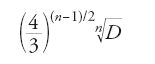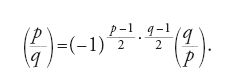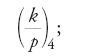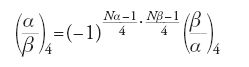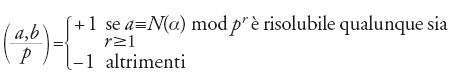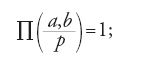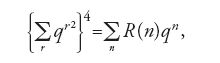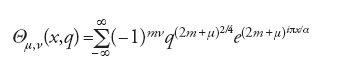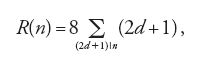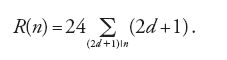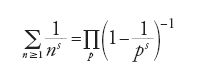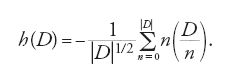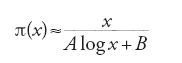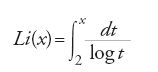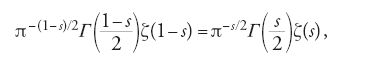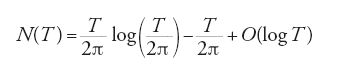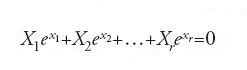L'Ottocento: matematica. Teoria dei numeri

L'Ottocento: matematica. Teoria dei numeri

Teoria dei numeri

Le tappe più significative dello sviluppo di un settore della scienza o dell'arte si accordano raramente con la suddivisione cronologica per secoli. La teoria dei numeri sembra però fare eccezione e il XIX sec. uniformarsi a essa. Nel 1801, a ventiquattro anni, Carl Friedrich Gauss (1777-1855) ha dato alla teoria quella che ne sarà la 'Bibbia': le sue Disquisitiones arithmeticae hanno costituito infatti per tutto l'Ottocento l'opera di riferimento, dalla quale molti autori hanno attinto notazioni, struttura, problematiche e dimostrazioni. Il secolo si chiuderà con un'altra summa, anch'essa destinata a influenzare a lungo la ricerca: nel 1897 David Hilbert (1862-1943) pubblicherà, su richiesta della Deutsche Mathematiker-Vereinigung (Unione matematica tedesca) un Bericht über die Theorie der algebraischen Zahlkörper (Relazione sulla teoria dei corpi numerici algebrici), chiamato comunemente Zahlbericht, in cui è offerta una sintesi originale delle nuove e più importanti scoperte della teoria algebrica dei numeri. Nella prefazione Hilbert descriveva anche le più importanti trasformazioni avvenute nel XIX sec., affermando che "la teoria dei numeri ha raggiunto l'età matura solo negli ultimi tempi" (Hilbert 1897 [1932-35, I, p. 65]).

Innanzitutto, alla fine del secolo gli argomenti erano ormai cambiati: con Gauss e con i suoi predecessori la teoria dei numeri si era occupata degli interi naturali, talvolta dei razionali, mentre lo Zahlbericht considerava prevalentemente campi di numeri algebrici, ossia insiemi di particolari numeri complessi dotati di una struttura algebrica.

In secondo luogo, la teoria dei numeri aveva ormai legami molto stretti con altri settori della matematica, come la teoria dei gruppi e l'analisi. Nel 1896, appena prima della pubblicazione dello Zahlbericht, che tratta solamente le origini del problema, Jacques Hadamard e Charles-Jean De la Vallée Poussin, indipendentemente l'uno dall'altro, utilizzarono le conoscenze più recenti sulle funzioni analitiche di una variabile complessa per descrivere la distribuzione, apparentemente non regolare, dei numeri primi.

Un ultimo aspetto di questa trasformazione si può cogliere nelle lettere, nelle prefazioni e nelle riviste: la teoria dei numeri aveva anche cambiato status. Marginale all'inizio del secolo, soltanto un esercizio riservato a qualche appassionato, nell'arco di alcuni decenni essa era divenuta, per usare le parole di Gauss, la "regina della matematica", l'incarnazione del nuovo modello della matematica pura esplorata "per l'onore dello spirito umano". "La teoria dei numeri", scrive nel 1859 Henry J.S. Smith in una relazione per la British Association for the Advancement of Science, "ha acquisito un crescente diritto all'attenzione dei matematici. È notevole sia per la quantità e l'importanza dei risultati ottenuti, sia per l'esattezza e il rigore delle dimostrazioni, la varietà dei metodi, le relazioni che stabilisce tra concetti apparentemente non correlati, sia infine per le numerose applicazioni ad altre parti dell'analisi alle quali si presta" (1859, p. 38).

La teoria dei numeri veniva spesso presentata come una attività che comporta disciplina personale e intellettuale e una pratica di lavoro che richiede grande attenzione per scoprire le regolarità dei fenomeni numerici, molta pazienza per isolare i concetti importanti e un'intensa concentrazione per fornire dimostrazioni corrette (Edwards 1977b; Goldstein 1989; Mehrtens 1990). D'altra parte, nello Zahlbericht Hilbert indicava alle altre branche della matematica la teoria dei numeri sia come esempio da seguire, sia come possibile fondamento nel quadro di uno sviluppo "sotto il segno del numero" di un'aritmetizzazione più spinta, garanzia di rigore. Quando al Congresso Internazionale dei matematici di Parigi del 1900 egli propose un programma di ricerche per il secolo a venire, sotto forma di ventitré problemi, ben sei di questi riguardavano la teoria dei numeri: ciò mostra chiaramente la notorietà acquisita e il ruolo decisivo che le veniva ormai attribuito.

Questo successo strepitoso non deve però illudere: si tratta infatti più di un successo di prestigio che di vera e propria produzione scientifica. Nello "Jahrbuch über die Fortschritte der Mathematik", che a partire dal 1869 recensì gli articoli di matematica pubblicati ovunque nel mondo, ogni anno e sino alla fine del secolo saranno dedicate alla teoria dei numeri solamente poche pagine: dal 2,5% al 4,5% del totale (Goldstein 1994). Nel 1889-1890 soltanto il 3% dei membri della Deutsche Mathematiker-Vereinigung erano autori di lavori in questo settore; essi diventarono l'11% dieci anni più tardi (forse per effetto dello Zahlbericht), per diminuire di nuovo negli anni successivi. Negli stessi periodi furono dedicati alla teoria dei numeri, rispettivamente, soltanto il 5% e il 3% degli articoli pubblicati dalla Societé Mathématique de France, l'analoga istituzione francese (Gispert 1996). Si era dunque lontani, nel lavoro quotidiano di ricerca, dal rilievo che la teoria dei numeri aveva nell'elenco dei problemi proposto da Hilbert.

Esistevano però differenze da paese a paese, come suggeriscono queste stesse cifre. Anche se la storiografia le riconosce un ruolo preminente, la teoria dei campi di numeri algebrici, così come viene presentata nello Zahlbericht, è una creazione quasi esclusivamente tedesca che, all'inizio del XX sec., mobilitò solamente un esiguo numero di specialisti. I principali temi di ricerca su scala europea ‒ si tratti della Francia, dell'Italia, dell'Inghilterra o della Russia ‒ erano ancora quelli più classici: divisibilità e numeri primi, analisi diofantea e teoria delle forme (studio, quest'ultimo, di polinomi a coefficienti interi o razionali da diversi punti di vista).

Le parti più innovative delle Disquisitiones arithmeticae, opera non agevolmente reperibile e la cui prima edizione era piena di errori tipografici, poterono esercitare una più ampia influenza soltanto grazie alle lezioni e agli articoli di Peter Gustav Lejeune Dirichlet, negli anni Trenta. La pubblicazione di queste lezioni a partire dal 1863 e la relazione presentata da Smith all'incirca nello stesso periodo accompagnarono le profonde ristrutturazioni della seconda metà del secolo. A tale riguardo, i sistemi di classificazione adottati nei manuali e nelle riviste scientifiche costituiscono un eccellente indicatore della formazione progressiva dei diversi filoni della teoria dei numeri e delle differenti valutazioni espresse dai vari gruppi di matematici. Ancora nel 1889 l'Index du répertoire bibliographique des sciences mathématiques, elaborato da una commissione internazionale, seguiva pressappoco l'indice delle Disquisitiones per indicare gli argomenti della teoria dei numeri, accontentandosi di aggiungere in fondo all'elenco qualche sezione supplementare che rendesse conto degli ultimi sviluppi, algebrici o analitici. L'Encyclopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen (Enciclopedia delle scienze matematiche, incluse le loro applicazioni), che rappresentava in parte il punto di vista del circolo di Christian Felix Klein (1849-1925) e alla quale collaborò anche Hilbert, riservò invece un posto importante ai campi di numeri algebrici e alla teoria analitica nel volume sulla teoria dei numeri, pubblicato nel 1900.

Se la teoria dei numeri subì nel XIX sec. profondi cambiamenti, questi non furono uniformi nel tempo e nello spazio; nemmeno nei suoi singoli settori tali cambiamenti furono recepiti, accettati e trasmessi ovunque nello stesso modo. Per semplicità di esposizione, ma anche perché costituiscono la fonte, se non la causa, della maggior parte dei progressi nel corso del secolo, si parlerà dapprima dello sviluppo dei temi classici della teoria; si ricorderanno poi le tappe principali che portarono dalle Disquisitiones allo Zahlbericht e alla costituzione di una nuova teoria algebrica dei numeri; per delineare infine, mediante qualche esempio, alcune delle nuove interazioni con l'analisi, sia reale sia complessa.

L'eredità di Legendre e di Gauss

Tav. I

La teoria dei numeri agli inizi del XIX sec. può essere ben rappresentata, più che dalle Disquisitiones, dall'Essai sur la théorie des nombres di Adrien-Marie Legendre (1752-1833). La prima edizione del 1798, raccoglieva, corredati da numerosi esempi, i principali risultati ottenuti fino a quel momento dai tre padri fondatori della teoria, Pierre Fermat (1601-1665), Leonhard Euler (1707-1783) e Joseph-Louis Lagrange (1736-1813), e dallo stesso Legendre. Altre due edizioni, nel 1808 e nel 1830, quest'ultima con il titolo di Théorie des nombres, riportavano alcuni contributi di Gauss. In queste opere si possono trovare numerosi studi sulle equazioni diofantee (equazioni definite da polinomi o sistemi di polinomi a coefficienti interi o razionali), i risultati sulla divisibilità di svariate espressioni algebriche e la rappresentazione degli interi mediante queste espressioni. Legendre discuteva anche alcuni casi noti del grande teorema di Fermat (l'equazione xⁿ+yⁿ=zⁿ non ammette soluzioni intere per n>2, a meno che x, y e z non siano tutti e tre nulli), dimostrava che ogni numero dispari, esclusi quelli della forma 8n+7, è somma di tre quadrati e compilava lunghe tavole dei divisori primi di varie espressioni (Tav. I).

Alcuni di questi problemi figurano anche nelle Disquisitiones. Gauss li aveva però raggruppati diversamente, modificandone quindi la struttura logica e le relazioni. Egli aveva introdotto la relazione di congruenza tra due interi modulo un intero m: due interi a e b sono 'congrui modulo m' se m divide la differenza a−b, o, ciò che è lo stesso, se a e b divisi per m danno lo stesso resto; in simboli: a≡b mod m. Questa notazione è assai opportuna, perché richiama l'attenzione sul fatto che le congruenze possono essere trattate come le uguaglianze (si possono cioè sommare, elevare a potenza, ecc.). Le prime quattro sezioni delle Disquisitiones sono dedicate alla risoluzione di congruenze di primo e di secondo grado e alle proprietà di divisibilità che ne conseguono. Il secondo tema, oggetto della lunghissima quinta sezione, riguarda lo studio delle forme quadratiche in due variabili. Il libro si conclude su un problema che secondo Gauss riguarda l'aritmetica soltanto in linea di principio: l'esame delle equazioni che traducono algebricamente la divisione del cerchio in n parti uguali, cioè xⁿ−1=0 e i suoi divisori, equazioni che, come si direbbe oggi, determinano le radici dell'unità (equazioni ciclotomiche). Gauss determinò le condizioni di natura aritmetica da imporre al grado n affinché le soluzioni siano costruibili con riga e compasso (n deve essere il prodotto di una potenza di 2 e di un numero primo della forma 2^r+1, per esempio 3, 5 o 17), esplicitando la costruzione per n=17. La soluzione di quest'ultimo problema, equivalente al problema di inscrivere in un cerchio un poligono regolare di 17 lati, rimasto irrisolto fin dall'Antichità, rese celebre Gauss.

Si tratta di questioni che, nell'impostazione di Legendre o in quella di Gauss, saranno spesso riprese e sviluppate nel corso del secolo. Joseph Liouville (1809-1882) costituisce un esempio straordinario in tal senso: egli dedicò molto spazio all'interno della propria rivista "Journal des mathématiques pures et appliquées" all'esame della divisibilità di espressioni algebriche. Non mancarono poi sviluppi originali. Angelo Genocchi, Adolphe Desboves, James J. Sylvester, Edouard Lucas studiarono le equazioni cubiche di tutti i tipi, cercando di determinare in quali casi si abbia un numero finito di soluzioni razionali e in quali sia possibile dedurle con un procedimento sistematico da una, due, tre, o più di esse. Interpretando queste equazioni come equazioni di curve piane si possono sfruttare, per ricerche di analisi diofantea, le costruzioni geometriche e i legami della geometria con la teoria degli invarianti. I risultati ottenuti furono utilizzati all'inizio del XX sec. nell'importante teoria aritmetica delle curve ellittiche (Schappacher 1990).

Lucas si interessò anche al problema di riconoscere i numeri primi a partire dalle equazioni ciclotomiche. Più precisamente, studiò le successioni u_n=(aⁿ−bⁿ)/(a−b) e v_n=aⁿ+bⁿ, nel caso in cui a e b siano le radici di un polinomio di secondo grado a coefficienti interi primi tra loro. Gli u_n, per n dispari, dividono l'espressione x2−aby2; Lucas ne dedusse la legge secondo la quale certi numeri primi compaiono e si propagano come divisori di termini della successione u_n. In particolare, se un numero p divide il termine u_p+1 ma non i termini il cui indice divide p+1, allora p è primo. Questo criterio è particolarmente adatto per dimostrare la primalità di numeri quali quelli di Mersenne (ossia di numeri del tipo 2^k−1) e le sue versioni più recenti fanno parte del gran numero di test utilizzati oggi in crittografia.

Il comportamento delle due serie u_n e v_n è simile a quello delle funzioni circolari seno e coseno. Lucas sperava di sviluppare successioni aritmetiche analoghe a partire da polinomi di grado superiore e ottenere in tal modo dei sostituti per funzioni più complesse. Egli era a conoscenza dei contributi che la teoria delle funzioni stava dando in quel periodo all'aritmetica (dei quali si tratterà più avanti), cercava tuttavia di evitarli perfezionando altri strumenti. Tale atteggiamento era tutt'altro che isolato: se infatti alcuni matematici del XIX sec. erano soliti sfruttare le connessioni tra settori diversi, altri si sforzavano al contrario di conformarsi il più possibile a quelle che consideravano le specificità del loro ambito di ricerca. Teorici dei numeri come, per esempio, Genocchi e Lucas si consideravano inoltre eredi di Fermat e di Euler; molti di loro si impegnavano anche in lavori di carattere bibliografico e storico: per esempio, Genocchi e Lucas pubblicarono articoli nel "Bullettino di bibliografia e di storia delle scienze matematiche e fisiche" di Baldassarre Boncompagni (1821-1894), la prima rivista interamente dedicata alla storia della matematica.

La teoria aritmetica delle forme, che occupava nel XIX sec. un posto centrale nella teoria dei numeri, ne fu storicamente il primo filone organizzato in modo coerente; per le forme quadratiche in due variabili ciò era già accaduto nel XVIII sec. a opera di Lagrange. Il nucleo più tecnico di questa teoria, trattata nei capitoli centrali delle Disquisitiones, richiamò per tutto il secolo l'attenzione di matematici prestigiosi, tra cui figurano Charles Hermite, Ferdinand Gotthold Eisenstein, Henry J.S. Smith, Camille Jordan, Jules-Henri Poincaré, Luigi Bianchi, Aleksandr Nikolaevič Korkin, Egor Ivanovič Zolotarev, Hermann Minkowski. La teoria delle forme ebbe inoltre relazioni molto strette, a volte anche conflittuali, con altre linee di sviluppo della teoria dei numeri e con diversi altri settori della matematica (come la teoria algebrica degli invarianti e la geometria, in particolare la geometria non euclidea) e con la fisica, anche se i legami con quest'ultima si accentueranno soprattutto nel XX secolo.

La natura delle questioni prese in esame si può spiegare agevolmente a partire dal caso della forma quadratica binaria, ossia un polinomio omogeneo in due variabili di secondo grado, f(x,y)=ax2+bxy+cy2. Come si è detto, uno dei primi problemi, già studiato da Fermat, era quello di pervenire a una rappresentazione di un numero intero n per mezzo di una forma, vale a dire di determinare (se esistono) due interi x e y (che per semplificare la discussione supporremo primi fra loro) tali che f(x,y)=n. È evidente che la forma f fornisce una rappresentazione del proprio coefficiente dominante a: basta prendere x=1 e y=0. Viceversa, se una forma f fornisce una rappresentazione di un intero n, allora esiste una trasformazione lineare a coefficienti interi e a determinante uguale a 1 tale che la forma quadratica trasformata abbia coefficiente dominante n. Due forme trasformate una nell'altra in questo modo si dicono equivalenti. I numeri rappresentati da una forma sono dunque i coefficienti dominanti di forme a questa equivalenti.

Il problema è allora quello di classificare le forme a meno di equivalenze e di determinarne gli invarianti caratteristici, cioè le espressioni funzioni dei coefficienti che sono identiche per due forme equivalenti. Il discriminante della forma, Δ=b2−4ac, è un invariante fondamentale; ma esistono anche invarianti propri del caso aritmetico, del caso cioè della forma a coefficienti interi (un esempio è dato dal massimo comun divisore dei coefficienti). Da Lagrange in poi i matematici si erano interessati anche al problema della riduzione: trovare per ciascuna classe di equivalenza una (o a volte più di una) forma particolarmente semplice e definire i cambiamenti di coordinate che consentono di trasformare in tale forma una forma qualunque della classe. Quando il discriminante Δ è negativo, vi è una sola forma per classe, che viene detta ridotta e i cui coefficienti soddisfano uno dei due sistemi di disuguaglianze: ∣b∣≤a⟨c, b+a≠0 oppure ∣b∣≤a=c, b≥0. La riduzione consiste nel riportarsi a questa forma con un numero finito di passi che si possano descrivere esplicitamente. Come mostrano le condizioni che definiscono una forma ridotta, vi è soltanto un numero finito di classi; Dirichlet ne diede unintorno al 1840, utilizzando strumenti analitici.

Non sempre un numero intero è rappresentato dalle forme di una sola classe: le Disquisitiones di Gauss mostrano come suddividere le classi in generi in modo che le classi che rappresentano un intero siano dello stesso genere e come riconoscere se un intero n possa essere rappresentato da una forma di dato genere soltanto in funzione dei resti di n modulo i divisori del discriminante Δ. Nell'esempio di Legendre presentato nella Tav. I vi è una sola classe per genere, ma ciò non è vero in generale.

Lo studio di forme più complesse, per esempio in più di due variabili o, in certi casi, di grado più elevato, è proseguito per tutto l'Ottocento. La situazione è diversa già nel caso di una forma quadratica binaria a discriminante positivo, perché non si ha più una definizione semplice che porti a una riduzione unica. La difficoltà si deve al fatto che in questo caso esistono infiniti cambiamenti di variabili (le 'sostituzioni automorfe', nel linguaggio dell'epoca) che lasciano invariata la forma. Furono proposte numerose alternative ed è in tale contesto che Charles Hermite (1822-1901), nel 1851, mise a punto il 'procedimento di riduzione continua', spesso utilizzato nella seconda metà del secolo. Alla forma iniziale f, che per via del segno del discriminante si può scrivere come prodotto di due forme di primo grado a coefficienti reali:

[1] f(x₁, x₂)=a(x₁+αx₂)(x₁+α'x₂),

Hermite associa una forma ausiliaria

[2] Φ(x₁, x₂)=(x₁+αx₂)²+λ(x₁+α'x₂)²,

dove λ è un parametro reale positivo. Il discriminante della forma [2] è negativo: Hermite considera allora ridotta la forma [1] se si può scegliere λ in modo tale che la [2] sia una forma ridotta (nel senso precisato sopra). Facendo variare λ con continuità e descrivendo le riduzioni successive necessarie, egli riuscì a definire la struttura delle forme automorfe alla forma iniziale [1]. L'esame delle forme automorfe consentì inoltre di scoprire legami importanti con la teoria dei gruppi: nel 1887 Poincaré mostrava come associare a una forma quadratica un sottogruppo di un gruppo fuchsiano.

È notevole il fatto che la concezione originaria dei problemi sulle forme, legata alla rappresentazione degli interi, abbia condotto a studiare innanzi tutto l'equivalenza di forme a meno di una trasformazione di coordinate a coefficienti interi, cosa che ora sappiamo essere estremamente difficile. Nella seconda metà del XIX sec., ci si accorse del fatto che considerare trasformazioni a coefficienti non più interi, ma razionali, semplifica di molto la classificazione. Smith poté così dimostrare nel 1867 che due forme quadratiche in n variabili, aventi lo stesso discriminante D, sono dello stesso genere se possono dedursi l'una dall'altra mediante una trasformazione lineare invertibile a coefficienti razionali di denominatore primo con 2D. Da questo risultato derivano importanti teoremi sulla rappresentazione dei numeri per mezzo di forme in più variabili. Nel 1881 l'Académie des Sciences di Parigi istituiva un premio per la risoluzione di questo problema nel caso di forme in cinque variabili: Smith protestò, richiamando l'attenzione sui suoi precedenti lavori, e alla fine il premio fu assegnato a lui (che tuttavia morì poco prima di riceverlo) e a un giovane matematico che aveva partecipato al concorso e che era destinato a divenire celeberrimo: Hermann Minkowski.

Nell'ultimo decennio del XIX sec. Minkowski studiò la classificazione delle forme quadratiche a meno di trasformazioni razionali, dimostrando che stabilire una tale equivalenza tra due forme significa dimostrare che esse si possono trasformare l'una nelltanto mediante cambiamenti di variabili a coefficienti reali quanto mediante cambiamenti modulo m (con m intero qualunque). Il vantaggio di sostituire una sola condizione con un'infinità di condizioni consiste nel fatto che queste ultime sono effettive. Si tratta di un punto di vista che cambierà notevolmente lo studio delle forme nel corso del XX secolo.

Un altro importante contributo fornito da Minkowski fu l'impiego di una rappresentazione geometrica delle forme. Questa Geometrie der Zahlen (Geometria dei numeri) verrà studiata con i suoi principali sviluppi nel Novecento. Va precisato però che essa si inscriveva in una linea di ricerca, nella quale le forme e anche la loro riduzione venivano interpretate, in vario modo, nel piano o nello spazio. Il processo di 'aritmetizzazione', raccomandato da Hilbert in nome del rigore, non escludeva una 'geometrizzazione' che favorisse anche l'Anschauung, la rappresentazione intuitiva delle relazioni aritmetiche o analitiche. Procedimenti che alcuni matematici vedevano come antagonisti e che altri invece consideravano come complementari (Mehrtens 1990; Schwermer 1991; Bordogna 1996).

Lo studio aritmetico delle forme non si limitava alle forme a coefficienti interi. In parte a causa dello sviluppo dello studio aritmetico di certi numeri complessi, erano ugualmente prese in considerazione anche le forme a coefficienti reali o complessi. Hermite cercò di determinare il valore minimo che può assumere una forma in n variabili per valori interi non nulli delle variabili. Per un fissato discriminante D, Hermite dimostrò che questo minimo è inferiore a

il punto essenziale è che questa maggiorazione dipende soltanto dal discriminante. Tra le conseguenze che Hermite ne trasse figura l'approssimazione simultanea di molti numeri mediante numeri razionali, risultato che fu poi migliorato dai matematici russi Korkin e Zolotarev e da Minkowski (Kolmogorov 1978).

La teoria dei campi di numeri algebrici da Gauss a Hilbert

Alla fine del XIX sec. lo Zahlbericht di Hilbert ratificava una trasformazione, parziale ma profonda, nella concezione stessa della teoria dei numeri e dei suoi oggetti di studio. Tale trasformazione aveva preso forma soltanto negli anni Settanta e sfruttava largamente il contemporaneo rinnovamento dell'algebra per l'impulso delle idee di Niels Henrik Abel (1802-1829) e di Evariste Galois (1811-1832), costituendo a sua volta un fattore importante per l'affermazione in algebra del punto di vista strutturale (Corry 1996). "La teoria dei campi di numeri" scrive Hilbert "è un edificio di meravigliosa bellezza e armonia". È bene avvertire però che l'armonia di cui parla Hilbert si fonda su elementi strettamente tecnici e che grandi rinnovamenti concettuali si giocano spesso su minimi dettagli.

La legge di reciprocità quadratica

Il problema principale che ha motivato queste ricerche ha avuto origine, ancora una volta, nel cuore della teoria delle forme: è il problema delle 'leggi di reciprocità'.

Se un numero primo p è rappresentato da una forma quadratica binaria di discriminante D, allora p è il coefficiente dominante di una forma f(x,y)=px2++bxy+cy2 a essa equivalente e quindi con lo stesso discriminante D=b2−4pc. D è perciò un quadrato modulo p, cioè è un residuo quadratico modulo p. Euler aveva dimostrato che, mentre perun numero intero a primo con p si ha a^p−1≡1 modp, a è un residuo quadratico precisamente quando a(^p−1)/2≡1 modp. Sarebbe quindi auspicabile un enunciato inverso, che dica direttamente quali discriminanti siano possibili per un numero primo p assegnato: questo è quanto la legge di reciprocità quadratica consente di ottenere. Risultati di questo tipo si trovano espressi già in Euler ma fu Legendre a introdurre una utile notazione ‒ il simbolo di Legendre ‒ enunciandone esplicitamente la proprietà cruciale. Per un numero primo p dispari e un intero a non divisibile per p Legendre definisce:

La legge di reciprocità quadratica fornisce allora una relazione sorprendente fra due numeri primi dispari p e q distinti:

In altri termini, p è un residuo quadratico modulo q se e solo se q è un residuo quadratico modulo p, salvo il caso in cui i due numeri sono della forma 4n+3, perché allora p è un residuo quadratico modulo q se e solo se q non è un residuo quadratico modulo p. Vi sono inoltre altre relazioni complementari che caratterizzano i numeri p per i quali 2 e −1 sono residui quadratici modulo p. Il simbolo di Legendre fu poi generalizzato da Jacobi al caso in cui p è un intero qualunque.

Legendre considerava la legge di reciprocità tra due numeri primi "la proposizione più notevole e più feconda della teoria dei numeri" (Legendre 1798 [1830, p. 238]), evidenziando un entusiasmo che era condiviso dalla maggior parte dei teorici dei numeri, impegnati o no che fossero negli sviluppi che ne sarebbero seguiti. Come scriveva ancora Helmut Hasse (1898-1979) nel 1950 "Gauss ha giustamente chiamato questa legge teorema fondamentale della teoria dei residui quadratici" [nelle Disquisitiones; nel suo diario Gauss chiama questo risultato theorema aureum]. Essa è divenuta il teorema centrale della nuova teoria dei numeri per le sue molteplici relazioni, formali e concettuali, con tutte le possibili questioni e teorie, come pure per le sue generalizzazioni nella teoria dei numeri algebrici" (Hasse 1950, p. 90).

Oltre agli aspetti teorici, ed è forse ciò che ne spiega il successo, la legge di reciprocità si era rivelata un efficace strumento per risolvere congruenze e per la determinazione effettiva dei divisori di espressioni quadratiche. Per esempio Legendre se ne era servito per dimostrare i suoi teoremi sui divisori di t2+au2, che richiedono di sapere per quali numeri primi p il numero a è un residuo quadratico. Il metodo usuale, che adotta il criterio di Euler, risulta molto faticoso se a e p sono grandi. Legendre (1798 [1830, pp. 245-246]) porta a titolo di esempio la dimostrazione che il numero primo 1013 non divide la forma t2+601: il criterio di Euler richiede il calcolo di 601506 modulo 1013, cioè 14 moltiplicazioni e 14 divisioni, mentre con la legge di reciprocità il numero di operazioni scende a 3 divisioni e a 3 fattorizzazioni semplicissime.

La legge di reciprocità ha alimentato anche un luogo comune nelle presentazioni usuali della teoria dei numeri del XIX sec.: "Gran parte delle sue teorie acquista un fascino particolare perché importanti proposizioni si possono spesso scoprire per semplice induzione, ma sono tuttavia di una tale profondità che non se ne trova la dimostrazione se non dopo molti tentativi" (Smith 1859, p. 39). La dimostrazione proposta da Legendre nell'Essai del 1798 era incompleta. Le due prime dimostrazioni soddisfacenti si trovano nelle Disquisitiones; Gauss ne propose in seguito altre quattro e un'altra, che dunque è almeno la settima, è stata trovata nei suoi scritti inediti. Altri autori affrontarono la questione tanto che, alla fine del secolo, si contavano una cinquantina di dimostrazioni, di lunghezza variabile e basate sui principî più diversi, mettendo in gioco la teoria delle forme quadratiche, le funzioni circolari, le permutazioni, l'induzione, senza contare le dimostrazioni fondate su vari lemmi aritmetici elementari.

Le leggi di reciprocità superiori

In questa ricerca di nuove dimostrazioni si manifestava il desiderio non soltanto di comprendere i fondamenti della legge di reciprocità ma anche di generalizzarla a residui di potenze superiori a 2 (Lemmermeyer 2000).

Il simbolo di Legendre associato al caso quadratico assume due valori, +1 e −1, le due radici quadrate di 1. Nei gradi superiori intervengono, in modo naturale, radici dell'unità di ordine superiore a 2, che non sono però interi ordinari. Ciò suggerì a Gauss che, per formulare e dimostrare una corretta legge di reciprocità biquadratica (cioè per le quarte potenze), occorresse "estendere il campo dell'aritmetica" ai numeri complessi (detti 'interi di Gauss') della forma a+bi, dove a e b sono interi usuali e i è una radice quarta dell'unità diversa da 1 e −1: "i teoremi sui residui quadratici risplendono in tutta la loro semplicità e bellezza soltanto quando si estende il campo dell'aritmetica alle quantità immaginarie" (Gauss 1876, p. 102). Nel 1831 Gauss spiegò come lavorare aritmeticamente con questi numeri. La 'norma' Nα di un intero di Gauss α=a+bi, è l'intero ordinario a2+b2, per definizione, il prodotto di tale numero per il suo coniugato. Esistono quattro interi di Gauss aventi norma uguale a uno: 1, −1, i, −i; essi fungono da unità. Un numero complesso primo (oggi diremmo 'irriducibile') è un numero divisibile solo per sé stesso e per le unità. Ogni intero di Gauss si decompone in modo essenzialmente unico, nel prodotto di interi di Gauss primi, e sussiste un algoritmo di divisione analogo a quello di Euclide. Va sottolineato il fatto, importante per quanto si dirà in seguito, che i numeri primi ordinari non sono necessariamente primi se considerati come interi di Gauss: per esempio, il numero 5 si decompone in (2+i)(2−i) e lo stesso accade per tutti i numeri primi della forma 4n +1 (essendo interi che si possono scrivere come somma di due quadrati). Il numero 2 si decompone in (−i)(1+i)2; solamente i numeri primi della forma 4n+3, come 7 o 19, sono primi anche come interi di Gauss.

Nel caso quadratico la legge di reciprocità si enuncia e si dimostra soltanto per i numeri primi dispari positivi; i casi 2 e −1 vengono discussi a parte. Gauss definisce alcune condizioni riguardanti gli interi complessi equivalenti a queste: un numero dispari è un numero non divisibile per 1+i, un numero primario è un numero a+ib tale che b è pari e a+b−1 è divisibile per 4 (ma sono possibili altre normalizzazioni). Per ogni numero primo p complesso dispari e ogni intero complesso k non divisibile per p è allora possibile definire un analogo del simbolo di Legendre nel modo seguente:

esso assume i valori 1, −1, i, −i. Gauss ottiene la legge di reciprocità biquadratica, espressa dalla formula seguente (nella quale α e β sono numeri primi primari):

e altre relazioni per le unità e per 1+i.

La dimostrazione della [7] non figura negli articoli di Gauss (Rowe 1988). Presumibilmente, essa fu data per la prima volta nelle lezioni di Carl Gustav Jacob Jacobi (1804-1851), nelle quali viene anche definita una legge analoga per i residui cubici, che utilizza una radice cubica di 1. Fu tuttavia Ferdinand Gotthold Eisenstein (1823-1852), verosimilmente in modo indipendente, a pubblicarne le dimostrazioni, suscitando il disappunto di Jacobi (Collison 1977). D'altra parte, Eisenstein e Jacobi fornirono molte dimostrazioni di queste leggi, oltre a esaminare anche il caso di altre potenze, ma gli ostacoli che si presentavano erano molto seri: l'algoritmo di Euclide non era più valido e le proprietà aritmetiche necessarie alla formulazione stessa della legge non potevano essere dimostrate.

I numeri ideali di Kummer

Ernst Eduard Kummer (1810-1893) deve la propria fama soprattutto ai lavori sul grande teorema di Fermat. Dopo la sua morte, alcuni matematici hanno voluto vedere in questo teorema la motivazione principale della sua opera e la spinta decisiva attraverso la quale la teoria dei numeri è giunta alla modernità. Tuttavia, come è stato dimostrato da recenti ricerche storiche (Edwards 1975, 1977a; Neumann 1981), fu piuttosto la ricerca delle leggi di reciprocità superiori a giocare un ruolo fondamentale nella genesi delle idee di Kummer. I numeri complessi dei quali si tratta di definire l'aritmetica sono quelli della forma:

[8] F(ζ)=a₀+a₁ζ+…+a_n-2ζ^n-2,

dove i coefficienti a_i sono interi ordinari e ζ è una radice n-esima dell'unità. Oggi questi numeri vengono detti 'interi ciclotomici' e il loro insieme si denota con ℤ[ζ_n]. Ci limiteremo qui, come Kummer, a trattare il caso che n sia un numero primo p dispari; in tal caso, se ζ è diverso da 1, esso è radice del 'polinomio minimo' X^p−1+X^p−2+…+1 e i suoi coniugati, ossia le altre radici di questo polinomio, sono le potenze di ζ. È naturale allora definire la norma NF(ζ) di un numero ciclotomico F(ζ) con la relazione

[9]  NF(ζ)=F(ζ)F(ζ²)…F(ζ^p-1);

NF(ζ) è un intero ordinario. Diversamente dal caso degli interi di Gauss, in generale non vi è soltanto un numero finito di unità, ovvero di numeri ciclotomici di norma uguale a 1; ma Leopold Kronecker, allievo e amico di Kummer, dimostrò per gli interi ciclotomici, e Dirichlet nel 1846 per numeri complessi più generali, che ogni unità è il prodotto di un numero finito di unità fondamentali, e che queste ultime sono in numero finito. I problemi relativi alle unità si controllano pertanto agevolmente.

Un fenomeno sorprendente, che sembra abbia molto turbato Kummer, è che per p≥23 viene meno l'unicità della fattorizzazione in elementi irriducibili. Dopo un intenso lavoro su una gran quantità di dati numerici, egli ebbe un'idea fondamentale: ottenere una decomposizione unica in fattori primi attraverso i cosiddetti 'fattori primi ideali' (Smith 1859; Edwards 1975, 1977a). Come affermava Smith nella relazione più sopra citata, "un numero ideale non ha esistenza quantitativa […]. L'affermazione che un dato numero complesso contiene un fattore ideale è solo un modo opportuno di esprimere un certo insieme di condizioni su congruenze soddisfatte dai coefficienti dei numeri complessi" (1859, p. 110). Kummer non presenta una vera e propria definizione di fattore ideale, limitandosi a fornire in maniera operativa il concetto di divisibilità di un numero ciclotomico per un tale fattore e, per giustificare questo concetto, ricorre a diverse analogie. Alcune di queste provengono dalla matematica e ricordano i tanti 'strani' oggetti, a cominciare dagli stessi numeri complessi, con i quali operavano i matematici dell'Ottocento. La più sorprendente delle analogie era però fornita dalla chimica: si possono effettivamente scoprire molti composti senza poterne isolare i componenti. In conclusione, a ogni numero ciclotomico resta associato un numero finito di fattori ideali con certi esponenti, univocamente determinati.

Tra il 1847 e il 1859 Kummer pubblicò alcuni articoli nei quali esponeva in modo particolareggiato i diversi aspetti della teoria e le sue applicazioni. Dimostrava che, poiché due fattori ideali sono equivalenti se sono deducibili l'uno dall'altro moltiplicandoli per un numero ciclotomico, il numero h delle classi di equivalenza dei fattori ideali è finito. Ogni potenza con esponente h di un fattore ideale è un numero ciclotomico. Un numero di classi pari a 1 equivale all'esistenza di una 'vera' fattorizzazione unica in numeri primi; ma il numero di classi di ℤ[ζ23] è già 3, e tale numero cresce rapidamente.

L'applicazione più spettacolare di queste idee fu quella che nel 1857 valse a Kummer un premio dell'Académie des Sciences di Parigi, anche se egli non aveva risolto completamente il problema proposto: dimostrare il grande teorema di Fermat. All'epoca si conoscevano dimostrazioni soltanto per interi inferiori a 7 (e pertanto anche per i loro multipli). Fissato un numero primo dispari p e due interi a e b non nulli, Kummer parte dall'identità

[10] a^p+b^p=(a+b)(a+ζb)…(a+ζ^p-1b).

Se il teorema di Fermat fosse falso, nella [10] il prodotto dei numeri ciclotomici a+ζⁱb dovrebbe essere una potenza con esponente p, ovvero c^p. Utilizzando una decomposizione in fattori primi ideali, Kummer deduce che tali fattori devono comparire con esponente p, e se p è primo con il numero delle classi di ℤ[ζ_p] (si dice allora che p è regolare) si può portare questa informazione dal livello dei fattori ideali a quello degli stessi numeri ciclotomici e dedurne una contraddizione. Kummer dimostrò così il teorema di Fermat per tutti i numeri primi regolari, in particolare per tutti i numeri inferiori a 100, salvo tre. Egli sperava che la lista delle eccezioni fosse finita, ma dall'inizio del XX sec. è noto che la situazione è ben diversa. Il teorema di Fermat è stato peraltro completamente dimostrato nel 1994, per vie del tutto diverse.

I risultati e il successo ottenuti non cambiarono l'opinione di Kummer sulla specifica importanza dei singoli problemi. Il teorema di Fermat era per lui solamente una curiosità e le leggi di reciprocità, queste "nemiche giurate", erano di grande interesse per i matematici. Kummer spiegava finalmente queste leggi non per i soli numeri ciclotomici, come avevano tentato di fare i suoi predecessori, ma anche per i fattori primi ideali (innovazione che consente di fornire una loro adeguata definizione) e riusciva a dimostrarle nel caso regolare, sviluppando inoltre un primo studio dei numeri formati da radici di interi ciclotomici, iniziando quella che sarà poi la 'teoria degli ampliamenti di Kummer'(Neumann 1979-80).

Lo sviluppo della teoria degli ideali

Le costruzioni di Kummer si applicano soltanto ai numeri ciclotomici, ma ciò è sufficiente per l'applicazione alle leggi di reciprocità e al teorema di Fermat. D'altra parte i matematici del XIX sec. si interessavano anche ad altri numeri algebrici, cioè ai numeri θ soluzioni di equazioni della forma a_nθⁿ+a_n−1θⁿ−1+…+a1θ+a0=0, con gli a_i interi ordinari. Lo studio aritmetico delle radici di polinomi quadratici si collega in modo naturale alla teoria delle forme quadratiche e presenta fenomeni analoghi a quelli messi in luce da Kummer: per esempio, dall'identità (1+2√−5)(1−2√−5)=21=3×7 risulta che anche per i numeri della forma a+b√−5, con a e b interi ordinari, viene meno l'unicità della fattorizzazione. Nascevano anche nuovi problemi, che rendevano difficile l'applicazione diretta delle idee di Kummer. Se ci si limita ai numeri della forma a+b√5, con a e b interi ordinari, risulta che, (1+√5)/2 è radice dell'equazione algebrica x2−x−1=0, la quale ha coefficiente direttore uguale a 1: malgrado il denominatore 2 che vi compare, tale radice deve essere considerata come un intero. Le generalizzazioni proposte differivano sotto vari aspetti: nei criteri da conservare, nei concetti presi in considerazione, ma anche nel modo stesso di definire nuovi concetti matematici e, più in generale, nella concezione stessa dei numeri.

Come già detto, Kummer non aveva dato una vera e propria definizione di fattore ideale di un numero di ℤ[ζ_p], avendo piuttosto fornito dei criteri per utilizzare questi fattori basati su congruenze modulo potenze di p. Verso il 1877 Zolotarev cercò di seguire la via indicata da Kummer per altri numeri algebrici F(θ) ottenuti, come i numeri ciclotomici, da polinomi in un dato numero algebrico θ. Zolotarev considerò il problema di individuare un procedimento costruttivo, a partire da congruenze, per fattorizzare i numeri primi ordinari in fattori ideali relativi ai numeri F(θ). Il problema dei denominatori di cui si è appena detto lo condusse a studiare, per ogni numero primo p, i numeri il cui denominatore è primo con p, e a sviluppare decomposizioni in fattori ideali specifici. Il lavoro rimase tuttavia incompleto e non sembra aver avuto un'influenza immediata. Esso costituisce nondimeno una testimonianza delle possibilità e dei limiti di un'impostazione algoritmica e locale, ossia di un'impostazione, come quella di Kummer, che considera separatamente cosa accade per ogni singolo numero primo. L'aspetto algoritmico ha conosciuto recentemente un rinnovato interesse e l'aspetto locale poté contare alla fine del XIX sec. su nuovi sostenitori di cui si parlerà più avanti.

Una maggiore diffusione e una grande influenza, anche se in modo molto diverso, ebbero altre due soluzioni, proposte da Richard Dedekind (1831-1916) e da Leopold Kronecker (1823-1891). Il punto di vista di Dedekind viene spiegato nel supplemento X della seconda edizione del corso di teoria dei numeri tenuto da Dirichlet nel 1871 e, in versioni a lungo rielaborate, nel supplemento XI delle edizioni successive. È un punto di vista assiomatico e insiemistico. Dedekind introduce la nozione fondamentale di campo (Körper) di numeri, cioè di un insieme di numeri complessi algebrici chiuso rispetto alle quattro operazioni. Per esempio, i numeri della forma a+b√5, con a e b razionali, formano un campo di numeri che oggi si indica con Q[√5]; nei casi considerati da Dedekind, i campi sono sempre generati da un solo numero algebrico. Egli mostra anche come interpretare il gruppo di Galois di un'equazione come gruppo di trasformazioni del campo generato dalle sue radici. Egli si interessa poi agli interi appartenenti al campo, definiti come gli elementi che sono radici di un'equazione del tipo θⁿ+a_n−1θⁿ−1+…+a1θ+a0=0 (nella quale il coefficiente del termine di grado più alto è uguale a 1); adottando questa definizione un numero come, per esempio, (1+√5)/2 è un intero del campo Q[√5]. Dedekind definisce anche il 'discriminante del campo': si tratta di un intero (ordinario) che gioca un ruolo simile a quello del suo omonimo nell'ambito delle forme quadratiche; per esempio, il discriminante del campo Q[√5] è uguale a 5.

Gli oggetti principali della teoria di Dedekind sono gli ideali. La terminologia rende omaggio a Kummer, ma tali ideali sono ora sottoinsiemi di interi algebrici, chiusi rispetto alle operazioni di addizione, sottrazione e moltiplicazione per tutti gli interi del campo. Per esempio, l'insieme (θ) ottenuto considerando tutti i multipli di un intero algebrico θ, è un ideale, detto 'ideale principale'. Due ideali che differiscano soltanto per moltiplicazione per un ideale principale sono considerati equivalenti e, come per le classi di forme quadratiche, il numero delle classi di ideali di Dedekind è finito.

È rispetto agli ideali, non rispetto agli interi algebrici, che Dedekind sviluppò la propria aritmetica. Fornendo le definizioni di ideale primo e di moltiplicazione fra ideali, dimostrò che ogni ideale si scrive in modo unico come prodotto di ideali primi. Esaminò anche come decomporre un ideale principale (p), generato da un numero primo ordinario p, in ideali primi in un campo di numeri; ma per alcuni numeri primi che dividono il discriminante sorgono grandi difficoltà, cosicché Dedekind riuscì a completare l'esame di tali casi particolari.

Dedekind applicò le proprie idee sia a questa generalizzazione delle ricerche di Kummer sia alla nozione di numero. Per esempio, definì i numeri reali a partire da insiemi di numeri razionali (Dugac 1976). Un insieme di "numeri veramente esistenti" gli sembrava più concreto di certi criteri di divisibilità, per quanto effettivi essi fossero. Davanti alla gran quantità di campi di numeri algebrici, ciascuno con le proprie sottili particolarità, Dedekind insisteva sulla superiorità delle idee pure rispetto ai calcoli e sull'importanza di una teoria, la più generale possibile, che agevolasse la dimostrazione dei risultati. Nel 1882 Dedekind elaborò con Heinrich Weber (1842-1913) una teoria delle funzioni algebriche di una variabile, ossia delle funzioni f(z) che soddisfano un'equazione polinomiale P(z,f(z))=0, basandosi su alcune analogie tra queste funzioni e i campi di numeri. Alla nozione di ideale primo corrisponde la nozione di punto sulla superficie di Riemann associata alla funzione: ne deriva l'abitudine di considerare 'locale' ciò che si riferisce a un numero o a un ideale primo. Per Dedekind e Weber si trattava soprattutto di utilizzare il grande rigore della teoria dei numeri per trasferirne dimostrazioni e nozioni in una materia che giudicavano mancare ancora di precisione (Corry 1996): il che illustra bene il nuovo ruolo attribuito alla teoria dei numeri.

L'analogia tra funzioni algebriche di una variabile e campi di numeri svolge un ruolo ancora più importante in Kronecker. Sebbene sembri aver elaborato una parte delle proprie idee sin dalla fine degli anni Cinquanta e che il suo lavoro sia stato anticipato da Kummer, Kronecker non pubblicò nulla prima del 1882 e, anche allora, si limitò sostanzialmente a formulare un programma. Il suo punto di vista rifletteva una posizione che egli difendeva con sempre maggior decisione: il solo fondamento legittimo della matematica, e dunque il solo che la renda legittima, sono gli interi ordinari: "Il buon Dio ha creato i numeri interi, tutto il resto è opera dell'uomo". Come per Kummer, il punto centrale della teoria è la definizione di divisibilità, ma la nozione di numero primo è molto meno importante che per Kummer e, a fortiori, per Dedekind, avendo il difetto, secondo Kronecker, di dipendere da uno specifico dominio di razionalità (nozione equivalente a quella di campo per Dedekind): il numero 5 non è più primo negli interi di Gauss. La teoria dei divisori di Kronecker si basa sulla determinazione, per mezzo di forme algebriche, del massimo comun divisore di più interi algebrici appartenenti a un fissato dominio di razionalità e, in definitiva, su calcoli fra interi ordinari (Edwards 1992).

Kronecker, come dichiara nell'articolo del 1882, preferiva estendere l'aritmetica secondo la dimensione aggiungendo nuove variabili, piuttosto che analiticamente con dei numeri complessi e le loro funzioni. Se si considerano equivalenti due polinomi in una variabile T a coefficienti razionali che differiscono per un multiplo di T2−5, lo studio dei polinomi a meno di questa equivalenza è identico allo studio del corpo Q[√5]; ma si tratta di un ampliamento per mezzo della nuova variabile T e non dell'aggiunta del numero √5. Sulla base di una teoria dei polinomi in più variabili Kronecker suggeriva la possibilità di un trattamento unificato della teoria dei numeri algebrici e di quella delle funzioni algebriche. Non si trattava di trasferire nozioni e risultati dall'una all'altra branca, ma di analogie profonde che avrebbero dovuto, in linea di principio, esprimersi con una completa identificazione entro un quadro comune. Le difficoltà del testo di Kronecker e del suo programma ne hanno presumibilmente ridotto le possibilità di influenza diretta sulla teoria dei numeri. Tale programma favorì però quell'avvicinamento fra teoria dei numeri e geometria algebrica che riceverà grande impulso dagli sviluppi dell'algebra astratta e che rivestirà un ruolo sempre più importante nel XX secolo.

Un allievo di Kronecker, Kurt Hensel, riuscì a risolvere il problema dei divisori del discriminante che Dedekind non aveva portato a termine e, nel 1897, a semplificarne notevolmente la dimostrazione affinando l'analogia con i corpi di funzioni. Hensel introdusse in teoria dei numeri l'equivalente delle serie di Puiseux dell'analisi (che descrivono il comportamento di una funzione algebrica nell'intorno di un punto), considerando in particolare serie del tipo ∑_n>_ka_npⁿ, con 0≤a_n⟨p e k intero fissato e serie analoghe associate a fattori primi nei corpi di numeri. Qualsiasi numero razionale si può rappresentare con una serie di questo tipo, ma l'idea fondamentale di Hensel fu quella di considerare tali serie come numeri (i 'numeri p-adici'). Egli se ne serviva come potente strumento per l'analisi locale dei numeri primi, allo stesso modo in cui aveva tentato di fare Zolotarev. In altri termini, Hensel mostrava come definire un continuo adeguato per la teoria dei numeri. I numeri p-adici fornivano inoltre un nuovo esempio di campo, stimolando così fin dai primi anni del XX sec. gli algebristi a studiare tale struttura.

Dalla teoria dei campi di numeri alla teoria dei campi di classi

Per il suo Zahlbericht David Hilbert scelse di fornire una sintesi originale dei risultati raggiunti, piuttosto che limitarsi a descriverli (Zassenhaus 1973); in particolare, voleva approfondire l'analogia con la teoria delle funzioni, cercando di definire gli equivalenti del teorema dei residui di Cauchy e del teorema di Riemann-Roch. Egli prendeva in esame le idee di Kronecker nella misura in cui le considerava utili alla dimostrazione di alcuni risultati (relativi, in particolare, ai divisori di un discriminante), ma privilegiava l'approccio di Dedekind, pur modificandolo in relazione ad alcuni aspetti importanti.

Anche Hilbert mise al centro della sua attenzione la nozione di campo di numeri generato da un numero algebrico, sviluppando sistematicamente i legami tra l'aritmetica di questi numeri e i risultati della teoria di Galois, relativi allo studio dell'equazione di grado minimo soddisfatta dal numero algebrico generatore del campo. Si è visto più volte come un numero primo ordinario p non resti in generale primo quando lo si consideri ‒ come ideale principale (p) ‒ in un campo di numeri algebrici K; Hilbert descrive, per mezzo di certi sottogruppi del gruppo di Galois, alcune caratteristiche della decomposizione di (p) in ideali primi degli interi di K, esaminando in dettaglio i casi particolari dei campi quadratici (generati cioè dalle radici di un'equazione quadratica), dei campi ciclotomici e delle loro estensioni cicliche (estensioni il cui gruppo di Galois è generato da un solo elemento).

Hilbert analizza anche alcuni problemi classici che hanno motivato lo sviluppo di tipo algebrico che si è descritto. Egli introduce un simbolo per i resti delle norme:

per tutti gli interi a e b (con b non quadrato) e per ogni primo p, dove N(α) denota la norma nel campo quadratico Q(√b). Il simbolo [11] vale 1 se p non divide b, e si ritrova il simbolo di Legendre se p=b. Le leggi di reciprocità si esprimono allora in una forma particolarmente interessante mediante la formula del prodotto:

nella [12] il prodotto è esteso a tutti i numeri primi, con un termine che rappresenta un numero primo 'all'infinito'. Hilbert riscrisse anche in modo più semplice gran parte delle Disquisitiones di Gauss e dei risultati di Kummer.

Hilbert si interessò molto al caso in cui non si considera necessariamente il campo dei numeri razionali, ma un campo di numeri qualunque (anche in questo caso l'analogia con i rivestimenti delle superfici di Riemann ha un ruolo importante). Egli era inoltre portato a congetturare l'esistenza, per ogni campo di numeri K, di un ampliamento H soddisfacente molte importanti proprietà: H doveva essere un corpo di Galois, ossia generato su K da un elemento algebrico. Doveva contenere tutti i coniugati di tale elemento e il suo gruppo di Galois su K doveva essere isomorfo al gruppo delle classi di ideali di K; nessun ideale di K doveva essere divisibile per il quadrato di un ideale primo di H (come avviene, per esempio, nel caso degli interi di Gauss con il numero primo 2 e, più in generale, con i divisori del discriminante). Infine, tutti gli ideali di K dovevano essere ideali principali di H. Presumibilmente nello stesso periodo e, a partire dal problema del tutto diverso della distribuzione degli ideali primi nelle classi di ideali (Frei 1989), anche Weber fu condotto a postulare l'esistenza di ampliamenti particolari, che egli chiamava campi di classi, con proprietà che riflettono alcuni aspetti della decomposizione degli ideali del campo di base. Si poteva sperare, in altri termini, di descrivere gli ampliamenti a partire da proprietà legate al campo. Queste congetture, nel caso di ampliamenti abeliani, sono state dimostrate e sviluppate nel corso del XX sec.: è la teoria dei campi di classi, le cui generalizzazioni al caso non abeliano (congetture di Langlands e di Bloch-Kato) occupano un posto importante nelle ricerche odierne di teoria dei numeri.

L'evoluzione qui rapidamente delineata ebbe un impatto decisivo non soltanto sulla teoria dei numeri ma anche sull'algebra astratta: le strutture di campo e di ideale che si considerano in algebra provengono dalla teoria dei numeri. Le congetture sui campi di classi dimostrano inoltre che le strutture algebriche erano divenute alla fine del XIX sec. oggetti di studio a pieno titolo. Ai nuovi problemi si rispondeva costruendo campi di numeri soddisfacenti certe condizioni.

Le relazioni fra analisi e teoria dei numeri

Fin dalla prima metà del XIX sec. erano stati pubblicati numerosi testi che nel titolo menzionano esplicitamente relazioni tra analisi e teoria dei numeri. Tale accostamento suscitava grande interesse, considerato che la classificazione tradizionale delle varie materie tendeva a separare il continuo, e pertanto l'analisi, dal discreto, in particolare della teoria dei numeri. La varietà di queste relazioni è sorprendente, sia che si tratti di applicazioni da un campo a un altro, come si è visto a proposito delle leggi di reciprocità, sia che si tratti di analogie (per es., con la teoria delle funzioni algebriche).

Funzioni ellittiche e modulari

Le funzioni circolari seno, coseno ed esponenziale complesso sono già comparse più volte in questo capitolo, sia nelle dimostrazioni che nello studio diretto di loro valori speciali, quali le radici dell'unità e i numeri ciclotomici. Un altro tipo di funzioni si presentava ai matematici del XIX sec.: le funzioni ellittiche, la cui teoria costituisce un tema prediletto dell'analisi e uno dei suoi strumenti più potenti. Come le funzioni circolari, le funzioni ellittiche sono periodiche, anzi doppiamente periodiche: per ogni funzione ellittica f esistono due numeri complessi ω1 e ω2, il cui rapporto è un numero complesso non reale, tale che f(ω1+z)==f(ω2+z)=f(z).

Nei Fundamenta nova theoriae functionum ellipticarum del 1829, Jacobi considera l'identità formale:

dove R(n) denota il numero di decomposizioni di un intero positivo n in somma di quattro quadrati interi. Serie analoghe erano già state utilizzate da Euler nel secolo precedente per il calcolo di partizioni di interi. Jacobi introduce le funzioni

dove μ e ν sono parametri interi, α è un numero complesso e ∣q∣⟨1. Egli esplicita le relazioni tra le varie funzioni Θμ,ν associate a differenti parametri; in particolare, i quozienti tra queste funzioni danno luogo a funzioni ellittiche doppiamente periodiche. Jacobi utilizza le proprietà di queste ultime per determinare il valore di R(n): per n dispari si ha

e per n pari

L'inadeguatezza del suo metodo per le decomposizioni in somma di cinque quadrati spinse l'Académie des Sciences di Parigi a bandire nel 1881 il premio che suscitò l'indignazione di Smith, come abbiamo visto sopra.

Un altro intervento delle funzioni ellittiche nella teoria dei numeri ha portato alla creazione di un campo di ricerca autonomo, la teoria della moltiplicazione complessa. Kronecker si era interessato molto ai lavori di Abel e di Galois sulle equazioni, ma non approvava l'impostazione che essi avevano seguito. Si trattava, in particolare, di rinunciare a una espressione esplicita delle radici per interessarsi soltanto alle loro relazioni, al gruppo di Galois dell'equazione: si ritrovano in questo atteggiamento le priorità di Kronecker. Le radici p-esime dell'unità, diverse da 1, soddisfano l'equazione x^p−1+x^p−2+…+1=0 e sono tutte potenze di una qualunque di esse. In altri termini, il gruppo di Galois dell'equazione è ciclico: una sola permutazione delle radici è sufficiente a generare tutte le altre. Nel 1853 Kronecker suggerì che deve sussistere una sorta di proposizione inversa, cioè che ogni equazione a coefficienti interi abeliana (ossia con gruppo di Galois abeliano, e dunque prodotto di gruppi ciclici) ha come radici funzioni razionali delle radici dell'unità. La dimostrazione completa fu data da Weber nel 1886. Kronecker immaginò una situazione analoga per equazioni che hanno per coefficienti interi di Gauss o, più in generale, interi di un campo quadratico a discriminante negativo, considerando l'uso di funzioni ellittiche. Come cosnz si esprime razionalmente in funzione di cosz così, per ogni funzione ellittica f(z), f(mz) è una funzione razionale di f(z). Tuttavia può anche accadere che una tale relazione sussista per valori di m non interi: è il caso della moltiplicazione complessa, quando il rapporto τ=ω1/ω2 dei periodi della funzione ellittica appartiene appunto a un campo quadratico immaginario. Le funzioni ellittiche possono essere classificate secondo il tipo di moltiplicazione complessa e ciascuna classe può essere descritta mediante un valore particolare di una funzione j, detta 'funzione modulare', che gode anche di interessanti proprietà di periodicità. Lo 'Jugendtraum' (il sogno di gioventù) di Kronecker, termine con il quale si fa oggi riferimento a questa idea, era di utilizzare le radici dell'unità e dei valori di questa funzione j per descrivere le radici delle equazioni a coefficienti in un campo quadratico immaginario. La versione corretta di tale enunciato, legato alla teoria dei campi di classi, è stata dimostrata solamente nel XX secolo.

La distribuzione dei numeri primi e la teoria analitica dei numeri

Un altro tema molto importante è la questione della distribuzione dei numeri primi. Si tratta in realtà di un vecchio problema: fin dal 1737 Euler aveva osservato che la divergenza nell'intorno di 1 della serie ζ(s)=∑_n≥11/n^s implica l'esistenza di una infinità di numeri primi. In effetti, per s>1 si ha:

e il prodotto a secondo membro della [17] è divergente soltanto se vi è una infinità di fattori. L'idea fu ripresa un secolo dopo da Dirichlet, in alcuni articoli del 1837 e 1839. Dirichlet introduce serie del tipo L(χ,s)=∑_n≥1_an/n^s, nelle quali i coefficienti a_n sono definiti aritmeticamente: un caso tipico è quello in cui a_n è il simbolo di Legendre-Jacobi (D/n) per D fissato. La proprietà fondamentale di tali serie è quella di riunire informazioni di carattere aritmetico in forma compatta e utilizzando un oggetto accessibile ai metodi analitici. Teoremi di carattere analitico su queste serie forniscono quindi informazioni sull'aritmetica che esse racchiudono. Nel caso in esame, i coefficienti dipendono da classi di congruenza e servono a isolare i numeri primi che appartengono a ciascuna classe. Dal fatto che L(χ, s) non si annulla per s=1, Dirichlet dedusse l'esistenza di infiniti numeri primi in ogni progressione aritmetica a+Km (con a e m primi fra loro). Per esempio, esistono infiniti numeri primi della forma 5K+2 o 6K+1. Risultato che Legendre aveva implicitamente utilizzato nei suoi tentativi di dimostrazione della legge di reciprocità quadratica.

Dirichlet utilizzò queste serie anche per determinare il numero h(D) delle classi di forme quadratiche in due variabili, di discriminante D. Per esempio, per un discriminante D⟨−4 egli ottiene:

Molti sforzi sono stati compiuti durante il XIX sec. per comprendere meglio la distribuzione dei numeri primi (Ellison 1978; Schwarz 1994). Si prestava attenzione in particolare alla funzione π(x), che conta i numeri primi inferiori a un fissato numero x. L'andamento sembrava del tutto irregolare e la speranza era riposta nel confronto con alcune funzioni analitiche. Fin dagli Essais sur la théorie des nombres, Legendre aveva proposto un equivalente asintotico

con x sufficientemente grande e A e B costanti determinate empiricamente. Nella prima metà del secolo furono effettuate numerose osservazioni su tavole di numeri (Echeverria 1992). Nel 1849 Gauss, utilizzando alcuni calcoli di Benjamin Goldschmidt per valori di x vicini a 3 milioni, suggeriva in una lettera che la funzione Li(x), il logaritmo integrale:

fornisse una approssimazione migliore. Ciò fu confermato dal matematico russo Pafnutij L´vovič Čebyšev (1821-1894), al quale si devono i primi risultati importanti in materia. In particolare egli corresse le stime proposte da Legendre, stabilendo che

Egli dimostrò anche che, se il rapporto di π(x) a (x/logx) tende a un limite, questo limite non può che essere 1, deducendo da queste stime una dimostrazione del postulato di Bertrand: per ogni n>3 esiste un numero primo fra n e 2n−2.

Le due approssimazioni mediante x/logx e Li(x) sono asintoticamente equivalenti. Come ha osservato Jacques Hadamard nell'articolo scritto per l'Encyclopédie des sciences mathématiques, la prima esprime il fatto che la probabilità di estrarre un numero primo, scegliendo a caso un numero tra 0 e x, è 1/logx e la seconda che la probabilità che un numero sufficientemente vicino a x sia primo è 1/logx.

L'analisi che interviene in questi risultati, e in quelli che seguirono subito dopo, è molto elementare (anche se di non agevole impiego), riguardando convergenza, integrazione e stime nel campo reale. Nel 1859 Riemann, nel suo unico articolo sulla teoria dei numeri, operava una trasformazione decisiva, suggerendo di applicare a questi problemi lo studio della funzione ζ(s) considerata come funzione di una variabile complessa, un campo di ricerca tra i più attivi dell'epoca ma anche tra i più difficili. La serie che definisce ζ(s) ha senso solo per Re(s)>1, ma Riemann dimostrò che ζ(s) soddisfa l'equazione funzionale

dove

è la funzione gamma di Euler, e che la [22] consente di definire un prolungamento analitico di ζ(s) a tutto il piano complesso, con un unico polo in s=1 di residuo 1. La [22] implica anche l'esistenza di zeri reali nei punti s=−2,−4,−6,…; nel piano complesso non vi possono essere zeri fuori della striscia compresa fra le due rette verticali Re(s)=0 e Re(s)=1. Riemann enunciò, quasi senza dimostrazione, alcune ulteriori proprietà della funzione così prolungata: essa ha una infinità di zeri nella detta striscia; più precisamente, vale la seguente relazione:

nella quale N(T) è il numero degli zeri di parte reale compresa fra 0 e 1 e di parte immaginaria compresa fra T e −T. La ζ può essere fattorizzata in un prodotto infinito di funzioni, ciascuna delle quali si annulla esattamente in uno degli zeri di ζ; tutti questi zeri si trovano sulla retta mediana Re(s)=1/2. Quest'ultima affermazione è la famosa 'ipotesi di Riemann', a tutt'oggi non ancora dimostrata. Le altre proprietà furono dimostrate, in particolare da Hadamard e von Mangoldt, solamente nell'ultimo decennio del XIX secolo. Il legame tra il comportamento degli zeri di ζ e la distribuzione dei numeri primi, della quale Riemann formula una versione precisa, segue dalla decomposizione della funzione ζ in un prodotto esteso a numeri primi, come detto più sopra: il logaritmo della funzione ζ tende a ∑p−^s e pertanto la localizzazione dei suoi zeri fornisce informazioni sulla funzione che conta i numeri primi.

Queste idee di Riemann interessavano soprattutto gli analisti. Il caso di Hadamard è abbastanza tipico: nella sua tesi di dottorato egli ottenne la fattorizzazione della funzione ζ mediante i suoi zeri e sviluppò una teoria più generale sulla determinazione di una funzione di variabile complessa a partire dai suoi zeri e dai suoi poli. Anche se appartengono propriamente alla teoria delle funzioni complesse, questi sviluppi permisero a Hadamard e a De la Vallée Poussin, indipendentemente ma nello stesso anno 1896, di dimostrare il teorema di distribuzione dei numeri primi. Le dimostrazioni sono diverse ma si basano entrambe sul fatto che la funzione ζ non si annulla sulla retta Re(s)=1. Charles-Jean De la Vallée Poussin integrò poi questa impostazione con le ricerche di Dirichlet per dimostrare che i numeri primi si distribuiscono uniformemente nelle diverse classi di congruenza. Sono state anche fornite diverse stime dei termini d'errore. Tutti questi studi avrebbero conosciuto un grande sviluppo a partire dal 1910, generando interazioni profonde fra teoria delle funzioni e teoria dei numeri.

Furono inoltre definite funzioni analoghe a ζ e L allo scopo di ottenere informazioni sulla distribuzione degli ideali primi nei campi di numeri. Per esempio, si può associare a un campo di numeri la sua funzione di Dedekind analoga alla funzione di Riemann; anch'essa possiede un solo polo in s=1, il cui residuo si esprime in funzione di dati aritmetici del campo; per un campo quadratico di discriminante −d≡1 mod 4, d≥5, il residuo è h/√d. In generale, i risultati analitici necessari non furono messi a punto prima del XX sec. e alcuni costituiscono ancora oggi problemi aperti. Va osservato tuttavia che queste funzioni hanno rivestito un ruolo molto importante nelle prime dimostrazioni di esistenza dei campi di classi.

Numeri trascendenti

Tra le questioni che ebbero pieno sviluppo soltanto nel XX sec. rilevante è l'esame delle proprietà dei numeri. Si è finora parlato soprattutto di numeri algebrici, ma un interesse parallelo, anche se ancora rivolto a casi particolari, si è manifestato per i numeri trascendenti, ossia non algebrici. Nel 1844 Joseph Liouville costruì, in modo piuttosto artificioso e nel quadro delle ricerche sull'approssimazione di un numero algebrico mediante numeri razionali, numeri di questo tipo che non possono essere soluzione di alcuna equazione algebrica a coefficienti interi.

Fu però Charles Hermite il primo a dimostrare che un numero ben noto in analisi, il numero e (il numero di Napier) è trascendente. La dimostrazione della trascendenza di π fu ottenuta nel 1882 da Carl Louis Ferdinand Lindemann, perfezionando alcune idee di Hermite. Egli ha dimostrato che l'equazione

non ha soluzioni per numeri algebrici distinti x_i e X_i se gli X_i non sono tutti nulli; in particolare, se x è un numero algebrico non nullo, senx, tanx, e^x sono sempre trascendenti e ciò dimostra che 2πi, e pertanto π, non può essere algebrico. Varie classificazioni delle quantità irrazionali venivano ormai proposte alla fine del secolo.

Per quanto concerne queste nuove interazioni fra teoria dei numeri e analisi, diversi matematici, come Dedekind e Weber, le ritenevano un mezzo per trasferire rigore da una disciplina all'altra; altri, come Lucas, sostenevano invece la necessità di evitarle per sviluppare metodi più omogenei. Hilbert vi vedeva la possibilità di collegare alla teoria dei numeri ulteriori branche della matematica in una prospettiva strutturale; altri, al contrario, vi vedevano la prova della dipendenza della teoria dei numeri da campi di ricerca diversi. Alludendo al metodo di Hermite, Poincaré concludeva:

L'analisi ci apre prospettive infinite che l'aritmetica nemmeno sospetta, consentendo di abbracciare con lo sguardo un insieme grandioso dall'aspetto semplice e simmetrico. Nella teoria dei numeri invece, dove regna l'imprevisto, la vista si ferma per così dire a ogni passo. Senza dubbio vi diranno che al di fuori del numero intero non c'è rigore e quindi non c'è verità matematica, che esso si nasconde dappertutto e che bisogna cercare di rendere trasparenti i veli che lo coprono, a costo di doversi rassegnare a innumerevoli ripetizioni inutili. Cerchiamo dunque di non essere così puristi e di portare invece riconoscenza al continuo che, anche se tutto nasce dal numero intero, è il solo in grado di farne nascere tutto. (1897b)

I problemi di Hilbert

I sei problemi proposti da Hilbert nel 1900 per la teoria dei numeri riguardano la maggior parte dei temi che sono stati qui trattati: trascendenza dei valori di certe funzioni complesse e di numeri della forma αβ, con α e β algebrici e β irrazionale; distribuzione degli ideali primi nei campi di numeri e ipotesi di Riemann; leggi di reciprocità generali; risoluzione algoritmica di un'equazione diofantea; forme quadratiche; estensione delle idee di Kronecker sulla caratterizzazione delle radici delle equazioni. I problemi di Hilbert hanno avuto grande influenza sugli sviluppi del XX secolo. Per ognuno di essi egli scelse la formulazione che più lo collegava ai suoi temi preferiti, in particolare alla teoria dei campi di numeri (fa eccezione il problema delle equazioni diofantee, che ha avuto sviluppi di natura logica).

Si sarebbe perciò tentati di concludere questa esposizione celebrando la vittoria della concezione strutturale della teoria dei numeri, ma ciò significherebbe restringere l'orizzonte della teoria. Vi sono stati invece matematici, e non dei minori, che nel XX sec. si formarono a Gottinga presso gli allievi di Hilbert, senza però adottarne in blocco l'impostazione. Le varie alternative favorirono il costituirsi di filoni importanti della futura teoria dei numeri. Nell'avvenire preconizzato da Hilbert colpisce l'assenza di due aspetti: la messa in atto effettiva di risultati teorici, per ritrovare per esempio i particolari più sottili dei diversi campi di numeri, e ovviamente la geometrizzazione della teoria dei numeri. Il fatto che questi aspetti abbiano anch'essi conosciuto sviluppi fecondi nel corso del XX sec. dimostra che le voci, se non discordanti almeno dissidenti, degli altri studiosi contemporanei di Hilbert si sono fatte sentire: non fu un sec. XIX unico e monolitico quello che ha ispirato la moderna teoria dei numeri.

Bibliografia

Bordogna 1996: Bordogna, Francesca, Interpreting the ideal. Embedding ideal numbers in the mathematical programs of Kummer, Dedekind and Klein, Berlin, Max-Planck-Institut für Wissenschaftsgeschichte, 1996.

Collison 1977: Collison, Marie, The origins of the cubic and biquadratic reciprocity laws, "Archive for the history of exact sciences", 16, 1977, pp. 63-69.

Corry 1996: Corry, Leo, Modern algebra and the rise of mathematical structures, Basel, Birkhäuser, 1996.

Dugac 1976: Dugac, Pierre, Richard Dedekind et les fondements des mathématiques, Paris, Vrin, 1976.

Echeverria 1992: Echeverria, Javier, Observations, problems and conjectures in number theory. The history of the prime number theorem, in: The space of mathematics. Philosophical, epistemological and historical explorations, edited by Javier Echeverria, Andoni Ibarra and Thomas Mormann, Berlin-New York, de Gruyter, 1992, pp. 230-252.

Edwards 1975: Edwards, Harold M., The background of Kummer's proof of Fermat's last theorem for regular primes, "Archive for history of exact sciences", 14, 1975, pp. 219-236.

‒ 1977a: Edwards, Harold M., Fermat's last theorem. A genetic introduction to algebraic number theory, New York-Berlin, Springer, 1977.

‒ 1977b: Edwards, Harold M., Postscript to 'The background of Kummer's proof of Fermat's last theorem for regular primes', "Archive for history of exact sciences", 17, 1977, pp. 381-394.

‒ 1980: Edwards, Harold M., The genesis of ideal theory, "Archive for the history of exact sciences", 23, 1980, pp. 321-378.

‒ 1992: Edwards, Harold M., Mathematical ideas, ideals and ideology, "Mathematical intelligencer", 14, 1992, pp. 6-18.

Ellison 1978: Ellison, William - Ellison, Fern, Théorie des nombres, in: Abrégé d'histoire des mathématiques 1700-1900, directeur de la publication Jean Dieudonné, Paris, Hermann, 1978, 2 v.; v. I: Algèbre, analyse classique, théorie des nombres, pp. 151-236.

Frei 1989: Frei, Günther, Heinrich Weber and the emergence of class field theory, in: The history of modern mathematics, edited by David E. Rowe and John McCleary, Boston, Academic Press, 1989-1994, 3 v.; v. I: Ideas and their reception, 1989, pp. 425-450.

‒ 1994a: Frei, Günther, Number theory, in: Companion encyclopedia of the history and philosophy of the mathematical sciences, edited by Ivor Grattan-Guinness, London-New York, Routledge, 1994, 2 v.; v. I, pp. 806-827.

‒ 1994b: Frei, Günther, The reciprocity law from Euler to Eisenstein, in: The intersection of history and mathematics, edited by Sasaki Chikira, Sugiura Mitsuo and Joseph W. Dauben, Basel-Boston-Berlin, Birkhäuser, 1994, pp. 67-90.

Gispert 1996: Gispert, Hélène - Tobies, Renate, A comparative study of the French and German mathematical societies before 1914, in: L'Europe mathématique. Histoires, mythes, identités, sous la direction de Catherine Goldstein, Jeremy Gray et Jim Ritter, Paris, Maison des sciences de l'homme, 1996, pp. 407-430.

Goldstein 1989: Goldstein, Catherine, Le métier des nombres aux XVIIe et XIXe siècles, in: Éléments d'histoire des sciences, sous la direction de Michel Serres, Paris, Bordas, 1989, pp. 274-295 (trad. ingl.: A history of scientific thought, edited by Michel Serres, Oxford, Blackwell, 1995, pp. 344-371).

‒ 1994: Goldstein, Catherine, La théorie des nombres dans les Notes aux comptes rendus de l'Académie des sciences (1870-1914). Un premier examen, "Rivista di storia della scienza", n.s., 2, 1994, pp. 137-160.

Hasse 1950: Hasse, Helmut, Vorlesungen über Zahlentheorie, Berlin, Göttingen - Heidelberg, Springer, 1950.

Houzel 1978: Houzel, Christian, Fonctions elliptiques et intégrales abéliennes, in: Abrégé d'histoire des mathématiques 1700-1900, directeur de la publication Jean Dieudonné, Paris, Hermann, 1978, 2 v.; v. II: Fonctions elliptiques, analyse fonctionnelle, topologie, géométrie différentielle, probabilités, logique mathématique, pp. 1-113.

Kolmogorov 1978: Matematika XIX veka. Matematičeskaja logika, algebra, teorija čisel, teorija verojatnostei, pod redaktsiei Andrei N. Kolmogorov i Adol'f P. Yuškevič, Moskvà, Nauka, 1978 (trad. ingl.: Mathematics of the 19th century. Mathematical logic, algebra, number theory, probability theory, edited by Andrei N. Kolmogorov and Adol'f P. Yushkevich, Basel, Birkhäuser, 1992, 3 v.).

Lemmermeyer 2000: Lemmermeyer, Franz, Reciprocity laws. From Euler to Eisenstein, Berlin-New York, Springer, 2000.

Mehrtens 1990: Mehrtens, Herbert, Moderne, Sprache, Mathematik. Eine Geschichte des Streits um die Grundlagen der Disziplin und des Subjekts formaler Systeme, Frankfurt a.M., Suhrkamp, 1990.

Neumann 1979-80: Neumann, Olaf, Zur Genesis der algebraischen Zahlentheorie. Bemerkungen aus heutiger Sicht über Gauß' Beiträge zu Zahlentheorie, Algebra und Funktionentheorie, "Zeitschrift für Geschichte der Naturwissenschaft, Technik un Medizin", 16/2, 1979, pp. 22-39; 17/1, 1980, pp. 32-48; 17/2, 1980, pp. 38-58.

‒ 1981: Neumann, Olaf, Über die Anstösse zu Kummers Schöpfung der "idealen complexen Zahlen", in: Mathematical perspectives. Essays in mathematics and its historical development, edited by Joseph W. Dauben, New York, Academic Press, 1981, pp. 179-199.

Rowe 1988: Rowe, David E., Gauss, Dirichlet and the law of biquadratic reciprocity, "Mathematical intelligencer", 10, 1988, pp. 13-26.

‒ 1989: Rowe, David E., Klein, Hilbert and the Göttingen mathematical tradition, "Osiris", 5, 1989, pp. 186-213.

Schappacher 1990: Schappacher, Norbert, Le développement de la loi de groupe sur une cubique, in: Séminaire de théorie des nombres. Paris, 1988-1989, edited by Catherine Goldstein, Basel-Boston, Birkhäuser, 1990, pp. 159-184.

Schwarz 1994: Schwarz, Wolfgang, Some remarks on the prime number theorem from 1896 to 1960, in: Development of mathematics, 1900-1950, edited by Jean-Paul Pier, Basel-Boston, Birkhäuser, 1994, pp. 565-616.

Schwermer 1991: Schwermer, Joachim, Räumliche Anschauung und Minima positiv definiter quadratischer Formen, "Jahresbericht der Deutschen Mathematiker-Vereinigung", 93, 1991, pp. 49-105.

Zassenhaus 1973: Zassenhaus, Hans, Zur Vorgeschichte des Zahlberichts, in: Hermann Minkowski, Briefe an David Hilbert, mit Beiträgen und hrsg. von Lily Rüdenberg und Hans Zassenhaus, Berlin, Springer, 1973, pp. 22-26.