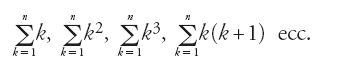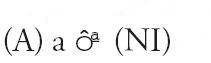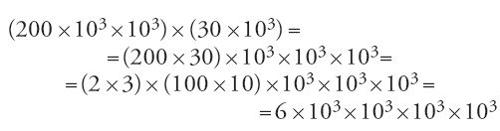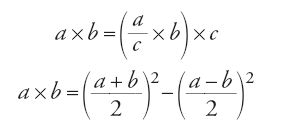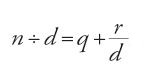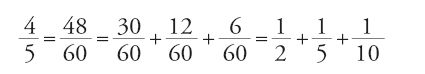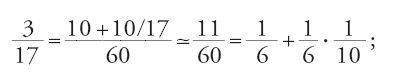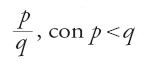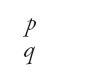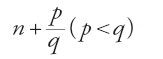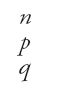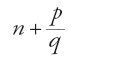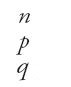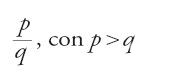La civiltà islamica: antiche e nuove tradizioni in matematica. Aritmetica

La civilta islamica: antiche e nuove tradizioni in matematica. Aritmetica

Aritmetica

Se ciò che in questa sede intendiamo per aritmetica si ricollega in generale al calcolo con quantità note, questo sembra a prima vista essere in rapporto con discipline che, anche se non del tutto indipendenti, ne sono comunque distinte: calcolo indiano basato sulla numerazione posizionale decimale, calcolo che come notazione utilizza la scrittura alfabetica dei numeri ereditata dai Greci (notazione abǧad); calcolo con le dita; calcolo "aereo"; calcolo sessagesimale, ecc. Numerose tradizioni aritmetiche coesistono infatti a partire dal IX sec. e si distinguono sia per le regole riguardanti le operazioni e i sistemi di numerazione sia per l'uso e i campi di applicazione. Si tratta di tradizioni diverse, che pongono ai matematici problemi teorici e pratici, ossia fondare su solide basi matematiche le regole di ciascuna di esse, ma anche rispondere alle sollecitazioni provenienti dall'amministrazione dello Stato a elaborare procedure che possano facilitare e razionalizzare l'uso di tali regole. È assai frequente inoltre che uno stesso matematico componga un trattato per ciascuna delle diverse aritmetiche: è il caso di Abū Bakr Muḥammad ibn al-Ḥasan al-Karaǧī (secc. X-XI), per fare soltanto un celebre esempio, autore di un libro, andato perduto, dedicato al calcolo indiano, e uno al calcolo non indiano del quale parleremo tra breve. Inoltre, come spiega Roshdi Rashed "il confronto, almeno implicito, tra le aritmetiche fa risaltare in maniera molto più chiara di prima la generalità e la natura astratta del concetto di operazione. Viste in questo modo, e in un certo senso sistematizzate, le operazioni rappresentano perciò mezzi per organizzare l'esposizione aritmetica. La presenza di più aritmetiche ha avuto infatti la conseguenza di relativizzare i sistemi di numerazione mostrando che il punto essenziale è dato dalla scelta della base e dalle operazioni da applicare" (1984a, p. 66). È quindi come se, in nome di questa comunanza di concezioni e di questo confronto implicito, le diverse tradizioni si inserissero in modo spontaneo in un insieme più ampio, anche se non precisamente definito. È di tale insieme che parleremo in questo capitolo.

Del resto gli autori di testi aritmetici fanno anch'essi riferimento a una disciplina più vasta, il ḥisāb (calcolo). Ma il ḥisāb va molto oltre lo stretto ambito dell'aritmetica nel senso in cui l'intendiamo oggi. Basterà, per convincersene, prendere in esame il contenuto dei trattati che dichiarano esplicitamente di rientrare in questo campo. La maggior parte di questi comprende infatti almeno un capitolo dedicato all'algebra, considerata allora sotto l'aspetto pratico e delle applicazioni, e destinato a fornire le regole operative per determinare le incognite, come pure altri procedimenti quali la regola della doppia falsa posizione. Alcuni trattati come al-Kāfī fī 'l-ḥisāb (Il sufficiente per il calcolo) di al-Karaǧī, o più tardi il Miftāḥ al-ḥisāb (La chiave del calcolo) di Ǧamšīd ġiyāṯ al-Dīn al-Kāšī (1380 ca.-1429), contengono inoltre un capitolo sulle regole del calcolo da usare per la misura delle aree e dei volumi.

Lo status del ḥisāb non è però facile da precisare. Esso fa chiaramente riferimento alla scienza dei numeri, ma esclude la teoria dei numeri ereditata dai libri aritmetici di Euclide e l'ariṯmāṭīqī, disciplina che per parte sua rinvia alla tradizione aritmetica dei neopitagorici e in particolare al libro di Nicomaco di Gerasa. È quanto lascia intendere Avicenna quando a conclusione dell'Aritmetica di al-Šifā' scrive: "Ecco quanto abbiamo voluto dire nella scienza dell'ariṯmāṭīqī. Abbiamo lasciato da parte alcuni casi, considerando che menzionarli in questa sede sarebbe stato estraneo alla regola di quest'arte. Nella scienza del ḥisāb resta ciò che a noi serve per usare i numeri e per determinarli. Ciò che infine resta per la pratica segue l'esempio dell'algebra e del muqābala e della scienza indiana dell'addizione e della sottrazione. Ma per quanto riguarda queste ultime è meglio considerarle tra le parti secondarie" (al-Ḥisābī, p. 69; Rashed 1984b, p. 33).

Tutto indica dunque che occorre considerare il ḥisāb soprattutto in relazione a un approccio pratico, fortemente segnato dal ruolo strumentale e applicativo che hanno le discipline come l'algebra, il calcolo indiano e loro analoghi, qui annoverate tra le "parti secondarie" della scienza dei numeri.

Il ruolo e l'influenza dell'algebra nella tradizione del ḥisāb si rivelano inoltre preponderanti per più di un aspetto. Occorre intanto osservare che non ci è pervenuto alcun trattato arabo di aritmetica anteriore al trattato di algebra di al-Ḫwārizmī, composto tra l'813 e l'830. Ciò non significa beninteso che il testo di al-Ḫwārizmī non sia stato preceduto da trattati di aritmetica; basta citare, tra molti altri, quello composto dal linguista e matematico al-Ḫalīl ibn Aḥmad (718-786), andato perduto. È molto probabile invece che fu proprio basandosi su una certa tradizione di aritmetica e di calcolo, della quale oggi si conosce molto poco, che al-Ḫwārizmī poté concepire la sua nuova teoria. Inoltre, il titolo che il matematico dette al suo libro, Kitāb al-Muḫtaṣar fī ḥisāb al-ǧabr wa-'l-muqābala (Libro conciso sul calcolo dell'algebra), sembra in qualche modo rendere conto dei rapporti esistenti inizialmente tra le due discipline: l'algebra è considerata come un 'calcolo' i cui campi di applicazione, descritti nella seconda parte dell'opera, vanno dalle transazioni commerciali, all'agrimensura, ai problemi di misura e di successione. Comunque, i trattati di ḥisāb posteriori alla comparsa dell'algebra risentiranno sempre più della nuova disciplina. Infatti, al di là dei punti che si occupano in modo più specifico di algebra, è innegabilmente lo sviluppo di questa materia che contribuirà a "razionalizzare una pratica empirica", per riprendere un'espressione di Roshdi Rashed (1984a, p. 63), e questo si verificherà almeno in due direzioni. In primo luogo favorendo l'emergere del concetto di operazione come principio di organizzazione dei trattati, in una sorta di ritorno del movimento di aritmetizzazione dell'algebra al quale si assiste fin dal X sec. con al-Karaǧī e i suoi successori; e permettendo, in secondo luogo, una presentazione più decisa degli algoritmi dell'aritmetica, ossia l'impostazione algoritmica, dotata ormai dei mezzi teorici che mancavano ai procedimenti di calcolo del passato, è diventata parte integrante della matematica.

I trattati di ḥisāb comprenderanno quindi necessariamente un certo numero di argomenti: interi e operazioni sugli interi, frazioni e operazioni sulle frazioni, algoritmi per l'estrazione della radice quadrata o eventualmente di ordine superiore, calcolo sessagesimale, determinazione delle incognite (algebra, doppia falsa posizione). Si ritroveranno frequentemente, in quanto costituiscono strumenti "dei quali si ha bisogno per determinare le incognite", come scriverà Ǧāmšīd Ġiyāṯ al-Dīn al-Kāšī, alcuni risultati relativi alla somma di determinate successioni come

(va osservato che all'epoca questi ultimi risultati sono utilizzati nelle branche più diverse della matematica e sono esposti anche nei trattati di algebra di al-Karaǧī e di al-Samaw᾽al, o in quelli che riguardano la matematica infinitesimale come quello di Ṯābit ibn Qurra). Più sopra abbiamo ricordato i problemi di misura delle superfici e dei volumi.

Non affronteremo tutti questi punti; anche se possono essere oggetto di una trattazione specifica nei libri di ḥisāb, di alcuni si parlerà in altri capitoli di questa Storia: algebra, metodi algoritmici per l'estrazione di radice, geometria pratica, analisi combinatoria, ecc., e a questi rimandiamo. In questa sede esporremo soltanto i fondamenti dei vari tipi di calcolo, rendendo conto di alcuni sviluppi come quelli che riguardano il concetto di frazione.

I sistemi di numerazione scritta

La scrittura dei numeri con le lettere sarà a lungo e largamente utilizzata dai matematici per varie ragioni, anche nei testi che trattano dei procedimenti di calcolo indiani. Per fare l'esempio di un manuale che sarà ampiamente diffuso, non si trovano cifre indiane né altri caratteri particolari che possano essere utilizzati allo stesso scopo nel Talḫīṣ a῾māl al-ḥisāb (Sommario delle operazioni del calcolo) del matematico marocchino Ibn al-Bannā᾽ (1256-1321), anche se questi descrive come operare con i numeri nel quadro della numerazione decimale posizionale, spiegando in particolare come manipolare le cifre.

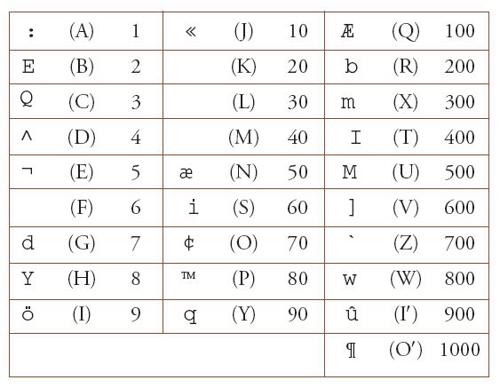
Oltre alla scrittura con le lettere, che è più una riproduzione del sistema di numerazione orale legato alla lingua che un vero e proprio sistema di numerazione scritta, diversi sistemi di scrittura dei numeri coesisteranno. In primo luogo, una scrittura alfabetica che si serve dei caratteri dell'alfabeto greco, o di quello arabo presi in un determinato ordine comune ad altre lingue semitiche. Questo ordine, detto abǧad, parola ottenuta prendendo di seguito le prime quattro lettere nell'ordine detto, dà origine al sistema di numerazione dello stesso nome, anch'esso chiamato ǧummal. Assegnando alle lettere i valori della tabella seguente (le ultime corrispondenze sono un po' diverse nel mondo musulmano occidentale), si può esprimere per esempio un numero come 389 con

(cioè X-P-I).

I caratteri greci (rūmī) saranno utilizzati fino a un periodo relativamente tardo, in particolare nel Maghreb e nell'Andalus, con qualche cambiamento di forma che ha in particolare dato origine a quelle che sono state chiamate 'cifre di Fes'. Ibn al-Bannā᾽ per esempio ha dedicato un opuscolo al calcolo con questi caratteri, intitolato al-Iqtiḍāb min al-῾amal bi-'l-rūmī fī 'l-ḥisāb (Breve trattato sulla pratica del calcolo coi numeri greci).

Contrariamente al calcolo indiano e a quello "aereo", di questo sistema alfabetico, che è decimale senza essere posizionale, sono pochi i testi che ci sono pervenuti e che indicano un procedimento specifico da seguire per effettuare le operazioni basandosi sulla numerazione scritta. Questo sistema continuò tuttavia a essere largamente usato per denotare i numeri anche molto dopo la diffusione del calcolo indiano; ciò senza pregiudicare l'uso di un modo di operare specifico per i calcoli, che poteva benissimo essere improntato su un altro sistema e, in particolare sul calcolo con le dita.

La notazione ǧummal è utilizzata anche in un altro contesto, quello del sistema posizionale sessagesimale, largamente usato dagli astronomi: le cifre da 1 a 59 di questo sistema vengono rappresentate dai numeri ai quali esse corrispondono nel sistema precedente, cioè da

,

una notazione che continuerà a essere utilizzata fino alla fine del XIX secolo. L'uso delle cifre ǧummal non è però esclusivo di questo sistema, come mostra l'esempio del trattato di Kūšyār ibn Labbān (X-XI sec.), nel quale le operazioni del calcolo sessagesimale sono presentate con cifre formate scrivendo i numeri corrispondenti e utilizzando le cifre indiane della numerazione decimale.

L'uso crescente del calcolo indiano contribuirà tuttavia a rendere sempre meno importante la grafia delle cifre, conservando come essenziale soltanto il principio della numerazione posizionale, qualunque sia la base. Nel primo libro di calcolo indiano che ci sia pervenuto in forma completa, Abū 'l-Ḥasan Aḥmad ibn Ibrāhīm al-Uqlīdisī (X sec.) scrive infatti: "è possibile sostituire queste nove cifre con altre, sia con cifre ǧummal, sia con cifre greche, sia con cifre arabe" (al-Fuṣūl fī 'l-ḥisāb al-hindī, p. 386). L'idea sembra essere così diffusa che viene ancora ripresa dall'autore di un lessico della lingua scientifica e filosofica dell'epoca, al-Ḫwārizmī al-Kātib (m. 990 ca.), che a proposito delle cifre ǧummal dichiara: "si può scrivere con queste cifre come fanno i calcolatori indiani, cioè si scrive con nove di queste cifre, dall'alif alla ṭā᾽, mettendo il segno 0 nelle caselle vuote, posto dello zero nel calcolo indiano, in modo da tener conto soltanto della disposizione" (Mafātīḥ al-῾ulūm, p. 178).

Quanto all'introduzione del calcolo indiano, e quindi della numerazione decimale posizionale, essa potrà aver luogo relativamente presto (sappiamo però poco sulla diffusione del nuovo sistema). La forma delle nove cifre e dello zero subisce vari cambiamenti secondo le regioni, per finire con le grafie tra loro diverse dell'Oriente e dell'Occidente musulmano (*,+,  ̗, -, ., /, 0, 1, 2 rispetto a 1, 2, 3, 4, 5, 6, 7, 8, 9).

Già nel 662 il vescovo siriaco Severo Sebokht, stabilitosi nella valle dell'Eufrate in Siria, esprimeva ammirazione per la scienza degli Indiani segnalando "i loro programmi di calcolo che superano tutto ciò che si può immaginare" e osservando che "questi calcoli si fanno con nove segni" (Nau 1910). Comunque sia, sembra sia stato lo stesso fondatore dell'algebra, Muḥammad ibn Mūsā al-Ḫwārizmī, a introdurre il nuovo sistema a Baghdad nella prima metà del IX secolo. Il trattato che il matematico dedicava al calcolo indiano è da considerarsi per il momento perduto; le versioni latine che sono giunti fino a noi costituiscono però una traccia dei primi lavori in arabo in questo campo dei quali si ha notizia. In particolare sembra che a partire da quest'opera si sia formata tutta una tradizione che raggiungerà la piena maturità nel X sec. con i trattati di al-Uqlīdisī e poi di Kūšyār ibn Labbān e dell'allievo di questi al-Ḥasan ῾Alī al-Nasawī.

Le necessità dell'amministrazione dello Stato e della società civile

Prima di iniziare l'esame del contenuto di questi libri occorre ritornare su quelle che possiamo definire le "determinazioni sociali dell'aritmetica" e che contribuiscono a spiegare sia la molteplicità dei lavori in questo campo, a opera di matematici e a partire dalla fine del IX sec., sia la forma adottata nella redazione di questi. Non ci resta che riprendere per esteso lo studio che su questo punto ha fatto Roshdi Rashed (1984a, pp. 62-66); di qui alla fine del presente paragrafo citeremo una parte di questo studio.

Come attestano gli stessi autori, i trattati di aritmetica nascono, almeno in parte, per le necessità dell'amministrazione. Nel trattato dal titolo Kitāb fī mā yaḥtāǧu ilay-hi al-kuttāb wa-'l-῾ummāl min ῾ilm al-ḥisāb (Delle necessità della scienza aritmetica dei funzionari amministrativi, degli esattori fiscali e altri), Abū 'l-Wafā᾽ al-Būzǧānī (940-998) presenta quest'ultimo come un libro che comprende l'insieme di ciò di cui hanno bisogno l'esperto e il principiante, il dipendente e il superiore in aritmetica, arte del funzionario (sinā῾at al-kitāba), pratica delle imposte fondiarie e ogni sorta di pratica in atto nei dīwān, proporzione, moltiplicazione, divisione, misure, tasse fondiarie, ripartizioni, cambi e altre pratiche utilizzate dalle varie categorie di persone per trattare gli affari e delle quali hanno bisogno per vivere.

La stessa preoccupazione si manifesta nel trattato al-Kāfī di al-Karaǧī. La si ritrova, anche se soltanto come indicazione, nei trattati di aritmetica indiana. È in questo modo che Ibn Labbān (intorno al 1000) scrive in conclusione della sua opera: "Questi fondamenti sono sufficienti sia per il calcolo astronomico che per le relazioni pratiche tra gli uomini". Al-Nasawī, suo allievo (1030 ca.) che aveva cominciato a comporre un trattato di aritmetica in persiano per l'amministrazione di Rayy, ne redasse poi una versione in arabo "affinché gli uomini ne facciano uso nei vari affari che intrattengono tra loro, e gli astronomi nella loro arte".

Si potrebbero moltiplicare gli esempi forniti dai matematici di questa generazione, cioè della fine del IX secolo. Possiamo infatti affermare che proprio durante l'Impero abbaside si assiste al consolidamento e allo sviluppo delle istituzioni amministrative al livello dell'impero; alla moltiplicazione su scala ridotta di queste istituzioni a livello delle province, a seguito dell'indebolimento del potere dei califfi; e infine alla comparsa di uno strato sociale, quello dei kuttāb (funzionari), legata al moltiplicarsi delle amministrazioni (dīwān) e della loro dimensione locale.

L'esistenza autonoma e il peso sociologico di questo ceto avevano destato stupore già negli storici dell'epoca: al-Ṭabarī, al-Ṣūlī, al-Mas῾ūdī, e soprattutto al-Ǧahšiyārī nel Kitāb al-Wuzarā᾽ wa-'l-kuttāb (Libro dei ministri e dei segretari) ne danno una descrizione particolareggiata. Sappiamo d'altra parte che l'arabizzazione dei dīwān era cominciata relativamente presto, tra il 700 e il 705 a seconda delle province, come ricordano al-Ǧahšiyārī e al-Kindī, lo storico.

Alla fine dell'Impero omayyade, uno di questi funzionari, Hārūn ibn ῾Abd al-Ḥamīd descriveva già il tipo ideale dei suoi colleghi. Da un testo conservato da al-Ǧahšiyārī e del quale parla Ibn Ḫaldūn, sappiamo che si tratta di un uomo colto che conosce bene l'aritmetica. Oltre alle qualità morali e sociali deve possedere conoscenze di arabo, storia, aritmetica e scienze religiose secondo le necessità del lavoro che svolge. È in questo senso che A. Metz scrive che il funzionario "è il rappresentante della cultura letteraria e tratta di scienze religiose soltanto per le necessità del proprio lavoro e della propria cultura". E aggiunge: "questo ceto di funzionari è ciò che distingue maggiormente lo Stato musulmano dall'Europa all'inizio del Medioevo".

È quindi l'esistenza di questi funzionari che spinge alla redazione di trattati per la loro formazione, non soltanto trattati di aritmetica, ma anche di geografia economica, come il celebre libro di Qudāma ibn Ǧa῾far sulle imposte fondiarie, di lessico della lingua filosofica, economica, scientifica dell'epoca, come quello di al-Ḫwārizmī al-Kātib, Mafātīh al-῾ulūm (Le chiavi delle scienze). Dīwān delle finanze, dīwān dell'esercito, dīwān degli uffici informazioni, dīwān della corrispondenza, e un buon numero di altri dīwān avevano tutti bisogno della contabilità finanziaria e chiedevano trattati di aritmetica sicuri e maneggevoli per la pratica del loro lavoro.

Ora, ciò che si è convenuto chiamare 'campo di esercizio' dell'aritmetica è costituito proprio da questi problemi posti ai funzionari dei dīwān. I capitoli 4 e 5 di Abū 'l-Wafā᾽ sono perciò dedicati ai problemi finanziari come tali, mentre il capitolo 6 riguarda le questioni di gestione dei beni, i pagamenti ai soldati, le licenze di transito da concedere o rifiutare ai battelli commerciali che percorrevano i fiumi e ai mercanti che circolavano lungo le strade, l'invio di corrispondenza e di corrieri e ogni altro affare che cadeva sotto l'amministrazione dei dīwān.

Si capisce subito, confrontando le due aritmetiche, che facilità e rapidità d'uso divennero presto criteri di preferenza. È proprio per sottolineare l'importanza dell'aritmetica indiana che al-Uqlīdisī metteva avanti questi valori pratici e scriveva:

La maggior parte degli esperti di aritmetica trae vantaggio a servirsene nella sua pratica: per quanto essa ha di facile e rapido, per il poco che bisogna ricordare, per la brevità del tempo impiegato a dare risposte, per quel poco di riflessione su ciò di cui essa si occupa, che essi si trovano necessariamente a disposizione. […] Diciamo dunque che si tratta di una scienza e di una pratica che richiedono uno strumento, come lo richiedono lo scrivano, il fabbricante, il cavaliere nella loro pratica; perché se manca al fabbricante, o se gli risulta difficile trovare ciò per cui esercita il proprio lavoro, non potrà ottenere ciò che gli serve; e capire ciò non è difficile né impossibile, e non c'è bisogno di preparazione. (al-Fuṣūl fī 'l-ḥisāb al-hindī, p. 48)

Sembra dunque che sia per rispondere alle due nuove necessità e conformemente a queste nuove norme che il matematico ritorna all'aritmetica digitale, o aritmetica indiana, della quale si propone di giustificare le regole e di organizzare l'esposizione.

Il calcolo indiano

Come suggerisce ampiamente il passo di al-Uqlīdisī ora visto, il modo di operare del calcolo indiano è stato a lungo dipendente da uno 'strumento', nel caso specifico una tavoletta detta taḫt (termine consacrato dall'uso) cosparsa di sabbia fine o di polvere (turāb, ġubār) per poter tracciare le cifre delle quali si aveva bisogno. La dipendenza originaria da questo dispositivo è il motivo di altre denominazioni per la disciplina, che si ritrovano sia nei biobibliografi sia nei matematici stessi. Così Naṣīr al-Dīn al-Ṭūsī (1201-1274) compone un trattato dal titolo Ǧawāmi῾ al-ḥisāb bi- 'l-taḫt wa-'l-turāb (Compendio del calcolo con la tavoletta e la polvere). Più tardi, quando l'uso della tavoletta sarà abbandonato a vantaggio di carta e penna, si ritroverà ancora traccia di questa origine in alcune espressioni come ḥurūf al-ġubār (cifre di polvere); il termine ġubār finirà per designare i nove caratteri utilizzati nell'Occidente musulmano in contrasto con i loro omologhi in Oriente, e a volte anche la disciplina stessa, come mostra il titolo di un manuale del matematico andaluso Abū 'l-Ḥasan ῾Alī al-Qalaṣādī (1412-1486), Kašf al-asrār ῾an ῾ilm ḥurūf al-ġubār (Lo svelamento dei segreti sulla scienza delle cifre ġubār).

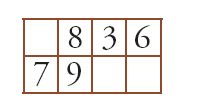
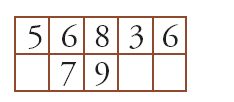
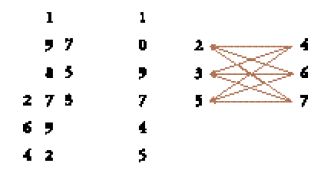
A questo modo di operare sono legati procedimenti di calcolo nel corso dei quali i risultati intermedi (e anche certi dati iniziali) sono cancellati uno dopo l'altro e sostituiti da altri, fino a che non si ottiene il risultato finale. Per illustrare l'uso della tavoletta riprendiamo uno degli esempi forniti da al-Uqlīdisī per la moltiplicazione, nel quale l'autore riprende un procedimento che viene descritto in tutti i libri di calcolo indiano (nelle opere più tarde che non fanno uso della tavoletta questo procedimento viene leggermente adattato). Per moltiplicare 836 per 79 si comincia con lo scrivere il secondo numero sotto il primo, con l'ultima cifra del secondo sotto la prima cifra del primo come segue:

Si moltiplica poi 8 per 7 e si scrive la cifra delle unità del risultato sopra il 7 e quello delle decine alla sua sinistra:

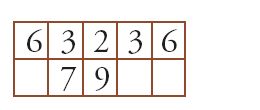
Si moltiplica poi 8 per 9, si sostituisce l'8 con la cifra delle unità del nuovo risultato (cioè 2) e si aggiunge quello delle decine (cioè 7) al risultato a sinistra:

Si sposta poi 79 di un posto verso destra:

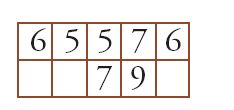
e si ricomincia l'operazione moltiplicando 3 per 7 e poi per 9; si ottiene:

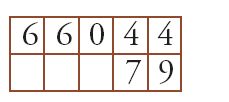
Si sposta di nuovo 79 di un posto verso destra, si moltiplica 6 per 7, poi per 9, e si ottiene:

dove la prima riga indica il risultato finale dell'operazione.

Le opere che trattano del calcolo indiano consistono allora di una presentazione di un certo numero di algoritmi che operano considerando le posizioni occupate dagli stessi nove caratteri. Il principale vantaggio, come afferma la maggioranza degli autori e come abbiamo sottolineato anche noi, è che la memoria viene poco sollecitata. Un inconveniente che oggi invece potremmo rilevare, oltre al fatto che manipolando la tavoletta ci si sporca, cosa che lo stesso al-Uqlīdisī menziona a proposito della diffusa prevenzione sull'aritmetica indiana, è la scomparsa dei risultati intermedi che rende impossibile controllare i calcoli. Assumono quindi importanza i procedimenti di verifica, come la prova del nove, che viene descritta nella maggior parte dei trattati.

Se si escludono le versioni latine del trattato di al-Uqlīdisī, nessuna delle quali si può considerare una traduzione fedele dall'originale arabo, il libro di al-Uqlīdisī, al-Fuṣūl fī 'l-ḥisāb al-hindī (Capitoli sul calcolo indiano), scritto a Damasco nell'anno 341 dell'egira (952-953), costituisce la prima esposizione completa di calcolo indiano a noi pervenuta. Oltre che per questa priorità, esso per certi versi deve essere considerato, se non come uno dei momenti fondanti della disciplina, almeno come uno dei punti fondamentali nella ricostituzione della sua storia, contenente in germe la maggior parte degli sviluppi successivi. Come l'autore stesso spiega nell'introduzione, l'intenzione che presiede alla redazione del trattato è quella di comporre un libro che esaurisca l'argomento, riprendendo in modo sistematico i lavori precedenti. Secondo al-Uqlīdisī si tratta di un progetto mai concepito prima di lui. Meglio ancora, egli non afferma soltanto di aver letto tutti i testi dei suoi predecessori, ma anche di essere stato il primo ad adattare al calcolo indiano tutti i procedimenti fondati sul calcolo con le dita e utilizzati fino ad allora nell'ambito dell'"aritmetica dei Greci e degli Arabi".

La prima parte del trattato di al-Uqlīdisī riguarda il calcolo indiano così come, dal suo punto di vista, era stato praticato fino ad allora. Vi si trova raccolto il grosso dei capitoli menzionati nelle versioni latine dell'opera di al-Ḫwārizmī e che serviranno a strutturare la disciplina presso gli autori successivi. In primo luogo un'esposizione del principio della numerazione decimale posizionale, l'introduzione delle nove cifre, della posizione (marātib) che permette di attribuire loro un valore, e del ruolo dello zero per designare i posti vuoti; in secondo luogo le descrizioni, prima nel caso degli interi, poi in quello delle frazioni e infine nel quadro del calcolo sessagesimale, delle procedure da seguire per la duplicazione, l'addizione, la sottrazione, la moltiplicazione, la divisione e l'estrazione di radice. In particolare, è in questa parte che viene descritto il procedimento che abbiamo esposto in dettaglio più sopra per la moltiplicazione degli interi.

Una seconda parte è dedicata a sviluppi supplementari che sono inseriti nel calcolo indiano, ma che provengono secondo l'autore da altre tradizioni aritmetiche. Vi si trovano esposti numerosi procedimenti alternativi per le operazioni, in particolare per la moltiplicazione, che noi presenteremo qui brevemente a titolo di esempio, e che si distinguono tra loro per la diversa disposizione nella scrittura dei numeri e per l'ordine secondo il quale si effettuano le operazioni intermedie. L'autore espone quindi di seguito tre tipi di moltiplicazioni: (a) una moltiplicazione "verticale" (ḍarb al-qā᾽im), nella quale il moltiplicando e il moltiplicatore sono scritti verticalmente e dove lo spazio che li separa è utilizzato come colonna di lavoro, così come lo era la riga superiore nel procedimento che abbiamo descritto sopra (ma contrariamente a quest'ultimo i due numeri iniziali restano visibili fino alla fine del calcolo, nelle figure rispettivamente 753 e 264, mentre nella colonna di lavoro compare solo 198.792 come risultato finale. (b) Una moltiplicazione "arborescente" (ḍarb al-mašǧar), che differisce dalla precedente per il posto della colonna di lavoro, posizionata questa volta a sinistra, e nella quale lo spazio tra i due numeri serve in questo caso a tracciare delle righe tra le cifre oggetto di prodotti parziali, ciò che permette di segnalare meglio i diversi passi del procedimento (nella figura la colonna di lavoro riporta il risultato finale, 109.745).

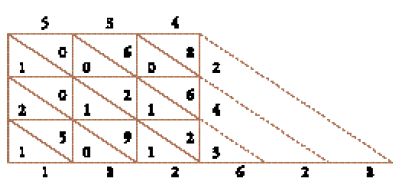
(c) Una moltiplicazione per 'caselle' (ḍarb al-buyūt), nella quale il moltiplicando e il moltiplicatore (534 e 342 nella tavola di al-Qalaṣādī qui sotto riportata) sono scritti perpendicolarmente l'uno all'altro, dando così luogo a una tabella le cui caselle, determinate dai diversi ordini dei due numeri, servono da spazio di lavoro nel quale si annotano i vari prodotti cifra per cifra prima di effettuare le somme (al-Uqlīdisī propone numerosi modi di operare per questo).

Questa molteplicità di procedimenti, in particolare per la moltiplicazione, resterà a lungo una delle caratteristiche delle opere a venire e che si rifanno alla tradizione del calcolo indiano. I vari metodi potranno assumere nomi diversi da un manuale all'altro, e potranno essere oggetto di qualche modifica. Si può così trovare il metodo delle 'caselle' sotto il nome di 'metodo delle tavole' (ǧadāwil) nel trattato al-Takmila fī 'l ḥisāb (Supplemento al calcolo) di Ibn Ṭāhir al-Baġdādī (m. 1037); nei trattati successivi lo stesso procedimento sarà presentato facendo comparire le diagonali di ciascuna casella, e il procedimento prenderà a volte, come nel Miftāḥ al-ḥisāb di al-Kāšī o nella Ḫulāṣat al-ḥisāb (La quintessenza del calcolo) di Bahā᾽ al-Dīn al-῾Āmilī (1547-1622), il nome di reticolo (šabaka).

Nella seconda parte dell'opera al-Uqlīdisī parla anche del principio della prova del nove per tutte le operazioni: addizione, sottrazione, moltiplicazione, divisione, estrazione di radice quadrata (le versioni latine del testo di al-Ḫwārizmī ne parlano solo per la moltiplicazione). Certo, il calcolo indiano si prestava particolarmente bene a questo genere di verifica: per ottenere i resti, al-Uqlīdisī utilizza infatti la proprietà secondo la quale un numero e la somma delle sue cifre in numerazione decimale sono congrui modulo 9. Più avanti ne dà una breve giustificazione, osservando che se si rappresenta dieci scrivendo 1 al secondo posto, e si sottrae 9, resta 1.

Si troveranno più tardi, presso altri autori come Naṣīr al-Dīn al-Ṭūsī o Ibn al-Bannā᾽, indicazioni per effettuare prove del 7, dell'8 e dell'11, accompagnate da vari algoritmi, basati sulla numerazione decimale, per determinare con facilità i resti modulo il numero scelto. Così per il calcolo dei resti modulo 11 al-Ṭūsī fornisce la regola che consiste nel sottrarre la somma delle cifre di posto pari da quella delle cifre di posto dispari. Ma c'è di più: sono questi procedimenti di verifica che sembrano aver portato i matematici, come se volessero generalizzare le regole, a dare risultati comuni sulle congruenze e a esporre le nozioni su queste in forma più esplicita. Così Ibn al-Bannā᾽, tra molti altri, distingue subito due tipi di sottrazione: una nella quale si sottrae semplicemente il numero più piccolo dal più grande, l'altra nella quale si ripete l'operazione fino a esaurimento con un eventuale resto. Questo resto, cercato in primo luogo per la verifica delle operazioni, troverà altre applicazioni. Ya῾īš ibn Ibrāhīm al-Umawī (m. 1489) ne fornisce una presentando alcuni criteri per riconoscere quadrati o cubi perfetti, facendo così entrare in gioco i residui quadratici e cubici modulo 7, 8, e 9.

Le opere di calcolo indiano, almeno le prime, si rivelano essere nel complesso soprattutto cataloghi ragionati, organizzati secondo le varie operazioni e la natura degli oggetti trattati (interi, frazioni, sistema sessagesimale), e di metodi pratici per lavorare con i numeri. In altre parole, più che chiarire cosa sono le operazioni, si tratta di proporre procedimenti, spesso più d'uno, per effettuarle. Per l'insistenza con cui ritorna sui vari metodi operativi, il calcolo indiano riveste così un carattere strumentale, già sottolineato come abbiamo visto da Avicenna, che in un certo senso l'oppone al calcolo "aereo" di cui parleremo. Inoltre è come se nei secc. X e XI questo modo di scrivere i numeri dipendesse soprattutto da un simbolismo fortemente collegato a un sistema di procedimenti tecnici e fosse usato come uno strumento, non potendo perciò pretendere, almeno in un primo tempo, di essere una rappresentazione universale.

Questo aspetto pratico e strumentale, rafforzato da spiccate preoccupazioni didattiche che si traducevano nella presenza di molti esempi, non impedisce però alcuni sviluppi concettuali che partono proprio dall'interno della disciplina. Abbiamo appena visto l'esempio delle congruenze, e sarà così anche con le frazioni decimali.

Inoltre, la diffusione del calcolo indiano, la superiorità pratica riconosciuta ai suoi procedimenti e, soprattutto, l'abbandono della tavoletta contribuiranno progressivamente ad attribuire alla numerazione decimale posizionale un nuovo status. Esso si avverte per esempio nell'uso della notazione in molti trattati che non sono di aritmetica indiana, e perfino in trattati di calcolo "aereo" (hawā᾽ī), come quello di al-Fārisī dei primi del XIV secolo. Già al-Uqlīdisī cercava, nell'ultima parte del suo libro, di adattare a un altro supporto, carta e penna, i procedimenti esposti all'inizio, sperando così di vincere le numerose resistenze riguardo al nuovo calcolo. I nuovi procedimenti presentati andavano però perfezionati: l'autore ricorreva ancora in modo massiccio alla notazione abǧad per i calcoli intermedi. Solo molti secoli dopo, con trattati come quelli di Ibn al-Bannā᾽ o di al-Kāšī, scomparirà il riferimento alla tavoletta, e spesso con questa (come nella prima delle due opere che abbiamo citato) ogni riferimento all'origine indiana di un'aritmetica in qualche modo ormai unificata, fondata sulla numerazione decimale posizionale ma che approfittava anche di lavori intrapresi nell'ambito del calcolo "aereo".

Il calcolo "aereo" ('hawā᾽ī')

Più o meno contemporanei del trattato di al-Uqlīdisī, in due libri di ḥisāb, già citati, composti da due matematici di prima grandezza che avevano entrambi dedicato opere al calcolo indiano, non si fa riferimento né ai procedimenti indiani né alla numerazione decimale posizionale: il Kitāb al-Manāzil al-sab῾ (Libro dei sette gradi) di Abū 'l-Wafā᾽ al-Būzǧānī e il Kāfī fī 'l-ḥisāb di al-Karaǧī. I numeri sono scritti in lettere senza alcun simbolismo, e sia l'addizione sia la sottrazione sono supposte note.

La maggior parte degli storici ha spesso presentato tali opere come riguardanti l'aritmetica dell'indigitazione. È vero che questi testi avevano entrambi una vocazione pratica esplicita, e si rivolgevano a un pubblico che, renitente all'uso del calcolo indiano, poteva eventualmente praticare il calcolo con le dita. Tuttavia non vi si trovano né indicazioni sulle posizioni delle dita per rappresentare i numeri, né su come servirsene. Da altri storici è stata attribuita a questi testi anche la qualifica di calcolo mentale, ma al-Karaǧī e Abū 'l-Wafā᾽ non danno una definizione particolare del tipo di aritmetica che espongono: qualche tempo dopo, sia negli scritti dei biobibliografi che dai matematici, essa sarà chiamata calcolo "aereo" (hawā᾽ī), a volte anche calcolo "aperto" (maftūḥ). Parallelamente allo sviluppo del calcolo indiano, questo metodo sarà in effetti all'origine di tutta una tradizione nella redazione dei trattati di ḥisāb. Citiamo a titolo di esempio opere che secondo al-Sinǧārī avrebbero composto Abū 'l-Qāsim ibn al-Samḥ (m. 1035) e al-Samaw᾽al (m. 1175), il voluminoso Asās al-qawā῾id fī uṣūl al-fawā᾽id (I fondamenti delle regole nei principî delle utilità) di Kamāl al-Dīn al-Fārisī (m. 1319), vasto commento di un trattato del suo maestro ῾Abd Allāh ibn Muḥammad ibn al-Ḫawwām (m. dopo il 1324), e più tardi ancora numerosi manuali di Šihāb al-Dīn Aḥmad ibn al-Hā᾽im (1352-1412), che saranno continuamente studiati fino al XIX secolo. Al-Fārisī, rispetto ai suoi predecessori, fornisce una spiegazione più dettagliata su come intende questa disciplina.

Se è certamente permesso denominare pratica questa parte (ḥisāb), non si usano però le estremità del corpo (ovvero le dita) né strumenti per ottenere ciò che si richiede. Allo stesso modo non si dice della logica che è pratica di per sé, per quanto si possa assimilare alle discipline pratiche; perché come le discipline pratiche ricercano procedimenti per alcuni materiali secondo modi particolari che portano a uno scopo, lo stesso accade con questi problemi, salvo che questi materiali sono esterni e ⟨i materiali dei problemi logici> sono di ordine intellettuale. È ciò di cui tratta il calcolo "aereo" che il libro comprende. Vi sono tuttavia nel ḥisāb metodi effettivamente pratici, come il calcolo con l'ausilio della tavoletta e della polvere. (Asās al-qawā῾id fī uṣūl al-fawā᾽id, p. 69)

Si trova così sottolineata per il calcolo "aereo" una dimensione di teoria pura, nel senso che non si ricorre né alle dita né a strumenti come la tavoletta e la polvere per il calcolo indiano. Non si tratta di fornire soltanto tecniche di risoluzione, ma, soprattutto, di interessarsi alla natura delle operazioni proponendone delle definizioni e rendendo espliciti i particolari con numerosi esempi, in modo da renderle comprensibili e dunque utilizzabili dal lettore, che in caso potrà sempre ricorrere ad altri procedimenti. "Se conosci il concetto della moltiplicazione e la sua definizione, ne conosci il calcolo", scrive al-Karaǧī (al-Kāfī fī 'l-ḥisāb, p. 37). Le operazioni non sono più semplicemente un principio di organizzazione, ma anche, assieme ai numeri e alle frazioni, gli oggetti stessi della disciplina, oggetti dei quali si cercano di stabilire i fondamenti concettuali, ritornando se necessario, come Abū 'l-Wafā᾽ e al-Fārisī, agli Elementi di Euclide e al rigore dell'esposizione che a essi è proprio. Inoltre non è certo un caso se matematici come al-Karaǧī e al-Samawa᾽al, due dei principali artefici dell'aritmetizzazione dell'algebra, si siano rivolti in questo modo verso l'aritmetica per meglio fondarne l'oggetto, approfittando dei progressi ottenuti dall'aver messo ordine nel calcolo algebrico e nel calcolo indiano. In un certo modo, al di là dell'opposizione tra i generi, questi autori non cercano affatto di opporsi al calcolo indiano in quanto tale: l'uso che al-Fārisī fa della numerazione decimale posizionale e delle cifre indiane gli permette di esplicitare meglio quanto si propone di fare, per esempio illustrando con una tavola l'operazione di moltiplicazione degli interi descritta prima di lui, in termini non molto diversi, da al-Karaǧī.

I fondamenti su cui si basa il calcolo "aereo" sono essenzialmente una concezione del numero intero come pluralità di unità, l'addizione e la sottrazione di questi interi, e il concetto di rapporto per definire le frazioni. Al-Fārisī giustifica la presenza dell'addizione e della sottrazione tra i principî della disciplina (e dunque il fatto che non vengono trattati nel calcolo "aereo") osservando che di queste si ha un'idea (taṣawwur) completa, ed è la ragione per la quale nemmeno Euclide le chiarisce, quando invece utilizza la sottrazione nella prima proposizione del libro degli Elementi dedicato ai numeri. Di rimando, è per obbedire a questa stessa esigenza di composizione teorica rigorosa che gli irrazionali trovano all'interno della disciplina un posto meno consolidato che altrove, in quanto non potevano beneficiare all'epoca di una costruzione propriamente aritmetica. Al-Fārisī spiega così, come introduzione alla sua opera, che se un numero che non è un quadrato perfetto ammette comunque una radice che si può maggiorare e minorare (così si ha 2⟨√5⟨3), la determinazione di questa radice è possibile soltanto per mezzo di rette e il ricorso a proposizioni euclidee: il suo "valore numerico" (῾adadiyya) resta ignoto agli uomini. Più avanti aggiunge: ciò che non ha un valore numerico è di competenza della geometria e non degli esprimibili (o aperti; maftūḥāt) del ḥisāb. Il che non impedisce che si possa trovare in queste stesse opere il tema delle radici quadrate dei numeri e della loro approssimazione, come in al-Karaǧī o nello stesso al-Fārisī. Ma oltre al fatto che questa menzione non è sistematica (Abū 'l-Wafā᾽ non affronta l'argomento), il trattamento e l'approssimazione delle radici irrazionali sembrano esposti quasi inopinatamente, in un modo spesso molto meno approfondito che non nelle opere di calcolo indiano, nelle quali costituisce un argomento a sé stante. Nelle loro opere di calcolo "aereo" al-Karaǧī e al-Fārisī si accontentano infatti di fornire per la radice quadrata di a²+r l'approssimazione a+r/(2a+1) già data da al-Uqlīdisī e da tutti i suoi successori, senza realmente cercare di migliorarla ed estenderla come faranno Kūšyār ibn Labbān, al-Nasawī e soprattutto al-Samaw᾽al nelle loro opere di calcolo indiano. Del resto, il procedimento di iterazione fornito da quest'ultimo aveva bisogno di una teoria delle frazioni decimali che trovasse la sua collocazione naturale nel quadro di quest'ultima disciplina.

La scrittura dei numeri con lettere costituisce dunque il supporto dell'esposizione del calcolo "aereo". Tuttavia ancora di più il sistema manifesta una certa dipendenza dalla lingua e dal carattere decimale della numerazione orale, dando luogo in particolare, come vedremo, a classificazioni propriamente linguistiche introdotte per trattare le frazioni. Riprendiamo come esempio l'esposizione di al-Karaǧī. Egli comincia con il definire tre nozioni per distinguere i numeri:

1) le posizioni (marātib) che corrispondono a quelle del calcolo indiano (la parola è la stessa). Le prime tre ‒ unità, decine e centinaia ‒ fondano il sistema e permettono di dare un nome alle successive mediante l'aggiunta del termine migliaia (migliaia, decine di migliaia, centinaia di migliaia, quindi migliaia di migliaia, decine di migliaia di migliaia, centinaia di migliaia di migliaia, ecc.);

2) i nodi (῾uqūd), il numero dei quali specifica il valore da attribuire a ogni posizione (così per le decine, dieci ha un solo "nodo", mentre sessanta ne ha sei); il numero di nodi per ciascuna posizione varia dunque da uno a nove e corrisponde in sostanza alla cifra del calcolo indiano (il termine ῾uqūd sembra però ripreso dal calcolo con le dita);

3) i nomi (asmā᾽) che intervengono nell'espressione dei numeri che sono dodici (da uno a nove, ai quali si aggiungono dieci, cento e mille). L'arabo permette di scrivere tutti i numeri mediante queste dodici radici senza utilizzarne altre, contrariamente ad altre lingue, come l'italiano, che fa uso di termini come venti.

I numeri si dividono pertanto in due categorie: i numeri semplici, che hanno una sola posizione (come 8, 20 o 30 mila) e quelli composti, che ne hanno più d'una (come 36). Per moltiplicare due numeri semplici si moltiplicano allora i due soli numeri di "nodi" presenti, e si applicano poi le regole per la moltiplicazione delle potenze di 10 date da al-Karaǧī nel linguaggio da lui introdotto. Si ha così, nell'esempio dello stesso matematico,

Per moltiplicare due numeri composti basta moltiplicare ognuno dei numeri semplici che formano il moltiplicatore per ognuno dei numeri semplici che formano il moltiplicando e sommare i risultati ottenuti. Si trova così espressa, in un modo particolarmente chiaro, una regola di distributività che sarà non semplicemente enunciata, ma anche dimostrata da al-Fārisī, il quale in tal modo accentuerà l'aspetto teorico dell'esposizione. Data la regola generale, al-Karaǧī può in seguito enunciare alcune regole che facilitano il calcolo in alcuni casi particolari, e che poggiano sulle proprietà stesse dell'operazione. Enuncia quindi, tra altre regole, le seguenti:

l'ultima regola può rivelarsi utile, come osserva l'autore, quando la somma dei due numeri a e b è un numero semplice.

L'esempio della moltiplicazione illustra l'attenzione che la pratica dell'aritmetica rivolgeva allora alla razionalizzazione. Questa razionalizzazione si fonda essenzialmente sulla lingua, un supporto che poteva sembrare più generale di un simbolismo legato a tecniche di soluzione particolari; ma l'influenza del calcolo indiano non sembra per questo meno preponderante. I "numeri di nodi" altro non sono che i corrispondenti "letterali" delle cifre della numerazione indiana, e occupano anch'essi un posto centrale nella struttura. Come se volesse operare questa identificazione ed esprimere un ordine tra le ragioni delle due nozioni, Muḥammad ibn ῾Alī al-Šahrazūrī (XII sec.), commentatore del trattato di al-Karaǧī, spiegherà, a posteriori, che gli Indiani hanno utilizzato nove forme numeriche per designare i numeri perché ogni posizione ha nove "nodi".

Le frazioni

La prima parte del libro di Abū 'l-Wafā᾽ è dedicata alle frazioni, e anzi si tratta della prima esposizione completa che oggi conosciamo. Se infatti l'autore in questa prima parte riporta i procedimenti largamente in uso prima di lui, li espone però secondo un ordine che partecipa dello stesso desiderio di razionalizzazione mostrato dalla pratica aritmetica, e che si trova particolarmente più nell'ambito del calcolo "aereo" che in quello del calcolo indiano. Inoltre, se contrariamente alla maggior parte degli autori di trattati di ḥisāb, Abū 'l-Wafā᾽ fa precedere da questa sezione l'esame delle operazioni sugli interi, è verosimilmente perché le frazioni costituiscono assieme agli interi gli oggetti primari della disciplina. In effetti per il calcolo indiano come per quello "aereo" la divisione tra interi è una divisione "senza resto", il cui risultato viene dato in generale mediante frazioni. Si ha così:

dove q ed r sono interi e r/d una frazione con r⟨d (nel procedimento di calcolo indiano il risultato viene presentato scrivendo in colonna q, r, d). Al-Uqlīdisī e al-Karaǧī organizzano diversamente la loro esposizione, e sono costretti a utilizzare il linguaggio delle frazioni prima ancora di averle introdotte, cosa che Abū 'l-Wafā᾽ evita. Per definire le frazioni quest'ultimo fa uso della nozione euclidea di rapporto e osserva che vi sono tre tipi di rapporto tra numeri: quello del più piccolo al più grande, quello del più grande al più piccolo, e quello tra due numeri uguali. Una frazione è allora, come nel caso dei risultati forniti dalla divisione di due interi, sempre un rapporto del primo tipo, cioè del più piccolo al più grande. Si ritroverà questo stesso concetto generale di frazione propria, almeno implicitamente, in tutti gli autori di trattati di aritmetica, di calcolo indiano e di calcolo "aereo". Posta la definizione, Abū 'l-Wafā᾽ passa alla classificazione delle frazioni di cui, per lui, si servono gli scrivani e i calcolatori:

1) le frazioni principali ("semplici" secondo altri autori), della forma 1/n, con 2≤n≤10, sono quelle che si possono definire con una sola parola. Le frazioni da un mezzo a un decimo sono le sole a rientrare in questo caso perché in arabo non vi sono, come invece in italiano, parole specifiche per un undicesimo o un dodicesimo (in questi casi si dice 'una parte di undici' o 'una parte di dodici');

2) le frazioni composte, che più tardi chiamerà "composte omogenee", della forma m/n, 2≤n≤10 e 2≤m⟨n;

3) le frazioni unite, come un mezzo di un quinto o un terzo di un settimo, che corrispondono a prodotti di frazioni principali come, per esempio, (1/2)(1/5) o (1/3)(1/7);

4) infine le frazioni "sorde" (aṣamm), che non si possono esprimere componendo frazioni dei tipi precedenti.

Abbiamo così due grandi categorie di frazioni: le esprimibili (munṭaq) e le sorde (aṣamm), secondo una distinzione che riprende i termini che in un altro ambito distinguono le quantità razionali (munṭaq) e irrazionali (aṣamm). Le prime si possono esprimere sotto forma di somme e prodotti di frazioni principali, le seconde hanno un denominatore comprendente un fattore primo superiore o uguale a 11; una classificazione fondata, quindi, su particolarità linguistiche, più che propriamente matematiche dei numeri.

L'eleganza suggerita dai calcolatori raccomandava inoltre la decomposizione di ogni frazione in somma di frazioni principali e unite (2/3 ha un ruolo particolare). Senza che fosse una regola, si preferiva perciò scrivere 3/4 come 1/2+1/4 o 2/5 come 1/3+(2/3)(1/10), e la maggior parte dei matematici continuerà a osservare questa forma di scrittura. Abū 'l-Wafā᾽ formula, nella prima parte del libro, un gran numero di regole per decomporre in questo modo le frazioni esprimibili o per dare alla frazioni sorde un'approssimazione dello stesso tipo. Il principio generale equivale a uno sviluppo delle frazioni in frazioni sessagesimali, che poi si esprimono per mezzo di frazioni del tipo richiesto. Per esempio:

o ancora

in quest'ultimo esempio l'approssimazione di 10/17 secondo lo stesso metodo aumenterebbe, secondo il commento dell'autore stesso, la precisione del risultato.

A questo sistema generale di frazioni se ne aggiungono altri due, che si ritroveranno in tutti i trattati di ḥisāb: in primo luogo, il sistema sessagesimale che abbiamo appena ricordato e nel quale i denominatori (60 o una sua potenza) sono impliciti e, in secondo luogo, quello che risulta dalle varie unità e frazioni di monete o di pesi e misure.

Alle operazioni già trattate nel caso degli interi si aggiungeranno quindi per le frazioni operazioni più specifiche, come la conversione tra i vari sistemi o ancora, più particolarmente (ma non solo) nel caso del calcolo "aereo", la decomposizione in frazioni principali, e operazioni ausiliarie, come la semplificazione e la riduzione allo stesso denominatore. Se presso al-Uqlīdisī il denominatore comune è ancora semplicemente il prodotto dei denominatori, la ricerca del minimo comune multiplo diventerà rapidamente, come in Abū 'l-Wafā᾽, al-Karaǧī o al-Baġdādī, il procedimento principale per effettuare una tale riduzione, così come per la semplificazione si ricorrerà al massimo comun divisore. Inoltre, l'insieme di queste operazioni fa nascere la necessità della decomposizione degli interi in fattori primi. Alcuni capitoli dedicati alla teoria elementare della divisibilità, e che rientrano quindi più in generale nella teoria dei numeri, compaiono così nei trattati di ḥisāb in relazione alle operazioni: l'algoritmo euclideo per la ricerca del massimo comun divisore viene pertanto ripreso da al-Karaǧī e da molti altri. In molte opere la teoria della divisibilità resta tuttavia legata in una certa misura al problema della denominazione delle frazioni e alla loro decomposizione in frazioni principali. Riprendendo per esempio la terminologia data da al-Fārisī, abbiamo le seguenti tre classi di numeri interi: (a) i numeri "sordi" (aṣamm), che non sono divisibili per i nove denominatori delle frazioni principali, come 11 o 143. Si tratta insomma di prodotti di numeri primi maggiori o uguali a 11; (b) i numeri "esprimibili" (munṭaq) o "aperti" (maftūḥ), che sono divisibili soltanto per i denominatori delle frazioni principali, come 8 o 25; (c) i numeri "comuni" (muštarik), che sono divisibili sia per numeri sordi che per numeri esprimibili, come 22 o 65. Così la decomposizione degli interi in fattori tenderà alla ricerca di fattori sordi primi, più che verso i fattori primi stessi. Il nome di "sordi" finirà per designare, nelle opere più tarde, solo i numeri primi maggiori o uguali a 11. Se in alcuni autori come Ibn al-Bannā᾽ o al-Qalaṣādī si incontra ancora il tema della decomposizione in frazioni principali e della ricerca di divisori sordi, nelle opere di calcolo indiano le frazioni compaiono per lo più nella forma generale

In al-Uqlīdisī e i suoi successori le frazioni sono indicate scrivendo in colonna

i numeri razionali positivi

scrivendo

forma che si ottiene, come abbiamo osservato, con il procedimento di divisione di due interi. Per evitare possibili confusioni nel trattamento di molti numeri razionali, si affermò progressivamente l'abitudine di introdurre un trattino per separare i vari termini, denotando in un primo tempo

con la forma in colonna

È poi nell'Occidente musulmano, come sembra, intorno alla scuola di Ibn al-Bannā᾽, che si instaura definitivamente l'abitudine di separare con un trattino numeratore e denominatore. Se si escludono le frazioni della forma

,

introdotte più tardi in Europa, si arriva a una concezione delle frazioni ordinarie vicine a quelle oggi prevalenti.

Conclusioni

La molteplicità delle tradizioni di scrittura dei trattati sul ḥisāb non deve indurre a fraintendere la natura di questa disciplina, la cui unitarietà è molto più profonda di quanto possa sembrare. Anche se si potrebbe porre l'accento sul modo tradizionale di scomporre le frazioni, esse sono oggetto di identiche concezioni nel calcolo indiano e in quello "aereo". Inoltre, il principio della numerazione decimale di posizione sottintende assai bene i due generi. Il calcolo sessagesimale, sistematicamente segnalato per il suo frequente uso in alcuni settori come l'astronomia, appariva come una diversa modalità di scrittura dei numeri dove cambia soltanto la base, fornendo spesso procedure di calcolo simili a quelle del calcolo decimale (a questo scopo sono utilizzate tavole di moltiplicazione in base 60).

Presentando una classificazione dei numeri in semplici e composti come nel calcolo "aereo", introducendo in seguito le cifre della numerazione decimale di posizione come il mezzo per indicare i 'nodi' di ciascun 'rango', proponendo una definizione per ogni operazione e sviluppando infine le procedure del calcolo indiano, opere come quelle di al-Kāšī non faranno altro che realizzare in modo effettivo questa unitarietà del ḥisāb, già in nuce. Si assisterà così all'ultimo atto di un processo che, a partire dall'introduzione della numerazione indiana e appoggiandosi a essa, condurrà a un approfondimento delle tecniche di calcolo, all'abbandono della tavoletta e della polvere, all'elaborazione di nuovi concetti come le frazioni decimali e a una seria riflessione sulla natura delle operazioni.

Bibliografia

Aghayani-Chavoshi 1996: Aghayani-Chavoshi, Jafar, L'oeuvre scientifique d'Abû al-Wafâ al-Buzjânî (Thèse de doctorat, Paris VII, 1996).

Nau 1910: Nau, François, La plus ancienne mention orientale des chiffres indiens, "Journal asiatique", 16, 1910, pp. 225-227.

Rashed 1984a: Rashed, Roshdi, Entre arithmétique et algèbre. Recherches sur l'histoire des mathématiques arabes, Paris, Les Belles Lettres, 1984.

‒ 1984b: Rashed, Roshdi: Mathématiques et philosophie chez Avicenne, in: Études sur Avicenne, édité par Jean Jolivet et Roshdi Rashed, Paris, Les Belles Lettres, 1984, pp. 29-39.

‒ 1992: Rashed, Roshdi, Optique et mathématiques. Recherches sur l'histoire de la pensée scientifique en arabe, Aldershot, Variorum, 1992.

‒ 1997: Histoire des sciences arabes, sous la direction de Roshdi Rashed avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v. (ed. orig.: Encyclopedia of the history of Arabic science, London-New York, Routledge, 1996, 3 v.).

Youschkevitch 1976: Youschkevitch, Adolf P., Les mathématiques arabes (VIII^e-XV^e siècles), Paris, Vrin, 1976.