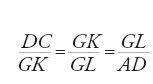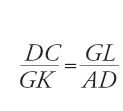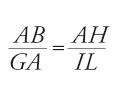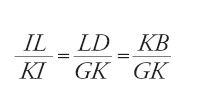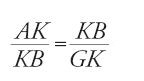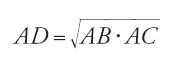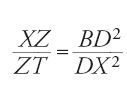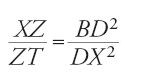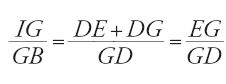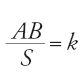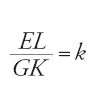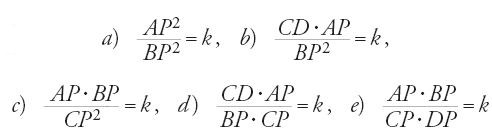La civiltà islamica: antiche e nuove tradizioni in matematica. Geometria delle coniche, luoghi, contatti e costruzioni
La civilta islamica: antiche e nuove tradizioni in matematica. Geometria delle coniche, luoghi, contatti e costruzioni
Geometria delle coniche, luoghi, contatti e costruzioni
L'opera di Apollonio di Perge segnò profondamente lo sviluppo della geometria tra il IX e l'XI secolo. Le Coniche, e la loro traduzione da parte degli stessi matematici, come Ṯābit ibn Qurra, diedero luogo a una vera e propria tradizione, all'origine della quale, nella prima metà del IX sec., quando non avevano ancora un accesso diretto e completo a quest'opera, troviamo i tre figli di Mūsā ibn Šākir. Saranno loro a tradurre le Coniche, dopo che Aḥmad ibn Mūsā, allora a Damasco, aveva rinvenuto i primi quattro libri nella redazione di Eutocio di Ascalona. Da quel momento le coniche avranno un ruolo fondamentale nella matematica. In algebra, la loro applicazione alla risoluzione geometrica delle equazioni di terzo grado darà il via, con la teoria di al-Ḫayyām (440-526/1048-1131), alla geometria algebrica; in geometria, i problemi solidi, alcuni ereditati dalla matematica greca, saranno risolti applicando sistematicamente l'intersezione di coniche e si moltiplicheranno fino a dare origine a una nuova disciplina, quella delle costruzioni geometriche, che si costituirà come tale soprattutto con Ibn al-Hayṯam (m. dopo il 1040). Anche le altre opere di Apollonio, andate in buona parte perdute, influenzeranno per lo stile e per il contenuto le ricerche di geometria dell'epoca. Il metodo di Apollonio, preciso e completo, fornisce un modello da seguire per l'esposizione della risoluzione di un problema: essa deve comportare un'analisi, una sintesi e una discussione dei vari casi possibili ('diorisma'). Si sviluppa l'analisi geometrica e con essa i problemi di luoghi e di contatti.
La fecondità di questa tradizione che riprende l'eredità di Apollonio non si esaurisce qui. L'applicazione delle coniche si estenderà a problemi appartenenti ad altri campi e ciò permetterà a sua volta la scoperta di nuove proprietà di queste curve. In ottica, le ricerche sugli specchi ustori condurranno, nella seconda metà del X sec., in particolare per opera di Ibn Sahl, allo studio delle proprietà focali e alla progettazione di strumenti per tracciare le coniche con un tratto continuo. I geometri di questa tradizione, "in possesso di una teoria delle coniche ben più approfondita di quella di cui disponeva Archimede" (Rashed 2000b, p. VI), riprendono le ricerche di quest'ultimo sulla misura delle superfici e dei volumi e sviluppano lo studio delle trasformazioni geometriche: omotetie, proiezioni e applicazioni affini. In un altro campo, a partire dallo studio dell'astrolabio essi concepiranno la prima teoria proiettiva locale della sfera.
L'applicazione delle coniche in particolari settori e la loro generalizzazione porteranno i matematici del X sec. a completare lo studio teorico di alcune proprietà di queste curve. È quanto farà Ibn Sahl, autore dell'opuscolo Fī ḫawāṣṣ al-quṭū῾ al-ṯalāṯa (Sulle proprietà delle tre coniche), nel quale studia alcune proprietà armoniche delle coniche invarianti per proiezione. Ibn al-Hayṯam scrive un trattato intitolato Fī tamām kitāb al-Maḫrūṭāt (Sul completamento delle Coniche), primo tentativo di restituzione del Libro VIII delle Coniche di Apollonio, andato da tempo perduto (probabilmente prima di Pappo). L'opera si presenta come una raccolta di problemi di costruzioni geometriche riguardanti rette associate a sezioni coniche: tangenti, diametri, lato retto (latus rectum); i problemi di geometria piana e solida sono risolti mediante l'intersezio ne di due coniche e l'autore cerca di stabilire un metodo che gli permetta di determinare l'esistenza e il numero dei punti d'intersezione di due coniche e di studiare, in particolare, il caso limite delle coniche tangenti. L'opera rientra nel quadro dei problemi di costruzioni geometriche risolti con metodi puramente geometrici, particolarità che conferisce loro a pieno titolo lo status di capitolo della geometria; più tardi questi lavori saranno ripresi da un punto di vista puramente algebrico, questa volta a opera di Šaraf al-Dīn al-Ṭūsī.
Prima di Ibn al-Hayṯam l'intersezione di coniche era stata considerata, da un punto di vista più generale, in rapporto con la continuità delle curve e aveva dato luogo a studi sulla possibilità di tracciarle con un tratto continuo. Oltre alle ricerche di Ibn Sahl, effettuate nel quadro dei suoi studi sugli strumenti ustori e della loro costruzione pratica, vi è la progettazione da parte di al-Qūhī di uno strumento, il compasso perfetto, capace di disegnare una conica con un movimento continuo; questo strumento fu studiato anche da al-Siǧzī, contemporaneo di Ibn Sahl. Nel XII sec. Ibn al-Ḥusayn cercherà di ricostruire lo studio di al-Qūhī. I lavori sul compasso perfetto, se mirano almeno in parte a risolvere il problema della costruibilità delle coniche nel piano e della loro continuità, rivelano anche il desiderio dei matematici di legittimare le costruzioni per intersezione di coniche per risolvere problemi solidi e di attribuire loro lo stesso status che avevano le costruzioni con riga e compasso per la risoluzione di problemi piani. Ciò condurrà i matematici in quella regione in cui si incontrano matematica e filosofia, che riguarda l'esame e la distinzione tra la costruzione di un oggetto matematico e la dimostrazione della sua esistenza. Le Coniche susciteranno nei matematici altre riflessioni d'ordine filosofico. Alla fine del X sec., al-Siǧzī s'interesserà al carattere di infinito della proprietà dell'asintoto di un'iperbole, cercando di fondare questa proprietà su solide basi.
I problemi di costruzione
I problemi di costruzione che tratteremo in questo paragrafo sono essenzialmente i problemi solidi: non risolubili con riga e compasso, ma risolvibili per intersezione di coniche. Si tratta sia di problemi ereditati dall'Antichità sia di altri posti in seguito. La ricerca di costruzioni geometriche ebbe inizio con i geometri greci, spinti a studiare curve diverse dalla circonferenza, in particolare le coniche, per risolvere appunto i problemi solidi. Secondo la testimonianza di Eutocio, già nel IV sec. Menecmo proponeva due metodi per determinare le due rette medie proporzionali tra due rette date (qui e nel seguito il termine 'retta' è equivalente al moderno 'segmento di retta'): uno di questi fa intervenire l'intersezione di una parabola e di un'iperbole, l'altro l'intersezione di due parabole. L'attribuzione di questa seconda costruzione a Menecmo è ancora oggetto di discussione tra gli storici; essa si trova anche in Diocle, contemporaneo di Apollonio. Fino alla vigilia del IX sec., gli studi sull'intersezione di coniche non hanno un carattere sistematico legato alla natura di problemi solidi; per questi ultimi si ricorreva anche a curve trascendenti (quadratrice, concoide) e soltanto Pappo sembra accordare la preferenza alle sezioni coniche. Inoltre, i geometri dell'età ellenistica non si preoccupano di dimostrare l'esistenza di un punto d'intersezione tra due coniche, un problema che non si porrà prima del X secolo. Sarà Ibn al-Hayṯam, all'inizio dell'XI sec., a imporre la norma dimostrativa che richiede l'esposizione dell'analisi e della sintesi.
Le Coniche di Apollonio svolgono nel IX sec. un ruolo preponderante nello sviluppo e nell'unificazione dei metodi di risoluzione dei problemi non risolvibili con riga e compasso. I problemi ereditati dai geometri greci sono ripresi in modo massiccio, gli studi a essi dedicati si moltiplicano, le risoluzioni per neũsis (ossia, riconducendosi a un problema di inclinazione) non sono più accettate (salvo qualche rara eccezione) e non si fa più ricorso alle curve trascendenti. L'unificazione di metodi applicati a problemi di natura molto diversa caratterizza, a partire dalla metà del IX sec., queste ricerche. Anche la comparsa dell'algebra nello stesso periodo ha grande importanza per la costituzione di questo nuovo campo d'interesse in geometria. Si assiste così a uno sviluppo in due direzioni. Da un lato, uno sviluppo di impronta 'ellenistica', come nel caso della costruzione dell'ettagono regolare, problema ispirato a uno scritto attribuito ad Archimede, ma senza che ci sia pervenuto alcun metodo completo. Si deve ai matematici del X sec. la stesura di una dozzina di trattati su questo tema; tutti propongono soluzioni basate sull'intersezione di coniche. Dall'altro lato, uno sviluppo, suggerito dall'algebra, che si emancipa dal contesto ellenistico, ossia si cerca di risolvere per mezzo delle coniche nuovi problemi espressi sotto forma di equazioni di terzo grado.
Tra i problemi più famosi ereditati dall'Antichità ellenistica, due furono ripresi dall'inizio della tradizione che si rifà ad Apollonio, ma anche precedentemente, nella prima metà del IX sec., rimanendo oggetto di ricerche per circa due secoli: la determinazione delle due rette medie proporzionali e la trisezione dell'angolo. Ippocrate di Chio fu il primo a dimostrare che il problema riguardante la determinazione delle due rette medie proporzionali è una derivazione da quello della duplicazione del cubo; una ventina di soluzioni sono riportate da Diocle, Pappo ed Eutocio. La trisezione dell'angolo è invece probabilmente legata alla costruzione di poligoni regolari.
Anche se numerose soluzioni erano state proposte nell'Antichità, e molte tra queste erano poi state trasmesse ai matematici arabi del IX sec. (alcune utilizzavano anche le coniche), entrambi questi problemi sono largamente ripresi tra il IX e l'XI secolo. Il testo più antico di questo periodo non appartiene ancora alla nuova tradizione apolloniana. Ha come autori i Banū Mūsā, dei quali abbiamo detto che non poterono utilizzare le Coniche di Apollonio se non molto tardi. Alla fine del loro trattato Kitāb ma῾rifat misāḥat al-aškāl al-basīṭa wa-'l-kuriyya (Libro per conoscere l'area delle figure piane e sferiche), che ci è pervenuto soltanto in due frammenti, completati per fortuna in una redazione di Naṣīr al-Dīn al-Ṭūsī nel XIII sec. e nella traduzione latina di Gherardo da Cremona (con il titolo Liber trium fratrum de geometria oppure Verba filiorum Moysi), gli autori presentano una risoluzione per ciascuno dei due problemi.
Le due rette medie proporzionali
Per quanto riguarda il problema delle due rette medie proporzionali, nella prop. 16 del trattato dei Banū Mūsā si trova il metodo che Eutocio riporta nel suo commento al Della sfera e del cilindro di Archimede, affermando che Eudemo lo attribuisce ad Archita (IV sec. a.C.). Quanto a loro, i Banū Mūsā attribuiscono il metodo, che si basa sull'intersezione di un cilindro retto, di un toro e di un cono retto, a Menelao. Nella prop. 17 essi elaborano un'altra soluzione, questa volta di natura meccanica, basata su uno strumento diverso da quello che Eutocio attribuisce a Platone. I lavori dei Banū Mūsā segnano la prima tappa negli studi sulle costruzioni geometriche, durante la quale i matematici s'interessano da vicino all'eredità greca e cominciano a sviluppare ricerche all'interno di quel quadro metodologico, aprendo la strada all'affermazione delle soluzioni per intersezioni di coniche e allo sviluppo di un numero notevole di studi in questa direzione.
Nella prima metà del X sec. Abū Ǧa῾far al-Ḫāzin riprende la risoluzione di Nicomede (attivo forse a Pergamo, nel II sec. a.C. ca.) mediante la concoide, che il geometra greco aveva ideato assieme a uno strumento per tracciarla. Secondo una testimonianza di al-Ḫayyām, al-Ḫāzin è il primo ad applicare le sezioni coniche alla risoluzione di un'equazione di terzo grado; egli è quindi uno dei primi rappresentanti della duplice tradizione cui abbiamo fatto riferimento. Propone una risoluzione della neũsis di Nicomede che fa uso dell'intersezione di un'iperbole e di un cerchio. A questo scopo egli utilizza la prop. 4 del Libro II delle Coniche, che permette di costruire l'iperbole a partire da un punto e dagli asintoti, e anche un'altra proprietà dell'iperbole che deriva dalla prop. 12 dello stesso libro di Apollonio, che egli cita. Nel presentare questa costruzione, al-Ḫāzin menziona esplicitamente i miglioramenti dovuti al metodo 'geometrico' (cioè mediante le coniche) rispetto al metodo 'strumentale' (cioè mediante neũsis).
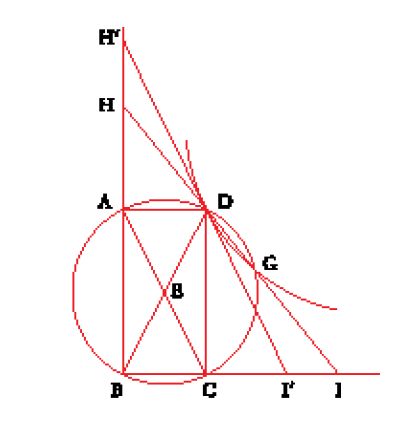
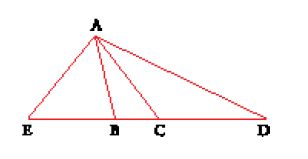
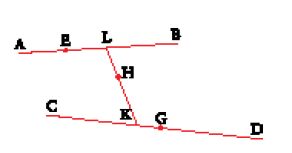
In un altro testo al-Ḫāzin propone nuovamente una risoluzione basata sull'intersezione di una circonferenza e di un'iperbole; questa volta però il metodo è diretto, senza neũsis. La redazione contiene soltanto la sintesi del problema (fig. 2). Se AB e BC sono le due rette date, di cui si cercano le due medie proporzionali, si costruisca il rettangolo ABCD di centro E e la circonferenza circoscritta. L'autore considera allora l'iperbole passante per D e di asintoti BA e BC e cerca di costruire un punto G, comune a questa curva e alla circonferenza, sia con un metodo geometrico sia con uno meccanico, senza dare precisazioni, ma non prima di aver definito il lato retto e il diametro dell'iperbole. Tracciando la retta passante per D e G, si ottengono sugli asintoti i punti H e I che determinano le rette cercate e tali che
Nella dimostrazione di al-Ḫāzin intervengono uguaglianze di rapporti in triangoli simili, come pure la proprietà secondo la quale IG=DH; essa corrisponde alla prop. 8 del Libro II delle Coniche, che egli non cita accontentandosi di precisare che aveva già dimostrato questa proprietà in precedenza.
In un testo attribuito a un certo Abū Bakr al-Harawī si trova un metodo simile a quello di al-Ḫāzin che abbiamo appena descritto; si tratta di un autore forse contemporaneo di al-Ḫāzin, se è lo stesso matematico e astronomo del quale parla al-Bīrūnī nel Kitāb Taḥdīd nihāyāt al-amākin li-taṣḥīḥ masāfāt al-masākin (Libro sulla determinazione delle coordinate delle località per rettificare il valore delle distanze fra loro) e che osserverà l'altezza del Sole nel 959. Questo metodo si basa sugli stessi principî, ma nella prima parte l'autore non precisa come costruire l'iperbole. All'inizio della dimostrazione egli si appoggia però al Libro II delle Coniche per affermare che IG=DH. Il metodo sarà ripreso nel XIII sec. da Naṣīr al-Dīn al-Ṭūsī, che completerà la dimostrazione dell'esistenza del punto di intersezione (oltre a D) tra la circonferenza e l'iperbole.
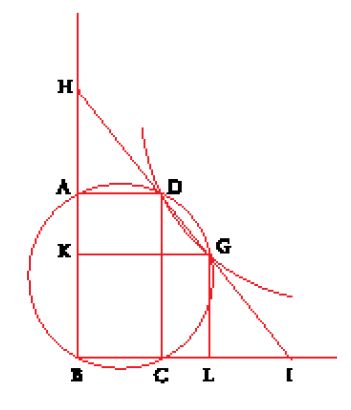
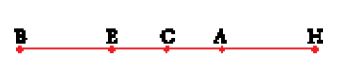
Questi tre testi presentano una soluzione 'completa' del problema così com'era stato studiato nell'Antichità da Apollonio, Filone di Bisanzio ed Erone di Alessandria. Questi ultimi costruivano il rettangolo avente per lati le due rette date, ma ottenevano poi i punti K e H utilizzando una riga mobile rotante intorno al punto B (modifichiamo qui le notazioni dei vari testi per poterci riferire alla fig. 3) e stabilendo condizioni opportune in ciascuno dei tre metodi. Pappo attribuisce ad Apollonio una risoluzione del problema per intersezione di coniche, ma senza altre precisazioni, in un passo che forse è un'interpolazione.
Sempre nel solco della stessa tradizione, al-Qūhī (seconda metà del X sec.) propone una risoluzione che segna una piccola rottura. Egli introduce le proiezioni sugli asintoti del punto G (fig. 3); le due medie proporzionali sono allora GK e GL (fa vedere che GK=CI e che GL=AH); la conclusione diventa
A partire dalla prop. 8 del Libro II delle Coniche, al-Qūhī dimostra la prima delle due uguaglianze, mentre un'applicazione della successiva prop. 12 del medesimo libro di Apollonio gli fornisce direttamente l'uguaglianza GK∙GL=AD∙DC, che dà subito
Questo cambiamento ha come conseguenza il fatto di rendere meno pesante la dimostrazione e apre la strada a un'interpretazione analitica (equazione dell'iperbole rispetto agli asintoti), analoga a quella moderna.
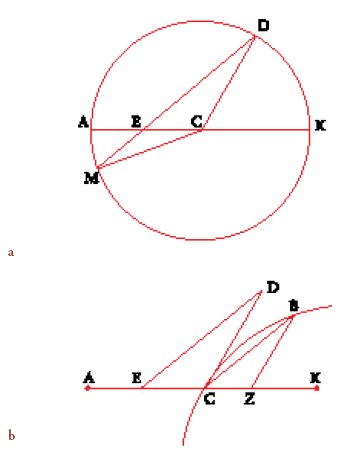
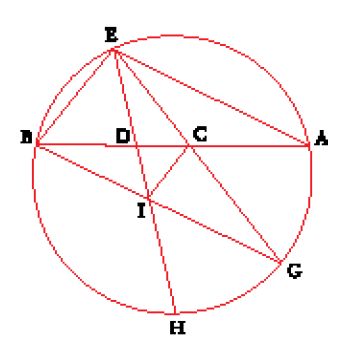
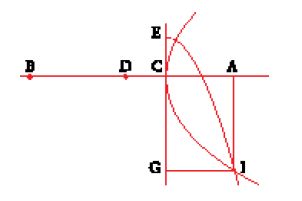
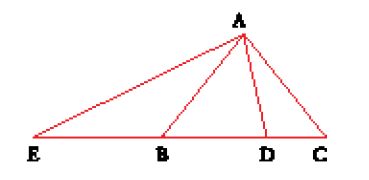
Nei frammenti che ci sono pervenuti del Kitāb al-Istikmāl (Libro del perfezionamento), attribuito con quasi assoluta certezza a Ibn Hūd al-Mu᾽taman, re di Saragozza tra il 1081 e il 1085, si trovano quattro costruzioni relative al problema delle due medie proporzionali. Vi si riconoscono i due metodi attribuiti a Menecmo, l'uno per intersezione di una parabola e di un'iperbole, l'altro per intersezione di due parabole; al-Ḫayyām riprenderà questo secondo metodo in uno dei lemmi necessari ai fondamenti teorici della Maqāla fī 'l-ǧabr wa-'l-muqābala (Trattato sull'algebra). Vi si trova anche, come quarto metodo, quello utilizzato da al-Ḫāzin e da al-Harawī, espresso nei termini di quest'ultimo (eccezion fatta per la menzione del centro del rettangolo). Quanto al terzo metodo, che consiste nell'intersezione di una circonferenza e di una parabola, ci è pervenuto solo in quest'opera, cosa che auto rizza Jan Hogendijk (1992-94) ad attribuirla a Ibn Hūd stesso. La costruzione comincia come nel metodo della circonferenza e dell'iperbole (fig. 4). Si costruiscono AB e BC tra loro perpendicolari e si traccia il cerchio circoscritto al triangolo ABC. Ibn Hūd pone BC>AB e definisce la parabola di asse CB, vertice C e parametro CB. Essa incontra il cerchio in un punto D (diverso da C). Se si traccia l'ordinata DE, si ha che ED ed EC sono le due rette medie proporzionali.
La dimostrazione si basa su alcune uguaglianze di rapporti tra triangoli simili e sul symptoma della parabola. I quattro metodi presentati da Ibn Hūd sono matematicamente legati: nei tre metodi che ne fanno uso la parabola è la stessa, e anche l'iperbole utilizzata in due dei quattro metodi è la stessa. Allo stato delle nostre conoscenze non possiamo però dedurne conseguenze sul piano storico.
La trisezione dell'angolo
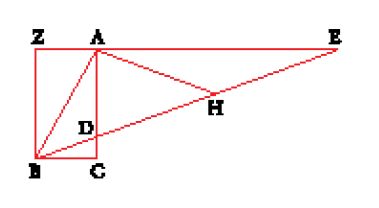
Nella Collezione matematica, Pappo ricorda che i primi geometri cercavano di dividere l'angolo in tre parti uguali con metodi piani (cioè con riga e compasso) perché non sapevano utilizzare le coniche. E fallivano, com'è ovvio, perché il problema è solido. Pappo fa notare inoltre che gli Antichi avevano ridotto il problema alla neũsis seguente: tracciare una retta passante per un punto dato e sulla quale due rette date stacchino una lunghezza assegnata. Enunciamo il problema con precisione (fig. 5): dato un rettangolo ABCD, tracciare una retta da A che tagli CD in E e il prolungamento di BC in Z, in modo che EZ abbia la stessa lunghezza di una data retta M. Pappo comincia risolvendo il problema mediante l'intersezione di un cerchio e di un'iperbole (Libro IV, prop. 31). La soluzione è data dal punto H, intersezione dell'iperbole passante per D, e di asintoti BA e BZ, e del cerchio di centro D passante per il punto K, situato sul prolungamento di AD e tale che DK=M. Basta allora proiettare H su BC parallelamente ad AB per ottenere Z. Pappo fornisce analisi e sintesi di questo problema.
Nella seguente prop. 32 egli dimostra come questa neũsis permetta di trisecare l'angolo. Sia ABC l'angolo in questione; supponiamo dapprima che sia acuto (fig. 6). Si costruisce il rettangolo ACBZ e si traccia la retta BE, dove E è sul prolungamento di ZA in modo che si abbia DE=2AB, dove D è il punto di intersezione delle rette BE e AC.
Questa costruzione è un caso particolare della proposizione precedente; Pappo mostra allora, nella sintesi, che l'angolo DBC è un terzo di ABC. Considera poi il caso in cui l'angolo ABC sia retto, caso in cui basta costruire un triangolo equilatero, poi quello in cui ABC sia ottuso, che egli risolve considerando l'angolo come somma di un angolo retto e di uno acuto. Nella successiva prop. 33 egli ritorna all'inizio della risoluzione della neũsis e riprende il problema della costruzione di un'iperbole a partire da un punto e dagli asintoti. Il problema è trattato da Apollonio, che ne dà la sintesi nella prop. 4 del Libro II delle Coniche. Pappo espone un'analisi (che poggia sulla prop. 3 del Libro II delle Coniche) e quindi una sintesi, equivalente a quella di Apollonio.
Il metodo descritto da Pappo nella Collezione matematica si ritrova in un testo attribuito a Ṯābit ibn Qurra, nel quale l'ordi ne delle diverse fasi è leggermente modificato. Ṯābit comincia infatti dove Pappo finisce, cioè con la costruzione dell'iper bole. Inoltre, espone solamente la sintesi, ma negli stessi termini, vale a dire quelli di Apollonio. Il problema della neũsis è trattato soltanto nella sintesi, che è simile a quella di Pappo. La trisezione dell'angolo è espressa in modo più succinto; non viene data la costruzione del rettangolo ACBZ ma la proiezione ortogonale di A su BC nel punto D. Infine, per l'angolo ABC non si distinguono i tre casi acuto, retto e ottuso.
In un'altra opera, che porta questa volta come autore uno dei Banū Mūsā, Aḥmad, ma la cui attribuzione è dubbia, ritroviamo il modo di procedere precedente: si comincia cioè con la costruzione di un'iperbole a partire dagli asintoti e da uno dei suoi punti. L'autore non dà dimostrazioni, accontentandosi di rimandare laconicamente alla dimostrazione di Apollonio. Ritroviamo poi la costruzione di Pappo, quella della trisezione vera e propria, e non quella di Ṯābit ibn Qurra. L'autore precisa, analogamente a Pappo, che in questa costruzione l'angolo è acuto. Osserva poi che il caso dell'angolo retto è facile (non lo tratta) e termina con l'angolo ottuso, proponendo due metodi. Il primo è quello esposto da Pappo; il secondo consiste nel prendere la metà dell'angolo ottuso, che è un angolo acuto, trisecarlo secondo il metodo precedente e prendere il doppio della parte ottenuta.
Alla fine del trattato già menzionato sull'area delle figure piane e sferiche, i Banū Mūsā presentano un'altra soluzione, del tutto indipendente dal metodo che abbiamo appena descritto, perché basata su una curva trascendente. Nella prop. 18 si trova infatti un procedimento ingegnoso che permette di descrivere un arco di concoide di cerchio. Questo metodo potrebbe essere stato ispirato dalla prop. 8 del Libro dei lemmi, un'opera attribuita senza certezza ad Archimede, in quanto essa può suggerire l'idea della concoide di cerchio e permettere così di riportare il problema della trisezione a una neũsis in modo abbastanza naturale (anche se questo non viene fatto nella proposizione detta). Tuttavia, anche se il Libro dei lemmi ci è pervenuto nella traduzione araba di Ṯābit ibn Qurra, nulla ci autorizza ad affermare che i Banū Mūsā l'abbiano utilizzata. Vi è poi una differenza importante, di carattere tecnico: essi utilizzano l'arco di concoide interno al cerchio, mentre nei Lemmi la neũsis si può risolvere mediante l'arco di concoide esterno al cerchio.
Nella prima metà del IX sec. l'impegno è quindi volto a riprodurre e a migliorare i metodi di epoca ellenistica che poggiavano su una neũsis, risolta mediante coniche o curve trascendenti. Dall'età ellenistica sono anche pervenuti due metodi di risoluzione dello stesso problema, questa volta senza ricorrere a una neũsis, e cioè due costruzioni ottenute direttamente a partire dalle sezioni coniche. Pappo ci rivela questi metodi, che si basano sull'intersezione di una circonferenza e di un'iperbole che egli chiama 'luogo solido', nel Libro IV della Collezione matematica, subito dopo il primo metodo che abbiamo descritto sopra (prop. 34). Questi due metodi diretti, senza neũsis, si applicano sia ad angoli acuti sia ottusi, cosa che non succedeva con il primo metodo.
Nella seconda metà del X sec., al-Siǧzī ci lascia una testimonianza importante sulle ricerche del tempo riguardanti la trisezione dell'angolo. Egli sostiene che tra gli studiosi antichi e moderni due soltanto hanno risolto il problema: Ṯābit ibn Qurra e al-Qūhī. Franz Woepcke (1851) poté quindi affermare, sulla base del trattato di al-Siǧzī nel suo complesso e della riconosciuta serietà del suo autore, che se certe fonti greche sulla trisezione dell'angolo erano note nel IX sec., non lo erano più un secolo dopo. Al-Siǧzī riporta il principio su cui poggiano i metodi dei due studiosi, riassumendo anche i metodi di numerosi contemporanei: Abū 'l-Ḥasan al-Harawī, al-Bīrūnī (che fornisce tre proposizioni) e al-Ṣāġānī. Egli stesso proporrà una costruzione che permette di dimostrare tutte le altre, compresa un'antica costruzione ottenuta mediante una neũsis, risolta utilizzando una riga mobile, che non è altro che la neũsis che si può ottenere a partire dalla già citata prop. 8 dei Lemmi. In quest'ultimo caso, al-Siǧzī rifiuta la soluzione per neũsis e precisa che occorre dimostrare questa proposizione mediante la geometria fissa, cioè per mezzo delle coniche.
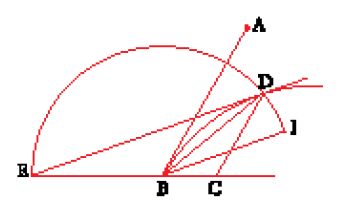
Il metodo esposto da al-Qūhī si fonda sull'intersezione di una circonferenza e di un'iperbole, ma è indipendente dai metodi che si trovano in Pappo. Per trisecare l'angolo dato ABC, al-Qūhī costruisce un'iperbole equilatera di vertice B, diametro BE e nella quale l'angolo delle ordinate con il diametro è uguale all'angolo ABC dato. Costruisce poi la circon ferenza di centro B e raggio BE, che taglia l'iperbole in D: l'angolo ABD vale allora un terzo dell'angolo ABC (fig. 7).
L'autore espone dettagliatamente l'analisi e la sintesi, mettendo da parte in un primo tempo il caso dell'angolo retto. La dimostrazione poggia su calcoli di angoli, sull'uguaglianza dei rapporti in triangoli simili e sulla prop. 21 del Libro I delle Coniche, che stabilisce, con le notazioni della figura, la relazione
qui tale rapporto vale 1 perché l'iperbole è equilatera. Cono sciamo altre versioni che riassumono il metodo di al-Qūhī, nelle quali la circonferenza non compare (ms. Aya Sofya 4830, f. 182r-v). Esse si limitano alla sintesi, in cui si costruisce l'iperbole (caratterizzandola nello stesso modo della prima versione) e si considera poi uno dei punti D della curva tale che la retta BD sia uguale al lato retto. La costruzione prende così la forma di una neũsis: inserire una retta BD di lunghezza data tra l'iperbole e il punto B. Ritroviamo questo stesso metodo in un breve testo anonimo posto in appendice al Fī tamām kitāb al-Maḫrūṭāt di Ibn al-Hayṯam e in un altro opuscolo anonimo, che fa parte della collezione di manoscritti copiata da al-Siǧzī negli anni 969-970 e che si trova a Parigi (BN, ar. 2457).
Torniamo ora al trattato di al-Siǧzī sulla trisezione dell'angolo. L'autore enuncia una proposizione di cui rivendica la scoperta e a partire dalla quale dimostra tutte le altre proposizioni dei contemporanei (fig. 8a): dato l'angolo KCD, si prenda un punto A sul prolungamento della retta CK, dal lato di C, tale che CA=CD. Si tracci da D una retta DE in modo che si abbia la relazione: DE∙EC+EC2=CD2. L'angolo CDE è allora uguale a un terzo dell'angolo dato KCD. Infatti, se si considera il cerchio di centro C e raggio CA, si ha CD2=AC2=EC2+AE∙EK=EC2+DE∙EM e dunque, per la re la zione precedente, EC=EM. Ne segue DEC=2EMC=2EDC e poiché DCK=DEC+EDC, l'angolo EDC è un terzo dell'angolo KCD di partenza.
Per ottenere il punto E (fig. 8b) al-Siǧzī costruisce un'iper bole equilatera di vertice C il cui diametro trasverso è uguale a CA e l'angolo delle ordinate con questo diametro è uguale all'angolo dato KCD. Determina un punto B dell'iperbole tale che CB=CD e costruisce poi la parallela a CB passante per D, che taglia la retta CA in E; si ha DE∙EC+EC2=CD2. Come nelle versioni che riassumono la soluzione di al-Qūhī, il problema è espresso come una neũsis, nel senso che il cerchio di centro C è sottinteso, anche se è esplicito nella prima parte del metodo che consiste nel dare la soluzione della trisezione a partire dal punto E. La costruzione del punto B è esattamente la stessa di quella di al-Qūhī, ma la differenza ri siede nel modo in cui viene sfruttata; al-Siǧzī basa la dimostrazione sulla costruzione del punto E, ed è questa costruzione che gli permette di dimostrare la validità degli altri metodi di trisezione dei quali era a conoscenza.
Nella prima metà dell'XI sec., Ibn al-Hayṯam, il matematico con il quale si concludono le due tradizioni che fanno riferimento ad Archimede e Apollonio, nel corso della sua descrizione di due delle quattro costruzioni diverse dell'ettagono regolare, sottolinea che tale problema si può ricondurre a quello della trisezione dell'angolo. Nella prima, la costruzione di un triangolo isoscele con angoli alla base che siano il triplo dell'angolo al vertice porta alla trisezione di uno degli angoli alla base e la soluzione si ottiene per intersezione di due iperboli, definite entrambe da un punto e dagli asintoti. Nella seconda, il triangolo da costruire è anch'esso isoscele, ma ora gli angoli alla base sono i due terzi dell'angolo al vertice, ed è l'angolo al vertice che viene diviso in tre parti uguali; anche qui il problema è risolto per intersezione di due iperboli definite da un punto e dagli asintoti. Quanto sopra ci porta direttamente all'argomento del paragrafo seguente.
La costruzione dell'ettagono regolare
Il punto di partenza delle ricerche del X sec. sulla costruzione dell'ettagono regolare inscritto in un cerchio è un testo, attribuito ad Archimede, nel quale il problema viene ridotto a un lemma, una parte del quale non è dimostrata ma data per acquisita. Nel lemma (fig. 9) si deve costruire una divisione di una retta (G,A,K,B) in modo tale che AB∙KB=GA2 e GK∙AK=KB2. Questa divisione ci fornisce il primo esempio di una serie di divisoni della retta, adoperate come relazioni che svolgono il ruolo di calcoli geometrici in questo contesto: la chiameremo 'divisione di tipo I'.
Per ottenere questa divisione si procede nel modo seguente. Sia ABCD un quadrato il cui lato BA viene prolungato nella direzione di A fino al punto E. Occorre allora disporre una riga con un'estremità in D in modo che i triangoli GAH e CID siano di uguale area e la riga tagli EA in G, BC in I e AC in H. Il punto K si ottiene tracciando la parallela ad AC passante per I. La posizione della riga, che assicura l'uguaglianza dei triangoli, non viene giustificata. Il lemma è in effetti una sorta di neũsis per costruire la divisione voluta. Si tratta di una soluzione che i matematici del X sec. giudicheranno non completamente dimostrata, e ciò li spingerà a riprendere lo studio del problema.
Una volta ammessa la posizione della retta DG, la dimostrazione del lemma viene fatta a partire dall'uguaglianza dell'area dei triangoli; essa implica CD∙IL=GA∙AH, da cui
Ma i triangoli rettangoli GAH, GKI e ILD sono simili e da questa similitudine si trae un certo numero di uguaglianze di rapporti. Si ottiene
,
da cui segue la prima uguaglianza cercata: AB∙KB=GA2. D'altra parte,
,
ma IL=LC=AK e KI=KB, da cui
,
che dà la seconda uguaglianza: GK∙AK=KB2. L'autore aggiunge, alla fine del lemma, che sussistono le seguenti di suguaglianze: GA>AK e KB>AK.
Dopo questo lemma, troviamo la sintesi della costruzione dell'ettagono a partire da un segmento AB (fig. 10) diviso dai punti C e D in modo che la divisione (A,C,D,B) sia di tipo I, analoga a quella del lemma. Ma in questa seconda proposizione si costruisce la divisione (A,C,D,B) nella quale sono dati i punti estremi A e B, e non C e B come richiederebbe il lemma. Vi è dunque un'incoerenza tra le due proposizioni. Sia E tale che CE=AC e DE=DB, e si consideri il cerchio circoscritto al triangolo AEB. Prolungando le rette EC ed ED fino al cerchio si ottengono i punti G e H; basta allora dividere in due parti uguali gli archi AE e BH per ottenere i sette vertici dell'ettagono regolare inscritto nel cerchio.
Questo testo pone problemi di autenticità. È menzionato da al-Nadīm, biobibliografo del X sec., nell'elenco dei lavori di Archimede noti in arabo, ma la sola versione che ci è pervenuta fu copiata nel XVIII sec. a partire dalla versione araba di un trattato sulla costruzione dell'ettagono attribuito ad Archimede. Nel Kitāb ῾Amal al-dā ᾽ira al-maqsūma bi-sab ῾at aqsām mutasāwiyya li-Aršimīdis, tarǧamat Abī 'l-Ḥasan Ṯābit ibn Qurra al-Ḥarrānī (Libro di Archimede sulla costruzione del cerchio suddiviso in sette settori di identica area, traduzione di Ṯābit ibn Qurra) l'attribuzione della traduzione, riportata nel titolo, non è confermata in altre fonti. Nella versione del XVIII sec. sono presenti gli abituali interventi matematici del copista, Muṣṭafā Ṣidqī. L'esame del testo rafforza il dubbio; infatti, delle diciotto proposizioni che lo compongono, soltanto le ultime due, la cui continuità logica presenta una lacuna, riguardano la costruzione cercata. A partire dalla testimonianza contenuta nei trattati dei matematici del X sec. che studiarono il lemma di Archimede, Roshdi Rashed (2000b) conclude che all'epoca esisteva un testo sull'ettagono regolare attribuito ad Archimede, la cui versione è diversa da quella copiata da Muṣṭafā Ṣidqī, perché lo strumento descritto come riga mobile è assente da tutte le citazioni del X secolo. Nulla si può dire del lavoro originale del matematico siracusano, se non che egli si interessava ai poligoni regolari inscritti in un cerchio. E tuttavia, il fatto che il lemma non sia dimostrato non è una buona ragione per non attribuirlo ad Archimede: egli fa così anche altrove, come nella prop. 4 del Libro II dell'opera Della sfera e del cilindro.
Possiamo dire allora, alla stregua dei matematici del X sec., che il problema dell'ettagono regolare fa parte dell'eredità greca, ma si distingue per la sua storia dagli altri problemi studiati in questa sede. La trisezione dell'angolo, la determinazione delle due medie proporzionali, ma anche il lemma di Archimede alla prop. 4 del Libro II del Della sfera e del cilindro, furono argomenti studiati attivamente nel periodo ellenistico (le testimonianze di Pappo ed Eutocio su questo punto sono eloquenti) e ripresi poi con lo stesso interesse a partire dal IX sec. (ricordiamo i Banū Mūsā, Ṯābit ibn Qurra, al-Māhānī). In compenso, dopo Archimede non si conoscono studi sulla costruzione geometrica dell'ettagono regolare prima dell'ultimo terzo del X sec., e ciò malgrado la conoscenza che se ne aveva nel secolo precedente, come dimostra una corrispondenza di Qusṭā ibn Lūqā. L'entusiasmo provocato dallo studio di questo problema nel X sec. si spiega forse con i nuovi interessi che nascono in questo periodo. Sul piano geometrico, il metodo di costruzione per mezzo delle coniche crea un nuovo campo di ricerca nel quale il problema dell'ettagono trova naturalmente il proprio posto, in mezzo ad altri il cui numero non fa che crescere. Sul piano algebrico, alcuni matematici come Abū 'l-Ǧūd si interessano alle equazioni di terzo grado e intendono scriverne la teoria. Il fatto che il nome di Archimede sia associato a questo problema è forse anch'esso una delle cause della vera e propria infatuazione che esso suscitò. Ci sono pervenuti non meno di dodici trattati sull'argomento, scritti in meno di mezzo secolo, e vi si trovano i nomi dei più grandi matematici del periodo: Abū 'l-Ǧūd, al-Siǧzī, al-Qūhī, al-Ṣāġānī, Ibn al-Hayṯam.
Un nuovo aspetto della ricerca scientifica compare in questo periodo: il rapporto con il potere. La posta in gioco è notevole, è legata al mecenatismo, ma anche all'accesso alle corti dei governanti; ciò provocherà quindi un aumento della competizione e susciterà polemiche, riguardanti in particolare le ricerche sull'ettagono regolare, che saranno contrassegnate da una vera e propria disputa tra Abū 'l-Ǧūd e al-Siǧzī, agli inizi degli anni Settanta del X sec., per un problema di priorità e di plagio. Un quarto di secolo più tardi al-Šannī ne scriverà la storia in modo fazioso, riaccendendo così il fuoco della polemica. La ragione di questa disputa risiede in una critica formulata da al-Siǧzī riguardo a una memoria scritta da Abū 'l-Ǧūd nel 968 o nel 969 per la risoluzione del problema dell'ettagono: secondo al-Siǧzī, il metodo sarebbe errato, in quanto l'autore avrebbe confuso due lemmi senza fornire la divisione della retta come aveva annunciato. La memoria di Abū 'l-Ǧūd, purtroppo, è andata perduta e non è quindi possibile giudicare la legittimità di queste critiche.
Rashed (2000b) ha dedicato un'analisi minuziosa alle varie fonti disponibili: le due memorie redatte da Abū 'l-Ǧūd dopo il suo primo lavoro, quella di al-Siǧzī, la versione di al-Šannī, come pure un testo anonimo che riprende uno dei lemmi di Abū 'l-Ǧūd. Dalla sua ricerca risulta che l'accusa di plagio ai danni di un altro matematico, Ibn Sahl, rivolta da al-Šannī ai due autori è ingiusta. Non è stato trovato alcun trattato di Ibn Sahl sull'argomento; forse al-Siǧzī, non riu scendo a correggere l'errore di Abū 'l-Ǧūd, si era rivolto a lui. Ma, al di là di questi giochi di influenze, l'analisi dell'errore che avrebbe commesso Abū 'l-Ǧūd getta luce sulla posta in gioco di queste ricerche, e cioè sul ruolo delle costruzioni e delle sezioni coniche in geometria. Tale conclusione a proposito della polemica sottolinea l'interesse che ha per lo storico una situazione come questa, rivelatasi feconda per la ricerca. Lo studio storico rivela l'esistenza di due gruppi di matematici: uno appunto impegnato nella polemica, che comprende al-Siǧzī, Abū 'l-Ǧūd, al-Šannī e suo malgrado Ibn Sahl; l'altro che raccoglie i matematici che invece non hanno preso parte a scambi di accuse, come al-Qūhī e al-Ṣāġānī. Nell'XI sec. Ibn al-Hayṯam farà una sintesi di tutti questi lavori in una memoria che, completando lo studio di tutti i metodi possibili, segnerà la fine di questa tradizione di ricerca.
Prendiamo ora in esame i vari contributi. Le ricerche sulla costruzione dell'ettagono seguono due direzioni. La prima procede lungo la strada tracciata dal testo attribuito ad Archimede e comprende i lavori nei quali si cerca di costruire la stessa divisione e lo stesso triangolo del lemma di Archimede, prendendo o no in considerazione l'uguaglianza delle aree dei triangoli GAH e CID (fig. 9), ma facendo sempre uso dell'intersezione di coniche; ne fanno parte le due memorie di al-Qūhī, quella di al-Ṣāġānī e il primo trattato di Ibn al-Hayṯam. Questa prima direzione presenta anche una ramificazione data dalla seguente generalizzazione del lemma di Archimede: il quadrato ABCD diventa un parallelogramma, e si cerca la retta DIHG tale che il rapporto tra i triangoli GAH e CID sia uguale a un rapporto dato. Un contributo a questo studio è dato dai lavori di Ibn Sahl, giunti a noi soltanto indirettamente nella sintesi fatta da al-Šannī per l'analisi di Ibn Sahl. Quest'ultimo risolve il problema nel caso in cui il rapporto dato è quello tra i triangoli GAH e CIH e al-Šannī riprende la prima generalizzazione adattando uno dei metodi di al-Qūhī. L'altra direzione di ricerca comprende indagini su divisioni e triangoli diversi da quelli di Archimede. Vi troviamo Abū 'l-Ǧūd, al-Siǧzī, Naṣr ibn ῾Abd Allāh e soprattutto il secondo trattato di Ibn al-Hayṯam, che chiude magistralmente questo capitolo, nel quale l'autore esaurisce tutti i casi possibili legati ai quattro tipi di triangoli, dimostrando che sono i soli. Egli è l'unico a realizzare uno studio di questo genere.
Infatti, in tutti questi trattati la costruzione dell'ettagono è ricondotta a quella di un triangolo inscritto nel poligono. In un ettagono regolare esistono solo quattro tipi di triangoli inscritti. Ciascuno di questi può essere caratterizzato da una terna di interi proporzionali alle misure degli angoli, tutti multipli di π/7: (1,5,1), (1,2,4), (1,3,3) e (3,2,2). A sua volta, la costruzione del triangolo si riporta alla divisione di un segmento di retta. Nell'insieme delle fonti disponibili si contano cinque diverse divisioni, come si vedrà nel seguito. La prima di esse è la già citata divisione di tipo I, quella del lemma di Archimede, che permette di costruire il triangolo (1,2,4) (il triangolo AEB della fig. 10). Tutti i lavori che seguono la prima direzione di ricerca si basano su questa divisione.
Nella sua prima memoria, risalente al 969-970, al-Qūhī riprende quindi il problema della costruzione dell'ettagono regolare in un cerchio dato, seguendo la via tracciata da Archimede. Espone l'analisi e la sintesi, dimostrando così l'intenzione di fornire tutti i dettagli del metodo. Per quanto riguarda l'analisi, egli considera un ettagono inscritto in un cerchio e sceglie tre vertici A, B, C tali che B e C siano conse cutivi e AB=2BC.
Dimostra che ABC=2ACB=4BAC, quindi il triangolo è del tipo (1,2,4); la scelta è la stessa del testo attribuito ad Archimede. Analizza poi la costruzione di questo triangolo prolungando la retta BC da entrambi i lati, fino a due punti D ed E tali che CD=CA e BE=BA.
Dimostra allora che la divisione (D,C,B,E) deve soddisfare le relazioni DB∙BC=BE2 e CE∙EB=CD2, e dunque che è di tipo I. Costruisce la divisione direttamente per mezzo dell'in tersezione di una parabola e di un'iperbole equilatera, senza passare per il quadrato del lemma di Archimede.
Si riconosce qui una delle caratteristiche delle ricerche di questo periodo che abbiamo già sottolineato. Al-Qūhī considera la costruzione basata sul quadrato, che porta all'uguaglianza dei triangoli GAH e CID (fig. 9), un passaggio inutile, in quanto le sezioni coniche si applicano direttamente a partire dalle relazioni della divisione di tipo I.
Nella sintesi egli parte da uno dei segmenti CD della divisione e costruisce una perpendicolare CE tale che CE=CD (fig. 13). Costruisce poi la parabola di asse EC, vertice E e lato retto CD e l'iperbole equilatera di asse CD e vertice C. Considera allora il punto d'intersezione I tra le due coniche, punto noto a partire dalla grandezza CD; tracciando l'ordinata AI si ottengono i punti A e B (ponendo BD=CG). L'autore non studia l'intersezione delle due curve e non spiega perché questo sia il punto da prendere in considerazione (l'altro non permetterebbe di costruire la divisione). Dimostra in compenso che in una divisione di tipo I i tre segmenti della retta sono ciascuno minore della somma degli altri due. Ciò assicura la costruibilità del triangolo (1,2,4) nella sintesi, riportando le lunghezze BD e CA come lati del triangolo di base CD. Ottenuto così il triangolo, non gli resta che costruire nel cerchio dato un triangolo simile mediante una similitudine. Al-Qūhī fonda quindi la sintesi sul segmento CD, che rappresenta il triangolo (1,2,4). Vedremo che Ibn al-Hayṯam tratterà il problema in maniera più completa a partire dalla retta AB da dividere e che ciò l'obbligherà a operare un'omotetia. Poiché il cerchio è dato, l'ultimo passo della costruzione di al-Qūhī richiede una similitudine. È un procedimento caratteristico dell'epoca che si ritrova in tutti gli autori, mentre nel testo attribuito ad Archimede il cerchio è circoscritto a un triangolo. Alcuni anni dopo, al-Qūhī dedicherà una seconda memoria allo stesso argomento. Essa segue esattamente lo stesso sviluppo dell'altra, ma questa volta il triangolo è del tipo (1,5,1) e per costruire la stessa divisione di tipo I vengono utilizzate due iperboli.
Tra questi due trattati di al-Qūhī troviamo il contributo di al-Ṣāġānī, che risale al 970, cioè a meno di un anno dopo la prima memoria di al-Qūhī. Al-Ṣāġānī comincia con l'analisi della costruzione dell'ettagono regolare che porta a un triangolo (1,2,4) e poi a una divisione di tipo I. I due primi passi sono identici a quelli di al-Qūhī; ma poi si ritorna al quadrato ed egli mostra, mediante l'analisi, che la divisione di tipo I si riduce a costruire la retta DIHG per avere l'uguaglianza delle aree dei triangoli GAH e CID (come nella fig. 9). Pone allora il problema della costruzione di questa retta, che risolve per analisi e sintesi grazie all'intersezione di due iperboli. A questo scopo, a partire dal quadrato AFID (fig. 15), egli costruisce i due rami dell'iperbole passante per F e C ‒ dove C soddisfa la relazione FI=IC ‒ e di asintoti AI e ID, e un'altra iperbole passante per I e di asintoti FA e AD. Caratterizza gli asintoti utilizzando le propp. 8 e 11 del Libro II delle Coniche di Apollonio. L'intersezione G di un ramo della prima iperbole con la seconda iperbole permette di costruire il punto B che dà la soluzione.
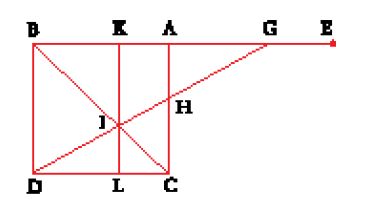
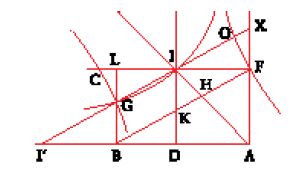
All'inizio dell'XI sec. il problema è ripreso da Ibn al-Hayṯam, che scrive due trattati. Come si è ricordato, la dimostrazione del lemma di Archimede, nel testo disponibile in arabo a partire dal IX sec., presenta una lacuna riguardo alla costruzione della retta DIHG (nel seguito riprendiamo le notazioni della fig. 9) ed è precisamente questa lacuna che Ibn al-Hayṯam si propone di colmare nel primo trattato. Giustifica la soluzione attribuita al geometra dell'Antichità come una scelta deliberata di non far intervenire le sezioni coniche, una spiegazione che sarà ripresa a proposito del lemma non dimostrato di Archimede nella prop. 4 del Libro II del Della sfera e del cilindro, nello stesso modo di al-Šannī. Abbiamo così numerose testimonianze, molto eloquenti, del posto che occupano le coniche nelle costruzioni geometriche nel periodo a cavallo tra i secc. X e XI. Partendo dalla costruzione della retta DIHG nel quadrato ABCD come si trova nel lemma, egli la riporta a una divisione diversa da quella di Archimede, nel modo seguente. Introducendo un nuovo punto L tale che AL=BA (fig. 16), la retta BL, con punto medio A, viene divisa in G in modo che
Ibn al-Hayṯam analizza poi questa costruzione e la riporta all'intersezione di due parabole con lo stesso vertice L, una di asse AL e l'altra avente per diametro una retta LQ inclinata di 45° su AL. Questa soluzione pone però un problema di forma, in quanto il lato retto della parabola di asse AL è definito a partire dal punto G; ciò obbliga, nella sintesi, a dare in anticipo il lato retto e a operare un'omotetia per ottenere la divisione cercata della retta data BL.
Ibn al-Hayṯam non dà la sintesi di questa prima soluzione, ma in compenso ne propone un'altra, della quale fornisce soltanto la sintesi. Egli costruisce direttamente una divisione di tipo I, senza passare per il quadrato, per mezzo dell'intersezione di due coniche (fig. 17). La soluzione è data dal punto N, intersezione della parabola di vertice E, asse EG e lato retto EH (metà della retta EI data all'inizio) e dell'iperbole passante per I e di asintoti HK e HS.
Egli dimostra che le due coniche si intersecano utilizzando una proprietà dell'asintoto e ottiene la divisione (E,H,F,G) di tipo I. Grazie a un'omotetia, che conserva i rapporti di questo tipo di divisione, passa a dividere la retta AB e conclude la sintesi costruendo un triangolo di tipo (1,2,4) e quindi un ettagono nel cerchio dato. Questo secondo metodo è simile a quello utilizzato da al-Qūhī nella sua prima memoria, con la differenza che Ibn al-Hayṯam comincia introducendo la retta AB da dividere, mentre al-Qūhī parte dal segmento CD. In generale, la memoria di Ibn al-Hayṯam s'inserisce nella tradizione di studi dell'ultimo terzo del X sec., tradizione che verrà invece interrotta con il suo secondo trattato. Vi sono altri due testi che stabiliscono la costruzione sulla quale giace l'uguaglianza delle aree dei triangoli GAH e CID (fig. 9), ma con un metodo che non è basato sulla divisione di tipo I: un testo del XIII sec., redatto da Kamāl al-Dīn ibn Yūnus, allievo di Šaraf al-Dīn al-Ṭūsī, che stabilisce direttamente l'equivalenza dei triangoli a partire dall'intersezione di due iperboli, e un testo anonimo.
Veniamo ora alla seconda direzione, diversa da quella che si è sviluppata sulla scia del lemma di Archimede, della ricerca sulla costruzione dell'ettagono regolare. Abū 'l-Ǧūd e al-Siǧzī riconducono la costruzione dell'ettagono a quella di un triangolo del tipo (1,3,3). Abū 'l-Ǧūd per primo, in base a quanto egli stesso dice, introduce una nuova divisione, che diremo 'divisione di tipo II': dividere un segmento AB mediante un punto C tale che
A partire da questa divisione (fig. 18) si può costruire un punto D tale che BD=BA e
Il punto D si trova sull'asse di AC e i triangoli ABD e ACD sono isosceli, del tipo (1,3,3). Mediante l'analisi, Abū 'l-Ǧūd dimostra che un triangolo (1,3,3) si riconduce alla divisione di tipo II di uno dei lati, quindi risolve il problema di questa divisione per intersezione di una parabola e di un'iperbole equilatera. Questa divisione sarà ripresa da al-Siǧzī, che utilizzerà, seguendo Ibn Sahl al quale si è rivolto per aiutarlo, le stesse curve di Abū 'l-Ǧūd.
Abū 'l-Ǧūd concepisce un'altra divisione, la 'divisione di tipo III', che ottiene aggiungendo un punto alla divisione di tipo II: un segmento AB diviso da un punto C nelle condizioni della divisione di tipo II [10], più un punto E tale che BE2=AB∙AC.
Questa divisione è equivalente a quella di tipo I. Infatti, (fig. 19) se (A,C,E,B) è di tipo III e se si prolunga BA di un segmento AH uguale a BE, allora (H,A,C,E) è di tipo I. Abū 'l-Ǧūd associa questa ulteriore divisione alla costruzione di un triangolo (1,3,3).
Nella sua seconda memoria su questo problema, Ibn al-Hayṯam studia tutti i triangoli possibili per costruire l'ettagono, uno dopo l'altro. Egli sarà portato a introdurre due nuove divisioni. Il primo caso è quello di un triangolo di tipo (1,3,3) che egli associa a una nuova divisione, la 'divisione di tipo IV', sconosciuta fino a quel momen to: dividere un segmento AC mediante i punti D ed E in modo che CE2=AC∙CD e CE2=AD∙DE.
La divisione (C,D,A) è di tipo II e il punto E si ottiene a partire da questi tre punti secondo la prima delle due relazioni. A partire da questa divisione di tipo IV si può costruire un punto B tale che BE=EA e CB=CE. I triangoli ABC e BCD sono del tipo (1,3,3). Per ottenere questa divisione Ibn al-Hayṯam procede intersecando due iperboli, delle quali una è equilatera.
Il secondo caso (fig. 21) è quello di un triangolo di tipo (3,2,2), che Ibn al-Hayṯam è il primo a prendere in considerazione. Si ottiene nell'ettagono a partire da vertici non consecutivi (è il solo caso di triangolo in cui nessun lato è uguale al lato dell'ettagono). L'analisi porta a una divisione di tipo III, data da Abū 'l-Ǧūd; anche questa divisione è ottenuta da Ibn al-Hayṯam per il tramite di due iperboli, una delle quali equilatera, e quindi il suo metodo si differenzia da quello di Abū 'l-Ǧūd.
Il terzo caso è quello del triangolo di tipo (1,5,1), la cui analisi porta lo studioso a un nuovo tipo di divisione, la 'divisio ne di tipo V' (fig. 22): dividere un segmento BC mediante due punti D ed E in modo che BE2=BC∙CD e CD2=BD∙DE.
A partire da questa divisione, si può costruire un punto A tale che EA=BE=CA. Ibn al-Hayṯam riesce a ottenere questa divisione a partire dall'intersezione di un'iperbole e di una parabola.
Per finire, l'autore della memoria ritorna sul caso del triangolo (1,2,4) e della divisione di tipo I, da lui trattata nel primo lavoro, ma come abbiamo visto proposta anche da altri. Questa volta però Ibn al-Hayṯam modifica il procedimento: comincia con il dimostrare che questo triangolo si può ottenere a partire da tutti quelli che ha appena studiato. Fornisce quindi l'analisi che permette di ricondurne la costruzione alla divisione di Archimede, che trova utilizzando le stesse curve del caso precedente.
Possiamo allora concludere che in tutti i casi studiati Ibn al-Hayṯam cerca di aprire nuove strade: è un'ulteriore dimostrazione, se ce ne fosse bisogno, che, al di là della costruzione dell'ettagono regolare, oggetto delle ricerche sono proprio le sezioni coniche, nonché i loro rapporti con le costruzioni geometriche, stabiliti attraverso relazioni che svolgono il ruolo di calcoli geometrici (le divisioni delle rette) e che il matematico ricerca in numero sempre maggiore, allo scopo di sistematizzarle. "Ibn al-Hayṯam sembra suggerire che il problema della scelta di una divisione conveniente non ha più importanza. Si può infatti effettuare la costruzione per mezzo di due coniche qualunque di un fascio, del quale sono fissati solo i punti base; ogni scelta di due coniche fornisce due symptomata che determinano una divisione del segmento" (Rashed 2000b, p. 381). Le ricerche sulla costruzione dell'ettagono regolare costituiscono quindi una parte essenziale del capitolo delle costruzioni geometriche basate sulle sezioni coniche, che si formò in quel periodo.
La divisione della retta nel Della sfera e del cilindro di Archimede
Nell'introduzione all'opera succitata, scritta per parte cipare alla polemica sulla costruzione dell'ettagono regolare, al-Šannī menziona la prop. 4 del Libro II del Della sfera e del ci lin dro, nella quale Archimede divide una sfera in due parti, che stanno tra loro in un dato rapporto, ricorrendo a un lemma che permette di dividere il diametro della sfera in un certo modo e che non dimostra. Al-Šannī precisa anzi che il matematico di Siracusa non avrebbe potuto dimostrare questo lemma a partire dai principî della geometria, come nel caso del lemma relativo all'ettagono regolare che abbiamo esaminato in precedenza. Egli non intende certo accusare Archimede di incapacità, ma vuole soltanto dire che Archimede si era limitato ai principî raccolti da Euclide negli Elementi. Una spiegazione che si riallaccia a quella che darà più tardi Ibn al-Hayṯam, e cioè che Archimede aveva appositamente scartato le sezioni coniche dall'opera Della sfera e del cilindro per non confondere i generi. Queste testimonianze traducono la concezione, che emerge alla fine del X sec. e si consolida con Ibn al-Hayṯam all'inizio dell'XI, secondo la quale le costruzioni geometriche ottenute mediante l'intersezione di coniche costituiscono un "corpo di dottrina particolare all'interno della geometria" (Rashed 2000b, p. 422).
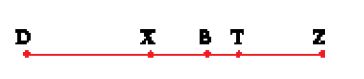
Il lemma utilizzato da Archimede nella citata proposizione del Della sfera e del cilindro può essere enunciato nel modo seguente:
dati due punti B e T su un segmento di retta DZ, dividere il segmento in un punto X tale che
Nessun testo a noi noto riporta una dimostrazione di Archimede di questo lemma, come osservava già Diocle, più giovane di Archimede di sole due generazioni, nel libro sugli specchi ustori. Nel suo commento all'opera di Archimede, Eutocio propone una dimostrazione basata sull'intersezione di una parabola e di un'iperbole. Alla fine del IX sec. il problema sarà oggetto di una traduzione in termini algebrici. Secondo la testimonianza di al-Ḫayyām, al-Māhānī fu il primo a ridurre il problema a un'equazione di terzo grado, risolta poi per mezzo di sezioni coniche da Abū Ǧa῾far al-Ḫāzin nel secolo seguente. Ma la via geometrica non è abbandonata: viene seguita da due autori che nelle loro costruzioni evitano espressamente ogni formulazione algebrica, al-Qūhī e Ibn al-Hayṯam, due importanti rappresentanti della tradizione apolloniana e archimedea già ricordata che contribuirono in modo considerevole, come abbiamo visto, alle ricerche sull'ettagono regolare.
Al-Qūhī enuncia il problema in termini leggermente diversi da quelli di Archimede: dati due segmenti DZ e C, determinare sulla retta DZ, tra D e Z oppure oltre Z, un punto X tale che
Questo enunciato è generale quanto quello di Archimede; esso consiste infatti nel prendere C tale che C3=ZT∙BD2. Il secondo membro è un volume dato, e dunque si può trovare C se si sa risolvere il problema delle due medie proporzionali.
Al-Qūhī esamina insieme i due casi, X interno e X esterno al segmento DZ (fig. 24). Afferma fin dall'inizio che nel primo caso, cioè nelle condizioni di Archimede, C deve essere tale che
Posto DE=C, costruisce il quadrato DEGH, la parabola di vertice Z, asse ZD e lato retto C e l'iperbole passante per G e di asintoti DE e DH. Le due curve si incontrano nel punto I. L'autore caratterizza la parabola tramite il sýmptōma (Coniche, I, prop. 11) IX2=C∙ZX e l'iperbole mediante gli asintoti (Coni che, II, prop. 12), cioè DE∙EG=DK∙KI, o ancora C2=IX∙XD. Trasformando queste due relazioni in uguaglianze di rapporti si ottiene la [13].
Egli prosegue poi lo studio, servendosi del lemma appena dimostrato per risolvere il problema seguente: applicare lungo un segmento dato ZD un parallelepipedo uguale a un solido dato, con un eccesso o un difetto pari a un cubo. Se C è il lato di un cubo equivalente al solido dato, allora il punto X costruito nel lemma precedente fornisce la soluzione, in quanto ZX∙DX2=C3. Generalizza poi il problema in modo che l'eccesso ‒ o il difetto ‒ sia non più un cubo, ma un parallelepipedo di forma nota. Per riprendere un'espressione di Roshdi Ra shed, l'estensione che dà al-Qūhī al problema di Archimede consiste in una sorta di generalizzazione del metodo di applicazione d'area presente nel Libro VI degli Elementi di Euclide alla dimensione 3, che si può di conseguenza chiamare un'applicazione di volume.
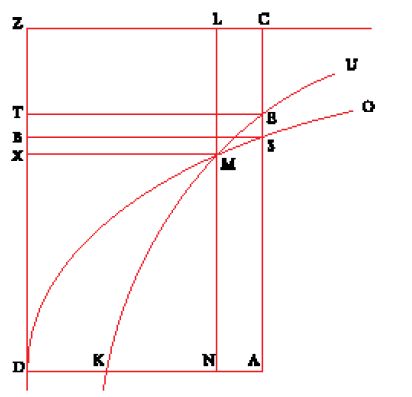
Ibn al-Hayṯam procede in modo diverso rispetto al suo predecessore (fig. 25). Segue strettamente le condizioni poste da Archimede e cerca il punto X all'interno del segmento DZ (ricordiamo che i punti T e B sono dati sul segmento DZ). Costruisce il rettangolo ZCAD tale che ZC=BD, poi traccia la parallela a ZC, passante per T, che taglia CA in E. Ottiene la soluzione intersecando l'iperbole passante per E e di asintoti CZ e ZD con la parabola di asse AD, vertice D e lato retto DB. Egli dimostra poi che le due curve si intersecano necessariamente in un punto che si trova sull'iperbole tra E e K, giu stificando il fatto che il punto E è esterno alla parabola, mentre K è interno, utilizzando a questo scopo le proprietà delle coniche relative ai rami infiniti e alla loro continuità. Il punto di intersezione M viene proiettato ortogonalmente su DZ nel punto X: Ibn al-Hayṯam dimostra quindi che X è tale che
basandosi sulla caratterizzazione della parabola con il sýmptōma MN2=BD∙DN e dell'iperbole con l''equazione' riferita agli asintoti: CE∙ET=ML∙MX.
Anche Eutocio ci ha lasciato una soluzione basata sull'intersezione di una parabola con un'iperbole, ma vi sono molte e importanti differenze tra le due soluzioni. Inizialmente, traducendo in termini algebrici le relazioni che caratterizzano le varie coniche, si vede che le equazioni risolte dai due matematici non sono le stesse. La scelta di Ibn al-Hayṯam di riportare le due curve agli stessi assi gli permette di semplificare la dimostrazione geometrica riguardo al calcolo dei rapporti e di avvicinarsi alla nozione di coordinate dei punti di una curva; ciò è confermato dal fatto che, diversamente da Eutocio, egli esprime le relazioni che caratterizzano le coniche sotto forma di uguaglianza di prodotti di segmenti. Eutocio poi non si preoccupa di dimostrare che le due coniche s'intersecano. Abbiamo già sottolineato che questo fatto è un aspetto dell'attività geometrica del periodo ellenistico. Infine, l'importanza che Ibn al-Hayṯam attribuisce a questo problema è soprattutto collegata alle sue ricerche sul corpus di costruzioni geometriche strettamente connesse con le coniche, corpus che prende forma sempre più chiaramente nella geometria dei primi anni dell'XI secolo. Le intenzioni espresse all'inizio dell'opera non lasciano dubbi: i problemi che fanno intervenire le sezioni coniche costituiscono un genere a parte, e ciò al tempo di Eutocio non era ancora ben stabilito. L'esempio esaminato illustra queste intenzioni e permette di cogliere meglio la profondità delle modifiche apportate alla geometria nel corso del X secolo.
Un'aggiunta al Libro II del Della sfera e del cilindro di Archimede
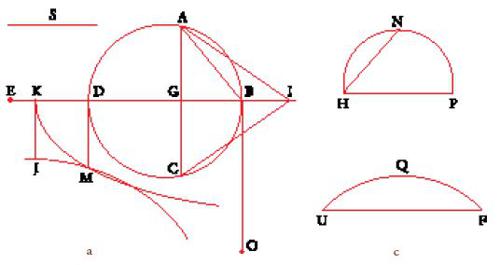
Nel Libro II del Della sfera e del cilindro, Archimede considera due problemi relativi alla costruzione di segmenti di sfera. Dati due segmenti di sfera, costruire un segmento simile al primo e avente lo stesso volume del secondo (prop. 5) e un segmento simile a uno dei due segmenti dati e avente la stessa superficie dell'altro (prop. 6). Nella seconda metà del X sec., al-Qūhī si propose di completare questi due problemi con un terzo, completamente nuovo: dati due segmenti di sfera, costruire un segmento che abbia la stessa superficie di uno dei due e lo stesso volume dell'altro. Questo problema è più difficile degli altri e inoltre richiede il ricorso alle sezioni coniche. Si può affermare che si tratta del problema di costruzione più difficile tra quelli considerati all'epoca; non si conoscono altri contributi alla sua soluzione. L'autore lo risolve per intersezione di un'iperbole equilatera e di una parabola e studia il limite di esistenza della soluzione, ossia il caso in cui le due curve sono tangenti.
Al-Qūhī comincia con il descrivere in maniera dettagliata l'analisi (fig. 26a). Sia ABC il segmento cercato, parte di una sfera di diametro BD, la cui posizione è nota a partire dal punto noto B. L'autore definisce due coni associati a ogni segmento di sfera. Il primo è il 'cono di segmento', che ha lo stesso volume del segmento di sfera, e per definirlo al-Qūhī rimanda alla prop. 2 del Libro II dell'opera di Archimede; il cono di segmento di ABC ha allora per base il cerchio di diametro AC e per vertice il punto I definito da
dove E è il punto che si trova sul prolungamento del diametro a una distanza da D pari al raggio. Il secondo cono è il 'cono di superficie': esso ha per base un cerchio che ha la stessa superficie del segmento e per altezza il raggio della propria base. Così, il cono di superficie per il segmento ABC è il cono di altezza AB e di base il cerchio di raggio AB (secondo le propp. 42 e 43 del Libro I del Della sfera e del cilindro). Questo raggio AB è determinato in quanto è nota la superficie del segmento ABC; di conseguenza, il volume di questo secondo cono, V′=(π/3)AB3, è anch'esso determinato. L'autore considera allora il rapporto k tra il cono di superficie e il cono di segmento, che ha un ruolo fondamentale nel suo ragionamento e che è noto perché sono noti superficie e volume del segmento.
L'analisi porta l'autore al punto M definito da DM=BG, sulla perpendicolare a BD passante per D. Il punto M si trova sulla parabola di vertice K, asse KB e lato retto S.Il vertice K è definito sul prolungamento del diametro della sfera dalla relazione
,
mentre il lato retto S è definito dalla relazione
Il punto M si trova anche sull'iperbole di asintoti BK e BO, tra loro perpendicolari, iperbole tale che il prodotto delle distanze da un suo punto qualunque agli asintoti sia uguale al prodotto BD∙BG=AB2.
Prima d'iniziare la sintesi, al-Qūhī studia l'esistenza di un punto d'intersezione tra la parabola e l'iperbole. Afferma che il rapporto k è maggiore o uguale al valore che corrisponde al caso in cui le due coniche sono tangenti, e studia questo caso dimostrando che G è allora il centro della sfera e ottenendo quindi k≥2/√2.
Passa quindi alla sintesi. Dati i segmenti di sfera HNP (fig. 26b) e UQF (fig. 26c), cerca un segmento ABC che abbia la stessa superficie di HNP (quindi AB=NH) e lo stesso volume di UQF. Dato un punto B sulla retta BE di posizione nota costruisce il punto K tale che
,
e definisce la retta S mediante
Si può allora tracciare la parabola di vertice K, asse BK e lato retto S, secondo la prop. 52 del Libro I delle Coniche, e dopo aver disegnato BO perpendicolare a BK in B e costrui to il punto J tale che BK∙KJ=NH2, si può tracciare anche l'iperbole passante per J e di asintoti BK e BO, secondo la prop. 4 del Libro II dell'opera di Apollonio. Affinché il problema ammetta soluzione, è necessario che le due coniche s'incontrino, diciamo in M. Non resta allora che proiettare ortogonalmente M su BK per ottenere D e dunque il diametro della sfera e, poiché DM=BG, è possibile costruire il segmento ABC. L'autore mostra che il segmento verifica le condizioni del problema.
Infine al-Qūhī discute le soluzioni in funzione del valore di k, ottenendo i risultati seguenti: se k⟨2/√2 il problema è impossibile; se k=2/√2 vi è una sola soluzione e il segmento cercato è una semisfera; se (2/√2)⟨k⟨(2/1) il problema ha due soluzioni, ossia un segmento più piccolo di una semisfera e un altro più grande; se k=2/1 il problema ammette ancora due soluzioni, una è l'intera sfera, l'altra un segmento la cui altezza è "circa un ottavo del diametro della sfera, o piuttosto più grande di questa di una piccola quantità" (Woepcke 1851, p. 113); infine, se 2/1⟨k il problema ha una sola soluzione, un segmento la cui altezza è minore di un ottavo del diametro della sfera. Termina così lo studio completo di un problema non facile dovuto a uno dei più grandi geometri della seconda metà del X secolo.
Le ricerche di analisi geometrica derivanti dai trattati perduti di Apollonio
Oltre al magistrale trattato sulle Coniche, Apollonio è autore di sei trattati, menzionati da Pappo nell'introduzione al Libro VII della Collezione matematica come appartenenti al campo dell'analisi, che sono: la Sezione di ragione, la Sezione di area, la Sezione determinata, i Contatti, le Inclinazioni e i Luoghi piani. Nessuno di questi ci è pervenuto in greco. Abbiamo una traduzione araba anonima della Sezione di ragione fatta verosimilmente nel IX secolo. I biografi e bibliografi arabi ricordano inoltre, tra le opere di Apollonio: la Sezione di area, la Sezione determinata (secondo il biografo e bibliografo al-Nadīm, ci sarebbe stato un tentativo di traduzione in arabo di quest'opera; il primo libro di questa traduzione anonima sarebbe stato corretto da Ṯābit ibn Qurra, mentre il secondo sarebbe rimasto incomprensibile) e i Contatti (opera per la quale non sono menzionati né traduzione né traduttore). I Luoghi piani e le Inclinazioni sono noti soltanto per alcuni enunciati che Pappo sostiene di aver riprodotto nella Collezione matematica; per quanto ne sappiamo, non sono stati tradotti in arabo.
La Sezione di ragione e la Sezione di area
Ecco l'enunciato del problema affrontato da Apollonio nell'opera la Sezione di ragione: se in un piano si hanno due rette infinite di posizioni assegnate, parallele o secanti, se si sceglie un punto su ciascuna di queste e se sono dati un rapporto e un punto non appartenente ad alcuna delle due, come tracciare da questo punto una terza retta che, intersecando le prime due, intercetti su di esse, a partire dai due punti noti, segmenti tali che il loro rapporto sia uguale al rapporto dato? Questo trattato in due libri è dedicato quindi a un solo problema (fig. 27): dato un rapporto k, due rette AB e CD e un punto H non appartenente né ad AB né a CD, E un punto di AB, G un punto di CD, determinare una retta HKL che tagli AB in L e CD in K e tale che
In assenza di una qualche nozione di valore assoluto, Apollonio è costretto a distinguere tutti i casi possibili e tutte le posizioni dei punti sulle rette. Nel Libro I studia allora il caso in cui le due rette sono parallele e poi, in quello delle rette secanti, il caso in cui uno dei due punti dati coincide con il punto di intersezione delle due rette. Il Libro II è dedicato allo studio del caso generale di due rette secanti e due punti dati distinti dal punto di intersezione, che egli riporta a un caso studiato in precedenza. Questo trattato, il solo del quale possediamo una versione araba, sarà per i geometri arabi, e in particolare per Ibrāhīm ibn Sinān (909-946) che lo cita nella sua autobiografia, Risāla fī waṣf al-ma῾ānī allatī istiḫrāǧu-hā fī 'l-handasa wa-῾ilm al-nuǧūm (Epistola sulla descrizione dei significati determinati dalla geometria e dalla scienza delle stelle), un modello di analisi e di sintesi classiche. In effetti, Apollonio, dopo aver attentamente distinto i vari casi, offre per ciascuno di essi un'analisi, che comprende una discussione (detta 'diorisma') dei casi possibili a seconda del valore del rapporto dato (offrendoci in tal modo uno degli esempi di diorisma di maggiore complessità della letteratura matematica ellenistica conosciuta), una sintesi e una dimostrazione del numero di soluzioni.
Ibn Sinān cita questo problema nel trattato Fī ṭarīq al-taḥlīl wa-'l-tarkīb fī 'l-masā᾽il al-handasiyya (L'analisi e la sintesi nei problemi geometrici) per illustrare la necessità di considerare tutti i casi nel corso dell'analisi e lo riprende in al-Masā᾽il al-muḫtāra (Antologia di problemi), ma dandone un'analisi sommaria, senza approfondire proprio lo studio del diorisma. Mostra soltanto, e rapidamente, che il caso generale delle rette secanti si riduce a quello particolare in cui uno dei due punti dati coincide con il punto d'intersezione delle due rette. Quest'ultimo caso viene a sua volta risolto con metodi di analisi geometrica che Ibn Sinān applica in al-Masā᾽il al-muḫtāra; riconducendo il problema alla determinazione di grandezze, egli procede in due tempi: dimostra innanzi tutto, con considerazioni geometriche, che le grandezze incognite sono soluzioni di sistemi di uguaglianze, che egli riporta in un secondo momento, con un cambiamento di grandezze incognite ed eliminazione di incognite tra più uguaglianze, a sistemi classici che ha già risolto geometricamente, in una continua alternanza tra sofisticate manipolazioni di grandezze e costruzioni geometriche. A questo scopo egli fa largo uso delle proprietà delle relazioni del tipo 'maggiore (o minore) rispetto a, secondo un rapporto assegnato', alcune delle quali sono studiate da Euclide nei Dati (deff. 11 e 12, propp. 10-21) e le altre stabilite da lui in persona. Queste definizioni e queste proprietà, utilizzate poco o nulla nella matematica ellenistica, sono formulate da Ibn Sinān in termini di uguaglianze tra grandezze; le proprietà che egli determina gli permettono di operare cambiamenti di incognite del tipo y=kx o y2=kx2 (dove x e y sono lunghezze e k un rapporto), e di eliminare un'incognita nei sistemi di tipo kx±k′y=a e mx±m′z=b (dove k,k′,m,m′ sono rapporti e x,y,z,a,b grandezze, lunghezze o superfici). In queste manipolazioni di grandezze e di rapporti Ibn Sinān non esce, contrariamente agli algebristi, dal quadro euclideo della geometria caratterizzato dal rispetto dell'omogeneità delle grandezze nei rapporti, nelle uguaglianze, o nei sistemi di uguaglianze.
Nella seconda metà del X sec. al-Siǧzī, nella Risāla fī 'l-masā᾽il al-muḫtāra (Epistola sull'antologia dei problemi), riporta un'analisi del problema della Sezione di ragione e la attribuisce al geometra Abū Sahl al-Qūhī, che riduce il caso generale al caso particolare nel quale uno dei due punti dati coincide con il punto d'intersezione delle due rette (analisi che è esattamente quella di Apollonio), ma soltanto in un caso che non comporta alcun diorisma. Al-Siǧzī presenta anche una sintesi (quella di Apollonio) nel caso particolare in cui uno dei due punti dati coincide con il punto d'intersezione di due rette, sempre in una configurazione che non comporta diorisma. Utilizza poi questo risultato per risolvere il problema di 'dividere un triangolo ABC in due triangoli dei quali è noto il rapporto tra le aree'.
La Sezione di area ci è nota soltanto per quel che ne dice Pappo, il quale enuncia il problema nei termini seguenti: "Tracciare da un punto dato una retta che intercetti su due rette di posizioni assegnate, e ciò fino ad alcuni punti dati su queste rette, dei segmenti che comprendano un'area equivalente a un'area data" (p. 481). Si tratta in pratica dello stesso problema del trattato precedente, che si suddivide nello stesso numero di casi, nel quale ora si richiede semplicemente che sia assegnato non il rapporto tra rette, ma il loro prodotto. Anche Ibn Sinān, in al-Masā᾽il al-muḫtāra, dà un'analisi di questo problema (con i metodi di analisi geometrica che abbiamo appena ricordato) senza attribuirla ad Apollonio, nel caso in cui le due rette date s'intersecano in un punto O. E ciò dapprima nel caso in cui uno dei punti dati è O stesso, dimostrando poi, con un metodo che s'ispira a quello applicato da Apollonio nella Sezione di ragione, che il caso generale si riconduce a questo caso particolare.
La Sezione determinata
Il testo di Pappo, la nostra sola fonte su questo problema, non è affatto chiaro: "Dividere in un punto una retta illimitata, in modo tale che il quadrato costruito su una delle rette comprese tra il punto e alcuni punti dati su tale retta, o il rettangolo incluso tra le rette ottenute, abbia un rapporto assegnato o con il quadrato di una di queste rette [o con il rettangolo costruito su una di queste rette e un'altra retta data altrove] o con il rettangolo costruito su due rette poste da un lato qualunque dei punti dati".
Siano dati quattro punti A,B,C,D allineati; si tratta quindi di determinare un punto P della retta ABCD tale che
È verosimile che Apollonio, nei due libri di questo trattato, abbia studiato tutte le configurazioni e tutti i possibili casi particolari del problema (che in generale si riduce a un'equazione di secondo grado, o piuttosto a un problema di applicazione di aree) e abbia discusso il numero di soluzioni in funzione del rapporto assegnato k, in vista di future applicazioni.
Si trova un'eco dei problemi della Sezione determinata nel Libro III del trattato di Ṯābit ibn Qurra Kitāb fī ta᾽līf al-nisab (Libro sulla composizione dei rapporti): egli risolve i problemi [22 b, c, d] in casi particolari che non richiedono discussione e mostra, mediante considerazioni metriche, che allora AP, BP e CP sono noti. Utilizza questo risultato per dimostrare che, quando un rapporto a/b è composto dei rapporti c/d ed e/f, allora: se il rapporto a/b è noto, assieme a una delle quattro grandezze c, d, e o f, e se anche il rapporto di due delle tre grandezze rimanenti è noto, insieme alla somma o alla differenza della terza grandezza e una delle prime due, allora le tre grandezze rimanenti sono determinate; se il rapporto a/b è noto, assieme a una delle quattro grandezze c, d, e o f, e se le somme o le differenze delle tre grandezze restanti sono note, allora le tre grandezze restanti sono determinate. Ibn Sinān in al-Masā᾽il al-muḫtāra risolve anche il caso [22 c] e ne fa un'analisi geometrica (che permette di costruire il punto dato con riga e compasso), in una configurazione che non richiede discussione.
Nella seconda metà del X sec. il matematico al-Qūhī, nel Kitāb Ṣan῾at al-asṭurlāb bi-'l-burhān (Libro sull'arte dell'astrolabio mediante dimostrazione) e nel Fī 'l-birkār al-tāmm (Libro del compasso perfetto) utilizza risultati che afferma di aver ottenuto in un altro trattato, Fī iḥdāṯ al-nuqaṭ ῾alā 'l-ḫuṭūṭ ῾alā nisab al-suṭūḥ (Sulla generazione dei punti sulle rette secondo rapporti i cui termini sono superfici). È possibile che questo trattato, che non ci è pervenuto e nel quale al-Qūhī, secondo le sue stesse parole, avrebbe risolto i problemi [22 b, d, e], ma limitandosi forse a configurazioni particolari, sia stato un tentativo di ricostituzione della Sezione determinata. Nel cap. 2 del Libro II del trattato sull'astrolabio, egli cerca di costruire l'astrolabio a partire dalla proiezione, sul piano dello strumento, di un cerchio parallelo all'orizzonte, dalla distanza del polo di questo cerchio dal polo della sfera e un terzo dato variabile; per risolvere il caso in cui questo terzo dato è il centro della sfera, al-Qūhī deve determinare un punto P che soddisfi [22 e] e, per il caso in cui il terzo dato è il raggio della sfera, un punto P che soddisfi [22 d]. Alla fine del Kitāb Ṣan῾at al-asṭurlāb bi-'l-burhān, in una sorta di allegato che costituisce il cap. 7 del Libro II, l'autore fa un'analisi di queste due proposizioni su una configurazione particolare e senza fornire la discussione. Ibn Sahl, nel suo commento al trattato di al-Qūhī, fornisce la sintesi corrispondente. Inoltre, nel Libro II del trattato che al-Qūhī dedica al compasso perfetto, quando vuole tracciare a partire da questo strumento una parabola dati l'asse, il vertice e il parametro, utilizza un punto P che soddisfa la [22 b] e rimanda semplicemente al trattato perduto senza dare alcuna indicazione sulla dimostrazione o su un'eventuale discussione; in seguito, nello stesso libro, procederà a due riprese nello stesso modo; da un lato, per descrivere un'iperbole, avrà bisogno di un punto P che soddisfi la [22 d], dall'altro lato, per descrivere un'ellisse, utilizzerà la stessa relazione.
Le Inclinazioni
I geometri dell'Antichità ellenistica hanno ricondotto un certo numero di problemi, e in particolare due dei grandi problemi solidi (cioè risolubili per intersezione di coniche), la trisezione dell'angolo e la duplicazione del cubo, a problemi d'inclinazione (neũsis). Ecco come Pappo definisce nella loro generalità questi problemi di neũsis: "Una retta si dice inclinata verso un punto quando prolungata arriva a questo punto […]. Il problema generale [delle Inclinazioni] si enuncia così: date due rette di posizione assegnata, inserire nell'intervallo tra loro una retta di data grandezza che sia inclinata verso un dato punto" (Inclinazioni, p. 501). Questi problemi di neũsis, difficili, non sono in generale risolvibili con riga e compasso (come nel caso dei problemi ai quali si riportano la trisezione dell'angolo e la duplicazione del cubo, i problemi solidi più antichi che abbiamo trattato in precedenza). Quando almeno una delle due curve è una retta, la concoide di Nicomede fornisce per i matematici greci un metodo generale di risoluzione.
Secondo Pappo, Apollonio avrebbe risolto nelle Inclinazioni i casi seguenti (che sono risolvibili con riga e compasso, e sono quindi, secondo la terminologia greca, problemi piani): "Dati in posizione un semicerchio e una retta ad angolo retto rispetto alla sua base [a], o due semicerchi aventi le basi sulla stessa retta [b], inserire nell'intervallo compreso tra queste due curve una retta di grandezza data e inclinata verso l'estremità del semicerchio. Poi, dato un rombo e prolungato uno dei suoi lati, inserire nell'angolo esterno una retta di data grandezza e inclinata verso l'angolo opposto [c]. Poi, dato un cerchio di posizione assegnata, inserirvi una retta di grandezza data e inclinata verso un punto dato [d]" (ibidem, pp. 501-502).
I casi (a), (d) e (c) si troverebbero risolti nel Libro I delle Inclinazioni, mentre l'intero Libro II sarebbe dedicato allo studio del caso (b) (i casi a e d sono relativamente banali). Anche se il trattato non è menzionato dai biografi e bibliografi arabi come facente parte delle opere di Apollonio e di esso non ci resta traccia, i matematici arabi si sono effettivamente posti problemi di questo tipo: al-Siǧzī risolve il problema "il rombo AB (cioè il rombo ACBE) e la retta H sono dati; prolungata CB fino a D, vogliamo tracciare AD in modo che KD sia uguale a H′", e lo fa con un metodo leggermente diverso da quello di Apollonio, almeno secondo quello che i lemmi di Pappo permettono di ricostruire. Al-Siǧzī attribuisce tuttavia ad Apollonio una soluzione del problema "i semicerchi sono sui diametri AB, AC e CB; vogliamo tracciare AD in modo che ED sia uguale a una retta nota" (D sul semicerchio AB, E sul semicerchio BC), senza indicarne però la fonte. Al-Siǧzī generalizza anche il problema al caso di due cerchi che s'intersecano con il punto dato, che è uno dei punti di intersezione. Stando ai lemmi di Pappo, Apollonio avrebbe anche risolto, nel Libro I, il problema delle Inclinazioni nel caso in cui le due rette di cui è data la posizione sono due semirette secanti, e in cui il punto dato si trova sulla bisettrice dell'angolo che esse formano (il lemma di Pappo fornisce il diorisma, cioè la condizione di esistenza della soluzione). Questo problema è analizzato da Ibn Sahl, mentre al-Šannī ne dà la sintesi e discute diverse possibilità. Al-Siǧzī da parte sua, rispondendo a una domanda posta dal matematico Abū 'l-Ǧūd ibn al-Layṯ, fornisce di questo problema sia la propria soluzione sia quella che egli attribuisce ad Apollonio, ma senza menzionare il diorisma.
I metodi di risoluzione di problemi solidi per neũsis saranno abbandonati a partire dal X sec., a vantaggio di metodi di risoluzione delle equazioni di terzo grado, ai quali si riducono mediante metodi geometrici basati su intersezioni di coniche; i problemi di neũsis cadranno dunque in disuso poco a poco. Considerato che i Banū Mūsā già risolvono, nel trattato sull'area delle figure piane e sferiche, il problema della trisezione dell'angolo intersecando una concoide di cerchio e una retta, l'uso di neũsis nel testo molto posteriore prima citato, che figura in appendice al trattato di Ibn al-Hayṯam Fī tamām kitāb al-Maḫrūṭāt e nel quale l'autore anonimo risolve il problema della trisezione dell'angolo per intersezione di una retta e di un'iperbole, non è altro che un vecchio ricordo.
I Luoghi piani
Questo trattato, che i bibliografi arabi non menzionano tra le opere di Apollonio, ci è noto soltanto per quanto riporta Pappo. Esso ha ispirato in modo significativo Pierre de Fermat. L'opera consta di due libri; l'argomento del Libro I, così come è descritto da Pappo, è il seguente: "Se da un punto dato, o da due, si tracciano due rette; se queste si riducono a una sola, o sono parallele, o formano un certo angolo; se sono in un dato rapporto o racchiudono una data area e se l'estremità di una di esse appartiene a un luogo piano di posizione assegnata, l'estremità dell'altra apparterrà anch'essa a un luogo piano di posizione assegnata, dello stesso genere del primo o di un genere diverso e che sarà situato in modo simile al primo rispetto alla retta o in modo opposto" (Luoghi piani, pp. 496-497).
Apollonio studiava dunque in questo trattato quello che Fermat nel XVII sec. interpreterà come immagini di rette e cerchi, di posizioni assegnate, per mezzo di un'omotetia (da un punto dato si tracciano due rette, che costituiscono una sola retta e sono tra loro in un rapporto dato), oppure per mezzo di una traslazione (da due punti dati si tracciano due rette parallele, con lo stesso verso, che sono tra loro nel rapporto di due cose uguali), o di una similitudine diretta (da un punto dato si tracciano due rette che formano un angolo assegnato e sono tra loro in un rapporto dato), o tramite un'inversione (da un punto dato si tracciano due rette che costituiscono una sola retta e determinano un'area data), o infine componendo tra loro queste diverse trasformazioni. A partire dal IX sec. sono stati sviluppati nella geometria araba, indipendentemente dai Luoghi piani, studi dello stesso tipo di quelli di Fermat.
Tra i diversi problemi risolti nel Libro II dei Luoghi piani figurano i seguenti: "Se due rette tracciate da due punti si intersecano, e i quadrati costruiti su queste rette differiscono per un'area data, il punto [d'intersezione] è legato a una retta determinata in posizione […]. Se queste rette sono in un rapporto dato, il punto sarà legato sia a una retta, sia a una circonferenza […]. Se due rette tracciate da due punti s'intersecano, e se il quadrato di una è rispetto al quadrato dell'altra più grande secondo un rapporto tra aree stabilito, il punto sta su una circonferenza determinata in posizione" (ibidem, pp. 498-499).
Pertanto in questi tre problemi del Libro II si tratta di determinare alcune curve di livello; più precisamente, dati due punti A e B: (a) se MA/MB=k (per un dato k), il punto M sta su una retta se k=1 e su un cerchio altrimenti; (b) se MA2−MB2=s (per una data area s), il punto M sta su una retta; (c) se MA2−kMB2=s (k≠1 è un rapporto dato, s una data area), il punto M sta su una circonferenza, eventualmente ridotta a un punto (ovvero non esiste, caso che Pappo non prende in considerazione). L'enunciato di questo terzo problema costituisce inoltre il solo uso conosciuto, nelle matematiche greco-ellenistiche, delle deff. 11 e 12 dei Dati di Euclide prima citate a proposito della Sezione di ragione: 'maggiore (o minore) rispetto a, secondo un rapporto stabilito'.
I matematici arabi si sono posti problemi di questo tipo, in particolare Ibn Sinān, che nel trattato al-Masā᾽il al-muḫtāra si interessa ai casi (a) e (c). Egli riporta innanzitutto tre dimostrazioni del problema (a): un'analisi che attribuisce ad Apollonio (l'unica indicazione che abbiamo di questa dimostrazione), una sintesi dovuta a lui stesso e infine la sintesi di suo nonno Ṯābit ibn Qurra. L'analisi di Apollonio si riduce a dimostrare che il punto H, baricentro del sistema {(A,1),(B,−k2)}, è il centro del cerchio cercato.
Nella sua sintesi, Ibn Sinān dimostra che il cerchio di diametro CD è il cerchio cercato, essendo C e D i baricentri dei sistemi {(A,1),(B,k)} e {(A,1),(B,−k)} rispettivamente. Anche la sintesi di Ṯābit ibn Qurra, diversa da quella di Ibn Sinān, si riduce a dimostrare che il cerchio cercato ha diametro CD, dove C è ancora il baricentro del sistema {(A,1),(B,k)}, mentre D è l'immagine secondo l'inversione di centro C, individuata dal prodotto CA∙CB del punto medio I di AB. In quest'opera si ha pertanto un'esposizione completa dei tre metodi classici di risoluzione di questo problema. Al-Siǧzī dimostra inoltre, nella Risāla fī 'l-masā᾽il al-muḫtāra, un lemma necessario alla risoluzione di (a), attribuendolo ad Apollonio senza tuttavia citare la fonte.
Il problema (a) ha anche ispirato a Ibn al-Hayṯam i trattati Fī 'l-taḥlīl wa-'l-tarkīb (Sull'analisi e la sintesi) e Fī'l-ma῾lūmāt (Sui noti) (nei due casi k=1 e k 1), in una forma differente (prop. 8: se si tracciano da due punti di posizione nota due rette che si incontrano in un punto in modo che esse siano uguali, allora il punto d'incontro si trova su una retta la cui posizione è determinata; prop. 9: se si tracciano da due punti di posizione nota due rette che si incontrano in un punto in modo che sia noto il rapporto dell'una all'altra, e che sia il rapporto della più grande alla più piccola, allora il punto d'incontro sta sulla circonferenza di un cerchio la cui posizione è determinata). In questa forma i problemi diventano teoremi di Fī 'l-ma῾lūmāt e tale formulazione risparmia a Ibn al-Hayṯam la sintesi. Una differenza importante tra Ibn Sinān e Ibn al-Hayṯam sta nel fatto che il primo risolve il problema geometrico dato, mentre il secondo lo trasforma in una ricerca esplicita del luogo dei punti soluzione.
Riguardo al problema (c), esso ha soluzione nel caso k>1 soltanto se
[23] k
AB2≥s
k-1
(il caso k⟨1 equivale a scambiare i ruoli di A e B). Ibn Sinān non menziona il diorisma, ma dà la sintesi di questo problema nel caso AB2≥s (condizione sufficiente), mostrando che allora il luogo dei punti è un cerchio di centro C, baricentro del sistema {(A,1),(B,−k)}, e che se in particolare si ha AB2=s, questo cerchio passa per B. Egli dichiara a proposito di questa dimostrazione di non ricordare la dimostrazione di Apollonio, ma afferma che è diversa dalla sua, mostrando così di averne avuto conoscenza se non altro indirettamente.
I Contatti
Pappo descrive così il problema dei Contatti: "Dati in posizione tre elementi qualunque tra punti, rette e cerchi, tracciare un cerchio il quale, passando per ciascuno dei punti dati (nel caso in cui sono dati i punti), sia tangente a ciascuna delle linee date" (p. 483). Come abbiamo ricordato, quest'opera di Apollonio è citata da alcuni matematici arabi sen-za dare riferimenti e senza dire che era disponibile una traduzione araba. L'argomento ha in ogni caso ispirato, nel X e nell'XI sec., numerosi geometri arabi, così come ispirerà più tardi in Europa, tra gli altri, Viète e Fermat. In primo luogo Ibn Sinān, che afferma di aver composto un'opera sui cerchi tangenti, che purtroppo non ci è pervenuta. Un'eco di questo lavoro si trova in al-Masā᾽il al-muḫtāra, nel quale Ibn Sinān ritorna su alcuni di questi problemi e sulle loro soluzioni. È inoltre presente un'analisi del problema di 'costruire un cerchio tangente a tre cerchi dati', identica a quella che, alla fine del XVI sec., sarà fatta da François Viète: mediante 'dilatazioni' egli riduce il problema, a seconda che i raggi dei tre cerchi dati siano uguali, o solo due lo siano, o siano tutti e tre diversi, ai problemi da lui stesso risolti in precedenza di 'costruire un cerchio passante per tre punti dati', 'costruire un cerchio passante per due punti assegnati e tangente a un cerchio dato', 'costruire un cerchio passante per un punto dato e tangente a due cerchi assegnati', rispettivamente. Quest'analisi è il punto di partenza della soluzione completa che ne dà Ibn al-Hayṯam nel trattato Fī 'l-taḥlīl wa-'l-tarkīb per esemplificare le sue teorie sull'analisi: egli non si accontenta più di dimostrare che il problema si riporta a uno già risolto, ma ne fa l'analisi nei vari casi possibili. Tuttavia, prima di Ibn al-Hayṯam tre matematici contemporanei di Ibn Sinān, e cioè Abū 'l-῾Abbās ibn Yaḥyā, Abū 'l-῾Alā᾽ ibn Abī 'l-Ḥusayn (Ibn Karnīb) e Abū Yaḥyā (al-Māwardī o al-Bāwardī), si sarebbero interessati ai problemi dei Contatti. Purtroppo, conosciamo le loro opere soltanto per quanto riporta lo stesso Ibn Sinān. Il primo dei tre avrebbe svolto un'analisi (della quale Ibn Sinān ricostituisce la sintesi) del problema di tracciare un cerchio tangente a due cerchi dati e a una retta data; la dimostrazione utilizza la proprietà prima citata dei Luoghi piani, secondo la quale il luogo dei punti M tali che AM2−kBM2=s è un cerchio, dove A e B sono due punti distinti dati, k un rapporto assegnato (k≠1) e s un'area data. Abū 'l-῾Alā᾽ e Abū Yaḥyā hanno da parte loro risolto, con dimostrazioni che Ibn Sinān riporta, il problema di tracciare un cerchio tangente a tre cerchi dati, nel caso (non trattato da Ibn Sinān) nel quale il cerchio cercato è interno a uno o due cerchi dati, ma non a tutti e tre; Abū 'l-῾Abbās ibn Yaḥyā, in un testo citato da Ibn Sinān, avrebbe analizzato il problema di tracciare un cerchio tangente a due cerchi dati e a una retta data basandosi sulla proprietà usata anche da Abū 'l-῾Abbās ibn Yaḥyā.
Queste dimostrazioni non sono quelle di Apollonio, almeno per come possono essere ricostruite mediante i lemmi di Pappo. Esse illustrano i metodi di analisi geometrica che si svilupparono nel X e nell'XI sec. a Baghdad, nell'ambiente dei geometri, e che abbiamo ricordato a proposito della Sezione di ragione. Le dimostrazioni di Apollonio, però, almeno nel caso di due di questi problemi, erano forse note in qualche forma ai matematici arabi. Infatti, al-Siǧzī, nella Risāla fī 'l-masā᾽il al-muḫtāra, risolve in due casi il problema (che attribuisce ad Apollonio) di inscrivere in un cerchio un triangolo, del quale due lati passano per due punti dati e il terzo è parallelo alla retta passante per questi due punti; questa proposizione permette ad Apollonio di costruire un cerchio passante per due punti dati e tangente a un cerchio dato. Analogamente, il problema di inscrivere in un cerchio un triangolo i cui lati passano per tre punti di posizione assegnata (problema al quale Apollonio riconduce quello di tracciare un cerchio tangente a tre cerchi dati) sarebbe stato analizzato dal matematico Ibn Sahl; il geometra al-Šannī ne dà la sintesi in tutti i casi.
Anche il problema dei Contatti è suscettibile di generalizzazioni. Così, Ibn Sinān risolve il problema di costruire un cerchio tangente a una retta data e tale che due rette date stacchino due archi di cerchio simili a due archi dati, anticipando il problema che più tardi porrà Blaise Pascal (Promotus Apollonius Gallus) a Fermat: dati tre cerchi, tre punti e tre linee qualunque, determinare un cerchio tangente ai cerchi, passante per i punti e che stacchi sulle linee alcuni archi che comprendano angoli dati. Un altro modo di generalizzare questo problema consiste nell'imporre solo due condizioni al cerchio dato; le soluzioni sono allora infinite e il problema diventa indeterminato. In realtà, si tratta di trovare il luogo descritto dal centro del cerchio. È quanto fa al-Qūhī in un piccolo trattato dal titolo Kitāb Marākiz al-dawā ᾽ir al-mutamāssa ῾alā al-ḫuṭūṭ bi-ṭarīq al-taḥlīl (Libro dei centri dei cerchi tangenti situati su delle linee con il metodo dell'analisi). Egli studia i sei casi possibili e, quando il cerchio cercato deve essere tangente a un cerchio dato, utilizza il metodo della 'dilatazione' ideato da Ibn Sinān per ricondurre, come fa al-Qūhī, questo caso a quello in cui il cerchio passa per un punto dato. Dimostra che il luogo del centro è una retta (nel caso di due punti dati o di due rette assegnate) o una conica: parabola (nel caso in cui sono dati un punto e una retta o un cerchio e una retta) o conica a centro (nel caso di un punto e di un cerchio oppure di due cerchi assegnati). Tale studio è simile a quello delle coniche come luoghi di punti definiti a partire dai fuochi, nel caso di coniche a centro, e dalla proprietà fuoco-direttrice nel caso della parabola.
Nel trattato Fī rasm al-quṭū῾ al-ṯalāṯa (Sul tracciato delle tre sezioni coniche), Ibn Sinān afferma anche che il centro di un cerchio passante per un punto dato e tangente a un cerchio dato sta su un'iperbole (punto assegnato esterno al cerchio dato, cerchio cercato tangente esternamente) o su un'ellisse (punto interno al cerchio dato, cerchio cercato tangente internamente). L'enunciato non è accompagnato da dimostrazioni; c'è invece un rinvio alla proposizione corrispondente delle Coniche di Apollonio.
Le proprietà focali e il tracciato delle coniche
Nella Collezione matematica Pappo considera a due riprese la proprietà fuoco-direttrice delle coniche, che è assente dalle Coniche di Apollonio. La prima volta, nel Libro IV come abbiamo visto, l'autore riporta una soluzione per trisecare l'angolo a partire da un cerchio e da un'iperbole, caratterizzando l'iperbole per mezzo di una relazione che mette in evidenza un'eccentricità uguale a 2. La seconda volta, nel Libro VII, Pappo commenta l'opera di Euclide sui Luoghi di superficie e propone un lemma nel quale dimostra la proprietà fuoco-direttrice per i tre tipi di coniche, allo scopo di caratterizzarle come luogo di punti. Nel caso della parabola, per esempio, Pappo mostra che il sýmptōma è espresso dalla relazione EZ2/(BZ2+ZC2)=1 che permette di determinare l'eccentricità, qui uguale a 1. Dimostra che ogni punto equidistante dal punto C e dalla retta DE sta sulla parabola e, viceversa, che ogni punto della parabola è equidistante da C e da DE.
Le applicazioni agli specchi ustori
La nozione di fuoco e la proprietà fuoco-direttrice per la parabola si trovano già molti secoli prima in Diocle (III-II sec. a.C.), ma con altri scopi. Egli studia, nel trattato sugli Specchi ustori, lo specchio parabolico e la proprietà secondo la quale i raggi incidenti parallelamente all'asse si riflettono in un medesimo punto. È allora indotto a considerare la proprietà fuoco-direttrice per determinare la parabola generatrice dello specchio di rivoluzione. Egli, tuttavia, non la considera una proprietà caratteristica della parabola: il suo scopo non è, come nel caso di Pappo, quello di definire la parabola come luogo di punti, ma di tracciare un luogo che poi verifica, mediante il sýmptōma, essere effettivamente una parabola.
Sebbene meno rigoroso dal punto di vista matematico, lo studio della parabola da parte di Antemio di Tralle (VI sec.) fa anch'esso intervenire il fuoco e la direttrice; lo scopo è quello del suo predecessore. L'autore parla della costruzione di uno specchio ustorio che permetta di concentrare in un punto raggi incidenti paralleli. Determina alcuni punti posti a una stessa distanza dal fuoco e dalla direttrice e costruisce le tangenti alla parabola. Non dimostra, tuttavia, che i punti così costruiti stanno su una parabola e la curva non viene esplicitata. Questa costruzione sarà ripresa nel IX sec. da al-Kindī. Antemio espone anche la prima forma del 'metodo del giardiniere' per costruire l'ellisse con un tratto continuo, metodo che si basa sulla proprietà bifocale dell'ellisse (Coniche, Libro III, prop. 52) secondo la quale la somma delle distanze tra un punto dell'ellisse e i due fuochi è costante ed è pari alla lunghezza dell'asse maggiore della curva.
Le ricerche condotte da Ibn Sahl sugli specchi ustori nella seconda metà del X sec. s'inscrivono in questa tradizione e nello stesso tempo la rinnovano: egli non si limita più soltanto allo studio delle proprietà ottiche delle coniche nel caso della riflessione, ma considera anche la rifrazione. Utilizza di nuovo la nozione di fuoco e concepisce anche l'idea di lenti piano-convesse e biconvesse.
Le ricerche geometriche sul tracciato delle coniche
Oltre alle ricerche di Ibn Sahl sul tracciato continuo delle coniche (cap. XXXIV), altri metodi, per punti o continui, nascono nello stesso periodo e si ritrovano negli studi di geometria pura, in relazione alle riflessioni sui legami tra esistenza e costruibilità. Secondo al-Nadīm, al-Ḥasan, uno dei Banū Mūsā, avrebbe redatto un trattato, Kitāb fī 'l-šakl al-mudawwar al-mustaṭīl (Libro sulla figura circolare allungata), riguardante l'ellisse considerata come sezione di un cilindro. Il trattato è andato perduto, ma secondo numerose testimonianze in nostro possesso, esso conteneva la descrizione del tracciato continuo dell'ellisse a partire dalla proprietà bifocale, nel quadro però di uno studio geometrico dell'ellisse e non più come un'applicazione per la costruzione di un oggetto a forma di ellisse.
Si è ricordato che all'epoca né al-Ḥasan, né i suoi fratelli avevano accesso a una versione comprensibile delle Coniche di Apollonio; difatti la traduzione dell'opera sarà fatta soltanto dopo la sua morte. Il trattato di al-Ḥasan ibn Mūsā sull'ellisse, del quale Ibn al-Samḥ ci ha conservato una versione, rappresentò il punto di partenza dello studio di Ṯābit ibn Qurra Fī quṭū῾ al-usṭuwāna wa-basīṭi-hā (Sulle sezioni del cilindro e sulla sua superficie laterale), condotto però con una conoscenza profonda dell'opera greca.
Meno di un secolo dopo, Ibn Sinān dedicherà il trattato Fī rasm al-quṭū῾ al-ṯalāṯa alla costruzione con riga e compasso del punto corrente per ciascuna delle tre coniche a partire da un cerchio (cerchi fissi, di diametro pari all'asse maggiore per l'ellisse o all'asse trasverso per l'iperbole, un cerchio variabile per la parabola). Per costruire un punto H della parabola di vertice D, asse individuato da DB e lato retto il segmento DB, egli prende un punto G dell'asse, posto al di fuori del segmento DB dalla parte di D. Costruisce quindi il cerchio di diametro BG che taglia la perpendicolare per D a DB nel punto E. Il punto H completa il rettangolo GDEH, ed è un punto che si trova effettivamente sulla parabola cercata, in quanto GH2=DE2=GD∙DB.
Per le coniche a centro, le costruzioni fanno intervenire trasformazioni geometriche, affini nel caso dell'ellisse, non affini in quello dell'iperbole. Ibn Sinān dimostra per prima cosa che i punti dell'ellisse si deducono dai punti corrispondenti del cerchio che ha come diametro l'asse maggiore mediante un'affinità ortogonale e ne deduce una costruzione con riga e compasso del punto mobile sull'ellisse. Mostra poi nel modo seguente che tutti i punti dell'iperbole si deducono da un punto del cerchio di diametro pari al diametro trasverso dell'iperbole: da un punto O di questo cerchio si traccia la tangente; essa taglia l'asse trasverso in un punto E e, se D è un punto della parallela alle ordinate passante per E e tale che il rapporto tra ED ed EO sia uguale a un rapporto assegnato, allora il punto D si trova sull'iperbole data. A partire da qui, egli dimostra che tutte le iperboli aventi lo stesso diametro trasverso e le cui ordinate forma-no un medesimo angolo con questo diametro si deducono, le une dalle altre, per affinità oblique. In quest'opera Ibn Sinān dà anche un procedimento di costruzione per punti dell'iperbole a partire dagli asintoti, riconducendo questa costruzione a quella di un punto M che divida un segmento dato AB in modo che il prodotto MA∙MB sia uguale a un'area data; tale problema dà luogo a una discussione e viene risolto in tutti i dettagli in un'altra sua opera.
La moltiplicazione dei problemi solidi e lo studio dell'esistenza delle soluzioni, cioè dei punti d'intersezione delle coniche, sono in parte i motivi che hanno spinto i geometri arabi a interrogarsi sulla natura profonda di queste curve, su come concepirle e in particolare sulla loro continuità. Quest'ultima proprietà, assieme alla nozione di convessità, si dimostra indispensabile allo studio dell'esistenza di punti d'intersezione di coniche. Ora, i metodi che consentono di tracciare le coniche per punti, anche quelli in cui intervengono trasformazioni geometriche, come nel caso delle coniche a centro nei lavori di Ibn Sinān, non assicurano del tutto questa continuità. Questa esigenza condurrà al-Qūhī a ideare uno strumento che egli chiamerà 'compasso perfetto' e che permetterà di tracciare le coniche con un movimento continuo.
Ci sono pervenuti altri due trattati sullo stesso strumento, uno a opera di al-Siǧzī, matematico dello stesso periodo, l'altro scritto molto più tardi, nel XII sec., da Ibn al-Ḥusayn, che cercherà di ricostruire l'opera di al-Qūhī.
Abbiamo esaminato in precedenza alcuni degli effetti che gli scritti di Apollonio hanno avuto sulle ricerche svolte dai matematici arabi a partire dalla metà del IX sec., in particolare per quanto riguarda le costruzioni geometriche, i problemi di luoghi e quelli di tangenza; questi studi sviluppano ed estendono alcuni capitoli della geometria ellenistica, ma emergono anche nuovi campi di ricerca. Tra i problemi tratti dalle opere andate perdute in greco, come la Sezione di ragione la Sezione di area o la Sezione determinata (e in misura minore le Inclinazioni, i Luoghi piani e i Contatti), sono gli enunciati, più delle soluzioni date da Apollonio, ad avere suscitato l'interesse dei geometri arabi dal IX all'XI sec., arricchendo le loro riflessioni. Di questi problemi essi hanno dato soluzioni originali, che spesso portavano il segno delle loro nuove concezioni dell'analisi geometrica. Per quanto concerne le Coniche, lo studio di quest'opera, diventata accessibile in arabo grazie ai Banū Mūsā, influenzò le ricerche sulla teoria delle coniche e i metodi di risoluzione dei problemi geometrici. Riguardo a questi ultimi, si deve sottolineare l'emergere di una nuova esigenza: le soluzioni dei problemi solidi dovevano essere ottenute per intersezione di coniche, nella grande maggioranza dei casi parabole o iperboli. La sistematizzazione degli studi ha comportato l'introduzione di una tecnica di 'calcoli geometrici' di base, che i geometri del X sec. hanno cercato di migliorare. In questo modo, le coniche sono associate sempre più sistematicamente ad alcune 'formule' (i sýmptōmata).
Lo studio dell'esistenza e del numero dei punti d'intersezione di due coniche, secondo i principî dell'analisi e della sintesi, diventa inseparabile dalla risoluzione sistematica dei problemi di costruzione mediante queste curve. Tali studi non sono più suggeriti, come nell'epoca ellenistica, dalla casualità di questo o di quel problema, ma da una volontà di esplorare sistematicamente il campo dei problemi solidi, e anche di quelli piani. Questa evoluzione, che traeva alimento dall'eredità archimedea, ha un punto di arrivo nell'opera di Ibn al-Hayṯam, che ha fatto delle costruzioni geometriche un capitolo della geometria a pieno titolo. Quasi un secolo dopo, suggerendo un metodo generale di risoluzione delle equazioni di grado minore o uguale a tre basato sull'intersezione di coniche, l'opera algebrica di al-Ḫayyām segnerà il completamento di queste ricerche.
Bibliografia
Abgrall 1995: Abgrall, Philippe, Les cercles tangents d'al-Qūhī, "Arabic sciences and philosophy", 5, 1995, pp. 263-295.
Bellosta 1991: Bellosta, Hélène, Ibrāhīm ibn Sinān: on analysis and synthesis, "Arabic sciences and philosophy", 1, 1991, pp. 211-232.
‒ 1997a: Bellosta, Hélène, Ibrāhīm ibn Sinān: Apollonius Arabicus, in: Perspectives arabes et médiévales sur la tradition scientifique et philosophique grecque, édité par Ahmad Hasnawi, Abdelali Elamrani-Jamal et Maroun Aouad, Leuven, Peeters; Paris, Institut du Monde Arabe, 1997, pp. 31-48.
‒ 1997b: Bellosta, Hélène, Les mathématiciens arabes et le problème des 'Contacts', "Oriens-Occidens. Cahiers du Centre d'histoire des sciences et des philosophies arabes et médiévales", 1, 1997, pp. 105-122.
Heath 1921: Heath, Thomas L., A history of Greek mathematics, Oxford, Clarendon, 1921, 2 v. (rist.: New York, Dover, 1981, 2 v.).
Hogendijk 1984: Hogendijk, Jan P., Al-Kūhī's construction of an equilateral pentagon in a given square, "Zeitschrift für Geschichte der arabisch-islamischen Wissenschaften", 1, 1984, pp. 100-144.
‒ 1992-94: Hogendijk, Jan P., Four constructions of two mean proportionals between two given lines in the Book of Perfection Istikmāl of al-Mu᾽taman ibn Hūd, "Journal for history of Arabic science", 10, 1992-1994, pp. 13-29.
Knorr 1989: Knorr, Wilbur, Textual studies in ancient and medieval geometry, Boston-Basel-Berlin, Birkhäuser, 1989.
Rashed 1986: al-Ṭūsī, Šaraf al-Dīn, Œeuvres mathématiques. Algèbre et géométrie au XIIe siècle, texte établi et traduit par Roshdi Rashed, Paris, Les Belles Lettres, 1986, 2 v.
‒ 1991: Rashed, Roshdi, L'analyse et la synthèse selon Ibn al-Haytham, in: Mathématiques et philosophie de l'antiquité à l'âge classique. Hommage à Jules Vuillemin, sous la direction de Roshdi Rashed, Paris, CNRS, 1991, pp. 131-162 (trad. ingl.: Analysis and synthesis according to Ibn al-Haytham, in: Artifacts, representations and social practice. Essays for Marx Wartofsky, edited by Carol C. Gould and Robert S. Cohen, Dordrecht, Kluwer, 1994, pp. 121-140).
‒ 1993-: Rashed, Roshdi, Math. inf.
‒ 1993a: Rashed, Roshdi, Géométrie et dioptrique au Xe siècle: Ibn Sahl, al-Qūhī et Ibn al-Haytham, Paris, Les Belles Lettres, 1993.
‒ 1993b: Rashed, Roshdi, Math. inf. II.
‒ 1996: Rashed, Roshdi, Math. inf. I.
‒ 1999: Rashed, Roshdi - Vahabzadeh, Bijan, Al-Khayyām mathématicien, Paris, Blanchard, 1999 (trad. ingl.: Omar Khayyam. The mathematician, New York, Bibliotheca Persica, 2000).
‒ 2000a: Rashed, Roshdi, Les catoptriciens grecs, textes établis, trad. et commentés par Roshdi Rashed, Paris, Les Belles Lettres, 2000-; v. I: Les miroirs ardents, 2000.
‒ 2000b: Rashed, Roshdi, Math. inf. III.
‒ 2000c: Rashed, Roshdi - Bellosta, Hélène, Ibrāhīm ibn Sinān. Logique et géométrie au Xe siècle, Leiden, E.J. Brill, 2000.
‒ 2002: Rashed, Roshdi, Math. inf. IV.
Sa῾idan 1984: Sa῾īdān, Aḥmad S., Taṯlīṯ al-zāwiya fī al-῾uṣūr al-islāmiyya, "Maǧalla ma῾had al-maḫṭūṭāt al-῾arabiyya", 28, 1984, pp. 99-137.
Sayili 1962: Sayılı, Aydın, The trisection of the angle by Abû Sahl Wayjan ibn Rustam al-Kûhî (fl. 970-988), "Belleten", 26, 1962, pp. 693-700.
Woepcke 1851: Woepcke, Franz, L'algèbre d'Omar Alkhayyāmī, publiée, traduite et accompagnée d'extraits de manuscrits inédits, Paris, Duprat, 1851 (v. anche Woepcke 1986, v. I, pp. 49-253).
‒ 1874: Woepcke, Franz, Trois traités arabes sur le compas parfait, "Notices et extraits des manuscrits de la Bibliothèque Impériale et autres bibliothèques", 22, 1874, pp. 1-175 (v. anche Woepcke 1986, v. II, pp. 560-734).
‒ 1986: Woepcke, Franz, Études sur les mathématiques arabo-islamiques, hrsg. von Fuat Sezgin, Frankfurt a.M., Institut für Geschichte der Arabisch-Islamischen Wissenschaften, 1986, 2 v.