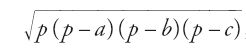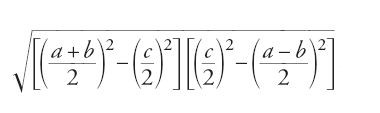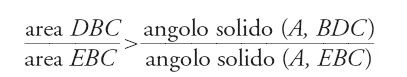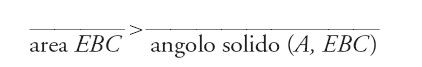La civiltà islamica: antiche e nuove tradizioni in matematica. Geometria: la tradizione euclidea rivisitata
La civilta islamica: antiche e nuove tradizioni in matematica. Geometria: la tradizione euclidea rivisitata
Geometria: la tradizione euclidea rivisitata
Introduzione
Fin dai primi sviluppi della geometria e, più in generale, della matematica scritta in arabo, gli Elementi di Euclide hanno costituito un manuale di riferimento inevitabile e di importanza basilare. La natura stessa dell'opera, concepita per raccogliere quelle proposizioni fondamentali ‒ gli 'elementi', appunto, non necessariamente 'elementari', però ‒ che permettessero di accedere alla maggior parte dei vari campi della matematica, fece sì che quest'opera di Euclide divenisse assai presto, come già era avvenuto nell'epoca greca ed ellenistica, un passaggio obbligato per lo studio dei testi di Archimede e Apollonio e la base principale su cui potevano essere sviluppate nuove ricerche e costruite intere teorie.
Tuttavia, anche se la geometria araba è senza dubbio erede diretta di quella greca, ben presto cominciò a mostrare caratteristiche peculiari, come l'interazione con l'algebra, per esempio, che esercitò un'influenza notevolissima e continua nello sviluppo di entrambe le discipline. Inoltre, l'attività geometrica andò via via mostrando orientamenti nuovi, ampliamenti del campo di ricerca, nuove esigenze dimostrative. Tuttavia, poiché gli Elementi continuarono sempre a essere l'indiscussa pietra angolare dell'edificio della geometria (perché in essi erano raccolti i fondamenti della disciplina), si può ben capire come, quasi inevitabilmente, divennero oggetto di commento, di tentativi di delucidazione, di correzione, di riscrittura, di ampliamento.
Cercare di descrivere cosa possa aver rappresentato lo sviluppo della tradizione euclidea per la matematica araba, porta dunque a prendere in considerazione in primo luogo i numerosi lavori, piuttosto eterogenei, cui diedero luogo gli Elementi. Tali lavori furono variamente alimentati da riflessioni che muovevano da preoccupazioni di tipo filosofico o da considerazioni di ordine più specificamente matematico. Nel seguito ci limiteremo a quei contributi che si riferiscono ai Libri I-IV, VI, XI e XIII degli Elementi, ossia quelli dedicati alla geometria; è appena il caso di ricordare che i restanti sei libri si occupano di altri oggetti: teoria delle proporzioni (Libro V), aritmetica e teoria dei numeri (Libri VII-IX), teoria delle grandezze irrazionali (Libro X) e matematica infinitesimale (Libro XII).
Ma cosa intendiamo, precisamente, con 'tradizione euclidea'? Per esempio, non ci sono dubbi che Euclide avesse scritto un trattato sulle coniche, ma sembra che esso fosse andato perduto già nel corso dell'Antichità, dato che il testo di Apollonio divenne rapidamente l'opera di riferimento. Nel contesto di questo capitolo, la locuzione 'tradizione euclidea' designerà soprattutto lo studio delle figure geometriche costruibili con riga e compasso, il che è del resto l'oggetto dei sette libri degli Elementi che abbiamo qui sopra citato. Il Libro I introduce, oltre alle definizioni, come la maggior parte degli altri libri, i postulati e le nozioni comuni che verranno utilizzati nel corso di tutto il resto dell'opera; tratta poi degli angoli, delle rette perpendicolari e parallele, e fornisce le principali proprietà dei triangoli e dei parallelogrammi. Il Libro II contiene i primi fondamenti della teoria dell'applicazione delle aree ai segmenti. Il Libro III affronta la teoria del cerchio e illustra le proprietà delle linee e degli angoli a esso inscritti. Il Libro IV tratta dei poligoni inscritti e circoscritti e fornisce le costruzioni dei principali poligoni regolari costruibili con riga e compasso (quadrato, pentagono, esagono, pentadecagono). Il Libro VI affronta le applicazioni della teoria delle proporzioni alla geometria piana e, in particolare, lo studio delle figure simili. Il Libro XI generalizza in tre dimensioni alcuni risultati dei Libri I e VI e introduce il concetto di angolo solido. Il Libro XIII è dedicato alla costruzione dei cinque poliedri regolari inscritti nella sfera.
Tuttavia, questi libri degli Elementi non sono i soli testi di Euclide a trattare di tali oggetti. Furono tradotte in arabo almeno altre due opere dedicate alla geometria piana, spesso etichettate come 'minori' rispetto agli Elementi, che si collocano anch'esse nel contesto di una geometria di riga e compasso. La prima è il libro dei Dati, che raccoglie proposizioni che insegnano come, se una figura geometrica ha certi elementi, necessariamente ne ha anche altri; esse trovano appli- cazione nel dominio dell'analisi. La seconda è il libro Divisioni delle figure, il cui testo originale greco è perduto; ne possediamo un riassunto e alcuni frammenti in lingua araba e talune tracce in lingua latina. Si tratta di una raccolta di problemi centrati intorno alla questione di dividere una figura data con una o più rette, in modo che le superfici ottenute stiano fra loro in un dato rapporto. Infine, i successori ellenistici di Euclide scrissero opere che si riallacciavano a questa tradizione; per la maggior parte sono o commenti agli Elementi (ma anche 'esercizi e complementi' relativi ad alcuni punti particolari), oppure opere che avevano più o meno le stesse finalità, di cui però ci sono rimaste soltanto alcune tracce in lingua araba. Lo sviluppo in arabo della tradizione euclidea si basò quindi su un corpus di testi greci piuttosto vasto. Cercheremo ora di precisare la sua estensione, per non rischiare di fornire al lettore false prospettive.
La trasmissione del 'Corpus' euclideo
Al-Nadīm, bibliografo del X sec., fornisce nel Kitāb al-Fihrist (Catalogo) una prima descrizione dell'attività di traduzione che gli Elementi stimolarono a partire dalla fine dell'VIII sec.; la sua testimonianza è corroborata da altre fonti che precisano le sue informazioni. Ne risulta non solo che quest'attività fu oggetto di molteplici e reiterate attenzioni, ma che fu anche incoraggiata dal potere politico dell'epoca. L'opera euclidea sarebbe stata tradotta due volte da al-Ḥaǧǧāǧ ibn Yūsuf ibn Maṭar: la prima volta durante il regno del califfo Hārūn al-Rašīd (r. 786-809), per ordine del suo primo ministro, Yaḥyā ibn Ḫālid ibn Barmak; la seconda durante il regno del califfo al-Ma᾽mūn (r. 813-833). In seguito, Isḥāq ibn Ḥunayn (m. 298/910), figlio del famoso traduttore Ḥunayn ibn Isḥāq, avrebbe condotto una terza traduzione, rivista poi dal matematico Ṯābit ibn Qurra (826-901). Infine, Abū ῾Uṯmān al-Dimašqī (inizio del X sec.) avrebbe anch'egli tradotto vari libri dell'opera di Euclide.
Della prima traduzione di al-Ḥaǧǧāǧ sembra che non ci sia pervenuto nulla, come del resto neanche di quella incompleta forse effettuata da al-Dimašqī. Si è creduto a lungo che la seconda traduzione di al-Ḥaǧǧāǧ fosse stata parzialmente trasmessa attraverso le ampie citazioni degli Elementi che si trovano in un importante commento a quest'opera, scritto nel corso della prima metà del X sec. da Abū 'l-῾Abbās al-Faḍl al-Nayrīzī; lavori recenti hanno però mostrato che i testi citati da questo commentatore potrebbero benissimo essere una riscrittura di al-Nayrīzī stesso, anche se basata sul testo di al-Ḥaǧǧāǧ. Alcuni frammenti attribuiti a questo traduttore sono però conservati in manoscritti di origine andalusa e ci permettono di apprezzare le differenze di formulazione fra la sua versione e quelle successive.
Nemmeno la traduzione attribuita a Isḥāq ibn Ḥunayn è oggi chiaramente identificabile in quanto tale. Sono stati finora recensiti circa venti manoscritti, che però sembrano contenere la versione corretta da Ṯābit ibn Qurra; ma uno studio comparato, esauriente e completo di tutte le copie disponibili resta ancora un lavoro da farsi, nonostante alcuni contributi in questa direzione (De Young 1984, 1992; Kunitzsch 1985). Sia come sia, bisogna osservare che il numero e l'ordine delle proposizioni nella versione Isḥāq-Ṯābit sono diversi da quelli dei manoscritti greci di cui si servì Johann Ludwig Heiberg per la sua edizione critica degli Elementi; Thomas Heath (1926) propose una lista di corrispondenze. Queste differenze testuali generarono, alla fine dell'Ottocento, un dibattito sull'importanza relativa che doveva essere assegnata alle traduzioni arabe nei confronti dei manoscritti greci, nell'ottica di una possibile ricostruzione dell'edificio euclideo originario (Klamroth 1881; Heiberg 1884); dibattito che ancora oggi non ha perduto la sua attualità (Knorr 1996; Rommevaux 2001).
Tuttavia, per quanto importante, l'analisi delle traduzioni arabe degli Elementi non può da sola esaurire la questione più generale della trasmissione del Corpus euclideo. Le varie versioni di cui disponiamo suggeriscono infatti l'utilizzazione da parte degli studiosi arabi di svariati manoscritti greci, senza dubbio imparentati, ma distinti; grazie ad alcuni di questi, fra l'altro, sembra che Ṯābit abbia potuto revisionare la traduzione di Isḥāq. D'altra parte, al-Nadīm ci segnala che uno dei suoi contemporanei, il medico Naẓīf ibn Yumn, avrebbe consultato una versione greca del Libro X che conteneva quaranta proposizioni in più rispetto alla versione abituale di questo testo e che Ibn Yumn stesso ne avrebbe tentato una traduzione. È dunque del tutto verosimile che, accanto ai testi che furono poi effettivamente tradotti, fosse trasmesso anche un gran numero di scolii; e non è detto che anche questi fossero trasportati in lingua araba. Per di più, Ṯābit ibn Qurra ‒ una delle grandi figure della storia della matematica araba ‒ era perfettamente in grado di consultare i trattati greci nella loro lingua originale; e altrettanto poteva fare ‒ per fornire soltanto un altro esempio ‒ anche Naẓīf ibn Yumn, che intrattenne un fitta corrispondenza con al-Siǧzī, uno dei matematici più interessanti della seconda metà del X sec. e di cui ci dovremo occupare più avanti.
Per poter dunque valutare con precisione ciò che della tradizione euclidea greca ed ellenistica fu trasmesso o meno, occorrerebbe poter esaminare, oltre alle traduzioni oggi accessibili, l'insieme dei testi arabi che dipendono da tale tradizione; ma, attualmente, siamo ben lontani da un simile traguardo. Ciononostante, le fonti che ci sono pervenute ci permettono comunque di presentare un panorama almeno approssimativo. Si possono distinguere, quindi, tre categorie di testi: quelli attribuiti a Euclide stesso; i commenti agli Elementi; le opere di altri autori.
Abbiamo qui sopra ricordato, fra i testi euclidei diversi dagli Elementi e riguardanti la geometria piana, i Dati e il libro Divisioni delle figure. Ci limitiamo a segnalare che, come nel caso degli Elementi, la traduzione dei Dati fu eseguita da Isḥāq e corretta successivamente da Ṯābit; anche questa versione presenta alcune varianti nell'ordine delle proposizioni rispetto ai manoscritti greci utilizzati da H. Menge per la sua edizione. Per quanto riguarda il libro Divisioni delle figure, il suo traduttore non è stato ancora identificato; ma anche in questo caso sembra che Ṯābit abbia rivisto la traduzione, forse allo scopo di fornire un'edizione completa e 'unificata' del Corpus geometrico euclideo in senso stretto. Alcuni autori hanno recentemente sollevato il problema della trasmissione nel mondo arabo e islamico di un'altra opera di Euclide, i Porismi, un testo di geometria 'non elementare', oggi perduto, e di cui parla Pappo (attivo agli inizi del IV sec. d.C.) nell'introduzione al Libro VII della sua Collezione matematica; ma non è stata addotta alcuna prova tangibile al riguardo.
Insieme agli Elementi, furono trasmessi vari commenti che rappresentarono forse il veicolo di molti scolii e dimostrazioni alternative. Il commento già citato di al-Nayrīzī è ricco di ampie citazioni tratte da quello di Erone di Alessandria (I sec. d.C.), relativo all'insieme dell'opera. È sempre al-Nayrīzī a citare il commento di Simplicio a proposito della teoria delle parallele e, sempre sullo stesso tema, quello di un certo Aġānis, che, in passato, si tendeva a identificare con Gemino. Per il momento non abbiamo nessuna prova di trasmissioni di altri commenti greci o ellenistici, salvo che per quello di Pappo al Libro X, di cui ci è pervenuta una traduzione araba. Per esempio, al-Nadīm non menziona mai Proclo in relazione agli Elementi, né la sua attività di commentatore euclideo agli altri testi di cui disponiamo sembra essere nota. Ciò non implica necessariamente che la letteratura antica relativa agli Elementi ereditata dal mondo islamico si riduca a questi pochi nomi. Il Kitāb al-Fihrist di al-Nadīm non è certo esaustivo; inoltre il commento di al-Nayrīzī presenta un gran numero di sviluppi e dimostrazioni alternative che questo autore non attribuisce a Erone e che sono abbastanza vicini a ciò che si può leggere in Proclo per poter ipotizzare l'eventuale esistenza di altre fonti, o che derivano dai commentari di Proclo al Libro I degli Elementi di Euclide, o che sono comuni a Proclo e ad al-Nayrīzī.
Infine, dobbiamo ricordare un certo numero di opere greche minori che, pur non essendo commenti veri e propri, sembrano rifarsi anch'esse a una tradizione euclidea intesa in senso lato, almeno nel modo in cui i matematici dell'epoca potevano comprenderla. Fra i tanti, citiamo innanzitutto il Libro dei lemmi attribuito ad Archimede, il cui testo greco è andato perduto e che spesso viene ritenuto apocrifo, in quanto non sembra all'altezza dell'ispirazione del grande siracusano; questo testo, tradotto da Ṯābit ibn Qurra e presentato da al-Nadīm e da altri come dipendente dagli 'elementi di geometria', contiene quindici proposizioni di geometria piana, fra cui alcune che trattano del cosiddetto 'arbelo' o 'trincetto del calzolaio'. Un secondo esempio è rappresentato dal Libro delle ipotesi di un certo Aqāṭun, autore greco il cui nome ci è noto solamente nella sua trascrizione araba; è un'opera di geometria piana elementare contenente quarantatré proposizioni, che potrebbe forse essere stata utilizzata nell'insegnamento alla fine del mondo antico. Di altre due opere oggi ci restano soltanto alcune citazioni fatte da autori successivi; si tratta degli Elementi di geometria di Menelao (I sec. d.C.), che Ṯābit, sempre secondo al-Nadīm, avrebbe elaborato in tre libri, e di quelli ‒ oggi perduti ‒ di Sereno di Antinoe (IV sec. d.C.), citati da al-Bīrūnī (362-442/973-1050 ca.) nel suo Istiḫrāǧ al-awtār fī 'l-dā᾽ira (Determinazione delle corde nel cerchio). Infine, citiamo le opere sui triangoli, che, sempre secondo al-Nadīm, sarebbero state composte da Archimede e da Menelao; in particolare, un manoscritto di un autore non ben identificato, conservato oggi a Hyderabad, potrebbe contenere, in tutto o in parte, la traduzione di Ṯābit ibn Qurra (Rasā᾽il ibn Qurra) del libro Sui triangoli di Archimede.
Di questo quadro generale vale la pena di sottolineare quattro elementi principali. In primo luogo, la trasmissione dal greco all'arabo del Corpus euclideo in senso lato ebbe un carattere massiccio. Secondariamente, questo processo avvenne con una grande attenzione alla costruzione del testo; ce lo testimonia l'intervento di Ṯābit ibn Qurra, che si appoggiava su una lingua e su un vocabolario ormai perfettamente fissati negli scritti di al-Kindī o dei Banū Mūsā già a partire dalla seconda metà del IX secolo. In terzo luogo, è da rilevare l'imperfezione e la parzialità delle nostre conoscenze dei materiali disponibili. Infine, bisogna riconoscere i limiti di un tentativo di ricostituzione esauriente del Corpus trasmesso, perché oggi molte opere sono ormai da considerarsi perdute sia in greco sia in arabo. Bisogna però evitare di sopravvalutare questo quarto problema. Infatti, dato che gli Elementi rimasero sempre la pietra angolare della geometria e raccoglievano i fondamenti della disciplina, essi costituirono l'obiettivo privilegiato dei commentatori e di coloro che si dedicarono a tentativi di rinnovamento. Per quanto i Dati o il Libro dei lemmi possano avere anch'essi stimolato la composizione di testi originali e per quanto il libro Divisioni delle figure o le opere perdute di Archimede e Menelao sui triangoli possano essere state in relazione con altre opere arabe su questi argomenti, tuttavia il riesame della tradizione euclidea si concentrò, com'è ovvio e naturale, sull'opera principe del matematico di Alessandria. È senza dubbio qui, più che in altri luoghi, che si potrà vedere il destino dei concetti euclidei, piegati e sforzati nel quadro di un'attività geometrica che si sviluppava in un contesto lievemente diverso da quello delle matematiche ellenistiche.
Dobbiamo ancora menzionare una categoria di testi che non sono traduzioni vere e proprie, ma che ebbero senza dubbio un ruolo nella diffusione del Corpus euclideo, senza essere peraltro non più di semplici compendi destinati all'insegnamento, o dei commenti in senso stretto. Intendiamo parlare di certe opere che potremmo chiamare 'nuove redazioni' o anche 'edizioni' (taḥrīr), opere che furono in genere composte sulla base di traduzioni precedenti. La più famosa fra queste è l'edizione degli Elementi di Euclide fatta da Naṣīr al-Dīn al-Ṭūsī (597-672/1201-1274), il Taḥrīr al-Uṣūl li-Uqlīdis, datata 1248 e scritta ‒ come il suo stesso autore dichiara ‒ sulla base delle traduzioni di al-Ḥaǧǧāǧ e di Ṯābit; se si tiene conto della quantità di copie che ne furono eseguite, sembra che quest'opera si sia rapidamente imposta come edizione di riferimento. Si aggiunga che al-Ṭūsī si dedicò all'edizione di molte altre opere, fra cui i Dati (basandosi sulla versione di Isḥāq-Ṯābit) e il Libro dei lemmi di Archimede (basandosi sul commento di Abū 'l-Ḥasan ῾Alī ibn Aḥmad al-Nasawī, che risale all'inizio dell'XI secolo).
Senza alcuna pretesa di completezza, non possiamo fare a meno di citare altre edizioni e parafrasi degli Elementi: l'edizione di uno Pseudo-Ṭūsī, probabilmente datata 1298 e redatta da un allievo di Naṣīr al-Dīn stesso, che si rifà anch'essa alle versioni di al-Ḥaǧǧāǧ e di Ṯābit e fornisce commenti notevolmente più ricchi della precedente; l'edizione di Muḥyī 'l-Dīn Yaḥyā ibn Muḥammad ibn Abī 'l-Šukr al-Maġribī (XIII sec.), di cui si attende ancora un'edizione e uno studio, nonostante alcuni autori contemporanei vi abbiano accennato; e, infine, gli Uṣūl al-handasa (I fondamenti della geometria) di Avicenna (980-1037), che costituiscono il primo libro della parte matematica della sua grande enciclopedia filosofica, al-Šifā᾽ (La guarigione). Quest'ultimo testo, a differenza delle opere che abbiamo ora citato, non si propone in maniera esplicita come un'edizione degli Elementi, anche se abbraccia l'intera opera euclidea e dipende da traduzioni precedenti (pare che certe varianti risalgano ad al-Ḥaǧǧāǧ); le dimostrazioni, che riprendono le argomentazioni di Euclide, sono scritte in genere con uno stile più raccolto.
Oltre a queste edizioni, gli scritti relativi agli Elementi sono numerosissimi; allo stato attuale degli studi si contano più di una sessantina di autori, fra i quali si trovano matematici di prima grandezza, come Ṯābit ibn Qurra, Abū Ǧa῾far al-Ḫāzin (metà del X sec.), Abū Sahl al-Qūhī (X sec.), Ibn al-Hayṯam (m. dopo il 1040 ca.), ῾Umar al-Ḫayyām (440-526/ 1048-1131) e molti altri. Non tutti i loro testi ci sono pervenuti; molti di essi non sono ancora stati editi né hanno, a fortiori, goduto dello studio che meriterebbero; e non tutti inoltre presentano lo stesso livello di interesse. Tuttavia, prima di affrontare nei prossimi paragrafi una descrizione dei loro contenuti scientifici, non sarà certo inutile tentare fin d'ora una panoramica generale (anche se succinta) dell'insieme di questi scritti.
Possiamo raccogliere in una prima famiglia i commenti circoscritti a parti ben delimitate dell'opera euclidea, se non addirittura a singole proposizioni. La maggior parte delle volte, ma non esclusivamente, in essi si affrontano aspetti che verranno trattati nei prossimi capitoli: il quinto postulato e la teoria delle parallele, il Libro V e la teoria delle proporzioni, il Libro X e le grandezze irrazionali. Altri testi si concentrano sui 'fondamenti' costituiti dalle definizioni, dalle nozioni comuni e dai postulati, secondo varie prospettive: una riflessione sulla natura della conoscenza matematica, come quella del filosofo al-Fārābī (257-339/870 ca.-950 ca.); la delucidazione di certi concetti, in connessione con lo sviluppo della ricerca matematica dell'epoca, come in Ibn al-Hayṯam; o, più semplicemente, il raggiungimento di certi scopi pedagogici. Un altro gruppo è costituito dai commenti alle proposizioni, che cercano di rispondere a possibili obiezioni alle dimostrazioni euclidee o propongono dimostrazioni alternative. Tali testi si rifanno a temi classici nella tradizione dei commenti agli Elementi, e si occupano di dimostrazioni relative a casi di figure trascurate da Euclide per non sovraccaricare la sua esposizione della ricerca di una dimostrazione diretta al posto di una per assurdo, e così via. Inoltre, fra i titoli segnalati dai bibliografi, troviamo 'aggiunte' (ziyādāt) a certe parti degli Elementi o dei Dati, o anche delle 'correzioni' (iṣlāḥ) agli Elementi; ma di questi testi ce ne è pervenuto un numero troppo piccolo perché sia oggi possibile andare oltre la suggestione di un titolo e precisarne la portata generale. Bisogna anche aggiungere al nostro elenco una considerevole quantità di compendi, e le opere di taglio enciclopedico, come l'Istikmāl (Perfezionamento) del matematico andaluso al-Mu᾽taman ibn Hūd (m. 478/1085) o l'enciclopedia di Quṭb al-Dīn al-Šīrāzī (634-710/1236-1311), nelle quali sono in genere contenute lunghe parti dedicate alla geometria piana che, con tutta evidenza, riprendono varie proposizioni degli Elementi.
Disponiamo dunque di una gamma di approcci molto vasta, dietro cui si possono leggere senza troppa difficoltà gli sforzi compiuti per dissipare le oscurità nascoste nelle opere che costituivano il retaggio della matematica antica, i tentativi di approfondimento e di ricostruzione o anche le nuove prospettive aperte da una ricerca che non mancò certo di esercitare la sua influenza sul modo di pensare e intendere i fondamenti delle discipline geometriche.
La tradizione degli 'Elementi'
I fondamenti e l'ordinamento degli 'elementi di geometria'
Il sistema di premesse che costituisce il punto di partenza delle catene deduttive dell'opera euclidea comprende, com'è noto, le definizioni, le 'domande' (o postulati) e le nozioni comuni. Lo status e la funzione di questi tre gruppi di enunciati rispondono grosso modo alle teorie dominanti all'epoca in cui furono redatti gli Elementi, e in particolare alla teoria della dimostrazione esposta negli Analitici secondi di Aristotele. Non si tratta dunque di un'assiomatica, almeno non nel senso che le attribuiamo oggi e che nascerà realmente soltanto nel XIX secolo. L'analisi critica dei fondamenti esposti negli Elementi risale però a molti secoli prima dell'Ottocento. Fra i matematici arabi essa si esercitò in particolare ‒ e fu una critica radicale ‒ a proposito del postulato delle parallele e della teoria delle proporzioni. Tuttavia, ci sono anche altri settori in cui troviamo testimonianze di mutamenti nella maniera di concepire l'edificio geometrico euclideo. È il caso del modo di trattare il problema dell'esistenza degli oggetti geometrici. Negli Elementi questa nozione di esistenza non è esplicitamente presente. Euclide inizia con il fornire definizioni di oggetti geometrici il cui scopo, sostenuto da un certo realismo, è quello di permettere di intendersi sul significato dei termini introdotti. Nel seguito dell'opera ha poi cura di non fare intervenire tali oggetti se non dopo che la loro costruzione sia stata ben fondata; la dimostrazione della proposizione corrispondente a tale costruzione assume in qualche modo il ruolo di una dimostrazione di esistenza. L'ordinamento degli Elementi deriva così da una restrizione di cui, nel mondo arabo, alcuni redattori di 'elementi' sembra abbiano voluto sbarazzarsi, almeno entro certi limiti, arrivando a proporre rimaneggiamenti fino ad allora inediti. È questo il caso di Abū Sahl al-Qūhī, cui è attribuito un rifacimento dei primi due libri degli Elementi. Il Libro I del rifacimento di al-Qūhī presenta in effetti una successione di proposizioni riguardanti le proprietà delle figure che copre la totalità del Libro I degli Elementi; l'ordine del testo originario è però sconvolto e ne sono esclusi tutti i problemi di costruzione. La coerenza di questo testo può essere colta soltanto quando ci si sia assicurati dell'esistenza di certi oggetti, come la perpendicolare (o la parallela) passante per un punto dato a una retta data; la retta passante per un punto di una retta data e che formi con questa un angolo dato; o un quadrato costruito su una retta data. Facciamo un esempio. La seconda proposizione del testo di al-Qūhī ha un enunciato che corrisponde a quello della prop. 13 del Libro I degli Elementi ('se una retta è innalzata su un'altra retta, essa forma angoli che sono entrambi retti o che hanno somma uguale a due retti'); la dimostrazione utilizza l'esistenza della perpendicolare a una retta in un punto, senza che sia stato proposto in precedenza un modo di costruirla (nel testo euclideo ciò viene invece fatto nella precedente prop. 11). La copia del testo di al-Qūhī di cui disponiamo non discute i fondamenti su cui l'autore si poteva appoggiare, né ci svela le sue intenzioni e motivazioni, il che rende difficile, almeno per il momento, inscriverlo in una prospettiva storica.
Notiamo tuttavia che si potrebbe rintracciare un approccio simile, che tende cioè a mettere da parte il problema delle costruzioni e, di conseguenza, quello dell'esistenza degli oggetti matematici, nei testi a scopo didattico della scuola di Naṣīr al-Dīn al-Ṭūsī, come gli Aškāl al-ta᾽sīs (Proposizioni fondamentali) di al-Samarqandī (fine XIII sec.). Anche se si tratta di un contesto che non è quello della ricerca, ci sembra opportuno segnalare questo testo perché ‒ oltre a sviluppare in qualche modo una strada abbozzata da predecessori assai più illustri ‒ conobbe una larghissima diffusione accompagnato da un commento di Qāḍī Zāda al-Rūmī (765-840/1364 ca.-1436 ca.). Il testo commentato di al-Samarqandī arrivò a soppiantare gli Elementi stessi come manuale primario nell'insegnamento in epoche tarde, provocando a sua volta la circolazione di un buon numero di ulteriori commenti e glosse.
Qualche decennio dopo al-Qūhī, Ibn al-Hayṯam affrontò ‒ questa volta esplicitamente ‒ la questione dell'esistenza degli oggetti matematici definiti all'inizio degli Elementi nel suo Šarḥ muṣādarāt kitāb Uqlīdis fī 'l-Uṣūl (Commento ai postulati degli Elementi di Euclide). Questo problema si poneva in un certo contesto; infatti, la soluzione dei problemi solidi aveva già portato il matematico a rafforzare, anche se su un piano diverso, la distinzione fra costruzione di un oggetto matematico e dimostrazione della sua esistenza. Nel suo trattato sull'opera euclidea Ibn al-Hayṯam si preoccupa di fornire un commento alle definizioni del Libro I, commento costituito, nella maggior parte dei casi, da due parti distinte: una dedicata a mostrare che le definizioni euclidee sono valide e pertinenti; l'altra mirata effettivamente al problema dell'esistenza degli oggetti così definiti. A questo scopo Ibn al-Hayṯam ricorre in maniera massiccia al movimento.
Riprendiamo l'esempio dell'angolo retto e della perpendicolare in un punto. Ibn al-Hayṯam considera una retta finita e un punto preso a caso su di essa; innalza in questo punto un'altra retta che anima di un moto di rotazione continuo. Nel corso di questo moto, uno degli angoli adiacenti a questa retta mobile cresce, mentre l'altro decresce: la retta passerà dunque necessariamente per una posizione in cui i due angoli saranno uguali, assicurando così l'esistenza dell'angolo retto e quella della perpendicolare in un punto. Questa giustificazione, che si basa in definitiva su una sorta di 'pre-topologia', si ritrova in altri matematici: per esempio, nel commento di Qāḍī Zāda al-Rūmī al libro di al-Samarqandī o, assai più tardi, in alcune edizioni degli Éléments de géométrie del matematico francese Adrien-Marie Legendre (1752-1833). Ibn al-Hayṯam fu il primo a proporre in modo così netto l'introduzione del moto nel cuore stesso dell'edificio geometrico; e ciò ebbe implicazioni che andarono ben al di là delle dimostrazioni di esistenza. In particolare, Ibn al-Hayṯam ne fece la base della sua Maqāla fī 'l-ma῾lūmāt (Trattato sui noti) e del suo approccio al problema del quinto postulato, come si potrà vedere in altri capitoli. Si consuma qui una rottura con la teoria aristotelica; per questo Ibn al-Hayṯam sarà criticato severamente da alcuni matematici successivi, fra cui ῾Umar al-Ḫayyām; ma altri riprenderanno la sua utilizzazione del moto per definire gli oggetti geometrici fondamentali, per fornire una prova di esistenza e dimostrare i postulati.
L'edizione degli Elementi compilata nel XIII sec. da Naṣīr al-Dīn al-Ṭūsī non contiene invece riferimenti al movimento. Accanto ai postulati euclidei però troviamo veri e propri postulati di esistenza: testimonianza di una comune volontà di arrivare a dare salde basi all'edificio della geometria. Leggiamo, per esempio: "È necessario in primo luogo postulare che il punto, la linea, la superficie ‒ e fra queste la retta e il piano ‒ e il cerchio esistano, e che [si possa] disegnare un punto su qualsiasi linea o superficie, e supporre una linea su qualsiasi superficie o passante per un qualsiasi punto" (Kitāb Uqlīdis, p. 3). L'edizione dello Pseudo-Ṭūsī riprende questi postulati di esistenza, aggiungendovi una dimostrazione dei primi postulati euclidei che si basa, come in Ibn al-Hayṯam e utilizzando gli stessi argomenti, sulla considerazione del movimento.
Le figure geometriche e le loro proprietà
La percezione stessa delle figure geometriche andò modificandosi a partire dal X sec., e questo fenomeno si manifesta nell'evoluzione dello stile espositivo di certe dimostrazioni, sempre più evidente. Questa evoluzione ha origine nell'osservazione ‒ che si può leggere in filigrana in matematici come al-Qūhī, oppure Ibrāhīm ibn Sinān (296-335/909-946) ‒ che certe dimostrazioni di Euclide o di Apollonio presentano ridondanze quando affrontano situazioni che, sul piano della dimostrazione, si limitano a generare una sostituzione del tipo aggiungere/sottrarre. Può darsi che tale evoluzione fosse stata influenzata dalla pratica degli algebristi; in ogni caso assistiamo alla nascita di una nuova tendenza, quella di assorbire, nel contesto di una stessa dimostrazione, situazioni che nel testo euclideo erano trattate in proposizioni separate, e che ora sono considerate come casi specifici, che non coinvolgono il problema geometrico di fondo. Quest'idea è esposta chiaramente da al-Siǧzī nei suoi Barāhīn kitāb Uqlīdis (Dimostrazioni del libro di Euclide), in cui propone di mettere insieme due proposizioni, per così dire 'gemelle', utilizzando una dimostrazione comune, allo scopo ‒ scrive ‒ di far risaltare una 'proprietà unica'. È questo il caso, per esempio, delle propp. 35 e 36 del Libro III (potenza di un punto, interno o esterno, rispetto a un cerchio), delle propp. 28 e 29 del Libro VI (applicare a una retta data un parallelogramma uguale a una figura data che sia mancante o eccedente di un parallelogramma simile a un parallelogramma dato), o ancora, nel Libro III, delle propp. 7 e 8 (v. sotto) e, nel Libro VI, delle propp. 14 o 15 e delle 16 e 17. Le eventuali differenze fra un caso e l'altro della figura sono specificate nell'interlinea del manoscritto, un po' come oggi scriveremmo 'rispettivamente …'. Si può dunque capire che, in certa misura, ciò che è in gioco qui non è altro che la neutralizzazione delle opposizioni dentro/fuori o aggiungere/sottrarre, atteggiamento questo che si cercherebbe invano negli autori greci. La possibilità di formulare proposizioni di questo tipo attraverso un enunciato comune è considerata in maniera esplicita da Naṣīr al-Dīn al-Ṭūsī nella sua edizione degli Elementi, senza però che si generi una modificazione dell'ordine espositivo dell'opera.
L'opera di al-Siǧzī ci permette di illustrare la posta in gioco. In generale questo autore assume la figura geometrica (šakl) come oggetto principale dell'attenzione del geometra. I compiti che si assegna sono di due ordini, nei quali si può qui riconoscere la distinzione tradizionale fra 'teorema' e 'problema'. Si tratta o di occuparsi delle proprietà delle figure (ḫawāṣṣ al-aškāl), o della loro costruzione (῾amal al-aškāl); si osservi, beninteso, che qui con šakl si intende la figura geometrica 'astratta', composta da elementi semplici come rette, cerchi, angoli, ecc., e non la rappresentazione o la figura effettivamente disegnata (ṣūra), che può essere d'ausilio a cogliere meglio la dimostrazione. Si può quindi presumere che la natura stessa dell'oggetto geometrico possa essere stata deformata e modificata. Prendiamo come esempio quello delle propp. 7 e 8 del Libro III, dedicate al confronto delle rette tracciate verso un cerchio da uno stesso punto, interno o esterno a esso. Al-Siǧzī propone un enunciato unico, comune, mostrando così che si tratta effettivamente di un'unica proposizione: ma il fatto che l'enunciato, la proprietà e la proposizione siano unici, impone che unica debba essere anche la šakl? È proprio questo che sembra intendere al-Siǧzī, come ci si potrebbe d'altronde aspettare. Comincia, come è d'uso, a sviluppare un esempio assegnando nomi ai punti e alle rette: "Sia AB il cerchio dato di centro C e D il punto dato. La situazione di questa figura [šakl] è secondo due casi di figura, perché il punto D è situato o all'interno del cerchio o all'esterno" (Barāhīn kitāb Uqlīdis fī 'l-Uṣūl ῾alā sabīl al-tawassu῾wa-'l-irtiyāḍ, f. 20r). Detto in altri termini, la figura geometrica è ciò che costituisce l'oggetto di una proposizione (si noti, inoltre, che i termini 'figura' e 'proposizione', in arabo, corrispondono a un unico termine, šakl); in questo caso la figura corrisponde ad assegnare un cerchio e un punto che non coincida con il suo centro, e quest'assegnazione, oggetto della riflessione del geometra, è unica, al di là di quanti casi di figura essa possa generare. Questa modificazione che va a toccare la natura stessa dell'oggetto geometrico, allo stesso titolo delle estensioni che discuteremo in seguito, costituisce un segno del fatto che il campo di ricerca sviluppato da Euclide nell'ambito della geometria piana non rimase affatto fisso e immutabile, ma poté essere arricchito senza che i suoi fondamenti fossero rimessi in discussione o radicalmente ridefiniti.
Nuovi strumenti per le costruzioni con riga e compasso: le estensioni del Libro II e della teoria delle applicazioni d'area
Fin dall'Antichità, la soluzione dei problemi di geometria piana o di quella dei solidi ha sempre rappresentato una parte importante del lavoro matematico. Nel X sec. questo tipo di attività fu particolarmente intensa, e divenne spesso occasione di sfide, discussioni, scambi di corrispondenza, generando al tempo stesso una riflessione di natura più filosofica sulla classificazione dei problemi o sull'analisi e la sintesi. Inoltre, i matematici dell'epoca apprezzavano in modo particolare il genere letterario costituito dalle raccolte di problemi scelti o dalle antologie; ne sono un esempio gli scritti di Ibrāhīm ibn Sinān, di Abū 'l-Ǧūd ibn al-Layṯ (X sec.), di Ibn ῾Irāq (X-XI sec.) e dello stesso al-Siǧzī. I problemi di costruzione con riga e compasso costituiscono naturalmente una parte essenziale di queste raccolte; e un numero significativo di esse era legato ai trattati oggi perduti di Apollonio: i Luoghi piani, i Contatti, le Inclinazioni. Accanto a queste antologie troviamo anche raccolte che, sull'esempio degli scritti di Apollonio, sono dedicate a particolari classi di problemi. Fra di esse si trovano gli scritti sui cerchi tangenti di Ibn Sinān, al-Qūhī e al-Siǧzī, la raccolta di al-Siǧzī dedicata al problema 'da un punto dato tracciare una retta che cada su due rette date' e quella di al-Qūhī sul problema 'da un punto dato tracciare due rette che formino un angolo dato'. In queste ultime due raccolte, le rette cercate devono soddisfare condizioni relative a lunghezze, aree o rapporti da esse individuati. I risultati ottenuti si trasformano a loro volta in altrettanti strumenti da utilizzare per risolvere con riga e compasso altri problemi geometrici.
D'altra parte, lo studio delle soluzioni con riga e compasso, così come avviene in altri campi della geometria, beneficiò del rinnovamento di certi strumenti, grazie all'uso crescente delle trasformazioni affini e, in particolare, delle omotetie; per esempio, al-Qūhī dimostra sostanzialmente che l'immagine di un cerchio tramite un'omotetia è ancora un cerchio, proprietà che viene più volte utilizzata nella soluzione dei problemi. Tuttavia, questo rinnovamento generale delle tecniche si colloca a volte in continuità diretta con la tradizione degli Elementi e troviamo vere e proprie estensioni e ampliamenti dell'opera euclidea. È questo ciò che accade nel caso del Libro II e in quello della teoria delle applicazioni d'area.
Vale la pena di ricordare che, a partire dalla pubblicazione del Kitāb al-Ǧabr wa-'l-muqābala (Libro dell'algebra) di al-Ḫwārizmī (prima metà IX sec.), le letture algebriche del Libro II degli Elementi si sono moltiplicate e diffuse per secoli, fra i matematici, ma ‒ assai più tardi ‒ anche fra gli stessi storici della scienza. Alla fine dell'Ottocento, H.G. Zeuthen introdusse l'espressione 'algebra geometrica' per descrivere la tecnica che Euclide espone nei Libri II e VI, nota fino ad allora come 'applicazione d'area'; in seguito, O. Neugebauer prima e S. Gandz poi proposero una visione in cui l'esposizione euclidea si riduceva a un travestimento geometrico di sedicenti 'procedure algebriche' babilonesi. Questo approccio è oggi vivacemente contestato da quegli storici che ritengono di dover restituire gli scritti euclidei alla tradizione che è loro propria, cioè a una tradizione fondamentalmente geometrica. Non abbiamo intenzione di entrare qui in questo dibattito; tuttavia non si può negare che, accostandosi ai lavori degli algebristi, la problematica delle applicazioni d'area poté arricchirsi e svilupparsi nel contesto arabo, pur continuando a vivere nel solco della tradizione propriamente geometrica di Euclide. Vediamo cosa avvenne nel X sec. nel caso di due matematici che abbiamo or ora incontrato, al-Qūhī e al-Siǧzī.
Ricordiamo brevemente che lo scopo del Libro II è quello di mettere in luce le relazioni fra i rettangoli 'determinati' da due rette (segmenti) date. La prop. 1, per esempio, tratta dei rettangoli costituiti da una retta data e da quelle che risultano dalla divisione di un'altra retta data in un numero arbitrario di segmenti; algebricamente essa può essere interpretata così: a(b+c+d+…)=ab+ac+ad+… La prop. 4 tratta dei quadrati costruiti su una retta data e su due sue parti qualunque (fig. 2); algebricamente equivale all'identità (a+b)2=a2+b2+2ab; la sua dimostrazione si fonda sulla descrizione dei rettangoli coinvolti nel problema geometrico.
Similmente, fino alla prop. 10, Euclide esamina ciò che risulta dalla divisione delle rette in parti uguali/diseguali e dall'aggiunta di una retta a una retta data. È da osservare che, forse a scapito della concisione, ma molto probabilmente con lo scopo di illustrare al meglio il suo metodo, Euclide rese le prime otto proposizioni indipendenti l'una dall'altra, fornendo per ciascuna di esse una dimostrazione che permettesse una visualizzazione geometrica dei rettangoli e dei quadrati in gioco.
Al-Qūhī (fig. 3) dimostra sostanzialmente che se la retta AB è divisa secondo i punti C e D, con AC=DB, e se CD è divisa in modo qualunque dal punto E, allora
[1] AD∙DB+CE∙ED=AE∙EB (prop. 16)
e
[2] AD2+DB2=AE2+EB2+2CE∙ED (prop. 22),
o anche che, se AB (fig. 4) è divisa in C e in D e AC=DB, se si aggiunge il segmento BE, allora
[3] AE∙EB +AD∙DB=CE∙ED (prop. 20)
e
[4] AE2+EB2=CE2+ED2+2AD∙EB (prop. 26).
Le reciproche di queste proposizioni mostrano che se una di queste relazioni è verificata, allora AC=DB.
Nella sua riscrittura del Libro II, al-Qūhī propone ventisette proposizioni. Dieci di esse corrispondono alle prime dieci del Libro II degli Elementi, nella maggior parte con nuove dimostrazioni; cinque ancora sono le reciproche di alcune proposizioni, che non si trovano in Euclide, formulate nei termini seguenti: se certe condizioni fra certi rettangoli sono verificate, allora un certo punto divide un certo segmento in due parti uguali, o un certo segmento è uguale a un certo altro. Le restanti dodici (ciascuna di esse con la sua reciproca) introducono sviluppi ulteriori, moltiplicando i punti in cui vengono divise le rette. Si noti che al-Qūhī non affronta le restanti quattro proposizioni del Libro II e, a quanto pare, per un motivo molto semplice: le propp. 11 e 14 sono problemi di costruzione che ‒ esattamente come nel caso del Libro I ‒ non interessano qui al-Qūhī, che è soprattutto preoccupato di esplicitare le proprietà delle figure. Quanto alle propp. 12 e 13 che generalizzano il teorema di Pitagora, egli le aveva esposte nel suo Libro I, in quanto si tratta di teoremi essenzialmente relativi a proprietà dei triangoli; inoltre, e soprattutto, essi sembrano estranei allo scopo della trattazione del Libro II, che è quello di esplicitare le relazioni fra i rettangoli generati da divisioni di segmenti dati.
A differenza di Euclide, al-Qūhī non fornisce alcuna visualizzazione dei rettangoli che entrano in gioco negli enunciati (il che non significa che la natura delle proposizioni presentate risulti profondamente modificata); le sue dimostrazioni sono più concise di quelle del suo modello e ‒ ulteriore differenza ‒ utilizzano il più possibile i risultati precedenti. Per esempio, per dimostrare la prop. 4 al-Qūhī utilizza in modo del tutto naturale le precedenti 2 e 3, fornendo così una dimostrazione assai simile a quella che Heath fa risalire al gesuita Cristoforo Clavio (1537-1612). Da questo punto di vista le sue dimostrazioni si avvicinano a quelle che al-Nayrīzī nel suo commento attribuisce a Erone, o a quelle che Heath definisce 'semi-algebriche', perché non offrono una visualizzazione geometrica del risultato. In realtà, il testo di al-Qūhī sembra testimoniare l'esistenza di approfondimenti di una tecnica euclidea assai utile nella soluzione di problemi geometrici e in cui ‒ a nostro avviso ‒ si cercherebbe invano una quantità di algebra maggiore di quella che si trova in Euclide.
Le proposizioni aggiunte al testo euclideo (dalla 16 alla 27) possono dunque essere lette come altrettanti strumenti inediti fondati sulle stesse tecniche di Euclide; strumenti che potevano rivelarsi preziosi in un'epoca di intensa attività geometrica, in cui le raccolte di problemi erano divenute un vero e proprio genere letterario e i matematici si sfidavano per provare le loro capacità di solutori. Notiamo anche che la preoccupazione di dotare le proposizioni delle loro reciproche è però nuova. Si esercitò qui, probabilmente, l'influenza delle riflessioni suscitate, a partire dagli inizi del X sec. (in particolare a partire da Ibrāhīm ibn Sinān), dal tema dell'analisi e della sintesi, e in particolare dal problema della reversibilità del procedimento analitico. È però difficile precisare ulteriormente questo punto, fintanto che non si sarà approfondito meglio quanto i matematici possano essersi giovati di tali risultati nei loro lavori originali.
Si giunge a conclusioni di questo tipo anche nel caso di al-Siǧzī. Nell'opera prima menzionata, Barāhīn kitāb Uqlīdis, che propone dimostrazioni alternative di proposizioni degli Elementi, sono utilizzati due tipi di dimostrazioni, senza che si possa individuare una qualunque preminenza di un tipo sull'altro. Da un lato, come in al-Qūhī, alcune dimostrazioni si basano sulle proposizioni precedenti; per di più le argomentazioni proposte sono a volte identiche in questi due autori, come nel caso, particolarmente elegante, della dimostrazione della prop. 6 del Libro II, che viene ricondotta alla prop. 5 utilizzando l'aggiunta di un segmento scelto in modo opportuno. In altri casi, al-Siǧzī riprende il metodo euclideo di 'visualizzazione' dei rettangoli, introdotti proprio là dove Euclide aveva scelto un'altra strada (è il caso delle propp. 9 e 10 del Libro II).
Tuttavia, nel testo di al-Siǧzī si trovano anche sviluppi ulteriori, sconosciuti alla letteratura matematica greca e che si collocano in continuità con la tradizione euclidea delle applicazioni di aree, fornendo al tempo stesso strumenti inediti per la soluzione dei problemi. È un altro punto di contatto con al-Qūhī; ma i nuovi sviluppi proposti da al-Siǧzī si muovono in una direzione diversa. Si tratta infatti non più del Libro II, ma delle propp. 28 e 29 del Libro VI degli Elementi. La dottrina euclidea consiste nell'applicare a una retta data un parallelogramma uguale a una figura rettilinea data cui manchi (rispettivamente: cui sia aggiunto) un parallelogramma simile a uno dato. Sia AB la retta data, C la figura rettilinea data, D il parallelogramma dato: la prop. 29, per esempio, fornisce il mezzo per costruire il parallelogramma AGHI che ha la stessa superficie di C e tale che il parallelogramma BGHJ sia simile a D.
Il caso più utilizzato di questo risultato è quello in cui D è un quadrato, il che facilita ulteriormente un'interpretazione algebrica di queste proposizioni, che possono essere tradotte in equazioni di secondo grado: in effetti si ottiene ax±x2=c, ovvero due delle tre equazioni trinomie canoniche.
I matematici faranno un uso massiccio di queste proposizioni, soprattutto nelle raccolte di problemi che si vanno producendo nel corso del X secolo. Il tentativo di al-Siǧzī di allargare il ventaglio di utilizzazione era dunque del tutto naturale. Egli infatti propone per queste due proposizioni una dimostrazione destinata a facilitare la dimostrazione di un corollario inesistente nel testo euclideo, ossia il caso in cui l'eccesso (o il difetto) non è più un parallelogramma, ma un triangolo. Adattando l'esempio precedente, si può applicare ad AB il trapezio AGJI, che ha la stessa superficie di C ed è tale che il triangolo BGJ sia simile al triangolo D.
L'utilità di questo risultato si manifesta quando si esamina l'uso che al-Siǧzī ne fa in altri luoghi, per esempio nella raccolta che dedica al problema della divisione delle figure (che affronteremo in seguito). Questi stessi problemi gli forniscono inoltre l'occasione di produrre un altro risultato, assente in Euclide, dato che si tratta di ciò che corrisponderebbe alla terza equazione trinomia canonica: x2=ax+c. Il lemma che dimostra consiste nell'applicare al segmento AB un parallelogramma AGHI simile al parallelogramma D dato e che ha un eccesso pari al parallelogramma BGHJ, di superficie uguale a quella di C.
In al-Qūhī, come in al-Siǧzī, questi sviluppi ulteriori non snaturano certo i tratti fondamentali dell'esposizione degli Elementi. Rappresentano tuttavia una testimonianza di una ricerca attiva che punta a dotarsi di nuovi strumenti e del perseguimento di una tradizione propriamente euclidea che, nella seconda metà del X sec., era sempre viva e vitale. Il discorso diventa però diverso se ci rivolgiamo a un altro opuscolo di al-Siǧzī, il Fī misāḥat al-ukar bi-'l-ukar (Sulla misura delle sfere per mezzo di sfere), in cui l'autore affronta oggetti geometrici tridimensionali. Ci troviamo di nuovo sulla scia del Libro II: al-Siǧzī applica a segmenti dei parallelepipedi rettangoli (o sfere che ammettano tali segmenti come diametri) e cerca di esplicitare le relazioni che risultano da una divisione di questi segmenti o dall'aggiunta di altri. Il vocabolario, fra l'altro, è identico, dato che si parla di parallelepipedi 'circondati' da questa o quella retta, e di rette che 'possono' certi cubi o certe sfere, allo stesso modo con cui in Euclide 'potevano' certi quadrati. Per di più, come nel caso del Libro II, il testo sarebbe suscettibile di essere interpretato algebricamente, producendo in questo caso però identità di terzo grado. Per esempio, la descrizione della suddivisione del cubo data da al-Siǧzī ‒ e, secoli dopo, da Christoff Rudolff (XVI sec.) o da Bonaventura Cavalieri (1598?-1647) ‒ fornirebbe l'identità: (a+b)3=a3+b3+3ab(a+b). In effetti, il cubo AG è la 'somma' dei cubi AE ed EG e dei tre parallelepipedi uguali BK, CD e HJ (fig. 8).
Ma le analogie con il Libro II si arrestano qui, e lo scopo di al-Siǧzī è evidentemente un altro e ben diverso. Non si tratta più ‒ è questo il punto fondamentale ‒ di approfondire e sviluppare una tecnica che può fornire strumenti utili per risolvere problemi: del resto, molti degli oggetti che intervengono nelle dimostrazioni (per es., il cubo equivalente all'eccesso del cubo AG sulla 'somma' dei cubi AE ed EG) non sono costruibili con riga e compasso. Anche se il progetto di al-Siǧzī è assai poco esplicito, tutto concorre a farci pensare che siamo in presenza di una ricerca più teoricamente marcata e le cui applicazioni sono assai meno sicure; di una ricerca, cioè, che punterebbe a esplicitare i protocolli di passaggio da una 'dimensione' a un'altra per mezzo della definizione di relazioni metriche. È in questo modo, in ogni caso, che si può interpretare la formulazione dei risultati in termini di sfere: quasi che per al-Siǧzī la sfera ‒ forse per motivi legati a una certa concezione del mondo o forse perché essa manifesta meglio l'isotropia dello spazio ‒ fosse più adatta del cubo a esprimere i suoi veri scopi, nonostante la maggior parte delle dimostrazioni si fondi su considerazioni relative a parallelepipedi. Per riprendere l'esempio precedente, abbiamo che l'eccesso della sfera grande sulle due sfere è uguale alla sfera che 'può' il lato del cubo uguale a tre solidi uguali, ciascuno dei quali è 'circondato' dal diametro della sfera grande e dai diametri delle due sfere. Ci sembra dunque che, nelle pieghe più intime di questa riflessione, si possa trovare l'idea di 'dimensione', nozione che dipende dal concetto di grado algebrico; idea affatto nuova in matematica, che emerge da una lettura rigidamente geometrica del Libro II degli Elementi.
Inoltre, sebbene niente di certo possa essere affermato a questo proposito, è possibile che al-Siǧzī abbia pensato di passare a una tappa successiva, vale a dire considerare oggetti di dimensione superiore a 3. Infatti, le due ultime proposizioni del suo opuscolo fanno supporre che egli abbia potuto trattare ipersfere in uno spazio a quattro dimensioni, poiché le relazioni metriche esposte si verificano soltanto in questo caso. Tuttavia, non avendo a disposizione una terminologia adeguata, l'autore non fa parola di ciò che potrebbe essere un tale spazio.
La geometria del triangolo
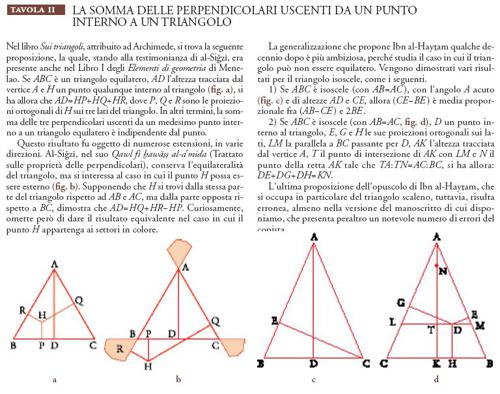
Ereditati dall'Antichità, alcuni problemi relativi alla geometria del triangolo divennero oggetto di estensioni o ispirarono nuove dimostrazioni alternative. Oltre alla generalizzazione del teorema di Pitagora e agli sviluppi relativi alla somma delle perpendicolari uscenti da un punto interno a un triangolo (per i quali si rinvia alle Tavv. I e II), un'idea concreta sia della preoccupazione di generalizzazione presente nei matematici islamici, sia di come questi sviluppi e questi metodi si inserissero nella ricerca dell'epoca è data dagli sviluppi relativi alla formula di Erone.
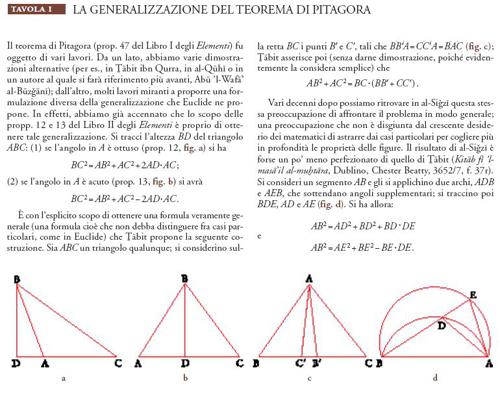
La formula, dimostrata da Erone di Alessandria nel Libro I della Metrica e nel capitolo 30 della Diottrica, afferma che l'area di un triangolo si può esprimere nella forma
dove a, b e c sono i lati e p è il semiperimetro del triangolo. È tuttavia probabile che questa formula sia anteriore a Erone. Al-Bīrūnī l'attribuisce ad Archimede (senza peraltro citare alcuna fonte, v. oltre). In ogni caso, la formula di Erone sembra essere divenuta molto presto nota e largamente diffusa nel mondo islamico, senza mai essere messa in connessione con il matematico alessandrino. Ṯābit ibn Qurra scrive, per esempio: "alcuni l'hanno attribuita all'India, altri hanno detto che è dovuta ai Bizantini" (Rashed 1996, p. 1029).
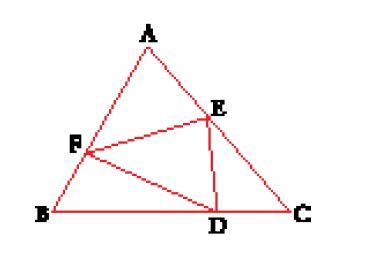
Il primo contributo arabo al riguardo sembra sia stato quello dei Banū Mūsā, Muḥammad, al-Ḥasan e Aḥmad (IX sec.). Nel loro Kitāb Ma῾rifat misāḥat al-aškāl al-basīṭa wa-'l-kuriyya (Libro per conoscere l'area delle figure piane e sferiche; noto nel mondo latino con il titolo Liber trium fratrum oppure Verba filiorum Moysi), che conobbe anch'esso una grande diffusione, questi tre matematici proposero una dimostrazione originale della formula, che fu ripresa poi da Leonardo Fibonacci, Luca Pacioli e molti altri. Il punto di partenza è lo stesso di quello di Erone (fig. 9): si considera il cerchio inscritto al triangolo ABC di centro E, tangente ai lati nei punti D, F e G. La costruzione successiva differisce però da quella eroniana: si prolunghino AB e AC fino a H e K in modo che BH=CG e CK=BG. È facile dimostrare che AH=AK=p. Si traccino poi le perpendicolari alle rette AH e AK nei punti H e K, che si intersecano in I, un punto che si trova sulla bisettrice dell'angolo BAC. Tracciata infine la perpendicolare IL alla retta BC, la dimostrazione può essere sviluppata manipolando i rapporti che derivano dalle uguaglianze e dalle similitudini dei triangoli rettangoli costruiti.
Nella maggior parte dei manoscritti che ci hanno conservato il trattato dei Banū Mūsā si trova aggiunta una dimostrazione praticamente identica a quella di Erone, dimostrazione che l'autore attribuisce però ad Abū Ǧa῾far al-Ḫāzin. Il principio su cui si basa consiste nel non prolungare AB e AC fino a H e K, ma prolungare solo la retta CB fino al punto indicato con V, in modo che VB=AF; e da qui segue che VC=p. Per mezzo di altre costruzioni ausiliarie, la dimostrazione viene ottenuta grazie ad argomenti analoghi a quello della precedente, ma utilizzando anche la proprietà dei quattro punti cociclici.
Verso la fine del X sec. Abū ῾Abd Allāh al-Šannī tentò una strada completamente diversa. In realtà egli dimostra un'espressione equivalente alla formula di Erone, e precisamente:
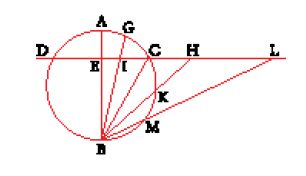
Comincia con il dimostrare un lemma che serve ad assicurare che (fig. 10a) se in un triangolo BMN, rettangolo in B, C è il punto di mezzo dell'ipotenusa e A è un punto qualunque del segmento CM, allora l'area Δ del triangolo ABC soddisfa l'espressione (4Δ)2=xx′yy′, dove x e y rappresentano rispettivamente i cateti BN e BM e, dato un triangolo simile a BMN e con vertice in A, x′ e y′ rappresentano i lati paralleli a BN e BM. Per dimostrare tale relazione, utilizza una doppia affinità ortogonale che trasforma BMN in un triangolo isoscele e, di conseguenza, l'angolo BCA in un angolo retto.
Prolungando BC fino a P (fig. 10b) in modo che si abbia CP=AC=b (e chiamando Q il punto di BC tale che CQ=b), si può applicare ai due trapezi isosceli APNB e AQBM il teorema di Tolomeo, che assicura che per ogni quadrilatero inscrittibile il prodotto delle diagonali è uguale alla somma dei prodotti dei lati opposti, il che fornisce un'espressione dei prodotti xx′ e yy′ e permette di ottenere il risultato.
Qualche decennio dopo ritroviamo l'espressione dell'area del triangolo nel già citato Istiḫrāǧ al-awtār fī 'l-dā᾽ira di al-Bīrūnī relativo alla determinazione delle corde nel cerchio grazie alle proprietà della 'retta a gomito' (al-ḫaṭṭ al-munḥanī) inscritta. Si ritorna qui alla formula eroniana, il cui enunciato al-Bīrūnī attribuisce ad Archimede; ma l'attribuzione della dimostrazione che l'accompagna è assai più dubbia: infatti essa si basa su un risultato che non viene in nessun modo collegato al nome di Archimede, in contrasto con il fatto che al-Bīrūnī cita sistematicamente i contributi di tutti i suoi predecessori. Per di più, in uno dei manoscritti di cui disponiamo, la dimostrazione di questo punto (scritta in modo diverso, ma utilizzando la stessa costruzione e le stesse argomentazioni) viene esplicitamente attribuita ad al-Šannī. Sia come sia, è importante sottolineare che questa dimostrazione è inserita in un libro dedicato alle proprietà della cosiddetta 'retta a gomito', diventando in qualche modo un'esemplificazione dell'interesse di questo argomento.
Siano AB e BC due corde di un cerchio, con AB maggiore di BC; la spezzata ABC è una retta a gomito inscritta nel cerchio (fig. 11a). Il punto D, punto di mezzo dell'arco AC, ha un ruolo centrale. In effetti, se si traccia la perpendicolare ad AB passante per D, si può dimostrare che il piede E di questa perpendicolare è il 'punto di mezzo' della retta a gomito ABC, nel senso che AE=EB+BC. Questa proposizione si trova nel libro Sui cerchi tangenti attribuito ad Archimede dalla tradizione araba, e al-Bīrūnī cita al proposito anche gli Elementi di geometria di Sereno e un discreto numero di suoi predecessori più immediati, quali al-Siǧzī e al-Šannī.
Tuttavia si può mostrare addirittura che, tracciate AC, AD e CD (fig. 11b), si ottiene il seguente risultato per le aree dei triangoli: (area del triangolo ADC)−(area del triangolo ABC)=DE∙EB.
Al-Bīrūnī fornisce tre dimostrazioni di questa proposizione: una ideata da lui stesso, una di un certo Abū Naṣr al-Ǧa῾dī e una di al-Šannī. Quest'ultimo risultato, insieme al precedente (che in effetti permette di dire che p=AE+AJ, con J punto medio di AC) fornisce la chiave per la dimostrazione della formula di Erone (nella figura le costruzioni ausiliarie utilizzate sono tratteggiate).
Riassumendo, possiamo dunque dire che fu grazie a tecniche derivate dalle ricerche della loro epoca che i matematici arabi poterono escogitare dimostrazioni molto diverse di un risultato largamente diffuso e conosciuto e che, tuttavia, sembra essere loro pervenuto senza alcun supporto dimostrativo.
La geometria del cerchio
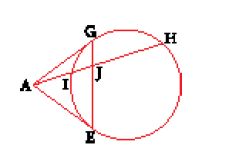
Il libro di al-Bīrūnī sulla retta a gomito (gnomone) ci indica come le proprietà metriche del cerchio siano state oggetto di un'esplorazione intensa. Ciò è vero, in particolare, per il trattato Fī ḫawāṣṣ al-dawā᾽ir (Sulle proprietà dei cerchi) che Ibn al-Hayṯam dedicò a tale figura. I risultati ottenuti in questo campo furono molti e di natura assai varia, per cui ci limiteremo qui a proporre due esempi di proprietà che dovevano rivelarsi particolarmente importanti per la storia della geometria. Nel X sec. al-Qūhī e al-Siǧzī forniscono, sostanzialmente, la proprietà che definisce poli e polari nel cerchio, un risultato già presente nella prop. 38 del Libro III delle Coniche di Apollonio, ma che ora è accompagnato da nuove dimostrazioni nel contesto di una geometria con riga e compasso. Nel Kitāb fī 'l-masā᾽il al-muḫtāra (Problemi scelti) di al-Siǧzī, tale proprietà è dimostrata nel modo seguente (fig. 12). Sia A un punto esterno a un cerchio; GE la retta congiungente i punti in cui le tangenti condotte da A incontrano il cerchio; AH una retta che incontri il cerchio in I e H e la congiungente GE in J; si ha allora che AH:AI=JH:JI.
Nello stesso trattato al-Siǧzī enuncia la proprietà generale per cui una retta e un cerchio sono immagini l'uno dell'altra in un'inversione che abbia per polo un punto del cerchio; un risultato utilizzato nel X sec. negli studi sull'astrolabio, nel caso particolare di un piano passante per il centro di una sfera. Nella formulazione di al-Siǧzī abbiamo che (fig. 13), se BA è un diametro del cerchio, DCL una retta perpendicolare a BA in E e BIG, BKH e BML rette uscenti da B, allora
[7] BA∙BE=BG∙BI=BC2=BK∙BH=BM∙BL.
Non sembra però che l'inversione, in quanto trasformazione del piano, sia stata utilizzata quanto lo furono le trasformazioni affini.
I poligoni regolari
Negli Elementi Euclide fornisce, come abbiamo detto, le costruzioni dei principali poligoni regolari costruibili con riga e compasso (quadrato, pentagono, esagono, ecc.). Il caso degli altri poligoni che, come l'ettagono o l'ennagono, non sono costruibili con riga e compasso, divenne oggetto, a partire dal X sec., di notevoli sviluppi. Tali ricerche, soprattutto nel caso dell'ettagono, divennero a loro volta un motore particolarmente importante per la sistemazione dell'uso delle sezioni coniche nella soluzione dei problemi solidi. Anche in un altro campo, quello del calcolo delle aree e della matematica infinitesimale, la problematica sui poligoni regolari provocò nuove ricerche. è da segnalare in primo luogo l'utilizzazione di successioni di poligoni per delimitare il cerchio o altre curve. Tale pratica produsse a volte, in modo quasi incidentale, un certo numero di risultati preparatori il cui unico oggetto era lo studio dei poligoni in sé. Per esempio, nel Kitāb Ma῾rifat misāḥat al-aškāl al-baṣīta wa-'l-kuriyya dei Banū Mūsā prima citato, si dimostra che l'area S di ogni poligono regolare di perimetro p, circoscritto a un cerchio di raggio r, vale S=pr/2; e se r′ è il raggio del cerchio circoscritto al poligono, l'area di questo cerchio è maggiore di pr′/2.
Lo studio dei poligoni viene affrontato anche ‒ in modo molto più sostanzioso e specifico ‒ nel quadro del teorema isoperimetrico: fra tutte le figure piane aventi ugual perimetro, il cerchio è quella che ha area massima. Sebbene queste ricerche appartengano più propriamente a un altro capitolo della matematica, citeremo ugualmente qui i risultati più importanti relativi ai poligoni. Negli scritti di al-Ḫāzin (metà del X sec.) e poi, qualche decennio dopo, in quelli di Ibn al-Hayṯam si trovano dimostrate proprietà come le seguenti: (1) fra due poligoni convessi, di cui uno sia regolare e l'altro qualunque, aventi ugual numero di lati e ugual perimetro, il poligono regolare ha area maggiore (al-Ḫāzin); (2) fra due poligoni regolari aventi lo stesso perimetro, ha area maggiore quello che ha un maggior numero di vertici (al-Ḫāzin e Ibn al-Hayṯam); (3) fra due poligoni regolari inscritti nello stesso cerchio, quello che ha maggior numero di lati ha perimetro maggiore e area maggiore (Ibn al-Hayṯam).
Stereometria
La situazione dei poliedri regolari differisce da quella dei poligoni: infatti sono solo cinque e negli Elementi sono tutti costruiti esplicitamente. In tutti e cinque i casi il metodo euclideo consiste nel costruire il poliedro utilizzando come dato soltanto il diametro della sfera, per dimostrare in un secondo tempo l'inscrittibilità del solido ottenuto. Euclide insiste sulla natura della relazione metrica fra lo spigolo del poliedro e il diametro della sfera. I matematici arabi affrontarono invece ‒ oltre a cercare approcci diversi a un problema di costruzione già risolto ‒ la scoperta e la costruzione dei poliedri semiregolari, vale a dire di quei poliedri inscrivibili le cui facce sono poligoni regolari non necessariamente identici. Ricordiamo in proposito che Pappo, nel Libro V della Collezione matematica, aveva elencato, senza dare indicazioni sulla loro costruzione, i tredici poliedri semiregolari proposti da Archimede in un libro oggi perduto: tuttavia sembra che né la Collezione di Pappo (eccezion fatta per il Libro VIII), né questo testo di Archimede siano stati trasmessi al mondo arabo e islamico.
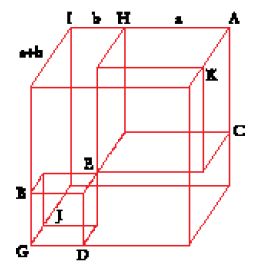
Nel IX sec. Ṯābit ibn Qurra dedicò un opuscolo alla costruzione di un poliedro inscrivibile a quattordici facce (sei quadrati e otto triangoli equilateri), ossia proprio uno dei tre decatetraedri proposti da Pappo.
Il suo metodo è l'opposto di quello seguito da Euclide per i poliedri regolari, nel senso che Ṯābit prima costruisce un poliedro inscritto nella sfera e dimostra poi che è semiregolare; inoltre non si interessa affatto alle relazioni metriche fra spigolo e diametro. In effetti, la costruzione inizia tracciando un esagono regolare AEFBCG inscritto in un cerchio massimo della sfera; tale esagono viene diviso in sei triangoli equilateri di vertice D, il centro della sfera. Si costruiscono poi sei tetraedri aventi per faccia questi sei triangoli: tre da un lato del piano dell'esagono (AEDH, FBDI e CGDK) e tre dall'altro. Per costruzione, i vertici di questi sei tetraedri (diversi da D) sono collocati sulla sfera. Congiungendo poi IH, IK, KH, FI, EH, AH, GK, CK e BI e i loro omologhi dall'altra parte del piano dell'esagono, per ottenere il decatetraedro basta dimostrare (utilizzando ripetutamente il teorema di Pitagora diretto e inverso) che EHIF è un quadrato.
Nel secolo successivo Abū 'l-Wafā᾽ al-Būzǧānī dedicò ai poliedri semiregolari l'ultimo capitolo del suo libro Fī mā yaḥtāǧu al-ṣāni῾ min al-a῾māl al-handasiyya (Sulle costruzioni geometriche indispensabili all'artigiano). In questo testo sono discusse le costruzioni dei cinque solidi regolari e di vari poliedri semiregolari. Ancor più che in Ṯābit, ci troviamo qui di fronte a una tendenza ormai affermata che si contrappone al procedimento euclideo: quella di far astrazione dalle considerazioni metriche per rivolgersi solamente alla forma del solido inscritto e alla descrizione dei procedimenti geometrici necessari per ottenerlo. Eloquentemente, Abū 'l-Wafā᾽ non formula il problema generale in termini di poliedri, ma ‒ in modo equivalente ‒ in termini di suddivisione della superficie della sfera in poligoni sferici equilateri ed equiangoli. Le costruzioni saranno quindi effettuate quasi esclusivamente sulla superficie della sfera, utilizzando in modo massiccio il tracciato di cerchi massimi. Meglio ancora, Abū 'l-Wafā᾽ si spingerà fino a tentare ‒ anche se nel caso dell'icosaedro la costruzione risulta erronea ‒ una soluzione che, per ogni solido, faccia a meno della conoscenza del diametro della sfera.
Consideriamo un esempio semplice, quello della costruzione del tetraedro. Si parte da tre cerchi massimi ortogonali a coppie, che formano dunque otto triangoli sferici equilateri (abbiamo così la costruzione dell'ottaedro); si considerino poi il centro di uno di questi triangoli e quello dei tre triangoli che gli sono opposti al vertice e si traccino quattro cerchi, ciascuno passante per tre di questi punti. La superficie sferica è stata così divisa in quattro triangoli sferici equilateri, il che equivale alla costruzione del tetraedro. Aggiungiamo che Abū 'l-Wafā᾽ propone un enunciato che non si trova né in Euclide né in Pappo (anche se nel Libro II di Ipsicle ci sono indicazioni in questo senso): il cubo e l'ottaedro, così come l'icosaedro e il dodecaedro sono poliedri duali, nel senso che il centro del poligono sferico dell'uno serve come vertice all'altro e viceversa.
Basandosi sul suo metodo, Abū 'l-Wafā᾽ fornisce anche vari procedimenti per la costruzione dei poliedri semiregolari, fondati tutti sullo stesso principio: suddividere la superficie sferica in modo corrispondente alla costruzione di un poliedro regolare, per ritagliare, per mezzo di cerchi massimi, opportuni poligoni sferici ai vertici. Egli ritrova in questo modo il decatetraedro di Ṯābit, ottenuto questa volta o ritagliando dei quadrati ai vertici di un ottaedro inscritto, o ritagliando dei triangoli equilateri ai vertici di un cubo inscritto. Abū 'l-Wafā᾽ propone inoltre la costruzione di quattro poliedri semiregolari nuovi, le cui facce sono: dodici pentagoni e venti triangoli (ritagliando pentagoni ai vertici di un icosaedro o triangoli ai vertici di un dodecaedro); dodici pentagoni e venti esagoni (ritagliando esagoni ai vertici di un icosaedro); sei quadrati e otto esagoni (ritagliando quadrati ai vertici di un ottaedro); quattro triangoli e quattro esagoni (ritagliando triangoli ai vertici di un tetraedro).
Oltre a questo rinnovamento dei procedimenti costruttivi e della teoria a essi associata, ritroviamo i poliedri regolari anche nel campo della matematica infinitesimale, in cui diventano oggetto di sviluppi analoghi a quello dei poligoni regolari. L'opera sopra citata di Ibn al-Hayṯam e dedicata allo studio degli isoperimetri e degli isepifani (solidi aventi la stessa superficie) comprende, in particolare, i seguenti risultati che, per forza di cose, riguardano solo tetraedri, ottaedri e icosaedri: fra due poliedri regolari simili che abbiano superficie totale uguale, ha maggior volume quello che ha il maggior numero di facce; e, fra due poliedri regolari aventi facce simili inscritti in una stessa sfera, ha maggiore superficie e maggiore volume quello che ha il maggior numero di facce. Per ottenere questi risultati, dimostrati in tutta generalità anche se il campo di applicazione si riduce a tre tipi di solidi, Ibn al-Hayṯam stabilisce cinque lemmi che trattano di disuguaglianze di rapporti fra angoli solidi e di rapporti fra aree.
Sembra che sia questa "la prima applicazione estensiva e importante dell'angolo solido e, pertanto, il primo studio di un certo peso di alcune delle sue proprietà" (Rashed 1993, p. 332). Negli Elementi il concetto di angolo solido è in effetti molto poco sviluppato: due sole proposizioni per enunciarne le proprietà. Nel Libro XI, la prop. 20 afferma che se un angolo solido è compreso fra tre angoli piani, la somma di due di loro è maggiore del terzo; e la prop. 21 dimostra che la somma degli angoli piani che formano un angolo solido è minore di quattro retti. Quest'ultimo enunciato viene utilizzato una sola volta, alla fine della prop. 18 del Libro XIII, per dimostrare che i poliedri regolari sono solo cinque; l'utilizzazione dell'angolo solido nei problemi di costruzione non va oltre la prop. 27 del Libro XI, che serve a costruire su una retta data un parallelepipedo simile a un parallelepipedo dato.
La prima innovazione di Ibn al-Hayṯam consiste nel considerare rapporti fra angoli solidi, ammettendo così che questi possano essere visti come grandezze. Nel suo Šarḥ muṣādarāt kitāb Uqlīdis fī 'l-Uṣūl, libro che probabilmente precedeva il lavoro che stiamo qui considerando, egli riprendeva ancora una delle obiezioni che allora circolavano correntemente contro il fatto che un angolo piano possa essere pensato come una grandezza: i multipli di un angolo possono essere nulli o non essere angoli, mentre i multipli di una grandezza devono sempre essere una grandezza. Nella dimostrazione di uno dei primi risultati del suo studio sugli isepifani, Qawl fī anna al-kura awsa῾ al-aškāl al-muǧassama (Opuscolo sulla sfera che è la più grande delle figure solide) Ibn al-Hayṯam considera precisamente ciò che corrisponde alla definizione euclidea di uguaglianza di rapporti, ossia gli equimultipli di angoli solidi: tali multipli sono anch'essi angoli solidi ‒ come Ibn al-Hayṯam stesso sottolinea ‒ e la dimostrazione si conclude con queste parole: "e se non si può prendere il multiplo in una sola sfera, si prenda il multiplo in due sfere o più" (Qawl fī anna al-kura, p. 408). Si vede qui emergere una modificazione radicale nella concezione della nozione di angolo solido, che non è più ‒ com'era in Euclide ‒ una semplice relazione, anche se si poteva suddividerla o addizionarla, ma una vera e propria grandezza il cui studio, se sviluppato, avrebbe potuto, nel caso piano, portare al concetto di congruenza modulo 2π.
Diamo qui due esempi dei cinque lemmi che, di fatto, costituiscono lo studio condotto sugli angoli solidi da Ibn al-Hayṯam; potranno dare un'idea dei risultati raggiunti:
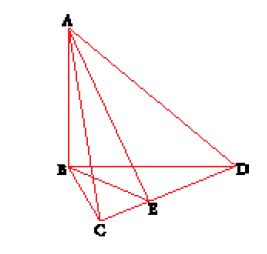
a) sia ABCD una piramide (fig. 15) tale che ABC∧≥π/2 e AB∧D≥π/2; se E è un punto di BD tale che AEC∧≥π/2 o A∧CE≥π/2, allora:
b) sia ABCD una piramide (fig. 16) tale che AB sia perpendicolare al piano (BCD) e B∧CD≥π/2; se E è un punto del segmento CD, allora:
area DBC angolo solido (A, BDC)
Il metodo utilizzato per dimostrare questi lemmi fa sì che tale trattato sia forse uno dei testi matematici più difficili dell'epoca: Ibn al-Hayṯam combina l'uso della proiezione conica con la determinazione infinitesimale di 'fette' piramidali. Siamo dunque assai lontani dalla tradizione degli Elementi propriamente detta; tuttavia fu proprio grazie all'integrazione con tecniche provenienti da altre tradizioni (proiezioni, matematica infinitesimale) che un concetto come quello di angolo solido poté conoscere un rinnovamento così notevole.
La divisione delle figure
La storia del trattato euclideo Divisioni delle figure e delle sue derivazioni è alquanto complessa. Come abbiamo osservato in precedenza, il testo greco è da considerarsi perduto, così come la traduzione araba fatta da Ṯābit ibn Qurra. Sembra che il testo arabo fosse stato tradotto in latino da Gherardo da Cremona, ma non ci è pervenuta nemmeno questa traduzione. Ci restano però interi capitoli dedicati alla soluzione di questo tipo di problemi composti da autori come Abū 'l-Wafā᾽ al-Būzǧānī (in arabo), ᾽Avrāhām bar Ḥiyya (in ebraico), e Leonardo Fibonacci, Giordano Nemorario o Luca Pacioli (in latino), i quali testimoniano l'esistenza di una tradizione reale.
Per precisare la portata dell'opera euclidea disponiamo tuttavia (a parte una testimonianza di Proclo) di un riassunto composto nel X sec. da al-Siǧzī, probabilmente sulla base della traduzione di Ṯābit. Questo riassunto fu ritrovato e tradotto in francese da Franz Woepcke nel 1851; recentemente è stata fatta un'edizione del testo arabo (Hogendijk 1993). È costituito da trentasei proposizioni di cui solamente quattro sono accompagnate da una dimostrazione, dato che al-Siǧzī pensava che le altre potessero essere dimostrate facilmente. Raymond Clare Archibald (1915) si basò su questo testo, oltre che sulla quarta sezione della Practica geometriae (1220) di Leonardo Fibonacci, per tentare la sua ricostruzione del trattato euclideo originale.
Inoltre, fino alla scoperta fatta da Woepcke, serpeggiò per lungo tempo la tentazione di attribuire a Euclide un trattato composto sullo stesso argomento da un certo Machometus Bagdedinus (Muḥammad al-Baġdādī) la cui esatta identità non è stata ancora precisata. Una copia latina di questo testo fu esemplata nel corso del XVI sec. dal matematico inglese John Dee (1527-1608), che utilizzò un manoscritto oggi non più disponibile; il testo di Dee fu pubblicato nel 1570 e David Gregory (1659-1708) l'aggiunse alla sua edizione degli Elementi.
I problemi di divisione di campi fra vari eredi sono certamente di origine assai antica e se ne possono trovare esempi nelle matematiche egizie e babilonesi. È possibile che l'opera euclidea Divisioni delle figure sia nata dal solco di queste tradizioni. Ma, nonostante autori come Abū 'l-Wafā᾽ o Leonardo Fibonacci utilizzino il pretesto dei campi da dividere fra gli aspiranti a un'eredità per introdurre i loro capitoli, non è però sicuro che il testo euclideo presentasse questo genere di considerazioni pratiche. Al contrario, la testimonianza di Proclo tende chiaramente a considerare il progetto euclideo sotto un aspetto molto più speculativo, completamente rivolto verso il concetto di figura. I metodi utilizzati per risolvere questi problemi variano anch'essi da un autore all'altro: in certuni le soluzioni sono completamente geometriche; in altri, come in Erone, presentano esemplificazioni numeriche; in altri ancora sono sostenute da tecniche algebriche.
Lasciando da parte due proposizioni in cui la figura considerata è un cerchio, o è limitata parzialmente da un arco di cerchio, le figure di cui si occupa il trattato euclideo ‒ almeno per come è descritto dal riassunto di al-Siǧzī ‒ sono triangoli o quadrilateri. Si tratta di dividere tali figure in due parti per mezzo di una trasversale passante per un punto dato o parallela a uno dei lati, in modo che queste due parti siano o uguali, o tali che una di esse sia una data parte della figura totale oppure in un rapporto dato con questa; a meno che non si tratti di dividere un triangolo o un trapezio in tre parti uguali servendosi di una retta parallela alla base, ma in questo caso il procedimento non differisce sostanzialmente da quello della divisione in due parti. Per risolvere questi problemi Euclide fa uso all'inizio di nozioni piuttosto elementari, ricavabili dagli Elementi: la prop. 19 del Libro VI (triangoli simili stanno fra loro come il quadrato del rapporto dei loro lati omologhi), la prop. 37 del Libro I (triangoli di stessa base posti fra due parallele sono uguali) e la prop. 1 del Libro VI (triangoli e parallelogrammi di stessa altezza stanno fra loro come le basi). Ricorda poi un caso particolare della prop. 28 di quest'ultimo libro (applicare a una retta data un rettangolo uguale a un rettangolo dato e mancante di un quadrato) per dimostrare nel seguito proposizioni più difficili. Il trattato euclideo è dunque organizzato in funzione di una scala di difficoltà crescente.
I lavori di Abū 'l-Wafā᾽, di Muḥammad al-Baġdādī, di Leonardo Fibonacci e degli altri autori latini rimangono tutti inquadrati in questo schema euclideo della divisione di una figura in due parti. Le loro trattazioni sono però organizzate in modi diversi, in funzione del crescere del numero dei lati della figura considerata. Tuttavia se Muḥammad arriva fino al pentagono e Fibonacci si spinge fino all'esagono, lo spirito generale è sempre il medesimo, dato che i problemi rimangono relativamente semplici e gli strumenti utilizzati sono sempre gli stessi, anche se si possono rilevare alcune variazioni fra un autore e un altro.
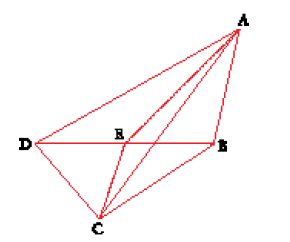
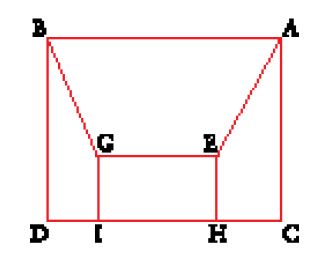
Diverso è invece il caso di un'altra categoria di problemi affrontati nel corso del X sec. in cui non ci si riduce più alla divisione della figura in due sole parti; tali problemi, di conseguenza, sono assai meno elementari. Ricordiamo che, sebbene al riguardo non possa essere stabilito alcun tipo di derivazione, problemi analoghi erano già affrontati nel Libro III della Metrica di Erone, testo dedicato alla divisione delle figure piane e solide. Un tipico problema, per esempio, è quello di dividere un triangolo ACB in quattro parti in modo che i triangoli AEF, ECD e BFD siano di uguale area e il triangolo EDF sia di area data (fig. 17).
Discussi all'epoca con i suoi corrispondenti, alcuni di questi problemi furono oggetto di una raccolta composta da al-Siǧzī; altri furono inseriti nel suo Kitāb fī 'l-masā᾽il al-muḫtāra, con problemi geometrici d'altra natura; il tutto unito dal filo conduttore del tema dell'analisi e della sintesi, dell'enunciazione dei diorismi e dei casi eventuali di indeterminazione: temi questi che costituivano all'epoca le attività geometriche più di moda. Al-Siǧzī risolve per esempio questo problema, che verrà ripreso due secoli dopo da Šaraf al-Dīn al-Ṭūsī (seconda metà del XIII sec.; fig. 18): dividere il parallelogramma ABDC in quattro parti, in modo che il parallelogramma EGIH e i trapezi ABGE, AEHC e BDIG stiano fra loro in certi rapporti dati. Šaraf al-Dīn al-Ṭūsī affronterà il problema considerando il caso particolare di un quadrato sottoponendolo a un trattamento algebrico.
Dato che gli strumenti euclidei elementari che abbiamo ricordato non potevano bastare per risolvere questi problemi, al-Siǧzī coglie l'occasione per estendere i risultati relativi all'applicazione delle aree, utilizzando in particolare due costruzioni che abbiamo citato prima (figg. 6 e 7): applicare a una retta data un parallelogramma con l'eccesso di un triangolo simile a un triangolo dato; applicare a una retta data un parallelogramma simile a un parallelogramma dato, con l'eccesso di un parallelogramma di area uguale a un'area data. È del resto naturale che i problemi di divisione di figure siano stati all'origine di questo genere di sviluppi, poiché il loro scopo consiste proprio nel passare da una condizione sulle aree a una condizione sui segmenti che le definiscono. In ogni caso, sia i risultati ottenuti sia il fatto che non ci siano fondamentali differenze nella trattazione fra questi problemi geometrici e altri discussi all'epoca, spingono questo campo di ricerca lontano da quello della geometria pratica cui certi autori hanno voluto ridurre il trattato euclideo.
La tradizione dei 'Dati'
I Dati, un testo legato strettamente al campo dell'analisi, entrarono naturalmente a far parte degli strumenti utilizzati dai geometri nella soluzione dei problemi. Con l'intensificarsi dell'attività geometrica, e prima ancora che si sviluppasse una riflessione più matura sul ruolo dell'analisi e della sintesi, alcuni matematici tentarono di estendere i risultati dei Dati euclidei, cioè di formulare nuove proposizioni con lo stesso stile: se in una figura certi elementi sono noti, allora anche altri saranno noti.
Ṯābit ibn Qurra compose un'opera al riguardo il cui titolo (al-Mafrūḍāt, Le ipotesi) era sinonimo di quello dato alla traduzione araba dell'opera di Euclide (al-Mu῾ṭayyāt); essa verrà ripresa in seguito da Naṣīr al-Dīn al-Ṭūsī. Anche se le prime dodici proposizioni di Ṯābit sono di fatto problemi di costruzione, la maggior parte dei trentasei enunciati di cui è composta l'opera affronta effettivamente il problema dell'estensione dei Dati, dimostrando vari risultati ‒ in particolare sul cerchio ‒ assenti nell'opera euclidea. Uno di questi è il seguente: se i lati di un triangolo sono noti, è noto il diametro del cerchio circoscritto. Un secondo risultato (fig. 19) afferma che, se AB è il diametro di un cerchio e DG ed EC due perpendicolari ad AB: (1) se DE, DG ed EC sono noti, anche AB è noto; (2) se AE e (BE−CE) sono noti, anche AB è noto.
Ma due fattori finiranno per segnare il destino dei Dati. In primo luogo, lo sviluppo dell'algebra modificherà in modo del tutto naturale il procedimento stesso dell'analisi in certi campi di ricerca, rendendo così obsoleto il riferimento all'opera euclidea. In secondo luogo, da un punto di vista più specificamente geometrico, lo sviluppo crescente della riflessione sull'analisi e la sintesi porterà Ibn al-Hayṯam, nella sua Maqāla fī 'l-ma῾lūmāt, a inserire le proposizioni dei Dati in un insieme più vasto, nel contesto di una ridefinizione dei fondamenti stessi della geometria. Ma con l'introduzione del moto fra i principî della geometria, ci si situava ormai al di fuori della tradizione euclidea propriamente detta.
Bibliografia
Abgrall 2002: Abgrall, Philippe, L'oeuvre mathématique d'al-Qūhī (Thèse de doctorat, Paris VII, 2002).
Aghayani-Chavoshi 1996: Aghayani-Chavoshi, Jafar, L'oeuvre scientifique d'Abû al-Wafâ al-Buzjânî (Thèse de doctorat, Paris VII, 1996).
Archibald 1915: Archibald, Raymond C., Euclid's book on divisions of figures, Cambridge, Cambridge University Press, 1915.
Bellosta 1997: Bellosta, Hélène, Les mathématiciens arabes et le problème des 'Contacts', "Oriens-Occidens. Cahiers du Centre d'histoire des sciences et des philosophies arabes et médiévales", 1, 1997, pp. 105-122.
Bessel-Hagen 1933: Bessel-Hagen, Erich - Spies, Otto, Ṯābit b. Qurras Abhandlung über einen halbregelmäßigen Vierzehnflächner, "Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik", 2, 1933, pp. 186-198.
Crozet 1993: Crozet, Pascal, L'idée de dimension chez al-Sijzī, "Arabic sciences and philosophy", 3, 1993, pp. 251-286.
‒ 1997: Crozet, Pascal, Al-Sijzī et les 'Éléments' d'Euclide: Commentaires et autres démonstrations des propositions, in: Perspectives arabes et médiévales sur la tradition scientifique et philosophique grecque. Actes du colloque de la SIHSPAI, Paris 1993, édités par Ahmad Hasnawi, Abde- lali Elamrani-Jamal et Maroun Aouad, Leuven, Peeters; Paris, Institut du Monde Arabe, 1997, pp. 61-77.
‒ 1999: Crozet, Pascal, À propos des figures dans les manuscrits arabes de géométrie: l'exemple de Siǧzī, in: Editing islamic manuscripts on science, edited by Yusuf Ibish, London, Al-Furqān Islamic Heritage Foundation, 1999 [1420], pp. 131-163.
‒ 2000: Crozet, Pascal, Les problèmes de division des figures au Xe siècle, présenté au colloque de la SIHSPAI, Tunisi, 28 nov.-2 déc. 2000.
De Young 1984: De Young, Gregg R., The Arabic textual traditions of Euclid's 'Elements', "Historia mathematica", 11, 1984, pp. 147-159.
‒ 1991-92: De Young, Gregg R., Abū Sahl's additions to Book II of Euclid's 'Elements', "Zeitschrift für Geschichte der arabisch-islamischen Wissenschaften", 7, 1991-1992, pp. 73-135.
‒ 1992: De Young, Gregg R., Isḥāq ibn Ḥunayn, Ḥunayn ibn Isḥāq, and the third Arabic translation of Euclid's 'Elements', "Historia mathematica", 19, 1992, pp. 188-199.
Dold-Samplonius 1977: Dold-Samplonius, Yvonne, Book of Assumptions by Aqāṭun. Text-critical edition (Diss., Amsterdam Univ., 1977).
Engroff 1980: Engroff, John W., The Arabic tradition of Euclid's Elements: Book V (Ph.D., Harvard University, 1980).
Freudenthal 1988: Freudenthal, Gad, La philosophie de la géométrie d'al-Fārābī. Son commentaire sur le début du Ier livre et le début du Ve livre des 'Eléments' d'Euclide, "Jerusalem studies in Arabic and Islam", 11, 1988, pp. 104-219.
Heath 1926: Heath, Thomas L., The thirteen books of Euclid's Elements, 2. ed., Cambridge, Cambridge University Press, 1926, 3 v. (rist.: New York, Dover, 1956).
Heiberg 1884: Heiberg, Johann L., Die arabische Tradition der Elemente Euklids, "Zeitschrift für Mathematik und Physik. Historisch-literarische Abteilung", 29, 1884, pp. 1-22.
Hogendijk 1987: Hogendijk, Jan P., On Euclid's lost porisms and its Arabic traces, "Bollettino di storia delle scienze matematiche", 7, 1987, 1, pp. 93-115.
‒ 1993: Hogendijk, Jan P., The Arabic version of Euclid's On divisions, in: Vestigia mathematica. Studies in medieval and early modern mathematics in honour of H.L.L. Busard, edited by Menso Folkerts and Jan P. Hogendijk, Amsterdam-Atlanta, Rodopi, 1993, pp. 143-160.
Id 1969: Id, Yusuf - Kennedy, Edward S., A medieval proof of Heron's formula, "Mathematics teacher", 62, 1969, pp. 297-302 (rist. in: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, edited by David A. King, Mary Helen Kennedy, Beirut, American University of Beirut, 1983, pp. 492-494).
Klamroth 1881: Klamroth, Martin, Über den arabischen Euklid, "Zeitschrift der Deutschen Morgenländischen Gesellschaft", 35, 1881, pp. 270-326.
Knorr 1996: Knorr, Wilbur R., The wrong text of Euclid: on Heiberg's text and its alternatives, "Centaurus", 38, 1996, pp. 208-276.
Kunitzsch 1985: Kunitzsch, Paul, Findings in some texts of Euclid's Elements (mediaeval transmission, Arabo-Latin), in: Mathemata. Festschrift für Helmuth Gericke, hrsg. von Menso Folkerts und Uta Lindgren, Stuttgart, Steiner, 1985, pp. 115-128.
Murdoch 1971: Murdoch, John, Euclid. Transmission of the Elements, in: Dictionary of scientific biography, edited by Charles C. Gillispie and Frederic L. Holmes, New York, Scribner, 1970-1990, 18 v.; v. IV, 1971, pp. 437-459.
Rashed 1991: Rashed, Roshdi, L'analyse et la synthèse selon Ibn al-Haytham, in: Mathématiques et philosophie de l'antiquité à l'âge classique. Hommage à Jules Vuillemin, sous la direction de Roshdi Rashed, Paris, CNRS, 1991, pp. 131-162 (trad. ingl.: Analysis and synthesis according to Ibn al-Haytham, in: Artifacts, representations and social practice. Essays for Marx Wartofsky, edited by Carol C. Gould and Robert S. Cohen, Dordrecht, Kluwer, 1994, pp. 121-140).
‒ 1993: Rashed, Roshdi, Math. inf. II.
‒ 1996: Rashed, Roshdi, Math. inf. I.
‒ 1997: Rashed, Roshdi, Histoire des sciences arabes, sous la direction de Roshdi Rashed avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v. (ed. orig.: Encyclopedia of the history of Arabic science, London-New York, Routledge, 1996, 3 v.).
‒ 1999: Rashed, Roshdi - Vahabzadeh, Bijan: Al-Khayyām mathématicien, Paris, Blanchard, 1999 (trad. ingl.: Omar Khayyam. The mathematician, New York, Bibliotheca Persica, 2000; senza i testi arabi).
‒ 2000: Rashed, Roshdi - Bellosta, Hélène: Ibrāhīm ibn Sinān. Logique et géométrie au Xe siècle, Leiden, E.J. Brill, 2000.
Rommevaux 2001: Rommevaux, Sabine - Djebbar, Ahmed - Vitrac, Bernard, Remarques sur l'histoire du texte des 'Éléments' d'Euclide, "Archive for history of exact sciences", 55, 2001, pp. 221-295.
Sayili 1958: Sayılı, Aydın, Šâbit ibn Kurra'nin Pitagor teoremini tamimi, "Belleten", 21, 1958, pp. 527-549.
‒ 1959: Sayılı, Aydın, Thābit ibn Qurra's generalization of the Pythagorean theorem, "Isis", 51, 1959, pp. 35-37.
Shamsi 1970: Shamsi, Fazal Ahmad, Properties of triangles in respect of perpendiculars, in: Ibn al-Haitham. Proceedings of the celebrations of 1000th anniversary, edited by Hakim Mohammed Said, Karachi, Hamdard Academy, 1970, pp. 228-246.
Sude 1974: Sude, Barbara Hooper, Ibn al-Haytham's commentary on the premises of Euclid's 'Elements' (Sharḥ muṣādarāt kitāb Uqlīdis fī al-Uṣūl), books I-VI (Diss., Princeton University, 1974).
Thaer 1942: Thaer, Clemens, Euklids Data in arabischer Fassung, "Hermes", 77, 1942, pp. 197-205.
Vernet 1971-75: Vernet, Juan - Catalá, María Asunción, Dos tratados del Arquímedes árabe. Tratado de los círculos tangentes y el Libro de los triángulos, Barcelona, Memorias de la Real Academia de Buenas Letras, 1971-1975 (rist. in: Vernet, Juan, Estudios sobre historia de la ciencia medieval, Barcelona, Universidad de Barcelona; Bellaterra, Universidad Autónoma de Barcelona, 1979, pp. 33-80).
Woepcke 1851: Woepcke, Franz, Notice sur des traductions arabes de deux ouvrages perdus d'Euclide, "Journal asiatique", s. V, 4, 1851, 18, pp. 217-247 (v. anche Woepcke 1986, v. I, pp. 17-47).
‒ 1855: Woepcke, Franz, Analyse et extrait d'un recueil de constructions géométriques par Abou-l Wafā, "Journal asiatique", s. V, 5, 1855, feb.-mar., pp. 218-256; apr., pp. 309-359 (v. anche Woepcke 1986, v. I, pp. 483-572).
‒ 1986: Woepcke, Franz, Études sur les mathématiques arabo-islamiques, hrsg. von Fuat Sezgin, Frankfurt a.M., Institut für Geschichte der Arabisch-Islamischen Wissenschaften, 1986, 2 v.