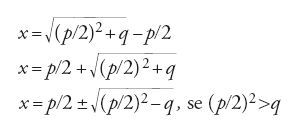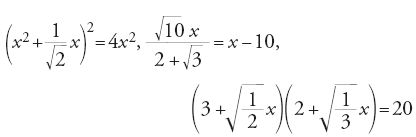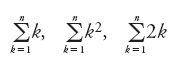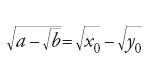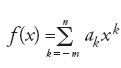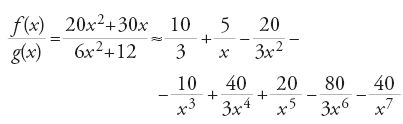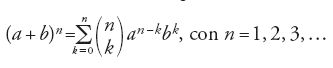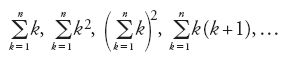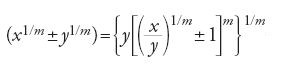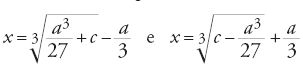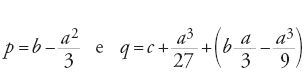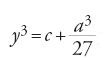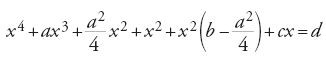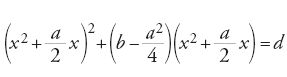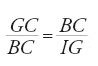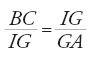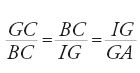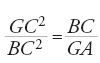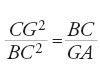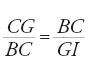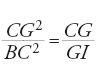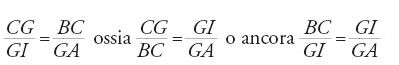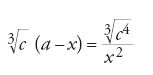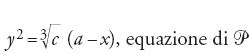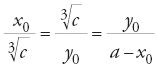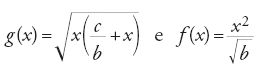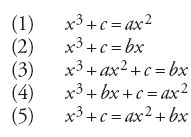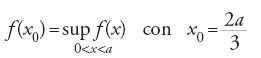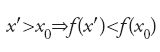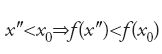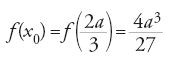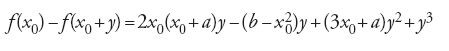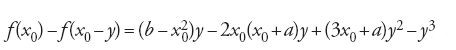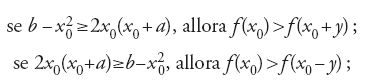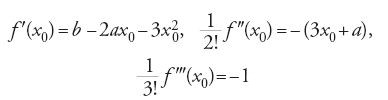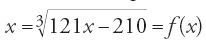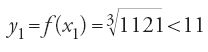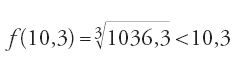La civiltà islamica: antiche e nuove tradizioni in matematica. L'algebra e il suo ruolo unificante
La civilta islamica: antiche e nuove tradizioni in matematica. L'algebra e il suo ruolo unificante
L'algebra e il suo ruolo unificante
La seconda metà del VII sec. vede il costituirsi dell'Impero islamico, il cui consolidamento istituzionale e culturale si verificherà durante il secolo successivo con la fioritura di molte discipline direttamente legate alla nuova società e alla sua ideologia. Si assiste così a numerosi tentativi di fondare e sviluppare discipline ermeneutiche e coraniche, linguistiche, giuridiche, storiche e teologiche. Per misurare l'ampiezza di questo movimento intellettuale senza precedenti basta pensare alle scuole di Kufa e di Bassora, nella seconda metà dell'VIII secolo. Non si sottolineerà mai abbastanza l'importanza che ha avuto all'epoca la ricerca in queste discipline: essa ha permesso la creazione dei mezzi necessari per recepire e integrare altre scienze, come la matematica e le discipline filosofiche, ed è sempre questa ricerca che ha anche favorito la domanda di tali materie, preparandone il terreno. Questa ricerca, perseguita, ampliata e diffusa in varie direzioni nel IX sec., ha condotto a due risultati epistemici fondamentali: una nuova classificazione delle scienze e una nuova concezione dell'enciclopedia del sapere. L'una e l'altra, stabilite sul terreno della ricerca scientifica vera e propria, saranno amplificate dalla presa di coscienza da parte dei filosofi. Per convincersene, basta leggere per esempio l'Iḥṣā᾽ al-῾ulūm (Enumerazione delle scienze) di al-Fārābī. Costituitasi all'inizio del IX sec., l'algebra ebbe un ruolo fondamentale in questa nuova classificazione come pure nella concezione della nuova enciclopedia. Ma questo evento, la nascita dell'algebra intorno all'820, non può essere compreso se non si chiarisce il contesto intellettuale dell'VIII sec. e non si tiene conto della domanda proveniente dalle ricerche effettuate nelle discipline sopra ricordate. È proprio questa domanda, infatti, che fornirà all'algebra dei campi di applicazione, cioè quella che può definirsi la sua ragione sociale.
Per delineare un quadro del contesto intellettuale (qualcuno direbbe epistemico) di questo secolo, sarebbero necessarie un'opera di vasto respiro e numerose competenze per evitare giudizi arbitrari. Noi ci limiteremo in questa sede a mettere in luce alcuni aspetti, basandoci su due esempi soltanto. Il primo si deve al fondatore della prosodia araba e della lessicografia, al-ḫalīl ibn Aḥmad, così come ai suoi successori; quest'ultimo ha elaborato gli elementi di analisi combinatoria necessari per i fondamenti della prosodia e per quello che sarà il primo dizionario di arabo. Il metodo consiste nell'elaborare a priori tutte le possibilità. Nella lessicografia, la parte foneticamente realizzata, secondo le regole della fonologia elaborate da lui stesso, costituisce la lingua reale. Questo modo di procedere era reso possibile da una concezione positiva della lingua, teologicamente neutra, e da una nuova concezione dell'oggetto linguistico. La lingua comprende sia la 'lingua divina' ‒ il Corano ‒ sia la 'lingua dei pagani' parlata dagli Arabi prima dell'Islam, che conosciamo grazie alla poesia e allo studio etnolinguistico, ben vivo all'epoca. Ma il fatto ancora più importante è che il nuovo oggetto linguistico è una combinazione di fonemi indipendente da ogni materia fonetica, un'associazione formale di fonemi che dà luogo a parole possibili, a prescindere dal valore fonetico e semantico.
In questa disciplina, come nella prosodia e in altre attività dell'epoca, le disposizioni e le combinazioni di elementi prive di significato producono, in quanto tali, conoscenze certe. Nel contesto intellettuale dell'VIII sec. una tale concezione dell'oggetto della conoscenza era dunque considerata ammissibile, e gli algebristi vi si adattarono perfettamente. Ricordiamo che lo stesso al-ḫalīl era un matematico; aveva anche composto un calcolo, che non ci è mai pervenuto.
L'attività di al-ḫalīl riflette un ulteriore aspetto dello scenario intellettuale del tempo: non vi sono compartimenti stagni tra arte e scienza, né nella pratica, né soprattutto sul piano teorico. Lo scopo di una scienza, per esempio la lessicografia, si trova al di fuori della scienza stessa, anche se ciò non le impedisce di essere apodittica: mira manifestamente a razionalizzare una pratica senza cessare di essere una teoria. Un'arte a sua volta può essere pensata come un mezzo tecnico per risolvere un problema teorico: la composizione della lingua, per restare nel nostro esempio. Anche un rapporto di questo tipo si addiceva agli algebristi. Questo esempio tratto dal campo linguistico mostra se non altro che alla vigilia della nascita dell'algebra era già stata elaborata una nozione di conoscenza apodittica, come pure dell'oggetto di questa conoscenza, che si addiceva perfettamente agli algebristi. In questo senso, il contesto intellettuale dell'VIII sec. era piuttosto favorevole alla nascita dell'algebra, rendendo facile e naturale l'inserimento di questa disciplina nell'ambito del sapere dell'epoca.
Il secondo esempio mostra come, fornendo all'algebra dei campi di applicazione, gli studiosi dell'VIII sec. parteciparono alla costruzione dei suoi vari capitoli. La giurisprudenza vede nascere in quello stesso periodo tre scuole principali, legate ai nomi di grandi maestri: Abū Ḥanīfa, il fondatore della scuola che porta il suo nome, morirà nel 767; l'allievo Abū Yūsuf nel 798; Mālik ibn Anas, capo della Scuola di Medina, nel 795; e infine al-Šāfi῾ī, fondatore della terza scuola, nell'820. Questi eminenti giuristi e i loro allievi scrivono anche di teoria del diritto, ed è per questo lavoro che i loro successori li paragonano, per la logica, ad Aristotele. Ma ciò che qui ci interessa è lo sviluppo in queste scuole, nel corso dell'VIII sec., di lavori di diritto civile relativi in particolare ai testamenti e alle successioni secondo le regole dettate dal Corano. Si tratta di regole spesso molto complesse che per essere rispettate con precisione richiedono l'invenzione di un vero e proprio calcolo, che si presenta subito come un calcolo di tipo algebrico. Muḥammad ibn Ḥasan al-Šaybānī (749-803), allievo di Abū Ḥanīfa e di Mālik ibn Anas, scrive un libro intitolato proprio Ḥisāb al-waṣāya (Calcolo dei testamenti). Vedremo che un intero capitolo, che costituisce i 5/12 del libro fondamentale di al-Ḫwārizmī, è dedicato a questo calcolo. Lo sviluppo di questo capitolo darà luogo a una disciplina algebrica che avrà lo stesso nome, o anche quello di ḥisāb al-farā᾽iḍ (Calcolo delle obbligazioni). Un campo di ricerca per algebristi e giuristi che sarà oggetto d'insegnamento nelle scuole di diritto, prima fra tutte la Madrasa Niẓāmiyya, quando queste saranno istituite nell'XI secolo.
Gli inizi dell'algebra: al-Ḫwārizmī
È in questo contesto che Muḥammad ibn Mūsā al-Ḫwārizmī scrive un libro dal titolo Kitāb al-ǧabr wa-'l-muqābala (Libro dell'algebra, noto semplicemente come Algebra). La pubblicazione di quest'opera durante il regno del califfo al-Ma᾽mūn (tra l'813 e l'833) è un avvenimento importante nella storia della matematica. Per la prima volta compare in un titolo il termine 'algebra' per denotare una disciplina ben distinta e dotata di un proprio vocabolario tecnico.
Al-ǧabr (algebra) è in effetti una parola araba, nome d'azione di un verbo, un maṣdar come dicono i grammatici, la cui radice ha il senso generale di rettificare qualcosa per mezzo di una costrizione (per es., rimettere a posto un osso rotto). Si tratta perciò di una parola della lingua comune che può ricoprire molti significati. Priva di qualunque significato tecnico prima di al-Ḫwārizmī, con lui ne avrà due: in associazione con un'altra parola, al-muqābala, indica una disciplina e allo stesso tempo un'operazione. I successori di al-Ḫwārizmī non tarderanno a privilegiare la prima parola per denominare la disciplina, e facendo derivare poi da questa sola parola il nome della professione, 'algebrista'. Ciò accade già con Ṯābit ibn Qurra (826-901). Ma anche la seconda parola indica un'operazione: 'restaurare' un'equazione, cioè aggiungere ai due membri i termini sottratti. Per esempio, nell'equazione che con la notazione moderna si scrive
[1] x2+c−bx=d, con c>d,
l'operazione 'algebra' consiste nell'aggiungere a entrambi i membri la quantità bx:
[2] x2+c=bx+d,
mentre l'operazione al-muqābala, cioè 'opposizione' o 'riduzione' equivale a:
[3] x2+(c−d)=bx.
Le due operazioni insieme hanno lo scopo di ridurre l'equazione originaria a uno dei tipi canonici definiti a priori da al-Ḫwārizmī.
Così tra l'813 e l'833, un matematico e astronomo di Baghdad, membro illustre del Bayt al-Ḥikma (Casa della sapienza) scrive un libro con questo titolo, utilizzando la detta terminologia tecnica. Questo fatto è cruciale, e tale viene riconosciuto dagli storici antichi e moderni. La sua importanza non sfuggì alla comunità matematica dell'epoca né a quella dei secoli successivi. A proposito di al-Ḫwārizmī, Abū Kāmil scrive: "colui che è giunto per primo al libro di algebra e di al-muqābala, colui che l'ha cominciato, e inventato tutti i fondamenti che vi si trovano" (Kitāb fī 'l-ǧabr wa-'l-muqābala, f. 2r). Sempre Abū Kāmil scrive: "nel mio secondo libro (al-waṣāya bi-'l-ǧabr) ho dato la prova dell'autorità e della priorità in algebra e al-muqābala di Muḥammad ibn Mūsā al-Ḫwārizmī, e ho risposto all'irruenza di Ibn Barza a proposito di quanto egli attribuisce a ῾Abd al-Ḥāmid, che dice essere suo nonno" (Ḥāǧǧī Ḫalīfa, Kašf al-ẓunūn, ed. Yatkaya, II, pp. 1407-1408).
Le testimonianze in questo senso abbondano e potremmo moltiplicarle. Sinān ibn al-Fatḥ, nell'introduzione dell'Opuscolo, menziona soltanto al-Ḫwārizmī attribuendogli l'algebra: "Muḥammad ibn Mūsā al-Ḫwārizmī ha composto un libro che ha chiamato algebra e al-muqābala".
Il libro di al-Ḫwārizmī non ha mai smesso di essere una fonte d'ispirazione e oggetto di commento da parte dei matematici, non soltanto in arabo e in persiano, ma anche in latino e nelle lingue dell'Europa occidentale. L'evento è in apparenza paradossale: alla novità della concezione, del vocabolario e dell'organizzazione dell'opera di al-Ḫwārizmī si contrappone la semplicità delle tecniche matematiche utilizzate, se confrontate con quelle delle composizioni matematiche celebri, per esempio le opere di Euclide e di Diofanto. Ma questa semplicità tecnica è dovuta proprio alla nuova concezione matematica di al-Ḫwārizmī. A un osservatore superficiale il suo libro può sembrare un'opera certamente pregevole, ma che non si segnala per la novità: la maggior parte delle idee di al-Ḫwārizmī si può ritrovare in questo o quel predecessore. Se alcuni punti del suo progetto, però, si possono rinvenire nei Babilonesi di 25 secoli prima, altri negli Elementi di Euclide, altri ancora nell'Aritmetica di Diofanto, in nessuno scritto precedente essi sono stati organizzati in quel modo dando vita a una nuova disciplina fino ad allora impensata. Vediamo quali sono questi punti, e qual è questa organizzazione. Lo scopo di questo studioso, mai perseguito prima di lui, è chiaro: elaborare una teoria delle equazioni risolubili per radicali, equazioni alle quali sono riducibili problemi sia aritmetici sia geometrici, per potersene servire nel calcolo, negli scambi commerciali, nei problemi di eredità, di misurazione dei terreni, ecc. La nuova disciplina è deliberatamente rivolta alle applicazioni: al-Ḫwārizmī lo dichiara apertamente fin dall'introduzione. Il campo di applicazione comprende problemi aritmetici e geometrici, e il libro è organizzato secondo questo scopo.
Nella prima parte del testo lo studioso definisce i termini primitivi della teoria. Questi, per l'esigenza della risoluzione per radicali e per via delle sue conoscenze nel campo, potevano riguardare soltanto le equazioni dei primi due gradi. Si tratta dell'incognita, detta indifferentemente 'radice' o 'cosa', del quadrato di questa, dei numeri razionali positivi, delle leggi dell'aritmetica riguardo alle quattro operazioni fondamentali, all'estrazione di radice, all'uguaglianza. I concetti principali introdotti in seguito da al-Ḫwārizmī sono l'equazione di primo grado, di secondo, i binomi e i trinomi relativi, la forma normale, le soluzioni algoritmiche e la dimostrazione della formula che fornisce la soluzione. Il concetto di equazione compare nel libro di al-Ḫwārizmī per indicare una classe infinita di problemi, e non come presso i Babilonesi al momento della soluzione di un problema particolare. D'altra parte le equazioni stesse non sono presentate nel corso dei problemi da risolvere, come nei Babilonesi e in Diofanto, ma fin dall'inizio, a partire dai termini primitivi le cui combinazioni debbono dare tutte le forme possibili. Egli introduce quindi, subito dopo aver definito i termini primitivi, i sei tipi seguenti di equazioni:
[4] ax2=bx, ax2=c, bx=c, ax2+bx=c, ax2+c=bx, ax2=bx+c.
Introduce in un secondo momento la nozione di forma normale richiedendo che ognuna delle equazioni precedenti sia ridotta alla corrispondente forma normale. In particolare, per i trinomi si ha:
[5] x2+px=q, x2=px+q, x2+q=px.
Successivamente passa alla determinazione delle formule algoritmiche delle soluzioni. Tratta allora i vari casi e ottiene rispettivamente formule equivalenti alle espressioni seguenti:
e in quest'ultimo caso precisa che se (p/2)2=q, "allora la radice del quadrato [māl] è uguale alla metà del numero delle radici, esattamente, senza eccesso né difetto"; se (p/2)2⟨q, "allora il problema è impossibile" (Kitāb al-ǧabr wa-'l-muqābala, ed. 1939, pp. 20-21).
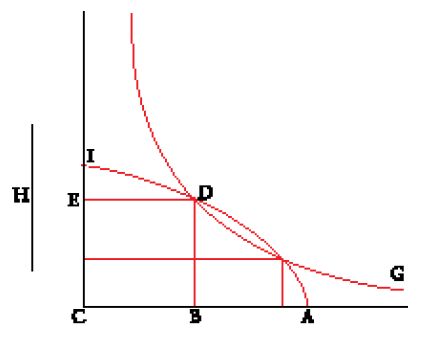
Al-Ḫwārizmī dimostra anche le varie formule, non algebricamente bensì mediante l'uguaglianza di aree, ispirato verosimilmente da una conoscenza recente degli Elementi di Euclide, tradotti da al-Ḥaǧǧāǧ ibn Maṭar, anch'egli al Bayt al-Ḥikma. Ognuna di queste dimostrazioni viene definita ῾illa (causa) della soluzione. Al-Ḫwārizmī non solo richiede una dimostrazione per ogni caso, ma a volte per un medesimo tipo di equazioni ne propone due. Tale esigenza mostra bene la distanza che separa al-Ḫwārizmī non soltanto dai Babilonesi, ma anche, per la sua sistematicità, da Diofanto. Per l'equazione x2+px=q, prende due segmenti AB=AC=x, quindi CD=BE=p/2 (fig. 1). Se la somma delle aree ABMC, BENM, DCMP è uguale a q, allora la superficie del quadrato AEOD è uguale a (p/2)2+q, da cui segue la soluzione:
Con al-Ḫwārizmī i concetti della nuova disciplina, e in particolare la cosa, cioè l'incognita, non denotano qualcosa di particolare, ma un oggetto che può essere indifferentemente numerico o geometrico, e d'altra parte gli algoritmi di risoluzione devono essere anch'essi oggetto di dimostrazione. È questo il contributo principale di al-Ḫwārizmī. Secondo lui tutti i problemi trattati in algebra, siano essi aritmetici o geometrici, devono essere riportati a un'equazione in una sola incognita a coefficienti razionali positivi e al più di secondo grado. Le operazioni algebriche ‒ trasposizione e riduzione ‒ si applicano per mettere l'equazione in forma normale. Ciò rende possibile l'idea della soluzione come procedura semplice di decisione, un algoritmo per ogni classe di problemi. La formula della soluzione è poi giustificata matematicamente da una dimostrazione di tipo geometrico, e al-Ḫwārizmī può allora scrivere che tutto ciò che è relativo all'algebra "deve condurre a uno dei sei tipi che ho descritto nel mio libro" (ibidem, p. 27).
Al-Ḫwārizmī inizia poi un breve studio di alcune proprietà dell'applicazione delle leggi elementari dell'aritmetica alle espressioni algebriche più semplici. Studia così i prodotti del tipo (a±bx)(c±dx), con a,b,c,d, numeri razionali positivi. Anche se all'apparenza rudimentale, si tratta comunque del primo tentativo di studio dedicato al calcolo algebrico in quanto tale; ai vari elementi di questo calcolo sono infatti dedicati capitoli relativamente autonomi. A questi capitoli ne seguono altri nei quali l'autore procede all'applicazione della teoria elaborata per risolvere problemi numerici e geometrici per poi trattare, infine, servendosi dell'algebra, problemi di eredità nei quali incontra questioni di analisi indeterminata.
All'inizio l'algebra si presenta perciò come una sorta di aritmetica, un'aritmetica delle incognite come qualcuno l'avrebbe chiamata dopo al-Ḫwārizmī, più generale non soltanto della 'logistica' ‒ essa permette infatti di risolvere i problemi di quest'ultima in modo più rigoroso grazie ai concetti che le sono propri ‒ ma anche di una geometria metrica. La nuova disciplina è infatti una teoria delle equazioni lineari e quadratiche a un'incognita risolubili per radicali, e del calcolo algebrico sulle espressioni relative, senza che si sia ancora concepita l'idea di polinomio. Osserviamo infine che questa nuova disciplina si costituisce senza ricorso ad alcun simbolismo, ma nei soli termini della lingua naturale. Si è però ben capito che i termini che entrano in combinazione, la cosa e il suo quadrato, sono visti come privi di un significato particolare, e funzionano per così dire come simboli. Un antico lettore, un giurista anonimo che ignorava ancora tutto del simbolismo, ha ideato una combinatoria dei giudizi giuridici, rappresentando ciascuno di essi con una lettera dell'alfabeto: "Designamo gli esempi [i giudizi] con lettere prive di significato in modo che queste siano produttive per sé stesse e non in ragione di una qualche materia esistenziale. Inoltre sono brevi e analoghe alle cose e ai quadrati (māl) che il calcolatore utilizza per determinare le incognite".
I successori di al-Ḫwārizmī: interpretazione geometrica e sviluppo del calcolo algebrico
Per cogliere l'idea che al-Ḫwārizmī aveva della nuova disciplina, come pure la fecondità di questa, non basta certo confrontare i suoi libri con le composizioni matematiche antiche. Occorre anche esaminare l'influenza che egli esercitò sui suoi contemporanei e i suoi successori, le ricerche cui la disciplina ha dato luogo, le tradizioni che ha saputo generare. Solamente allora questo studioso potrà mostrarsi nella sua vera dimensione storica. Ora uno degli aspetti essenziali del libro di al-Ḫwārizmī è proprio il fatto di aver immediatamente suscitato una corrente di ricerca in algebra. Al-Nadīm, biobibliografo del X sec. ci fornisce già una lunga lista dei contemporanei e dei successori di al-Ḫwārizmī che continuano le ricerche da lui iniziate. Tra gli altri vi figurano Ibn Turk, Sind ibn ῾Alī, Abū Ḥanīfa al-Dīnawarī, al-Ṣaydalānī, Ṯābit ibn Qurra, Abū Kāmil, Sinān ibn al-Fatḥ, al-Ḥubūbī, Abū 'l-Wafā᾽ al-Būzǧānī. Anche se un buon numero degli scritti di questi autori sono andati perduti, quelli che restano permettono di restituire le grandi linee di questa tradizione. Non è possibile però nei limiti di questo capitolo analizzare i singoli contributi; cercheremo soltanto di mettere in luce le principali linee dello sviluppo dell'algebra nel solco tracciato da al-Ḫwārizmī.
Al tempo di al-Ḫwārizmī e subito dopo si assiste in primo luogo all'estensione delle ricerche già intraprese da quest'ultimo: la teoria delle equazioni di secondo grado, il calcolo algebrico, l'analisi indeterminata e l'applicazione dell'algebra a problemi di successione, di ripartizione, e così via. La ricerca nella teoria delle equazioni ha preso strade diverse. La prima è quella già tracciata dallo stesso al-Ḫwārizmī, ma questa volta migliorandone le dimostrazioni protogeometriche: è la via seguita da ῾Abd al-Ḥāmid ibn Turk, che senza aggiungere nulla di nuovo riprende una discussione più serrata della dimostrazione. Più importante è quella seguita da Ṯābit ibn Qurra un po' più tardi. Questi ritorna infatti agli Elementi di Euclide, sia per stabilire una base geometrica più solida alle dimostrazioni di al-Ḫwārizmī, sia per tradurre in termini geometrici le equazioni di secondo grado. Ibn Qurra è d'altronde il primo che distingue nettamente tra i due metodi algebrico e geometrico cercando però di dimostrare che conducono allo stesso risultato, cioè all'interpretazione geometrica dei procedimenti algebrici. Nella sua opera Ibn Qurra comincia infatti con il dimostrare che l'equazione x2+px=q si può risolvere utilizzando la prop. 6 del Libro II degli Elementi. Alla fine della dimostrazione scrive: "questa via è in accordo con quella degli algebristi (aṣḥāb al-ǧabr)" (Fī taṣḥīḥ masā ᾽il al-ǧabr bi-'l-barāhīn al-handasiyya, f. 245r). Procede analogamente per x2+q=px e x2=px+q utilizzando rispettivamente le propp. 5 e 6 del Libro II degli Elementi, mostrando per ciascuna proposizione la corrispondenza con la soluzione algebrica, e scrive: "La via per risolvere questo problema, e quello che lo precede, mediante la geometria, è la via della risoluzione mediante l'algebra" (ibidem, f. 246v).
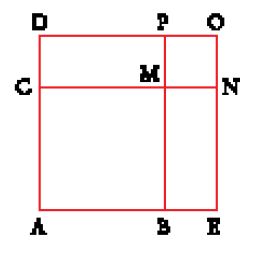
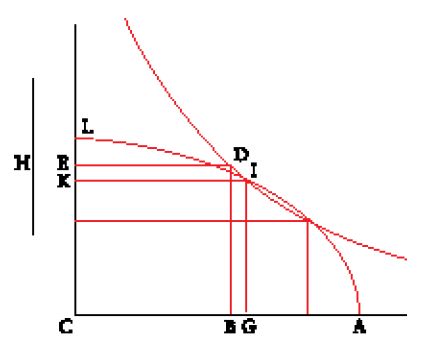
Ṯābit ibn Qurra sembra essere stato il primo a stabilire un parallelo tra al-Ḫwārizmī ed Euclide dando a un tempo un'interpretazione geometrica dell'algebra del primo e un'interpretazione algebrica della geometria del Libro II degli Elementi. Se l'espressione 'l'algebra geometrica dei Greci' che gli storici usano ha un senso, è solo dopo al-Ḫwārizmī e con Ṯābit ibn Qurra. Consideriamo ora un esempio dello studio di Ibn Qurra, importante per l'algebra e per la sua storia. Riprendiamo l'esempio della prima equazione di al-Ḫwārizmī, x2+px=q. Ibn Qurra pone x2 uguale a un quadrato ABCD (fig. 2); considera poi un'unità u, che è un'unità di lunghezza se l'incognita è una grandezza geometrica, ed è uguale a 1 se è un numero. Pone successivamente BE=pu; è chiaro che AB=xu. Ibn Qurra procede quindi con il seguente calcolo. Si ha AB∙BE=px=area (DE), e dunque area (CE)=x2+px=q, un numero noto. Il prodotto di EA per AB è noto e la retta (vale a dire, il segmento) BE anche; il problema si riporta quindi a un problema geometrico: "Una retta BE è nota, la si prolunghi di una retta AB in modo che il prodotto di EA per AB sia noto. Ora, nella sesta proposizione del Libro VI degli Elementi si dimostra che se si divide in due metà la retta BE nel punto F, il prodotto di EA per AB più il quadrato di BF è uguale al quadrato di AF. Ma il prodotto di EA per AB è noto e il quadrato di BF è noto, dunque il quadrato di AF è noto e AF è noto. Se si sottrae BF, che è noto, resta AB noto ed è la radice" (ibidem).
Ibn Qurra stabilisce allora la corrispondenza tra il metodo degli algebristi e quello dei geometri, e scrive:
Questa strada è in accordo con quella degli algebristi per risolvere questo problema. Quando questi (gli algebristi) considerano la metà del numero delle radici (p/2) è come quando noi consideriamo la metà della retta BE; e quando essi moltiplicano quella per sé stessa [(p/2)2], è come quando noi consideriamo il quadrato della metà di BE. Quando essi aggiungono il numero [q] a quanto hanno ottenuto è come quando noi aggiungiamo il prodotto di EA per AB per ottenere il quadrato della somma di AB più la metà della retta BE. Quando essi prendono la radice quadrata della somma è come quando noi diciamo: la somma di AB più la metà della retta BE è nota se è noto il quadrato. Quando essi sottraggono la metà del numero delle radici è come quando noi sottraiamo la metà di BE. Quando essi ottengono il resto, che è la grandezza della radice, è come quando noi sottraiamo la retta BF per ottenere il resto ottenendo AB. (ibidem, f. 245v)
Se abbiamo citato questo passo interamente, a dispetto della sua lunghezza, è perché volevamo mostrare che la doppia interpretazione di Ibn Qurra, geometrica in riferimento ad al-Ḫwārizmī, algebrica riguardo a Euclide, è a un tempo intenzionale e rigorosa.
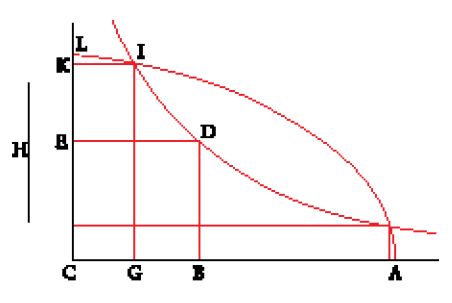
Altri matematici seguiranno un cammino analogo per fondare una teoria geometrica delle equazioni; faranno però appello al procedimento euclideo dell'applicazione delle aree, cioè al Libro VI degli Elementi. Uno di questi matematici scrive, in un manoscritto anonimo falsamente attribuito ad Abū Kāmil, copiato nel 581/1185:
Abbiamo mostrato che il procedimento che ha condotto alla determinazione dei lati di quadrati incogniti in ciascuna delle tre equazioni trinomie è quello esposto da Euclide alla fine del sesto libro della sua opera sugli Elementi, che consiste nell'applicare a una retta data un parallelogramma che rispetto al parallelogramma intero sia più grande o più piccolo di un quadrato. Infatti il lato del quadrato eccedente è il lato del quadrato incognito nel primo trinomio e nel secondo trinomio [x2+q=px, x2+px=q], e nel terzo trinomio è la somma della retta alla quale è applicato il parallelogramma e del lato del quadrato eccedente. (Mashhad, Āstān-i Quds, 5325, f. 24r-v)
Tuttavia, la traduzione geometrica da parte di Ibn Qurra delle equazioni di al-Ḫwārizmī si rivelerà particolarmente importante, come vedremo, per lo sviluppo della teoria delle equazioni algebriche. Un'altra traduzione, un po' differente, si ebbe quasi nello stesso periodo, e fu anch'essa fondamentale per lo sviluppo di tale teoria: la traduzione dei problemi di geometria in termini algebrici. Al-Māhānī, contemporaneo di Ibn Qurra, oltre a cominciare a tradurre certi problemi biquadratici del Libro X degli Elementi in equazioni algebriche, traduce anche un problema solido, vale a dire quello dato nell'opera Della sfera e del cilindro di Archimede, in un'equazione di terzo grado.
Un'altra direzione di sviluppo della teoria delle equazioni seguita all'epoca fu quella della ricerca della forma generale delle equazioni quadratiche
[8] ax2n+xn=c, ax2n+c=bxn, ax2n=bxn+c,
come possiamo verificare tra gli altri in Abū Kāmil e in Sinān ibn al-Fatḥ.
Si assiste inoltre, dopo al-Ḫwārizmī, all'estensione del calcolo algebrico. È questo forse il principale tema di ricerca, e il più diffuso presso gli algebristi che vennero dopo di lui. Si cominciò con l'estendere i termini stessi dell'algebra fino alla sesta potenza dell'incognita, come in Sinān ibn al-Fatḥ, e fino all'ottava, come in Abū Kāmil. Sinān ibn al-Fatḥ definisce in modo moltiplicativo queste potenze, a differenza di Abū Kāmil, che ne dà una definizione additiva. Sono però i lavori in campo algebrico di quest'ultimo che segnano l'epoca e anche la storia dell'algebra stessa. Oltre all'estensione del calcolo algebrico, il suo Kitāb fī 'l-ǧabr wa-'l-muqābala comprende un nuovo capitolo dell'algebra, l'analisi indeterminata o analisi diofantea razionale. Così, dopo aver ripreso la teoria delle equazioni dando dimostrazioni più rigorose di quelle dei suoi predecessori, egli studia in modo molto più approfondito ed esteso le operazioni aritmetiche sui binomi e i trinomi, dimostrando ogni volta il risultato ottenuto. Enuncia e giustifica la regola dei segni e stabilisce le regole del calcolo sulle frazioni prima di passare ai sistemi di equazioni lineari in più incognite e alle equazioni a coefficienti irrazionali, come per esempio
Abū Kāmil introduce nella sua algebra mezzi numerici ausiliari, alcuni dei quali si troverebbero in un libro di al-Ḫwārizmī andato perduto, come
e studia poi numerosi problemi che si riportano a equazioni di secondo grado.
Si vede così come le ricerche dei successori di al-Ḫwārizmī, soprattutto Abū Kāmil, abbiano contribuito tanto alla teoria delle equazioni quanto all'estensione del calcolo algebrico ai numeri razionali e irrazionali. Le ricerche di Abū Kāmil sull'analisi indeterminata ebbero un'enorme influenza sullo sviluppo di questa disciplina, fornendole un nuovo senso e allo stesso tempo un nuovo status. Questo tipo di analisi si ritroverà in seguito in ogni trattato che si proponga di offrire un quadro completo della materia.
L'aritmetizzazione dell'algebra: al-Karaǧī e i suoi successori
Non si può capire la storia dell'algebra se non si evidenziano i contributi di due linee di ricerca sviluppatesi durante il periodo che abbiamo considerato sopra. Il primo riguarda lo studio di quantità irrazionali, sia in relazione al Libro X degli Elementi, sia indipendentemente da questo. Si possono ricordare, tra i molti altri matematici che hanno partecipato a queste ricerche, i nomi di al-Māhānī, Sulaymān ibn ῾Iṣma, al-Ḫāzin, al-Aḥwāzī, Yūḥannā ibn Yūsuf, al-Hāšimī. Non elencheremo qui i diversi contributi; vogliamo soltanto sottolineare che in questi lavori si è notevolmente sviluppato il calcolo con gli irrazionali, e che a volte si è anche cominciato a leggere parti del Libro X degli Elementi di Euclide alla luce dell'algebra di al-Ḫwārizmī. Per fare un solo esempio, consideriamo il caso di al-Māhānī, del IX sec., che richiede di calcolare la radice quadrata di cinque apòtomi. Per estrarre la radice del primo, l'autore propone di "procedere con il metodo dell'algebra e di al-muqābala" (Tafsīr al-maqāla al-῾āšira min kitāb Uqlīdis, f. 182r), cioè porre a=x+y, b=4xy, e ricondursi all'equazione x2+(b/4)=ax. Si determina in questo modo la più grande radice positiva x0, si calcola y0 e si ottiene:
Ricordiamo che, nel linguaggio euclideo sulle rette irrazionali, a+√b è un primo binomio, con a e b razionali, a>√b, √b irrazionale e
razionale, e la retta coniugata a−√b è una prima apòtome.
Al-Māhānī continua poi con le quattro apòtomi seguenti. Per esempio, per la seconda √b−a, con b=45 e a=5, egli si riporta all'equazione
[12] x4+(625/16)=(65/2)x2.
In tal modo, questi matematici non hanno soltanto esteso il calcolo algebrico alle quantità irrazionali, ma hanno dato una conferma del fatto che l'algebra è uno strumento generale.
La seconda linea di ricerca nasce dalla traduzione araba dell'Aritmetica di Diofanto, e in particolare dalla lettura di questo libro in termini algebrici. Intorno all'870 Qusṭā ibn Lūqā traduce sette libri dell'Aritmetica con il titolo significativo Ṣinā῾at al-ǧabr (L'arte dell'algebra). Per rendere il greco di Diofanto il traduttore ricorre al linguaggio di al-Ḫwārizmī, indirizzando verso la nuova disciplina il contenuto del libro. Anche se non è un'opera di algebra nel senso di al-Ḫwārizmī, essa contiene nondimeno tecniche di calcolo algebrico molto efficaci per quell'epoca: sostituzioni, eliminazioni, cambiamenti di variabile, ecc. Fu oggetto di commenti da parte di matematici come lo stesso traduttore Ibn Lūqā, purtroppo perduti, e un secolo più tardi Abū 'l-Wafā᾽ al-Būzǧānī. Sappiamo però che quest'ultimo nel suo commento voleva dare le dimostrazioni delle soluzioni proposte da Diofanto. In un testo che ci è pervenuto, intitolato Fī ǧam῾ aḍlā῾ al-murabba῾āt wa-'l-muka῾ ῾abāt wa-aḫḏ tafāḍuli-hā (Sulla somma dei lati dei quadrati e dei cubi e sulle loro differenze), egli dimostra la formula del binomio, spesso utilizzata nell'Aritmetica, per n=2 e n=3.
Comunque, questo progresso del calcolo algebrico, sia perché si estese ad altri campi sia per la quantità dei risultati tecnici ottenuti, portò a un rinnovamento della disciplina stessa. Nell'XI sec., un secolo e mezzo dopo al-Ḫwārizmī, al-Karaǧī, matematico di Baghdad, concepisce un nuovo progetto di ricerca: applicare l'aritmetica all'algebra, vale a dire studiare in modo sistematico l'applicazione delle leggi dell'aritmetica e di certi suoi algoritmi alle espresssioni algebriche e in particolare ai polinomi. Ed è proprio questo calcolo sulle espressioni algebriche della forma:
con m e n interi non negativi, che diventa l'oggetto principale dell'algebra. La teoria delle equazioni algebriche è certamente sempre presente, ma occupa un posto modesto nelle preoccupazioni degli algebristi. Si comprende quindi come i libri di algebra subiscano modifiche non solo di contenuto ma anche di organizzazione.
Al-Karaǧī dedica molti scritti a questo nuovo progetto, in particolare al-Faḫrī fī'l-ǧabr wa-'l-muqābala (L'algebra dedicata a Faḫr al-Mulk) e al-Badī῾ fī'l-ḥisāb (L'innovatore del calcolo). Si tratta di testi che saranno studiati, ripresi e commentati dai matematici fino al XVII sec., e che quindi per secoli saranno al centro delle ricerche di algebra aritmetica. L'opera di al-Ḫwārizmī si trasformerà invece in un'esposizione storicamente importante, ma commentata da matematici non di primo piano. Senza ripercorrere la storia di sei secoli di algebra, illustriamo ora l'influenza dell'opera di al-Karaǧī rivolgendo l'attenzione a uno dei suoi successori del XII sec., al-Samaw᾽al (m. 1174). Il suo libro di algebra, al-Bāhir (Lo splendore), comprende le opere principali di al-Karaǧī, tra cui quelle che abbiamo precedentemente citato. Al-Samaw᾽al comincia con il definire la nozione di potenza algebrica in tutta la sua generalità; a partire dalla definizione x0=1 egli dà una regola equivalente alla xmxn=xm+n, con m e n interi.
Ecco cosa scrive al-Samaw᾽al dopo aver elencato in una tavola le potenze a destra e a sinistra di x0: "se due potenze si trovano ai due lati dell'unità, e a partire da una di queste contiamo nella direzione dell'unità il numero di elementi della tavola che separano l'altra potenza dall'unità, e il numero è dalla parte dell'unità. Se le due potenze si trovano dalla stessa parte dell'unità allora contiamo nella direzione opposta all'unità" (Al-Bāhir en Algèbre d'as-Samaw᾽al, p. 19)
Segue poi lo studio delle operazioni aritmetiche sui monomi e i polinomi, in particolare la divisibilità dei polinomi, come pure l'approssimazione delle frazioni mediante gli elementi dell'anello dei polinomi. Per esempio:
dove al-Samaw᾽al ottiene uno sviluppo limitato di f(x)/g(x) valido per x abbastanza grande.
Troviamo poi l'estrazione di radice quadrata di un polinomio a coefficienti razionali. A tutti questi calcoli sui polinomi al-Karaǧī aveva dedicato uno scritto, andato perduto ma fortunatamente citato da al-Samaw᾽al, nel quale egli determina la formula dello sviluppo delle potenze del binomio e la tavola dei coefficienti corrispondenti:
Nel quadro della dimostrazione di questa formula, compare come procedimento di dimostrazione in matematica l'induzione completa finita in una forma antiquata. Tra i mezzi di calcolo ausiliario al-Samaw᾽al fornisce, seguendo al-Karaǧī, le somme di varie progressioni numeriche assieme alle dimostrazioni delle stesse:
Segue poi la risposta alla domanda "come si possono utilizzare la moltiplicazione, la divisione, l'addizione, la sottrazione e l'estrazione di radice per le quantità irrazionali?" (ibidem, p. 37). La risposta a questa domanda porta al-Karaǧī e i suoi successori a leggere deliberatamente in modo algebrico il Libro X degli Elementi, a estendere all'infinito i monomi e i binomi in esso contenuti, e a proporre regole di calcolo tra le quali si trovano formulate esplicitamente quelle di al-Māhānī:
[17] (x1/n)1/m=(x1/m)1/n e x1/m=(xn)1/mn
assieme ad altre come questa:
Vi si trova anche un importante capitolo sull'analisi diofantea razionale e un altro sulla risoluzione di sistemi di equazioni lineari a più incognite. Al-Samaw᾽al dà un sistema di 210 equazioni lineari a 10 incognite.
A partire dai lavori di al-Karaǧī vediamo costituirsi una linea di ricerca in algebra, una tradizione ben caratterizzata sia per il contenuto sia per l'organizzazione dei singoli lavori. Questi ultimi, per dirla con Ibn al-Bannā᾽, nei secc. XIII e XIV "quasi non si riescono a contare" (Kitāb fī 'l-ǧabr wa-'l-muqābala, f. 1). Per citare solo alcuni autori troviamo opere di al-Šahrazūrī, Ibn Abī Turāb, Ibn al-Ḫaššāb, i maestri di al-Samaw᾽al; lo stesso al-Samaw᾽al, Ibn al-Ḫawwām, al-Tanūḫī, Kamāl al-Dīn al-Fārisī, Ibn al-Bannā᾽e, più tardi, al-Kāšī, al-Yazdī e altri ancora.
All'interno di questa linea di ricerca il capitolo della teoria delle equazioni algebriche propriamente detto, senza essere un capitolo centrale, fa comunque progressi. Come i suoi predecessori, anche al-Karaǧī considera le equazioni quadratiche; tuttavia alcuni suoi successori tentano di studiare la soluzione delle equazioni cubiche e di quarto grado. Così al-Sulamī (XII sec.), che cerca una soluzione per radicali dell'equazione cubica in al-Muqaddima al-kāfiya fī ḥisāb al-ǧabr wa-'l-muqābala (L'introduzione sufficiente al calcolo algebrico), un testo che testimonia l'interesse dei matematici dell'epoca per la soluzione per radicali dell'equazione cubica. Egli considera come possibili due tipi di equazione:
[19] x3+ax2+bx=c e x3+bx=ax2+c,
imponendo tuttavia la condizione a2=3b, che esprime così: "Questo tipo [il primo] ha due condizioni: una è la proporzionalità, l'altra che un terzo del numero di quadrati x2 sia uguale alla radice quadrata di un terzo del numero di cose. Se le due condizioni sono soddisfatte esso è realizzabile" (Collection Paul Sbāṭ, n° 5, ff. 92v-93r). Per 'proporzionalità', come spiegherà in seguito, egli intende l'uguaglianza 1/x=x/x2=x2/x3…, mentre la seconda condizione è quella detta. Per il secondo tipo aggiunge una condizione ulteriore: "Le cose devono essere con il cubo". Se le cose sono nello stesso membro dei quadrati, l'autore ricorda che non vi sono ancora metodi noti. Per ognuna delle due equazioni dà quindi una radice reale positiva:
Possiamo ricostruire il procedimento di al-Sulamī come segue: egli riporta l'equazione alla forma normale mediante una trasformazione affine, ma invece di cercarne il discriminante, annulla il coefficiente della prima potenza dell'incognita per ricondurre il problema a quello dell'estrazione di una radice cubica. Così, per esempio, per l'equazione del primo tipo considera la trasformazione affine x y−a/3; l'equazione si riscrive:
[21] y3+py−q=0,
dove
posto b=a2/3, ne segue
,
da cui y, e quindi x.
Per il secondo tipo applica la trasformazione x y+a/3. Infine considera l'equazione
[24] x3=ax2+bx+c
e ricorda che non si può risolvere con la trasformazione x y+
+a/3. In questo caso si cade su un numero negativo, cioè b=−a2/3, cosa che al-Sulamī non poteva ammettere.
Prosegue quindi con un'equazione di quarto grado, cercando, in modo molto naturale, di determinare il cambiamento di variabile che la riduce a un'equazione quadratica, cioè formando la prima parte di un quadrato. Per esempio, per l'equazione
[25] x4+ax3+bx2+cx=d,
con a=2, b=6, c=5 e d=66, trova la soluzione x=2.
Il metodo di al-Sulamī è il seguente: pone a=2 e b−1=c, cioè b=6 e c=5, così che b≥1.
L'equazione si riscrive come:
[26] (x2+x)2+(b−1)(x2+x)=d.
Posto
[27] x2+x=y,
si ha y2+(b−1)y=d, equazione di secondo grado che ha una radice positiva y1. Si risolve quindi l'equazione x2+x=y1 che ha anch'essa una radice positiva. Per b=1 e c=0 l'equazione diventa (x2+x)2=d, e l'equazione x2+x=√d ha una radice positiva. Per b=0 si ha c=−1; l'equazione si scrive
[28] (x2+x)2=x2+x+d,
da cui y2=y+d; per ogni valore di d si ha un valore di y1, e basta dunque risolvere x2+x=y1. Se a 2 il metodo si applica ancora; l'equazione si riscrive come:
,
da cui
Posto x2+(a/2)x=y, si ha y2+(b−a2/4)y=d, equazione che ha una radice positiva; si risolve infine x2+(a/2)x=y1, equazione che ha ugualmente una radice positiva.
Riassumendo, qualunque sia a positivo, se b e c sono positivi e soddisfano la condizione b−a2/4=2c/a, si può risolvere l'equazione iniziale ponendo y=x2+(a/2)x. L'equazione avrà in tutti i casi una radice positiva.
Tentativi di questo genere, attribuiti al matematico italiano Dardi (magister Dardi) del XIV sec., sono frequenti nella tradizione algebrica iniziata da al-Karaǧī. Così, per esempio, il matematico Ibn al-Bannā᾽, anche se riconosce implicitamente la difficoltà di risolvere per radicali le equazioni di terzo grado, a eccezione di x3=a, quando scrive che le equazioni che "si riportano a gradi diversi [dal secondo] non si possono risolvere per via algebrica escluse quelle in cui un cubo uguaglia un numero" (Kitāb fī 'l-ǧabr wa-'l-muqābala, f. 26v), prende in considerazione l'equazione
[31] x4+2x3=x+30,
che egli risolve nel modo seguente. La riscrive come
[32] x4+2x3+x2=x2+x+30,
che a sua volta si riscrive come (x2+x)2=x2+x+30. Posto y=x2+x, si ha y2=y+30, che risolta fornisce y=6; risolvendo x2+x=6 poi trova x=2, che è una soluzione della [31].
È ancora troppo presto per conoscere con precisione il contributo dato dai matematici che si rifanno a questa tradizione alla risoluzione delle equazioni di terzo e quarto grado. Ma le testimonianze che abbiamo fornito mostrano che, contrariamente a quanto si credeva, alcuni di loro hanno cercato di andare oltre i risultati di al-Karaǧī.
La geometrizzazione dell'algebra: al-Ḫayyām
Gli algebristi con tendenza all'impostazione aritmetica cercavano soluzioni per radicali delle equazioni e volevano dare una giustificazione dell'algoritmo di risoluzione. A volte lo stesso matematico dà due giustificazioni, una geometrica e l'altra algebrica (è il caso di Abū Kāmil). Per l'equazione di terzo grado mancava non solo la soluzione per radicali ma anche la giustificazione dell'algoritmo della soluzione, in quanto la soluzione non è costruibile con riga e compasso. I matematici di questa tradizione erano perfettamente consci di questo fatto; uno di loro scriveva molto prima del 1185: "Poiché l'incognita che si vuole determinare e conoscere in ciascuno di questi polinomi è il lato del cubo che in essi compare, e poiché l'analisi porta ad applicare un parallelepipedo rettangolo noto a una retta nota, e che ecceda o difetti di un cubo il parallelepipedo intero; e si può fare la sintesi di ciò soltanto mediante le sezioni coniche" (Mashha, Āstān-i Quds, 5325, f. 25).
Il ricorso alle sezioni coniche, destinato esplicitamente a risolvere equazioni di terzo grado, ha presto seguito le prime traduzioni algebriche dei problemi solidi. Esso si ritrova, nel IX sec., nel lavoro di al-Māhānī sul lemma di Archimede (Tav. I).
Gli altri problemi, come la trisezione dell'angolo, le due medie proporzionali e in particolare l'ettagono regolare, non tarderanno a essere tradotti in termini algebrici. D'altronde, davanti sia alla difficoltà ricordata sopra, sia a quella di risolvere per radicali le equazioni di terzo grado, matematici come al-Ḫāzin, Ibn ῾Irāq, Abū 'l-Ǧūd ibn al-Layṯ e al-Šannī sono stati condotti a tradurre queste equazioni in termini geometrici (Tav. II).
Diventava così possibile applicare allo studio di queste equazioni una tecnica d'uso corrente a quel tempo nell'esame di problemi solidi, e cioè l'intersezione di coniche. È questo il motivo principale della geometrizzazione della teoria delle equazioni algebriche. Questa volta, contrariamente a Ṯābit ibn Qurra, non si cerca di tradurre geometricamente le equazioni algebriche per trovare l'equivalente geometrico della soluzione algebrica già ottenuta, ma di determinare mediante la geometria le radici positive dell'equazione che non si riescono a ottenere altrimenti. I tentativi di al-Ḫāzin, al-Qūhī, Ibn al-Layṯ, al-Šannī, al-Bīrūnī, ecc., sono altrettanti contributi parziali, finché al-Ḫayyām non concepisce il progetto di elaborare una teoria delle equazioni di grado inferiore o uguale a 3. Al-Ḫayyām (1048-1131) vuole intanto superare le ricerche di tipo frammentario, cioè legate a questa o quella forma dell'equazione di terzo grado, per elaborare invece una teoria delle equazioni proponendo contemporaneamente un nuovo metodo di redazione. Studia allora tutti i tipi di equazioni di terzo grado, classificati in modo formale secondo la di stribuzione tra i due membri dell'equazione dei termini noti, di quelli di primo grado, di secondo e di terzo. Per ciascuno di questi tipi al-Ḫayyām trova la costruzione di una radice positiva mediante l'intersezione di due coniche.
Così, per esempio, per risolvere l'equazione 'un cubo più un numero uguale a dei quadrati', cioè
[33] x3+c=ax2,
procede come segue. Sia AC=a; allora a>x. Sia H un segmento tale che H3=c. Si possono presentare tre casi: H=AC, H>AC e H⟨AC. Al-Ḫayyām comincia con l'esaminare questi casi.
Se H=AC, il problema è impossibile. Infatti, tre sono i casi che si presentano a seconda che si supponga la soluzione x0 ugua le, maggiore o minore di H: per x0=H, si ha ax20=H3=c, e ciò è impossibile; per x0⟨H, si ha ax20⟨c, da cui ax20⟨c⟨x30+c, e ciò è assurdo; per x0>H, si ha x30>ax20, e ciò è assurdo.
Se H>AC, il problema è a fortiori impossibile. Infatti per x0=H, si ha x0>a e x30>ax20, e ciò è impossibile; per x0⟨H, si ha ax20⟨H3=c in quanto H>a, e ciò è ugualmen te impossibile; per x0>H, si ha x30>ax20, in quanto H>a, e ciò è impossibile. Si ha così la condizione necessaria H⟨AC, cioè c⟨a3.
Poiché H⟨AC, prendiamo un punto B su AC tale che BC=H, ed esaminiamo i tre casi a seconda che BC=AB, BC>AB e BC⟨AB. Consideriamo il primo caso, per BC=AB (fig. 5), che corrisponde alla condizione algebrica c1/3=a/2. Completiamo il quadrato DC e tracciamo l'iperbole A passante per D e che ammette AC e CE per asintoti. Tracciamo anche la parabola P di vertice A, asse AC e lato retto BC. La parabola P passa per D in quanto DB2=AB∙BC, e questa è l'equazione della parabola; dunque A e P si intersecano in D. Ma P incontra A, come osserva al-Ḫayyām senza, però, darne giustificazione, in un altro punto. Nel secondo caso, con BC>AB (fig. 6), o equivalentemente c1/3>a/2, completiamo di nuovo il quadrato DC; tracciamo l'iperbole A passante per D e la parabola P. Il punto D è esterno alla parabola perché DB2>AB∙BC. Se P e A si intersecano o sono tangenti in un punto D1 D, la proiezione di D1 su AC si trova necessariamente tra A e B, e il problema è possibile, altrimenti no. Per la dimostrazione di questa conclusione si veda il commento. Infine, nel terzo caso, BC⟨AB ossia c1/3⟨a/2, il punto D è interno alla parabola P; A e P si incontrano dunque in due punti (fig. 7).
In tutti e tre i casi sia I una delle due intersezioni di A con P. Nel secondo caso (fig. 6) si procede nel modo seguente. Sia G la proiezione di I su CA. Si ha uguaglianza tra le superfici IGCK e DBCE, co me segue dall'equazione di A, e dunque
I però appartiene a P, per cui IG2=GA∙BC, e dunque
,
per cui
,
e
,
da cui c=BC3=GC2∙GA, e quindi
[38] c+GC3=GC2(GA+GC)=GC2∙CA=a∙GC2,
per cui GC è soluzione. Si procede analogamente negli altri due casi. Nel terzo caso, si hanno due soluzioni distinte corrispondenti alle due intersezioni di A e P.
Commentiamo ora il testo di al-Ḫayyām. Si è notato che al-Ḫayyām dimostra che se c1/3≤a/2, il problema è sempre possibile. Il caso a/2⟨c1/3⟨a merita di essere discusso. Per la scelta delle due curve ausiliarie A e P si riporta l'equazione alla proporzione
si introduce GI perpendicolare a BC tale che
di modo che
e l'equazione diventa:
Il punto I tale che CG∙GI=BC2 e GI2=BC∙GA si trova all'intersezione dell'iperbole A e della parabola P.
Si osserva d'altra parte che questa scelta delle curve coincide con quella dell'equazione x3+ax2=c, studiata in preceden za da al-Ḫayyām. La sola differenza, che rende conto del cambiamento di segno dei coefficienti, è che la concavità dell'iperbole è rivolta nell'altro senso.
In altri termini, consideriamo il sistema di assi (CA, CE), cioè (Ox,Oy), e sia il punto D(c1/3, c1/3). L'equazione si riscrive come segue
poiché zero non è soluzione. Poniamo:
e
Nel primo caso, se c1/3=a/2, allora D appartiene a P in quanto c2/3=c1/3(a−c1/3). Al-Ḫayyām afferma allora che P e A si intersecano anche in un altro punto I(x,y): il problema ha due soluzioni. Per ottenere la seconda, sappiamo che se c1/3=a/2, x1=c1/3 è soluzione, e la seconda radice è x2=c1/3(1+√5)/2.
Nel secondo caso, se c1/3>a/2, il punto D è esterno a P in quanto c2/3>c1/3(a−c1/3). Se dunque A e P hanno due punti di intersezione o se sono tangenti in un punto, le loro ascisse soddisfano c1/3⟨x⟨a, e il problema ha una soluzione se le due curve sono tangenti, due se si intersecano in due punti, nessuna se non si intersecano. Le ascisse dei due punti di intersezione sono dalla stessa parte di BC=c1/3; dimostriamo che sono più grandi. Il polinomio x3−ax2+c raggiunge il minimo per x=2a/3 e vale allora (27c−4a3)/27; la condizione di esistenza delle radici è dunque
Osserviamo che le ordinate y1, y2 dei punti di ascissa x=2a/3 rispettivamente sull'iperbole e sulla parabola sono dati da y1=3c2/3/2a e y22=ac1/3/3; la condizione
significa che y1≤y2, cioè che il punto dell'iperbole è interno alla parabola. Il valore 2a/3 si trova tra le due radici dell'equazione e occorre verificare che c1/3⟨2a/3, cioè 27c⟨8a3, conseguenza della condizione di esistenza.
Nel terzo caso, se c1/3⟨a/2, A e P si intersecano necessariamente in due punti e il problema ha due soluzioni. Infatti, se un punto I(x0,y0) appartiene a A e a P si ha
da cui c=x20(a−x0). Osserviamo infine che, se la condizione c1/3⟨a si ottiene facilmente confrontando i 'pesi' rispettivi dei monomi dell'equazione (da x3⟨ax2 segue x⟨a, e da c⟨ax2⟨a3 segue c1/3⟨a), è più difficile ottenere la condizione c1/3⟨x⟨a senza considerazioni geometriche sul comportamento asintotico delle curve. Poiché CE è un asintoto di A, tutti i punti di quest'ultima hanno ascissa a destra di C. Ma per costruzione tutti i punti di P hanno ascissa a sinistra di A. Ne segue che ogni punto dell'intersezione di A e P si proietta tra C e A, da cui 0⟨x⟨a. Dalla convessità di A e dalla concavità di P segue che le due curve non si possono intersecare a sinistra del punto D. Se dunque (x,y) è un punto di intersezione si ha c1/3⟨x, da cui la condizione c1/3⟨x⟨a. È forse in questo modo, o in uno equivalente, che al-Ḫayyām ha trovato questa disuguaglianza.
Questa discussione di al-Ḫayyām algebrista, vale a dire le condizioni da lui trovate, è un passo avanti sulla strada che condurrà a stabilire l'esistenza della radice positiva. Tuttavia, non si tratta ancora di condizioni necessarie e sufficienti. Per completarle, il successore di al-Ḫayyām, Šaraf al-Dīn al-Ṭūsī seguirà un altro percorso, determinando dapprima il massimo della quantità x2(a−x).
Per elaborare questa nuova teoria al-Ḫayyām ha dovuto comprendere e formulare meglio i nuovi rapporti tra geometria e algebra. Ricordiamo in proposito che il concetto fondamentale introdotto da al-Ḫayyām è quello di unità di misura, il quale, opportunamente definito in relazione a quello di dimensione, permette l'applicazione della geometria all'algebra. Ora, questa applicazione ha spinto al-Ḫayyām in due direzioni che a prima vista possono sembrare paradossali: mentre l'algebra si identifica adesso con la teoria delle equazioni algebriche, quest'ultima sembra ormai, anche se ancora timidamente, trascendere la separazione tra l'algebra e la geometria. La teoria delle equazioni è più che mai un luogo dove si incontrano algebra e geometria e sempre più ragionamenti e metodi analitici. La traduzione concreta di questa situazione è la comparsa di memorie dedicate solo alla teoria delle equazioni, come quella di al-Ḫayyām. In effetti, contrariamente agli studiosi algebrico-aritmetici, al-Ḫayyām elimina dal suo trattato i capitoli dedicati ai polinomi, alla loro aritmetica, allo studio degli irrazionali algebrici, ecc. In compenso delinea un nuovo modello di redazione: comincia con una discussione del concetto di grandezza algebrica per poi definire quello di unità di misura. Dà poi i lemmi necessari e una classificazione formale delle equazioni ‒ in funzione del numero di termini ‒ per esaminare in ordine di difficoltà crescente le equazioni binomie di secondo e terzo grado, quelle trinomie di secondo e terzo grado e infine le equazioni che contengono l'inversa dell'incognita. Il trattato contiene due risultati eccezionali, che gli storici di solito attribuiscono a Descartes: una soluzione generale di tutte le equazioni di terzo grado per intersezione di due coniche, e un calcolo geometrico reso possibile dalla scelta di una lunghezza presa come unità, restando però, contrariamente a Descartes, fedele alla regola dell'omogeneità.
Si osservi che al-Ḫayyām non si ferma qui, ma cerca anche di dare una soluzione numerica approssimata dell'equazione cubica. Così, in una memoria dal titolo Risāla fī qismat rub῾ al-dā᾽ira (Epistola sulla divisione di un quarto di cerchio), nella quale annuncia il suo nuovo progetto sulla teoria delle equazioni, giunge a una soluzione numerica approssimata per mezzo di tavole trigonometriche.
La trasformazione della teoria delle equazioni algebriche: Šaraf al-Dīn al-Ṭūsī
Fino a poco tempo fa si pensava che il contributo dei matematici dell'epoca alla teoria delle equazioni algebriche fosse limitato ad al-Ḫayyām e alla sua opera. In realtà non è affatto così. Se è vero che l'opera di al-Ḫayyām è all'origine di una vera e propria tradizione, è anche vero che soltanto mezzo secolo dopo la sua morte questa tradizione andò incontro a una profonda trasformazione.
Secondo testimonianze storiche, il discepolo di al-Ḫayyām, Šaraf al-Dīn al-Mas῾ūdī, avrebbe composto un libro sulla teoria delle equazioni e la risoluzione delle equazioni di terzo grado. Questo libro, tuttavia, se veramente è stato scritto, non ci è pervenuto. Due generazioni dopo al-Ḫayyām incontriamo una delle opere più importanti di questa tradizione: il trattato al-Mu῾ādalāt (Le equazioni) di Šaraf al-Dīn al-Ṭūsī. Questo trattato (1170 ca.) introduce importanti innovazioni rispetto a quello di al-Ḫayyām: i procedimenti di al-Ṭūsī non sono più di carattere globale e algebrico, bensì locale e analitico. Un cambiamento radicale, particolarmente importante nella storia della matematica classica e che merita di essere analizzato più diffusamente.
Il trattato di al-Ṭūsī si apre con lo studio di due coniche che saranno utilizzate nel seguito. Si tratta della parabola e dell'iperbole, alle quali, per esaurire le curve utilizzate, occorre aggiungere il cerchio, supposto noto. Al-Ṭūsī sembra infatti supporre che il lettore abbia familiarità con l'equazione del cerchio, ottenuta a partire dalla potenza di un punto rispetto proprio al cerchio, e dedica questa parte preliminare della sua opera a stabilire l'equazione della parabola e dell'iperbole equilatera rispetto a due sistemi di assi.
Segue poi una classificazione delle equazioni di grado inferiore o uguale al terzo. Contrariamente ad al-Ḫayyām egli opta per un criterio di classificazione non intrinseco, bensì estrinseco. Laddove al-Ḫayyām, come abbiamo visto, classifica le equazioni secondo il numero dei monomi che contengono, al-Ṭūsī sceglie come criterio l'esistenza o meno di soluzioni positive: le equazioni sono cioè classificate a seconda che ammettano o no dei 'casi impossibili'. Si capisce facilmente allora perché il trattato consti di due sole parti, che corrispondono all'alternativa detta. Nella prima, al-Ṭūsī tratta la risoluzione di venti equazioni, procedendo per ciascun caso alla costruzione geometrica delle radici, alla determinazione del discriminante per le equazioni di secondo grado, e infine alla risoluzione numerica con il metodo detto di Ruffini-Horner, che egli applica alle equazioni polinomiali e non più soltanto all'estrazione della radice di un numero.
Possiamo già a questo punto individuare gli elementi costitutivi della teoria delle equazioni nel XII sec. nel solco della tradizione di al-Ḫayyām: costruzione geometrica delle radici, risoluzione numerica delle equazioni e, infine, richiamo delle soluzioni per radicali dell'equazione di secondo grado, riscoperta questa volta a partire dalla costruzione geometrica. Nella prima parte, dopo aver studiato le equazioni di secondo grado e l'equazione x3=c, al-Ṭūsī prende in esame otto equazioni di terzo grado. Le prime sette hanno tutte una sola radice positiva (possono avere anche radici negative, che al-Ṭūsī però non determina). Per studiare queste equazioni egli sceglie due curve di secondo grado, più precisamente due archi di curva. Dimostra mediante considerazioni di carattere geometrico che gli archi considerati hanno un punto di intersezione la cui ascissa soddisfa l'equazione proposta (possono avere altri punti di intersezione). Le proprietà geometriche descritte da al-Ṭūsī, a meno di qualche precisazione che egli passa sotto silenzio, ma che segue dai dati scelti, sono proprietà caratteristiche e conducono pertanto alle equazioni delle curve utilizzate. Grazie all'uso dei termini 'interno' ed 'esterno' al-Ṭūsī fa appello alla continuità delle curve e alla loro convessità. Si può tradurre in questi termini il procedimento utilizzato per l'equazione
[47] x3−bx=c, con b,c>0.
Egli considera infatti le due espressioni
e dimostra che, se esistono α e β tali che (f−g)(α)>0 e (f−g)(β)⟨0, allora esiste γ compreso tra α e β tale che (f−g)(γ)=0.
In questa prima parte al-Ṭūsī studia, come al-Ḫayyām, soprattutto la costruzione geometrica delle radici positive di queste venti equazioni di grado ≤3; quelle che restano saranno riportate infatti, mediante trasformazioni affini, all'una o all'altra di queste equazioni. In modo analogo a quello di al-Ḫayyām, egli procede per costruzioni geometriche piane se l'equazione ridotta è di primo o secondo grado, per costruzioni che fanno intervenire due delle tre curve dette se l'equazione ridotta è di terzo grado.
Anche se questa parte del trattato dipende dal contributo di al-Ḫayyām, vi sono già alcune differenze, le cui conseguenze si vedranno nella seconda parte. Al-Ṭūsī dimostra infatti l'esistenza del punto d'intersezione di due curve per tutte le equazione studiate, mentre al-Ḫayyām affronta questo studio solo per la ventesima equazione. Introduce anche nozioni alle quali ricorrerà in modo massiccio nella seconda parte, come le trasformazioni affini e la distanza di un punto da una retta.
La seconda parte del trattato è dedicata alle cinque equazioni che ammettono, secondo l'espressione di al-Ṭūsī, 'casi impossibili', cioè casi in cui non vi sono soluzioni positive. Sono le seguenti:
Contrariamente ad al-Ḫayyām, al-Ṭūsī non si poteva accontentare semplicemente di constatare l'esistenza di questi 'casi impossibili'. Volendo infatti dimostrare l'esistenza dei punti d'intersezione e, di conseguenza, quella delle radi ci, egli doveva caratterizzare tali casi e spiegarli. Ora è proprio questo problema di carattere tecnico, e gli interrogativi che ne scaturiscono, che conducono al-Ṭūsī a rompere con la tradizione di al-Ḫayyām per modificare il progetto iniziale. Per cogliere questo profondo cambiamento occorre analizzare il modo di procedere di al-Ṭūsī.
Ognuna delle cinque equazioni si scrive nella forma f(x)=c, dove f è un polinomio. Per caratterizzare i 'casi impossibili' al-Ṭūsī studia infatti l'intersezione della curva di equazione y=f(x) con la retta y=c. In effetti egli considera un arco della cur va, quello per il quale si ha simultaneamente x>0 e y=f(x)>0, che può non esistere; per al-Ṭūsī il problema ha senso solo se x>0 e f(x)>0, e in ognuno dei casi dà le condizioni affinché f(x) sia strettamente positiva. Nell'equazione (1) deve allora aversi 0⟨x⟨a, nella (2) si richiede 0⟨x⟨√b; la (3) dà ancora 0⟨x⟨√b, condizione che non è sufficiente. Al-Ṭūsī deve quindi considerare la relazione tra l'esistenza delle soluzioni e la posizione della costante c in rapporto al massimo della funzione polinomiale. È a questo proposito che egli introduce nuovi concetti, nuovi procedimenti e un nuovo linguaggio; anzi, definisce un nuovo oggetto. Comincia così con il formulare la nozione di massimo di un'espressione algebrica, che egli chiama "il numero più grande (al-῾adad al-a῾ẓam)". Sia f(x0)=c0 il massimo di f(x) nel punto (x0,c0). Al-Ṭūsī determina poi le radici di f(x)=0, cioè l'intersezione della curva con l'asse delle ascisse, e ne deduce infine le limitazioni delle radici di f(x)=c.
Tutto il problema si riduce ora alla determinazione del valore di x che fornisce il massimo di f(x). Egli procede allora risolvendo un'equazione che altro non è, in notazione diversa, che la f′(x)=0, dove f′ è un polinomio, la derivata di f. Ma prima di considerare il problema cruciale della derivata vogliamo sottolineare il cambiamento di punto di vista e l'introduzione dell'analisi locale. Cominciamo ricordando i risultati di al-Ṭūsī. Per l'equazione (1) la derivata ammette due radici, 0 e 2a/3, che danno rispettivamente un minimo f(0)=0 e un massimo f(2a/3)=c0. D'altra parte l'equazione f(x)=0 ammette una radice doppia λ1=0 e una positiva λ2=a. Al-Ṭūsī conclude allora che se c⟨c0 l'equazione (1) ha due radici positive x1 e x2 tali che λ1=0⟨x1⟨x0⟨x2⟨λ2=a. Osserviamo che esiste una terza radice x3, negativa, che al-Ṭūsī non considera. Per le equazioni (2), (3) e (5) il ragionamento è analogo. Nei tre casi la derivata ammette due radici di segno opposto. La radice positiva x0 dà il massimo c0=f(x0) e l'equazione f(x)=0 ammette tre radici semplici, delle quali una è negativa e le altre due sono λ1=0 e λ2; ne segue la conclusione precedente.
Per meglio illustrare il modo di procedere di al-Ṭūsī riassumiamo la sua discussione dell'equazione (1). L'equazione si riscrive come segue: c=x2(a−x)=f(x). Al-Ṭūsī considera tre casi: se c>4a3/27, il problema è secondo lui impossibile (ammette una radice negativa); se c=4a3/27, determina la radice doppia x0=2a/3 (senza riconoscere la radice negativa); e se c⟨4a3/27, determina le due radici positive con 0⟨x1⟨2a/3⟨x2⟨a. Studia allora il massimo di f(x), e dimostra che
mostrando dapprima che:
e quindi
e da [51] e [52] deduce [50].
Per trovare x0=2a/3, al-Ṭūsī risolve f′(x)=0. Calcola poi
e ciò gli permette di giustificare i tre casi considerati in precedenza. Determina poi le due radici positive x1 e x2. Pone x2=x0+y, trasformazione affine che porta all'equazio ne y3+ay2=k, con k=c0−c=4a3/27−c, equazione già risolta nella prima parte del trattato. Giustifica quindi questa trasformazione affine. Proce de poi analogamente con la trasformazione affine x1=y+a−x2, dove y è una soluzione positiva di un'equazione risolta in precedenza nel trattato. Al-Ṭūsī giustifica anche quest'ultima trasformazione affine mostrando che x1 x0 e x1 x2.
Nell'equazione (4) sorge una difficoltà: il massimo f(x0) può essere negativo. Al-Ṭūsī impone allora una condizione af finché si abbia f(x0)>0 e procede poi come prima. L'equazione f′(x)=0 ha allora due radici x′0 e x0 (x′0⟨x0), alle quali corrispondono rispettivamente un minimo negativo e un massimo positivo. Al-Ṭūsī considera solo la radice x0 e determina c0=f(x0). D'altra parte l'equazione f(x)=0 ammette in questo caso tre radici, e cioè 0, λ1>0, λ2>0, con λ1⟨λ2. Egli ne deduce che per c⟨c0 l'equazione (4) ha due radici positive x1 e x2 tali che 0⟨λ1⟨x1⟨x0⟨x2⟨λ2.
Questa rapida ricapitolazione mostra che la presenza della nozione di derivata non è né casuale né secondaria, ma è invece intenzionale. È vero, d'altra parte, che non è la prima volta che si incontra nell'opera di al-Ṭūsī l'espressione della derivata, poiché è già stata introdotta per costruire il metodo di risoluzione numerica delle equazioni. Questo metodo segue infatti il seguente ordine: si determina la prima cifra della radice e il suo ordine decimale; la radice si scrive cioè x=s0+y con s0=σ010r (dove r è l'ordine decimale). Per quanto riguarda la seconda cifra si ricorre all'equazione in y, f(s0+y)=0; l'algoritmo, noto come algoritmo di Ruffini-Horner, si applica poi per determinare i vari termini della precedente equazione cubica in y. L'algoritmo introdotto da al-Ṭūsī serve a disporre i calcoli in modo da effettuare meno moltiplicazioni possibili, ed è una leggera modificazione dell'algoritmo di Ruffini-Horner adattato alle equazioni di terzo grado. Al-Ṭūsī introduce allora, come coefficiente di y, il valore f′(s0) della derivata di f nel punto s0; ottiene la cifra più alta di y, cioè la seconda cifra della radice cercata, prendendo la parte intera di −f(s0)/f′(s0); si riconosce qui il metodo detto 'di Newton' per la risoluzione approssimata delle equazioni. Dopo aver determinato la seconda cifra, che è la prima di y, si ripete l'algoritmo sull'equazione in y per trovare una terza cifra, e si continua così finché non si ottiene la radice, che nei casi considerati da al-Ṭūsī è intera (Tav. III).
Ma anche se non fosse intera si troverebbero le cifre dopo la virgola nello stesso modo. I successori di al-Ṭūsī hanno proceduto in questo modo nel caso della radice non intera, come si vede dal testo di al-Iṣfahānī del XVIII secolo.
Se la presenza dell'espressione della derivata non può essere messa in dubbio, resta il fatto che al-Ṭūsī non spiega come sia giunto a questa nozione. Per meglio cogliere l'originalità del suo modo di procedere, consideriamo l'esempio dell'equazione (3), che si riscrive come f(x)=x(b−ax−x2)=c. Il problema principale è quello di trovare il valore x0 di x per il quale il massimo viene raggiunto. Spiegando il passaggio dall'equazione (3) a due equazioni risolte in precedenza per mezzo delle trasformazioni affini x→y=x−x0 e x→y=x0−x, al-Ṭūsī fornisce:
e
Egli confronta f(x0) con f(x0+y) e con f(x0−y) osservando che nell'intervallo ]0, λ2[, i termini y2(3x0+a+y) e y2(3x0+a−y) sono positivi. Dalle due uguaglianze [54] e [55] deduce poi che
di conseguenza, se b−x20=2x0(x0+a), si ha che f(x0)>f(x0+y) e f(x0)>f(x0−y). Ossia, se x0 è la radice positiva dell'equazione
[57] f′(x)=b−2ax−3x2=0,
allora f(x0)è il massimo di f(x)nell'intervallo considerato. Osserviamo che le due uguaglianze corrispondono allo sviluppo di Taylor con
Il procedimento di al-Ṭūsī consiste dunque nell'ordinare f(x0+y) e f(x0−y) secondo le potenze di y e dimostrare che il massimo viene raggiunto quando il coefficiente di y in questo sviluppo è zero. Il valore di x che rende massima f(x) è dunque la radice positiva dell'equazione f′(x)=0. Le trasformazioni affini x→x0±y, con x0 radice di f′(x)=0 permettono di far scomparire il termine in y. È verosimile che sia a partire da questa proprietà che al-Ṭūsī scopre l'equazione derivata f′(x)=0, forse in relazione alla curva che rappresenta f, ma che egli non disegna mai: per y piccolo, la parte principale dello sviluppo di f(x0±y) è in y2, e quindi non cambia di segno con y. Il procedimento di al-Ṭūsī e quello di Fermat sulla ricerca di massimi e minimi dei polinomi si somigliano come due gocce d'acqua.
Così, la teoria delle equazioni non è più soltanto un capitolo dell'algebra, ma investe un campo più vasto. In essa il matematico unisce lo studio geometrico delle equazioni e la loro risoluzione numerica. Pone e risolve il problema delle condizioni di possibilità di ciascuna equazione, e ciò lo porta a studiare in modo sistematico il massimo di un polinomio di terzo grado per mezzo dell'equazione derivata. Nel corso della risoluzione numerica al-Ṭūsī non applica soltanto algoritmi dove si incontra di nuovo la nozione di derivata di un polinomio, ma cerca di giustificare questi algoritmi mediante la nozione di 'polinomi dominanti'. È chiaro che si tratta di una matematica di alto livello per l'epoca: si arriva ai limiti di una ricerca condotta senza disporre di un efficace simbolismo. Tutta la ricerca di al-Ṭūsī si sviluppa infatti nella lingua naturale, senza simbolismo, se si esclude quello delle tavole, il che rende questa ricerca particolarmente complicata. Una tale difficoltà si presenta infatti come un ostacolo, non soltanto al progresso interno della sua stessa ricerca, ma anche alla trasmissione dei risultati. In altri termini, non appena il matematico manipola nozioni analitiche come quelle ricordate sopra, la lingua naturale diventa presto inadeguata a esprimere i concetti e le operazioni a esse relative, costituendo un limite all'innovazione e alla diffusione di questo tipo di conoscenze. I successori di al-Ṭūsī si scontrarono verosimilmente contro lo stesso ostacolo, finché non vi fu una vera trasformazione della notazione matematica, a partire principalmente da Descartes.
Tuttavia, l'esempio di al-Ṭūsī basta a dimostrare che la teoria delle equazioni non solo si è trasformata a partire da al-Ḫayyām, ma non ha mai smesso di allontanarsi, sempre più, dalla ricerca di soluzioni per radicali. Ha finito così per coprire un campo vasto, comprendendo settori che più tardi apparterranno alla geometria analitica o all'analisi.
Il destino della teoria delle equazioni
Qual è stato il destino di questa teoria delle equazioni di terzo grado fondata da al-Ḫayyām e trasformata da al-Ṭūsī? Una vera risposta a questa domanda potrà darla soltanto la ricerca futura (ma non bisogna farsi illusioni). Per andare oltre al-Ḫayyām e al-Ṭūsī occorreva non soltanto un efficace simbolismo (e non solo semplici abbreviazioni come se ne trovano, per es., in al-Qalaṣādī), ma soprattutto un nuovo programma matematico che andasse al di là delle coniche per intraprendere lo studio delle curve algebriche tramite le loro equazioni. I veri successori di al-Ḫayyām e di al-Ṭūsī si chiamano insomma Descartes e Fermat. Questa visione non impedisce però di seguire sul terreno della storia della matematica araba i lavori dei successori di al-Ḫayyām e di al-Ṭūsī. Il primo è il discepolo di al-Ṭūsī, il matematico Kamāl al-Dīn ibn Yūnus, di Mosul. Egli riprende l'equazione più difficile considerata da al-Ḫayyām e al-Ṭūsī, la venticinquesima nella loro classificazione:
[59] x3+c=ax2+bx.
Al-Ḫayyām distingue tre casi, a seconda che c⟨ab, c=ab o c>ab, e determina nel primo caso la più grande radice positiva x2>a. Šaraf al-Dīn al-Ṭūsī dà invece una discussione completa. Se a=√b, dimostra che l'equazione 3x2−2ax−a3=0 ha come radice positiva x0=a, e si trova c0=ab; ne segue che c⟨ab è condizione necessaria e sufficiente affinché l'equazione [59] ammetta due radici positive 0⟨x1⟨a⟨x2⟨2a. Negli altri due casi che egli prende in considerazione, a>√b e a⟨√b, discute in modo analogo le condizioni necessarie e sufficienti per l'esistenza di radici positive.
Ibn Yūnus sembra partire dallo studio di al-Ḫayyām per completarlo, determinando cioè la più piccola radice positiva. Procede utilizzando due metodi per determinare una radice x1⟨a. Il secondo metodo corrisponde a quello di al-Ḫayyām: intersezione di un'iperbole equilatera e di una seconda iperbole. Si tratta quindi di una ricerca nel solco tracciato da al-Ḫayyām, che intende completare lo studio iniziato da quest'ultimo seguendone il metodo o utilizzandone uno analogo.
L'astronomo e matematico Aṯīr al-Dīn al-Abharī (m. 1262), allievo di Kamāl al-Dīn ibn Yūnus, compose un trattato di al gebra che ci è pervenuto, per ammissione stessa del copista, mutilo. Nella parte di cui disponiamo egli applica all'equazione x3=a il metodo di risoluzione numerica di al-Ṭūsī, e negli stessi termini. Egli ha anche familiarità con le trasformazioni affini che permettono di ridurre un'equazione a un'altra. Così, anche quando espone i tre tipi canonici dell'equazione di secondo grado, egli considera x2=px+q, ricorda che x>p, pone x=y+p e si riporta all'equazione già studiata y2+py=q.
Al-Ḫilāṭī, un altro algebrista dell'epoca, ricorda che al-Ṭūsī era "il maestro del suo maestro", che aveva studiato le equazioni di terzo grado, ma che egli stesso era fedele alla tradizione di al-Karaǧī (Nūr al-dalāla fī ῾ilm al-ǧabr wa-'l-muqābala, f. 2). Altre testimonianze dell'epoca ricordano al-Ṭūsī, ma nulla ci è ancora pervenuto che indichi che qualche matematico abbia ripreso la sua teoria.
Ancora più tardi, nel XVIII sec., al-Iṣfahānī, un matematico della Scuola di Isfahan, presenta nel suo trattato un metodo interessante per la ricerca di una radice positiva dell'equazione di terzo grado fondata sulla proprietà del punto fisso. L'ha appreso da antichi predecessori, come fece per il metodo di al-Ṭūsī? È così, verosimilmente, anche se al momento non abbiamo prove decisive. Viene fornita rapidamente un'esposizione del metodo applicato all'esempio dello stesso al-Iṣfahānī. Si tratta di risolvere l'equazione
[60] x3+210=121x,
con x reale positivo. Si scrive l'equazione nella forma:
prendendo poi x1=11, allora
Prende un valore approssimato per difetto di x1, cioè 10,3, e trova
Ponendo x2=10,3 e y2=f(x2)=(1036,3)1/3, prende poi un valore approssimato per difetto di x2, cioè 10,1. Si trova:
Prende allora x3=10,1, e così di seguito. I primi termini di questa successione sono
[65] x1=11>x2=10,3>x3=10,1>…
Al-Iṣfahānī sceglie il valore 11 in un modo un po' diverso. Invece della funzione f ne considera una che la maggiora, cioè g(x)=(121x)1/3, e cerca una radice x1 della nuova equazione x=g(x), ciò che assicura che x1=11>x0 se x0 è la radice cercata.
Anche se possiamo scorgere tracce del libro di al-Ṭūsī negli scritti dei suoi successori, non conosciamo al momento commenti riguardo alla sua algebra. È possibile che vi siano stati, ma non crediamo che possano aver superato l'opera di al-Ṭūsī senza disporre del simbolismo necessario allo sviluppo delle nozioni analitiche contenute nel suo trattato.
Bibliografia
van Egmond 1983: Egmond, Warren van, The algebra of Maestro Dardi of Pisa, "Historia mathematica", 10, 1983, pp. 399-421.
Hunger 1963: Hunger, Herbert - Vogel, Kurt, Ein byzantinisches Rechenbuch des 15. Jahrhunderts. 100 Aufgaben aus dem Codex Vindobonensis Phil. Gr. 65, Wien, Böhlau, 1963.
Rashed 1974: Rashed, Roshdi, Résolution des équations numériques et algèbre: Sharaf al-Dīn al-Ṭūsī, Viète, "Archive for history of exact sciences ", 12, 1974, pp. 244-290 (rist. in: Rashed, Roshdi, Entre arithmétique et algèbre. Recherches sur l'histoire des mathématiques arabes, Paris, Les Belles Lettres,1984, pp. 147-194).
‒ 1984: Rashed, Roshdi, Entre arithmétique et algèbre. Recherches sur l'histoire des mathématiques arabes, Paris, Les Belles Lettres, 1984 (trad. ingl.: The development of Arabic mathematics. Between arithmetic and algebra, Dordrecht-Boston, Kluwer, 1994).
‒ 1986: al-Ṭūsī, Šaraf al-Dīn, Oeuvres mathématiques. Algèbre et géométrie au XIIe siècle, texte établi et traduit par Roshdi Rashed, Paris, Les Belles Lettres, 1986, 2 v.
‒ 1997a: Rashed, Roshdi, L'algèbre, in: Histoire des sciences arabes, sous la direction de Roshdi Rashed avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v.; v. II: Mathématiques et physique, pp. 31-54 (ed. orig.: Encyclopedia of the history of Arabic science, London-New York, Routledge, 1996, 3 v.).
‒ 1997b: Rashed, Roshdi, La Géométrie de Descartes et la distinction entre courbes géométriques et courbes mécaniques, in: Descartes et le Moyen Âge, édité par Joël Biard et Roshdi Rashed, Paris, Vrin, 1997, pp. 1-22.
‒ 1999: Rashed, Roshdi - Vahabzadeh, Bijan, Al-Khayyām mathématicien, Paris, Blanchard, 1999 (trad. ingl.: Omar Khayyam. The mathematician, New York, Bibliotheca Persica, 2000).
‒ 2001: Rashed, Roshdi, Fermat and algebraic geometry, "Historia scientiarum", 11, 2001, 1, pp. 24-47.
Sayili 1962: Sayılı, Aydın, Logical necessities in mixed equations by ῾Abd al-Ḥāmid ibn Turk and the algebra of his time, Ankara, 1962.