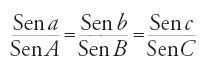La civiltà islamica: antiche e nuove tradizioni in matematica. La matematica applicata all'astrologia

La civilta islamica: antiche e nuove tradizioni in matematica. La matematica applicata all'astrologia

La matematica applicata all'astrologia

L'astrologia può essere definita come la disciplina basata sull'assunto che i corpi celesti, in particolare il Sole e la Luna, insieme ai cinque pianeti facilmente visibili, esercitano il loro influsso su tutti gli avvenimenti terreni, e che questi influssi sono così potenti e pervasivi da condizionare la vita quotidiana di tutti gli esseri umani. Ne consegue che l'astrologo, se in possesso di informazioni sufficienti, può predire gli eventi della vita di ogni persona, oppure ricostruire l'esistenza di un individuo morto da tempo, sempre che gli vengano forniti i dati richiesti.

Le informazioni richieste dall'astrologo consistono quasi esclusivamente in una serie di dati che danno la posizione nel cielo dei sette corpi celesti prima indicati. Ora, è compito dell'astronomo determinare le posizioni planetarie in momenti dati, ed egli usa la matematica per svolgere tale mansione. La matematica applicata all'astrologia è in linea generale simile a quella applicata all'astronomia antica. Poiché l'astronomia ha a che fare con oggetti nello spazio, quindi con la geometria, si fa riferimento alla geometria piana, sferica e solida. Inoltre, si devono calcolare le distanze tra coppie di oggetti, il che comporta un richiamo alla trigonometria, piana e sferica, o suoi equivalenti. Queste branche della matematica si svilupparono a un livello utile intorno al III sec. a.C. e fu allora che l'astronomia e l'astrologia fecero entrambe la loro apparizione. A quel tempo, però, così come nei successivi diciassette secoli, si era poco propensi a tenere separate le due discipline. Piuttosto, esse erano considerate come un insieme costituente un'unica, valida scienza delle stelle; ogni astronomo tendeva a essere anche astrologo, e viceversa.

Nel seguito sono presentate le definizioni delle operazioni e dei concetti astronomici utilizzati anche in astrologia, ed è descritto uno strumento, l'astrolabio, che fornisce una soluzione rapida ed elegante a un problema fondamentale dell'astrologia. Viene anche esaminato il contenuto della trigonometria medievale, che è alquanto diversa dal suo corrispondente moderno; la trigonometria è applicata praticamente nella soluzione di tutti i problemi astrologici. Quindi sono descritte le procedure mediante le quali si formulano le predizioni nell'astrologia genetliaca (compilazione degli oroscopi), la branca principale dell'astrologia; e infine sono considerati due esempi dell'astrologia delle congiunzioni, che sovrappone alcuni schemi cronologici periodici all'astrologia classica. I successivi progressi della cosmologia fecero sì che l'astrologia venisse relegata al suo ruolo attuale, vale a dire quello di pseudoscienza.

Le basi dell'astrologia

L'astrologia nasce dall'incontro della tradizione divinatoria babilonese, basata sugli astri, con la prima teoria planetaria elaborata dai Greci in grado di determinare con precisione le posizioni planetarie. Verso il 285 a.C. un caldeo, Beroso, fondò una scuola nell'isola di Coo, nel Mediterraneo, e pubblicò un'opera in greco intitolata Babyloniaká, che oltre a una storia di Babilonia includeva le numerose, anche se poco sistematiche, regole babilonesi per la divinazione basata sulle configurazioni delle stelle. L'opera ricevette una buona pubblicità e divenne molto nota nel mondo greco.

La teoria astronomica fu sviluppata principalmente da tre studiosi greci attivi ad Alessandria. Aristarco di Samo (IV-III sec. a.C.) fu il primo studioso a noi noto ad aver proposto un Universo eliocentrico, anticipando così Copernico di circa diciassette secoli. Apollonio (III sec. a.C. ca.) studiò il moto di un punto rotante lungo un cerchio detto 'epiciclo' che a sua volta ruota lungo la circonferenza di un cerchio più grande detto 'deferente'. I risultati conseguiti da Apollonio sono essenziali per predire i momenti in cui il moto apparente in avanti di un pianeta cessa e diventa retrogrado. Di importanza molto superiore fu, infine, Ipparco (attivo intorno al II sec. a.C.), il più eminente degli astronomi antichi. Egli utilizzò combinazioni di epicicli con deferenti eccentrici per sviluppare modelli del moto dei cinque pianeti. Riguardo agli altri due astri, la sua precisa determinazione del mese lunare medio portò ai successivi miglioramenti nel modello della Luna, e lo stesso avvenne per il Sole grazie alla sua scoperta della precessione. Egli sviluppò una branca della matematica che possiamo chiamare il 'calcolo delle corde'. Applicandolo a qualsiasi figura piana o sferica si possono conseguire tutti i risultati ottenibili con la trigonometria. Il calcolo impiegava soltanto una funzione, quella di una corda di arco su una circonferenza di raggio 60, e si basava solamente su un teorema, quello di Menelao. Dal momento che tale teorema considera un intero quadrilatero piuttosto che un triangolo, la matematica che ne discende non può essere denominata trigonometria.

Tolomeo di Alessandria (attivo intorno al 150 d.C.) fu il primo e il più grande di una lunga serie di astronomi-astrologi. I suoi modelli planetari, descritti nell'Almagesto, predicevano le posizioni con un'accuratezza superiore a quella di qualunque altro suo predecessore. Questo miglioramento era dovuto alle sue personali osservazioni, ma egli raggiunse la maggior parte dei risultati aggiungendo alle semplici combinazioni di deferente ed epiciclo un ingegnoso meccanismo a manovella. I precedenti modelli lunari portavano a risultati erronei alle quadrature (cioè a 90° di distanza dal Sole); anche questi furono corretti grazie all'introduzione di un meccanismo simile. Il risultato fu che i modelli tolemaici continuarono a dominare incontrastati e a essere usati per molto più di un millennio. Il contributo dato all'astrologia dalla sua Tetrabiblos è di natura molto diversa. In quest'opera egli espose, in modo chiaro e completo, la teoria, la nomenclatura e le operazioni dell'astrologia così come era praticata ai suoi tempi; essa rimane la fonte principale di informazione sull'astrologia antica e su gran parte di quella medievale. Tutto ciò che è stato aggiunto successivamente si fonda sull'astrologia classica.

Per descrivere la disciplina che risultò dall'amalgama delle credenze sulle stelle e dell'astronomia pura, è necessario definire un certo numero di concetti astronomici, che sono essenziali anche all'astrologia propriamente detta. Si chiama 'eclittica' il percorso nel cielo tra le stelle fisse che il Sole traccia apparentemente ogni anno. Essa è pertanto anche un cerchio massimo della sfera celeste, quest'ultima essendo una sfera di raggio infinitamente grande avente lo stesso centro della Terra. Molti degli oggetti con cui avremo a che fare si trovano sulla superficie della sfera celeste. Si chiama 'equatore celeste' il circolo massimo sulla sfera celeste il cui polo è il Polo Nord celeste. L'eclittica e l'equatore celeste si intersecano in due punti, uno dei quali è il 'punto vernale'. Partendo dal punto vernale, l'eclittica viene divisa in dodici archi uguali. Ogni arco costituisce un segno (zodiacale) e prende il nome da una costellazione. Gli astrologi usano i segni per indicare la posizione di un pianeta o di una stella, talvolta utilizzando semplicemente il nome della costellazione, altre volte con maggior precisione, fornendo anche i gradi all'interno del segno.

La longitudine di un corpo celeste (rappresentata dal simbolo λ) è la distanza lungo l'eclittica, misurata nella direzione positiva, ovvero antioraria (da ponente a levante), che congiunge il punto vernale con la base della perpendicolare che unisce il corpo celeste all'eclittica. Si chiama 'ascendente' il punto dell'eclittica all'incrocio con l'orizzonte orientale in un momento dato. Fissato un punto sull'eclittica si definisce la sua 'ascensione obliqua' A_φ(λ) nel modo seguente. Si faccia ruotare la sfera celeste in modo che il punto dato si trovi sull'ascendente: l'ascensione obliqua del punto dato è la distanza sull'equatore celeste dal punto vernale all'intersezione dell'equatore con l'orizzonte orientale della località.

Si noti che poiché l'angolo tra l'equatore e l'orizzonte è il complementare della latitudine φ della località, l'insieme di funzioni dell'ascensione obliqua è divisibile in famiglie di funzioni. In ognuna di tali funzioni la variabile indipendente è λ. L'insieme di tutte le funzioni che hanno lo stesso valore del parametro φ costituisce una famiglia. Il meridiano di ogni località è il circolo massimo verticale che passa per il Polo Nord celeste.

L'eclittica viene divisa anche in una seconda serie di dodici archi, chiamati 'case' (o loci), da non confondere con i segni zodiacali. Le case trovano applicazione soltanto in astrologia; esse sono definite nella seguente maniera alquanto complicata. Quattro punti eclittici costituiscono i cardines (o centri); due di questi quattro cardini sono l'ascendente e il suo punto opposto, che tramonterà sotto l'orizzonte nel momento in cui l'altro sorge; gli altri due cardini sono il 'medio cielo' superiore e inferiore che corrispondono ai punti di intersezione dell'eclittica con il meridiano, uno sopra, l'altro sotto l'orizzonte. Ciascuno dei quattro archi formati dalla successione dei cardini viene poi diviso in tre segmenti per dare luogo alle dodici case. La trisezione è il metodo più semplice di suddivisione, ma è poco elegante, e nel corso del tempo furono elaborati e applicati altri sistemi. In realtà, il calcolo delle case costituisce di per sé un argomento di studio.

Un pianeta è detto 'in aspetto' con un altro se i due sono separati da certe distanze. Si ha 'opposizione' quando i due pianeti si trovano alle estremità di un diametro; l'aspetto 'trigono' si ha quando la distanza corrisponde al lato di un triangolo equilatero inscritto nell'eclittica; il 'quartile' quando corrisponde al lato di un quadrilatero; e il 'sestile' a quello di un esagono regolare. Ogni segno si trova in aspetto trigono con altri due segni; ognuno di questi raggruppamenti di tre segni è chiamato 'triplicità' (o 'triangolo') e naturalmente ci sono quattro triplicità. Le triplicità prendono il nome dai quattro elementi aristotelici: fuoco, terra, aria e acqua. Infine, se due pianeti si trovano nello stesso segno o, in modo più significativo, se hanno la stessa longitudine, si dice che sono 'in congiunzione'. Alle congiunzioni di speciali coppie di pianeti è stata attribuita una particolare importanza. In effetti, l'astrologia delle congiunzioni ha finito per svilupparsi come una dottrina completa e quasi indipendente.

L'astrolabio

Ottenere in breve tempo la determinazione dell'ascendente, fondamentale per l'astrologia, presentava molte difficoltà. Tuttavia, con l'ausilio di un astrolabio l'astrologo era in grado di trovare l'ascendente in modo rapido e preciso. Questo strumento, che si basa su un'elegante applicazione della proiezione stereografica, è insieme uno strumento di osservazione e un calcolatore analogico. Esso è composto da un disco circolare di metallo con un allungamento per la sospensione intorno al bordo (che si tiene sospeso al pollice per mezzo di un anello inserito all'estremo di un diametro). Nel centro del disco è montata un'alidada, o diottra, libera di ruotare sul piano del disco. Una delle facce dello strumento presenta una concavità, in modo tale che possa esservi inserito e fissato un disco di diametro leggermente inferiore a quello dello strumento. Su questo disco è incisa una famiglia di cerchi, che sono le proiezioni stereografiche di circoli di altezza costante (sulla sfera celeste), a cominciare dall'orizzonte. Tale proiezione è stata realizzata in modo da essere valida per la latitudine della località dove l'astrolabio viene usato. Il centro di proiezione è posto al centro dello strumento ed è la proiezione del Polo Nord.

La seconda componente dello strumento è la 'rete' o 'ragno'. Essa è ciò che rimane di un secondo disco di metallo che aveva lo stesso diametro del primo. Tutto il metallo di cui era fatto è stato tagliato e asportato a eccezione di un sottile bordo intorno al margine, una sottile striscia circolare all'interno, un'estremità della quale è la proiezione stereografica dell'eclittica, e di punti che indicano molte delle stelle più brillanti, le 'stelle dell'astrolabio'. Tutto ciò è tenuto in posizione da strisce di connessione che partono dal margine della rete. Le rappresentazioni delle stelle sono le estremità aguzze di queste strisce. L'eclittica è suddivisa in gradi, così che la rappresentazione del Sole può essere posizionata sull'eclittica secondo la sua longitudine al momento dell'osservazione. La rete è libera di ruotare e così facendo essa traccia i percorsi giornalieri nel cielo del Sole e delle stelle sullo sfondo fisso dei cerchi di altezza.

Quando l'evento, normalmente una nascita, si verifica, ne viene informato l'astrologo. Immediatamente egli osserva l'altezza con l'alidada. Se è giorno, egli prende l'altezza del Sole, se è notte, usa una stella. In entrambi i casi, egli fa ruotare la rete fino a quando la proiezione del corpo appena osservato si trova in corrispondenza del cerchio per quella altezza. Ciò consente di fissare la posizione della sfera celeste rispetto all'orizzonte locale e di leggere l'ascendente sulla rete, essendo questo la longitudine del punto dell'eclittica preso sull'orizzonte orientale.

Le funzioni trigonometriche nell'astronomia medievale

Caratteristico dell'astrologia è l'impiego delle note funzioni trigonometriche di seno, coseno e tangente. Tuttavia, in epoca medievale queste funzioni differivano dai loro corrispondenti moderni, nel senso che i loro valori erano un multiplo costante della funzione moderna. Quindi, il seno medievale (indicato con l'iniziale maiuscola per distinguerlo da quello moderno) era Senx=60 senx. L'uso del numero 60 come raggio del cerchio fondamentale era naturale, poiché esso è la base del sistema sessagesimale. Nel sistema di numerazione posizionale sessagesimale dei Babilonesi, 60 si scriveva 1;0,0, dove il punto e virgola separa la parte intera da quella frazionaria. L'aritmetica medievale era soltanto parzialmente sessagesimale, ma l'influsso babilonese si rivelò persistente.

La costante adottata per le tangenti e le cotangenti era diversa da quella usata per il seno e il coseno. Entrambe le funzioni erano definite come formalizzazioni di antichi schemi per il calcolo delle ombre. Questi erano sequenze di numeri interi che assegnavano ogni ora del giorno alla lunghezza dell'ombra proiettata da uno gnomone standard. Così, la tangente medievale era definita come Tanx=gtanx, dove g è la lunghezza dello gnomone nelle allora ordinarie unità; il valore più diffuso era g=12, ma ci sono molte tavole di tangenti in cui g è invece pari a 6,5 o 7.

Intorno al IX sec. furono riconosciute le identità di base che connettevano le quattro funzioni. Restava da trovare la soluzione completa del triangolo, sia piano sia sferico, vale a dire: dato un triangolo di cui siano noti un numero di lati e di angoli sufficienti per determinarlo, trovare le formule per calcolare i rimanenti lati e angoli sconosciuti. Un esempio di soluzione è dato dalla legge del seno per i triangoli sferici, che afferma che per ogni triangolo si ha

dove la maiuscola indica l'angolo e la stessa lettera in minuscolo indica il lato opposto all'angolo. Un'elegante prova fu data da Abū 'l-Wafā᾽, un persiano attivo a Baghdad intorno al 970. Le linee principali del suo ragionamento possono essere indicate nel modo seguente: il triangolo originario viene diviso in due triangoli rettangoli tramite una costruzione che utilizza soltanto cerchi massimi. Ciò determina la formazione di una coppia di triangoli rettangoli in aggiunta alla coppia all'interno del triangolo originario; ciascuno dei due triangoli esterni ha in comune un angolo con uno dei due triangoli interni. Successivamente si applica due volte un teorema precedentemente provato e simile alla legge del seno (la differenza consiste nel fatto che il teorema fa uso dei seni dell'ipotenusa, che non esistono nei triangoli scaleni). Nondimeno, le due applicazioni implicano quattro rapporti, quindi otto quantità di cui due sono quadranti, e altre due sono identiche. Queste quattro quantità possono essere eliminate dalle due espressioni, mentre le restanti danno luogo a un'unica espressione che prova la legge del seno. Una singola applicazione della legge del seno conduce alla formula

[2] δ = arcSen (Senε Senλ/60),

che dà la declinazione δ di un punto dell'eclittica, ovvero la sua distanza dall'equatore, in termini del parametro ε, l'angolo tra l'equatore e l'eclittica, e della longitudine λ del punto. Quando, nel corso del X sec., fu accumulato un numero di tali formule sufficiente a consentire la soluzione di ogni triangolo, la trigonometria medievale fu completa.

Astrologia genetliaca e astrologia divinatoria

Il postulato fondamentale della branca più importante dell'astrologia, l'astrologia genetliaca, è che si possono dedurre gli eventi della vita di ogni persona dall'oroscopo della sua nascita. L'oroscopo è un documento che dà la longitudine dell'ascendente, della Luna, del Sole e dei pianeti, nonché i nodi lunari ascendente e discendente, all'istante della nascita. Talvolta vi vengono introdotte anche le collocazioni delle case. L'individuo per il quale si elabora l'oroscopo è indicato come il 'nativo'.

Tra le serie di longitudini da calcolare, la più importante è quella dell'ascendente, perché molte delle predizioni dipendono dalle posizioni di diversi pianeti rispetto a esso. Nello stesso tempo, la sua determinazione è di gran lunga la più difficile. I movimenti planetari sono relativamente lenti e perciò le loro posizioni non risentono del passare del tempo. Al contrario, l'ascendente dipende dalla rotazione giornaliera; quindi esso attraversa un intero segno zodiacale in un paio d'ore e un piccolo errore sul tempo della nascita può comportare seri errori nell'interpretazione.

Per cogliere l'ascendente, l'astrologo attende fuori della camera dove avverrà la nascita, ed è prontamente informato appena essa avviene. È suo interesse preparare un diagramma completo dell'oroscopo da consegnare al committente, ed elaborare un'interpretazione il più rapidamente possibile. Se egli ha a disposizione un astrolabio può trovare l'ascendente con una sola osservazione, tuttavia è bene che abbia a portata di mano anche le effemeridi. Il libro delle effemeridi infatti elenca le posizioni planetarie già calcolate, a intervalli frequenti, per l'anno in corso. Interpolando per la data in esame, l'astrologo completa l'oroscopo con il minimo impiego di tempo.

Rimane la questione dell'interpretazione. A tale scopo, l'astrologo ha a disposizione un'immensa letteratura contenente indicazioni. Ciascun pianeta, segno e casa è dotato di molteplici poteri, proprietà e qualità (benevolenza, malevolenza, amicizia, inimicizia, obbedienza, sesso, malattie, successi). Inoltre, in una coppia di pianeti in aspetto, ciascuno può influenzare i poteri e le proprietà dell'altro. Tuttavia, questo tipo di attività non coinvolge in alcun modo la matematica che è già stata applicata.

Una seconda branca dell'astrologia è l'astrologia divinatoria, che si può suddividere a sua volta in due categorie. La prima è il metodo per determinare il momento propizio in cui si realizza un dato evento. Al fine di risolvere tale questione, l'astrologo o gli astrologi coinvolti probabilmente calcolavano il suddetto momento propizio partendo dagli aspetti presenti dei cieli, ed elaborando quindi l'oroscopo. Questo doveva essere esaminato attentamente e poteva essere accettato o, più probabilmente, usato come base per un'altra scelta. Se necessario, la procedura poteva continuare. Il secondo tipo di divinazione consisteva nel rispondere a un richiedente che aveva rivolto una domanda specifica. Di nuovo la soluzione richiedeva l'interpretazione di un oroscopo, elaborato, in questo caso, per il momento in cui la domanda era posta. In ogni caso, le regole che governavano l'interpretazione erano essenzialmente quelle usate per le nascite.

Astrologia delle congiunzioni

Durante il lungo intervallo trascorso tra l'epoca di Tolomeo e l'VIII sec., in quello che sarebbe diventato il mondo islamico, si continuò a praticare l'astrologia degli oroscopi tradizionale. I cambiamenti nella teoria furono pochi, ma vi fu un lento miglioramento dei parametri astronomici su cui si basava. Contemporaneamente, nell'Iran sasanide le antiche idee sui cicli cronologici furono utilizzate nel calcolo degli oroscopi per produrre una serie di opere che possiamo chiamare 'storie del mondo', le quali si basavano sulle serie di congiunzioni dei due pianeti più lenti, Saturno e Giove.

Ogni congiunzione di tali pianeti poteva preannunciare un evento religioso, politico o naturale di un certo rilievo. Queste congiunzioni si succedono a intervalli di circa vent'anni; ciò implica che se una particolare congiunzione si verifica, per esempio, nella triplicità del fuoco, la successiva salterà tre segni per apparire in un segno diverso, ma nella stessa triplicità. Tuttavia, in conseguenza del moto medio dei due pianeti, le congiunzioni successive avanzano lentamente nell'eclittica, penetrando infine nella triplicità successiva, in questo caso quella della Terra. Questi passaggi di triplicità si succedono gli uni agli altri a intervalli di circa 238 o 259 anni, a seconda che servano dodici o tredici congiunzioni prima che si verifichi il passaggio. Si supponeva che i passaggi coincidessero con eventi di gran lunga più importanti di quelli associati alle semplici congiunzioni.

Un ciclo di quattro passaggi esaurisce tutte e quattro le triplicità, tornando a quella originaria, nel nostro esempio quella del fuoco. Questo percorso si compie in un periodo di tempo dell'ordine del millennio, e il completamento di questo ciclo può annunciare l'avvento di un profeta che fonda una nuova religione, o una questione di importanza mondiale.

L'astrologo più influente del Medioevo fu Abū Ma῾šar (noto anche come Albumasar, 787-886). Originario di Balkh, da giovane soggiornò in Iraq, e a Baghdad studiò con diversi maestri fino a divenire un ardente proselito dell'astrologia.

Compose numerose opere che contribuirono ad accrescere la sua fama; tuttavia, i quarantuno libri da lui scritti, per la maggior parte, rappresentano un'esposizione della validità dell'astrologia o delle sue applicazioni pratiche. La popolarità di Abū Ma῾šar, a questo punto, ci impone di parlare del suo sistema cosmologico, che costituisce una variante dell'astrologia delle congiunzioni basata su un anno mondiale, di elaborazione persiana, di 360.000 anni. In esso Abū Ma῾šar ipotizza l'inizio di una grande congiunzione da parte di tutti i pianeti nel punto vernale. Il loro movimento, infatti, era tale che alla fine dell'anno mondiale essi ritornavano tutti nel punto iniziale. L'anno mondiale era suddiviso in tre serie di cicli più brevi, ognuna con caratteristiche proprie. L'unica matematica richiesta in aggiunta per costruire il sistema era un leggero aggiustamento con parametri di moto medio ricavati da fonti indiane e iraniane.

Se la matematica rese possibile il sorgere dell'astrologia, fu proprio lo sviluppo della stessa disciplina che, dopo un lungo periodo di tempo, fece perdere a questa materia ogni credibilità. Tale processo ebbe inizio quando Copernico (1473-1543) comprese che era molto più semplice considerare la rotazione di tutti i pianeti, inclusa la Terra, intorno al Sole, piuttosto che mettere la Terra al centro dell'Universo. L'eliocentrismo andò incontro a ulteriori sviluppi nel XVI sec. con Johannes Kepler (1571-1630), che fu egli stesso astrologo. Le sue accurate osservazioni portarono a dimostrare che le orbite dei pianeti non sono circolari bensì ellittiche e che in ciascuna di queste il Sole occupa uno dei due fuochi. La questione fu, infine, risolta in maniera defintiva da Isaac Newton (1642-1727), il quale con la legge di gravitazione universale, da lui provata con il calcolo infinitesimale, trasformò la teoria planetaria cinetica in una branca della fisica. Una conseguenza è che nell'immenso Universo l'uomo abita un pianeta in orbita attorno a una piccola stella tra le galassie. L'idea che fosse possibile prevedere qualsiasi azione umana basandosi sulla posizione degli altri pianeti in orbita al momento della nascita apparve palesemente assurda. Tuttavia, l'astrologia è ancora oggi largamente praticata.

Bibliografia

Bouché-Leclercq 1899: Bouché-Leclercq, Auguste, L'astrologie grecque, Paris, Leroux, 1899.

Gibbs 1984: Gibbs, Sharon - Saliba, George, Planispheric astrolabes from the National Museum of American History, Washington, Smithsonian Institution Press, 1984.

Heath 1921: Heath, Thomas L., A history of Greek mathematics, Oxford, Clarendon, 1921, 2 v. (rist.: New York, Dover, 1981, 2 v.).

Kennedy 1969: Kennedy, Edward S., The history of trigonometry, in: Historical topics for the mathematics classroom, Washington, National Council of Teachers of Mathematics, 1969, pp. 333-359 (rist. in: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983, pp. 3-29).

‒ 1971: Kennedy, Edward S. - Pingree, David, The astrological history of Māshā᾽allāh, Cambridge (Mass.), Harvard University Press, 1971.

‒ 1972: Kennedy, Edward S. - Krikorian-Preisler, Haiganoush, The astrological doctrine of projecting the rays, "Al-Abhath", 25, 1972, pp. 3-15.

‒ 1983a: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983.

‒ 1983b: Kennedy, Edward S., The world-year concept in islamic astrology, in: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983, pp. 351-371.

‒ 1985: Kennedy, Edward S., Spherical astronomy in Kāshī's Khāqānī Zīj, "Zeitschrift für Geschichte der arabisch-islamischen Wissenschaften", 2, 1985, pp. 1-46.

‒ 1995-96: Kennedy, Edward S., Treatise V of Kāshī's Khāqānī Zīj: determination of the ascendent, "Zeitschrift für Geschichte der arabisch-islamischen Wissenschaften", 10, 1995-1996, pp. 123-144.

‒ 1996: Kennedy, Edward S., The astrological houses as defined by medieval islamic astronomers, in: From Bagdad to Barcelona. Studies in the islamic exact sciences in honour of Juan Vernet, edición por Josep Casulleras y Julio Samsó, Barcelona, Instituto Millás Vallicrosa de Historia de la Ciencia Árabe, 1996, pp. 535-578.

‒ 1998: Kennedy, Edward S., Astronomy and astrology in the medieval islamic world, Aldershot-Brookfield (Vt.), Ashgate, 1998.

Neugebauer 1959: Neugebauer, Otto - Van Hoesen, Henry B., Greek horoscopes, Philadelphia, American Philosophical Society, 1959.

North 1986: North, John D., Horoscopes and history, London, Warburg Institute, 1986.

Pingree 1968: Pingree, David, The thousands of Abū Ma῾shar, London, Warburg Institute, 1968.

‒ 1997: Pingree, David, Māshā᾽allāh: Greek, Pahlavi, Arabic and Latin astrology, in: Perspectives arabes et médiévales sur la tradition scientifique et philosophique grecque. Actes du colloque de la SIHSPAI, Paris 1993, édités par Ahmad Hasnawi, Abdelali Elamrani-Jamal et Maroun Aouad, Leuven, Peeters; Paris, Institut du Monde Arabe, 1997, pp. 123-126.