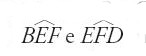La civiltà islamica: antiche e nuove tradizioni in matematica. La teoria delle parallele
La civilta islamica: antiche e nuove tradizioni in matematica. La teoria delle parallele
La teoria delle parallele
Secondo la def. 23 che Euclide fornisce nel Libro I degli Elementi, rette che giacciono in uno stesso piano sono parallele se, prolungate in entrambe le direzioni, non si incontrano. La teoria costruita su questa definizione creava difficoltà già prima di Euclide. Aristotele, parlando della petizione di principio, osservava che "è proprio questo l'errore commesso da coloro che ritengono di tracciare rette parallele: essi infatti non si accorgono di assumere premesse tali da non poter essere dimostrate, a meno che le rette non si presuppongano già parallele" (Analytica priora, II, 16, 65a 4). Filopono (filosofo cristiano del VI sec. d.C.) commentava, non senza qualche oscurità, il passo di Aristotele in questi termini: "essi ammettono che sia possibile tracciare rette parallele a partire dal cerchio meridiano e suppongono, per così dire, che un punto cada sul piano di questo cerchio e così tracciano le rette. E così si suppone quello che si cerca, perché colui che non ammette la genesi delle parallele non ammetterà nemmeno il punto di cui si sta parlando".
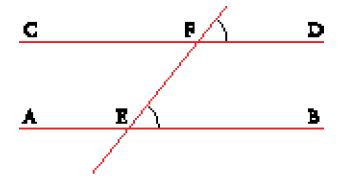
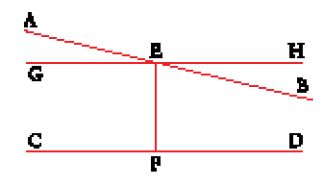
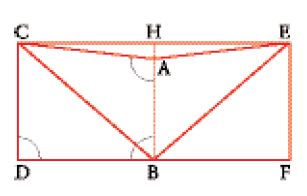
Lo storico della matematica Thomas Heath interpretava il commento di Filopono nel senso che in esso si parla di un punto estremamente lontano nel piano, tale cioè che le rette che passano per questo punto possano essere considerate parallele; in altre parole la critica di Aristotele si appunterebbe su una concezione del parallelismo come identità di direzione. Aristotele (Analytica priora, II, 17, 66a 11) osserva poi che esistono ipotesi che porterebbero alla falsa conclusione che le parallele si incontrino: (1) se si suppone che l'angolo interno sia più grande dell'angolo esterno; (2) se si suppone che la somma degli angoli di un triangolo sia maggiore di due angoli retti. L'ipotesi (1) si riferisce agli angoli in E e in F formati da una trasversale EF a due rette parallele AB e CD (fig. 1). Discuteremo in seguito l'interpretazione di queste due ipotesi.
La teoria delle parallele dunque aveva creato problemi e suscitato discussioni approfondite fin dall'epoca di Aristotele. Euclide diede una soluzione alle difficoltà che questi aveva segnalato con l'introduzione del suo famoso postulato V, detto 'postulato delle parallele': "se una retta [EF nella fig. 1] venendo a cadere su due rette [AB e CD] forma gli angoli interni e dalla stessa parte
[
]
minori di due angoli retti [cioè tali che la loro somma sia minore di due retti], le due rette prolungate illimitatamente verranno a incontrarsi da quella parte in cui sono gli angoli minori di due retti" (Elementa, Libro I). Questo postulato permise a Euclide di edificare una teoria coerente delle parallele, riconducendo il parallelismo a una proprietà degli angoli che una trasversale forma tagliando le due rette. Il suo carattere ad hoc, tuttavia, non soddisfaceva i geometri; e un altro motivo di insoddisfazione nasceva dalla sua somiglianza con il reciproco di un teorema dimostrato nel Libro I, prop. 28, la cui dimostrazione non necessita del postulato V. Siamo qui di fronte all'origine di un capitolo del tutto peculiare della storia della geometria: la storia degli sforzi compiuti per sostituire la definizione euclidea con un'altra, o per dimostrare il postulato V a partire dalle altre ipotesi euclidee, o, infine, per dimostrarlo sulla base di un postulato più soddisfacente che potesse prenderne il posto.
Gli studi sulla teoria delle parallele continuarono fino all'inizio dell'Ottocento, quando (del tutto inaspettatamente) si scoprì che si poteva sostituire il postulato V con un altro ‒ del tipo, per esempio, delle ipotesi (1) e (2) di Aristotele ‒ e costruire su questa base una nuova geometria altrettanto coerente di quella euclidea, ma incompatibile con essa. Ci vollero circa quarant'anni perché la portata della scoperta delle geometrie non euclidee cominciasse a essere avvertita, ma essa ebbe effetti assai profondi.
Si possono distinguere vari periodi nella storia della teoria delle parallele: il periodo ellenistico, noto grazie al commento al Libro I degli Elementi da parte del filosofo neoplatonico Proclo di Costantinopoli (In primum Euclidis elementorum librum commentarii, V sec. d.C.); il periodo arabo, che ci ha lasciato molti testi originali; il XVI e XVII sec. in Europa; e, infine, la scoperta della geometria non euclidea. Proprio alcuni testi arabi, tradotti in latino fra il XII e il XVI sec., ispirarono i lavori su questo argomento di John Wallis e di Girolamo Saccheri. Fino a non molto tempo fa era questa la sola parte della geometria araba nota agli storici; in questo capitolo tratteremo della storia delle parallele fino alla fine dell'impatto delle matematiche arabe.
Il periodo ellenistico
La definizione euclidea di parallelismo pone immediatamente problemi, sia perché si fonda su una proprietà negativa, sia perché coinvolge l'infinito, in quanto, per verificare che due rette sono parallele, occorre prolungarle indefinitamente (o illimitatamente, in greco eis ápeiron). Di conseguenza, alcuni autori cercarono di sostituire questa definizione. La prima idea fu quella di dire che due rette sono parallele se hanno la stessa 'direzione'; tuttavia, abbiamo appena visto che si tratta di una petizione di principio (la direzione è definita a partire dal parallelismo). Un'altra idea che emerse fu quella di fondare il parallelismo sull''equidistanza': due rette sono parallele se tutte le perpendicolari abbassate da un punto di una retta sull'altra sono uguali. Questa definizione, secondo Proclo, si trovava nel filosofo stoico Posidonio e poi nel suo allievo Gemino di Rodi. Un'altra testimonianza di questa definizione si incontra in una citazione del neoplatonico Simplicio di Cilicia, conservataci dal matematico arabo al-Nayrīzī (900 d.C. ca.); questi attribuisce la definizione a un tal Aġānis altrimenti sconosciuto. Tuttavia, come osserverà Saccheri all'inizio del Settecento, nulla prova che esistano rette che si mantengano a distanza costante; anche se ‒ come vedremo fra breve ‒ si può dimostrare l'esistenza di tali rette utilizzando la definizione euclidea e il postulato V. La definizione basata sull'equidistanza non è dunque soddisfacente, ma la vedremo ripresentarsi numerose volte nel corso della storia.
Nel Libro I degli Elementi, Euclide dimostra l'esistenza di rette parallele (secondo la sua definizione) utilizzando la prop. 16: l'angolo esterno ACD del triangolo ABC è maggiore di ciascuno dei due angoli interni a lui opposti ABC e BAC.
Per dimostrare questo fatto, si congiunga B con E, punto medio del lato opposto AC e si prolunghi BE fino a F in modo che BE=EF. I triangoli AEB e CEF risultano allora uguali (per il primo criterio di uguaglianza dei triangoli dato nel Libro I, prop. 4) e l'angolo BAC sarà dunque uguale all'angolo FCE. Il lato CF di quest'angolo è contenuto nell'angolo esterno ACD, e dunque l'angolo esterno è maggiore di FCE (per la nozione comune V, ossia che il tutto è maggiore della parte). Ne segue la tesi.
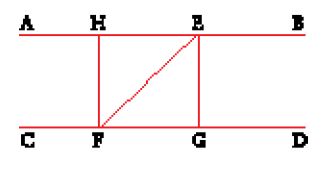
Grazie alla prop. 16 Euclide può dimostrare la prop. 27, secondo la quale, se due rette AB e CD formano con la trasversale EF angoli alterni interni FEB ed EFC uguali, allora le due rette sono parallele.
Infatti, supponiamo, per assurdo, che le rette AB e CD si incontrino in un punto G. Allora l'angolo esterno EFC del triangolo EFG sarebbe uguale all'angolo interno opposto FEB, contro la prop. 16. Dalla prop. 27 segue immediatamente la prop. 28, la quale afferma (fig. 3) che, se la somma degli angoli coniugati interni FEB ed EFD posti dalla stessa parte rispetto alla trasversale è uguale a due retti, le rette AB e CD saranno parallele (basta osservare che la somma
vale due angoli retti).
La prop. 29 è la reciproca delle due precedenti 27 e 28, ma per la sua dimostrazione è necessario far uso del postulato V. Essa afferma che se AB e CD sono parallele, gli angoli alterni interni formati dalla trasversale EF sono uguali e gli angoli interni dalla stessa parte sono supplementari (ossia la loro somma è uguale a due retti). La dimostrazione procede per assurdo: se fosse, per esempio,
,
sommando
a entrambi si otterrebbe che
sarebbe minore di
cioè di due angoli retti. Allora, per il postulato V, se si prolungassero AB e CD dalla parte di B e di D, esse si dovrebbero incontrare, contro l'ipotesi che le rette siano parallele.
In tal modo, le propp. 27, 28 e 29 del Libro I degli Elementi riconducono il parallelismo a una proprietà angolare, enunciabile in termini positivi e in cui non interviene l'infinito. Euclide poteva così, nella successiva prop. 33 dello stesso Libro I, stabilire l'esistenza dei parallelogrammi, il che equivale a una dimostrazione dell'equidistanza di due rette parallele.
Tuttavia, come abbiamo già osservato, l'enunciato del postulato V non soddisfaceva i matematici. Come scrive Proclo nel commento al Libro I degli Elementi di Euclide "non bisogna considerarlo fra i postulati, bensì è un teorema che presenta molte difficoltà, che Tolomeo cercò di risolvere in un suo trattato, e che necessita per la dimostrazione di molte definizioni e teoremi. D'altro canto, lo stesso Euclide ha dimostrato il reciproco di questa asserzione". La prima idea di dimostrazione segnalata da Proclo consiste nel dire che, se gli angoli interni coniugati (ossia, dalla stessa parte della trasversale EF) hanno somma minore di due retti, allora ci deve essere convergenza (sýnesis) delle rette AB e CD dalla parte di questi angoli, e che queste rette devono dunque incontrarsi. Tuttavia, ricorda Proclo citando Gemino, AB e CD potrebbero avvicinarsi sempre più senza mai toccarsi: potrebbero cioè essere rette 'asintote', come avviene nel caso dell'iperbole e del suo asintoto, appunto. Non si può dunque concludere nulla sull'intersezione delle rette se non si stabilisce preventivamente che due rette non possono essere asintote. E in effetti, nella geometria non euclidea detta 'iperbolica', le parallele sono asintote da una parte e si allontanano dall'altra.
Proclo riporta poi la dimostrazione di Tolomeo nel modo seguente. Supponiamo che AB e CD siano parallele; si vuole dimostrare che la somma
è uguale a due angoli retti. Se fosse maggiore di due retti,
sarebbe minore di due retti, perché la somma dei quattro angoli è uguale a quattro retti. Ora, secondo Tolomeo, poiché le due rette sono parallele tanto da una parte quanto dall'altra, anche la somma
dovrebbe essere maggiore di due retti, come dalla parte di A e di C, il che è assurdo. Questo ragionamento suppone implicitamente che il parallelismo 'fissi' il valore, rispetto a due angoli retti, della somma degli angoli interni dalla stessa parte di una trasversale; ma è proprio questa ipotesi implicita ciò che si dovrebbe dimostrare e Tolomeo cade così in un circolo vizioso.
Proclo propone anche una sua dimostrazione. Essa si basa su un postulato tratto da Aristotele, secondo il quale due rette che escono da uno stesso punto, se prolungate indefinitamente, si allontanano l'una dall'altra più di qualunque distanza assegnabile (De caelo, I, 5, 271b 28). Tuttavia Proclo suppone anche, implicitamente, che le distanze dei punti di una retta AB da una sua parallela CD rimangano limitate, il che non è altro che una forma debole della proprietà di equidistanza.
Egli, infatti, dimostra innanzitutto che, se una retta ('semiretta', secondo la terminologia moderna) EF taglia AB (fig. 4), il suo prolungamento deve tagliare necessariamente anche la parallela CD ad AB, perché il prolungamento FG si allontana indefinitamente da AB (principio di Aristotele), mentre la distanza fra AB e CD resta limitata. Ora, nella situazione prevista dal postulato V, si suppone piuttosto che la somma
(fig. 5) sia minore di due angoli retti e se ne vuole dedurre che AB e CD si incontrano dalla parte di B e D. Proclo dimostra il postulato nel modo seguente. Si tracci GH passante per E in modo che
sia uguale a due angoli retti; ciò garantisce (per la prop. 28 prima citata) che GH e CD siano parallele. Ma siccome AB incontra GH, AB incontrerà anche CD.
Il frammento di Simplicio tradotto in arabo e citato da al-Nayrīzī nel suo Šarḥ Uqlīdis, commento agli Elementi, contiene un tentativo di dimostrazione del postulato V a opera di un misterioso Aġānis. Le parallele sono definite, come abbiamo visto, per il tramite della proprietà di equidistanza e su questa base si dimostra che la distanza è data dalle rette perpendicolari alle due parallele. La dimostrazione della prop. 29 risulta facile (fig. 6): si traccino, dalle estremità E e F della trasversale considerata, rispettivamente la perpendicolare EG a CD e la perpendicolare FH ad AB. I triangoli rettangoli FHE ed EGF hanno in comune l'ipotenusa EF, e i lati FH ed EG sono uguali (per l'equidistanza); quindi i due triangoli sono uguali e pertanto anche gli angoli alterni interni AEF e DFE sono uguali. Aġānis ne deduce, come Proclo, l'unicità della parallela a una retta data passante per un punto esterno a essa.
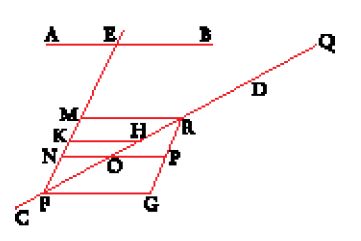
Infine, per dimostrare il postulato V, Aġānis fa ricorso al cosiddetto postulato o 'assioma di Archimede' (fig. 7). Da un punto H di CD si tracci HK parallela ad AB che incontri la trasversale EF in K. Sia M il punto medio di EF, N il punto medio di MF e così via. Per l'assioma di Archimede si arriverà in questo modo a un punto situato fra K e F, per esempio N. Il segmento NF=EF/2n sarà infatti più piccolo di KF per n abbastanza grande. Aġānis traccia ora NO parallela ad AB: questa retta incontra CD in O, fra F e H (perché deve uscire dal triangolo FKH). A questo punto egli costruisce Q, sul prolungamento di CD in modo che FQ=2nFO; e per i punti di suddivisione di FQ (quale R) traccia le parallele a EF (come RG). I triangoli NOF e POR sono uguali (per il secondo criterio di uguaglianza dei triangoli, dato nella prop. 26 del Libro I degli Elementi), in quanto FO=OR e sono uguali anche gli angoli adiacenti corrispondenti; infatti
(per la prop. 29) e
in quanto angoli opposti al vertice (applicando la prop. 15). Pertanto RP=FN e d'altra parte il parallelogramma FNPG mostra che FN=GP. Di conseguenza, RG=MF e MR è parallela a FG, quindi anche ad AB. Ripetendo il ragionamento si finisce con l'ottenere che EQ è parallela ad AB e dunque che il punto Q di CD si trova sulla retta AB.
La teoria delle parallele nella matematica araba
Il più antico commentatore arabo che si sia occupato del postulato delle parallele sembra essere stato al-Ǧawharī, che scrisse un Iṣlāḥ li-kitāb al-Uṣūl (Rettifica al libro degli Elementi). Questo testo non ci è pervenuto, ma è citato nel XIII sec. da Naṣīr al-Dīn al-Ṭūsī. In esso si ammetteva implicitamente che, se la conclusione della prop. 29 del Libro I degli Elementi (cioè l'uguaglianza degli angoli alterni formati da una trasversale che interseca due rette parallele) è vera per una trasversale che tagli due rette parallele date, allora è vera per tutte le trasversali; su questa base si può stabilire che le parallele si mantengono a distanza costante l'una dall'altra. Al-Ǧawharī dimostrava poi il postulato V, stabilendo in primo luogo che si può tracciare per un punto interno a un angolo dato una retta che incontri i due lati dell'angolo; questa proprietà sarà utilizzata anche da Naṣīr al-Dīn al-Ṭūsī e ‒ molto più tardi, nel 1800 ‒ da Adrien-Marie Legendre. Per quanto riguarda al-Nayrīzī, oltre al commento a Euclide (nel quale, come si è detto, cita Simplicio e Aġānis parlando della teoria delle parallele), aveva composto un'operetta, la Risāla fī 'l-muṣādara al-mašhūra li-Uqlīdis (Epistola sul celebre postulato di Euclide), in cui riprendeva le stesse idee che Simplicio attribuisce ad Aġānis. Il suo commento è importante, per la diffusione che ebbe grazie alla traduzione latina che ne fece Gherardo da Cremona nel XII sec., in cui era indicato con il nome latinizzato di Anaritius.
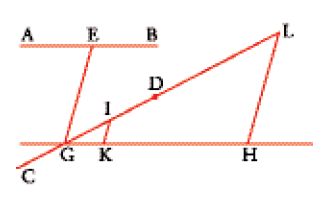
Il grande astronomo e matematico Ṯābit ibn Qurra (826-901) scrisse due trattati sul problema: la Maqāla fī burhān al-muṣādara al-mašhūra min Uqlīdis (Trattato sulla dimostrazione del celebre postulato di Euclide) e la Maqāla fī anna al-ḫaṭṭayn iḏā uḫriǧā ilā 'l-zāwiyatayn aqall min al-qā'imatayn iltaqayā (Trattato sul fatto che due rette tracciate ad angoli minori di due retti si incontrano). Nel primo di questi testi egli non utilizza mai il termine arabo mutawāzī (parallela); parla invece di rette 'che non si avvicinano né si allontanano', optando dunque per il concetto di equidistanza come fondamento della teoria. Egli suppone che se due rette si allontanano in una direzione si debbano necessariamente avvicinare nell'altra, e viceversa; ciò gli permette di dimostrare che l'ipotesi degli angoli alterni interni uguali implica l'equidistanza delle due rette. Di conseguenza, la dimostrazione della prop. 29 non presenta più alcuna difficoltà. Anche Ṯābit utilizza di nuovo l'assioma di Archimede per dimostrare il postulato V, ma in modo più semplice rispetto ad Aġānis e al-Nayrīzī. Si supponga (fig. 8) che le rette AB e CD formino con la trasversale EG gli angoli BEG ed EGD, la cui somma sia minore di due retti: si vuole dimostrare che tali rette, prolungate dalla parte di questi angoli, si devono incontrare. Si tracci GH parallela a AB e si conduca da un punto I di CD la parallela IK a EG, che incontri GH in K. Se IK è maggiore di EG, CD incontra AB fra G e I. Altrimenti, si raddoppia GI e si ricomincia, fino a ottenere GL=2nGI, tale che LH sia maggiore di EG (l'assioma di Archimede garantisce, infatti, che ciò è possibile).
Nel suo secondo trattato Ṯābit faceva invece ricorso al movimento. Quest'idea la ritroviamo anche in Ibn al-Hay- ṯam (m. dopo il 1040), che dedicò due opere alla teoria delle parallele: lo šarḥ muṣādarāt kitāb Uqlīdis fī 'l-Uṣūl (Commento ai postulati dell'opera di Euclide sugli Elementi) e il Kitāb fī ḥall šukūk kitāb Uqlīdis fī 'l-Uṣūl (Libro sulla soluzione dei dubbi intorno agli Elementi di Euclide). Una volta di più, Ibn al-Hayṯam criticava la definizione euclidea delle parallele: non si può rappresentare chiaramente la nozione euclidea di parallelismo a causa dell'intervento dell'infinito nella definizione. Egli sostituiva il parallelismo con l'equidistanza, ma proponeva ‒ come già Ṯābit prima di lui ‒ un tentativo di dimostrazione del fatto che il luogo dei punti che abbiano distanza data da una retta data (da una parte di questa retta) è una retta. A tal fine, utilizzava il movimento facendo descrivere a un segmento EF un 'movimento semplice', in modo che F descrivesse una retta fissa AB e il segmento EF restasse sempre perpendicolare ad AB. Questo movimento semplice (che apparentemente consiste in una traslazione uniforme) non è evidentemente definito da Ibn al-Hayṯam; egli cerca di superare la difficoltà con prolisse spiegazioni, per concludere che tutti i punti di EF descrivono linee 'uguali e simili'. Il punto E descrive dunque una retta, esattamente come l'altro estremo F, e questa retta si mantiene a una distanza costante da AB.
Il ricorso al moto è un tratto caratteristico della geometria di Ibn al-Hayṯam, ma la vera novità compare nella sua dimostrazione del postulato delle parallele. Egli, infatti, cerca di dimostrarlo per assurdo, assumendo la sua negazione e deducendone una contraddizione. Molti altri autori lo seguiranno per questa strada, fino alla scoperta della geometria non euclidea.
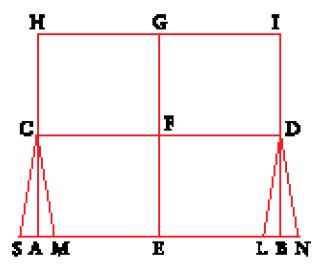
Si traccino le perpendicolari AC e BD alle estremità del segmento AB e da un punto C di AC si abbassi la perpendicolare CD su BD (fig. 9). Si ottiene così un quadrilatero ABCD che ha tre angoli retti per costruzione e basterà dimostrare che anche il quarto angolo ACD è retto. Si tratta, insomma, secondo il nuovo punto di vista di Ibn al-Hayṯam, di dimostrare l'esistenza del rettangolo per fondare la teoria delle parallele. A questo fine si dimostra che CD=AB, fatto che implica l'uguaglianza dei triangoli rettangoli BAC e CDB. Per dimostrare la relazione CD=AB, Ibn al-Hayṯam mostra che le ipotesi CD>AB e CD⟨AB conducono entrambe a contraddizione. Si prolunghi CA oltre A fino a E, in modo che sia AE=CA, e da E si abbassi la perpendicolare EF sul prolungamento di DB. Poiché l'angolo BAE è retto, i triangoli ABC e ABE sono uguali (di nuovo per la prop. 4 del Libro I); quindi BC=BE e gli angoli CBA, EBA sono uguali; sono dunque uguali gli angoli CBD ed EBF, in quanto complementari di angoli uguali. Di conseguenza, i triangoli CBD ed EBF sono uguali e quindi EF=CD. Ora, se per esempio fosse CD>AB, anche EF sarebbe maggiore di AB. Si sposti allora EF lungo DF mantenendolo perpendicolare: l'estremità E descriverà una retta EHC equidistante da FBD; e quando F giungerà in B, E giungerà in H e dovrebbe essere BH>BA. Il che è assurdo, perché le rette EAC ed EHC racchiuderebbero uno spazio. Allo stesso modo si dimostra che è impossibile che sia CD⟨AB.
῾Umar al-Ḫayyām (1048-1131) criticò violentemente Ibn al-Hayṯam per aver introdotto il moto in geometria, proponendo a sua volta una dimostrazione per assurdo del postulato V. L'idea è analoga a quella di Ibn al-Hayṯam, ma invece di utilizzare il movimento, al-Ḫayyām fece ricorso a un principio enunciato esplicitamente e da lui attribuito ad Aristotele (o, meglio, 'al Filosofo'). Il principio ‒ di cui non si trova traccia negli scritti di Aristotele oggi noti ‒ è il seguente: "due rette che convergono si incontrano ed è impossibile che due rette convergenti divergano nella direzione di convergenza". Questo principio contiene due asserzioni: la prima esclude la possibilità dell'esistenza di rette asintote e risponde alle obiezioni del tipo di quelle sollevate da Gemino; la seconda esclude il caso per cui due rette possano avvicinarsi fino a una perpendicolare comune e allontanarsi tra loro dopo averla superata. Entrambi i casi si presentano effettivamente nella geometria iperbolica.
Anche al-Ḫayyām costruisce un quadrilatero (fig. 10) tracciando le perpendicolari AC e BD a un segmento AB e riportando in alto AC=BD. Dimostra poi che gli angoli ACD e BDC sono uguali: l'esistenza del rettangolo si riduce al fatto che questi angoli sono retti.
Si tracci la perpendicolare EF al punto di mezzo di AB; si dimostra che essa incontra CD ad angoli retti nel suo punto di mezzo F. Il quadrilatero AEFC è dunque analogo a quello di Ibn al-Hayṯam (con tre angoli retti). Si prolunghi allora EF oltre F fino al punto G in modo che FG=EF e si tracci HI, la perpendicolare in G a EG, che incontrerà i prolungamenti di AC e BD in H e I rispettivamente. Per assicurare l'esistenza dei punti H e I è necessaria un'ipotesi supplementare, che al-Ḫayyām introduce implicitamente: l'equidistanza delle parallele AH ed EG, o BI ed EG. In effetti, in geometria non euclidea i punti H e I non sempre esistono.
Si ottiene dunque un nuovo quadrilatero CDIH. Ribaltandolo rispetto a CD, si otterrà il quadrilatero CDLM se l'angolo ACD è ottuso (e dunque
è acuto) e il quadrilatero CDNS se
è acuto; ne segue che HI>AB nel caso di angolo acuto e HI⟨AB se l'angolo è ottuso. Si può ricominciare la costruzione a partire dal quadrilatero ABIH; continuando in questo modo si otterrà che le rette AC e BD, prolungate oltre C e D, divergono nell'ipotesi dell'angolo acuto e convergono nell'ipotesi dell'angolo ottuso. Queste conclusioni sono perfettamente valide e possono essere considerate come i primi due enunciati di geometria non euclidea, per quanto al-Ḫayyām non pensi affatto a prospettive del genere. Egli, invece, per ottenere le contraddizioni che si aspetta, nota che si avranno le stesse proprietà per i prolungamenti di CA e di DB dall'altra parte di AB: nell'ipotesi dell'angolo acuto le rette divergono dalle due parti della loro perpendicolare comune AB, e convergono nell'ipotesi dell'angolo ottuso. Il principio che egli attribuisce ad Aristotele gli permette allora di escludere l'una e l'altra di queste conclusioni e di dimostrare sia che i lati opposti di un rettangolo sono uguali sia che le parallele sono equidistanti. A questo punto è in grado di dimostrare la prop. 29 di Euclide e il postulato delle parallele.
Le teorie di al-Ǧawharī, di Ibn al-Hayṯam e di ῾Umar al-Ḫayyām sono esposte da Naṣīr al-Dīn al-Ṭūsī (1201-1274) nella sua Risāla al-šāfiya ῾an al-šakk fī 'l-ḫuṭūṭ al-mutawāziya (Epistola che guarisce i dubbi sulle rette parallele).
Al-Ṭūsī proponeva poi una sua dimostrazione che si ispirava a quella di al-Ḫayyām, utilizzava l'assioma di Archimede (come quella di al-Nayrīzī) e supponeva l'esistenza di una retta passante per un punto interno a un angolo e che incontri i due lati dell'angolo (come in quella di al-Ǧawharī). Egli riprese poi questa dimostrazione nel Taḥrīr al-Uṣūl li-Uqlīdis (Redazione degli Elementi di Euclide), esplicitando l'ipotesi che gli occorreva per arrivare alla conclusione. L'ipotesi, che assomiglia al principio che al-Ḫayyām attribuiva al Filosofo, è la seguente: tutte le rette di una superficie piana cui s'imponga di allontanarsi in una direzione data, non possono essere destinate ad avvicinarsi in questa direzione senza secarsi.
La dimostrazione riprende il quadrilatero di al-Ḫayyām (fig. 10), provando che si tratta di un rettangolo. Se gli angoli ‒ uguali ‒ in C e in D fossero ottusi (rispettivamente acuti), AB e CD si allontanerebbero (rispettivamente, si avvicinerebbero) in direzione di B e di D; accadrebbe però la stessa cosa, per simmetria, in direzione di A e di C, il che è assurdo per l'ipotesi formulata. Per stabilire questa proprietà di allontanamento o di avvicinamento, al-Ṭūsī costruisce una sequenza di triangoli rettangoli i cui angoli retti si trovano alternativamente su AB e su CD e l'ipotenusa di ciascuno dei quali è un lato dell'angolo retto del triangolo seguente o del precedente. Così facendo stabilisce, come al-Ḫayyām prima di lui, una proprietà di geometria non euclidea: le rette AB e CD hanno in comune un'unica perpendicolare (quella che congiunge i punti di mezzo di AB e CD) e la variazione della distanza di AB da CD cambia senso passando attraverso questa perpendicolare comune, che è la distanza massima nell'ipotesi dell'angolo ottuso (geometria sferica) e la distanza minima nell'ipotesi dell'angolo acuto (geometria iperbolica).
Una variante della dimostrazione di al-Ṭūsī si trova in una seconda versione del Taḥrīr al-Uṣūl li-Uqlīdis, attribuita anch'essa ad al-Ṭūsī ma sicuramente a lui posteriore. Tale versione fu stampata in arabo a Roma nel 1594 e fu tradotta in latino dall'arabista Edward Pococke (1604-1691) su richiesta di John Wallis. Quest'ultimo inserì la traduzione di Pococke nell'edizione delle sue opere, apparsa nel 1693; il testo contenuto nelle opere di Wallis servì da punto di riferimento a Saccheri. Ci troviamo qui di fronte a una preziosa testimonianza delle vie di trasmissione dalle matematiche arabe a quelle latine. Si aggiunga che Wallis fece poi tradurre in latino la prima versione della dimostrazione di al-Ṭūsī; il manoscritto di questa traduzione si trova alla Bodleian Library di Oxford, nell'esemplare personale che Wallis conservò delle sue opere. Non è impossibile che Saccheri lo conoscesse.
Gli sviluppi successivi della geometria araba in materia si possono trovare in alcuni testi ebraici, ma soprattuto in testi latini. Un commento anonimo, scritto in ebraico, degli Elementi di Euclide propone un'idea di dimostrazione che si ritrova, attribuita a Mōšeh ha-Lēwî di Siviglia (XIII sec.), in un'opera intitolata Colui che rende retta la curva e attribuita a un certo Maestro Alfonso (XIV sec., forse Alfonso di Valladolid). Questa dimostrazione ricorda quella di Proclo, ma invece di invocare il principio di Aristotele e una condizione di limitatezza della distanza fra due rette parallele Mōšeh sposta 'in immaginazione' EH in modo che E descriva EF e che l'angolo HEF rimanga uguale a sé stesso. Egli spiega poi che la retta EH, che nella sua posizione iniziale incontra AB, non può separarsene nel corso del moto "se non raggiungendo la sua estremità prima di tale separazione". Questa eventualità è però da escludersi perché le rette sono "senza limite" e ne risulta che EH, nella sua posizione finale FD, incontra ancora AB. Questo ragionamento è forse un'eco di altri che si possono leggere in alcuni testi arabi di carattere filosofico, per esempio in Avicenna (980-1037).
Maestro Alfonso rimprovera a Mōšeh ha-Lēwî di considerare rette infinite in atto e critica anche le dimostrazioni di Ibn al-Hayṯam e di Aġānis. Tuttavia, le sue critiche mostrano una conoscenza assai superficiale di questi testi: non vede, per esempio, che Ibn al-Hayṯam utilizza il movimento per dimostrare che il luogo dei punti equidistanti da una retta data è ancora una retta; e rimprovera alla dimostrazione di Aġānis di ammettere l'equidistanza delle parallele e di non conformarsi alla definizione euclidea. Maestro Alfonso presenta poi la propria dimostrazione, in cui utilizza la sovrapposizione di due parallelogrammi per stabilire l'esistenza del rettangolo, la quale, tuttavia, è invalidata da un grossolano circolo vizioso.
Il terzo autore di lingua ebraica che ha tentato una dimostrazione del postulato V è Lēwî ben Gēršôm (Gersonide, 1288-1344). Egli scrisse un commento ai primi cinque libri degli Elementi e un opuscolo sulla teoria delle parallele di cui ci è pervenuto soltanto l'inizio. Il postulato di Euclide è sostituito dal seguente: "la linea [retta] che è inclinata [rispetto a un'altra linea retta] si avvicina [alla seconda] dalla parte in cui si forma l'angolo acuto". In questo enunciato ‒ chiaramente ripreso dalla versione dello Pseudo-Ṭūsī ‒ l'angolo acuto è quello formato dalla retta inclinata e da una perpendicolare abbassata sulla seconda retta. Si sottintende che l'angolo acuto si trovi dalla stessa parte (quella dell'inclinazione), qualunque sia la perpendicolare. Lēwî ben Gēršôm ne deduce, nel suo lemma 1, che i quattro angoli di un quadrilatero non possono essere tutti acuti o tutti ottusi, altrimenti due lati opposti sarebbero inclinati l'uno verso l'altro nelle due direzioni, cosa che contraddice l'enunciato. Si può allora dimostrare l'esistenza di un parallelogramma e che i suoi angoli opposti sono uguali. A questo punto Lēwî ben Gēršôm può provare l'esistenza di un rettangolo (costruito a partire da un triangolo isoscele) ragionando su una figura che somiglia molto a quella di al-Ḫayyām. Dimostra poi che la somma dei due angoli acuti di un triangolo rettangolo è uguale a un angolo retto e che la somma dei tre angoli di un triangolo qualunque è uguale a due retti. La dimostrazione del postulato V viene ricondotta, attraverso l'assioma di Archimede, al caso in cui la retta trasversale EF sia perpendicolare a una delle due rette AB o CD.
La teoria delle parallele nella tradizione latina
A partire dal XVI sec. vari autori di lingua latina cominciano a interessarsi al postulato delle parallele. Nel 1560 esce a Padova, curata da Francesco Barozzi, la traduzione latina del commento di Proclo agli Elementi di Euclide. Sulla scia di Barozzi, Federico Commandino pubblica una traduzione latina degli Elementi con il commento di Proclo (1572), in cui alla definizione euclidea del parallelismo aggiunge quella basata sull'equidistanza. Cristoforo Clavio, nella seconda edizione del suo Euclide (1589), definisce il parallelismo mediante l'equidistanza e propone una dimostrazione del postulato euclideo vicina a quella di al-Ṭūsī. Pietro Antonio Cataldi compone una Operetta delle linee rette equidistanti e non equidistanti (1603) in cui segue la stessa via, ammettendo che se due rette non si mantengono equidistanti, convergono in una direzione e divergono nell'altra. Andreas Tacquet definisce anch'egli il parallelismo per mezzo dell'equidistanza nei suoi Elementa geometriae planae et solidae del 1654. Giovanni Alfonso Borelli, nel suo Euclides restitutus (1658), cerca di stabilire la possibilità dell'equidistanza di due rette utilizzando un ragionamento analogo a quello di Ibn al-Hayṯam, facendo cioè muovere un segmento che abbia uno dei suoi estremi su una retta perpendicolarmente a tale retta; egli conosceva forse il ragionamento di Ibn al-Hayṯam attraverso ciò che ne scrive al-Ṭūsī.
Una teoria delle parallele molto simile a quella dello Pseudo-Ṭūsī si può trovare nei Nouveaux élémens de géométrie (1667) di Antoine Arnauld. Nel Libro VI egli spiega che la proprietà dell'equidistanza ‒ una proprietà positiva ‒ fornisce una definizione del parallelismo più soddisfacente di quella fondata sulla proprietà negativa usata da Euclide: due rette non si devono mai incontrare. Ammette poi che se due rette sono inclinate una verso l'altra, l'inclinazione rimane sempre dalla stessa parte. La definizione di parallelismo per mezzo dell'equidistanza si ritrova anche negli Élémens de géométrie di Gilles Personne de Roberval, testo la cui redazione definitiva risale al 1675, ma pubblicato soltanto recentemente (1996). Roberval adotta un assioma che assomiglia in modo impressionante a quello di al-Ṭūsī: se si prolungano dalla stessa parte due rette (segmenti di retta) che giacciano sullo stesso piano e l'una si scosta continuamente dall'altra, ossia le distanze della prima dalla seconda diventano continuamente maggiori, tali rette, se sono prolungate dalla parte opposta, prima di incontrarsi si avvicineranno ‒ ossia le distanze della prima dalla seconda diventeranno minori. Grazie a questo assioma Roberval può garantirsi l'esistenza delle rette equidistanti e dei rettangoli, e dimostrare poi il postulato V utilizzando l'assioma di Archimede.
Un curioso tentativo di dimostrare che "il luogo dei punti che hanno distanza data da una retta data è una retta" si può leggere nell'Euclide restituto, overo gli antichi elementi geometrici ristaurati e facilitati (1680) di Giordano Vitale.
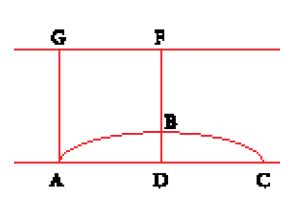
Per provare che la curva convessa ABC (fig. 12) non può trovarsi a distanza costante da una retta, Vitale costruisce la corda AC e traccia dal punto B la perpendicolare BD alla corda. Prendendo AD come base, costruisce un quadrilatero ADFG del tipo di quello di Ibn al-Ḫayyām (con angoli retti in A e in D e i lati AG e DF uguali) e osserva che BF è minore di AG e dunque la curva ABC non si trova tutta alla stessa distanza dalla retta GF. Tuttavia, ne deduce illegittimamente (la retta GF infatti ha proprietà particolari) che non si trova alla stessa distanza da nessun'altra retta.
Si può dunque osservare che, rispetto a ciò che la matematica araba aveva realizzato, non ci furono novità sostanziali riguardanti la teoria delle parallele fino a oltre la metà del XVII secolo. Idee nuove si trovano in autori posteriori, come ora vedremo. John Wallis dedicò due lezioni (nel 1651 e nel 1663) alla teoria delle parallele: esse sono stampate nell'edizione delle sue opere (1693) con il titolo De postulato quinto e Definitione quinta libri sexti Euclidis: disceptatio geometrica. In questo testo Wallis mostra che l'esistenza di triangoli simili, grandi quanto si voglia, basta per dedurre il postulato euclideo delle parallele. E l'esistenza di questi triangoli gli sembrava tanto più facile da ammettere, in quanto il postulato III di Euclide può essere interpretato come un postulato di esistenza di cerchi simili di dimensioni qualsiasi.
Supponendo che le rette AC′ e Bb (fig. 13) formino con la trasversale AB angoli C′AB e ABb la cui somma sia minore di due angoli retti, Wallis costruisce la retta Ab′ che forma con BA (prolungata oltre A) un angolo uguale ad ABb, di modo che questa nuova retta si trovi nell'angolo supplementare di C′AB. Facendo poi muovere Ab′ fino a B′b″ in modo che formi sempre lo stesso angolo con AB, egli osserva che, se B′ non è troppo lontano da A, B′b″ incontra AC′, formando così un triangolo AB′C′. Allora basta costruire un triangolo ABC simile ad AB′C′ per ottenere l'intersezione C di AC′ e di Bb.
Girolamo Saccheri affronta il problema delle parallele nell'Euclides ab omni naevo vindicatus: sive conatus geometricus quo stabiliuntur prima ipsa universae geometriae principia, pubblicato postumo a Milano nel 1733, l'anno stesso della morte dell'autore. Saccheri segue la strada della dimostrazione per assurdo, in modo simile a quanto già aveva fatto al-Ḫayyām. Tuttavia, nella sua opera lo sviluppo delle proprietà deducibili dalle due ipotesi dell'angolo acuto e dell'angolo ottuso è perseguito con un'ampiezza del tutto nuova. La sua figura di base è il quadrilatero di al-Ḫayyām (fig. 10); egli dimostra che se l'angolo in C è acuto (rispettivamente, retto od ottuso) nel caso di una figura, allora sarà acuto (o retto od ottuso) in tutti i casi. Saccheri riuscì a eliminare facilmente l'ipotesi dell'angolo ottuso, perché se ne può dedurre il postulato delle parallele e, di conseguenza, tutta la geometria euclidea; in particolare, se ne può dedurre che l'angolo ottuso deve essere retto, il che è assurdo. In effetti, la geometria dell'angolo ottuso è incompatibile con l'infinità della retta e con la prop. 16 del Libro I degli Elementi. L'ipotesi dell'angolo acuto fu per Saccheri fonte di problemi assai maggiori, tanto che a essa consacrò la maggior parte del suo Euclides ab omni naevo vindicatus. In questa ricerca scoprì molte proprietà di geometria iperbolica, come il fatto che due rette che non si incontrano possiedono un'unica perpendicolare comune, a partire dalla quale divergono da entrambi i lati, a meno che non siano rette asintote da una parte e divergano dall'altra; in quest'ultimo caso, dovrebbe esistere una perpendicolare comune nel punto all'infinito, dove si incontrano. Tuttavia, secondo Saccheri, questa proprietà "ripugna" alla natura della linea retta. Anche se, nel corso del Settecento, Johann Heinrich Lambert riscoprirà il quadrilatero di Ibn al-Hayṯam, è con Saccheri e con il suo Euclides ab omni naevo vindicatus che si sviluppa pienamente la teoria delle parallele così come si era delineata nell'ambito della matematica araba.
Bibliografia
Bonola 1906: Bonola, Roberto, La geometria non euclidea. Esposizione storico-critica del suo sviluppo, Bologna, Zanichelli, 1906.
Cassinet 1986: Cassinet, Jean, Transmission à l'Occident des travaux des mathématiciens de l'Islam au XIIIe siècle sur le cinquième postulat d'Euclide, "Cahiers d'histoire des mathématiques de Toulouse", 9, 1986, pp. 1-17.
Engel 1895: Theorie der Parallellinien von Euclid bis auf Gauss. Eine Urkundensammlung zur Vorgeschichte der nichteuklidischen Geometrie, hrsg. von Friedrich Engel und Paul Stäckel, Leipzig, Teubner, 1895.
Heath 1926: Heath, Thomas L., The thirteen books of Euclid's Elements, 2. ed., Cambridge, Cambridge University Press, 1926, 3 v. (rist.: New York, Dover, 1956).
Lévy 1992: Lévy, Tony, Gersonide, le Pseudo-Ṭūsī et le postulat des parallèles. Les mathématiques en hébreu et leurs sources arabes, "Arabic sciences and philosophy", 2, 1992, pp. 39-82.
Pont 1986: Pont, Jean-Claude, L'aventure des parallèles. Histoire de la géométrie non euclidienne: précurseurs et attardés, Berne, Lang, 1986.
Roberval 1996: Roberval, Gilles-Personne de, Éléments de géométrie de G.P. de Roberval, textes réunis et présentés par Vincent Jullien, préface de Jean Dhombres, Paris, Vrin, 1996.
Rosenfeld 1988: Rosenfeld, Boris A., Non Euclidean geometry, Berlin, Springer, 1988.
‒ 1997: Rosenfeld, Boris A. - Youschkevitch, Adolf P., Géométrie, in: Histoire des sciences arabes, sous la direction de Roshdi Rashed avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v.; v. II: Mathématiques et physique, pp. 121-162 (ed. orig.: Encyclopedia of the history of Arabic science, London-New York, Routledge, 1996, 3 v.).