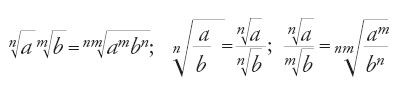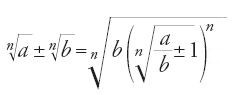La civiltà islamica: antiche e nuove tradizioni in matematica. La tradizione araba del Libro X degli Elementi

La civilta islamica: antiche e nuove tradizioni in matematica. La tradizione araba del Libro X degli Elementi

La tradizione araba del Libro X degli Elementi

La storia delle letture arabe del Libro X degli Elementi è strettamente connessa a quella dell'estensione del concetto di numero alle quantità irrazionali e delle sue conseguenze in algebra. Nel corpus della matematica greca si trovano testi aritmetici e testi geometrici. Gli oggetti dell'aritmetica sono gli interi naturali strettamente maggiori di 1. Infatti '1' non è un numero, è l'unità costitutiva dei numeri. D'altra parte, gli oggetti della geometria non sono tutti rappresentabili numericamente (discuteremo in dettaglio il problema) e dunque le operazioni aritmetiche non possono essere estese a essi in modo diretto. Vedremo come la tradizione araba del Libro X abbia realizzato tale estensione in un contesto algebrico e quali conseguenze ne siano immediatamente derivate.

I pitagorici, avendo l'obiettivo di ricondurre ogni cosa al numero, avevano dovuto necessariamente occuparsi del problema di come trattare aritmeticamente le grandezze continue. Ma due ostacoli si opponevano a questo progetto. Il primo era costituito dal fatto che un segmento può essere diviso all'infinito (Achille e la tartaruga), il che implica che non è possibile determinare un'unità di misura indivisibile comune a tutte le grandezze continue. La seconda difficoltà dipendeva dal fatto che per qualsiasi grandezza è possibile trovarne una dello stesso genere tale che le due non abbiano una misura comune. Per esempio, dato un segmento, la diagonale del quadrato costruito su di esso non ha misura comune con il segmento stesso: i due segmenti sono incommensurabili. Il secondo ostacolo è più serio del primo, dato che stabilisce che esistono due grandezze dello stesso genere prive di misura comune; mentre il primo implica l'incommensurabilità soltanto per un'infinità di segmenti.

Il progetto di un'aritmetica del continuo sembrava dunque impossibile. La geometria, dominio naturale delle grandezze continue, era la sola soluzione per poterle trattare: è questo l'oggetto del Libro X degli Elementi di Euclide. Esso si presenta come una risposta, fondata sulle nozioni di grandezze razionali e irrazionali, al problema posto ai matematici greci dalla scoperta dell'incommensurabilità. Euclide fissa una retta (un segmento) ‒ che chiama 'razionale posta' ‒ e l'utilizza come riferimento per sviluppare lo studio geometrico del continuo.

Nel IX sec. al-Ḫwārizmī fondò il linguaggio algebrico, costituito da termini astratti che permettono di rappresentare tanto i problemi aritmetici quanto quelli geometrici sotto forma di equazioni. In seguito i matematici arabi poterono estendere il dominio dei numeri alle quantità irrazionali reali positive e definite da radicali qualunque e operare su di esse. La difficoltà di questa problematica (operare sul continuo) suscitò numerose ricerche: dalla traduzione dei problemi quadratici del Libro X in equazioni algebriche di secondo grado, alla soluzione di queste equazioni, allo sviluppo del calcolo algebrico e di quello sulle quantità irrazionali multinomiali (a più termini). Questi studi avrebbero condotto a contraddizioni e problemi che, grazie al contatto con altre tradizioni matematiche, avrebbero indirizzato l'algebra su una strada autonoma: quella del calcolo formale sulle espressioni polinomiali e irrazionali.

Nella seconda metà del XIX sec. Franz Woepcke (1856), eminente storico della matematica, dedicò uno studio al commento di Pappo al Libro X degli Elementi di Euclide, conservatoci nella traduzione araba di Abū ῾Uṯmān al-Dimašqī. Nel 1930 William Thomson forniva un'edizione del commento di Pappo, corredata da una traduzione inglese e da uno studio (Junge 1930). Sarà però Roshdi Rashed, all'inizio degli anni Settanta (Ahmad 1972), a riconoscere il ruolo svolto dai commenti arabi al Libro X nello sviluppo dell'algebra, sia per ciò che riguarda l'estensione del dominio dei numeri agli irrazionali definiti tramite radicali, sia per quanto attiene agli sviluppi del calcolo algebrico che si sviluppò parallelamente e per analogia con il calcolo sulle quantità irrazionali. Lo stesso Rashed elaborò poi queste sue conclusioni, mostrando come l'algebra di al-Ḫwārizmī avesse dato luogo a due opposte linee di ricerca. Da un lato Ṯābit ibn Qurra fondò la teoria delle equazioni di secondo grado sulle dimostrazioni geometriche; dall'altro si sviluppò una corrente di ricerca che puntava alla traduzione dei problemi geometrici in termini algebrici. Al-Māhānī, Sulaymān ibn ῾Iṣma, al-Ḫāzin, al-Ahwāzī e altri ancora tradussero nei loro commenti i problemi quadratici del Libro X in equazioni algebriche; al-Māhānī e al-Ḫāzin tradussero in equazioni cubiche i problemi solidi proposti nell'opera Della sfera e del cilindro di Archimede. Rashed (1997) ha mostrato che tali lavori si collocano in quella linea di ricerca che, iniziata con la traduzione in arabo (e in linguaggio algebrico) di Qusṭā ibn Lūqā dell'Aritmetica di Diofanto, sfocerà nel progetto di al-Karaǧī di aritmetizzazione dell'algebra. Negli ultimi anni sono stati condotti studi sui primi commentatori arabi del Libro X, in modo da poter disporre di edizioni e analisi dettagliate (in russo, Matvievskaja 1972, 1977 e 1978; e in francese, Ben Miled 1999b). La nostra conoscenza della tradizione araba del Libro X si fonda dunque su studi abbastanza recenti, relativi ad alcuni dei 23 testi arabi finora noti che trattano particolarmente del Libro X. Questa conoscenza va completandosi attraverso lo studio diretto dei manoscritti che ci sono pervenuti e ciò rende possibile fornire una presentazione sintetica che tenga conto anche degli sviluppi storici in altri campi della matematica.

Il Libro X e il commento di Pappo

I concetti su cui si fonda il Libro X sono la commensurabilità e l'incommensurabilità, applicate alle grandezze lineari e piane. È evidente che esistono grandezze commensurabili (per es., un segmento è commensurabile con un altro che sia il doppio di esso). D'altro canto sappiamo che la diagonale di un quadrato è incommensurabile con il suo lato. Due rette (segmenti) saranno dette 'commensurabili in potenza' se i quadrati costruiti su di esse sono commensurabili. Altrimenti sono 'incommensurabili in potenza'. Si osserva subito che due rette commensurabili lo sono anche in potenza, mentre in generale il contrario non è vero: la diagonale di un quadrato è commensurabile in potenza con il suo lato, senza essergli però commensurabile.

Euclide fissa una retta arbitraria, detta 'razionale posta', e chiama 'razionali' tutte le rette che risultano commensurabili o commensurabili in potenza con la razionale posta. Le altre rette sono dette 'irrazionali'. Il quadrato della razionale posta e tutte le superfici con esso commensurabili sono chiamati 'razionali'. La coerenza fra le due definizioni di razionalità ‒ una per le rette, l'altra per le superfici ‒ deriva dal fatto che i quadrati di rette razionali sono superfici razionali. Bisogna rilevare che la razionalità delle rette e delle superfici sono nozioni che dipendono dalla scelta (arbitraria) della razionale posta.

Se si fissa il lato di un quadrato come razionale posta, la diagonale del quadrato non sarà una retta irrazionale, come ci si potrebbe forse aspettare: essa infatti è commensurabile in potenza con la razionale posta. Esistono, naturalmente, rette irrazionali. Euclide ne costruisce in un primo tempo tredici diverse. La prima è la 'mediale': se si considerano due rette razionali che siano commensurabili in potenza, ma non commensurabili (per es., il lato di un quadrato e la sua diagonale), il rettangolo costruito su queste due rette è una superficie irrazionale; e il lato del quadrato equivalente a tale superficie è una retta irrazionale detta 'mediale'. Ripetendo tale costruzione, partendo questa volta da una retta razionale e da una mediale, Euclide ottiene una nuova retta irrazionale detta anch'essa mediale; e continuando così, a partire dall'ultima mediale costruita, può definire un'infinità di mediali di ordini successivi.

Dopo la mediale, sono definite altre dodici rette irrazionali. Sei di loro sono le somme (geometriche) di due rette incommensurabili che verificano, di volta in volta, proprietà diverse. Le altre sei sono le rette a esse coniugate (vale a dire, sono le rette ottenute per differenza delle due rette incommensurabili, anziché per somma). Per esempio, la retta 'binomiale' è la somma di due rette razionali (dette 'nomi' della binomiale) incommensurabili ma commensurabili in potenza; la sua coniugata è detta 'apotome', ed è la differenza di due rette commensurabili soltanto in potenza. La retta 'maggiore' è la somma di due rette incommensurabili in potenza, che formano una superficie mediale e tali che la somma dei loro quadrati produce una superficie razionale. La retta 'minore' è la coniugata della maggiore. In un secondo tempo, Euclide introduce una distinzione fra sei diverse rette binomiali e le sei apotomi a esse coniugate, in funzione delle proprietà soddisfatte dai nomi della binomiale. Per esempio: se la differenza dei quadrati dei due nomi di una binomiale è una superficie uguale a un quadrato il cui lato risulta incommensurabile col più grande dei due nomi della binomiale e se tale nome risulta razionale, tale retta è detta 'quarta binomiale'. La 'quarta apotome' è la sua coniugata.

Queste definizioni, a priori piuttosto oscure, acquistano senso nel contesto delle propp. 54-65 e 91-102 del Libro X. In esse Euclide stabilisce le relazioni fra le dodici rette irrazionali e le sei binomiali e le sei apotomi. Per esempio, nella prop. 94 viene stabilito che il rettangolo formato da una retta razionale e dalla quarta apotome è equivalente a un quadrato il cui lato è la retta 'minore'. Reciprocamente, la prop. 100 stabilisce che se un rettangolo ha per lato una retta razionale ed è equivalente a un quadrato il cui lato sia la retta 'minore', allora l'altro suo lato è la quarta apotome. È bene sottolineare che le proposizioni in questione sono tutte di tipo geometrico: si fondano su costruzioni con riga e compasso e su dimostrazioni in cui intervengono proporzionalità fra coppie di grandezze e coppie di numeri.

Nella prima metà del IV sec. d.C., Pappo di Alessandria scrisse un commento al Libro X degli Elementi che ci è pervenuto unicamente attraverso la traduzione araba di al-Dimašqī, che risale alla prima metà del X sec. (Woepcke 1856; Junge 1930). Nel suo commento, Pappo parla delle origini pitagoriche dello studio dell'incommensurabilità e del ruolo avuto da Teeteto in queste ricerche, spiegando che la mediale veniva associata alla geometria, la binomiale all'aritmetica e l'apotome all'armonia. Egli sottolinea il fatto che la nozione di razionalità è relativa, ricordando che le grandezze sono razionali per convenzione e non per natura. Nel suo commento si ritrova la distinzione, presente in Platone, fra rette razionali in lunghezza e razionali soltanto in potenza, distinzione che sarà ripresa sistematicamente dagli algebristi arabi che affronteranno questa materia. Oltre a descrivere le mediali, le binomiali e le apotomi di Euclide, Pappo definiva anche trinomi e polinomi ottenuti mescolando somme e differenze in modo da produre una retta irrazionale: a suo avviso tutte le rette irrazionali derivano dalle razionali in tre soli modi: proporzionalità (le mediali), somme e differenze (binomiali, apotomi, trinomi e polinomi). Chiama 'irrazionali ordinate' le grandezze irrazionali definite da Euclide, mentre le altre (cioè le varie grandezze polinomiali) sono dette 'irrazionali non ordinate'. Secondo Pappo, le mediali sono irrazionali che hanno una natura simile a quella delle razionali. Le irrazionali ordinate non se ne distaccano troppo, mentre quelle non ordinate ne differiscono considerevolmente. Pappo ci informa dei lavori che Apollonio (III sec. a.C.) aveva svolto in questo campo, descrivendo le irrazionali non ordinate in contrapposizione alle irrazionali euclidee. È questa mancanza di ordine che spinge Pappo a sostenere l'esistenza di una quantità infinita di grandezze irrazionali.

Il testo di Pappo non rompe con la tradizione euclidea di trattare le grandezze irrazionali in modo geometrico; d'altra parte, l'assenza di una teoria matematica che integri nel suo linguaggio oggetti geometrici e aritmetici continua a impedire di operare aritmeticamente sulle grandezze incommensurabili. Ma, considerando grandezze irrazionali polinomiali (rette composte da un numero arbitrario di rette incommensurabili a coppie), Pappo getta un seme che germoglierà e sboccerà nel solco dell'algebra araba, in cui il trattamento aritmetico di queste quantità si rivelerà finalmente possibile.

I commentari arabi del IX e X sec.: una risposta al problema del trattamento aritmetico del continuo

I successori di al-Ḫwārizmī svilupparono naturalmente lo studio delle equazioni algebriche. Matematici come Sinān ibn al-Fatḥ e Abū Kāmil approfondirono lo studio delle equazioni quadratiche, introducendo potenze dell'incognita fino al sesto grado. Sinān ibn al-Fatḥ, procedendo per analogia con la numerazione decimale (che era chiamata numerazione indiana), arrivò persino a introdurre tutte le potenze intere dell'incognita. Furono sviluppate sia regole di calcolo algebrico sia regole per la manipolazione delle quantità irrazionali, come quelle che compaiono nei coefficienti delle equazioni studiate da Abū Kāmil. Si rendeva dunque necessario arrivare a una concezione teorica delle quantità irrazionali che compaiono nelle soluzioni delle equazioni; d'altra parte, bisognava poter sviluppare i calcoli algebrici anche sulle quantità irrazionali e sui termini dell'algebra, ormai estesi a tutte le potenze dell'incognita. Lo sviluppo di questi due problemi dovette molto alla lettura che gli algebristi arabi fecero del Libro X degli Elementi.

Con l'invenzione della teoria algebrica di al-Ḫwārizmī, all'inizio del IX sec., i matematici erano ormai in possesso di un linguaggio capace di un'astrazione superiore rispetto a quelli dell'aritmetica e della geometria. Le varie combinazioni di termini algebrici permettevano di descrivere sia i problemi geometrici sia quelli aritmetici in un'unica forma, quella delle equazioni. Inversamente, la medesima equazione poteva essere interpretata aritmeticamente o geometricamente. Era diventato così teoricamente possibile trattare le grandezze continue con gli strumenti operativi dell'aritmetica, estesi alle espressioni algebriche. In un primo tempo ciò rese necessaria un'opera di traduzione dei problemi geometrici in equazioni algebriche; questo lavoro coinvolse, fra l'altro, i problemi del Libro X. A questo compito si dedicarono numerosi matematici del IX e X sec., che scrissero commenti spesso intitolati 'Spiegazione', 'Interpretazione', o 'Chiarificazione' del Libro X degli Elementi di Euclide.

Sappiamo che nel IX sec. furono scritti almeno due commenti arabi al Libro X: quello di Sind ibn ῾Alī, che allo stato attuale delle ricerche è da considerarsi perduto, e quello di al-Māhānī, di cui ci è pervenuto solo l'inizio (la prima edizione di questo commento, corredata da un'analisi del testo e da una traduzione francese, è presentata in Ben Miled 1999). Al X sec. risalgono invece i commenti di Ibn ῾Iṣma, di al-Ḫāzin, di al-Ahwāzī, di Yūḥannā ibn Yūsuf e di al-Hāšimī, che si sono tutti conservati. Altri commenti di questo secolo ci sono pervenuti nelle traduzioni latine: quello di al-Nayrīzī, tradotto da Gherardo da Cremona, e un commento attribuibile ad Abū Bakr Muḥammad ibn Zakariyyā al-Rāzī. È noto inoltre che al-Arǧānī e al-Anṭākī scrissero anch'essi dei commenti, che però non sono stati sin qui reperiti. Bisogna infine citare un commento anonimo, risalente a prima della metà del X sec., che potrebbe essere l'ultima parte del commento di al-Māhānī.

Le quantità numeriche irrazionali e l'estensione del dominio numerico

L'algebrizzazione del Libro X doveva passare attraverso la traduzione delle grandezze geometriche razionali e irrazionali di Euclide in quantità che potessero essere trattate algebricamente, ovvero in quantità numeriche. Nei commenti al Libro X si svilupparono così due diverse definizioni numeriche delle grandezze razionali e irrazionali.

Verso la metà del IX sec. al-Māhānī scrisse un Tafsīr al-maqāla al-῾āšira min kitāb Uqlīdis (Commento al Libro X di Euclide), in cui interpretava le rette razionali come grandezze di cui si può 'pronunciare' il valore numerico. Tutti i numeri che oggi chiamiamo razionali positivi sono per lui razionali, dato che possono essere 'pronunciabili' o esprimibili senza radicali. Per contro, al-Māhānī definiva le rette surdae o irrazionali come rette di cui non si può 'esprimere la grandezza, né pronunciare la quantità'. Sono dunque surdae le radici quadrate (o cubiche, o di ordine superiore) di quei numeri che non siano quadrati (o cubi, o potenze d'ordine superiore). Per esempio, 2 è razionale perché è esprimibile con la parola 'due', mentre la quantità radice di 2 è surda, perché non è direttamente esprimibile: si può esprimere solo il suo quadrato. Le quantità surdae di questo tipo vengono chiamate 'semplici' o 'monomie'. Sono surdae anche le somme o le differenze, scritte in forma irriducibile, in cui interviene almeno un termine surdus. In tal caso, ossia quando la forma irriducibile risulta composta, al-Māhānī parla di 'quantità surdae composte'. Occorre osservare che le sue definizioni riguardano soltanto i numeri reali positivi definiti per radicali, nonostante la sua definizione di quantità surdae possa essere generalizzata allo stesso modo a tutti i numeri irrazionali, tranne rarissime eccezioni, come il numero e oppure il numero π, che hanno ricevuto nomi particolari.

Accanto a questa definizione, di ispirazione aristotelica, che si basava sulla possibilità di esprimere una certa quantità, se ne aggiunse un'altra. Nel suo commento al Libro X, Ibn ῾Iṣma attribuiva alla razionale posta il valore 1, l'unità dei numeri. Ogni quantità che misura una grandezza commensurabile con la razionale posta è dunque commensurabile con 1, e viene detta razionale; le altre quantità sono dette irrazionali o surdae. Gli esempi forniti mostrano che le quantità prese in considerazione sono quantità numeriche. Infine, ragionando sulla commensurabilità, Ibn ῾Iṣma arriva alla stessa interpretazione numerica delle grandezze razionali e surdae che al-Māhānī aveva fornito all'inizio del suo commento. Anche al-Ḫāzin lo seguirà su questa strada; in un'epistola sul Libro X, intitolata Tafsīr ṣadr al-maqāla al-῾āšira min kitāb Uqlīdis (Commento al principio del Libro X di Euclide), spiega che la razionale posta è un'unità delle lunghezze, poiché essa è uno, perché è tramite la sua unità che le grandezze vengono contate una volta o molte volte.

L'idea di associare l'unità dei numeri a una grandezza geometrica arbitraria non era nuova. Era stata alla base, fra l'altro, dei lavori dei geometri infinitesimali e la si trova già nel IX sec. in un testo dei Banū Mūsā. Però Ibn ῾Iṣma e al-Ḫāzin utilizzeranno questa unità associata alle grandezze geometriche per definire le quantità irrazionali e per trattarle come numeri. In seguito, ῾Umar al-Ḫayyām (riprendendo la tradizione di algebristi come al-Māhānī, al-Ḫāzin, Abū Naṣr ibn ῾Irāq e Abū 'l-Ǧūd che avevano tentato lo studio dell'equazione cubica) introdurrà l'unità di misura per rappresentare una conica per mezzo di un'equazione algebrica in un sistema di due coordinate, arrivando così a risolvere tutte le equazioni di grado minore o uguale a tre per mezzo di intersezioni di coniche.

Il passo successivo all'introduzione delle quantità numeriche razionali e surdae era di collegarle alle grandezze irrazionali introdotte da Euclide. I commentatori del Libro X associarono queste grandezze alle loro 'misure' numeriche, in modo da generare una parte dell'insieme delle quantità surdae. Le binomiali di Euclide si trasformarono in quantità numeriche binomie, ovvero in quelle quantità numeriche che 'misurano' le rette binomiali, ove si sia associata l'unità alla razionale posta: la quantità 'uno più radice di due' ne è un esempio. Per quanto riguarda le rette razionali di Euclide, nelle interpretazioni numeriche che ci sono pervenute le rette commensurabili con la razionale posta diventano le quantità numeriche razionali o, come si trova a volte specificato, 'razionali in lunghezza' (in termini moderni, gli elementi di ℚ*₊); mentre le grandezze razionali che sono commensurabili soltanto in potenza con la razionale posta diventano le quantità numeriche razionali solamente in potenza: non essendo razionali in lunghezza, sono da collocare fra le quantità surdae, cui naturalmente appartengono tutte le grandezze irrazionali. A partire da questo punto si può riscontrare che, nelle opere matematiche in cui entrano in gioco quantità irrazionali, il dominio dei numeri si è ormai ampliato. Ne fanno parte i 'semplici' (ovvero, le quantità razionali o le radici n-esime di a, dove a appartiene a ℕ* o a ℚ*₊* e n appartiene a ℕ*) e i 'composti' (costruiti con i semplici per mezzo di somme e differenze e in cui compaiono almeno o un semplice razionale e un semplice surdus, o due semplici surdi e incommensurabili fra loro). Il complesso di questi oggetti forma ciò che oggi chiamiamo insieme dei numeri reali positivi definibili per radicali. Se in Euclide il concetto di razionalità era relativo, e dipendeva dalla razionale posta, la sua traduzione in termini algebrici lo rende assoluto: la razionalità o la irrazionalità di una quantità numerica diventa una proprietà intrinseca della quantità considerata.

Costituzione delle equazioni e calcoli algebrici

Queste grandezze irrazionali generalizzate e interpretate numericamente diventano termini dell'algebra, sottoposte ai calcoli algebrici e accettate come soluzioni di equazioni. Dato che i problemi studiati nel Libro X erano di tipo quadratico, i matematici arabi poterono tradurre certe proposizioni in equazioni di secondo grado e lavorare sulle loro soluzioni. In questo modo il calcolo sulle quantità surdae e il calcolo algebrico si svilupparono parallelamente, alimentandosi a vicenda, fino ai lavori di al-Karaǧī e poi di al-Samaw᾽al, che nell'XI e XII sec. formalizzeranno questi due calcoli nell'ambito di una stessa trattazione, utilizzando algoritmi simili.

Tav. I

Vari autori (fra cui Ibn ῾Iṣma, al-Ḫāzin, al-Ahwāzī e l'anonimo che potrebbe forse identificarsi con al-Māhānī) si impegnarono in letture algebriche delle propp. 54-65 e 91-102 del Libro X, riconducendo le loro dimostrazioni alla soluzione di equazioni di secondo grado (propp. 54-59 e 91-96) o al calcolo algebrico di un prodotto di fattori (propp. 60-65 e 97-102). Ci limiteremo qui a fornire due esempi: le propp. 91 e 97 che furono trattate dalla maggior parte dei commentatori. La prop. 91 afferma che il lato del quadrato uguale al rettangolo costruito su una retta razionale e l'apotome prima è la retta apotome. La traduzione algebrica di questa proposizione si presenta sotto forma di calcolo: si tratta di calcolare numericamente la radice dell'apotome prima e di mostrare che questa radice corrisponde alla quantità apotome. Tale calcolo si riconduce alla soluzione di un'equazione di secondo grado, la cui soluzione è assicurata dall'algoritmo descritto nel Kitāb al-ǧabr wa-'l-muqābala (Libro dell'algebra) di al-Ḫwārizmī (Tav. I).

Reciprocamente, la prop. 97 stabilisce che se un lato di un rettangolo è una retta razionale e il rettangolo è uguale a un quadrato il cui lato è la retta apotome, allora l'altro lato del rettangolo è la prima apotome. La traduzione algebrica di questa proposizione si riduce di nuovo a un calcolo. Attribuendo il valore 'uno' alla retta razionale, occorre verificare algebricamente che il quadrato della quantità numerica 'prima apotome' è uguale alla quantità numerica 'apotome'. La prop. 97 è dunque la reciproca della 91 ed è presentata dai commentatori arabi come una verifica di quest'ultima. La dimostrazione utilizza varie tecniche del calcolo algebrico e consiste essenzialmente nello sviluppo del quadrato di una differenza, composta da due termini separati dalla parola 'meno'. Tale parola era comparsa, fino a questo momento, con il ruolo di operatore fra due numeri, di cui il primo era maggiore del secondo. Ma con lo svilupparsi della necessità di trattare prodotti di espressioni composte, divenne necessario trattare il 'meno' non più come un operatore, ma come un attributo del numero che esso precedeva. Per esempio, per sviluppare (a−b)(c−d), dove a e b sono due quantità numeriche incommensurabili, al pari di c e d (il che vieta la possibilità di semplificare le espressioni contenute nelle parentesi), gli algebristi dell'epoca effettuano il prodotto di a (contato positivamente) per c (anch'esso positivo), poi di a (positivo) per d (considerato negativamente), poi di b (negativo) per c (positivo) e, infine, di b e d (entrambi contati negativamente); dopodiché, considerano la somma dei quattro termini così ottenuti. Le regole di calcolo sono le seguenti: il prodotto di due quantità contate positivamente o negativamente produce una quantità da contarsi positivamente; mentre il prodotto di una quantità contata positivamente per una contata negativamente produce una quantità da contarsi negativamente. La somma di una quantità contata positivamente e di una contata negativamente (che sia minore della prima in valore assoluto) è la differenza delle due quantità. Evidentemente, non viene stabilito alcun ordinamento fra quantità negative, positive e nulle.

Le incoerenze della traduzione algebrica dei risultati geometrici

La traduzione algebrica di un testo puramente geometrico diede luogo per lo meno a due incoerenze. La prima si situava a livello di nomenclatura, in quanto i nomi attribuiti nel Libro X alle varie grandezze riflettono procedure di costruzione geometrica. Accadeva così che le quantità numeriche corrispondenti a queste grandezze ‒ frutto di definizioni algebriche ‒ ereditassero nomi che ne fornivano una descrizione poco appropriata, se non addirittura fuorviante. La seconda incoerenza riguardava il senso stesso delle proposizioni. Mentre nel Libro X il fine delle varie proposizioni era evidente da un punto di vista geometrico, non succedeva altrettanto per le forme algebriche che assumevano, delle quali sfuggiva la motivazione. Alcune proposizioni, tradotte in linguaggio algebrico, perdevano il proprio significato.

Consideriamo dapprima il problema della nomenclatura. Nel Libro X, la 'retta di due mediali' è la somma di due mediali commensurabili soltanto in potenza. Euclide distingue fra la 'prima di due mediali' (caso in cui il rettangolo costruito sulle due mediali è razionale) e la 'seconda di due mediali' (in cui tale rettangolo è una superficie mediale). Nei commenti arabi le rette di due mediali compaiono in forme algebriche del tipo a+b, dove a e b sono radici 2ⁿ-esime di numeri razionali positivi non quadrati, tali che a/b non sia razionale (per es., ⁴√8+⁴√2 o ⁴√12+⁴√3). La prima di due mediali, in questi commenti, è tale che il prodotto dei due termini è una quantità razionale (⁴√8+⁴√2 è una prima di due mediali, dato che il prodotto delle due componenti è uguale a 2). La seconda di due mediali è tale che il prodotto delle componenti risulta una quantità razionale in potenza e non mediale come voleva la definizione geometrica (per i commentatori arabi ⁴√12+⁴√3, per es., è una seconda di due mediali, dato che il prodotto delle componenti è √6, che è razionale in potenza).

La definizione algebrica della seconda di due mediali differisce quindi dalla definizione geometrica di Euclide. Secondo la definizione geometrica essa è 'la somma di due rette mediali che racchiudono un'area mediale' e non 'la somma di due quantità mediali il cui prodotto è una quantità razionale in potenza'. Si osservi che, trattandosi di superfici, tale definizione non avrebbe senso nel contesto geometrico del Libro X. La differenza fra le due definizioni deriva dal fatto che, associando un valore numerico alle grandezze continue, la distinzione fra rette e superfici viene a perdersi. Il valore numerico associato a una retta razionale, commensurabile solamente in potenza con la razionale posta, è dello stesso ordine di quello associato a una superficie mediale. Per esempio, il valore numerico associato alla diagonale del quadrato che ha come lato la razionale posta è √2; ma √2 è anche il valore associato all'area del rettangolo che ha per lati la razionale posta e la diagonale del quadrato suddetto. Per gli algebristi arabi, tale valore è razionale in potenza.

Si ritrovano le stesse differenze tra definizioni algebriche e geometriche nei casi della retta maggiore, di quella che 'può una razionale e una mediale', di quella che 'può due mediali' e nelle rispettive grandezze coniugate. La retta che 'può una razionale e una mediale', per esempio, ha questo nome perché è definita geometricamente come somma di due rette incommensurabili in potenza e tali che il rettangolo costruito su di esse è una superficie razionale, mentre la somma dei loro quadrati deve essere una superficie mediale. Il nome di questa retta è dunque ben giustificato. Numericamente, essa è definita come somma di due rette incommensurabili, il cui prodotto è una quantità razionale e la somma dei loro quadrati è razionale in potenza. Da questo punto di vista il nome 'retta che può una razionale e una mediale' non è più così scontato. Al-Ahwāzī era consapevole di questa situazione. Nel suo commento al Libro X tradusse numericamente le grandezze geometriche irrazionali di Euclide. Di fronte al problema qui delineato giustificava la nomenclatura fornendo due distinte classificazioni numeriche per le quantità irrazionali: una per le quantità numeriche che rappresentano linee e una per quelle che rappresentano superfici, e per questa strada arrivò ad applicare ai numeri argomentazioni di tipo geometrico.

La traduzione algebrica del Libro X degli Elementi non generò problemi di coerenza soltanto a livello di nomenclatura. Un secondo tipo di incoerenza si manifestò con la traduzione di alcune proposizioni. Infatti, ciò che è giustificabile geometricamente, non sempre lo è anche da un punto di vista algebrico. Le propp. 54-59 e 91-96 si riducono a costruzioni di rette a partire da rettangoli. Nella forma algebrizzata che assumono nei commenti arabi, si trasformano nel problema di estrarre la radice di una quantità composta, il cui obiettivo è la trasformazione di un'espressione algebrica (la radice quadrata di una quantità composta da due termini) in una più semplice (una quantità composta da due termini).

In forma algebrica, la prop. 91 equivale all'estrazione della radice quadrata della prima apotome: prendiamo come esempio la radice quadrata di 'nove meno radice di quarantacinque'. Una volta effettuato il calcolo, tale radice risulta uguale alla differenza 'radice di sette e mezzo meno radice di uno e mezzo'. La radice quadrata di un'espressione composta da due termini è stata dunque ridotta a un'espressione di due termini, quindi a una forma più semplice. Questa semplificazione dell'espressione è resa possibile dalla condizione, verificata dalle tre prime apotomi, sulla differenza fra i quadrati del 'Tutto' e del 'Congruo' che deve corrispondere a un quadrato il cui lato sia commensurabile in lunghezza con il Tutto (Tav. I). Tuttavia la quarta, la quinta e la sesta apotome non verificano questa condizione, e il calcolo delle loro radici quadrate non porta alla semplificazione descritta. Se si effettua tale calcolo (il che corrisponde alla traduzione algebrica delle propp. 94-96) si ottengono infatti nuovamente radici quadrate di apotomi, ovvero espressioni con la stessa struttura sintattica di partenza.

Si vede qui come il criterio di semplicità sintattica sia intrinseco all'algebra, ma non alla geometria. Può accadere, infatti, che uno dei termini della quantità ottenuta come risultato sia dello stesso tipo della quantità di partenza (la radice quadrata di una quantità composta di due termini). La semplificazione cercata algebricamente non può allora avere luogo, anche reiterando l'operazione. Il commento anonimo prima citato, quasi certamente opera di al-Māhānī, deplora questa situazione. Cercando la radice quadrata di un'apotome quarta, ottiene una differenza fra due espressioni, di cui l'una è la radice quadrata di una quarta binomiale, vale a dire la radice quadrata di una quantità composta, e l'altra la radice quadrata di un'apotome quarta, anch'essa radice quadrata di una quantità composta. Scrive: "la ricerca della radice della quarta apotome necessita di conoscere la radice prima di arrivare al risultato, come avviene in questa fase del problema che si ripete perpetuamente" (Ben Miled 1999b, pp. 112-113). Tuttavia, egli finisce con l'accettare la forma del risultato, perché è quella dell'irrazionalità minore ottenuta nella prop. 94 che sta traducendo algebricamente.

Di conseguenza, se le proposizioni di Euclide rispondono a esigenze geometriche ‒ in questo caso la trasformazione di una superficie in una retta di cui siano noti i nomi ‒, la loro traduzione nel linguaggio dell'algebra che troviamo nei commentatori arabi non sempre ha un movente algebrico equivalente. Alcune proposizioni, una volta che siano state algebrizzate, risultano prive di motivazione propria. Così, anche se permisero agli algebristi di concepire e generalizzare le grandezze irrazionali e di estendere a loro le regole dell'aritmetica, i commenti al Libro X presentano aspetti contraddittori, sintomatici del fatto che la classificazione delle rette irrazionali operata da Euclide in un contesto geometrico era ormai divenuta obsoleta. Assistiamo in questo modo alla fine di un genere della letteratura matematica araba, quello dei commenti che tentano di seguire, ancorché parzialmente, l'esposizione euclidea.

Il Libro X nelle matematiche arabe dell'XI e XII secolo

Nel corso dei secoli seguenti il Libro X degli Elementi continuò a essere presente nei testi algebrici. Le grandezze irrazionali erano state generalizzate nella cornice dell'algebra. In seguito alcuni algebristi si impegnarono in una riflessione sulla natura delle quantità irrazionali e del loro status nei confronti dei numeri; altri, invece, si dedicarono a sviluppare sistematicamente le regole dei calcoli che le governavano, parallelamente allo sviluppo del calcolo algebrico.

La riflessione sulle quantità irrazionali

Abū ῾Abd Allāh al-Ḥasan ibn Muḥammad ibn Ḥamla, noto come Ibn al-Baġdādī e attivo tra la fine del X sec. e l'inizio dell'XI, scrisse una Risāla fī 'l-maqādīr al-muštaraka wa-'l-mutabāyina (Epistola sulle grandezze commensurabili e incommensurabili). In questo testo, dopo aver discusso in cosa consista la differenza fra i numeri e le grandezze (i primi permettono di numerare le seconde), definisce il numero come una proprietà generale, inerente a ogni insieme di grandezze omogenee o eterogenee. I numeri sono in corrispondenza con ogni insieme di oggetti.

Rappresentando i numeri con segmenti di retta, Ibn al-Baġdādī stabilisce una corrispondenza fra numeri e grandezze razionali. Queste sono costituite dall'unità delle grandezze, dai suoi multipli e dalle sue frazioni, e il rapporto di due di esse è uguale a quello che un numero ha con un numero. Le grandezze irrazionali sono quelle che non sono uguali a parti delle grandezze razionali; egli fa osservare che le grandezze irrazionali del Libro X soddisfano queste proprietà. Per distinguere le grandezze dai numeri il suo testo si sofferma sul concetto di radice quadrata, notando che la radice quadrata di un numero è media proporzionale fra il numero dato e l'unità (a:√a=√a:1), mentre la radice quadrata di una grandezza è media proporzionale fra la grandezza e l'unità delle grandezze. Secondo tali definizioni la radice quadrata di un numero può esistere o non esistere (caso che si verifica quando il numero non è un quadrato), mentre la radice quadrata di una grandezza esiste sempre. Ibn al-Baġdādī osserva inoltre che questi due concetti di radice vengono spesso confusi, e che tale confusione porta a ridurre la radice quadrata di una grandezza al numero che essa rappresenta.

Egli discute poi la rappresentazione grafica delle operazioni algebriche sulle grandezze, mostrando come il prodotto di due grandezze omogenee sia una grandezza omogenea a esse, distaccandosi così dal principio di omogeneità a cui la matematica greca era sempre rimasta fedele. Adotta anche una notazione originale: stabilisce una corrispondenza fra le radici 2ⁿ-esime dei numeri e le radici 2ⁿ-esime delle grandezze (si osservi che queste producono le rette razionali in potenza e tutte le mediali), indicando con un cerchio le grandezze irrazionali del prim'ordine (radici quadrate), con due cerchi quelle del second'ordine (radici quarte) e così via. Seguendo questo percorso ottiene un risultato molto importante: la dimostrazione dell'esistenza di un'infinità di grandezze irrazionali fra due grandezze intere. Il suo ragionamento si svolge nel modo seguente. Se m è un numero intero che rappresenta una grandezza, egli considera le radici 2ⁿ-esime degli interi compresi fra m²ⁿ e (m+1)²ⁿ. Dato che n può essere grande a piacere, ne segue che ci sono infiniti irrazionali compresi fra m e m+1. Corollario di questa proposizione è che esiste un'infinità di grandezze irrazionali comprese fra due grandezze razionali. La domanda che ci si pone è: Ibn al-Baġdādī, o uno dei suoi successori, se ne era reso conto?

I matematici arabi dovettero confrontarsi con le problematiche sollevate dalle quantità irrazionali anche in campi appartenenti a tradizioni diverse da quelle derivate dal Libro X degli Elementi di Euclide. La concezione euclidea tradizionale del numero, che era basata sulla nozione di unità indivisibile, in alcun modo poteva applicarsi alle quantità surdae e questo portò a interrogarsi sulla loro natura. Discuteremo brevemente gli approcci di due fra i matematici più illustri di questo periodo.

In un commento al Libro V degli Elementi, al-Ḫayyām affrontò il problema dei rapporti fra grandezze incommensurabili. La definizione del rapporto per mezzo dell'antifairesi, che egli adottò seguendo al-Māhānī e altri, gli permise di associare un rapporto a una successione di numeri razionali (che corrisponde al nostro sviluppo in frazione continua) e di considerare i rapporti come grandezze. Basandosi su un'unità indivisibile per misurare le quantità razionali e irrazionali (al modo di Ibn ῾Iṣma e al-Ḫāzin nei loro commenti al Libro X), collegava le quantità surdae e i rapporti di grandezze, anche incommensurabili, ai numeri. E discuteva del problema di valutare se un rapporto

comprende il numero nella sua essenza; o se invece è inseparabile dal numero; o se è congiunto al numero estrinsecamente alla sua essenza a causa di un'altra cosa; o se è congiunto al numero a causa di una cosa inseparabile dalla sua essenza senza che si abbia bisogno di un'asserzione estrinseca: è questo uno studio filosofico cui il geometra non si deve assolutamente dedicare. Ma occorre sapere che quando si parla qui della composizione del rapporto, se ne parla in quanto esso è congiunto alle nozioni di numero e di unità o in potenza o in atto. [Parlando dei rapporti incommensurabili e della loro conoscenza effettiva, aggiunge][…] non vogliamo con questo dire che sia in nostro potere modellare questa nozione in tutte le grandezze, cioè che facciamo ciò che qui diciamo grazie a una regola dell'arte. Vogliamo al contrario sostenere che non è impossibile che essa esista nell'intelletto. E la nostra incapacità di farlo non indica che la cosa sia impossibile in sé. Comprendi, dunque, queste nozioni. (Rashed 1999, pp. 374, 378-380)

Nella tradizione archimedea e, in particolare, nel calcolo delle aree e dei volumi i geometri infinitesimali dovettero manipolare rapporti di grandezze incommensurabili e considerare successioni convergenti a quantità irrazionali. Dovettero confrontarsi anche con la determinazione effettiva dei valori delle quantità irrazionali. Ibn al-Hayṯam affrontò il problema in un testo in cui dimostra la possibilità della quadratura del cerchio. Assumendo come dati il rapporto di una lunula a un cerchio e la quadratura della lunula, egli deduce la possibilità della quadratura del cerchio. È evidente che non si tratta di una dimostrazione della quadratura del cerchio con riga e compasso: sappiamo oggi che il rapporto lunula/cerchio è trascendente e, per questo motivo, la dimostrazione di Ibn al-Hayṯam non consiste in una procedura effettiva. Egli scrive: "le verità delle nozioni intelligibili non hanno bisogno di essere trovate o determinate in atto dall'uomo, ma se la dimostrazione stabilisce la possibilità di tale nozione, allora essa diventa vera, che l'uomo la determini in atto o no" (Rashed 1993, pp. 96-97). Così, una volta che le grandezze irrazionali si guadagnarono un posto fra le quantità numeriche, si pose il problema del calcolo effettivo dei loro valori. Se tali valori non potevano essere conosciuti, occorreva, per calcolare con le quantità irrazionali, sviluppare tecniche di calcolo formale simili a quelle del calcolo polinomiale che si stava elaborando.

Il calcolo algebrico

Al-Ḫwārizmī, seguito da Abū Kāmil e da Sinān ibn al-Fatḥ, aveva avviato nel suo Kitāb al-Ǧabr wa-'l-muqābala lo studio del calcolo algebrico. Anche Qusṭā ibn Lūqā e Abū al-Wafā᾽ al-Būzǧānī (le cui opere si inscrivono nella tradizione dell'Aritmetica di Diofanto) si erano incamminati in questa direzione. Nello stesso periodo al-Māhānī, Ibn ῾Iṣma, al-Ḫāzin, al-Ahwāzī e altri avevano sviluppato, traducendo il Libro X in linguaggio algebrico, alcune tecniche di calcolo che potevano essere applicate alle grandezze irrazionali composte. Fu sulla scia di queste tradizioni che, nell'XI sec., al-Karaǧī, nel suo al-Badī῾ fī 'l-ḥisāb (L'innovatore nel calcolo) e nel suo al-Faḫrī fī 'l-ǧabr wa-'l-muqābala (L'algebra dedicata a Faḫr al-Mulk), concepì il progetto di applicare sistematicamente le leggi dell'aritmetica alle espressioni algebriche; nel secolo successivo, al-Samaw᾽al, con al-Bāhir fī ῾ilm al-ḥisāb (Lo splendore della scienza del calcolo), riprese i suoi lavori e li portò a compimento. In questi autori si legge un chiaro riferimento al Libro X, dato che ne forniscono una lettura ormai direttamente legata alle tecniche del calcolo algebrico. Essi presentano una definizione generale e graduata su più livelli delle quantità irrazionali semplici, o monomi.

Al-Karaǧī inizia con il definire i numeri interi come quantità razionali in assoluto: sono i monomi di primo livello. Definisce poi le quantità razionali in potenza (le radici quadrate degli interi non quadrati), ottenendo così i monomi di secondo livello. I monomi di terzo livello sono le radici cubiche degli interi che non sono cubi perfetti, mentre quelli del quarto livello sono le quantità mediali (le radici quarte), definite con riferimento al lato del quadrato del loro quadrato. Al quinto livello troviamo i lati del quadrato del cubo, al sesto i lati del cubo del cubo e così via. Al-Karaǧī ottiene le quantità irrazionali polinomiali componendo per somma e differenza le quantità monomie: si tratta cioè di espressioni composte da termini semplici rappresentanti quantità razionali e quantità irrazionali incommensurabili a due a due. In questo modo costruisce esplicitamente gli irrazionali positivi costruibili per radicali qualunque. È una costruzione al modo di al-Māhānī, con la differenza però che a quest'ultimo era mancata una definizione chiara delle radici n-esime di ordine qualunque. Tuttavia, la differenza più importante è che l'obiettivo di al-Karaǧī non era più quello di tradurre in equazioni algebriche le proposizioni del Libro X. Il testo degli Elementi viene lasciato da parte per affrontare la descrizione degli algoritmi di calcolo sulle quantità irrazionali: le regole di calcolo del prodotto, della somma e della differenza di quantità irrazionali composte. Egli si applicò anche allo studio della divisione e dell'estrazione della radice quadrata.

Seguendo le sue orme, al-Samaw᾽al generalizzò i termini dell'algebra a tutte le potenze (positive, negative e nulla) dell'incognita, grazie a una rappresentazione per mezzo di una tavola al cui centro era posta la potenza zero, da un lato le potenze positive e dall'altro quelle negative. In modo analogo, le quantità irrazionali semplici erano definite in una tavola per livelli successivi: le radici n-esime dei numeri risultavano simmetriche alle potenze n-esime dei numeri. I numeri razionali e irrazionali positivi costruiti per radicali qualunque erano anch'essi definiti in modo analogo ai polinomi a coefficienti interi in x e 1/x. Guidato da queste analogie, al-Samaw᾽al chiamò le potenze dell'incognita 'semplici' o 'monomi incogniti', denominando le quantità irrazionali come 'semplici' o 'monomi noti'. I polinomi in senso ampio sono le 'quantità composte incognite', mentre le quantità irrazionali composte sono dette 'quantità composte note'. Vengono poi forniti gli algoritmi per le quattro operazioni di base sulle quantità composte incognite e per l'estrazione della radice quadrata (dove il polinomio sia un quadrato). Parimenti, sfruttando l'analogia introdotta, vengono presentati gli algoritmi per le quattro operazioni sulle quantità composte note e per l'estrazione della loro radice quadrata.

Esattamente come il commentatore anonimo che, per potere operare calcoli sulle apotomi, era stato condotto a manipolare quantità negative, al-Samaw᾽al stabilì le regole di calcolo sulle quantità negative per potere ottenere una descrizione completa dei suoi algoritmi:

a) se x⟨0 e y>0, allora xy⟨0; se x⟨0 e y⟨0, allora xy>0; se x>0 e y>0, allora xy>0;

b) se x⟨0 e y>0, allora x−y⟨0; se x⟨0, y⟨0 e ∣x∣⟨∣y∣, allora x−y>0;

c) se x>0, allora 0−x⟨0 ; se x⟨0, allora 0−x>0.

Fra le regole di calcolo sugli irrazionali stabilite da al-Karaǧī e da al-Samaw᾽al possiamo menzionare la seguente: per ogni n, m interi positivi

Il testo di al-Samaw᾽al ci informa inoltre che la formula nota oggi come 'binomio di Newton' era stata dimostrata da al-Karaǧī per le potenze intere positive; ci fornisce quindi la sua dimostrazione per induzione, accompagnata da una tavola triangolare che dà i coefficienti dello sviluppo del polinomio. Sulla base di questa formula egli ne poteva stabilire altre, come, per esempio, la seguente: per ogni n intero positivo

Euclide aveva inserito nel Libro X alcune proposizioni che forniscono le costruzioni geometriche delle rette irrazionali, via via che esse sono definite. Al-Samaw᾽al riprende queste proposizioni e dimostra come per ciascuno dei numeri irrazionali che corrispondono alle rette irrazionali euclidee si può assegnare una formula algebrica che permette di produrne un'infinità.

Il ruolo del Libro X degli Elementi fu quindi centrale per coloro che affrontarono i primi sviluppi dell'algebra. In un primo momento, nel IX e nel X sec., tale studio consistette nell'applicazione dell'algebra di al-Ḫwārizmī alla geometria di Euclide; successivamente, al-Karaǧī e al-Samaw᾽al generalizzarono le leggi dell'aritmetica alle espressioni algebriche. Ma, accanto a queste ricerche, non bisogna dimenticare che ci fu anche chi affrontò lo studio del Libro X indipendentemente dall'algebra: nel seguito discuteremo le ricerche che Ibn al-Hayṯam condusse in questo senso nell'XI secolo.

Ibn al-Hayṯam e il Libro X

Ci sono pervenuti tre testi di Ibn al-Hayṯam sul Libro X: un opuscolo che discute la prop. 1 e i capitoli che trattano del Libro X nello Šarḥ muṣādarāt kitāb Uqlīdis fī 'l-Uṣūl (Commento ai postulati degli Elementi di Euclide) e nel Kitāb fī ḥall šukūk kitāb Uqlīdis fī 'l-Uṣūl (Libro sulla soluzione dei dubbi intorno agli Elementi di Euclide), scritto in cui viene anche ripreso il testo dell'opuscolo.

Il capitolo sul Libro X dello Šarḥ muṣādarāt kitāb Uqlīdis fī 'l-Uṣūl è di natura puramente geometrica, inscritto com'è nella tradizione del commento di Pappo di Alessandria, che i matematici arabi conobbero nella traduzione di al-Dimašqī. Ibn al-Hayṯam comincia con l'esporre ciò che a suo avviso rappresenta lo scopo e il filo conduttore del testo euclideo. Euclide ‒ afferma ‒ vuole qui distinguere i vari tipi di rapporti, mentre nel Libro V aveva definito il rapporto ed espresso le sue proprietà generali. Lo stile di Ibn al-Hayṯam è dimostrativo.

Se si comincia con il porre una retta, essa possiede un'infinità di rette a essa commensurabili, alcune soltanto in lunghezza, altre in potenza e in lunghezza. Ciò egli [Euclide] l'ha dimostrato in questo libro, in cui non dimostra nient'altro che questo; tale è infatti il suo scopo. È quello di discutere in dettaglio le specie di rapporti, perché ogni retta, che non sia commensurabile con la prima retta posta all'inizio, ha un rapporto con questa prima retta che è di una specie diversa dalla specie del rapporto di un'altra retta non commensurabile con la prima. È dunque chiaro che il suo scopo è quello di discutere in dettaglio le specie dei rapporti. (Šarḥ muṣādarāt kitāb Uqlīdis fī 'l-Uṣūl, Tunisi, Biblioteca Nazionale, 16167, c. 51v)

Il ragionamento si sviluppa poi secondo queste linee. Dato che il rapporto 'della maggior parte delle grandezze' può essere ricondotto a quello di due rette; dato che il rapporto di due rette 'è più chiaro' per il fatto che si può sempre applicare una retta a un'altra per evidenziarne la differenza, cosa che non sempre avviene con gli altri tipi di grandezze; dato che si possono considerare i quadrati e i cubi delle rette, il che non è possibile con le superfici e i volumi; e dato che se si ottengono i rapporti fra le rette si ottengono anche i rapporti fra i loro quadrati e i loro cubi, per tutti questi motivi, 'è più comodo' analizzare i rapporti delle rette piuttosto che quelli fra altre grandezze.

Ibn al-Hayṯam esplicita a questo punto le varie specie di rapporti mediante ragionamenti di proporzionalità fra alcune grandezze geometriche e i numeri, utilizzando il concetto di commensurabilità e dopo aver fissato una retta di riferimento. Ricapitola le sue conclusioni in questi termini. Data una retta, tutte le rette sono: o commensurabili con essa, in numero infinito; o incommensurabili con essa, in numero infinito. Fissata una di queste rette incommensurabili con la retta data, alcune rette sono commensurabili con essa, mentre le altre sono incommensurabili, e non hanno tutte lo stesso tipo di rapporto con la retta posta all'inizio. Successivamente, Ibn al-Hayṯam arriva a spiegare che razionale vuol dire 'pronunciabile' rispetto alla retta di riferimento. Poiché essa è fissata arbitrariamente, ne conclude che la razionalità è un concetto relativo, che non appartiene all''essenza' delle grandezze.

Anche nel capitolo sul Libro X del Fī ḥall šukūk egli attira l'attenzione sulla relatività del concetto di razionalità. In questo modo stabilisce la necessità di definire la commensurabilità e l'incommensurabilità, i concetti su cui è fondato l'intero Libro X. Ibn al-Hayṯam enuncia le proposizioni di Euclide che a suo avviso sono problematiche: o perché le loro dimostrazioni assumono come note ipotesi non altrimenti dimostrate (nel qual caso provvede a completare la dimostrazione), o perché sono oggetto di dibattito, come accade nel caso della prop. 1.

La prop. 1 del Libro X degli Elementi afferma che, date due grandezze omogenee, se si toglie da quella più grande una parte maggiore della sua metà, e dalla parte rimanente se ne toglie un'altra maggiore della sua metà, e si continua di seguito in questo modo, si finisce per ottenere un residuo più piccolo della grandezza minore delle due date all'inizio. Questa proposizione occupa un posto particolare nel contesto del Libro X, dato che non è direttamente in relazione con la teoria euclidea delle grandezze irrazionali, anche se funge da lemma per la prop. 2. Inoltre, la prop. 1 afferma sostanzialmente che non è possibile fissare un'unità delle grandezze che ci permetta di affrontare aritmeticamente il problema del continuo. Questo fatto, come abbiamo visto nella precedente trattazione, contribuì (insieme con la scoperta dell'esistenza di coppie di grandezze incommensurabili) a rendere necessaria l'analisi condotta more geometrico nel Libro X. Ma occorre anche segnalare che è nel Libro XII che questa proposizione trova la sua più naturale applicazione, accanto al metodo di esaustione.

Secondo Ibn al-Hayṯam questa proposizione risulta equivoca: i matematici la considerano unicamente in un senso particolare, quello per cui la grandezza che viene tolta è strettamente superiore alla metà della grandezza data (è sotto questa forma che si trova nel Libro X). Pertanto generalizza la proposizione, dimostrandola nel caso in cui la grandezza che viene detratta si trovi in un qualunque rapporto (strettamente compreso fra 0 e 1) con la grandezza data. Questo passo fu a sua volta criticato da Ibn al-Sarī, un autore di Baghdad, attivo nella prima metà del XII secolo. Questi sosteneva che Ibn al-Hayṯam avesse mancato di generalità nel mantenere lo stesso rapporto fra grandezza tolta e grandezza data passando da una fase all'altra del processo; tale critica, per quanto sottile, non è esattamente fondata (Rashed 1993).

Questo dialogo è una testimonianza dell'interesse suscitato dalla prop. 1. I geometri infinitesimali ‒ Ibn al-Hayṯam fu un esponente di primo piano di questa tendenza ‒ l'utilizzarono per studiare le aree e i volumi di superfici e corpi ricurvi, seguendo il metodo di esaustione. L'interesse di Ibn al-Sarī, matematico e filosofo, era però di natura differente. Fra i suoi scritti matematici, si trova la correzione di un errore commesso da al-Qūhī nella dimostrazione del rapporto fra diametro e circonferenza del cerchio, e anche quattro scritti mirati a confutare alcune critiche formulate da Ibn al-Hayṯam sugli Elementi, fra cui quella sulla prop. 1.

Il destino dei commentari arabi al Libro X dopo il XIII secolo

Le quantità irrazionali si erano ormai affermate e intervenivano insieme ai numeri nei libri di aritmetica e di algebra. Nei decenni successivi, i commenti al Libro X si fecero più rari, limitandosi strettamente agli irrazionali definiti da Euclide. Nella seconda metà del XIII sec., ῾Imād al-Dīn ibn al-Ḫawwām scrisse una Risāla fī fahm al-maqāla al- ῾ašira al muta ῾alliqa min kitāb Uqlīdis (Epistola per comprendere il Libro X di Euclide). Anche se questo breve testo fornisce una descrizione limitata delle grandezze irrazionali del Libro X, appartiene comunque alla tradizione algebrica dei secoli precedenti: si continua a far ricorso a termini presi in prestito dalla geometria, ma le grandezze considerate sono quantità numeriche. La classificazione delle grandezze irrazionali non si fonda sulla commensurabilità (come in Euclide o in Ibn al-Hayṯam), ma sulla loro rappresentazione algebrica sotto forma di quantità semplici o composte. L'ordine delle proposizioni è modificato rispetto al testo degli Elementi, in modo da rispondere alle esigenze del punto di vista algebrico. Ibn al-Ḫawwām inizia con il distinguere le linee monomie da quelle composte, diversamente da Euclide che operava in prima istanza una distinzione fra rette razionali e irrazionali, entrambe definite sulla base della nozione di commensurabilità. Questa distinzione si spiega con il fatto che Ibn al-Ḫawwām non definisce, ma descrive la classificazione derivata dalla tradizione algebrica. In tale tradizione il monomio si oppone al polinomio (quantità composta) perché i calcoli relativi ai polinomi necessitano di regole particolari di cui non c'è invece bisogno per i calcoli sulle quantità monomie. In questo testo si ritrovano gli stessi problemi di nomenclatura che, come si è visto, afflissero gli algebristi del X sec., ma questa volta il linguaggio era ormai fissato e divenuto quello di una versione algebrica del Libro X.

Nel XIII sec. le parti del Libro X più importanti per la conoscenza del continuo erano ormai acquisite. Mancava tuttavia una parte notevole: lo studio degli irrazionali (algebrici o trascendenti) non definibili per radicali; ma queste quantità erano inaccessibili a una tradizione che traeva la sua origine dal Libro X. Nel corso di quattro secoli, dunque, il Libro X degli Elementi fu una fonte importante cui attinsero molti matematici di lingua araba. Grazie ai chiarimenti forniti dall'algebra, questo testo contribuì a determinare molti progressi della matematica, dando origine, come il postulato delle parallele, il Libro I e il Libro V, a una ricerca costante.

Bibliografia

Ahmad 1972: Al-Bāhir en algèbre d'al-Samaw᾽al, édition, notes et introduction par Salah Ahmad et Roshdi Rashed, Damasco, Imprimerie de l'Université de Damas, 1972.

Ben Miled 1998: Ben Miled, Marouane, Le commentaire du Livre X des Éléments par Ibn al-Khawwām, présenté au colloque de la SIHSPAI, Cordoue, 9-11 décembre 1998.

‒ 1999a: Ben Miled, Marouane, De l'unité de mesure chez al-Khayyām et ses prédécesseurs, présenté au colloque international ῾Umar al-Khayyām, mathématicien, philosophe et poète, organisé à Paris, en septembre 1999, par le Projet Bayt al-Hikma de l'Unesco, 1999.

‒ 1999b: Ben Miled, Marouane, Les commentaires d'al-Māhānī et d'un anonyme du Livre X des Éléments d'Euclide, "Arabic sciences and philosophy", 9, 1999, pp. 89-156.

Junge 1930: Junge, Gustav - Thomson, William, The commentary of Pappus on book X of Euclid's Elements, Arabic text and translation by William Thomson, Cambridge, Harvard University Press, 1930 (rist.: New York, Johnson, 1968).

Matvievskaja 1972: Matvievskaja, Galina P., Materialy k istorii učenija o čisle na srednevekovom Vostoke, in: Iz istorii točnych nauk na srednevekovom bližnem i srednem Vostoke, Taškent, Fan, 1972, pp. 76-169.

‒ 1977: Matvievskaja, Galina P., Desjataja kniga Načal Evklida v srednevekovich arabskich kommentarijach, in: Matematika i astronomija v trudach učenich srednevekovogo Vostoka, Taškent, 1977, pp. 4-81.

‒ 1978: Matvievskaja, Galina P., Nekotorye arabskie kommentarii k desjatoj knige Načal Evklida, in: Matematika i astronomija na srednevekovom Vostoke, Taškent, 1978, pp. 3-87.

‒ 1987: Matvievskaja, Galina P., The theory of quadratic irrationals in medieval oriental mathematics, in: From deferent to equant. A volume of studies in the history of science in the ancient and medieval Near East in honor of E.S. Kennedy, edited by David A. King and George Saliba, New-York, New York Academy of Sciences, 1987, pp. 267-271.

Rashed 1984: Rashed, Roshdi, L'idée de l'algèbre selon al-Khwārizmī, in: Rashed, Roshdi, Entre arithmétique et algèbre. Recherches sur l'histoire des mathématiques arabes, Paris, Les Belles Lettres, 1984, pp. 17-29.

‒ 1993: Rashed, Roshdi, Math. inf. II.

‒ 1996: Rashed, Roshdi, Math. inf. I.

‒ 1997: Rashed, Roshdi, L'algèbre, in: Histoire des sciences arabes, sous la direction de Roshdi Rashed avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v.; v. II: Mathématiques et physique, pp. 31-54 (ed. orig.: Encyclopedia of the history of Arabic science, London-New York, Routledge, 1996, 3 v.).

‒ 1999: Rashed, Roshdi - Vahabzadeh, Bijan, Al-Khayyām mathématicien, Paris, Blanchard, 1999 (trad. ingl.: Omar Khayyam. The mathematician, New York, Bibliotheca Persica, 2000).

‒ 2000: Rashed, Roshdi, Math. inf. III.

‒ 2002: Rashed, Roshdi, Math. inf. IV.

Vahabzadeh 1997-98: Vahabzadeh, Bijan, Trois commentaires arabes sur les concepts de rapport et de proportionnalité (Thèse de doctorat, Paris VII, 1997-1998).

Woepcke 1856: Woepcke, Franz, Essai d'une restitution des travaux perdus d'Apollonius sur les quantités irrationnelles d'après des indications tirées d'un manuscrit arabe, "Mémoires présentés par divers savants à l'Académie des sciences de l'Institut Nationale de France, et imprimés par son ordre. Sciences mathématiques et physiques", 14, 1856, pp. 658-720 (v. anche Woepcke 1986, v. I, pp. 648-671).

‒ 1986: Woepcke, Franz, Études sur les mathématiques arabo-islamiques, hrsg. von Fuat Sezgin, Frankfurt a.M., Institut für Geschichte der Arabisch-Islamischen Wissenschaften, 1986, 2 v.