La civiltà islamica: osservazioni, calcolo e modelli in astronomia. La scienza nautica
La civilta islamica: osservazioni, calcolo e modelli in astronomia. La scienza nautica
La scienza nautica
Il 'sapere' nautico si fonda principalmente sulle esperienze accumulate dai navigatori. Si tratta nondimeno di una 'scienza', che si pone all'incrocio tra diverse discipline, in particolare astronomia, geografia e meteorologia, senza dimenticare la questione degli strumenti di misurazione e di osservazione.
È difficile scrivere la storia della scienza nautica araba, perché non abbiamo a disposizione i testi antichi. I soli disponibili risalgono alla fine del XV sec. e all'inizio del XVI e trattano soltanto dell'arte di navigare nell'Oceano Indiano. La presente esposizione sarà perciò limitata all'analisi di due soli autori, Ibn Māǧid e Sulaymān al-Mahrī, entrambi uomini di mare. Essi si situano, in qualche modo, al termine di una tradizione di cui sono gli eredi e della quale non possiamo rintracciare lo sviluppo storico a causa dello stato attuale della nostra conoscenza delle fonti.
Sarà opportuno ricordare innanzi tutto il quadro storico e geografico nel quale si inscrivono i lavori di questi due autori, menzionando anche le rotte e le imbarcazioni che utilizzavano, e poi alcune nozioni elementari di navigazione, sia antica sia moderna, con una terminologia marittima succinta. Tutto ciò è indispensabile per poter seguire la presentazione e l'analisi dei testi e cogliere l'importanza di ciò che l'esperienza nautica araba ha permesso di acquisire.
La situazione geografica e storica
L'esperienza dei due navigatori Ibn Māǧid e al-Mahrī s'inscrive in un quadro geografico ben preciso, quello dell'Oceano Indiano. Via tradizionale di contatti tra le civiltà dell'Occidente (romana prima, araba poi) e quella cinese, è il regno di venti regolari e alterni, i monsoni, che hanno sempre favorito scambi commerciali molto attivi tra le diverse rive che su di esso si affacciano.
L'epoca che consideriamo si estende nell'arco di circa un secolo (1450-1550) e nel complesso corrisponde, per l'Europa occidentale, al periodo di transizione tra il Medioevo e l'Età moderna. È l'epoca delle 'grandi scoperte', che vede i Portoghesi circumnavigare l'Africa e penetrare nell'Oceano Indiano, il quale era stato per più di mezzo millennio dominio incontrastato di Arabi, Persiani, Indiani e Cinesi. Nell'Oceano Indiano gli Arabi disponevano di due punti d'appoggio principali: uno era la costa orientale dell'Africa nel vassallato di Oman, con numerosi porti (trentasette, sembra), dei quali i principali erano Mogadiscio e soprattutto Malindi (nell'attuale Kenia), Kilwa (Tanzania) e Sofala (Mozambico); l'altro, dal 1206, era il sultanato di Delhi, che nel 1310 controllava quasi tutta la penisola del Deccan. I marinai arabi erano dunque spinti a navigare, con l'aiuto dei monsoni di sud-ovest, tra questi due poli e anche oltre, verso gli stretti. Intorno al 1420, una nave indiana (o araba) doppia il Capo ed entra nell'Atlantico.
Chi navigava lungo queste rotte incrociava i marinai cinesi che si spingevano fin lì. Già nel 1402 in una mappa coreana si trova rappresentata la punta dell'Africa. Nel 1405 cominciano le grandi spedizioni marittime dell'ammiraglio cinese Zheng He; questi raggiunge più volte l'Indonesia e l'India, le supera, getta l'ancora in Africa nel 1417 e vi ritorna nel 1431-1433. Si può allora dire che l'Oceano Indiano era in comproprietà tra i Cinesi e gli Arabi? Sembra che la presenza degli Arabi sia stata più costante e di ordine essenzialmente commerciale.
Nel XV sec. la chiusura della via della seta, dovuta alla politica xenofoba e isolazionista dei Ming, dà ai musulmani il monopolio del commercio tra Oriente e Occidente, che essi sfrutteranno fino all'arrivo dei Portoghesi. Questi ultimi in effetti navigheranno anno dopo anno intorno a tutto il continente africano. Bartolomeo Dias raggiunge il Capo nel 1488, Vasco de Gama costeggia il Mozambico (dove a Quelimane incontra quattro vascelli arabi con un pesante carico d'oro, di gioielli, di diamanti e di spezie). Il sultano di Malindi, per rivaleggiare con quello di Mombasa, procura a Vasco il miglior timoniere dell'Oceano Indiano, Ibn Māǧid, noto dal 1462 per i suoi trattati di nautica. Questi guida in ventitré giorni la flotta portoghese a Calicut (a sud di Mahé, nell'attuale Kerala). Anche se questa impresa denota un navigatore affermato, l'identificazione di quest'ultimo con Ibn Māǧid non è dimostrata in modo irrefutabile. Comunque sia, fu un uomo di mare arabo che divenne lo strumento involontario se non proprio dell'estromissione degli Arabi dalla navigazione nell'Oceano Indiano ‒ perché essa prosegue attivamente ancora oggi tra Africa orientale, Somalia, penisola araba, sub-continente indiano e Laccadive-Maldive ‒ almeno della fine di una 'riserva di caccia'.
Le rotte e le imbarcazioni
Il fenomeno del monsone favoriva l'instaurazione di rotte regolari, gestite da famiglie di navigatori. Partendo dai porti dell'Africa, attivi e tra loro concorrenti, e dopo aver fatto scalo lungo la costa occidentale dell'India (Goa o Calicut), i navigatori arabi si spingevano fino in Malesia. È meno certo che arrivassero fino in Cina (si parla, al riguardo, di un'agenzia commerciale a Canton). Scortavano da ovest a est oro e avorio, materie di base per realizzare oggetti di lusso, e schiavi. Il carico di ritorno comprendeva cotone, soia, spezie, ceramiche e porcellane.
Era quindi soprattutto il monsone a stabilire quali fossero le rotte da seguire: da novembre a marzo, l'aria dall'India (fresca) verso l'Africa (calda) dà luogo al monsone di nord-est; a partire da aprile, il Sole riscalda l'India e provoca un'inversione della direzione del monsone, che soffia da sud-ovest. Da giugno a settembre, il monsone spazza il Mare d'Arabia e il Golfo del Bengala in tutta la loro estensione.
C'erano due tipi di viaggi. Da una parte la rotta che serviva Malacca; per varie ragioni, essa girava attorno a Ceylon tenendosene molto lontana (si percepivano solamente i vapori condensati che ricoprivano i rilievi, o, di notte, lampi di luce), per poi continuare, con l'aiuto delle osservazioni, verso le isole Nicobare. Dall'altra parte la traversata dell'India verso Oman, quando il monsone dell'est si avviava al termine; si faceva inizialmente rotta verso Socotra, che a volte si scorgeva prima che si facessero sentire i soffi iniziali del monsone contrario. Allora, rasentando il vento si risaliva verso l'Arabia, per poi costeggiarla. Se la si mancava, si doveva ritornare in India e aspettare parecchi mesi; per bene che andasse, si raddoppiava il percorso iniziale. I percorsi seguiti a priori in linea retta, come per esempio la risalita del Mar Rosso, comportavano anch'essi gravi pericoli.
L'intrico degli scambi marittimi presenta tuttavia elementi di rottura. Così, a sud-est di Sumatra, oltre Singapore, nel Golfo del Bengala, nello stesso Golfo Arabo-Persico e anche a nord di Gedda, i manoscritti lasciano intuire l'esistenza di vari divieti. In compenso, la precisione delle cifre riguardanti la latitudine tra la Sonda, le Chagos e Pemba, suggerisce legami diretti e recenti. Se al-Mahrī scrive che "i marinai del mare indiano e i cristiani sono d'accordo su questo valore […] ma la gente della Cina, di Giava e più oltre su un altro", ci sembra che documenti ancora ignoti, ma indispensabili per completare le nostre conoscenze, siano piuttosto da cercare in India e in Portogallo.
A causa delle caratteristiche meteorologiche la navigazione nell'Oceano Indiano richiede imbarcazioni veloci, in grado di navigare quasi controvento e soprattutto adatte a venti che soffiano di traverso o da poppa. I butri ‒ che s'incontrano ancor oggi, in legni di tek montati uno sull'altro, con il dritto di prora allungato e la poppa con il quadro rialzato ‒, i baghla, i sambuchi, sono tutti armati con la vela 'araba' ad antenna, montata secondo l'uso locale; si tratta di eccellenti navi stagionali, lunghe e sottili. Sappiamo che le imbarcazioni del tempo di Ibn Māǧid e di al-Mahrī erano in grado di navigare controvento a fine stagione, e dunque con deboli brezze, per raggiungere il porto e non lasciarsi sorprendere dal cambiamento di direzione del monsone durante un eventuale ancoraggio in terra straniera. Non conosciamo però con precisione come queste navi fossero costruite e armate, del resto tutte in modo diverso. I disegni probabilmente più somiglianti figurano su alcune carte portoghesi dell'inizio del XVI secolo. Vi si riconosce un modello di timone ancora in uso talvolta in imbarcazioni a due alberi, con il timoniere praticamente ai piedi dell'albero posteriore.
Le fonti dello studio delle conoscenze nautiche degli Arabi
Non si tratta, ora, di passare in rassegna dettagliatamente le conoscenze di nautica che avevano gli Arabi, quanto piuttosto di cogliere l'essenza dell'esperienza di due navigatori nelle parti settentrionale e occidentale ‒ e ben oltre per Ibn Māǧid ‒ dell'Oceano Indiano, nel periodo che va dal 1450 al 1550. Si tratta di conoscenze che riguardano zone limitate, come d'altronde è riconosciuto anche dal più competente dei due, cioè da Ibn Māǧid, il quale, probabilmente a causa della collaborazione con i Portoghesi, consiglia ai suoi compatrioti dell'Oceano Indiano di "andare a scuola dai Franchi [cioè dagli Occidentali] da cui ora vengono la scienza e l'arte del navigare". Questa esperienza di una tecnica essenzialmente pratica ed empirica è riportata in vari manoscritti che vanno dal 1460 al 1550 circa. Sono le copie giunte fino a noi di questi manoscritti, che hanno dato luogo alla maggior parte delle glosse che costituiscono la sostanza del presente capitolo.
Ibn Māǧid e al-Mahrī sono entrambi navigatori. Se il primo raggiunge i vertici dell'arte della navigazione con la spedizione di Vasco de Gama del 1496, e conosce dunque l'irruzione dei Portoghesi in quello che era un 'lago arabo', al-Mahrī viene probabilmente subito dopo. Secondo varie ipotesi egli sarebbe morto tra il 1511 e il 1554. La datazione dei suoi libri è dunque un problema delicato, tanto più che alcune delle sue opere, nello stato in cui le conosciamo, si citano a vicenda. I manoscritti che si utilizzano sono i tre seguenti: il 992, conservato presso gli Studi orientali dell'Accademia delle Scienze di Pietroburgo (ff. 82r-106r) e che consta di alcuni libri di Ibn Māǧid; i manoscritti 2292, contenente i libri di Ibn Māǧid, e 2559, che contiene i libri di Ibn Māǧid e di al-Mahrī, entrambi del Fondo arabo della Bibliothèque Nationale di Parigi. Nessuno di questi manoscritti è originale; si tratta di copie con numerose varianti e glosse, quando il confronto tra i due testi è possibile, nelle quali sono riportati titoli di libri a noi ancora sconosciuti.
L'Oceano Indiano era luogo di frequenti incontri e anche di collaborazioni e scambi tra i naviganti. Quando si parla di 'sapere arabo' va perciò tenuto presente che molto è dovuto ai navigatori cinesi, mentre l'abbondante letteratura portoghese in ambito nautico del XVI sec. ricorre in parte all'eredità di Ibn Māǧid e dei suoi contemporanei. Possiamo perciò affermare che il sapere nautico va al di là delle epoche e delle zone d'influenza. È un thesaurus comune, ripreso da predecessori e concorrenti e arricchito da ogni nuova generazione. La presenza secolare dominante dei navigatori arabi nell'Oceano Indiano riserva tuttavia un ruolo particolarmente importante agli insegnamenti di Ibn Māǧid e al-Mahrī.
Detto ciò, sappiamo che le istruzioni nautiche pubblicate in arabo intorno al X sec. sono in gran parte traduzioni. I trattati originali in arabo composti più tardi segnalano divergenze tra Arabi, Ormuziani, Indiani, ecc. Molto prima di Marco Polo si conoscevano nell'Andalus libri di astronomia detti Sind, e Marco Polo stesso riportava procedimenti e documenti di navigatori dell'Estremo Oriente. Vi erano anche carte cinesi e giavanesi. Ci si aspetta quindi di dover confrontare i libri nautici arabi con molti altri testi dello stesso genere. I Portoghesi hanno poi approfittato di queste fonti preliminari, arricchendole con le loro osservazioni: infatti, si hanno "nel solo periodo che va dal 1538 al 1552 più di 4700 documenti, quasi tutti in portoghese e quasi tutti inediti" (Aubin 1972). Lo studio delle istruzioni di Ibn Māǧid e al-Mahrī dovrà dunque basarsi sul confronto con un insieme di testi di epoche diverse.
Prima di passare all'analisi critica degli autori ‒ un'analisi che comporta talvolta questioni di autenticità, e cioè il problema della fedeltà delle copie all'originale ‒, bisogna superare l'ostacolo della lingua. Le istruzioni nautiche arabe sono redatte in termini che consideriamo in certi casi troppo vaghi. Tuttavia, a volte essi sono più precisi di alcuni termini in uso oggi, anche tenendo conto della stabilità dell'arabo nel corso dei secoli. In tal modo, 'punto di mura' e 'punto di scotta' erano espressi all'epoca, come oggigiorno, tramite termini caratteristici; al contrario, in alcuni casi, destra e sinistra erano detti nello stesso modo. Esempi di questo tipo sono molto frequenti.
Con quale spirito affrontare la lettura di Ibn Māǧid e di al-Mahrī? Con quale atteggiamento critico un lettore competente deve valutare le loro affermazioni?
A prima vista, un lettore esperto di nautica resta sedotto dalla sobrietà e dalla chiarezza di al-Mahrī, mentre Ibn Māǧid si rivela confusionario e pretenzioso. In seguito, però, la verifica scientifica delle affermazioni degli autori e la maggiore familiarità di Ibn Māǧid con la pratica della navigazione conducono a una diversa conclusione: Ibn Māǧid ha percorso i mari molto più del suo 'rivale', e se si può vedere in al-Mahrī uno studioso stimolato dalla curiosità delle cose di mare, in Ibn Māǧid si può riconoscere soprattutto un navigatore esperto. I suoi libri, destinati apparentemente agli apprendisti piloti, sono irti di difficoltà: quei versi sono pieni di rievocazioni e allusioni, e alcune indicazioni lasciano intendere il resto a un lettore ben informato e acuto. Tecniche di esegesi potranno poi affinare le indispensabili ricerche per decidere l'autenticità di certi testi. Così, nella Sufaliyya (Sulle profondità), uno dei tre scritti di nautica del ms. 992, alcuni passaggi sembrano apocrifi a causa di enormità, inammissibili da parte di Ibn Māǧid e difficilmente spiegabili con la disattenzione di un copista.
Si osserverà infine che Ibn Māǧid, tradizionalmente considerato un uomo pratico, tace a proposito della teoria della latitudine ricavata da un'altezza meridiana ‒ nonostante parli di tavole di declinazione ‒, mentre al-Mahrī tratta questo punto in modo magistrale; anche se poi, omettendo di adattare la formula alle latitudini sud, tradisce il fatto di non aver oltrepassato l'equatore, il che spiega la parzialità di alcuni dei suoi risultati.
Lo studio di Ibn Māǧid e di al-Mahrī porta a chiedersi dove tracciare la linea di separazione tra scienza ed esperienza pratica. Un navigatore come il primo, empirista e tradizionalista, ha fatto a lungo ricorso a veri e propri esperimenti. Tuttavia, è sufficiente ciò per considerare questi due navigatori uomini di scienza? Si può comunque attribuire ad al-Mahrī la qualifica di studioso, semplicemente curioso delle cose di mare, e a Ibn Māǧid quella di artigiano, un 'fuoriclasse' nella sua arte, malgrado fosse una personalità incontestabilmente piena di difetti.
Come abbiamo in precedenza detto non si tratta in questa sede di esporre in modo specialistico le conoscenze nautiche degli Arabi, ma piuttosto di cercare di progredire, spesso solamente con congetture, nella comprensione di un sapere largamente imperfetto, privo di una propria coerenza complessiva.
Non bisogna pensare ai navigatori arabi, e in particolare a Ibn Māǧid, come a ufficiali di quarto intenti a rilevare mede o astri con la precisione che l'epoca consentiva e a riportare su una carta un triangolo per correggere un punto stimato mediante uno osservato. Utilizzando la propria esperienza e quella dei suoi predecessori, Ibn Māǧid praticava ciò che potremmo definire una 'stima con correzioni'. Le carte erano probabilmente utilizzate soltanto come promemoria delle distanze tra i vari luoghi o degli orientamenti generali delle coste e delle posizioni dei porti; non permettevano molto di più. Per localizzare un'imbarcazione si poteva ricorrere all'altezza di un astro; per il resto, le 'istruzioni nautiche', le conoscenze dei timonieri e la loro intuizione determinavano la stima. Se l'Oceano Indiano è un mare di venti stabili, con tutti i vantaggi già segnalati, la regolarità dei monsoni non è tale da rendere superflua una buona valutazione della forza e della direzione dei venti e delle correnti.
Le unità di misura utilizzate
Pare lecito porsi la domanda su quali unità di misura utilizzassero gli Arabi precedentemente all'adozione del sistema metrico. Essenzialmente essi usavano le dita, gli zam e le tirfa. Come oggigiorno, è a partire dalla misura dell'altezza che si determina una distanza: zam e tirfa si definiscono in rapporto al dito; tuttavia, la nozione di unità di misura invariante non è ancora del tutto familiare alla mentalità del tempo. Si tratta di un grosso ostacolo, aggravato dall'assenza di strumenti sufficientemente precisi, che impedisce una pratica scientifica vera e propria. Tuttavia, in fondo, se le variazioni sono di un ordine di grandezza paragonabile al grado di precisione delle osservazioni, la non invarianza delle unità di misura non risulta molto importante.
a) Le 'dita' e il dubbān. Le dita erano misurate con i 'legni' (v. oltre) e pertanto la misura massima era di 12 dita, cioè di 20° circa. Quindi, si poteva misurare soltanto l'altezza delle stelle basse.
Nel corso dei secoli si è fatto riferimento al dito, al palmo, al cubito, al piede, ecc. come unità di misura. Tuttavia, voler misurare 'dita', cioè angoli molto piccoli, su tavolette incise con il coltello, è certamente un'impresa. L'accuratezza nelle altezze raggiungeva 20′ e probabilmente anche meno; i casi di accuratezza inferiore a 5′, infatti, sono troppo frequenti per poter essere attribuiti al caso. Si ricorreva dunque alla mano, che fornisce il dubbān, termine che designa l'angolo coperto da 4 dita, campione grossolano anche se personalizzato; i navigatori del tempo di Ibn Māǧid potevano certamente ottenere lo standard delle 4 dita dalla rotazione della Stella Polare, se il diametro non cambiava con il tempo; comunque, il cielo forniva un sistema di riferimento invariante, in quanto la distanza angolare tra la maggior parte delle stelle rimane stabile per secoli.
Il termine dubbān è utilizzato per due stelle, tra le quali α dell'Auriga, una delle preferite da Ibn Māǧid: "α Aurigae ha un dubbān, il suo è [β], e a sud del dubbān c'è una stella della stessa grandezza [θ] che si chiama il dubbān del dubbān, e distano l'una dall'altra 4 dita". Malgrado ciò Ibn Māǧid non si richiama mai formalmente a questa taratura per i legni, al contrario di al-Mahrī: "i legni del dubbān di misura devono corrispondere al dubbān di α Aurigae alla culminazione del Leone e gli altri legni saranno corretti suddividendoli secondo questo campione, che è una misura angolare più precisa di quella ottenuta stendendo un braccio".
La distanza angolare tra α e β è di 7;36°, e di 7;42° quella tra β e θ. Dato che non esistono esempi di misure precise non verticali prese con i legni, e poiché alla culminazione data α e β sono in verticale, nel paese di al-Mahrī, intorno a 30° di altezza, il sistema di riferimento è ben definito per il dubbān sui legni di 4 dita. In queste condizioni, la misura con i legni dà un errore di circa 1°: l'angolo osservato è di 6;40° (da confrontare con l'angolo effettivo di 7;36°), e ciò implica che il braccio doveva contrarsi da h1 a h2.
Per fissare le idee e arrivare a un'equivalenza tra dita, tali da corrispondere alle meridiane di alcune stelle osservate da Ibn Māǧid, abbiamo fatto numerose correzioni in uno spirito 'moderno', riguardanti la rifrazione (deviazione dei raggi dovuta agli strati dell'atmosfera), l'altezza vera (l'altezza del punto di osservazione sul mare influisce sull'altezza misurata dell'astro), la Stella Polare (che non si trova al Nord vero). L'altezza vera della Stella Polare alla meridiana fornisce la latitudine del luogo; il risultato di questi calcoli dà la 'tavola delle dita' o delle altezze misurate in dita (Tav. IV).
Abbiamo utilizzato le osservazioni delle stelle riportate da Ibn Māǧid abbandonando, salvo in caso di accordo, al-Mahrī, poco affidabile malgrado le sue qualità scientifiche.
Questa tavola è il risultato di un gran numero di confronti tra le meridiane di α della Croce del Sud, di α di Eridano e soprattutto della Stella Polare e di alcune stelle accoppiate considerate quasi alla meridiana. La media delle differenze tra il secondo e il dodicesimo valore, 1;36°, corrisponde alla cifra data dai Portoghesi. Quanto all'enorme primo dito, esso si può spiegare con l'indeterminatezza dell'orizzonte notturno, che costringe ad alzare i legni in modo esagerato per distinguere nettamente l'orizzonte dalla loro parte inferiore. L'ipotesi sembra confermata dal fatto che le misure valutate utilizzando l'accoppiamento di brillanti stelle del Sud, troppo alte per essere misurate con il metodo della meridiana, sono esagerate (a volte anche di un grado); in effetti: "α Carinae e β Centauri […] devono essere misurate al chiaro di Luna, come è caratteristico per le stelle del Sud". La nitidezza della linea dell'orizzonte con la luce della Luna permette infatti di non alzare esageratamente i legni e di ottenere, di conseguenza, un valore dell'altezza non gonfiato.
Il lettore moderno resta sorpreso dalla diversità delle dita in questa tavola; gli Arabi invece non si ponevano il problema di sapere se le dita avevano valori diversi. Un'analisi accurata dei testi, che appesantirebbe questo studio senza renderlo più valido, permetterebbe di ridurre alcune inesattezze nella rilevazione di determinate altezze, sebbene non tutte.
b) Gli zam. Le distanze stimate erano misurate secondo l'unità zam, che al-Mahrī definisce opportunamente nel modo seguente: "lo zam è di due tipi, definito [o d'uso] e tecnico. Il primo è un ottavo di un percorso tale che una stella aumenta o diminuisce in altezza di un dito, andando verso di essa o dandole le spalle, in teoria o realmente". Altrove egli qualifica anche come "vero" o "in senso proprio" (ḥaqqī) lo zam ottenuto con una misura; bisogna osservare che si doveva operare con la stella alla meridiana, e al-Mahrī ne era probabilmente cosciente, mentre ai suoi inizi Ibn Māǧid credeva che il procedimento fosse valido qualunque fosse l'azimut della stella osservata purché si situasse lungo l'asse dell'imbarcazione (ciò è falso dal punto di vista matematico).
Al-Mahrī precisa che lo zam 'definito' implica "un vento stabile e di forza media". In compenso non tratta di zam d'insieme (possibile interpretazione di ǧumma) di cui Ibn Māǧid parla invece abbondantemente e segnatamente in questo modo: "il valore esatto degli zam d'insieme tecnici supera gli zam delle rotte e delle distanze effettivamente percorse"; passo che permette di mettere in discussione la stima di alcune distanze. Con gli zam d'insieme Ibn Māǧid vuole soltanto definire un certo standard: "Questo è il valore che io do in zam di tre ore, in navigazione normale; il lettore lo adatterà a seconda dei casi". In questo modo, egli si avvicina allo zam 'definito' di al-Mahrī, tanto più che distingue ancora tra zam 'pesanti' e 'leggeri', lo zam pesante tipico essendo evidentemente quello che si realizza in tempo di bonaccia e in assenza di correnti.
Più inatteso è tuttavia il modo in cui Ibn Māǧid utilizza questi aggettivi per regioni particolari, e dunque in funzione della meteorologia che è loro propria. L'estratto che segue proviene dalla "particolarità delle particolarità" (o "carattere delle proporzioni", ḍarībat al-ḍarā᾽ib), dove Ibn Māǧid associa queste distanze a variazioni di altezza di astri, ritenute misurabili mediante l'osservazione astronomica in scostamenti dal meridiano (ciò che equivarrebbe a ottenere una componente in longitudine!): "la distanza stimata del primo rombo è pesante […] non la si calcola da Hadmati al vostro Muluk [da 2;35° a 1;50° N nelle Maldive] come la si calcola da Bab el-Mandeb a Zuqur, né da Muruti a Brawa [Somalia orientale]".
Vi sono grandi differenze tra i percorsi citati; il più 'leggero' si trova in Somalia dove il monsone di nord-est è fresco e regolare, con una buona corrente favorevole. È un monsone che segna il più lungo periodo dell'anno in cui si può navigare da queste parti, mentre i velieri si preparano a salpare ai primi segni del monsone di sud-ovest, che si annuncia con piccole brezze, per evitarne la violenza più tardi. Questa relatività dell'unità di misura era poi aggravata dalla variabilità dei percorsi descritti. Ibn Māǧid dichiara: "da quel punto della Somalia ad Aden vi sono 20 zam, a volte meno se il tempo è sereno grazie al monsone da est". Questo passo mostra che le distanze non erano calcolate necessariamente tra la normale del punto di partenza e quella del punto d'arrivo. Ciò non presenta inconvenienti per lunghi percorsi, ed è una probabile spiegazione di velocità a volte sorprendenti su percorsi brevi.
La Ḍarība (La particolarità; non datata), come pure la ḏahabiyya (La dorata) o la Ḥāwiya (La comprensiva), trattano in modo analogo queste distanze misurate in zam variabili (inaccettabili, come sappiamo, perché equiparate all'osservazione della longitudine). Ora, se la Ḥāwiya risale alle prime esperienze di Ibn Māǧid, fin dall'inizio della Ḍarība l'autore parla della propria età adulta, e dunque o Ibn Māǧid sbaglia nel perseverare diabolicum (ma ciò da parte sua è poco verosimile), oppure non ha capito la corrispondenza con la longitudine. Se il rapporto tra la distanza e il tempo è un dato relativo, non per questo è meno probabile che lo zam 'teorico', preso come campione un ottavo di dito, avesse un valore quantificabile in 12 miglia (da ca. 1500 m l'una). Dal canto suo, al-Mahrī stabilisce il 'valore matematico dello zam' prendendo il dito come campione: "gli astronomi sanno bene che la rivoluzione della Stella Polare [che i marinai prendono come misura di 4 dita] è di 6° e 6/7 [ciò che è esatto per il 1505], dunque 1 dito è pari a 1° e 5/7, e 1° a 1 zam meno un terzo"; ciò che dà allo zam un valore di 12,82 miglia (19,2 km ca.), valore ammissibile.
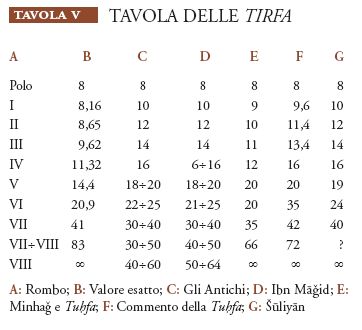
c) Le tirfa (e le deviazioni). Una tirfa è la distanza da percorrere in ogni rombo (ossia per ogni trentaduesima parte della rosa della bussola, 11;15°) per vedere la meridiana di un astro variare di un dito. Qui, ancora, ci troviamo di fronte alla nozione di unità di misura relativa, a noi divenuta estranea, ma che appariva naturale prima dell'astrazione che ha portato alla nozione di misura assoluta, in un ambiente abituato a basarsi unicamente sull'osservazione di dati concreti.
Le tirfa erano classificate secondo l'obliquità della rotta rispetto al meridiano: le meno inclinate (rombi da 1 a 5) si chiamavano ruḥuwayyāt o raḥawiyyāt, le altre šaqaqāt. Ibn Māǧid ne parla in particolare quando, a proposito delle rotte dirette press'a poco a ovest o a est (dunque a proposito della distanza stimata lungo queste direzioni, che è poco affidabile), precisa: "per le raḥawiyyāt la stima è preferibile […] soprattutto se è in accordo con l'osservazione, mentre per le šaqaqāt sono preferibili le sole altezze"; ciò è abbastanza logico in ragione della totale inefficacia dell'osservazione del meridiano rispetto agli spostamenti in direzione ovest o est.
Citiamo ancora i manākib (deviazioni, oblique, o aree di direzione intermedia tra i punti cardinali secondo l'accezione comune in Europa) che rappresentavano i percorsi tra il meridiano e le masāfāt, distanze per antonomasia a est od ovest.
La tavola delle tirfa qui riportata (Tav. V; i valori sono espressi in zam) raccoglie gli elementi di varie distanze sparse nei libri di Ibn Māǧid e di al-Mahrī. I loro punti di vista teorici avrebbero dovuto affermarsi senza ambiguità in una tavola di questo tipo. E tuttavia sorprende già il valore definito dato alle tirfa est od ovest, in realtà infinite.
Per quanto riguarda al-Mahrī, abbiamo visto che non si possono datare con precisione i suoi scritti e dunque giudicare come progredisse la sua esperienza. Egli si limita spesso a riportare, senza verificarle, informazioni raccolte da altri navigatori. Nel suo commento alla Tuḥfa (Il dono prezioso), egli fornisce dati di diverse scuole tra cui quelle dei marinai di Coromandel, dei quali dà dati approssimati, anche se basati "sul quarto di cerchio trascurato dai timonieri […] e questa è la mia scuola".
Precedentemente, al-Mahrī aveva rettificato i dati dei primi 4 rombi, integrandoli con frazioni approssimate e ricorrendo ancora al metodo dei quarti di seno. In tal modo si constata che, per quanto i valori dei primi 4 rombi siano i meno imprecisi della tavola, il confronto con i navigatori di Coromandel fornisce cifre notevolmente inesatte, salvo nel settimo rombo (mentre egli non ne fornisce per il rombo seguente). Poiché sarebbe un abuso accusare i copisti di questa accumulazione di errori, detti approssimazioni, la scienza di al-Mahrī (una vera scienza peraltro) ha capitolato davanti a una questione tanto elementare da essere illustrata mediante la costruzione, al suolo, di una rosa sulla quale le persone si muovono verso i rombi tracciati materialmente.
Le carte
Nonostante i manoscritti parlino di effemeridi e sebbene esistessero carte ‒ mai citate nei testi e del tutto scomparse, alcune delle quali note però ai Portoghesi ‒, si navigava nell'Oceano Indiano, intorno al 1500, senza utilizzare né carte né effemeridi; ci si serviva di un calendario approssimativo e di numerose istruzioni nautiche. L'esperienza faceva il resto.
È probabile in effetti che le carte di allora non sarebbero state di alcuna utilità per determinare la posizione in mare, in quanto la precisione delle distanze tra le coste era inferiore all'incertezza della posizione stimata, che era corretta mediante le osservazioni astronomiche.
I manoscritti di Ibn Māǧid e di al-Mahrī, che sono un modello delle istruzioni nautiche in uso allora, forniscono distanze marittime ‒ e terrestri nel caso di Ibn Māǧid ‒ ad altezza di ogni dito (Stella Polare, stelle β e γ dell'Orsa Minore, ε e ζ dell'Orsa Maggiore). La misura di queste distanze rispetto alla trama dei meridiani permetteva di fare rotta su un luogo; il tutto concordava abbastanza bene con le rotte costiere, un fatto curioso data l'espressione di questi orientamenti in termini di rotte vere e rombi in cifra tonda. A volte si ha invece discordanza nei dettagli per una particolare regione, per esempio il 'Golfo berbero'. La carta nella fig. 4 permette di confrontare la forma delle coste tratta dalle opere di Ibn Māǧid e di al-Mahrī con quella reale.
Al-Mahrī elenca metodicamente le distanze, come fa a volte anche Ibn Māǧid. L'uno e l'altro sono talvolta complementari, con alcune divergenze quando trattano delle stesse zone. Coordinare il tutto non fu cosa facile. Un esempio tra i più evidenti riguarda l'altezza di 5 dita della Stella Polare, che si estende tra Bargamlah (il Margabeleh delle nostre carte, presso Assab) e Tawahi (Tavoy, in Birmania). Gli errori in latitudine rivelano sulla carta le zone sconosciute agli Arabi, in primis l'Australia (Timor), disegnata con un tratto verticale in una posizione presunta (niente distanze), e la cui toponimia è relativamente recente. Il Madagascar figura sotto due profili; quello della costa occidentale è di Ibn Māǧid.
Per l'Estremo Oriente i dati divengono confusi subito dopo Malacca. A Sumatra la riva occidentale presenta alcuni errori importanti; vi sono due dita di differenza tra la Sonda di Ibn Māǧid e quella di al-Mahrī; Bali è sempre a ovest di Giava. C'e anche confusione, sebbene in misura minore, a nord della linea Ceylon-Nicobar, in quanto, secondo Ibn Māǧid "pochi Arabi frequentano il Bengala, il Siam e l'est dell'India". La presenza di quest'isola mitica, Tirm Turi, si spiega, più ancora dell'incertezza riguardo alle Seychelles e soprattutto alle Mascarene, con il fatto che i velieri non si arrischiavano mai nella 'zona delle calme equatoriali'. Quanto a Karm Danwa (o Diwa), spostato in longitudine come la costa dell'Africa e la Sonda, esso non attesta forse migrazioni relativamente recenti degli Indonesiani? Ibn Māǧid rettifica nella Qiblat al-islām (La direzione della preghiera dell'Islam) alcune nozioni della sua epoca. Il controllo dei suoi orientamenti conferma ‒ salvo per luoghi lontani dal mare e per il Madagascar, troppo esteso ‒ il profilo di ricostruzione della carta.
Queste carte presentavano insomma gravi incertezze; nei manoscritti non vi è traccia della loro utilizzazione effettiva in mare e sembra che i geografi arabi le abbiano ignorate del tutto. A queste carte ‒ che si potrebbero indicare come 'carte dei marinai' piuttosto che 'carte marittime' e che erano state elaborate da gente pratica di mare ‒ bisogna nondimeno riconoscere, prima dello sviluppo della cartografia iberica, il merito di proporre al navigatore una sorta di identikit di regioni nelle quali, avendo come sola guida la tradizione, avrebbe navigato ignorandone la geografia.
Gli strumenti
a) La bussola (e la declinazione). Sebbene per la navigazione dispongano di ausili radioelettrici, in assenza di mede direzionali, ossia di segnali direzionali fissi, i navigatori ricorrono ancora alla bussola, che i marinai francesi e di altri paesi chiamano 'compasso'.
Il termine si trova già nell'accezione dell'epoca in Ibn Māǧid, a proposito dei popoli mediterranei. La presenza di un ago magnetico, sistemato in un abitacolo, è data per certa, anche se nessuno è in grado di precisarne la disposizione effettiva. Due punti meritano però attenzione: intanto, ibra e samaka indicano effettivamente l'ago, ma il secondo termine è utilizzato soltanto due volte. Inoltre, si può avanzare l'ipotesi di una cassa con un asse di supporto, basandosi su un passo (anche se è l'unico) di un commento sui difetti della bussola "dovuti alla pesantezza della rosa e alla cattiva qualità della sua calotta". Privo di supporto su un asse, l'ago non avrebbe potuto muoversi liberamente senza urtare i bordi del contenitore. E come mai allora, riguardo ai difetti della bussola, non si fa menzione di casse o contenitori? Il marinaio capisce immediatamente che con il termine 'pesantezza' s'intende riferirsi a una forza direttrice troppo debole perché si possano attuare rapidamente correzioni dopo rollii o cambiamenti di rotta nelle imbardate.
Per mantenere la rotta poteva essere d'aiuto, di giorno, una fiamma di stoffa che permetteva di localizzare il vento in modo da poter governare meglio l'imbarcazione rispetto a esso. Tuttavia, nell'ipotesi di un ago poggiato su un asse tramite un cappelletto in una scatola-abitacolo, come si può determinare la rotta tenuta? Vi sono due configurazioni elementari. Nella prima, la vaschetta dell'abitacolo, solidale all'imbarcazione, è graduata, ma al contrario: se l'imbarcazione fa rotta verso nord-ovest, la gradazione nord-ovest sarà a destra del nord e l'ago punterà verso di essa. Nella seconda, viceversa, per una rosa graduata sostenuta dall'ago e dunque solidale con esso, è sufficiente un solo segno sull'abitacolo, che può non essere circolare. Tale segno designa la parte anteriore dell'imbarcazione (la nostra 'linea di fede') e deve essere posto di fronte, o quasi, alla tacca che indica la rotta.
La seconda configurazione è la più comoda perché il timoniere guarda sempre davanti a sé, quasi inconsciamente, la rotta, mentre con la prima deve comunque fare riferimento alla punta dell'ago che si trova in posizione variabile rispetto alla rotta, che manterrà, quindi, meno facilmente. Governare con le stelle è una variante della prima configurazione. C'è da chiedersi se i due modi non possano allora essere stati presenti contemporaneamente in quest'epoca di transizione. Ciò spiegherebbe perché i testi utilizzano indistintamente i termini al-ḥaqqa (lett. il solo abitacolo), bayt al-ibra (lett. la sede dell'ago) e al-dā᾽ira (lett. la rosa).
Si pone infine la questione dell'illuminazione della bussola. Sappiamo che si bruciava della nafta, probabilmente in occasione di qualche celebrazione ‒ per esempio, all'arrivo a Nicobar Grande: "accendete la nafta e imbandierate". Non sappiamo però se ci fosse una fiammella, opportunamente protetta, per illuminare la bussola.
Resta poi la questione della 'declinazione': se il ferro o l'acciaio influenzano la bussola, questa 'deviazione', che varia con la rotta, si combina con la 'declinazione' magnetica ‒ dovuta al fatto che l'ago della bussola indica il N del campo magnetico terrestre, e non quello geografico, indipendentemente dalla rotta ‒ per dare la 'variazione'. Benché Ibn Māǧid e al-Mahrī mettano in guardia contro gli errori di rotta dovuti alla bussola (deriva, ecc.), si cercherebbe invano una definizione formale della declinazione. Tuttavia, in due casi, essi si domandano se i timonieri non si siano accorti di un evento inspiegabile. La prima citazione, di Ibn Māǧid, riporta alla samaka. Si tratta effettivamente dell'ago in quanto "essa [la rotta] è falsata soltanto da […] o per difetti nell'abitacolo dell'ago [a forma di] pesce [che] si chiama pesce della scatola (samaka)". E più oltre: "il timoniere crede di seguire una [data] rotta ma se ne discosta a causa della scarsa conoscenza della stessa, o della cattiva disposizione di un abitacolo, o [a causa] di un ago o di un ago che ha toccato la pietra 'farqadosa' [tale quale, est od ovest farqad o faraqad designava l'Orsa Minore]". Al-Mahrī è meno vago: "è possibile che alcune rose indichino il N-NO". Infatti, siccome seguendo rotte note dalla tradizione si giungeva in porto (salvo errori personali nell'applicazione delle istruzioni), non c'era motivo di preoccuparsi se l'ago non indicava esattamente il N; inoltre non erano in molti ad accorgersene.
b) I legni. Intorno alla prima metà del XVI sec., per misurare l'altezza di un astro si erano affermate due tecniche: la prima consisteva nel misurare l'angolo compreso tra l'astro e l'orizzonte, mentre l'altra consisteva nel localizzare l'astro su una o più tavolette, graduate in 'dita', facendo coincidere il bordo inferiore di queste con la linea dell'orizzonte.
Pur non dilungandoci su come puntare correttamente con un solo occhio l'orizzonte e simultaneamente un dato astro, si ricorderà tuttavia l'importanza delle difficoltà inerenti alla costante instabilità dell'imbarcazione e a quella, relativa, del braccio che sostiene lo strumento di misura: occorre puntare rapidamente e gli obiettivi (punti o linee) sono a volte confusi. Insomma, prima delle rilevazioni elettroniche né i legni né un sestante davano altezze esatte ed era l'abilità dell'operatore che a volte suppliva alla mancanza di precisione. Detto ciò, è possibile stabilire, basandoci sui testi in nostro possesso, la frequenza con cui, al tempo di Ibn Māǧid e di al-Mahrī, si faceva uso di apparecchi graduati, come il quadrante e l'astrolabio? Con la parola 'legno', ḫašabāt, più raramente ḫušb o ḫušub, plurale di ḫašaba, si designava lo strumento per misurare l'altezza di un astro sull'orizzonte. Al singolare la parola si trova in un'espressione usata frequentemente per indicare una posizione di stelle a una medesima altezza: fī ḫašaba wāḥida. Le divergenze tra i commentatori moderni suggeriscono prudenza nell'analizzare i testi che trattano dell'uso dei 'legni'.
Quando Barros parla di strumenti arabi 'inattesi' (tra cui un quadrante) che servono a misurare l'altezza del Sole, c'è da chiedersi se si tratti di una forma di sensazionalismo o di una sorta di imbroglio da parte di chi ci vuole informare e che poco dopo confesserà di servirsi solo di legni. Lo stesso accade, in modo più sottile, nel Muḥīṭ di Çelebī (traduzione interpretata di alcuni libri di Ibn Māǧid e di al-Mahrī, che fu redatta in turco nel 1553 e tradotta in tedesco da Hammer-Purgstall e dal tedesco in inglese da Princep), che aggiunge alla traduzione un commento sulla descrizione degli strumenti di misura. Çelebī descrive in maniera dettagliata le caratteristiche delle gradazioni di uno strumento a legni munito di un filo graduato del quale precisa ‒ seguendo così al-Mahrī ‒ che esso era soggetto ad allentarsi.
Al-Mahrī ricorda anche l'uso simultaneo di entrambe le tecniche: "l'altezza [presa con lo strumento] a mano che corrisponde ai legni per misurare, e l'altezza [presa con lo strumento] graduato [gradi sull'arco di cerchio] non varia con l'aumento dell'altezza delle stelle, contrariamente alla misura a mano" (il termine ḥaṭabāt al posto di ḫašabāt è usato solamente da lui). Questa citazione sembra alludere a strumenti quali l'astrolabio, che hanno come riferimento la verticale vera, e quanto dice al-Mahrī sembra riferirsi inevitabilmente a misure che, come è noto, furono prese a terra. Al-Mahrī parla in seguito di un altro apparecchio a filo: "proporzionalmente all'altezza della mano il filo si allenta a causa dell'avvicinamento dell'apparecchio all'occhio, e la misura si riduce". Come si può allentare un filo fatto per restare teso? Secondo I. Khoury ciò si spiega attribuendo a ḫayṭ il significato di filo immaginario, di linea teorica.
Comunque sia, ricordiamo ora quanto ci insegnano Ibn Māǧid e al-Mahrī sui legni, tecnica che ci appare come la più utilizzata ‒ e anzi praticamente la sola ‒ all'epoca. Vediamo esattamente cosa dicono, sebbene ne parlino poco:
La condizione [necessaria] delle misure è che, sui quattro grandi legni, esse siano deboli, sui quattro legni medi siano comuni [o normali, abituali=senza correzione]; tra la stella e il legno [occorre lasciare] un filo, e un filo anche tra il legno e l'acqua, come il taglio di un coltello, a vista dell'osservatore; e la condizione sui legni piccoli è che siano deboli […].
Mettere tra la stella osservata e la direzione del tuo viso 7 rombi (78;45°) come da nord ad al-ṭayr [che sarebbero invece 8 rombi (90°)] e i legni grandi sono di misura debole; tendi la mano al massimo, e i quattro legni piccoli sono forti; contrai la mano al massimo, per i quattro medi la loro misura è normale, e ciò allo scopo di allargare il lembo di orizzonte e ridurne la parte superiore […].
La miglior misura è quella presa con i legni medi, né grandi né piccoli […].
Si può dunque ipotizzare un insieme di tre tavolette crescenti per serie di 4 dita in 4 dita, ciascuna delle quali forma, per esempio, un insieme rigido in quanto non se ne conosce la disposizione effettiva. Invece di una gradazione come quella dei gradini di una scala, è possibile che si tracciassero sui legni segni di colore alternativamente chiaro e scuro (da cui il termine hadba). Si possono pensare tutte le frazioni, perché era necessario poter leggere un dito e anche sottomultipli.
Vediamo ora una possibile realizzazione dello strumento. L'ideale sarebbe stato una ripartizione di 3 elementi congiunti, di 4 dita ciascuno, su un settore il cui raggio fosse centrato sull'occhio, e che fossero una realizzazione concreta delle corde ab´ (legni piccoli), hc (medi) e gd´ (grandi). Poiché non era così (si sarebbe trattato allora di un quadrante o dell'astrolabio) e dal momento che si teneva ciascun legno per la parte superiore, il problema da risolvere si presenta come segue: misurare in successione, mediante le tavolette di 4, 8 e 12 dita, angoli che hanno tra loro una differenza costante di 4 dita, visti dall'occhio (posto in o), aob´, aoc, aod´. Tenuta costantemente tesa, la mano percorre un arco di cerchio bcd, con centro sulla spalla; in questo modo le quattro dita sulle tavolette (uguali per definizione) evidentemente non vanno bene. Supponiamo allora il problema risolto, prendendo come punto di partenza c, quarto dei legni medi (dunque 8 dita), con la mano tesa normalmente. Quindi, a 4 dita di scarto in verticale su c tracciamo due rette parallele all'orizzonte. Il quarto dei legni piccoli (4 dita) e il quarto dei grandi (12 dita) tagliano l'arco con centro nell'occhio rispettivamente in b´ e in d´, punti nei quali conviene quindi porre la parte superiore delle tavolette. La mano si è dunque 'estesa' da f a g e 'contratta' da e ad a.
c) Altri strumenti. Abbiamo visto come i due autori alludessero all'utilizzazione di strumenti diversi dai legni per misurare l'altezza degli astri. Non è del tutto infondata l'ipotesi di uno strumento provvisto di un filo materiale, tipo kamāl, che avrebbe fatto la sua comparsa intorno al 1540, nel quale il filo servisse evidentemente a misurare la tangente dell'angolo dell'altezza, e dunque l'angolo stesso. Come ha osservato G. Tibbets nel 1971, Ibn Māǧid e al-Mahrī non parlano mai del kamal, o kamāl, uno strumento che molti sono invece convinti fosse utilizzato all'epoca. Tra le varie ragioni di questa convinzione c'è la tendenza di Ibn Māǧid a usare superlativi, tra cui kamalān (ottimamente); ciò è all'origine di varie sviste. Così, quando Ibn Māǧid, doppiando le Laccadive (Fāl o Fālat) e basandosi sul fatto che gli imperativi stagionali fanno sì che in una data epoca non bisogna doppiarle troppo al largo, scrive: "non lasciar cadere la Stella Polare e [se necessario] vira verso nord, non ci si allontana certo [verso sud] di 3 kamalān [leggere 'forte']", il termine 'forte' (kamalān) appare ambiguo; Ibn Māǧid l'aveva utilizzato in precedenza, nelle opere in versi; 'forte' e 'debole' sono espressi di solito in modo diverso.
Quanto all'astrolabio propriamente detto, alcuni affermano che era in uso presso i navigatori arabi che si basavano soltanto sull'altezza quantificata (in gradi arrotondati), detta 'presa con l'astrolabio'. Ibn Māǧid cita alcune coordinate in gradi, ma le aveva tratte dai libri di geografia. Dal canto suo al-Mahrī fornisce alcune altezze in dita prese con lo 'strumento munito di divisioni'. Tuttavia, considerate migliaia di altezze in dita prese con i legni, è evidente che lo strumento di misura usuale non era l'astrolabio. Anche il quadrante ‒ altro cerchio, o frazione di cerchio, suddiviso in parti uguali ‒ figura tra gli strumenti menzionati nei testi.
Il calendario e le istruzioni nautiche
Nei mari ad accentuato regime stagionale la navigazione dipende del tutto dalle stagioni. Come determinare precisamente un dato primo giorno nell'anno solare, se le stelle subiscono una precessione rispetto al Sole?
Nella realizzazione del calendario l'umanità ha dovuto affrontare difficoltà tali da dover attendere la riforma gregoriana della fine del XVI sec. per trovare soluzioni accettabili. Vediamo a che punto erano, un secolo prima, i navigatori dell'Oceano Indiano.
Secondo il computo che si trova nei manoscritti nautici, si determinava l'inizio dell'anno ‒ primo giorno di nawrūz (o nayrūz o nīrūz) ‒ a partire dalla comparsa all'alba della casa della Corona (nella Bilancia) in una declinazione di 15°. Questo primo nīrūz cadeva intorno all'attuale 20 novembre. Le difficoltà di compilare un calendario invariante hanno inizio qui, perché questo 'anno variabile' che cominciava al nīrūz constava di 365 giorni interi; gli anni bisestili non rientravano dunque nel computo. Il primo giorno di nīrūz si spostava pertanto di più di tre mesi in quattro o cinque secoli; e ricordiamo che i grandi astronomi arabi scrivono a partire dal IX secolo. Di fronte all'ampiezza di questo scarto, lo spostamento dovuto alla precessione diventa trascurabile. Comunque, questo rapido computo era utilizzato al tempo di Ibn Māǧid e continuò a esserlo nell'Oceano Indiano, sebbene in forma diversa da una regione all'altra, senza fondarsi più sulla Corona.
Una seconda difficoltà consisteva nel fatto che la comparsa di una stella varia in funzione della latitudine e della declinazione, fenomeno del quale Ibn Māǧid era al corrente. Gli astronomi dei 'grandi libri', come egli li chiama, osservavano ogni alba e ogni tramonto eliaco senza tenere conto della declinazione, come se operassero all'equatore, mentre l'osservazione aveva luogo sopra 25° N. Nei manoscritti nautici le loro testimonianze relative alle case lunari sono copiate quasi esattamente, giorno per giorno. Verso la fine del XV sec., a 15° N, la stella α della Bilancia sorgeva effettivamente verso il 20 novembre attuale, e un navigatore come Ibn Māǧid, che scrutava con assiduità la volta stellata, poteva benissimo averlo notato. Poiché tutto ciò è in accordo, a meno di una decina di giorni, con le affermazioni avanzate nel X sec., egli sarà tentato di relativizzare il fenomeno: "succede che si dica che la data dei viaggi ritardi di un grado l'anno". Al-Mahrī, tuttavia, vede la questione diversamente: "evolve di un quarto di giro l'anno", una nuova dimostrazione della differenza di carattere dei due.
Di fronte a queste irregolarità, più o meno ben percepite, di un calendario fondato su una sola stella, ci si può chiedere quale fosse il comportamento dei marinai dell'epoca. Se si tiene conto, da un lato, dell'eredità tecnica caduta rapidamente in disuso presso i marinai di oggi, e dall'altro lato della pratica, molto frequente, di riunioni di tipo 'seminariale' tenute dai capitani a bordo delle proprie imbarcazioni o presso sensali nel corso delle quali ci si scambiavano informazioni di ogni genere, si può avanzare l'idea di un consenso che, intorno al 1450, richiedeva che si salpasse da una certa regione verso un'altra in certe date al nīrūz, quasi sempre con una tolleranza di dieci giorni, raramente di cinque. Alcuni lustri più tardi, dopo varie esperienze su determinate rotte, confronti in riunioni e sotto l'autorità di timonieri di fama, si applicavano a poco a poco correzioni da cinque a dieci giorni a quanto precedentemente convenuto, fino a una revisione globale, da cui il passaggio agli errori attuali. Un consenso che ricalcava il calendario dei viaggi su quello dei monsoni. Il termine stesso di monsone, di origine araba, implica un'idea di periodicità stagionale: le date dei viaggi si chiamavano infatti mawāsim (stagioni).
La suddivisione in periodi dei venti caratteristici avviene ovviamente in nīrūz. L'inventario dei periodi di viaggio inseriti in questa suddivisione elementare è in realtà molto complicato. Lo schema che segue tiene conto di numerosi microclimi che possono implicare un'inversione dello schema e anche la soppressione della chiusura del mare (ġalaq al-baḥr). Può inoltre accadere che un testo parli di un vento non coerente con un luogo o una stagione; la comprensione di questi passi dipende anche dal significato che i termini utilizzati hanno in una località specifica.
La chiusura del mare è la stagione in cui non si naviga e si resta, per quanto possibile, in famiglia nel porto in cui si arma l'imbarcazione. Dall'inizio di giugno a metà agosto si scatena il monsone di sud-ovest. Sulle carte stagionali attuali, una delle curve che riportano la forza del vento presenta, per luglio e all'est di Socotra, una forma allungata che delimita la zona più fortemente spazzata dal vento (il 'fagiolo' dei marinai francesi); zona che le imbarcazioni di debole potenza che fanno rotta verso ovest devono evitare. La stagione del monsone di sud-ovest, il monsone stesso e i suoi numerosi derivati costituiscono i kaws, anche se il termine equivalente, dabūr o dabbūr, si applica in particolare al vento stesso.
Con la fine della chiusura del mare, nel periodo tra agosto e settembre, comincia la grande stagione (al-mawsim al-kabīr) quasi ovunque esente da cattivo tempo. Essa comprende l'ultimo periodo dei venti di sud-ovest, favorevole alla navigazione (damanī o dimanī), tutto il monsone di nord-est (aziyab o saba) da ottobre ad aprile, e infine l'inizio del monsone di sud-ovest, detto inizio (o testa) di kaws, o fine della (grande) stagione (anwal, ra᾽s al-kaws o āḫir al-mawsim al-kabīr), anch'esso favorevole alla navigazione da fine aprile a fine maggio; dopodiché è impossibile navigare.
Mentre oggi l'espressione 'istruzioni nautiche' si riferisce a un documento essenziale della biblioteca del navigatore, che raccoglie tutte le informazioni utili in mare che non riguardano le carte e le misurazioni, gli scritti di Ibn Māǧid e di al-Mahrī ‒ raccolte complessive di indicazioni e consigli ai marinai riguardanti i loro mari ‒ costituivano, assieme agli strumenti descritti e alla loro esperienza, i soli ausili alla navigazione effettivamente utilizzabili. Il paragrafo seguente è quindi un'esposizione, centrata sui problemi più importanti che si presentano in mare, delle istruzioni nautiche essenziali di cui disponevano i marinai arabi nel XVI sec. nell'Oceano Indiano.
Le tecniche del punto in mare secondo la stima e l'osservazione astronomica
Il punto, o più precisamente la posizione dell'imbarcazione in mare, dipende dal percorso stimato, rettificato appena possibile dalla misura dell'altezza di astri noti e osservabili, il tutto in riferimento alle istruzioni nautiche e all'esperienza dell'ufficiale di rotta, per il quale contano la rotta, la velocità effettiva stimata e l'altezza degli astri. Come abbiamo visto, la distanza era calcolata in zam; per questo motivo, i passi dei manoscritti di Ibn Māǧid e al-Mahrī più importanti per i naviganti riguardano la precisione della rotta e l'altezza delle stelle.
Ricordiamo ancora che, fino a quando non fu commercializzato il cronometro ‒ strumento affidabile in tutti i climi e per lunghi periodi ‒ cioè soltanto da circa 150 anni, i marinai potevano osservare abitualmente soltanto la latitudine. Sicuramente, procedimenti basati sulla misurazione della distanza della Luna sulla volta celeste da certe stelle e sull'uso di tavole di tali distanze a seconda dell'epoca dell'anno consentivano di valutare la longitudine, anche in mare, ma si richiedevano conoscenze che non erano alla portata della maggior parte dei navigatori.
Nella navigazione araba, effettuata principalmente tra coste orientate grosso modo a nord, la conoscenza della longitudine non poteva essere che approssimativa, senza seri inconvenienti; non ne parleremo dunque più, se non occasionalmente. Tuttavia è chiaro che coordinare una latitudine osservata con una longitudine stimata a distanza rappresentava già, dal punto di vista tecnico, un'impresa di non poco conto.
La precisione della rotta
La questione della precisione con cui si teneva la rotta su lunghi tragitti era legata a contingenze di ordine pratico. In realtà non c'era precisione e la suddivisione più fine della rosa in rombi (quella che si ha nell'Oceano Indiano) non superava 2°. Ibn Māǧid sembra parlare di una navigazione di lungo corso a 1/4 di rombo, cioè con una precisione di poco inferiore a 3°. Enumera i vari tipi di rotta: costiera, diretta al largo e quella che chiama 'per deduzione' (in confronto a un'altra supposta corretta). Si mostra critico riguardo alle distanze stimate ammesse dagli Antichi, le tirfa.
Un'imbarcazione va in direzione sud-est (SE), da Mascate a Aden [fino a] lasciare 4 zam tra essa e lo scoglio a nord delle Laccadive […] la rotta di una seconda imbarcazione che vuole raggiungere questa scogliera si trova a 4/7 di rombo tra SE e SE1/4E [in realtà da SE1/4E verso SE: Ibn Māǧid fa spesso queste approssimazioni], e raggiunge la scogliera dopo un percorso di 7 tirfa e avrà navigato [oltre al primo] 28/7 di 4 zam […] perciò le tirfa sono errate […] in quanto, in un percorso come nell'altro, le distanze sono pari a 117 zam […].
La spiegazione che diamo di questo passo, un po' ellittico ma importante, è la seguente: la rotta sud-est porta effettivamente a 4 zam (48 miglia) dallo scoglio, di cui si suppone di conoscere la latitudine, a 5 dita, così come Mascate è a 12 dita, perché 12−5=7. Per la seconda imbarcazione, la rotta sarebbe piuttosto a 6/8 di rombo (8;26°), senza le approssimazioni che Ibn Māǧid è solito fare; ma prendiamo piuttosto 5/7. Le due imbarcazioni hanno percorso 7 tirfa; se la tirfa di sud-est è di 16 zam e quella di SE1/4E di 18 zam, la differenza è di 2 zam. Per calcolare il percorso supplementare della seconda, Ibn Māǧid fa la proporzione di questa differenza con 2/7(7/7−5/7=2/7), che dà 2×7×2/7=28/7, cioè 4 zam (il testo citato dice tuttavia '28/7 di 4 zam'; la ragione per la quale sembra necessario correggerlo è la seguente: l'originale riportava probabilmente a῾nī arba῾a e il copista ha trascritto ῾an arba῾a, poi, per farlo quadrare con i 28/7, pensò che la proporzione non poteva essere che 4/7 ‒ e non 5/7 o meglio 6/8 ‒, valore che moltiplicato per 7 tirfa dà effettivamente 28/7).
La verifica si effettua facilmente a partire dai due rombi, per il percorso supplementare della seconda imbarcazione, sia sottraendo dal percorso SE1/4E i 5/7 della differenza tra i due percorsi (18−16=2; 2×7×5/7=10; 126−10=116), sia aggiungendo al percorso della prima i 2/7 di 14, cioè 4, che sommato a 112 dà ancora 116. Resta da spiegare il valore di 117 che dà il testo, valore comune ai due percorsi. Ora, il primo è senz'altro 112+4, e il calcolo precedente lo conferma. Si tratta dunque di un nuovo passaggio da 16 a 17 nella copia? Comunque sia, a meno di uno zam, la dimostrazione di Ibn Māǧid è corretta.
Osserviamo per concludere che nessun timoniere avrebbe osato fare rotta direttamente su questo enorme e temibile scoglio che affiora invisibile dai fondali insondabili, dove un portoghese si era perso con tutto il carico di persone e cose durante il suo secondo viaggio. Ibn Māǧid non si preoccupa nemmeno di mettere in guardia i naviganti. In circostanze analoghe anche al-Mahrī parla di quinti di rombo, ma in totale i due autori non fanno riferimento a più di quattro esempi di questo genere. Per questo è difficile affermare, sulla base di tali argomenti, che le suddivisioni fini fossero realmente operative sulle rotte oceaniche.
In compenso, nel caso di mare chiuso, possiamo citare un esempio tratto da Ibn Māǧid, dove accadeva effettivamente che si navigasse al quarto di rombo: nel Mar Rosso, al termine di una o l'altra delle varie rotte seguite scendendo da Gedda a Siban (alias Jebel Tir), picco che dall'alto dei suoi 245 metri domina la zona in cui si trova ed è circondato da fondali scoscesi (fig. 11). Ora, nel Mar Rosso, i banchi di scogli più o meno fitti si estendono molto al largo; lungo la costa araba sorgono da fondali molto profondi, mentre lungo la costa 'straniera' sono spesso preceduti da fondali accessibili.
Risalendo, i marinai cercavano nondimeno riposo sulle coste arabe; la sera, infatti, gli scogli si vedono meglio grazie al Sole al tramonto, anche se radente. Inoltre, i venti laschi durante la risalita subiscono inversioni frequenti, mentre quando si scende il vento soffia in modo meno irregolare; è questo probabilmente il motivo per cui Ibn Māǧid moltiplica le altezze degli astri durante la risalita e ne dà solo raramente durante la discesa.
Alcune di queste rotte terminavano a ovest di Siban. Ma dopo un percorso di più di 300 miglia a partire da Gedda, cioè grosso modo dopo i 17° (intorno a 7 dita e 1/2 di altezza massima della Stella Polare) la prudenza è di rigore: dove siamo in longitudine? La mappa nella fig. 11 mostra i fondali che si possono sondare intorno alle Dahlak, sui quali si distinguono appena, qua e là, scogli bassi coperti di sabbia e raramente di vegetazione. Sapendo che la rotta è verso SE1/4S, Ibn Māǧid consiglia allora, se la sonda risponde segnalando uno scadere verso ovest, di tenersi tra 35 e 24 m di profondità, se necessario "piegando verso SE di 1/4, 1/3 o 1/2 di rombo". Con la manovra descritta si era sicuri di tenersi al largo dagli scogli che affioravano in superficie. Infine, evitando i pericoli della costa araba e, in assenza di mede, orientandosi verso Huatib e Hajouat per mezzo dei fondali scandagliabili, essi si ingegnavano a non mancare la meda straordinaria costituita da Siban, prima di affrontare altri pericoli a sud.
In conclusione, l'esempio della rotta, una pura visione della mente, in direzione del temuto scoglio delle Fāl (Laccadive), come quello delle contingenze immediate da trattare con abilità nel Mar Rosso, corroborano l'ipotesi di una disposizione della bussola che permette una tenuta effettiva di un quarto di rombo.
L'altezza delle stelle
Poiché nella navigazione stimata la posizione dell'imbarcazione viene generalmente controllata riferendosi all'altezza delle stelle citate nelle 'istruzioni nautiche', queste altezze svolgono un ruolo centrale nei manoscritti nautici arabi.
a) Osservazioni preliminari. Sembra opportuno sottolineare i seguenti quattro punti. Se le coordinate eclittiche delle stelle sono considerate fisse, e grosso modo lo sono, in compenso le coordinate equatoriali, le sole che servono per l'osservazione della latitudine, sono instabili. L'evoluzione di queste ultime, tuttavia, è molto lenta (dell'ordine di 15′ in 40 anni), e si comprende come non sia stata notata dai navigatori dell'epoca. Inoltre, i marinai arabi utilizzavano soltanto le stelle, proprio in ragione della loro fissità; insieme alla semplice identificazione degli astri, una lunga esperienza (aiutata, in caso di perdita del giornale di bordo, dalla memoria prodigiosa che si sviluppa a contatto permanente con la Natura) era sufficiente a questi autentici marinai di lungo corso. Per di più, al di là delle esigenze scientifiche, le effemeridi impiegate attualmente dai marinai si situano ancora, per la semplicità dei calcoli, in un Universo geocentrico, e ciò ci permette di ricostruire facilmente i procedimenti dei marinai di una volta. Infine, nella misurazione delle altezze delle stelle alla metà del XVI sec. occorre tenere conto della relativa mancanza di precisione degli strumenti, dell'instabilità della piattaforma e dell'assenza di correzioni (rifrazione, ecc.).
Per entrare un po' nella mentalità di questi marinai, relativamente alla navigazione d'alto mare ‒ "quelle tali stelle sono alla tale altezza e dunque mi trovo nel tal punto" ‒, occorre fare ricorso al notevole senso empirico insito nei mezzi rudimentali dei quali allora si disponeva; gli Spagnoli chiamano ancora el pratico il pilota che prende la guida di una nave nei punti delicati.
b) Le altezze accoppiate. Sui legni, che allora costituivano il solo strumento d'uso corrente, non si superavano le 12 dita, e non si scendeva quasi mai al di sotto delle 3; i marinai avevano scoperto effetti anormali, dovuti alla rifrazione, ad altezze molto basse, come afferma Ibn Māǧid: "non c'è niente di buono se una stella è bassa sull'acqua". La scala delle altezze meridiane delle stelle era perciò molto compressa. Per ovviarvi, i marinai avevano notato che, a una data altezza di riferimento alla latitudine L definita dall'altezza meridiana di una data stella a, accadeva che due stelle, per esempio b e c, si trovassero in un certo istante a una stessa altezza h.
Nel caso più frequente, c tramonta e b sorge; ma potevano anche sorgere entrambe, b e d, o tramontare, c ed e; d'altra parte, anche le loro declinazioni avevano un ruolo, e portavano lo stesso nome, b e d, b ed e, ecc. Si diceva che si trovavano "su un solo legno o in uguaglianza [i῾tidāl]", ma si usavano anche altre espressioni, sinonimi esatti o con qualche sfumatura di significato, secondo le situazioni in cui ci si trovava e che erano molto diverse.
Se da un lato la resa delle osservazioni meridiane è teoricamente del 100%, dall'altro quella degli accoppiamenti va da 0 a 100, ciò dipende dalla declinazione e dall'azimut delle stelle considerate. Il senso empirico di Ibn Māǧid, il "primario", sembra averlo condotto a un notevole acume al riguardo; infatti, egli integra spesso gli accoppiamenti di stelle con proporzioni che sembrano implicare un certo grado di precisione. Al contrario, al-Mahrī, in modo piuttosto singolare, non si è accorto di questo fatto evidente, e si è limitato a dire in proposito quanto segue: "La presa dell'altezza è tanto più soddisfacente quanto più la stella osservata è al meridiano al momento dell'osservazione; il motivo di questa maggior precisione sta nel fatto che allora vi è perfezionamento [rifinitura, interruzione], né aumento né diminuizione […] al contrario delle misure a lato (del meridiano), incerte in ragione della rapidità del loro corso".
Effettivamente, la relativa stabilità momentanea di una stella in culminazione, anche nelle regioni equatoriali, permette un'osservazione più sicura che non la rapidità ascensionale di astri molto distanti dal meridiano. L'elenco delle stelle raccomandate da al-Mahrī comprende nove posizioni; nei quattro meridiani egli rivendica la paternità di quella di α Pavonis, valida durante il monsone occidentale che comporta tre mesi di chiusura del mare. Le coppie sono β e γ dell'Orsa Minore, ε e ζ dell'Orsa Maggiore, α e β Centauri e Canopo-Achernar; ma le altezze non concordano da un testo all'altro.
Secondo le sue abitudini, Ibn Māǧid non propone un elenco coerente di accoppiamenti. Soltanto una verifica volta per volta permette di estrarre dai manoscritti un inventario di una sessantina di coppie, con alcuni doppioni. Bisogna poi impegnarsi in un lavoro notevole: ottenere il valore di ciascuna coppia e poi controllare matematicamente questi valori. Nel seguito ci limiteremo a cogliere le grandi linee degli accoppiamenti, per poi enunciare i risultati del controllo matematico, e valutare quindi, dopo averne descritte le tecniche, quali garanzie venivano offerte.
La presenza nella Ḥāwiya ‒ scritta da Ibn Māǧid in gioventù, sempre che sia integralmente una sua opera ‒ di numerose coppie (oltre alle classiche stelle delle due Orse si trovano α e β Centauri, Vega-Sirio, Achernar, α-Fenice, Achernar-Vega) fa pensare che sia stato lui a inaugurare questo modo di procedere, dedicandosi poi accanitamente a svilupparlo, anche se in modo frammentario e a volte esoterico. Sono pochi, infine, gli accoppiamenti che coprono una gamma estesa di latitudini e che sono accompagnati da considerazioni relative ai periodi favorevoli ai viaggi e alle osservazioni.
Schematicamente, si riconoscono i seguenti tre tipi di accoppiamento. (1) Uno degli astri è vicino al meridiano, l'altro ne è distante e la sua velocità ascensionale sostituisce l'ora locale all'istante voluto, in quanto la lentezza del compagno implica una certa attesa. Il tipo è quello del "bastone, o appoggio, dei capitani" (῾asā o ukkāz al-rabbābīn): Achernar non lontano dal meridiano e Sirio lontano dall'azimut. La fascia di latitudine va da 25;36° a 19° N, poi scende in 'immobilizzazione' di una delle stelle (il procedimento di integrazione è descritto più avanti). I passaggi che riguardano la coppia non presentano grandi difficoltà a condizione di essere al corrente dei diversi nomi delle stelle, delle situazioni geografiche e di avere familiarità con lo stile di Ibn Māǧid. Altrove, astrolabio alla mano (in gradi interi), egli dà l'uguaglianza della Capra e di Canopo. (2) Le due stelle sono in una declinazione qualunque; è raro tuttavia che una di esse si trovi a meno di 45° e l'altra resti qualunque. Il modello è dato dalla Grande Solitaria (al-fard al-kabīr), ζ dell'Orsa Maggiore e α dell'Ariete. L'analisi di questa coppia comporta molte difficoltà. I risultati sono eccellenti durante il monsone dell'est tra 19° e 14;30°, e durante il monsone dell'ovest tra 18° e 24° N. Si superano allora 20′ di approssimazione per raggiungere perfino 1;30°, e ciò è aberrante. Ibn Māǧid riporta il valore di questa coppia in tutto il mondo, perfino nel 'mare dei Rūm' (il Mediterraneo). Altrove si accontenta di definirlo come 'scarso' nel paese di Zanǧ, e come 'grande' a latitudini maggiori. Ma perché non dice nulla di questa coppia nei viaggi in Malacca, in cui si doppiava Ceylon molto al largo, e nemmeno all'altezza della Somalia, come l'abbiamo visto fare a proposito dei bachi che transitavano da quelle parti? (3) Si tratta piuttosto di una variante dei due casi precedenti, denominata 'immobilizzazione' (qayyid), abbastanza originale da meritare un esame a parte. Accade che l'ora del gemellaggio comporta un'impossibilità di osservare, per esempio quando si verifica di giorno. Ibn Māǧid vi pone rimedio riconoscendo a una coppia delle disuguaglianze tali che si osserva una delle stelle a una data altezza, sempre la stessa, in qualche modo immobilizzata lungo una fascia di latitudine all'interno della quale la compagna segue una gradazione molto grande.
Occorre segnalare in Ibn Māǧid la nozione di 'permutazione' (ibdāl). Nell'utilizzare coppie le cui differenze di ascensione retta sono prossime a 12 ore ‒ ne fa parte la Grande Solitaria ‒, queste stelle, che si trovano su meridiani quasi opposti, ritrovano di nuovo l'uguaglianza dell'altezza circa 12 ore più tardi. Beninteso, la seconda volta tale uguaglianza è diversa dalla prima; il fenomeno non ha luogo nel corso di una stessa notte, salvo a latitudini maggiori in inverno, ma questi marinai non facevano mai osservazioni oltre 25° N o S. Questa particolarità della permutazione ha per applicazione quella di favorire l'entrata in gioco dell''immobilizzazione'.
Per terminare chiediamoci se Ibn Māǧid abbia colto la relazione tra errori di posizione ed efficacia degli accoppiamenti. Se nulla ci autorizza ad affermarlo, resta il fatto che, in una parte delle caratteristiche (ḍarā᾽ib, cioè rendimento) delle quali precisa per ogni coppia la "disposizione" (tartīb), è andato spesso vicino alla verità: "cambiando latitudine, l'altezza di tale coppia, o della compagna dell'immobilizzata, evolve di frazioni di dito per ogni dito intero di meridiano". Ma i margini di latitudine non erano forse troppo stretti perché potessero rivelargli delle instabilità in qualche coppia?
c) Coordinamento tra misura delle altezze e lettura della carta. Non era sempre facile; diamone due esempi estremi. Scendendo verso sud, che doveva già trovarsi in basso nella carta perché era detto sāfil (basso, appunto), la saldatura tra i riferimenti alla Stella Polare e alla coppia β e γ dell'Orsa Minore è perfetta. In compenso, il ponte tra queste ed ε e ζ dell'Orsa Maggiore dava luogo a una controversia che aveva una sua giustificazione. La discordanza tra osservazioni astronomiche e disegno della carta era piuttosto ampia, in particolare per il Sud del Madagascar e le isole Mascarene, con l'eccezione delle Comore, indicate in modo molto preciso. Questo significa che la navigazione degli Arabi si era interrotta, come era avvenuto per Malacca verso est o Gedda verso nord? I marinai arabi raggiungevano tuttavia Sofala in vari modi. Su una delle rotte lungo costa si vivono intensamente, con Ibn Māǧid, i tormenti dei navigatori, vittime di correnti violente "come a Cambay" nelle acque agitate e pericolosamente basse vicino all'immenso delta dello Zambesi. Quanto alla rotta di altura, si bordeggiava dapprima verso sud-sudest prima di virare fino all'altezza di Mambone-Chiluan, rotta esatta a meno di 20′.
Queste inesattezze casuali contrastano con la precisione di Ibn Māǧid riguardo alle altezze misurate per mezzo della Croce del Sud nel Mar Rosso. Una di queste è di particolare interesse. È innanzitutto un esempio unico di equivalenza con la Stella Polare (7,25 dita); sono due meridiane uguali e opposte, che danno i valori 16;33° e 16;36° N, cifre sorprendentemente vicine. Inoltre, essa dà la posizione di due scogli traditori in una serie corallina al largo delle Farasan, sulla quale le carte attuali sono incerte. Sarebbe curioso vederne precisato uno dei punti grazie a un documento del XV secolo. Ammirevole solidarietà dei marinai di ogni tempo!
Questi studi e riflessioni sparsi su documenti singolarmente privi anch'essi di una coerenza complessiva non hanno la pretesa di fare il punto sulla scienza nautica araba nell'Oceano Indiano intorno al 1500. Come abbiamo accennato, restano ancora da scoprire, interpretare e utilizzare numerose fonti, sparse negli archivi dei paesi che hanno avuto un ruolo nella complessa storia della navigazione nell'Oceano Indiano. Le pagine precedenti rappresentano soltanto un modesto contributo a un più ampio sforzo collettivo, che non avrà mai lo scopo di arricchire l'odierna scienza della navigazione perché siamo ormai entrati senza ritorno in un'altra dimensione, quella della navigazione assistita dall'elettronica. Il nostro contributo non sarà allora soltanto un addio nostalgico dei marinai del sestante e del compasso ai loro predecessori della bussola e dei legni? Un ultimo segno di complicità tra marinai della plancia, prima di cedere il passo agli oscuri accoliti delle centrali operative? Pensarla così significherebbe offendere pesantemente i due marinai, Ibn Māǧid e al-Mahrī (uno certo più 'marinaio' dell'altro), che abbiamo imparato ad apprezzare malgrado i difetti, che anzi ce li fanno sentire più vicini. E vorrebbe anche dire dimenticare che essi erano gli eredi, a dispetto delle inesattezze 'scientifiche', di una prestigiosa tradizione secolare di rigore del pensiero, come testimonia anche il presente studio.
Bibliografia
Ahmad 1947: Ahmad, Nafis, Muslim contribution to geography, Lahore, Ashraf, 1947.
de Albuquerque 1972: de Albuquerque, Luis, Quelques commentaires sur la navigation orientale, Paris, Fondation C. Gulbenkian, 1972.
Aubin 1972: Aubin, Jean, Quelques remarques sur l'étude de l'Océan Indien au XVIe siècle, Coimbra, Junta de Investigações do Ultramar, 1972.
Bagrow 1951: Bagrow, Leo, Die Geschichte der Kartographie, Berlin, Safari, 1951.
‒ 1955: Bagrow, Leo, A tale from the Bosphorus, "Imago Mundi", 12, 1955, pp. 25-29.
Chumovski 1957: Chumovski, Teodor A., Ṯalāṯ rāḥmanaǧāt li-Aḥmad ibn Māǧid, Mosca-Leningrado, 1957.
Ferrand 1921-28: Instructions nautiques et routiers arabes et portugais des XVe et XVIe siècles, reproduits, traduits et annotés par Gabriel Ferrand, Paris, Geuthner, 1921-1928, 3 v.
‒ 1924: Ferrand, Gabriel, L'élément persan dans les textes nautiques arabes des XVe et XVIe siècles, Paris, Imprimerie Nationale, 1924.
Grosset-Grange 1972: Grosset-Grange, Henri, Noms d'étoiles, quelques termes particuliers, "Arabica", 19, 1972, pp. 240-245.
‒ 1973: Grosset-Grange, Henri, Analyse des voyages d'Inde à Malacca, "Navigation", 81, 1973, pp. 97-109.
‒ 1976: Grosset-Grange, Henri, Une carte nautique arabe, "Acta geographica", 27, 1976, pp. 33-46.
‒ 1977: Grosset-Grange, Henri, Noms d'étoiles, quelques termes particuliers, "Arabica", 24, 1977, pp. 42-46.
‒ 1977-79: Grosset-Grange, Henri, La science nautique arabe, "Jeune Marine", 1977-1979, 16-21, 23-29.
‒ 1978: Grosset-Grange, Henri, La côte africaine dans les routiers nautiques arabes, "Azania", 13, 1978, pp. 1-17.
‒ 1979: Grosset-Grange, Henri, Noms d'étoiles, quelques termes particuliers, "Arabica", 26, 1979, pp. 90-98.
‒ 1993: Grosset-Grange, Henri, Glossaire nautique arabe ancien et moderne de l'Océan Indien, Paris, CTHS, 1993.
Kammerer 1936: Le routier de Dom Joam de Castro: l'exploration de la mer Rouge par les Portugais en 1541, traduit du portugais d'après le ms. du British Museum, avec introduction et notes par Albert Kammerer, Paris, Geuthner, 1936.
Khoury 1971a: Ibn Māǧid, Kitāb al-Fawā᾽id, édité par I. Khoury, Damasco, Académie Arabe de Damas, 1971.
‒ 1971b: Ibn Māǧid, Al-Ḥāwiya, présenté et édité par I. Khoury, "Bulletin d'études orientales", 1971.
Kunitzsch 1967: Kunitzsch, Paul, Zur Stellung der Nautikertexte innerhalb der Sternnomenklatur der Araber, "Der Islam", 43, 1967, p. 53 e segg.
‒ 1969: Kunitzsch, Paul, Zur Stellung der Nautikertexte innerhalb der Sternnomenklatur der Araber, "Der Islam", 56, 1969, p. 305 e segg.
Serjeant 1963: Serjeant, Robert B., The Portuguese of the South Arabian Coast, Oxford, Clarendon, 1963.
Sihab 1982: Šihāb, H.S., Fann al-milāḥa ῾inda 'l-῾Arab, Beirut, 1982.
‒ 1983: Šihāb, H.S., al-Dalīl al-baḥrī ῾inda 'l-῾Arab, Kuwait, 1983.
‒ 1984: Šihāb, H.S., Ṭuruq al-milāḥa al-taqlīdiyya fī 'l-Ḫalīǧ al-῾Arabī, Kuwait, 1984.
Tibbetts 1971: Tibbetts, Gerald R., Arab navigation in the Indian Ocean before the coming of the Portuguese, London, Luzac, 1971.
Villiers 1966: Villiers, Alan J., Sons of Sinbad. An account of sailing with the Arabs in their dhows, in the Red Sea, around the coasts of Arabia, and to Zanzibar and Tanganyika, pearling in the Persian gulf, and the life of the shipmasters, the mariners and merchants of Kuwait, Portway-Bath, Cedric Chivers, 1966 (1. ed.: London, Hodder & Stoughton, 1940).