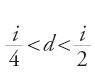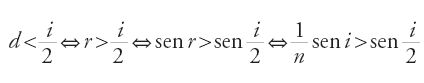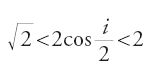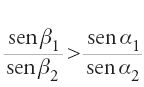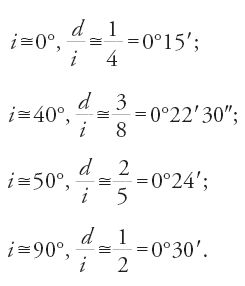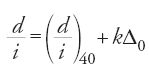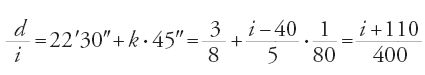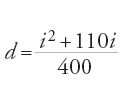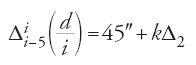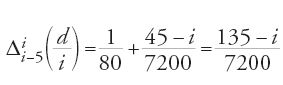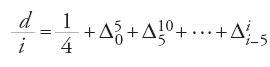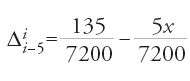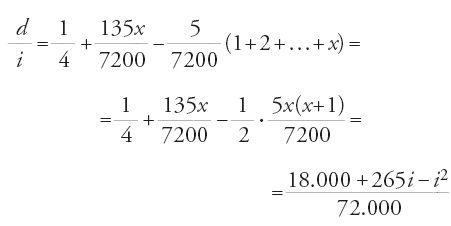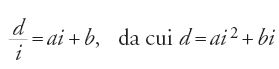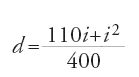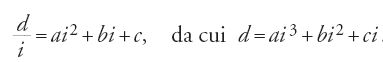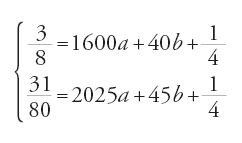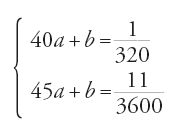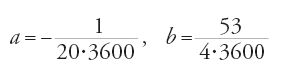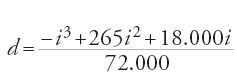La civiltà islamica: teoria fisica, metodo sperimentale e conoscenza approssimata. Specchi ustori, anaclastica e diottrica
La civilta islamica: teoria fisica, metodo sperimentale e conoscenza approssimata. Specchi ustori, anaclastica e diottrica
Specchi ustori, anaclastica e diottrica
Esiste una particolare classe di oggetti di interesse scientifico nella quale theōría e téchnai si trovano intrecciate. Se si vuole descrivere qualcuno di questi oggetti non basta pertanto fare appello ai concetti e alle loro relazioni, ma occorre anche illustrare i procedimenti tecnici necessari alla sua fabbricazione. Allo storico della scienza deve quindi accompagnarsi lo storico della tecnica. Le cose si complicano se gli oggetti appartengono a un passato lontano, se la loro origine si perde agli albori dell'astronomia, della geometria e della statica. È il caso di meridiane, astrolabi, leve, bilance, mesolabi, specchi ustori e altri strumenti matematici costruiti dai geometri e dagli ingegneri dell'Antichità. Si tratta di strumenti di pertinenza della matematica applicata che si presentano come oggetti tecnici a scopo pratico e socialmente utili. Poco importa se questa utilità è reale o è dovuta piuttosto all'immaginario sociale: in entrambi i casi attribuisce all'oggetto geometrico-tecnico una finalità che va oltre le conoscenze che rappresenta. L'astrolabio, per esempio, non si riduce né alle conoscenze di astronomia sulle quali si basa, né ai procedimenti utilizzati dall'artigiano per costruirlo; esso comprende sia la reale utilità che ha per l'astronomo, sia quella congetturata dall'astrologo e dal medico. È da questa molteplice utilità che nasce la domanda sociale per l'istituzione della professione di 'astrolabista' riconosciuta da storici e biobibliografi del IX e X secolo.
Astrolabi, specchi ustori (che, secondo la tradizione, furono impiegati da Archimede per incendiare le navi romane al largo di Siracusa), lenti, ecc., non furono soltanto oggetti di trasmissione del sapere scientifico, ma anche vettori della sua propagazione. Si impone dunque una riflessione su questa trasmissione, e su come tali strumenti si siano inseriti nelle diverse tradizioni. È quanto faremo ora, dapprima per quanto riguarda gli specchi ustori ‒ dalla trasmissione dei trattati in greco fino alle ricerche di Ibn Sahl (fine del X sec.) e Ibn al-Hayṯam (m. dopo il 1040) ‒, e poi per quanto riguarda le lenti. In tal modo ripercorreremo la via che ha condotto, negli studi di ottica, dalla catottrica all'anaclastica, e da questa alla diottrica.
La ricezione della tradizione greca sugli specchi ustori: dalla geometria delle coniche alla catottrica
Se ci chiediamo cosa poteva significare nel mondo greco uno specchio ustorio (dal latino ustus), la risposta è che era concepito come un órganon, una macchina delicata da costruire e destinata a uso pratico. Questo scopo pratico, vero o presunto, attribuito allo specchio, ha avuto un ruolo importante di stimolo alla ricerca, a partire dal II sec. a.C. almeno, e fino al XVIII sec., richiamando l'attenzione sia di geometri di valore sia di matematici di minor prestigio. D'altra parte, nel corso di queste ricerche, gli specchi ustori hanno posto problemi che per essere risolti hanno richiesto il concorso di conoscenze tecniche e di varie discipline quali la geometria, la catottrica (ossia lo studio dei fenomeni di riflessione dei raggi di luce), e a volte anche l'astronomia. Esamineremo dapprima gli specchi ustori parabolici, passando da Alessandria a Bisanzio, per poi spostarci a Baghdad (dove lavorava Ibn Sahl), al Cairo (la città di Ibn al-Hayṯam, noto anche come Alhazen), e nell'Europa del Sud, cioè nei centri più rinomati per la ricerca scientifica fino al XVII sec. circa.
Lo specchio parabolico
L'opera più antica e più ricca di informazioni sugli specchi ustori a noi pervenuta è quella di Diocle, vissuto dopo Archimede (che cita, assieme al suo corrispondente Dositeo, compagno di Conone di Alessandria). L'esame congiunto di varie testimonianze e del suo lessico suggerisce che egli appartenesse alla generazione degli 'archimedei' e vivesse a cavallo fra il III e il II sec. a.C. Le sue ricerche non si iscrivono nella tradizione di Apollonio, suo contemporaneo, ma in quella di Conone e di Archimede.
La sua opera Kitāb fī 'l-marāyā al-muḥriqa (Sugli specchi ustori), che ci è pervenuta soltanto nella versione araba, comincia con un gruppo di proposizioni che trattano degli specchi ustori parabolici (propp. 1, 4 e 5) e sferici (propp. 2 e 3), i due tipi di specchi che interessavano particolarmente agli autori antichi. L'introduzione dell'opera fornisce le prime importanti informazioni sulle conoscenze relative agli specchi parabolici possedute nel II sec. a.C. Diocle riferisce dell'esistenza di un'importante tradizione di ricerca risalente alla Scuola di Conone e ad altri in contatto epistolare con Archimede; tradizione di cui avrebbero fatto parte matematici come Dositeo e astronomi come Ippodamo (quest'ultimo non è stato ancora identificato). Ci informa, inoltre, che in numerose città questi specchi erano usati per accendere fuochi nei templi in occasione di particolari feste, o per far funzionare certi gnomoni, ricordando che fu Ippodamo a porre il problema ‒ in seguito risolto da Dositeo ‒ di determinare la forma dello specchio in modo che i raggi solari si riflettessero in un unico punto e qui si incendiassero.
Nello studio dello specchio parabolico, Diocle comincia con il dimostrare la proprietà focale della parabola, utilizzando allo scopo le proprietà della sottotangente e della sottonormale.
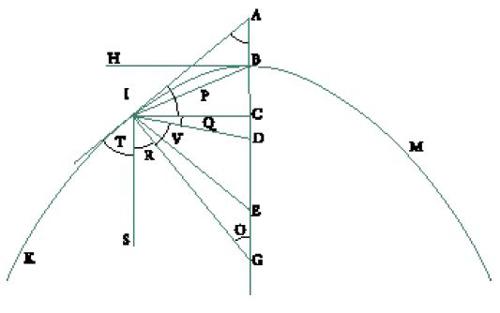
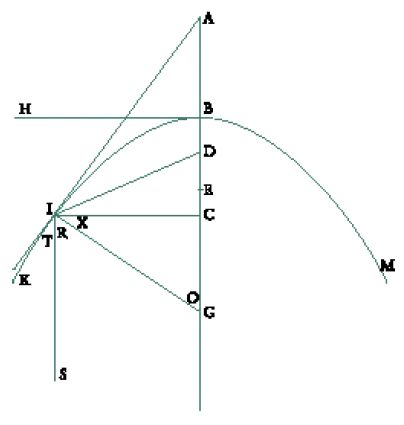
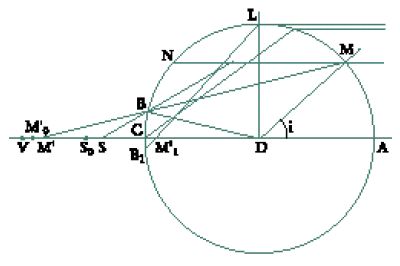
Sia data una parabola di vertice B e di fuoco D, e sia E il punto definito da BE=2BD. Sia I un punto di questa parabola, C la sua proiezione sull'asse, IA e IG rispettivamente la tangente e la normale in I. Allora si ha CB=BA e CG=BE. Diocle dimostra che D è il punto medio di AG, considerando i due casi BC⟨BE (fig. 1) e BC>BE (fig. 2)
Egli dimostra poi che se la superficie interna del paraboloide generato dalla rotazione di un arco della parabola attorno all'asse è riflettente e l'asse è diretto verso il Sole, allora i raggi solari incidenti sullo specchio si riflettono nel fuoco. Per poter costruire tale specchio, Diocle determina quale parabola genera uno specchio parabolico di rotazione in modo tale che i raggi riflessi si incontrino in un punto posto a una data distanza dal centro dello specchio; spiega poi come fabbricare, seguendo questa costruzione, un modello dello specchio. Al tempo di Diocle, e proprio con lui, i matematici avevano dunque iniziato lo studio della proprietà anaclastica della parabola (ossia la caratteristica ottica che riguarda la focalizzazione della luce), messo in evidenza la proprietà 'fuoco-direttrice' e costruito un modello di specchio parabolico su basi geometriche. Tuttavia, se si guarda al di là dei semplici risultati e si cerca di cogliere lo spirito di queste ricerche, ci si accorge che esse rientrano nel quadro della geometria delle coniche. Sono infatti le proprietà anaclastiche delle curve che attirano l'attenzione dei matematici; le conseguenze di queste per l'ottica sono anch'esse rilevanti, ma si tratta di un interesse secondario.
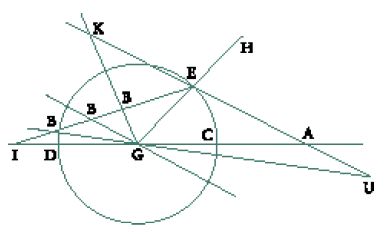
Oltre al testo di Diocle esistono altri due importanti trattati sugli specchi ustori, uno di un certo Dtrūms e l'altro di Antemio (Tav. I).
Dell'autore del primo trattato che, perduto in greco, ci è giunto in arabo, non sappiamo nulla; il nome è palesemente alterato. Se si prova a correggere quello che è probabilmente un errore di trascrizione, si arriva a Dīdūms, cioè Didimo. Comunque, si tratti di Didimo o di qualche altro studioso, l'originale dell'opera è in greco. La parte che riguarda gli specchi ustori consta di sei proposizioni, quattro sugli specchi parabolici e due su quelli sferici. La costruzione dello specchio parabolico si basa su un metodo di costruzione per punti della parabola che, pur relativamente semplice, non si trova, a nostra conoscenza, in nessun altro studio sugli specchi ustori.
Il terzo trattato greco sugli specchi ustori tradotto in arabo è dello scienziato bizantino Antemio di Tralle (VI sec. d.C.); si tratta del più noto, oggi come allora, dei lavori scritti in greco su questo tema, tradotto in arabo più volte nel IX sec.; una di queste versioni è più completa dell'originale greco che sfortunatamente ci è pervenuto mutilo. In questo testo, Antemio studia più tipi di specchi: gli ellissoidali, un sistema di numerosi specchi piani e i parabolici. Per meglio comprendere il contributo di Antemio e le ragioni dell'accoglienza ricevuta, va ricordato che siamo in effetti di fronte a un cambiamento di prospettiva. Questo autore infatti non appartiene, contrariamente ai suoi predecessori, alla tradizione della geometria delle coniche. Egli prende come punto di partenza la leggenda dell'incendio della flotta di Marcello da parte di Archimede durante l'assedio di Siracusa, e vuole stabilirne la veridicità risolvendo il problema di come far giungere i raggi solari in un punto che si trovi a una data distanza. Esamina quindi un certo numero di specchi prima di soffermarsi su quello parabolico e di procedere alla costruzione per punti e tangenti di una parabola di cui sono noti fuoco e direttrice. Complessivamente, il trattato di Antemio si colloca in una prospettiva più di catottrica che di geometria delle coniche; fu questa la prospettiva che s'impose, notevolmente rinforzata, quando la tradizione greca fu trasmessa agli scienziati arabi, assicurando al libro di Antemio una fama che altri scritti non conobbero.
I principali testi greci sugli specchi parabolici furono tradotti in arabo nel IX secolo. Non abbiamo alcuna traccia dell'impatto che ebbero gli studi di Diocle e di Dtrūms; sappiamo invece che l'opera di Antemio fu ampiamente consultata. Essa fu commentata dal filosofo e scienziato al-Kindī (m. 866 ca.), citata ampiamente da Aḥmad ibn ῾Īsā ‒ autore di una raccolta delle opere di ottica di al-Kindī e di Ḥunayn ibn Isḥāq (m. 877) ‒ e fu ripresa integralmente nel trattato di ῾Uṭārid del X secolo. Alla fine del X sec., Ibn Sahl cita la leggenda di Archimede menzionata da Antemio e riprende lo studio dello specchio ellissoidale, mentre Ibn al-Hayṯam, nel suo trattato sullo specchio parabolico, oltre ad Archimede cita soltanto Antemio. Se confrontato con i testi di Diocle e di Dtrūms, lo studio di Antemio appare tuttavia meno rigoroso, una debolezza che non poteva sfuggire a matematici del calibro di Ibn Sahl o di Ibn al-Hayṯam. Il successo del trattato di Antemio era dunque verosimilmente dovuto alla novità di prospettiva che lasciava intravedere in filigrana.
Gli specchi sferici ed ellissoidali
Lo specchio parabolico non è il solo specchio ustorio studiato dai matematici greci. È noto l'interesse per lo specchio sferico espresso nella prop. 30 della Catottrica, opera attribuita a Euclide. Questa proposizione contiene un risultato di natura matematica sullo specchio sferico che Diocle rifiutava, perché riguardante la riflessione su uno specchio sferico concavo, orientato in direzione del Sole, di raggi non paralleli (si suppone infatti, implicitamente, che il Sole sia una sorgente a distanza finita). Anche Diocle si era occupato dello specchio sferico: nelle propp. 2 e 3 del suo trattato studia quale riflessione dei raggi paralleli al diametro e incidenti su una calotta sferica (che egli determina) provoca il fuoco più intenso. Dello specchio sferico, d'altra parte, Dtrūms aveva fornito l'esposizione più completa di tutta la letteratura greca. Nella prop. 5 del suo trattato egli studia la riflessione sul cerchio dei raggi paralleli a un diametro, allo scopo di determinare i punti in cui i raggi riflessi incontrano il diametro; ancora, nella prop. 6, Dtrūms si propone di determinare qual è lo specchio sferico che garantisce il fuoco più intenso, e dimostra che è quello costruito su un arco pari a un terzo della circonferenza. L'unico altro testo greco nel quale questo specchio è trattato è il celebre frammento di Bobbio, mai tradotto in arabo.
Al contrario, Antemio non si occupa dello specchio sferico. Egli prende in considerazione altri tre tipi di specchi, di cui il primo è quello ellissoidale. Esso ha come superficie uno sferoide allungato, generato dalla rotazione di un settore ellittico intorno all'asse principale, e permette di risolvere la seguente questione: "come fare sì che in un dato luogo, a tutte le ore e in ogni stagione, un raggio di Sole cada sempre nello stesso punto". Antemio comincia con il costruire la curva per punti, mostra poi che si tratta di un'ellisse e infine traccia questa ellisse con un tratto continuo secondo il ben noto metodo del giardiniere.
L'analisi dello scritto di Antemio non lascia dubbi sul fatto che egli conoscesse le proprietà matematiche, che sono applicate senza essere enunciate esplicitamente. Per costruire un'ellisse per punti, per esempio, egli applica il metodo delle tangenti, che si basa su due proprietà. La prima non è altro che la prop. 48 del Libro III delle Coniche di Apollonio: le rette condotte dal punto di contatto ai fuochi formano con la tangente angoli uguali. La seconda è la seguente: la retta che unisce un fuoco al punto di intersezione di due tangenti biseca l'angolo formato dalle rette che congiungono il fuoco con i punti di contatto. Antemio dimostra poi che la curva ottenuta soddisfa due proprietà dell'ellisse. La prima è quella che permette di tracciare la curva per punti: dati due punti fissi A e B del piano, e una lunghezza a, ogni punto M della curva soddisfa la relazione MA+MB=2a; A e B sono i due fuochi e 2a è la lunghezza dell'asse maggiore. La seconda proprietà si può esprimere come segue: a ogni punto P del cerchio di centro B e raggio 2a corrisponde un punto M della curva, che si ottiene come intersezione di BP e dell'asse di AP che è tangente in M alla curva. È infine mostrato il procedimento per tracciare l'ellisse in modo continuo. Antemio elabora inoltre un sistema di specchi esagonali ‒ allo scopo di ottenere la concentrazione dei raggi riflessi in un punto che si trova a una distanza assegnata per incendiarlo ‒ e, come si rileva dalla versione araba, anche uno specchio a forma di catino.
Questo, essenzialmente, è quanto era stato trasmesso con le traduzioni in arabo delle opere greche sugli specchi ustori allorché gli studiosi del IX sec. intrapresero le loro ricerche. Tali traduzioni sono state almeno in parte stimolate dalle ricerche di questi studiosi e perciò non potevano che essere critiche. Veniamo ora a questi studiosi.
Gli specchi ustori nei secc. IX-XI: dall'anaclastica alla diottrica
Al-Kindī, Ibn Lūqā e i loro successori
Negli studi sugli specchi ustori all'epoca delle traduzioni in arabo dei testi greci colpisce un certo cambiamento di prospettiva, strettamente legato all'emergere di un nuovo carattere della ricerca su questo tema nel IX sec.: essa rientra ormai nel campo della catottrica, con il risultato che chi si occupa di ottica o di catottrica si interessa anche di specchi ustori. È il caso di al-Kindī, di Qusṭā ibn Lūqā, suo contemporaneo, e dei loro successori. Né Diocle, né Dtrūms, né l'autore del frammento di Bobbio, né ‒ malgrado le notevoli differenze che abbiamo sottolineato ‒ lo stesso Antemio, avevano condotto anche ricerche di ottica. A quanto sembra, il primo a unificare i diversi campi di ricerca, modificandone così la prospettiva, fu al-Kindī. Egli scrisse l'Ottica ‒ che ebbe grande fama ed è nota con il titolo De aspectibus della traduzione latina del testo arabo perduto ‒ e il Kitāb fī taqwīm al-ḫaṭā᾽ wā-'l-muškilāt allatī li-Uqlīdis fī 'l-Manāẓir (Sulla rettifica degli errori e delle difficoltà riscontrabili nell'Ottica di Euclide). Si devono a lui anche molti trattati di catottrica e uno scritto sugli specchi ustori dal titolo Kitāb fī 'l-šu῾ā῾āt [al-šamsiyya] (Libro sui raggi [solari]).
Qusṭā ibn Lūqā scrisse un trattato di catottrica e, secondo quanto affermano antichi biobibliografi, anche uno sugli specchi ustori. Ibn ῾Īsā ‒ che successe nel X sec. ai due studiosi e fu autore anche di una raccolta delle opere di al-Kindī ‒ raggruppò in uno stesso volume ottica, catottrica, ottica meteorologica e specchi ustori. È chiaro da questi dati che la trasmissione delle conoscenze in atto nel IX sec. non fu una semplice consegna di risultati: è evidente che essa è accompagnata da un rinnovamento che, già presente negli autori del IX sec., si rivelerà più tardi in tutta la sua importanza. Alla fine del secolo successivo, l'opera di Ibn Sahl dimostrerà la portata dell'unificazione operata da al-Kindī e dai suoi contemporanei e che sarà completata con la nascita di un nuovo capitolo dell'ottica, l'anaclastica.
Accanto a questa corrente che è la principale, alcuni matematici, tra i quali Abū 'l-Wafā᾽ al-Būzǧānī (940-997 o 998), intrapresero ricerche su particolari tipi di specchi ustori nell'ambito della geometria pratica. Si tratta di ricerche che non hanno più lo status che avevano nella matematica greca; aspetto, questo, che gli storici dell'ottica non hanno approfondito a sufficienza.
Nel trattato sugli specchi ustori, come nella maggior parte dei suoi scritti di ottica, al-Kindī continuò il lavoro dei suoi predecessori greci e bizantini, ma da una posizione critica, scelta deliberatamente e più volte proclamata. Scrivendo il Kitāb fī 'l-šu῾ā῾āt, egli intese esplicitamente rimediare alle insufficienze dello studio di Antemio e completarlo. Mentre Antemio riteneva vera la leggenda dell'incendio della flotta romana da parte di Archimede, senza però addurre prove a sostegno, al-Kindī si propose di fornire le dimostrazioni necessarie, oltre a estendere le ricerche ad altri tipi di specchi.
Il suo studio ha inizio con la costruzione di uno specchio ustorio di forma conica, considerando a questo scopo un sistema formato da due specchi posti sulle facce di un diedro. Al-Kindī prosegue poi con la costruzione di uno specchio sferico concavo, con l'asse sempre in direzione del Sole e, supponendo che i raggi siano incidenti sui punti del cerchio che limita lo specchio, dimostra che i raggi riflessi corrispondenti incontrano l'asse in uno stesso punto. Distingue inoltre vari casi, a seconda del rapporto tra l'arco che definisce lo specchio e il cerchio massimo della sfera che contiene l'arco. Dopo aver costruito lo specchio sferico, al-Kindī ritorna a un problema considerato da Antemio, ossia quello relativo alla costruzione di venticinque specchi esagonali che permettano di riflettere in uno stesso punto i raggi solari che cadono nel loro centro. Egli affronta questo problema nella prop. 14 del suo trattato, dove si propone di costruire uno specchio "molto più perfezionato di quello di Antemio". A partire da un poligono regolare di ventiquattro lati, costruisce una piramide regolare a ventiquattro facce, tale che i raggi solari incidenti nel centro delle basi di queste facce, prese come specchi, si riflettano in uno stesso punto dell'asse della piramide. L'opera termina con la costruzione di uno specchio parabolico: il procedimento ‒ costruzione per punti e tangenti di una parabola di cui sono noti fuoco e direttrice ‒ è del tutto analogo a quello di Antemio.
Il Kitāb fī 'l-šu῾ā῾āt non è la sola opera che al-Kindī dedicò agli specchi ustori. Tracce di un'altra opera, ossia il Kitāb fī ῾amāl al-marāyā al-muḥriqa (Libro sulla costruzione degli specchi ustori), andata perduta, sono state recentemente individuate in una raccolta dovuta a Ibn ῾Īsā. D'altra parte, come abbiamo detto, nel IX sec. al-Kindī non fu l'unico a occuparsi di specchi ustori. Qusṭā ibn Lūqā considerò questi specchi un argomento di grande importanza, e dedicò a esso un libro oggi perduto. Nel Kitāb fī ῾ilal mā ya῾riḍu fī 'l-marāyā min iḫṭilāf al-manāẓir (Libro delle cause della diversità di prospettive che si produce negli specchi), il suo trattato di catottrica che invece ci è pervenuto, egli pone attenzione alle proprietà anaclastiche degli specchi, un interesse che più tardi si ritroverà nei lavori di Aḥmad ibn ῾Īsā e di ῾Uṭārid. Si tratta di nomi e titoli di opere che potrebbero moltiplicarsi con il progredire delle ricerche storiche, ma che già ora permettono di poter parlare di una tradizione di ricerca di catottrica sugli specchi ustori.
Questa tradizione non fu però la sola. Ce ne fu una seconda, come abbiamo visto, nel quadro della geometria pratica, con autori come Abū 'l-Wafā᾽ al-Būzǧānī, che nel trattato dal titolo Kitāb fī mā yaḥtāǧu al-ṣāni῾ min al-a῾māl al-handasiyya (La geometria di cui ha bisogno l'artigiano) si occupò dello specchio parabolico secondo due metodi, uno dei quali ripreso da Ibrāhīm ibn Sīnān. Il libro, un manuale di procedimenti per la fabbricazione destinato agli artigiani, non contiene dimostrazioni ‒ anche se l'autore, che era un matematico, certamente le conosceva ‒, limitandosi a spiegare come tracciare la parabola e fabbricare lo specchio. Un commento sul contributo di Abū 'l-Wafā᾽ al-Būzǧānī fu espresso più tardi da al-Ġundiǧānī, un matematico interessato alla catottrica.
Entrambe le direzioni di ricerca non si limitano al commento di quanto ereditato dai Greci. Si tratta invece di studi indipendenti dalla tradizione greca, come dimostra il confronto tra lo studio dello specchio sferico di al-Kindī e quelli degli autori che lo hanno preceduto (Diocle, Dtrūms, il frammento di Bobbio, Antemio). Simili conclusioni si ottengono confrontando lo scritto di Abū 'l-Wafā᾽ sullo specchio parabolico con quelli degli autori greci.
Ibn Sahl e Ibn al-Hayṯam
Verso la fine del X sec. la tradizione di ricerca di catottrica sugli specchi ustori subisce una trasformazione e si conclude con l'opera di due matematici, Ibn Sahl e Ibn al-Hayṯam. Con Ibn Sahl, infatti, viene posto un nuovo problema: provocare l'accensione di un fuoco in un dato punto mediante raggi provenienti da una sorgente luminosa vicina o lontana, per mezzo non soltanto della riflessione ma anche della rifrazione. Per risolvere questo problema, Ibn Sahl considera i seguenti elementi: da una parte, il fuoco dovuto alla riflessione (a) o alla rifrazione (b); dall'altra, il caso in cui i raggi possono essere considerati paralleli (c), e in cui essi escono da un punto a distanza finita (d). Le diverse combinazioni di questi quattro elementi costituiscono gli argomenti dei vari capitoli del Kitāb al-Ḥarrāqāt (Libro degli strumenti ustori). Così, combinando (a) e (c) si ha il caso di raggi paralleli con sorgente a distanza infinita che causano un fuoco per riflessione; l'esempio del sistema catottrico scelto da Ibn Sahl per questo caso è lo specchio parabolico che riflette i raggi del Sole. Da (a) e (d) si ha il caso di raggi uscenti da un punto a distanza finita e fuoco prodotto per riflessione; l'esempio è quello dello specchio ellissoidale. Con (b) e (c) si hanno raggi paralleli che causano il fuoco per rifrazione e come esempio la lente convessa; e infine (b) e (d) conducono alla lente biconvessa. Per ciascuno di questi casi Ibn Sahl non soltanto spiega il funzionamento ideale dello specchio o della lente, ma descrive anche la loro effettiva costruzione chiarendo come tracciare le curve corrispondenti.
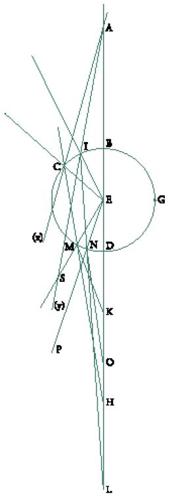
Con Ibn Sahl assistiamo quindi alla nascita della disciplina che si occupa degli 'strumenti ustori' (ḥarrāqāt) in generale, che tratta cioè insieme specchi e lenti (sullo studio di Ibn Sahl degli specchi parabolici ed ellissoidali, v. Tav. II).
Lo studio degli specchi ustori è con lui saldamente ancorato alla catottrica, e diventa quindi parte dell'ottica geometrica. Dopo il decennio 980-990 (Ibn Sahl scrive il Kitāb al-Ḥarrāqāt tra il 983 e il 985) si assiste a una delle prime riforme dell'ottica per opera di Ibn al-Hayṯam: combinare geometria ed esperimenti per trattare i fenomeni di propagazione della luce. La ricerca sugli specchi ustori aveva in qualche modo precorso questa riforma, perché aveva fin dall'inizio preso in considerazione la propagazione della luce approfittando della sperimentazione che la costruzione di essi permetteva. Seguendo Ibn Sahl, Ibn al-Hayṯam insiste sull'importanza del piano tangente, e si occupa anch'egli delle proprietà anaclastiche. Il suo studio dello specchio parabolico, per esempio, non è molto diverso da quello di Ibn Sahl, ma con una differenza non trascurabile: Ibn al-Hayṯam mette l'accento sul contenuto fisico delle nozioni geometriche, come quelle di raggio e di fascio luminoso. All'inizio egli prende in esame le proprietà anaclastiche della parabola e prosegue con quelle del paraboloide di rivoluzione, per poi soffermarsi sulla costruzione effettiva dello specchio. Spiega come costruire le lastre di acciaio, distinguendone due tipi, quelle del vertice e quelle del centro della sezione; per uno specchio ovoidale si utilizza una lastra del primo tipo, scegliendo la sezione retta della parabola a partire dalla distanza del punto nel quale si vuole provocare il fuoco, e cioè pari a quattro volte questa distanza; per uno specchio parabolico a forma di anello, invece, la lastra si determina supponendo noti la distanza dal punto che si vuole incendiare e la sezione retta della parabola.
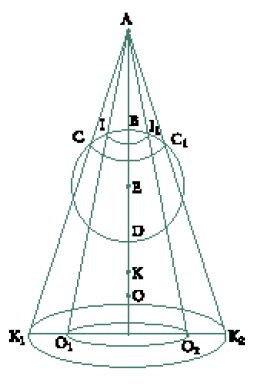
Oltre al trattato sullo specchio parabolico, Ibn al-Hayṯam, ne scrisse uno anche sullo specchio sferico nel quale si manifesta questo nuovo interesse per il contenuto fisico della questione, sottolineando in tal modo la novità della ricerca e dello stile (Tav. IIIa e IIIb).
Lo sviluppo degli studi sugli specchi ustori, dall'epoca della trasmissione dei risultati dei Greci fino a Ibn al-Hayṯam non si può ridurre a una somma di risultati, né a un semplice perfezionamento delle tecniche. Per effetto di un rinnovamento di prospettiva, è il significato stesso dell'oggetto delle ricerche che cambia. Le ricerche di Ibn al-Hayṯam influirono più di tutte sugli studi di ottica e sugli specchi ustori in lingua araba e, grazie alla traduzione del Kitāb al-Manāẓir (Libro dell'ottica) e della Maqāla fī 'l-marāyā al-muḥriqa bi-'l-quṭū῾ (Trattato sugli specchi ustori parabolici), anche su quelli in lingua latina. L'impatto sulle due aree culturali non fu però lo stesso, come vedremo dall'esempio degli specchi parabolici.
Diffusione della ricerca anaclastica di Ibn al-Hayṯam in arabo e in latino
Il trattato sullo specchio parabolico di Ibn al-Hayṯam, redatto al Cairo prima degli anni Quaranta dell'XI sec., non fu diffuso soltanto in arabo ma, a partire dal XII sec., anche in latino. La differenza che, almeno per un certo periodo, ha contraddistinto il modo in cui queste due versioni sono state recepite è ricca di insegnamenti riguardo alle vie della trasmissione di tali conoscenze: la linea di demarcazione passa, per così dire, tra ottica e geometria.
Ampiamente diffuso in arabo, il trattato fu commentato a Baghdad, nell'Est e nell'Ovest islamico, come opera di ottica e non di geometria; chi era interessato alla teoria delle coniche aveva ampiamente modo di rivolgersi altrove. Il solo sviluppo a noi noto delle ricerche contenute in questo lavoro riguarda tecniche di ottica, e non ha nulla di geometrico. Ciò non deve meravigliare, perché l'ottica ha una tradizione ben consolidata, con autori propri, e una bibliografia e una problematica tutte sue. Quanto alla ricerca teorica delle coniche, essa era troppo avanzata nel mondo islamico dell'epoca perché chi vi si dedicasse dovesse cercare informazioni nello scritto di Ibn al-Hayṯam.
Per la versione in latino, nel XII sec., le cose vanno diversamente. La traduzione di Gherardo da Cremona (1114 ca.-1187) non rispondeva a una richiesta proveniente da ricerche in campo ottico: non si può, infatti, ancora propriamente parlare di ricerche in questo campo nel mondo della latinità. Piuttosto, con questa traduzione la teoria delle coniche diventa per la prima volta accessibile in latino. Scrive Marshall Clagett: "prima del XII secolo le coniche in Occidente erano sconosciute […]. Le prime tracce si hanno con la traduzione in latino di due opere di Alhazen [cioè Ibn al-Hayṯam]. La prima è il Liber de speculis comburentibus, a cura di Gherardo da Cremona […]" (Clagett 1980, p. 3). Perché iniziassero le ricerche di ottica, infatti, occorreva attendere la traduzione dei trattati di al-Kindī e di Ibn al-Hayṯam. L'influenza dello scritto di anaclastica di Ibn al-Hayṯam fu di notevole rilevanza nel campo della geometria delle coniche, come ha dimostrato Marshall Clagett con lo studio di opere quali l'anonimo Speculi almukefi compositio o il Libellus de seccione mukefi di Johannes Fusoris.
Il ruolo del trattato di Ibn al-Hayṯam sugli specchi ustori nel mondo arabo, nell'ambito di una tradizione di ricerca ben stabilita da oltre due secoli, può essere illustrato dall'esempio di un autore finora sconosciuto, Ibn Ṣāliḥ, al quale si deve una voluminosa opera su tali specchi, che riporta numerosi passi del trattato di Ibn al-Hayṯam.
Lo scritto di Ibn Ṣāliḥ comincia con alcune considerazioni sulla teoria delle coniche, in un linguaggio che combina quelli degli Elementi di Euclide e delle Coniche di Apollonio (a questo proposito va ricordato il pericolo cui si va incontro nel cercare di stabilire una cronologia fra due autori basandosi soltanto sulla lingua). Si passa poi allo specchio parabolico. La difficoltà principale che l'autore avverte è di ordine tecnico: come curvare uno specchio parabolico con una superficie abbastanza grande in modo da aumentare l'intensità del fuoco causato. Uno specchio del genere era difficile, se non impossibile, da costruire per un artigiano dell'epoca. L'idea era allora quella di perdere un po' in focalizzazione per guadagnare in superficie.
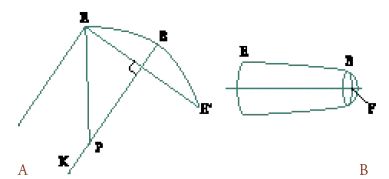
Ricordando lo studio dello specchio 'a forma di anello' di Ibn al-Hayṯam, nel quale l'asse è sempre l'asse del paraboloide e il punto d'incendio è il fuoco del paraboloide, si può scegliere l'arco EB che genera un tale specchio in modo che il fuoco F sia a una distanza data dal centro del cerchio descritto dal punto E.
Ibn Ṣāliḥ considera allora uno specchio concavo generato dall'arco EB per rotazione attorno alla normale BK nel punto B; BK sarà dunque l'asse dello specchio (fig. 4A). Tutti i raggi paralleli a BK e incidenti sul cerchio generato da E si riflettono in un punto P di BK. La distanza BP dipende dal punto E che determina il bordo dello specchio. Un raggio parallelo a BK e incidente in un punto qualunque dello specchio incontrerà l'asse in un punto diverso da P, più vicino a B. Ibn Ṣāliḥ procede alla determinazione di questi punti. Non c'è perciò un solo punto d'incendio, ma una concentrazione di raggi riflessi nei pressi dell'asse BK. Egli espone poi un procedimento che permette di ottenere un arco di parabola come sezione piana di un tronco di cono di rivoluzione (fig. 4B), e descrive in dettaglio le tecniche necessarie alla costruzione di uno specchio di questa forma.
Ibn Ṣāliḥ ritiene questo tipo di specchio mai immaginato prima, in seguito a una limitazione di carattere tecnico. Né i materiali, né le tecniche disponibili all'epoca permettevano la costruzione di uno specchio parabolico di grande curvatura. Questa dialettica tra la tradizione concettuale sviluppata a partire da al-Kindī e quella tecnica percorre, nelle opere in lingua araba, tutta la storia degli specchi parabolici e degli specchi ustori in generale.
La teoria geometrica delle lenti di Ibn Sahl
La teoria geometrica delle lenti compare per la prima volta nel Kitāb al-Ḥarrāqāt di Ibn Sahl. Si tratta di un fatto importante, che spinge a una revisione della storia della diottrica com'è stata scritta fino a oggi: non si può più infatti considerare l'anaclastica come una creazione della fine del XVI sec. poiché essa ha origine in questo trattato scritto a Baghdad negli anni 983-985. Il tentativo di ricorrere alla rifrazione per provocare l'accensione di un fuoco portò Ibn Sahl alla considerazione di un'altra conica, l'iperbole, e allo studio delle lenti di cristallo. Per comprendere la soluzione che egli diede a questo problema, occorre farsi un'idea delle conoscenze sulla rifrazione di cui era in possesso. Ibn Sahl conosceva bene l'Ottica di Tolomeo; mentre studiava il Libro V di quest'opera ‒ nel quale si parla di rifrazione ‒ scrisse una breve memoria sulla trasparenza della sfera celeste, che aveva intenzione di includere in un commento generale al libro. In questa memoria, Ibn Sahl applicò alcuni risultati tratti appunto dall'Ottica di Tolomeo, come la legge secondo la quale il raggio incidente e quello riflesso stanno in uno stesso piano che contiene anche la normale e sono disposti da una parte e dall'altra di questa. Allo stesso modo, egli utilizzò la regola per cui la massima trasparenza si ottiene con l'angolo più grande, la regola cioè secondo la quale la rifrazione dipende per ampiezza e direzione dalla differenza di opacità tra i due mezzi attraversati dalla luce; essa si allontana dalla normale nel passaggio da un mezzo più denso a uno meno denso, mentre vi si avvicina nel caso contrario. In altri termini, se i1 è l'angolo di incidenza nel mezzo I, e i2 l'angolo di rifrazione nel mezzo II, essendo i1 e i2 angoli acuti con i1>i2, allora il mezzo I è meno opaco del mezzo II.
Le conoscenze di Ibn Sahl sulla rifrazione non si limitano però a quanto appreso dall'Ottica di Tolomeo; non soltanto egli andò oltre, ma procedette anche in modo diverso da Tolomeo. Per esempio, la nozione di 'mezzo' ha per Ibn Sahl un'importanza maggiore. Ogni mezzo, compresa la sfera celeste, ha un certo grado di opacità che lo definisce, ovvero come dice Ibn al-Hayṯam interpretando Ibn Sahl "non c'è un limite per la trasparenza: per ogni corpo trasparente se ne può sempre trovare uno che lo è di più" (Maqāla fī 'l-ḍaw᾽, p. 218). Tuttavia la vera originalità di Ibn Sahl sta nell'aver posto per la prima volta il problema dell'accensione di un fuoco per rifrazione. Al centro del suo studio sulla rifrazione delle lenti c'è la nozione di 'rapporto costante': il mezzo non è più definito dall'opacità, ma si caratterizza tramite questo rapporto. Postulato ma mai calcolato da Ibn Sahl, esso non è altro che l'inverso di ciò che, in termini moderni, è chiamato indice di rifrazione n del mezzo rispetto all'aria; nel suo trattato è dunque l'inverso dell'indice di rifrazione del cristallo rispetto all'aria (Tav. IVa e IVb).
Fu lo studio degli specchi ustori che portò Ibn Sahl alle prime ricerche di diottrica. In effetti, interrogandosi sul fuoco provocato in un punto, posto a una data distanza, non soltanto per riflessione ma anche per rifrazione da raggi paralleli o uscenti da un'unica sorgente a distanza finita, egli si trovò naturalmente a intraprendere ricerche di anaclastica. Ciò che invece rese possibile le ricerche di catottrica e, anzi, la nascita stessa di questo capitolo dell'ottica fu la sua magistrale conoscenza della teoria delle coniche, come testimoniato dal Kitāb al-Ḥarrāqāt e da altri lavori (Rashed 1993). Nello studio delle lenti come in quello sugli specchi ustori, ci si trova di fronte allo scopo pratico di ottenere l'accensione di un fuoco in un punto posto a una data distanza. In entrambi i casi, ciò è ottenuto applicando ai fenomeni luminosi le proprietà di alcune strutture geometriche, in particolare quelle offerte dalla teoria delle coniche. L'oggetto che si costruisce, sia uno specchio sia una lente, deve adattarsi a queste strutture geometriche. Si tratta di una conoscenza che non è dunque fine a sé stessa, ma che in qualche modo tende a fondere arte e scienza. In termini moderni, si potrebbe dire che si tratta della costruzione di modelli facendo uso di strumenti matematici per rispondere all'esigenza pratica di accendere un fuoco a partire da una sorgente vicina o lontana.
In questa costruzione di modelli, ciò che si cerca di concettualizzare non è tanto il funzionamento ideale del fenomeno, quanto piuttosto gli elementi necessari a rispondere alla domanda posta dalle applicazioni. In questo senso, il nuovo capitolo della diottrica si differenzia da quello, ben più antico, degli specchi ustori soltanto per la complessità degli elementi in gioco e la raffinatezza delle strutture matematiche considerate.
Una tale analogia epistemica tra le ricerche di catottrica sugli specchi ustori e quelle di diottrica sulle lenti rinvia certamente al fatto che le seconde costituiscono una generalizzazione delle prime, ma riguarda soprattutto l'uso che è fatto nelle due discipline del metodo dei modelli. Non bisogna perciò stupirsi se le conoscenze che esse offrono sono simili: in entrambi i casi, lo stile è essenzialmente geometrico e non impone al matematico di optare per una particolare teoria, riguardante per esempio la natura della luce o le ragioni fisiche della riflessione e della rifrazione. Questa è la situazione nella quale si trova Ibn Sahl, da ciò che si può dedurre dagli scritti che ci sono pervenuti. Malgrado lo scopo sia quello di provocare un fuoco in un punto, lo studio è puramente geometrico: in effetti, in nessun momento l'esperimento, pur presente, interviene a sostegno della dimostrazione. Ibn Sahl si limita all'elaborazione e alla costruzione del modello geometrico che servirà a fabbricare la sagoma della lente, e con ciò si considera portato a termine il progetto di stabilire come provocare il fuoco. Così facendo, egli affina lo studio geometrico e lo fa progredire. Quanto al valore pratico del modello e alla sua efficacia sarà l'uso a dimostrarne la validità.
Con questa breve analisi si è cercato di chiarire il senso del contributo di Ibn Sahl e dei primi passi della diottrica nonché le ragioni del ritorno d'interesse per il fenomeno della rifrazione; crediamo che sia la prima volta, dopo l'Ottica di Tolomeo, che si possa parlare di un effettivo progresso in questo campo. Lettore e commentatore dello studioso di Alessandria, Ibn Sahl sapeva che il raggio incidente e quello rifratto sono su un piano che contiene la normale e si trovano da parti opposte di esso. Conosceva anche il principio della reversibilità del cammino dei raggi luminosi e la legge denominata 'legge di Snellius', della quale fu lo scopritore. Come abbiamo visto, infatti, fu lui a introdurre il rapporto tra il raggio rifratto e la distanza tra l'immagine e il punto d'incidenza (CE/CH nella sua notazione), come rapporto costante per un certo mezzo rispetto all'aria.
Tuttavia, nello studio delle lenti Ibn Sahl considerò un solo tipo di raggi: quelli paralleli all'asse nel caso di lenti convesse e quelli uscenti dal fuoco di una delle facce iperboliche nel caso di lenti biconvesse. In entrambi i casi, ottiene la convergenza di tutti i raggi rifratti in un solo punto dell'asse. D'altra parte, non sente poi alcun bisogno di enunciare esplicitamente le leggi e le regole di cui si serve. Tale discrezione non autorizza dubbi sul fatto che egli conoscesse questi principî, ma non è da considerarsi casuale. Essa sembra dovuta al fatto che egli non cerca una spiegazione fisica del fenomeno della rifrazione: nei suoi scritti, in effetti, non vi è alcun tentativo di giustificare questo modo di propagazione della luce. Le cose andranno in modo molto diverso quando si inizieranno ad affrontare i problemi posti dall'immagine di un oggetto osservato attraverso una lente, e non si potranno quindi evitare le difficoltà poste dallo stigmatismo e dall'aberrazione. Ancora non presenti nel Kitāb al-Ḥarrāqāt di Ibn Sahl, questi problemi emergeranno con Ibn al-Hayṯam, spingendolo a ridefinire i rapporti tra le condizioni della visione, della luce e della sua propagazione.
Ibn al-Hayṯam e lo sviluppo della diottrica
La scoperta del Kitāb al-Ḥarrāqāt di Ibn Sahl spinge a una riflessione sui rapporti tra questi e Ibn al-Hayṯam. Sarebbe stato davvero sorprendente se un contributo così importante nella storia dell'ottica e senz'altro eccezionale per l'epoca non avesse avuto eredi. Sarebbe stato non meno sorprendente se uno scritto di questo rilievo non avesse avuto un ruolo centrale nel preparare la strada a un'opera rivoluzionaria come quella di Ibn al-Hayṯam. Dobbiamo allora interrogarci sul progresso degli studi nella storia della diottrica dopo Ibn Sahl, e dunque in particolare nell'opera di Ibn al-Hayṯam.
I lavori di Ibn Sahl impongono di riconsiderare le conoscenze di diottrica alla vigilia del contributo di Ibn al-Hayṯam. Non è infatti più possibile presentare questo contributo soltanto nel solco della tradizione dell'Ottica di Tolomeo, anche se in qualche modo in opposizione a essa. I lavori di Ibn Sahl permettono di considerare l'opera di Ibn al-Hayṯam, non più come isolata, ma in un contesto più ampio. Siamo fin d'ora in grado di valutare le conseguenze di questa nuova situazione, e di porre una domanda precedentemente impensabile. Intanto, la conoscenza dell'opera di Ibn Sahl rivela che gli scritti di Ibn al-Hayṯam contengono temi di ricerca sfuggiti finora agli storici, anche ai migliori tra questi come Mustafa Nazif. Certi che la ricerca sulle lenti e sui diottri appartenesse a un'altra epoca, molto più tarda, gli storici non hanno considerato a fondo gli studi che Ibn al-Hayṯam ha dedicato a questo argomento. Quanto alla domanda, essa riguarda la legge della costanza dell'indice di rifrazione nota come legge di Snell: perché questa legge, scoperta da Ibn Sahl, non è ripresa da Ibn al-Hayṯam, che ritorna invece alla considerazione del rapporto tra gli angoli?
Nel Libro VII del Kitāb al-Manāẓir Ibn al-Hayṯam tratta del diottro sferico. Si nota una differenza fondamentale con Ibn Sahl: nell'opera di Ibn al-Hayṯam lo studio del diottro fa parte di un capitolo dedicato al problema dell'immagine ottica, e dunque non è separato dal problema della visione. In questo studio sono considerati due casi, a seconda che la sorgente, puntiforme e a distanza finita, si trovi dal lato della concavità o della convessità della superficie sferica del diottro; segue, subito dopo, lo studio dell'immagine di un punto per mezzo del diottro.
In tal modo sono trattate sia la propagazione della luce all'interno del diottro, sia l'immagine e la sua posizione. Ibn al-Hayṯam dimostra che se il raggio BE (fig. 5) si rifrange nel punto A, punti distinti della retta BE hanno immagini separate.
Il suo ragionamento si può riassumere così: se la retta GB è parallela alla retta EA, l'immagine di B sarà all'infinito su EA, altrimenti si troverà in un punto come K o U. Se lo studio geometrico che egli fa sul punto d'intersezione del raggio rifratto EA e del raggio GB normale alla sfera è giusto, le conclusioni fisiche non lo sono. Come ha spiegato Nazif (1942-43), l'errore nasce dal fatto che "Ibn al-Hayṯam suppone che l'immagine si trovi sulla perpendicolare condotta dal punto visibile alla superficie, nel punto d'incontro tra il raggio riflesso o rifratto verso l'occhio con la detta perpendicolare. Ciò è vero soltanto per la riflessione su superfici piane. Per altre superfici, o per la rifrazione su superfici piane o no, ciò è vero unicamente se i punti di incidenza sono molto vicini al piede della perpendicolare condotta dal centro dell'occhio alla superficie" (p. 781).
La stessa critica fu fatta sei secoli fa da Kamāl al-Dīn al-Fārisī (m. 718/1319). Si tratta, comunque, di imprecisioni che nulla tolgono all'importanza di questo studio del diottro sferico, terminato il quale Ibn al-Hayṯam affronta quello sulla sfera di cristallo trasparente e omogenea, cioè la lente sferica, interessandosi in particolare alle immagini degli oggetti che essa offre. Si limita però all'esame di un caso soltanto, quello in cui l'occhio e l'oggetto si trovano su uno stesso diametro; vale a dire, egli studia l'immagine attraverso una lente sferica di un oggetto situato in una particolare posizione sul diametro che passa per l'occhio. Cercheremo ora di dare un'idea dell'esposizione di Ibn al-Hayṯam (il quale tuttavia dedica un intero capitolo allo studio dell'immagine di un oggetto perpendicolare o meno al diametro passante per l'occhio e visto per rifrazione su una superficie sferica).
Il modo di procedere ricorda quello di Ibn Sahl nello studio della lente biconvessa iperbolica. Ibn al-Hayṯam considera separatamente due diottri e applica i risultati ottenuti in precedenza. Per il diottro di vertice B si è nel primo caso già considerato. Egli parte dunque dalla conclusione relativa all'aberrazione e considera (fig. 6) un segmento i cui estremi H e L forniscono ciascuno un raggio che si rifrange in A. Siano HC e LI questi raggi. Da ogni punto del segmento HL parte uno e un solo raggio che si rifrange in un punto dell'arco CI verso il punto A (Ibn al-Hayṯam non dimostra che in questo caso i raggi HC e LI si intersecano). I raggi HC e LI incontrano il diottro di vertice D rispettivamente in M e in N. Il raggio IN, all'interno della sfera, proviene perciò da un raggio NO più distante dalla normale EN, e il raggio CM proviene da un raggio MK. Da ogni punto del segmento KO parte dunque un raggio che subisce due rifrazioni, una sull'arco MN, l'altra sull'arco CI, prima di giungere nel punto A. Per rotazione attorno ad AD ciascuno dei due archi genera un settore sferico. Un raggio uscente da un punto del segmento KO e incidente sul settore generato dall'arco MN subisce una rifrazione su questo settore e quindi una rifrazione sul settore generato dall'arco IC per poi terminare in A. I raggi uscenti da K e incidenti sul cerchio descritto da M sono, in effetti, rifratti verso un punto del cerchio descritto da C e rifratti una seconda volta verso A. Si ha un risultato analogo per ogni punto di KO. L'immagine del segmento KO è dunque il punto A. Ponendo l'occhio in A si vede il segmento KO sotto forma di anello in quanto i raggi che colpiscono l'occhio si trovano tra il cono generato dalla retta AC e quello generato dalla retta AI (fig. 7).
Ibn al-Hayṯam suggerisce poi il seguente esperimento. Si prenda per oggetto una pallina di cera, molto piccola, tinta di nero, e una sfera di cristallo o di vetro il più possibile perfetta. L'occhio, il centro della sfera e quello della pallina siano allineati. Per un'opportuna posizione della pallina lungo quest'asse l'osservatore vedrà un anello di colore nero; se necessario, si sposta l'anello avanti e indietro per pervenire a questa posizione. Ibn al-Hayṯam studia quindi cosa succede se si sostituisce la sfera con un cilindro di direttrice circolare BCD e di generatrici perpendicolari al piano BCD. L'occhio vede il segmento KO non più sotto forma di anello ma come due segmenti separati. Osserviamo che, nel corso del suo lavoro, per studiare l'immagine di un segmento che è porzione di un segmento definito dall'aberrazione sferica, Ibn al-Hayṯam utilizza l'aberrazione sferica di un punto a distanza finita nel caso del diottro.
Dopo le ricerche sul diottro e la lente sferica del Kitāb al-Manāẓir, Ibn al-Hayṯam ritorna sul problema della sfera ustoria in uno scritto (Fī 'l-kura al-muḥriqa) che sarà oggetto di un commento di al-Fārisī e che, per riconoscimento unanime, è uno dei punti più alti nel campo dell'ottica classica. Questo scritto ci interessa per varie ragioni: in primo luogo, in esso sono chiariti e precisati certi risultati sulla lente sferica da lui ottenuti in precedenza; inoltre, è qui ripreso il problema dell'uso della lente sferica come lente ustoria. Si tratta pertanto di un testo che permette di seguire l'evoluzione del pensiero di Ibn al-Hayṯam sulla lente sferica, esaminando il modo in cui egli affronta il problema di come generare un fuoco mediante una lente per rifrazione posto da Ibn Sahl.
Ibn al-Hayṯam comincia con l'introdurre numerosi lemmi, due dei quali di particolare importanza. Il primo afferma che l'angolo di deviazione nel vetro è più piccolo della metà dell'angolo di incidenza e più grande di un quarto di questo. Come ricorda lo stesso Ibn al-Hayṯam, si tratta di una proposizione del Libro V dell'Ottica di Tolomeo. Per l'indice n=3/2 si ha allora:
,
dove i è l'angolo di incidenza e d quello di deviazione. Mentre la prima parte di questa disuguaglianza sussiste per ogni i, la seconda non vale sempre. Si ha infatti d+r=i e seni=nsenr, da cui
Ne segue che
[3] (2/n) cos(i/2)>1 ovvero 2cos(i/2)>n.
Poiché 0⟨i⟨π/2, si ha:
Se n⟨√2, allora la disuguaglianza d⟨i/2 è soddisfatta per i∩[0, π/2]; se √2⟨n⟨2, d⟨i/2 è soddisfatta per 0⟨i⟨i0, dove i0 è tale che cos(i0/2)=n/2; se n>2, d⟨i/2 non è soddisfatta per alcun valore di i.
Il secondo lemma è il seguente. Siano α e β due archi di un cerchio. Supponiamo che α>β, α=α1+α2, β=β1+β2 con α2/α1=β2/β1=k⟨1 e α1⟨π/2 (da cui α2⟨π/2 e β2⟨β1⟨π/2). Allora,
Utilizzando questi due lemmi insieme alle regole di rifrazione a lui dovute, Ibn al-Hayṯam studia la propagazione di un fascio di raggi paralleli incidenti su una sfera di vetro o di cristallo, procedendo per tappe come segue. In una prima proposizione egli dimostra che tutti i raggi paralleli incidenti su una sfera trasparente con uno stesso angolo di incidenza i convergono, dopo due rifrazioni, verso uno stesso punto del diametro parallelo ai raggi; punto che è il fuoco associato all'incidenza i. In una seconda proposizione, Ibn al-Hayṯam mostra che la deviazione totale è il doppio di ciascuna delle deviazioni, dimostrando successivamente, per assurdo, che un dato punto S sul diametro e oltre C può essere raggiunto soltanto a partire da M: S corrisponde, cioè, a una sola incidenza (fig. 8). Ancora, in una terza proposizione egli fa vedere come a due incidenze i e i′ corrispondano due punti distinti appartenenti al diametro parallelo ai raggi incidenti; mentre, in una quarta proposizione perviene al seguente risultato: se i′>i i punti S e S′ corrispondenti sono tali che CS′⟨CS; in queste ipotesi, al crescere di i, la distanza CS diminuisce; a un dato punto S corrisponde dunque una sola incidenza.
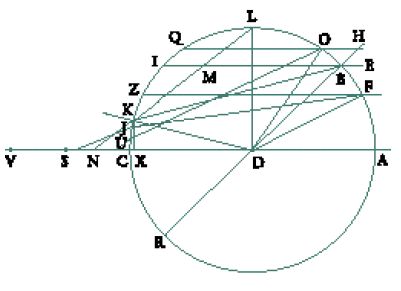
Ibn al-Hayṯam si propone poi di determinare gli estremi del segmento sul quale si trovano i punti S. Per fare questo, deve studiare le posizioni del punto B ‒ punto di seconda rifrazione ‒ al variare dell'incidenza. Si tratta, a nostra conoscenza, del primo studio esplicito dell'aberrazione sferica per raggi paralleli incidenti su una superficie di vetro e che subiscono due rifrazioni. In questo studio Ibn al-Hayṯam ricorre ai dati numerici dell'Ottica di Tolomeo per i=40° e i=50°, ottenendo il seguente risultato: i due raggi associati a questi valori di i, BK e B′K rispettivamente, sono incidenti su uno stesso punto K, quello per cui l'arco CK è di 10°. Il raggio BK si rifrange poi in direzione di un punto N tale che L, K, N sono allineati (fig. 9). Non è precisata la posizione del punto N′ associato a i=40°; l'autore si limita ad affermare che è distinto da N. Egli dimostra poi che a un punto O tale che l'arco AO supera i 50° corrisponde un raggio rifratto OU ‒ con U tra K e C ‒ e un punto S tra N e C tale che CS⟨CN. A un punto F tale che l'arco AF⟨40° corrisponde un raggio rifratto FJ ‒ con J tra K e C ‒ e un punto S oltre N′ tale che CS>CN′. Prova inoltre che si ha sempre CS⟨CV (=DR). Se ne deduce che al crescere di i da 0 a π/2 il punto S si sposta sul segmento VC da V verso C.
Si deve osservare che Ibn al-Hayṯam non considera i raggi per i quali i è compreso tra 40° e 50°, e tali che S appartiene al segmento NN′. Afferma soltanto che N è distinto da N′, ma apparentemente senza tenerne conto. Procede poi alla valutazione di CN, trovando che è circa un quinto di DR, senza calcolare il valore di CN′. Ibn al-Hayṯam scrive a questo proposito che i raggi che si rifrangono verso CN sono più numerosi di quelli che si rifrangono verso NV. Qui occorre correggere il testo e leggere CN′ e N′V: si rifrangono infatti su N′V i raggi di incidenza tra 0° e 40° e su CN′ quelli tra 40° e 90°. Se si prende come S0 il centro di CV, i raggi rifratti su CS0 sono molto più numerosi di quelli rifratti su S0V, da ciò deriva un incendio migliore su CS0 che è di lunghezza uguale a un quarto del diametro.
L'esame in termini moderni di quanto ottenuto da Ibn al-Hayṯam lascia intravedere alcune inesattezze, che nulla tolgono però al valore degli strumenti concettuali applicati all'analisi del fenomeno della focalizzazione della luce che si propaga secondo traiettorie parallele al diametro della sfera.
Apparentemente, queste inesattezze sono dovute, più che alla legge di Snellius, all'approssimazione dei valori numerici considerati e al ricorso ai rapporti angolari. Rimane comunque l'individuazione dell'aberrazione sferica per raggi di questo tipo; pur diffidando dei valori numerici, Ibn al-Hayṯam mostrò di voler dare una descrizione quantitativa dell'aberrazione e di fatto egli tentò di definire l'intervallo dei punti S, anche se a partire da due soli valori della rifrazione, corrispondenti alle incidenze di 40° e 50°. Sia in questo trattato sulla sfera ustoria sia nel Libro VII del Kitāb al-Manāẓir, nonché in altri scritti sulla rifrazione, Ibn al-Hayṯam espone le proprie ricerche in modo in parte paradossale: inventa, monta e descrive con molta cura vari dispositivi sperimentali, per l'epoca molto raffinati, che permettono di determinare valori numerici, ma nella maggior parte dei casi omette poi di riportare questi valori. Quando gli capita, come nel caso delle sfere ustorie, di ricorrere ai valori numerici, lo fa con economia e circospezione. Questo atteggiamento, già notato da altri studiosi, è dovuto probabilmente a due motivi. Il primo rinvia allo stile della pratica scientifica: la descrizione quantitativa non sembra ancora essere una norma vincolante. Il secondo motivo, verosimilmente legato al primo, riguarda il fatto che i dispositivi sperimentali potevano dare soltanto valori approssimati; e, d'altronde, Ibn al-Hayṯam non poteva considerare in altro modo i valori desunti dall'Ottica di Tolomeo. La ricerca di carattere quantitativo sarà ripresa più tardi da al-Fārisī che, approfondendola, porterà a compimento il progetto del suo predecessore.
La sfera ustoria e l'introduzione dei metodi algoritmici: Kamāl al-Dīn al-Fārisī
Nel commento alla Maqāla fī 'l-kura al-muḥriqa (Trattato sulla sfera ustoria) di Ibn al-Hayṯam, al-Fārisī si dilunga in particolare sullo studio quantitativo iniziato da questi. Il passaggio che egli dedica a questo sviluppo dell'ottica in senso quantitativo è considerato dagli studiosi uno dei contributi più importanti della storia di tale disciplina, non soltanto per la profondità, ma anche e soprattutto per le rappresentazioni di tipo funzionale ante litteram introdotte. In questo passaggio, al-Fārisī si diffonde in considerazioni teoriche sulle relazioni tra angoli d'incidenza, di deviazione e di rifrazione, e sulle differenze del primo ordine; inoltre, fa seguire a esse una tabella dove sono esaminati i valori numerici di queste grandezze, per incidenze comprese tra 0°59′ e 89°59′, di 5° in 5°. Al-Fārisī ricorda infine che per il calcolo ha fatto ricorso a un metodo raffinato, del genere di quello detto qaws al-ḫilāf (arco della differenza). Di questo metodo si conosceva allora solamente il nome, e si era cercato di stabilire in cosa consistesse basandosi proprio sui valori della tabella riportata da al-Fārisī. Anche noi ci trovammo in questa medesima situazione quando scoprimmo in uno dei manoscritti del commento di al-Fārisī una glossa, quasi certamente dovuta all'autore, che fornisce una spiegazione di questo metodo d'interpolazione, preso in prestito, come suggerisce il nome, dalle ricerche in campo astronomico. Oggi possiamo perciò capire il commento di al-Fārisī senza dover ricorrere ad alcuna congettura di sorta.
Abbiamo visto che Ibn al-Hayṯam aveva stabilito che se un raggio IM d'incidenza i si rifrange secondo MB, si ha l'arco CB=2r−i=i−2d e, partendo dai valori di Tolomeo, egli dà, per i=40° e i=50°,
,
ottenendo così lo stesso punto K per entrambe le incidenze. Ma con l'indice n uguale per esempio a 3/2 si ottiene, per i=40°, 2r−i 10°44′, e, per i=50°, 2r−i 11°26′, e posto
si ha che φ presenta un massimo per i=i0=49°48′. Ci si può chiedere perché Ibn al-Hayṯam abbia considerato lo stesso punto K per le incidenze di 40° e 50°. Forse aveva preso i valori di Tolomeo senza rifare le misure, oppure erano i metodi sperimentali di cui disponeva che gli impedivano di ottenere una precisione maggiore.
Abbiamo anche notato come Ibn al-Hayṯam non avesse considerato la posizione del punto B per i compreso tra 40° e 50°, cioè il comportamento della funzione φ in questo intervallo. È qui che interviene al-Fārisī, precisando le variazioni di d e di r, e con ciò quella dell'arco CB. Al-Fārisī inizia con lo studio della differenza del primo ordine Δ(2r−i)=Δr−Δd, dimostrando l'esistenza di un'incidenza i0 compresa tra 40° e 50° ‒ valore che egli definisce 'di separazione' ‒, in modo tale che:
a) per i⟨i+Δi⟨i0 si ha Δr>Δd e Δr−Δd decresce, tendendo a zero per i che tende a i0;
b) per i0⟨i⟨i+Δi si ha Δr⟨Δd e Δd−Δr cresce al crescere di i.
Nel primo caso si ha allora Δ(r−d)=Δ(2r−i)>0 e nel secondo Δ(r−d)⟨0, ciò mette in evidenza l'esistenza di un massimo in corrispondenza del valore i0 dell'incidenza. Dopo aver enunciato questi risultati al-Fārisī presenta la sua tabella. L'esame dei valori di d, r, Δd, Δr in funzione di i mostra che la tabella consta di due parti, corrispondenti a i⟨i0 e i>i0. Per i valori di i presi di 10° in 10°, a partire da 40° fino a 90°, i risultati di al-Fārisī coincidono con quelli di Tolomeo, coincidenza che viene però meno per i⟨40°. Per comprendere la ragione di questa differenza, occorre risalire al metodo usato per la costruzione della tabella, metodo che l'autore stesso definisce 'sottile'.
Al-Fārisī vuole calcolare d per una variazione di i da 0° a 90° di 5° in 5°, e anche di grado in grado, sotto due assunzioni: i dati di Tolomeo per i=40° e i=50°, come nel caso di Ibn al-Hayṯam, e la limitazione [1] stabilita da quest'ultimo. Si ottiene un primo gruppo di valori:
Al-Fārisī divide allora l'intervallo [0°, 90°] in 18 parti che separa in tre gruppi: otto intervalli da 0° a 40°, due da 40° a 50° e ancora otto da 50° a 90°. Su queste 18 parti l'accrescimento medio di d/i è Δ(d/i)=(1/4):18=0°0′50″. Ma:
per i∈[0°, 40°] si ha Δ(d/i)=56″15‴;
per i∈[40°, 50°] si ha Δ(d/i)=45″;
per i∈[50°, 90°] si ha Δ(d/i)=45″.
Per evitare un'eccessiva discontinuità nella successione degli accrescimenti per intervalli di 5°, è necessario apportare una correzione. Al-Fārisī sapeva che una qualunque correzione di Δ(d/i) tra 40° e 90° avrebbe modificato il risultato del calcolo di d per i=50°. Questo risultato è però un dato, e dunque egli decide di mantenere costante Δ(d/i) nell'intervallo [40°, 90°], cioè Δ(d/i)=Δ0=45″, e di apportare una correzione in [0°, 40°]. In questo modo, per ogni intervallo Δi=5° in [0°, 40°] si ha Δ(d/i)−Δ0=11″15‴, ciò che dà 1′30″ per gli otto intervalli. Al-Fārisī suppone che Δ(d/i) decresca in ciascun intervallo di una stessa quantità Δ2=Δ[Δ(d/i)] fino ad arrivare a Δ0=45″ al nono intervallo. Deve dunque aversi:
[8] (1+2+…+8)Δ2=1′30″
da cui
[9] 36Δ2=1′30″ e Δ2=2″30‴.
Si ottengono così accrescimenti corretti sui primi otto intervalli. Partendo da questi e dagli accrescimenti costanti sui dieci intervalli seguenti, al-Fārisī dà i rapporti d/i per valori di i multipli di 5°, deducendone i valori di d che compaiono nella sua tabella. Il calcolo di d per i=15° e i=35° fornisce rispettivamente d=4°31′52″30‴ e d=12°39′47″30‴, che sono arrotondati ai valori superiori.
Riassumendo, nel metodo di al-Fārisī si suppone: (a) Δ(d/i) costante nell'intervallo [40°, 90°]; (b) Δ[Δ(d/i)] costante nell'intervallo [0°, 40°], ottenendo un'espressione di d/i in funzione di i. Così:
in [40°, 90°], per i multiplo di 5°, si ha
,
che, per k=(i−40)/5, diventa
,
da cui
Si riconosce qui la formula di Kepler, implicita nelle tavole di Tolomeo riprese da Witelo. Essa permette di ricostruire interamente la tavola dei valori di Tolomeo per valori di i che variano di 10° in 10° e, nella tavola di al-Fārisī, i valori di d per i che varia di 5° in 5°, ma soltanto nell'intervallo [40°, 90°].
Nell'intervallo [0°, 40°], Δ2 è costante, e vale 2″30‴==2,5/3600. I valori di Δii−5, tenuto conto del valore Δ4540=45″, sono perciò i seguenti:
che, per k=(45−i)/5, diventa
Per valori di i multipli di 5° abbiamo poi:
Per i=5x, x∈{1, 2,…,8}, si ha
,
da cui
Il metodo di al-Fārisī consiste dunque nell'approssimazione della funzione φ(i)=d/i nell'intervallo [40°, 90°] con una funzione lineare, e nell'intervallo [0°, 40°] con un polinomio di secondo grado. Si ottengono così per d un'espressione polinomiale di secondo grado nel primo caso e una di terzo grado nel secondo. Il calcolo è allora più semplice:
per i∈[40°, 90°],
Ne segue, per i=40° e d=15°,
[19] 15=1600a+40b,
e per i=50° e d=20°,
[20] 20=2500a+50b.
Il sistema di queste due equazioni fornisce a=1/400 e b=11/40, da cui
per i∈[0°, 45°], il ragionamento di al-Fārisī ci permette di associare l'intervallo [40°, 45°] sia alla seconda parte sia alla prima per correggere gli intervalli:
Per i=0°, d/i=1/4; per i=40°, d/i=3/8; e per i=45°, d/i=31/80, calcolato secondo la d/i=(110+i)/400. Ne segue il sistema:
equivalente a
che ha le soluzioni
da cui
Queste formule permettono di calcolare un valore approssimato di d per variazioni di i di un grado, o per qualunque valore di i, come aveva promesso al-Fārisī, affermando anche che questi risultati si sarebbero potuti ottenere per interpolazione lineare in ciascuno degli intervalli di ampiezza Δi=5° determinati secondo la sua tabella. Calcoliamo, a titolo di esempio, d per i=12° con i due metodi. Dalla precedente espressione per d si ottiene:
Per interpolazione lineare si ottiene, invece:
[28] d10=2°51'15", d15=4°31'53", ∆d=1°40'38",
[28] ∆12=d10+2/53∆d =2°51'15"+4'14"=3°31'29".
I risultati differiscono dunque di un minuto circa.
Si deve notare che, contrariamente a quanto è stato suggerito, al-Fārisī non fa intervenire, per 40°⟨i⟨90°, le differenze del secondo ordine, Δ2, e, per 0°⟨i⟨40°, quelle del terzo, Δ3=Δ(Δ2). Il metodo che abbiamo esposto non richiede infatti la considerazione di questi valori. Del resto, le funzioni sono di secondo e di terzo grado, e quindi conducono ovviamente a differenze del secondo (Δ2) e del terzo ordine (Δ3) costanti. Questo metodo di interpolazione del secondo ordine, che sembra risalga ad al-Ḫāzin (X sec.), si ritroverà più tardi nelle tavole astronomiche note come Zīǧ-i Ḫāqānī di al-Kāšī.
Con l'analisi precedente del metodo seguito da al-Fārisī, si è cercato di renderne esplicite le intenzioni. Al-Fārisī era un fisico, ma, come hanno dimostrato studi recenti, era anche un algebrista e un teorico dei numeri. Egli cercava un algoritmo che potesse esprimere la dipendenza funzionale tra gli angoli di incidenza e gli angoli di deviazione, per poi dedurne i valori della deviazione per un'incidenza qualunque e in due mezzi determinati. Come abbiamo visto, egli suddivide l'intervallo [0°, 90°] in due parti, nelle quali approssima la funzione f(i)=d/i con una funzione lineare su [40°, 90°] e un polinomio di secondo grado su [0°, 40°]. Raccorda poi le due interpolazioni, imponendo alla prima differenza di essere la stessa per i=40°, o, per usare un altro linguaggio, imponendo alla parabola e alla retta di intersecarsi in due punti vicini di ascissa i=40° e i=45°. C'è da notare che, se invece di procedere, come l'autore, cercando le differenze finite delle due funzioni che compongono l'algoritmo, si calcolano le derivate, si trovano rispettivamente i valori 37/14.400 e 37/14.800; dimostrazione a posteriori della precisione voluta da al-Fārisī.
Questo modo di procedere non è né quello di Tolomeo né quello di un ricercatore che conosca la legge di Snell. Senza dubbio, al-Fārisī e Tolomeo fanno entrambi ricorso a metodi ispirati verosimilmente a quelli degli astronomi. Il metodo di al-Fārisī non consiste però nel tradurre in una progressione aritmetica una serie di valori numerici ottenuti mediante osservazioni, come invece accadeva nell'astronomia antica (ed è in questo senso che Albert Lejeune (1957) spiega il procedimento di Tolomeo). Non soltanto il metodo è matematicamente più fine, ma riposa in ultima analisi solamente su due osservazioni, quelle corrispondenti alle due incidenze di 40° e 50° prese, tramite Ibn al-Hayṯam, da Tolomeo, stimando in 1/4 il valore di d/i vicino a 0° e in 1/2 quello vicino a 90°.
Per determinare la differenza seconda nell'intervallo [0°, 40°] al-Fārisī sfrutta la differenza prima tra 0° e 45° ottenuta con l'algoritmo relativo all'intervallo [40°, 90°]. Egli cerca dunque di ottenere mediante l'algoritmo tutti i valori a partire da due sole osservazioni; il calcolo doveva prevedere, con grande precisione, i valori non misurati. La tabella composta da al-Fārisī non ha perciò lo scopo di riportare tutti, o in parte, i risultati, grezzi o corretti, delle osservazioni, ma solamente alcuni dei valori che si possono ottenere con metodi algebrici a partire da due osservazioni. Un calcolo che non è quindi soltanto lo strumento di una ricerca di carattere quantitativo e di precisione, ma che è investito di un potere euristico, in questa che è la parte più fisica dell'ottica geometrica.
Il metodo resta tuttavia intrinsecamente limitato, poiché la funzione lineare, così come la funzione polinomiale di secondo grado, è legata alle condizioni dell'esperimento della rifrazione nei due mezzi, aria e vetro. La difficoltà non sta dunque nello strumento matematico, ma nell'impostazione concettuale di al-Fārisī: egli pensa in termini di una classe particolare di dati di osservazioni, senza preoccuparsi di caratterizzare intrinsecamente questa classe rispetto alle altre.
Al-Fārisī non intraprese questa ricerca soltanto per commentare il testo di Ibn al-Hayṯam; il suo studio aveva ambizioni più ampie, e sarà poi utilizzato nelle sue magistrali ricerche sull'arcobaleno e sull'alone, nelle quali egli ritorna al problema della visione attraverso una sfera trasparente, apportando anche innovazioni nella teoria dei colori.
Conclusioni
Promossa a partire dal IX sec., la ricerca sugli specchi ustori non soltanto ha stimolato la traduzione in arabo della parte essenziale dell'eredità greca in questo settore, ma ha anche spinto a situare questa eredità, assieme alle scoperte recenti, nella nuova prospettiva dell'ottica: gli specchi ustori, da sempre di pertinenza della matematica applicata, lo sono ora anche dell'ottica. Il passo compiuto da al-Kindī affinché lo studio di tali specchi fosse riconosciuto come parte integrante della catottrica ha senza dubbio dato un nuovo impulso alle ricerche in campo ottico. Circa un secolo più tardi, Ibn Sahl procede alla seconda importante trasformazione, ponendo il problema del fuoco provocato da strumenti ustori che non siano specchi. Si ha qui la prima teoria geometrica delle lenti e della loro fabbricazione, teoria vista come parte di una nuova disciplina, lo studio degli strumenti ustori in generale. La ricerca sulle lenti risultò così una continuazione di quella sugli specchi ustori, ed ebbe il merito di ridare vita al capitolo sulla rifrazione che apparentemente era rimasto al punto in cui l'aveva lasciato Tolomeo. Si tratta di cinquant'anni che segnano profondamente la storia dell'ottica. Con Ibn Sahl, lo si è detto, le ricerche di diottrica fanno parte di un campo più vasto che tratta insieme specchi ustori e lenti ustorie. Tuttavia, nel corso delle sue ricerche, spinto dalla propria formazione in geometria e conoscendo le leggi dell'ottica geometrica (propagazione rettilinea, riflessione, rifrazione, reversibilità del cammino dei raggi luminosi), questi s'interessò principalmente delle proprietà ottiche delle coniche legate alla focalizzazione della luce: questo studio delle tre sezioni coniche segna l'inizio dell'anaclastica. Inoltre, utilizzando soprattutto mezzi meccanici per la descrizione grafica di tali curve, egli realizzò strumenti che permettevano la concentrazione della luce.
Ibn Sahl ha creato dunque un campo di ricerca sugli strumenti ustori e, quasi in più, la diottrica. Ma, spinto dalla sua prospettiva prevalentemente geometrica a pensare non soltanto all'ellisse e alla parabola ma anche all'iperbole come curve anaclastiche, fu naturalmente portato a scoprire la legge della costanza dell'indice, o legge di Snell. Si comprende quindi perché la diottrica, quando nasce con Ibn Sahl, tratti soltanto ciò che riguarda la propagazione della luce, senza preoccuparsi dei problemi della visione, e anzi mostrando una certa indifferenza nei loro confronti.
Mezzo secolo più tardi la diottrica amplia il proprio orizzonte e gode di uno status completamente diverso. Con Ibn al-Hayṯam viene meno l'idea della diottrica come geometria delle lenti: per studiare le lenti occorre, secondo le sue parole, "unire matematica e fisica". Si tratta di un passo decisivo, e suggerisce che il campo che Ibn Sahl aveva delimitato, la disciplina degli strumenti ustori, ebbe vita breve, non resistendo ai colpi inferti da un autore il quale è più un fisico che un matematico. Un insieme di scopi pratici non basta per definire un campo di studi e di ricerche.
La riforma di Ibn al-Hayṯam modificò le condizioni della ricerca diottrica: da allora, si studiarono diottri e lenti non soltanto come strumenti ardenti, ma anche come strumenti ottici. Diventò naturale, allora, rivolgere l'attenzione al problema della formazione delle immagini e della loro localizzazione mediante questi strumenti. Tuttavia, Ibn al-Hayṯam, spinto dalle nuove norme da lui stesso introdotte ‒ in particolare quella della sperimentazione come categoria di prova in fisica ‒, promosse certe ricerche di tipo qualitativo. Ancora timida e moderata, questa ricerca prenderà poi la direzione a essa impressa dal commentatore di Ibn al-Hayṯam, Kamāl al-Dīn al-Fārisī.
Bibliografia
Clagett 1980: Archimedes in the Middle Ages, edited by Marshall Clagett, Philadelphia, American Philosophical Society, 1964-1984, 5 v., 13 t.; v. IV: A supplement on the medieval Latin traditions of conic sections (1150-1566), 1: Texts and analysis, 1980.
Heath 1907: Heath, Thomas L., The fragment of Anthemius on burning mirrors and the 'Fragmentum mathematicum Bobiense', "Bibliotheca mathematica", s. III, 7, 1907, pp. 225-233.
Heiberg 1909-10: Heiberg, Johann L. - Wiedemann, Eilhard, Ibn al-Haiṯams Schrift über parabolische Hohlspiegel, "Bibliotheca mathematica", s. III, 10, 1909-1910, pp. 201-237.
Lejeune 1957: Lejeune A., Recherches sur la catoptrique grecque d'après les sources antiques et médiévales, Bruxelles, Palais des Académies, 1957.
Mawaldi 1988: Mawaldi, Moustafa, L'algèbre de Kamāl al-Dīn al-Fārisī, édition critique, analyse mathématique et étude historique (Thèse de doctorat, Paris, Sorbonne Nouvelle, 1988, 3 v.).
Nazif 1942-43: Naẓīf, Muṣṭafā, Al-Ḥasan ibn al-Hayṯam, buhūṯu-hu wa-kušūfu-hu al-baṣariyya, Il Cairo, Ǧāmi῾at Fu᾽ād al-Awwal, 1942-1943, 2 v.
‒ 1958: Naẓīf, Muṣṭafā, Kamāl al-Dīn al-Fārisī wa ba῾ḍ buḥūṯi-hi fī ῾ilm al-ḍaw᾽, "Publications of the Egyptian society for the history of science", 2, 1958, pp. 65-100.
Rashed 1968: Rashed, Roshdi, Le Discours de la lumière d'Ibn al-Haytham: traduction française critique, "Revue d'histoire des sciences", 21, 1968, pp. 197-224.
‒ 1970: Rashed, Roshdi, Optique géométrique et doctrine optique chez Ibn al-Haytham, "Archive for history of exact sciences", 6, 1970, pp. 271-298.
‒ 1978: Rashed, Roshdi, Lumière et vision: l'application des mathématiques dans l'optique d'Alhazen, in: Roemer et la vitesse de la lumière, avant-propos de René Taton, Paris, Vrin, 1978, pp. 19-44 (rist. in: Rashed, Roshdi, Optique et mathématiques. Recherches sur l'histoire de la pensée scientifique en arabe, Aldershot, Variorum, 1992, v. IV).
‒ 1982: Rashed, Roshdi, Matériaux pour l'histoire des nombres amiables et de l'analyse combinatoire, "Journal for the history of Arabic sciences", 6, 1982, pp. 209-278.
‒ 1984: Rashed, Roshdi, Entre arithmétique et algèbre. Recherches sur l'histoire des mathématiques arabes, Paris, Les Belles Lettres, 1984 (trad. ingl.: The development of Arabic mathematics. Between arithmetic and algebra, Dordrecht-Boston, Kluwer, 1994).
‒ 1990: Rashed, Roshdi, A pioneer in anaclastics. Ibn Sahl on burning mirrors and lenses, "Isis", 81, 1990, pp. 464-491.
‒ 1992a: Rashed, Roshdi, Optique et mathématiques. Recherches sur l'histoire de la pensée scientifique en arabe, Aldershot, Variorum, 1992.
‒ 1992b: Rashed, Roshdi, De Constantinople à Bagdad: Anthémius de Tralles et al-Kindī, in: La Syrie de Byzance à l'Islam (VIIe-VIIIe siècles), publiés par Pierre Canivet et Jean-Paul Rey-Coquais, Damasco, Institut Français de Damas, 1992, pp. 165-170.
‒ 1993a: Rashed, Roshdi, Math. inf. II.
‒ 1993b: Rashed, Roshdi, Géométrie et dioptrique au Xe siècle: Ibn Sahl, al-Qūhī et Ibn al-Haytham, Paris, Les Belles Lettres, 1993.
‒ 1995: Rashed, Roshdi, Conic sections and burning mirrors. An example of the application of ancient and classical mathematics, in: Physics, philosophy and the scientific community. Essays in the philosophy and history of the natural sciences and mathematics in honor of Robert S. Cohen, edited by Kostas Gauroglu [et al.], Dordrecht-Boston, Kluwer, 1995, pp. 357-376.
‒ 1996: Rashed, Roshdi, Math. inf. I.
‒ 1997a: Œuvres philosophiques et scientifiques d'al-Kindī, Leiden-New York, E.J. Brill, 1997-1998, 4 v.; v. I: L'optique et la catoptrique, par Roshdi Rashed, 1997.
‒ 1997b: Rashed, Roshdi, Dioclès et 'Dtrūms': deux traités sur les miroirs ardents, "Mélanges de l'Institut dominicain d'études orientales du Caire", 23, 1997, pp. 1-155.
‒ 2000: Les catoptriciens grecs, textes établis, trad. et commentés par Roshdi Rashed, Paris, Les Belles Lettres, 2000-; v. I: Les miroirs ardents, 2000.
Schramm 1965: Schramm, Mathias, Steps towards the idea of function: A comparison between Eastern and Western science in the Middle Ages, "History of science", 4, 1965, pp. 70-103.
Wiedemann 1910: Wiedemann, Eilhard, Beiträge zur Geschichte der Naturwissenschaften. Über die Brechung des Lichtes in Kugeln nach Ibn al-Haiṯam und Kamāl al-Dīn al-Fārisī, "Sitzungsberichte der Physikalisch-medizinischen Sozietät in Erlangen", 42, 1910, pp. 15-58 (rist. in: Wiedemann, Eilhard, Aufsätze zur arabischen Wissenschaftsgeschichte, hrsg. von Wolfdietrich Fischer, Hildesheim-New York, Olms, 1970, 2 v.; v. I, pp. 597-640).
Winter 1949: Winter, Henry J.J. - ῾Arafat, Walid, Ibn al-Haytham on the paraboloidal focussing mirror, "Journal of the Royal Asiatic Society of Bengal Science", s. III, 15, 1949, 1, pp. 25-40.
‒ 1950: Winter, Henry J.J. - ῾Arafat, Walid, A discourse on the concave spherical mirror by Ibn al-Haytham, "Journal of the Royal Asiatic Society of Bengal science", s. III, 16, 1950, pp. 1-6.
Woepcke 1855: Woepcke, Franz, Analyse et extraits d'un recueil de constructions géométriques par Abou-l Wafā, "Journal asiatique", s. V, 5, 1855, pp. 309-359.