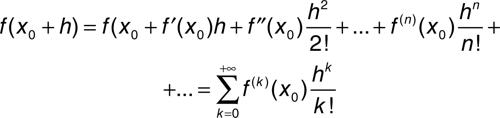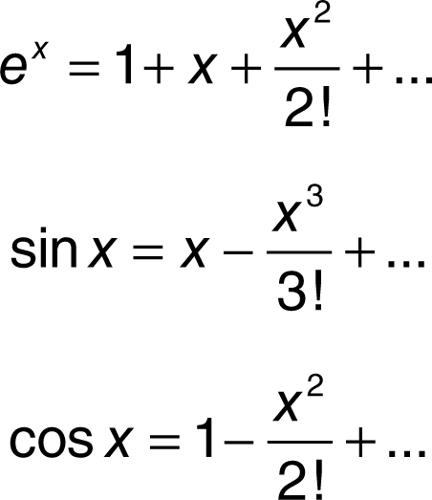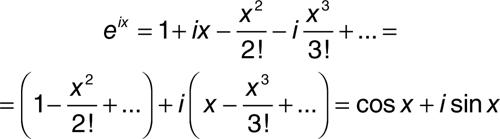La formula matematica piu bella

La formula matematica piu bella

La formula matematica più bella

La formula e^iπ = −1 è considerata pressoché unanimemente la formula matematica più elegante. Per la sua semplicità. Perché è semplicemente bella: unisce le due più famose costanti matematiche (e e π), le due unità dell’insieme dei numeri reali e dei numeri complessi (1 e i) e magari anche lo zero se la si scrive nella forma e^iπ + 1 = 0. Perché è affascinante e misteriosa: si prende un numero come π (che vuol dire 3,14 ecc.), lo si moltiplica per i (già questo prodotto qualche problema lo crea: che numero si ottiene moltiplicando π per i ?), si eleva e (anche in questo caso: 2,71 ecc.) al risultato della moltiplicazione e si ottiene −1. Ma l’esponenziale non era una funzione sempre positiva? Com’è possibile che calcoli così complicati si semplifichino a tal punto da dare alla fine come risultato −1?

Naturalmente, sostenere che e^iπ = −1 è la formula più elegante e bella della matematica porta a chiedersi che rapporto c’è tra la stessa matematica e l’estetica, quali sono i criteri estetici intrinseci alla matematica, quali caratteri tra i risultati che questa ottiene sono significativi dal punto di vista estetico. Quanto osservato a proposito di e^iπ = −1 sembra premiare la semplicità e la brevità: è difficile dare un giudizio positivo di un enunciato che a prima vista non si capisce o di una dimostrazione troppo lunga e articolata. C’è poi – molto importante – la presenza delle contrapposizioni: l’alternarsi tra aspettativa e realizzazioni, tra sorpresa e unitarietà, tra tensione e calma; la combinazione di semplice e complesso; lo studio della differenza nella similarità e della similarità nella differenza. Sono criteri esplicitati, tra gli altri, dal matematico inglese G.H. Hardy, per il quale il valore estetico in matematica proviene appunto in primo luogo da economia, inevitabilità e sorpresa.

La formula e^iπ = −1 è di solito associata al nome di Eulero. L’attribuzione è sostanzialmente corretta, ma non va comunque dimenticato il merito del matematico inglese R. Cotes che nel 1714 pubblicò un teorema sui numeri complessi che, nel linguaggio moderno, afferma che e^iα = cosα + isinα. Nel 1743 Eulero dimostrò che

Dalle precedenti formule segue il risultato di Cotes (che Eulero in ogni modo riscoprì autonomamente nel 1748). Leonhard Euler è uno dei più grandi matematici di tutti i tempi. Eulero – questo il nome nella forma italianizzata – insegnò all’Accademia di Pietroburgo, accettando poi di trasferirsi nel 1741 nella nuova Accademia prussiana di Berlino (anche se affetto da una progressiva forma di cecità) per tornare definitivamente a Pietroburgo su invito di Caterina la Grande. La sua fama è dovuta anche alla straordinaria produttività scientifica, quasi 900 titoli fra trattati e memorie. Le Lettere a una principessa tedesca, nate occasionalmente dalle lezioni impartite per corrispondenza a una nipote di Federico ii di Prussia, documentano i suoi interessi estesi alla fisica, alla filosofia e alla divulgazione del pensiero scientifico.

La dimostrazione della formula di Eulero può essere ottenuta abbastanza semplicemente partendo dalla formula di De Moivre relativa alla potenza di un numero complesso scritto in forma trigonometrica: z = r(cosα + isinα). Si ha allora (cosnα + isinnα) = (cosα + isinα)ⁿ da cui, ponendo α = x/n, si ricava

Ora, per x assegnato e per n sempre più grande, cos(x/n) differirà di poco da 1 mentre sin(x/n) è asintoticamente uguale a x/n. Si ottiene pertanto la seguente formula limite per n → ∞:

Per x = π si ha a questo punto e^iπ = −1.

Un’altra dimostrazione più formale è basata sugli sviluppi in serie di Taylor. Se una funzione ƒ ammette nell’intervallo [x₀ −r, x₀ + r] derivate di qualunque ordine ed esistono due numeri K e M per cui risulta Iƒ ⁽ⁿ⁾(x)I ≤ KM^N per ogni n e per ogni x dell’intervallo considerato, si può allora scrivere:

Cioè nell’intervallo considerato la funzione ƒ può essere sviluppata in serie di potenze. Si ottengono così in particolare, per x₀ = 0, gli sviluppi in serie di potenze delle funzioni esponenziale, seno, coseno, validi per ogni x reale:

Si consideri adesso nel campo complesso la serie

per la quale si dimostra la convergenza assoluta per ogni z. Si può allora porre la sua somma uguale a e^z con una scelta giustificata dal fatto che, per z ∈ R, si ritrova il risultato già noto nel caso reale:

Ponendo in particolare z = ix e ricordando le successive potenze di i si ottiene:

Da e^ix = cosx + isinx, si ha, per x = π, la formula di Eulero.