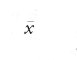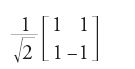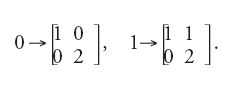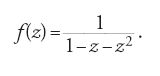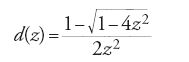La grande scienza. Automi e linguaggi formali
La grande scienza. Automi e linguaggi formali
Automi e linguaggi formali
La teoria degli automi e dei linguaggi formali ha lo scopo di descrivere le proprietà delle successioni di simboli. Tali successioni si presentano in situazioni diverse, dai processi che si svolgono in tempi discreti alle catene di molecole. La teoria ha pertanto un aspetto interdisciplinare, che cercheremo di illustrare più avanti.
La teoria matematica applicata, che si è sviluppata parallelamente alla necessità di formalizzare e descrivere i processi legati all'uso del computer e agli strumenti di comunicazione, ha però un'origine strettamente matematica; essa risale ai lavori di logici dei primi decenni del Novecento, quali Emil L. Post, Alonzo Church e Alan M. Turing, motivati dalla necessità di dare un fondamento alla nozione di dimostrazione matematica sulla via inaugurata dai lavori di David Hilbert. Dopo la Seconda guerra mondiale, in seguito allo sviluppo dei computer e delle telecomunicazioni e del rinnovato interesse per lo studio delle funzioni del cervello umano, Claude E. Shannon, Stephen C. Kleene e John von Neumann hanno esteso questo primo approccio. Negli anni Sessanta l'interesse dei linguisti è stato stimolato dai lavori di Noam A. Chomsky, sostenitore dell'uso dei metodi formali nella descrizione dei linguaggi naturali. Lo sviluppo della biologia molecolare ha poi portato a considerare le catene di molecole formate dai genomi come successioni di simboli sull'alfabeto costituito dalle basi: un ulteriore motivo per occuparsi di proprietà come le ripetizioni delle occorrenze di simboli o delle similarità tra successioni.
Nella classica gerarchia di Chomsky, per descrivere i linguaggi formali si introducono quattro livelli di complessità crescente: a stati finiti, context-free, context-sensitive e ricorsivamente computabili. Cercheremo di dare un'idea di questi livelli, fornendo le necessarie definizioni in modo piuttosto informale e sottolineando gli sviluppi più recenti. Nella prima parte tratteremo della teoria degli automi finiti, mettendo in evidenza i legami con altri campi della matematica, in particolare con la teoria dei semigruppi e dei linguaggi razionali. Prenderemo in considerazione anche i legami con la logica, come pure l'estensione dei linguaggi a oggetti infiniti, e introdurremo poi la dinamica simbolica attraverso la nozione di sistema dinamico simbolico.
Nella seconda parte ci occuperemo invece del secondo livello della gerarchia di Chomsky, i linguaggi context-free, sottolineando il legame tra grammatiche context-free e 'automi a pila' e fornendo recenti risultati sugli automi a pila deterministici. Come nel caso degli automi finiti, menzioneremo anche i legami con la teoria dei gruppi, inclusi alcuni importanti risultati sui gruppi context-free.
Il quarto e ultimo livello della gerarchia è costituito dalla classe dei linguaggi ricorsivamente enumerabili. Essa viene introdotta mediante le macchine di Turing. Definiremo anche la corrispondente classe di funzioni ricorsive intere. Parleremo poi delle classi di complessità P, NP e PSPAZIO, includendo anche il famoso problema aperto P≠NP.
Considereremo quindi due campi di ricerca vicini allo studio dei linguaggi formali. Il primo è quello delle serie formali, un campo che ha importanti applicazioni nella combinatoria enumerativa e nell'analisi degli algoritmi. Il secondo è la combinatoria delle parole, una branca della combinatoria molto attiva, con collegamenti con vari campi dell'algebra e della teoria dei numeri.
Parleremo infine delle applicazioni dei linguaggi formali e degli automi. Queste riguardano la progettazione di software e la concezione di compilatori, il trattamento di testi e la loro compressione, il trattamento dei linguaggi naturali e infine gli studi sul genoma.
Una bibliografia commentata concluderà questo saggio; essa ha lo scopo di aiutare il lettore che voglia approfondire particolari aspetti di questa disciplina.
Automi finiti
L'idea di automa finito compare esplicitamente negli anni Cinquanta in un lavoro di Kleene (1956). È il modello più semplice di computazione e, più generalmente, di comportamento di un sistema. Si tratta semplicemente di un controllo discreto dotato di una memoria finita. Il primo teorema in proposito è l'equivalenza tra il modello dell'automa finito e la descrizione di successioni di simboli ottenute utilizzando i tre simboli logici primitivi di unione, prodotto di insiemi e iterazione. Le espressioni costruite in questo modo sono dette 'espressioni razionali'; un linguaggio descritto da un'espressione razionale è detto anch'esso razionale. Il teorema di Kleene afferma che un linguaggio è razionale se e solo se è riconosciuto da un automa finito. Tale risultato ha una dimostrazione costruttiva che fornisce un algoritmo implementato in numerosi sistemi pratici (v. oltre). L'articolo di Kleene ha un precedente in quello di Warren S. McCulloch e Walter Pitts A logical calculus of the ideas immanent in nervous activity (1943), nel quale gli autori si proponevano di descrivere il comportamento del cervello umano mediante un modello di neuroni e sinapsi. I primi articoli di teoria degli automi hanno anche legami con la teoria dei circuiti. Un circuito sequenziale, nel quale l'uscita dipende da un segnale di entrata, è ben descritto da un automa finito.
La fig. 1 rappresenta un automa finito. Esso ha due 'stati' 1 e 2. Lo stato 1 è iniziale, 1 e 2 sono entrambi finali. Gli archi sono etichettati con i simboli a e b. L'insieme delle parole, che sono etichette di cammini dallo stato iniziale a uno stato finale, è l'insieme di tutte le parole su a e b nelle quali a è sempre immediatamente seguito da b. Per il teorema di Kleene questo insieme di parole si può anche descrivere con un'espressione razionale, e cioè: (ab+b)*(ε+a), dove ε denota la parola vuota, + l'unione e l'asterisco l'iterazione.
La star-height
La star-height (altezza, o profondità, dell'operazione di iterazione) di un linguaggio razionale X si definisce semplicemente: è il più piccolo numero, su tutte le espressioni razionali che descrivono X, di simboli di iterazione nidificati che compaiono nell'espressione. Quindi la star-height è 0 se e soltanto se il linguaggio è finito (non vi sono iterazioni). La star-height dell'espressione che descrive un linguaggio non è sempre la minima possibile. Per esempio, le espressioni (a*b)*a* e (a+b)* descrivono entrambe l'insieme di tutte le parole su a e b; la prima ha star-height 2, ma la seconda 1. Il problema del calcolo della star-height di un linguaggio razionale è stato sollevato fin dagli albori della teoria degli automi e risolto, in linea di principio, da Kosaburo Hashiguchi (1987), il quale ha dimostrato che la star-height è ricorsivamente computabile. Restano da studiare metodi efficienti per calcolarla, oppure dimostrare che non ne esistono. Un problema strettamente collegato a questo è ancora aperto: quale sia il minimo valore della star-height di espressioni razionali più generali, cioè quelle nelle quali si ammette l'uso della complementazione. Non si conoscono attualmente esempi di star-height maggiore di 1 per queste espressioni.
Teoremi di decomposizione
Due automi finiti possono essere composti per formarne un terzo. Ciò si vede facilmente quando gli automi hanno un output, perché allora definiscono funzioni sulle parole che possono essere composte nel solito modo. Un notevole risultato è stato ottenuto da Keneth Krohn e John L. Rhodes negli anni Sessanta (Krohn e Rhodes 1965). Si tratta di un teorema di decomposizione che afferma che ogni automa finito si può ottenere componendo automi di due tipi: (1) 'automi a gruppo', nei quali le azioni dei simboli sugli stati sono biunivoche; (2) 'automi reset', nei quali l'automa ricorda soltanto l'ultimo simbolo letto.
Questo risultato si applica ai semigruppi finiti e fornisce un teorema di decomposizione per semigruppi. Il teorema corrispondente per gruppi finiti è la nota decomposizione di un gruppo finito nei gruppi semplici che si ottengono a partire da una serie di composizione. Il calcolo della complessità di un semigruppo finito, nel senso del minimo numero di gruppi che compaiono in una decomposizione, è un problema aperto.
Semigruppi e varietà
Si comprese presto che gli automi finiti sono strettamente legati ai semigruppi finiti, ottenendo così l'analogo algebrico della definizione di riconoscibilità da parte di un automa finito. Si possono infatti caratterizzare i linguaggi razionali come quelli che sono riconosciuti da un morfismo su un semigruppo finito, cioè della forma X=φ−1(Y) per qualche morfismo φ:A*→S su un semigruppo finito S, con Y⊂S. Esiste altresì un semigruppo S minimo per ogni X, detto 'semigruppo sintattico' di X.
Il primo importante risultato in questa direzione è il teorema di Schützenberger sui linguaggi star-free. Diamo alcune definizioni. Un linguaggio star-free è un linguaggio che si può ottenere limitando le operazioni razionali, escludendo l'operazione di iterazione, ma ammettendo tutte le operazioni booleane, compresa la complementazione. Per esempio, l'insieme delle successioni di 0 e 1 con le due cifre che si alternano è un linguaggio star-free, in quanto si può ottenere come il complementare dell'insieme delle successioni aventi qualche blocco 00 o 11. Inoltre, un semigruppo finito S si dice 'aperiodico' se esiste un intero n≥1 tale che per ogni x∈S si abbia xn+1=xn. Allora il teorema di Schützenberger afferma che un linguaggio razionale è star-free se e soltanto se è riconosciuto da un semigruppo aperiodico.
La teoria delle varietà di linguaggi razionali si deve a Samuel Eilenberg (1974, 1976). Si tratta in un certo senso del punto di arrivo degli sforzi degli anni precedenti, perché sistema in un quadro unificato molti fatti noti. Formalmente, una varietà di semigruppi è una famiglia di semigruppi finiti chiusa rispetto ai morfismi, al prodotto diretto di due semigruppi e ai sottosemigruppi. Tecnicamente si dovrebbe chiamare 'pseudovarietà' in quanto non è chiusa rispetto a prodotti diretti arbitrari, come nella teoria di Birkhoff. Gli esempi principali sono la varietà dei semigruppi aperiodici e molte sue sottovarietà. Un teorema generale afferma che esiste una corrispondenza tra varietà di semigruppi e famiglie di linguaggi razionali dette anche varietà di linguaggi, nel senso che i semigruppi sono i semigruppi sintattici dei corrispondenti linguaggi. La varietà dei semigruppi aperiodici corrisponde così a quella dei linguaggi star-free.
Una nozione interessante è quella di localizzazione di una varietà V. Un semigruppo S si dice appartenere 'localmente' alla varietà V se, per ogni idempotente e∈S, il semigruppo eSe appartiene a V. Si può dimostrare che la famiglia di questi semigruppi è ancora una varietà; si denota con LV. Per esempio, la varietà dei semigruppi aperiodici coincide con la varietà dei semigruppi localmente banali.
Un altro esempio interessante è dato dalla varietà dei linguaggi localmente testabili. Un linguaggio X si dice 'localmente testabile' se esiste un intero k tale che la proprietà w∈X dipende soltanto dall'insieme dei blocchi di lunghezza k di w. Un semigruppo è idempotente se x=x2 e commutativo se xy=yx, identicamente. Per un importante teorema di McNaughton, Brzozowski e Simon, un linguaggio è localmente testabile se e solo se il suo monoide sintattico è localmente idempotente e commutativo (Eilenberg 1976).
Automi e logica
Si deve a Richard Büchi l'idea di utilizzare gli automi finiti in un contesto nel quale a prima vista essi non compaiono, e cioè nella logica formale. Dai lavori di Kurt Gödel degli anni Trenta era noto che la teoria logica degli interi con le operazioni + e × è indecidibile; ciò lasciava aperta la ricerca di sottoteorie decidibili. Un primo risultato era stato ottenuto da Thomas Pressburger, il quale dimostrò che la teoria degli interi con + come unico operatore è decidibile. Büchi ottenne negli anni Sessanta la decidibilità di un'altra porzione della logica: la teoria monadica del secondo ordine degli interi con successore. La dimostrazione si basa su una riduzione ad automi finiti: l'idea è di considerare un insieme di interi come una successione binaria infinita. Per esempio, l'insieme dei numeri pari corrisponde alla successione 1010101…
I lavori di Büchi hanno aperto un nuovo campo di ricerca, in due direzioni. Una riguarda l'estensione della teoria degli automi finiti a parole infinite (v. oltre); l'altra, lo studio dei legami tra teoria degli automi e logica formale. In questo quadro, Büchi ha dimostrato che i linguaggi razionali sono precisamente quelli che si possono definire in un linguaggio logico che permetta di confrontare le posizioni delle lettere nelle parole e l'uso di quantificatori su insiemi di posizioni (teoria monadica del secondo ordine degli interi con ⟨). Ciò ha aperto la strada alla caratterizzazione in termini di automi di altre classi di teorie logiche.
Una delle prime motivazioni per lo studio dei linguaggi star-free è stata l'osservazione fatta da Robert McNaughton che essi corrispondono alla parte del primo ordine (cioè senza variabili di insiemi) della detta teoria. Più recentemente è stata introdotta una variante di questa logica, la 'logica temporale', che viene applicata alla verifica dei programmi.
Parole infinite e alberi
Il lavoro di Büchi ha dato luogo a una teoria dei linguaggi, detti talvolta ω-linguaggi, nella quale gli elementi non sono parole finite bensì infinite. Tutte le nozioni note nel caso finito si traducono nel caso infinito, anche se le dimostrazioni sono notevolmente più difficili. Per esempio, i fatti fondamentali riguardanti i linguaggi razionali, come la chiusura rispetto alle operazioni booleane, nel caso infinito diventano un risultato molto delicato, dovuto a Büchi, che fa uso del teorema di Ramsey. Analogamente, gli algoritmi di determinazione degli automi finiti diventano, nel caso infinito, un difficile teorema di McNaughton.
Oltre alle parole, si possono definire automi su alberi, anche infiniti. L'idea è semplicemente che processare un albero dall'alto in basso significa duplicare copie dell'automa in ogni figlio del vertice attuale. Lo stato raggiunto nelle foglie (o gli stati infinitamente ripetuti se l'albero è infinito) determina l'accettazione o meno dell'albero da parte dell'automa. Il risultato più noto in questo campo è il teorema di complementazione di Rabin. La dimostrazione si può capire meglio grazie a una serie di idee avanzate da Juri Gurevich e Leo Harrington, il cui punto chiave è l'uso di strategie vincenti in giochi combinatori. L'idea è la seguente: si può descrivere e processare un albero con un automa come un gioco tra due persone. Una di queste (detta l''Automa') sceglie una transizione dell'automa, l'altra (detta l''Esploratore') sceglie una direzione nell'albero. L'Automa ha una strategia vincente se e solo se l'automa accetta l'albero.
Dinamica simbolica
Gli automi finiti hanno numerose relazioni con la 'dinamica simbolica', una teoria sviluppata originariamente da Harold M. Morse e Gustav A. Hedlund. Si tratta di una teoria che studia sistemi dinamici simbolici dati da insiemi di parole doppiamente infinite, invarianti rispetto allo shift e topologicamente chiusi. L'esempio più semplice è l'insieme delle successioni binarie su {a,b} nelle quali non compaiono mai due b consecutive; è il sistema detto della 'sezione aurea'. Di particolare interesse sono i 'subshifts di tipo finito' introdotti da Robert F. Williams, che si possono definire proibendo che compaiano alcune parole, in numero finito. Così il sistema della sezione aurea è un subshift di tipo finito, mentre l'insieme delle parole prive di quadrati non lo è. L''entropia' h(S) di un subshift S è il limite di (1/n)log un, dove un è il numero dei possibili blocchi di lunghezza n di S. Per il sistema della sezione aurea si ha un+1=un+un−1, per cui l'entropia è log φ, dove φ è la sezione aurea, e ciò spiega il nome dato a questo sistema. Un bel risultato della teoria è il teorema di Krieger, che afferma che è possibile immergere strettamente un sottoshift di tipo finito S in un altro T se e solo se: 1) h(S)⟨h(T); 2) pn(S)≤pn(T), per n≥1, dove pn(S) è il numero di punti di periodo n in S. I subshift di tipo finito hanno uno stretto legame con i codici circolari che si studiano nella teoria dei linguaggi formali (Berstel e Perrin 1985).
Automi e gruppi
La 'teoria computazionale dei gruppi' è una branca della teoria dei gruppi che si occupa di computazioni con i gruppi, in particolare con quelli presentati con generatori e relazioni. Molti algoritmi classici, come l'algoritmo di Todd-Coxeter per l'enumerazione delle classi laterali di un sottogruppo, si possono considerare come algoritmi su automi. Una rappresentazione di permutazione di un gruppo finito è un caso particolare di un automa finito (Sims 1994).
La teoria dei gruppi automatici ha origine nel lavoro di molti ricercatori, fra i quali geometri come William P. Thurston e teorici della teoria computazionale dei gruppi come John J. Cannon. Un gruppo si dice 'automatico' se si può rappresentare come un insieme R di parole su un alfabeto A, in modo che per ogni a∈A, la relazione (r,s) su R definita da
sia razionale sincrona
(
denota l'elemento di R corrispondente a x). Una relazione tra parole è razionale sincrona se è un sottoinsieme razionale di (A×A)* (a meno di un'aggiunta - padding - a destra per rendere di uguale lunghezza le parole di una coppia). I risultati fondamentali di questa teoria mostrano che i gruppi automatici hanno piacevoli proprietà (come il fatto che il problema della parola è facilmente risolubile) e che gruppi interessanti, come i gruppi discreti della geometria iperbolica, o gruppi iperbolici, sono automatici.
Grammatiche 'context-free'
La nozione di grammatica context-free è tecnicamente semplice: si tratta di un sistema di regole di riscrittura che servono a formare insiemi di parole su un dato alfabeto. Essa appare esplicitamente nel lavoro di Chomsky (1956) nel quale si cerca un modello per la sintassi dei linguaggi naturali. Le grammatiche sono dette grammatiche a 'struttura di frase' e si basano su idee di analisi sintattica introdotte da Zelig Harris negli anni Quaranta (Harris 1946). Vi sono precedenti nei lavori di logici sui sistemi formali, in particolare Turing (1936-37), A. Thue e E. Post (Post 1936). Parallelamente, e apparentemente in modo indipendente, lo stesso concetto è stato sviluppato dai primi inventori dei linguaggi di programmazione. In particolare, John W. Backus ha utilizzato la forma detta ora BNF (Backus-Naur form) per descrivere la sintassi del linguaggio ALGOL.
a) Linguaggi context-free. Una grammatica context-free (indipendente dal contesto) è un insieme di regole della forma x→w, dove x è un simbolo non terminale (variabile) e w una parola sull'alfabeto misto di simboli terminali e non terminali. Una 'derivazione' consiste nel sostituire un certo numero di volte una variabile mediante l'applicazione di una regola. Il linguaggio 'generato' dalla grammatica è l'insieme delle parole sull'alfabeto terminale che si possono derivare a partire da un simbolo iniziale detto 'assioma'.
Per esempio, la grammatica con una variabile σ e due simboli terminali +, v, e con le due regole σ→+vv e σ→v genera tutte le espressioni additive nella notazione prefissa polacca con v come simbolo operando. Il linguaggio generato è anche detto linguaggio di Lukasiewicz.
Un linguaggio è context-free se e solo se è generato da una grammatica context-free. È facile dimostrare che i linguaggi context-free sono chiusi rispetto a un certo numero di operazioni (compresa l'intersezione con un linguaggio razionale), ma non rispetto alla complementazione.
b) Automi a pila. La nozione di linguaggio context-free è strettamente legata a quella di 'automa a pila'. Si tratta di un automa non deterministico, con una memoria che può essere illimitata ma accessibile unicamente attraverso una modalità ristretta detta 'pila', nella quale è permesso l'accesso soltanto all'ultimo elemento, in un sistema first in-last out. Una parola è accettata da questo automa se esiste un calcolo che porti alla pila vuota. Un risultato elementare afferma che un linguaggio è context-free se e solo se è accettato da un automa a pila.
Il problema dell'equivalenza tra automi a pila (non deterministici) è un problema indecidibile; è infatti chiaramente equivalente a quello dell'equivalenza tra grammatiche context-free. Un problema rimasto a lungo aperto è la decidibilità dell'equivalenza di automi a pila deterministici; esso è stato risolto positivamente da Géraud Sénizergues (Sénizergues 1997, 2002).
c) Gruppi context-free. Un esempio fondamentale di linguaggio context-free è il linguaggio di Dyck, dal nome di uno studioso di teoria dei gruppi (che però appartiene a un periodo precedente a quello delle grammatiche context-free). È il linguaggio delle espressioni ben formate che utilizzano n tipi di parentesi ed è generato dalla grammatica le cui regole sono S→anSān, per n=1,2,… più la regola S→ε.Una versione più simmetrica utilizza anche le regole S→ānSan.
Si tratta in pratica dell'insieme delle parole sull'alfabeto An⋃Ān equivalenti all'identità nel gruppo libero su An.
Più in generale, un gruppo si dice context-free se ammette una presentazione G=⟨A∣R⟩ tale che l'insieme L(G) delle parole su An⋃Ān che si cancellano modulo le relazioni di R è un linguaggio context-free. Un gruppo libero è context-free in quanto il linguaggio di Dyck lo è. Anche un gruppo finito è context-free: il linguaggio L(G) è infatti razionale per qualunque presentazione. Un importante teorema di Muller e Schupp afferma che un gruppo è context-free se e solo se è libero-per-finito (un'estensione di un gruppo libero per un gruppo finito).
d) Sistemi di riscrittura. Molti sistemi computazionali, in particolare quelli che trattano di gruppi, fanno uso di sistemi di riscrittura per ottenere la forma ridotta degli elementi. Per esempio, il procedimento di riduzione di una parola su ai e āi alla corrispondente forma ridotta nel gruppo libero sui simboli āi si può realizzare applicando le regole di riduzione auāi →ε, āi ai →ε.
L'unicità della parola ridotta esprime la proprietà di 'confluenza' del sistema di riscrittura, cioè il fatto che esso fornisce un risultato indipendente dal modo in cui le regole sono applicate. Le cose vanno diversamente se le regole sono del tipo aa→ε, bb→ε, ab→c; in questo caso infatti da aab si possono derivare sia b sia ac. Una coppia come la (b, ac), che consta di due parole irriducibili derivate dalla stessa parola, si definisce 'coppia critica'.
Esiste un algoritmo che permette di completare un sistema di riscrittura e trasformarlo in un uno confluente senza alterare la relazione di equivalenza. Dovuto a Donald E. Knuth e Peter B. Bendix, esso cerca le coppie critiche e le aggiunge (con un opportuno orientamento) alle regole di riduzione. Nell'esempio precedente, aggiungendo le coppie ac→b e cb→a si ottiene un sistema confluente (per un gruppo che è context-free).
e) Una teoria algebrica. È possibile dare una definizione interamente algebrica dei linguaggi context-free. Essa si basa sull'idea che le grammatiche possono essere considerate come un sistema di equazioni. Una caratterizzazione che fa uso del quoziente sinistro di un linguaggio X per una parola u, definito come u−1X={v∣uv∈X}. Questi insiemi si possono usare per caratterizzare i linguaggi razionali. Infatti, un linguaggio è razionale se e solo se l'insieme dei suoi quozienti sinistri è finito. Una famiglia F di sottoinsiemi di A* si dice 'stabile' se u−1X∈F per u∈A* e X∈F. Si possono caratterizzare i linguaggi context-free su A come gli elementi di una sottoalgebra finitamente generata dell'algebra dei sottoinsiemi di A*. Per esempio, il linguaggio di Lukasiewicz L sull'alfabeto {a,b} soddisfa l'equazione L=b+aLL. Così gli insiemi a−1L=L2 e b−1L=ε appartengono all'algebra generata da L.
Computabilità
Riguardo alla classe più grande contenente tutti i linguaggi riconoscibili da macchine, vi sono almeno due modi di affrontarla: uno mediante un modello di macchina (macchina di Turing), l'altro mediante una classe di funzioni (funzioni ricorsive). Questo aspetto era presente anche nel caso dei linguaggi razionali e context-free: nel primo caso avevamo automi finiti ed espressioni razionali, nel secondo automi a pila e grammatiche.
Macchine di Turing
Una macchina di Turing opera con una memoria infinita (in realtà è sufficiente una parola su un alfabeto fissato, detto 'nastro') sulla quale si può leggere e scrivere. La macchina ha inoltre un insieme finito di stati, e si dice che riconosce la parola w data come input se si ferma in uno stato finale. È importante osservare che può anche non fermarsi mai (come ben sanno i programmatori: ogni programmatore ha scritto un programma che entra in un loop).
Un linguaggio L si dice 'ricorsivamente enumerabile' se è riconosciuto da una macchina di Turing. Si dice 'ricorsivamente computabile' (o semplicemente computabile, o decidibile) se è ricorsivamente enumerabile e anche il suo complementare lo è. In modo equivalente, L è computabile se è riconosciuto da una macchina di Turing che si ferma sempre. Un tipico linguaggio indecidibile è l'insieme delle coppie (⟨M⟩, x), dove M è una macchina di Turing, opportunamente codificata da una parola, e x è una parola tale che M si ferma se ha x come input.
Ricorsività
Le funzioni ricorsive si possono definire come funzioni sulle parole, ma è più semplice definirle sugli interi come funzioni numeriche f(x1,x2,...,xp) di p variabili intere a valori interi (a questo livello non è molto importante in quanto gli interi si possono codificare con parole, e viceversa). La classe delle funzioni ricorsive consta delle funzioni che si possono ottenere dalle funzioni iniziali (proiezione, successore e costanti) mediante le seguenti operazioni: (1) composizione; (2) ricorsione primitiva; (3) minimizzazione.
La ricorsione primitiva permette di costruire una funzione f a partire da funzioni g, h mediante f(0, x)=g(x) e f(k+1, x)= =h(f(k,x),k,x). La minimizzazione permette di costruire da una funzione g una funzione f tale che f(x) è il minimo intero m per il quale g(x,m)=0.
È un risultato classico che le funzioni ricorsive e le macchine di Turing, come pure molti altri formalismi, definiscono le stesse classi di oggetti computabili. Che esse corrispondano a ciò che si intende per computabile è un'affermazione nota come 'tesi di Church'. Ovviamente questa nozione di computabilità non tiene conto del tempo e dello spazio occorrenti per effettuare il calcolo, e in questo senso non è realistica. Nel prossimo paragrafo consideriamo il problema della quantità di risorse disponibili.
Classi di complessità
La classe dei linguaggi ricorsivi contiene sottoclassi naturali definite in base alle risorse necessarie per riconoscere una parola di lunghezza n. Le restrizioni possono riguardare sia lo spazio sia il tempo impiegato dalla macchina. Una classe importante è la classe P dei linguaggi (o algoritmi) polinomiali: il tempo impiegato per una computazione da una macchina di Turing deterministica è maggiorato da una funzione polinomiale. Un'altra classe importante è la classe NP: è definita come la P, ma ammette però anche macchine di Turing non deterministiche. Si ha così che un linguaggio è in NP se esiste una ricerca in un albero binario di altezza polinomiale che fornisce il risultato. Un tipico problema della classe NP è la soddisfacibilità delle formule booleane. Queste formule, che sono del tipo
[1] (x∨¬y)∧(¬x∨z)∧…,
comprendono connettivi booleani e la negazione con le variabili x,y,… Per ogni scelta dei valori {vero, falso} per le variabili, è facile verificare se la formula è vera o falsa. Ne segue che il problema di trovare un insieme di valori per i quali la formula è valida è in NP. Si può anche dimostrare che si tratta di un problema NP-completo, nel senso che ogni problema in NP si può ridurre a questo in un tempo polinomiale. Ovviamente P⊂NP; è ragionevole supporre che P≠NP, ma ciò non è stato ancora dimostrato, e anzi costituisce uno dei problemi centrali della teoria computazionale. Per citare una classe definita da restrizioni sullo spazio, la classe PSPAZIO è la classe dei linguaggi riconosciuti da una macchina di Turing che lavora in uno spazio di dimensione maggiorata da un polinomio nella lunghezza dell'input. Si ha NP⊂PSPAZIO. Un tipico problema della classe PSPAZIO è la soddisfacibilità delle formule booleane con quantificatori, per esempio:
[2] ∀x∀y(x∧¬y∨∃z((x∧z)∨(y∧z))).
Un recente risultato caratterizza la classe PSPAZIO in termini di dimostrazioni interattive, una forma moderna del dialogo socratico. Fa uso della nozione di macchina di Turing probabilistica, nella quale le transizioni avvengono in modo casuale: l'accettazione di un dato input x viene sostituita dalla probabilità che x sia accettato. Vi sono due macchine di Turing, il 'Dimostratore' e il 'Verificatore'; l'input è un enunciato da dimostrare. Le due macchine comunicano a ogni passo e il numero dei passi è limitato da un polinomio. Un linguaggio L è in IP (interattivo polinomiale) se esiste una macchina di Turing probabilistica V (il Verificatore) che lavora in tempo polinomiale e tale che x∈L se e solo se esiste una macchina di Turing D (il Dimostratore) tale che x è accettato dalla coppia (D,V) con probabilità maggiore di 1−ε, con ε⟨1/2. Un esempio di problema della classe IP è quello del non-isomorfismo dei grafi. Il Verificatore sceglie a caso un indice i∈{1,2} e una permutazione π, e invia al Dimostratore il grafo H=π(Gi). Il Verificatore trova j∈{1,2} tale che Gj e H sono isomorfi, e accetta se i=j. Joseph Shamir nel 1989 ha dimostrato che si ha IP=PSPAZIO.
Teoria computazionale quantistica
La teoria computazionale quantistica nasce da un suggerimento del fisico Richard P. Feynman (1982), secondo il quale la macchina di Turing può non essere in generale il modello adatto per simulare un sistema fisico quantistico. Gli inizi della teoria risalgono agli anni Novanta, in particolare a David Deutsch (1985). L'idea è di far uso di uno spazio degli stati rappresentato da uno spazio vettoriale di dimensione finita sul campo dei numeri complessi; le transizioni sono trasformazioni unitarie di tale spazio. Uno stato quantistico è un vettore di norma 1.
In tal modo le norme delle coordinate si possono interpretare come la probabilità di trovarsi in un dato stato ordinario. Per esempio, la trasformazione a matrice ortogonale:
trasforma il vettore [1,0] (interpretato come un bit che vale 0 con probabilità 1) nel vettore [1√2,1√2] (dove il bit ha la stessa probabilità di assumere uno dei due valori 0 o 1). Il risultato più importante è dovuto a Peter W. Shor (1997): esso afferma che la fattorizzazione di un intero è polinomiale nel senso della complessità quantistica (mentre si pensa che non appartenga alla classe P della complessità ordinaria).
Complessità di un circuito
Il calcolo del valore di una funzione booleana di n variabili dà luogo a un circuito: si tratta semplicemente di un grafo orientato aciclico con 2n nodi sorgente, e nel quale ciascun nodo è una funzione OR o una funzione AND (fig. 2).
Un tale circuito riconosce un insieme di parole in {0,1}n, e precisamente quelle che corrispondono al valore 1 della funzione. Denotiamo con AC0 la classe dei linguaggi riconosciuti, per ciascuna lunghezza n, da circuiti di dimensione limitata da un polinomio in n e profondità limitata da una costante. La classe più ristretta NC1 è costituita dai linguaggi riconosciuti da circuiti nei quali la profondità, invece che costante, può essere logaritmica, ma il grado entrante di ciascuna porta AND od OR è 2. Si ha AC0⊂NC1. È stato dimostrato (Furst et al. 1984) che l'inclusione è propria: la funzione parità (che ovviamente è in NC1) non sta in AC0. Ulteriori lavori, iniziati da David A. Barrington e Denis Therien (Straubing 1994), hanno dimostrato che vi è un legame tra la complessità di un circuito e le varietà di semigruppi. In particolare, il fatto che la funzione parità non appartiene ad AC0 è una conseguenza del fatto che i linguaggi razionali di AC0 sono i linguaggi star-free.
Serie formali
Invece di considerare semplicemente insiemi di parole, è naturale dal punto di vista matematico considerare funzioni dall'insieme delle parole a valori in un insieme di numeri. L'interpretazione di una parola su 0 e 1 come sviluppo di un intero in base 2 è un esempio di funzione di questo tipo. Essa si può calcolare come l'elemento in alto a destra della matrice ottenuta con la sostituzione:
Questa impostazione permette di considerare importanti nozioni, come quella di molteplicità (quando i valori sono numeri interi) e quella di probabilità (quando i valori sono numeri reali).
Serie razionali
Formalmente, queste funzioni sono spesso chiamate serie formali e denotate come somma:
[5] ∑(S,w)w
di parole w con un coefficiente (S,w). Una serie su un alfabeto A si dice razionale se esiste un morfismo μ da A* nel monoide delle matrici n×n tale che (S,w)=λμ(w)γ per opportuni vettori λ e γ. Questa impostazione algebrica ha il vantaggio di permettere una semplificazione di molti concetti. I linguaggi razionali corrispondono così a soluzioni di sistemi di equazioni lineari. Per esempio, il linguaggio razionale X=(ab+b)* è la soluzione dell'equazione X=(ab+b)X+1. La serie generatrice f(z)=∑nfnzn del numero di parole di lunghezza n in X è allora la frazione razionale:
Serie algebriche
Analogamente, i linguaggi context-free corrispondono a soluzioni di equazioni algebriche. Per esempio, il linguaggio di Dyck generato dalla grammatica D→aDbD∣ε è semplicemente la soluzione dell'equazione D=aDbD+1. Di conseguenza la serie generatrice d(z)=∑ndnzn del numero dn di parole di lunghezza n in D è la serie:
soluzione dell'equazione z2d(z)2−d(z)+1=0.
Le serie formali hanno trovato importanti applicazioni nell'analisi degli algoritmi (Sedgewick e Flajolet 1996) e nella combinatoria enumerativa.
Combinatoria delle parole
I problemi combinatori che riguardano parole sono stati studiati molto presto; i lavori di Thue (1906, 1912) segnano un momento storico. Il risultato più classico, dovuto originariamente a Thue e poi dimostrato più volte in seguito, è l'esistenza di parole infinite prive di quadrati. Un quadrato in una parola è un fattore della forma ww, cioè ripetuto due volte di seguito. Il modo più semplice di ottenere una parola priva di quadrati è il seguente. Si prenda la parola di Thue-Morse
[8] t=abbabaab…
definita come segue. Sia β(n) il numero di 1 nello sviluppo binario di n; allora tn=a, se β(n) è pari e tn=b se è dispari. Si formi quindi la parola:
[9] m=abcacbabcbac…
che è la controimmagine di t nella sostituzione seguente:
[10] a→abb, b→ab, c→a.
Si può allora dimostrare che m è priva di quadrati.
La parola di Thue-Morse non è ovviamente priva di quadrati, in quanto è definita su un alfabeto binario e ogni parola binaria abbastanza lunga ha un quadrato. Tuttavia è priva di cubi, e anche di più: non contiene sovrapposizioni, ovvero fattori della forma uvuvu con u non vuota. Lo studio delle ripetizioni nelle parole ha fatto molti progressi dal lavoro iniziale di Thue.
Parole sturmiane
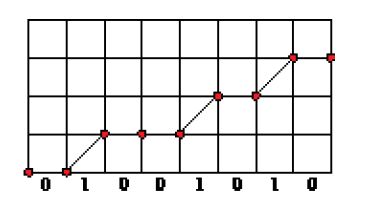
Le parole sturmiane hanno una lunga storia, che risale all'astronomo Johann Bernoulli. Una delle definizioni equivalenti di parola sturmiana è quella di una parola infinita x tale che per ogni n il numero p(n) di blocchi distinti di lunghezza n che vi compaiono è n+1 (si può dimostrare che se p(n)≤n, allora è una costante, e la parola x è definitivamente periodica). L'esempio più semplice di parola sturmiana è la parola di Fibonacci:
[11] f=01001010…
che è il punto fisso della sostituzione 0→01, 1→0. Vi sono tre fattori di lunghezza 2, cioè 00,01 e 10 e quattro fattori di lunghezza 3, cioè 001,010,100 e 101. Si ha anche un'altra definizione della parola di Fibonacci che usa approssimazioni di irrazionali mediante razionali. Infatti, sia s la successione:
[12] sn=⌊(n+1)α⌋−⌊nα⌋,
dove α=1/φ2 con φ=(1+√5)/2, e dove ⌊x⌋ è il massimo intero contenuto in x. Si ha allora s=0f. Questa formula mostra che i simboli fn si possono interpretare come l'approssimazione di una retta di pendenza α con punti a coordinate intere (fig. 3). Per un teorema di Morse e Hedlund, le parole sturmiane si possono anche definire come quelle che hanno n+1 fattori di lunghezza n, o per mezzo di una formula come la [12] con α numero irrazionale.
Equazioni in parole
Le equazioni in parole costituiscono un attivo campo di ricerca. Una tale equazione è semplicemente una coppia x=y di due parole su un alfabeto A∪X di costanti da A e incognite da X. Una soluzione è una sostituzione di una parola su A per ciascuna delle incognite x∈X. Per esempio, l'equazione ax=yb ha la soluzione x=b, y=a. Gennady S. Makanin ha dimostrato per primo che l'esistenza di una soluzione è un problema decidibile.
Applicazioni
Menzioniamo brevemente alcune applicazioni pratiche delle nozioni e dei metodi che abbiamo descritto.
a) Compilatori. La possibilità di compilare in modo efficiente un linguaggio di programmazione di alto livello si può considerare uno dei grandi successi nella storia dell'informatica. Il primo compilatore Fortran fu scritto da Backus negli anni Cinquanta. Da allora centinaia di linguaggi di programmazione sono stati ideati, e scrivere un compilatore fa parte del processare un linguaggio. Il legame con i linguaggi formali è per grandi linee il seguente. La parte lessicale di un compilatore che tratta nozioni di basso livello, come il format dell'input, è descritta da automi finiti. Esistono molti strumenti di software per facilitare l'implementazione di questa parte, che va sotto il nome di 'analisi lessicale'. La sintassi di un linguaggio di programmazione viene inoltre generalmente descritta per mezzo di una grammatica context-free (o di un formalismo equivalente). Il procedimento che controlla la correttezza sintattica (e che computa la struttura sintattica) è noto come 'analisi sintattica' e si effettua con metodi che implementano una forma di automa a pila. La traduzione dal linguaggio sorgente al linguaggio oggetto (un qualche tipo di linguaggio macchina di basso livello) costituisce la terza parte, che implementa l'attraversamento di un albero che può essere descritto da una 'grammatica ad attributi'.
La possibilità di far uso dei metodi della teoria dei linguaggi formali per costruire compilatori viene considerata qualcosa di veramente straordinario.
b) Trattamento di testi. I problemi che comporta il trattamento dei testi sono di livello relativamente basso, ma importanti per la vita di ogni giorno. Essi comprendono l'uso dei processori di parole per un pubblico generale, ma anche tecniche più complicate per produrre testi stampati di alta qualità.
Un campo di ricerca molto attivo è quello degli algoritmi di pattern matching (confronto di schemi). Il più famoso di questi è l'algoritmo di Knuth, Morris e Pratt (Knuth et al. 1977) che permette di localizzare una parola w in un testo t in un tempo proporzionale alla somma delle lunghezze di w e t (e non al loro prodotto, come nell'algoritmo ingenuo che cerca tutte le possibili posizioni di w in t). Questo algoritmo è strettamente legato al calcolo dell'automa minimo che riconosce l'insieme delle parole che terminano con w.
Esistono poi numerosi algoritmi per la compressione dei testi, importante per velocizzarne la trasmissione e ridurne le dimensioni per l'archiviazione. Molti di questi algoritmi si basano su idee che rientrano nel campo degli automi finiti e dei linguaggi formali. Uno dei più famosi è il metodo di Ziv-Lempel che fattorizza l'input in blocchi x1x2…xn… dove xn è la parola più corta tra quelle che non si trovano nella lista (x1,x2,…,xn−1).
c) Linguaggi naturali. Come abbiamo visto, automi e grammatiche sono stati usati fin dall'inizio per processare i linguaggi naturali. Gli automi finiti sono largamente utilizzati (spesso in questo contesto sotto il nome di 'reti di transizione'), con applicazioni alla descrizione di fenomeni di fonetica e di lessicografia, o per la descrizione di frasi elementari (Roche e Schabes 1997). L'uso di grammatiche permette di trattare strutture nidificate come quelle generate da clausole subordinate.
d) Genomi. I progressi della biologia molecolare, e in particolare la scoperta del codice genetico, hanno aperto un nuovo campo di ricerca, la 'biologia computazionale', che tratta sequenze di significato biologico come oggetti computazionali (Waterman 1995).
Numerosi algoritmi sono stati applicati all'analisi di queste sequenze, alcuni pensati appositamente. Uno dei più famosi è il confronto tra sequenze basato sulla ricerca della più lunga sequenza comune. Dovuto originariamente a Daniel S. Hirschberg, è stato riscoperto da vari autori. Permette di determinare, mediante una tecnica detta 'programmazione dinamica', la più lunga sottosequenza comune di due sequenze in un tempo proporzionale al prodotto delle lunghezze delle due (Gusfield 1997). Questa tecnica, che è oggetto di attive ricerche, si può considerare come una sorta di string matching (confronto di sequenze).
Bibliografia
Esistono molti testi che trattano di automi e linguaggi formali; pochi però forniscono una rassegna completa dell'argomento. Ciò è dovuto probabilmente ai diversi punti di vista assunti sia sul versante matematico, sia in quello dell'informatica o dell'ingegneria. Il testo classico per gli informatici è quello di Hopcroft e Ullman (1979), che tratta di automi finiti, grammatiche context-free e anche di computabilità e macchine di Turing. I due volumi di Eilenberg (1974, 1976) si occupano di automi con molteplicità, semigruppi e varietà; la loro pubblicazione ha rappresentato una pietra miliare in questo campo, sia per la qualità della presentazione che per la raffinatezza matematica. Il libretto di Conway (1971), è elegante e stimolante per l'originalità del punto di vista. Testi classici sui linguaggi formali sono quelli di Salomaa e Soittola (1978) e di Berstel e Reutenauer (1988). La serie dei Lothaire (1982, 2002, 2003) ha lo scopo di fornire dei manuali nel campo della combinatoria delle parole. L'Handbook of theoretical computer science di Leeuwen (1990a e b) tratta tutti i campi dell'informatica teorica. Il volume B contiene capitoli di rassegna sugli automi finiti, parole infinite, grammatiche context-free, computabilità, ecc. Più specificamente, l'Handbook of formal languages è una fonte di informazioni su tutti gli aspetti dei linguaggi formali, compresi molti di quelli qui trattati.
Aho 1986: Aho, Alfred V. - Sethi, Ravi - Ullman, Jeffrey D., Compilers, principles, techniques and tools, Reading (Mass.), Addison-Wesley, 1986.
Backus 1959: Backus, John W., The syntax and semantics of the proposed international algebraic language of the Zürich ACM-GAMM conference, Proceedings of the International conference on information processing, Paris, UNESCO, 1959, pp. 125-132,
Bell 1990: Bell, Thimothy - Cleary, John - Witten, Ian, Text compression, Englewood Cliffs (N.J.), Prentice Hall, 1990.
Berstel, Boasson 1996: Berstel, Jean - Boasson, Luc, Towards an algebraic theory of context-free languages, "Fund inform", 25, 1996, pp. 217-239.
Berstel, Perrin 1985: Berstel, Jean - Perrin, Dominique, Theory of codes, New York, Academic Press, 1985.
Berstel, Reutenauer 1988: Berstel, Jean - Reutenauer, Christophe, Rational series and their languages, Berlin-London, Springer, 1988.
Book, Otto 1993: Book, Ronald - Otto, Friedrich, String-rewriting systems, New York, Springer, 1993.
Chomsky 1956: Chomsky, Noam, Three models for the description of language, in: Symposium on information theory held at MIT, September 1956, "IRE transactions on information theory", IT-2, 3, 1956.
Chomsky 1957: Chomsky, Noam, Syntactic structures, 's-Gravenhage, Mouton, 1957 (trad. it.: Le strutture della sintassi, introduzione, traduzione e note di Francesco Antinucci, Bari, Laterza, 1970).
Conway 1971: Conway, John H., Regular algebra and finite machines, London, Chapman and Hall, 1971.
Crochemore, Rytter 1994: Crochemore, Maxime - Rytter, Wojciech, Text algorithms, Oxford, Oxford University Press, 1994.
Deutsch 1985: Deutsch, David, Quantum theory, the Church-Turing principle and the universal quantum computer, "Proceedings of the Royal Society of London", A400, 1985, pp. 97-117.
Eilenberg 1974: Eilenberg, Samuel, Automata, languages and machines, A, New York-London, Academic Press, 1974.
Eilenberg 1976: Eilenberg, Samuel, Automata, languages and machines, B, New York-London, Academic Press, 1976.
Epstein 1992: Epstein, David B.A. e altri, Word processing in groups, Boston (Mass.), Jones and Bartlett, 1992.
Feynman 1982: Feynman, Richard, Simulating physics with computers, "International journal of theoretical physics", 21, 1982, pp. 467-488.
Furst 1984: Furst, Merrick - Saxe, James B. -Sipser, Michael, Parity, circuits and the polynomial time hierarchy,"Mathematical system theory", 17, 1984, pp. 13-27.
Greibach 1981: Greibach, Sheila, Formal languages: origins and directions, "Annals of the history of computing", 3, 1981, pp. 14-41.
Gross, Lentin 1967: Gross, Maurice - Lentin, André, Notions sur les grammaires formelles, Paris, Gauthier-Villars, 1967.
Gusfield 1997: Gusfield, Dan, Algorithms on strings, trees, and sequences, Cambridge, Cambridge University Press, 1997.
Harris 1946: Harris, Zelig, From morpheme to utterance, "Language", 22, 1946, pp. 161-183.
Hashiguchi 1987: Hashiguchi, Kosaburo, Algorithms for determining relative star heigth and star lighting, "Information and computation", 78, 1987, pp. 124-169.
Hopcroft, Ullman 1979: Hopcroft, John E. - Ullman, Jeffrey D., Introduction to automata theory, "Languages and computation", Reading (Mass.)-London, Addison Wesley, 1979.
Kleene 1956: Kleene, Stephen C., Representation of events in nerve nets and finite automata, in: Automata studies, edited by Claude E. Shannon and John McCarthy, Princeton (N.J.), Princeton University Press, 1956, pp. 3-42.
Knuth 1977: Knuth, Donald E. - Morris, James H. - Pratt, Vaughan R., Fast pattern matching in strings, "SIAM journal on computing", 6, 1977, pp. 323-350.
Krohn, Rhodes 1965: Krohn, Keneth - Rhodes, John L., Algebraic theory of machines, I. Prime decomposition theorem for finite semigroups and machines, "Transactions of the American Mathematical Society", 116, 1965, pp. 450-464.
Lallement 1979: Lallement, Gerard, Semigroups and combinatorial applications, New York, Wiley, 1979.
van Leeuwen 1990a: van Leeuwen, Jan, Handbook of theoretical computer science, vol. A: Algorithms and complexity, Amsterdam, North Holland, 1990.
van Leeuwen 1990b: van Leeuwen, Jan, Handbook of theoretical computer science, vol. B: Formal models and semantics, Amsterdam, North Holland, 1990.
Lind, Marcus 1996: Lind, Douglas - Marcus, Brian, Symbolic dynamics and coding, Cambridge, Cambridge University Press, 1996.
Lothaire 1982: Lothaire, M., Combinatorics on words, Cambridge, Cambridge University Press, 1982.
Lothaire 2002: Lothaire, M., Algebraic combinatorics on words, Cambridge, Cambridge University Press, 2002.
Lothaire 2003: Lothaire, M., Applied combinatorics on words, Cambridge, Cambridge University Press, 2003.
McCulloch, Pitts 1943: McCulloch, Warren - Pitts, Walter, A logical calculus of the ideas immanent in nervous activity, "Bulletin of mathematical biophysics", 5, 1943, pp. 115-133.
McNaughton, Papert 1971: McNaughton, Robert - Papert, Seymour, Counter-free automata, Cambridge (Mass.), Massachusetts Institute of Technology Press, 1971.
Muller, Schupp 1983: Muller, David E. - Schupp, Paul E., Groups, the theory of ends, and context-free languages, "Journal of computer and system sciences", 26, 1983, pp. 295-310.
Perrin, Pin 2003: Perrin, Dominique - Pin, Jean-Eric, Infinite words, automata, semigroups, logic and games, Amsterdam, Elsevier, 2003.
Post 1936: Post, Emil L., Finite combinatory processes-formulation 1, "Journal of symbolic logic", 1, 1936, pp. 103-105.
Post 1943: Post, Emil L., Formal reductions of the general combinatorial decision problem, "American journal of mathematics", 65, 1943, pp. 197-215.
Rabin, Scott 1959: Rabin, Michael O. - Scott, Dana, Finite automata and their decision problems, "IBM journal of research and development", 3, 1959, pp. 114-125 (rist. in: Sequential machines, edited by Elisabeth F. Moore, Reading (Mass.), Addison-Wesley, 1964, pp. 63-91).
Roche, Schabes 1997: Roche, Emmanuel - Schabes, Yves, Finite-state language processing, Cambridge (Mass.), Massachusetts Institute of Technology Press, 1997.
Rozenberg, Salomaa 1997: Rozenberg, Grzegorz - Salomaa, Arto, Handbook of formal languages, 3 v. (I: Word, language, grammar; II: Linear modeling, background and application; III: Beyond words), Berlin-New York, Springer, 1997.
Salomaa, Soittola 1978: Salomaa, Arto - Soittola, Matti, Automatic-theoretic aspects of formal power series, New York, Springer, 1978.
Sankoff, Kruskal 1983: Time warps, string edits, and macromolecules: the theory and practice of sequence comparison, edited by David Sankoff and Joseph B. Kruskal, Reading (Mass.), Addison-Wesley, 1983.
Schöning, Pruim 1998: Schöning, Uwe - Pruim, Randall, Gems of theoretical computer science, Berlin-London, Springer, 1998.
Sedgewick, Flajolet 1996: Sedgewick, Robert - Flajolet, Philippe, Analysis of algorithms, Reading (Mass.), Addison-Wesley, 1996.
Sénizergues 1997: Sénizergues, Géraud, The equivalence problem for deterministic pushdown automata is decidable, Proceedings ICALP 97, "Lecture notes in computer science", 1256, 1997, pp. 671-681.
Sénizergues 2002: Sénizergues, Géraud, L(A) = L(B)? A simplified decidability proof, "Theoretical computer science", 281, 2002, pp. 555-608.
Shor 1997: Shor, Peter W., Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer, "SIAM journal on computing", 26, 1997, pp. 1484-1509.
Sims 1994: Sims, Charles, Computation with finitely presented groups, in: Encyclopedia of mathematics and its applications, XLVIII, Cambridge, Cambridge University Press, 1994.
Straubing 1994: Straubing, Howard, Finite automata, formal logic, and circuit complexity, Boston, Birkhäuser, 1994.
Thue 1906: Thue, Axel, Über unendliche Zeichenreihen, "Norske Videnskabers Selskabs skrifter I", Matematisk-Naturvidenskapelig Klasse, 7, 1906, pp. 1-22.
Thue 1912: Thue, Axel, Über die gegenseitige Lage gleicher Teile gewisser Zeichenreihen, "Norske Videnskabers Selskabs skrifter I", Matematisk-Naturvidenskapelig Klasse, 1, 1912, pp. 1-67.
Turing, 1936-37: Turing, Alan M., On computable numbers with an application to the Entscheidungsproblem, "Proceedings of the London Mathematical Society", 42, 1936-1937, pp. 230-265.
Waterman 1995: Waterman, Michael S., Introduction to computational biology, London, Chapman and Hall, 1995.