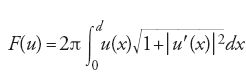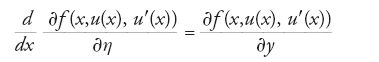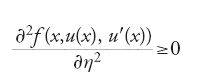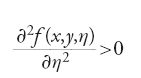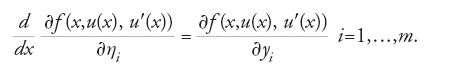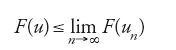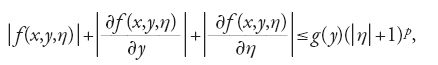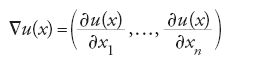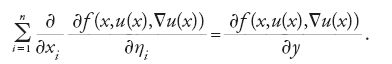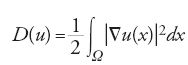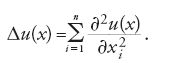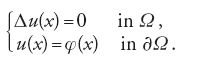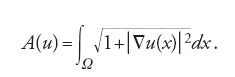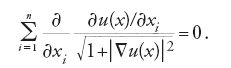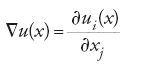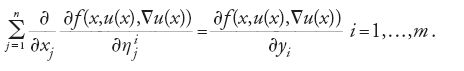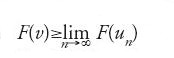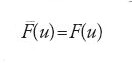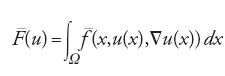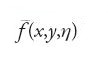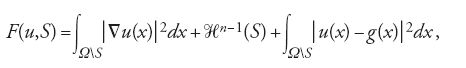La grande scienza. Calcolo delle variazioni
La grande scienza. Calcolo delle variazioni
Calcolo delle variazioni
Un problema di grande importanza nella matematica pura e applicata è la ricerca dei valori massimi o minimi di grandezze dipendenti da variabili di tipo numerico o geometrico. I casi più semplici riguardano grandezze che dipendono da un numero reale o, più in generale, da un numero finito di variabili reali, e possono essere risolti utilizzando i metodi di base del calcolo differenziale.
Più interessanti sono i problemi di massimo o di minimo per grandezze che dipendono da enti matematici che non possono essere individuati da un numero finito di parametri. Un tipico esempio sono le grandezze dipendenti da curve o superfici, quali la lunghezza o l'area, o più in generale le grandezze dipendenti da funzioni di una o più variabili reali. Tali problemi hanno richiesto lo sviluppo di metodologie specifiche, che vanno sotto il nome di 'calcolo delle variazioni', di cui ci occuperemo in questo articolo.
Non considereremo invece i 'problemi di controllo ottimo', introdotti da L.S. Pontrjagin e dalla sua scuola alla fine degli anni Cinquanta. Si tratta di problemi di massimo o di minimo per grandezze che dipendono dalle soluzioni di un'equazione differenziale ordinaria, dipendente a sua volta da un numero finito di funzioni, chiamate 'controlli', che devono essere scelte in modo da ottimizzare il risultato. Questi problemi, di grande importanza per le applicazioni tecnologiche, hanno determinato il rapido sviluppo di una nuova branca dell'analisi matematica, la 'teoria del controllo'.
Per illustrare in maniera elementare le problematiche e i metodi del calcolo delle variazioni, conviene partire da un esempio classico: il problema della 'superficie di rotazione di area minima'. Consideriamo due circonferenze di raggio R1 e R2 su due distinti piani ortogonali alla retta r passante per i due centri; il problema consiste nel trovare, tra tutte le superfici di rotazione di asse r aventi per contorno queste due circonferenze, quella di area minima.
Per formulare il problema in maniera analitica, fissiamo un sistema di coordinate cartesiane su un piano contenente r in modo tale che r sia l'asse delle x, il centro della prima circonferenza abbia coordinate (0,0), e il centro della seconda abbia coordinate (d,0), con d>0. Qualora la superficie di rotazione sia generata da una curva del piano esprimibile come grafico di una funzione positiva y=u(x), la sua area è data dalla classica formula
dove u′ è la derivata della funzione u.
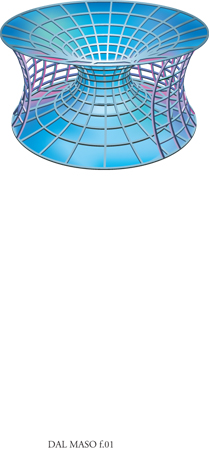
Il problema da esaminare consiste quindi nella ricerca del minimo del funzionale F(u) tra tutte le funzioni u che soddisfano le condizioni agli estremi u(0)=R1 e u(d)=R2, le quali equivalgono al fatto che la superficie abbia per contorno le due circonferenze. Come vedremo, la funzione che realizza il minimo, quando esiste, deve soddisfare un'equazione differenziale, detta 'equazione di Euler', che in questo caso ha come soluzione esplicita le funzioni u(x)=(1/c1)cosh(c1x+c2), dove coshα è il 'coseno iperbolico' di α definito da cosh α=(eα+e−α)/2, mentre le costanti c1 e c2 vanno scelte in modo che valgano le condizioni agli estremi u(0)=R1 e u(d)=R2. Il grafico di queste funzioni è una curva denominata 'catenaria', perché rappresenta la configurazione di equilibrio di un cavo pesante flessibile e inestensibile (catena) fissato agli estremi e soggetto soltanto all'azione della forza di gravità. Dunque, la superficie minima di rotazione, quando esiste, è una 'catenoide', ossia una superficie ottenuta ruotando una catenaria (fig. 1).
Una semplice analisi mostra che per alcuni valori di R1, R2 e d non esiste alcuna coppia di costanti c1, c2 che soddisfi le condizioni al contorno, per altri valori vi è una sola coppia, mentre per altri ancora vi sono due coppie. Un'analisi più accurata mostra che nei primi due casi il problema di minimo non ha soluzione. Nel terzo caso si hanno due catenoidi, una interna e una esterna, di cui quella esterna ha l'area più piccola. Quest'ultima realizza il minimo se, e solo se, la sua area è minore o uguale alla somma delle aree dei due cerchi; questo è l'unico caso in cui il problema di minimo ha soluzione. Esso si verifica quando la distanza d tra i due centri è abbastanza piccola rispetto ai raggi R1 e R2. Nei casi in cui il minimo non esiste, il limite inferiore delle aree delle superfici di rotazione è dato dalla somma delle aree dei due cerchi.
Già tale esempio mostra in maniera chiara una delle problematiche del calcolo delle variazioni: non si tratta soltanto di trovare il minimo, ma anche di stabilire con precisione sotto quali condizioni questo minimo esista.
Tranne pochi esempi nei quali i punti di minimo possono essere descritti attraverso funzioni elementari, nella maggior parte dei casi ci si deve accontentare di uno studio di carattere qualitativo, che serve anche come base per ottenere una soluzione numerica approssimata. Possiamo dividere i problemi affrontati dal calcolo delle variazioni in tre grandi gruppi: (a) determinare condizioni qualitative, sui funzionali da minimizzare e sulle condizioni al contorno, che garantiscano l'esistenza di un minimo; (b) trovare condizioni sulla funzione incognita che siano necessarie e sufficienti per la minimalità: si tratta di condizioni di tipo differenziale, che collegano il problema di minimo con quello di risolvere un'equazione differenziale con determinate condizioni al contorno; (c) dimostrare proprietà qualitative delle funzioni che realizzano il minimo, la più importante delle quali è la 'regolarità': le soluzioni di certi problemi di minimo hanno derivate continue di qualsiasi ordine nel loro dominio di definizione, o almeno in gran parte di esso.
Funzionali integrali per funzioni di una variabile
Molti problemi classici riguardano la ricerca dei minimi di funzionali integrali dipendenti da una funzione u di una variabile reale e dalla sua derivata u′. Si tratta di funzionali del tipo
[2] F(u)=∫baf(x,u(x), u'(x))dx,
dove [a,b] è un intervallo della retta reale ℝ e f(x,y,η) è una funzione regolare di tre variabili reali. Dati due numeri reali α e β, si considera il problema di trovare un minimo di F(u) tra tutte le funzioni u sufficientemente regolari che verificano le 'condizioni agli estremi' u(a)=α e u(b)=β.
Seguendo lo sviluppo storico, cominciamo con l'esaminare le principali 'condizioni di minimalità'. Esse sono ottenute confrontando il valore di F in un punto di minimo u con il valore ottenuto aggiungendo a u una 'variazione' ammissibile v. Le approssimazioni di F(u+v)−F(u) al primo o al secondo ordine rispetto a v determinano la 'variazione prima e seconda' di F nel punto u, il cui studio porta alle seguenti condizioni necessarie di minimalità.
Condizioni necessarie di Euler e di Legendre
Se u è un punto di minimo di [2] con assegnate condizioni agli estremi, allora vale l'eguaglianza
per ogni punto x dell'intervallo [a,b], dove ∂f/∂y e ∂f/∂η sono le derivate parziali di f rispetto a y e η. Questa condizione necessaria di minimalità, detta 'equazione di Euler', è un'equazione differenziale ordinaria, in generale non lineare, del secondo ordine rispetto alla funzione incognita u. Le sue soluzioni sono chiamate 'estremali', oppure 'punti stazionari' o 'punti critici' di F.
Esempi elementari mostrano che non tutti i punti stazionari sono punti di minimo. Un caso molto semplice in cui ogni punto critico è anche punto di minimo è quello in cui il funzionale F è 'convesso', cioè
[4] F(λu+(1-λ)ν)≤λF(u)+(1-λ)F(ν)
per ogni coppia di funzioni u e v e per ogni numero λ compreso tra 0 e 1. Se poi F è 'strettamente convesso', cioè se la [4] vale con la disuguaglianza stretta per u diversa da v, allora il problema di minimo ha al più una soluzione.
La 'condizione necessaria di Legendre' stabilisce che ogni soluzione u del problema di minimo deve soddisfare la disuguaglianza
per ogni punto x dell'intervallo [a,b].
Minimi locali e condizione sufficiente di Jacobi
Una funzione u verificante le condizioni agli estremi è un 'minimo locale' se esiste una costante δ>0 tale che F(u)≤F(v) per ogni funzione v con gli stessi valori agli estremi e con ∣v(x)−u(x)∣⟨δ in ogni punto di [a,b]. Le condizioni necessarie di Euler e di Legendre valgono anche per i minimi locali. Supponiamo che
per ogni (x,y,η). La 'condizione sufficiente di Jacobi' stabilisce che, se u è un'estremale e se l'intervallo [a,b] è abbastanza piccolo, in un senso tecnico ben preciso, allora u è un minimo locale.
Il caso vettoriale
Se la funzione u(x) prende i suoi valori nello spazio euclideo m-dimensionale ℝm, possiamo esprimerla mediante le sue coordinate (u1(x),…,um(x)), e la sua derivata u′(x) è data da (u′1(x),…,u′m(x)). Il funzionale F, di cui si cerca il minimo, si può ancora scrivere nella forma [2], ma questa volta f(x,y,η) è definita per x in [a,b] e per y=(y1,…,ym) e η=(η1,…,ηm) in ℝm. L'equazione di Euler diventa allora un sistema di m equazioni differenziali ordinarie nelle m funzioni incognite u1,…,um:
Le condizioni di Legendre e di Jacobi continuano a valere con ovvie modifiche.
C'è un legame molto stretto tra questi problemi di minimo e la meccanica dei sistemi con un numero finito di gradi di libertà. Nella formulazione di Lagrange le equazioni del moto di un sistema meccanico a m gradi di libertà con vincoli olonomi indipendenti dal tempo e soggetto soltanto a forze conservative si scrivono nella forma [7], dove x rappresenta il tempo, u(x) individua lo stato del sistema, f è la differenza tra l'energia cinetica e l'energia potenziale, e F rappresenta l''azione' del sistema.
I legami tra funzionale e sistema di Euler permettono di dimostrare il 'principio di minima azione': la traiettoria u seguita da un sistema meccanico è sempre un'estremale dell'azione e in generale è un minimo locale se l'intervallo è abbastanza piccolo; in particolari condizioni è anche un minimo assoluto.
Metodi diretti e semicontinuità
Fino alla seconda metà dell'Ottocento i matematici non si erano curati di dimostrare l'esistenza del minimo nei problemi di calcolo delle variazioni. Si presupponeva che un funzionale integrale limitato inferiormente dovesse avere un punto di minimo, e ci si concentrava piuttosto sulle condizioni di minimalità, in modo da individuare i punti di minimo risolvendo un'equazione differenziale. Alcuni esempi proposti da Karl Theodor Wilhelm Weierstrass (1815-1897) mostrarono però che ci possono essere funzionali integrali non negativi, con f molto regolare, che non hanno punti di minimo.
Per risolvere il problema dell'esistenza del minimo si possono utilizzare le condizioni sufficienti di Jacobi o altre, più generali, di Weierstrass, che però richiedono di trovare in via preliminare una soluzione dell'equazione di Euler [3] che soddisfi le condizioni agli estremi. Quest'ultimo problema, che riguarda la teoria delle equazioni differenziali non lineari del secondo ordine, è piuttosto difficile e richiede ipotesi molto forti sulla funzione integranda f.
A partire dagli ultimi anni dell'Ottocento si è cominciato a seguire una strada del tutto diversa, i cosiddetti 'metodi diretti', che permettono di dimostrare l'esistenza del minimo senza impiegare l'equazione di Euler. I primi risultati in questo senso sono dovuti a David Hilbert (1900) per l'integrale di Dirichlet, di cui parleremo in seguito. La sistemazione definitiva dei metodi diretti per funzionali dipendenti da funzioni di una variabile è stata realizzata da Leonida Tonelli (1885-1946), che ha utilizzato a tale scopo la nozione di semicontinuità.
Dato uno spazio astratto U, dotato di una nozione di convergenza, una funzione F definita su U è 'semicontinua inferiormente' se, per ogni u in U e per ogni successione un convergente a u in U, si ha
ogni volta che il limite indicato esiste. Si dice che F è 'coercitiva' se ogni successione un in U, con F(un) limitata superiormente, ha una sottosuccessione che converge a un elemento di U.
Un classico ragionamento introdotto da Weierstrass per provare l'esistenza del massimo e del minimo di una funzione continua definita su un intervallo chiuso e limitato dimostra che ogni funzione semicontinua inferiormente e coercitiva ha un punto di minimo.
Il teorema di esistenza di Tonelli
Lo spazio in cui si ambienta lo studio del funzionale [2] è lo spazio AC([a,b]) delle funzioni 'assolutamente continue' su [a,b]. Si tratta di uno spazio compreso tra lo spazio C0([a,b]) delle funzioni continue su [a,b] e lo spazio C1([a,b]) delle funzioni dotate di derivata prima continua su [a,b].
In base a un classico teorema di Henri-Léon Lebesgue (1875-1941), ogni funzione u di AC([a,b]) è derivabile in tutti i punti di [a,b], eccettuato al più un insieme di punti di misura unidimensionale nulla, e quindi F(u) è ben definito dalla [2]. La nozione di convergenza impiegata in AC([a,b]) è l'usuale convergenza uniforme: un 'converge uniformente' a u se il massimo nell'intervallo [a,b] dello scarto ∣un(x)−u(x)∣ tende a zero per n tendente all'infinito.
Supponiamo che f(x,y,η) sia continua, convessa rispetto a η, ed esistano un esponente p>1 e due costanti c0>0 e c1>0 tali che
[9] f (x,y,η)≥c0∣η∣p-c1(∣y∣+1).
Dai risultati di Tonelli, dimostrati originariamente sotto ipotesi meno generali, si ottiene che F è semicontinuo inferiormente nello spazio AC([a,b]) rispetto alla convergenza uniforme, ed è pure coercitivo sull'insieme delle funzioni che soddisfano le condizioni agli estremi. Ne segue che il problema di minimo per [2] ha soluzione. Un risultato analogo vale nel caso vettoriale.
Regolarità delle soluzioni
Il teorema di esistenza di Tonelli è ottenuto a condizione di ampliare lo spazio in cui si cercano le soluzioni. Precedentemente esse venivano cercate in C1([a,b]) o tutt'al più nello spazio delle funzioni C1 a tratti. Sorge allora il problema di stabilire sotto quali condizioni su f la soluzione in AC([a,b]) trovata con i metodi diretti appartenga a C1([a,b]).
Se f ha derivate parziali continue fino all'ordine k≥2, verifica la [6] e la [9] e se inoltre esiste una funzione continua g tale che
allora ogni soluzione u del problema di minimo su AC([a,b]) ha derivate continue fino all'ordine k su [a,b]. Questo risultato continua a valere, con ovvie modifiche, nel caso vettoriale.
Più difficile è il seguente teorema di 'regolarità parziale' di Tonelli (1915). Se f ha derivate continue di qualsiasi ordine e soddisfa la [6], e u è una soluzione del problema di minimo su AC([a,b]), allora esiste un insieme chiuso E, di misura unidimensionale nulla, fuori dal quale u ha derivate continue di qualsiasi ordine. L'estensione di questo risultato al caso vettoriale è dovuta a F.H. Clarke e R.B. Vinter (1985). Di recente è stato dimostrato che per ogni insieme chiuso E, di misura nulla, esiste una funzione f regolare che soddisfa le ipotesi del teorema di Tonelli e ha un punto di minimo che non ha derivata finita nei punti di E.
Fenomeno di Lavrentiev
Nel 1926 M. Lavrentiev osservò che vi sono casi in cui la soluzione u in AC([a,b]) non solo non è regolare in tutto [a,b], ma addirittura non può essere approssimata con funzioni regolari, nel senso che non esiste alcuna successione un in C1([a,b]) tale che F(un) tenda a F(u). È questo il 'fenomeno di Lavrentiev', molto studiato negli anni Ottanta e Novanta. Vi sono esempi in cui f è una funzione polinomiale, soddisfa la [6] e la [9] e ha un punto di minimo u in AC([a,b]), e un diverso punto di minimo v in C1([a,b]), con F(u)⟨F(v). Questi esempi hanno imposto lo sviluppo di tecniche numeriche nuove per l'approssimazione dei minimi che presentano punti singolari, in quanto i metodi numerici tradizionali risultano inadeguati se non è possibile l'approssimazione con funzioni di classe C1([a,b]).
Geodetiche
Un classico problema che rientra nel quadro dei funzionali integrali considerati finora è quello delle geodetiche su una superficie. Una 'geodetica minimale' è una curva sulla superficie avente lunghezza minore o uguale a quella delle altre curve sulla superficie con gli stessi estremi, mentre una 'geodetica' è una curva i cui archi sufficientemente piccoli sono geodetiche minimali. Per esempio, ogni arco di cerchio massimo è una geodetica sulla sfera, mentre solo quelli di ampiezza minore o uguale a 180° sono geodetiche minimali. Analogamente ogni arco di elica cilindrica è una geodetica sul cilindro, mentre solo quelli che non si avvolgono per più di mezzo giro sono minimali.
Il teorema di Hopf-Rinow (1931) garantisce che, se due punti di una superficie chiusa possono essere congiunti da una curva sulla superficie, allora possono essere congiunti anche da una geodetica minimale. Questo risultato ha un'estensione naturale al caso di 'varietà riemanniane' di dimensione arbitraria, che costituiscono l'analogo a più dimensioni della nozione di superficie.
Altri risultati molto importanti riguardano le geodetiche chiuse. Il teorema di Birkhoff (1917) assicura che su ogni superficie bidimensionale del tipo della sfera c'è almeno una geodetica chiusa, e il successivo teorema di Lyusternik-Schnirelmann (1929) garantisce che ce ne sono almeno tre senza autointersezioni. In dimensione più alta ogni varietà riemanniana del tipo della sfera n-dimensionale ha almeno una geodetica chiusa (Birkhoff 1927) e il risultato vale anche nel caso generale di varietà compatte (Lyusternik e Fet 1951). Usando strumenti topologici più raffinati sono stati ottenuti in seguito molti altri risultati di notevole interesse riguardanti il numero delle geodetiche congiungenti due punti, anche in presenza di ostacoli, o nel caso più difficile delle 'varietà lorentziane' usate nella teoria della relatività generale.
Problemi per integrali multipli: caso scalare
Consideriamo ora il caso dei funzionali F dipendenti da funzioni u a valori reali definite su una regione limitata ω dello spazio euclideo n-dimensionale ℝn, con bordo ∂ω sufficientemente regolare. Esaminiamo in particolare i funzionali del tipo
[11] F(u)=∫Ωf(x,u(x),∇u(x))dx,
dove f(x,y,η) è una funzione definita per x=(x1,…,xn) in ω, y in ℝ, e η=(η1,…,ηn) in ℝn. Qui e in seguito
è il 'gradiente' della funzione u e dx=dx1…dxn indica l'integrazione rispetto alla misura n-dimensionale. Le condizioni agli estremi sono sostituite, in questo caso, da una 'condizione al contorno': si richiede che u coincida con una funzione assegnata φ in ogni punto di ∂ω.
Equazione di Euler
L'equazione di Euler per il funzionale [11] è un'equazione differenziale alle derivate parziali del secondo ordine in ω, che si scrive
Le ipotesi che faremo in seguito per garantire l'esistenza di un punto di minimo implicano che l'equazione di Euler sia di tipo ellittico. In molti casi è difficile dimostrare l'esistenza di una soluzione della [13] che soddisfi le condizioni al contorno usando solo i metodi della teoria delle equazioni differenziali. Si preferisce quindi capovolgere i termini del problema, ottenendo l'esistenza di una soluzione dell'equazione di Euler a partire dall'esistenza di un minimo fornita dai metodi diretti del calcolo delle variazioni, che garantiscono il risultato in ipotesi molto generali.
Si è così venuto a creare nella seconda metà del Novecento uno stretto legame tra il calcolo delle variazioni e lo studio delle 'equazioni ellittiche non lineari': i risultati più completi sono stati ottenuti per quelle che possono essere viste come equazione di Euler di un funzionale di tipo [11]. Per lo studio delle soluzioni della [13] è importante trovare non solo un punto di minimo della [11], ma anche gli eventuali punti critici. Un'intera branca dell''analisi non lineare', che va sotto il nome di 'metodi variazionali', si è sviluppata per ottenere risultati di esistenza e molteplicità per i punti critici della [11]. Si tratta di una linea di ricerca molto attiva, che sta ottenendo notevoli risultati in molti problemi di interesse geometrico o fisico-matematico.
Teoremi di esistenza per integrali multipli
Per applicare i metodi diretti al caso degli integrali multipli del tipo [11] è opportuno utilizzare gli spazi di Lebesgue e di Sobolev. Dato un esponente p≥1, lo spazio di Lebesgue Lp(ω) è costituito dalle funzioni u definite su ω tali che ∣u∣p sia integrabile nel senso di Lebesgue. Si dice che uk converge a u in Lp(ω) se l'integrale di ∣uk−u∣p tende a zero per k tendente all'infinito.
Usando un procedimento che ha trovato una sistemazione definitiva nella teoria delle distribuzioni sviluppata negli anni Cinquanta da L. Schwartz, è possibile introdurre una nozione debole di derivata parziale per funzioni u di Lp(ω), che coincide con quella usuale se u ha derivate parziali continue.
Lo spazio di Sobolev W1,p(ω) è costituito delle funzioni u in Lp(ω) le cui derivate parziali deboli ∂u/∂xi appartengono a Lp(ω) per i=1,…,n. Dato che è possibile definire la 'traccia' sul bordo ∂ω di ogni funzione u di W1,p(ω), la condizione al contorno u(x)=φ(x) su ∂ω va intesa nel senso delle tracce.
Supponiamo che f(x,y,η) sia semicontinua inferiormente rispetto a (y,η), sia convessa rispetto a η, e che valga la [9] con un esponente p>1, dove ∣η∣ è ora la norma euclidea del vettore η=(η1,…,ηn), definita da ∣η∣2=∣η1∣2+…+∣ηn∣2. Il funzionale F è allora semicontinuo inferiormente su W1,p(ω) rispetto alla convergenza Lp(ω). In questa forma generale, in cui non viene richiesta la continuità di f, tale risultato è stato ottenuto, con diverse dimostrazioni, da C. Olech nel 1976 e da A.D. Ioffe nel 1977.
Utilizzando la teoria degli spazi di Sobolev, sviluppata tra gli anni Trenta e gli anni Cinquanta, si verifica che nelle ipotesi avanzate il funzionale F è anche coercitivo rispetto alla convergenza Lp(ω) sullo spazio delle funzioni u in W1,p(ω) aventi traccia assegnata su ∂ω. Applicando i metodi diretti del calcolo delle variazioni, si deduce quindi che il problema di minimo ha soluzione in W1,p(ω) se c'è almeno una funzione di W1,p(ω) che ha φ come traccia su ∂ω.
Regolarità delle soluzioni
Sotto opportune condizioni su f, che sono verificate in molti casi significativi, tutte le soluzioni del problema di minimo in W1,p(ω) hanno derivate continue di qualsiasi ordine in ω, sono anzi funzioni analitiche, cioè sviluppabili in serie di potenze nell'intorno di ciascun punto di ω. Questo risultato, che costituisce la soluzione del diciannovesimo dei 23 problemi proposti da Hilbert nella sua celebre conferenza al Congresso Mondiale dei Matematici di Parigi del 1900, nel caso di dimensione n arbitraria è una conseguenza del teorema di hölderianità di Ennio De Giorgi e John Nash per le soluzioni di equazioni ellittiche lineari. Esso è stato dimostrato nel 1957 per p=2 ed esteso poco dopo al caso p≠2 a opera di vari autori.
Integrale di Dirichlet e funzioni armoniche
Un classico problema per integrali multipli riguarda l''integrale di Dirichlet'
che ha uno stretto legame con l''operatore di Laplace'
Infatti l'equazione di Laplace Δu(x)=0, le cui soluzioni sono dette funzioni 'armoniche', è l'equazione di Euler dell'integrale di Dirichlet. Poiché tale funzionale è convesso, se φ è abbastanza regolare le soluzioni del problema di minimo per D(u) con condizione al contorno φ coincidono con le soluzioni del 'problema di Dirichlet' per l'equazione di Laplace
Questa equivalenza fu usata da Hilbert nel 1900 per dare la prima dimostrazione rigorosa dell'esistenza della soluzione del problema di Dirichlet, nel caso di domini limitati e uniformemente convessi del piano con bordo sufficientemente regolare.
Con metodi analoghi si studia l''equazione di Poisson' Δu(x)=f(x), che compare in moltissimi problemi di fisica matematica riguardanti mezzi lineari omogenei e isotropi, tra i quali i problemi di elettrostatica, di campi gravitazionali e di equilibrio di membrane elastiche.
La nozione di integrale di Dirichlet può essere estesa al caso in cui u sia una funzione definita su una varietà riemanniana e prenda i suoi valori in un'altra varietà riemanniana. In tal caso i punti stazionari sono le 'mappe armoniche' tra le due varietà, lo studio delle quali è legato a interessanti questioni di topologia e di geometria differenziale.
Superfici cartesiane di area minima
Se u ha derivate parziali continue, l'area del suo grafico è data da
Il problema di minimo per il funzionale A(u), con le condizioni al contorno u(x)=φ(x) su ∂ω, è detto 'problema dell'area minima in forma cartesiana'.
La richiesta che la superficie minima sia di tipo cartesiano, cioè rappresentabile come grafico di una funzione, impone alcune restrizioni geometriche su ∂ω e su φ. Per esempio, se ω è una corona circolare e φ è costante in ciascuna delle due componenti del bordo, si dimostra che la superficie cartesiana di area minima esiste se, e solo se, le costanti sono vicine tra loro.
Se invece ω è una regione piana uniformenente convessa e φ è abbastanza regolare, il problema dell'area minima in forma cartesiana ha una e una sola soluzione. La dimostrazione, dovuta a A. Haar (1927), utilizza il metodo di Hilbert per l'integrale di Dirichlet. L'estensione al caso n-dimensionale è stata ottenuta da M. Miranda (1965). Servendosi di metodi più raffinati, H. Jenkins e J. Serrin (1968) hanno dimostrato che è possibile alleggerire le ipotesi geometriche su ω e di regolarità su φ.
L'equazione di Euler del funzionale A(u) è detta 'equazione delle superfici minime'; essa esprime la proprietà geometrica che il grafico di u abbia curvatura media nulla:
Un'importante proprietà di questa equazione per n=2 è il 'teorema di Bernstein': ogni soluzione della [18] definita su tutto il piano ha come grafico un piano. Dopo la dimostrazione di S. Bernstein (1915) rimase aperto per molti anni il problema analogo in dimensione più alta. Si trattava di stabilire se ogni soluzione u della [18] definita su tutto ℝn avesse per grafico un iperpiano, cioè si potesse scrivere come u(x)=a0+a1x1+…+anxn con opportune costanti a0, a1,…,an.
Questa proprietà è stata dimostrata da De Giorgi (1965) per n=3 e da F.J. Almgren (1966) per n=4. Il caso n≤7 è stato risolto positivamente da J. Simons (1968). Invece per n≥8 il teorema di Bernstein non vale, come mostra un controesempio di Bombieri, De Giorgi e Giusti (1969).
Problemi per integrali multipli: caso vettoriale
Prendiamo ora in considerazione il caso in cui u prende i suoi valori nello spazio euclideo m-dimensionale ℝm. Il funzionale F è ancora del tipo [11], ma in questa ipotesi
è una matrice m×n e, di conseguenza, f(x,y,η) è una funzione definita per x=(x1,…,xn) in ω, y=(y1,…,ym) in ℝm, e η=(ηij) nello spazio delle matrici m×n. Problemi di minimo per questi funzionali sono stati molto studiati a partire dalla fine degli anni Settanta per il loro legame con problemi di elasticità non lineare.
L'equazione di Euler diventa un sistema di m equazioni alle derivate parziali del secondo ordine nelle m funzioni incognite u1,…,um:
Teoremi di esistenza nel caso vettoriale
I risultati del caso scalare si estendono senza difficoltà al caso vettoriale, ma, mentre per m=1 il teorema di semicontinuità esposto sopra è ottimale, nel senso che l'ipotesi di convessità di f(x,y,η) rispetto a η è necessaria per la semicontinuità inferiore di F, nel caso vettoriale m>1 vi sono funzionali, di notevole interesse nella teoria dell'elasticità non lineare, che sono semicontinui inferiormente senza che f sia convessa rispetto alla matrice η=(ηij).
Nel caso m>1 la condizione che risulta necessaria e, con ipotesi aggiuntive, anche sufficiente per la semicontinuità inferiore dei funzionali integrali, è la 'quasi convessità', introdotta da Charles B. Morrey nel 1952. Una funzione g(η), definita nello spazio delle matrici η=(ηij) di tipo m×n, si dice 'quasi convessa' se, fissato un cubo Q n-dimensionale di lato uno, vale la disuguaglianza
[21] g(η)≤∫Ωg(η+∇ψ(x))dx
per ogni matrice η e per ciascuna funzione ψ definita su Q, a valori in ℝm, nulla sul bordo di Q e dotata di derivate parziali continue.
Ogni funzione convessa risulta quasi convessa, e le due nozioni coincidono se n=1 oppure m=1. Una sottoclasse particolarmente interessante di funzioni quasi convesse è quella delle funzioni 'policonvesse' (Ball 1977), cioè delle funzioni del tipo g(η)=h(M(η)), dove h è una funzione convessa e M(η) indica il vettore le cui componenti sono i determinanti di tutte le sottomatrici quadrate, dette minori, della matrice η=(ηij). Semplici esempi mostrano che vi sono funzioni policonvesse che non sono convesse.
Siano Lp(ω;ℝm) e W1,p(ω;ℝm) gli spazi delle funzioni u, definite su ω e a valori in ℝm, le cui componenti u1,…,um appartengono a Lp(ω) e a W1,p(ω). Supponiamo che f(x,y,η) sia continua rispetto a (y,η) e quasi convessa rispetto a η. Supponiamo inoltre che valga la [9] con un esponente p>1 e che esista una costante c2>0 tale che
[22] f(x,y,η)≤c2(∣η∣+∣y∣+1)p.
Il funzionale F definito dalla [11] è allora semicontinuo inferiormente su W1,p(ω;ℝm) rispetto alla convergenza Lp(ω;ℝm), definita componente per componente. Questo risultato, dimostrato da Morrey (1952) in una forma leggermente diversa, è stato esteso da Emilio Acerbi e Nicola Fusco (1984) al caso in cui f(x,y,η) sia discontinua rispetto a x. La coercitività si dimostra come nel caso scalare, e dunque i metodi diretti assicurano che il problema di minimo per F con condizione al contorno φ ha soluzione in W1,p(ω;ℝm) se esiste almeno una funzione di W1,p(ω;ℝm) che ha φ come traccia su ∂ω.
Un importante problema aperto del calcolo delle variazioni per le funzioni vettoriali è trovare una caratterizzazione più maneggevole delle funzioni quasi convesse. È noto che tutte le funzioni quasi convesse sono 'convesse di rango uno', cioè verificano la disuguaglianza
[23] g(λξ+(1-λ)η)≤λg(ξ)+(1-λ)g(η)
per ogni λ compreso tra 0 e 1 e per ogni coppia di matrici ξ e η tali che la differenza ξ−η abbia rango minore o uguale a uno, cioè tutte le sue sottomatrici quadrate di ordine maggiore di uno abbiano determinante nullo. Morrey (1966) aveva congetturato che la convessità di rango uno implicasse la quasi convessità, ma un controesempio di Vladimir Sverák (1992) ha mostrato che ciò non è vero, almeno per n≥2 e m≥3. Recenti risultati di Jan Kristensen (1998) mostrano che nessuna condizione di natura locale su g può essere equivalente alla quasi convessità.
Un altro problema aperto consiste nell'indebolire l'ipotesi [22] che interviene nel teorema di semicontinuità e che esclude molti funzionali interessanti per le applicazioni all'elasticità non lineare.
Regolarità parziale delle soluzioni
Nel caso vettoriale non sempre i punti di minimo sono regolari in tutto il dominio ω. Il primo esempio di funzionale regolare con punti di minimo discontinui è dovuto a Enrico Giusti e Mario Miranda (1968). È possibile, sotto opportune ipotesi, ottenere risultati di 'regolarità parziale', cioè dimostrare che la soluzione della [11] ha derivate continue di qualsiasi ordine in un sottoinsieme ω0 di ω che differisce da ω per un insieme di misura n-dimensionale nulla. Questi risultati sono stati ottenuti a partire dalla fine degli anni Settanta per f convessa in η, ed estesi al caso quasi convesso negli anni Ottanta.
Rilassamento di problemi di minimo
Se un funzionale F su uno spazio astratto U non è semicontinuo inferiormente, il problema di minimo può non avere soluzione. È utile allora considerare il 'funzionale rilassato'
,
definito come il più grande funzionale semicontinuo inferiormente che sia minore o uguale a F. Se F è coercitivo, lo è anche
,
e dunque
ha punti di minimo in U, che si possono caratterizzare come limiti di 'successioni minimizzanti' di F, dove con questo termine s'intende una successione un in U tale che
per ogni v in U.
Il funzionale rilassato appare dunque uno strumento utile per individuare le successioni minimizzanti di F. In qualche caso fortunato si verifica anche che
su un punto di minimo di
,
e ciò permette di affermare che u è un punto di minimo anche di F.
In molti casi, se F è un funzionale integrale, lo è anche
Per esempio, se F è definito da [11] con u vettoriale, e f è continua rispetto a (y,η) e verifica la [9] e la [22] con p>1, allora il funzionale rilassato
rispetto alla convergenza Lp(ω;ℝm) è dato da
dove
è la più grande funzione quasi convessa in η che sia minore o uguale a f(x,y,η) (Dacorogna 1982; Acerbi e Fusco 1984).
Una situazione molto interessante si presenta quando la [9] e la [22] valgono con p=1. Lo spazio di Sobolev W1,1(ω;ℝm) non è adatto in questo caso all'uso dei metodi diretti, perché viene a mancare la coercitività. È quindi opportuno estendere il funzionale a uno spazio ancora più ampio, lo spazio BV(ω;ℝm) delle funzioni a variazione limitata su ω a valori in ℝm. L'estensione più conveniente si ottiene con il metodo del rilassamento: si considera il più grande funzionale che sia semicontinuo inferiormente su BV(ω;ℝm) rispetto alla convergenza L1(ω;ℝm) e che sia minore o uguale a F su W1,1(ω;ℝm). Formule di rappresentazione per tali funzionali rilassati, che permettono di studiare le proprietà dei punti di minimo, sono state ottenute sotto varie ipotesi, negli anni Ottanta nel caso m=1, negli anni Novanta nel caso generale.
Γ-convergenza
A partire dagli anni Settanta De Giorgi e i suoi collaboratori hanno sviluppato una nozione di convergenza per funzionali, la γ-convergenza, che unifica diverse nozioni di convergenza variazionale e garantisce la convergenza dei punti di minimo, in presenza di opportune condizioni di coercitività uniforme.
I risultati più interessanti riguardano la stabilità di alcune classi di funzionali integrali. Il seguente risultato, che discende da un recente teorema di G. Bouchitté, I. Fonseca, G. Leoni e L. Mascarenhas (2002), comprende gran parte di quelli precedenti: se Fk è una successione di funzionali definiti dalla [11] e le corrispondenti fk verificano la [9] e la [22] con costanti indipendenti da k, allora esiste una sottosuccessione Fkj che Γ-converge a un funzionale F0, che è ancora definito dalla [11] con una funzione f0(x,y,η), convessa in η nel caso m=1 e quasi convessa nel caso m>1. Da ciò segue che se uj sono punti di minimo di Fkj con un'assegnata condizione al contorno, allora uj ha una sottosuccessione che converge a un punto di minimo u0 di F0 con le stesse condizioni al contorno, e l'intera successione uj converge a u0 se tale punto di minimo è unico.
In certi casi è possibile calcolare f0 a partire dalle fk. Per esempio, questo accade nei cosiddetti 'problemi di omogeneizzazione', nei quali si considerano integrandi della forma fk(x,y,η)=f(kx,y,η), con f(x,y,η) periodica rispetto a x, studiati da P. Marcellini (1978) per m=1 e da A. Braides (1985) e S. Müller (1987) per m>1. Questi problemi sono legati allo studio del comportamento macroscopico di materiali elastici non omogenei a struttura microscopica di tipo periodico. Il funzionale F0 rappresenta allora l'energia elastica di un materiale omogeneo che, in un senso tecnico molto preciso se il periodo della struttura microscopica è piccolo, ha un comportamento vicino a quello del materiale non omogeneo.
Problemi geometrici
Il maggiore problema geometrico del calcolo delle variazioni è quello delle superfici di area minima, detto anche 'problema di Plateau' in onore del fisico belga Joseph-Antoine-Ferdinand Plateau (1801-1883) che nel suo trattato del 1873 descrisse un gran numero di esperimenti su pellicole liquide sottili. Egli notò che un filo chiuso, di qualunque forma, delimita sempre almeno una pellicola di acqua saponata in equilibrio stabile. In base alla teoria della capillarità ogni pellicola ha un'energia potenziale proporzionale alla sua area, e dunque le pellicole in equilibrio stabile corrispondono a superfici di area minima tra quelle di uguale contorno.
Superfici minime parametriche
Per una formulazione rigorosa del problema di Plateau va precisata la nozione di superficie. Si può usare la forma parametrica x=x(u,v), y=y(u,v), z=z(u,v), chiedendo che il punto (u,v) vari, per esempio, nel cerchio unitario. Si parla allora di 'superfici del tipo del disco'. Cercando il minimo in questa classe, il problema di Plateau si formula nel modo seguente: assegnata una curva semplice chiusa Γ nello spazio tridimensionale, trovare le superfici del tipo del disco di area minima tra quelle aventi Γ per contorno (fig. 2).
L'esistenza di una soluzione per un'arbitraria curva semplice chiusa di lunghezza finita è stata dimostrata da J. Douglas (1930) e, indipendentemente, da T. Radó. Una notevole semplificazione fu trovata da R. Courant (1936) e, indipendentemente, da Tonelli. Un risultato del tutto analogo vale quando Γ sia una curva semplice chiusa di lunghezza finita in ℝn e si cerchi in tale spazio una superficie bidimensionale del tipo del disco, di area minima tra quelle aventi Γ per contorno.
Frontiere di area minima
I metodi utilizzati per le superfici minime del tipo del disco non si estendono al caso di varietà di dimensione k in ℝn con 2⟨k⟨n.
Se k=n−1, è possibile formulare e risolvere interessanti problemi di area minima mediante la teoria dei perimetri introdotta da R. Caccioppoli e De Giorgi negli anni Cinquanta del sec. XX. Data una regione ω di ℝn, è possibile definire per ogni sottoinsieme E di ℝn un ben determinato valore P(E,ω), finito o infinito, detto 'perimetro' di E in ω, che, se il bordo di E è sufficientemente regolare, coincide con la misura (n−1)-dimensionale della porzione del bordo di E interna a ω.
Si dice che un insieme E ha 'frontiera minima' in un dominio limitato ω se P(E,ω)⟨+∞ e P(E,ω)≤P(F,ω) per ogni altro insieme F che coincida con E vicino al bordo di Ω. Il problema più importante in questo approccio, in cui, almeno inizialmente, si considerano anche insiemi E molto irregolari, consiste nel dimostrare la regolarità degli insiemi con frontiera localmente minima. Per n≤7 i risultati ottenuti da De Giorgi negli anni Sessanta permettono di stabilire che, se E ha frontiera minima in Ω, allora la parte del bordo di E interna a Ω è una varietà (n−1)-dimensionale regolare. Nel caso n=8 il cono di Simons, costituito dai punti le cui coordinate (x1,…,x8) soddisfano la disuguaglianza
è un esempio di insieme E la cui frontiera, pur non essendo regolare nel punto di coordinate (0,…,0), è minima in ogni dominio limitato Ω contenuto in ℝ8 (Bombieri et al. 1969). Nel caso n≥8 Herbert Federer (1970) ha dimostrato che, se E ha frontiera minima in Ω, allora la parte del bordo di E contenuta in Ω è una varietà (n−1)-dimensionale regolare, eccettuato un insieme singolare di dimensione minore o uguale a n−8.
Questi metodi permettono di ottenere risultati analoghi di esistenza e di regolarità per altri problemi di natura geometrica, quali, per esempio, quelli di area minima a volume assegnato, tra cui rientra il classico problema isoperimetrico, formulato qui in condizioni di estrema generalità. A questo proposito De Giorgi (1958) ha dimostrato che tra tutti gli insiemi di misura n-dimensionale assegnata in ℝn, la sfera ha perimetro minimo.
Varietà minime di dimensione arbitraria
Nello spazio ℝn l'analogo k-dimensionale del problema di Plateau è il seguente: assegnata una varietà regolare orientata Γ di dimensione k−1, limitata e priva di bordo, trovare una varietà k-dimensionale orientata S di misura k-dimensionale minima tra quelle aventi γ come bordo orientato.
Seguendo un metodo abituale nel moderno calcolo delle variazioni, anche questo problema è stato risolto introducendo una formulazione debole, in cui si amplia la classe ove si cerca il minimo, includendovi oggetti anche molto irregolari. In questo caso si utilizza la teoria delle 'correnti rettificabili': una generalizzazione della nozione di varietà k-dimensionale orientata, che include diversi nuovi enti identificabili con varietà anche molto irregolari, ma per i quali si può ancora parlare, in un senso tecnico ben preciso, di bordo orientato e di misura k-dimensionale.
L'esistenza di una soluzione nello spazio delle correnti rettificabili si ottiene con i metodi diretti grazie al teorema di compattezza di Federer e W.H. Fleming (1960). Per quanto riguarda la regolarità delle soluzioni, vi sono risultati parziali per 1⟨k⟨n−1 e risultati completi nel caso k=n−1 che utilizzano le tecniche sviluppate nella teoria dei perimetri: se n≤7, allora le correnti minime di dimensione n−1 sono varietà regolari al di fuori di γ, mentre, se n≥8, esse possono presentare un insieme singolare di dimensione minore o uguale a n−8 (Federer 1970).
Problemi con discontinuità libera
Si tratta di problemi di minimo nei quali la funzione incognita u presenta, in posizione da determinarsi, una superficie di discontinuità S che influisce sul valore del funzionale da minimizzare. Nei casi più comuni questo contiene, oltre a un termine dipendente da S, un integrale di volume, dipendente dalla funzione u e dalle sue derivate sul complementare di S. Questi problemi mescolano dunque le caratteristiche dei problemi di minimo per funzionali integrali con quelle dei problemi di tipo geometrico.
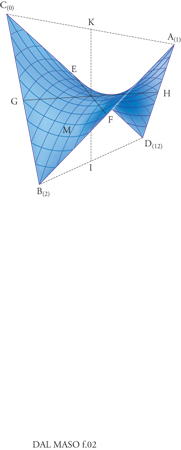
Il primo di tali problemi è stato proposto nel 1985 da D. Mumford e J. Shah in relazione allo studio della segmentazione delle immagini nella teoria della visione. Questioni analoghe si incontrano in vari rami della fisica matematica, per esempio nello studio della meccanica delle fratture. Data una funzione limitata g definita su una regione limitata Ω di ℝn, il problema consiste nel trovare il minimo del funzionale
dove Ω∖S indica l'insieme dei punti di Ω che non stanno in S e ℋn-1(S) indica la misura (n−1)-dimensionale di S. La principale novità consiste nel fatto che vi sono due incognite di natura diversa rispetto alle quali va cercato il minimo: l'insieme S, che varia tra i sottoinsiemi di Ω di misura (n−1)-dimensionale finita, e la funzione u, che varia tra le funzioni dotate di derivate parziali continue su Ω∖S.
La soluzione di questo problema è stata ottenuta dimostrando prima, con i metodi diretti, l'esistenza di un'opportuna soluzione generalizzata in un nuovo spazio funzionale introdotto da Luigi Ambrosio e De Giorgi nel 1988, e mostrando successivamente, con un primo teorema di regolarità, che tale soluzione generalizzata risolve il problema proposto (De Giorgi et al. 1989). Un successivo teorema di regolarità ha mostrato che l'insieme S corrispondente a un punto di minimo è una varietà regolare di dimensione n−1, a meno di un insieme singolare avente misura (n−1)-dimensionale nulla (Ambrosio e Pallara 1997a; Ambrosio et al. 1997b), mentre la regolarità della funzione u segue dai risultati classici per i minimi dell'integrale di Dirichlet.
Rimangono aperti problemi interessanti a proposito della struttura dell'insieme singolare della varietà S. In particolare non è noto se per n=2 questo insieme singolare sia costituito da un numero finito di punti.
Bibliografia
Acerbi 1984: Acerbi, Emilio - Fusco, Nicola, Semicontinuity problems in the calculus of variations, "Archives for rational mechanics and analysis", 86, 1984, pp. 125-145.
Ambrosio 1997a: Ambrosio, Luigi - Pallara, Diego, Partial regularity of free discontinuity sets, I, "Annali della Scuola Normale Superiore di Pisa. Classe di scienze", 26, 1997, pp. 1-38.
Ambrosio 1997b: Ambrosio, Luigi - Fusco, Nicola - Pallara, Diego, Partial regularity of free discontinuity sets, II, "Annali della Scuola Normale Superiore di Pisa. Classe di scienze", 26, 1997, pp. 39-62.
Ambrosio 2000: Ambrosio, Luigi - Fusco, Nicola - Pallara, Diego, Functions of bounded variation and free discontinuity problems, Oxford, Oxford University Press, 2000.
Ball 1977: Ball, John L., Convexity conditions and existence theorems in nonlinear elasticity, "Archives for rational mechanics and analysis", 63, 1977, pp. 337-403.
Birkhoff 1927: Birkhoff, George David, Dynamical systems, New York, American Mathematical Society, 1927.
Bombieri 1969: Bombieri, Enrico - De Giorgi, Ennio - Giusti, Enrico, Minimal cones and the Bernstein problem, "Inventiones mathematicae", 7, 1969, pp. 243-268.
Braides, Defranceschi 1998: Braides, Andrea - Defranceschi, Annalisa, Homogenization of multiple integrals (Oxford lecture series in mathematics and its applications, 12), Oxford, Clarendon Press, 1998.
Buttazzo 1989: Buttazzo, Giuseppe, Semicontinuity, relaxation and integral representation in the calculus of variations, New York, Wiley, 1989.
Buttazzo 1998: Buttazzo, Giuseppe - Giaquinta, Mariano - Hildebrandt, Stefan, One dimensional variational problems, Oxford, Oxford University Press, 1998.
Cesari 1983: Cesari, Lamberto, Optimization - Theory and applications, (Application of mathematics, XVII), New York, Springer, 1983.
Dacorogna 1982: Dacorogna, Bernard, Quasiconvexity and relaxation of nonconvex problems in the calculus of variations, "Journal of functional analysis", 46, 1982, pp. 102-118.
Dacorogna 1989: Dacorogna, Bernard, Direct methods in the calculus of variations, Berlin, Springer, 1989.
Dal Maso 1993: Dal Maso, Gianni, An introduction to gamma-convergence, Boston, Birkhäuser, 1993.
De Giorgi 1989: De Giorgi, Ennio - Carriero, Mary Elizabeth - Leaci, Antonio, Existence theorem for a minimum problem with free discontinuity sets, "Archives for rational mechanics and analysis", 108, 1989, pp. 195-218.
Dierkes 1992: Dierkes, Ulrich - Hildebrandt, Stefan - Küster, Albrecht - Wohlrab, Ortwin, Minimal surfaces, Berlin, Springer, 1992.
Dolzmann 2003: Dolzmann, Georg, Variational methods for crystalline microstructure - Analysis and computation, (Lecture notes in mathematics), Berlin, Springer, 2003.
Ekeland, Temam 1974: Ekeland, Ivar - Temam, Roger, Analyse convexe et problèmes variationnels, Paris, Dunod, 1974.
Federer 1969: Federer, Herbert, Geometric measure theory, Berlin, Springer, 1969.
Federer 1970: Federer, Herbert, The singular sets of area minimizing rectifiable currents with codimension one and area minimizing flat chains modulo two with arbitrary codimension, "Bulletin of American Mathematical Society", 76, 1970, pp. 767-771.
Giaquinta 1998: Giaquinta, Mariano - Modica, Giuseppe - Soucek, Jiri, Cartesian currents in the calculus of variations, Berlin, Springer, 1998.
Giaquinta, Hildebrandt 1995: Giaquinta, Mariano - Hildebrandt, Stefan, Calculus of variations, Berlin, Springer, 1995.
Giusti 1984: Giusti, Enrico, Minimal surfaces and functions of bounded variation, Boston, Birkhäuser, 1984.
Giusti 1994: Giusti, Enrico, Metodi diretti nel calcolo delle variazioni, Bologna, Unione Matematica Italiana, 1994.
Jost, Li-Jost 1998: Jost, Jürgen - Li-Jost, Xianqing, Calculus of variations, Cambridge, Cambridge University Press, 1998.
Lyusternik 1951: Lyusternik, Lazar´ Aronovich - Fet, Abram I´iã, Variational problems on closed manifolds (in russo), "Doklady Akademii Nauk SSSR", n.s., 81, 1951, pp. 17-18.
Masiello 1994: Masiello, Antonio, Variational methods in Lorentzian geometry, Harlow, Addison-Wesley-Longman, 1994.
Massari, Miranda 1984: Massari, Umberto - Miranda, Mario, Minimal surfaces of codimension one, Amsterdam, North-Holland, 1984.
Milyutin, Osmolovskii 1998: Milyutin, Alexei Alekseevich - Osmolovskii, Nikolai Pavlovich, Calculus of variations and optimal control, Providence, American Mathematical Society, 1998.
Morel, Solimini 1995: Morel, Jean-Michel - Solimini, Sergio, Variational methods in image segmentation, Boston, Birkhäuser, 1995.
Morgan 1988: Morgan, Frank, Geometric measure theory: a beginners guide, New York, Academic Press, 1988.
Morrey 1966: Morrey, Charles B., Multiple integrals in the calculus of variations, Berlin, Springer, 1966.
Nitsche 1989: Nitsche, Johannes C., Lectures on minimal surfaces, Cambridge, Cambridge University Press, 1989.
Struwe 1988: Struwe, Michael, Plateau's problem and the calculus of variations, Princeton, Princeton University Press, 1988.
Struwe 1990: Struwe, Michael, Variational methods, Berlin, Springer, 1990.
Virga 1994: Virga, Epifanio G., Variational theories for liquid crystals, London, Chapman & Hall, 1994.
Young 1969: Young, Laurence Chisholm, Lectures on the calculus of variations, Philadelphia, WB Saunders Company, 1969.