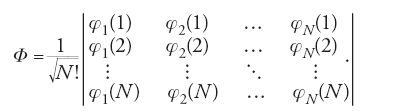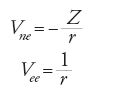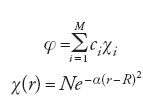La grande scienza. Chimica quantistica

La grande scienza. Chimica quantistica

Chimica quantistica

La materia è costituita da nuclei atomici ed elettroni che interagendo formano gli atomi e le molecole, i quali a loro volta danno origine alla materia inorganica, organica e biologica che ci circonda e di cui siamo formati. Le interazioni tra queste particelle stanno alla base delle principali funzioni che determinano i processi naturali. Le regole per descrivere su basi riduzionistiche le caratteristiche strutturali ed energetiche delle molecole sono quelle della meccanica quantistica che furono formulate nella prima metà del secolo scorso. In linea di principio, pertanto, la descrizione dei processi chimici dovrebbe costituire un 'semplice esercizio' di meccanica quantistica. In realtà i calcoli che si devono affrontare sono talmente complessi che la prospettiva di raggiungere tali obiettivi ha dovuto essere procrastinata sin quasi alla fine del secolo scorso, quando la disponibilità di supercalcolatori ha permesso di affrontare in modo concreto lo studio dei sistemi a molti corpi, formati dai nuclei atomici e dagli elettroni che gravitano attorno a essi.

Fintanto che i menzionati mezzi di calcolo non sono diventati di agevole applicazione, la chimica quantistica ha potuto affrontare solo problemi di carattere concettuale o fruire di modelli semiempirici mutuati dalle conoscenze sperimentali. Il primo esempio significativo di applicazione della meccanica quantistica alla chimica, che risale al 1927 ed è dovuto a Walter Heitler e Fritz London, è stato lo studio del legame covalente presente nella molecola di idrogeno. Anche se i calcoli furono condotti in modo approssimato, per cui fornivano un valore dell'energia di legame che ammontava a circa il 60% di quello sperimentale, il risultato ottenuto si rivelò di notevole interesse concettuale poiché forniva una chiara interpretazione della natura del legame chimico, che sino ad allora era stato giustificato mediante regole euristiche.

L'approccio che viene seguito per valutare l'energia dei sistemi atomici e molecolari si basa sulla soluzione dell'equazione proposta da Erwin Schrödinger nel 1926 (Schrödinger 1926a, b), la cui forma è:

[1] (T+V)ψ=Eψ.

Essa appartiene alla classe delle equazioni differenziali agli autovalori. I termini T e V sono operatori che agiscono sulla funzione d'onda ψ, dipendente dalle coordinate spaziali (x,y,z) delle particelle presenti nel sistema. Il quadrato di ψ fornisce la probabilità di trovare queste ultime in determinate posizioni dello spazio. Si può allora osservare che l'effetto dell'operatore T+V è quello di lasciare la funzione d'onda immutata eccetto che per un fattore moltiplicativo E. L'operatore T si riferisce all'energia cinetica e, se si misura l'energia in unità atomiche (unità di lunghezza uguale al raggio di Bohr, carica e massa dell'elettrone uguali a 1), esso assume la seguente forma differenziale: −(1/2)(∂²/∂x²+∂²/∂y²+∂²/∂z²). V esprime invece la somma delle energie coulombiane di interazione fra i nuclei e gli elettroni e degli elettroni fra di loro. L'operatore H=T+V viene chiamato 'hamiltoniano', mentre il termine moltiplicativo E che compare al secondo membro fornisce l'energia del sistema. L'equazione di Schrödinger costituisce un'equazione differenziale di secondo ordine rispetto alla funzione ψ, la quale risulta continua, finita in ogni punto dello spazio e a un sol valore solo se E assume una serie di valori discontinui che corrispondono a quelli dei livelli energetici del sistema riscontrati sperimentalmente. Per l'atomo di idrogeno è possibile risolverla analiticamente, ottenendo delle funzioni d'onda monoelettroniche chiamate 'orbitali atomici', dotate di tipiche configurazioni spaziali.

L'equazione di Schrödinger non tiene conto degli effetti relativistici. Nel 1928 Paul-Adrien-Maurice Dirac dimostrò come essa potesse essere modificata per inglobare tali effetti (Dirac 1928), ottenendo un'equazione che, pur essendo formalmente analoga a quella di Schrödinger, ha la caratteristica peculiare di contenere ben quattro componenti della funzione d'onda. La risoluzione dell'equazione di Dirac per un elettrone libero mostra che esso possiede un momento angolare intrinseco chiamato spin, che può assumere due valori, uguali rispettivamente a 1/2ℏ e a -1/2ℏ. Inoltre la presenza di stati con energia negativa ha permesso di anticipare rispetto all'esperienza l'esistenza di un'antiparticella dell'elettrone, che è stata chiamata positrone. Per molecole contenenti elementi con numero atomico minore di 36 (fino al kripto), la differenza tra i risultati dell'equazione di Dirac e di quella di Schrödinger è minore di pochi punti percentuali e pertanto, essendo l'equazione di Schrödinger notevolmente meno complicata di quella di Dirac, nella chimica quantistica gli effetti relativistici sono spesso trascurati (perlomeno finché non si ha a che fare con elementi molto pesanti). L'aspetto che non può essere ignorato è la presenza dei due valori per lo spin e in particolare il fatto che l'elettrone appartiene alla classe delle particelle elementari aventi spin semintero, chiamate fermioni. Una legge fondamentale della fisica stabilisce che un sistema di fermioni deve essere descritto da una funzione d'onda antisimmetrica, cioè tale che essa cambia di segno quando le posizioni di due elettroni, che vengono indicati con 1 e 2, sono scambiate fra di loro:

[2] ψ(1,2)=−ψ(2,1).

Questo fatto ha l'importante conseguenza che la probabilità che due elettroni aventi lo stesso spin si trovino nella stessa posizione è nulla, in accordo con il principio di esclusione di Pauli (1925), secondo il quale due elettroni non possono avere tutti i numeri quantici identici. In base a questo principio e al cosiddetto principio di Aufbau, che stabilisce che nello stato fondamentale gli elettroni occupano gli orbitali con la minima energia, è possibile dedurre le caratteristiche peculiari della tavola degli elementi di Mendelev.

Dal 1928 le equazioni fondamentali della meccanica quantistica erano quindi note. Gli sviluppi successivi che hanno avuto luogo durante gli ultimi 70 anni riguardano principalmente l'individuazione di metodi matematici che permettono di risolvere l'equazione di Schrödinger per sistemi contenenti più particelle, tanto che Dirac nel 1929 fece un'affermazione ormai diventata famosa: "Le leggi fisiche soggiacenti alla teoria matematica di una vasta parte della fisica e di tutta la chimica sono del tutto note e la difficoltà consiste solo nel fatto che l'esatta applicazione di queste leggi porta a equazioni troppo complicate per essere solubili".

Soluzioni approssimate

Per sistemi con più di due particelle l'equazione di Schrödinger non può essere risolta analiticamente, ma è necessario utilizzare metodi numerici. In sostanza non si può scrivere la funzione d'onda mediante le consuete funzioni matematiche polinomiali, esponenziali e trigonometriche con le quali si potrebbe direttamente calcolare il valore di ψ in qualunque punto dello spazio. Una soluzione numerica viene ottenuta mediante una sequenza iterativa di calcoli per i quali deve essere definito anche un adeguato criterio per individuarne la convergenza, cioè il punto in cui cessare il procedimento iterativo. Ovviamente è possibile ridurre l'incertezza dei valori numerici ottenuti con un maggiore sforzo computazionale, per esempio aumentando il numero di iterazioni. Si può così raggiungere il grado di precisione desiderato, purché si disponga di sufficienti risorse di calcolo. Si pongono allora i seguenti problemi: quanto accurati devono essere i risultati desiderati? Come si può realizzare tale precisione nel modo più efficiente?

La risposta alla prima domanda dipende dal problema specifico che si sta affrontando. Per esempio, Wlodzimierz Kolos e Lutoslaw Wolniewicz nel 1964 hanno evidenziato che il valore dell'energia di dissociazione sperimentale della molecola di idrogeno (H₂) non era corretto (Kolos e Wolniewicz 1964). Ciò ha richiesto di risolvere l'equazione di Schrödinger con una precisione di 10⁻⁷ , risultato che ha costituito, a quel tempo, uno sforzo di calcolo significativo. Se viceversa si desidera effettuare una selezione iniziale di molecole che risultino possibili candidati per nuovi farmaci, non è richiesta una precisione così elevata, ma la risposta dei calcoli deve essere veloce per poter esaminare molte migliaia di strutture. Nel corso degli anni sono stati formulati diversi metodi per ottenere risposte con un grado variabile di precisione e velocità.

L'approssimazione di Born-Oppenheimer

Un passo essenziale per applicare metodi approssimati alla risoluzione dell'equazione di Schrödinger consiste nel separare il movimento dei nuclei da quello degli elettroni. Tale separazione sarebbe rigorosa solo se ai nuclei si potesse attribuire una massa infinita. In questo caso essi risulterebbero immobili rispetto agli elettroni che vi gravitano attorno. Questa approssimazione fu suggerita da Max Born e Robert Oppenheimer nel 1927 e porta i loro nomi. Nella realtà il rapporto delle masse non è ovviamente infinito, ma ha un valore di 1836 per l'atomo d'idrogeno e un valore intorno a 20.000 per la maggior parte delle molecole organiche. L'approssimazione di Born-Oppenheimer introduce allora errori dell'ordine di 10⁻⁵, che in quasi tutti i casi comportano una precisione minore di quella desiderata.

fig. 1

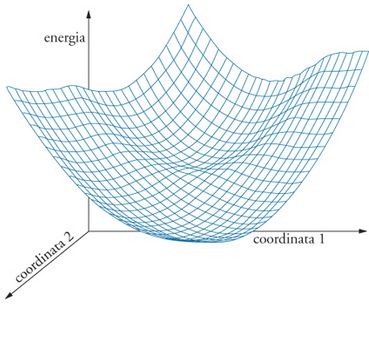
Assumendo valida l'approssimazione di Born-Oppenheimer, il problema viene affrontato in due stadi: si risolve l'equazione di Schrödinger rispetto agli elettroni, con i nuclei in una posizione volta per volta fissata, e successivamente si studia il movimento dei nuclei. Come risultato del primo stadio si ottiene l'energia degli elettroni in funzione delle posizioni dei nuclei. Si tratta di una funzione multidimensionale, che nel caso semplice bidimensionale ha la forma illustrata nella fig. 1.

L'energia elettronica gioca il ruolo di un'energia potenziale per i nuclei, per cui il suo andamento in funzione delle coordinate spaziali dei nuclei viene denominato 'superficie di energia potenziale'. Quando tale superficie è disponibile, i movimenti nucleari possono essere descritti su di essa con metodi classici o quantistici.

L'energia cinetica dei nuclei è legata alla temperatura del sistema. Per temperature relativamente basse essi passano quasi tutto il tempo vicino alla parte inferiore delle buche di energia della superficie di energia potenziale. Se l'energia cinetica è molto minore della barriera di energia che separa le differenti buche, con buona approssimazione si può studiare il movimento nucleare mediante un'espansione in serie di Taylor al secondo ordine dell'energia potenziale attorno al suo minimo. In questa impostazione i moti dei nuclei sono descritti da funzioni armoniche le cui frequenze di vibrazione possono essere misurate, per esempio, con la spettroscopia infrarossa o Raman. Se i nuclei si comportassero in pieno accordo con le leggi della meccanica classica, la loro posizione alla temperatura di 0 K (zero assoluto) dovrebbe essere esattamente determinata dalla posizione di un minimo di energia della superficie di energia potenziale. In realtà, in conseguenza del carattere quantistico del loro moto, i nuclei non possono essere localizzati in una posizione specifica per cui anche allo zero assoluto essi oscillano intorno alla posizione di minima energia; questa vibrazione viene chiamata 'vibrazione di punto zero'.

Le coordinate del minimo di energia sono strettamente legate alla struttura molecolare, cioè alle lunghezze e agli angoli di legame. Differenti minimi sulla superficie di energia potenziale corrispondono allora a differenti strutture o a molecole diverse che hanno la stessa formula bruta, come si verifica per esempio per l'etanolo (CH₃CH₂OH) e l'etere dimetilico (CH₃OCH₃). La differenza di energia di tali minimi determina la stabilità relativa delle molecole.

Le proprietà della superficie di energia potenziale determinano anche la velocità con la quale avviene una reazione chimica. Una reazione corrisponde infatti al movimento degli atomi da un minimo a un altro sulla superficie di energia potenziale, e ciò si realizza in modo più agevole se il moto ha luogo lungo il percorso di reazione che coinvolge il minimo investimento di energia. Il punto a più alta energia lungo questo percorso descrive un complesso molecolare che viene chiamato 'stato di transizione', e la variazione di energia associata alla sua formazione a partire dai reagenti viene chiamata energia di attivazione (E_a) della reazione. Essa determina direttamente la velocità di reazione attraverso l'equazione di Arrhenius

[3]  k=Ae^-Ea/RT

dove il fattore preesponenziale A riflette la frequenza delle collisioni fra le molecole (in una reazione bimolecolare).

Per poter prevedere la struttura molecolare, la stabilità e la reattività chimica di una molecola, si deve risolvere l'equazione elettronica di Schrödinger per un dato insieme di posizioni nucleari e poi esaminare la superficie di energia potenziale per determinarne i minimi di energia e i percorsi di reazione di minima energia. In pratica la ricerca dei minimi di energia e degli stati di transizione viene perseguita tramite una procedura di ottimizzazione a partire da una conveniente geometria iniziale. In questo modo si devono calcolare solo le regioni significative della superficie di energia potenziale. I metodi usati per questo tipo di calcolo verranno trattati nei prossimi paragrafi.

Modelli a particelle indipendenti

Dato un sistema molecolare costituito da N=1,2,…,i,… elettroni, il comportamento di ciascuno di essi può essere descritto mediante orbitali molecolari φ(i), analoghi a quelli atomici precedentemente menzionati, ma delocalizzati in tutta la molecola. Questi orbitali vengono in genere formulati combinando linearmente gli orbitali atomici attraverso opportuni coefficienti. Lo stato dell'intero sistema viene invece descritto mediante una funzione d'onda globale φ, costruita dalle stesse φ(i), ed espressa sotto la seguente forma di determinante (determinante di Slater):

Questa espressione garantisce infatti che risulti soddisfatta la caratteristica di antisimmetria della funzione d'onda contemplata dal principio di Pauli. Il calcolo dell'energia corrispondente a tale stato può essere effettuato solo mediante metodi numerici approssimati, fruendo di un principio variazionale, compatibile con l'equazione di Schrödinger, in base al quale i coefficienti impiegati nella costruzione degli orbitali molecolari devono assumere valori tali da minimizzare l'energia.

Un possibile primo passo può essere quello di trascurare le interazioni tra gli elettroni, considerando solamente l'attrazione tra i nuclei e gli elettroni. Questo approccio è simile a quello che si applica in astronomia nello studio del moto dei pianeti nel Sistema solare quando le loro interazioni reciproche vengono trascurate. In quest'ultimo caso si tratta di un buon modello poiché tutti i pianeti sono molto leggeri rispetto al Sole e quindi la forza (gravitazionale) tra essi è più piccola di quella che si manifesta fra il Sole e i pianeti (per la Terra, per es., la forza dovuta a Giove è 25.000 volte più piccola di quella del Sole). Per gli atomi, però, l'interazione (coulombiana) tra due elettroni V_ee è confrontabile con l'attrazione esercitata dal nucleo V_ne, dalla quale differisce solamente per un fattore uguale al numero atomico Z:

dove r indica le distanze coinvolte.

Inoltre, gli elettroni interagiscono a coppie. Così, per esempio, per un atomo come il carbonio con una carica nucleare di 6, ci sono 6 termini attrattivi con una grandezza relativa di −6, mentre ci sono 15 termini repulsivi ciascuno con una grandezza di +1. Un calcolo reale mostra che la repulsione totale elettrone-elettrone ammonta al 14% dell'attrazione tra il nucleo e gli elettroni. Per un atomo o per una molecola trascurare l'interazione elettrone-elettrone costituisce allora un'approssimazione mediocre.

Un'approssimazione migliore può essere realizzata includendo l'interazione fra gli elettroni mediante un campo medio definito da tutti gli altri elettroni. In questo modo, se si assume di conoscere gli orbitali di tutti gli elettroni tranne uno, si può determinare la forma di questo orbitale risolvendo l'equazione di Schrödinger in quanto si deve fronteggiare un problema a un unico elettrone. Ma poiché ciò vale per ogni elettrone, occorre applicare la seguente sequenza iterativa: (1) si sceglie opportunamente un orbitale per ciascun elettrone; (2) si risolve l'equazione di Schrödinger per il primo elettrone, tenendo fissati gli altri orbitali; (3) si mantiene inalterato l'orbitale così ottenuto e si risolve l'equazione di Schrödinger per il secondo; (4) si tengono fissati il primo e il secondo orbitale e si risolve l'equazione di Schrödinger per il terzo, e così via; (5) si confrontano i nuovi orbitali con i precedenti e se il cambiamento è sufficientemente piccolo si termina l'iterazione, altrimenti si riparte dal punto (2).

Quando la sequenza iterativa ha raggiunto la convergenza, si è ottenuto un insieme completo di orbitali che descrivono la distribuzione di tutti gli elettroni tenendo conto della repulsione media che si esercita fra le coppie elettroniche. La sequenza iterativa determina un campo elettrico che è compatibile con sé stesso, per questo chiamato 'autocompatibile' o 'autoconsistente'. In realtà la repulsione fra due elettroni è un po' minore dell'effetto medio descritto in questa approssimazione, perché le due particelle tenderanno dinamicamente a evitare di trovarsi nella stessa regione dello spazio nello stesso tempo. L'errore che ne consegue nel calcolo dell'energia è tipicamente inferiore all'1%; questa precisione, caratteristica dei modelli a particelle indipendenti, si ottiene anche per sistemi molecolari abbastanza grandi.

L'applicazione della procedura autoconsistente per la determinazione degli orbitali, combinata con il requisito fondamentale che la funzione d'onda totale sia antisimmetrica rispetto allo scambio di qualunque coppia di elettroni, è nota come 'metodo di Hartree-Fock', ed è stata sviluppata indipendentemente da John C. Slater (1930) e da Vladimir A. Fock (1930), a partire da un precedente lavoro di Douglas R. Hartree (1928).

Le equazioni di Hartree-Fock sono un insieme di equazioni differenziali (dall'operatore energia cinetica) e integrali (dall'operatore energia potenziale) accoppiate. Nel 1951 Clemens C.J. Roothaan e George C. Hall mostrarono che le equazioni di Hartree-Fock possono essere trasformate in un insieme di equazioni lineari, molto più adatte per i calcoli numerici (Roothaan 1951; Hall 1951). Il trucco per ottenere questa trasformazione consiste nello sviluppare gli orbitali molecolari non noti in un insieme di funzioni note χ_i, chiamato 'insieme di base'. Per sistemi molecolari queste funzioni di base sono normalmente localizzate sui nuclei e hanno la forma delle funzioni gaussiane, particolarmente adatte per il calcolo degli integrali che esprimono l'interazione fra gli elettroni:

In linea di principio si può utilizzare qualunque tipo di funzione di base, purché se ne includa un numero sufficientemente elevato. Per sistemi estesi, come gli elettroni all'interno di un metallo, le funzioni di base scelte sono spesso le onde piane, che in questi casi si rivelano più adeguate nel descrivere le caratteristiche delle funzioni d'onda:

[7]  χ(r)=Ne^ikz

dove k è il numero d'onda e i l'unità immaginaria.

Pertanto, indipendentemente dalla scelta delle funzioni di base, il problema di determinare gli orbitali di Hartree-Fock si trasforma in quello di trovare i coefficienti sconosciuti c_i dello sviluppo [6]. Poiché il numero delle funzioni di base è definito dall'utilizzatore, la precisione del risultato può essere aumentata aggiungendo altre funzioni di base.

Anche se il modello di Hartree-Fock fornisce più del 99% dell'energia totale, quest'ultima è però così elevata che la rimanente frazione può risultare una quantità molto significativa. Per l'atomo di neon, per esempio, l'energia totale e l'energia di Hartree-Fock sono rispettivamente 338.800 kJ/mol e 337.500 kJ/mol. L'errore del metodo di Hartree-Fock è quindi di 1300 kJ/mol, che va confrontato con il valore tipico dell'energia di legame, pari a 400 kJ/mol. L'errore assoluto nel modello di Hartree-Fock è significativamente più grande dell'energia richiesta per rompere completamente un legame chimico, fatto che sembrerebbe invalidare il metodo per qualunque uso realistico. Fortunatamente la maggior parte delle quantità chimiche di interesse sono collegate a differenze di energia e non a valori assoluti. Poiché una grande parte dell'errore nel modello di Hartree-Fock è costante, in molti casi le differenze di energia possono essere calcolate con una ragionevole precisione. Per esempio, il valore calcolato della barriera di energia per la rotazione intorno al legame C‒C nell'etano (H₃C‒CH₃) ammonta a 12,7 kJ/mol, che va paragonato al valore sperimentale di 12,2 kJ/mol e all'energia totale dell'etano di 208.000 kJ/mol. L'errore di Hartree-Fock di circa 1000 kJ/mol sull'energia assoluta è quindi ridotto a 0,5 kJ/mol nella differenza di energia tra le due conformazioni. La capacità di calcolare queste differenze molto piccole sottraendo due quantità grandi è stata paragonata da Charles A. Coulson alla determinazione del peso del capitano di una nave pesando la nave con e senza il capitano a bordo e sottraendo i due valori.

Sebbene il metodo di Hartree-Fock possa dare buoni risultati per molti problemi, in genere esso fallisce ogni volta che ci sono riarrangiamenti sostanziali nella distribuzione elettronica, per esempio quando si verifica la rottura e la formazione di legami chimici. In tali situazioni la cancellazione dell'errore viene a mancare e il metodo di Hartree-Fock conseguentemente produce risultati mediocri o scorretti. Diviene allora importante descrivere l'effetto dinamico in virtù del quale gli elettroni si evitano l'un l'altro. In un quadro classico ciò riflette il fatto che i movimenti degli elettroni devono essere correlati, per cui se uno di essi si trova in un lato della molecola, un altro preferisce stare nell'altro lato per minimizzare la repulsione. La cosiddetta 'energia di correlazione' è definita come la differenza tra l'energia esatta e quella ottenuta dal modello di Hartree-Fock:

[8] E_corr=E_esatta−E_HF.

Il calcolo dell'energia di correlazione è lo scopo principale dei metodi a molti corpi.

Metodi a molti corpi

Il metodo più tradizionale, usato ormai raramente nelle ricerche moderne, è quello delle 'interazioni fra configurazioni' (CI, configuration interaction). In questo metodo la funzione d'onda di un sistema di N elettroni viene espressa mediante un insieme di funzioni base φ_i, ciascuna espressa come determinante di Slater, attraverso lo sviluppo seguente:

Se si parte da un insieme di M orbitali si può generare un totale di K_MN determinanti di Slater (dove K_MN è il numero di combinazioni di M oggetti a N a N), ottenuti scegliendo in tutti i modi possibili N orbitali. Il calcolo dei coefficienti dello sviluppo viene condotto minimizzando l'energia del sistema. Analogamente a quanto si verifica nel metodo di Hartree-Fock, in cui il numero delle funzioni di base determina la precisione degli orbitali, nel metodo CI il numero di determinanti di Slater condiziona l'accuratezza del risultato ottenuto, e quindi quella con cui si valuta l'energia elettronica di correlazione. Poiché il numero di determinanti di Slater può divenire estremamente grande anche per un valore abbastanza piccolo di N e M, è necessario limitare la scelta a particolari sottogruppi. Tuttavia, la possibilità di includere gradualmente un numero sempre più elevato di determinanti di Slater offre una procedura sistematica per conseguire la precisione desiderata, sebbene le risorse di calcolo richieste possano diventare proibitivamente grandi.

Un approccio alternativo è quello della teoria delle perturbazioni a molti corpi troncata al secondo ordine, sviluppato da Christian Møller e Milton S. Plesset (1934). Si tratta di un metodo meno costoso dal punto di vista del calcolo, che può fornire approssimativamente l'80% dell'energia di correlazione. Purtroppo questo approccio, anche se consente di stimare velocemente l'effetto della correlazione elettronica, presenta uno svantaggio: in alcuni casi la serie perturbativa diverge, per cui risulta necessario includere termini aggiuntivi nello sviluppo. L'estensione a ordini sempre più elevati va sotto il nome di 'metodo dei cluster accoppiati' e può portare a risultati molto accurati, ma richiede un notevole costo di calcolo.

Metodi approssimati a molti corpi o a particelle pseudo-indipendenti

Un metodo alternativo per 'risolvere' l'equazione di Schrödinger è noto come 'teoria del funzionale della densità'. Questo approccio discende da un teorema di Pierre Hohenberg e Walter Kohn, formulato nel 1964, mediante il quale si dimostra che l'energia totale di un sistema è univocamente determinata dalla sua densità elettronica (Hohenberg e Kohn 1964). Pertanto, invece di determinare la funzione d'onda e costruire da essa la densità elettronica (che tra l'altro ha un ben definito significato fisico ed è misurabile sperimentalmente), in linea di principio si può invertire la procedura operando direttamente sulla densità elettronica. Il funzionale che connette l'energia alla densità elettronica è però ignoto: il teorema menzionato dimostra solamente che esso esiste ed è unico.

Nel 1965 Kohn e Lu J. Sham mostrarono che una grande parte dell'energia può essere calcolata da una somma di contributi valutati mediante una densità elettronica ottenuta a sua volta da opportuni orbitali molecolari. L'espressione dell'energia è simile a quella presente nella teoria di Hartree-Fock, ma contiene un ulteriore contributo, chiamato 'energia di scambio-correlazione' che è responsabile di una percentuale relativamente piccola dell'energia totale. Per il caso speciale in cui la densità elettronica sia costante e uniforme, si conoscono accorgimenti esatti per calcolare l'energia di scambio-correlazione, ma sfortunatamente i sistemi atomici e molecolari risultano descritti in modo mediocre nel caso in cui si impieghi questa approssimazione. Comunque, questi metodi, detti 'di densità locale', forniscono risultati paragonabili a quelli del metodo di Hartree-Fock e la comunità dei fisici li ha a lungo preferiti. Un significativo miglioramento per i sistemi chimici venne conseguito intorno al 1990, quando furono proposte diverse espressioni del funzionale dell'energia di scambio-correlazione dipendenti sia dalla densità elettronica sia dalla sua derivata prima (Becke 1988; Lee et al. 1988). Molti di questi funzionali danno risultati di qualità simile a quelli dei metodi a molti corpi precedentemente descritti per il calcolo dell'energia di correlazione, come quello dei cluster accoppiati, ma a un costo di calcolo più basso. In realtà il metodo del funzionale della densità, nelle sue varie forme corrispondenti a quelle del termine esprimente l'energia di scambio-correlazione, può essere considerato come un miglioramento del metodo di Hartree-Fock, nel quale la correlazione elettronica è scritta come una funzione parametrica della densità elettronica. L'esecuzione dei calcoli è molto simile a quella del metodo di Hartree-Fock, in quanto si devono risolvere equazioni a un elettrone, invece che equazioni a molti corpi. In conclusione, il metodo del funzionale della densità fornisce in molti casi risultati più accurati della teoria di Hartree-Fock, con un costo di calcolo quasi uguale, ma presenta lo svantaggio di non offrire un modo sistematico per migliorare i risultati verso il limite esatto, come invece si verifica negli altri casi.

Metodi approssimati parametrizzati

Per sistemi di grandi dimensioni possono non essere disponibili le risorse di calcolo necessarie per applicare i metodi di Hartree-Fock o del funzionale della densità. Per tali applicazioni, o per fare uno screening rapido di un grande numero di strutture possibili, può essere utile impiegare metodi che contengono approssimazioni ma che consentono un rapido ottenimento dei risultati desiderati. Tali metodi sono quasi tutti derivati dal metodo di Hartree-Fock trascurando termini che sono ritenuti piccoli o semplicemente la cui presenza aumenta il tempo di calcolo. Per compensare parzialmente gli errori, le quantità rimanenti sono spesso considerate alla stregua di parametri che, invece di essere valutati esplicitamente, vengono adattati ai risultati sperimentali. A seconda del punto di vista, questi metodi possono essere considerati sia come metodi di Hartree-Fock approssimati sia come funzioni di interpolazione sofisticate di risultati sperimentali. I più noti sono stati sviluppati da un gruppo di ricerca che fa capo a Michael J.S. Dewar (Dewar et al. 1985) e sono conosciuti con gli acronimi MNDO, AM1 e PM3.

Gerarchia dei modelli teorici

fig. 2

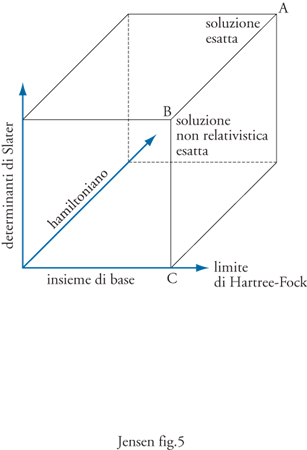
È possibile illustrare gli aspetti peculiari della ricerca di soluzioni approssimate dell'equazione di Schrödinger mediante un sistema di coordinate tridimensionali, come illustrato nella fig. 2. L'asse dell'hamiltoniano caratterizza gli effetti di cui si tiene conto nella formulazione dell'hamiltoniano stesso. Per esempio, nella formulazione di Schrödinger non si descrivono gli effetti relativistici, mentre un hamiltoniano corrispondente al metodo del funzionale della densità risponde solo in maniera approssimata degli effetti dovuti alla correlazione elettronica, compatibilmente con la bontà dei funzionali di correlazione-scambio disponibili. L'asse dei determinanti di Slater quantifica la frazione dell'energia di correlazione elettronica di cui si può tenere conto con un dato hamiltoniano. Infine, l'asse dell'insieme di base determina l'accuratezza con la quale possono essere descritte le funzioni monoelettroniche, ovvero gli orbitali molecolari. Poiché il numero dei determinanti di Slater dipende a sua volta dal numero di orbitali considerati, le loro caratteristiche determinano indirettamente anche l'ammontare dell'energia di correlazione elettronica di cui si riesce a tenere conto.

Nel cubo rappresentato nella fig. 2 sono evidenziati tre punti nodali. Quello indicato con A corrisponde a un hamiltoniano esatto, un insieme infinito di funzioni di base e l'inclusione di tutti i determinanti di Slater. A questo limite il sistema quantistico è risolto esattamente, includendo anche gli effetti relativistici. Quello indicato con B corrisponde all'hamiltoniano di Schrödinger, un insieme infinito di funzioni di base e l'inclusione di tutti i determinanti di Slater: il sistema quantistico è risolto esattamente nell'approssimazione non relativistica. Quello indicato con C corrisponde all'hamiltoniano di Schrödinger, un insieme infinito di base, ma un solo determinante di Slater: il sistema quantistico è risolto esattamente nel limite non relativistico e tenendo conto della repulsione elettrone-elettrone solo come effetto medio. Il corrispondente limite di Kohn-Sham è un po' spostato lungo l'asse dell'hamiltoniano e corrisponde alla risoluzione esatta del sistema quantistico nell'ambito di un'approssimazione compatibile con una forma parzialmente empirica dell'hamiltoniano. Sebbene la formulazione gerarchica delle soluzioni illustrata nella fig. 2 fosse nota già nel 1929, è stato solo con l'avvento dei calcolatori elettronici, a partire dagli anni Cinquanta, che è divenuto possibile risolvere i sistemi con più di due elettroni con una precisione ragionevole. Nel primo periodo (1960-1980) la scarsità delle risorse di calcolo restrinse i calcoli ai metodi approssimati semiempirici e ai calcoli Hartree-Fock con piccoli insiemi di funzioni di base. Tali calcoli all'inizio diedero risultati qualitativi e solo per sistemi sufficientemente piccoli. Negli anni Ottanta si è verificato il maggior sviluppo dei metodi per il calcolo della correlazione elettronica e i risultati hanno iniziato a raggiungere un'accuratezza che qualche volta poteva essere paragonata a quella dei risultati sperimentali. Gli anni Novanta hanno visto un ulteriore sviluppo dei metodi dei cluster accoppiati e specialmente del metodo del funzionale della densità. La combinazione di un continuo aumento della potenza di calcolo e di un miglioramento dei programmi di calcolo ha reso possibile l'avvicinamento alla soluzione 'esatta' dell'equazione di Schrödinger per sistemi piccoli. In vista di questo scopo, sono stati anche intrapresi i metodi per risolvere l'equazione di Dirac, anche se attualmente essi risultano ancora poco sviluppati. Con gli anni Duemila l'avvento di potenti calcolatori paralleli ha reso possibile in alcuni casi il calcolo di talune proprietà molecolari con una precisione maggiore di quella ottenibile dagli esperimenti. Inoltre, grazie all'avvento di metodi caratterizzati da un costo di calcolo contenuto, come quello del funzionale della densità, risulta ora possibile affrontare calcoli relativi a sistemi con centinaia o migliaia di atomi.

Qualità dei risultati

Le grandezze chimico-fisiche ottenibili mediante i metodi della chimica quantistica si possono classificare in tre categorie: (a) quantità strutturali; (b) quantità energetiche; (c) proprietà molecolari.

Le quantità strutturali si riferiscono tipicamente al calcolo della geometria di una molecola o di un sistema esteso come un metallo o una lega. Ciò significa calcolare la superficie di energia potenziale del sistema in esame per poterne individuare, attraverso una ottimizzazione, i suoi minimi. Poiché la posizione di questi ultimi dipende unicamente dai valori relativi delle energie di configurazioni geometriche strettamente collegate (in accordo alla topologia della superficie di energia potenziale), la previsione delle caratteristiche strutturali è relativamente insensibile all'accuratezza della funzione d'onda. Pertanto, anche il metodo di Hartree-Fock o del funzionale della densità nella sua più semplice approssimazione possono spesso fornire risultati in buon accordo con gli esperimenti. Metodi più sofisticati sono in grado di dare risultati addirittura più accurati di quelli che attualmente si possono ottenere sperimentalmente.

Le quantità energetiche si riferiscono alla stabilità delle molecole, espressa quantitativamente attraverso un confronto fra le energie di differenti strutture. La qualità di tali previsioni dipende significativamente dalla somiglianza delle strutture paragonate. Per esempio, la differenza di energia fra differenti conformazioni della stessa molecola è relativamente facile da valutare. All'altro estremo si trova invece la differenza di energia tra una molecola e i suoi componenti atomici, il cui calcolo corrisponde al valore sperimentale dell'energia di atomizzazione della molecola stessa. Con i metodi di calcolo più recenti tali quantità possono essere stimate con un'accuratezza di 5 kJ/mol per sistemi il cui numero di elettroni non superi 100.

Le proprietà molecolari sono grandezze che esprimono il modo in cui il sistema risponde a una perturbazione esterna, quale un campo elettrico o una radiazione di una certa lunghezza d'onda. Fra esse rientrano la polarizzabilità e l'iperpolarizzabilità, importanti nell'ottica non lineare o nell'assorbimento di luce con successiva emissione a diverse lunghezze d'onda. Nel caso in cui la lunghezza d'onda della luce incidente sia abbastanza piccola, è possibile che l'assorbimento porti alla rottura di legami molecolari e a una successiva reazione chimica.

Ulteriori proprietà spettroscopiche sono quelle che consentono di prevedere lo spettro molecolare vibrazionale o quello di risonanza magnetica nucleare. Talvolta è difficile calcolare queste proprietà con un'accuratezza confrontabile a quella relativa alle strutture e all'energia. In molti casi, comunque, sono difficili da effettuare anche i corrispondenti esperimenti per cui, curiosamente, esistono esempi nei quali i valori teorici risultano più affidabili di quelli sperimentali.

Sviluppi futuri

Le ricerche in corso procedono lungo diverse linee, che si possono così riassumere: (a) sviluppo di metodi di calcolo più accurati, per quanto concerne l'inclusione esplicita degli effetti dovuti agli ordini più alti dei calcoli perturbativi sulla correlazione elettronica e lo sviluppo di termini di correlazione-scambio del funzionale della densità più accurati. Per il basso costo di calcolo coinvolto in questi metodi, si tratta di un'area particolarmente interessante e potenzialmente molto utile. (b) Sviluppo di metodi per risolvere l'equazione relativistica di Dirac, importante per sistemi che contengono atomi della parte inferiore della tavola periodica (atomi pesanti). Sebbene si possa fruire di molti degli accorgimenti impiegati per risolvere l'equazione di Schrödinger, è comunque necessario intensificare in modo significativo le ricerche per superare i problemi dovuti all'alta complessità dell'equazione di Dirac. (c) Formulazione più efficiente dei metodi esistenti per lo sviluppo dei calcoli. Il 'Santo Graal' in questo caso consiste nell'elaborare metodologie la cui applicazione vari linearmente con le dimensioni dei sistemi. Questo obiettivo è stato sostanzialmente raggiunto per i modelli a particelle indipendenti, come quello di Hartree-Fock e del funzionale della densità, e alcuni promettenti tentativi sono stati eseguiti anche per metodi in cui appare esplicitamente la correlazione. Nella formulazione tradizionale dei metodi accurati per trattare la correlazione, come quello dei cluster accoppiati, l'entità dei calcoli varia con la settima potenza della dimensione della molecola. Pertanto un aumento nel potere di calcolo di un fattore 100.000 permette solo un aumento della dimensione del sistema di un fattore 5. Affinché questi metodi diventino di utilità generale è essenziale che tale variazione con le dimensioni del sistema, fisicamente non giustificabile, venga ridotta. (d) Sviluppo di approcci più efficienti per applicare i metodi esistenti. In questo quadro risulta di particolare importanza l'impiego di cluster di calcolatori costituiti da diversi computer appartenenti ai ricercatori stessi, che consentirebbe di conseguire una potenza di calcolo senza precedenti con una spesa modesta. Tuttavia, ottenere un software che funzioni efficientemente in parallelo o su centinaia di tali macchine non è un compito banale e può richiedere significative riorganizzazioni dei codici di calcolo e forse una riformulazione degli stessi algoritmi.

Molti aspetti importanti della moderna ricerca biologica, medica e tecnologica sono una diretta conseguenza delle informazioni di cui si può disporre sulle strutture atomiche e molecolari, e pertanto l'abilità di effettuarne dettagliate descrizioni con i metodi di calcolo della chimica quantistica apre la possibilità non solo di approfondire la conoscenza della Natura, ma anche di disporre di uno strumento utile per la progettazione di nuovi sistemi di interesse tecnologico e pratico. Per questa ragione è probabile che le applicazioni chimiche della meccanica quantistica giocheranno in futuro un ruolo sempre più importante in numerosi settori delle scienze applicate.

Bibliografia

Becke 1988: Becke, Axel D., Density-functional exchange-energy approximation with correct asymptotic behavior, "Physical review", A38, 1988, pp. 3098-3100.

Born, Oppenheimer 1927: Born, Max - Oppenheimer, Robert, Zur Quantentheorie der Molekule, "Annalen der Physik", 84, 1927, pp. 457-484.

Dewar 1985: Dewar, Michael J.S. - Zoebisch, Eve G. - Healy, Eamonn F. - Stewart, James J.P., AM1: a general purpose quantum mechanical molecular model, "Journal of the American chemical society", 107, 1985, pp. 3902-3909.

Dirac 1928: Dirac, Paul-Adrien-Maurice, The quantum theory of the electron, "Proceedings of the Royal Society of London", A117, 1928, pp. 610-621; A118, 1928, pp. 351-361.

Dirac 1929: Dirac, Paul-Adrien-Maurice, Quantum mechanics of many electron systems, "Proceedings of the Royal Society of London", A123, 1929, pp. 714-733.

Fock 1930: Fock, Vladimir A., Näherungsmethode zur Lösung der quantenmechanischen Meherkörperproblems, "Zeitschrift für Physik", 61, 1930, pp. 126-148.

Hall 1951: Hall, George G., The molecular orbital theory of chemical valency. VIII. A method of calculating ionization potentials, "Proceedings of the Royal Society of London", A205, 1951, pp. 541-552.

Hartree 1928: Hartree, Douglas R., The wave mechanics of an atom with a son-Coulomb centralfield, "Proceedings of the Cambridge Philosophical Society", 24, 1928, pp. 89-132.

Hohenberg, Kohn 1964: Hohenberg, Pierre - Kohn, Walter, Inhomogeneous electron gas, "Physical review", B136, 1964, pp. 864-B871.

Jacobsen 2001: Jacobsen, Claus J.H. e altri, Catalyst design by interpolation in the periodic table: bimetallic ammonia synthesis catalysts, "Journal of the American chemical society", 123, 2001, pp. 8404-8405.

Kohn, Sham 1965: Kohn, Walter - Sham, Lu J., Self-consistent equations including exchange and correlation effects, "Physical review", A140, 1965, pp. A1133-A1138.

Kolos, Wolniewicz 1964: Kolos, Wlodzimierz - Wolniewicz, Lutoslaw, Accurate adiabatic treatment of the ground state of the hydrogen molecule, "Journal für Chemie und Physik", 41, 1964, p. 3663 e segg.

Lee 1988: Lee, Clengteh - Yang, Weitao - Parr, Robert G., Development of the Colle Salvetti correlation-energy formula into a functional of the electron density, "Physical review", B37, 1988, pp. 785-789.

Møller, Plesset 1934: Møller, Christian - Plesset, Milton S., Note on approximation treatment for many-electron systems, "Physical review", 46, 1934, pp. 618-622.

Moscatelli 2003: Moscatelli, Davide - Cavallotti, Carlo - Masi, Maurizio - Carrà, Sergio, A quantum chemistry investigation of the gas phase and surface chemistry of the MOCVD of ZnSe, "Journal of crystal growth", 248, 2003, pp. 31-36.

Pauli 1925: Pauli, Wolfgang, Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Complexstructur des Spektren, "Zeitschrift für Physik", 31, 1925, pp. 765-783.

Roothaan 1951: Roothaan, Clemens C.J., New developments in molecular orbital theory, "Review of modern physics", 23, 1951, pp. 69-89.

Schrödinger 1926a: Schrödinger, Erwin, An undulatory theory of the mechanics of atoms and molecules, "Physical review", 28, 1926, pp. 1049-1070.

Schrödinger 1926b: Schrödinger, Erwin, Quantisierung als Eigenwertproblem, "Annalen der Physik", 79, 1926, pp. 361-376, 489-527; 80, 1926, pp. 437-490; 81, 1926, pp. 109-139.

Slater 1929: Slater, John C., The theory of complex spectra, "Physical review", 34, 1929, pp. 1293-1322.

Slater 1930: Slater, John C., Note on Hartree's method, "Physical review", 35, 1930, pp. 210-211.