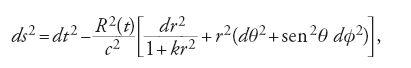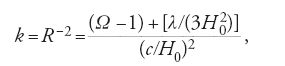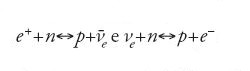La grande scienza. Cosmologia

La grande scienza. Cosmologia

Cosmologia

Il 1925 può essere considerato l'anno in cui nacquero, nel loro aspetto moderno, le scienze dell'astrofisica extragalattica e della cosmologia astrofisica. In quell'anno, infatti, Edwin P. Hubble (1889-1953), dello statunitense Mount Wilson Observatory, in California, fornì la prova definitiva della natura extragalattica delle nebulose spirali (Hubble 1925). Egli scoprì 22 stelle variabili Cefeidi nella nebulosa spirale M33 e 12 nella M31, per le quali valeva esattamente la stessa relazione periodo-luminosità trovata per le Cefeidi nelle nubi di Magellano; fu, inoltre, in grado di ottenere una buona stima della distanza di queste galassie dalla Terra, pari a circa 285.000 anni luce, distanza di gran lunga maggiore del massimo valore attribuito al raggio della nostra Galassia da Harlow Shapley (1885-1972), anch'egli del Mount Wilson Observatory.

Hubble iniziò immediatamente a servirsi delle nebulose extragalattiche, o galassie, per comprendere la struttura su larga scala dell'Universo. Infatti, nel 1926 egli pubblicò il primo studio importante sulle proprietà delle galassie, lavoro in cui è riportato il suo famoso schema di classificazione, che distingue i principali tipi di galassie in ellittiche, spirali normali, spirali barrate e irregolari. Tale schema di classificazione è convenzionalmente presentato nella forma di un diagramma a diapason, che interpretò come una sequenza morfologica evolutiva, secondo cui le galassie si sviluppano evolvendosi da forme ellittiche/sferiche - a sinistra nel diagramma - in una serie di forme a spirale. Questa congettura si dimostrò totalmente errata, tuttavia i termini di galassie di 'primo tipo' e di galassie di 'tipo avanzato' sono rimasti nell'uso corrente.

Hubble si accorse che il conteggio del numero di galassie la cui luminosità supera una data magnitudine apparente fornisce una prova dell'omogeneità della distribuzione delle galassie nell'Universo. Il conteggio si estendeva fino alla magnitudine 16,7 e aumentava con la magnitudine apparente, esattamente come atteso per una distribuzione uniforme di galassie.

In seguito, Hubble stimò le masse tipiche delle galassie; di qui dedusse che la densità di massa media dell'Universo fosse ϱ=1,5×10⁻²⁸ kg m⁻³. Adottando il modello di Universo statico di Einstein, risultò, assumendo la geometria sferica, un raggio di curvatura di 27.000 Mpc e un numero di galassie, in questo Universo supposto chiuso, pari a 3,5×10¹⁵. Così, nel 1926, le idee della cosmologia relativistica furono per la prima volta applicate all'Universo delle galassie.

fig. 2

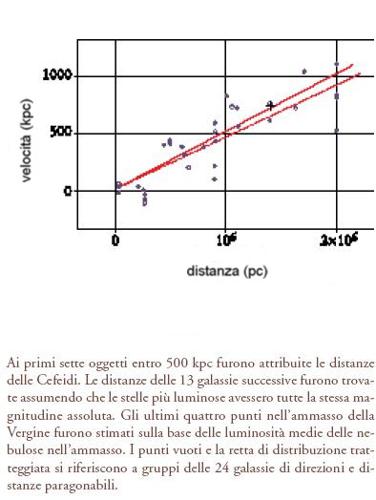
Queste importanti intuizioni furono presto seguite da una scoperta ancora più ragguardevole. Nel 1917 lo statunitense Vesto M. Slipher (1875-1969), del Lowell Observatory, aveva pubblicato le sue pionieristiche osservazioni spettroscopiche su 25 galassie spirali. Le velocità delle galassie, dedotte dallo spostamento Doppler osservato nelle loro righe di assorbimento, erano tipicamente di circa 570 km s⁻¹, ossia di gran lunga maggiori della velocità di qualsiasi oggetto noto nella nostra Galassia. Inoltre, la maggior parte delle velocità corrispondeva a galassie che si allontanavano dal Sistema solare, cioè le righe spettroscopiche erano spostate verso lunghezze d'onda maggiori (verso il rosso, da cui il termine red shift dato a tale fenomeno). Nel 1922 l'astrofisico tedesco Carl Wilhelm Wirtz (1876-1939), dell'Università di Kiel, aveva concluso che, usando i dati in modo appropriato, emergeva una dipendenza approssimativamente lineare delle velocità dalla magnitudine apparente. Nel 1929 Hubble raccolse le distanze approssimative di 24 galassie, di cui erano state misurate le velocità prevalentemente da Slipher, entro 2 Mpc di distanza dalla nostra Galassia. Da questi pochi dati, Hubble dedusse la sua famosa relazione red shift-distanza (Hubble 1929); se i red shift sono interpretati come gli spostamenti Doppler delle galassie, dovuti alle loro velocità di recessione v, questa relazione può essere scritta v=H₀r, dove H₀ è la costante di Hubble e r è la distanza delle galassie dalla Terra (fig. 2). Un tale risultato era già previsto nel modello di Universo derivato dalla teoria della relatività generale (RG) di Albert Einstein.

Le origini della cosmologia relativistica

Nel 1916, l'anno dopo la pubblicazione della teoria della RG nella sua forma definitiva, Wilhelm de Sitter e Paul Ehrenfest suggerirono, contemporaneamente, che uno spazio-tempo sferico a 4 dimensioni eliminava il problema delle condizioni al contorno all'infinito, questione insuperabile nei modelli cosmologici newtoniani. Nel 1917 Einstein si accorse che con la RG aveva formulato per la prima volta una teoria da cui si potevano inferire modelli completamente autoconsistenti dell'intero Universo (Einstein 1917). Si doveva peraltro includere, nella struttura della RG, ciò che egli chiamò 'principio di Mach', ossia che il sistema di riferimento inerziale locale deve essere determinato dalla distribuzione su grande scala della materia nell'Universo. Era poi necessario affrontare un ulteriore problema, per la prima volta notato da Newton, vale a dire che i modelli di Universo statico risultano instabili sotto gravità. Einstein propose di risolvere entrambi i problemi introducendo nelle equazioni di campo un termine aggiuntivo, la 'costante cosmologica' λ. In termini newtoniani, la costante cosmologica corrisponde a una forza repulsiva f che agisce su una particella di prova a distanza r, f=(1/3)λr. A differenza della gravità, questa forza è indipendente dalla densità di materia. Il termine λ ha un'influenza trascurabile sulla scala delle dimensioni del Sistema solare, è invece apprezzabile sulle scale cosmologiche.

Dalle equazioni di campo di Einstein della RG, segue che la geometria dell'Universo statico di Einstein è chiusa e il raggio di curvatura delle sezioni geometriche è R_c=c/(4πGϱ₀)^1/2, dove G è la costante della gravitazione, c la velocità della luce nel vuoto e ϱ₀ la densità dell'Universo statico. Il valore di λ è proporzionale alla densità media dell'Universo, λ=4πGϱ₀. Einstein credeva di aver incorporato il principio di Mach nella RG, poiché essenzialmente pensava che non esistessero soluzioni statiche delle equazioni di campo in assenza di materia.

Quasi immediatamente, de Sitter mostrò che tale risultato non era stato raggiunto. Egli trovò soluzioni delle equazioni di campo di Einstein in assenza di materia, ϱ=p=0, dove p è la pressione. Anche se nell'Universo non vi fosse materia, una particella di prova si sposterebbe, comunque, nello spazio-tempo, su una traiettoria perfettamente definita. Peraltro, come lo stesso de Sitter osservò: "Se non esiste nessuna forma di materia oltre al corpuscolo di prova, ha senso attribuirgli una massa inerziale?". Inoltre, de Sitter previde che le galassie distanti sarebbero state osservate attraverso un red shift, benché nella sua soluzione la metrica fosse stazionaria; fu per questo che tale fenomeno fu chiamato 'effetto de Sitter'.

Nel 1922 Kornel Lanczos mostrò che la soluzione di de Sitter poteva essere scritta nella forma di una metrica nella quale le particelle di prova si spostano con una velocità esponenzialmente crescente. Quasi contemporaneamente Aleksandr A. Fridman pubblicò il primo dei suoi due famosi articoli sulla cosmologia relativistica (Fridman 1922), nel quale trovò soluzioni per modelli di universi in espansione caratterizzati da geometrie spaziali chiuse, tra cui quelli che si espandono fino a un raggio massimo e quindi collassano in una singolarità. Due anni dopo, nel secondo articolo, precisò che vi sono anche soluzioni che si espandono illimitatamente, caratterizzate da una geometria iperbolica (Fridman 1924). Queste soluzioni corrispondono esattamente ai modelli standard della RG e sono a ragione note come modelli di Fridman.

Questi risultati rimasero nell'ombra finché, nel 1927, il belga Georges Lemaître scoprì le stesse soluzioni e quindi emerse l'importanza dei contributi pionieristici di Fridman. Lemaître e Howard P. Robertson, dell'Università di Princeton, sapevano già nel 1928 che le soluzioni di Fridman avrebbero portato localmente a una relazione velocità-distanza. Lemaître derivò quello che egli stesso definì 'effetto Doppler apparente', nel quale "le velocità di allontanamento delle nebulose extragalattiche sono un effetto cosmico dell'espansione dell'Universo" con v∝r (Lemaître 1927). Robertson trovò un risultato simile: "si dovrebbe attendere […] una correlazione v≈cl/R", dove l è la distanza e v la velocità di allontanamento (Robertson 1928); dallo studio delle galassie vicine, egli ricavò un valore della costante di Hubble pari a 500 km s⁻¹ Mpc⁻¹.

La scoperta della relazione velocità-distanza per le galassie fu interpretata come prova dell'espansione dell'Universo nel suo insieme. Rimaneva il problema di interpretazione dei concetti di tempo e di distanza nella cosmologia, poiché le equazioni di campo potevano essere formulate in qualsiasi sistema di riferimento. Il problema fu risolto indipendentemente da Robertson e Arthur Geoffrey Walker (Robertson 1935; Walker 1936). Per modelli del mondo isotropi e omogenei, essi mostrarono che la metrica dello spazio-tempo doveva avere la forma

dove k è la curvatura dello spazio nell'era corrente, (r, θ, ϕ) sono le coordinate polari rispetto a un osservatore di riferimento e R(t) è il fattore di scala che descrive come cambiano le distanze tra due elementi qualsiasi di linea con il tempo cosmico t. Questa metrica è nota come metrica di Robertson-Walker e contiene tutte le geometrie coerenti con le ipotesi di isotropia e omogeneità dell'Universo; la curvatura k=R⁻², dove R è il citato raggio di curvatura delle sezioni spaziali dello spazio curvo isotropo, può essere positiva, negativa o nulla. La descrizione fisica dell'espansione è contenuta nel fattore di scala R(t).

Con la scoperta della relazione velocità-distanza Einstein si pentì di aver incluso la costante cosmologica nelle equazioni di campo. Secondo George Gamow, insigne membro dell'Università di Washington, Einstein dichiarò che l'introduzione della costante cosmologica era stato l'errore più grave della sua vita (Gamow 1970, p. 44). Nel 1932 Einstein e de Sitter mostrarono che vi è una soluzione speciale delle equazioni con λ=0 e k=0, corrispondenti alle sezioni dello spazio euclideo (Einstein e de Sitter 1932). Secondo questo modello di Einstein-de Sitter, si ha una densità nell'era corrente di ϱ₀=3H₀²/(8πG). Ci si riferisce spesso a questa densità come alla 'densità critica' e al modello di Einstein-de Sitter come al 'modello critico', in quanto esso separa i modelli che si espandono illimitatamente con geometrie aperte e iperboliche da quelli che sono destinati a collassare in una singolarità e che hanno geometria sferica chiusa. Quando Einstein e de Sitter inserirono H₀=500 km s⁻¹ Mpc⁻¹ nell'espressione per ϱ₀, trovarono ϱ₀=4×10⁻²⁵ kg m⁻³. Benché questo valore fosse piuttosto maggiore della densità media nelle galassie derivata da Hubble, essi argomentarono che potesse essere dell'ordine di grandezza giusto perché nell'Universo potrebbe essere presente una considerevole quantità di 'materia oscura'.

La cosmologia astrofisica fino al 1939

La materia oscura

L'evidenza astrofisica della materia oscura non tardò ad arrivare. Nel 1933 Fritz Zwicky del Caltech di Pasadena, in California, effettuò i primi studi dinamici sugli ammassi ricchi di galassie, in particolare, sull'ammasso della Chioma di Berenice (Coma; Zwicky 1933). Nel metodo che Zwicky usò per stimare la massa totale dell'ammasso figura il teorema del viriale, che era stato derivato nel 1916 da Arthur S. Eddington (1882-1944), dell'Osservatorio di Greenwich, per valutare le masse degli ammassi stellari (Eddington 1916). Il teorema collega l'energia cinetica interna totale delle galassie in un ammasso, T=(1/2)M⟨v²⟩, alla sua energia potenziale gravitazionale all'equilibrio statistico, sotto la gravità, U=GM²/(2R_cl), con R_cl raggio dell'ammasso. Eddington mostrò che T=(1/2)∣U∣, da cui si calcola la massa dell'ammasso, M≈R_cl ⟨v²⟩/G.

Zwicky misurò la dispersione di velocità ⟨v²⟩ delle galassie nell'ammasso di Coma e trovò che vi era una quantità maggiore di massa di quella che poteva essere stimata in base alle parti visibili delle galassie. In unità solari, il rapporto tra massa e luminosità ottica di una galassia come la nostra è circa 3, mentre per l'ammasso di Coma si trovò che tale rapporto è circa 500; perciò vi deve essere materia circa 100 volte più 'oscura' o nascosta di quella visibile nell'ammasso. Gli studi pionieristici di Zwicky sono stati confermati da tutti quelli successivi sugli ammassi ricchi di galassie.

I modelli di Universo di Eddington-Lemaître

Malgrado Einstein avesse rinnegato la costante cosmologica λ, rimaneva un problema molto grave per i modelli nei quali si pone λ uguale a zero. In tutti questi modelli, infatti, l'età dell'Universo è minore di H₀⁻¹. Usando la stima di Hubble di H₀=500 km s⁻¹ Mpc⁻¹, l'età dell'Universo risulta minore di 2×10⁹ anni; tale valutazione entra in conflitto con l'età della Terra derivata dai rapporti di abbondanze di specie radioattive con lunga vita media, che, a quel tempo, davano un'età di almeno 2,5×10⁹ anni.

Eddington e Lemaître capirono che questo problema poteva essere eliminato supponendo λ positivo (Eddington 1930; Lemaître 1931a). L'effetto di una costante cosmologica positiva è di opporsi alla forza di attrazione gravitazionale quando la dimensione dell'Universo è diventata abbastanza grande. Tra le soluzioni delle equazioni di Einstein ci sono dei casi speciali che rimangono nello stato statico di Einstein per un periodo arbitrariamente lungo e quindi si espandono allontanandosi da questo stato, sotto l'influenza del termine cosmologico. In tali modelli di Eddington-Lemaître, l'età dell'Universo potrebbe essere arbitrariamente lunga e, perciò, come Eddington stesso affermò, l'Universo avrebbe una 'eternità logaritmica' sulla quale ripiegarsi. Questo argomento risolve il conflitto tra le stime della costante di Hubble e l'età della Terra.

L'origine degli elementi chimici

Negli anni Trenta, vi erano due ragioni per prendere in considerazione la sintesi degli elementi chimici durante gli stadi iniziali dei modelli di Fridman. In primo luogo, sembrava che le abbondanze chimiche degli elementi nelle stelle fossero eccezionalmente uniformi; in secondo luogo, sembrava che le parti interne delle stelle non fossero abbastanza calde perché vi avesse luogo la nucleosintesi degli elementi chimici. Un punto di partenza per una soluzione cosmologica di questo problema era calcolare le abbondanze all'equilibrio degli elementi a una temperatura molto alta e assumere che, se la densità e la temperatura fossero diminuite in modo sufficientemente rapido, queste abbondanze sarebbero rimaste 'congelate'.

Nel 1931 Lemaître propose che lo stato iniziale dei modelli di Fridman consistesse in quello che egli definì un 'atomo primordiale' (Lemaître 1931b). In seguito alla scoperta del neutrone nel 1932, questo stato fu pensato come un mare di neutroni tenuti fortemente insieme. Si suppose che i neutroni primordiali fossero decaduti in protoni e che, in interazioni nucleari successive, si fossero formati sia gli elementi chimici sia i raggi cosmici. Queste idee alimentarono l'approccio di Gamow al problema dell'origine degli elementi chimici. Nel 1946 egli estrapolò i modelli di Fridman fino a epoche in cui le densità e le temperature erano abbastanza alte affinché avesse luogo la nucleosintesi, e trovò che la scala di tempo dell'Universo in questi stadi iniziali era troppo breve perché si potesse stabilire una distribuzione di equilibrio degli elementi (Gamow 1946).

Il problema cosmologico nel 1939

Alla fine degli anni Trenta tutti pensavano che la soluzione del problema cosmologico consistesse nella determinazione dei parametri che definiscono i modelli di Fridman. Questo divenne uno dei grandi obiettivi dei programmi di osservazione che avrebbero impegnato il telescopio da 200 pollici del Monte Palomar e la generazione successiva di telescopi della classe da 4 metri. La sfida consisteva nel misurare precisamente i parametri che caratterizzano l'Universo: la costante di Hubble, H₀=(dR/dt)/R; il parametro di decelerazione, q₀=−(d²R/dt²)/(dR/dt)²; la curvatura dello spazio, k=R⁻²; la densità media di materia nell'Universo, ϱ, e, in particolare, se si supera o meno la densità critica ϱ_crit; l'età dell'Universo, T₀; e la costante cosmologica, λ. Tutti questi dati non sono indipendenti; infatti, secondo la RG,

con q₀=Ω/2-λ/(3H²₀); Ω=ϱ/ϱ_crit è noto come parametro di densità. La determinazione di questi parametri, una delle sfide osservative più ambiziose dell'astronomia di ogni tempo, e i progressi rispetto alle tecniche tradizionali dell'astronomia ottica risultarono però molto più difficili di quanto si era sperato negli anni Trenta. Tuttavia, prospettive completamente diverse si sarebbero profilate dopo la Seconda guerra mondiale, quando per le osservazioni astronomiche divenne disponibile l'intero spettro elettromagnetico e furono scoperti approcci completamente nuovi alla determinazione dei parametri cosmologici e dell'origine della struttura dell'Universo.

L'Universo delle galassie

Le galassie

A seguito degli studi pionieristici di Hubble sulle proprietà delle galassie, riassunti nel suo libro The realm of the nebulae (1936), furono raggiunti risultati definitivi da un punto di vista quantitativo. La distribuzione, per unità di volume, delle luminosità tra galassie di tutti i tipi può essere rappresentata straordinariamente bene dalla forma della funzione di luminosità introdotta da Paul Schechter nel 1976:

[3]  Φ(L) dL=AL^-α exp(-L/L*) dL.

Il valore di L* corrisponde al taglio della funzione di luminosità e si ha L*≈10¹⁰ L_⊙, dove L_⊙ è la luminosità del Sole (Schechter 1976). Si trovò che l'indice α ha un valore di circa 0,25, cioè la funzione di luminosità ha una lunga coda che si estende alle galassie nane, scoperte da Zwicky negli ultimi anni Trenta. La nostra Galassia ha una luminosità di circa 0,5 L*.

La determinazione della distribuzione della massa all'interno delle galassie attraverso le osservazioni risultò molto difficile tuttavia, dagli ultimi anni Settanta in avanti, furono disponibili tubi convertitori di immagine e rivelatori CCD (charge coupled device), per cui aumentò notevolmente la capacità di catturare spettri a due dimensioni utilizzando spettrografi a fenditura lunga. Vera C. Rubin e i suoi colleghi della Carnegie Institution effettuarono studi sistematici delle curve di rotazione di varie galassie in tutte le loro parti interne, utilizzando righe di emissione strette (Rubin et al. 1980). Tali osservazioni furono completate da misure di radioonde della riga a 21 cm dell'idrogeno neutro; fu così possibile determinare le curve di velocità delle galassie spirali, a distanze radiali molto più grandi di quelle consentite dalle osservazioni ottiche.

Risultò che, nelle regioni più esterne delle galassie, le curve di velocità sono eccezionalmente piatte, v_rot=costante. Segue che, se si assume una distribuzione di massa sfericamente simmetrica, si ha che M(⟨r)∝r, cioè la massa totale entro il raggio r cresce linearmente con la distanza dal centro. Questo risultato contrasta fortemente con la diminuzione quasi esponenziale della luminosità superficiale delle galassie spirali a distanza r dal centro. Il rapporto massa-luminosità deve quindi aumentare significativamente nelle regioni esterne delle galassie spirali. Vi deve essere una grande quantità di materia oscura negli aloni delle galassie, all'incirca 10 volte la quantità di materia visibile. Risultati simili per galassie ellittiche furono trovati da Virginia L. Trimble, dagli studi su alcuni ammassi globulari, e da Daniel G. Fabricant e altri, dalla distribuzione delle loro luminosità superficiali di raggi X. Un argomento astrofisico per l'esistenza di tali aloni oscuri attorno alle galassie spirali fu presentato nel 1973 da Jeremiah P. Ostriker e P. James E. Peebles; essi evidenziarono che i dischi interni rotanti sono soggetti a un'instabilità di barra, a meno che non vi sia un alone stabilizzante che contenga una frazione significativa della massa del sistema (Ostriker e Peebles 1973).

Gli ammassi di galassie

Le galassie si raggruppano su una gamma molto ampia di scale fisiche, da piccoli gruppi, che contengono solo alcune galassie, ad ammassi giganti e superammassi. Gli ammassi più ricchi hanno tempi di attraversamento, t_c=R/v, che sono molto minori dell'età dell'Universo e quindi è certo che essi sono entrati in uno stato di equilibrio statistico sotto gravità. Applicando il teorema del viriale, le masse degli ammassi possono spingersi fino a 3×10¹⁵ M_⊙, ossia, come per la prima volta notato da Zwicky, a un valore molto maggiore di quello che si potrebbe inferire dalla luce delle galassie.

Le osservazioni effettuate nei primi anni Settanta con l'osservatorio di raggi X Uhuru mostrarono che alcuni ammassi ricchi di galassie sono sorgenti intense di raggi X la cui emissione è diffusa e riempie una frazione significativa della buca di potenziale gravitazionale dell'ammasso. Sensatamente questa radiazione venne collegata a quella di frenamento del gas caldo all'interno dell'ammasso; prova evidente di questo fenomeno fu la scoperta, realizzata dal satellite Ariel V, di righe di emissione nella banda di ferro altamente ionizzato, Fe XXV e Fe XXVI (Mitchell et al. 1976). Il gas all'interno dell'ammasso dà un contributo significativo alla massa totale dello stesso, tuttavia è ancora approssimativamente un ordine di grandezza in meno di quanto richiesto perché l'ammasso si formi a causa dell'attrazione gravitazionale. Le misure di raggi X rappresentano uno dei più efficaci mezzi per determinare la distribuzione di massa negli ammassi e hanno confermato che questi sono dominati dinamicamente dalla materia oscura.

Una conseguenza della presenza di gas molto caldo nell'ammasso è che i fotoni a bassa energia della radiazione cosmica di microonde sono diffusi a energie maggiori per diffusione Compton, derivante dall'urto elastico di protoni contro elettroni; tale processo fu descritto per la prima volta nel 1969 (Sunyaev e Zeldovich 1970b). Poiché lo spettro della radiazione di fondo risulta spostato verso energie leggermente più alte, si determina una diminuzione della sua intensità nella regione di Rayleigh-Jeans in direzione dell'ammasso di galassie. L'effetto di Sunyaev-Zeldovich coinvolge soltanto circa una parte su 3000 dell'intensità di fondo ed è stato osservato da Mark Birkinshaw e dai suoi colleghi dell'Università di Bristol solamente nel 1990.

La descrizione più semplice dell'evoluzione dinamica di un gruppo di galassie inizia con il collasso di una protogalassia. In esso si realizzano enormi gradienti di potenziale gravitazionale - è, infatti, improbabile che il collasso sia a perfetta simmetria sferica - e il sistema di galassie si rilassa sotto l'influenza di queste perturbazioni. Tale processo, descritto per la prima volta nel 1967 da Donald Lynden-Bell, è noto come 'rilassamento violento'. Le galassie dell'ammasso raggiungono rapidamente un equilibrio dinamico in cui, indipendentemente dalla loro massa, hanno la stessa distribuzione di velocità; questa previsione teorica è compatibile con le osservazioni, effettuate negli ammassi, delle velocità delle galassie con masse diverse.

Proprio come nei casi di particolari galassie interagenti, intense forze mareali possono causare la disgregazione delle galassie e, in particolare, le grandi galassie tendono a distruggere e a inglobare quelle più piccole. Questo processo, descritto da Ostriker e Scott D. Tremaine nel 1975 e spesso chiamato 'cannibalismo galattico', fornisce una buona spiegazione dell'origine delle galassie ellittiche supergiganti, osservate nei centri di molti ammassi ricchi (Ostriker e Tremaine 1975).

Le proprietà di raggruppamento delle galassie su scale maggiori degli ammassi di galassie furono quantificate tramite funzioni di correlazione da Hiroo Totsuji e Taro Kihara nel 1969 e questo approccio fu poi sviluppato ampiamente da Peebles e dai suoi colleghi. La funzione di correlazione a due punti per le galassie può essere scritta:

[4]  N(r) dV=N₀[1+ξ(r)] dV,

dove N(r) descrive la densità in numero delle galassie a distanza radiale r da una qualsiasi galassia data e ξ(r) esprime di quanto aumenta la probabilità di trovare una galassia a distanza r, rispetto a una distribuzione uniforme N₀. La funzione N(r) può essere descritta da una legge di potenza, ξ(r)=(r/r₀)^−γ‚ dove γ=1,8 e r₀≈8 Mpc. Tale funzione, infatti, rappresenta bene il fenomeno di raggruppamento delle galassie su scale da circa 200 kpc a 10 Mpc. Su scale maggiori di 10 Mpc, la funzione diminuisce più rapidamente al crescere della dimensione fisica.

fig. 3

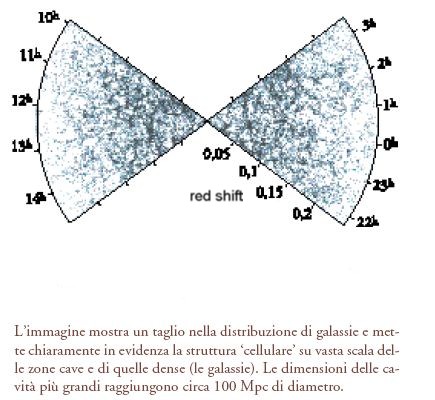
Negli anni Settanta Peebles e i suoi colleghi utilizzarono i conteggi delle galassie di Lick per dimostrare che, su scale maggiori di quelle degli ammassi, la distribuzione delle galassie ha un aspetto fibroso e cellulare, dove le zone vuote sono fino a 30÷50 volte più grandi degli ammassi di galassie (fig. 3). Nel 1986 J. Richard Gott e i suoi colleghi di Princeton mostrarono che la topologia della distribuzione delle galassie su grande scala è simile a una spugna, in quanto sia le zone intergalattiche sia le galassie sono connesse con continuità in tutto l'Universo locale. Si tratta delle strutture più grandi che si conoscono dell'Universo.

Gamow e il 'big bang'

I primi calcoli dettagliati delle abbondanze degli elementi, calcolate nel quadro del modello di Lemaître dell''atomo primordiale', furono eseguiti nel 1942 da Subrahmanyan Chandrasekhar e Louis R. Henrich. In base a essi, fu confermato quanto atteso secondo la teoria all'equilibrio, cioè che, se gli elementi sono in equilibrio a temperature di circa 10¹⁰ K e a densità attorno a 10⁹ kg m⁻³, le loro abbondanze dovrebbero essere inversamente proporzionali alle loro energie di legame. Era tuttavia palese il disaccordo con le abbondanze osservate: gli elementi leggeri, quali il litio, il berillio e il boro, risultavano ampiamente in eccesso rispetto alle abbondanze calcolate; il ferro e gli elementi con numeri di massa maggiori erano di circa 70 in difetto. Questa incompatibilità suggerì l'esistenza di processi di non equilibrio, fino ad allora non considerati.

Nel 1946 Gamow trovò che la scala di tempo sulla quale era avvenuta l'espansione iniziale dell'Universo era troppo breve perché potesse stabilirsi un'abbondanza di equilibrio degli elementi. Una volta determinate le sezioni d'urto di cattura dei neutroni (ciò avvenne nel 1946, in seguito a studi di fisica nucleare eseguiti durante la Seconda guerra mondiale), si trovò una correlazione inversa fra queste sezioni d'urto e le abbondanze relative degli elementi. Nei primi calcoli eseguiti da Gamow e Ralph A. Alpher, nei quali si adottò un modello di Universo statico, si assunse l'esistenza di un mare di neutroni e si suppose che la nucleosintesi avesse avuto luogo soltanto dopo che la temperatura era scesa al di sotto di kT=0,1 MeV (in unità energetiche; k è la costante di Boltzmann). Questa teoria fu pubblicata nel 1948 da Alpher, Hans Bethe e Gamow e vi si trova un accordo ragionevole con le abbondanze osservate degli elementi. L'articolo attirò l'attenzione sulla necessità di avere una fase calda e densa nell'Universo, nell'ipotesi di una sintesi cosmologica degli elementi (Alpher et al. 1948).

Nello stesso anno, Alpher e Robert C. Herman eseguirono calcoli più accurati, in cui era prevista un'espansione cosmica (Alpher e Herman 1948). Essi compresero che, a temperature così alte, l'Universo iniziale era costituito più da radiazione che da materia e risolsero in questo modo il problema della storia dell'Universo precedente alla fase in cui erano stati raggiunti gli 0,1 MeV. Essi pervennero alla giusta conclusione che quello che rimaneva, raffreddato, delle fasi iniziali calde dovesse essere presente nell'Universo attuale e previdero inoltre che la temperatura di fondo termico dovesse essere di circa 5 K.

Vi era, tuttavia, un problema basilare: non esistono nuclei stabili con numeri di massa 5 e 8. Enrico Fermi e Anthony Turkevich calcolarono l'evoluzione delle abbondanze nucleari degli elementi leggeri usando 28 reazioni nucleari per elementi fino a numero di massa 7, in un Universo in espansione dominato da radiazione; questi risultati furono pubblicati da Alpher e Herman nel 1950. Tali calcoli mostrarono che solamente una parte su 10⁷ della massa iniziale poteva essere convertita in elementi più pesanti dell'elio.

Nel 1950 Chushiro Hayashi indicò che, nell'Universo iniziale, neutroni e protoni furono portati all'equilibrio termico dalle interazioni deboli

soltanto a temperature dieci volte maggiori di quelle a cui avvenne la nucleosintesi (Hayashi 1950). Più o meno alla stessa temperatura aveva avuto luogo la produzione di coppie elettrone-positrone. Così, invece di assumere arbitrariamente come condizione iniziale un mare di neutroni, si potrebbero calcolare esattamente le abbondanze all'equilibrio di protoni, neutroni, elettroni e di tutti gli altri costituenti dell'Universo iniziale. Nel 1953 Alpher, James W. Follin e Herman determinarono l'evoluzione del rapporto protoni-neutroni nell'espansione dell'Universo e ottennero una risposta eccezionalmente simile a quella conseguita con calcoli moderni (Alpher et al. 1953). Queste idee furono, tuttavia, superate dalla comprensione della nucleosintesi degli elementi chimici nelle stelle.

La cosmologia dello stato stazionario e la radioastronomia

Immediatamente dopo la guerra molte nuove idee si facevano strada. Edward A. Milne aveva sviluppato la sua teoria della 'relatività cinematica', nella quale sono presenti due tempi, uno associato a fenomeni dinamici, l'altro a fenomeni elettromagnetici. Paul-Adrien-Maurice Dirac era stato impressionato dalle coincidenze tra i numeri molto grandi della fisica e le proprietà dell'Universo - per esempio, il quadrato del rapporto tra l'intensità della forza elettromagnetica e quella della forza gravitazionale è approssimativamente uguale al numero di protoni nell'Universo - e dalla corrispondenza tra questi grandi numeri egli derivò, nel 1937, l'idea che la costante gravitazionale possa variare nel tempo. Eddington aveva sviluppato la sua teoria fondamentale, nella quale la costante cosmologica appariva come una costante fondamentale della Natura.

La cosmologia dello stato stazionario fu inventata da Hermann Bondi, Thomas Gold e Fred Hoyle nel 1948. Essi estesero il principio cosmologico a quello che chiamarono il principio cosmologico perfetto, secondo cui l'Universo presenta a tutti gli osservatori fondamentali sempre la stessa immagine su vasta scala (Bondi e Gold 1948; Hoyle 1948). Da qui si ricava che la costante di Hubble è una costante fondamentale della Natura. Il principio cosmologico perfetto porta a una metrica unica per la dinamica dell'Universo con curvatura spaziale nulla.

A causa dell'espansione dell'Universo, allo scopo di sostituire la materia che si disperde deve esserne creata continuamente altra; la velocità di creazione è di una particella al metro cubo ogni 300.000 anni. Una conseguenza di questa teoria è che l'età dell'Universo sia infinita e che, al contrario, l'età degli oggetti tipici osservati nell'Universo locale sia soltanto (1/3)H^-1₀.

Fu negli ultimi anni Quaranta, durante un programma radiofonico sulla cosmologia, che Hoyle introdusse il termine piuttosto dispregiativo di big bang per descrivere i modelli Fridman caratterizzati da una singolarità iniziale (concetto assente nel modello di stato stazionario).

Hoyle affermò di aver trovato mezzi alternativi per comprendere la formazione degli elementi chimici nella nucleosintesi stellare; queste considerazioni lo portarono nel 1954 a predire la risonanza tre-alfa per la formazione del carbonio nelle stelle e alla pubblicazione di importanti articoli sui processi di nucleosintesi stellare (Burbidge et al. 1957). A seguito di queste nuove intuizioni, le abbondanze degli elementi chimici non furono più considerate come prova di una qualche fase iniziale calda dell'Universo.

Negli anni Cinquanta furono raggiunti due risultati di importanza cruciale per la cosmologia. Il primo riguardava il valore della costante di Hubble. Al convegno dell'Unione astronomica internazionale, svoltosi a Roma nel 1952, Walter Baade annunciò che la distanza dalla Nebulosa Andromeda (M31) era stata sottovalutata di un fattore 2; la costante di Hubble veniva quindi ridotta a 250 km s⁻¹ Mpc⁻¹ e  H^-1₀ aumentato a 4×10⁹ anni. Nel 1956 Milton L. Humason, Nicholas U. Mayall e Allan R. Sandage rideterminarono la costante di Hubble abbassandone ulteriormente il valore a 180 km s⁻¹ Mpc⁻¹ (Humason et al. 1956). Queste correzioni eliminarono la discrepanza fra l'età della Terra e l'età dell'Universo, calcolata secondo i modelli Fridman con λ=0.

Il secondo risultato deriva dalle indagini effettuate sulle sorgenti radio extragalattiche. La radioastronomia fu una delle nuove discipline che seguirono agli sviluppi tecnologici della Seconda guerra mondiale. Durante la seconda indagine su sorgenti radio a Cambridge, intrapresa nel 1954, Martin Ryle e i suoi colleghi trovarono che le sorgenti compatte erano distribuite uniformemente nel cielo e che il loro numero aumentava enormemente quando la misura si estendeva a densità di flusso via via più deboli. In qualsiasi modello euclideo uniforme ci si aspetta che il numero di sorgenti più luminose di una certa densità di flusso S soddisfi la relazione N(≥S)∝S^−3/2; tuttavia, a densità di flusso più deboli, Ryle trovò un quantità maggiore di sorgenti deboli rispetto a quanto previsto dalla legge N(≥S)∝S⁻³.

Egli concluse che l'unica interpretazione ragionevole consisteva nel fatto che vi fosse una densità in numero di radiosorgenti extragalattiche molto maggiore a grandi distanze, e perciò a epoche cosmiche precedenti, piuttosto che a distanze ravvicinate. Come Ryle espresse nella sua Halley Lecture, "sembra non ci sia alcun modo di spiegare le osservazioni in termini di una teoria di stato stazionario" (Ryle 1955).

Un anno dopo, il gruppo di Sydney, diretto da Bernard Mills, completò le misure radio del cielo meridionale usando come antenne le cosiddette 'croci di Mills' (insieme di antenne perpendicolari tra loro caratterizzate da un fascio molto stretto) e trovò il conteggio delle sorgenti pari a N(≥S)∝S^−1,65; tale risultato non era significativamente diverso dall'aspettativa dei modelli cosmologici uniformi. Il problema dei conteggi di Cambridge consisteva nel fatto che essi si estendevano a densità superficiali di sorgenti tali che le densità di flusso delle sorgenti più deboli erano sopravvalutate; tale fenomeno è noto come 'confusione'. Peter A.G. Scheuer elaborò una procedura statistica per derivare i conteggi delle sorgenti direttamente dalle registrazioni delle misure e trovò che la pendenza dei conteggi delle sorgenti era in effetti −1,8, che ora si sa essere la pendenza corretta (Scheuer 1957).

La risoluzione della controversia arrivò con ulteriori indagini, meno sensibili agli effetti di confusione delle sorgenti, che permisero di ottenere posizioni precise e identificazioni ottiche. Queste mostrarono che le conclusioni di Ryle del 1955 erano fondamentalmente corrette. I programmi di riconoscimento ottico condussero, nei primi anni Sessanta, alla scoperta dei quasar. A metà degli anni Sessanta, si ottenne la prova schiacciante che ci fosse un grande eccesso di radiosorgenti extragalattiche e quasar per grandi red shift, contrariamente alle aspettative della teoria dello stato stazionario.

Il problema dell'elio e la scoperta della radiazione di fondo cosmico di microonde

Nel 1961 Donald E. Osterbrock e John B. Rogerson mostrarono che l'abbondanza frazionaria di elio sembrava essere eccezionalmente uniforme dovunque potesse essere osservata e corrispondeva a circa il 25% della massa totale. Nel 1964 C. Robert O'Dell, Manuel Peimbert e Thomas D. Kinman trovarono che anche in una nebulosa planetaria nel vecchio ammasso sferico M15 era presente abbondanza di elio per circa il 25%; viceversa gli elementi pesanti risultavano molto impoveriti rispetto alle abbondanze cosmiche.

Nello stesso anno Hoyle e Roger J. Tayler ripeterono i calcoli relativi alla nucleosintesi primordiale; trovarono che circa il 25% di elio è sintetizzato nel big bang, in perfetto accordo con i dati osservati, e che questo risultato è essenzialmente indipendente dalla attuale densità barionica (Hoyle e Tayler 1964). Tuttavia essi non indicarono che le radiazioni associate all'Universo iniziale caldo dovessero ancora essere individuabili sulle lunghezze d'onda del centimetro. La previsione di Alpher e Herman era stata più o meno accantonata nel momento in cui la teoria di Gamow della nucleosintesi primordiale non era riuscita a spiegare la creazione degli elementi.

Nel 1965, fu scoperta, più o meno incidentalmente, la radiazione di fondo di microonde dagli statunitensi Arno A. Penzias e Robert W. Wilson. Usando un'antenna a tromba di 20 piedi, progettata per le telecomunicazioni, essi notavano, dovunque puntassero il telescopio al cielo, un rumore imprevisto con temperatura di 3,5±1 K (Penzias e Wilson 1965). Il gruppo di Robert H. Dicke a Princeton stava tentando esattamente questo esperimento per rilevare ciò che restava, raffreddato, del big bang; si capì subito che Penzias e Wilson avevano scoperto il segnale cercato dai fisici di Princeton. Dopo alcuni mesi, due di questi fisici, Peter Roll e David Wilkinson, misurarono una temperatura di fondo di 3,0±0,5 K a una lunghezza d'onda di 3,2 cm, che confermava la natura di corpo nero dello spettro di fondo.

In precedenza si era trovata, dallo studio di deboli righe di assorbimento interstellari, associate alle molecole CH, CH⁺ e CN, una componente diffusa di radiazione dell'ordine del millimetro. Nel 1941 Andrew McKellar aveva mostrato che la temperatura di eccitazione necessaria per popolare i primi stati eccitati di queste molecole era 2,3 K, ma l'origine di tale eccitazione era sconosciuta (McKellar 1941). In seguito furono effettuate molte osservazioni della radiazione di fondo cosmico di microonde, che culminarono in misure eccellenti realizzate dal satellite COBE (Cosmic background explorer); esse mostrarono che lo spettro della radiazione è esattamente quello di un corpo nero in cui la temperatura della radiazione è di 2,725±0,01 K (Mather et al. 1990).

Nel 1967 Robert V. Wagoner, William A. Fowler e Hoyle ripeterono l'analisi eseguita da Hoyle e Tayler utilizzando molte più sezioni d'urto di interazioni nucleari per nuclei leggeri, sapendo che la temperatura di radiazione di fondo era circa 2,7 K (Wagoner et al. 1967). Oltre all'elio, furono previste le abbondanze degli altri prodotti di nucleosintesi, ossia del deuterio, dell'³He e del ⁷Li, e si trovò che queste dipendevano dalla densità media attuale dei barioni nell'Universo. L'importanza di tali elementi leggeri consiste nel fatto che essi non sono sintetizzati, ma distrutti, nelle stelle.

Le righe interstellari di assorbimento del deuterio furono scoperte, nella regione ultravioletta dello spettro, da Rogerson e Donald G. York nel 1973 a partire da osservazioni realizzate dal satellite Copernicus (Rogerson e York 1973). Fu trovata un'abbondanza in massa di deuterio interstellare 1,5×10⁻⁵ volte minore rispetto a quella dell'idrogeno. Osservazioni effettuate nel 1977 mostrarono che la stessa abbondanza di deuterio si trova lungo le linee radiali di altre stelle. Questi risultati permisero di porre un limite superiore alla densità media barionica dell'Universo di 1,5×10⁻²⁸ kg m⁻³, che è di almeno un ordine di grandezza in meno rispetto alla densità cosmologica critica.

Fu stimato da Hoyle e Tayler, da Peebles e dal gruppo di Mosca, cui apparteneva Zeldovich, che la nucleosintesi degli elementi leggeri fornisce un importante strumento diagnostico per la dinamica dell'Universo all'epoca della nucleosintesi. Furono posti limiti su una qualsiasi possibile variazione della costante gravitazionale con il tempo cosmico; il numero delle specie ammissibili di neutrini fu limitato a 3 - risultato successivamente confermato dagli esperimenti con il LEP (Large electron-positron collider) al CERN.

Alla fine degli anni Sessanta, la radiazione di fondo cosmico di microonde e le abbondanze cosmiche degli elementi leggeri vennero universalmente riconosciute come prove inconfutabili delle fasi iniziali calde dell'Universo e, perciò, la cosmologia astrofisica assunse come riferimento standard lo scenario del big bang.

Il problema cosmologico classico

Immediatamente dopo la Seconda guerra mondiale, lo strumento principale della ricerca cosmologica era il telescopio da 200 pollici del Monte Palomar, commissionato nel 1948. Nel 1961 Sandage pubblicò un articolo in cui discuteva svariati approcci per la determinazione della costante di Hubble e del parametro di decelerazione q₀.

La costante di Hubble e l'età dell'Universo

Nel 1956 fu ottenuta da Sandage un'ottima stima della costante di Hubble: H₀=75 km s⁻¹ Mpc⁻¹. Nello stesso anno i già citati Humason, Mayall e Sandage mostrarono che, per galassie prese a caso, c'è una grande dispersione nella relazione red shift-magnitudine; ciò rende inadeguato l'ultilizzo di tale relazione per la determinazione dei parametri cosmologici (Humason et al. 1956). Sandage mostrò, tuttavia, che le magnitudini assolute delle galassie più luminose degli ammassi hanno una dispersione molto più stretta, di circa 0,3 (Sandage 1968). Si potrebbe trovare la costante di Hubble se questa relazione potesse essere verificata misurando la magnitudine assoluta delle galassie più luminose in ammassi ricchi vicini.

Dal 1970 agli ultimi anni Novanta, il valore della costante di Hubble fu una questione controversa. In una lunga serie di articoli, Sandage e Gustav Tammann trovarono valori di H₀≈50 km s⁻¹ Mpc⁻¹, mentre Vaucouleurs, Aaronson, Mould e i loro collaboratori trovarono valori di circa 80 km s⁻¹ Mpc⁻¹. La controversia si risolse attraverso un notevole impegno collettivo di un ampio gruppo di astronomi, che misurarono precisamente le distanze delle galassie vicine; a tale scopo furono effettuate le osservazioni sulle Cefeidi variabili nell'ammasso della Vergine attraverso il telescopio spaziale Hubble; il risultato finale di questo programma fu un valore di 70±7 km s⁻¹ Mpc⁻¹, dove gli errori sono 1−σ (Freedman et al. 2001). Tale valore è compatibile con molti approcci indipendenti in cui H₀ cade nell'intervallo tra 60 e 75 km s⁻¹ Mpc⁻¹.

Come abbiamo detto, il valore della costante di Hubble è strettamente legato all'età dell'Universo. Una delle tecniche migliori per il calcolo di tale età, inventata nel 1952 da Sandage e Martin Schwarzschild, implica il confronto dei diagrammi di Herzsprung-Russell (ossia della luminosità in funzione della temperatura superficiale delle stelle) relativi agli ammassi sferici più vecchi e poveri di metallo con quanto ci si può attendere in base alla teoria dell'evoluzione stellare utilizzando la diramazione della sequenza principale verso il braccio delle stelle giganti. Per il vecchio ammasso sferico 47 Tucanae, la migliore stima prevede che l'abbondanza degli elementi pesanti sia soltanto il 20% del valore solare e che l'età dell'ammasso sia di (1,2-1,4)×10¹⁰ anni. Per confronto, la scala di tempo H₀⁻¹ che corrisponde al valore attuale della costante di Hubble sta nell'intervallo (1,27-1,55)×10¹⁰ anni. Questi valori sono simili a quelli determinati dalla cronologia dei nuclei cosmici e dal periodo di raffreddamento delle stelle nane bianche.

Il parametro di decelerazione

fig. 4

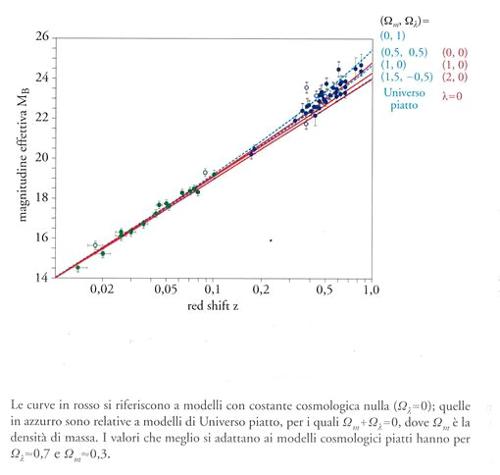
La relazione red shift-magnitudine per le galassie più luminose degli ammassi è esattamente lineare, ma vale solo per i red shift fino a z≈0,5, per i quali le differenze tra i vari modelli cosmologici sono relativamente piccole (z è il rapporto tra la velocità di allontanamento della galassia e la velocità della luce). Inoltre, devono essere apportate opportune correzioni sia a causa di correlazioni sottili fra le proprietà delle galassie più luminose degli ammassi sia a causa di effetti relativi all'evoluzione delle loro popolazioni stellari. Le incertezze risultanti nel valore del parametro di decelerazione q₀ sono abbastanza grandi, tanto che Sandage concluse che q₀=1±1 (Sandage 1995). Problemi simili sono presenti in altri metodi usati nella determinazione dei parametri cosmologici, per esempio nella relazione infrarosso-magnitudine K, valida per le radiogalassie. Un metodo promettente per la determinazione dei parametri cosmologici è stato perseguito attraverso l'uso di supernovae di tipo Ia. Queste supernovae sono associate alla morte delle stelle nane bianche, che raccolgono sulle loro superfici materia proveniente dalla stella più piccola di un sistema binario. Esiste una correlazione fra la luminosità massima di queste supernovae e la durata della fase di massima intensità; una volta apportate le correzioni per questa correlazione, si rileva che tali oggetti sono i migliori indicatori di distanza disponibili. La relazione red shift-magnitudine per tali supernovae fino a red shift vicini a 1 (le osservazioni si possono effettuare comunque anche a red shift maggiori) mostra che i modelli cosmologici nei quali si assume nulla la costante cosmologica non sono molto rappresentativi (fig. 4). Combinati con le osservazioni dello spettro delle fluttuazioni nella radiazione di fondo cosmico di microonde, questi dati forniscono una prova convincente della limitatezza del valore della costante cosmologica.

L'evoluzione cosmologica delle galassie attive

Esiste ora una prova convincente del fatto che le proprietà delle galassie di qualsiasi tipo e delle galassie attive evolvano con il tempo cosmico. Nel 1968 Michael Rowan-Robinson e Maarten Schmidt svilupparono indipendentemente una procedura, il cosiddetto 'V/V_max test', per mostrare che i quasar radio sono situati verso i limiti dei loro volumi osservabili (Rowan-Robinson 1968; Schmidt 1968). Da allora, sono state eseguite numerose indagini sistematiche per definire la forma precisa dell'evoluzione cosmologica delle radiogalassie e delle popolazioni dei quasar radio. Lo studio più ambizioso in tal senso fu completato da James S. Dunlop e John A. Peacock nel 1990.

fig. 5

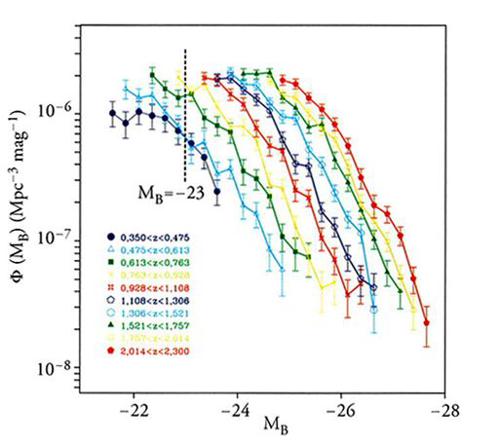
Nei primi anni Ottanta, le indagini sistematiche di quasar selezionati otticamente mostrarono che anch'essi esibiscono una forte evoluzione cosmologica, simile a quella dei quasar radio. Patrick S. Osmer rilevò che vi era un numero di grandi oggetti spostati verso il rosso inferiore a quello atteso in base ai modelli evolutivi utilizzati per spiegare le distribuzioni degli oggetti a z≈2. Negli anni Ottanta e Novanta la disponibilità di strumenti in grado di misurare le alte velocità permise di intraprendere vaste e complete indagini di quasar in cui si utilizzava la fotometria multicolore. Ne risultò un campionamento completo dei quasar con red shift via via crescenti. Di recente l'indagine digitale del cielo, realizzata da Alfred P. Sloan, ha permesso di scoprire quasar con red shift fino a 6,4. Una qualche misura dell'intensità dei cambiamenti evolutivi può essere osservata (fig. 5) nell'evoluzione della funzione di luminosità di un campione molto grande di quasar, scelti otticamente dall'indagine sul quasar 2dF.

Nel 1982 furono eseguite le prime indagini approfondite sui raggi X visibili nel cielo dall'Osservatorio spaziale Einstein; vi si trovò la prova di un eccesso di sorgenti deboli di raggi X associate alle galassie attive. La prova definitiva dell'evoluzione cosmologica della popolazione di sorgenti di raggi X fu derivata da minuziose indagini eseguite dal satellite ROSAT (Roentgen satellite), lanciato nel 1991. Accurati conteggi di sorgenti di raggi X, operati da Günther Hasinger e dai suoi colleghi nel 1993, mostrano esattamente la stessa forma dei conteggi delle radiosorgenti e dei quasar: la pendenza dei conteggi supera l'aspettazione euclidea alle alte densità di flusso, ma vi è convergenza alle densità di flusso più deboli (Hasinger et al. 1993).

Sembra che le popolazioni di galassie attive di tutti i tipi esibiscano la stessa forma di evoluzione con il tempo cosmico, che può essere descritta assumendo che le luminosità medie delle sorgenti cambino come L=L₀(1+z)³ nell'intervallo di red shift 0⟨z⟨2. A red shift più grandi, le luminosità medie non possono continuare ad aumentare come (1+z)³, e la densità dello spazio solidale con questi oggetti diminuisce a grandi red shift. C'è un comune accordo nel pensare che la popolazione di galassie attive dovesse essere notevolmente più energetica quando l'Universo aveva un'età di circa il 20-25% della sua età attuale.

Il parametro densità

L'analisi di Hubble della densità media di massa nelle galassie fu ripetuta nel 1958 da Jan H. Oort, che trovò un valore di 3,1×10⁻²⁸ kg m⁻³, assumendo che la costante di Hubble fosse 180 km s⁻¹ Mpc⁻¹ (Oort 1958). Questo valore non è molto diverso da quelli attuali. Nel 1978 James E. Gunn espresse lo stesso risultato in termini del rapporto massa/luminosità necessario affinché l'Universo abbia la densità cosmologica critica. Egli trovò (M/L)_crit=2600 h, valore di gran lunga maggiore di quelli rilevati nelle nostre vicinanze, nel piano della Galassia; h è il valore della costante di Hubble in unità pari a 100 km s⁻¹ Mpc⁻¹. Se si tenesse conto della materia oscura presente nelle galassie, il rapporto tra la massa totale e la luminosità sarebbe molto più grande, M/L≈(100÷150)h. Negli ammassi ricchi di galassie, il valore tipico di M/L, in cui si includa la materia oscura, è dell'ordine di 250 h. Questi valori di M/L sono significativamente minori del valore necessario per un Universo chiuso.

Tali risultati riflettono il punto di vista, generalmente accettato, secondo cui, determinando la densità di massa dei sistemi legati, la densità di massa totale nell'Universo risulta di circa 5-10 volte minore di quella necessaria per un Universo chiuso. Negli anni Ottanta, il teorema del viriale cosmico fu applicato da Marc Davis e Peebles alle velocità casuali di galassie non appartenenti a un ammasso. Questi studi suggerirono che il parametro densità di massa ω_m potesse essere più grande di 0,2. Un risultato simile fu trovato studiando la caduta di galassie in superammassi e in altri sistemi su grande scala, come il Grande Attrattore (superammasso di galassie la cui esistenza a circa 150 milioni di anni-luce è stata ipotizzata per spiegare particolari movimenti delle galassie): ricordiamo che tale caduta si verifica a causa della presenza di un oggetto molto compatto, come una stella di neutroni o un buco nero, in cui si forma un plasma caldo. Recenti studi hanno utilizzato più di 100.000 galassie provenienti dall'indagine 2dF per misurare statisticamente la velocità media di caduta delle galassie nelle strutture su larga scala (Peacock et al. 2001). Se il valore della costante di Hubble è di 70 km s⁻¹ Mpc⁻¹, si ha ω_m=0,3. La maggior parte della massa nell'Universo deve essere in qualche forma non barionica, in quanto le osservazioni dell'abbondanza cosmica di deuterio indicano che il parametro attuale di densità barionica ω_B non può essere maggiore di 0,02 h⁻².

La formazione di galassie e le strutture su vasta scala nell'Universo

I modelli di Friedman sono isotropi e omogenei e quindi il passo successivo nello sviluppo di modelli più realistici è includere piccole perturbazioni e studiare come queste evolvano sotto gravità. Tale problema fu risolto nel 1902 da James H. Jeans per il caso di un mezzo stazionario. Secondo Jeans, perché si abbia il collasso, la forza gravitazionale con cui la materia attrae la perturbazione deve superare i gradienti di pressione che resistono al collasso. L'analisi fu ripetuta per il caso di perturbazioni sfericamente simmetriche in un mezzo in espansione da Lemaître nel 1933 e da Richard C. Tolman nel 1934, e la soluzione generale fu trovata da Evgenii Lifshitz nel 1946 (Lemaître 1933; Tolman 1934; Lifshitz 1946). La condizione per il collasso gravitazionale è esattamente la stessa del criterio di Jeans e, in particolare, la velocità di crescita delle perturbazioni non è più esponenziale ma soltanto una potenza Δ∝t^2/3. Ne consegue che le fluttuazioni dalle quali si è formata la struttura su vasta scala dell'Universo non possono essersi sviluppate da perturbazioni infinitesimali. Per questa ragione, Lemaître, Tolman e Lifshitz inferirono che le galassie non potessero essersi formate per collasso gravitazionale.

In seguito, altri studiosi dichiararono che la soluzione era includere perturbazioni limitate nell'Universo iniziale e seguire come il loro spettro di massa si fosse sviluppato nel tempo. Negli anni Sessanta la scuola di Mosca, guidata da Zeldovich, Igor D. Novikov e i loro colleghi, e Peebles a Princeton aprirono la strada allo studio della formazione delle strutture. A un red shift sufficientemente grande, la scala della perturbazione è uguale a quella dell'orizzonte, r=ct, dove t è l'età dell'Universo. Nel 1964 Novikov mostrò che, per formare strutture sulla scala delle galassie e degli ammassi di galassie e garantire la formazione di galassie nell'epoca corrente, le perturbazioni di densità sulla scala dell'orizzonte dovevano avere ampiezza Δ≈10⁻⁴.

La scoperta della radiazione di fondo cosmica di microonde nel 1965 ebbe un impatto eccezionale su questi studi poiché si poterono determinare in dettaglio la storia termica del gas intergalattico e pregalattico. La temperatura della radiazione di fondo cambia con un fattore di scala dato dalla relazione T=T₀(1+z); così, a un red shift z≈1500 la temperatura della radiazione è di circa 4000 K; a tale temperatura, nella coda della distribuzione di Planck, ci sono fotoni sufficienti a ionizzare tutto l'idrogeno intergalattico. L'epoca corrispondente è nota come 'epoca di ricombinazione', e, in epoche precedenti, l'idrogeno era completamente ionizzato. Poco prima, la densità di massa inerziale della radiazione era uguale alla densità di massa della materia, ϱc²=aT⁴ e, in tempi ancora precedenti, la dinamica dell'Universo era dominata dalla radiazione.

Lo studio dell'accoppiamento materia-radiazione per mezzo della diffusione di elettroni fu completato da Ray J. Weymann nel 1966 e ulteriori dettagli furono aggiunti nel 1969 da Zeldovich e Rashid A. Sunyaev. Essi mostrarono che, durante le epoche dominate dalla radiazione, materia e radiazione furono mantenute in strettissimo contatto termico dalla diffusione Compton finché il gas intergalattico rimase ionizzato. Ciò permise di determinare la velocità del suono e, perciò, la lunghezza di Jeans, in tutte le epoche precedenti a quella di ricombinazione.

Nel 1968 Joseph Silk mostrò che, durante le epoche precedenti alla ricombinazione, le onde sonore nel plasma dominato dalla radiazione erano smorzate dai ripetuti urti degli elettroni e, così, sarebbero state dissipate le perturbazioni con massa inferiore a circa 10¹² M_⊙ (Silk 1968). All'epoca della ricombinazione sarebbero sopravvissute soltanto strutture apprezzabili sulla scala delle grandi galassie, degli ammassi di galassie e ancora più grandi. Nei primi anni Settanta Edward R. Harrison e Zeldovich mostrarono che le strutture su vasta scala dell'Universo potevano essere spiegate se lo spettro delle fluttuazioni di massa, nelle primissime fasi dell'Universo, aveva la forma Δ(M)∝M^−2/3, che corrisponde a uno spettro di potenza delle fluttuazioni iniziali della forma ∣Δ_k²∣∝kⁿ, con n=1, e di ampiezza di ≈10⁻⁴ (Harrison 1970; Zeldovich 1972). Questo spettro di Harrison-Zeldovich ha l'interessante caratteristica che le fluttuazioni sulle varie scale di massa hanno la stessa ampiezza quando attraversano l'orizzonte.

Negli anni Settanta furono sviluppati due scenari diversi per l'origine delle strutture dell'Universo. Nel modello adiabatico, le perturbazioni iniziali erano onde sonore adiabatiche prima della ricombinazione e le strutture nell'Universo adiabatico si formarono, in epoche relativamente successive, dalla frammentazione di strutture su vasta scala che arrivavano ad ampiezze di δϱ/ϱ∼1. Nel modello alternativo sono, invece, implicate, nel plasma precedente alla ricombinazione, perturbazioni isotermiche in equilibrio con la pressione della radiazione di fondo. Queste non avrebbero subito alcuno smorzamento cosicché le masse, su tutte le scale, sarebbero sopravvissute fino all'epoca della ricombinazione. Le galassie e gli ammassi di galassie si sarebbero, quindi, formati attraverso un processo di raggruppamento gerarchico. La rappresentazione adiabatica può essere pensata come un processo top-down, nel senso che si sarebbero formate prima le strutture della scala più grande. Al contrario, il modello isotermico corrisponde a un processo bottom-up, in cui gli oggetti in scala ridotta si sarebbero uniti per formare strutture più grandi.

Le fluttuazioni di densità all'epoca della ricombinazione lasciarono tracce sulla radiazione di fondo cosmico di microonde. Secondo le ricerche di Sunyaev e Zeldovich, effettuate nel 1970, le fluttuazioni di temperatura su piccole scale angolari sono associate a quelle adiabatiche e alla diffusione Doppler del primo ordine, dovuta al collasso delle perturbazioni (Sunyaev e Zeldovich 1970a). Su scale più grandi ci si aspettava che le fluttuazioni di temperatura fossero causate dal red shift gravitazionale che la radiazione subisce sfuggendo dalle perturbazioni di densità sulla scala più grande - fenomeno noto come 'effetto Sachs-Wolfe', dal nome dei due studiosi, Raymond K. Sachs e Arthur M. Wolfe, che lo discussero nel 1967. Le ampiezze predette delle fluttuazioni erano ΔT/T≈10⁻³-10⁻⁴ e i modelli cosmologici puramente barionici entrarono in serio conflitto con le osservazioni, in cui si continuavano a migliorare i limiti dell'ampiezza delle fluttuazioni. Questi problemi erano accentuati dai limiti della densità barionica posti dalla nucleosintesi primordiale, che mostravano che, se il parametro di densità fosse 1, la maggior parte della materia nell'Universo dovrebbe essere in qualche forma non barionica.

Una possibile soluzione a questi problemi apparve nel 1980, quando Valentin A. Lyubimov e i suoi collaboratori riferirono che il neutrino elettronico ha una massa a riposo finita di circa 30 eV. Negli anni Settanta gli ungheresi George Marx e Alexander S. Szalay avevano considerato i neutrini con massa a riposo finita quali possibili costituenti della materia oscura e avevano studiato il loro ruolo nella formazione delle galassie. Zeldovich e i suoi colleghi svilupparono una nuova versione del modello adiabatico in cui l'Universo era dominato da neutrini con massa a riposo finita. I neutrini interagiscono molto debolmente con la materia e quindi si svincolano agilmente dalle perturbazioni di densità. Soltanto le perturbazioni sulla scala in assoluto più grande, con masse M≥10¹⁶ M_⊙, sopravvivrebbero all'epoca della ricombinazione. Nel 1970 Zeldovich scoprì una soluzione per lo sviluppo non lineare di una nube che collassa e mostrò che le perturbazioni su grande scala potrebbero formare superfici piatte (sheets e pancakes), in grado di spiegare la struttura filamentosa su grande scala, osservata nella distribuzione delle galassie (Zeldovich 1970). Le ampiezze delle fluttuazioni di temperatura nella radiazione di fondo di microonde sarebbero state molto ridotte poiché le fluttuazioni nella materia barionica sarebbero state poco ampie durante le fasi critiche in cui, per ultimi, furono diffusi i fotoni di fondo.

Si crede ora che il risultato di Lyubimov sia sbagliato: il limite superiore della massa a riposo del neutrino elettronico risulta minore di circa 1 eV. Nel 1979 Tremaine e Gunn mostrarono come i vincoli nello spazio delle fasi associato ai fermioni, quali sono i neutrini, potevano essere utilizzati per fissare limiti inferiori per le loro masse (Tremaine e Gunn 1979). Mentre i neutrini a 30 eV potrebbero legare gli ammassi e gli aloni delle galassie giganti, quelli necessari per legare le galassie nane dovrebbero avere masse maggiori di 30 eV. Più di recente, la scoperta delle oscillazioni dei neutrini suggerisce fortemente che le masse di questi, sebbene finite, siano di molto inferiori a 1 eV ed è quindi improbabile che essi giochino un ruolo importante in cosmologia.

Nei primi anni Ottanta si capì che esistono numerosi modi per spiegare la materia oscura secondo le teorie della fisica delle particelle, per esempio includendovi gli assioni, le particelle supersimmetriche, come il gravitino o il fotino, e le particelle debolmente interagenti, quali il neutrino; i fisici delle particelle iniziarono così a considerare seriamente l'Universo primordiale come laboratorio per i loro studi. Nel 1982 Peebles introdusse la locuzione 'materia oscura fredda' per denotare molti tipi esotici di particella, collettivamente noti come 'particelle massive debolmente interagenti' (o WIMPS, weakly interacting massive particles), che potrebbero essersi create nei primi minuti dell'Universo e che, quindi, ora sarebbero molto fredde.

Nello scenario della materia oscura fredda, le perturbazioni non sono distrutte dal flusso libero poiché la materia è molto fredda. Dopo l'epoca della ricombinazione, la materia barionica collassa in buche di potenziale via via più profonde nella materia oscura. Dopo la ricombinazione, galassie, gruppi e ammassi si formano per un processo di raggruppamento gerarchico. Un formalismo eccezionalmente efficace nella esposizione di questo processo fu presentato nel 1974 da William H. Press e Schechter; esso fornisce una buona descrizione di come, per una data funzione di massa, la funzione di massa di oggetti di masse diverse si sviluppi nel tempo (Press e Schechter 1974). Il confronto con le simulazioni, realizzate con gli attuali supercomputer, ha mostrato che il formalismo di Press-Schechter è un'utile descrizione del modo in cui si sviluppa la struttura nell'Universo dopo la ricombinazione. Molti modelli alternativi sul ruolo della materia oscura nella formazione delle galassie sono stati verificati attraverso molteplici analisi e simulazioni al computer. Gli scenari in cui la materia oscura fredda ha un termine λ finito possono spiegare molte caratteristiche della distribuzione delle galassie nell'Universo, per quanto possa restare sconosciuta la natura della materia oscura.

Fluttuazioni di temperatura su scale angolari maggiori o uguali a 10° furono scoperte nel 1992 dal satellite COBE con un'ampiezza di ΔI/I≈10⁻⁵ (Smoot et al. 1992). Queste osservazioni dimostrarono che l'Universo è isotropo a una risoluzione migliore di una parte su 10⁵, sulle più grandi scale accessibili. La ricerca delle fluttuazioni di temperatura nella radiazione di fondo su scala minore o uguale a 1° fu di importanza cruciale, perché su queste scale il Modello standard della materia oscura fredda fa predizioni molto forti sulla presenza di picchi acustici, o di Sacharov, nello spettro di potenza delle fluttuazioni. Andrei D. Sacharov aveva, infatti, predetto la presenza di questi picchi in un articolo del 1965, alcuni mesi prima della scoperta della radiazione di fondo cosmico di microonde (Sacharov 1965). I picchi sono associati al fatto che le fluttuazioni nel plasma dominato dalla radiazione sono onde sonore dopo che esse hanno attraversato l'orizzonte, e vi è un numero limitato di oscillazioni tra quel momento e l'epoca in cui le fluttuazioni lasciano il loro segno sulla radiazione di fondo, durante l'epoca della ricombinazione. L'origine di questi picchi e la loro importanza per la cosmologia furono notate da Sunyaev e Zeldovich nei loro articoli del 1970 (Sunyaev e Zeldovich 1970a).

fig. 7

tab. 1

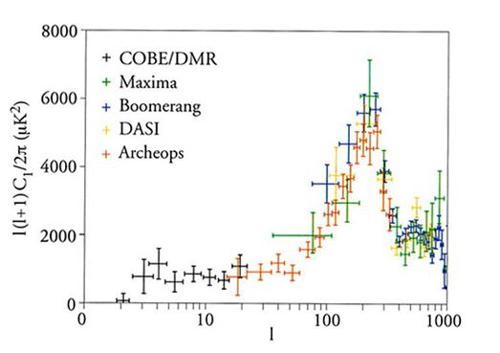
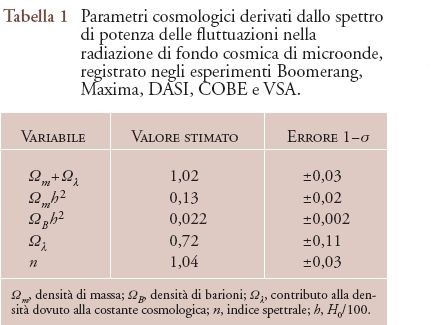
La misura delle proprietà dettagliate dello spettro di potenza delle fluttuazioni nella radiazione di fondo cosmico fornisce mezzi molto potenti, non soltanto per testare la teoria dell'origine delle strutture, ma anche per determinare i valori dei parametri cosmologici. All'epoca della ricombinazione, le fluttuazioni erano ancora nel regime lineare e, quindi, dato un insieme di parametri di ingresso, si possono eseguire con precisione i calcoli dello spettro predetto delle perturbazioni di temperatura. Dal 2002 esistono prove convincenti della scoperta del primo e del secondo picco predetti nello spettro di potenza delle fluttuazioni, dati che permettono di realizzare valutazioni eccezionalmente precise dei parametri cosmologici (fig. 7). La scala angolare sulla quale si osserva il primo picco è di importanza fondamentale poiché è determinata principalmente dalla geometria generale dell'Universo. Fisicamente, questo picco corrisponde alla scala dell'orizzonte sonoro per le fluttuazioni nel plasma di fotoni e barioni, all'epoca della ricombinazione. Si può trovare un insieme concorde di parametri cosmologici che è consistente con i valori provenienti dai risultati delle supernovae di tipo Ia, e si può determinare dinamicamente la densità media di materia oscura fredda e quella barionica nell'Universo, a partire da argomenti relativi alla nucleosintesi primordiale (tab. 1). Questo risultato è davvero sorprendente.

I primi istanti dell'Universo

Malgrado l'indubbio successo del modello standard della materia oscura fredda con valore finito della costante cosmologica, è necessario fin dal principio stabilire in esso ben quattro assunzioni: (a) l'Universo deve essere isotropo; (b) vi deve essere stata un'asimmetria molto piccola tra barioni e antibarioni nei primi istanti dell'Universo; (c) l'Universo si deve essere costituito con una geometria piatta; (d) uno spettro iniziale di fluttuazioni deve essere stato presente nell'Universo primordiale.

La prima condizione deriva dal fatto che, in un lontano passato, la scala dell'orizzonte racchiudeva sempre meno massa e, quindi, ci si domanda perché oggi l'Universo dovrebbe essere così isotropo sulle scale più grandi. Il secondo requisito scaturisce dal fatto che l'attuale rapporto tra fotoni e barioni è N_γ/N_B=4×10⁷/(ω_B h²), dove ω_B è il parametro di densità di barioni e h=H₀/100. Se i fotoni non sono né creati né distrutti, questo rapporto è conservato. A temperature di circa 10¹⁰ K, dal campo dei fotoni si producono coppie elettrone-positrone. In un'epoca antecedente, a una temperatura più alta, si ha produzione di coppie barione-antibarione con il risultato che ci deve essere stata una leggera asimmetria nel rapporto barioni-antibarioni nella primissima fase dell'Universo. Nel 1965 Zeldovich mostrò che, se l'Universo fosse simmetrico rispetto a materia e antimateria, l'attuale rapporto fotoni su barioni-antibarioni sarebbe di circa 10¹⁸. Furono proposti vari modelli di Universo con simmetria barionica, da Hannes Alfvén e Oskar B. Klein nel 1962 e da Roland Omnes nel 1969, che però non riuscirono a dimostrare come materia e antimateria si fossero potute separare nell'Universo iniziale. La terza condizione, notata da Dicke e Peebles nel 1979, consegue dal fatto che, secondo i modelli cosmologici standard, se l'Universo si fosse costituito con un valore del parametro di densità diverso dal valore critico ω=1, si sarebbe allontanato molto rapidamente da ω=1 in epoche successive. Ci si chiede, dunque, perché l'Universo sia così vicino all'Universo piatto con ω_m+ω_Λ=1.

Nel 1967 Sacharov suggerì che l'asimmetria barioni-antibarioni potesse essere associata al tipo di rottura di simmetria osservato nei decadimenti dei mesoni K (Sacharov 1967). Ci si aspetta che si verifichino tipi simili di rottura di simmetria nelle teorie di grande unificazione delle particelle elementari a temperature molto alte e, perciò, Sacharov propose tre regole che devono essere soddisfatte affinché sia osservata un'asimmetria barioni-antibarioni: (a) la conservazione del numero barionico deve essere violata; (b) C (la coniugazione di carica) e CP (la coniugazione di carica combinata con la parità) devono essere violate; (c) l'asimmetria si deve creare sotto condizioni di non equilibrio.

Il più importante sviluppo concettuale si verificò nel 1981 quando Alan Guth propose il modello inflazionario per le fasi iniziali dell'Universo (Guth 1981). Già precedentemente, vi erano stati sviluppi che suggerivano una simile ipotesi. Nel 1968, infatti, Zeldovich aveva osservato che è possibile un'interpretazione fisica della costante cosmologica λ, associata a fluttuazioni di punto zero del vuoto. Andrei D. Linde nel 1974 e Sidney A. Bludman e Malvin A. Ruderman nel 1977 avevano mostrato che i campi scalari di Higgs hanno proprietà simili a quelli che porterebbero a una costante cosmologica positiva.

Guth mostrò che l'espansione esponenziale iniziale dell'Universo da un lato risolverebbe il problema dell'isotropia dell'Universo su larga scala e, dall'altro, lo avrebbe condotto verso una geometria spaziale piatta. Gli effetti di questa espansione inflazionaria sono di portare particelle inizialmente vicine oltre l'orizzonte locale e di spiegare, così, l'isotropia su grande scala dell'Universo. Alla fine dell'espansione esponenziale, l'Universo si trasforma nel modello cosmologico standard di Friedman, dominato dalla radiazione, che, avendo una geometria assolutamente piatta, deve avere ω_m+ω_Λ=1. Il modello fu revisionato nel 1982 da Linde, nonché da Andreas Albrecht e Paul J. Steinhardt, per risolvere le incompatibilità con il modello originale: il passaggio alle soluzioni di Friedman sarebbe dovuto avvenire molto più lentamente e gradualmente.

Dal 1982 gli studi si sono concentrati sulla primissima evoluzione inflazionaria dell'Universo, in epoche in cui l'età dell'Universo era compresa tra 10⁻³⁴ e 10⁻³² secondi. Tra gli ulteriori successi ottenuti da questa teoria vi è l'aver evidenziato che le fluttuazioni quantistiche nei campi, che guidano l'espansione inflazionaria, sono amplificate nel processo stesso e dalla teoria si deduce immediatamente la forma dello spettro di Harrison-Zeldovich. Ciononostante non esiste ancora un'evidenza fisica di questa fase di espansione inflazionaria.

Bibliografia

Alpher 1948: Alpher, Ralph A. - Bethe, Hans - Gamow, George, The origin of the chemical elements, "Physical review", 73, 1948, pp. 803-804.

Alpher, Herman 1948: Alpher, Ralph A. - Herman, Robert C., Evolution of the Universe, "Nature", 162, 1948, pp. 774-775.

Alpher 1953: Alpher, Ralph A. - Follin, James W. - Herman, Robert C., Physical conditions in the initial stages of the expanding Universe, "Physical review", 92, 1953, pp. 1347-1361.

Bondi, Gold 1948: Bondi, Hermann - Gold, Thomas, The steady-state theory of the expanding Universe, "Monthly notices of the Royal Astronomical Society", 108, 1948, pp. 252-270.

Burbidge 1957: Burbidge, E. Margaret - Burbidge, Geoffrey R. - Fowler, William A. - Hoyle, Fred, Synthesis of the elements in stars, "Reviews of modern physics", 29, 1957, pp. 547-650.

Dunlop, Peacock 1990: Dunlop, James S. - Peacock, John A., The redshift cut-off in the luminosity function of radio galaxies and quasars, "Monthly notices of the Royal Astronomical Society", 247, 1990, pp. 19-42.

Eddington 1916: Eddington, Arthur S., The kinetic energy of a star cluster, "Monthly notices of the Royal Astronomical Society", 76, 1916, pp. 525-528.

Eddington 1930: Eddington, Arthur S., On the instability of Einstein's spherical world, "Monthly notices of the Royal Astronomical Society", 90, 1930, pp. 668-678.

Einstein 1917: Einstein, Albert, Cosmological considerations on the general theory of relativity, "Sitzungsberichte der deutschen Akademie der Wissenschaften zu Berlin", 1, 1917, pp. 142-152.

Einstein, Sitter 1932: Einstein, Albert - Sitter, Wilhelm de, On the relation between the expansion and the mean density of the Universe, "Proceedings of the National Academy of Sciences", 18, 1932, pp. 213-214.

Freedman 2001: Freedman, Wendy L. e altri, Final results from the Hubble space telescope key project to measure the Hubble constant, "Astrophysical journal", 533, 2001, pp. 47-72.

Fridman 1922: Fridman, Aleksandr A., On the curvature of space, "Zeitschrift für Physik", 10, 1922, pp. 377-386.

Fridman 1924: Fridman, Aleksandr A., On the possibility of a world with constant negative curvature, "Zeitschrift für Physik", 12, 1924, pp. 326-332.

Gamow 1946: Gamow, George, Expanding Universe and the origin of elements, "Physical review", 70, 1946, pp. 572-573.

Gamow 1970: Gamow, George, My world line, New York, Viking Press, 1970.

Guth 1981: Guth, Alan, Inflationary Universe: a possible solution to the horizon and flatness problems, "Physical review", D23, 1981, pp. 347-356.

Harrison 1970: Harrison, Edward R., Fluctuations at the threshold of classical cosmology, "Physical review", D1, 1970, pp. 2726-2730.

Hasinger 1993: Hasinger, Günther e altri, A deep X-ray survey in the Lockman Hole and the soft X-ray N-Log, "Astronomy and astrophysics", 275, 1993, pp. 1-15.

Hayashi 1950: Chushiro Hayashi, Proton-neutron concentration ratio in the expanding Universe at the stages preceding the formation of the elements, "Progress of theoretical physics (Japan)", 5, 1950, pp. 224-235.

Hoyle 1948: Hoyle, Fred, A new model for the expanding Universe, "Monthly notices of the Royal Astronomical Society", 108, 1948, pp. 372-382.

Hoyle 1954: Hoyle, Fred, On nuclear reactions occurring in very hot stars. I. The synthesis of elements from carbon to nickel, "Astrophysical journal supplement", 1, 1954, pp. 121-146.

Hoyle, Tayler 1964: Hoyle, Fred - Tayler, Roger J., The mystery of the cosmic helium abundance, "Nature", 203, 1964, pp. 1108-1110.

Hubble 1925: Hubble, Edwin P., Cepheids in spiral nebulae, "Publications of the American Astronomical Society", 5, 1925, pp. 261-264.

Hubble 1926: Hubble, Edwin P., Extra-galactic nebulae, "Astrophysical journal", 64, 1926, pp. 321-369.

Hubble 1929: Hubble, Edwin P., A relation between distance and radial velocity among extra-galactic nebulae, "Proceedings of the National Academy of Sciences", 15, 1929, pp. 168-173.

Humason 1956: Humason, Milton L. - Mayall, Nicholas U. - Sandage, Allan R., Redshifts and magnitudes of extra-galactic nebulae, "Astronomical journal", 61, 1956, pp. 97-162.

Jeans 1902: Jeans, James H., The stability of a spherical nebula, "Philosophical transactions of the Royal Society of London", 199, 1902, pp. 1-53.

Lemaître 1927: Lemaître, Georges, Un univers de masse constante de rayon variable rendant compte de la vitesse radiale des nébuleuses extra galactiques, "Annales de la Société scientifique de Bruxelles", A47, 1927, pp. 49-59 (trad. ingl.: A homogeneous Universe of constant mass and increasing radius, accounting for the radial velocity of extra-galactic nebulae, "Monthly notices of the Royal Astronomical Society", 91, 1931, pp. 483-490).

Lemaître 1931a: Lemaître, Georges, The expanding Universe, "Monthly notices of the Royal Astronomical Society", 91, 1931, pp. 490-501.

Lemaître 1931b: Lemaître, Georges, The beginning of the world from the point of view of quantum theory, "Nature", 127, 1931, p. 706.

Lemaître 1933: Lemaître, Georges, Spherical condensation in the expanding universe, "Comptes rendus de l'Académie des Sciences", 196, 1933, pp. 903-904.

Lifshitz 1946: Lifshitz, Evgenii, On the gravitational stability of the expanding Universe, "Journal of physics, Academy of Sciences of the USSR", 10, 1946, pp. 116-129.

Lynden-Bell 1967: Lynden-Bell, Donald, Statistical mechanics of violent relaxation in stellar systems, "Monthly notices of the Royal Astronomical Society", 136, 1967, pp. 101-121.

Mather 1990: Mather, John e altri, A preliminary measurement of the cosmic microwave background spectrum by the Cosmic Background Explorer, "Astrophysical journal", 354, 1990, pp. L37-L40.

Matthews, Sandage 1963: Matthews, Thomas A. - Sandage, Allan R., Optical identification of 3C 48, 3C 196 and 3C 286 with stellar objects, "Astrophysical journal", 138, 1963, pp. 30-56.

McKellar 1941: McKellar, Andrew, Molecular lines from the lowest states of the atomic molecules composed of atoms probably present in interstellar spaces, "Publications of the Dominion Astrophysical Observatory (Victoria)", 7, 1941, pp. 251-272.

Milne 1948: Milne, Edward Arthur, Kinematic relativity, Oxford, Clarendon Press, 1948.

Mitchell 1976: Mitchell, Richard J. - Culhane, John Leonard - Davison, P.J.N. - Ives, J.C., Ariel 5 Observations of the X-ray spectrum of the Perseus cluster, "Monthly notices of the Royal Astronomical Society", 175, 1976, pp. 29P-34P.

Oort 1958: Oort, Jan H., Distribution of galaxies and density in the Universe, Solvay Conference on The structure and evolution of the Universe, Bruxelles, Institut International de Physique Solvay, 1958, pp. 163-181.

Ostriker, Peebles 1973: Ostriker, Jeremiah P. - Peebles, P. James E., A numerical study of the stability of flattened galaxies: or, can cold galaxies survive?, "Astrophysical journal", 186, 1973, pp. 467-480.

Ostriker, Tremaine 1975: Ostriker, Jeremiah P. - Tremaine, Scott D., Another evolutionary correction to the luminosity of Giant galaxies, "Astrophysical journal", 202, 1975, pp. L113-L117.

Peacock 2001: Peacock, John A. e altri, A measurement of the cosmological mass density from clustering in the 2dF galaxy redshift survey, "Nature", 410, 2001, pp. 169-173.

Penzias, Wilson 1965: Penzias, Arno A. - Wilson, Robert W., A measurement of excess antenna temperature at 4080 MHz, "Astrophysical journal", 142, 1965, pp. 419-421.

Press, Schechter 1974: Press, William H. - Schechter, Paul, Formation of galaxies and clusters of galaxies by self-similar gravitational condensation, "Astrophysical journal", 187, 1974, pp. 425-438.

Robertson 1928: Robertson, Howard P., On relativistic cosmology, "Philosophical magazine", 5, 1928, pp. 835-848.

Robertson 1935: Robertson, Howard P., Kinematics and world structure, "Astrophysical journal", 82, 1935, pp. 284-301.

Rogerson, York 1973: Rogerson, John B. - York, Donald G., Interstellar deuterium abundance in the direction of Beta Centauri, "Astrophysical journal", 186, 1973, pp. L95-L98.

Rowan-Robinson 1968: Rowan-Robinson, Michael, The determination of the evolutionary properties of quasars by means of the luminosity-volume test, "Monthly notices of the Royal Astronomical Society", 141, 1968, pp. 445-458.

Rubin 1980: Rubin, Vera C. - Thonnard, Norbert - Ford, W. Kent jr, Rotational properties of 21 Sc galaxies with a large range of luminosities and Radii from NGC 4605 (R=4 kpc) to UGC2885 (R=122 kpc), "Astrophysical journal", 238, 1980, pp. 471-487.

Ryle 1955: Ryle, Martin, Radio stars and their cosmological significance, "The Observatory", 75, 1955, pp. 137-147.

Sachs, Wolfe 1967: Sachs, Raymond K. - Wolfe, Arthur M., Perturbations of a cosmological model and angular variations in the microwave background, "Astrophysical journal", 147, 1967, pp. 73-90.

Sacharov 1965: Sacharov, Andrei D., The initial stage of an expanding Universe and the appearance of a nonuniform distribution of matter, 1965. "Zhurnal eksperimental´noi i teoreticheskoi fiziki", 49, 1965, pp. 345-358.

Sacharov 1967: Sacharov, Andrei D., Violation of CP invariance, C asymmetry, and baryon asymmetry of the Universe, "JETP Letters", 5, 1967, pp. 32-35.

Sandage 1961: Sandage, Allan R., The ability of the 200-inch telescope to discriminate between selected world models, "Astrophysical journal", 133, 1961, pp. 355-392.

Sandage 1968: Sandage, Allan R., Observational cosmology, "The Observatory", 88, 1968, pp. 91-106.

Sandage 1995: Sandage, Allan R., Practical cosmology: inventing the past, in: Sandage, Allan R. - Kron, Richard K. - Longair, Malcolm S., The deep Universe, edited by Bruno Binggeli and Roland Buser, Berlin, Springer, 1995, pp. 1-232.

Schechter 1976: Schechter, Paul, An analytic expression for the luminosity function of galaxies, "Astrophysical journal", 203, 1976, pp. 297-306.

Scheuer 1957: Scheuer, Peter A.G., A statistical method for analysing observations of faint radio stars, "Proceedings of the Cambridge Philosophical Society", 53, 1957, pp. 764-773.

Schmidt 1963: Schmidt, Maarten, 3C 273: A star-like object with large red-shift, "Nature", 197, 1963, p. 1040.

Schmidt 1968: Schmidt, Maarten, Space distribution and luminosity functions of quasi-stellar sources, "Astrophysical journal", 151, 1968, pp. 393-409.

Silk 1968: Silk, Joseph, Cosmic black-body radiation and galaxy formation, "Astrophysical journal", 151, 1968, pp. 459-471.

Smoot 1992: Smoot, George F. e altri, Structure in the COBE differential microwave radiometer first-year maps, "Astrophysical journal", 396, 1992, pp. L1-L5.

Sunyaev, Zeldovich 1970a: Sunyaev, Rashid A. - Zeldovich, Yakov B., Small-scale fluctuations of relic radiation, "Astrophysics and space science", 7, 1970, pp. 3-19.

Sunyaev, Zeldovich 1970b: Sunyaev, Rashid A. - Zeldovich, Yakov B., Interaction of matter and radiation in the hot model of the Universe, "Astrophysics and space science", 7, 1970, pp. 21-30.

Tolman 1934: Tolman, Richard C., Effect of inhomogeneity on cosmological models, "Proceedings of the National Academy of Sciences", 20, 1934, pp. 169-176.

Totsuji, Kihara 1969: Totsuji, Hiroo - Kihara, Taro, The correlation function for the distribution of galaxies, "Publications of the Astronomical Society of Japan", 21, 1969, pp. 221-229.

Tremaine, Gunn 1979: Tremaine, Scott D. - Gunn, James E., Dynamical role of light neutral leptons in cosmology, "Physical review letters", 42, 1979, pp. 407-410.

Wagoner 1967: Wagoner, Robert V. - Fowler, William A. - Hoyle, Fred, On the synthesis of elements at very high temperatures, "Astrophysical journal", 148, 1967, pp. 3-49.

Walker 1936: Walker, Arthur Geoffrey, On Milne's theory of world structure, "Proceedings of the London Mathematical Society", s. 2, 42, 1936, pp. 90-127.

Zeldovich, Sunyaev 1969: Zeldovich, Yakov B. - Sunyaev, Rashid A., The interaction of matter and radiation in a hot-model Universe, "Astrophysics and space science, 4, 1969, pp. 301-316.

Zeldovich 1970: Zeldovich, Yakov B., Gravitational instability: an approximate theory for large density perturbations, "Astronomy and astrophysics", 5, 1970, pp. 84-89.

Zeldovich 1972: Zeldovich, Yakov B., A hypothesis, unifying the structure and the entropy of the Universe, "Monthly notices of the Royal Astronomical Society", 160, 1972, pp. 1P-3P.

Zwicky 1933: Zwicky, Fritz, The redshift of extragalactic nebulae, "Helvetica physica acta", 6, 1933, pp. 110-118.