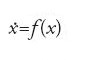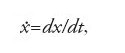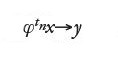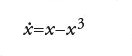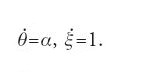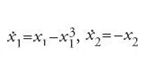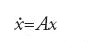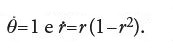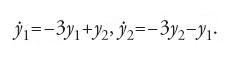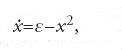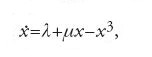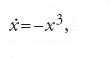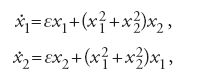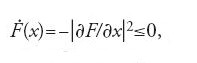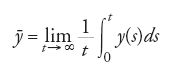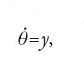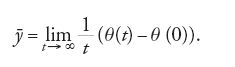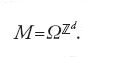La grande scienza. Sistemi dinamici
La grande scienza. Sistemi dinamici
Sistemi dinamici
Il nostro Universo è formato da oggetti che si muovono nello spazio e le cui caratteristiche cambiano continuamente. Gli scienziati pensano che il moto di molti sistemi sia soggetto a leggi deterministiche, cioè che la conoscenza dello stato del sistema in un dato istante determini gli stati in tutti gli istanti seguenti. La teoria dei sistemi dinamici, che nacque e si sviluppò nel XX sec., fa uso di strumenti provenienti da diverse parti della matematica, e si ispira a idee e impostazioni mutuate dalla fisica e dall'ingegneria. A loro volta i sistemi dinamici hanno influenzato molte branche della matematica, e forse soltanto il calcolo delle probabilità può vantare un'analoga varietà di applicazioni e di successi a problemi del mondo 'reale'.
Scopo di questo saggio è illustrare sulla base di alcuni semplici esempi le numerose idee e nozioni della teoria dei sistemi dinamici, sacrificando la generalità della trattazione a vantaggio della semplicità e della chiarezza dell'esposizione.
Per costruire un modello di un particolare sistema occorre definire in maniera accurata lo stato del sistema stesso e precisare una legge che ne descriva l'evoluzione. Uno stato è descritto da un insieme di variabili, o coordinate; l'insieme di tutti gli stati è lo 'spazio delle fasi'. Per esempio, in un modello del moto di Luna, Terra e Sole, rappresentati come punti materiali e ignorando tutti gli altri oggetti celesti, lo stato del sistema è dato dalla posizione e dalla velocità di ciascuno di questi tre corpi. La legge che governa l'evoluzione del sistema è quella di Newton, che esprime la forza come prodotto della massa per l'accelerazione e in cui la forza è data dall'attrazione gravitazionale. Per il moto di un fluido incompressibile lo stato del sistema è descritto assegnando in ogni punto la velocità del fluido, e la legge che ne regola l'evoluzione è l'equazione differenziale alle derivate parziali nota come equazione di Navier-Stokes. Nella teoria dei circuiti, lo stato del sistema è dato dalla differenza di potenziale e dall'intensità della corrente; le leggi che governano il moto sono equazioni differenziali ordinarie dedotte dalle leggi di Kirchhoff. Nel caso della vibrazione di una corda, il modello più semplice è quello in cui lo stato è dato dalla posizione e dalla velocità della corda in ogni suo punto; il movimento è descritto da un'equazione differenziale alle derivate parziali detta equazione delle onde. Nella teoria delle reazioni chimiche, come variabili di stato si possono considerare le concentrazioni delle varie sostanze; il movimento è descritto da un'equazione differenziale ordinaria o da una alle derivate parziali che tenga conto della possibilità di diffusione della sostanza.
In questi modelli il tempo varia con continuità; in molte situazioni è però più realistico considerare un tempo discreto. Può infatti accadere che sia possibile osservare un sistema soltanto a intervalli di tempo regolari. In questo caso la legge che regola il moto del sistema è data da una trasformazione (applicazione) che determina lo stato al tempo n+1, noto quello al tempo n.
Per esempio, nella 'dinamica delle popolazioni' un modello è costituito da un'applicazione che determina il numero xn+1 di individui della (n+1)-esima generazione in funzione del numero xn dell'n-esima. La più semplice di queste è la xn+1=axn-bx2n, dove a>0 è il tasso di crescita, e dove il termine quadratico impedisce una crescita infinita. La dinamica si può interpretare come competizione degli individui di una specie per una risorsa disponibile in quantità finita (b>0).
Nei reticoli cristallini che constano di differenti elementi, si hanno disposizioni diverse degli elementi grazie alle loro proprietà attrattive e repulsive nei confronti dei vicini. Data la disposizione iniziale degli elementi nel reticolo, le leggi che governano queste proprietà attrattive e repulsive possono essere espresse da un'applicazione definita sul reticolo che determina il modo in cui gli elementi si sistemano via via in una disposizione stabile.
Una volta specificati lo spazio delle fasi e la legge che governa l'evoluzione dello stato si può passare a discutere la dinamica del sistema. Come si è detto il tempo può essere considerato un parametro discreto o continuo. Indichiamo con X lo spazio delle fasi, che supponiamo essere uno spazio metrico completo di dimensione finita perché la presentazione è più semplice e permette di evitare l'introduzione di molti altri concetti, necessari nel caso della dimensione infinita. Per semplificare la discussione supponiamo anche che la legge che governa il moto dipenda solo dallo stato e non dal tempo; la dinamica è cioè governata dalla struttura interna del sistema e non da forze esterne. Un tale sistema si dice 'autonomo'.
A titolo d'esempio consideriamo l'equazione differenziale
dove
e sia φtx la soluzione dell'equazione al tempo t con valore x per t=0, cioè φ0x=x. Supponiamo che la soluzione che passa per x sia unica, cioè, se x, y sono due punti per i quali esiste t0 tale che
allora φtx=φty per ogni t. Poiché f non dipende esplicitamente da t, il sistema è autonomo e, per ogni s, φt+sx è anche una soluzione con valore iniziale φsx per t=0. Ma anche φtφsx è una soluzione con valore iniziale φsx per t=0, e pertanto l'unicità della soluzione implica φt+sx=φtφsx per ogni t e s; questa proprietà è detta di 'semigruppo'.
In generale, se supponiamo che il nostro sistema sia autonomo e che il suo stato futuro sia univocamente determinato dal valore iniziale (determinismo) e, inoltre, che φtx denoti lo stato del sistema al tempo t con valore iniziale x per t=0, allora φ0x=x e φt+sx=φtφsx. Ogni funzione φtx continua rispetto a t e x e che soddisfi le suddette proprietà è un 'sistema dinamico'.
Per discutere le proprietà dei sistemi dinamici abbiamo bisogno di introdurre alcuni termini e definizioni. Per un dato x, l''orbita positiva' γ+(x) di x è l'insieme ∪t≥0φtx, e l''orbita' γ(x) di x è l'insieme ∪t∈ℝφtx, se φtx è definito per t negativo. L'insieme ω-limite ω(x) di x è l'insieme dei punti y per i quali esiste una successione tn→∞ tale che
per n→∞. L'insieme α-limite α(x) di x è definito analogamente con tn→−∞. Un insieme J è 'invariante' per φt se φtJ=J per ogni t. Una relazione fondamentale tra questi concetti è la seguente: se γ+(x) è limitata, allora ω(x) esiste ed è compatto e invariante. Un insieme J si dice 'minimale' se è invariante e minimale rispetto all'invarianza, cioè se K è un insieme invariante contenuto in J, allora K=J.
Consideriamo alcuni semplici esempi per illustrare questi concetti. Un punto di equilibrio di un sistema di equazioni differenziali
è un punto x0 tale che f(x0)=0. Tutti i punti di equilibrio sono invarianti e minimali. Per esempio, per l'equazione scalare
vi sono tre punti di equilibrio: 0, 1,−1. Se x0∈(0,1), allora γ(x0)=(0,1), ω(x0)={1}, α(x0)={0}. Se x0>1 allora γ(x0)=(0,∞), ω(x0)={1}.
Una soluzione periodica p(t) di un'equazione differenziale
è una soluzione che ha la seguente proprietà: esiste T>0 tale che p(t+T)=p(t) per ogni t. Il minimo numero T con questa proprietà si chiama periodo. L'orbita γ(p(0)) è una curva chiusa invariante e minimale.
Un altro esempio, un po' più complicato, è il seguente. Siano θ e ξ due angoli che descrivono un toro, e supponiamo di avere un'equazione differenziale sul toro con flusso descritto dalle equazioni
Se α è irrazionale, allora l'orbita γ(θ0ξ0) è tutto il toro. Il solo insieme minimale è il toro stesso.
L'insieme di tutte le orbite di un sistema dinamico è la 'struttura delle orbite' o 'flusso' del sistema dinamico. Di primaria importanza sono le proprietà qualitative del flusso: quali sono gli insiemi minimali, gli insiemi limite e quelli stabili? Dov'è che il sistema passa la maggior parte del tempo? Possiamo assegnare una misura, o probabilità, che il sistema si trovi in un certo stato (misura invariante, teoria ergodica)? Come varia la struttura delle orbite quando la legge che governa il moto cambia di poco (stabilità strutturale e biforcazione)?
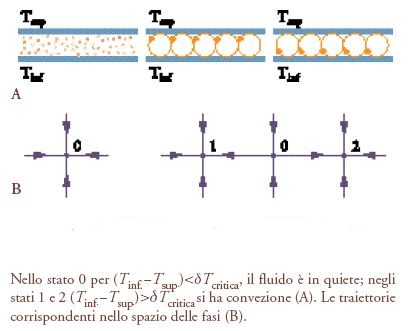
Nei paragrafi che seguono vogliamo discutere alcuni importanti sviluppi della disciplina, concentrandoci su equazioni differenziali ordinarie e sulle applicazioni differenziabili. Come vedremo, la struttura delle orbite di molti sistemi dinamici non è sensibile a piccole perturbazioni dei processi che definiscono il flusso, mentre in molti sistemi fisici la struttura orbitale cambia quando i parametri fisici variano su larga scala. I valori dei parametri per i quali la struttura delle orbite varia da un tipo a un altro sono chiamati 'punti di biforcazione'. Per esempio, consideriamo un recipiente che contiene acqua, e che viene riscaldato in basso a una temperatura T mentre la superficie dell'acqua viene mantenuta a temperatura costante T0. Si osserva che vi sono valori critici del parametro differenza di temperatura T−T0 per i quali il moto delle particelle d'acqua subisce un cambiamento di struttura. Considerato come sistema dinamico, ciò significa un cambiamento nella struttura delle orbite. Per certi aspetti, i punti di biforcazione sono i sistemi dinamici più interessanti, perché il cambiamento nella struttura delle orbite della dinamica si accompagna spesso a qualche tipo di scambio di stabilità e all'introduzione di una dinamica molto complicata (caos), eccetera. Numerosi sforzi sono stati fatti per capire i tipi più elementari, ma molto importanti, di biforcazione. È notevole quanto queste idee siano entrate a far parte del vocabolario dei ricercatori, al punto che sono stati ideati nuovi esperimenti a partire dalla teoria. Nei congressi scientifici sono descritte ricerche sperimentali in laboratorio o di simulazione numerica, osservazioni di fenomeni dinamici e si propongono modelli matematici appositamente introdotti per studiare certi tipi di biforcazione, che poi si verificano con esperimenti. I modelli suggeriscono nuovi fenomeni fisici e l'allestimento di nuove esperienze per osservarli.
Quando i sistemi sono molto grandi o molto complessi può essere necessario procedere diversamente per capirne la dinamica. Per esempio, è impossibile osservare il moto di ogni singola particella per capire il moto di un gas in un recipiente. Occorre trovare qualche altro modo per misurare la complessità della dinamica. In situazioni di questo genere è naturale associare una misura di probabilità, per esempio la probabilità che una particella si trovi in una data regione dello spazio con una data velocità. Tutto ciò rientra nel quadro della teoria ergodica, una teoria nata in meccanica statistica e che sta portando a una comprensione fondamentale dei principî di base che regolano la statistica delle traiettorie.
Più oltre daremo maggiori dettagli su questi concetti illustrandoli nel modo più semplice possibile. Non possiamo qui prendere in considerazione gli sviluppi più recenti, che estendono molte idee a equazioni differenziali alle derivate parziali e a equazioni differenziali per moti determinati non solo dal presente, ma anche da parte o da tutto il passato. Vogliamo tuttavia sottolineare che lo sviluppo della teoria in dimensione infinita ha avuto un ruolo importante per colmare la lacuna tra la teoria matematica e le applicazioni: la maggior parte dei modelli fisici si basa su sistemi a infinite dimensioni.
Proprietà locali e globali
Anche se lo scopo principale dello studio dei sistemi dinamici è comprendere le proprietà del flusso globale, è però naturale, e importante, cominciare la discussione dal comportamento delle orbite nelle vicinanze di semplici insiemi invarianti.
Consideriamo dapprima un sistema dinamico continuo generato dalle soluzioni di un'equazione differenziale ordinaria
La funzione f è il 'campo vettoriale' che definisce il sistema dinamico. Sia φtx0 la soluzione per un punto iniziale x0 al tempo t=0. Un punto x0 è un 'punto di equilibrio' se f(x0)=0, cioè se φtx0=x0. Se x0 è un punto di equilibrio l'orbita che passa per x0 si riduce a x0 stesso.
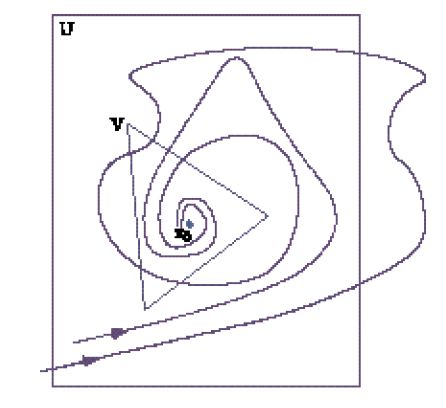
Seguendo Aleksandr Michajlovič Ljapunov, un punto di equilibrio x0 si dice 'stabile' se per ogni intorno U di x0 esiste un intorno V di x0 tale che per ogni y in U, la soluzione φty che passa per y è in V per tutti i t≥0 (fig. 1).
Il punto di equilibrio x0 è 'asintoticamente stabile' se è stabile, ed esiste un intorno W di x0 tale che per ogni y in W, φty→x0 per t→∞. Il punto di equilibrio x0 è 'instabile' se non è stabile.
Per esempio, se x è uno scalare e f(x)=x−x3, i punti di equilibrio dell'equazione differenziale sono x=0, x=1, x=−1. Poiché f(x)(x+1)⟨0 per x≠−1 e nelle vicinanze di −1, la soluzione dell'equazione con valore iniziale nelle vicinanze di −1 tende a −1 per t→∞ e il punto di equilibrio −1 è asintoticamente stabile. Lo stesso vale per +1. È anche facile vedere che la soluzione x=0 è instabile, in quanto una soluzione con valore iniziale vicino a 0 ma non uguale a 0 si allontana da 0 al crescere di t.
Consideriamo ora il semplice sistema nel piano
i punti di equilibrio sono (−1,0), (0,0), (1,0). Poiché ogni soluzione (x1(t),x2(t)) ha la proprietà che x2→0 per t→∞, i punti (−1,0) e (1,0) sono asintoticamente stabili e il punto (0,0) è instabile in quanto la soluzione con dati iniziali sull'asse x1 vicini a 0 si allontana da (0,0) al crescere di t. Osserviamo anche che la soluzione con dati iniziali sull'asse x2 si avvicina a (0,0) per t→∞ (fig. 2).
Gli esempi precedenti motivano le seguenti definizioni. Se x0 è un punto di equilibrio per
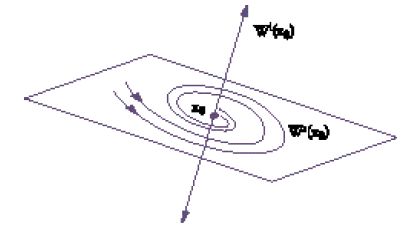
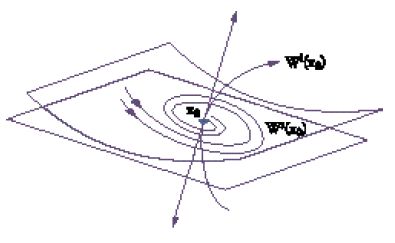
l''insieme stabile Ws(x0) di x0' è l'insieme dei punti y per i quali la soluzione φty tende a x0 per t→∞, l'insieme instabile Wi(x0) di x0, è l'insieme dei punti per i quali la soluzione tende a x0 quando t→−∞. Il comportamento delle orbite vicino a x0 dipende principalmente dagli autovalori del sistema linearizzato y.=Ay, dove A=∂f(x0)/∂y e ∂f(x)/∂x è la matrice jacobiana di f. Nell'esempio precedente, le matrici jacobiane nei punti di equilibrio (−1,0), (0,0), (1,0) sono rispettivamente diag(−2,−1), diag (1,−1) e diag(−2,−1).
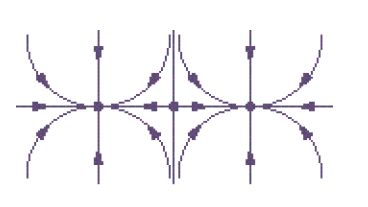
Diremo che x0 è 'iperbolico' se gli autovalori λ di A= =∂f(x0)/∂x hanno tutti la parte reale non nulla. Se x0 è iperbolico, l'insieme stabile per l'equazione lineare
è lo spazio lineare generato dagli autospazi degli autovalori con parte reale negativa. L'insieme instabile è generato dagli autospazi degli autovalori con parte reale positiva. Per questa equazione lineare il flusso è rappresentato nella fig. 3.
Un famoso risultato di Ljapunov-Hadamard-Perron afferma che gli insiemi Ws(x0) e Wi(x0) dell'equazione non lineare sono varietà lisce tangenti a quelle dell'equazione lineare nei punti di equilibrio. Ne segue che il comportamento locale nelle vicinanze di un punto di equilibrio iperbolico è determinato dalla linearizzazione (fig. 4). Diremo che un punto di equilibrio è un 'punto sella' se la linearizzazione ammette almeno un autovalore con parte reale positiva e almeno uno con parte reale negativa. Nell'esempio considerato prima l'origine (0,0) è un punto sella.
Un'altra nozione, molto importante, della teoria dei sistemi dinamici è quella di orbita periodica. Una soluzione p(t) dell'equazione differenziale
si dice 'T-periodica' se esiste un numero reale T>0 tale che p(t+T)=p(t) per ogni t. Nello spazio delle fasi, l'orbita γ=γp descritta da una soluzione T-periodica p è una curva chiusa. Inoltre, ogni curva chiusa invariante dell'equazione che non contenga punti di equilibrio deve corrispondere a una soluzione periodica dell'equazione. Una semplice equazione nel piano che ha una soluzione periodica è:
Infatti, introducendo le coordinate polari x1=rcosθ, x2=−rsenθ, si ha
Il cerchio r=1 è invariante, non contiene punti di equilibrio e pertanto è un'orbita periodica (fig. 5). Inoltre, quest'orbita periodica è stabile nel senso che è l'insieme ω-limite di ogni orbita con dati iniziali a essa vicini in realtà, con qualunque dato iniziale meno l'origine.
Consideriamo ora le proprietà globali del flusso. Nel 1937 Aleksandr A. Andronov e Lev S. Pontrjagin hanno introdotto il concetto di 'stabilità strutturale' per individuare sistemi per i quali le proprietà qualitative della struttura delle orbite definite dall'equazione differenziale non cambiano per piccole variazioni del campo vettoriale. Questo concetto conduce alla nozione di 'equivalenza topologica' di sistemi dinamici. Due sistemi dinamici (φt,M), (ψt,N) con spazio delle fasi M e N sono topologicamente equivalenti se esiste un omeomorfismo h:M→N che manda orbite di (φt,M) in orbite di (ψt,N) e conserva la direzione del tempo (si può cambiare la parametrizzazione del tempo ma non la direzione). In altri termini, le proprietà topologiche della struttura delle orbite dei due sistemi sono le stesse. Queste orbite possono essere di struttura diversa. Per esempio, nel piano, il sistema lineare
è topologicamente equivalente al sistema lineare
Nella fig. 6 le orbite appaiono piuttosto diverse, ma sono topologicamente equivalenti.
Diremo che (φt,M) è 'strutturalmente stabile' se esiste un ε>0 tale che, per ogni (ψt,N) per il quale la distanza tra ψt e φt nella topologia C1 è minore di ε, risulta (ψt,N) topologicamente equivalente a (φt,M). Come esempio prendiamo le equazioni [1] nel piano e limitiamo le nostre considerazioni al disco x21+x22≤2. Si può dimostrare che questo sistema è strutturalmente stabile. Il punto di equilibrio 0 e l'orbita periodica sono iperbolici, e pertanto, in caso di perturbazione, esiste un punto di equilibrio iperbolico e un'orbita iperbolica vicina all'originale. Il punto importante nella dimostrazione che questi flussi sono topologicamente equivalenti è provare che lo sono nelle vicinanze dei punti di equilibrio e delle orbite periodiche. Ciò si ottiene utilizzando un famoso risultato di Grobman e Hartman, secondo il quale l'iperbolicità implica l'equivalenza topologica locale.
Nella definizione originale di stabilità strutturale di Andronov e Pontrjagin si richiedeva che l'omeomorfismo che conserva la struttura delle orbite fosse vicino all'identità. La definizione che abbiamo dato, dovuta a Solomon Lefschetz e Mauricio Peixoto, è stata introdotta per facilitare la verifica dell'equivalenza topologica. Inoltre, il fatto che l'insieme dei sistemi strutturalmente stabili sia aperto segue immediatamente dalla definizione.
Un sistema dinamico (φt,M) si dice 'punto di biforcazione' nello spazio dei sistemi dinamici su M se non è strutturalmente stabile.
I punti di biforcazione sono particolarmente interessanti perché in questi la struttura topologica delle orbite cambia per piccole variazioni del campo vettoriale. In un sistema reale questi punti corrispondono a una riorganizzazione della configurazione delle orbite del sistema. Un esempio di riorganizzazione è l'inizio della convezione cellulare in uno strato orizzontale di fluido riscaldato dal basso. L'aumento della differenza di temperatura tra la parte superiore e quella inferiore del fluido non dà origine a un movimento macroscopico del fluido se la differenza è al di sotto di un dato valore critico. Quando la differenza supera questo valore compare una convezione cellulare. Nel modello matematico (le equazioni dell'idrodinamica o la loro approssimazione finita), la comparsa di queste cellule corrisponde a una biforcazione dovuta alla nascita di uno stato di equilibrio non zero (fig. 7), se il modello descrive soltanto l'ampiezza dei modi, e alla nascita di soluzioni periodiche se descrive anche la fase.
È molto importante disporre di una classificazione dei punti di biforcazione elementari per farsi un'idea del modo in cui può cambiare la struttura delle orbite. Nelle applicazioni, i parametri di particolare interesse e che influenzano fortemente il flusso non sono molti. Se un sistema dinamico si trova in un punto di biforcazione di uno spazio di parametri, e quindi non è strutturalmente stabile, è importante classificare i comportamenti possibili del sistema quando i parametri variano in un piccolo intorno del valore di biforcazione. In molti casi interessanti è possibile presentare una famiglia di sistemi dinamici dipendente da un numero finito di parametri λ=(λ1,…,λn) tale che per λ=0 questa famiglia sia topologicamente equivalente a un sistema in un punto di biforcazione, e la variazione del parametro in un intorno di λ=0 fornisca tutti i possibili comportamenti dinamici vicino al punto di biforcazione. Una tale famiglia si dice 'dispiegamento' della biforcazione.
Per esempio, se la biforcazione è il risultato del cambiamento di stabilità di un punto di equilibrio, e se ciò è dovuto al fatto che nel valore critico del parametro esiste un autovalore della linearizzazione semplice e non nullo, allora la biforcazione può essere analizzata discutendo un'equazione differenziale scalare con parametri. In questa situazione il tipo di biforcazione più semplice, ma molto importante, è quello in cui
dove ε è un parametro reale. Limitiamo la discussione al caso in cui ε∈[−0,5,0,5] e x∈[−1,1]. Il sistema è strutturalmente stabile se ε≠0. Se ε⟨0 non vi sono punti di equilibrio; se ε>0 vi sono due punti di equilibrio (fig.8). Di conseguenza il flusso per ε>0 non può essere topologicamente equivalente a un flusso per ε⟨0. Questa biforcazione si chiama 'a punto sella'.
La biforcazione che segue in ordine di importanza è quella determinata dall'equazione scalare
dove λ e μ sono piccoli parametri reali e x∈[−1,1]. Due parametri sono necessari per capire i cambiamenti che hanno luogo nelle vicinanze dell'equazione
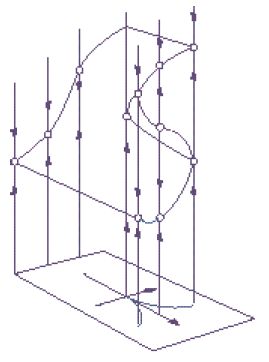
in quanto sono necessari due parametri per descrivere tutti i modi possibili in cui il grafico di una funzione cubica può cambiare. La fig. 9 mostra i vari flussi possibili. Questa biforcazione si chiama 'cuspide'. Nel caso particolare λ=0 (lungo l'asse μ) è detta biforcazione 'a forcella'.
È possibile che la stabilità di un punto di equilibrio cambi facendo attraversare l'asse immaginario a una coppia di autovalori complessi. In questo caso si può dimostrare che il cambiamento nella struttura del flusso è descritto da un sistema planare. Il più semplice tipo di biforcazione possibile è descritto dalle equazioni:
dove ε è un parametro reale. Usando coordinate polari, il flusso come funzione di ε è dato nella fig. 10. Questa biforcazione è dinamica, a differenza di quella statica vista sopra, e prende il nome di 'biforcazione di Poincaré-Andronov-Hopf'.
Consideriamo ora alcune questioni riguardanti le equazioni differenziali nel piano. Perché un problema sia trattabile, occorre imporre una condizione sul campo vettoriale che impedisca alle soluzioni di trovarsi nei pressi dell'infinito. Il sistema dinamico si dice 'dissipativo' se esiste un insieme limitato nel quale tutte le orbite alla fine entrano e vi rimangono. Se il sistema è dissipativo esiste un 'attrattore globale
,
cioè un insieme compatto invariante che contiene l'insieme ω-limite di ogni orbita. È allora possibile dimostrare che esiste un intorno di
la cui frontiera è una curva liscia e il campo vettoriale è diretto verso l'interno di questa curva. Nel discutere di stabilità strutturale per un sistema dissipativo possiamo limitarci a un insieme limitato la cui frontiera soddisfi la proprietà suddetta. Questa discussione permette di motivare il seguente problema. Supponiamo che il campo vettoriale sia trasversale alla frontiera del disco unitario e sia diretto verso l'interno (qualunque altro insieme aperto con frontiera liscia andrebbe bene). In questa classe di campi vettoriali Andronov e Pontrjagin hanno caratterizzato i campi strutturalmente stabili come quelli che hanno le proprietà seguenti: (1) tutti i punti di equilibrio sono iperbolici; (2) tutte le orbite periodiche sono iperboliche; (3) le varietà stabili e instabili dei punti sella non si intersecano.
La discussione precedente mostra che (1), (2) e (3) sono certamente necessarie; dimostrare che sono anche sufficienti richiede invece molto lavoro.
Peixoto ha dimostrato successivamente che la stessa caratterizzazione sussiste quando lo spazio delle fasi è una qualunque varietà bidimensionale liscia. Inoltre, l'insieme dei campi vettoriali strutturalmente stabili è aperto e denso nell'insieme dei campi vettoriali C1.
Nel piano, se il sistema non è strutturalmente stabile, abbiamo visto alcune delle biforcazioni elementari che possono aver luogo. Se consideriamo soltanto famiglie di campi vettoriali a un parametro nel piano, è importante classificare quelle per le quali le biforcazioni sono del tipo più semplice. Una classificazione completa di queste famiglie a un parametro è stata ottenuta grazie agli sforzi congiunti di Andronov, E.A. Leontovich, I.I. Gordon, A.G. Majer e Jorge Sotomayor, e comprende le biforcazioni locali nelle vicinanze di un punto di equilibrio dato da un punto sella e le biforcazioni di tipo Poincaré-Andronov-Hopf come pure numerose altre. Ricordiamo, tra quelle globali, solo una delle più interessanti. È possibile che vi sia un''orbita omoclina' per un punto sella x0, cioè che esista un punto
tale che gli insiemi α- e ω-limite di
siano il punto x0. In un punto di biforcazione di questo tipo la rottura di un'orbita omoclina può dar luogo a un'orbita periodica (fig. 11).
Con una teoria dei sistemi strutturalmente stabili nel piano come questa, interessante e piuttosto semplice, è naturale considerare concetti analoghi in spazi di dimensione superiore. In dimensione maggiore di due sono possibili molti tipi di dinamica; cominciamo con i più semplici, cioè con i sistemi gradiente. Un campo vettoriale f si dice gradiente se f=−∂F/∂x dove F è una funzione scalare. Se consideriamo il modo in cui la funzione F(x(t)) varia lungo le soluzioni vediamo che
cioè che la funzione F(x(t)) è non crescente lungo le soluzioni. Se le soluzioni sono limitate, allora ognuna deve tendere a un punto di equilibrio, cioè a un punto critico della funzione F. Se supponiamo che i punti di equilibrio siano iperbolici, allora sono massimi, minimi o punti sella elementari del grafico della funzione F (fig. 12). Palais e Smale hanno caratterizzato i campi vettoriali gradiente strutturalmente stabili come quelli per i quali i punti di equilibrio sono iperbolici, con varietà stabili e instabili che si intersecano trasversalmente. L'insieme di questi campi vettoriali è altresì aperto e denso.
I sistemi strutturalmente stabili sono certamente tra i più importanti tra quelli che si incontrano nelle applicazioni; si è molto discusso per chiarire nei particolari le proprietà della struttura delle orbite. Questi sistemi non sono però densi, come ha dimostrato Smale con un esempio ammirevole. L'esempio più famoso proveniente dalle applicazioni e che mostra la non densità di sistemi strutturalmente stabili è quello dei sistemi di Lorentz, derivato da un'approssimazione di Galerkin dell'equazione di Navier-Stokes che descrive la convezione di un flusso fluido. Può anche servire come modello semplicissimo di laser. Se l'insieme dei parametri è un dominio il sistema ha un insieme attrattivo invariante, il cosiddetto attrattore di Lorentz, che cambia di struttura cambiando valore ai parametri, ma rimane però attrattivo.
Come osservato in precedenza, in dimensione maggiore di due si presentano vari tipi di dinamica. Ne discuteremo alcuni. Se un punto di equilibrio x0 è iperbolico, allora una piccola variazione C1 nel campo vettoriale non fa cambiare il flusso in un intorno di x0. In effetti, per il campo vettoriale perturbato vi è un punto di equilibrio nelle vicinanze di x0, questo punto è iperbolico e vi sono varietà lisce stabili e instabili tangenti alle varietà, dovute alla linearizzazione del campo vettoriale in quel punto. Inoltre, nelle vicinanze di x0 il flusso dell'equazione non perturbata è topologicamente equivalente a quello del campo vettoriale perturbato (teorema di Grobman-Hartman).
Per un'orbita iperbolica periodica γ si può utilizzare la mappa di Poincaré (Tav. I) e, con una piccola perturbazione C1 del campo vettoriale, ottenere un'orbita iperbolica periodica vicina, con varietà stabili e instabili; si può inoltre applicare il teorema di Grobman-Hartman per le mappe e scoprire che le proprietà topologiche dei flussi sono equivalenti in un intorno di γ.
Il comportamento globale delle varietà stabili e instabili di un punto di equilibrio o di un'orbita periodica può dar luogo a strutture molto complicate nello spazio delle fasi. È possibile in effetti osservare un comportamento di tipo casuale nella dinamica anche se il flusso definito dall'equazione differenziale è deterministico. Affermare che il flusso è deterministico significa dire che il comportamento futuro del sistema è determinato dallo stato iniziale. Ciò non implica la previdibilità: la conoscenza dell'orbita del valore iniziale x0 può non servire per determinare l'orbita di un altro valore x1 molto vicino a x0. Il moto può infatti mostrare una 'dipendenza critica dalle condizioni iniziali', nel senso che due orbite con dati iniziali estremamente vicini possono allontanarsi molto l'una dall'altra e poi riavvicinarsi, e ripetere l'operazione infinite volte. Questi moti vengono genericamente chiamati 'caotici'.
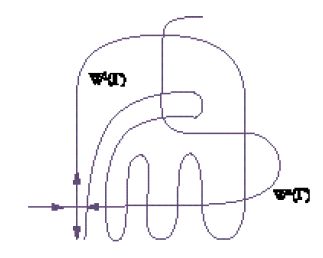
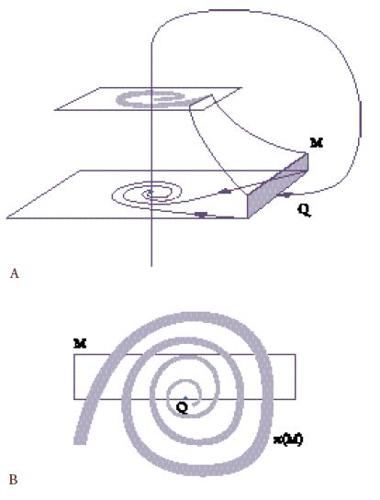
Per cominciare a discutere di questo fenomeno complicato consideriamo il comportamento nelle vicinanze di un'orbita periodica. Per ogni orbita periodica iperbolica le varietà stabile Ws(γ) e instabile Wi(γ) si possono intersecare in un'orbita che è omoclina a γ (fig. 13). Effettuando una piccola perturbazione del campo vettoriale, se necessario, possiamo supporre che le varietà Ws(γ) e Wi(γ) siano trasversali lungo questa orbita. Data l'intersezione trasversale di queste varietà, una piccola perturbazione del campo vettoriale non disturba la struttura omoclina. È quindi importante capire il comportamento nelle vicinanze di questa orbita.
A tale scopo è opportuno considerare una trasversale Q a γ e il comportamento delle iterate della mappa di Poincaré su Q. Le varietà stabili e instabili di γ intersecano Q infinite volte e la loro intersezione in Q è trasversale. Queste intersezioni sono piccoli archi che si intersecano trasversalmente (fig. 13). Iterando un certo numero di volte π, ciascun piccolo arco di Q interseca Q con un altro piccolo arco che fa parte della varietà stabile o instabile di γ.
Poincaré è stato il primo a osservare che in applicazioni particolari questo complicato comportamento può effettivamente manifestarsi. La comprensione completa di questo importante fenomeno ha richiesto moltissimo tempo e l'impegno di numerosi matematici, tra i quali George David Birkhoff negli anni Trenta, Stephen Smale e Leonid P. Shil´nikov negli anni Sessanta.
È piuttosto difficile dare una descrizione dettagliata di questa complessità; comunque, la fig. 13 mostra che deve essere insolita. Descriveremo brevemente il risultato matematico discutendone alcune implicazioni, e per questo abbiamo bisogno di alcune considerazioni di dinamica simbolica. Sia λ un insieme di simboli λ1,λ2,…, e sia Σ l'insieme delle successioni doppiamente infinite a={aj, j=0,±1,±2,…}, dove ciascun aj è un elemento di λ. Per esempio, se λ={0,1}, gli elementi di Σ sono successioni doppiamente infinite di 0 e 1. Definiamo lo shift σ su Σ come σa=b, dove b={bj, j=0,±1,±2,…}, bj=aj+1. Una topologia naturale rende Σ uno spazio metrico. Per questo sistema il comportamento delle traiettorie si riflette esattamente nelle proprietà delle successioni corrispondenti. Una traiettoria periodica corrisponde a una successione periodica, due traiettorie tra loro asintotiche hanno gli stessi simboli da un certo punto in poi, ecc. Diventa quindi molto proficuo utilizzare questi sistemi dinamici simbolici astratti per la descrizione del comportamento delle traiettorie di un sistema.
Sia ora γ un'orbita periodica iperbolica con un'intersezione trasversale non vuota tra Ws(γ) e Wi(γ), e siano π la mappa di Poincaré e Q la trasversale. Se x è un punto nel campo di definizione di π che non appartiene alla varietà stabile di γ, esiste un intero q tale che πqx non appartiene a Q. Se inoltre x appartiene alla varietà instabile di γ, o è vicino a un suo punto, esiste un intero k tale che πkx appartenga a Q. Dato un punto x in Q e nell'intersezione delle varietà stabili e instabili di γ, e un intorno V di x, sia Jk l'insieme invariante massimale di πk in V. Si può dimostrare che esiste un intero k tale che il flusso definito da π e ristretto a Jk sia topologicamente coniugato allo shift sinistro σ su Σ, dove l'insieme λ che serve a definire Σ consta di due soli simboli, per esempio 0 e 1.
Le implicazioni di questa equivalenza topologica sono sorprendenti. Per esempio, per ogni numero finito p>k esiste una successione (p+1)-periodica che contiene p zeri tra due 1, e pertanto in Jk vi sono infinite orbite periodiche. Se prendiamo una successione nella quale i p numeri sono scelti a caso, allora il moto lungo l'orbita in γ è casuale. Si può anche dimostrare che il moto su Jk mostra la sensibilità alle condizioni iniziali che abbiamo descritto prima.
Consideriamo ora un'orbita omoclina in un punto di equilibrio. La struttura del flusso nelle vicinanze di quest'orbita dipende fortemente dagli autovalori della linearizzazione. Se gli autovalori dominanti delle varietà stabile e instabile sono semplici e reali, allora in generale una piccola perturbazione rompe l'orbita. Il nuovo flusso non è molto complicato, ma può contenere un'ulteriore orbita periodica, come accade anche nel piano.
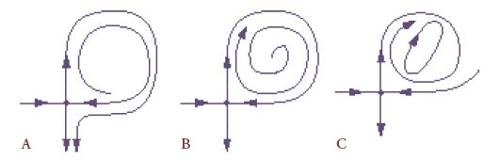
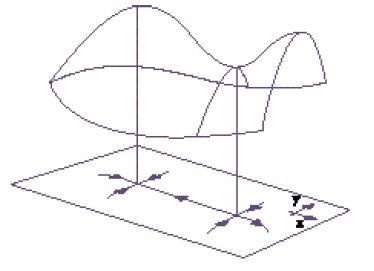
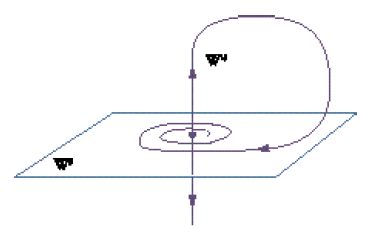
Se gli autovalori dominanti della varietà stabile o di quella instabile sono complessi, l'orbita prende il nome di 'orbita di Shil´nikov' (fig. 14).
Supponiamo di essere in tre dimensioni e che la dimensione della varietà instabile sia 1 con autovalore λ>0 e quella della varietà stabile sia 2 con autovalori complessi α±iβ. Se λ⟨α, il che vuol dire che il tasso di espansione dal punto di equilibrio è superiore a quello di contrazione verso di esso, allora il flusso può essere molto complicato in un intorno di questa orbita.
La fig. 15 dà un'indicazione del perché il comportamento nelle vicinanze di tale orbita abbia una struttura complicata. Se consideriamo una piccola lastra orizzontale come quella della figura, allora il flusso trasforma l'orbita in una struttura a spirale che ritorna a intersecarla in un modo che ricorda quanto accade con l'intersezione trasversale delle varietà stabili e instabili di un'orbita periodica, anche se è più complicato.
La descrizione matematica del flusso si ottiene utilizzando la dinamica simbolica come nel caso di un'orbita periodica; la differenza principale sta nel fatto che ora l'insieme λ consta di un numero infinito di simboli λ1, λ2,… Sia ora γ un'orbita di Shil´nikov con tasso di espansione maggiore di quello di contrazione, e per un dato piccolo intorno U di γ sia J il massimo insieme invariante di U. Allora, genericamente nello spazio dei campi vettoriali C1, la mappa di Poincaré per il flusso del campo vettoriale ristretta a J è coniugata topologicamente allo shift σ su Σ e l'insieme λ che serve a definire Σ deve contenere infiniti simboli. A causa di quest'ultimo elemento il flusso è più complicato rispetto al caso di un'orbita periodica iperbolica con intersezione trasversale delle varietà stabili e instabili.
La descrizione del comportamento delle orbite fornito dalla dinamica simbolica è in generale approssimativa. Nei casi più semplici, come quello dei sistemi strutturalmente stabili del piano, il comportamento di un'orbita è così semplice che la dinamica simbolica non fornisce molte più informazioni. D'altra parte, quando tutte le orbite in qualche insieme invariante non banale sono instabili, come nel caso delle strutture omocline menzionate sopra, la dinamica simbolica è in grado di offrire una descrizione qualitativa rigorosa del comportamento delle orbite. A volte, mediante la tecnica delle partizioni di Andrej Markov si può utilizzare la dinamica simbolica per costruire una buona misura invariante e applicare i potenti strumenti della teoria ergodica.
Il concetto di stabilità strutturale e di biforcazione di Andronov è un'idea matematica generale che si può adattare, ed è stato fatto, ad altre situazioni, come la teoria delle singolarità delle funzioni differenziabili, la classificazione di curve e varietà algebriche, ecc.; si tratta di idee e metodi che sono ormai parte integrante del vocabolario di fisici e ingegneri. Suddivisioni dello spazio dei parametri per un particolare sistema in regioni che mostrano comportamenti dinamici diversi sono ormai consuete nella ricerca in molti campi delle scienze naturali. Nell'ingegneria elettrotecnica, in ricerche connesse con il laser, e in altri campi, sono stati sviluppati strumenti particolari che determinano, direttamente dai dati sperimentali, le curve o le superfici relative alla biforcazione di Poincaré-Andronov-Hopf. Attualmente, le nozioni, la terminologia e i risultati della teoria dei sistemi dinamici sono parte essenziale del bagaglio degli specialisti delle scienze non lineari.
È importante sottolineare che molte caratteristiche fisiche dei processi dinamici reali sono adeguatamente rappresentate nella teoria dei sistemi dinamici. Per esempio, il modello di giunzioni di Josephson è descritto dalle equazioni:
dove r è una corrente adimensionale e y una differenza di potenziale anch'essa adimensionale. Nel modello, la quantità
è una buona misura delle caratteristiche tensione-corrente. Poiché
abbiamo:
Questa quantità è detta 'numero di rotazione di fase'. Per alcuni valori dei parametri si ha un toro invariante per l'equazione differenziale. In questo caso il numero di rotazione di fase è il numero di rotazione di Poincaré sul toro, e le caratteristiche tensione-corrente sono determinate dal modo in cui il numero di rotazione di Poincaré dipende dal parametro r. Il grafico di questa funzione fornisce informazioni dettagliate sul modo in cui la dinamica dell'equazione dipende da r. Il grafico tipico, detto 'scala del diavolo', è una funzione monotona che è costante sui razionali p/q, dove p e q corrispondono al numero di armoniche con le quali ha luogo un moto periodico.
Per altri valori dei parametri il sistema ha un'orbita periodica iperbolica per la quale le varietà stabili e instabili si intersecano. Per valori prossimi a questi si è dimostrato sperimentalmente che le caratteristiche di tensione-corrente sono sensibili ai dati iniziali anche nelle stesse condizioni sperimentali (che corrispondono all'intersezione trasversale delle varietà stabili e instabili delle orbite periodiche).
Sistemi dinamici estesi
La comparsa di potenti computer ha portato alla creazione di una nuova disciplina che possiamo chiamare matematica sperimentale, e che ha permesso di esplorare problemi matematici che erano, e sono tuttora, fuori della portata dei metodi analitici rigorosi. In seguito a questi esperimenti sono stati introdotti modelli matematici che possono essere simulati al computer.
Tradizionalmente modelli di sistemi dinamici estesi sono rappresentati da equazioni differenziali alle derivate parziali. Tuttavia a causa sia dell'estrema difficoltà dell'analisi rigorosa sia della necessaria discretizzazione per i moderni esperimenti al computer, sono stati introdotti sistemi dinamici con spazio fisico discreto.
Il primo di questi modelli, detti 'automi cellulari' (AC), è stato introdotto da John von Neumann come l'esempio più semplice che può esibire il medesimo processo di autoriproduzione riscontrabile in Natura e nei computer. Più precisamente, è un esempio di programmi che si autoriproducono o di sistemi di intelligenza artificiale capaci di apprendimento adattativo. Gli automi cellulari sono stati usati come modello di morfogenesi, di creazione di forme in mezzi attivi, eccetera. Lo spazio fisico di un AC è un reticolo, per esempio il reticolo ℤd⊂ℝd, e lo spazio delle fasi M è l'insieme di tutte le applicazioni ℤd→ω, dove ω è un insieme finito. Consideriamo un semplice esempio, il voter model (modello dell'elettore), in cui ω={+1,−1}, d=1, e la dinamica è data da:
dove i∈ℤ. Questo sistema dinamico ha infiniti punti fissi: sono le successioni infinite con le seguenti proprietà: se Xi=1, allora o Xi−1 oppure Xi+1 è uguale a 1, e analogamente per Xi=−1. Vi è anche l'orbita 2-periodica, quella della successione in cui Xi=1, Xi+1=−1. Tutte le altre orbite tendono a punti fissi. La dinamica (temporale) è estremamente semplice, ma il comportamento spaziale delle soluzioni può essere molto complicato.
Il problema principale della dinamica degli AC è trovare tutte le distribuzioni di equilibrio (misure invarianti rispetto alla dinamica). Nell'esempio precedente le distribuzioni sono determinate dai punti fissi e dalle orbite periodiche. Vi sono però molti AC con comportamento caotico, sia temporale sia spaziale, e il problema di descriverne le misure invarianti non è banale.
Recentemente è stata introdotta un'altra classe di sistemi dinamici estesi, i cosiddetti 'reticoli di mappe accoppiate' (CML, coupled map lattices) o più in generale 'sistemi dinamici su reticoli' (LDS, lattice dynamical systems). Lo spazio fisico di un LDS è sempre un reticolo ℤd⊂ℝd, e la differenza tra un LDS e un AC è che lo spazio delle fasi locale ω è continuo (per es., una varietà). La dinamica di un LDS è generata da un sistema dinamico locale (una funzione f : ω→ω) e da interazioni spaziali. Supponiamo per semplicità ω=[0,1] e d=1. Allora lo stato del sistema è dato da un insieme doppiamente infinito di numeri xi, i∈ℤd, 0≤xi≤1, e lo spazio delle fasi è
Lo spazio delle fasi è il cubo di dimensione infinita, mentre la dinamica è generata da una φ:M→M. La scelta più semplice per φ è:
dove ε>0 rappresenta la forza dell'accoppiamento, f è la mappa locale e la funzione g rappresenta il tipo di accoppiamento presente tra i punti del reticolo.
Vi è un altro sistema dinamico che agisce anch'esso sullo spazio delle fasi M. Questo sistema dinamico è generato dallo shift spaziale Sj del reticolo ℤd, dove j=(j1,j2,…,jd) è un punto arbitrario di ℤd. Se d=1, S è semplicemente lo shift di una coordinata su ℤ1 (per es., verso sinistra): (Sx)i=xi+1.
Nelle applicazioni, in particolare negli esperimenti con sistemi estesi, si usano ampiamente termini come caos spazio-temporale, intermittenza, strutture coerenti, ecc. Queste nozioni, pur vaghe, sono state di aiuto nello sviluppo della ricca fenomenologia dell'evoluzione dei sistemi dinamici estesi.
La teoria vera e propria comincia però con la definizione precisa dei fenomeni fondamentali. Il primo passo nello sviluppo della teoria del moto caotico dei sistemi dinamici estesi (teoria del caos spazio-temporale) è definire con esattezza cosa voglia dire moto caotico. Intuitivamente, caos spazio-temporale significa che due misure effettuate nello stesso punto dello spazio fisico hanno traiettorie che diventano quasi indipendenti dopo un lungo periodo di tempo (caos temporale), così come quasi indipendenti diventano due misure prese nello stesso istante ma in due punti distinti dello spazio fisico delle fasi, se la distanza tra questi punti è sufficientemente grande (caos spaziale).
Per dare una definizione di caos spazio-temporale che formalizzi questa nozione intuitiva abbiamo intanto che lo shift S e lo shift temporale φ commutano, e che insieme generano un semigruppo di shift spazio-temporali nello spazio delle fasi M. Per ε=0 si ha φ=f, e possiamo vedere l'influenza di f sulla dinamica dello spazio e del tempo sostituendo le iterate fn della mappa f con φn°Sm e facendo tendere n e/o m all'infinito. Se f è sufficientemente caotica abbiamo un mixing spazio-tempo per ε=0. Infatti, tutte le correlazioni spaziali sono identicamente nulle perché non vi sono interazioni spaziali, e le correlazioni temporali decadono a zero perché la mappa locale f è mixing. Ne segue che se l'accoppiamento spaziale degli elementi del reticolo è abbastanza debole (ε piccolo) vi è caos spazio-temporale nel sistema esteso. Per alcune classi di CML è stata dimostrata la validità di questa idea.
Ma è la dinamica temporale, piuttosto che quella spaziale, che governa effettivamente l'evoluzione dei sistemi dinamici spazialmente estesi. In particolare si può dimostrare esplicitamente per alcune classi di questi sistemi che la dinamica locale determina effettivamente la struttura spaziale delle soluzioni (struttura spazio-temporale). Infatti, più la dinamica locale diventa complessa, più diventa complessa la struttura spaziale delle orbite.
Bibliografia
Afraimovich, Bunimovich 1995: Afraimovich, Valentin S. - Bunimovich, Leonid A., Density of defects and spatial entropy in extended systems, "Physica D", 80, 1995, pp. 277-288.
Andronov, Pontrjagin 1937: Andronov, Alexandr A. - Pontrjagin, Lev S., Systems grossieres, "Doklady Akademii Nauk SSSR", 14, 1937, pp. 247-250.
Andronov 1966: Andronov, Alexandr A. - Leontovich, Evgeniia A. - Gordon, I.I. - Maier, A.G., Qualitative theory of second-order dynamical systems, Moscow, Nauka, 1966.
Andronov 1973: Andronov, Alexandr A. - Leontovich, Evgeniia A. - Gordon, I.I. - Maier, A.G., Theory of bifurcations of dynamical systems on a plane, Israel program for science translations, New York, Wiley, 1973.
Anosov 1967: Anosov, Dmitrii V., Geodesic flows on closed riemannian manifolds with negative curvature, "Proceedings of the Steklov institute of mathematics", 90, 1967, pp. 1-235.
Arnold 1978: Arnold, Vladimir Igorevich, Mathematical methods of classical mechanics, New York-Berlin-Heidelberg, Springer, 1978.
Arnold 1994: Dynamical systems V: bifurcation theory and catastrophe theory, edited by Vladimir Igorevich Arnold, New York-Berlin-Heidelberg, Springer, 1994.
Babin, Vishik 1991: Babin, Anatoli V. - Vishik, Mark I., Attractor of evolution equations, Amsterdam, North Holland, 1991.
Bunimovich, Sinai 1988: Bunimovich, Leonid A. - Sinai, Yakov G., Space-time chaos in coupled map lattices, "Nonlinearity", 1, 1988, pp. 491-516.
Guckenheimer, Holmes 1983: Guckenheimer, John - Holmes, Philip J., Nonlinear oscillations, dynamical systems and bifurcations of vector fields, New York-Berlin-Heidelberg, Springer, 1983.
Hale 1988: Hale, Jack K., Asymptotic behavior of dissipative systems, Providence (RI), American Mathematical Society, 1988.
Hale, Koçak 1991: Hale, Jack K. - Koçak, Hüseyin, Dynamics and bifurcations, (Texts in applied mathematics, 3), New York-London, Springer, 1991.
Hale, Verduyin Lunel 1993: Hale, Jack K. - Verduyin Lunel, Sjoerd M., Introduction to functional differential equations, (Applied mathematical sciences, 99), New York-London, Springer, 1993.
von Neumann 1932: von Neumann, John, Zur Operatoren methode in der Klassishen Mechanik, "Annal of mathematics", 33, 1932, pp. 587-645.
von Neumann 1951: von Neumann, John, The general and logical theory of automata, in: Cerebral mechanisms in behaviour, edited by Lloyd A. Jeffreys, New York, Wiley, 1951.
Palis, de Melo 1982: Palis, Jacob jr - de Melo, Welington, Geometric theory of dynamical systems, New York-Berlin-Heidelberg, Springer, 1982.
Peixoto 1962: Peixoto, Mauricio M., Structural stability on two-dimensional manifolds, "Topology", 1, 1962, pp. 101-120.
Smale 1967: Smale, Stephen, Differentiable dynamical systems, "Bulletin of the American mathematical society", 73, 1967, pp. 747-817.
Smale 1966: Smale, Stephen, Structurally stable systems are not dense, "American journal of mathematics", 88, 1966, pp. 491-496.
Sinai 2000: Dynamical systems, ergodic theory and applications, edited by Yakov G. Sinai, Berlin-London, Springer, 2000.
Shil´nikov 1967: Shil´nikov, Leonid P., On a Poincaré-Birkhoff problem, "Mathematics of the USSR sbornik", 3, 1967, pp. 353-371.
Shil´nikov 1970: Shil´nikov, Leonid P., A contribution to the problem of the structure of an extended neighborhood of a rough equilibrium state of saddle-focus type, "Mathematics of the USSR sbornik", 10, 1970, pp. 91-102.
Sotomayor 1973: Sotomayor, Jorge, Generic one-parameter families of vector fields on two-dimensional manifolds, "Publications mathématiques. Institut des Hautes Études Scientifiques", 43, 1973, pp. 5-46.
Temam 1988: Temam, Roger, Infinite-dimensional dynamical systems in mechanics and physics, (Applied mathematical sciences, 68), New York- London, Springer, 1988.