La grande scienza. Sistemi disordinati
La grande scienza. Sistemi disordinati
Sistemi disordinati
I sistemi disordinati sono estremamente comuni e appaiono con svariate forme e componenti in discipline molto differenti, fra cui la fisica dello stato solido, la neurobiologia, le scienze computazionali, le teorie evolutive, l'economia e le scienze sociali. Nella terminologia corrente, questi sono sistemi composti da un gran numero di parti microscopiche, che sono in interazione fra di loro in maniera non uniforme: ciascun componente ha la sua individualità e interagisce con gli altri in maniera peculiare. Come vedremo meglio in seguito, spesso la forma dettagliata di queste interazioni dipende da variabili casuali e perciò tali sistemi sono chiamati disordinati. Nell'ultimo quarto del XX sec. ci si è resi conto che questi sistemi possono presentare un comportamento collettivo emergente estremamente ricco e complesso, che solo in alcuni casi è stato compreso fino a fondo e il cui studio è uno dei campi più interessanti della ricerca attuale, con molti risvolti interdisciplinari. I primi studi sistematici sono stati compiuti nell'ambito della fisica e successivamente sono nate le applicazioni in campi differenti: per questo motivo discuteremo innanzi tutto il caso della materia condensata.
In fisica, il disordine appare spesso, ma con caratteristiche molto diverse a seconda dei casi. Per esempio sia i gas sia i liquidi sono disordinati. Nei gas le molecole si muovono rapidamente senza avere una posizione fissa e sono completamente disordinati. Nei liquidi la densità è più alta e le posizioni di atomi vicini sono correlate, ma non esiste una correlazione fra atomi lontani. Nei solidi cristallini gli atomi sono ordinati periodicamente nello spazio su distanze macroscopiche (ossia grandi rispetto alla separazione interatomica media) e ognuno rimane 'congelato' nella posizione che aveva al momento della formazione del cristallo, a parte piccole oscillazioni di origine termica di modesta ampiezza rispetto alla scala interatomica e deboli fenomeni di diffusione, che tuttavia sono irrilevanti in questo contesto.
La transizione di fase da uno stato mobile a uno congelato è una transizione dal disordine all'ordine, da uno stato di simmetria minore a uno di simmetria maggiore. La definizione di disordine che abbiamo usato per i gas e per i liquidi non è quella adottata di solito quando si parla di sistemi disordinati, benché molto dell'interesse con cui essi sono considerati coinvolga concetti di transizione di fase da stati in rapido movimento a stati a tutti gli effetti congelati. Nel contesto che ci interessa, l'espressione è usata per riferirsi a sistemi in cui alcune proprietà delle parti costituenti microscopiche sono sia congelate (o variabili molto lentamente) sia non periodiche spazialmente (come in un cristallo). Esempi di solidi disordinati sono le leghe metalliche, in cui i siti del reticolo cristallino sono occupati a caso da atomi di tipi diversi, e i vetri, in cui le posizioni atomiche sono ancora praticamente congelate ma senza alcuna periodicità. In questi casi, ci sono altre proprietà degli elementi costitutivi che evolvono velocemente, per esempio quelle associate con il moto elettronico o l'orientamento degli spin.
Storicamente, già prima del XX sec., era stata raggiunta una buona comprensione dei gas e delle equazioni che controllano i mezzi continui. Nella prima metà del Novecento la teoria dei cristalli era stata approfondita tenendo conto non solo degli aspetti macroscopici ma anche della loro struttura periodica microscopica. La scoperta della meccanica quantistica permise di sviluppare, nel secondo quarto del secolo, la teoria quantistica dei solidi ponendo le basi teoriche per la successiva comprensione della differenza tra metalli, isolanti e semiconduttori, senza che ancora venissero alla luce nuovi effetti significativi dovuti al disordine. Solo nella seconda metà del secolo cambia l'impostazione dello studio dei sistemi disordinati: il disordine non è più una noiosa complicazione, ma diventa riferimento fondamentale per l'interpretazione di comportamenti qualitativamente nuovi.
Alcuni sistemi disordinati 'semplici'
Gli aspetti dei sistemi disordinati di maggiore interesse scientifico e con possibili applicazioni riguardano gli effetti del disordine 'congelato' (dovuto alla presenza di componenti del sistema che non possono muoversi) sulla mobilità delle altre componenti del sistema che non sono congelate. In ogni caso, prima di affrontare questa problematica è opportuno descrivere alcuni esempi di comportamento dovuti al disordine congelato in cui tali effetti sulla mobilità non risultano importanti.
Un primo esempio è l'origine del colore di molte gemme causata da impurità isolate presenti nel cristallo: queste agiscono in pratica come singoli atomi e hanno uno spettro discreto dei livelli energetici che risuonano a frequenze ottiche discrete; di conseguenza, le impurità, assorbendo queste frequenze dalla luce bianca incidente, appaiono colorate. Un secondo esempio è quello relativo alla resistenza elettrica nei metalli normali, che persiste anche scendendo alle temperature più basse, a causa della diffusione degli elettroni dovuta alle impurità (fanno eccezione i superconduttori dove la resistenza crolla a zero al di sotto di una certa temperatura critica). Un ulteriore esempio è connesso con la variazione della densità degli elettroni capaci di trasportare la corrente che viene realizzata in un solido cambiando la proporzione delle costituenti atomiche. Questa variazione può modificare notevolmente il comportamento del sistema, con conseguenze molto importanti. In diversi chip a semiconduttore, un attento drogaggio (aggiunta di impurità) permette di ottenere effetti fondamentali che sono il cuore di molti strumenti elettronici (come il raddrizzamento e l'amplificazione). In altri casi il cambiamento nella densità degli elettroni di conduzione è all'origine di effetti collettivi che possono anche dare luogo a una transizione di fase in cui cambiano le proprietà qualitative del sistema: un magnete si può smagnetizzare o un metallo normale (o addirittura un isolante) può diventare un superconduttore.
Un altro concetto facilmente visualizzabile, che coinvolge il disordine, è quello della percolazione. Consideriamo un insieme di elementi, conduttori o isolanti, scelti a caso, connessi tra loro a formare un circuito (per es., un recipiente pieno di biglie, alcune di vetro, altre di metallo). L'intero circuito condurrà da una parte all'altra solo se esiste un cammino continuo di elementi conduttori tra le due parti. Questa proprietà è detta percolazione. Si possono altresì avere esclusivamente elementi conduttori, con connessioni variabili, che abbiano capacità diverse di portare la corrente (per es., un mucchio di aghi gettato su un tavolo). La conduttività dipenderà dal numero e dalla resistenza dei cammini conduttori. Analogie abbondano in molti contesti: per esempio, nei solidi potenzialmente magnetici, i 'nodi' del circuito potrebbero essere atomi, alcuni dei quali con momento magnetico, e gli 'elementi conduttori' interazioni che cercano di orientare i momenti magnetici paralellamente l'uno rispetto all'altro; in questo caso l'analogo della percolazione è l'apparire di un ordine magnetico macroscopico spontaneo (ordine nel senso specificato sopra).
Per i fisici, uno dei motivi di interesse fondamentale in tali sistemi sta nel fatto che la transizione dalla fase non percolante a quella percolante mostra un comportamento critico caratterizzato dall'universalità degli esponenti che descrivono l'andamento verso la soglia di percolazione; proprietà macroscopiche seguono leggi di potenza in funzione della deviazione della densità del disordine dal suo valore critico, con esponenti che dipendono soltanto dalla classe generale e non dai dettagli della struttura microscopica del sistema. Lo studio dei fenomeni critici e della loro universalità è stata una delle più grandi sfide intellettuali degli ultimi trent'anni del XX secolo.
Esistono molte estensioni dei semplici problemi di percolazione sopra menzionati: per esempio lo studio della distribuzione, forma e struttura di gruppi di elementi mutuamente connessi e della loro crescita e interconnessione all'aggiungersi di nuovi elementi. Molte sono le applicazioni: la 'percolazione invasiva', di rilevanza nell'estrazione petrolifera, in cui un fluido che si diffonde in un sistema di pori di dimensione variabile sceglie a ogni passo il poro adiacente più grande ancora aperto; la 'percolazione diretta' (condizionata) d'interesse nella determinazione dei percorsi di fiumi (e affluenti) che scorrono da una data pendenza.
Un effetto diverso del disordine congelato è il fenomeno della localizzazione elettronica. In assenza di disordine le funzioni d'onda degli elettroni nei metalli si estendono all'intero solido, permettendo la conduzione elettronica una volta applicata una differenza di potenziale. Quando è presente il disordine nei potenziali locali avvertiti dagli elettroni, alcune funzioni d'onda diventano localizzate nelle regioni dove il potenziale è più attrattivo per effetto di fluttuazioni statistiche. Se il potenziale indotto dal disordine è sufficientemente grande, la conduzione elettrica si annulla completamente al tendere della temperatura allo zero assoluto, mentre in un metallo normale rimane diversa da zero realizzando una transizione metallo-isolante. A temperatura non nulla, le fluttua- zioni termiche possono sempre avere luogo e indurre il passaggio della corrente elettrica, ma nella fase isolante ogni conduzione risultante è piccola e di tipo non metallico. Questo fenomeno è più intenso in sistemi unidimensionali o bidimensionali. In sistemi lineari (unidimensionali) qualsiasi disordine macroscopico è sufficiente a prevenire la conduzione metallica. Anche in questo caso ci sono interessanti fluttuazioni critiche ed effetti caratterizzati da esponenti universali vicini ai valori critici del disordine. La localizzazione è, inoltre, alla base del notevole effetto Hall quantistico, dove nette discontinuità delle proprietà del sistema al variare dei parametri di controllo permettono la misura di una costante fondamentale (la carica dell'elettrone in unità opportune) con la più alta precisione conosciuta.
Sistemi complessi
Concentriamoci ora, in particolare, su una della più grandi rivoluzioni concettuali dell'ultimo quarto del Novecento, che ha condotto a implicazioni sia pratiche sia teoriche assai ampie in molte aree della scienza ed è scaturita dall'aver considerato sistemi che combinano il disordine congelato con un'altra caratteristica nota come 'frustrazione'. Quest'ultima proprietà si riferisce a situazioni nelle quali le propensioni di componenti o gruppi di componenti del sistema sono in conflitto le une con le altre, cosicché non tutte possono essere simultaneamente soddisfatte e diventano essenziali accomodamenti (per es., Caio vuole andare in vacanza assieme a Tizio e Sempronio, che non si possono sopportare reciprocamente).
Alcuni esempi di sistemi frustrati si trovano nella fisica della materia condensata, ma anche in biologia, nelle scienze computazionali, nei problemi decisionali e di decodificazione e nelle scienze sociali. Una delle caratteristiche chiave di tali sistemi è di possedere molti stati globali metastabili, cioè stati dell'intero sistema nei quali una modifica della condizione di un qualsivoglia individuo porterebbe a un abbassamento della qualità di tutto l'insieme. Uno, o più, di questi stati del sistema sarà il migliore compromesso possibile, ma di solito è difficile determinarlo a priori. Piuttosto si è spesso indotti (o la Natura lo è) a cercare tale 'miglior soluzione' mediante alcune procedure iterative, che sfortunatamente passano con molta difficoltà le barriere presenti tra gli stati metastabili: in questo modo la dinamica può essere estremamente lenta (caratteristica presente nei vetri e in molti problemi pratici di difficile ottimizzazione). D'altro canto, in alcune situazioni, le barriere tra gli stati metastabili possono anche tornare utili, come nel caso della memoria neurale.
In generale si chiamano complessi quei sistemi in cui il comportamento macroscopico, molto più ricco di quello dei suoi singoli 'ingredienti' microscopici, evolve mediante la loro cooperazione. Nello studio di tali sistemi spesso si ricorre a modelli minimali in cui le componenti microscopiche individuali e le loro interazioni sono semplici, nello spirito della ricerca di proprietà qualitative universali, in modo da distinguere la complessità dalla mera complicazione.
Lo studio del comportamento complesso in quanto conseguenza della combinazione di disordine e frustrazione è nato indipendentemente in ambiti diversi. Tuttavia, può essere conveniente esaminare la questione nel contesto della fisica dello stato solido dove una sequenza di sviluppi ha portato a progressi concettuali, quantitativi e applicativi molto fruttiferi, attraverso una combinazione di analisi matematica, simulazione numerica ed esperimenti. Il punto di partenza di questa vicenda è apparentemente angusto e oscuro, ma la ricaduta è stata ampia. Nei primi anni Settanta del Novecento, esperimenti su alcune leghe metalliche mostrarono quel che sembrava essere un'atipica transizione di fase da una fase paramagnetica ad alta temperatura (disordinata) a una magneticamente congelata a temperatura inferiore, che non era di tipo ferromagnetico normale o antiferromagnetico periodico ma, piuttosto, mostrava momenti magnetici congelati in una sorta di ordinamento amorfo, a cui fu dato il nome di 'vetro di spin'. I tentativi di costruire un modello teorico di questo comportamento svelarono i concetti già menzionati e più tardi continuarono a fornire modi di quantificarli e di estendere le idee sviluppate ad altri campi.
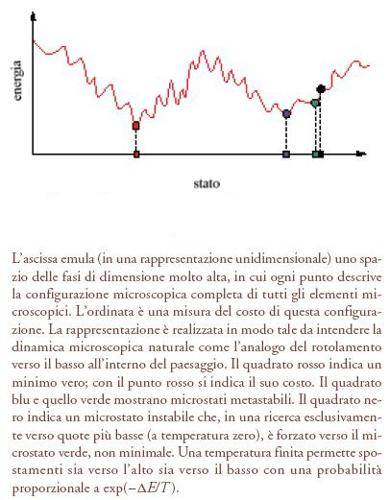
Un semplice modello minimale, che presenta le caratteristiche chiave, possiede momenti magnetici atomici (spin) che possono assumere solo due stati (convenzionalmente su e giù); i momenti magnetici interagiscono a coppie, a volte in maniera ferromagnetica, favorendo l'allineamento della coppia di spin, entrambi su o entrambi giù, a volte in maniera antiferromagnetica, favorendo allineamenti opposti, uno spin su e l'altro giù. Se le interazioni sono ferromagnetiche o antiferromagnetiche a caso, allora si hanno gli ingredienti per un vetro di spin; cammini di interazione chiusi con un numero dispari di interazioni antiferromagnetiche non possono essere completamente soddisfatti e si ha frustrazione. Inoltre, non c'è periodicità nella natura di questi 'cicli' frustrati. Tale problema può essere quantificato attribuendo un costo cumulativo (o energia nel linguaggio della fisica) a tutte le interazioni non soddisfatte. Studi di questo modello dimostrano che ci sono molti stati metastabili in cui il ribaltamento di ogni singolo spin determina un aumento del costo. L'energia è una funzione delle configurazioni microscopiche con moltissimi minimi locali. Usando un linguaggio figurativo possiamo dire che è presente un paesaggio energetico 'corrugato' nello spazio (a molte dimensioni) dei possibili stati, dove ci sono molte valli, cime e passi: la dinamica dei ribaltamenti degli spin è alla ricerca dell'equilibrio corrispondente al moto locale in questo paesaggio (fig. 1). In tale rappresentazione, un sistema a temperatura nulla corrisponde al caso in cui gli unici spostamenti permessi sono verso il basso. A temperatura finita sono ammessi anche movimenti verso l'alto con probabilità proporzionale a exp(−ΔE/T), dove ΔE è il costo energetico e T la temperatura assoluta, ma è ancora difficile uscire da una regione metastabile per andare verso una molto diversa, a causa della combinazione di barriere energetiche e cammini labirintici, almeno finché la temperatura non è notevolmente aumentata e non diventa più alta di una temperatura critica.
A temperatura finita, la quantità rilevante per l'equilibrio termodinamico è l'energia libera, che include pure effetti entropici, ma un simile paesaggio corrugato è spesso presente anche se consideriamo la dipendenza di altre quantità macroscopiche. Prendendo in esame l'energia libera, il paesaggio diventa meno corrugato all'aumentare della temperatura. Per la termodinamica di equilibrio contano soltanto gli stati a più bassa energia libera e a una certa temperatura critica avviene una transizione a una fase paramagnetica non ordinata. Al di sotto di questa temperatura, anche per un modello così semplice, si presenta una struttura di stati metastabili gerarchica e molto ricca. Dinamicamente, all'abbassarsi della temperatura, c'è una corrispondente transizione tra un comportamento di rilassamento veloce e quello lento tipico dei vetri. Nella fase a bassa temperatura si riscontra il fenomeno dell'invecchiamento, in cui è presente una memoria a lungo termine della storia passata del sistema. L'analisi di questo modello per i vetri di spin ha svelato molte sottigliezze che hanno messo alla prova modi di pensare e metodologie convenzionali. La loro scoperta ha, in cambio, arricchito la nostra comprensione e il nostro bagaglio tecnico stimolando esperimenti e nuove scoperte.
Se questa fosse stata la fine della storia i vetri di spin sarebbero rimasti un oscuro (anche se appassionante) episodio nella storia dei solidi. In realtà, dato che molti dei concetti e delle tecniche sviluppatesi per studiare questo semplice modello hanno applicazioni significativamente più ampie, esso è diventato un paradigma per un più vasto studio dei sistemi complessi. Una delle tante applicazioni riguarda i problemi 'duri' di ottimizzazione in cui i conflitti impediscono una soluzione facile. Essi sono interessanti sia in molti casi pratici sia come problemi fondamentali nelle scienze computazionali, per esempio per le classificazioni in gradi di difficoltà, per confermare l'esistenza di soluzioni e per inventare algoritmi efficienti.
Una questione esemplare è trovare la partizione ottimale, importante in molti problemi pratici nei quali un processo decisionale (o uno strumento elettronico) deve essere diviso in blocchi di taglia simile e nei quali il trasferimento di segnale tra blocchi diversi sia più lento di quello all'interno dei blocchi stessi, e quindi ottimizzato. Ciò è illustrato dal seguente problema di partizione dei grafi. Avendo un 'grafo' in cui i vertici siano connessi a coppie, a caso, da 'spigoli', bisogna trovare la maniera di separare i vertici in due gruppi che abbiano lo stesso numero di elementi ma con il numero minimo di spigoli tra i due gruppi (problema del taglio minimale, detto anche Mincut). Questo problema può essere messo in rapporto con una variante del semplice vetro di spin prima discusso: l'assegnare un vertice a uno o all'altro dei due gruppi corrisponde allo stato verso l'alto o verso il basso dello spin, la condizione che il grafo abbia uno spigolo tra due vertici o meno corrisponde alla presenza o assenza casuale di legami di interazione ferromagnetici; la frustrazione è data dal vincolo che i due gruppi devono essere delle stesse dimensioni. Il disordine interviene poiché non c'è in generale una relazione semplice tra la connettività richiesta dalla rete relativa al problema in esame e la necessità di una separazione semplice. Questo è il caso di molti altri problemi di ottimizzazione e si assumerà implicitamente nel seguito. Maxcut è un problema simile in cui l'obiettivo è trovare una maniera di separare i vertici in due gruppi avendo il numero massimo di spigoli tra i due gruppi; esso si trasforma in un analogo vetro di spin con legami antiferromagnetici o assenti.
In entrambi i casi si è interessati ai grafi casuali (o effettivamente casuali, dal punto di vista di questi problemi decisionali). Si ha, quindi, quella combinazione di frustrazione e disordine che porta nuovamente a una topologia complessa ruvida del paesaggio della funzione costo; in questo caso il costo è il negativo del numero di spigoli scambiati tra le due sezioni. Maxcut e Mincut sono evidentemente problemi complessi noti nelle scienze computazionali come NP-hard (una famosa congettura afferma che il tempo di calcolo necessario per risolvere il più difficile problema NP-hard con N elementi aumenti necessariamente come l'esponenziale di N). È chiaro che, quando il numero di vertici diventa grande, non si possono prevedere tutte le possibili soluzioni in quanto il loro numero aumenta esponenzialmente con quello dei vertici stessi. Non si può neppure utilizzare una procedura semplice di discesa lungo il gradiente del paesaggio effettivo perché esso è ruvido.
L'analogia con i vetri di spin, tuttavia, apre anche le porte all'utilizzazione di tecniche della fisica statistica per trovare soluzioni a problemi tipici e sviluppare algoritmi per casi specifici di questo e altri problemi di ottimizzazione. Una di queste tecniche, ormai usuale nella ricerca di settore, è la ricottura simulata (simulated annealing, in analogia con il processo di ricottura, usato in metallurgia, in cui la temperatura è abbassata gradualmente in modo da rimuovere i difetti): si introduce una 'temperatura di ricottura' artificiale permettendo spostamenti probabilistici verso l'alto, analoghi a quelli consentiti dalla temperatura reale nei vetri di spin fisici e si utilizza una dinamica di ricerca algoritmica efficiente in cui tale temperatura è gradualmente ridotta. Tuttavia quando la frustrazione è forte anche questa procedura è rallentata dalla dinamica lenta caratteristica dei vetri di spin; sono stati pertanto effettuati molti sforzi per escogitare algoritmi migliori, ispirati dalla comprensione teorica e/o dalla biologia ma che spesso coinvolgono anche dinamiche al computer prive di controparti in Natura: per esempio la 'tempratura parallela' (parallel tempering), in cui un sistema è simulato simultaneamente a parecchie temperature diverse e gli stati ottenuti vengono scambiati regolarmente.
Metodi di ottimizzazione e applicazioni
Tanto i modelli di vetro di spin quanto gli esempi di ottimizzazione sopra menzionati, con interazioni a coppie tra entità binarie, presentano simultaneamente transizioni termodinamiche e dinamiche quando i loro parametri di controllo (come la temperatura) variano attraversando i valori critici. Esiste, però, un'altra classe di problemi in cui le transizioni dinamiche non permettono di realizzare le transizioni termodinamiche quando si variano i parametri di controllo per passare dallo stato non vetroso a quello vetroso. Nei vetri di spin questo si verifica nei modelli in cui le interazioni fra spin non hanno una simmetria di riflessione semplice, con la temperatura come parametro di controllo naturale. Nelle scienze computazionali ciò è esemplificato dai problemi, detti K-SAT, consistenti nel trovare valori di quantità booleane che soddisfino simultaneamente molte 'clausole' di lunghezza K; in questo caso il parametro di controllo è il rapporto tra il numero di clausole e quello di variabili; dove, nel limite di molte clausole, la soddisfazione è possibile se questo rapporto è al di sotto di un certo valore critico.
Di fatto, il trasferimento dei concetti e delle tecniche dei vetri di spin ha permesso l'identificazione di due rapporti critici nel problema K-SAT. Un primo valore separa la fase in cui le clausole possono essere tutte contemporaneamente soddisfatte (SAT) e la fase in cui nessuna configurazione è in grado di soddisfare un numero così elevato di condizioni (UNSAT): siamo in presenza dell'analogo di una transizione termodinamica. Un secondo rapporto (più basso del primo) è invece analogo della transizione dinamica (o di stabilità marginale), corrispondente al sorgere di una regione di difficile soddisfazione compresa tra SAT e UNSAT. Di particolare interesse è stata l'applicazione di una tecnica sviluppata per lo studio degli stati fondamentali dei vetri di spin sui reticoli diluiti, che ha fornito un nuovo algoritmo per risolvere problemi di soddisfazione.
Una situazione simile, di doppia transizione, è importante anche per i codici correttori d'errore. L'informazione trasmessa attraverso canali in presenza di rumore è soggetta a una distorsione tra la trasmissione e la ricezione ed è necessario aggiungere ridondanza al messaggio per rendere possibili interpretazioni prive di errori. Claude E. Shannon mostrò che la decodifica senza errori è possibile, in linea di principio, introducendo una opportuna ridondanza nei codici trasmessi e calcolò la ridondanza minima necessaria. Trovare un algoritmo che funzioni in tempi non eccessivamente lunghi e che raggiunga il limite di Shannon per la ridondanza minima si è rivelata una meta irraggiungibile, tuttavia il controllo di parità (parity-check) a bassa densità fornisce, al momento, uno degli approcci migliori. Questi codici presentano una somiglianza con i ferromagneti con interazioni a molti spin che, se opportunamente interpretati, diventano vetri di spin con interazioni a molti spin. La decodifica è un problema di ottimizzazione. I codici basati su interazioni a due spin non raggiungono il limite di Shannon, mentre esistono codici che coinvolgono interazioni di ordine più alto, dove il limite di Shannon risulta l'analogo della loro transizione termodinamica, mentre l'algoritmo di decodifica è una dinamica soggetta a una transizione di incollamento (sticking) che avviene prima di aver raggiunto questo limite. Uno degli scopi della ricerca corrente è trovare codici con transizione dinamica più vicino possibile al limite di Shannon.
Queste applicazioni avvalorano il metodo in base al quale a volte si studia accuratamente un modello semplificato che si allontana, anche notevolmente, dalla realtà, in modo da ottenere problemi che si possono risolvere analiticamente e quindi arrivare a una comprensione profonda delle cause del comportamento del sistema. Nei veri vetri di spin solamente gli spin vicini interagiscono, ma non sono risolubili analiticamente. Le loro controparti teoriche, dove tutti gli spin interagiscono (ossia le interazioni hanno una portata infinita), sono invece risolubili e le loro soluzioni hanno prodotto concetti e tecniche nuove. Quanto tutto ciò si applichi ai vetri di spin reali dei materiali solidi rimane un punto controverso, tuttaia molte delle analogie al di fuori della fisica, come quelle sopra riportate, hanno interazioni con portata infinita e in questo caso la teoria è certamente ben fondata.
Applicazioni biologiche
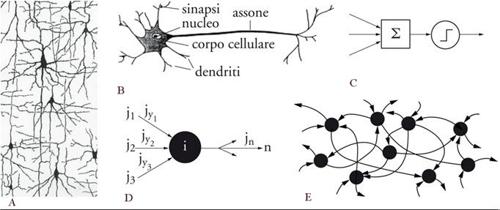
Un'altra analogia nasce quando si prende in considerazione la modellizzazione della memoria neurale associativa, sia come idealizzazione del cervello - benché le reali operazioni biologiche non siano ancora completamente chiare - sia in quanto strumento artificiale affidabile che impara dall'esperienza. La fig. 2 illustra il processo di modellizzazione: sono mostrate una sezione di cervello, dove le 'gocce' triangolari sono i neuroni da cui emergono gli assoni che a loro volta conducono, attraverso le sinapsi, ad altri neuroni, e differenti rappresentazioni provenienti da ambiti disciplinari diversi.
Un'immagine neurale è caratterizzata da uno stato globale (configurazione) di tutti i neuroni; un'immagine memorizzata è ben ricostruita se c'è un'elevata somiglianza (o sovrapposizione) tra lo stato neurale globale corrente e quello corrispondente all'immagine memorizzata: questa somiglianza può essere definita come la frazione di stati individuali dei singoli neuroni coincidenti nei due casi. La memoria associativa consiste allora nell'avere il sistema che si muove dinamicamente verso stati che corrispondono a immagini immagazzinate a partire da inizializzazioni distorte. Questo processo può essere immaginato ancora una volta come un flusso attraverso un paesaggio corrugato nello spazio degli stati neurali globali, in cui i minimi corrispondono a memorie immagazzinate e i bacini di ricordo associativo sono le regioni da cui il flusso dinamico muove verso i minimi. Per immagazzinare numerose memorie si richiede che il paesaggio abbia molti minimi, cosa che a sua volta impone frustrazione nelle interazioni sinaptiche. Nel caso in cui le immagini da memorizzare siano effettivamente scorrelate tra loro, entra in gioco il disordine.
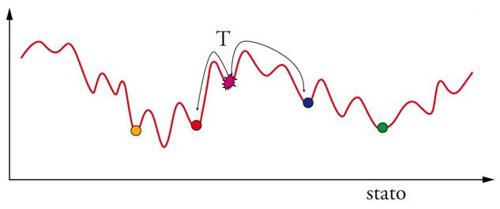
Durante l'apprendimento le sinapsi vengono istruite a modificare il paesaggio energetico e a collocare i minimi in posizione corretta, e questo processo è più lento. Ciò è illustrato nella fig. 3, dove si mostra come, in sistemi ipersemplificati, può aver luogo il ricordo schizofrenico (in cui l'immagine finale è una combinazione di due immagini differenti): quest'effetto indesiderato è però eliminabile se nel sistema è presente un rumore stocastico, che gioca un ruolo simile alla temperatura.
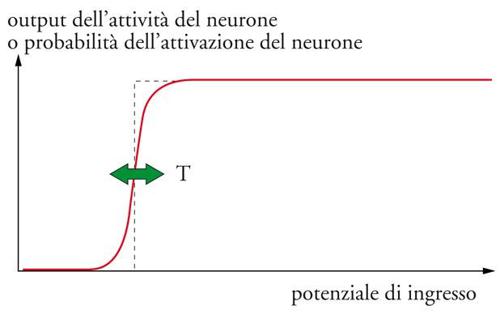
Analizziamo l'analogia con i vetri di spin un po' più nel dettaglio. I neuroni possono operare a diverse velocità e quando lo fanno inviano, attraverso le sinapsi, segnali ad altri neuroni che possono essere sia eccitatori (amplificando l'azione del neurone di partenza) sia inibitori (tendendo a disattivarlo). Questi casi sono l'equivalente delle interazioni ferromagnetiche e antiferromagnetiche che causano frustrazione nei vetri di spin. Nel modello più semplice il segnale (o potenziale) di entrata ricevuto da un neurone è la somma dei prodotti delle frequenze di attivazione dei neuroni afferenti e della corrispondente efficienza delle loro sinapsi collegate al neurone considerato. Il suo input conseguentemente determina l'attività del neurone afferente, attraverso una funzione di risposta a forma di sigmoide (gradino arrotondato, fig. 4). L'arrotondamento del gradino è l'analogo della temperatura nelle figure mostrate prima. Le tecniche sviluppate per la comprensione dei vetri di spin sono state utili nell'analisi quantitativa di questi modelli di reti neurali oltre che nei progressi teorici.
Un altro esempio biologico di sistemi disordinati è quello connesso all'evoluzione delle specie in cui alcune di esse favoriscono e altre impediscono la riproduzione di altre specie. Supponiamo che il sistema sia arrivato in qualche modo a una configurazione di questo tipo e analizziamo l'evoluzione successiva. Studi numerici indicano che dopo un tempo molto superiore a quello di una singola generazione, numerose specie vengono eliminate lasciando solamente sottoinsiemi di specie con un adattamento ottimizzato che ricorda gli stati metastabili dei sistemi complessi.
Un ulteriore esempio di sistemi che sono ragionevolmente rilevanti per la biologia, dove sia il disordine sia la frustrazione sono presenti, è costituito dagli eteropolimeri casuali, dove ci sono interazioni tra monomeri tanto repulsive quanto attrattive: possiamo presumere che le attuali proteine si siano evolute partendo da un sistema simile. La maggior parte degli eteropolimeri casuali si ripiega con difficoltà, mentre al contrario, una piccola parte, con sequenze particolarmente fortunate, si ripiega molto più facilmente, come se nel loro paesaggio energetico ci fosse un imbuto che porta verso uno stato ripiegato. È probabile che queste sequenze siano state selezionate a partire dal brodo primordiale da un lenta dinamica riproduttiva che favorisce gli eteropolimeri che ripiegano meglio.
Disordine autoindotto
Finora sono stati esaminati sistemi in cui il disordine congelato è presente nella forma degli ingredienti microscopici o delle regole. Tuttavia si può ottenere pure un disordine autoindotto in presenza di un rilassamento vetroso, anche con ingredienti microscopici e regole di interazione puramente omogenee. Attualmente si pensa che questo accada per i vetri strutturali (quelli delle finestre), benché, in pratica, essi spesso debbano essere costituiti da miscele per prevenire la cristallizzazione. Tali sistemi sono stati modellizzati in numerosi modi; per quanto riguarda i vetri covalenti come reticoli casuali di vertici con legami in direzioni preferenziali o in termini di atomi con forze centrali che si possono autointrappolare in gabbie (come in un ingorgo stradale), oppure più metaforicamente in termini di sistemi con trappole o dinamiche vincolate.
È interessante notare che progressi significativi nella comprensione e modellizzazione dei cosiddetti vetri fragili sono derivati da analogie con caratteristiche rilevate inizialmente nei modelli artificiali dei vetri di spin con insolite interazioni di portata infinita tra due o più spin; queste caratteristiche furono dapprima ravvisate nell'analisi formale ma la cui generalizzazione fu identificata seguendo una concettualizzazione fisica appropriata. Una di queste identificazioni ha coinvolto il concetto di invecchiamento nei vetri, per cui il comportamento di un sistema dipende da quanto tempo esso è rimasto alla temperatura considerata, con comportamento secondo legge di scala che dipende dal rapporto tra il tempo passato dall'inizio delle misure e quello intercorso prima che le misure iniziassero. Un'ulteriore identificazione è che un vetro non all'equilibrio può apparire come un sistema la cui temperatura è più alta rispetto a quella ambiente. Altre sono la determinazione e la spiegazione di una certa quantità di temperature diverse, caratteristiche di cambi di regime.
Ci sono anche molti altri problemi in cui il disordine è autoindotto, per esempio quelli di deposito casuale o di erosione delle valli da parte dei fiumi. Ciò conduce ad altre questioni, quali le dimensioni (frattali) effettive dei volumi, delle superfici o dei contorni risultanti; per esempio, la lunghezza delle coste di un'isola o di un paese peninsulare (come la Gran Bretagna o l'Italia) dipende dalla lunghezza del regolo che si usa per misurarla. Molti di questi problemi coinvolgono quella che si chiama la 'criticità autoorganizzata', in cui i sistemi si evolvono, con la loro dinamica naturale, verso situazioni nelle quali si trovano leggi di scala autosimili analoghe a quelle di una normale transizione di fase termodinamica ma senza che, per raggiungere il punto critico, si abbia bisogno di regolare un parametro di controllo esterno. Un classico esempio è la sabbia asciutta fatta cadere in un mucchio, che raggiunge in maniera naturale un particolare angolo di pendenza.
Le polveri sono sistemi disordinati che presentano caratteristiche ulteriormente stimolanti. Esse possono fluire come liquidi e si possono comprimere come vetri. Nel caso specifico la temperatura è essenzialmente irrilevante e il suo ruolo è svolto dalla compattezza, legata alla derivata dell'entropia configurazionale rispetto al volume. Al momento attuale non è chiaro quanto gli opportuni concetti e relazioni termodinamiche si possano applicare a questi sistemi, pur essendoci analogie molto strette.
Un altro gruppo di sistemi disordinati per i quali l'entropia è più importante dell'energia è quello dei polimeri fusi e solidi; per esempio, l'origine primaria dell'elasticità della gomma è entropica. L'entropia fa contrarre i polimeri come spaghetti disordinati. Il moto di un singolo polimero è ostacolato dall'incapacità dei polimeri stessi di attraversarsi a vicenda, causando un moto (detto reptation in quanto contorto, come quello di un serpente) di un polimero attraverso tubi formati dagli altri polimeri. La vulcanizzazione aggiunge legami tra i polimeri nel punto in cui si incrociano quando si effettua, e ciò vuol dire che da quel momento in poi i polimeri mantengono questi legami incrociati e tutte le restrizioni topologiche risultanti come vincoli sulla loro dinamica e termodinamica.
I sistemi sociali ed economici forniscono molti altri scenari per i sistemi disordinati e frustrati: spesso sono composti da numerosi individui e gruppi caratterizzati da obiettivi, opinioni e inclinazioni differenti, che si influenzano l'un l'altro per trovare un compromesso. Capire e controllare tali sistemi ha, chiaramente, conseguenze potenziali molto importanti.
Concludendo, i sistemi disordinati con molti agenti in interazione sono estremamente frequenti ed è un obiettivo affascinante arrivare a una loro comprensione, sia qualitativa sia quantitativa, che possa essere utile in casi concreti. Come disse Philip W. Anderson poco più di trenta anni fa, 'more is different' e come sanno tutti, anche gli scienziati, 'la vita è bella perché è varia'.
Bibliografia
Amit 1989: Amit, Daniel J., Modeling brain function, Cambridge-New York, Cambridge University Press, 1989.
Anderson 1958: Anderson, Philip W., Absence of diffusion in certain random lattices, "Physical review", 109, 1958, pp. 1492-1501.
Anderson 1972: Anderson, Philip W., More is different, "Science", 177, 1972, pp. 393-396.
Anderson 1988: Anderson, Philip W. - Arrow, Kenneth J. - Pines, David, The economy as an evolving complex system, Redwood City (CA), Addison, Wesley, 1988.
Anderson 1988-90: Anderson, Philip W., Spin-glass I-VII, "Physics today", 41/1, 1988, pp. 9-11; 41/3, 1988, p. 9; 41/6, 1988, pp. 9-11; 41/9, 1988, pp. 9-11; 42/7, 1989, pp. 9-11; 42/9, 1989, pp. 9-11; 43/3, 1990, pp. 9-11.
Bak, Sneppen 1993: Bak, Per - Sneppen, Kim, Punctuated equilibrium and criticality in a simple model of evolution, "Physical review letters", 71, 1993, pp. 4083-4086.
Garey, Johnson 1979: Garey, Michael R. - Johnson, David S., Computers and intractability. A guide to the theory of NP-completeness, New York, Freeman, 1979.
Mandelbrot 1975: Mandelbrot, Benoit B., Les objects fractals: form, hasard et dimension, Paris, Flammarion, 1975.
Mandelbrot 1982: Mandelbrot, Benoit B., The fractal geometry of nature, San Francisco, Freeman, 1982.
Martin 2001: Martin, Olivier C. - Monasson, Remy - Zecchina, Riccardo, Statistical mechanics methods and phase transitions in optimization problems, "Theoretical computer science", 265, 2001, pp. 3-67.
Mèzard 1986: Mèzard, Marc - Parisi, Giorgio - Virasoro, Miguelangel, Spin-glass theory and beyond, Singapore, World Scientific Publishing, 1986.
Sherrington, Kirkpatrick 1975: Sherrington, David - Kirkpatrick, Scott, Solvable model of a spin-glass, "Physical review letters", 35, 1975, pp. 1792-1796.
Sourlas 1989: Sourlas, Nicolas, Spin-glass models as error-correcting codes, "Nature", 339, 1989, pp. 693-694.
Stauffer, Aharony 1994: Stauffer, Dietrich - Aharony, Amnon, Introduction to percolation theory, 2. ed., London, Taylor & Francis, 1994 (1. ed.: 1985).