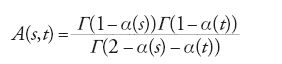La grande scienza. Teoria delle stringhe: una testimonianza
La grande scienza. Teoria delle stringhe: una testimonianza
Teoria delle stringhe: una testimonianza
La parola serendipità deriva dal racconto persiano dei tre principi di Serendippo che scoprivano casualmente, ma fortunosamente, cose che non stavano cercando. In campo scientifico essa identifica una categoria di scoperte inattese in cui si colloca senza dubbio quella che aprì le porte alla teoria delle stringhe alla fine degli anni Sessanta e all'inizio degli anni Settanta del secolo scorso. Nella prospettiva di una teoria unificata della gravità quantistica, la teoria delle stringhe, o della corda, è oggi considerata quella avente le migliori potenzialità.
Come per molte altre scoperte, è difficile definire esattamente dove la storia di tale teoria abbia avuto inizio. Le sue origini risiedono nella teoria della matrice S, che risale a Werner Heisenberg e, successivamente, a Geoffrey Chew e al suo gruppo di ricerca. Secondo l'impostazione della matrice S, gli unici concetti che possono essere definiti in maniera precisa in fisica sono le ampiezze di scattering per particelle stabili quali protone o elettrone. Un evento di scattering coinvolge sempre particelle originate a una distanza infinita dal centro di scattering in corrispondenza del quale reagiscono, producendo eventualmente nuove particelle, per poi allontanarsi all'infinito. Secondo la meccanica quantistica, la probabilità di un certo risultato finale è data in termini di un'ampiezza dipendente dalle energie e dagli impulsi delle particelle che si avvicinano e di quelle che si allontanano. L'insieme di tali ampiezze è detto matrice S o matrice di scattering.
La teoria quantistica dei campi cerca di costruire processi di scattering da eventi locali più dettagliati. Chew e i suoi colleghi ne astrassero varie caratteristiche matematiche della matrice S, tra cui le sue proprietà analitiche, in funzione dell'energia e dei momenti, oltre alla sua unitarietà e invarianza di Lorentz. I sostenitori della matrice S speravano che questi astratti vincoli matematici sarebbero stati in grado di determinare completamente non solo la matrice S ma anche i tipi di particelle che eventualmente avrebbero potuto subire lo scattering. Diversi studiosi non si trovavano d'accordo sul fatto che l'impostazione relativa alla matrice S si potesse applicare a tutta la fisica, inclusa l'elettrodinamica e la gravità, piuttosto che soltanto alla fisica degli adroni. In ogni caso, gran parte degli sforzi si concentrarono sulla descrizione degli adroni e delle loro interazioni forti.
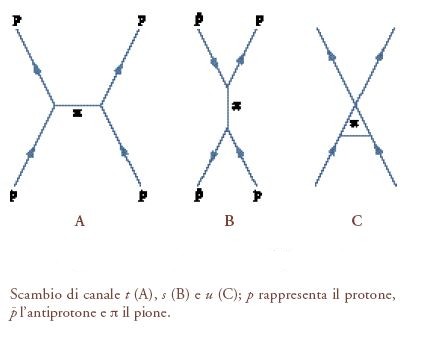
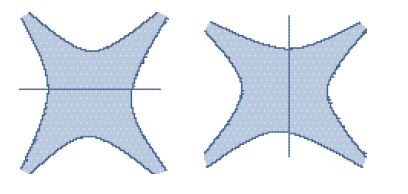
Una delle caratteristiche della teoria quantistica dei campi era rappresentata dal fatto che i processi di scattering potevano essere costruiti sulla base dei diagrammi di Feynman; i più semplici tra questi erano in grado di descrivere lo scambio di particelle. Un esempio di scambio di particelle è rappresentato da un mesone emesso da un protone e assorbito da un altro. Se il mesone è un pione, questo processo è detto scambio di pione. Esiste, tuttavia, un altro tipo di scambio che può avvenire se un protone urta un antiprotone. In questo caso il protone e l'antiprotone possono formare un pione 'virtuale', che successivamente ricrea una coppia protone-antiprotone. Il primo tipo di processo si chiama 'scambio di canale t' e il secondo 'scambio di canale s'. È possibile anche un terzo contributo, detto 'scambio di canale u'. I tre tipi di scambio sono illustrati nella fig. 1. Nel caso protone-antiprotone entrambi i tipi di scambio sono possibili: lo scambio di pioni tra protone e antiprotone, così come pure la generazione di un pione virtuale, seguito da una nuova creazione di un protone e di un antiprotone. La teoria quantistica dei campi, indica che le due ampiezze dovrebbero essere sommate come contributi distinti alla matrice S.
Dal momento che gli adroni non sono semplici particelle puntiformi, essi possono essere eccitati in modi simili a quelli delle molecole, degli atomi e dei nuclei, e assumere uno spin in modo tale da aumentare il loro momento angolare, oltre a dare vita a una serie di oscillazioni pulsanti. Questo di per sé costituì un importante suggerimento sia per la teoria dei quark sia per quella delle stringhe relativa agli adroni. Tuttavia, per quelli che lavoravano alla teoria della matrice S ciò significava che l'ampiezza di scattering non coinvolgeva soltanto lo scambio di oggetti semplici come il pione, ma anche tutti gli stati eccitati dei pioni a massa più alta. In effetti, sembrava (ed è ancora così) che la sequenza di stati eccitati, nota anche con il nome di 'risonanze', fosse infinita. Come un oscillatore armonico, un adrone sembra avere un numero infinito di stati eccitati di energia sempre più alta. Ogni risonanza dovrebbe essere aggiunta nel canale s, nel canale t oppure nel canale u, come un contributo all'ampiezza di scattering e in questo modo il risultato sarebbe una somma infinita. L'intera torre di stati eccitati potrebbe essere parametrizzata mediante la cosiddetta traiettoria di Regge. La traiettoria rappresentava una sequenza di stati eccitati di momento angolare, o spin, crescente, e di massa crescente. Non si parlava di scambio di stati di particelle individuali ma di scambio di intere traiettorie. L'idea più ovvia era che si dovessero aggiungere le ampiezze per tutti i possibili oggetti scambiati nei canali s, t e u.
Fu quindi una sorpresa quando tre giovani fisici di Berkeley, Louise A. Dolan, David Horn e Christof Schmidt, affermarono che i vari scambi nei diversi canali potevano essere ridondanti. Essi, quando cominciarono ad aggiungere le ampiezze per tutte le infinite eccitazioni nel canale s, osservarono che il risultato somigliava molto alla somma degli scambi nel canale t. Tale ridondanza fu chiamata dualità. Questo fu il primo dei molti tipi di dualità che i teorici delle stringhe continuano a scoprire anche più di trent'anni dopo la nascita della teoria.
Successivamente al lavoro di Dolan, Horn e Schmidt, Gabriele Veneziano, che allora si trovava al Weizmann Institute of Science in Israele, iniziò una ricerca matematica per trovare un'espressione esatta di un'ampiezza che avrebbe dovuto possedere la ridondanza di Dolan, Horn e Schmidt. Sorprendentemente, manipolando semplici funzioni gamma, egli conseguì in poco tempo l'obiettivo. La funzione risultante
è la famosa ampiezza di Veneziano (α è la traiettoria di Regge). Si trovò che l'ampiezza completa era costituita da una somma di tre termini di questo tipo ma, a differenza dei diagrammi convenzionali di Feynman, i singoli termini non corrispondevano ai tre canali s, t e u. Al contrario, ogni ampiezza di Veneziano era correlata a una coppia di canali. Pertanto ci sarebbe stato un termine di tipo (s,t), uno di tipo (s,u) e uno di tipo (t,u). Ampiezze di questo tipo descrivono i processi di scattering che coinvolgono un totale di quattro particelle; due particelle iniziali si urtano e il risultato è rappresentato da due particelle che si allontanano. A quel tempo il meccanismo di collisione era ignoto. In effetti, i difensori della teoria della matrice S talvolta assunsero la posizione estrema secondo cui la caratterizzazione del meccanismo era priva di senso. L'analiticità, l'unitarietà e l'invarianza di Lorentz era tutto quello che veniva richiesto.
Subito dopo l'articolo rivoluzionario di Veneziano, furono scoperte le ampiezze per processi più complicati che coinvolgevano numeri più elevati di particelle. Fu scoperta, per esempio, un'ampiezza che era in grado di descrivere cinque particelle tutte assieme e una collisione in cui due particelle iniziali producevano tre particelle finali. Di nuovo, i diversi possibili processi di scambio tra particelle erano ridondanti. L'ampiezza generale a n-particelle fu ben presto costruita da diversi gruppi di ricercatori e il risultato fu chiamato 'modello a risonanza duale'.
La scoperta della teoria delle stringhe
Quanto segue è un resoconto personale sull'origine della teoria delle stringhe, basato sulle mie esperienze dirette. Il mio primo contatto con l'importante formula di Veneziano risale alla fine del 1968, quando uno dei suoi colleghi del Weizmann Institute of Science fece una breve visita a New York, dove io ero un professore ordinario di ventinove anni. Hector Rubinstein, entusiasta del nuovo lavoro, passò la giornata a spiegarlo a Yakir Aharonov e a me; parlava così velocemente che non riuscivo a seguirlo ma, alla fine, scrisse il prodotto di funzioni gamma scoperto da Veneziano. La formula era talmente semplice che ebbi la sensazione che dietro di essa dovesse esservi un meccanismo semplice. Dalla formula di Veneziano era possibile desumere le masse delle particelle eccitate che sono scambiate nei canali s e t. Il quadrato della massa cresce, infatti, linearmente con il momento angolare. Le eccitazioni non sono tutte uniformemente distanziate in massa, ma piuttosto nel quadrato della massa. Questo fatto mi colpì. In passato avevo lavorato alla teoria quantistica dei campi in un sistema di riferimento il cui momento era portato a infinito. Oggi un riferimento di questo tipo viene definito struttura 'a cono di luce' ma a quel tempo si chiamava 'a momento infinito' (IMF, infinite momentum frame). Una caratteristica fondamentale del riferimento a momento infinito era rappresentata dal fatto che l'energia era sostituita dal quadrato della massa. Pertanto gli stati eccitati della formula di Veneziano erano uniformemente distanziati nell'energia dell'IMF. Inoltre la separazione lineare è associata con uno dei sistemi più semplici della meccanica quantistica, l'oscillatore armonico. Evidentemente gli adroni descritti dalla nuova formula erano costituiti da un qualche tipo di oscillatore ed erano equivalenti a particelle ai capi di una molla.
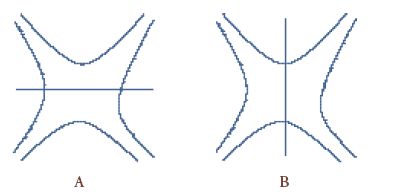
All'incirca nello stesso periodo, o forse poco tempo prima, Jonathan Rosner e Haim Harari, indipendentemente l'uno dell'altro, svilupparono un'interpretazione molto interessante della dualità di Dolan, Horn e Schmidt per il caso dello scattering dei mesoni. Questi studiosi disegnarono alcuni diagrammi che erano diversi da quelli soliti di Feynman. Essi immaginarono che ogni mesone potesse essere considerato come una coppia quark-antiquark. Il processo fondamentale di scattering coinvolgeva una coppia di questo tipo per ogni mesone entrante o uscente. Le linee dei quark potevano essere congiunte per formare un diagramma simile a quelli mostrati nella fig. 2. L'aspetto entusiasmante di questi diagrammi era costituito dal fatto che essi potevano essere tagliati in modi che rivelavano sia il contenuto di canale s sia quello di canale t.
L'opinione generale a quel tempo era che il successo della formula di Veneziano e delle sue generalizzazioni costituisse un'importante conferma del punto di vista della matrice S, confutando nel contempo la teoria quantistica dei campi e qualunque teoria microscopica che potesse costituire il fondamento del processo di scattering. Per quanto io ricordi, solamente un esiguo gruppo di persone assunse la posizione opposta, sostenendo cioè che l'estrema semplicità della teoria indicasse una rappresentazione molto elegante del processo di collisione; oltre a me soltanto Yoichiro Nambu, Holger Bech Nielsen e il suo relatore, Ziro Koba, cominciarono a pensare a una teoria dinamica che facesse da fondamento all'ampiezza di Veneziano e dalla quale fosse possibile derivare il modello a risonanza duale.
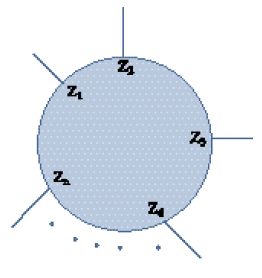
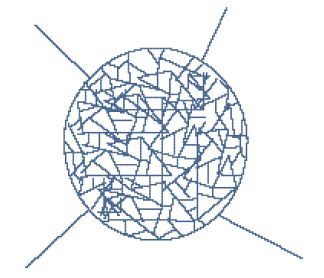
Koba e Nielsen realizzarono un lavoro molto accurato, nel quale derivavano una forma semplice e suggestiva per la funzione generale a n-punti (in cui le ampiezze coinvolgono un numero totale di n-particelle). La loro costruzione coinvolgeva il disegno di un disco di raggio unitario sul piano complesso (fig. 3). Le particelle entranti e uscenti erano rappresentate da punti sulla circonferenza delimitante e l'ampiezza era data da un integrale calcolato sulle loro posizioni su questo circolo. L'integrando aveva una forma analitica molto semplice. Il fatto che Koba e Nielsen abbiano pensato in termini di un disco, invece che su una circonferenza, suggerisce che essi avessero in mente un modello in cui l'interno del disco rappresentasse un qualche materiale che riempiva una superficie bidimensionale.
Conoscevo il lavoro di Koba e Nielsen ed esso mi fece pensare a una rappresentazione spaziotemporale bidimensionale che implicasse superfici bidimensionali nello spazio-tempo distese tra contorni disegnati da quark. Con Graham Frye disegnammo diverse figure simili alla fig. 4, in cui i diagrammi di quark di Harari e Rosner erano riempiti con qualcosa che chiamammo world sheet. Credo che fummo i primi nel 1969 a usare questo termine. Tutti gli articoli che scrivemmo in quel periodo in cui si trattava il concetto del world sheet furono respinti dal "Physical review".
Nonostante il mio interesse per la rappresentazione a world sheet, non fu questa l'occasione che mi spinse all'idea della stringa. La motivazione principale fu data dall'analogia con l'oscillatore armonico nella struttura a momento infinito. La somiglianza dello spettro delle risonanze con un oscillatore armonico mi convinse a costruire un modello semplice di coppia quark-antiquark, connessa da un potenziale a oscillatore armonico nel contesto dell'IMF. Successivamente passai a definire operatori di vertice per l'emissione e assorbimento di quanti da parte dei quark. Gli operatori di vertice rappresentavano semplicemente l'assorbimento del momento del quanto da parte del quark e avevano la forma, oggi familiare, exp (ikx). È importante notare che le ampiezze di scattering dei quanti da parte degli oscillatori erano integrali molto simili a quelli di Koba e Nielsen. Sebbene fossero simili, tuttavia, a essi mancavano tutte le importanti proprietà di dualità. Quando portai a compimento la pubblicazione per "Physical review", mi accorsi che l'ingrediente mancante era la stringa continua che connetteva i quark. Misi quindi in evidenza alla fine dell'articolo che si poteva costruire un modello di gran lunga migliore in cui i quark erano connessi mediante un continuo armonico simile a un elastico.
Ciò che mi condusse alla rappresentazione mediante una corda elastica non fu l'idea del world sheet o la rappresentazione di Koba e Nielsen. L'idea aveva a che fare, piuttosto, con una strana proprietà spaziotemporale delle ampiezze di Veneziano o più generalmente ampiezze che coinvolgevano traiettorie di Regge. In generale, dalle proprietà di sezioni d'urto differenziali per i processi di scattering è possibile dedurre la dimensione degli oggetti coinvolti negli urti. In effetti, è proprio questo il modo in cui Rutherford stabilì che il nucleo non è puntiforme, ed è anche il modo in cui Hofstadter determinò la dimensione dei nuclei facendo urtare su di essi degli elettroni. Se si supponeva che l'ampiezza di Veneziano rappresentasse dati reali per una collisione, era possibile dedurre le dimensioni delle particelle coinvolte nella collisione stessa. In questo modo però si giunse a un risultato paradossale: la dimensione teorica di un adrone dipendeva dal suo momento. Il raggio di un adrone, difatti, sembrava crescere come la radice quadrata dell'energia delle particelle coinvolte nella collisione. Passai molto tempo a pensare a questo fatto singolare, prima di accorgermi del punto fondamentale.
È oggi ben noto ai teorici delle stringhe che le oscillazioni di punto zero di un semplice oscillatore armonico gli conferiscono un raggio indipendente dall'energia. Ma un continuo armonico, come una stringa elastica, possiede un numero infinito di modi di oscillazione di frequenza non limitata. Al crescere dei modi, sono aggiunte frequenze sempre più alte e le oscillazioni di punto zero propagano la funzione d'onda su una regione di spazio crescente. Combinando questa circostanza con il fatto che una reazione a una data energia potrebbe essere sensibile solo a modi con frequenza inferiore rispetto all'energia stessa, si ottiene il risultato che il raggio apparente cresce con l'energia. Un rapido calcolo rivelò esattamente che il comportamento sarebbe stato corretto se i quark fossero stati connessi da una stringa elastica idealizzata invece che da una stringa singola. Sapevo senza alcun dubbio di essere sulla strada giusta e che il modello della risonanza duale era in realtà una teoria di stringhe elastiche. Ricordo distintamente che ero talmente esaltato dalla scoperta da non essere in grado di completare il calcolo delle ampiezze d'urto, ma inviai comunque al "Physical review" un articolo sul modello basato sull'oscillatore armonico con un commento sulle stringhe. In pochi giorni riuscii nuovamente a concentrarmi e a completare il calcolo per le stringhe.
Ero assolutamente convinto che avrei ottenuto l'ampiezza di Veneziano, e così fu. Scoprii anche, dato poco confortante, che lo stato fondamentale dell'adrone descritto da questo sistema era un tachione, un fatto che, credo, fosse sconosciuto. Quando il relativo articolo fu finalmente pronto, scelsi di mandarlo al prestigioso "Physical review letters" che si proclamava disponibile a pubblicare unicamente le comunicazioni più importanti e urgenti.
L'articolo fu respinto dal recensore con due motivazioni. Innanzi tutto esso non conteneva predizioni sperimentali. In secondo luogo erano note altre derivazioni che consentivano di giungere alla formula di Veneziano, in particolare una che derivava dalla teoria della matrice S. Mi opposi a questa bocciatura, ma senza successo. Alla fine l'editore, Samuel Goldschmidt, suggerì che il "Physical review", non avendo degli standard di qualità altrettanto elevati, forse sarebbe stato disponibile a pubblicare il lavoro, che comunque avrei dovuto riesaminare completamente. Il tutto richiese altri tre mesi, ma l'articolo fu finalmente accettato. Proprio in quel periodo, un'ulteriore delusione mi fu causata dall'aver saputo che il grande fisico Nambu aveva anche lui scoperto l'interpretazione a stringhe del modello della risonanza duale. Il suo articolo non era stato pubblicato in un giornale scientifico, ma negli atti di una conferenza e questa è la ragione per cui io non ebbi modo di leggerlo per diversi mesi. A questo punto Nielsen aveva anch'egli formulato il modello di risonanza duale in una forma che era equivalente alla teoria delle stringhe. Secondo il suo modello, il disco di Koba-Nielsen aveva precisamente il significato di un materiale continuo che poteva essere attraversato dal momento. Il momento fluiva dentro e fuori dalle particelle esterne. La teoria di Nielsen era identica a quella di Nambu e alla mia ed era espressa in termini di momento, anziché di posizione.
Le limitazioni della teoria delle stringhe per gli adroni
Poco dopo la scoperta della teoria delle stringhe, cominciai a rendermi conto che essa, nel modo in cui era formulata allora, non era una teoria plausibile degli adroni. Alcuni aspetti erano insoddisfacenti e anzitutto l'inaspettata circostanza per cui lo stato fondamentale era un tachione. Questo significa che il quadrato della sua massa è negativo. Da un lavoro precedente sui tachioni, pubblicato con Aharonov e Arthur Komar, sapevo che questo implicava l'instabilità del vuoto, una condizione che invalidava la teoria. La mia opinione personale era che il tachione poteva essere eliminato in qualche modo, e in seguito ciò si verificò nella teoria delle superstringhe. Inoltre lo spettro conteneva particelle vettoriali prive di massa simili a fotoni. Questa però non era una circostanza positiva poiché la teoria doveva descrivere gli adroni, fortemente interagenti, e non il fotone, caratterizzato da deboli interazioni. Ero anche dell'opinione che questa particella potesse essere rimossa, anche se ciò si rivelò essere molto più difficile dell'eliminazione del tachione. Ciononostante la mia preoccupazione più grande riguardava l'accoppiamento dei fotoni con gli adroni. I fotoni interagiscono con un adrone mediante la densità di carica elettrica e la corrente dell'adrone. Il problema riguardava le stesse oscillazioni di punto zero della stringa: esse facevano sembrare il suo raggio crescente con l'energia e avevano anche l'effetto di distribuire la carica elettrica su un raggio infinito. Questa circostanza era in completa contraddizione con gli esperimenti. Quando veniva sondata mediante fotoni, la carica elettrica di un adrone si spandeva solo su una piccola dimensione dell'ordine di 10−12 cm. Infatti non sembrava esserci alcun modo per ottenere una teoria con dualità di Dolen, Horn e Schmidt che non comportasse anche adroni dotati di raggio elettromagnetico infinito. Ci sono voluti trentadue anni per risolvere questo problema, ma adesso sembra che tutti gli ostacoli alla teoria delle stringhe degli adroni siano stati finalmente rimossi. In quel primo periodo cominciai a credere che il modello continuo a stringhe avesse soltanto un significato idealizzato. Sospettavo che un adrone fosse in realtà composto da partoni, così come sostenuto da Feynman e Bjorken, e che, per qualche motivo, i partoni fossero distribuiti su una stringa monodimensionale in modo tale che il limite continuo fosse solo un'idealizzazione matematica. In quel periodo iniziai una corrispondenza con Nielsen. Questi, che viveva a Copenaghen, venne poi a trovarmi a New York, dove collaborammo all'interpretazione a partoni delle stringhe. Infatti, anche Nielsen pensava che la teoria del continuo potesse essere solo un'approssimazione. La sua idea era che il world sheet fosse in realtà un network molto denso di propagatori e vertici di un qualche diagramma di Feynman di ordine molto alto che descrivesse partoni interagenti (fig. 5). Se il diagramma fosse stato planare, i partoni avrebbero formato stringhe. Insieme formulammo un principio d'azione per le stringhe che facemmo derivare dai diagrammi planari densi. Il principio d'azione è oggi noto con il nome di azione di Polyakov, ma apparve per la prima volta nell'articolo che scrissi insieme a Nielsen e al suo collega, Aage Kraemer. Allora non sapevamo perché i diagrammi principali di Feynman di una teoria dovessero essere planari. Dopo qualche anno Gerard't Hooft trovò che il cosiddetto limite a grande N della teoria di Yang-Mills aveva esattamente questa proprietà.
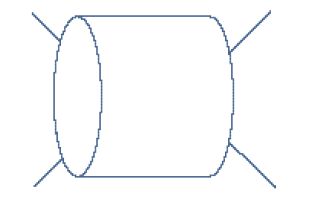
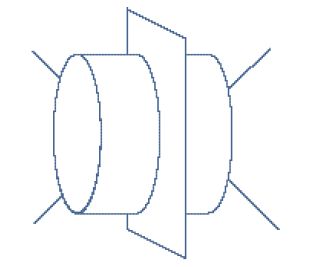
In quel periodo la matematica della teoria delle stringhe stava progredendo. Si comprese fin dall'inizio che l'ampiezza di Veneziano e il modello di risonanze duali erano soltanto i primi termini di una espansione simile all'espansione in diagrammi di Feynman. Il world sheet corrispondente all'ampiezza di Veneziano possedeva la topologia di un disco il cui contorno era il luogo cui si attaccavano le particelle esterne. Molti si accorsero che una teoria coerente avrebbe avuto bisogno di una somma su tutte le topologie, proprio come la teoria quantistica dei campi richiede una somma sui diagrammi di Feynman. Le topologie più complesse avrebbero giocato il ruolo dei diagrammi a loop. Il diagramma successivo al disco avrebbe coinvolto un world sheet dotato di una topologia di un anello con due contorni. Le particelle esterne potevano essere inserite in corrispondenza di uno qualunque dei contorni esterni. Il primo tentativo di calcolare un diagramma di anello fu portato a termine da Kikkawa, Salita e Virasoro, poco dopo la prima pubblicazione delle ampiezze del modello a risonanza duale. Insieme a Graham Frye tentai il primo calcolo di un diagramma ad anello non planare, ossia con vertici su entrambi i bordi. Il diagramma da noi calcolato è riportato nella fig. 6. Esso ci interessava in particolar modo perché, come Harari aveva notato in precedenza, coinvolgeva un nuovo canale che egli identificò con la cosiddetta 'traiettoria di Regge del Pomerone'. Tutti i canali precedenti implicavano stringhe dotate di porzioni terminali, in altre parole quelle che oggi sono chiamate stringhe aperte. Il nuovo canale, che si forma quando l'anello viene tagliato come nella fig. 7, coinvolge delle stringhe chiuse. Ciò suggerì per la prima volta che una teoria delle stringhe consistente comprendeva necessariamente delle stringhe chiuse.
Il calcolo eseguito in collaborazione con Frye portava a un comportamento inaccettabile, dal punto di vista matematico, per lo spettro delle stringhe chiuse. Invece di generare uno spettro discreto, come ci si sarebbe potuto aspettare, il calcolo dette uno spettro continuo. Non riuscimmo a comprendere la cosa, ma da lì a breve Claud Lovelace fornì una spiegazione piuttosto bizzarra. La formula che avevo derivato insieme a Frye dipendeva dal numero di dimensioni dello spazio-tempo. Non venne mai in mente, né a noi né a nessun altro, di prendere in considerazione non soltanto quattro dimensioni. Dopo tutto eravamo interessati al mondo reale degli ordinari barioni e mesoni. Lovelace notò che se la dimensionalità veniva sostituita dal veramente incredibile numero 26, le proprietà matematiche dell'ampiezza dell'anello erano esattamente quelle che ci si sarebbe aspettati se fosse esistita una nuova traiettoria di adroni descritti da stringhe chiuse. Questo rappresentava soltanto un'ulteriore evidenza circa il fatto che la teoria matematica delle stringhe era troppo idealizzata per descrivere in maniera appropriata gli adroni.
La teoria presentava ancora seri difetti anche qualora si fosse ignorata la necessità delle 26 dimensioni. Lo spettro a stringhe chiuse conteneva un nuovo tachione che avrebbe ulteriormente destabilizzato il vuoto. Inoltre apparvero delle nuove particelle prive di massa, una con spin zero e un'altra con spin 2. Adroni con spin del genere erano noti, ma erano piuttosto pesanti. Non c'era posto nella teoria per mesoni privi di massa, con l'unica possibile eccezione del pione e queste nuove particelle non assomigliavano assolutamente ai pioni. Un altro problema serio della teoria, per come era stata formulata allora, è che in essa in realtà non c'erano fermioni come i protoni, ma soltanto bosoni.
La teoria delle superstringhe avrebbe in seguito modificato questi aspetti. I tachioni sarebbero stati eliminati, la dimensionalità dello spazio-tempo sarebbe stata ridotta a 10, o addirittura a un numero più basso, grazie all'espediente di Kaluza-Klein di rendere le dimensioni compatte, e i fermioni sarebbero scaturiti come conseguenza necessaria della supersimmetria. Tuttavia, non furono risolti né il problema delle particelle prive di massa con spin 2 e spin 0 né il problema dei raggi infiniti di carica. Nel frattempo un'altra teoria degli adroni si stava rapidamente affermando. La nuova teoria era molto più convenzionale e si basava sui metodi, precedentemente scartati, della teoria quantistica dei campi. La cromodinamica quantistica (QCD, quantum chromodynamics) è una teoria strutturalmente simile all'elettrodinamica quantistica, in cui i quark sostituiscono gli elettroni e i gluoni sostituiscono i protoni. Il problema più grande che la QCD doveva affrontare era il confinamento apparente dei quark all'interno degli adroni. La teoria delle stringhe presentava anch'essa i suoi quark che erano sempre localizzati in corrispondenza degli estremi delle stringhe aperte. Nella teoria delle stringhe era assolutamente normale che i quark non potessero mai essere liberati dagli adroni poiché, ogni volta che una stringa si rompeva, si creava una coppia quark-antiquark in corrispondenza dei punti terminali che si erano formati. Un quark libero non poteva esistere più di quanto potesse esistere una stringa con una sola parte terminale. Nella QCD però i quark erano legati per effetto dello scambio di gluoni, nello stesso modo in cui l'atomo è legato dallo scambio fotonico. Le forze leganti in un atomo non sono abbastanza forti da poter evitare che un elettrone venga espulso e non si comprendeva perché lo scambio di gluoni dovesse essere diverso.
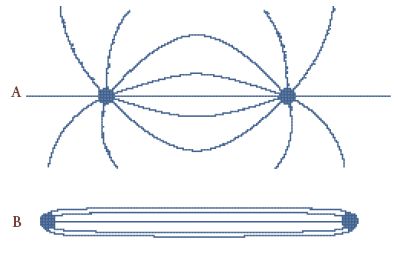
Tuttavia all'inizio degli anni Settanta i concetti della QCD e una teoria approssimata delle stringhe diedero origine alla teoria moderna del confinamento dei quark. Vennero proposte tre argomentazioni strettamente correlate che dimostrarono una connessione tra la teoria delle stringhe e la QCD. 'T Hooft e, indipendentemente, John Kogut e io, focalizzammo la nostra attenzione sulle proprietà non lineari del campo gluonico. La QCD è una teoria del tipo Yang-Mills e, come tale, le sue equazioni sono non lineari in modo più significativo della teoria di Maxwell del campo elettromagnetico. Basandoci sulla scoperta della libertà asintotica, 't Hooft, Kogut e io postulammo che le linee del flusso cromoelettrico si sarebbero legate in tubi simili ai tubi di flusso magnetico di Abrikosov nei superconduttori (fig. 8). Osservato a una certa distanza, il tubo di flusso si sarebbe comportato come una stringa e avrebbe legato alcuni quark in maniera permanente. Da un punto di vista microscopico, però, essi sarebbero stati composti da gluoni non lineari della QCD. Questo spiegherebbe il successo qualitativo della teoria delle stringhe nel descrivere le traiettorie di Regge di adroni eccitati, senza la necessità che la teoria delle stringhe idealizzata sia matematicamente esatta.
L'altro sviluppo che ebbe un effetto profondo fu la scoperta di 't Hooft del limite a grande N della teoria di Yang-Mills. 'T Hooft rilevò che nel limite di un numero molto grande di colori, la QCD era dominata da grafici di Feynman planari. Pertanto i diagrammi planari densi di Nielsen e la catena di partoni che io stesso avevo intuito divennero conseguenze naturali della QCD.
Teoria delle superstringhe
La teoria delle superstringhe fu inventata prima della scoperta della supersimmetria. Ebbe inizio con il tentativo da parte di Pierre Ramond di incorporare alcuni fermioni nella teoria delle stringhe. La motivazione era senza dubbio quella di includere i barioni nella teoria degli adroni. La teoria originale delle stringhe è solitamente indicata come teoria delle stringhe bosoniche poiché tutte le particelle nello spettro sono bosoni. Dal punto di vista matematico, la teoria è descritta da una stringa i cui gradi di libertà sono le coordinate spaziotemporali dei punti lungo la stringa. Le coordinate spaziotemporali sono variabili commutanti. Ramond argomentò che per descrivere la natura di spin semi-intero dei fermioni sarebbero stati necessari alcuni gradi di libertà addizionali, e pertanto aggiunse alcuni gradi anticommutanti lungo la stringa. Ramond stava studiando alcune stringhe aperte e trovò che lo stato fondamentale di questa nuova spinning string era veramente un fermione come il protone ma, sfortunatamente, di massa infinitamente piccola; nuovamente un successo e un fallimento nello stesso tempo. Seguendo il lavoro di Ramond, André Neveu e John Schwarz introdussero una leggera modifica del modello delle stringhe fermioniche di Ramond e scoprirono una teoria che fu chiamata modello del pione duale. La teoria conteneva fermioni simili al nucleone, oltre a bosoni che per svariati motivi si comportavano come pioni. Molti ebbero la sensazione che il modello del pione duale fosse infatti prossimo alla realtà delle cose. La teoria, in realtà, era ben lontana dall'essere perfetta e, oltre al fatto che il nucleone era privo di massa, il pione era un tachione. Queste insufficienze della teoria non sono mai state eliminate.
In seguito al lavoro di Neveu e di Schwarz, fu portato a termine un miglioramento tecnico che permise di sbarazzarsi di tutti i tachioni nel modello del pione duale. Questo lavoro fu opera di Ferdinando Gliozzi, Joel Scherk e David I. Olive, che si accorsero che interi settori della teoria potevano essere rimossi in maniera consistente. Tra le particelle che potevano essere eliminate c'erano i fastidiosi tachioni che rendevano il vuoto instabile. Assieme ai tachioni si sarebbe però eliminato anche il pione. Il risultato fu una teoria matematica dall'impressionante coerenza che adesso chiamiamo teoria delle superstringhe, ma che chiaramente presentava poche ovvie connessioni con lo spettro dell'adrone. A quel punto la maggior parte dei teorici delle particelle distolse la propria attenzione dalla teoria delle stringhe per avvicinarsi alla QCD. Ci sono voluti quasi 30 anni prima che i teorici tornassero alla teoria delle stringhe come struttura matematica per lo studio degli adroni in aggiunta alla QCD, ma durante tutto questo periodo si conosceva soltanto una vaga connessione tra il confinamento dei quark e il comportamento a stringhe della QCD.