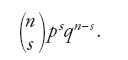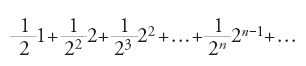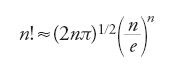La Rivoluzione scientifica: i domini della conoscenza. La nascita del calcolo delle probabilità
La Rivoluzione scientifica: i domini della conoscenza. La nascita del calcolo delle probabilita
La nascita del calcolo delle probabilità
Introduzione
Il carteggio del 1654 tra Blaise Pascal e Pierre de Fermat in merito ad alcuni problemi teorici sollevati dai giochi d'azzardo è generalmente posto all'origine del calcolo delle probabilità. In realtà, quest'ambito del pensiero matematico ha avuto una lunga evoluzione, legata sia al perfezionamento delle scienze matematiche, sotto l'aspetto dei contenuti e del simbolismo, sia, come si vedrà, ad alcuni mutamenti religiosi, economici e sociali.
Nell'Antichità le prime riflessioni sull'idea di probabilità si svilupparono intorno a questioni riguardanti la vita comune, i giochi d'azzardo, le scienze naturali, giuridiche e mediche. Erano timidi approcci a problemi legati all'incertezza o alla casualità, nei quali, però non emergevano né riferimenti precisi alla possibilità di misurare numericamente la probabilità, né tentativi di formularne una teoria, né indicazioni di regole e leggi che ne definissero il concetto. In alcuni casi le spiegazioni erano legate al divino; in altri, il termine 'probabile' era usato, come accade oggi nel linguaggio comune, senza tenere conto della sua portata teorica.
La riflessione sul concetto di 'caso' nell'Antichità coinvolgeva anche questioni legate alla considerazione del futuro e dei fatti 'misteriosi' (spesso attribuiti alla volontà divina), per affrontare le quali era stata necessaria una preliminare elaborazione dello statuto stesso del concetto di 'probabile' che ritardò l'avvio di un approccio formale al problema. In un ambito completamente diverso, come quello dei giochi d'azzardo, la possibilità di effettuare valutazioni a priori presentava indubbi vantaggi e la riflessione sulla probabilità avrebbe potuto giocare un ruolo fondamentale. Ciononostante, le prime riflessioni sui giochi d'azzardo cominciano ad apparire solo nel Tardo Medioevo, quando diversi studiosi si cimentarono nella risoluzione di problemi sul lancio dei dadi e sui giochi ripetuti. I primi, più semplici, erano strettamente connessi al calcolo combinatorio e solitamente riguardavano il motivo per cui alcune uscite erano più frequenti di altre. Quelli relativi ai giochi ripetuti, invece, possono essere sintetizzati nel problema noto come 'problema delle parti o dei punti' che consiste nel seguente quesito: due o più giocatori disputano una serie di partite di un gioco, e il vincitore è colui che per primo si assicura un numero prefissato n di partite; se, per qualche motivo, il gioco è interrotto prima che siano state giocate tutte le n partite, come deve essere divisa la posta in gioco? Il primo tentativo di soluzione viene proposto alla fine del XIV sec. dall'anonimo autore delle Regole del'alzibra, considerando il caso seguente: "Due uomini giuochano a scacchi e fanno [posta] d'un ducato a 3 giuochi, viene caso ch'el primo vince 2 giuochi al 2°, adomando non giocando più, quanto arà ad avere vinto lo primo al 2° del lo ducato" (Firenze, Biblioteca Nazionale, Magliabecchiano Cl. XI, 120, f. 29r). La soluzione proposta era puramente algebrica e conteneva un banale errore di calcolo. Luca Pacioli nella Summa de aritmetica (1494) propose una soluzione, ancora errata; Peverone nel 1558 e Pietro Cataneo (o de' Catani) di Siena nel 1559 si avvicinarono, invece, alla soluzione esatta.
L'ambiente in cui incominciava a prendere forma il calcolo delle probabilità era quello dei giochi d'azzardo: intorno al 1630, anche Galileo Galilei, nel breve scritto Sopra le scoperte dei dadi, si misurò con un quesito che gli era stato proposto da alcuni giocatori (Tav. I). Tuttavia si trattava di un ambiente poco favorevole a un rapido sviluppo della disciplina, sia perché poco 'scientifico' sia perché i giochi, per quanto largamente praticati, erano osteggiati da Stato e Chiesa.
Il periodo che precede il 1654, data del carteggio Fermat-Pascal, può essere considerato come la 'preistoria' del calcolo delle probabilità. Cosa contiene di così importante questa corrispondenza da indurci a considerarla come l'origine del calcolo delle probabilità?
L'approccio risolutivo dei tentativi precedenti era meramente empirico e consisteva nella risoluzione, per lo più algebrica, di casi particolari, senza un'effettiva considerazione formale dell'idea di 'caso'. è proprio dall'interesse per questo aspetto che trae origine l'affermazione del calcolo delle probabilità come disciplina autonoma e, successivamente, la possibilità di introdurre un formalismo matematico specifico. In questo senso, Pascal e Fermat non furono i soli protagonisti della nascita di questa teoria: intorno al 1660 un folto gruppo di studiosi, indipendentemente l'uno dall'altro, riuscì a cogliere gli aspetti principali del calcolo delle probabilità, avviandone lo sviluppo formale e le sue varie applicazioni.
La nascita di una nuova disciplina
Gli sviluppi del pensiero matematico avvenuti durante il XVII sec. vennero favoriti, oltre che dalle opere di singoli autori, anche dalla feconda circolazione delle nuove conoscenze: gruppi di scienziati si organizzarono in accademie e società; si realizzarono le prime stampe periodiche a scopi scientifici; si intensificarono gli incontri e gli scambi epistolari fra studiosi, stimolati sia da alcuni personaggi che assunsero il ruolo di intermediari e divulgatori ‒ il più noto di questi fu il frate dell'ordine dei minimi Marin Mersenne, attivo a Parigi ‒, sia dalla consuetudine di allegare alle lettere pregiati esemplari a stampa. In questa atmosfera di intensa vitalità intellettuale, anche le problematiche legate ai giochi d'azzardo divennero tema di studio e di discussione tra i principali matematici del tempo, tra i quali Pascal e Fermat.
Le origini
Il cavaliere de Méré diede un impulso importante all'applicazione della teoria della probabilità al gioco. Erudito, appassionato di quesiti sul gioco d'azzardo, propose alcune questioni di carattere probabilistico, fra cui il cosiddetto 'problema delle parti', che abbiamo appena descritto. Il quesito fu sottoposto a Pascal, già famoso per le sue scoperte sulla cicloide, mentre frequentava uno dei salotti culturali di Parigi, quello riunito intorno al duca di Roannez.
Pascal risolse il problema e, il 29 luglio 1654, scrisse a Fermat per avere una conferma dell'esattezza della propria soluzione: egli considerava due giocatori che puntano 32 monete ciascuno sulla vincita di tre partite di un certo gioco, inizialmente supponendo che il primo giocatore avesse vinto due partite e il secondo una. Allora, con la partita successiva, si delineavano due situazioni: "se il primo vince, gli toccano 64 [monete]; se egli perde gli toccano 32 [monete]. Dunque se essi vogliono arrischiare questa partita e separarsi senza giocarla, il primo deve dire: "Io sono sicuro di avere 32 monete, poiché la perdita stessa me le dà; ma per le altre 32, può essere che le avrò io, può essere che le avrete voi; il rischio è uguale; dividiamo dunque queste 32 monete a metà e datemi, oltre queste, le mie 32 che sono per me sicure". Egli avrà dunque 48 monete e l'altro 16" (Fermat, Oeuvres, II, p. 290). Altri possibili casi, in cui, per esempio, il primo giocatore aveva una o due partite vinte e il secondo nessuna, venivano risolti analogamente.
Iniziò, così, uno dei più famosi scambi epistolari della storia della matematica, in cui Pascal e Fermat confrontarono le loro soluzioni di vari problemi legati ai giochi d'azzardo e in cui, indipendentemente l'uno dall'altro, risolsero il 'problema delle parti'. Il caso risolto da Fermat riguardava due giocatori che, giocando più partite, si trovano nella situazione in cui mancano due partite al primo e tre al secondo per vincere la posta e si ricerca come questa debba essere spartita. Poiché il gioco si poteva risolvere in quattro partite, il metodo risolutivo consisteva nel calcolare tutti i possibili esiti delle quattro partite, valutare quante fossero favorevoli al primo giocatore e quante al secondo e dividere la posta seguendo questa proporzione.
Anche se nel carteggio tra Pascal e Fermat non emerge un metodo generale per risolvere il 'problema delle parti' e non si parla esplicitamente di probabilità, queste lettere contengono nuovi criteri di valutazione, e per questo possono essere considerate l'atto di nascita del calcolo delle probabilità.
Negli stessi anni della corrispondenza tra Pascal e Fermat, diversi studiosi si occuparono di questioni inerenti al calcolo delle probabilità e, nonostante rimanessero ancorati agli schemi offerti dallo studio dei giochi, iniziarono a sviluppare alcune 'regole' più generali.
Lo stesso Pascal, in un manoscritto del 1653, proponeva una soluzione generale del 'problema delle parti' mediante l'uso del 'triangolo aritmetico', già presente nei lavori di vari matematici tedeschi (Stiefel, Rudolff, Apiano) e italiani (Cardano, Tartaglia). Esso consiste in un triangolo di numeri costruito mediante semplici relazioni, oggi note come proprietà delle combinazioni di m oggetti di classe k, o di classe k−1, ecc. Il manoscritto, rinvenuto fra le carte di Pascal dopo la sua morte, fu pubblicato nel 1665 col titolo Traité du triangle arithmétique; la sua importanza consisteva anche nel fatto che, con la soluzione generale del 'problema delle parti', per la prima volta veniva chiarita la relazione esistente tra il triangolo aritmetico e i coefficienti binomiali.
Il 1655 vede l'ingresso nella storia del calcolo delle probabilità del matematico olandese Christiaan Huygens. Durante un viaggio a Parigi, dove conobbe Claude Mylon e Gilles Personne de Roberval, egli venne a conoscenza dei problemi relativi ai giochi d'azzardo su cui si erano cimentati Pascal e Fermat. Tornato in Olanda, Huygens cominciò subito a lavorare sulle stesse questioni e, nel 1656, inviò un manoscritto a Parigi, pubblicato nel 1657 col titolo Tractatus de ratiociniis in ludo aleae. Si tratta della traduzione latina, impostata da Huygens e realizzata dal matematico Frans van Schooten, dell'originale olandese, che fu pubblicato solo nel 1660 (Tav. II).
Con l'impostazione formale tipica degli scritti di Huygens, il trattato presentava la soluzione di molti quesiti legati ai giochi casuali, tra cui il 'problema delle parti', quello della 'rovina dei giocatori' e altri, relativi al lancio dei dadi.
Il caso più semplice del problema della 'rovina dei giocatori' è illustrato dal seguente quesito: "due giocatori A e B possiedono rispettivamente m e n gettoni e le probabilità di vincere, a ogni colpo, stanno tra loro come a sta a b; chi perde dà al vincitore un gettone e la partita è vinta quando un giocatore giunge a possedere m+n gettoni; determinare la probabilità, per ciascun giocatore, di vincere" (Bottazzini 1992, p. 370).
Nella parte finale Huygens riportava alcuni problemi proposti da Pascal e Fermat e da lui riformulati, che costituirono per più di mezzo secolo le questioni classiche nella teoria delle probabilità. Abraham de Moivre, Jakob I Bernoulli, Nicolaas Struyck, Pierre Rémond de Montmort e John Arbuthnot pubblicarono soluzioni di alcuni di questi problemi sui quali si cimentarono, tra gli altri, anche Jan Hudde, Spinoza e Leibniz.
L'importanza del trattato di Huygens era dovuta non solo al fatto di costituire il primo lavoro interamente dedicato al calcolo delle probabilità, ma anche all'introduzione della nozione di 'speranza matematica' (expectatio geometrica): "in un gioco d'azzardo, l'expectatio di un giocatore di ottenere qualcosa è quella quantità tale che, se il giocatore la possedesse, allora di nuovo egli potrebbe pervenire alla stessa expectatio con un gioco equo, cioè con un gioco che non miri a danneggiare nessuno [...]. Proposizione I. Se con uguale facilità posso ottenere a oppure b, allora la mia expectatio è (a+b)/2 […]" (ed. Dupont, pp. 36-42).
Huygens cercò inoltre di giustificare rigorosamente un metodo per determinare il prezzo equo di un gioco, ma si trovò a dover affrontare molte difficoltà di carattere sia concettuale sia linguistico.
Fin dall'inizio emerge infatti l'aspetto 'duale' dell'idea di probabilità: da un lato essa riguardava l'indicazione di regole all'interno di processi casuali, mentre dall'altro rivelava una natura epistemica, in relazione alla valutazione dei gradi ragionevoli di credenza in proposizioni prive di contenuto statistico. Così, da un lato tendevano a svilupparsi gli studi su nozioni e teoremi di probabilità in connessione con le prime applicazioni nel campo della fisica, dell'astronomia e della statistica, e in relazione anche a settori come la demografia o le scienze attuariali; dall'altro, fervevano le discussioni tra sostenitori di dottrine diverse, come i probabilisti e i giansenisti, in relazione all'aspetto epistemico dell'idea di probabilità.
Fra i matematici che si occuparono del primo problema alla fine del XVII sec. troviamo Jan Hudde, Jan de Witt, che pubblicò nel 1671 un trattato sulle rendite vitalizie (Waerdye van Lif-renten naer proportie van Los-senten) e che nella corrispondenza con Huygens si occupò dei risultati ottenuti mediante l'uso delle tavole della mortalità e delle rendite vitalizie, e John Graunt, che rese pubblici i risultati dei suoi studi di demografia nelle Natural and political observations del 1662. In relazione all'aspetto epistemico, sono importanti i capitoli finali della Logique, ou l'art de penser di Antoine Arnauld (1612-1694) e Pierre Nicole (1625-1695), attivi, come Pascal, a Port Royal. Tuttavia, non vi era una netta separazione tra questi due aspetti dell'applicazione del calcolo delle probabilità: lo stesso Pascal per dimostrare che era 'conveniente' credere nell'esistenza di Dio, utilizzò un ragionamento probabilistico in ambiti che, di per sé, coinvolgevano questioni di fede e di comportamento e non l'idea di casualità.
Poiché il calcolo delle probabilità ha avuto origine dallo studio dei giochi casuali, dove l'enumerazione dei casi possibili e dei casi favorevoli solitamente utilizzava il calcolo combinatorio, quest'ultimo si sviluppò, in un primo tempo, simultaneamente al calcolo delle probabilità. Nella seconda metà del Seicento, infatti, diversi lavori sono dedicati all'argomento, come la Dissertatio de arte combinatoria di Leibniz (la tesi di laurea presentata nel 1666 e ristampata, a sua insaputa, nel 1690) e un'operetta di John Wallis, pubblicata nel 1685, Discourse of combinations, alternations, and aliquot parts, in cui l'autore calcolava i numeri delle combinazioni e delle permutazioni che si possono ottenere con un certo numero di elementi. Questo legame sarà ancora più evidente negli anni successivi, in virtù della costante presenza nei testi sul calcolo delle probabilità di una parte dedicata esclusivamente al calcolo combinatorio.
I primi sviluppi
L'interesse per il calcolo delle probabilità si diffuse rapidamente, sia per motivi di carattere teorico, legati allo studio dei giochi, sia per ragioni di carattere applicativo.
Il Settecento fu, per questo nuovo tipo di calcolo, un secolo ricco di pubblicazioni, di scoperte e di ampliamenti a cui si accompagnarono varie discussioni sulla possibilità, o meno, di considerarlo allo stesso livello delle altre discipline della matematica.
Nonostante questo fermento, e malgrado vari tentativi di sistemazione e la dimostrazione di alcuni teoremi fondamentali, come il teorema di Bernoulli (se p è la probabilità costante di un evento in una prova e se, su n prove eseguite, m risultano favorevoli all'evento, la probabilità che risulti |(m/n)−p|⟨ε tende a 1 quando n tende all'infinito, comunque sia prefissato ε>0), mancava ancora una definizione chiara dei concetti fondamentali. Era noto che per calcolare la probabilità di un evento si dovesse dividere il numero dei casi favorevoli per il numero dei casi possibili; ma, come abbiamo già accennato, i problemi nascevano quando si doveva attribuire un significato a tale rapporto, o spiegare cosa si intendesse effettivamente per 'casi favorevoli' e 'casi possibili'. Si dovrà attendere l'inizio dell'Ottocento per trovare una prima sistemazione organica degli argomenti, mediante l'enunciazione di principî generali e la definizione classica del concetto di probabilità, proposta da Laplace.
Gli studi relativi al calcolo delle probabilità compiuti tra la fine del Seicento e l'inizio del Settecento si articolano in una serie di pubblicazioni ancora incentrate principalmente sui giochi, ma con impostazioni e contenuti più elaborati: tra le più note ricordiamo l'Ars conjectandi di Jakob I Bernoulli, l'Essai d'analyse sur les jeux de hasard di Pierre Rémond de Montmort, il De mensura sortis, seu de probabilitate eventuum in ludis a casu fortuito pendentibus e la Doctrine of chances di Abraham de Moivre.
L'opera di Jakob I Bernoulli, elaborata prima del 1705 ma pubblicata solo nel 1713 dal nipote Nikolaus I Bernoulli, riproponeva, nella prima parte, il trattato di Huygens completato da alcune Annotationes, utili per chiarire proposizioni, dimostrare teoremi o risolvere alcuni degli esercizi proposti dallo stesso Huygens. Bernoulli commenta così la prima proposizione di Huygens: "La parola expectatio, non è qui intesa nel suo senso ordinario […]; qui dovremmo intendere questa parola come la speranza di ottenere il meglio, diminuita della paura di ottenere il peggio. Così il valore della nostra speranza significa sempre qualcosa a metà tra il meglio che possiamo sperare e il peggio che possiamo temere" (ed. Dupont, p. 50). La seconda parte dell'opera era dedicata al calcolo combinatorio. Essa forniva un'esposizione chiara e completa dei risultati fino ad allora raggiunti e la discussione di alcune nuove formule utili nell'applicazione del calcolo delle probabilità, e fu utilizzata come libro di testo per la teoria delle combinazioni durante tutto il XVIII secolo. L'autore quindi proponeva, nella terza parte dell'opera, 24 problemi legati ai giochi insieme alle loro dettagliate soluzioni.
Tra i molteplici risultati ottenuti da Bernoulli, ricordiamo la dimostrazione completa della formula del binomio per potenze intere positive (il primo a proporre la formula nella sua forma generale per qualsiasi esponente razionale, ma senza fornirne la dimostrazione, fu Isaac Newton) e la considerazione dei cosiddetti 'numeri di Bernoulli'. Inoltre, il testo di Bernoulli contiene la soluzione di alcuni casi del cosiddetto 'problema delle prove ripetute', corrispondente alla seguente formulazione: se p è la probabilità costante di un evento e q quella dell'evento contrario, qual è la probabilità che in n prove l'evento si verifichi esattamente s volte? Questo problema in termini moderni ha come risposta la quantità:
Ma il risultato forse più celebre dell'Ars conjectandi è il cosiddetto 'teorema d'oro', cioè la legge dei grandi numeri nella sua forma più semplice, che Bernoulli enunciò all'inizio della quarta parte (e che fu anche argomento della sua corrispondenza con Leibniz) nel modo seguente:
chiameremo fecondi o fertili quei casi nei quali può capitare un qualunque evento, e sterili quei casi nei quali lo stesso evento non può capitare; e chiamerò prove feconde o fertili quelle alle quali si osserva che tocca qualcuno dei casi sterili. Pertanto, il numero dei casi fertili sia in rapporto, preciso o approssimato, con il numero dei casi sterili come r/s, e sia in rapporto con il numero di tutti i casi come r/(r+s), cioè r/t, rapporto evidentemente racchiuso fra i due limiti (r+1)/t e (r−1)/t. Si deve dimostrare che, dopo un certo numero di prove (poniamo c), accade più frequentemente che il numero dei casi fertili, confrontato con il numero di tutti i casi osservati, ha un rapporto né maggiore di (r+1)/t, né minore di (r−1)/t. (p. 236)
Sempre nella quarta parte Bernoulli affrontava anche alcune questioni filosofiche relative alla probabilità, affermando, per esempio, che "la probabilità è un grado di certezza e differisce dalla certezza assoluta come la parte dal tutto". Calcolare la probabilità è un'arte: "l'arte di congetturare è definita qui come l'arte di misurare le probabilità delle cose", per poter scegliere sempre il tragitto migliore. Quest'ultima sezione doveva anche contenere delle applicazioni del calcolo delle probabilità in civilibus, moralibus et economicis, ma la morte improvvisa dell'autore ne impedì il compimento.
Considerata l'importanza dei contributi di Bernoulli, alcuni autori sono arrivati a sostenere che la storia della nascita del calcolo delle probabilità si possa concludere con l'Ars conjectandi; tuttavia, in questo contesto, risultano rilevanti anche i contributi di Montmort e di de Moivre. Il primo pubblicò nel 1708 l'Essai d'analyse sur les jeux de hasard, seguito da una seconda edizione pubblicata nel 1713, arricchita del carteggio tenuto dall'autore con Nikolaus I Bernoulli. L'opera iniziava con una sezione sull'analisi combinatoria e le sue applicazioni al calcolo delle probabilità, e proseguiva poi con l'analisi di una grande varietà di giochi come il tric-trac, il faraone, il lanzichenecco e molti altri. Nella seconda edizione, all'interno del carteggio tenuto con Nikolaus I Bernoulli, troviamo un problema, proposto all'autore dallo stesso Nikolaus, che in seguito acquistò una certa importanza: due giocatori A e B giocano con una moneta, continuando a lanciare fino a che non compare testa. Se compare al primo lancio, B paga 1 corona ad A, se testa compare per la prima volta al secondo lancio, B paga 2 corone ad A, se compare per la prima volta al terzo lancio B paga 4 corone, se compare per la prima volta all'n-esimo lancio B paga 2n−1 corone. Quale somma A dovrebbe pagare a B, prima del gioco, perché B accetti di giocare?
Nella soluzione di questo problema nasceva un paradosso, perché calcolando la speranza matematica di A, la somma che A avrebbe dovuto pagare risultava infinita, ovvero:
Daniel Bernoulli (1700-1782) pubblicò un primo tentativo di soluzione di questo paradosso durante la sua permanenza a San Pietroburgo, e per questo il problema è oggi noto come 'paradosso di Pietroburgo'.
I contributi di Abraham de Moivre sono contenuti principalmente nel De mensura sortis, seu de probabilitate eventuum in ludis a casu fortuito pendentibus del 1711 e nella Doctrine of chances del 1718, seguita da altre due edizioni del 1738 e 1756. In questi lavori de Moivre risolse numerosi problemi sia legati allo studio dei giochi sia relativi a questioni di matematica attuariale e alle rendite vitalizie. La sua impostazione era fortemente algebrica e su questa strada cercò di sviluppare procedimenti e notazioni generali per il calcolo delle probabilità. Risolse, tra l'altro, il 'problema delle parti' nel caso nuovo di giocatori con abilità diverse; presentò la soluzione di alcuni casi del 'problema delle prove ripetute' e di un caso particolare del 'problema della rovina dei giocatori', generalizzandone la soluzione; studiò casi complessi del 'problema delle concordanze' e varie questioni relative al 'problema della durata del gioco'. Il 'problema delle concordanze' consiste nel determinare la probabilità che, estraendo successivamente da un'urna n palle numerate, si estragga, almeno una volta, una palla che porta il numero uguale al numero d'ordine dell'estrazione (cioè si abbia 'concordanza'). Il 'problema della durata del gioco' si pone, invece, in questi termini: all'inizio del gioco A possiede a monete e ha p probabilità di vincere, B possiede b monete e ha q=1−p probabilità di vittoria. Colui che perde a ogni gioco dà una moneta al vincitore. Qual è la probabilità che A possa perdere tutto il suo capitale, prima di riuscire a vincere tutte le monete di B?
De Moivre ottenne, indipendentemente da James Stirling (1692-1770), la famosa approssimazione nota oggi come 'formula di de Moivre-Stirling':
e apportò notevoli contributi al teorema di Bernoulli, che espose in un lavoro del 1730, i Miscellanea analitica; questi risultati furono integrati all'inizio dell'Ottocento da Laplace, che giunse a enunciare anche il secondo teorema fondamentale del limite, noto oggi come 'teorema di de Moivre-Laplace'.
Bibliografia
Bottazzini 1992: Bottazzini, Umberto - Freguglia, Paolo - Toti Rigatelli, Laura, Fonti per la storia della matematica, Firenze, Sansoni, 1992.
Boyer 1968: Boyer, Carl B., A history of mathematics, New York, Wiley, 1968 (trad. it.: Storia della matematica, a cura di A. Carugo, Milano, Mondatori, 1980).
Costantini 1970: Costantini, Domenico, Fondamenti del calcolo delle probabilità, Milano, Feltrinelli, 1970.
‒ 1982: Costantini, Domenico - Geymonat, Ludovico, Filosofia della probabilità, Milano, Feltrinelli, 1982.
Garibaldi 1982: Garibaldi, Antonio C., Sulla preistoria del calcolo delle probabilità, in: La storia delle matematiche in Italia, a cura di Oscar Montaldo e Lucia Grugnetti, Cagliari, Università-Istituti di Matematica delle Facoltà di Scienze e Ingegneria, 1982, pp. 377-384.
Geymonat 1962: Geymonat, Ludovico, Storia della matematica, in: Storia delle scienze, a cura di Nicola Abbagnano, Torino, UTET, 1962, 4 v.
‒ 1975: Geymonat, Ludovico, Storia del pensiero filosofico e scientifico, Milano, Garzanti, 1975, 9 v.; v. III: Il Settecento, 1975; v. IV: L'Ottocento, 1975.
Hacking 1975: Hacking, Ian, The emergence of probability. A philosophical study of early ideas about probability, induction and statistical inference, London, Cambridge University Press, 1975 (trad. it.: L'emergenza della probabilità. Ricerca filosofica sulle origini delle idee di probabilità, induzione e inferenza statistica, Milano, Il Saggiatore, 1987).
Loria 1929-33: Loria, Gino, Storia delle matematiche. Dall'alba della civiltà al secolo XIX, Torino, Sten, 1929-1933, 3 v. (2. ed.: Milano, Hoepli, 1950; rist. anast.: Milano, Cisalpino-La Goliardica, 1982).
Maistrov 1967: Maistrov, Leonid E., Teoriià veroiàtnostei, istoricheskii ocherk, Moskvà, Izdatel'stvo Nauka, 1967 (trad. ingl.: Probability theory. A historical sketch, transl. and edited by Samuel Kotz, New York, Academic Press, 1974).
Pearson 1970: Studies in the history of statistics and probability, selected and edited by Egon Sharpe Pearson, Maurice Kendall, London, Griffin, 1970.
Sheynin 1974: Sheynin, Oskar B., On the prehistory of the theory of probability, "Archive for history of exact sciences", 12, 1974, pp. 97-141.
‒ 1977: Sheynin, Oskar B., Early history of the theory of probability, "Archive for history of exact sciences", 17, 1977, pp. 201-219.
Todhunter 1865: Todhunter, Isaac, A history of the mathematical theory of probability. From the time of Pascal to that of Laplace, Cambridge, Macmillan, 1865 (rist.: New York, Chelsea, 1949; Bronx (N.Y.), Chelsea, 1965).