La Rivoluzione scientifica: i domini della conoscenza. La sintesi newtoniana
La Rivoluzione scientifica: i domini della conoscenza. La sintesi newtoniana
La sintesi newtoniana
Le opere maggiori di Newton
Isaac Newton rese pubbliche due sole opere, destinate a grande fama: i Philosophiae naturalis principia mathematica (1687) e l'Opticks (1704). La teoria della luce e dei colori, trattata in quest'ultima opera, era già nota nei suoi punti salienti dal febbraio del 1672, quando fu stampata in una breve memoria nelle "Philosophical Transactions". Niente, invece, aveva lasciato presagire la prima, il cui contenuto, il 28 aprile 1686, è incisivamente descritto in questo modo: "Il Dr. Vincent ha presentato alla [Royal] Society un trattato manoscritto […] di Isaac Newton, in cui egli fornisce una dimostrazione matematica dell'ipotesi copernicana come proposta da Kepler, e descrive tutti i fenomeni dei moti celesti con l'unica supposizione di una gravitazione verso il centro del Sole decrescente reciprocamente come i quadrati delle distanze da esso" (Cohen 1971, p. 130).
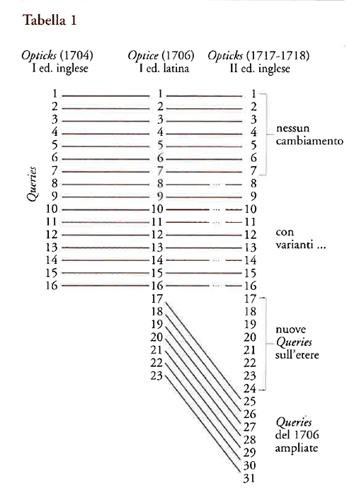
Le due opere si presentarono ai lettori in una successione cronologica non corrispondente a quella della loro effettiva elaborazione, ed ebbero fortuna diversa, pur concorrendo entrambe a costituire una parte rilevante della fisica classica. I Principia, vivente Newton, furono riediti nel 1713 e nel 1726, con revisioni e aggiunte, tra cui lo Scholium generale e le Regulae philosophandi. Anche l'Opticks ebbe due successive edizioni, nel 1717 e nel 1721, con un numero crescente di Queries. Diversamente dai Principia, che Newton non volle mai far tradurre, nel corso della sua vita l'Opticks ebbe anche due edizioni latine (1706, 1709) e una francese (1720), che ne favorirono la circolazione nel Continente.
Le opere edite di Newton esercitarono un ruolo egemonico nel Settecento grazie a una numerosa schiera di interpreti ‒ tra i quali Henry Pemberton, Colin Maclaurin, Francesco Algarotti e Voltaire ‒ che le divulgarono. Il contributo di Newton alla nuova scienza fu a poco a poco isolato da quello dei suoi illustri predecessori ‒ Niccolò Copernico, Galileo Galilei, Johannes Kepler, René Descartes, Robert Boyle, Robert Hooke e Christiaan Huygens ‒ e presentato spesso come una rivoluzione che aveva fornito alla scienza la forma che avrebbe dovuto conservare.
Gli storici della scienza si sono trovati così di fronte a un difficile compito. Essi hanno dovuto, da un lato, riannodare i fili interrotti con la tradizione della filosofia naturale cinque-seicentesca; dall'altro, ripristinare il senso originario della fisica newtoniana, liberandola dalle interpretazioni successive, oltre che dei divulgatori, anche dei più intelligenti continuatori, quali Joseph-Louis Lagrange e Pierre-Simon de Laplace.
Queste analisi storiche hanno avuto, e continuano ad avere, il loro centro nella grande quantità di manoscritti che hanno preparato le opere maggiori di Newton. Inoltre, la vastità delle sue attività intellettuali quasi in ogni campo del sapere seicentesco (matematica, alchimia, interpretazione della Scrittura, profezie, cronologia e metafisica) ha posto, e continua a porre, il problema dell'effettiva incidenza di questo sapere sulla formazione della scienza newtoniana. Non è qui il caso, tuttavia, di discutere fino a che punto il recupero di queste ampie informazioni storiche abbia migliorato la nostra conoscenza dei risultati scientifici ottenuti da Newton.
Il metodo
In una lettera a Henry Oldenburg del 21 settembre 1672 troviamo la prima dichiarazione esplicita di Newton sul metodo in seguito adottato nelle opere edite: "Per adempiere il vostro invito […] compilai una serie di tali esperimenti con il proposito di ridurre la teoria dei colori a proposizioni e di provare ogni proposizione con uno o più di questi esperimenti mediante l'aiuto di nozioni comuni redatte in forma di definizioni e assiomi ad imitazione del metodo con il quale i matematici sono soliti provare le loro dottrine" (The correspondence, I, p. 237).
Newton intende sottoporre le proposizioni della teoria a un doppio processo di verifica: una prova sperimentale e una prova deduttiva. Il metodo dei matematici si ispira evidentemente a quello di Euclide. Tuttavia Newton non dà seguito a quanto promesso, adducendo il pretesto di avere altri impegni. Dal 1672 al 1684, infatti, si dedica a un intenso studio delle profezie bibliche e a ricerche alchemiche.
In un inedito Trattato sull'Apocalisse, risalente a questo periodo, Newton propone un metodo molto simile a quello descritto nella lettera a Oldenburg: "Considerando […] la grande importanza di queste scritture e il pericolo di errare nella loro interpretazione, è nostro interesse procedere con ogni circospezione. E per questo scopo farò uso di questo Metodo. Per prima cosa porrò certe Regole generali di Interpretazione, la cui considerazione può preparare il giudizio del Lettore e renderlo in grado di sapere quando una interpretazione è genuina e qual è la migliore di due interpretazioni" (p. 19).
Il metodo applicato nel Trattato sull'Apocalisse rivela l'intento esplicito di evitare l'incertezza: "Con questi mezzi il linguaggio dei profeti diventerà certo e la libertà di forzarlo a immaginazioni private sarà esclusa. Chiamo definizioni i punti a cui riduco queste parole" (ibidem). Stabilite le regole e le definizioni, occorre provare con il loro aiuto le proposizioni del testo sacro: "Premesse queste cose, paragono le parti dell'Apocalisse l'una con l'altra e le riassumo in ordine […]. E faccio questo stendendo la sostanza della profezia in proposizioni, e aggiungendo le ragioni della verità di ogni proposizione" (ibidem).
Se esaminiamo le proposizioni del Trattato sull'Apocalisse è evidente che esse non sono provate in modo esclusivamente deduttivo, a partire dalle definizioni, ma anche aggiungendo liste di argomenti particolari, conformi alle regole. Il Trattato sull'Apocalisse è pertanto la prima realizzazione compiuta di un metodo che consente di provare le proposizioni per mezzo di particolari sottoposti a regole e con l'aiuto di definizioni.
Nel manoscritto De gravitatione et aequipondio fluidorum, di datazione incerta, Newton ripropone qualcosa di analogo:
Conviene trattare la scienza della gravità e dell'equilibrio dei fluidi, e dei solidi nei fluidi, con due metodi. Per quanto attiene alle scienze matematiche, è giusto che io astragga quanto più è possibile dalla contemplazione fisica. Perciò ho deciso di dimostrare con rigore more geometrarum le sue singole proposizioni da principî astratti e abbastanza noti a chi legge […]. Quindi poiché questa dottrina si ritiene essere in qualche modo affine alla filosofia naturale, in quanto è volta ad analizzare moltissimi suoi fenomeni […] non eviterò di illustrare copiosamente le proposizioni anche con esperimenti. (Unpublished scientific papers of Isaac Newton, p. 90)
Il primo metodo si avvale di lemmi, proposizioni e corollari, il secondo di scoli, più adatti alla libera discussione filosofica.
Il metodo abbozzato da Newton in questi primi progetti di lavoro è una sintesi di riflessioni e procedure ampiamente presenti nella cultura del suo tempo. Le opere più influenti, per quanto riguarda gli intenti dichiarati, furono quelle di Descartes; per le procedure, quelle di Galilei. Anche la tradizione classica della geometria e la logica aristotelica, mediata da Robert Sanderson (1587-1663) ‒ la fonte principale delle regole del Trattato sull'Apocalisse ‒ influirono sulla messa a punto del metodo newtoniano. Non bisogna tuttavia confondere il metodo assiomatico-deduttivo, abbinato alle prove sperimentali, con lo sviluppo delle tecniche matematiche nell'analisi della Natura, sviluppo che nei Principia conosce progressi decisivi. Il primo era un metodo di dottrina, un modo per ordinare e sistemare il contenuto di una disciplina, cui Newton aggiunse le fonti sperimentali; il secondo, un potente metodo d'invenzione, suscettibile di indefinito perfezionamento. Di fatto, tuttavia, Newton subordinò il secondo metodo al primo.
L'ottica
Le prime annotazioni di Newton sulla luce e sui colori, a commento delle esperienze effettuate con il prisma (v. cap. XL), si trovano nel taccuino del Trinity College di Cambridge e furono stese durante gli anni 1664-1665. Esse rivelano una curiosa interazione tra le ipotesi meccanicistiche cartesiane e gli esperimenti tratti da Boyle. Il nucleo fondamentale della nuova teoria è raggiunto subito: il prisma separa per rifrazione i raggi colorati, dotati di differenti velocità; il bianco, il grigio e il nero non sono che una mescolanza di raggi colorati. A conferma dell'ipotesi della diversa rifrangibilità dei raggi è riportata l'esperienza fatta con un filo colorato, per metà blu e per metà rosso, che osservato attraverso un prisma contro uno sfondo scuro appare spezzato. Questo esperimento, lievemente modificato, costituirà la proposizione 1, teorema I, dell'edizione dell'Opticks del 1704. Johann Wolfgang von Goethe nella Farbenlehre (1810) inizierà la sua critica dell'ottica newtoniana proprio rifiutando tale esperimento perché riesce soltanto su fondo scuro.
Il primo nucleo teorico, tuttavia, fu successivamente sviluppato nelle Lectiones opticae (1670-1671 ca.) in cui Newton tentò di sviluppare matematicamente i risultati dei suoi esperimenti. Questo tentativo si inseriva in un'aperta polemica contro l'ottica geometrica: "I cultori di geometria fino ad ora hanno vaneggiato su una certa proprietà della luce che si riferisce alle rifrazioni, mentre suppongono tacitamente per le loro dimostrazioni una certa ipotesi fisica non bene stabilita" (Cambridge, University Library, Add. 4002, f. 1).
L'ipotesi fisica in questione era l'omogeneità della luce bianca e la sua diversa rifrangibilità, la nuova proprietà scoperta da Newton.
Questo giudizio è in accordo con le dichiarazioni metodologiche contemporanee di Newton, e sintetizza le caratteristiche espresse fino ad allora dalla 'nuova scienza': l'approccio sperimentale e l'uso 'fisico' della matematica. Nelle Lectiones, infatti, Newton tratta i colori come proprietà fisiche, corrispondenti a gradi di rifrazione della luce, matematicamente determinabili, tanto che non si sarebbe potuto spiegarli isolatamente. Di conseguenza, le Lectiones si propongono di "mostrare quanto la matematica valga in filosofia naturale" (ibidem, f. 23). In questo caso Newton interpreta tutte le scienze matematiche tramandate dagli Antichi (l'astronomia, la geografia, l'ottica, la meccanica, ecc.) come fondate fisicamente, e quindi come parti integranti della filosofia naturale. Su questo fondamento, esorta "i cultori della geometria ad accingersi a un più stretto esame della Natura, e gli amanti della scienza naturale ad appropriarsi prima della geometria […] affinché filosofando i cultori di geometria e esercitando la geometria i filosofi, otteniamo al posto di congetture e cose probabili […] una scienza della Natura finalmente confermata con la più alta evidenza" (ibidem).
Nella New theory about light and colours, del febbraio 1672, composta in poco più di due settimane, Newton non ripropose più il sogno di unificare la matematica e la filosofia naturale contenuto nelle Lectiones. In forma autobiografica, fornì un picaresco e improbabile resoconto della sua scoperta, servendosi di pochi risultati di molte decine di esperimenti e facendo solo alcuni accenni ‒ significativamente omessi nella stampa ‒ alla convinzione che la scienza dei colori fosse matematica e altrettanto certa, come ogni altra parte dell'ottica geometrica. Le polemiche che scoppiarono immediatamente dopo la pubblicazione della New theory distolsero Newton dalla pubblicazione delle Lectiones e lo indussero ad abbandonare per parecchi anni le ricerche di ottica. In effetti, il programma scientifico abbozzato nelle Lectiones fu realizzato compiutamente solo nei Principia.
La pubblicazione tarda dell'Opticks, in cui Newton rinunciò alla compiuta matematizzazione della sua teoria della luce, come in parte aveva tentato nelle Lectiones, ne favorì, in realtà, l'ampia diffusione e fortuna. L'Opticks fu accolta come il modello di una scienza sperimentale indipendente da spiegazioni meccanicistiche e da complicati calcoli matematici.
Nonostante la teoria della diversa rifrangibilità dei raggi di luce fosse concepita all'inizio sulla base di alcune ipotesi meccanicistiche (diverse velocità dei raggi o diversa grandezza dei corpuscoli), a partire dalla memoria del 1672 Newton optò per una concezione sostanzialistica dei colori, ritenendoli proprietà essenziali e irriducibili della luce. Il famoso experimentum crucis, ivi descritto, ha la funzione di mostrare, una volta rifratta la luce bianca, l'immutabilità dei colori, pur sottoposti a ulteriori rifrazioni o riflessioni. Newton dedusse da questo esperimento l'impossibilità che l'azione del mezzo rifrangente inducesse modificazioni meccaniche nei raggi luminosi.
L'Opticks è opera composita, in cui il Libro I ha una struttura assiomatico-deduttiva, corrispondente al metodo descritto a Oldenburg nel 1672, e contiene molti risultati ed esperienze delle Lectiones. Il Libro II riporta le osservazioni sulle riflessioni, le rifrazioni e i colori dei corpi sottili trasparenti, e coincide con il Discours of observations, inviato nel 1675 alla Royal Society. Il brevissimo Libro III, che Newton dichiara di aver lasciato imperfetto, è dedicato alle osservazioni sulle inflessioni dei raggi di luce, in altre parole al fenomeno della diffrazione, scoperto da Francesco Maria Grimaldi (1618-1663). Al termine di questo libro, Newton elencò alcune domande (Queries), che erano a un tempo indicazioni per indagini successive e ipotesi esplicative sulla natura della luce.
Nelle successive edizioni dell'Opticks, Newton aggiunse e modificò diverse Queries (tab. 1), ed estese, soprattutto quelle sull'etere, all'intera filosofia della Natura.
Sulla scia del primo tentativo fallito di ripetere l'experimentum crucis, compiuto nel 1681 da Edme Mariotte, il contenuto sperimentale dell'Opticks fu oggetto di numerose critiche in Francia e in Italia. Il successo di molte prove successive occultò il fatto che la teoria della luce di Newton era prevalentemente speculativa e in alcuni casi connessa alle proposizioni sperimentali mediante argomenti retorici.
I 'Philosophiae naturalis principia mathematica'
La legge dell'inverso del quadrato
La voce Of gravity and levity del taccuino del Trinity College attesta che, dal 1664 al 1665, Newton si occupò anche della gravità. Il suo punto di partenza è una citazione dai Principia philosophiae di Descartes, secondo cui la materia che causa la gravità deve passare attraverso tutti i pori di un corpo. La voce contiene già forti obiezioni contro i vortici eterei cartesiani; in particolare, Newton mostra come i "raggi di gravità" dovrebbero essere proporzionali alla superficie dei corpi, e conclude in questo modo: "La gravità dei corpi è come la loro solidità, perché tutti i corpi discendono spazi uguali in tempi uguali, considerata la resistenza dell'aria ecc." (McGuire 1983, p. 431). Questa conclusione ‒ che richiama la legge di caduta dei gravi di Galilei ‒ implica, al contrario, che la gravità agisca in proporzione alle masse.
Prima del 1669, Newton affrontò anche il problema di calcolare a quale distanza dalla circonferenza, un corpo che la percorresse con moto uniforme, sarebbe trasportato, nel tempo di una rivoluzione, se in un punto dato fosse libero di muoversi lungo la tangente della circonferenza stessa.
Il manoscritto che raccoglie queste osservazioni richiama, sia nella figura (fig. 3) sia nell'intento di stabilire se la rotazione della Terra possa allontanare i corpi posti sulla sua superficie, la Giornata Seconda del Dialogo sopra i due massimi sistemi del mondo di Galilei, in cui è impostata la ricerca del moto lungo la tangente. Galilei considera anche la distanza esterna come equivalente all'azione della gravità verso il centro. Per questo Newton congettura che tali distanze sarebbero proporzionali al quadrato dei tempi, secondo la legge di Galilei. Il problema potrebbe essere stato suggerito a Newton anche da un esperimento di Giovanni Alfonso Borelli nelle Theoricae Mediceorum planetarum, del 1666, che prevede il movimento di una sfera all'interno di un circolo di legno in rotazione.
Alcuni storici preferiscono riconoscere in questo primo scritto di Newton l'influenza esclusiva di Descartes, segnatamente della sua seconda legge della Natura, espressa nei Principia philosophiae, che senza dubbio Newton conosceva. Tuttavia non si comprenderebbe come, in tal caso, sia utilizzata per il calcolo la legge di caduta dei gravi di Galilei, la cui dimostrazione non fu mai accettata da Descartes, e che Newton nel Trinity notebook utilizza proprio contro l'ipotesi dei vortici cartesiani.
Infine, al termine del corollario che segue il calcolo, Newton combina l'argomento iniziale con la terza legge di Kepler, concludendo che, supposta l'orbita circolare, gli sforzi (conatus) di allontanamento dei pianeti dal Sole vanno come l'inverso dei quadrati delle loro distanze da esso.
In un altro taccuino, il Waste book, iniziato nel 1665, si trovano abbozzate due diverse tecniche matematiche per risolvere il medesimo problema. Newton calcola la forza con cui un globo in rotazione in una sfera preme, nel suo sforzo di allontanamento dal centro, la superficie della sfera stessa. Considera tre specifiche varianti del problema: il moto del globo lungo un percorso quadrato inscritto in un cerchio; lungo un percorso poligonale inscritto nello stesso cerchio; lungo il cerchio stesso, considerato come un poligono di un numero illimitato di lati.
Nel Waste book è abbozzato anche il problema della corrispondenza tra il moto circolare e quello ellittico. Newton fa corrispondere le forze in ciascun punto di un'ellisse con quelle di un cerchio tangente quel punto e di uguale curvatura, una tecnica poi effettivamente utilizzata. È chiaro che Newton stava pensando al sistema copernicano rivisto secondo le leggi di Kepler, allo scopo di utilizzare i risultati dell'analisi del moto circolare uniforme per il problema, matematicamente più complesso, del moto ellittico.
I risultati idealizzati di queste tecniche possono anche essere considerati indipendenti da qualunque presupposto fisico o metafisico connesso con i concetti di moto e di gravità. Le loro radici, tuttavia, sono le opere di Galilei e dei galileiani, di Descartes e di Thomas Hobbes (1588-1679), anche se nessuno di loro aveva messo a punto un calcolo matematico indipendente dalla base empirica, moderatamente idealizzata, da cui avevano ricavato i principî della loro meccanica.
Nel 1679 Hooke scrisse a Newton, chiedendogli un parere circa l'ipotesi che i moti celesti dei pianeti fossero composti di un movimento rettilineo lungo la tangente e di un movimento attrattivo verso il corpo centrale. Fu questa l'occasione che indusse Newton a ripensare alle tecniche della sua dinamica celeste, finché nel 1684, dopo l'incontro con Edmond Halley, gli spedì il De motu corporum in gyrum, il primo abbozzo dei Principia. In questo breve trattato Newton mette a punto, utilizzando un poligono che si approssima al moto continuo di un pianeta nella sua orbita, la dimostrazione della seconda legge di Kepler, concludendo che tutti i corpi orbitanti descrivono, per l'azione continua di una forza centripeta, aree proporzionali ai tempi, con i raggi condotti verso il centro della forza. Nei teoremi e nei problemi successivi egli usa la tecnica del manoscritto, anteriore al 1669, e non l'approssimazione poligonale del Waste book. Newton dimostra che, per mantenere il moto ellittico di un pianeta intorno a un fuoco dell'ellisse, la forza centripeta ivi collocata deve essere inversamente proporzionale al quadrato della distanza tra il fuoco e il pianeta.
È curioso che qualche storico abbia difeso la rivendicazione di priorità di Hooke nella scoperta di questa legge. Le innovazioni, in quell'impresa eclettica e collettiva che è la scienza moderna, si sviluppano spesso in modo graduale, e nel Seicento furono proprio le interpretazioni meccaniche del moto circolare a subire una notevole evoluzione. Quando Newton scrive a Halley, il 20 giugno 1686, per difendersi dall'accusa di plagio, elenca le possibili fonti di Hooke (che probabilmente sono anche le sue), mostrando, senza possibilità di dubbio, che la legge dell'inverso del quadrato era una conoscenza collettiva, di cui si scopriva l'importanza a poco a poco. Kepler aveva definito questa legge sulla diffusione della luce. Ismaël Boulliau (1605-1694) la estese alle forze magnetiche o di altro genere, irradiate dal centro alla periferia (in proporzione alla superficie della circonferenza, quindi all'inverso di r2). Le opere postume di Hooke attestano che fu attraverso questa via che egli formulò l'ipotesi della legge dell'inverso del quadrato per la gravitazione. Inoltre, Huygens aveva calcolato nell'Horologium oscillatorium (1673) il valore della forza centrifuga, da cui non era difficile ricavare matematicamente la proporzionalità con l'inverso del quadrato. In seguito, Newton, negli Scolii classici ‒ note che intendeva aggiungere ai Principia e che risalgono agli anni Novanta ‒ sostenne che questa stessa legge era in qualche modo conosciuta anche dagli Antichi.
La Praefatio ad lectorem del 1686 e l'assiomatizzazione dei Principia
Nella prefazione del 1686 alla prima edizione dei Principia, Newton rende pubblica la sua proposta di affrontare la filosofia naturale, richiamandosi da un lato alla 'meccanica razionale' degli Antichi e, dall'altro, alla ricerca moderna di leggi matematiche dei fenomeni naturali. I due metodi separati, proposti nel De gravitatione, si fondono così in uno solo. Nonostante gli Antichi avessero distinto la meccanica razionale da quella pratica, e la geometria da entrambe, Newton propone di annullare ogni distinzione. A questo scopo, la sua attenzione si sposta sulla geometria per criticare il suo secolare isolamento dalla realtà. I principî della geometria non sono geometrici, ma fisici e precisamente meccanici: "Le descrizioni di rette e di circoli sono problemi, ma non geometrici. La soluzione di questi ultimi si postula dalla meccanica, in geometria si insegna l'uso delle soluzioni. E la geometria si gloria che con così pochi principî presi altrove domini così tante cose. La geometria dunque si fonda sulla pratica meccanica, e non è nient'altro che quella parte della meccanica universale, che propone e dimostra accuratamente l'arte della misura" (Principia, ed. Koyré, p. 15).
La meccanica razionale degli Antichi era limitata alle cinque potenze spettanti alle arti manuali, e Newton intende coltivare non le arti ma la filosofia, e scrivere non sulle potenze manuali ma su quelle naturali, ampliando i confini in cui solitamente erano rinchiuse la geometria e la meccanica, sia pratica sia razionale. Newton conclude che, poiché la geometria postula i suoi principî dalla meccanica, la filosofia può postularli dalla geometria e trattare le forze naturali sia attrattive sia impulsive, quali la gravità, la leggerezza, la forza elastica, la resistenza dei fluidi: "E perciò proponiamo questi nostri principî, come principî matematici di filosofia" (ibidem, p. 16).
Lo scopo dichiarato è quello di investigare le forze della Natura iniziando dai fenomeni del moto (intorno ai quali sono formulati i principî matematici ossia meccanici), e quindi, a partire da queste forze, di dimostrare gli altri fenomeni. Questo compito è assolto nei primi due libri dei Principia, e nel terzo lo stesso schema è adottato per spiegare il Sistema del mondo.
Newton auspica che lo stesso modo di ragionare si dimostri altrettanto efficace per spiegare il microcosmo (i legami delle particelle tra loro, lo spirito elettrico, la fermentazione, la vita). I filosofi, infatti, continuano invano a sondare la natura del microcosmo, come in precedenza avevano cercato invano le leggi del macrocosmo. I Principia sono dunque un diverso modo di filosofare; ne esisterà forse qualche altro ancora più efficace, ma certamente bisogna escludere quelli del passato, e quello ipotetico dei cartesiani.
Con poche eccezioni, gli interpreti recenti hanno trascurato la prefazione ai Principia, considerando spesso l'opera di Newton come una triviale applicazione della matematica tout court alla realtà. Nell'intenzione dell'autore, tuttavia, i Principia sono un'opera filosofica, alla cui elaborazione concorrono tre tradizioni di ricerca che in precedenza erano distinte e operavano separatamente: la tradizione sperimentale, quella matematica e quella filosofica. La sintesi fatta da Newton raggiunge nei Principia il risultato più maturo, dopo i tentativi incompleti di combinazione delle medesime tradizioni nell'ottica, nell'interpretazione della Scrittura e nel De gravitatione. I Principia sono dunque un'opera composita, che riflette un metodo semplice e unitario solo in apparenza.
L'assiomatizzazione che precede i tre libri dei Principia offre un chiaro esempio di questo metodo combinato. La struttura dei Principia è assiomatico-deduttiva, nel senso che Newton aveva indicato a Oldenburg nel 1672, quindi con l'avvertenza che, sia le definizioni sia gli assiomi, derivando dai fenomeni naturali, sono illustrabili mediante esperimenti. Newton postula tre axiomata o leges motus, la cui doppia denominazione indica già la combinazione di cui si parla nella prefazione, vale a dire che si tratta di principî matematici (axiomata) e di filosofia (leges). Ciò risulta ancora più evidente se confrontiamo gli assiomi o leggi con le definizioni che ne chiariscono i termini. Newton ha la cattiva abitudine di tornare al linguaggio ordinario dopo aver posto le definizioni: per esempio, chiamerà indifferentemente "corpo" o "massa" la quantità di materia, e "moto" la quantità di moto.
Definizione I
La quantità di materia è la misura del medesimo che deriva dal prodotto della sua densità per il volume.
Definizione II
La quantità di moto è la misura del medesimo che deriva dal prodotto della velocità e della quantità di materia.
Definizione III
La forza insita (vis insita) della materia è una potenza di resistere, grazie a cui ciascun corpo, per quanto sta in lui, persevera nel suo stato, sia di quiete sia di moto rettilineo uniforme.
Definizione IV
Una forza impressa è un'azione esercitata su un corpo, per mutare il suo stato, sia di quiete sia di moto rettilineo uniforme.
Legge I
Ogni corpo persevera nel suo stato di quiete o di moto uniforme in linea retta, a meno che non sia costretto a mutare il proprio stato da forze impresse. (Principia, ed. Koyré, pp. 39-41 e 54)
La prima legge è concettualmente fondata sull'analisi del moto parabolico di Galilei (Giornata Quarta dei Discorsi e dimostrazioni intorno a due nuove scienze matematiche), come è chiaro dal commento di Newton: "I proiettili perseverano nei loro moti, a meno che non siano ritardati dalla resistenza dell'aria e non siano spinti in basso dalla forza di gravità" (ibidem, p. 54). Del tutto fuorviante, invece, la sua somiglianza con la formulazione della prima legge di Natura che Descartes espone nei Principia philosophiae. Descartes ritiene che il corpo perseveri nei suoi stati di moto o di quiete perché non c'è nulla che lo muova o lo faccia fermare. Newton sostiene, invece, che esiste sempre una vis insita che mantiene lo stato di quiete o di moto (ibidem, def. III). Come esplicita il commento di questa stessa definizione: "Questa [forza] è sempre proporzionale al suo corpo [def. I], e non differisce affatto dall'inerzia della massa, se non nel modo di concepirla. A causa dell'inerzia della materia accade che ogni corpo sia distolto con difficoltà dal suo stato sia di quiete sia di moto. Onde la forza insita si può chiamare con il nome assai significativo di forza di inerzia" (ibidem, p. 40).
Di conseguenza, la vis insita è una forza realmente esercitata dal corpo ogni volta che vi è applicata una qualunque forza impressa (def. IV). Per quanto strano possa sembrare, questa concezione discende direttamente dalla voce Of gravity and levity del Trinity notebook del 1664, quando Newton scopre il caso particolare della proporzionalità tra la massa (in quanto vis insita) e il peso (in quanto vis impressa). La concezione della vis insita di Newton è una concezione filosofica alternativa a quella cartesiana, come risulterà chiaro dal commento alla regola III.
Questo ci consente una migliore comprensione della seconda legge.
Definizione VIII
La quantità motrice di una forza centripeta è la misura della stessa, proporzionale al moto che genera in un dato tempo.
Legge II
Il mutamento di moto è proporzionale alla forza motrice impressa, e avviene nella direzione della linea retta in cui quella forza è impressa. (Principia, ed. Koyré pp. 44 e 54)
Dal commento si evince che Newton intende la forza impressa sia come forza impulsiva (simul et semel) sia come forza continua (gradatim et successive). Questa legge richiama le tecniche matematiche impiegate da Newton prima del 1669. Poiché la vis insita è correlata alla vis impressa, nel caso di una forza impulsiva (che Newton aveva utilizzato nel Waste book), il mutamento di moto è proporzionale agli incrementi discreti della quantità di moto (Δmv); nel caso di una forza continua, il mutamento di moto avviene secondo un'accelerazione uniforme (ma). Quest'ultimo punto interessa Newton soprattutto in un caso particolare, quello delle forze centripete, oggetto delle definizioni VI, VII e VIII. La definizione VII stabilisce la proporzionalità tra la forza centripeta acceleratrice e la velocità che essa genera in un tempo dato. Dalle definizioni VII e VIII Newton ricava la seguente proporzione: "La forza acceleratrice sta alla forza motrice come la velocità al moto. Infatti la quantità di moto si ottiene dal prodotto della velocità e della quantità di materia, e la forza motrice dal prodotto della forza acceleratrice e della stessa quantità di materia" (ibidem, p. 45).
Se, in un tempo dato, la forza acceleratrice è proporzionale alla velocità e la forza motrice alla quantità di moto (mv), la forza motrice, nello stesso tempo, sarà data dal prodotto della forza acceleratrice per la quantità di materia o massa. Indichiamo con Fa la forza acceleratrice, con Fm la forza motrice, con v la velocità, e con (mv) la quantità di moto; la proporzione affermata nel passo sopra citato è la seguente:
[1] Fa/Fm=v/(m×v),
da cui
[2] Fm=Fa×(m×v)/v=Fa×m.
Ma l'azione della forza acceleratrice Fa è appunto l'accelerazione a come risulta dal commento alla definizione VII, e dunque la forza motrice è data dal prodotto dell'accelerazione per la massa
[3] Fm=a×m
come se la forza motrice fosse costituita dalla somma delle accelerazioni subite dalle singole particelle di un corpo: "Infatti la somma delle azioni della forza acceleratrice nelle singole parti di un corpo, costituisce la forza motrice dell'intero corpo" (ibidem).
Si potrebbe anche dire che la definizione VIII è la forma che prende la seconda legge nel caso delle forze centripete che agiscono ininterrottamente. Questo risultato è indipendente dalla specie fisica della forza centripeta considerata, poiché la definizione riguarda un concetto matematico, non fisico. L'esempio che Newton porta è tuttavia desunto dalla gravità, e fornisce la possibilità immediata di un confronto tra una definizione matematica e un fenomeno fisico, in conformità con il metodo descritto nella prefazione. Pertanto, poiché presso la superficie della Terra la gravità acceleratrice (forza acceleratrice gravitazionale) è la medesima per tutti i corpi, essi subiranno un'accelerazione uguale e dunque la gravità motrice (forza motrice gravitazionale) o peso sarà direttamente proporzionale alla massa. Se infatti P è la gravità motrice e g l'azione della gravità acceleratrice, ossia l'accelerazione di gravità, allora dalla relazione [3] risulterà la proporzionalità diretta tra peso e massa:
[4] P=g×m.
Diminuendo l'azione della gravità acceleratrice con la distanza, decresce l'accelerazione g, resta costante la massa m, e il peso P diminuisce in ugual misura della gravità acceleratrice, risultando come il prodotto dell'accelerazione di gravità per la massa: "Per cui presso la superficie della Terra, dove la gravità acceleratrice o forza gravitazionale è la medesima in tutti i corpi, la gravità motrice o peso è in proporzione al corpo: ma se si salisse in regioni dove la gravità acceleratrice è minore, il peso diminuirebbe in ugual misura, e sarebbe sempre come il prodotto del corpo e della gravità acceleratrice" (ibidem).
La terza legge è enunciata in questo modo: "Legge III. A un'azione corrisponde sempre una reazione uguale e contraria: ossia, le azioni reciproche di due corpi sono sempre uguali e dirette in senso contrario" (ibidem, p. 55).
Se ogni corpo conserva la propria vis insita, opporrà una resistenza pari all'impulso di un altro corpo, e poiché resistenza e impulso sono termini reciproci, le due azioni sono identiche. Dalla seconda legge segue che i mutamenti delle quantità di moto derivati da queste azioni saranno uguali e diretti in senso contrario lungo la stessa linea retta.
La seconda legge può essere considerata un'estensione della prima: se lo stato di un corpo muta con l'applicazione di una forza impressa (prima legge), una successiva forza impressa uguale o doppia provocherà un mutamento uguale o doppio dello stato del corpo. Se infatti il mutamento non fosse tale, una qualche parte della forza impressa non muterebbe lo stato del corpo, e ciò sarebbe contro la prima legge.
Analoga considerazione può essere fatta per la terza legge: se un corpo muta lo stato inerziale di un altro corpo con la propria azione, anche il suo stesso stato inerziale deve subire un'azione dall'altro corpo. Se questa azione non fosse uguale e contraria, una qualche parte dell'azione non sarebbe esercitata da nessuna forza, e ciò sarebbe contro la prima e la seconda legge.
Le tre leggi, dunque, altro non sono che tre diverse formulazioni dell'inerzia della materia, vale a dire della potenza di resistere.
La definizione I e la definizione III, infatti, illustrano due diverse concezioni della massa: solo la prima è propriamente una definizione matematica, la seconda, come si è osservato, è un concetto filosofico, che esprime una proprietà irriducibile o essenziale della materia. Le otto definizioni infatti non sono omogenee: come illustrato nella fig. 5, la III e la IV non sono definizioni di quantità, come le prime due e le ultime, ma rispettivamente di una potenza e di un'azione (esemplificata dalla forza centripeta nella def. V). Non sono neppure semplici definizioni linguistiche, ma hanno il loro fondamento nella tradizione filosofica e sperimentale.
L'assiomatizzazione dei Principia non ha ovviamente quel carattere di accuratezza matematica raggiunto dalla meccanica successiva e non solo perché ancora non poteva averlo: l'intento di Newton non è tanto quello di costruire una meccanica razionale, quanto di proporre una filosofia della Natura fondata su principî matematici. Come si evince dalla prefazione, gli stessi principî matematici, ossia meccanici, hanno poi la propria origine nelle potenze naturali, riconducibili ai fenomeni fisici. Non sorprende, quindi, che sia impossibile tradurre con esattezza le definizioni di Newton nelle formule meccaniche oggi invalse. Per esempio, la formula f=m×a non è concettualmente equivalente, se non in modo banale, a Fm=a×m (ricavata dalla def. VIII ed esemplificata con il peso del corpo).
Lo scolio sullo spazio e sul tempo
Le definizioni che aprono i Principia sono seguite da un ampio scolio sul tempo e sullo spazio (e sui concetti derivati di luogo e moto) distinti in assoluti e relativi, veri e apparenti, matematici e comuni (v. cap. XXX). Questo scolio ha avuto una lunga e tormentata elaborazione, documentata dalle numerose stesure conservate nella Portsmouth Collection. Una di queste è contenuta in un manoscritto (Add. 3965) databile intorno al 1684. In esso vi sono, rispettivamente, quattro definizioni del tempo e dello spazio assoluti e relativi, prive, se confrontate con quelle dei Principia, delle qualificazioni di veri e apparenti, matematici e comuni. Un breve commento segue la terza definizione di questo testo, che si ritrova, quasi identico, nello scolio dei Principia. Il commento è il seguente (in corsivo la parte omessa nei Principia):
Come l'ordine delle parti del tempo è immutabile così anche quello delle parti dello spazio. Siano mosse queste dai loro luoghi e saranno mosse da se stesse. Infatti i tempi e gli spazi sono i luoghi di sé stessi e di tutte le cose. Tutte le cose sono situate nel tempo rispetto all'ordine di successione, nello spazio rispetto all'ordine della posizione. è proprio della loro essenza di essere luoghi, ed è assurdo che i luoghi primari siano mossi. Inoltre sia una parte di spazio mossa da una forza applicata e l'intero spazio, applicata una forza di tale quantità a tutte le parti all'infinito, sarà mosso, cosa che è di nuovo assurda. (Cambridge, University Library, Add. 3965, f. 25r)
Questa è una sintesi di molti concetti contenuti nel De gravitatione, in particolare il paragone tra l'ordine delle parti del tempo e quelle dello spazio, l'assurdità che un luogo possa essere mosso da sé stesso e l'affermazione che i tempi e gli spazi sono i luoghi di sé stessi e di tutte le cose in essi situate.
L'immutabilità dei luoghi primari, che nel De gravitatione aveva fondamento nello spazio, inteso come effetto emanativo di Dio, ente primariamente esistente e di natura immutabile, è ora, come nei Principia, un corollario della concezione stessa di luogo.
La quarta definizione del manoscritto Add. 3965 ha come oggetto lo spazio relativo che è considerato immobile rispetto a qualcosa di sensibile, pur senza esserlo veramente. Esso è dunque sempre mobile e coinciderebbe con il corpo stesso, se soltanto fosse impenetrabile.
Newton ha operato, così, un'ulteriore astrazione sulla quantità determinata di estensione, dotata di mobilità e impenetrabilità, che è la definizione di corpo data nel De gravitatione, isolando, mediante la posizione, quantità determinate di estensione, dotate unicamente di mobilità. Anche queste quantità, come quelle corporee, si distinguono numericamente dalle corrispondenti quantità dello spazio assoluto. Soltanto quest'ultimo però esisterebbe veramente. La quinta definizione del manoscritto è quella di corpo, che nei Principia è sostituita dalla definizione di quantità di materia: "I corpi cadono sotto i sensi di tutti come cose mobili che non possono penetrarsi vicendevolmente" (Cambridge, University Library, Add. 3965, f. 25r).
In conclusione, i più importanti concetti metafisici trattati nel De gravitatione, chiaramente dipendenti dalla divisione ontologica di Pierre Gassendi (1592-1655), secondo il quale lo spazio e il tempo hanno un particolare modo di esistere che non compete né alle sostanze né agli accidenti, sono conservati nello scolio sullo spazio e il tempo dei Principia. Qui Newton opera almeno su tre livelli, che corrispondono a varie fasi della sua riflessione: il primo è quello metafisico, che appare da pochi indizi (lo spazio e il tempo sono immobili o mobili; hanno una natura o non l'hanno; i luoghi sono mutabili o immutabili per essenza) e ha alle spalle la prolissa digressione del De gravitatione; il secondo è quello fisico, per cui spazio e tempo sono veri se esistono in rerum natura o apparenti se si riducono a semplici relazioni fenomeniche; il terzo è quello matematico, in cui essi sono trattati come quantità confrontabili con l'esperienza (le osservazioni astronomiche e i fenomeni naturali). Questi tre livelli corrispondono e spiegano i tre noti attributi, che non sono affatto sinonimi, con cui Newton distingue lo spazio e il tempo nei Principia: assoluti, veri, matematici, in contrapposizione a relativi, apparenti e comuni.
I confini tra le tradizionali scienze teoretiche (fisica, matematica, metafisica), di ascendenza aristotelica, sono consapevolmente, anche se faticosamente, abbattuti da Newton nel tentativo di costruire una scienza unitaria, di cui i Principia rappresenterebbero appunto l'avvio.
I tre libri dei Principia
I Principia mantengono nella propria struttura i tre livelli che si riconoscono nello scolio sullo spazio e sul tempo. Il livello matematico è quello più sviluppato, soprattutto nei primi due libri, in cui Newton usa il linguaggio delle proporzioni geometriche e della geometria euclidea; in parte ricorre anche al proprio metodo delle quantità infinitamente evanescenti. Quanto all'uso del calcolo, leggiamo in un abbozzo di lettera a Pierre Des Maizeaux, databile intorno al 1720: "Ho scritto il libro dei Principî negli anni 1684, 1685, 1686, e nello scriverlo ho molto usato il metodo delle flussioni diretto e inverso, ma non ho riportato i calcoli nel libro stesso perché fu scritto con il metodo della sintesi come tutta la geometria dovrebbe essere. E dal tempo in cui scrissi quel libro, ho dimenticato a poco a poco i metodi con cui lo scrissi" (Cohen 1971, p. 296).
Gli storici hanno dubitato finora che questa affermazione fosse fondata, ma altri studi hanno mostrato, sulla base dei manoscritti raccolti nei Mathematical papers, che Newton era effettivamente in grado di affrontare i problemi dinamici proposti nei Principia, mediante il calcolo delle flussioni.
Mentre il Libro I è dedicato alla dimostrazione matematica delle tre leggi di Kepler, il Libro II si occupa dei moti in mezzi resistenti, come l'aria e i liquidi di diversa densità, e include uno studio matematico dei movimenti ondulatori e dei suoni. Newton si occupa anche del modo in cui le onde si diffondono attraversando piccole fessure, concludendo che, poiché la luce si propaga in linea retta anche attraverso di esse, la sua natura non può essere colta dalle teorie ondulatorie, come quelle di Descartes e Hooke. Alla fine si comprende che l'intento principale del Libro II è la confutazione della teoria dei vortici materiali di Descartes, poiché il movimento dei pianeti lungo le loro orbite risulta incompatibile con la resistenza di un qualunque mezzo celeste.
Il livello fisico dei Principia è manifesto soprattutto nel Libro III. Consideriamo la proposizione 11, problema VI del Libro I: "Si muova un corpo lungo un'ellisse: si richiede la legge della forza centripeta che tende a un fuoco dell'ellisse" (ed. Koyré, p. 118). Newton dimostra che tale forza è soggetta alla legge dell'inverso del quadrato, vale a dire che la forza centripeta è inversamente proporzionale al quadrato della distanza del corpo dal fuoco dell'ellisse. Nella dimostrazione egli usa la tecnica geometrica, integrata con il metodo delle prime e ultime ragioni e le leggi del moto. Nel Libro III, Newton ricava dai fenomeni che i pianeti si muovono lungo ellissi aventi come fuoco il centro del Sole, con forze centripete (la loro gravità), dirette verso il Sole: per la proposizione 11 del Libro I tali forze saranno inversamente proporzionali ai quadrati delle distanze dal centro del Sole.
La verità fisica di questa conclusione, tuttavia, si fonda sulla possibilità di poter riconoscere e distinguere i moti veri da quelli apparenti. Tutto l'edificio matematico dei Principia risulterebbe inutile, da un punto di vista fisico, se tale distinzione fosse impossibile. Alla fine dello scolio sullo spazio e sul tempo, Newton elenca le condizioni per riconoscere il moto vero: esso è sempre mutato da forze impresse sul corpo mosso, non così il moto relativo. Se fossero applicate forze uguali e in uguali direzioni a tutti i corpi con i quali sussiste la relazione di moto, il moto relativo risulterebbe immutato. Ne segue che, a meno di non pervenire a un luogo immoto nello spazio assoluto, non è possibile conoscere, mediante la traslazione in linea retta di un corpo rispetto a un altro, la quantità del suo moto assoluto, anche in presenza di una forza impressa. Newton adotta una duplice soluzione: (a) introduce un'ipotesi nel Libro III secondo cui: "il centro del sistema del mondo è in quiete" (ibidem, p. 586), e ne ricava la conseguenza che il centro comune di gravità della Terra, del Sole e di tutti i pianeti è in quiete (assoluta); (b) sostiene che nel moto circolare è sempre possibile riconoscere il moto vero da quello apparente, perché nel moto circolare vero si nota un effetto (le forze di allontanamento dall'asse) assente nel moto circolare relativo. Il famoso esperimento della secchia sospesa, analizzato da Newton con grande maestria retorica, ha lo scopo di illustrare questo punto.
La 'girofilia' di Newton potrebbe anche essere interpretata come un residuo dell'antica tradizione che riconosceva nel moto circolare un segno della perfezione celeste. Di fatto, le sue fonti sono almeno due: la scuola galileiana (forse Galilei stesso, ma certamente Borelli) e soprattutto Descartes. Già nel commento alla definizione V, Newton analizza l'esempio della pietra nella fionda negli stessi termini espressi da Descartes nei Principia philosophiae, riconoscendo nel conatus di allontanamento dal centro non solo una forza reale ma, come nell'esperimento della secchia, l''unica' forza reale in grado di identificare un moto vero.
Le proposizioni matematiche del Libro I forniscono la soluzione, con la stessa tecnica già illustrata per le orbite ellittiche dei pianeti, del movimento orbitale dei satelliti e delle comete. La legge di gravitazione universale, dopo che Newton ha dimostrato che la forza centripeta tra la Luna e la Terra è quella stessa forza che chiamiamo "gravità" (Principia, III, prop. 4, teorema IV), segue al riconoscimento che le forze centripete nei moti orbitali dei satelliti e dei pianeti sono proporzionali alle masse. Infatti tali forze accelerano ugualmente corpi ineguali, i quali descriverebbero, nella discesa verso il centro da uguali distanze, spazi uguali in tempi uguali (ibidem, prop. 6, teorema VI). È la stessa conclusione annotata nel Trinity notebook. La teoria gravitazionale è utilizzata per la spiegazione delle maree e per la previsione dei moti lunari. Il Libro III contiene anche la spiegazione dell'appiattimento della Terra ai poli, per effetto della sua rotazione, e quella della precessione degli equinozi.
Il livello metafisico dei Principia, nella prima edizione, può apparire trascurabile, ma le fondamentali definizioni di massa come vis insita, di spazio e di tempo assoluti, di luogo immobile e di moto vero rimandano a una complessa elaborazione di concetti metafisici della tradizione filosofica, assai evidenti nel De gravitatione, e riaffioranti in seguito nelle Regulae philosophandi, nello Scholium generale delle successive edizioni dei Principia e nelle Queries dell'Opticks.
Le 'Regulae philosophandi' e lo 'Scholium generale'
La storia editoriale delle Regulae philosophandi di Newton è riassunta nella Tav. I. Una regola V (che è piuttosto un chiarimento del termine 'ipotesi' usato nella IV) rimase manoscritta. Nell'edizione dei Principia del 1713, l'ipotesi III della prima edizione fu rimossa e la IV fu spostata dopo la proposizione 10 del Libro III sotto il titolo 'ipotesi I'.
Quali sono le fonti delle Regulae dei Principia? È certo che esse sono state precedute da una serie più numerosa di regole, elaborate per l'interpretazione del Trattato sull'Apocalisse negli anni Settanta del Seicento. Nella composizione di queste, Newton prese spunto da un manuale di logica scolastica, il Logicae artis compendium di Robert Sanderson, uno dei suoi primi acquisti come studente a Cambridge.
Sanderson elenca alcune leggi comuni (brevità, armonia, unità, connessione) al 'duplice metodo d'invenzione e di dottrina'. Le regole o canoni, secondo Sanderson, riguardano le scienze pratiche e non quelle teoriche, come la fisica e la geometria. Newton abbandona completamente questa distinzione, come risulta chiaro nella prefazione alla prima edizione dei Principia, in cui sostiene che la geometria stessa è fondata sulla pratica meccanica. Proprio per questo, egli ricava le proprie regole promiscuamente dal metodo d'invenzione e dalle leggi del metodo di dottrina, così come sono descritte da Sanderson. Allo stesso modo in cui le regole del Trattato sull'Apocalisse servivano a ordinare i luoghi della Scrittura, così quelle dei Principia hanno la funzione di collegare i fenomeni naturali secondo nessi causali.
Queste regole furono lette nel Settecento, e giustamente, come il canone della scienza sperimentale. Eppure in esse non vi è molto di più oltre la riproposta dell'induzione aristotelica. Il giovane Newton ne aveva trovato la definizione nel Logicae artis compendium di Sanderson: "Induzione, mediante la quale usiamo più esperienze collegate per costituire una conclusione universale" (p. 237). Il contenuto delle regole, tuttavia, rivela un'attenta rielaborazione delle discussioni metodologiche seicentesche.
Così la regola I non consente la distinzione tra verità fisica e verità matematica, filosofica la prima e ipotetica la seconda. Le cause vere devono salvare i fenomeni e, viceversa, quel che salva i fenomeni deve essere anche vero. Sotto il 'rasoio di Newton' cadono le note posizioni di Roberto Bellarmino (1542-1621) e di Andreas Osiander (1498-1552) e l'intera fisica di Descartes, che, purché fossero salvi i fenomeni, ammetteva indifferentemente ipotesi vere o false.
Per il lettore inconsapevole di questi riferimenti impliciti, la regola I risulta banale o generica, tanto più che si appoggia quasi completamente alla seconda come a una sua conseguenza.
In realtà, la regola II è quella più oscura: che cosa significa, infatti, "effetti naturali dello stesso genere"? Nient'altro che "effetti che hanno la medesima causa". Solo in tal caso gli effetti sono congeneri. La regola II si risolve così in una tautologia. L'avvertenza "per quanto sia possibile" non attenua la difficoltà, ma la sposta soltanto. Il problema sarà affrontato nella regola IV. L'ultima regola, tuttavia, attenua la prima, nel senso che ne corregge il dogmatismo: le cause ricavate dai fenomeni per induzione devono essere ritenute vere, finché non se ne abbia una conoscenza più accurata o siano riconosciute delle eccezioni. L'ipotesi del Libro III, che afferma la quiete assoluta del centro del sistema del mondo, avvicina l'opera di Newton alla fisica cartesiana più di quanto egli stesso, e gli interpreti di oggi, siano disposti ad ammettere. Infatti Newton salva i fenomeni con i suoi principî matematici di filosofia naturale indipendentemente dalla falsità o verità di quell'ipotesi.
La regola III è duplice: la prima parte sancisce un principio metafisico, vale a dire che esistono qualità essenziali dei corpi (come la vis insita della materia o i colori semplici), non soggetti all'intentio e alla remissio, di aristotelica memoria; la seconda introduce la base induttiva sperimentale, in seguito rafforzata nella regola IV. Nell'edizione del 1726 Newton aggiunge, come esempio dei due diversi modi di raggiungere una conclusione universale, la differenza fondamentale tra la forza insita, essenziale ai corpi, e la gravità, che quadra generalmente con gli esperimenti, ma, poiché diminuisce, non è essenziale. Proprio nel commento alla regola III, l'esempio di induzione riportato da Newton, la cui conclusione è la gravitazione universale, concorda in tutto con la definizione di induzione di Sanderson.
Lo Scholium generale dei Principia
Nel De gravitatione leggiamo un'affermazione di Newton sorprendente: "Potrei mostrare che l'analogia tra le facoltà divine e le nostre è più grande di quanto sia stato avvertito finora dai filosofi. Che siamo stati creati ad immagine di Dio, lo attesta la Sacra Scrittura. E la sua immagine splenderebbe più chiaramente in noi se solo simulasse nelle facoltà che ci ha accordato il potere di creazione nello stesso grado come i suoi altri attributi" (Unpublished scientific papers, p. 108).
L'analogia tra Dio e l'uomo non è soltanto un dato teologico. Newton la pone a fondamento della sua concezione della materia, poiché Dio sta alla materia come l'uomo al suo corpo. La volontà umana è il 'tipo' di quella divina. Ogni difficoltà che concerne la natura della materia può così essere ridotta alla facoltà di muovere il nostro corpo, la quale, in virtù dell'analogia, simula il potere creativo di Dio: "Così ho dedotto la descrizione di questa natura corporea dalla facoltà di muovere i nostri corpi, tanto che tutte le difficoltà possono essere ricondotte infine a quel concetto" (ibidem, p. 107).
Su questo fondamento teologico, Newton per molti anni cercò di mettere a punto la teoria di un etere immateriale per fornire una spiegazione unitaria sia del movimento volontario sia delle forze che agiscono nel microcosmo, come le attrazioni elettriche e magnetiche.
Lo Scholium generale dei Principia, forse uno degli scritti più famosi di Newton, ribadisce la somiglianza tra Dio e l'uomo, ed è il risultato della sua continua riflessione su Dio, il mondo e l'uomo.
All'inizio troviamo esposte le difficoltà, ricavate dal Libro II, che si possono opporre all'ipotesi cartesiana dei vortici. Quindi Newton afferma che i moti regolari dell'Universo non hanno origine da cause meccaniche e perciò esso non poté nascere senza l'intenzione e il dominio di un ente intelligente e potente, il quale, con la sua reale onnipresenza nello spazio, assicura la regolarità e l'armonia dell'Universo.
Gli attributi della divinità non sono soltanto quelli che i filosofi gli hanno riconosciuto: l'eternità, l'infinità e l'assoluta perfezione. Dio è una parola relativa, che si riferisce al dominio sui servi. Un Dio senza dominio, provvidenza e cause finali non è nient'altro che fato e Natura. Il Dio di Newton è il Dio Signore e Re, il Pantocratore, il quale, oltre che nel mondo, si manifesta nella Bibbia; qui egli si ispira ai Sermons di Isaac Barrow (1630-1677), il matematico teologo che gli aveva ceduto la cattedra lucasiana di Cambridge.
Contro i deisti, Newton nega con vigore che Dio sia l'anima del mondo: la sua onnipresenza non è virtuale, ma sostanziale. Non è il tempo e lo spazio, ma esistendo sempre e ovunque, costituisce la durata e lo spazio. Di conseguenza, Newton sostiene un fenomenismo radicale: "Vediamo soltanto le figure e i colori dei corpi, udiamo soltanto i suoni, tocchiamo soltanto le superfici esterne, annusiamo i soli odori, e gustiamo i sapori: non conosciamo le sostanze intime con nessun senso, nessun atto di riflessione; e molto meno abbiamo idea della sostanza di Dio" (Principia, ed. Koyré, p. 763).
Nel De gravitatione, la materia poteva essere pensata, senza contraddizione, priva di una sostanza indipendente dalla volontà di Dio. L'orientamento sostanzialistico di Newton, così evidente nella memoria sui colori del 1672 e nella concezione sia della vis insita della materia sia dello spazio e del tempo assoluti, sembra essersi volto in un fenomenismo puro. Tuttavia questo fenomenismo è giustificato dalla sostanziale presenza di Dio nel mondo ed equivale a dire che non possiamo conoscere le "sostanze intime", perché non conosciamo la sostanza di Dio. Per questo, la filosofia naturale parla di Dio soprattutto a partire dai fenomeni.
Dopo questa dichiarazione di fenomenismo, non sorprende che Newton affermi di non conoscere che cosa sia la gravità, ma solo di sapere che non è una forza meccanica. La sua azione, che si estende dovunque e a immense distanze, è indispensabile per l'ordine e l'armonia dell'Universo. La causa della gravitazione universale, tuttavia, non ha potuto essere ricavata dai fenomeni, e quindi Newton non 'finge ipotesi'. Si dice 'ipotesi' qualunque spiegazione che non sia tratta dai fenomeni, e nella filosofia sperimentale non devono essere ammesse ipotesi di nessun genere (metafisiche, fisiche, delle qualità occulte, meccaniche). Il rifiuto delle ipotesi è dunque l'estrema conseguenza della concezione della materia nel suo intimo rapporto con Dio.
Si tratta di una forma di scetticismo? Probabilmente sì, se ci poniamo di fronte unicamente al grandioso scenario teologico e metafisico tratteggiato da Newton nello Scholium generale; sicuramente no, se consideriamo che, proprio su questo scenario, la conoscenza della realtà è possibile grazie all'armonia della Natura, al riverbero di Dio presente in essa. I semi di questa conoscenza, come attestano gli Scoli classici, si trovano nella prisca sapientia, nella cronologia biblica, nell'alchimia. La stessa struttura geometrica del mondo, altro non è che un pallido riflesso della geometria divina.
Al termine dello Scholium generale, Newton spiega che, a causa della scarsità degli esperimenti, non può parlare di quello
spirito [cioè effluvio] sottilissimo, che pervade i grossi corpi e si nasconde in essi; per la cui forza e azione le particelle dei corpi si attraggono, e divenute contigue aderiscono; e i corpi elettrici agiscono a distanze maggiori, tanto respingendo quanto attraendo i corpuscoli vicini; e la luce viene emessa, riflessa, rifratta e inflessa, e scalda i corpi; e ogni sensazione viene eccitata, e le membra degli animali sono mosse dalla volontà, essendo propagate le vibrazioni di questo spirito attraverso i filamenti solidi dei nervi dagli organi esterni di senso al cervello e dal cervello ai muscoli. (Principia, ed. Koyré, p. 764)
È interessante il contrasto tra la precedente sospensione del giudizio sull'attrazione gravitazionale e l'ammissione di altre azioni a distanza, assai meno note della gravità. Questo passo, in effetti, è ciò che sopravvive, nell'opera pubblicata, di un'appendice ai Principia, di cui rimangono due manoscritti: il De motu et sensatione animalium e il De vita et morte vegetabili. In quest'ultimo troviamo esplicitamente espressa l'intenzione di Newton di unificare mediante l'attrazione, positiva o negativa, tutte le forze agenti nel macrocosmo e nel microcosmo:
Sembra che tutti i corpi densi siano costituiti di particelle elettriche e abbiano anche alcune particelle magnetiche. E nello stesso modo in cui l'attrazione di gravità è sufficiente a spiegare i maggiori movimenti dei pianeti, delle comete e del nostro mare, così le forze elettriche e magnetiche sembrano essere sufficienti a spiegare le azioni e i movimenti delle particelle di qualsiasi corpo fra di loro; ammesso ovviamente che le particelle elettriche agiscano sempre fortissimo alle piccole distanze, ma alle grandi distanze non possano agire se il loro potere non sia eccitato dalla frizione o dall'azione del vivere o da qualche altra azione. (p. 86)
Che rapporto c'è tra attrazione gravitazionale e attrazione elettrica? A questo proposito, occorre tenere in massimo conto l'analogia tra Dio e l'uomo, ripetutamente affermata da Newton: come la volontà dell'uomo agisce sul corpo e lo muove tramite lo spirito elettrico, così Dio potrebbe agire sul mondo mediante la gravità.
Nelle nuove Queries dell'Opticks, dalla 17 alla 24, Newton parla dell'etere come di un effluvio o di un'emanazione, senza preoccuparsi più, come in precedenza, della sua densità. Un etere denso, infatti, produrrebbe una resistenza che le leggi dei moti planetari non rivelano. L'attrazione elettrica, che non fa diminuire o aumentare sensibilmente il peso di un corpo, gli consente di aggirare questa difficoltà. Un mezzo analogo all'elettricità potrebbe esistere nel vuoto senza suscitare resistenza alcuna, giacché è proprio dello spirito elettrico permeare liberamente i corpi solidi. In seguito a "qualche altra azione", questo spirito potrebbe produrre la gravitazione dei grandi corpi l'uno verso l'altro e nello stesso tempo essere il mezzo che unisce "l'anima pensante e il corpo non pensante", Dio e il mondo (Cambridge, University Library, Add. 3970, f. 241r).
La materia densa e l'etere elettrico non sono più in attrito: "Sembra che tutti i corpi densi siano costituiti di particelle elettriche" (ibidem), ossia di particelle quasi prive di massa. Newton continua ad affermare di non sapere che cosa sia questo etere: in realtà, ora dubita di sapere che cosa sia la materia. Qualunque cosa sia, non è più concepita da Newton in opposizione all'anima pensante.
Bibliografia
Brackenridge 1995: Brackenridge, J. Bruce, The key to Newton's dynamics. The Kepler problem and the Principia. Containing an English translation of sections 1, 2, and of book one from the first (1687) edition of Newton's 'Mathematical principles of natural philosophy', Berkeley, University of California Press, 1995.
Casini 1981: Casini, Paolo, Newton. Gli scolii classici, "Giornale critico della filosofia italiana", 60-62, 1981, pp. 7-53.
Cohen 1971: Cohen, I. Bernard, Introduction to Newton's 'Principia', Cambridge (Mass.), Harvard University Press, 1971.
Guicciardini 1999: Guicciardini, Niccolò, Reading the 'Principia'. The debate on Newton's mathematical methods for natural philosophy from 1687 to 1736, Cambridge-New York, Cambridge University Press, 1999.
Koyré 1972: Koyré, Alexandre, Studi newtoniani, Torino, Einaudi, 1972 (ed. orig.: Newtonian studies, Chicago, University of Chicago Press, 1965).
McGuire 1983: McGuire, James E. - Tamny, Martin, Certain philosophical questions. Newton's Trinity notebook, Cambridge-New York, Cambridge University Press, 1983.
‒ 2001: McGuire, James E., The fate of the date. The theology of Newton's 'Principia' revisited, in: Scienza e sacra scrittura nel XVII secolo, a cura di Maurizio Mamiani, Napoli, Vivarium, 2001, pp. 197-227.
Mamiani 1976: Mamiani, Maurizio, Isaac Newton filosofo della natura. Le lezioni giovanili di ottica e la genesi del metodo newtoniano, Firenze, La Nuova Italia, 1976.
‒ 1986: Mamiani, Maurizio, Il prisma di Newton. I meccanismi dell'invenzione scientifica, Roma-Bari, Laterza, 1986.
‒ 1991: Mamiani, Maurizio, The rhetoric of certainty. Newton's method in science and in the interpretation of the Apocalypse, in: Persuading science. The art of scientific rhetoric, edited by Marcello Pera and William R. Shea, Canton (Mass.), Science History Publications, 1991, pp. 157-172.
‒ 1992: Mamiani, Maurizio - Trucco, Emanuela, Newton e i fenomeni della vita, "Nuncius", 6, 1992, pp. 69-77.
‒ 2001a: Mamiani, Maurizio, To twist the meaning. Newton's 'Regulae philosophandi' revisited, in: Isaac Newton's natural philosophy, edited by Jed Z. Buchwald and I. Bernard Cohen, Cambridge (Mass.), MIT, 2001, pp. 3-14.
‒ 2001b: Mamiani, Maurizio, Das Entschlüsseln der Apokalypse. Newton, das Unternehmen der Wissenschaft und die Sprache der Träume, in: Barock. Neue Sichtweisen einer Epoche, hrsg. von Peter J. Burgard, Wien, Böhlau, 2001, pp. 179-187.
Nauenberg 1994: Nauenberg, Michael, Newton's early computational method for dynamics, "Archive for history of exact sciences", 46, 1994, pp. 221-252.