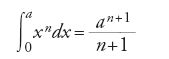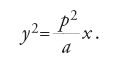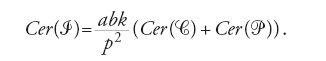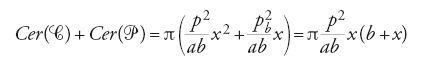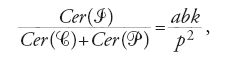La Rivoluzione scientifica: i domini della conoscenza. Le innovazioni di Luca Valerio e di Bonaventura Cavalieri
La Rivoluzione scientifica: i domini della conoscenza. Le innovazioni di Luca Valerio e di Bonaventura Cavalieri
Le innovazioni di Luca Valerio e di Bonaventura Cavalieri
L'eredità greca e l'opera di Valerio e Cavalieri
La riscoperta della geometria e della matematica greca che si verificò nel XVI sec. è alla radice di molte rivoluzioni concettuali del Seicento. È quasi impossibile immaginare Galilei senza Archimede, o Descartes senza Apollonio e Pappo. Non va dimenticato, però, che tale processo di riscoperta non fu una trasmissione meccanica delle conoscenze e dei metodi matematici antichi. Leggere Archimede o Apollonio ‒ e a maggior ragione tradurli e commentarli ‒ significò reinterpretarli. Le lacune e le corruzioni nella tradizione dei testi scientifici antichi, per non parlare di una cesura temporale durata secoli, implicavano necessariamente questa reinterpretazione. È ciò che avviene, in misura maggiore o minore, con tutti i campioni della riscoperta dei classici. Il caso di Francesco Maurolico (1494-1575) ‒ con le libertà totali che si prendeva rispetto ai testi che andava studiando ‒ è esemplare; ma uno studio attento potrebbe rivelare la presenza di questo fenomeno anche in Federico Commandino (1509-1575), assai più attento al rispetto filologico dei testi antichi.
La stagione della riscoperta può considerarsi chiusa nel 1575, anno in cui muoiono Maurolico e Commandino; da quel momento inizia la fase della riappropriazione. Riappropriarsi di Archimede significa completarne e riprenderne l'opera; implica una riflessione metodologica sul complesso della geometria di misura e sulle sue relazioni con la meccanica. Un discorso analogo, anche se assai più complesso, vale per la geometria di posizione e le problematiche legate al metodo di analisi e sintesi.
È in questo processo di riappropriazione e di reinterpretazione che si iscrive l'opera di Luca Valerio (1553-1618) e di Bonaventura Cavalieri (1598 ca.-1647). Il primo operò un radicale cambiamento dal punto di vista metodologico, aprendo prospettive per la ricerca che si spingevano ben al di là del panorama della geometria classica; il secondo si inoltrò in questo nuovo territorio edificandovi il suo metodo degli indivisibili. In un certo senso, Valerio è il Cristoforo Colombo della situazione, che scopre un nuovo mondo credendo di essere giunto alle rive del Catai; mentre Cavalieri è l'Hernán Cortés che in quel nuovo mondo pone le fondamenta di un nuovo impero.
Punto di partenza di entrambi furono gli oggetti, i metodi e le tecniche dimostrative della geometria classica e in particolare di quella archimedea. Varrà la pena di spendere qualche parola su di essi, per poter poi meglio apprezzare la portata dell'opera di questi due innovatori.
Oggetti e metodi della matematica greca
Un dato che differenzia profondamente la matematica greca dalla nostra è che gli oggetti della geometria classica sono sempre particolari, dati attraverso una procedura costruttiva più o meno assiomatizzata. Gli assiomi di Euclide permettono l'esistenza di rette e cerchi; una procedura implicita (tagliare un dato cono con un dato piano) permette l'esistenza delle sezioni coniche di Apollonio. Lo scopo della geometria è, per i Greci, quello di studiare tali oggetti e di determinarne le proprietà.
Questo atteggiamento è assai diverso da quello moderno, postcartesiano. Per noi un'ellisse è il luogo di zeri di un'equazione di secondo grado, o, in trattazioni più elementari, 'il luogo dei punti tali che la somma delle distanze da due punti fissi è costante'. La proprietà preesiste all'oggetto che, a priori, potrebbe anche essere vuoto. Per i Greci, invece, l'ellisse è l'oggetto determinato da un piano che tagli un cono incontrandone tutte le generatrici: tale curva esiste, dunque, ma se ne ignorano tutte le proprietà, che dovranno essere indagate. Non a caso i fuochi dell'ellisse e dell'iperbole sono introdotti da Apollonio solo alla fine del Libro III delle sue Coniche. L'oggetto preesiste alle sue proprietà. Una conseguenza immediata di tale modo di considerare gli oggetti geometrici, è che, per i Greci, non possono esistere oggetti generali. Nella geometria classica non esiste qualcosa di simile alle nostre 'curve'. Esistono varie linee curve ‒ come il cerchio, le coniche, la concoide, la cissoide, la spirale, la quadratrice ‒ ma non esiste un'unica categoria concettuale che le abbracci tutte. Ciascuna di queste curve è definita da una speciale procedura; anche se in alcuni casi una certa curva ottenuta con una certa procedura potrà essere identificata con un'altra curva ottenuta con un'altra procedura. Per esempio, la circonferenza euclidea si identificherà con la sezione parallela o subcontraria di un cono; la sezione del cono che produce l'ellisse si identificherà con la sezione obliqua del cilindro; tuttavia ogni curva manterrà la sua identità, la sua singolarità. Inoltre, non esistendo oggetti generali, non possono esistere nemmeno metodi generali: nella geometria di misura archimedea non c'è nulla di simile al nostro calcolo integrale, il quale si applica a certe classi di funzioni che rispondano a determinati requisiti. Anche se in Archimede troviamo metodi per il calcolo di aree e volumi in cui ricorrono concetti e tecniche che ricordano i nostri, c'è una differenza fondamentale: tali metodi intervengono sempre ad hoc, a seconda del tipo di situazione che si deve affrontare. Così, la quadratura della parabola (almeno nella sua forma meccanica) verrà trattata in modo radicalmente diverso da quella del cerchio; per lo studio delle spirali si svilupperanno metodi del tutto diversi da quelli concepiti per i conoidi e gli sferoidi, a loro volta ancora diversi da quelli utilizzati per determinare il rapporto fra la sfera e il cilindro ad essa circoscritto. Si usa dire che Archimede e i Greci utilizzassero il 'metodo di esaustione'. Ma, a rigor di termini, tale metodo non esiste nella geometria greca, almeno come metodo codificato di determinazione di rapporti volumetrici. È vero che tutta una serie di teoremi di Euclide e di Archimede si basano su una tecnica comune: per provare che due figure sono uguali, si dimostra con una doppia riduzione all'assurdo che una delle due non può essere né maggiore né minore dell'altra, e tale doppia riduzione è in genere ottenuta lavorando su figure 'note' che si approssimano alla figura data. Ma, come abbiamo accennato prima, la messa in opera di questa tecnica è soggetta ad amplissimi margini di variabilità. Bisogna anche aggiungere che, per quanto ci è dato sapere, era sfruttata appieno soltanto da Archimede e con considerevole difficoltà, come attesta la lettera con cui inviava a Dositeo i Conoidi e sferoidi. Il 'metodo di esaustione', insomma, è una comoda etichetta storiografica che permette di identificare a posteriori procedure che possiedono un'indubbia analogia, ma nulla di più.
La svolta metodologica di Valerio
Come accennavamo in precedenza, la figura di Valerio rappresenta il momento di passaggio fra la matematica rinascimentale e umanistica, ancora orientata al recupero e alla comprensione dei classici, e quella moderna. Il suo De centro gravitatis solidorum (1604) è un libro di importanza epocale: pur rimanendo fedele al linguaggio della matematica archimedea, il De centro può essere considerato l'ultimo testo della geometria di misura antica. In esso, infatti, erano proposti metodi e punti di vista talmente nuovi che, dopo Valerio, la geometria sarà costretta a prendere strade che la porteranno a staccarsi definitivamente dal modello greco. Non a caso, la lettura di questo testo entusiasmò Galilei al punto da spingerlo a dichiarare che Valerio era il "nuovo Archimede dell'età nostra" e da indurlo ad abbandonare le sue ricerche giovanili nel campo dei centri di gravità dei solidi. Inoltre la sua influenza sui matematici del primo Seicento ‒ Cavalieri, Torricelli, Guldin e altri ancora ‒ è palpabile e ben documentabile.
Il problema che Valerio affrontava e risolveva nel De centro era quello di determinare il centro di gravità di tutti i solidi allora conosciuti: sfera, cono, piramide, prisma, cilindro, poliedri, paraboloide, iperboloide, ellissoide, e loro parti. Dovrebbe esser chiaro, da quanto si è detto, che l'approccio classico non aveva esteso lo studio delle figure solide al di là di quelle considerate da Euclide o da Archimede: per brevità chiameremo questo gruppo eterogeneo di oggetti 'solidi archimedei'.
Quello affrontato da Valerio era un problema aperto e fra i più studiati dalla matematica della fine del XVI sec., anche perché si poneva come il necessario completamento dell'opera di Archimede, che trattava solo dei centri di gravità delle figure piane. Commandino aveva pubblicato nel 1565 un Liber de centro gravitatis solidorum che però era ben lungi dall'essere soddisfacente: molte dimostrazioni lasciavano a desiderare e, soprattutto, i casi più spinosi non erano nemmeno stati affrontati (per es., la determinazione dei centri di gravità dei segmenti della sfera e dell'ellissoide, nonché del centro di gravità dell'iperboloide di rotazione). Altri studiosi si erano cimentati in questa impresa: Francesco Maurolico, Simon Stevin, il giovane Galilei, lo stesso maestro di Valerio, Cristoforo Clavio. Tuttavia, o i risultati non erano stati pubblicati, o non avevano conosciuto una grande diffusione. E, in nessun caso, si era mai arrivati alla determinazione dei centri di gravità dell'emisfero e dell'iperboloide. Un aspetto comune a tutti i tentativi cinquecenteschi che ci sono pervenuti è la sostanziale adesione al modello antico: i centri di gravità dei vari solidi erano affrontati caso per caso, introducendo tecniche ad hoc per ogni solido studiato. Valerio seguì un'altra strada. Invece di affrontare singolarmente il problema della determinazione dei centri di gravità e delle quadrature, costruì una vasta architettura di teoremi relativi a un'intera classe di figure ‒ le figure digradanti circa axim e circa diametrum ‒ dotate di un asse di simmetria e le cui sezioni vanno costantemente decrescendo. In questa costruzione egli inquadrò la ricerca della determinazione delle quadrature e dei centri di gravità delle figure particolari che si trovava ad affrontare.
Valerio compiva così un passo fondamentale di distacco dal modello classico. Per anticipare un esempio che tratteremo estesamente in seguito, la determinazione del centro di gravità dell'iperboloide (come osserva con orgoglio Valerio, "antea tentata nemini") è ridotta all'applicazione di un teorema generale riguardante i centri di gravità delle figure circa axim e circa diametrum. Di tale rottura metodologica Valerio era pienamente consapevole ed essa ebbe una grande influenza sulla matematica successiva, in particolare su Cavalieri, che fu profondamente influenzato anche da singole tecniche utilizzate da Valerio, contenenti molti aspetti di quello che sarà il metodo degli indivisibili.
La seconda importante innovazione metodologica di Valerio è l'invenzione del 'metodo di esaustione'. Ci rendiamo benissimo conto che con questa affermazione ci opponiamo a gran parte della storiografia comunemente accettata. Tuttavia è a Valerio che per primo si deve far risalire la formalizzazione di un metodo per affrontare i confronti volumetrici, quale è quello codificato nei primi tre teoremi del Libro II del De centro: un passo, questo, che segue un distacco netto dall'accettazione di un 'modo di fare' più o meno standardizzato.
C'è anche una terza innovazione, più complessa da descrivere. In Valerio si può infatti osservare un primo tentativo di separare la quantità dalla forma nelle figure della geometria. Si tratta di un passo compiuto con mille cautele e mille esitazioni; ma sta di fatto che si possono trovare numerosi luoghi della sua opera in cui egli tratta le figure della geometria come pezzi ricomponibili e distaccabili, avvicinandosi a una dissoluzione completa della forma a favore di pure considerazioni quantitative. È questa una delle innovazioni più importanti, ma, al tempo stesso, è proprio qui che si possono riscontrare con maggiore chiarezza i limiti della sua impostazione, ancora legata al modello archimedeo.
Valerio introdusse dunque importanti cambiamenti e novità nella matematica del suo tempo, in special modo sul piano metodologico. Tuttavia, come tutti gli innovatori, si ritrovò a cavallo fra il vecchio e il nuovo. I suoi metodi generali si trovano mescolati ad argomenti tradizionali, senza che, almeno a prima vista, si riesca bene a capirne il motivo. Sembra quasi che, spaventato dalla sua stessa audacia innovativa, cercasse rifugio nel porto sicuro dello stile archimedeo.
Gli indivisibili di Cavalieri
Cavalieri inizia la sua opera là dove Valerio aveva smarrito il sentiero. Una caratteristica della sua Geometria indivisibilibus continuorum nova quadam ratione promota (1635) è infatti non tanto o non solo di proporre un metodo generale (quello degli indivisibili, appunto) per affrontare i problemi di quadratura e di determinazione di centri di gravità, quanto quello di proporre una teoria capace di inquadrare questo nuovo strumento nel contesto della geometria.
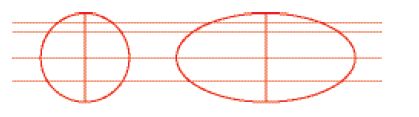
Già in Valerio infatti (e in altri autori del primo Seicento come Bartolomeo Sovero, 1576-1629) si trova l'uso di quello che sarà poi chiamato il 'principio di Cavalieri': se due figure piane sono poste tra due rette parallele, e se condotte due rette qualunque si troverà che le porzioni staccate dalle due figure sono sempre proporzionali, allora le figure staranno fra loro come una delle linee in una figura alla linea corrispondente dell'altra (fig. 3).
Anche in Valerio è dimostrato un principio del genere, in un caso particolare (e più complicato), quello della determinazione dei centri di gravità di certe classi di figure; e lo si può trovare anche in Sovero, ma dimostrato limitatamente alle sezioni coniche. Cavalieri, al contrario, vuole dimostrare le basi del suo metodo, per classi di figure arbitrarie, una volta per tutte. E dimostrare significa per lui cercare di far rientrare le idee innovatrici che propone nella teoria euclidea delle proporzioni.
Questa duplice esigenza (rigorose dimostrazioni geometriche e generalità dell'oggetto cui esse si devono applicare) è all'origine non solo della sua opera, ma anche del destino che sarebbe toccato al metodo e alla teoria degli indivisibili. A un metodo chiaro si contrappone una teoria oscura e involuta nelle dimostrazioni. Assistiamo così a un impressionante successo del metodo, che permette a Cavalieri di conseguire rapidamente non solo i risultati della matematica classica e quelli più recenti ottenuti dalla ricerca del primo Seicento (per es., quelli di Valerio e quelli raggiunti da Kepler con i 'nuovi' solidi da lui introdotti), ma anche risultati decisamente nuovi come la determinazione delle quadrature delle parabole di ordine superiore ‒ in linguaggio moderno la dimostrazione che
‒ o lo studio dei centri di gravità di solidi a densità variabile. Il metodo, oltre che dallo stesso Cavalieri, è adottato e in vario modo sviluppato da matematici di primo piano: Torricelli, Pascal, Roberval, Wallis, per non citarne che alcuni. Un successo impressionante, destinato a durare per molti decenni e a sopravvivere addirittura ‒ almeno per qualche tempo ‒ all'invenzione del calcolo infinitesimale.
A fronte di questi risultati sta, come dicevamo, l'oscurità della teoria. Discuteremo più avanti gli aspetti teorici (o, se si vuole, 'fondazionali') degli indivisibili, ma vale la pena di rilevare fin da ora un punto importante. Abbiamo sottolineato che, nella matematica greca non esistono oggetti generali. È bene però precisare che esiste un'importante eccezione: la teoria delle proporzioni fra grandezze, codificata da Euclide nel Libro V degli Elementi. La teoria euclidea delle proporzioni si presenta infatti come una dottrina compatta e generale che può essere applicata a qualsiasi sorta di ente geometrico: linee, superfici, solidi. Anzi, nel corso del Medioevo e, soprattutto, del XVI sec. e dei primi anni del XVII, si era precisata una tendenza di ricerca che puntava a includere nell'ambito della teoria tutto ciò che 'in qualche modo ha l'odore di quantità': suoni, pesi, velocità, pesi specifici. La teoria delle proporzioni diventa, soprattutto in Galilei, lo strumento con cui costruire modelli geometrici del mondo fisico. Ma bisogna ricordare che si tratta di uno strumento che conosce limitazioni e rigidità assai pesanti. La riflessione di Galilei sulle leggi del moto e i suoi tentativi di costruire un modello matematico in cui fosse possibile dedurre la legge oraria della caduta dei gravi (gli spazi percorsi sono proporzionali ai quadrati dei tempi di caduta) possono essere letti come una continua lotta contro le rigidità e le angustie dello strumento matematico di cui disponeva. Al tempo stesso, la generalità della teoria euclidea appare quasi eccessiva e soggetta ad ampi margini di ambiguità: mai in Euclide o in altre parti del corpus matematico classico è precisato cosa siano le grandezze di cui la teoria delle proporzioni si occupa.
Torniamo allora a Cavalieri. Costruire una teoria degli indivisibili fondata su dimostrazioni geometriche e capace di trattare classi di figure arbitrarie significa dover confrontarsi con l'unica teoria disponibile dotata di altrettanta generalità. Cavalieri deve cioè far vedere che i suoi indivisibili (o, meglio, 'tutte le linee' ‒ "omnes lineae" ‒ di una figura) possono essere trattati dalla teoria delle proporzioni; ossia mostrare che 'tutte le linee' di una figura costituiscono un nuovo oggetto matematico, capace di soddisfare le definizioni euclidee del Libro V. Impresa non facile, dati i limiti e le costrizioni imposti da un tale modello, e per di più ambiziosa, che porterà la teoria di Cavalieri a scontrarsi con numerose obiezioni e critiche. È infatti contro il tentativo di trasformare gli indivisibili in un nuovo oggetto geometrico che si scaglieranno i numerosi oppositori di Cavalieri, primo di tutti il gesuita Paul Guldin (1577-1643). La critica di Guldin si appunta infatti su di un'ambiguità sostanziale del nuovo oggetto che Cavalieri vuole introdurre in geometria: 'tutte le linee' di una figura sono infinite e, pertanto, non possono rientrare fra le grandezze euclidee.
In effetti, come è stato più volte sottolineato (Giusti 1980, 1982, 1999), gli indivisibili di Cavalieri ‒ nonostante gli sforzi del loro creatore ‒ non riusciranno mai a staccarsi dal carattere strumentale: "alla domanda: quali sono tutte le linee di questa figura? non si può rispondere che indicando la figura stessa" (Giusti 1999, p. 54). Persino le meditazioni di Cavalieri su come fornire al suo metodo salde basi geometriche, esposte nelle Exercitationes geometricae sex (1647), lo porteranno a sviluppare una risposta in qualche modo di retroguardia: a tentare cioè di giustificare gli indivisibili alla luce dei metodi classici. È questa l'essenza del cosiddetto 'secondo metodo degli indivisibili' in cui è implicita una rinuncia a formalizzare in modo autonomo il concetto di 'tutte le linee'.
Reinseriti nell'ambito dei metodi della geometria classica, gli indivisibili regrediscono a pure tecniche di dimostrazione, che sopravviveranno solo fin quando riusciranno a dare dei risultati. Alla fine del secolo, una volta esaurita la loro forza, essi svaniranno per lasciare il posto ai metodi più potenti del calcolo infinitesimale. (Giusti 1999, p. 55)
Anche il tentativo e il successo di Cavalieri sembrano dunque, alla fin fine, arenarsi nelle stesse secche in cui si era smarrita la via regia di Valerio.
Il linguaggio della teoria classica delle proporzioni e, più in generale, il contesto matematico ereditato dalla geometria greca non permettevano di sviluppare problemi generali adeguati ai metodi generali che erano stati introdotti. La via verso questi metodi era stata aperta da Valerio, portata molto avanti da Cavalieri; ma, da un lato, gli oggetti con cui tali metodi si confrontavano erano stati praticamente esauriti dal successo dei metodi stessi; dall'altro difficoltà teoriche apparentemente insormontabili si ergevano di fronte al tentativo di trasformare i nuovi strumenti dimostrativi in oggetti autonomi di ricerca.
Luca Valerio
Un problema aperto: la determinazione dei centri di gravità dei solidi
Come abbiamo accennato, nella seconda metà del Cinquecento lo studio dei centri di gravità destava molto interesse. Nel 1565 Commandino era arrivato a determinare i centri di gravità della piramide e del cono e a fornire una dimostrazione per quello del paraboloide (o 'conoide parabolico', secondo la terminologia dell'epoca). Va però osservato che era giunto a un tale risultato studiando i Galleggianti di Archimede e deducendone che il centro di gravità del paraboloide divide l'asse nel rapporto 1:2. È evidente che tentare la dimostrazione di un risultato noto è assai più facile che cercare la determinazione di un centro di gravità la cui posizione sia sconosciuta; e infatti per tutto il XVI sec. non fu fatto nessun progresso in direzione della determinazione del centro di gravità dell'iperboloide di rotazione (conoide iperbolico) o dell'emisfero o del semiellissoide (emisferoide).
Questi solidi (conoidi parabolico e iperbolico, e sferoidi) erano peraltro ben noti ai cultori di geometria archimedea, poiché Archimede aveva dedicato loro un intero libro, i Conoidi e sferoidi, nel quale determinava il rapporto fra il conoide o una parte di sferoide e il cilindro circoscritto (per es., il conoide parabolico è la metà del cilindro). Una trattazione esauriente dei centri di gravità dei solidi doveva necessariamente affrontare questi solidi archimedei. A tale scopo, il primo passo consisteva nel dimostrare che il loro centro di gravità si trova sull'asse; una dimostrazione i cui materiali erano già reperibili in Archimede.
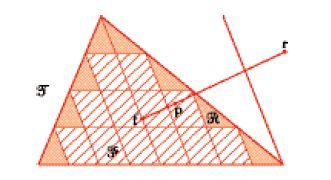
Nell'Equilibrio dei piani (propp. I.13 e II.4) si dimostra infatti che i centri di gravità del triangolo e di un segmento di parabola si trovano, rispettivamente, sulla mediana e sul diametro: si inscriva (fig. 6) nel triangolo ℑ una figura ℱ fatta di parallelogrammi.
Si sa che: (a) il centro di gravità della figura inscritta ℱ si trova sempre sulla mediana; (b) il residuo ℛ=ℑ−ℱ può essere reso piccolo a piacere prendendo l'altezza dei singoli parallelogrammi abbastanza piccola (fatto che si dimostra facendo ricorso, essenzialmente, alla X.1. degli Elementi e al cosiddetto 'postulato di Eudosso-Archimede').
Si supponga ora che il centro di gravità dell'intero triangolo ℱ non cada sulla mediana, ma nel punto p. Sia f il centro di gravità della figura inscritta ℱ: esso dovrà però trovarsi sulla mediana. Siccome ℱ+ℛ=ℑ, il centro di gravità r del 'residuo' ℛ si trova sul prolungamento della retta fp, in modo che rp:pf=ℱ:R. Poiché ℛ può essere piccolo a piacere (cioè, il rapporto ℱ:R grande a piacere), e p è un punto fisso fuori della mediana, il punto r, centro di gravità di ℛ, al diminuire di ℛ, sarebbe scacciato fuori dal triangolo, anzi, fuori dal semipiano in cui si trova il triangolo, il che è assurdo.
Per la parabola la costruzione delle figure approssimanti è assai diversa (Archimede utilizza i poligoni introdotti nella quadratura geometrica della parabola), ma l'idea fondamentale della dimostrazione è la stessa.
Le due dimostrazioni dell'Equilibrio dei piani si basano dunque sulla stessa idea: per dimostrare che il centro di gravità di una figura dotata di diametro o di asse cade sul diametro o sull'asse, basta disporre di figure approssimanti aventi centro di gravità sull'asse. Questo punto era stato in qualche modo colto da Commandino, che nel suo Liber de centro gravitatis aveva proposto una serie di dimostrazioni da cui si evinceva che i centri di gravità della piramide, del cono, di una porzione di sfera o di sferoide e del conoide parabolico o iperbolico si trovavano sull'asse (inteso come la retta che congiunge il vertice con il centro di gravità della base). Commandino cominciava con il dimostrare che a tali figure si possono inscrivere e circoscrivere figure a scalini fatte di cilindri (prismi nel caso della piramide) in modo tale che la differenza fra la figura inscritta e circoscritta possa essere resa piccola a piacere.
La tecnica seguita da Commandino per ottenere questi lemmi di approssimazione ricalcava da vicino quelle usate da Archimede nei Conoidi e sferoidi, in particolare quella della proposizione 19 secondo la quale la differenza fra lo scaloide circoscritto e quello inscritto è uguale al cilindretto di base (fig. 7). Tale tecnica era stata condensata da Archimede in un'unica proposizione, in cui si trattano simultaneamente i due conoidi (parabolico e iperbolico) e i due sferoidi (allungato e appiattito). Commandino, riprendendola, la suddivide in vari enunciati, uno per ciascuna delle figure che considera. Il procedimento è di questo tipo:
a) si circoscriva al conoide o allo sferoide una figura a scalini formata da cilindri;
b) la differenza delle figure circoscritte e inscritte è uguale al cilindretto base (qui è utilizzata la 'monotonia' del conoide o dello sferoide);
c) tale differenza può essere piccola a piacere, dato che il cilindretto può essere preso più piccolo di qualsiasi quantità prefissata.
È importante osservare che, per eseguire la costruzione, in tutti i casi considerati Archimede e Commandino sfruttano la 'monotonia' della figura in questione, ossia il fatto che le sezioni vanno costantemente decrescendo dalla base verso il vertice: non a caso è esplicitamente specificato che la porzione di sfera o di sferoide non deve essere maggiore della metà.
Ottenute così le sue figure approssimanti, Commandino passa a dimostrare che il centro di gravità del cono o della piramide (Liber de centro gravitatis, prop. 14) e del conoide parabolico o di una porzione di sfera o di sferoide (ibidem, prop. 15) si trova sull'asse, ricalcando da vicino la tecnica usata da Archimede per il triangolo e la parabola. Questo risultato, pur non eccessivamente difficile da ottenere, è però importante. Infatti esso ‒ sia pure con dimostrazioni alquanto farraginose e tediosamente ripetitive ‒ coniuga due tecniche archimedee: quella di approssimazione dei Conoidi e sferoidi e quella per la dimostrazione dell'appartenenza del centro di gravità all'asse. È da notare che Commandino era consapevole della sostanziale identità di tecnica dimostrativa, tanto che la dimostrazione della proposizione 13 (approssimazione di una porzione di sfera) consiste in un rinvio ai Conoidi e sferoidi, sottolineando che la tecnica è la stessa di quella appena utilizzata per il cono o il tronco di cono (propp. 11 e 12). Allo stesso modo, dopo aver dimostrato ‒ utilizzando la tecnica usata da Archimede nell'Equilibrio dei piani ‒ che il centro di gravità del cono e della piramide si devono trovare sull'asse (prop. 14), Commandino passa a dimostrare lo stesso fatto per i conoidi e la porzione di sfera o di sferoide e scrive: "La dimostrazione sarà simile a quella che abbiamo dato qui sopra per il cono o il tronco di cono, per non stare a ripetere inultilmente tante volte le stesse cose" (Liber de centro gravitatis, prop. 15).
Tuttavia, benché si rendesse conto che la dimostrazione è la stessa per tutte le figure, non si preoccupò affatto di estrarre un metodo generale, limitandosi ad aggiungere all'opera di Archimede alcuni teoremi come avrebbe potuto fare Archimede stesso.
Un nuovo punto di vista
Non c'è il minimo dubbio che fu proprio lo studio dell'opera di Commandino una delle fonti principali di riflessione metodologica di Luca Valerio, come afferma egli stesso nella prefazione del De centro gravitatis solidorum: "Sono partito cercando di rifare il lavoro di Commandino e vedendo se potevo trovare altre vie dimostrative che mi portassero, non solo a far meglio di lui, ma anche a spingermi più lontano" (De centro gravitatis solidorum, pref., pp. 1-2). Per cercare di dare un'idea delle novità introdotte da Valerio utilizzeremo un teorema relativamente semplice, la proposizione 22 del Libro I, la cui dimostrazione deriva molto probabilmente da quella riflessione metodologica sul libro di Commandino cui accennavamo sopra: "Il centro di gravità di ogni figura circa diametrum in alteram partem deficiens si trova sul diametro" (ibidem, prop. I.22, p. 47).
Ci serviremo di esso per spiegare cosa siano le figure circa diametrum e circa axim e per vedere come Valerio trasformi le tecniche dimostrative preesistenti nella definizione di un nuovo oggetto di indagine: le figure digradanti.
Abbiamo visto che per dimostrare la posizione del centro di gravità di una figura piana dotata di diametro (nel senso di una retta che dimezzi tutte le corde tracciate secondo una direzione assegnata) o di asse (inteso come la retta che congiunga il vertice di una figura solida con il centro di gravità della sua base) basta approssimare tale figura con altre, il cui centro di gravità cada per l'appunto sull'asse o sul diametro. Commandino aveva ben chiarito questo punto. Resta ora da chiedersi quali proprietà occorra supporre per poter costruire le figure approssimanti necessarie, una volta assegnata una figura dotata di diametro. Abbiamo già accennato alla risposta: è sufficiente che la figura goda di una proprietà di 'monotonia' ‒ cioè che le sezioni che il diametro dimezza vadano costantemente decrescendo dalla base della figura verso il suo vertice, il punto cioè in cui il diametro incontra la figura stessa. Valerio si pose questa domanda e trovò la risposta che abbiamo appena ricordato, compiendo così un salto di generalità notevole rispetto ad Archimede o a Commandino. Inoltre, trasformò una proprietà (la monotonia) dei conoidi, che permetteva di utilizzare una certa tecnica dimostrativa, in una definizione ‒ quella delle figure "digradanti intorno a un diametro o intorno a un asse" ‒ che gli assicurasse automaticamente l'esistenza delle figure approssimanti:
Definizione 2. Una figura piana circa diametrum è una figura in cui una retta, detta diametro della figura, divide a metà tutte le parallele ad una qualche retta, aventi gli estremi sulla figura stessa. (ibidem, I, def. 2, p. 3)
Definizione 7. Se una figura solida si può tagliare con piani paralleli in modo che tutte le sezioni abbiano un centro e siano tra loro simili e inoltre esiste una retta che passi per i centri delle basi opposte (come nel cilindro), o per il vertice e il centro della base (come nel cono, nell'emisfero o nel conoide), attraversando i centri di tutte le predette sezioni, chiameremo tale retta asse della figura stessa e il solido, solido circa axim. Si chiamerà poi solido "digradante intorno a un asse" [circa axim in alteram partem deficiens] se tra due qualsiasi delle predette sezioni quella più vicina al vertice (o alla base minore) è sempre la più piccola, e ciò sia nel caso che la figura abbia una base sola o due, disuguali e parallele. (ibidem, I, def. 7, pp. 4-5)
Il lettore potrà forse osservare che Valerio non introduce esplicitamente per le figure circa diametrum la proprietà di monotonia di cui parlavamo, ovvero che le corde dimezzate vadano costantemente decrescendo. Si tratta di una delle tante imperfezioni e oscurità che si possono trovare nel De centro. E tuttavia l'uso che intende fare di tali definizioni è chiarissimo. Infatti, poste queste basi, gli risulta assai facile dimostrare un teorema di approssimazione che valga non più in molti casi, ma per tutta la classe di figure che è stata così introdotta. Nelle proposizioni 6 e 11 del Libro I si legge:
Proposizione 6. Si può iscrivere ad ogni figura digradante intorno a un diametro [circa diametrum in alteram partem deficiens] una figura fatta di parallelogrammi tutti di ugual altezza e circoscriverne un'altra, in modo che la circoscritta superi l'inscritta per una superficie minore di qualsiasi grandezza assegnata. (ibidem, prop. I.6, p. 14)
Proposizione 11. Ad ogni solido digradante intorno a un asse, la cui base sia un cerchio (o un'ellisse) si può iscrivere una figura fatta di cilindri (o di porzioni di cilindro) tutti di uguale altezza e circoscriverne un'altra, in modo che la circoscritta superi l'inscritta per un eccesso minore di una qualsiasi grandezza assegnata. (ibidem, prop. I.11, p. 26)
La dimostrazione ricalca le linee delle analoghe dimostrazioni di Archimede e Commandino. Vale però la pena di sottolineare ancora una volta il passo che è qui compiuto: Valerio non soltanto dimostra in un colpo solo tutto ciò che Archimede e Commandino avevano dimostrato al riguardo, ma introduce un teorema generale, riguardante un nuovo oggetto ‒ le figure digradanti ‒ che sfrutterà abbondantemente nel corso della sua opera e non soltanto per i casi fin qui considerati. La geometria finora conosceva esclusivamente oggetti nominati: adesso, per la prima volta, sono introdotte classi di curve definite in base a una proprietà. Così, sempre in un colpo solo, Valerio può facilmente dimostrare la proposizione I.22: ogni figura digradante intorno a un diametro ha il suo centro di gravità sul diametro. La teoria delle figure digradanti introdotte dalle definizioni 2 e 7 ha già un corpus di teoremi, piccolo, ma importante: un teorema di approssimazione e uno sulla posizione del centro di gravità.
Si potrebbe obiettare che procedimenti simili non erano del tutto ignoti alla geometria classica e che, per esempio, Apollonio aveva definito il diametro e l'asse per una curva qualsiasi, mentre Archimede aveva abbondato in lemmi 'generali' su grandezze non meglio specificate. La somiglianza, tuttavia, è a nostro avviso soltanto superficiale. Il diametro apolloniano delle curve o i lemmi archimedei sulle grandezze si riferiscono a oggetti generici, non generali, mentre i teoremi di Valerio (di cui abbiamo visto per ora solamente un piccolo esempio) si riferiscono a classi di figure ben definite da una serie di proprietà. Inoltre non ci è noto alcun uso del concetto di diametro al di fuori della teoria delle sezioni coniche, e i lemmi che Archimede introduce sono appunto lemmi, proposizioni finalizzate ad essere utilizzate nel corso di un teorema successivo. I risultati di Valerio, invece, si propongono come una teoria riguardante gli oggetti che ha introdotto: le figure digradanti. Un mutamento di prospettiva assai notevole rispetto alla geometria classica che il Rinascimento aveva ereditato.
L'invenzione del metodo di esaustione
Il contributo di Valerio allo svincolamento della matematica dal paradigma classico non si esaurisce peraltro in quello che abbiamo qui sopra descritto. Di pari importanza è la generalizzazione, da parte sua, delle tecniche di approssimazione di Euclide e di Archimede. Quello che nella matematica greca era stato un 'modo di fare' mai codificato esattamente e che soltanto pochi grandi matematici (forse il solo Archimede) riuscivano a dominare, diventa in Valerio un vero metodo generale. Nelle prime tre proposizioni del Libro II del De centro, Valerio propone infatti un metodo che può riassumersi in questi termini: se, date due grandezze A e B, si possono determinare delle grandezze approssimanti E e F (tali cioè che le differenze A−E e B−F possano essere rese piccole a piacere) che stanno in un rapporto costante, allora anche A e B staranno nello stesso rapporto.
In questo modo Valerio riusciva a estrarre dalle ricette archimedee un principio generale: un metodo, appunto. C'è chi ha voluto vedere in queste proposizioni di Valerio un'anticipazione del concetto di limite, facendo di Valerio un precursore di Cauchy: le proposizioni in questione equivarrebbero al teorema di analisi che afferma che il limite di un rapporto è uguale al rapporto dei limiti.
A noi sembra assai più fruttuoso pensare Valerio come il vero inventore del 'metodo di esaustione'. Non a caso, nel XVII sec. il suo approccio al problema dell'approssimazione sarà ampiamente ripreso. Al riguardo si possono citare, fra gli altri, Giovanni Alfonso Borelli, con il suo Euclides restitutus (1658), e Gilles Personne de Roberval (éléments de géométrie). Sarà inoltre proprio un matematico uscito dalla scuola di Clavio, Grégoire de Saint-Vincent, a inventare il nome per il metodo che Valerio era riuscito per primo a codificare.
Le prime tre proposizioni del De centro e le applicazioni che Valerio ne fa sono notissime. La più famosa è senz'altro la determinazione del volume dell'emisfero, il risultato per cui Galilei lo loderà nei Discorsi come "nuovo Archimede". Ma si potrebbero citare anche la determinazione del volume del paraboloide, del tronco di cono, e altre ancora. Non ci sembra il caso di riportarne un esempio, mentre vale la pena di sottolineare l'analogia che sussiste fra il passaggio da una proprietà di certe figure alla definizione della classe delle figure digradanti, da una parte, e la generalizzazione delle tecniche di approssimazione greche, trasformate ora in un metodo di dimostrazione uniforme, dall'altra. Le prime tre proposizioni del Libro II, nel loro insieme, permettono di trattare in modo automatico tutti i casi che nella geometria greca richiedevano argomentazioni complicate per passare dall'esistenza di figure inscritte (o circoscritte) che soddisfacessero certe condizioni, alle conclusioni volute.
Si tratta di un metodo che rimane tutto interno al paradigma della teoria euclidea delle proporzioni, di cui costituisce una sorta di sviluppo. I primi tre teoremi del Libro II sono utilizzati esattamente allo stesso modo dei teoremi generali del Libro V degli Elementi, là dove Euclide aveva stabilito tutta una serie di tecniche per trattare le proporzioni fra grandezze: permutando, componendo, ex aequali; tecniche che, nel linguaggio della geometria greca, sono citate ogni volta che si pone la necessità di dedurre una proporzione da un'altra. In casi particolari, molto complessi, un'opportuna serie di lemmi posti all'inizio di un'opera ‒ è il caso di vari scritti di Archimede ‒ serve a condensare una tecnica che, applicata nel corso di un teorema, tenderebbe a oscurare le linee della dimostrazione. Ci sembra che la stessa analisi possa essere ripetuta per i teoremi di Valerio, che vengono a essere, nell'economia della sua opera, una sorta di 'lemmi generali' da citare ogni volta che sarà necessario. Non possono essere visti disgiunti dalle loro applicazioni, che si tratti del rapporto del tronco di cono al cilindro circoscritto o del paraboloide al cono a lui inscritto. Non entreremo qui nel merito di una discussione della letteratura che ha voluto vedere in Valerio un precursore dei concetti del calcolo e dell'analisi. Ci limiteremo a osservare come il contributo di Valerio non possa in alcun modo essere visto come una trasformazione del modello della teoria delle proporzioni in una teoria che permetta un calcolo effettivo con i limiti, intesi in senso moderno. Il suo contributo rimane inscritto nel paradigma classico, pur apportandovi una modifica essenziale: un metodo generale che permette di trattare in modo uniforme i problemi di quadratura. Più che il precursore della teoria dei limiti, Valerio è l'inventore del metodo di esaustione.
Un teorema generale
Se Valerio si fosse fermato a questo punto ‒ a ridimostrare cioè in generale risultati già noti in casi particolari ‒, ciò che abbiamo visto finora non sarebbe particolarmente significativo. Da un lato, infatti, non avrebbe aggiunto alcunché di nuovo alle conoscenze matematiche esistenti; dall'altro, dato che i membri delle sue classi di figure digradanti che erano noti all'epoca si riducono essenzialmente a solidi e a figure piane già studiate da Archimede e dal suo seguace Commandino, la sua operazione sarebbe stata puramente nominalistica. La sua stessa via regia (quella condensata nelle propp. 1-3 del Libro II del De centro) avrebbe rivestito un interesse molto limitato, dato che in definitiva era utilizzata soltanto per ricavare in modo più conciso e uniforme risultati ben noti. Molti problemi relativi alla geometria di misura sarebbero stati meglio inquadrati, certo, ma l'introduzione di oggetti e metodi generali non avrebbe portato alcun reale accrescimento delle conoscenze matematiche.
Tuttavia, le cose stanno altrimenti. Le figure digradanti di Valerio non sono infatti solamente una comoda etichetta che permette di esprimere molti risultati noti con pochi teoremi, ma sono anche un mezzo di invenzione e scoperta.
Abbiamo visto che uno dei problemi centrali della ricerca matematica dell'epoca era quello di riuscire a determinare i centri di gravità dell'ellissoide e dell'iperboloide, oltre che una dimostrazione corretta del centro del paraboloide. Fu studiando quest'ultimo problema che Valerio ebbe un'intuizione geniale. È relativamente facile rendersi conto (come era accaduto a Maurolico e anche al giovane Galilei) che la determinazione del centro di gravità del paraboloide può essere ridotta facilmente a quella del triangolo. I cerchi-sezione del paraboloide, infatti, sono proporzionali ai quadrati del loro raggio: ma il loro raggio è l'ordinata della parabola generatrice e il suo quadrato è proporzionale all'ascissa, che, a sua volta, è l'altezza del triangolo inscritto nel paraboloide, la quale è ovviamente proporzionale alla base del triangolo stesso. La conclusione è che le sezioni del paraboloide sono proporzionali alle sezioni del triangolo. A partire da qui non è troppo difficile, impiegando approssimanti a scalini composte da cilindri per il paraboloide e da rettangoli per il triangolo, far vedere che il centro di gravità del paraboloide e del triangolo devono coincidere. Ora, siccome il centro del triangolo è noto, si determinerà anche quello del paraboloide.
L'intuizione di Valerio si può riassumere in questi termini: il caso del paraboloide e del triangolo ci insegna che per trovare il centro di gravità di una figura digradante F1 basterà trovare un'altra figura F2 il cui centro di gravità sia noto e tale che le sezioni di F1 e F2 siano proporzionali. In tal caso il centro di gravità di F1 coinciderà con quello di F2.
Si tratta, in altre parole, di ottenere un teorema generale riguardante i centri di gravità delle figure digradanti. Non è certo qui il caso di esporre nei dettagli la strada che Valerio seguì per arrivare alla dimostrazione di un teorema del genere. Ci basti dire che egli riuscì a escogitare una dimostrazione che funzionava per una classe molto ampia di figure digradanti e che è esposta nelle proposizioni 25-32 del Libro II del De centro. Il tutto culmina nella proposizione 32: due figure aventi stesso asse e sezioni proporzionali avranno lo stesso centro di gravità.
Bisogna però rilevare almeno un punto: il teorema II.32 del De centro ha una portata rivoluzionaria, essendo il primo teorema a dimostrare un risultato importante e innovativo per una classe di figure. Con questo risultato Valerio poneva la matematica occidentale su una strada completamente nuova. Non solo rispetto a quella greca; persino gli Arabi, che pure nel campo delle 'matematiche infinitesimali' avevano ottenuto risultati notevolissimi ed estremamente raffinati, non erano riusciti a superare questa soglia: a passare cioè dalla considerazione di singole figure allo studio di classi, che diventano l'oggetto della ricerca.
Il teorema II.32 si rivelerà, nelle mani di Valerio, uno strumento potente. Abbiamo già dato un cenno della dimostrazione che tratta il caso del conoide parabolico: alla luce di quanto abbiamo detto, risulterà chiaro quali siano ora le sue linee portanti. Per prima cosa Valerio dimostra che il triangolo e il conoide parabolico sono due figure digradanti 'logaritmicamente convesse' e che le sezioni del triangolo e del conoide sono proporzionali. A questo punto le ipotesi di II.32 sono soddisfatte e gli basta applicare il suo teorema generale per ottenere il risultato: il centro di gravità del conoide parabolico divide l'asse nel rapporto di 2:1. Per la geometria rinascimentale il centro di gravità del conoide parabolico era stato una sorta di extrema Thule: nessuno, nemmeno Maurolico ‒ forse il maggiore matematico del XVI sec. ‒, era riuscito a spingersi oltre. Inoltre il risultato era già noto dai Galleggianti di Archimede e proprio questo aveva guidato Commandino nel suo tentativo di proporre una dimostrazione convincente. Valerio si spinge ben al di là di queste colonne d'Ercole: riesce con facilità a determinare centri di gravità del tutto sconosciuti alla matematica del suo tempo, in particolare quello dell'emisfero e dell'emisferoide e ‒ soprattutto ‒ quello dell'iperboloide (conoide iperbolico), che è sicuramente uno dei risultati più difficilmente ottenibili nel contesto della matematica classico-rinascimentale.
Tuttavia, come vedremo, ci sono molte ombre nell'uso che propone della proposizione II.32; la sua via regia tende qui a smarrirsi in un labirinto, che noi tenteremo di esplorare.
Esitazioni e involuzioni
La situazione di fronte alla quale si trova il lettore del Libro III del De centro è decisamente paradossale. Da un lato, infatti, Valerio trova i risultati assai notevoli cui accennavamo, distaccandosi ancora di più dall'impostazione classica: sviluppa, almeno in parte, un modo di concepire le relazioni fra le figure assai più quantitativo di quanto la matematica classica avesse mai fatto. Dall'altro, quasi spaventato dalla sua stessa audacia, accanto a questo modo di procedere presenta dimostrazioni alternative e ai suoi occhi "magis naturales", in cui abbandona non solo le innovazioni più radicali, ma i principî stessi elaborati in precedenza: la via regia e il metodo del teorema II.32. Questa oscillazione fra innovazione radicale e aderenza al paradigma classico è forse una delle cause principali dell'oscurità e delle difficoltà di lettura che affliggono buona parte dei Libri II e III del De centro.
Illustreremo la situazione descrivendo ‒ sia pur sommariamente ‒ i vari modi con cui è affrontata la determinazione del centro di gravità dell'iperboloide. Valerio ne offre tre dimostrazioni, la prima delle quali è contenuta nella proposizione 43 del secondo libro. Sia A un iperboloide, generato dalla rotazione dell'iperbole ABC attorno all'asse BD. Il lato trasverso dell'iperbole sia BE. Dalla proprietà (o sintomo) dell'iperbole, per un qualsiasi punto S sulla curva si ha:
[1] SQ2:BQ×QE=CD2:BD×DE=costante
Spiegheremo la dimostrazione di Valerio in termini algebrici. È una scelta che porta a non essere del tutto fedeli all'argomento, ma che ha il vantaggio di sottolineare alcuni punti essenziali, almeno a noi lettori moderni che non maneggiamo più con altrettanta facilità il linguaggio della teoria delle proporzioni.
Sia BD=a, BE=b e si pensi a un sistema di coordinate con origine in B. Sia k il rapporto costante nel sintomo dell'iperbole. L'equazione di questa iperbole diventa: y2=kx(b+x), ossia y2=kx2+bkx.
Ora, il membro di sinistra, y2, è proporzionale al cerchio-sezione dell'iperboloide che si ottiene tagliando con un piano SZ parallelo alla base (in altre parole, il cerchio di diametro SZ è uguale a πy2). Il membro di destra, invece, si divide in due parti: kx2 (proporzionale al quadrato dell'ascissa BQ=x) e bkx (proporzionale all'ascissa stessa). Si tratta allora di costruire due figure le cui sezioni siano proporzionali a queste due parti del secondo membro. A questo scopo, prendiamo un qualsiasi punto M su AD e poniamo MD=p. Si tracci una parabola MBN passante per M, di asse BD e vertice B, la cui equazione sarà:
Facendo ruotare la parabola si genererà il paraboloide P. Allo stesso modo, si consideri poi un triangolo BKD (il punto K è preso sulla linea AD in modo che MD2:DK2=BE:BD=b:a) e il cono C che si ottiene facendo ruotare tale triangolo intorno all'asse x.
Tagliando tutti questi solidi di rotazione (l'iperboloide A, il cono C e il paraboloide P) con un generico piano SZ, parallelo alla base (e quindi perpendicolare all'asse), le sezioni che si otterranno saranno cerchi: Cer(A), Cer(C) e Cer(P) rispettivamente. Allora si mostra facilmente che:
Posto BQ=x, si ha infatti:
e Cer(A)=πy2=πkx(b+x). Dalla [3] si ha dunque che
e da qui segue immediatamente che, per le due figure A e C+P, sono soddisfatte le condizioni della proposizione II.32. Di conseguenza il baricentro dell'iperboloide A si situa nello stesso punto del baricentro della figura C+P, il cono C e il paraboloide P 'presi insieme'. Poiché i baricentri e le grandezze del cono e del paraboloide sono già noti, si può poi facilmente determinare il baricentro dell'iperboloide A, utilizzando la legge della leva.
Ciò che ci sembra il punto più interessante di questa dimostrazione non è il fatto che si stia facendo uso di concetti infinitesimali, utilizzati peraltro una volta sola, incapsulati una volta per tutte nel teorema II.32. Il punto centrale, a nostro avviso, è la dissoluzione dell'iperboloide in figure i cui baricentri sono noti e di cui sono noti i rapporti volumetrici. E, cosa che impressiona ancora di più, il centro di gravità dell'iperboloide A è ricondotto al centro di gravità di un solido impossibile, un vero mostro: la somma, sezione per sezione, del cono C e del paraboloide P. Questo oggetto, C+P, non è un solido normale, che possa esistere nel senso comune del termine e nell'intuizione spaziale della geometria classica; inoltre il cono e il paraboloide sono determinati in modo puramente formale, a partire da un'analisi (nel senso chimico del termine) del sintomo dell'iperboloide. In questo senso, più che figure geometriche dotate di una loro vita, sono degli 'strumenti', come dei pezzi riutilizzabili.
Insomma: l'oggetto dell'interesse slitta dalle figure in quanto tali, dotate di forma e posizione, alle relazioni quantitative che intercorrono fra di esse o, meglio, alle relazioni che intercorrono fra le loro sezioni.
Tuttavia, come abbiamo accennato, Valerio sembra spaventarsi della sua stessa audacia. Se nel Libro II determina il centro di gravità dell'iperboloide utilizzando il 'mostro' C+P, e addirittura teorizza questa procedura in un apposito corollario alla proposizione II.32 ‒ asserendo che il teorema appena dimostrato mantiene la sua validità anche se al posto delle singole figure se ne considera la loro somma ‒, nel Libro III il gioco si complica alquanto, al punto che Valerio arriverà a proporre una dimostrazione 'ottima', in cui non soltanto non è fatto uso di mostri né del teorema II.32, ma nemmeno dei teoremi generali sulle figure digradanti introdotti nel Libro I (in particolare del teorema I.11).
Continuiamo a trattare il caso dell'iperboloide, quello in cui è più evidente questo processo di 'normalizzazione' delle relazioni quantitative. Evidentemente insoddisfatto della soluzione che abbiamo appena esposto, Luca Valerio non soltanto ne propone un'altra nel Libro III, ma aggiunge addirittura un'Appendix dedicata esplicitamente alla trattazione di questo solido secondo una via magis naturalis. Apparentemente, lo scopo di questa triplicazione della determinazione del centro di gravità del conoide iperbolico è l'eliminazione del ricorso a figure mostruose.
Nella proposizione III.39 il calcolo del baricentro dell'iperboloide è ricondotto alla determinazione del baricentro di un altro triangolo parabolico. Si consideri l'iperboloide il cui asse abbia lunghezza s, generato dalla rotazione intorno all'asse x dell'iperbole avente vertice nell'origine, lato trasverso 2a e la cui equazione è ora: y2=k2x2+2ak2x, nonché la parabola
passante per l'origine e per il punto (s,t), dove
Le sezioni dell'iperboloide e del 'triangolo parabolico' ℱ compreso fra il grafico della parabola e il suo simmetrico rispetto all'asse x sono evidentemente proporzionali, e di conseguenza l'iperboloide e ℱ hanno lo stesso centro di gravità. Anche in questo caso, la determinazione del centro di gravità di ℱ è ricondotta (attraverso dimostrazioni alquanto complesse) al centro di gravità del segmento parabolico. Viene spontanea la domanda: perché mai Valerio sente il bisogno di abbandonare la tecnica utilizzata in II.43, pagando il prezzo di dover introdurre il triangolo parabolico ℱ e di dover eseguire una serie di complicate argomentazioni per poterne ricavare il centro di gravità? La risposta la fornisce egli stesso, nelle ultime righe del De centro:
E qui saremmo arrivati alla fine del terzo libro, senonché, quando ormai il secondo era già finito di stampare mi venne in mente un'altra via più naturale (via magis naturalis) riguardante il centro di gravità del conoide iperbolico. Essa (andrebbe inserita nel secondo libro, ma l'espongo ora, nelle sette proposizioni della seguente Appendice) giunge alla conclusione dividendo il detto conoide in un conoide parabolico di stesso vertice e asse e nella figura solida rimanente, senza utilizzare la composizione di due figure circoscritte fatte di cilindri. (ibidem, III, p. 179, corsivi nostri)
Come si vede, è esplicitamente rinnegato il metodo utilizzato in II.43 che si basava sulla dissoluzione della forma delle figure a favore di pure considerazioni quantitative. E possiamo essere grati alle vicende che portarono a una stampa affrettata del De centro se possiamo oggi leggere quelle considerazioni: se Valerio avesse avuto un po' più di tempo le avrebbe inesorabilmente espunte. Questa ricerca di una via magis naturalis spiega quindi abbastanza bene l'introduzione di un oggetto (il triangolo parabolico) che richiede ragionamenti assai più complicati della scomposizione dell'iperboloide in un paraboloide e in un cono. Ma c'è, come dicevamo, di più: nell'Appendix al Libro III del De centro si assiste infatti a un vero e proprio ribaltamento metodologico.
Vediamo la cosa più da vicino. L'idea di Valerio è quella di scavare una 'scodella parabolica' all'interno dell'iperboloide. In effetti, considerata l'iperbole generatrice: y2=k2x2+2ak2x, la parabola y2=2ak2x genererà un paraboloide P il cui vertice e il cui asse sono gli stessi dell'iperboloide A. Se indichiamo con S la scodella iperbolico-parabolica che si ottiene scavando via il paraboloide, S risulta uguale al cono C generato dalla rotazione di y=kx intorno all'asse x. Sarebbe assai facile dimostrare che le tre figure in gioco sono 'logaritmicamente convesse' e che quindi, a norma della II.32, C e S hanno lo stesso centro di gravità. Siccome poi A=S+P e i centri di gravità di S e P sono noti, si potrebbe ricavare facilmente il centro di A, dato che è possibile calcolare il rapporto P:S. Questa, almeno, è la dimostrazione che ci si aspetterebbe conoscendo la proposizione II.32. Invece il metodo generale indicato da questo teorema, che aveva guidato Valerio per tutto il secondo e terzo libro, è abbandonato. Al contrario, il rapporto P:S è calcolato inscrivendo e circoscrivendo cilindri e utilizzando il 'metodo di esaustione' sviluppato nelle prime tre proposizioni del Libro II (III, Appendix, prop. 3). Addirittura sono ripetute le dimostrazioni di approssimazione già fatte in generale (prop. I.11) per il conoide parabolico e per il conoide iperbolico (III, Appendix, propp. 4 e 5). Infine, nella proposizione 6, nel calcolare il centro di gravità della scodella iperbolico-parabolica S, Valerio, per evitare di invocare la proposizione II.32 sembra rifarsi a una proposizione del Libro I (I.38) che non potrebbe qui applicare, dato che essa è esplicitamente enunciata per figure convesse.
C'è di che rimanere perplessi. Qui non è stato solamente eliminato l'uso dei mostri, o l'uso delle figure come pezzi ricomponibili e riutilizzabili. È tutto l'impianto metodologico del De centro che traballa. La via regia si perde in una via magis naturalis, che assomiglia da vicino alle strade battute da Archimede e da Euclide.
Un nuovo oggetto: tutte le linee
La lezione metodologica di Valerio, nonostante le esitazioni e i ripiegamenti che abbiamo ora descritto, non sarebbe però andata perduta. Nella prefazione alla Geometria, Cavalieri cita i risultati del De centro fra quelli che lo ispirarono a concepire il suo metodo. Naturalmente, la teoria degli indivisibili è molto complessa e ciò che qui presenteremo può essere considerato, nel migliore dei casi, una semplice introduzione. Tuttavia, ciò che ci premeva di più era mostrare l'emergere di nuove idee e di nuove metodologie: da questo punto di vista ci è sembrato più importante dedicare maggior spazio a Valerio e alla sua opera ‒ poco nota e poco studiata dalla letteratura ‒ piuttosto che a Cavalieri.
L'idea fondamentale della Geometria è che sia possibile confrontare fra loro due figure mettendo in relazione i loro 'indivisibili', o meglio 'tutte le linee' delle due figure. Questo concetto di 'tutte le linee' Cavalieri lo introduce immediatamente nella prima definizione:
Se si tracciano due piani paralleli passanti per due tangenti opposte ad una data figura piana qualsivoglia, e se uno di questi piani (che siano perpendicolari o inclinati rispetto al piano della figura assegnata) viene mosso verso l'altro rimanendogli sempre parallelo fino a che non coincida con esso, allora le singole linee prodotte durante il corso dell'intero movimento dall'intersezione del piano che viene mosso e di quello della figura, prese tutte insieme, verranno dette "Tutte le linee [omnes lineae] di tale figura, presa una di esse come direzione [regula]". (Geometria indivisibilibus, II, def. 1)
Se ci limitiamo (come fa perlopiù Cavalieri) al caso del retto transito, ovvero al caso in cui i due piani sono perpendicolari al piano della figura, 'tutte le linee' della figura si ottengono dal movimento di una linea che si muove parallelamente a sé stessa: sono i suoi indivisibili.
Analogamente, gli indivisibili delle figure solide saranno caratterizzati da 'tutti i piani della figura', che si ottengono intersecandola con un piano che si muove parallelamente a sé stesso.
Lo scopo dell'introduzione degli indivisibili è enunciato chiaramente nella proposizione II.3: "Le figure piane stanno fra loro nello stesso rapporto di tutte le loro linee, prese secondo una qualunque direzione; e anche le figure solide stanno fra loro nel rapporto di tutti i loro piani, presi secondo una direzione qualunque".
Una lettura affrettata potrebbe far sembrare che Cavalieri si stia muovendo sulla scia di Valerio, e del suo teorema II.32. Volendo, il teorema di Valerio si potrebbe rileggere infatti in questi termini: se gli indivisibili di due figure digradanti (e 'logaritmicamente convesse') sono proporzionali a due a due, allora le figure hanno lo stesso centro di gravità. O potrebbe sembrare che Cavalieri (e di ciò l'accuseranno puntualmente i suoi oppositori) stia seguendo l'esempio di Bartolomeo Sovero, che nel Libro V della Curvi ac recti proportio (1630) aveva dimostrato un principio simile ma soltanto relativamente alle sezioni coniche. In effetti, le cose stanno assai diversamente. In primo luogo, le somiglianze con Valerio e Sovero si fermano quasi subito, almeno ove sia questione della proposizione II.3 della Geometria. Quei metodi infatti prevedono il confronto degli indivisibili di due figure coppia per coppia: qui invece Cavalieri parla della 'collezione' di tutte le linee (o di tutti i piani) delle due figure, che devono poter essere confrontate fra di loro, nel senso euclideo del termine: tutte le linee di una figura devono poter essere trattate come grandezze che hanno rapporto fra loro, a norma delle definizioni del Libro V degli Elementi e in particolare della definizione V.4: "Si dice che due grandezze dello stesso genere hanno rapporto fra loro se, moltiplicate si superano l'un l'altra".
Ed è proprio da qui che comincia la Geometria di Cavalieri: la proposizione 1 del Libro II vuole dimostrare che tutte le linee di una figura piana formano una classe di grandezze aventi rapporto fra loro.
La stessa impostazione del libro svela quindi lo scopo di Cavalieri: non si tratta tanto di introdurre un nuovo metodo dimostrativo, quanto di far accettare dalla geometria un nuovo oggetto; accanto alla classe delle figure piane deve trovare posto anche quella di 'tutte le linee' delle figure piane. Basti dire che Cavalieri cerca di dare agli indivisibili lo status di grandezze indipendenti: 'tutte le linee' di una figura potranno essere confrontate, ordinate, sommate come le figure geometriche stesse.
Questo approccio 'fondazionale' e rivolto a figure generali (tali anche rispetto a Valerio e non soltanto al modello greco, poiché è persino sparito il riferimento a proprietà specifiche quali la monotonia) permette ovviamente a Cavalieri di ottenere risultati di grande generalità con mezzi relativamente semplici. Per esempio, può introdurre il concetto di figure simili in generale (Geometria indivisibilibus, I, def. 10) e dimostrare, in generale, che figure piane simili stanno fra loro come i quadrati di due lati omologhi (ibidem, II, prop. 11) nonché un analogo risultato per i solidi.
Sulla base del principio introdotto nella proposizione II.3 (e II.4), Cavalieri fu in grado di ricavare una serie impressionante di risultati: in particolare di determinare il volume di un gran numero di solidi di rotazione, ottenuti facendo ruotare intorno a un asse segmenti di sezioni coniche. Molti di questi erano i solidi che Johannes Kepler aveva introdotto nella Nova stereometria (1615): Cavalieri faceva così vedere che la propria teoria reggeva il confronto con i più recenti risultati, senza dover ricorrere, come aveva fatto Kepler, a concetti infinitesimali. La geometria poteva veramente essere promota dagli indivisibili, poiché con essi si potevano ottenere nuovi risultati senza abbandonare il rigore euclideo.
Tale serie di risultati, inoltre, si poteva ottenere da una coppia di concetti: quello di solidi simili e quello di solidi mutuamente simili. Il primo è introdotto nel Libro II della Geometria: può essere visto come un solido i cui indivisibili ('tutti i piani' del solido), presi rispetto a una certa direzione, sono tutti simili fra loro. In pratica, data una figura F situata su un piano verticale, essa determinerà il profilo del solido, mentre le sue sezioni orizzontali dovranno essere tutte simili a un'altra data figura G. In questo modo un solido simile generato da un triangolo (F) per mezzo di un cerchio (G) sarà un cono; un paraboloide sarà generato da una parabola per mezzo di un cerchio. Se poi date due figure F1 e F2 da esse si generano due solidi per mezzo della stessa figura G, i due solidi generati saranno detti mutuamente (ad invicem) simili.
La proposizione fondamentale che Cavalieri riesce a dimostrare al riguardo è che il rapporto fra due solidi mutuamente simili non dipende dalla figura G per mezzo della quale sono generati, ma soltanto dalle due figure F1 e F2; stando così le cose, come figura G può essere scelto un quadrato e il rapporto fra i due solidi sarà uguale al rapporto di 'tutti i quadrati' (ovvero di tutti i quadrati costruiti su 'tutte le linee') di F1 e di F2: si tratta del teorema II.33 della Geometria, di cui vediamo ora brevemente la dimostrazione. Consideriamo due solidi simili, S1=Σ(F1,G) e T1=Σ(F1,Q), dove Q è un quadrato. Ovviamente non si tratta di due solidi mutuamente simili; ma se tagliamo i due solidi con un piano orizzontale otterremo per S1 una figura simile a G e per T1 una figura simile al quadrato Q. Il rapporto fra queste sezioni è lo stesso per tutti i piani, dato che le figure piane simili stanno fra loro nel rapporto dei quadrati di due linee omologhe (si ricordi che la figura generatrice F1 è la stessa per i due solidi S1 e T1).
Interviene a questo punto uno dei principî più usati da Cavalieri, che è una generalizzazione di un teorema euclideo: "ut unum ad unum, sic omnia ad omnia". In Euclide tale principio è utilizzato nel modo seguente: se a1:b1=a2:b2=…=an:bn, ne deriva che la somma di tutti gli antecedenti sta a quella di tutti i conseguenti come un antecedente a un conseguente: (a1+a2+a3+…+an):(b1+b2+b3+…+bn)=a1:b1.
Cavalieri generalizza questo teorema (ibidem, II, corollario alla prop. II.4) a un numero indefinito di grandezze; e dato che per ogni piano le sezioni di S1 stanno alle sezioni di T1 sempre nello stesso rapporto ("unum ad unum"), così anche tutte le sezioni di S1, prese collettivamente, staranno a tutte le sezioni di T1 prese collettivamente ("sic omnia ad omnia") nel rapporto dato; e quindi, grazie alla proposizione II.3, (o, meglio, come vedremo fra breve, alla II.4), anche i due solidi S1 e T1.
Ovviamente lo stesso ragionamento si può ripetere per i due solidi S2=Σ(F2,G) e T2=Σ(F2,Q). In conclusione: S1:T1==S2:T2 da cui, permutando, segue subito che i due solidi S1 e S2 stanno fra loro come tutti i loro quadrati.
Un esempio semplicissimo basterà a illustrare la forza del teorema. È ben noto che una piramide a base quadrata è un terzo del prisma avente stessa base e stessa altezza: il risultato di Cavalieri permette di dedurre che lo stesso risultato varrà non soltanto per il cono e il cilindro usuali (fatto anch'esso ben noto), ma per il cono e il cilindro generalizzati, ovverossia costruiti per mezzo di una figura arbitraria, risultato tutt'altro che facile da provare. Inoltre, sempre grazie a questo teorema, Cavalieri sarà in grado di dimostrare i risultati cui accennavamo sopra.
Difficoltà di una teoria
La dimostrazione che abbiamo ora delineato mostra bene nella pratica quello che Cavalieri chiama "il primo metodo degli indivisibili", in cui 'tutte le linee' di una figura sono considerate collettivamente. Varrà la pena però di fermarci un attimo a riflettere sulle fondamenta teoriche su cui tale metodo è stato edificato.
Per poter trattare 'tutte le linee' o 'tutti i piani' di una figura come grandezze cui applicare la teoria delle proporzioni, Cavalieri deve ovviamente stabilire un modo di confrontare fra loro queste grandezze. Deve poter dire come, date due collezioni del genere, si stabilisca se siano una maggiore dell'altra o uguali; deve poter stabilire come sommarle e dimostrare che si tratta di grandezze 'archimedee' ossia che esiste un multiplo dell'una che supera l'altra. Questi compiti sono affidati alle primissime proposizioni del Libro II della Geometria. Le analisi che, indipendentemente, ne hanno fatto Enrico Giusti (1980) e Kirsti Andersen (1985) concordano nell'indicare la debolezza strutturale di questo programma. Particolarmente debole è la dimostrazione della proposizione II.2: "'Tutte le linee' di figure piane uguali sono uguali". L'idea è quella di sovrapporre parzialmente le due figure, di togliere i pezzi in comune (che, essendo congruenti, avranno tutte le loro linee congruenti, grazie a un apposito postulato) e di ripetere il procedimento, fino a che non resti più nulla. Come si vede niente garantisce (anzi!) che il procedimento non si debba ripetere all'infinito. Problemi analoghi gravano la dimostrazione della proposizione II.3, quella su cui si fonda il metodo del confronto collettivo degli indivisibili. Giusti conclude le sue osservazioni su questo punto notando che le regole introdotte da Cavalieri per rendere 'tutte le linee' di una figura una grandezza geometrica si riducono, in ultima analisi, a questo: le collezioni di indivisibili sono sommate e confrontate con le stesse identiche regole delle figure da cui derivano. Così gli indivisibili di una figura diventano indistinguibili dalla figura stessa e i teoremi II.2 e II.3 si risolvono in tautologie.
Altrettanto strutturalmente debole è il principio "ut unum ad unum, sic omnia ad omnia", che abbiamo visto all'opera qui sopra. Esso interviene per la prima volta nella proposizione II.4, in cui Cavalieri vuole dimostrare che, se due figure (piane o solide) hanno ugual altezza e se le sezioni fatte nelle due figure da piani paralleli alle basi hanno sempre lo stesso rapporto, allora anche le due figure stanno nello stesso rapporto. È qui che interviene il principio: siccome le singole sezioni altro non sono che singoli indivisibili delle due figure, applicando tale principio si ricaverà che come un indivisibile sta a un indivisibile, così tutti gli indivisibili della prima figura staranno a tutti quelli della seconda. E, applicando la proposizione II.3 seguirà il risultato.
Assai stranamente questo principio è enunciato come un 'corollario' della proposizione II.4, pur non essendo una sua immediata conseguenza, ma piuttosto un suo presupposto; inoltre, nonostante il chiaro richiamo a una proposizione euclidea, si tratta di un'estrapolazione indimostrabile e basata su equivoci. In primo luogo si passa, come abbiamo già rilevato, da un numero finito di rapporti a un numero infinito; in secondo luogo, laddove Euclide considera la somma degli antecendenti e dei conseguenti, Cavalieri è lontanissimo dal volere compiere un passo del genere. Sommare infinite grandezze lo porterebbe a violare l'assioma di Archimede e a escludere gli indivisibili dalle grandezze che hanno rapporto fra loro, motivazioni che già lo avevano spinto a rifiutare l'approccio kepleriano che consisteva nel fornire agli indivisibili uno spessore infinitesimo. Così, preferisce assonanze verbali: a tutte le linee corrispondono tutti gli antecedenti, presi cioè collettivamente.
In queste difficoltà di Cavalieri possiamo vedere un esempio concreto di un fenomeno più generale che abbiano già riscontrato in Luca Valerio, quando abbiamo notato un'estrema riluttanza a trattare relazioni puramente quantitative, indipendenti dalla forma. L'introduzione della teoria degli indivisibili può effettivamente essere letta come un passo nel senso della strada che Valerio aveva aperto e che non aveva avuto il coraggio di percorrere fino in fondo. Ed è un passo molto deciso: lo scopo iniziale di Cavalieri (che, peraltro, non sarà mai del tutto abbandonato) era appunto quello di dissolvere la rigidità formale delle figure nella duttilità della collezione dei loro indivisibili. Ma ci si scontra qui in un altro ostacolo: di fronte al programma di produrre una teoria geometrica capace di trattare figure del tutto generali, si pone la rigidità della teoria delle proporzioni. Il programma di Cavalieri, come abbiamo appena visto, si rivela assai difficile da percorrere: 'tutte le linee' di una figura sono indistinguibili dalla figura stessa, ed è solamente a costo dell'introduzione del principio ut unum che Cavalieri riesce a superare la difficoltà.
Il secondo metodo degli indivisibili e le Exercitationes
Si farebbe un torto alla sensibilità matematica e logica di Cavalieri pensando che non si fosse reso conto delle difficoltà strutturali della sua teoria. Non è un caso infatti che, quando nel 1634 la stampa dei primi cinque libri della Geometria era già terminata e si stava cominciando a stampare il sesto, egli decise di aggiungere un settimo libro "perché dubito che a molti sia forsi per dar fastidio quel concetto delle infinite linee o piani" (Cavalieri a Galilei, 22 luglio 1634, Carteggio).
E in una lettera successiva, sempre a Galilei (2 ottobre 1634), Cavalieri ribadisce le proprie esitazioni: trattare l'infinito "porta seco tanti dubbi" e per poterli mettere a tacere ha ridimostrato le sue conclusioni nel Libro VII con un nuovo metodo "esente da tal infinità". Il nuovo metodo è quello che Cavalieri chiama "secondo metodo degli indivisibili" o metodo 'distributivo': "Figure piane quali si vogliano poste tra le medesime parallele ‒ nelle quali, condotte quali si vogliano linee parallele alle parallele stesse, le porzioni racchiuse di una quale si voglia linea retta stanno fra loro come le porzioni di un'altra qual si voglia retta racchiusa nelle medesime figure (le linee omologhe essendo sempre prese nella medesima figura) ‒ avranno fra loro lo stesso rapporto che hanno tra di loro le dette porzioni" (Geometria indivisibilibus, VII, prop. 2).
È questo quello che sarà poi noto come il 'principio di Cavalieri', della cui fortuna e destino abbiamo già accennato e di cui tra breve discuteremo l'impianto teorico. Ma notiamo subito che siamo passati da una situazione in cui era in gioco la legittimità di un nuovo oggetto matematico (la collezione di 'tutte le linee') a una in cui si tratta, più modestamente, di introdurre un nuovo metodo dimostrativo. In altri termini, il secondo metodo degli indivisibili si avvicina molto al metodo di Valerio per il calcolo dei centri di gravità: racchiudere in una serie di dimostrazioni i ragionamenti che permettono di fornire una prova, una volta per tutte, delle tecniche di confronto fra due figure. Non si tratta quindi di una mera semplificazione della teoria, ma piuttosto di un suo abbandono.
Va detto che le critiche attese da Cavalieri ai suoi fondamenti teorici arrivarono puntualmente. Le più violente furono quelle sollevate da Paul Guldin nel Libro IV del De centro gravitatis o Centrobaryca, pubblicato a Graz nel 1641. Si trattava di critiche pesanti, che andavano da accuse di plagio più o meno pretestuose nei confronti di Kepler e di Sovero a critiche ai fondamenti del metodo. Come abbiamo già accennato fu proprio per rispondere alle accuse di Guldin e per cercare di chiarire le basi teoriche degli indivisibili che Cavalieri fu spinto a scrivere le Exercitationes, dove, nell'Exercitatio II, si può trovare il più alto tentativo di ottenere una dimostrazione rigorosa del secondo metodo degli indivisibili.
Per dimostrare la proposizione 2 del Libro VII della Geometria è necessario riuscire a dimostrare preliminarmente che, se le sezioni di due figure sono ordinatamente uguali, anche le figure lo saranno. Cavalieri non rinuncia a muoversi nella più grande generalità: le sue figure possono non solamente essere piane o solide, ma anche concave, dotate di buchi al loro interno: insomma, dei veri mostri rispetto all'immaginario dell'epoca, abituato alle regolari figure della geometria classica. Per superare le critiche di Guldin, egli tenta di ridurre questa varietà a un caso che abbiamo già incontrato: le figure digradanti considerate da Valerio. Come abbiamo visto è relativamente facile, usando metodi classici ‒ mutuati sostanzialmente da Archimede e filtrati dalla lettura del De centro di Valerio ‒, dimostrare per le figure digradanti che è possibile passare dall'uguaglianza delle sezioni all'uguaglianza delle figure stesse (Exercitatio II, lemma 2). Su questa base Cavalieri tenta poi di trattare il caso generale; ma qui è costretto a inserire tacitamente tutta una serie di ipotesi: che le figure considerate siano scomponibili in un numero finito di figure digradanti, che abbiano un numero finito di buchi al loro interno e simili. Il caso delle figure piane è, in quest'ottica, relativamente semplice; seguire i suoi ragionamenti per il caso dei solidi è invece un compito arduo. Ne era consapevole lo stesso Cavalieri che, scrivendo a Torricelli il 10 marzo 1643, rilevava l'estrema difficoltà dell'impresa.
Nella sistemazione del secondo metodo degli indivisibili fornita nelle Exercitationes, osserviamo dunque un riavvicinamento anche tecnico alle parti più avanzate dell'opera di Valerio. La teoria degli indivisibili ripiega in un metodo, che è giustificato utilizzando tecniche di cristallina classicità.
Vino nuovo in otri vecchi
Cavalieri come Valerio, dunque? A prima vista sembrerebbe di si. Entrambi introducono innovazioni metodologiche radicali, ed entrambi ripiegano. C'è però una differenza importante da segnalare: se Valerio, giunto alla fine della sua opera, sembra quasi rinnegarla per ritornare nell'alveo della tradizione archimedea, Cavalieri persino nelle Exercitationes, un'opera scritta a scopi essenzialmente difensivi, non rinuncerà a esporre la sua teoria sugli indivisibili e tantomeno a utilizzare e a vantare la validità teorica del suo metodo, sia pure nella versione più addomesticata del confronto distributivo. È vero, certamente, che le basi teoriche di quest'ultimo sono ridotte a tecniche di tipo valeriano; e si potrebbe dire, con una battuta, che se Valerio si rifugia in Archimede, Cavalieri si rifugia in Valerio.
Ma il punto è ormai acquisito e la geometria dopo Valerio e, soprattutto, dopo Cavalieri si staccherà definitivamente da una delle caratteristiche fondamentali del modello classico: lo studio di singole figure. L'introduzione di classi di figure generali e, di conseguenza, l'introduzione di metodi generali per trattarle entrerà così a far parte definitivamente della ricerca matematica.
Certamente, anche in Cavalieri e oltre, la ricerca è pur sempre ingabbiata nel linguaggio e nelle angustie della teoria delle proporzioni, un linguaggio nato per descrivere figure con posizioni fisse e con relazioni posizionali con altre figure. E nonostante che nei secc. XVI e XVII molti sforzi fossero stati compiuti per trasformarla in un linguaggio in cui si potessero esprimere relazioni astratte fra grandezze, rimaneva pur sempre un linguaggio estremamente rigido, strutturalmente incapace di trattare in modo efficace situazioni in cui venissero coinvolte infinità di oggetti (si pensi al principio ut unum). Ma era l'unico linguaggio disponibile, il cui schema concettuale ‒ al quale aderivano tanto Cavalieri quanto Valerio ‒ rese la geometria estremamente complessa e oscura; ed è forse da qui che deriva la diffusa immagine di un Cavalieri difficilissimo da leggere.
C'è anche un altro aspetto da mettere in conto. Abbiamo più volte detto che la geometria greca non tratta oggetti generali, il che implica una drastica limitazione degli oggetti da trattare, e di conseguenza dei problemi da affrontare. Il De centro di Valerio aveva praticamente esaurito tutto ciò che era disponibile sul 'mercato matematico' in materia di centri di gravità. La Geometria di Cavalieri si era spinta anche più in là: trattava praticamente tutti i problemi di quadratura, riuscendo a dominare anche i nuovi solidi kepleriani, le parabole di ordine superiore, o problemi atipici come la determinazione del centro di gravità di un corpo a densità variabile. Ma, rispetto all'innovazione radicale di considerare non più singoli oggetti (parabole, sfere, conoidi o quant'altro), ma classi di figure, tutto ciò sembra un po' poco. Da un lato abbiamo una visione e metodi generalissimi; dall'altro tali metodi e tale visione non trovano un campo sufficientemente vasto e al tempo stesso sufficientemente delimitato su cui esercitarsi. Insomma: il linguaggio della teoria delle proporzioni e il contesto problematico ereditato dalla geometria greca non permettevano di sviluppare problemi generali adeguati ai metodi generali che erano stati introdotti. La via verso questi metodi era stata aperta da Valerio, portata molto avanti da Cavalieri, ma sembrava che rimanesse da fare ben poco.
Sarà l'introduzione dell'ars analytica in geometria a sfondare queste mura elleniche. Seguendo un percorso del tutto parallelo a quello sviluppato nell'alveo della tradizione archimedea, la riflessione di François Viète doterà la geometria di un nuovo linguaggio, quello algebrico, grazie al quale Descartes, identificando la curva con la sua equazione, avrebbe di lì a poco aperto ai matematici un mondo letteralmente infinito, spezzando per sempre il modello greco. La nuova geometria cartesiana proponeva finalmente ambiti problematici (in particolare quello della ricerca delle tangenti a una curva algebrica e della determinazione dei massimi e dei minimi) sufficientemente precisi e sufficientemente ampi.
Da qui, oltre che dalla riflessione e dalla ricerca sugli indivisibili, sarebbe nato il calcolo infinitesimale. È difficile però immaginare Leibniz senza Cavalieri, così come è difficile immaginare quest'ultimo senza Valerio. Non si può immaginare il radicale rinnovamento che la matematica doveva conoscere nella seconda metà del Seicento senza le novità metodologiche e teoriche del De centro gravitatis solidorum e della Geometria indivisibilibus. Si potrebbe dire, per concludere, che Valerio e Cavalieri misero del buon vino nuovo in un otre vecchio. Di per sé non è una cosa fatta bene. Il vino nuovo va messo in otri nuovi; ma, nel caso specifico, quel vino, ribollendo, spezzò l'otre. Fuor di metafora, mise in crisi le rigidità del paradigma classico e contribuì a creare il contesto concettuale che avrebbe portato alla nascita della matematica moderna.
Bibliografia
Andersen 1985: Andersen, Kirsti, Cavalieri's methods of indivisibles, "Archive for history of exact sciences", 31, 1985, pp. 295-367.
Baldini 1991: Baldini, Ugo - Napolitani, Pier Daniele, Per una biografia di Luca Valerio. Fonti edite e inedite per una ricostruzione della sua carriera scientifica, "Bollettino di storia delle scienze matematiche", 11, 1991, pp. 3-157.
Giusti 1980: Giusti, Enrico, Bonaventura Cavalieri and the theory of indivisibles, Roma, Cremonese, 1980.
‒ 1982: Giusti, Enrico, Dopo Cavalieri. La discussione sugli indivisibili, in: La storia delle matematiche in Italia, a cura di Oscar Montaldo e Lucia Grugnetti, Cagliari, Università-Istituti di Matematica delle Facoltà di Scienze e Ingegneria, 1982, pp. 85-114.
‒ 1999: Giusti, Enrico, Ipotesi sulla natura degli oggetti matematici, Torino, Bollati Boringhieri, 1999.
Monti 1990: Monti, Pietro, Fra Bonaventura Cavalieri, Alberti, Intra, 1990.