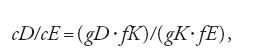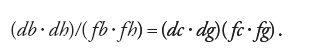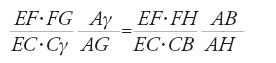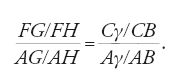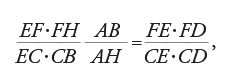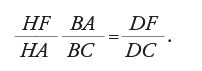La Rivoluzione scientifica: i domini della conoscenza. Lo sviluppo della matematica di Apollonio: Desargues, Pascal…
La Rivoluzione scientifica: i domini della conoscenza. Lo sviluppo della matematica di Apollonio: Desargues, Pascal¿
Lo sviluppo della matematica di Apollonio: Desargues, Pascal e le sezioni coniche
La matematica, o se vogliamo essere più precisi, la geometria di tradizione apolloniana, ebbe da un lato nella Géométrie (1637) di René Descartes uno sviluppo nuovo, conforme alle innovative concezioni cartesiane; dall'altro, grazie a Girard Desargues (Première proposition géométrique, 1636; Brouillon projet, 1639) e Blaise Pascal (Essay pour les coniques, 1639-1640), notevoli arricchimenti e ampliamenti concettuali secondo le tradizionali tecniche sintetiche. Vale la pena ricordare che le Coniche di Apollonio ebbero la loro prima edizio ne a stampa a Venezia nel 1537, tradotte in latino da Giovanni Battista Memmo, lettore di matematica a Venezia. L'opera era stata già studiata da Regiomontano e aveva suscitato l'interesse di Giorgio Valla (1447-1500) e Johann Werner (1468-1522). Commandino pubblicherà una nuova traduzione delle Coniche nel 1566, coredandola con parti del VII libro delle Collectiones di Pappo. Già in questo periodo le sezioni coniche sono coinvolte nella prospettiva (o perspectiva), nella costruzione di specchi ustori e delle linee orarie (per la realizzazione di orologi solari). A queste tematiche, che riguardano gli aspetti applicativi delle nozioni inerenti alle sezioni coniche, sono legati i nomi di matematici quali Giovanni Battista Benedetti, Cristoforo Clavio e Francesco Maurolico. A quest'ultimo si deve una traduzione dei primi quattro libri e la 'divinazione' (ricostruzione) del quinto e sesto libro dell'opera di Apollonio, redatti nel 1547 ma pubblicati nel 1654.
Uno dei temi centrali della Géométrie di Descartes è il cosiddetto 'problema di Pappo', che consiste nella determinazione di luoghi geometrici piani a partire da alcune relazioni che intercorrono tra le distanze di un punto generico da segmenti assegnati. Descartes giunge, abbandonando anche il principio di omogeneità dimensionale, all'equazione (cartesiana) di tale luogo. Nella Géométrie è appunto riportato il passo dalle Collectiones mathematicae di Pappo in cui quest'ultimo riconduce ad Apollonio la prima formulazione del problema. La nascita della geometria cartesiana è dunque intimamente legata alla tradizione di Apollonio e Pappo. Ma questa stessa tradizione è all'origine anche di altri importanti sviluppi della matematica seicentesca.
Nel Cinquecento (e anche prima) si era avuto un proliferare di interessanti trattati di perspectiva, molti dei quali utilizzavano lo strumento geometrico. Con tecniche basate sulla teoria delle proporzioni, questi trattatisti, che spesso erano anche pittori e architetti di fama, riuscivano a rappresentare le "degradazioni dall'occhio", ovvero le modalità con cui si poteva riprodurre in un piano un oggetto, in modo tale che apparisse al nostro occhio come se fosse tridimensionale. Il collegamento con la tradizione classica riguarda la costruzione di planisferi (il Planisphaerium di Tolomeo era stato tradotto in latino nel 1507), nonché le realizzazioni sceniche e gli argomenti studiati nell'Ottica e nella Catottrica di Euclide. Le tecniche della prospettiva furono presentate non solamente come regole pratiche per disegnare conformemente a come all'occhio appare la realtà osservata, ma furono anche descritte da un punto di vista geometrico, introducendo così di rimando nuovi spunti di riflessione nell'ambito di questa disciplina. Di particolare interesse matematico furono i trattati Della pictura (1435, stampato nel 1511) di Leon Battista Alberti, De prospectiva pingendi (1472-1475) di Piero della Francesca, Trattato della pittura (inizio del sec. XVI, stampato nel 1651) di Leonardo da Vinci, La perspectiva di Euclide (1573) nella traduzione di Egnazio Danti, i Perspectivae libri sex (1600) di Guidobaldo Dal Monte e il De sciagraphia (1605) di Simon Stevin; tra questi, il trattato di Piero riveste un'importanza notevole.
Nella prima metà del Seicento questi aspetti furono ripresi e ben studiati da architetti, pittori, scultori e matematici. Come vedremo, nelle loro opere Desargues, che era un architetto, e Pascal, che oltre alla filosofia seppe coltivare egregiamente interessi matematici, presentarono risultati geometrici, legati concettualmente alle tecniche prospettiche, che segnarono di fatto la nascita di nozioni e tematiche che sarebbero divenute proprie della geometria proiettiva. Furono introdotti elementi 'ideali' assimilabili a quelli che oggi chiamiamo 'punto improprio' e 'retta impropria', a livello concettuale, rendendo possibile un ampliamento dello spazio euclideo. Anche in questi sviluppi la teoria delle proporzioni gioca un ruolo determinante, permettendo di ottenere, come vedremo, rilevanti proprietà geometriche di carattere intrinsecamente proiettivo, nonostante il contesto di riferimento resti sempre euclideo.
Va evidenziato poi che alcune proposizioni (dalla 129 alla 145) del Libro VII delle Collectiones mathematicae di Pappo, che riguardano una sorta di teoria delle trasversali, presentano nozioni di carattere proiettivo, come (espresse nel linguaggio attuale) condizioni di allineamento fra tre punti oppure l'invarianza del birapporto. L'opera di Pappo, tradotta da Commandino, fu pubblicata postuma a spese del duca di Urbino, Francesco II, nel 1588; alcune sue proposizioni (VI.43, VI.42) mostrano forti analogie con altre contenute nella Perspectiva (pubblicata nel 1535) di Witelo, e precisamente le I. 22, I. 38, I. 39.
I lavori di Girard Desargues
Girard Desargues (1591-1661) di Lione, autodidatta, fu architetto e ingegnere militare; studiò le Coniche di Apollonio con l'obiettivo di svilupparne i contenuti alla luce di nozioni e considerazioni che provenivano da tecniche di perspectiva. L'opera di Desargues ha avuto un ruolo cruciale per l'analisi geometrica della prospettiva, anche se i suoi risultati non ebbero nell'immediato il successo e il seguito che era lecito aspettarsi. In essa era ampliato il bagaglio delle nozioni primitive euclidee ed era considerata in sostanza la nozione di trasformazione proiettiva; era inoltre messa in luce l'invarianza per tali trasformazioni di relazioni tra punti, come nel caso dell'involuzione, nozione introdotta esplicitamente da Desargues. I lavori desarguesiani che è necessario tenere presenti sono la Première proposition géométrique, pubblicata da Abraham Bosse nella Manière universelle de M. Desargues pour pratiquer la perspective (1648) e il Brouillon projet d'une atteinte aux événements des rencontres d'une cône avec un plane et aux événements des contrariétés de entre les actions des puissances ou forces, del 1639, che conobbe però una scarsissima circolazione fino al XIX secolo. Cominceremo dal primo, in cui è illustrato il teorema, noto come teorema dei triangoli omologici. Si tratta di un teorema molto significativo che stabilisce sotto certe ipotesi l'allineamento fra tre punti, permettendo, in altre parole, di costruire tre punti allineati per giungere, a partire da essi, alla costruzione di due triangoli legati tra loro omologicamente. Va altresì sottolineato che questo teorema può valere sia nel piano sia nello spazio.
Desargues e Bosse, Première proposition géométrique
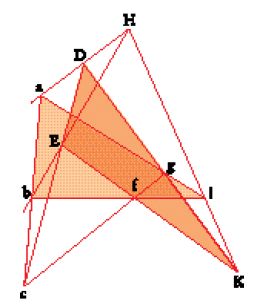
Se le rette HDa, HEb, HlK; cED, cba; lga, DgK; lfb, EfK si trovano su due piani distinti o nello stesso piano, allora i punti c, f, g ‒ rispettivamente punti di intersezione di cba con cED; di EfK con bfl; di agl con DgK ‒ si trovano su una stessa retta (cioè sono allineati), e viceversa (fig. 2).
Il teorema è dapprima dimostrato per lo spazio, cioè quando i piani abl e DEK sono distinti, e poi per il piano, ossia quando i due triangoli giacciono su uno stesso piano. Cominciamo dunque dal primo caso, in cui le rette abc, lga, lfb, che costituiscono il triangolo abl, sono nello stesso piano, mentre le rette DEc, DgK e KfE si trovano in un altro piano. Poiché i punti c, f, g appartengono a entrambi i piani si trovano dunque sulla retta cfg, intersezione tra i due piani. Passiamo ora al secondo caso (quello in cui i due triangoli giacciono su uno stesso piano), per il quale Desargues ricorre al cosiddetto 'teorema di Menelao-Tolomeo' (limitatamente al caso della geometria piana); in particolare ne utilizza l'inversa. Allora, con riferimento alla fig. 2, il suddetto teorema stabilisce che, essendo
i punti c, f, g sono allineati.
Desargues, Brouillon projet
Passiamo ora al Brouillon projet, del 1639, un'opera che, nonostante sia un semplice progetto, presenta un'articolazione dell'esposizione e prospettive d'indagine nell'ambito geometrico di particolare novità. Anche in questo lavoro il teorema di Menelao-Tolomeo gioca un ruolo cruciale nelle dimostrazioni di fondamentali risultati di significato proiettivo e Desargues lo richiama esplicitamente (sempre per il caso piano). Cominciamo presentando le definizioni desarguesiane, relative a ciò che noi chiamiamo elementi impropri e quindi alla nozione, sempre introdotta da Desargues, di 'involuzione'.
Diremo, con Desargues, che più linee rette sono tra loro di uno stesso ordine ("ordonnance des lignes droites") se sono tra loro tutte parallele oppure se tutte si incontrano in un medesimo punto. Sia nell'uno sia nell'altro caso tali rette tendono a un punto, detto punto 'traguardo' di rette di uno stesso ordine ("but d'une ordonnance de droites"). Diremo che più piani sono tra loro di uno stesso ordine ("ordonnance de plans") se sono tra loro tutti paralleli oppure se si incontrano tutti in una medesima retta. Sia nell'uno sia nell'altro caso essi tendono a una retta. La retta a cui tendono i piani è detta asse 'traguardo' di piani di uno stesso ordine ("but d'une ordonnance de plans").
Come si può osservare immediatamente, Desargues mette in evidenza il fatto che punti e rette all'infinito hanno, da un punto di vista proiettivo, le stesse caratteristiche dei rispettivi enti al finito; come questi, infatti, possono ottenersi per mezzo di intersezioni (all'infinito) di rette e di piani. Desargues presenta poi nel modo seguente la generazione del fascio di rette (e analogamente del fascio di piani): "Supponendo che una retta infinita avente un punto immobile si muova con tutta la sua lunghezza, si vede che alle diverse posizioni che prende in questo movimento essa dà le diverse rette di un medesimo fascio il cui centro è il punto immobile" (Brouillon projet in L'oeuvre mathématique, p. 146).
Questo tipo di generazione dei fasci richiama alla mente la nozione di 'verso di percorrenza' per un fascio di rette, dal momento che la retta generatrice può muoversi secondo due versi opposti a partire da una posizione iniziale. In quest'ordine di idee troviamo anche la considerazione che se un punto fisso, centro del fascio, è al finito, allora ogni punto della retta diverso dal centro traccia in questo movimento una circonferenza; mentre se il punto fisso è all'infinito, ciascuno dei punti della retta genera ancora una retta perpendicolare alla retta che si muove. In questo modo Desargues individua una sorta di legame tra la linea retta infinita e il cerchio.
Come abbiamo accennato, Desargues introduce la nozione di 'involuzione' fra sei punti su di una retta, che svolgerà un ruolo cruciale anche nello studio delle coniche. Dato un punto O su di una retta e le seguenti tre coppie di segmenti (detti 'bracci'): Oa, Oa′; Ob, Ob′; Oc, Oc′, se i rettangoli costruiti sulle tre coppie di segmenti sono uguali, cioè se:
[2] Oa ∙Oa'=Ob ∙Ob'=Oc ∙Oc'
allora i sei punti (detti 'nodi') a, a′; b, b′; c, c′ si dicono in involuzione.
Desargues fa vedere facilmente come l'involuzione possa essere caratterizzata mediante relazioni che non coinvolgono il punto O (detto 'ceppo' dell'involuzione). Infatti si arriva, partendo dalla [2], a:
[3] (b'c ∙ b'c')/(bc' ∙ bc)=(b'a ∙ b'a')/(a'b ∙ ab)
Analogamente Desargues stabilisce che:
[4] (c'b ∙c'b')/(cb ∙ cb') = (c'a ∙c'a')/(ca ∙ca')
[5] (a'b ∙ a'b')/(ab ∙ ab') = (a'c ∙ a'c')/(ac ∙ ac')
Otteniamo dunque il seguente enunciato:
Siano dati sei punti a, a′; b, b′; c, c′ su di una retta. Le [3], [4], [5] caratterizzano ciascuna l'involuzione dei sei punti in questione.
Desargues richiama quindi, come si diceva, il teorema di Menelao-Tolomeo e lo applicherà come lemma a due teoremi di spiccato carattere proiettivo. Cominciamo da quello che oggi è chiamato 'teorema del quadrangolo completo'. Per quadrangolo completo si intende la figura piana, formata da quattro punti (detti vertici) a tre a tre non allineati e dalle rette che essi determinano. Queste rette saranno sei e sono dette lati. Vale la pena osservare che tale nozione non è descritta in questi termini nelle opere di Desargues, anche se viene chiaramente utilizzata.
Teorema 1: Con riferimento alla fig. 5, se tre coppie di lati opposti di un quadrangolo completo sono intersecati da una retta che non passa per i vertici del quadrangolo, allora i sei punti individuati sono in involuzione.
Il seguente teorema mostra ‒ come diremmo oggi ‒ l'invarianza dell'involuzione per proiezione.
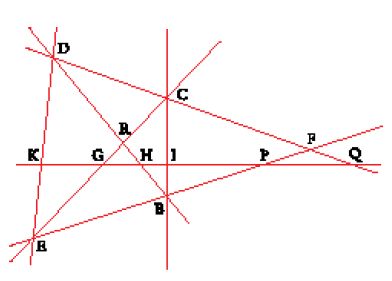
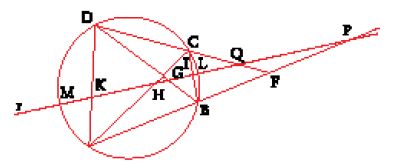
Teorema 2: Con riferimento alla fig. 6, quando, in una retta GH, per tre coppie di punti B, H; D, F; C, G disposti tra loro in involuzione passano tre coppie di rette di un medesimo fascio di centro K, ossia FK, DK; BK, HK; CK, GK, queste tre coppie di rette individuano su qualsiasi altra retta che le interseca (non appartenente al fascio) ancora tre coppie di punti b, h; d, f; c, g in involuzione.
Va precisato che se il punto K, centro del fascio, si trova a distanza infinita, vale a dire se è improprio, allora le rette del fascio sono parallele e di conseguenza staccano segmenti in proporzione su due trasversali qualsiasi. Quindi, per il cosiddetto 'teorema di Talete', se tra i segmenti staccati su una trasversale valgono relazioni che determinano una involuzione, le stesse relazioni valgono sui segmenti corrispondenti staccati sull'altra trasversale. Se il punto K è invece un punto proprio, bisogna per esempio dimostrare (vedi [6]) che se
[6] (DB ∙ DH)/(FB ∙ FH) = (DC ∙ DG)/(FC ∙ FG)
allora:
Questa importante proposizione ci dice appunto che l'involuzione è un invariante rispetto alle operazioni di proiezione e di sezione.
Le coniche secondo Desargues
I risultati che abbiamo visto nel precedente paragrafo furono applicati da Desargues, sempre nel Brouillon projet, allo studio delle coniche. Egli definì le coniche come proiezioni del cerchio, riuscendo a cogliere proprietà generali di tipo proiettivo. Secondo Desargues, la generazione delle coniche avviene tenendo presente le seguenti situazioni di base. Se una retta che ha un punto immobile si muove lungo una circonferenza, si possono avere due casi: (a) il punto immobile è nel piano della circonferenza e allora la retta con le sue posizioni successive descrive un fascio, che può essere proprio o improprio a seconda che il punto immobile sia a distanza finita o infinita; (b) il punto immobile è fuori del piano del cerchio e allora otterremo una figura solida, che chiameremo 'cono' se il punto è a distanza finita, 'cilindro' se è a distanza infinita. Come si può osservare, cono e cilindro sono visti in modo unitario. Proseguendo, Desargues richiama nozioni elementari sulle sezioni coniche in modo alquanto simile ad Apollonio.
Presenteremo ora uno dei risultati fondamentali del Brouillon projet, ossia il teorema relativo al quadrangolo completo inscritto in una conica e tagliato da una trasversale.
Teorema 3: Dato un quadrilatero inscritto in una conica, una retta secante, non passante per alcun vertice del quadrangolo, taglia la conica in due punti che sono coniugati nell'involuzione a cui appartengono le tre coppie di punti segnate, sulla retta stessa, dalle coppie di lati opposti del quadrangolo.
Facendo riferimento alla fig. 8, innanzi tutto va precisato che una coppia di punti è coniugata in una involuzione caratterizzata da sei punti assegnati (tre coppie) se, sostituita a una delle coppie date, non modifica l'involuzione medesima. Si dimostra allora che i punti L, M soddisfano a una delle relazioni previste dal teorema [6]. Desargues si riferisce in prima istanza al caso in cui la conica si riduce al cerchio e dimostra quindi la validità del teorema nel caso del cerchio. Dopo di che, sfruttando la caratterizzazione delle coniche quali sezioni di coni generati dalla rotazione di una retta attorno a un cerchio, deduce che ogni conica si può proiettare in un cerchio. Poiché l'involuzione, come aveva mostrato, è invariante per proiezione e per sezione, quanto provato per il cerchio varrà per ogni altra sezione conica. Pertanto il teorema è dimostrato utilizzando in modo cruciale l'invarianza dell'involuzione per proiezione e sezione.
Desargues conclude affermando che questo tipo di dimostrazione, "bene intesa, si applica in numerose occasioni". In questo modo è riconosciuto dall'autore il ruolo determinante "del metodo proiettivo che gli serve da guida" nelle indagini proposte nel Brouillon projet (in L'Oeuvre mathématique, p. 137 e segg.).
Le coniche secondo Blaise Pascal
Blaise Pascal, nell'Essay pour les coniques (1639-1640), studiò alcune notevoli proprietà delle coniche facendo riferimento ai metodi desarguesiani. Sull'influenza esercitata da Desargues su Pascal, la storiografia matematica è pressoché unanime, talché possiamo considerare i risultati pascaliani come un ampliamento e una parziale evoluzione di quelli desarguesiani. Illustreremo l'Essay, così come lo leggiamo nell'edizione di René Taton del 1951 (pp. 190-194), e alcuni teoremi di Pascal, con l'avviso che l'autore non ne dà la dimostrazione. Dopo alcune definizioni è enunciato il ben noto teorema pascaliano dell'esagono inscritto in una conica. Prima di riportarlo è però opportuno premettere proprio la definizione iniziale: "quando più rette concorrono a uno stesso punto oppure sono tutte tra loro parallele, allora queste rette vengono dette dello stesso ordine o dello stesso ordinamento". Si tratta di un concetto del tutto analogo a quanto espresso da Desargues con "ordonnance des lignes droites".
Pascal, Essay pour les coniques
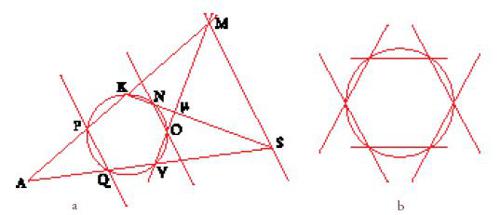
Teorema 1: Nel piano ove giacciono i punti M, S, Q (fig. 10), dal punto M partano le due rette MK, MV e dal punto S partano le due rette SK, SV; siano K l'incontro delle rette SK, MK; V l'incontro delle rette MV, SV; A l'incontro delle rette MA, SA e μ l'incontro delle rette MV, SK. Per due dei quattro punti A, K, μ, V che non siano nella stessa retta con i punti M, S, come i punti K, V, passi la circonferenza di un cerchio che incontra le rette MV, MK, SV, SK nei punti O, P, Q, N; allora diciamo che le rette MS, NO, PQ sono dello stesso ordine.
Questo teorema, come possiamo constatare dalla fig. 10a, è la formulazione del caso relativo alla circonferenza del teorema dell'esagono (o esalatero) completo. Abbiamo infatti l'esagono QPKNOV inscritto nella circonferenza. I lati opposti tra loro sono KN, QV; PK, VO; PQ, NO; di questi i primi due si incontrano nel punto S, i secondi nel punto M, mentre l'ultima coppia, nel caso prospettato dal teorema, è dello stesso ordine di MS. Vale a dire che le rette PQ e NO o sono parallele alla retta MS e quindi si incontrano nel punto improprio (come rappresentato nella fig. 10a), oppure hanno in comune con MS un punto al finito. In entrambe le eventualità vediamo che le tre coppie di lati opposti dell'esagono si incontrano in tre punti che sono allineati. La fig. 10b mostra l'esagono regolare inscritto in un cerchio; qui si trovano tre punti impropri tutti situati nella retta impropria.
Teorema 2: Se per una stessa retta passano più piani che sono tagliati da un altro piano, tutte le linee delle sezioni di questi piani sono dello stesso ordine della retta per la quale passano i detti piani.
Teorema 3: Posti come lemmi i precedenti [Pascal, teor. 1 e teor. 2] e qualche facile conseguenza di essi, dimostreremo che, poste le stesse condizioni del [Pascal, teor. 1], se per i punti K e V passa una qualunque sezione del cono che taglia le rette MK, MV, SK, SV, nei punti P, O, S, Q, le rette MS, NO, PQ saranno dello stesso ordine.
Come si può facilmente constatare il [Pascal, teor. 3] estende a qualunque conica il [Pascal, teor. 1], mentre il [Pascal, teor. 2] permette il passaggio per proiezione, stabilendo che tutte le rette che si incontrano nel piano della fig. 10 si incontreranno anche nel piano in cui verrà proiettata la conica. È immediato cogliere l'analogia metodologica tra il modo di procedere di Desargues nel Brouillon projet nella dimostrazione del [Desargues, teor. 3] e quello di Pascal: dapprima si dimostra una proprietà per il cerchio e poi la si estende per proiezione o sezione a una conica qualunque. Va osservato che quando la conica degenera, come diremmo oggi, in una coppia di rette, ci ritroviamo nel caso prospettato dalla proposizione VII.139 delle Collectiones di Pappo.
Vediamo di seguito qualche altra proposizione di particolare interesse presente nell'Essay.
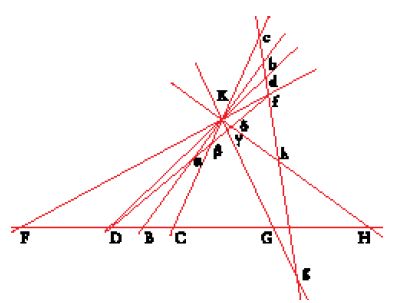
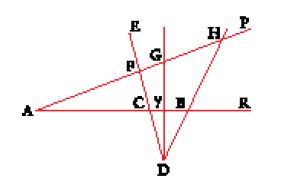
Teorema 4: Se sono date tre rette DE, DG, DH, tagliate dalle rette AP e AR nei punti F, G, H, C, γ, B, si può determinare sulla retta DC un punto E in modo tale che il rapporto composto dal rapporto del rettangolo EF, FG al rettangolo EC, Cγ e da quello del segmento Aγ al segmento AG risulti uguale al rapporto composto dal rapporto del rettangolo EF, FH al rettangolo EC, CB e dal rapporto del segmento AB al segmento AH (fig. 11).
Questo teorema espresso in formule afferma che:
che equivale a:
La [9] in termini moderni stabilisce l'uguaglianza tra il birapporto (FAGH) e il birapporto (CAγB) prescindendo dai segni. Questo teorema corrisponde alla proposizione VII.129 delle Collectiones di Pappo.
Teorema 5: Sulla base di [Pascal, teor. 4], si può dimostrare che:
ovvero:
La [11] non esprime altro che la versione piana del teorema di Menelao-Tolomeo, riproposto e utilizzato, come abbiamo visto, anche da Desargues, sia nel Brouillon projet sia nella dimostrazione del teorema dei triangoli omologici.
Ci si potrà domandare inoltre perché il filosofo Pascal scrisse in modo significativo di geometria e in generale di matematica. La risposta non è molto difficile se si pensa che in quel secolo altri illustri filosofi (come Descartes, Malebranche e più tardi Leibniz) si interessarono di matematica. In primo luogo era la formazione di base che avvicinava questi studiosi alla matematica più avanzata del tempo e quindi la necessità di riconsiderarla nei loro rispettivi impianti filosofici. In secondo luogo la tradizione matematica era in qualche modo legata, seppur nel suo autonomo sviluppo, a talune interessanti questioni filosofiche che nel Cinquecento ebbero come epicentro il dibattito sulla certitudo mathematicarum.
Descartes, Desargues e Pascal
Concludiamo qui la nostra presentazione dei risultati di Desargues e di Pascal con qualche succinta considerazione sui rapporti tra Descartes, Desargues e Pascal, i quali si conobbero grazie al polo di attrazione e di discussione culturale realizzato da Marin Mersenne.
In una lettera che Descartes invia a Desargues, datata 19 giugno 1639, si fa riferimento al Brouillon projet che appunto Mersenne aveva provveduto a inviargli. Nella prima parte della lettera Descartes afferma di non condividere la scelta desarguesiana di introdurre una nuova terminologia matematica (il cui unico termine rimasto è forse la parola 'involuzione'). A suo avviso, infatti, i dotti fanno riferimento alla tradizione classica che per le coniche risale ad Apollonio, mentre qualora ci si voglia rivolgere a coloro che praticano la prospettiva e l'architettura, l'impegno matematico prospettato nel Projet sarebbe inevitabilmente poco apprezzato. Il parere di Descartes è poi rappresentato emblematicamente nel passo poco sotto riportato, dove si coglie altresí non solo il suggerimento a servirsi dell'aritmetica per far geometria, ma anche lo scarso apprezzamento dei metodi sintetici: "A questo proposito a me sembra che, per rendere le vostre dimostrazioni più semplici, non sarebbero fuor di luogo termini e calcolo aritmetici, così come faccio io nella mia Géométrie; poiché sono più numerose le persone che conoscono cosa sia una moltiplicazione di quelle che sanno cosa sia la composizione tra i rapporti, ecc." (AT, II, p. 555). Descartes conclude poi ritenendo opportuna la proposta desarguesiana di unificare la nozione di punto al finito e all'infinito.
In una lettera a Descartes datata 12 novembre 1639 Mersenne aveva usato termini assai lusinghieri per descrivere la precoce e brillante intelligenza matematica di Pascal. Nell'aprile del 1640 Descartes ebbe sotto mano l'Essay e lo considerò una vera e propria filiazione delle concezioni desarguesiane.
L'impostazione e i metodi di Desargues non ebbero successo nel mondo matematico dell'epoca, se si eccettua l'interesse mostrato da Abraham Bosse e Philippe de La Hire, e per una loro riscoperta si dovrà attendere il XIX secolo. Nella seconda metà del Seicento, a caratterizzare gli sviluppi della geometria e della matematica furono i metodi cartesiani, indubbiamente anche per le loro potenzialità tecniche.
Le idee innovatrici di Descartes e Pascal nel campo dello studio matematico della perspectiva, in connessione con la teoria delle coniche, costituiscono un contributo di importanza cruciale, che sarà adeguatamente apprezzato solo a partire dai primi anni dell'Ottocento, soprattutto grazie a Jean-Victor Poncelet. Non si può fare a meno di rilevare che, nonostante le nuove elaborazioni teoriche, le nuove analisi logiche e la diversità di contesti e di linguaggi, la sostanza di questi teoremi e il loro genuino significato geometrico sono rimasti quasi immutati, pur avendo assunto un diverso ruolo dal punto di vista teorico.
Non si può infine non rammentare che il teorema di Desargues sui triangoli omologici e quello di Pascal sull'esagono ricoprono un ruolo cruciale nell'impianto teorico dei Grundlagen der Geometrie (1899) di David Hilbert, il trattato che nell'Età contemporanea rivisita in modo fortemente originale la geometria elementare euclidea e proiettiva.
Bibliografia
Bottazzini 1992: Bottazzini, Umberto - Freguglia, Paolo - Toti Rigatelli, Laura, Fonti per la storia della matematica, Firenze, Sansoni, 1992.
Boyer 1968: Boyer, Carl B., A history of mathematics, New York, Wiley, 1968 (trad. it.: Storia della matematica, a cura di A. Carugo, Milano, Mondadori, 1980).
Brigaglia 1997: Brigaglia, Aldo, La ricostruzione dei libri V e VI delle Coniche da parte di Francesco Maurolico, "Bollettino di storia delle scienze matematiche", 17, 1997, pp. 267-307.
Clagett 1980: Archimedes in the Middle Ages, edited by Marshall Clagett, Madison, University of Wisconsin Press; Philadelphia, American Philosophical Society, 1964-1984, 5 v.; v. IV/1-2: A supplement on the medieval Latin tradition of conic sections (1150-1566), 1980.
Costantini 1970: Costantini, Domenico, Fondamenti del calcolo delle probabilità, Milano, Feltrinelli, 1970.
‒ 1982: Costantini, Domenico - Geymonat, Ludovico, Filosofia della probabilità, Milano, Feltrinelli, 1982.
Dhombres 1994: Desargues en son temps, sous la direction de Jean G. Dhombres et Joël Sakarovitch, Paris, Blanchard, 1994.
Freguglia 1999: Freguglia, Paolo, La geometria fra tradizione e innovazione, Torino, Bollati Boringhieri, 1999.
Garibaldi 1982: Garibaldi, Antonio C., Sulla preistoria del calcolo delle probabilità, in: La storia delle matematiche in Italia, a cura di Oscar Montaldo e Lucia Grugnetti, Cagliari, Università-Istituti di Matematica delle Facoltà di Scienze e Ingegneria, 1982, pp. 377-384.
Geymonat 1962: Geymonat, Ludovico, Storia della matematica, in: Storia delle scienze, a cura di Nicola Abbagnano, Torino, UTET, 1962, 4 v.
‒ 1975: Geymonat, Ludovico, Storia del pensiero filosofico e scientifico, Milano, Garzanti, 1975, 9 v.; v. III: Il Settecento, 1975; v. IV: L'Ottocento, 1975.
Hacking 1975: Hacking, Ian, The emergence of probability. A philosophical study of early ideas about probability, induction and statistical inference, London, Cambridge University Press, 1975 (trad. it.: L'emergenza della probabilità. Ricerca filosofica sulle origini delle idee di probabilità, induzione e inferenza statistica, Milano, Il Saggiatore, 1987).
Loria 1950: Loria, Gino, Storia delle matematiche. Dall'alba della civiltà al secolo XIX, 2. ed., Milano, Hoepli, 1950 (1. ed.: Torino, Sten, 1929-1933, 3 v.; rist. anast.: Milano, Cisalpino-La Goliardica, 1982).
Maistrov 1967: Maistrov, Leonid E., Teoriià veroiàtnostei, istoricheskii ocherk, Moskvà, Izdatel'stvo Nauka, 1967 (trad. ingl.: Probability theory. A historical sketch, transl. and edited by Samuel Kotz, New York, Academic Press, 1974).
Pearson 1970: Studies in the history of statistics and probability, selected and edited by Egon Sharpe Pearson, Maurice Kendall, London, Griffin, 1970.
Sheynin 1974: Sheynin, Oskar B., On the prehistory of the theory of probability, "Archive for history of exact sciences", 12, 1974, pp. 97-141.
‒ 1977: Sheynin, Oskar B., Early history of the theory of probability, "Archive for history of exact sciences", 17, 1977, pp. 201-219.
Todhunter 1865: Todhunter, Isaac, A history of the mathematical theory of probability. From the time of Pascal to that of Laplace, Cambridge, Macmillan, 1865 (rist.: New York, Chelsea, 1949; Bronx (N.Y.), Chelsea, 1965).