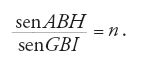La Rivoluzione scientifica: i domini della conoscenza. Ottica
La Rivoluzione scientifica: i domini della conoscenza. Ottica
Ottica
Nei cento anni intercorsi tra la pubblicazione della principale opera ottica di Johannes Kepler, i Paralipomena (1604), e l'Opticks (1704) di Isaac Newton, l'ottica passò attraverso una radicale trasformazione e ampliò notevolmente il proprio campo d'azione. Kepler formulò una nuova teoria della visione e gettò le basi della moderna teoria della formazione delle immagini ottiche. Quando, alcuni anni più tardi, Galilei inventò il telescopio astronomico, Kepler fu quasi subito in grado di spiegare il suo funzionamento e quello delle lenti. Da quel momento, il telescopio fu la forza trainante di buona parte della scienza ottica del XVII sec.: l'ottica geometrica diventò uno dei rami più complessi delle scienze matematiche e furono in molti a occuparsi dello studio teorico e pratico delle lenti e del telescopio. L'ottica fisica ‒ lo studio della Natura e delle proprietà della luce ‒ divenne uno dei principali rami dell'ottica man mano che la sperimentazione rivelava un numero sorprendente di nuove proprietà della luce, come l'interferenza, la diffrazione, la doppia rifrazione e la polarizzazione.
Kepler
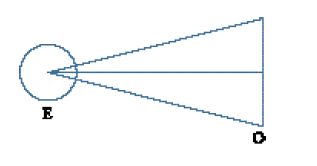
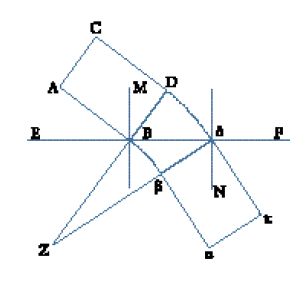
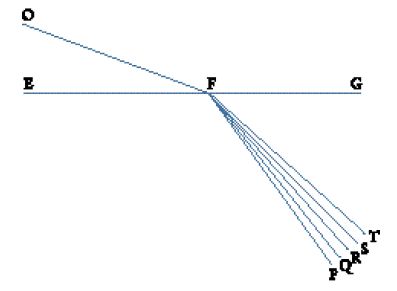
Quando, al volgere del XVII sec., Kepler iniziò a occuparsi di ottica, questa scienza era già passata attraverso un'importante rivoluzione nel Medioevo a opera di Ibn al-Hayṯam (965-1041 ca.), noto in Occidente come Alhazen. Nell'ottica greca, si riteneva che la luce si dirigesse seguendo raggi rettilinei dall'occhio verso l'oggetto della visione, per poi ritornare all'occhio. Ciò dava origine a un cono visuale con il vertice nell'occhio (E) e la base nell'oggetto (O), consentendo la geometrizzazione della visione (fig. 2).
Alhazen sostenne, invece, che gli oggetti visibili emettono raggi da ogni punto della loro superficie verso tutte le direzioni e che sono questi raggi a raggiungere l'occhio. Tuttavia ciò avrebbe provocato una visione confusa perché a ciascun punto dell'occhio i raggi sarebbero arrivati da ogni punto dell'oggetto. Per evitare questo problema, sostenne che soltanto un raggio tra quelli emessi da ciascun punto dell'oggetto, e cioè quello che cade perpendicolarmente sul cristallino, contribuisce alla visione, perché è più forte degli altri. Con questo argomento, Alhazen fu in grado di recuperare il cono visuale della tradizione dell'ottica geometrica, con la base nell'oggetto e il vertice nell'occhio e con un unico raggio proveniente da ciascun punto. La nuova teoria ottica di Alhazen fu adottata nell'Occidente latino. Il suo principale esponente fu Witelo (attivo nel 1220 ca.) la cui Optica, sostanzialmente una parafrasi di Alhazen, fu pubblicata nel 1572.
La camera obscura
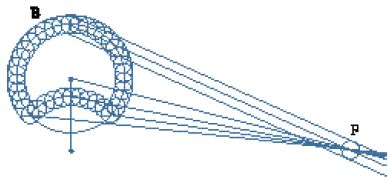
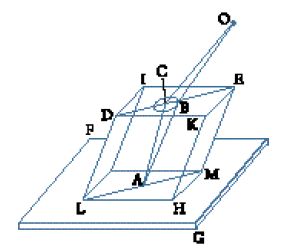
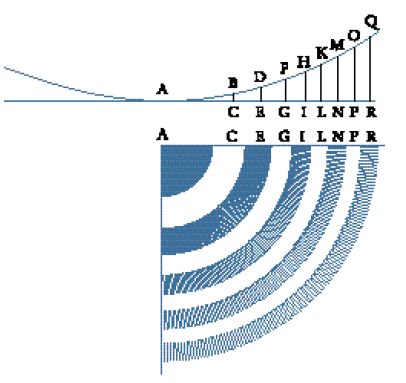
La descrizione di un'eclissi solare osservata nel 1598 dall'astronomo Tycho Brahe diede impulso alla ricerca di Kepler nel campo dell'ottica. Tycho osservò l'eclissi solare con una camera obscura, un apparecchio che consisteva in una tavola con un piccolo foro, attraverso il quale passava la luce che poi cadeva su uno schermo. Calcolando le dimensioni della Luna durante un'eclissi solare, scoprì che esse risultavano notevolmente inferiori (20% in meno) rispetto a quando la Luna non si trovava vicino al Sole. Capire come si forma un'immagine nella camera oscura era un antico e irrisolto problema dell'ottica. Non si riusciva a spiegare per quale motivo l'immagine non assumesse la forma del foro, per esempio perché l'immagine del Sole proiettata attraverso un'apertura triangolare fosse circolare e non triangolare; il problema era stato risolto, nei Photismi de lumine et umbra ad perspectivam et radiorum incidentiam facientes, da Francesco Maurolico verso il 1521 ma il suo lavoro non fu pubblicato fino al 1611, dopo la soluzione fornita indipendentemente da Kepler. Quest'ultimo si rese conto che la spiegazione del perché la Luna apparisse stranamente piccola doveva provenire dall'ottica, e iniziò pertanto a leggere i trattati medievali sull'argomento, ossia la Perspectiva di Witelo e la Perspectiva communis di Peckham. Li trovò oscuri e inutili. Per risolvere il problema, adottò una tecnica largamente usata dalla prospettiva lineare, con molta probabilità quella descritta da Albrecht Dürer nella Underweysung der Messung (Istituzioni di matematica, 1525), che gli consentiva di visualizzare in tre dimensioni l'irraggiamento da un corpo luminoso. Tese un filo dall'angolo di un libro (che rappresentava un corpo luminoso) attraverso un foro di forma poligonale e tracciò sul pavimento l'immagine che ne risultava: "In questo modo si creava sul pavimento una figura simile al foro. La stessa cosa avveniva quando un altro filo veniva aggiunto dal secondo, terzo e quarto angolo del libro, come pure dagli infiniti punti dei bordi del libro. In questo modo, infinite immagini del foro disposte lungo una stretta fila delineavano la grande figura quadrangolare del libro sul pavimento" (Kepler, Ad Vitellionem paralipomena, ed. Donahue, p. 56).
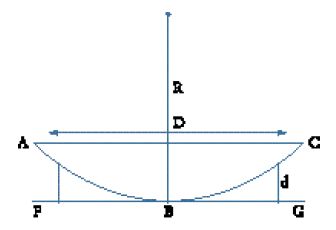
Kepler scoprì che l'immagine in una camera oscura era composta da un numero infinito di immagini del foro (F) che insieme formavano un'immagine della sorgente luminosa (B) (fig. 3). In particolare, dimostrò che l'immagine di un'eclissi parziale è composta da immagini sovrapposte del foro. Quando lo schermo è molto distante dal foro, l'immagine assume la forma dell'oggetto o della sorgente luminosa. Kepler fu in grado di risolvere quantitativamente il problema e di effettuare correzioni per le osservazioni astronomiche. La sua soluzione lo convinse del fatto che il progresso dell'astronomia sarebbe stato ostacolato fino a che non fosse stata raggiunta una vera conoscenza dell'occhio e della visione.
La teoria della visione
Kepler formulò le sue teorie nel quinto capitolo del suo innovativo contributo all'ottica, modestamente intitolato Ad Vitellionem paralipomena. Per affermare la propria teoria della visione, egli doveva scardinare due principî fondamentali dell'ottica medievale, uno anatomico e l'altro fisico. I suoi predecessori nello studio dell'ottica avevano sostenuto che l'umore cristallino è l'organo principale della visione, ma avevano affermato anche che i raggi che portano l'immagine continuano attraverso l'occhio fino al nervo ottico op. Per Kepler questa idea era incompatibile con la moderna anatomia di Andrea Vesalio (1514-1564) e di Felix Platter (1536-1614). Nel 1583 Platter aveva affermato che la retina, che riveste la parte posteriore dell'occhio, è la sede del potere visivo, mentre l'umore cristallino non è altro che una sorta di lente d'ingrandimento.
Kepler rifiutò anche l'argomento di Alhazen per cui soltanto quel raggio che cade perpendicolarmente da ciascun punto di un oggetto sull'occhio e lo attraversa senza rifrazione è quello che effettivamente lo penetra, perché tutti gli altri sono indeboliti dalla rifrazione e perciò difficilmente percepibili. Egli sostenne, invece, che i raggi obliqui adiacenti a quello perpendicolare sono scarsamente rifratti ed essendo la loro efficacia visiva quasi pari a quella dei raggi perpendicolari, non potevano essere ignorati. Questa critica era il frutto di una profonda rielaborazione della scienza ottica. Nella tradizione 'prospettivista' le immagini erano formate da un singolo raggio da ciascun punto dell'oggetto, ma Kepler ora esigeva che uno stretto cono o 'pennello' di raggi (come lo chiamò più tardi), venisse preso in considerazione nella formazione delle immagini. In questo modo, ridefinì la formazione dell'immagine e le leggi per calcolarne l'ubicazione. Stabilì che l'immagine si trova nel luogo in cui un pennello di raggi riflessi o rifratti diverge o sembra divergere. Nella Dioptrice (1611), Kepler per indicare tali raggi introdusse il termine penicilli, che evidentemente mutuò dal mondo dell'arte, così come la sua soluzione al problema delle immagini della camera oscura era stata dedotta dalla tradizione artistica. Un penicillum era un pennello da pittore e Kepler parlava dei pennelli che dipingevano (depingo) un'immagine o un quadro (pictura). Evidentemente, egli era fortemente influenzato dal mondo dell'arte.
Kepler spiegava la visione con la formazione sulla retina di un'immagine reale, ma rovesciata, del mondo esterno. Per giungere a questa nuova spiegazione, si rifece a una serie di osservazioni effettuate con una sfera di vetro riempita d'acqua. Rappresentando l'occhio con una sfera colma d'acqua, che talvolta collocava dietro una piccola apertura o finestrella per creare una camera oscura, egli dimostrò sperimentalmente che un'immagine o un disegno si formano con nitidezza su uno schermo collocato dietro la sfera. Questa osservazione non era nuova. Giambattista Della Porta (1535 ca.-1615), nella Magia naturalis ‒ che Kepler aveva letto ‒, aveva già osservato che quando una lente è collocata dietro un piccolo foro, le immagini diventano molto più nitide. Della Porta era arrivato perfino a paragonare l'occhio a una camera oscura, ipotizzando che il cristallino fosse analogo allo schermo sul quale le immagini sono proiettate in una camera oscura; Kepler, invece, lo riteneva simile a una lente collocata nel foro di una camera.
Grazie a questi esperimenti, sembra che Kepler nel corso delle sue ricerche abbia ben presto raggiunto la convinzione che una camera oscura con una lente potesse servire come modello per l'occhio e la visione. Dato che nessuno sapeva come funzionasse una lente, dovette studiare la traiettoria dei raggi attraverso un globo di vetro in varie condizioni, basandosi sulla conoscenza ‒ acquisita sperimentalmente ‒ del fatto che i raggi, sottoposti a varie condizioni, avrebbero effettivamente prodotto un'immagine.
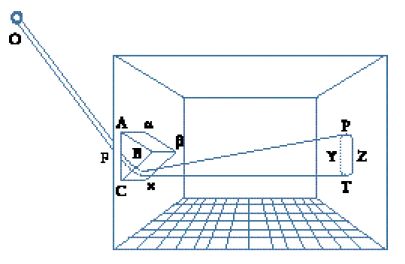
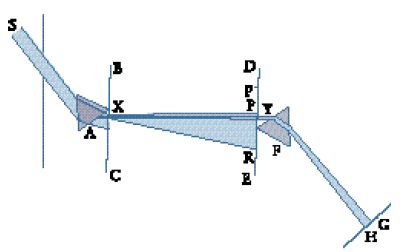
Kepler non presentò mai uno schema che illustrasse la formazione dell'immagine completa sulla retina. La spiegazione più famosa e autorevole della sua teoria fu presentata da René Descartes nella Dioptrique (1637). Il contesto che precedette la presentazione cartesiana ci può aiutare a capire quanto la teoria di Kepler fosse largamente accettata. L'astronomo gesuita Christoph Scheiner (1573-1650) l'aveva presentata nei suoi libri di ottica, che furono pubblicati nel terzo decennio del secolo, senza tuttavia rivelarne l'autore. Scheiner aveva concepito un'ingegnosa dimostrazione ‒ eseguita per la prima volta a Roma nel 1625 ‒ dell'immagine capovolta sulla retina, utilizzando occhi che erano stati prelevati da animali morti di recente. Eliminò le membrane posteriori dell'occhio in modo che la retina potesse essere vista da dietro l'occhio stesso, e collocò quest'ultimo nel foro di una camera oscura. Era dunque possibile vedere chiaramente sulla retina traslucida un'immagine rovesciata del mondo esterno. L'illustrazione dell'occhio di Descartes (di dimensioni esagerate) mostra un oggetto VXY all'esterno dell'occhio, che viene collocato in una camera oscura molto buia, e un uomo che osserva l'immagine RST sulla retina; sono visibili i coni di irraggiamento sovrapposti al cristallino e l'immagine rovesciata rispetto all'oggetto. Il fascio di raggi provenienti dal punto V, sulla sinistra, per esempio, passa attraverso la pupilla ed è rifratto ogni volta che attraversa la superficie del cristallino prima di convergere nel punto R sulla destra; analogamente, i raggi dal punto Y sulla destra convergono nel punto T sulla sinistra. Questo straordinario esperimento fu eseguito frequentemente e ripetuto circa tre decenni più tardi dal giovane Newton.
Il modello fornito da Kepler per l'occhio era di estrema semplicità: il foro della camera oscura rappresenta la pupilla, la sfera il cristallino e lo schermo la retina. Egli sapeva che il cristallino era lenticolare e non sferico; tuttavia sostenne che, a causa del circostante umore acqueo o fluido, la rifrazione che ne risultava non poteva essere molto diversa da quella di una sfera. L'aspetto più problematico della nuova teoria fu l'immagine invertita e rovesciata nella retina, che gli scienziati del Medioevo e del Rinascimento avevano cercato con grandi sforzi di evitare. Kepler ammise di "aver brancolato nel buio per lungo tempo" su questo problema, ma le sue analisi geometriche portavano necessariamente a tale conclusione. Dichiarò che la soluzione non era assolutamente di competenza della scienza dell'ottica geometrica, ma della filosofia. Sostenne con convinzione che la scienza ottica si occupa di sostanze trasparenti e non si estende alle sostanze opache dei nervi e del cervello.
Kepler aveva fornito ben più di una nuova teoria della visione, con il concetto di 'pennello di raggi' e la sua trattazione della formazione dell'immagine aveva gettato le basi per una nuova ottica. Le sue 'figure' sono quello che ora si definisce immagine reale, immagine che può essere proiettata su uno schermo, mentre i suoi predecessori avevano considerato solo immagini virtuali, che richiedono un occhio per essere percepite. Eliminando l'occhio come elemento fondamentale per l'ottica, Kepler prepara la strada alla nuova filosofia ‒ a cui Descartes aderisce con grande slancio ‒ che considera la luce semplicemente come un'entità fisica che suscita in noi sensazioni associabili con il mondo esterno e che trasforma l'ottica nello studio delle proprietà dell'irraggiamento.
La capacità di Kepler di ottenere risultati fondamentali e complessi con un modello così semplice, quasi banale, di rifrazione in una sfera acquea, fu un'impresa straordinaria ottenuta grazie a un abile ragionamento fisico e a un'analisi meticolosa dei suoi esperimenti. Dovette analizzare le sue osservazioni con le sfere e le fenditure come egli stesso confessa: "la varietà di queste cose è così vasta e presenta costantemente delle novità che, se non si è molto accorti, si rischia di venire facilmente confusi. Tanto è vero questo, che io stesso sono stato bloccato per lungo tempo" (Ad Vitellionem paralipomena, ed. Donahue, p. 212).
L'analisi geometrica della rifrazione fu in gran parte qualitativa, descrittiva e approssimata. Kepler fallì nel tentativo di formulare la vera legge di rifrazione e fece uso di una legge approssimata, secondo la quale l'angolo di rifrazione è proporzionale all'angolo di incidenza, con cui poté calcolare la traiettoria dei raggi rifratti in una sfera e stabilire che il suo punto focale era uguale al suo raggio. "Ho disperato ‒ si lamentò ‒ di poter definire geometricamente il punto preciso dove avviene l'estrema intersezione. Ti prego, lettore: dammi il tuo aiuto" (ibidem, p. 205).
Dopo l'annuncio galileiano del telescopio astronomico, Kepler fu in grado di spiegare nella Dioptrice sia il suo funzionamento sia quello delle sue lenti, ma gli fu possibile determinare il punto focale soltanto per una singola superficie sferica e per una lente equiconvessa sottile. Molte delle innovazioni di Kepler erano confuse, poco metodiche e incomplete e le successive generazioni di scienziati svilupparono ulteriormente i suoi studi. Fu soltanto nel 1647 che Bonaventura Cavalieri dedusse alcuni principî per i punti focali delle lenti sottili. Nel corso del secolo, matematici come James Gregory, Isaac Barrow, Newton, Christiaan Huygens, i fratelli Jakob I e Johann I Bernoulli, ed Edmond Halley formularono teorie sulle immagini ottiche e determinarono leggi per la definizione dell'aberrazione sferica, delle curve caustiche e dei punti immagine per qualsiasi lente: tutti risultati che in definitiva si basavano sui principî di Kepler.
Descartes
Nella Dioptrique, Descartes sintetizzò e approfondì le teorie ottiche di Kepler, ma lo fece con uno stile assai più lucido e accessibile di quello kepleriano. Di conseguenza, la conoscenza della teoria della visione di Kepler ebbe maggiore diffusione grazie proprio all'opera di Descartes. Nonostante non lo avesse citato nel suo libro, Descartes in una lettera del 31 marzo 1638 a Marin Mersenne ammise: "Kepler è stato il mio primo maestro di ottica" (AT, II, p. 86). Obiettivo della Dioptrique è descrivere i modi per migliorare la visione, in particolare con il telescopio, e a tal fine essa si occupa dell'anatomia oculare, della rifrazione e della sua misurazione, del disegno e della molatura delle lenti. Il contributo più rilevante è la pubblicazione della legge di rifrazione, generalmente nota come la legge di Snell. Per lungo tempo si ritenne che Descartes avesse 'preso in prestito' la legge da Willebrord Snell, anche perché l'accusa (avallata poi da Newton) era stata lanciata da uno scienziato di fama come Huygens, che aveva visto il manoscritto di Snell. Ora si accetta in linea di massima che l'idea sia stata elaborata autonomamente da Thomas Harriot, intorno al 1600, da Snell verso la metà degli anni Venti del secolo e, all'incirca nello stesso periodo, da Descartes stesso.
Rifrazione e filosofia meccanica
Sin dall'Antichità gli scienziati s'impegnarono nella ricerca della legge di rifrazione, che avrebbe sostituito le approssimazioni di cui si faceva uso, e la scoperta della legge permise allo studio delle lenti e dell'ottica geometrica di fondarsi su solide basi. Nella Dioptrique, Descartes ricavò la legge paragonando il movimento della luce a una palla che, dopo essere passata attraverso l'aria da A a B, entra in una conca d'acqua nel punto B, dove la resistenza dell'acqua sotto i punti CBE ne rallenta la velocità. Egli considerò che il movimento della palla consistesse di due componenti: una, BE, parallela alla superficie, e l'altra, EI, perpendicolare a essa, e dedusse che soltanto la componente della velocità perpendicolare alla superficie risultava modificata. Fu quindi in grado di dimostrare (in notazione moderna) che il rapporto fra il seno dell'angolo di incidenza ABH e il seno dell'angolo di rifrazione GBI è costante (tale costante è oggi nota come indice di rifrazione n), ovvero:
L'impiego di questa analogia pose però il problema che, mentre una palla entrando in una sostanza più densa come l'acqua rallenta, se si vuole spiegare la rifrazione della luce nell'acqua e nel vetro usando questo modello, se ne deve dedurre che la luce si muove più velocemente in sostanze più dense. Finché Newton non diede una giustificazione fisica di questo risultato apparentemente paradossale, esso fu considerato come un ostacolo per qualsiasi teoria dell'emissione della luce. Gli storici sono oggi ragionevolmente sicuri che Descartes in realtà non scoprì la legge mediante questa analogia. Così come la scoperta cartesiana dell'esatta formulazione della legge di rifrazione fu importante per il futuro sviluppo dell'ottica, altrettanto importante fu la sua derivazione meccanica; essa stabilisce un nuovo standard per la scienza del XVII sec., basandosi su un modello matematico che seguiva i principî della meccanica.
Descartes fu il più autorevole esponente di un nuovo approccio alla filosofia naturale, la 'filosofia meccanica', che sosteneva che tutti i fenomeni naturali dovevano essere spiegati soltanto con la materia e i suoi movimenti, escludendo ogni riferimento a cause immateriali, come le forze, le forme e le specie della Scolastica. Nella Dioptrique scrive che gli oggetti non possiedono qualità, come la dolcezza e il colore, che corrispondono alla nostra sensazione dei medesimi, ma soltanto le qualità primarie della dimensione, della forma e del moto che causano in noi movimenti; era convinto che le immagini nella nostra mente non assomiglino in nessun modo alle cose che esse rappresentano. Anche se sulla retina dell'occhio si forma un'immagine degli oggetti, "non bisogna tuttavia per nulla credere [...] che sia per mezzo di tale somiglianza che essa faccia in modo che noi li percepiamo, come se nel nostro cervello vi fossero ancora altri occhi coi quali potessimo vederla" (OS, II, p. 252). Secondo Descartes, il nervo ottico, che si estende dall'occhio al cervello, consiste di minuscole fibre che sono stimolate dalla luce e trasmettono il movimento al cervello. è grazie a questi moti che noi percepiamo il mondo esterno, e per lo scienziato moderno si tratta soltanto di conoscere come essi possano permettere alla mente di percepire tutte le diverse qualità degli oggetti ai quali si rapportano, non di conoscere come le immagini stesse assomiglino agli oggetti che esse rappresentano. Descartes aveva raccolto la sfida di Kepler: bisognava dare una spiegazione al processo della visione dopo che l'immagine si è formata sulla retina; Descartes rifiutò l'ipotesi che un'immagine sia trasmessa al cervello e, nello stesso tempo che vi sia, in realtà, un altro occhio nel cervello che percepisce l'immagine. A questo punto, la psicologia deve fornire una spiegazione. Ovviamente né Descartes né gli altri filosofi meccanici fecero molti progressi nel chiarire come i movimenti nel nostro cervello corrispondano alla nostra percezione del mondo esterno.
Una volta in possesso della legge della rifrazione, Descartes riuscì a elaborare la forma delle lenti che avrebbero messo la luce perfettamente a fuoco. Kepler aveva già dimostrato in modo convincente che le superfici sferiche non mettono a fuoco in un singolo punto, ma piuttosto sulla superficie caustica. Fu logica aspirazione degli studiosi di ottica, per migliorare i telescopi, arrivare a definire quelle forme che avrebbero eliminato questa aberrazione mettendo a fuoco la luce proveniente da un singolo punto in un singolo punto. Nella Géométrie, uno dei tre saggi pubblicati con il Discours de la méthode, Descartes definì una serie di curve, ora note come ovali cartesiani, che mettevano perfettamente a fuoco. Nelle condizioni che si verificano nell'ottica applicata, questi ovali si riducono a ellissi e iperboli. Nella Dioptrique, descrisse lenti con varie combinazioni di superfici ellittiche, iperboliche, sferiche e piane, che avrebbero diretto la luce nel modo richiesto. Per motivi tecnici, Descartes pensò che le superfici iperboliche sarebbero state più facili da molare di quelle ellittiche, e tentò di produrle con l'aiuto di abili costruttori di strumenti, descrivendo nella Dioptrique le sue macchine per la molatura. Gli sforzi di Descartes indirizzarono l'ottica del XVII sec. verso la ricerca sulle lenti a forma ellittica e iperbolica, nel tentativo di eliminare le gravi aberrazioni causate dalle lenti sferiche. Questo sforzo risultò vano, poiché la tecnologia del Seicento non era in grado di realizzare una tale molatura di precisione.
L'arcobaleno
Les météores, il terzo dei saggi introdotti dal Discours de la méthode, contenevano l'innovativa spiegazione dell'arcobaleno fornita da Descartes. L'arcobaleno, sin dall'Antichità, aveva catturato l'immaginazione popolare e scientifica, ma non si era ancora ottenuta una spiegazione soddisfacente delle sue cause fisiche, delle sue dimensioni e dei suoi colori. All'inizio del XIII sec., Teodorico di Vriberg (m. 1310 ca.) ne aveva correttamente spiegato la formazione con la riflessione e la rifrazione della luce del Sole nelle gocce di pioggia, ma il suo trattato sull'arcobaleno fu pubblicato solo in epoca moderna. La spiegazione di Descartes si articola in modo notevolmente metodico, ma non sappiamo se tale fu anche la sua ricerca.
Come altri prima di lui, Descartes dedusse che gli arcobaleni dipendevano dall'azione della luce sulle gocce di pioggia, dato che archi di luce possono apparire tanto negli spruzzi delle fontane quanto nel cielo. Egli ripeté un esperimento ben noto: riempì un globo di vetro con l'acqua e lo posizionò in modo tale che la luce del Sole potesse attraversarlo. Scoprì così che se la luce entrava lungo la direzione dei raggi AB, FG e l'occhio era nel punto E, quando collocava il globo in BCD, la parte D appariva "completamente rossa e incomparabilmente più brillante del resto", e l'angolo DEM misurava circa 42°. Quando l'angolo DEM era aumentato leggermente, il colore rosso scompariva, ma se l'angolo era lievemente ridotto, si rendevano visibili il giallo, il blu e altri colori. Quando guardava la parte K dell'ampolla e l'angolo KEM era di circa 52°, allora K appariva di colore rosso, ma non così brillante come D; aumentando ancora l'angolo, si scorgevano altri colori. Se il cielo fosse stato riempito con questi globi, una serie continua di macchie rosse ‒ archi rossi ‒ si sarebbe formata a 42° e 52° e gli altri colori sarebbero apparsi accanto a essi; questo dunque spiegava gli arcobaleni primari e secondari. I dettagli di tali osservazioni e misurazioni erano una novità.
Per stabilire quali raggi causassero l'arcobaleno, Descartes scoprì che interrompendo il cammino dei raggi AB, BC, CD, o CE, i colori sparivano. Pertanto, l'arcobaleno primario era formato da un raggio che era rifratto in B e poi procedeva verso C dove veniva riflesso verso D e nuovamente rifratto nell'uscire dalla goccia. In modo analogo, Descartes determinò che l'arcobaleno secondario era formato da un raggio che entrava nella goccia nel punto G e si rifletteva quindi due volte nella goccia nei punti H e I, prima di uscire nel punto K. Doveva ora spiegare perché soltanto i raggi che portavano questi particolari angoli causassero l'arcobaleno.
Per risolvere il problema, Descartes studiò i colori che si formano in un prisma di vetro, notoriamente analoghi a quelli dell'arcobaleno. Sistemò il prisma in modo che i raggi penetrassero la prima faccia NM perpendicolarmente, senza rifrazione, e poi passassero attraverso una fenditura DE, praticata nella base NP coperta con carta nera, e infine proiettassero i loro colori sullo schermo PF. Ritrovò sullo schermo tutti i colori dell'arcobaleno, con il rosso sempre nel margine F e il blu in H. Da questo esperimento concluse che una rifrazione da sola è sufficiente a dare origine ai colori ‒ a condizione di non essere annullata da una seconda rifrazione su una superficie parallela alla prima, come nel vetro di una finestra, che non produce alcun colore ‒ e che la superficie non deve essere necessariamente curva come nella goccia di pioggia. Dato che i colori scomparivano togliendo la carta nera, dedusse inoltre che per la loro produzione era necessaria l'ombra o l'eliminazione della luce.
Per spiegare perché più raggi si riflettono nei nostri occhi sotto determinati angoli, Descartes realizzò una serie di ventisette calcoli della traiettoria dei raggi attraverso le gocce di pioggia sferiche a differenti angoli di incidenza: "Ho trovato che dopo una riflessione e due rifrazioni ve ne sono molti di più [raggi] che possono essere visti sotto un angolo da 41 a 42 gradi che sotto alcun altro minore e che non se ne dà alcuno che possa essere visto sotto un angolo maggiore". Per l'arcobaleno secondario, scoprì che "se ne danno molti di più [raggi] che pervengono al nostro occhio sotto un angolo da 51 a 52 gradi che sotto alcun altro maggiore e che non se ne dà alcuno che pervenga sotto uno minore" (OS, II, pp. 476-477). Descartes aveva calcolato che l'arcobaleno primario si forma quando l'inclinazione del raggio emergente DE rispetto al raggio incidente AB è massima; cioè, quasi tutti i raggi escono dalla goccia a circa 41°30′ e nessuno emerge con un angolo superiore. Per l'arcobaleno secondario il suo calcolo equivaleva a determinare il minimo dell'inclinazione dei raggi emergenti e incidenti. Dagli esperimenti con il prisma, aveva concluso che è necessaria un'ombra o un'interruzione della luce perché appaia il colore, come era confermato dai suoi calcoli. Egli non sapeva che Harriot aveva già stabilito le condizioni generali per la formazione dell'arcobaleno. La soluzione di Descartes comportava calcoli molto pesanti e, dopo di lui, matematici come René-François de Sluse (1622-1685), Barrow, Halley e Newton lavorarono alla deduzione di leggi generali sulla formazione dei due arcobaleni e alla dimostrazione che le inclinazioni dei raggi incidenti ed emergenti rappresentano un massimo e un minimo.
Per poter comprendere la spiegazione cartesiana dei colori dell'arcobaleno, dobbiamo innanzitutto considerare la sua concezione della natura della luce. Nei Principia philosophiae (1644) spiegò che l'intero spazio è pieno di un elemento molto sottile, l'etere, composto da piccole sfere tonde in contatto l'una con l'altra. Negli spazi astronomici queste particelle nell'etere formano i vortici celesti che trasportano i pianeti nelle loro orbite. Le particelle ancora più piccole e di grande mobilità, che secondo l'ipotesi di Descartes formano una fonte luminosa come il Sole, premono contro le minuscole e perfettamente solide sfere di etere; questa pressione è istantaneamente propagata, senza alcun movimento, in linee rette verso tutte le direzioni. Se rammentiamo che Descartes dedusse la legge di Snell ipotizzando che la luce consistesse nell'emissione di particelle, questi due modelli sembrerebbero contraddirsi. Descartes lo negò sostenendo con convinzione che la sua deduzione della legge di rifrazione aveva soltanto utilizzato un'analogia e che la pressione dell'etere obbediva alle stesse leggi che regolano il movimento reale di un corpuscolo. In questo modo, i suoi scritti paradossalmente incoraggiarono sia i sostenitori di una teoria dell'emissione sia quelli della teoria ondulatoria o del continuum.
Gli esperimenti di Descartes con il prisma lo portarono a ipotizzare un motivo per cui la luce che passa attraverso un prisma è sempre rossa da un lato del raggio e blu dall'altro lato. Egli sostenne che, quando un raggio di luce avanza in un mezzo omogeneo, le minuscole sfere dell'etere ruotano uniformemente. Tuttavia, quando il raggio incontra una superficie rifrangente, il ritmo di rotazione delle sfere cambia, poiché esse saranno circondate da sfere che si muovono a diverse velocità. Nella fig. 8 le ombre nei punti D ed E che delimitano i due lati del raggio fanno sì che ‒ secondo Descartes ‒ le sfere sul lato DF del raggio aumentino la velocità, e quelle sul lato EH la diminuiscano. L'ipotesi che il blu sia più lento o tenda a muoversi con 'minore forza' del rosso, più veloce, evoca una teoria tradizionale per cui i colori derivano dalla modificazione della luce solare e quelli scuri, come blu e viola, sono molto più deboli dei vivaci rosso e giallo. La spiegazione cartesiana dell'origine dei colori partiva dal presupposto che questi nascano da una modificazione della luce solare ‒ una rotazione che si modifica ‒ e non esistano autonomamente nella luce solare prima della modifica indotta dalla rifrazione. Questa spiegazione del colore, nota come teoria della modificazione, fu adottata quasi universalmente fino a Newton.
Descartes aveva respinto la teoria scolastica secondo la quale i corpi possiedono qualità sensibili come il colore, e ora rifiutava la distinzione tra i colori 'apparenti' della luce, visti in fenomeni transitori come l'arcobaleno o lo spettro prismatico, e quelli 'reali' o permanenti dei corpi. I colori permanenti erano considerati qualità intrinseche dei corpi rivelate dalla luce, mentre i colori apparenti erano originati da una qualche modificazione della luce solare. Descartes sosteneva che il colore ‒ qualsiasi sia la sua fonte, un arcobaleno o un corpo ‒ è una sensazione suscitata dalla luce nel cervello, e che colori diversi sono generati da proprietà diverse della luce. Di conseguenza, per studiare il colore, deve essere studiata soltanto la luce colorata. Questo programma cartesiano fu vastamente adottato dalla generazione successiva e condusse direttamente all'opera di Newton.
Gli scritti scientifici di Descartes, la Dioptrique, le Météores e la Géométrie, pubblicati contemporaneamente, ebbero un'influenza enorme. Essi giocarono un ruolo fondamentale nell'orientamento delle ricerche in ottica geometrica e nel campo della progettazione e della molatura delle lenti, incoraggiando al tempo stesso gli studi sulla natura della luce e l'ottica fisica. Benché sia generalmente noto come filosofo razionalista (e in realtà lo fu), Descartes si impegnò anche in importanti ricerche sperimentali. Prima di lui, il prisma non era uno strumento sconosciuto per lo studio dei colori, ma egli contribuì a farlo diventare nella seconda metà del secolo un importante strumento di ricerca. Il suo stile scientifico ‒ l'adozione della filosofia meccanicistica, i tentativi di sviluppare modelli matematici e meccanici per la rifrazione e il colore, e la sua propensione a proporre meccanismi ipotetici per spiegare particolari fenomeni ‒ stimolò la crescita dell'ottica fisica. Dopo Descartes, i filosofi naturali proposero liberamente spiegazioni corpuscolari di fenomeni invisibili, quali la composizione dell'etere e della materia, fenomeni che causavano la rifrazione o la propagazione rettilinea della luce.
Hobbes e la nascita di una teoria ondulatoria della luce
Il conflitto tra la teoria ondulatoria e quella dell'emissione, che si concluse soltanto nel primo trentennio del XIX sec. con la vittoria della teoria ondulatoria, si originò alla fine del XVII sec., quando Huygens propose una teoria ondulatoria soddisfacente. Alcuni elementi fondamentali erano stati presentati per la prima volta nel 1644 nell'opera di Thomas Hobbes. Lo sviluppo della teoria ondulatoria riflette ciò che stava a cuore alla filosofia meccanicistica verso la metà del secolo, e cioè fornire una descrizione matematica completa della propagazione di un moto in un fluido, l'etere. I concetti più importanti, che sarebbero emersi dopo mezzo secolo di studi, furono quello di 'fronte d'onda' (il 'fronte' lungo cui avanza una perturbazione in un fluido) e quello di 'raggi', intesi ora come costruzioni mentali, cioè come traiettorie perpendicolari rispetto ai fronti d'onda realmente esistenti.
Al fine di evitare confusione, chiamerò 'teoria di emissione' qualsiasi teoria che comporti il trasporto di materia da una sorgente luminosa all'occhio e 'teoria ondulatoria' qualsiasi teoria che comporti la propagazione di uno stato (come una pressione o un moto) attraverso un mezzo circostante. Una teoria ondulatoria comporta i seguenti concetti: un fronte d'onda come luogo di un moto in un fluido; il raggio come la linea perpendicolare al fronte d'onda; la periodicità. Una teoria ondulatoria rappresenta un caso particolare della più generale teoria del continuum e, per la precisione, nessuna teoria ondulatoria fu presentata nel XVII sec., poiché nessuno era in possesso di tutti e tre i concetti. La teoria della luce di Descartes era una teoria del continuum, ma, come abbiamo visto, non comprendeva il moto, né i fronti d'onda, né la periodicità. Un raggio, per Descartes, come per quasi tutti gli scienziati del XVII sec., era un'entità realmente esistente che si dirigeva in linea retta dalla sorgente all'occhio, così come era rappresentato nell'ottica geometrica sin dall'Antichità. Per i sostenitori della teoria dell'emissione, un raggio di luce rappresentava la traiettoria percorsa dai corpuscoli emessi dalla sorgente luminosa, proprio come la palla nel modello cartesiano della rifrazione.
La teoria della luce di Hobbes, esposta nel Tractatus opticus, fu pubblicata nel 1644 come parte della Universae geometriae mixtaeque mathematicae synopsis di Mersenne. Lo scopo di Hobbes era formulare una teoria meccanicistica del continuum in sostituzione di quelle scolastiche che, pur comportando anch'esse una teoria del continuum, erano decisamente non meccanicistiche. La sua prima ipotesi stabilisce la base meccanicistica: "ogni azione è un moto locale nell'agente, così come ogni effetto è un moto locale nel soggetto". La terza ipotesi descrive chiaramente la natura del moto ondulatorio:
Nella visione, né l'oggetto né alcuna delle sue parti si spostano dal loro posto verso l'occhio. Affinché il moto possa essere prodotto a qualsiasi distanza, non è necessario che quel corpo, da cui il moto trae origine, percorra l'intero spazio attraverso il quale il moto si propaga; è sufficiente che esso produca un moto quasi impercettibile verso ciò che gli sta più vicino, di modo che ciò che si trova più vicino, spinto dal suo posto, a suo volta spinga ciò che gli è accanto, e in questo modo un moto si propagherà tanto lontano quanto si voglia. (Tractatus, in Opera, V, pp. 217-218)
Tutte le sorgenti luminose si espandono e si contraggono continuamente e fanno sì che il moto si propaghi nelle zone intorno all'occhio, dalle quali passa al cervello attraverso il nervo ottico. La reazione del cervello è la sensazione di luce. Secondo la teoria di Hobbes, non sono le singole parti della sorgente luminosa a vibrare, ma è l'intera sorgente che vibra tutta insieme, come un cuore. Se questa ipotesi fosse vera, però, non vedremmo, come in effetti vediamo, i singoli punti sulla superficie del corpo luminoso, ma soltanto il suo centro. Gli studiosi successivi provvidero ben presto a rettificare questa ipotesi.
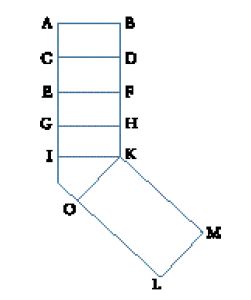
Hobbes formulò poi i nuovi concetti di 'raggio di luce' e 'linea di luce'. Egli definisce un raggio di luce come la traiettoria attraverso la quale il moto proveniente da un corpo luminoso si propaga attraverso un mezzo e sostiene che, poiché esso rappresenta il moto di un corpo, deve avere tre dimensioni e non può essere semplicemente una linea. Se Hobbes non avesse aggiunto altro alla sua definizione, potrebbe sembrare che egli adottasse l'opinione medievale che tutti i raggi luminosi hanno una qualche ampiezza. Tuttavia, egli propose anche altre definizioni: quella di un raggio rettilineo che, quando viene tagliato attraverso il suo asse è un parallelogrammo, come ABIK, e quella di un raggio rifratto, che si forma da due raggi diritti ABIK e KOLM e una parte intermedia IKO (fig. 10). Infine, aggiunse il nuovo concetto di linea di luce: "La linea di luce da cui iniziano i lati di un raggio (per es., linea AB da cui hanno inizio i lati AI, BK) io la chiamo semplicemente una linea di luce. Tuttavia, ognuna delle linee che derivano dalla linea di luce a seguito di un'estensione continua (come CD, EF, ecc.), le denomino linee di luce propagata" (ibidem, pp. 222-223). Poiché la 'linea di luce propagata' di Hobbes rappresenta una porzione di un fronte d'onda propagato, rispetto a cui i raggi sono sempre perpendicolari (come lo stesso Hobbes avrebbe più tardi dichiarato), la chiameremo 'fronte dei raggi'. Hobbes considera questi raggi come porzioni infinitesimali di un'onda, in modo che essi diventino equivalenti alle linee matematiche della tradizionale ottica geometrica.
Per spiegare la causa della rifrazione e dedurre la legge di Snell, Hobbes utilizza un'analogia. Quando un raggio si muove attraverso un mezzo omogeneo, la linea di luce AB si muove in modo costante verso IK, come se fosse il lato di un cilindro rotante. Tuttavia, quando esso incontra un nuovo mezzo dove le parti del fronte dei raggi non si muovono più con la stessa velocità, Hobbes considera che AB rappresenti un tronco di cono avente come basi AE e BF (fig. 11). Se il cono rotola, allora le basi "proprio come due ruote diverse" descriveranno gli archi circolari AH e BR, il cui centro comune G sarà il vertice di un cono e AHBR sarà la traiettoria del fronte dei raggi. A questo punto, la legge di Snell può essere facilmente dedotta dal modello di Hobbes. Tuttavia, questi formulò una spiegazione differente, per cui utilizzerò le deduzioni molto più chiare tratte dalla Perspectiva horaria (1648) di Emmanuel Maignan e dalle Lectiones XVIII (1669) di Barrow, che si basavano su quelle di Hobbes. Nella fig. 12 EF rappresenta la linea di demarcazione tra il mezzo più rarefatto che si trova nella parte superiore (per es., l'aria) e quello più denso presente nella parte inferiore (per es., acqua o vetro). Hobbes, dissentendo da Descartes, afferma che la luce si muove più lentamente in un elemento più denso. Quando il raggio di luce ABCD incontra il mezzo più denso, il punto B inizierà a muoversi più lentamente prima di D, che si trova ancora nel mezzo rarefatto. Le due parti si muoveranno a velocità diverse, e il fronte dei raggi ruoterà intorno al punto Z percorrendo una traiettoria curva DδBβ fino a che l'estremità superiore δ entrerà nel mezzo più denso e il raggio procederà nuovamente con un'unica velocità seguendo una traiettoria rettilinea. Quando il punto Z è scelto in modo appropriato, è facile dimostrare che la legge di Snell è verificata. Dato che i raggi di Hobbes hanno una larghezza infinitesimale, la traiettoria curva deve essere intesa come impercettibile.
Fino alla fine del Settecento, la deduzione di Hobbes della legge di rifrazione fu l'unica valida alternativa meccanica a quella di Descartes. Se Maignan e Barrow adottarono la derivazione di Hobbes della legge di Snell, respinsero però la sua teoria ondulatoria e sostennero quella dell'emissione della luce. Hobbes modificò le proprie idee sulla natura della luce e la rifrazione in trattati di ottica successivi, mai pubblicati. Il Tractatus opticus segna comunque l'inizio dei tentativi effettuati nel XVII sec. per sviluppare una descrizione matematica e meccanica di un moto che si propaga in un mezzo fluido. Non dovremmo, tuttavia, sopravvalutare i risultati raggiunti da Hobbes con i suoi fronti di raggi e raggi perpendicolari, poiché egli stava ancora lavorando con una sola entità, i raggi fisici, e non con due, raggi e onde.
L'ottica fisica
Negli anni Sessanta del XVII sec. vi fu un fiorire di lavori sperimentali che rivelarono nuove proprietà della luce e diedero l'avvio allo studio sperimentale delle sue proprietà fisiche. In un libro pubblicato postumo nel 1665, Francesco Maria Grimaldi (1618-1663) annunciò l'esistenza di una nuova proprietà della luce, la diffrazione; nello stesso anno Robert Hooke pubblicò una ricerca su una nuova classe di colori, quelli delle lamine sottili, o fenomeni di interferenza; nel 1669 Erasmus Bartholin rivelò l'esistenza di una sostanza con una doppia rifrazione. In quello stesso decennio, Robert Boyle pubblicò un trattato enciclopedico sul colore e Newton portò avanti le sue famose ricerche sulla natura della luce solare, del colore e dei colori delle lamine sottili, i cui risultati furono pubblicati soltanto nel decennio successivo.
La diffrazione
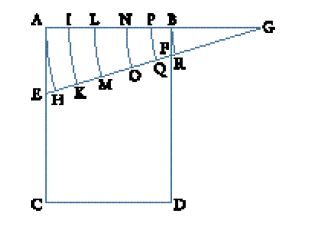
Nel trattato Physico-mathesis de lumine, coloribus et iride (1665) Grimaldi osservava che fasci di luce molto sottili non viaggiano in linea retta, violando così i principî fondamentali dell'ottica, e denominò questo fenomeno 'diffrazione'. Faceva entrare la luce del Sole in una stanza buia, attraverso un piccolo foro AB di 1/60 di pollice di diametro, inserendo quindi un ostacolo sottile FE, quale un capello o un filo, nel fascio di luce. Osservandone l'ombra su uno schermo bianco CD collocato sul pavimento, Grimaldi rilevò una serie di nuove caratteristiche nell'ombra MN: in primo luogo essa era molto più larga di quanto avrebbe dovuto essere secondo le leggi universalmente accettate dell'ottica geometrica. Calcolò le dimensioni dell'ombra in conformità al principio ordinario che la luce viaggia in linea retta e stabilì che esse avrebbero dovuto essere pari a IL, cioè un valore inferiore a quello dell'ombra osservata MN. Ciò significava che la luce non procedeva in linea retta e che, in questo caso, curvava verso l'esterno. Per arrivare a tale conclusione, si presume che Grimaldi abbia eseguito attente misurazioni, che in ogni caso non furono pubblicate. In secondo luogo, si accorse che un po' di luce invadeva l'interno di questa ombra, là dove avrebbe dovuto essere completamente buio. Infine scoprì tre frange di luce colorate, separate da bande scure, all'esterno dell'ombra.
In un altro esperimento, Grimaldi sostituì l'ostacolo sottile FE con uno schermo in cui era stato praticato un piccolo foro. Scoprì che il raggio di luce era molto più ampio di quanto avrebbe dovuto essere se la luce avesse viaggiato in linea retta dal foro verso lo schermo. Grimaldi tentò di spiegare la diffrazione, ipotizzando che la luce fosse un fluido corpuscolare che si spandeva o diffondeva quando incontrava un ostacolo. Tuttavia, in una seconda parte del libro, relativamente breve, ammise che dopotutto la luce avrebbe potuto anche non essere materiale, come aveva sostenuto nella prima parte, e lasciò la questione aperta. è stato spesso insinuato che il gesuita Grimaldi aggiunse questa seconda parte poiché non desiderava, o non gli era consentito, opporsi alla posizione già accettata dalla Scolastica.
La diffrazione è ora considerata una delle più significative scoperte del XVII sec., ma inizialmente ebbe scarsa influenza sull'orientamento della ricerca ottica. Probabilmente una serie di fattori contribuì a ritardare l'accettazione di questo nuovo fenomeno. In primo luogo, il libro di Grimaldi era redatto in uno stile scolastico prolisso, con argomenti, obiezioni e confutazioni che ne rendevano difficile l'apprezzamento da parte dei moderni. Soltanto le prime undici pagine, delle cinquecentoventicinque di cui era composto il libro, erano dedicate agli esperimenti sulla diffrazione. La mancata descrizione delle misurazioni rese le sue conclusioni meno interessanti e più difficili da confermare. In Francia la diffrazione non era generalmente accettata come fenomeno nuovo. Philippe de La Hire ed Edme Mariotte, due tra i più importanti filosofi sperimentali francesi, ripeterono alcuni degli esperimenti di Grimaldi nel 1679, di fronte all'Académie des Sciences, e li giudicarono inconcludenti. Huygens, uno dei membri dell'Académie, nella sua relazione sulla teoria ondulatoria non mostrò alcun interesse per la diffrazione.
La diffrazione ebbe migliore accoglienza in Inghilterra, dove Hooke la studiò da un punto di vista sperimentale nel 1675; egli potrebbe aver scoperto qualche fenomeno di diffrazione autonomamente, ma l'opera di Grimaldi fu divulgata in Inghilterra contemporaneamente alla sua ed è difficile stabilire se Hooke conoscesse il lavoro di Grimaldi quando iniziò le proprie ricerche. Dopo aver portato a termine i suoi esperimenti, la definì in maniera inequivocabile come un fenomeno nuovo e si dichiarò convinto che "questa straordinaria penombra non può in alcun modo essere attribuita ai comuni principî della luce ma a qualche nuova proprietà, in virtù della quale la luce devia dalle linee rette, contrariamente a quanto è stato finora affermato dagli scrittori di ottica" (The posthumous works, pp. 189-190). Newton assistette alla presentazione di Hooke alla Royal Society e inoltre era a conoscenza del lavoro di Grimaldi, grazie alla descrizione contenuta nel volume di Honoré Fabri, Dialogi physici quorum primus est de lumine (1669). Più tardi Newton affrontò l'argomento sia nei Principia sia nell'Opticks. Tuttavia né Hooke né Newton fecero grandi progressi nel cercare di comprendere la complessità del fenomeno, né tanto meno nel trovarne la spiegazione.
Hooke e i colori delle lamine sottili
La Micrographia (1665) di Hooke è un resoconto elegantemente illustrato di osservazioni microscopiche che colpirono l'immaginazione dei suoi contemporanei ed è anche una vera e propria cornucopia di filosofia naturale, contenente parti dedicate alla luce e al colore. Lo scopo di Hooke era utilizzare una teoria ondulatoria per illustrare i diversi modi in cui hanno origine i colori. Iniziò spiegando in che modo questi si formino in lamine sottili di mica, in bolle di sapone, vetro e altre sostanze; poi enunciò la sua teoria ondulatoria e spiegò anche come si producono i colori nella rifrazione.
I colori che si creano su pellicole sottili, come l'olio sull'acqua, erano stati osservati per millenni ed erano stati descritti da Johann Marcus Marci von Kronland (1595-1667) e da Boyle, ma Hooke fu il primo a riconoscere che la loro origine era sostanzialmente diversa da quella dei colori prodotti per rifrazione; quelli delle lamine sottili costituivano una sfida speciale per Hooke, poiché sembravano in contrasto con i principî dell'ottica stabiliti da Descartes e generalmente accettati.
Descartes aveva sostenuto che, per la produzione del colore, era necessaria almeno una rifrazione che non doveva essere annullata con il passaggio attraverso una seconda superficie parallela alla prima, e che doveva essere presente una separazione tra luce e ombra. Hooke constatò che una sottile lamina di mica contravviene a entrambi questi principî, poiché non comporta evidentemente alcuna ombra; e le due rifrazioni che si verificano nel penetrare attraverso la superficie superiore della lamina sottile e nell'uscire dalla stessa dopo la riflessione nella superficie inferiore, sono per simmetria equivalenti al passaggio in linea retta attraverso una lamina di spessore doppio. Hooke considerava le sue osservazioni dei colori nelle lamine sottili di mica come un esperimento cruciale per respingere la teoria dei colori di Descartes. Inoltre Hooke dimostrò che la spiegazione fornita da Descartes per l'arcobaleno aveva lo stesso difetto, poiché dopo due rifrazioni e una riflessione la luce emerge come se fosse parallela al raggio incidente. All'inizio dei suoi studi scientifici, il giovane Newton lesse la Micrographia di Hooke e notò, condividendola, questa confutazione della spiegazione dei colori dell'arcobaleno data da Descartes (lo stesso Newton fu però altrettanto critico nei confronti della teoria di Hooke). Condivideva anche il parere di Hooke circa la necessità di partire da nuovi principî per elaborare una teoria esplicativa dei colori delle lamine sottili. Prima che Hooke potesse spiegare come si formavano questi colori, enunciò la sua teoria della luce.
Nella teoria del continuum della luce elaborata da Hooke, ogni punto di una sorgente luminosa ‒ e non l'intera sorgente come sosteneva Hobbes ‒ vibra rapidamente e le vibrazioni si diffondono per mezzo di impulsi attraverso il mezzo circostante, con velocità finita, lungo linee rette e in tutte le direzioni. Hooke osservò anche che un movimento in un mezzo omogeneo si diffonde sfericamente in tutte le direzioni e che i raggi sono le linee perpendicolari ai fronti d'onda. Tutti questi fattori rappresentavano un evidente progresso rispetto alla teoria di Hobbes, di cui Hooke era a conoscenza. Per spiegare la generazione dei colori nella rifrazione, adottò il concetto di Hobbes di un raggio fisico e abbandonò l'idea che i raggi fossero perpendicolari ai fronti d'onda. Hooke trasse da Descartes la legge di Snell e il principio che la luce si muove più rapidamente in un mezzo denso ‒ come il vetro o l'acqua ‒ che nell'aria. Adottando l'ipotesi cartesiana secondo la quale la luce aumenta la propria velocità quando penetra nel vetro, i fronti dei raggi (o degli impulsi) di Hooke diventano obliqui rispetto ai raggi stessi dopo la rifrazione. Egli utilizzò questi fronti obliqui di impulsi per spiegare la formazione dei colori nella rifrazione. Secondo Hooke il lato principale CK dell'impulso CHK genera il blu, il lato GI il rosso e l'intensità di ciascun colore cambia dal bordo verso l'interno; per esempio il bordo GI varia da rosso cupo a giallo. Tutti gli altri colori hanno origine da questi due, il verde per esempio si forma dal blu e dal giallo. Hooke ipotizzò così l'origine dei colori prodotti per rifrazione nell'arcobaleno e nel prisma; per spiegare quelli delle lamine sottili, si richiamò a una teoria completamente diversa, basata sulle vibrazioni degli impulsi.
Hooke osservò che quando una lamina di mica era di spessore uniforme, il suo colore era uguale su tutta la superficie, ma che il colore mutava nelle lamine con spessori diversi. Scoprì inoltre che quando lo spessore della lamina variava in modo uniforme, come in un cuneo, la serie dei colori osservati si ripeteva: rosso, giallo, verde, blu e viola; rosso, giallo, verde, blu e viola; e così via per dieci e anche venti volte. Abilmente dedusse da questa ripetizione che tali colori erano un fenomeno periodico e ipotizzò che gli impulsi, o onde di luce, fossero periodici, oppure che gli impulsi fossero separati da intervalli regolari. Hooke spiegò i colori prodotti dalle lamine sottili in termini di variazione della distanza tra due fronti di impulsi, riflessi sulla prima e sulla seconda superficie della lamina sottile. Così sulla prima superficie della pellicola sottile AB il raggio incidente o impulso di luce solare ab in parte si riflette lungo cd e in parte è trasmesso. L'impulso trasmesso (indicato con la linea tratteggiata) si riflette sulla seconda superficie EF ed emerge dalla prima superficie come ef, è attenuato e segue l'impulso cd, più intenso: "questo impulso confuso o raddoppiato, la cui parte più intensa è quella che precede e quella più debole quella che segue, produce […] la sensazione di un giallo" (Micrographia, p. 66).
Man mano che la pellicola diviene più spessa, il raggio ef cade più distante dietro cd e si produce il rosso; e quando diventa ancora più spessa (a sinistra), la parte più debole precede quella più forte e si produce il blu.
La spiegazione dei colori delle lamine sottili fornita da Hooke ha in qualche modo una sorprendente rassomiglianza con il principio di interferenza proposto successivamente da Thomas Young (1773-1829), come Young stesso riconobbe. Tuttavia, poiché Hooke si avvaleva di una teoria della modificazione del colore, la formazione di tutti i colori dalla pellicola sottile dipendeva esclusivamente dalla distanza tra i due fronti di impulsi. La spiegazione di Hooke mancava di un numero sufficiente di variabili fisiche indipendenti, per poter rendere conto di tutti i fenomeni osservati. Le rifrazioni nella pellicola creavano soltanto un colore per ogni spessore, piuttosto che separare un certo numero di colori preesistenti, come Newton avrebbe ipotizzato pochi anni dopo. Hooke terminò la sua relazione sui colori delle lamine sottili con un nota di delusione e lanciò una sfida "del più grande interesse in questa hypothesis": misurare lo spessore delle lamine. Malgrado i suoi sforzi, infatti non era stato in grado di determinare a quale particolare spessore appaiono i colori, dato che le lamine erano "così eccessivamente sottili" e il suo microscopio "così imperfetto".
Una volta completata la sua descrizione delle varie fonti di colore, Hooke passò a occuparsi dell'origine del colore dei corpi. Questi ‒ secondo la sua ipotesi ‒ sono composti da particelle 'tingenti' trasparenti, E, F, G, H, disperse in modo uniforme in un mezzo trasparente e dotate di diverso potere rifrangente. Per spiegare l'origine dei colori, egli adottò la stessa teoria utilizzata per le lamine sottili, quella di un duplice fronte di impulsi in cui l'impulso più debole può precedere quello più intenso e produrre il blu, oppure seguirlo e produrre il rosso e il giallo. Se le particelle tingenti rallentano gli impulsi di luce (come illustrato), allora si forma il rosso, poiché, man mano che un impulso avanza attraverso le particelle tingenti di un corpo, si forma gradualmente un debole impulso PPP (linea tratteggiata) che segue quello più forte OO; ma se la luce si muove più celermente attraverso le particelle tingenti, allora si formano i blu. Con la sua teoria del colore dei corpi, Hooke fu il primo ad affrontare l'argomento seguendo i principî della filosofia meccanicista. Prima di lui, i filosofi meccanicisti avevano dedicato la loro attenzione esclusivamente alla rifrazione.
Hooke aveva presentato la più esauriente teoria del colore e dell'ottica fisica mai formulata, occupandosi dei colori che hanno origine dalla rifrazione, dalle lamine sottili ‒ a tal proposito fu il primo a capire che si trattava di una specie di colore diversa da quella prodotta con la rifrazione ‒ e dai corpi, e dieci anni più tardi aggiunse una relazione sulla diffrazione. Anticipò la teoria ondulatoria introducendo novità quali le vibrazioni in ogni punto della sorgente luminosa, una velocità finita di propagazione per le onde e la periodicità. Tuttavia, il suo interesse dominante era indirizzato a spiegare il colore e ciò lo portò a introdurre raggi che, dopo la rifrazione, risultavano obliqui rispetto ai fronti d'onda.
Bartholin e la doppia rifrazione
Nel 1668 il re Federico III di Danimarca inviò una spedizione in Islanda con l'incarico di riportare a Copenaghen alcuni campioni di un cristallo raro ‒ lo spato d'Islanda ‒ le cui proprietà erano ancora sconosciute agli scienziati. L'anno seguente, Erasmus Bartholin pubblicò negli Experimenta crystalli Islandici disdiaclastici la prima relazione sulle strane proprietà ottiche di questo cristallo, attraverso il quale si formano due immagini invece di una sola. Collocando tale cristallo sopra un foglio di carta sul quale è stato apposto un segno A, questo segno, visto attraverso il cristallo, produce due immagini (fig. 17). Se il cristallo viene fatto ruotare, si vede una delle immagini (B) ruotare intorno all'altra (C) che rimane ferma. In questo cristallo esistono due serie di raggi rifratti, una sola delle quali obbedisce alla normale legge di rifrazione, la legge di Snell. Nel piano definito dallo spigolo EM e dalla linea DE che biseca l'angolo della faccia superiore del cristallo (che Huygens più tardi definì la 'sezione principale'), i raggi rimangono nel piano di rifrazione, ma il raggio 'straordinario' negli altri piani si comporta diversamente. Bartholin diede a questi raggi i nomi con i quali sono ancora oggi noti: raggi 'ordinari' e 'straordinari'. Un altro esperimento dimostrò che la seconda immagine non è causata da una riflessione sui lati del cristallo. Essa pertanto dovrebbe essere attribuita a una rifrazione inusuale. Bartholin riuscì a fornire una trattazione matematica per la costruzione con la quale Descartes aveva determinato la rifrazione del raggio straordinario, eliminando così la sensazione di crisi e di novità sorprendente. Tuttavia la sua costruzione si applicava solamente alla sezione principale, e in aggiunta a ciò Bartholin non propose alcuna spiegazione fisica del bizzarro comportamento della luce all'interno del cristallo. La sua relazione suscitò scalpore e ben presto i cristalli furono disponibili a Londra e a Parigi. Huygens ‒ che più tardi avrebbe elaborato la sua teoria ondulatoria, stimolato soprattutto dalla sfida generata dalla possibilità di dare una spiegazione alla doppia rifrazione ‒ ne venne a conoscenza mentre era a Parigi.
Colore
Il colore, come si è potuto osservare, fu un argomento di grande interesse per gli scienziati del XVII sec. ed è pertanto opportuno esaminare tale questione prima della teoria del colore di Newton. Già verso l'inizio del secolo, le teorie sul colore avevano subito un cambiamento radicale. Aristotele aveva sostenuto che tutti i colori 'cromatici', come il rosso, il giallo e il blu, derivano da varie mescolanze di bianco e di nero. Diede ai colori un ordine lineare che, partendo dal bianco e passando per il giallo, il rosso, il viola, il verde e il blu, giungeva fino al nero, ossia una classificazione dei colori in base alla loro saturazione o alla loro brillantezza e non, come si fa attualmente, in base alla cromaticità determinata dalla lunghezza d'onda. La natura fondamentale del bianco e del nero fu spesso espressa in termini diversi, benché equivalenti, come luce e ombra, o oscurità. Aristotele elaborò anche un'altra teoria, che ebbe grande influenza per molto tempo, relativamente all'origine dei colori nell'arcobaleno. Spiegò che tali colori sono generati dall'attenuarsi e dall'oscurarsi della luce riflessa dalle nuvole oppure vista attraverso di esse; man mano che questa luce si oscura, passa dal rosso al verde e dal verde al blu. Le idee di Aristotele, che attribuivano una supremazia concettuale alla luce e all'ombra, o al bianco e al nero, condussero alle teorie della modificazione del colore di cui abbiamo parlato, e sarebbero state contestate dagli artisti del Rinascimento.
Fin verso la fine del XIII sec., gli artisti evitarono di mescolare i pigmenti, tranne che con il bianco e con il nero; ma già attorno al 1400 tale uso era diventato comune. Leon Battista Alberti nel De pictura, scritto in latino nel 1435 e tradotto in italiano l'anno successivo, diede una chiara prova di questo nuovo interesse, rompendo decisamente con le idee di Aristotele su bianco e nero e separando drasticamente questi ultimi due dai colori cromatici. Scrisse Alberti che il pittore poteva essere certo che il bianco e il nero non sono veri colori ma, si potrebbe dire, moderatori di colori. Egli suggerì come alternativa che la quasi infinita varietà di colori derivasse dai quattro primari (il rosso, il verde, il blu e il giallo), assieme ai 'moderatori' bianco e nero. La ricerca di un piccolo numero di cromatici primari, dai quali potevano derivare tutti gli altri colori, era cominciata.
All'inizio del Seicento quattro studiosi ‒ nel 1601 Guido Antonio Scarmiglioni, nel 1609 Louis Savot e Anselmus Boetius de Boodt e nel 1613 il gesuita François d'Aguilon ‒ conclusero questa ricerca e, indipendentemente l'uno dall'altro, annunciarono la scoperta dei tre colori primari dei pittori ‒ il rosso, il giallo e il blu ‒, dai quali (assieme al bianco e al nero) possono derivare tutti gli altri, ma che a loro volta non possono derivare da altri. Questi studiosi avevano una buona conoscenza delle scienze o della medicina e si intendevano anche di pittura. In realtà d'Aguilon nell'elaborazione delle sue idee potrebbe aver collaborato con l'amico fiammingo Peter Paul Rubens (1577-1640), il pittore che disegnò un certo numero di illustrazioni per gli Opticorum libri sex (1613) di d'Aguilon. Era qui formulata con grande chiarezza la teoria dei tre colori primari e l'opera ebbe grande influenza, anche perché i gesuiti svolsero un ruolo di primo piano nell'insegnamento delle scienze nel Seicento. L'opera contiene quello che è probabilmente il primo schema mai pubblicato sulla mescolanza dei colori, in cui si mostra come i tre colori primari mescolati a due a due producono i secondari; mentre aggiungendo bianco e nero a uno qualsiasi di questi cambia solo la loro intensità, ma non la tonalità.
Le idee di d'Aguilon sono la dimostrazione che all'inizio del Seicento il concetto che la mescolanza di bianco e nero non avrebbe prodotto niente altro che grigio si stava affermando sempre di più, sia tra gli artisti sia tra i filosofi naturali. Fino ad allora tutte le teorie della modificazione del colore avevano sostenuto che i colori si formano in qualche modo dalla mescolanza del bianco o della luce con l'ombra o con il nero. Il crescente rifiuto dell'idea che il bianco e il nero potessero dare origine ai colori portò a nuove formulazioni della teoria della modificazione. Descartes, per esempio, attribuiva i colori alle varie rotazioni delle piccole sfere che compongono l'etere. è vero che egli aveva affermato che l'ombra era necessaria per la produzione del colore nell'arcobaleno, ma ciò non costituiva una caratteristica di fondo della sua teoria del colore. Spiegò che i corpi sono di vari colori poiché le loro superfici trasmettono varie rotazioni alla luce da essi riflessa, e ciò è la causa per cui sono visti di colore rosso, blu, e così via. Analogamente, la teoria dei corpi colorati di Hooke abbandonava l'idea che il colore nascesse dalla luce e dall'ombra e lo faceva dipendere dall'intensità relativa di impulsi o onde di luce consecutivi quando attraversano i corpuscoli tingenti.
Gli Experiments and considerations touching colours (1664) di Boyle, insieme alla Micrographia di Hooke, pubblicata l'anno successivo, rappresentano il culmine della teoria meccanica dei colori. L'obiettivo di Boyle era quello di dimostrare che i colori dei corpi si spiegano meglio se si attribuisce la loro origine a una qualche modificazione della luce incidente causata dai corpuscoli dei corpi e che essi non sono qualità intrinseche dei corpi. Boyle attribuiva i colori dei corpi principalmente alla riflessione delle loro parti superficiali. Descrisse molto dettagliatamente gli innumerevoli modi in cui i corpuscoli dei corpi potevano formare superfici con strutture differenti, che avrebbero modificato la luce incidente producendo tutta la gamma dei colori. Essendo chimico, dedicò buona parte della sua opera alla descrizione dei colori generati attraverso reazioni chimiche, tra le quali la più famosa fu il test dell'indicatore di colore per gli acidi e le basi: si accorse che aggiungendo acidi a soluzioni vegetali di colore blu, queste diventano rosse, se invece viene introdotta una base, diventano verdi. Il testo di Boyle fu molto in voga nel Settecento per il gran numero di esperimenti e di osservazioni che esso conteneva. Oltre agli esperimenti chimici, Boyle descrisse quelli che riguardavano la mescolanza dei colori, alcuni dei quali furono realizzati utilizzando un prisma, "il più utile strumento che gli uomini abbiano finora usato per la contemplazione dei colori" (Experiments, p. 227).
Verso la metà del secolo, gli scienziati avevano ormai cominciato ad abbandonare molte delle idee aristoteliche sul colore: la distinzione tra colori reali e apparenti, quella tra luce e colore ‒ dato che tutta la luce causava una sensazione di colore ‒, il principio che bianco e nero producevano colori e le teorie della modificazione basate su bianco e nero. Tuttavia, anche se la concezione matura della modificazione andava mutando, le teorie della modificazione non venivano abbandonate. Anzi, i nuovi filosofi ipotizzavano che sia i colori reali, cioè quelli dei corpi, sia quelli apparenti rappresentassero una qualche forma di modificazione della luce bianca. Newton sfidò direttamente le teorie della modificazione proponendo un'idea completamente nuova sulla natura del colore.
Newton e il colore
Nel periodo tra il 1664 e il 1666, ancora studente all'Università di Cambridge, Newton si immerse nello studio della tradizione ottica contemporanea ‒ leggendo le opere di Descartes, Hooke, Boyle e, probabilmente, anche quelle di Kepler e di Scheiner ‒ e ben presto iniziò ad ampliare questa tradizione. Nonostante avesse formulato la sua teoria della natura composta della luce solare già nel 1666‒ e ne avesse fatto l'oggetto delle lezioni che tenne all'Università di Cambridge tra il 1670 e il 1672, dopo essere stato designato professore di matematica ‒, fu soltanto nel febbraio del 1672 che acconsentì a pubblicarla nelle "Philosophical Transactions". All'epoca in cui fu data alle stampe la teoria ‒ si trattava della sua prima pubblicazione ‒ Newton era praticamente sconosciuto e le controversie e le critiche che seguirono contribuirono ad alimentare la sua riluttanza a pubblicare. Nel 1666 anch'egli aveva effettuato ricerche sulle lamine sottili, ma procrastinò la divulgazione del lavoro fino al 1675. Successivamente abbandonò lo studio dell'ottica fino a che, dopo la pubblicazione dei Principia nel 1687, cominciò a scrivere l'Opticks. All'inizio dell'ultimo decennio del Seicento, mentre lavorava a tale opera, affrontò nuovamente la ricerca sull'ottica, studiando i colori delle lamine spesse e la diffrazione ma, ancora una volta, rimandò di più di dieci anni la pubblicazione dei risultati.
Una nuova teoria del colore
Nel trattato New theory about light and colours, pubblicato nel 1672, Newton presentò la teoria del colore come se la strada seguita per arrivare alla scoperta fosse stata facile, ma dai suoi scritti rimasti inediti sappiamo che fu assai complessa. Base della teoria fu un semplice esperimento di cui sviluppò numerose varianti (fig. 19). In una stanza oscurata fece penetrare un raggio di luce solare OF attraverso un piccolo foro e quindi lo trasmise attraverso un prisma ABCαβϰ, collocato in maniera tale che il raggio avesse la stessa inclinazione sia in entrata sia in uscita. Osservando l'immagine del Sole su uno schermo posto su un muro a 22 piedi (6,70 m ca.) di distanza, scoprì che tale immagine, invece di essere tonda, coerentemente con la dominante teoria della rifrazione, era oblunga e colorata, e per definirla coniò il termine 'spettro'. Scoprì che la lunghezza dell'immagine era circa cinque volte maggiore della larghezza, a sua volta uguale al diametro dell'immagine circolare del Sole. Il problema che si poneva era quello di capire perché l'immagine si allungasse in modo così 'stravagante'.
Per scoprire la causa dell'allungamento, Newton si avvalse di ciò che chiamava l'experimentum crucis ‒ un termine che aveva ripreso da Boyle ‒, con il quale poté stabilire definitivamente la corretta spiegazione della lunghezza dello spettro (fig. 20). Prese due tavole BC e DE, sulle quali erano stati praticati due piccoli fori, e le collocò a 12 piedi (3,66 m ca.) l'una dall'altra. Il foro X nella prima tavola consentiva soltanto il passaggio di una piccola porzione dello spettro proiettato dal prisma A collocato di fronte alla tavola; ruotando il prisma venivano trasmesse porzioni diverse. La porzione di luce trasmessa passava successivamente attraverso il secondo foro Y fino a incontrare un altro prisma F ed era quindi proiettata su uno schermo. I due fori assicuravano che tutti i raggi cadessero sul secondo prisma quasi esattamente con lo stesso angolo di incidenza. Newton scoprì che il raggio che aveva subito una maggiore rifrazione nel primo prisma subiva una maggiore rifrazione anche nel secondo prisma. Arrivò quindi alla seguente conclusione: "E così si è stabilito che la vera causa della lunghezza di quella immagine non era altro che il fatto che la luce consiste di raggi diversamente rifrangibili, i quali, indipendentemente da eventuali differenze nella loro incidenza, erano trasmessi, a seconda dei loro gradi di rifrangibilità, verso parti differenti della parete" (The correspondence, I, p. 95).
L'affermazione di Newton che la luce solare è costituita da "raggi diversamente rifrangibili" significa, tradotta in termini moderni, che essa è composta da raggi con differenti indici di rifrazione. Nella fig. 21 un raggio di luce solare OF si decompone per rifrazione sulla superficie di separazione EG in raggi di diversa rifrangibilità e colore, con il rosso che subisce la rifrazione minore in T e il viola quella maggiore in P. Ognuno di questi diversi tipi di raggi è inclinato o rifratto in misura differente e ognuno di essi obbedisce alla legge di rifrazione, ma con un indice di rifrazione diverso.
Avendo stabilito l'elemento più radicale della sua teoria, e cioè che la luce del Sole è composta, Newton affrontò l'argomento del colore. Scoprì che esiste una corrispondenza costante tra grado di rifrangibilità e colore, vale a dire che i raggi rossi subiscono sempre una rifrazione minore, i raggi viola una maggiore, i raggi verdi una intermedia, e così via. Verificò che qualunque fosse il modo in cui tentava di modificare il colore di qualsiasi tipo di raggio (riflessione, rifrazione, trasmissione, o in altro modo), questo rimaneva inalterato. Tuttavia, quando raggi di diversi colori si mischiano tra loro, il colore appare effettivamente mutato; per esempio, se raggi rossi e raggi gialli si mescolano, producono il colore arancione.
Per risolvere il problema, Newton introdusse una distinzione tra colori semplici o primari ‒ i colori puri dello spettro, rosso, giallo, verde, blu e viola, con le loro gradazioni intermedie ‒ e i colori che si compongono con essi. Benché questi due tipi appaiano identici all'occhio ‒ per esempio, un arancione 'spettrale' e un arancione costituito da rosso e giallo ‒ i colori semplici o primari sono formati in realtà da raggi aventi un unico grado di rifrangibilità, mentre quelli composti sono una mescolanza di raggi con differenti gradi di rifrangibilità. È sempre possibile distinguerli mediante la rifrazione in un prisma che separa i raggi aventi rifrangibilità diverse, la cui combinazione dà luogo a colori compositi, mentre lascia inalterati quelli semplici.
"Ma la più sorprendente e meravigliosa composizione è stata quella del colore bianco […] esso è sempre composto" (ibidem, p. 98). Il bianco è costituito dagli innumerevoli colori dello spettro. Questa era la parte più rivoluzionaria della teoria di Newton, dato che la luce solare per millenni era stata considerata semplice e pura e si riteneva che i colori fossero in qualche modo una modificazione di tale luce. Gran parte del linguaggio letterario e religioso occidentale utilizzava l'immagine della luce solare quale simbolo di purezza e semplicità, e la radiosità del Sole era praticamente identificata con il divino. Newton rovesciò tutte queste convinzioni. Per lui la luce solare era una mescolanza impura ed eterogenea di diversi tipi di raggi, ognuno di colore diverso, ed erano questi colori ad essere semplici e omogenei. "I colori non sono modificazioni della luce provocate da rifrazioni, o riflessioni di corpi naturali (come è generalmente ritenuto), ma proprietà originali e innate" (ibidem, p. 97). Pertanto, rifiutò categoricamente le teorie della modificazione (o della "qualificazione", com'egli stesso diceva). Ogniqualvolta appaiono i colori, sono soltanto scomposizioni della luce solare; si trovano già nella luce e non vengono mai creati; appaiono in un prisma dato che la rifrazione separa i diversi colori l'uno dall'altro, inclinando ognuno di essi in diversa misura, a seconda della sua rifrangibilità. La teoria del colore fu il fondamento di tutta la successiva ricerca ottica di Newton.
La teoria della composizione della luce bianca e del diverso grado di rifrangibilità formulata da Newton, benché inizialmente non fosse stata ben accolta, divenne una delle basi dell'ottica moderna. Già nei primi mesi dopo la pubblicazione fu criticata, fra gli altri, da Hooke, dal gesuita francese Ignace-Baptiste-Gaston Pardies e da Huygens; Newton fu impegnato a difenderla contro vari corrispondenti fino al 1676. Furono diversi i fattori che contribuirono all'insorgere di numerose contestazioni alla teoria di Newton; la sua radicalità e il capovolgimento di tante idee già consolidate provocarono una naturale resistenza e sarebbe stato necessario un certo periodo di tempo perché essa fosse assimilata dalla comunità scientifica. Newton stesso contribuì a ostacolarne l'accettazione pubblicando un saggio tanto conciso, e con due sole figure, da sconfinare nell'oscurità.
Solamente dopo che Pardies (uno scienziato sagace) ebbe messo in discussione per ben due volte il significato dell'experimentum crucis, Newton pensò di pubblicare un'esposizione chiara della sua teoria, accompagnandola con un grafico. In un'epoca in cui si dava molta importanza ai risultati sperimentali, egli decise di presentare soltanto tre esperimenti; lo stile dell'esposizione era provocatorio, con affermazioni talmente perentorie sulla certezza della sua teoria ‒ "risultati di massimo rigore […] ottenuti mediante sperimentazioni che hanno portato a conclusioni dirette ed esenti da qualsiasi ombra di dubbio" ‒ che l'editore delle "Philosophical Transactions" fu costretto a depennarle (ibidem, pp. 96-97). Newton presentò inoltre la sua teoria come una sfida alla verità della legge di Snell, che nel frattempo stava riscuotendo vasti consensi, anziché come un semplice ampliamento della medesima.
Essenzialmente, le obiezioni alla teoria di Newton si suddividevano in tre ampie categorie. La prima riguardava la rifrangibilità ineguale, e Newton fornì prontamente chiarimenti e sviluppò ulteriori esperimenti e argomentazioni. Questo aspetto fu accettato relativamente presto, perché estendeva in parte l'ambito dell'ottica geometrica. La graduale affermazione della rifrangibilità ineguale fu essenziale per l'accettazione di tutta la teoria. Accolto il concetto che la luce solare fosse composta di raggi rifratti in modo diverso, già era stato compiuto un enorme passo in avanti verso l'accettazione dell'idea, ancor più rivoluzionaria, che essa potesse essere composta da raggi di colori diversi. La seconda categoria di obiezioni riguardava la natura della luce e le teorie della modificazione del colore. Hooke, Pardies e Huygens, che sostenevano una teoria ondulatoria, intuirono che Newton era favorevole a una teoria dell'emissione: la loro preoccupazione era che la sua teoria del colore fosse incompatibile con quella ondulatoria. Newton non negò di credere alla teoria dell'emissione, ma ribadì che non aveva nulla a che fare con quella del colore. Per rassicurare gli antagonisti che la sua teoria non dipendeva dai corpuscoli di luce, spiegò come la teoria ondulatoria poteva esservi adattata.
Se i sostenitori della teoria ondulatoria avessero assunto che la luce solare fosse composta da una mescolanza di onde aventi varie lunghezze ('profondità' o 'grandezze') ‒ ognuna delle quali dotata di un diverso grado di rifrazione e capace di eccitare un colore diverso ‒ la loro teoria sarebbe stata compatibile con quella del colore di Newton senza alcun bisogno di adottare corpuscoli di luce. Nelle risposte Newton difese la sua nuova teoria del colore contro quelle della modificazione, ma nessuno dei suoi critici cambiò parere. La terza categoria di critiche riguardava la natura del colore e del bianco e Newton fu costretto a chiarire le sue idee su questi punti. Sia Newton sia i suoi critici avevano assimilato i risultati della tradizione artistica sul colore. Pardies obiettava che una combinazione di pigmenti di tutti i colori non produce il bianco, come sosteneva Newton, ma un colore cupo, scuro. Newton non replicò che una mescolanza di pigmenti avrebbe dato risultati diversi rispetto a una mescolanza di luci, perché, come tutti i contemporanei, accettava che fossero equivalenti. Nella risposta si rifece, piuttosto, al parere dominante nella tradizione artistica e cioè che bianco, grigio e nero formavano una scala cromatica separata e diversa da quella dei colori: poiché ciascun pigmento in una mescolanza riflette soltanto una piccola percentuale della luce incidente, il risultato della mescolanza avrebbe dovuto essere molto scuro e non intensamente bianco, così come effettivamente avviene. Newton riuscì in questo modo a trasformare una critica in un punto a favore della sua teoria, dimostrando che tali conclusioni concordavano con la nuova tradizione artistica, i cui risultati stavano continuamente guadagnando sostegno tra gli scienziati.
Hooke e Huygens sollevarono obiezioni riguardanti l'innumerevole quantità di colori primari di Newton, ritenendo "assolutamente inutile moltiplicare entità senza alcun bisogno", dato che i pittori possono ottenere tutti i colori mescolandone soltanto tre (ibidem, p. 113). Newton finì con il riconoscere che la sua concezione di colore semplice o primario era diversa da quella dei pittori: si basava infatti sulla rifrangibilità dei raggi, cioè sulla loro composizione fisica. I raggi semplici hanno un solo grado di rifrangibilità e quando attraversano un prisma rimangono inalterati, mentre un raggio composto ‒ per esempio un arancione risultante dalla combinazione di rosso e giallo ‒ sarebbe scomposto dal prisma in due raggi di rifrangibilità diversa. Malgrado appaiano identici ai sensi, i due colori differiscono nella composizione fisica. Con la denominazione di 'primario', Newton intendeva i componenti elementari e fisicamente irriducibili della luce, che si distinguono per la loro proprietà fisica di rifrangibilità. Questo concetto di 'primario' è diverso rispetto a quello della tradizione artistica di mescolanza dei pigmenti, in cui i colori primari sono quegli elementi dai quali si possono ottenere tutti gli altri colori e che, a loro volta, non possono in alcun caso derivare dalla mescolanza di altri colori. I critici convinsero Newton ad accettare questa concezione e in una lettera a Huygens egli introdusse i nuovi termini 'semplice e omogeneo' invece di 'primario'. Tuttavia, trent'anni più tardi usò nuovamente il termine 'primario' nell'Opticks, sia nella proposizione basilare della sua teoria ‒ "il bianco della luce solare si compone di tutti i colori primari" ‒ sia in un altro importante brano dello stesso libro. Inoltre, mentre nei primi scritti si riferisce agli innumerevoli colori dello spettro, nell'Opticks parla solo dei sette colori principali. Forse questi cambiamenti furono in parte motivati dal desiderio di sanare la discrepanza tra i suoi innumerevoli colori dello spettro e i tre colori primari dei pittori. In tal modo, la sua nuova teoria si accordava con la rielaborazione del concetto di colore del mondo artistico che, cominciata con Alberti, soltanto all'inizio del XVIII sec. fu assimilata nella tradizione scientifica.
Nonostante la teoria di Newton fosse stata oggetto di molte critiche nel periodo subito successivo alla pubblicazione, riuscì gradualmente ad affermarsi in Gran Bretagna dove, all'epoca della prima edizione dell'Opticks, nel 1704, aveva già raggiunto un vasto consenso. Non fu la stessa cosa nell'Europa continentale. Nel 1681 Mariotte effettuò una verifica sperimentale della teoria di Newton, poco dopo la sua pubblicazione, e ne rese noti i risultati dichiarando che l'esperimento era fallito. Egli aveva fatto passare una sottilissima porzione di uno spettro prodotto da un prisma in un secondo prisma posto a grande distanza dal primo. Secondo quanto affermato dal principio dell'immutabilità dei colori di Newton, Mariotte si aspettava che i colori rimanessero invariati; trovò invece una mescolanza, per esempio un raggio viola che produceva sfumature rosse e gialle. Per qualche inspiegabile motivo, Newton non aveva chiarito ‒ prima della pubblicazione dell'Opticks ‒ come separare raggi immutabili di un unico colore. Egli venne a conoscenza dell'esperimento di Mariotte dopo la pubblicazione dell'Opticks e soltanto allora fu in grado di dimostrare che i raggi di Mariotte non erano in realtà raggi di un unico colore, come egli aveva creduto. L'esperimento di Mariotte, benché scarsamente conosciuto in Gran Bretagna, era molto noto nell'Europa continentale, dove divenne il maggiore ostacolo all'accettazione della teoria di Newton.
I colori delle lamine sottili
Nel suo studio sui colori delle lamine sottili Newton dimostrò sperimentalmente la periodicità della luce, stabilendo nel contempo, nel campo della fisica, un nuovo livello di precisione, raggiunto in precedenza soltanto dall'astronomia. Nel 1666 aveva risolto, almeno in linea di principio, il problema del colore delle lamine sottili; nello stesso periodo, stava leggendo la Micrographia di Hooke ed era impegnato nella stesura di un primo resoconto della nuova teoria del colore. Newton condusse una ricerca sistematica sui colori delle lamine sottili intorno al 1671. Tuttavia, fu soltanto verso la fine del 1675 che inviò una relazione sull'argomento alla Royal Society, che fu letta nel corso delle riunioni. Ma Newton non acconsentì alla pubblicazione. Gran parte del Libro II dell'Opticks è una revisione della relazione letta alla Royal Society.
Hooke, a causa dell'estrema sottigliezza, non era stato in grado di misurare lo spessore di una lamina sulla quale appariva un particolare colore. Il successo ottenuto da Newton nel misurare tale spessore derivò dalla scelta di un dispositivo sperimentale in cui lo spessore era definito dalla geometria del dispositivo stesso. Collocando una lente convessa ABC sopra una lamina di vetro piana FBG, lo spessore dello strato d'aria ABCGBF tra la lente e la superficie di vetro piana poteva essere facilmente determinato applicando una ben nota formula di Euclide (fig. 22). Quando la lente era vista dall'alto e illuminata dalla luce solare, egli osservava una serie alternata di anelli diversamente colorati chiari e scuri ‒ ora noti come 'anelli di Newton' ‒ che circondavano una zona nera nel punto di contatto al centro della lente. Per calcolare lo spessore dello strato d'aria, Newton doveva soltanto misurare il diametro degli anelli colorati e calcolare il raggio della lente (grandezze entrambe di dimensioni ragionevoli). Se si indica il diametro di uno qualsiasi di questi cerchi colorati con D, lo spessore dello strato d'aria che produce quel cerchio con d e il raggio della lente con R, allora, utilizzando la proposizione III. 36 degli Elementi di Euclide, si può facilmente dimostrare che d=D2/8R. Calcolando il diametro di anelli successivi e dimostrando che i quadrati dei diametri aumentano come i numeri interi, Newton stabilì che i cerchi appaiono secondo multipli interi dello spessore dello strato d'aria misurato al primo anello. In questo modo dimostrò quantitativamente l'ipotesi di Hooke secondo la quale i colori mostrano una periodicità. Egli scoprì che lo spessore dello strato d'aria, o intervallo tra le lamine, che produce il giallo era di 1/80.000 di pollice (0,318 μm). Durante la stesura dell'Opticks perfezionò la misurazione e ricalcolò il valore in 1/89.000 di pollice (0,285 μm). Questo valore è fondamentale perché risulta essere pari a metà della lunghezza d'onda nella teoria ondulatoria della luce. Il valore che Newton ottenne da questo nuovo calcolo è molto vicino a quello attuale.
Il trattato di Newton sui colori delle lamine sottili fu pubblicato nel 1675 corredato da un saggio dal titolo An hypothesis explaining the properties of light discoursed of in my several papers, in cui egli spiega la periodicità degli anelli con le vibrazioni esistenti nell'etere che pervadono tutta la materia. Nonostante Newton fosse favorevole a una teoria dell'emissione, l'etere era una componente essenziale dei suoi ragionamenti di fisica, come lo era per la teoria ondulatoria di Hooke. Quando un corpuscolo cade sulla superficie superiore di uno strato sottile d'aria, provoca alcune vibrazioni in esso. A un certo spessore BC dello strato d'aria (fig. 23), il corpuscolo troverà una compressione nelle vibrazioni quando raggiungerà la seconda superficie e sarà riflesso in direzione contraria, formando un anello di colore chiaro; quando lo spessore raddoppia ‒ DE ‒ incontrerà una rarefazione e passerà oltre formando un anello scuro, e così via, in progressione aritmetica, conformemente alle osservazioni. Poiché Newton riteneva che i corpuscoli luminosi di colori diversi fossero tra di loro in qualche modo intrinsecamente differenti ‒ per dimensione, forza, o altro ‒ le vibrazioni da essi provocate dovevano essere di diverse dimensioni. Egli suppose che le vibrazioni rosse fossero maggiori rispetto a quelle viola e, così come aveva osservato, che formassero cerchi più grandi. Gli appunti e gli articoli inediti di Newton dimostrano che questo modello di vibrazioni dell'etere ebbe un ruolo fondamentale nello sviluppo della sua teoria. Le ipotesi come quelle dei corpuscoli di luce e delle vibrazioni eteree, sosteneva Newton, non dovrebbero essere mescolate con i risultati dimostrati sperimentalmente, a meno di non voler inficiare la certezza dei risultati. Spiegò di aver inviato la sua hypothesis alla Royal Society insieme alla relazione contenente le osservazioni, per rendere queste ultime più agevolmente comprensibili, sottolineando tuttavia che nessuno doveva confondere la certezza delle osservazioni con le ipotesi.
Quando Newton inserì il suo precedente lavoro sulle lamine sottili nel Libro II dell'Opticks, trasformò le vibrazioni nell'etere in 'impulsi di facile riflessione e rifrazione' e le promosse a principio incontrovertibile. Gli impulsi furono quindi considerati come una proprietà della luce e non dell'etere. Mentre stava scrivendo l'Opticks, all'inizio dell'ultimo decennio del Seicento, Newton aveva scoperto un nuovo fenomeno, i colori delle lamine spesse: anelli visibili in specchi sferici di 1/4 di pollice di spessore (6,35 mm). Ritenne che ciò fosse una prova sufficiente per dimostrare che la periodicità deve essere considerata una proprietà generale della luce e fu in grado di fornirne una spiegazione con le stesse lunghezze di vibrazione I e con la teoria fisico-matematica utilizzata per le lamine sottili, nonché di stimare la dimensione degli anelli colorati delle lamine spesse con la stessa precisione con cui l'aveva fatto per le lamine sottili. Questo nuovo fenomeno fu illustrato nell'Opticks (Libro II, parte IV). Dal momento che Newton riteneva che non fosse opportuno mescolare le ipotesi con principî scientifici stabiliti, dovette rinunciare ai suoi corpuscoli di luce e alle vibrazioni eteree. Ciò si tradusse in una teoria degli impulsi famigerata per la sua oscurità. Questi impulsi periodici avevano alcune proprietà matematiche delle onde, con gli intervalli tra impulsi che corrispondevano alla metà della lunghezza d'onda. La misurazione effettuata da Newton dei colori delle lamine sottili e della lunghezza delle vibrazioni è uno dei punti più alti raggiunti dalla scienza sperimentale del XVII sec., per il livello di precisione raggiunto e per aver dimostrato che la periodicità è una proprietà della luce.
L'Opticks e la natura della luce
L'Opticks, pubblicata nel 1704, quasi quarant'anni dopo che Newton aveva iniziato le sue ricerche nel campo dell'ottica, era il risultato finale dei suoi studi. Includeva una nuova esposizione della teoria della luce e del colore nel Libro I, i risultati della ricerca sulle lamine sottili nel Libro II e un nuovo lavoro inedito, realizzato nei primi anni dell'ultimo decennio del Seicento sui colori delle lamine spesse e la diffrazione, nei Libri II e III. I risultati sperimentali e le teorie di Newton divennero il fondamento dell'ottica nel XVIII sec., ma per più di un secolo l'Opticks servì anche come modello per la scienza sperimentale. Newton inserì nella parte finale dell'opera una serie di sedici brevi questioni (Queries) che servivano a presentare le sue speculazioni sulla natura della luce e i fenomeni ottici. Le questioni furono via via aumentate fino a che diventarono quasi un quarto dell'opera stessa: nella traduzione latina del 1706 ne aggiunse altre sette e nella seconda edizione inglese del 1717 ancora otto. Le Queries trattavano buona parte dei temi della filosofia naturale ed erano incentrate in particolare sulla luce, la chimica e la teoria della materia. Anch'esse furono di grande importanza per la filosofia naturale del XVIII secolo.
Benché Newton fosse già famoso per i Principia, pubblicati nel 1687, la sua teoria del colore non era molto nota nell'Europa continentale (l'Opticks fu data alle stampe solo nel 1704). La pubblicazione di questa opera chiara ed esauriente modificò la situazione assai rapidamente e nel giro di un decennio la nuova teoria della luce e del colore era ben avviata verso l'accettazione generale. Favorevole accoglienza alla teoria di Newton si ebbe in tutta Europa: in Francia, Nicolas Malebranche le diede il suo appoggio nel 1707 e Jean-Jacques Dortous de Mairan nel 1716; in Italia, Celestino Galiani e Francesco Bianchini a Roma nel 1707 e Giovanni Poleni a Venezia nel 1709; in Olanda Herman Boerhaave nel 1708; nei territori di lingua tedesca Johann I Bernoulli poco prima del 1710 e Christian Wolff nel 1710. Un evento fondamentale per l'accettazione della teoria si verificò quando, nel 1713, Wolff sfidò Newton sulla rivista "Acta Eruditorum" a rispondere all'esperimento di Mariotte, dimostrando l'esistenza di raggi immutabili di un solo colore, un concetto centrale nella teoria di Newton. Questi aveva all'epoca settant'anni e chiese a Jean-Théophile Desaguliers, che si occupava della realizzazione degli esperimenti alla Royal Society, di eseguire le prove richieste. Desaguliers effettuò con successo gli esperimenti nel 1713 e li ripeté frequentemente a Londra per i visitatori, liberandosi così definitivamente dallo spettro dell'esperimento di Mariotte.
Molti leggevano l'Opticks per conoscere le teorie di Newton sulla natura della luce, in particolare le Queries, in cui egli sostiene con fervore una teoria dell'emissione. Sin da quando aveva cominciato a interessarsi all'ottica, Newton aveva interpretato tali fenomeni attraverso una teoria corpuscolare della luce, che utilizzò metodicamente soprattutto nella ricerca sulla rifrazione e la dispersione cromatica (la misura in cui i raggi di differenti colori sono separati tra loro dalla rifrazione, l'angolo TFP nella fig. 21). Il suo scopo era quello di dedurre misurazioni quantitative di questi effetti con un approccio rigorosamente meccanicista. La spiegazione data da Descartes alla riflessione e alla rifrazione, che Newton apprese quando era studente, lasciò una traccia profonda in lui e i suoi tentativi di deduzione della legge di rifrazione e di dispersione riflettono il modello cartesiano. La più radicale rielaborazione del modello di Descartes avvenne nei Principia, dove introdusse il concetto di forza.
Newton dedicò una sezione di tale opera (Libro I, sez. XIV) allo sviluppo dell'analogia tra i raggi di luce e il moto dei corpuscoli in un campo di forze. Ipotizzò che sui corpuscoli di luce venisse esercitata dal corpo rifrangente una forza intensa e a corto raggio, che agiva in una minuscola zona sopra e sotto la superficie rifrangente e perpendicolare a essa. Il moto delle particelle in questo campo era esattamente come quello di un proiettile che 'cade' nel campo gravitazionale della Terra. Newton dimostrò che la traiettoria nella zona del campo di forza è una parabola ("da ciò che ha dimostrato Galileo") e che la traiettoria del corpuscolo avrebbe obbedito alla legge di Snell. Poiché presumeva che il campo di forza dovesse agire soltanto a distanza microscopica, la traiettoria curva sarebbe stata impercettibile. Negli anni Quaranta del Settecento la maggior parte degli scienziati aveva ormai accettato il concetto di forza; a questo punto il modello di Newton forniva una risposta soddisfacente all'enigma ‒ già evidente nella deduzione di Descartes della legge di Snell ‒ della maggiore velocità del moto di un corpo in un mezzo denso: in un corpo più denso esiste una maggiore quantità di materia che esercita una maggiore forza di accelerazione sui corpuscoli di luce.
In uno scolio a questa sezione dei Principia Newton suggerì che le forze a corto raggio che agiscono sui corpuscoli di luce potessero spiegare la diffrazione. Alcuni anni dopo, mentre stava completando l'Opticks, tentò di realizzare questo progetto e iniziò una ricerca sperimentale sulla diffrazione. I risultati di questo lavoro diventarono l'ultimo libro dell'Opticks. I suoi scritti inediti dimostrano che, secondo Newton, la diffrazione avviene quando i corpuscoli di luce passano molto vicino al bordo di un corpo e vengono deflessi dalle forze a corto raggio dei corpuscoli del corpo. Egli seppe sviluppare questo modello in forma matematica e con esso realizzò misurazioni e calcoli. Dopo aver completato questa ricerca, eseguì un nuovo esperimento, i cui risultati confutarono in maniera definitiva il modello basato su forze e corpuscoli. Quando diede alle stampe l'Opticks, Newton la rivide eliminando i risultati che erano stati ottenuti con il modello corpuscoli-forze. Di conseguenza, benché l'opera presenti alcune interessanti osservazioni sperimentali, in realtà contribuì in scarsa misura a spiegare la natura della diffrazione.
Lo scopo di questa sezione dei Principia era quello di dimostrare che l'ottica corpuscolare poteva essere accolta nel regno della nuova scienza matematica della meccanica e che, in particolar modo, poteva spiegare le cause dei diversi colori e della rifrangibilità dei raggi luminosi. In realtà, come fu dimostrato successivamente, le interpretazioni più naturali del suo modello erano o insostenibili da un punto di vista fisico o in contrasto con le osservazioni, e quindi non potevano essere applicate al colore, ossia proprio alla sua scoperta più significativa nel campo dell'ottica. Newton concluse lo scolio della sezione XIV dei Principia rammentando ai lettori che stava soltanto proponendo un'analogia e non ipotizzando che la luce fosse realmente composta da corpuscoli. Ma la prospettiva di poter unificare l'ottica e la meccanica era di tale interesse che per più di un secolo Newton e i suoi successori tentarono di fornire una spiegazione meccanica dell'azione dei corpi sui corpuscoli di luce.
Le limitazioni metodologiche di Newton non gli consentirono di sostenere la teoria corpuscolare della luce nell'Opticks.
Egli tuttavia considerò tale teoria nelle questioni speculative allegate all'opera. Nella Query 29 si interroga: "I raggi di luce sono corpi minuscoli emessi da sostanze luminose?" e fornisce prove che fanno ritenere che la risposta potrebbe essere affermativa (ed. 1952, p. 370). Nella Query 31 sostiene l'esistenza di forze ottiche a corto raggio d'azione: "Forse che le minuscole particelle dei corpi non hanno alcune potenze, virtù o forze per mezzo delle quali agiscono a distanza, non soltanto sui raggi della luce per rifletterli, rifrangerli e fletterli, ma anche l'una sull'altra producendo gran parte dei fenomeni della Natura?" (ibidem, pp. 375-376). Newton non si limitò a presentare ogni prova di cui potesse disporre a favore della teoria dell'emissione, ma mosse un certo numero di questioni contro la teoria ondulatoria. La sua principale obiezione, avanzata sin dall'inizio degli studi sull'ottica, era la seguente: se la luce fosse una pressione o il moto di un mezzo come l'etere, violerebbe la legge della propagazione rettilinea e si esaurirebbe come le onde del suono e dell'acqua. Si spinse fino ad attaccare il capolavoro della teoria ondulatoria di Huygens ‒ la spiegazione della doppia rifrazione ‒ cercando di sostituirlo con la sua legge, che si sarebbe poi rivelata errata.
Huygens e la teoria ondulatoria della luce
La teoria ondulatoria di Huygens rappresenta il culmine della concezione meccanicistica della luce nel XVII sec., iniziata con Hobbes e Descartes. Il suo approccio alla teoria della luce è di tipo cinematico (la cinematica è lo studio del moto prescindendo dalle forze che lo causano) e si basa in pratica su un solo principio, la velocità finita della luce. Nel Traité de la lumière (pubblicato nel 1690 ma scritto nel 1678), Huygens formulò i concetti di 'raggio' e di 'fronte d'onda' nella loro più completa generalità matematica e fisica. Considerando un fronte d'onda come il luogo dei punti raggiunti da un moto o una perturbazione nell'etere in un determinato momento, fu in grado di dimostrare che, nei mezzi omogenei, i raggi sono sempre perpendicolari ai fronti d'onda e di conseguenza gli fu possibile utilizzare questi concetti per spiegare l'insolita rifrazione nello spato d'Islanda.
Pardies aveva scritto un trattato sulla teoria ondulatoria. Huygens aveva discusso di ottica con lui e aveva letto alcune parti del suo manoscritto, ora perduto. Il testo si è però parzialmente conservato in quanto alcuni brani furono pubblicati dal confratello di Pardies, il gesuita Pierre Ango (1640-1694). Questi, tuttavia, confuse il proprio lavoro con quello di Pardies, di cui omise tra l'altro alcune parti, ed è difficile identificare con certezza i concetti di Pardies. Egli andò oltre i raggi fisici di Hobbes e Hooke e riconobbe che i raggi sono semplicemente le perpendicolari ai fronti d'onda. Secondo Huygens, non era stato Pardies a sviluppare il suo principio ‒ il maggior contributo di Huygens all'ottica ‒ e non c'è motivo di dubitare della sua affermazione. Resta tuttavia da chiarire in quale misura Huygens fu influenzato da Pardies.
Huygens iniziò il Traité dichiarando la sua fedeltà alla filosofia meccanicistica e adottando l'idea ‒ in netta contraddizione con Descartes ‒ che la luce è un moto, "per lo meno nella vera filosofia, in cui si concepiscono le cause di tutti gli effetti naturali in termini di moti meccanici" (OC, XIX, p. 454). Sin dall'inizio della ricerca, Huygens era partito dal presupposto ‒ di nuovo in contrasto con Descartes ‒ che la velocità della luce fosse finita, poiché il suo scopo era quello di descrivere il moto della luce in forma meccanica e matematica, e in questa prospettiva l'infinito rimaneva precluso all'indagine scientifica. Fu quindi soddisfatto quando, nel 1676, Ole Christensen Rømer calcolò la velocità della luce basandosi su osservazioni dei satelliti di Giove, fatto che Huygens non mancò di illustrare all'inizio del Traité.
Huygens assumeva che ciascun punto di un corpo luminoso vibrasse e inviasse onde ‒ o piuttosto impulsi, poiché negava la periodicità della luce ‒ attraverso l'etere. Rielaborando un suo precedente studio pionieristico sulla collisione delle sfere, fu in grado di dedurre le proprietà di un moto propagato attraverso un mezzo elastico e di sviluppare una teoria delle onde luminose matematicamente complessa. Come Descartes, ipotizzava che l'etere fosse composto da minuscole sfere in contatto tra loro, ma, rifiutando l'idea 'incomprensibile' di Descartes per cui la luce si sarebbe propagata istantaneamente, sostenne che le sfere dovevano essere elastiche. Riconobbe che in un mezzo elastico la velocità di propagazione di un impulso sarebbe stata la stessa, sia che le particelle ricevessero un impulso forte sia che ne ricevessero uno debole, e ciò significava che la luce doveva viaggiare a velocità costante. Infine, dal suo studio sulla collisione delle palle da biliardo egli sapeva che la stessa palla può servire a trasmettere simultaneamente diversi moti, così come i raggi di luce si incrociano nello spazio senza interferire l'uno con l'altro. L'etere di Huygens aveva tutte le proprietà necessarie per sviluppare una teoria ondulatoria.
Huygens utilizzò il suo etere 'a palle da biliardo' per fornire il più brillante contributo all'ottica, 'il principio di Huygens', secondo cui i fronti d'onda vengono generati da onde elementari più piccole. Osservò che le particelle di etere si toccano l'una con l'altra su tutti i lati e comunicano un loro moto qualsiasi a tutte le particelle che le circondano: per esempio, se una particella B colpisce la particella A, questo impatto verrà trasmesso a tutte le particelle che circondano quest'ultima. Di conseguenza, ciascuna particella, per esempio B diventa il centro della propria onda particolare KCL (une onde particulière). Questa onda elementare toccherà (oppure sarà tangente a) l'onda principale DCF nel punto C nello stesso istante in cui la stessa onda principale raggiunge DCF. Analogamente, tutte le onde particolari da tutti gli altri punti (b, d, ecc.) raggiungeranno DCF nello stesso istante e insieme formeranno l'onda principale o fronte d'onda. Se immaginiamo che BG sia un piccolo foro e che HB e GI siano opachi, Huygens spiega che le onde particolari oltre le linee AC e AE sono troppo deboli per poter essere percepite. In questo modo Huygens non sta soltanto spiegando la propagazione rettilinea, ma anche negando l'esistenza della diffrazione. Evidentemente non era convinto della validità della scoperta di Grimaldi.
Il 'principio di Huygens' consiste di tre assunzioni: (1) ciascun punto di un fronte d'onda è il centro di onde particolari; (2) il fronte d'onda è determinato dalla tangente comune alle estremità di queste onde elementari; (3) le onde particolari sono percepibili soltanto nel luogo definito dalla loro tangente comune. Le tre condizioni insieme definiscono il fronte d'onda come luogo dei punti raggiunti da una perturbazione in un dato momento. La terza condizione da sola equivale ad affermare che i raggi sono perpendicolari ai fronti d'onda. Huygens definisce in questo modo le onde, i raggi e le relazioni tra di essi.
Nella prima parte del Traité Huygens ammette che le onde particolari servono soltanto a complicare la situazione, ma promette che ciò che segue le giustificherà. Successivamente mette da parte le piccole sfere di etere, di cui in realtà si è servito soltanto per la proprietà dell'elasticità, e applica il 'principio di Huygens' come mezzo per descrivere la propagazione dei fronti d'onda nei casi di maggiore complessità. Si occupa prima dei problemi elementari della riflessione e della rifrazione di onde piane su superfici piane, poi della rifrazione in mezzi non omogenei, come l'atmosfera, in relazione alla quale spiega il motivo per cui i raggi luminosi non sembrano seguire un percorso rettilineo nell'aria. I due capitoli finali raggiungono un livello fisico-matematico assai raffinato. Nell'ultimo di essi Huygens risolve elegantemente il problema del rapporto tra teoria ondulatoria e ottica geometrica utilizzando la matematica delle evolute e delle evolventi (che aveva ideato tempo addietro) e mette in relazione la soluzione ottenuta con la caustica. I risultati così conseguiti erano all'avanguardia della fisica matematica dell'epoca.
Il risultato più originale e significativo della sua teoria ondulatoria fu la spiegazione della doppia rifrazione nello spato d'Islanda. Imitando Newton, in una lettera a Leibniz Huygens più tardi definì questa spiegazione il suo experimentum crucis. Spiegò che era stato costretto a condurre una ricerca sulla doppia rifrazione poiché nel cristallo il raggio rifratto in modo anomalo è obliquo rispetto al fronte d'onda, contrariamente al principio per il quale i raggi sono sempre perpendicolari a esso. Per spiegare come fosse possibile che apparissero due serie di raggi rifratti nello spato d'Islanda, sostenne che all'interno del cristallo vengono generate due serie di onde particolari: una di onde con la consueta forma sferica e l'altra di onde sferoidali. Ipotizzò che, mentre le onde regolari sferiche si propagano attraverso l'etere riempiendo i pori del cristallo, quelle sferoidali si propagano indifferentemente sia nell'etere sia nelle particelle che compongono il cristallo. Con le onde sferoidali fu in grado di produrre raggi obliqui rispetto al fronte d'onda. Quando l'onda piana RHhhC cade sul cristallo nei punti ATB, si propaga mediante onde particolari di forma sferoidale SNT, ecc., e i raggi AN e BQ saranno obliqui rispetto alla tangente comune o fronte d'onda NQ. L'interpretazione fisica delle onde di forma non sferica consiste dunque nel fatto che le onde luminose straordinarie viaggiano con differenti velocità in differenti direzioni all'interno del cristallo. Una volta stabilito che le onde sferoidali potevano spiegare il fenomeno, Huygens calcolò sperimentalmente i parametri e l'orientamento degli sferoidi. Definì la sua spiegazione della doppia rifrazione il suo experimentum crucis perché la sua idea delle onde particolari e il 'principio di Huygens' erano confermati soltanto nella doppia rifrazione. Tutti gli altri fenomeni di cui si era occupato potevano essere spiegati senza il 'principio di Huygens'. Coloro che accettarono questo principio ‒ e non furono molti prima del XIX sec. ‒ lo fecero, infatti, a causa della doppia rifrazione. Lo sforzo attuato da Newton per screditare la spiegazione di Huygens della doppia rifrazione e per sostituirla con la propria, rende evidente la consapevolezza della sua importanza.
Nel Traité, Huygens annunciò la scoperta di un nuovo fenomeno: la polarizzazione della luce, per usare la denominazione in uso all'inizio del XIX secolo. Quando Huygens collocava due cristalli uno sopra l'altro con i lati paralleli e trasmetteva i due raggi BC e BD prodotti nel primo cristallo attraverso il secondo cristallo, i raggi non venivano nuovamente divisi in due raggi. Il raggio ordinario era nuovamente rifratto in modo regolare e l'altro in modo irregolare. Se il cristallo inferiore era collocato perpendicolarmente rispetto al superiore, il raggio DG, che era rifratto in maniera regolare nel primo cristallo, si rifrangeva in modo irregolare nel secondo. A complicare ulteriormente le cose si aggiunse la sua scoperta che in tutte le altre posizioni del cristallo inferiore i raggi DG e CE erano nuovamente divisi in due raggi, così che da un raggio AB se ne creavano quattro. Huygens confessò che il fenomeno lo aveva sconcertato e che non poteva spiegare perché, nonostante i raggi CE e DG rimanessero gli stessi, la posizione del secondo cristallo causasse soltanto in alcuni casi un'ulteriore divisione dei raggi.
Il Traité de la lumière di Huygens affrontava in maniera elegante ed efficace una vasta gamma di fenomeni, ma, fatta eccezione per la doppia rifrazione, si limitò a illustrare le classiche proprietà della luce, riflessione e rifrazione, lasciando in disparte gran parte dell'ottica fisica, cioè la diffrazione, i colori delle lamine sottili e spesse e il colore. I suoi studi sulla doppia rifrazione e sulla polarizzazione, e con essi la teoria ondulatoria, non furono sviluppati in maniera significativa se non all'inizio del XIX secolo.
Conclusioni
Alla fine del XVII sec., la scienza dell'ottica assomigliava molto poco a quella di inizio secolo. La teoria della visione di Kepler fornì principî completamente nuovi all'ottica classica e l'ottica geometrica fu orientata verso lo studio delle lenti e degli strumenti ottici; verso la fine del secolo, quest'ultima rappresentava ormai una parte complessa della fisica matematica cui diedero il proprio contributo i matematici più eminenti. La nuova scienza sperimentale dell'ottica fisica fu soprattutto una creazione del Seicento. Affrontare teoricamente le proprietà della luce che si erano scoperte ‒ la diffrazione, i colori delle lamine sottili e spesse (fenomeni oggi noti come fenomeni di interferenza), la doppia rifrazione e la polarizzazione ‒ poneva difficoltà notevoli. Nel caso della diffrazione, la più difficile da trattare, se si eccettuano alcune speculazioni qualitative, si fecero pochi progressi. Newton aveva dimostrato che i colori delle lamine sottili e spesse sono fenomeni periodici e vi aveva dedicato un'esauriente ricerca sperimentale, ma la sua spiegazione ‒ la teoria degli impulsi ‒ fu generalmente ignorata. Huygens aveva presentato una soluzione per la doppia rifrazione che spiegava il fenomeno quantitativamente, ma essa era collegata alla sua teoria ondulatoria, che non aveva riscosso un vasto consenso. La polarizzazione, che aveva scoperto, mise in difficoltà lui e gli altri. Il colore, oggetto di studi millenari, fu il più rilevante successo dell'ottica fisica del XVII sec.; teoria e sperimentazione erano state in questo caso strette alleate. Verso la fine del secolo, e particolarmente nel lavoro di Huygens, la teoria ondulatoria poggiava su solidi principî ma il conflitto con quella corpuscolare era appena iniziato, anche perché le varie teorie non erano ancora completamente articolate. Newton attaccò la teoria ondulatoria, ma questo avvenne soprattutto nell'Opticks, all'inizio del secolo successivo.
Bibliografia
Armogathe 1987: Armogathe, Jean-Robert, L'arc-en-ciel dans les Météores, in: Le Discours et sa méthode, publié sous la direction de Nicolas Grimaldi et Jean-Luc Marion, Paris, PUF, 1987, pp. 145-162.
‒ 2000: Armogathe, Jean-Robert, The rainbow. A privileged epistemological model, in: Descartes' natural philosophy, edited by Stephen Gaukroger [et al.], London-New York, Routledge, 2000, pp. 249-257.
Casini 1993: Casini, Paolo, The reception of Newton's 'Opticks' in Italy, in: Renaissance and revolution. Humanists, scholars, craftsmen and natural philosophers in early modern Europe, edited and introd. by Judith Field and Frank A.J.L. James, Cambridge-New York, Cambridge University Press, 1993, pp. 215-227.
Crombie 1967: Crombie, Alistair C., The mechanistic hypothesis and the scientific study of vision. Some optical ideas as a background invention of the microscope, in: Historical aspects of microscopy, edited by Savile Bradbury and Gerard L'E. Turner, Cambridge, Heffer, 1967, pp. 3-112.
Gaukroger 1995: Gaukroger, Stephen, Descartes. An intellectual biography, Oxford, Clarendon, 1995.
Hall 1993: Hall, A. Rupert, All was light. An introduction to Newton's 'Opticks', Oxford, Clarendon, 1993.
Lindberg 1976: Lindberg, David C., Theories of vision from al-Kindi to Kepler, Chicago, University of Chicago, 1976.
Mamiani 1976: Mamiani, Maurizio, Isaac Newton filosofo della natura. Le lezioni giovanili di ottica e la genesi del metodo newtoniano, Firenze, La Nuova Italia, 1976.
‒ 1986: Mamiani, Maurizio, Il prisma di Newton. I meccanismi dell'invenzione scientifica, Roma-Bari, Laterza, 1986.
Sabra 1981: Sabra, Abd-al-Hamid I., Theories of light from Descartes to Newton, Cambridge-New York, Cambridge University Press, 1981 (1. ed.: London, Oldbourne, 1967).
Shapiro 1973: Shapiro, Alan E., Kinematic optics. A study of the wave theory in the seventeenth century, "Archive for history of exact sciences", 11, 1973, pp. 134-266.
‒ 1993: Shapiro, Alan E., Fits, passions, and paroxysms. Physics, method, and chemistry and Newton's theories of colored bodies and fits of easy reflection, Cambridge-New York, Cambridge University Press, 1993.
‒ 1994: Shapiro, Alan E., Artists' colors and Newton's colors, "Isis", 85, 1994, pp. 600-630.
‒ 1996: Shapiro, Alan E., The gradual acceptance of Newton's theory of light and color, 1672-1727, "Perspectives on science", 4, 1996, pp. 59-140.
Straker 1981: Straker, Stephen M., Kepler, Tycho, and the 'optical part of astronomy'. The genesis of Kepler's theory of pinhole images, "Archive for history of exact sciences", 24, 1981, pp. 267-293.
Westfall 1962: Westfall, Richard S., The development of Newton's theory of color, "Isis", 53, 1962, pp. 339-358.
‒ 1965: Westfall, Richard S., Isaac Newton's coloured circles twixt two contiguous glasses, "Archive for history of exact sciences", 2, 1965, pp. 181-196.