La scienza in Cina: dai Qin-Han ai Tang. La Cina e le zone limitrofe
La scienza in Cina: dai Qin-Han ai Tang. La Cina e le zone limitrofe
La Cina e le zone limitrofe
Agli inizi del I millennio d.C. il buddhismo cominciò a diffondersi al di fuori dell'India e, in tal modo, svolse un ruolo cruciale nel trasmettere elementi della cultura indiana ai paesi confinanti; infatti, il buddhismo non era soltanto un insieme di credenze religiose, ma comprendeva anche ciò che secondo i parametri moderni si potrebbe definire 'sapere scientifico'. Nei testi buddhisti cinesi le conoscenze di origine indiana erano suddivise in cinque categorie: dottrine linguistiche e grammaticali, conoscenze tecniche (per es., architettura e preparazione dei calendari), medicina e farmacopea, logica e conoscenza del sé interiore; tutte queste discipline erano oggetto di studio nei monasteri buddhisti. La medicina tradizionale indiana, insieme ad alcune conoscenze esoteriche e pratiche magiche, si propagò grazie al buddhismo nell'Asia centrale, meridionale e sudorientale, dove è tuttora praticata. Non sorprende, dunque, che anche l'astronomia e l'astrologia fossero esportate dal buddhismo fuori dell'India verso le aree culturali limitrofe. Peraltro, è da notare che tali conoscenze non esercitarono un'influenza significativa su quei settori della società che non si erano convertiti al buddhismo, né gli intellettuali cinesi, formatisi nell'ambito della tradizione accademica autoctona, mostrarono un grande interesse per le nozioni scientifiche di origine buddhista.
La trasmissione scientifica, oltre che dall'India alla Cina, deve essere avvenuta anche nella direzione opposta, tuttavia mancano testimonianze in proposito. Le scarne informazioni sulla Cina contenute nei testi classici sanscriti si limitano a un occasionale riferimento a questo paese chiamato, con nome sanscrito, Cīna; la più antica attestazione di questo termine si trova nel Trattato sull'utile (Arthaśāstra), un manuale sull'arte del buon governo opera di Kauṭilya, generalmente identificato con un ministro del sovrano Candragupta della dinastia Maurya, che regnò sull'India settentrionale agli inizi del III sec. a.C., dove la Cina è menzionata come il 'paese della seta'.
Un antico testo astrologico indiano e le sue traduzioni cinesi
Il più antico testo di astrologia indiano conosciuto in Cina fu le Gesta di Śārdūlakarṇa (Śārdūlakarṇāvadāna), parte del gruppo di testi buddhisti noti come avadāna ('gesta'), uno dei rari testi sanscriti nel quale sia sistematicamente trattata la fase iniziale dell'astrologia indiana. La data di quest'opera non è conosciuta, ma un esame dei contenuti mostra che il nucleo originale fu composto in un'epoca in cui gli Indiani sapevano dell'esistenza dei sette pianeti, ma ignoravano ancora l'ordine in cui questi si susseguivano nell'arco della settimana, il che permette di datarla al I o II sec. d.C. Il primo testo sanscrito in cui si accenna alla sequenza settimanale dei pianeti è lo Yavanajātaka (lett. Oroscopo greco, od Oroscopia secondo gli Occidentali, 269-270 d.C.) di Sphujidhvaja, ma anche in quest'opera il concetto di giorno della settimana non appare ancora ben definito. Di conseguenza, se un testo sanscrito fa riferimento alla sequenza dei giorni della settimana, si può dedurre che esso appartenga, in tutto o nella sezione pertinente, a un'epoca successiva all'Oroscopo greco.
Una delle caratteristiche dell'astrologia indiana del periodo più antico è la relativa mancanza d'interesse per i pianeti: i pronostici erano formulati in base alla posizione della Luna in rapporto alle ventotto o ventisette costellazioni chiamate nakṣatra o 'case lunari'. Questo tipo di divinazione può dunque essere definito 'astrologia lunare' per distinguerla dall'astrologia planetaria dei secoli successivi.
Le Gesta di Śārdūlakarṇa sono state tradotte in cinese più volte; la più antica versione ancora esistente, eseguita da Zhu Lüyan e Zhiqian verso la metà del III sec., porta il titolo di Aforismi dell'elefante (Modengqie jing, ovvero Mātaṇgasūtra); lo stesso testo fu tradotto col titolo di Sūtra delle ventotto case lunari del principe Śārdūla (Shetoujian taizi ershiba xiu jing) da Zhu Fahu (266-313 ca., noto anche come Dharmarakṣa) verso la fine del III o agli inizi del IV secolo. In seguito, poiché contenevano elementi di astrologia, queste traduzioni furono considerate come testi appartenenti alla tradizione del buddhismo tantrico e pertanto incluse nella sezione tantrica del Canone buddhista (Tripiṭaka) cinese.
Gli Aforismi dell'elefante si compongono di sette capitoli. I primi quattro raccontano la storia d'amore tra un discepolo del Buddha chiamato Ānanda e una ragazza fuori casta di nome Prakṛti e le loro vite precedenti in cui essi erano rispettivamente il principe fuori casta Śārdūla e la figlia di un brahmano; le conoscenze astrologiche insegnate dal padre del principe costituiscono l'oggetto dei rimanenti tre capitoli.
Il quinto capitolo tratta delle ventotto o ventisette case lunari; il fatto che le case siano ventotto o ventisette è significativo, perché i testi indiani più antichi contano ventotto case a intervalli irregolari, mentre i testi successivi ne contano ventisette, ciascuna delle quali occupa il medesimo spazio di 13°20′; quest'ultimo sistema è simile a quello dei dodici segni zodiacali nell'astrologia occidentale. È dunque degno di nota il fatto che tanto il testo sanscrito quanto la traduzione cinese contengano brani in cui si prendono in considerazione soltanto ventisette case lunari; all'epoca della composizione dell'originale sanscrito i due sistemi dovevano coesistere. Poiché il concetto di ventotto case lunari a intervalli irregolari ha una controparte assai simile nel xiu o 'casa lunare' dell'astronomia cinese e nelle manāzil o 'stazioni' dell'astronomia islamica, la questione del suo luogo di origine è controversa. È assai probabile che il sistema indiano e quello cinese si siano evoluti indipendentemente l'uno dall'altro; infatti, soltanto un terzo circa delle ventotto case nei due sistemi fa riferimento alla stessa stella o allo stesso gruppo di stelle. Negli Aforismi dell'elefante, tuttavia, tutti i nomi indiani dei nakṣatra o 'case lunari' sono stati tradotti nei nomi dei corrispondenti xiu cinesi come se fossero equivalenti.
Il modo di contare le case lunari a partire dalle Kṛttikā (in questo caso identiche al mao cinese e alle Pleiadi occidentali) appartiene al sistema indiano più antico. Nei testi successivi la prima casa lunare è considerata quella di Aśvinī (β e γ Arietis). Lo spostamento del punto d'inizio del sistema delle coordinate fu dovuto alla precessione degli equinozi; le Pleiadi erano in prossimità dell'equinozio di primavera intorno al 2300 a.C., ed è in base a questo che gli Indiani rivendicano l'antichità della loro tradizione astronomica.
Per ciascuna casa lunare gli Aforismi dell'elefante descrivono i seguenti elementi: il numero di stelle che la compongono, la sua configurazione e la sua ampiezza (nell'unità giorno-notte in cui la Luna vi sosta), la divinità che la presiede, le offerte per la divinità e la famiglia (gotra in sanscrito) cui essa appartiene. Alla fine del capitolo si elencano i nomi di sette astri ‒ nell'ordine il Sole, la Luna, Marte, Giove, Saturno, Venere e Mercurio ‒ cui si affiancano Luohou (trascrizione fonetica del termine sanscrito Rāhu, il demone che provoca le eclissi) e una cometa (o più comete, non essendovi distinzione tra singolare e plurale in cinese). L'ordine dei sette astri è importante dal punto di vista astronomico poiché sembra che i cinque pianeti siano stati suddivisi in due gruppi, quelli superiori (Marte, Giove e Saturno) e quelli inferiori (Venere e Mercurio); va anche sottolineato il fatto che la cometa (o le comete) non è chiamata Jidu (trascrizione fonetica del termine sanscrito Ketu), ma è annoverata come nono 'pianeta'. Soltanto in seguito, nella letteratura sanscrita Ketu iniziò a essere considerato come la coda di Rāhu; nel VI sec. Varāhamihira riteneva ancora che i ketavaḥ (plurale di Ketu) fossero comete. Il termine Ketu compare in due brani delle Gesta di Śārdūlakarṇa, ma entrambi sono compresi nell'ultima metà del testo, che è considerato un'aggiunta posteriore.
Il sesto capitolo descrive il carattere dei neonati e la loro occupazione futura e raccomanda i lavori da compiere quotidianamente a seconda della posizione della Luna in ciascuna casa, in base alla quale sono inoltre predetti gli eventi sociali, guerre e disordini, raccolti, condizioni climatiche, malattie ed epidemie. Anche gli effetti delle eclissi lunari e i terremoti sono classificati in base alla casa in cui si trova la Luna nel momento in cui si verificano.
Il settimo capitolo offre numerose informazioni significative per la storia dell'astronomia; gli argomenti trattati sono i seguenti.
a) Si fornisce la lunghezza del giorno e della notte in occasione dell'undicesimo mese (solstizio d'inverno) e del quinto mese (solstizio d'estate), nonché del secondo mese e dell'ottavo mese (i due equinozi). La proporzione tra il giorno più lungo e quello più corto è indicata come 18:12 (3:2); tale valore s'incontra nel Membro ausiliario del Veda sull'astronomia (Jyotiṣavedāṅga), il più antico testo indiano sul calendario, come pure nei testi cuneiformi babilonesi; è possibile dunque che non sia frutto di effettive osservazioni della lunghezza del giorno, ma sia stato semplicemente trasmesso alla Cina dall'India e, in origine, dalla Mesopotamia, senza subire modificazioni.
b) Sono elencati i nomi delle unità di tempo a iniziare dal chana, una trascrizione fonetica del sanscrito kṣaṇa, per finire con l'anno; sia kṣaṇa sia chana significano generalmente 'istante', ma in quanto unità di tempo rappresentano i 4/5 di un secondo.
c) Si precisa la lunghezza dell'ombra di un uomo nel 'secondo mese' dall'alba al tramonto a intervalli di un fen (solitamente il termine fen è usato come traduzione di vari termini sanscriti che significano 'minuto', ma nel caso specifico traduce muhūrta, cioè un trentesimo di giorno, ossia 48 minuti). Sono inoltre elencate le traduzioni cinesi del nome indiano di ciascuno dei trenta muhūrta, si fa menzione del metodo di misurazione del tempo mediante la clessidra e si enumerano le unità di lunghezza e di peso.
d) Le malattie, con la relativa prognosi fausta o infausta, e il numero di giorni che devono trascorrere prima della liberazione di una persona tenuta prigioniera sono associati alla casa in cui staziona la Luna.
e) Si descrive un metodo di divinazione in base alle verruche derivato dalla fisiognomonica indiana; trattazioni più dettagliate dell'argomento si trovano nei testi sanscriti di divinazione così come nella letteratura buddhista cinese.
f) È fornita la lunghezza dell'ombra di uno gnomone a mezzogiorno nel giorno centrale di ciascuno dei dodici mesi.
La parte più interessante del testo si trova alla fine del settimo capitolo, dove sono trattati il ciclo d'intercalazione di diciannove anni, l'ordine settimanale dei sette pianeti e i loro periodi siderali, tutti elementi di probabile origine ellenistica; in India, infatti, il ciclo di diciannove anni non era comunemente usato. Benché in Cina l'equivalente del ciclo metonico di diciannove anni fosse conosciuto già prima della dinastia degli Han anteriori (206 a.C.-9 d.C.), è possibile che i traduttori degli Aforismi dell'elefante ne avessero appreso l'esistenza da fonti occidentali. Ciò appare particolarmente significativo in quanto né l'unico testo sanscrito giunto sino a noi né l'altra traduzione cinese realizzata mezzo secolo più tardi contengono tali elementi. Gli Aforismi dell'elefante risalgono al periodo in cui l'astronomia e l'astrologia ellenistiche erano appena state introdotte in India; a meno che la parte in questione non sia un'interpolazione posteriore, si può ipotizzare che i traduttori, originari dell'Asia centrale, avessero ottenuto le nuove nozioni da fonti occidentali senza la mediazione indiana, incorporandole poi nella loro traduzione del testo buddhista. In alternativa, si può supporre che esistesse una differente versione del testo sanscrito e che su di essa si basi la traduzione cinese nota come Aforismi dell'elefante.
Malgrado l'altra traduzione cinese delle Gesta di Śārdūlakarṇa, ossia il Sūtra delle ventotto case lunari del principe Śārdūla, sia apparsa circa cinquant'anni più tardi, sembra che il suo traduttore non conoscesse la prima traduzione e che si sia servito di un testo sanscrito notevolmente diverso da quello usato per gli Aforismi dell'elefante, giacché le due traduzioni divergono in maniera sostanziale. Un esempio è fornito dal confronto dei nomi delle ventotto case lunari nei due testi. Come si è detto, gli Aforismi dell'elefante rendevano i nomi indiani dei nakṣatra con i nomi cinesi, già esistenti, dei xiu, sebbene le stelle che componevano i nakṣatra non fossero sempre le stesse di quelle dei xiu. Il Sūtra delle ventotto case lunari del principe Śārdūla, invece, cercava di tradurre il significato originale dei nomi sanscriti in maniera per quanto possibile letterale; la prima casa, per esempio, era chiamata mingcheng o 'fama', perché il nome sanscrito Kṛttikā era erroneamente interpretato come se fosse connesso alla parola kīrti, per l'appunto 'fama'; il nome della seconda casa, Rohiṇī, era tradotto come zhangyu o 'crescita', perché era correttamente ritenuto un derivato del verbo ruh- 'crescere'.
Come si accennava sopra, il testo sanscrito e la prima traduzione cinese annoverano a volte soltanto ventisette case lunari, omettendo niu (in sanscrito Abhijit, le tre stelle della Lira). Il Sūtra delle ventotto case lunari del principe Śārdūla fa invece costantemente riferimento a ventotto xiu, dal che si può dedurre che fosse basato su una recensione più antica del testo sanscrito.
I testi di epoca Tang
Prima dell'inizio del VII sec. l'astronomia indiana aveva compiuto notevoli progressi grazie a personalità come Āryabhaṭa (n. 476 d.C.) e Brahmagupta (n. 598 d.C.), e la nuova astrologia oroscopica di origine ellenistica si era ormai ampiamente diffusa in tutta l'India. Il periodo Tang (618-907) segnò l'acme degli scambi culturali tra la Cina e i paesi stranieri. In quegli anni la capitale Chang'an (l'odierna Xi'an) fiorì come centro internazionale ove si affollavano ambasciatori, missionari, rifugiati e viaggiatori. Anche alcuni studiosi buddhisti indiani visitarono la Cina e vi si stabilirono, contribuendo alla diffusione delle conoscenze scientifiche indiane.
Il Canone per la divinazione dell'era Kaiyuan dei grandi Tang (Da Tang kaiyuan zhanjing) è un'enorme raccolta di testi compilata nel VI anno di regno dell'imperatore Xuanzong (718 d.C.) della dinastia Tang. La raccolta comprende il Calendario Jiuzhi (Jiuzhi li), un testo astronomico di origine indiana, scritto da Qutan Xida (trascrizione fonetica di Gotama Siddhartha), un funzionario dell'Ufficio astronomico reale di Chang'an; come suggerisce il nome, Qutan Xida era un discendente di una famiglia indiana di nome Gotama. Nel 1977 è stato rinvenuto in un villaggio della provincia dello Shanxi l'epitaffio di Qutan Zhuan, il figlio di Qutan Xida. Quest'ultimo era figlio di Qutan Luo, direttore dell'Ufficio astronomico della dinastia Tang, che compose alla fine del VII sec. un nuovo calendario di cui fece omaggio alla celebre imperatrice Wu Zetian (690-704).
Il Calendario Jiuzhi riveste un'importanza fondamentale, essendo l'unico testo cinese che attesti la trasmissione dell'astronomia matematica indiana in Cina. Il termine jiuzhi nel titolo dell'opera è una traduzione del sanscrito navagraha, letteralmente i 'nove ghermitori', ossia i nove 'pianeti', comprendenti anche i due pianeti immaginari Rāhu e Ketu; la concezione dei nove pianeti era considerata caratteristica dell'astronomia indiana, ed è per questo che il termine fu usato nel titolo. All'inizio dell'opera si attribuisce la conoscenza dell'astronomia a "un veggente esperto nei cinque" in questo contesto 'cinque' si riferisce molto probabilmente alle cinque scuole astronomiche le cui dottrine sono riassunte nell'Esposizione dei cinque siddhānta (Pañcasiddhāntikā), composta da Varāhamihira intorno alla metà del VI sec., ed è possibile che Qutan Xida abbia tratto alcune nozioni da tale opera (Yabuuti 1979). Pingree ha messo in evidenza i paralleli esistenti tra gli argomenti trattati nei due testi, ma, oltre all'Esposizione dei cinque siddhānta, Qutan Xida doveva conoscere molte altre fonti sanscrite. Yano (1979) ha sostenuto che il Calendario Jiuzhi mostra forti affinità con il testo intitolato Bocconcini (Khaṇḍakhādyaka) di Brahmagupta, la cui epoca è il 23 marzo (domenica) 665; l'epoca del Calendario Jiuzhi è il 20 marzo (domenica) 657 e i due testi forniscono un'identica tavola per l'equazione solare.
Il Calendario Jiuzhi è un manuale per il computo del calendario del tipo detto karaṇa, nella tradizionale classificazione dei testi astronomici indiani. Si elencheranno qui di seguito in breve diversi argomenti trattati nel testo dai quali si possono trarre importanti informazioni dal punto di vista storico (poiché il testo originale cinese non è rigidamente suddiviso in capitoli, adottiamo la divisione in 37 capitoli proposta da Yabuuti 1979).
a) Nel primo capitolo sono introdotti i simboli numerici indiani e il metodo di calcolo scritto in cui essi sono usati; nella forma in cui ci è pervenuto, il testo non ha conservato gli originali simboli grafici per le cifre, ma la spiegazione non lascia adito a dubbi: "Ciascuna cifra è scritta con un solo tratto; quando un numero è contato in decine, avanza alla posizione superiore e in ogni spazio vuoto si mette sempre un punto. La cifra riceve quindi sempre un contrassegno e di conseguenza non possono esservi errori nel determinare la posizione" (Yabuuti 1979, p. 12).
Questo metodo di calcolo è esattamente quello cui fanno riferimento i testi posteriori chiamandolo calcolo sulla 'tavola di sabbia'. È interessante notare che per lo zero si usava un punto anziché un cerchio, poiché tali informazioni paleografiche s'incontrano raramente nei testi sanscriti. Benché Qutan Xida affermi che con le cifre il calcolo risultava facile 'per gli occhi', non si hanno testimonianze della diffusione di questo metodo tra i suoi colleghi cinesi.
b) Insieme alle unità sessagesimali di gradi e minuti, furono introdotti per la prima volta i segni zodiacali (1 segno = 30 gradi), tradotti con il termine xiang, sostituito circa cinquant'anni dopo da gong (v. oltre). La divisione del cerchio celeste in 360 'gradi' era un'idea innovativa, poiché nell'astronomia tradizionale cinese il numero di 'gradi' del cerchio celeste equivaleva al numero di giorni di un anno solare, e dunque l'unità di spazio dipendeva dall'unità di tempo. La nozione di 360 gradi celesti non fu accettata dai Cinesi sino all'introduzione dell'astronomia islamica nel periodo Yuan (1279-1368).
c) Alla fine del terzo capitolo è esposto il metodo per ottenere la settimana di sette giorni, e precisamente: quando i giorni accumulati a partire dall'epoca prescelta sono divisi per sette, il resto di 1 corrisponde al 'giorno di Marte' (martedì), quello di 2 al 'giorno di Mercurio' (mercoledì), e così via, perché si presuppone che l'epoca cada di lunedì (dunque in questo caso il resto è 0). Questa è la più antica attestazione del calcolo dei giorni della settimana in Cina. È chiaro che Qutan Xida era consapevole dell'importanza che i giorni della settimana governati dai pianeti avevano per l'astrologia, poiché annota che "la divinazione per i giorni governati dai sette astri dovrà essere descritta separatamente" (ibidem, p. 14).
d) In base ai valori della durata della luce diurna elencati nel cap. 11, si può approssimativamente stimare la latitudine geografica cui essi fanno riferimento; il risultato è di ca. 34°, che corrisponde alla latitudine di Chang'an, la capitale della dinastia Tang.
e) Nel cap. 21, subito prima di occuparsi del problema delle eclissi, il Calendario Jiuzhi introduce la tavola indiana dei seni. Non si tratta né di quella contenuta nell'Esposizione dei cinque siddhānta, in cui il raggio (R) del cerchio che funge da unità di misura vale 120, né di quella dei Bocconcini di Brahmagupta (dove R=150), bensì di quella del Trattato di Āryabhaṭa (Āryabhaṭīya, 499 d.C.), in cui i ventiquattro valori dei seni e le loro differenze Δ sono dati a intervalli, in notazione sessagesimale, di 3;45° ‒ cioè, in notazione usuale, 3° e 45/60 di grado, come dire 3°45′ ‒ dell'argomento α, per un raggio di 3438 minuti (v. La scienza indiana, cap. X). Questi valori erano ottenuti mediante una regola per la differenza dei seni e, di conseguenza, cinque valori deviano dai valori corretti di un minuto (1/60 di grado; Hayashi 1997). È interessante osservare che tutti i valori riportati nel Trattato di Āryabhaṭa furono riprodotti senza variazioni di alcun genere nel Calendario Jiuzhi; malgrado la tavola fosse adoperata nell'algoritmo del calcolo delle eclissi, l'importanza teorica delle funzioni trigonometriche non era compresa appieno dagli astronomi-matematici cinesi di quell'epoca. Nel tardo XIII sec. le funzioni trigonometriche furono reintrodotte in Cina insieme all'astronomia islamica, tuttavia furono utilizzate soltanto nell'ambito dei calcoli astronomici e non come strumento matematico per fini generali.
f) L'ultimo argomento di rilievo presentato nel testo riguarda la componente latitudinale della parallasse lunare, che è un fattore essenziale per calcolare le eclissi solari; anche questa era una novità per l'astronomia cinese, ma non ricevette l'attenzione che avrebbe meritato.
Il Calendario Jiuzhi aveva semplicemente lo scopo di fornire gli elementi essenziali per il computo del calendario; al di là dei giorni della settimana governati dai rispettivi pianeti, Qutan Xida non dà altre informazioni sui pianeti. Malgrado questo testo contenesse parecchie novità sostanziali che avrebbero potuto contribuire al progresso dell'astronomia, gli studiosi cinesi non prestarono molta attenzione all'aspetto teorico dell'astronomia matematica indiana, probabilmente perché potevano ottenere risultati migliori servendosi dei propri metodi. Difatti, gli autori posteriori si riferirono a volte al Calendario Jiuzhi definendolo un calendario 'grossolano', poiché ciò che contava ai loro occhi era l'accuratezza numerica piuttosto che l'innovazione teorica.
La diffusione del buddhismo tantrico coincise con la fase conclusiva del buddhismo indiano, che assorbì in quel periodo numerosi elementi della cultura tantrica hindu, in particolare per quanto riguarda i campi dell'astronomia, dell'astrologia e della medicina; in tal modo il buddhismo tantrico divenne il principale veicolo di trasmissione della cultura indiana ai paesi confinanti.
Il monaco Yixing (673-727) fu non soltanto una personalità eminente del buddhismo tantrico, ma anche uno dei più celebri astronomi cinesi. Egli scelse alcune opere tantriche che entrarono a far parte della raccolta di testi buddhisti cinesi. Una di queste, le Regole rituali per le case e gli astri (Xiuyao yigui), prescrive i rituali per le case lunari e gli dèi dei pianeti, servendosi di speciali posizioni delle dita (mudrā), formule sacre (mantra) e offerte. Gli dèi dei pianeti sono disposti secondo l'ordine dei giorni della settimana, seguiti da Luohou (Rāhu) e Jidu (Ketu), rispettivamente l'ottavo e il nono dio (o meglio demone) planetario, due divinità demoniache che avevano origine nella mitologia hindu. Un mostro dalla forma di drago, che aveva rubato e bevuto il nettare divino (la medicina dell'immortalità), fu punito per la sua azione dal dio Śiva, che lo tagliò in due; avendo bevuto il nettare dell'immortalità, il mostro però non morì e sopravvisse diviso nella testa (Rāhu) e nella coda (Ketu), che di tanto in tanto si vendicano divorando il Sole e la Luna, ossia provocando le eclissi solari e lunari.
Nelle Regole rituali per le case e gli astri si accenna all'ascendente di un oroscopo, ma non si trova ancora alcuna esposizione sistematica delle dodici 'posizioni' astrologiche (domus o 'case' nell'astrologia occidentale). Un'altra opera dello stesso genere ha il titolo di Brahmā, le horā e i nove graha (Fantian huoluo jiuyao). È interessante notare che il termine sanscrito horā (con cui si designava anche un'unità di spazio rappresentata dalla metà di un segno zodiacale, ossia equivalente a 15°) è una trascrizione fonetica del greco hō´ra, poi reso foneticamente in cinese come huoluo; la parola greca è anche all'origine del termine italiano 'ora', oltre a figurare come primo membro del composto 'oroscopo'.
Le Regole rituali per le case e gli astri menzionano anche un altro testo intitolato Yusi jing, che va probabilmente identificato con il Libro di Tolomeo (Duli yusi jing) citato da altre fonti cinesi; la prima parola del titolo di quest'opera deriva infatti dal nome dell'astronomo greco Tolomeo, autore anche di un trattato di astrologia, la Tetrabiblos. In Cina il testo del Libro di Tolomeo è andato perduto, ma in Giappone ne sopravvivono alcuni frammenti, sotto forma di citazioni in opere di astrologi buddhisti del periodo Heian (794-1192), in cui è menzionata la parola che equivale al termine tecnico astrologico 'trigono'. È molto probabile, pertanto, che una sorta di sintesi dell'astrologia greca, associata al nome di Tolomeo, sia stata trasmessa alla Cina e da qui al Giappone.
La scelta di testi curata da Yixing riflette la natura cosmopolita della dinastia Tang; testi astrologici, provenienti non soltanto dall'India, ma anche dalla Persia, dall'Asia centrale e da regioni ancora più occidentali, si fondono con la tradizione astrologica cinese. Questo caratteristico sincretismo è ancora più evidente nelle opere di cui si parlerà in seguito.
Yixing fu l'ideatore del celebre Calendario Dayan (Dayan li), ufficialmente in uso tra il 729 e il 761 d.C. Tale calendario si basa su un metodo d'interpolazione molto avanzato, praticamente identico a un caso particolare del metodo d'interpolazione di Gauss. Sebbene appaia probabile che Yixing avesse familiarità con la cultura indiana, è difficile valutare l'influsso della tradizione matematica indiana sul suo metodo.
Il Sūtra delle case e degli astri (Xiuyao jing) è un trattato di astrologia composto verso la metà dell'VIII sec. dal monaco buddhista di origine indiana Amoghavajra (705-774). Il titolo completo dell'opera può essere tradotto come Sūtra predicato dal Bodhisattva Mañjuśrī e dai santi sulle ore e i giorni fausti e infausti, e sulle case lunari e gli astri buoni e cattivi (Wenshu shi li busa ji zhu xian suoshuo ji xiong shiri shan'e xiuyao jing). Il testo è stato stampato in Giappone come numero 1299 del Taishō Daizōkyō, il Canone buddhista (Tripiṭaka) pubblicato durante il periodo Taishō, tra il 1912 e il 1926, ma, sempre in Giappone, ne esistono anche numerosi manoscritti antichi che presentano lezioni di gran lunga migliori. Amoghavajra era nato nell'India settentrionale da una famiglia di brahmani; dopo la morte dei genitori si recò in Cina, dove si convertì al buddhismo tantrico all'età di quindici anni, assumendo il nome cinese Bukong Jingang. Ardente adepto del culto di Mañjuśrī, uno dei più popolari bodhisattva ('colui la cui essenza è conoscenza perfetta'), viaggiò nel Sud dell'India per raccogliere testi buddhisti tantrici e, tornato in Cina, impartì oralmente la sua conoscenza dell'astrologia indiana al discepolo Shiyao, che provvide a metterla per iscritto nel 759. Questa prima traduzione, che riproduceva l'eloquio di Amoghavajra, mantenendo dunque una forte impronta indiana, non era forbita come i trattati cinesi, né presentava un'organizzazione sistematica degli argomenti. Allo scopo di diffondere il libro in Cina, Amoghavajra incaricò uno studioso cinese non buddhista, Yang Jingfeng, di riorganizzare la materia e rivedere la lingua. Successivamente, nel 764, il testo fu considerato come uno dei sūtra (jing) buddhisti attribuiti a Mañjuśrī, mentre Amoghavajra vi appose il proprio nome come 'traduttore'. Alla fine della nuova versione, Yang aggiunse un capitolo intitolato Calcolo del giorno governato dai [sette] astri, che era in effetti un estratto del corrispondente capitolo del Calendario Jiuzhi menzionato sopra.
Dopo il completamento della revisione, la versione originale di Shiyao non fu messa da parte, ma continuò a coesistere accanto all'altra ‒ cosa non insolita tra i buddhisti ‒, causando una certa confusione. Le due traduzioni, risultato di frequenti modifiche, aggiunte e cancellazioni, finirono per essere considerate due parti consecutive di un unico testo, che in questa forma fu incluso nella sezione tantrica del Tripiṭaka, sia nella recensione della dinastia Ming (1368-1644) sia in quella coreana del XIII secolo. È interessante notare che quando nell'806 il testo fu portato in Giappone dal monaco buddhista Konghai (il fondatore della setta Shingon), le due versioni non avevano subito ancora modifiche sostanziali, e in seguito rimasero intatte, continuando a essere usate l'una a fianco dell'altra. Ciò è dimostrato dal fatto che il capitolo aggiunto da Yang, il quale manca nelle recensioni del Tripiṭaka, figura invece come 'settimo capitolo' della prima parte (cioè, la nuova versione di Yang) nei manoscritti antichi giapponesi.
I contenuti del Sūtra delle case e degli astri sono illustrati già dal titolo; i due argomenti principali sono infatti i xiu ('case lunari') e gli yao ('astri'). Come si è detto, la divinazione basata sulla posizione della Luna nelle case appartiene alla tradizione indiana più antica, mentre quella fondata sui pianeti in rapporto ai segni zodiacali e alle dodici posizioni astrologiche rappresenta la nuova fase dell'astrologia arrivata dall'Occidente. In Cina il concetto di una settimana di sette giorni governati dagli astri sembra fosse ancora una novità all'epoca di Amoghavajra, che osserva: "Se all'improvviso vi capitasse di non ricordare il giorno della settimana, è consigliabile chiederlo a un sogdiano, o a un persiano, o alla gente delle cinque Indie" (Taishō shinshu Daizōkyō, II, p. 398). Amoghavajra dà i nomi dei giorni della settimana in tre lingue; quelli sogdiani e sanscriti sono resi foneticamente in caratteri cinesi, mentre quelli persiani sono trascrizioni fonetiche in cinese dei numeri persiani da uno a sette.
Anche i segni zodiacali costituiscono un'innovazione in campo astrologico; il concetto di segno zodiacale era già presente nel Calendario Jiuzhi, ma la lista completa dei nomi è attestata per la prima volta nel Sūtra delle case e degli astri. Quest'ultimo, benché contenga gli elementi essenziali dell'astrologia indiana dell'VIII sec., è un testo tutt'altro che professionale; tra le poche nozioni aggiunte da Amoghavajra agli insegnamenti astrologici delle Gesta di Śārdūlakarṇa (Śārdūlakarṇavadāna) figurano le ventisette case lunari distanziate da intervalli regolari e la descrizione completa della settimana, ma non si fornisce alcun metodo per il calcolo delle posizioni planetarie, né si fa riferimento ai dettagli tecnici dell'astrologia oroscopica. Non sorprende dunque che i lettori cinesi non siano stati attratti da questo testo, che sopravvisse tuttavia tra i buddhisti, incorporato nel canone, fino a esercitare una vasta influenza, soprattutto in Giappone durante il periodo Heian.
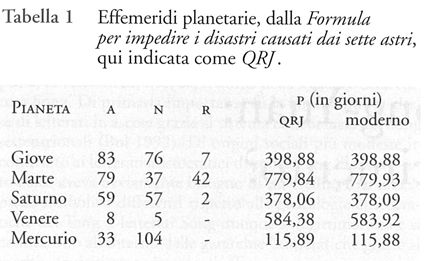
Il testo cinese della Formula per impedire i disastri causati dai sette astri (Qiyao rangzai jue), incluso nella sezione tantrica del Tripiṭaka, è stato scritto intorno all'800 d.C. da un "brahmano dell'India occidentale di nome Jin Juzha", di cui è impossibile ricostruire il nome sanscrito. L'interesse dell'opera consiste nel fatto che contiene una sorta di effemeridi planetarie; ecco un sommario dei suoi contenuti:
a) i metodi per esorcizzare gli dèi dei sette astri, cioè, nell'ordine, il Sole, la Luna, Giove, Marte, Saturno, Venere e Mercurio;
b) una tavola dell'estensione in gradi delle ventotto case lunari, divise in base ai quattro punti cardinali; si tratta della divisione tradizionale cinese, e il totale di 366 gradi è un'approssimazione della lunghezza in giorni di un anno siderale;
c) una tavola delle posizioni astrologiche fauste e infauste per ciascuno dei sette astri; il termine gong, che nel Sūtra delle case e degli astri era usato per i dodici segni zodiacali, è usato qui anche per le dodici posizioni, e la stessa ambiguità si riscontra anche nei testi sanscriti;
d) una tavola delle dodici posizioni astrologiche (corrispondenti al latino domus, 'case', la prima delle quali corrisponde all'ascendente) e dei loro significati;
e) un diagramma della versione in xiu del cosiddetto 'uomo zodiacale' (kālapuruṣa, in sanscrito), in cui le parti del corpo umano sono equiparate alle case lunari, per mostrare la corrispondenza tra macrocosmo e microcosmo;
f) la trascrizione fonetica in cinese di formule sacre (mantra) rivolte ai sette astri;
g) le effemeridi per i cinque pianeti, Rāhu (il nodo ascendente della Luna) e Ketu. In questo testo Ketu è presentato come l'apogeo lunare, anziché come le comete o la coda di Rāhu, significato insolito che fu conservato dagli astrologi buddhisti giapponesi;
h) descrizione nell'ordine delle immagini di Venere, Giove, Mercurio, Marte e Saturno, per consentire ai fedeli di preparare dipinti o statue per il culto;
i) varie combinazioni tra case lunari e pianeti, e gli effetti del giorno della settimana;
l) una tavola della posizione quotidiana del Sole;
m) il rapporto tra i cinque pianeti e le dodici 'posizioni'.
Caratteristica di questo testo è la mescolanza di elementi cinesi, indiani e centroasiatici; il sistema di coordinate basato sulle case lunari è quello dell'astronomia tradizionale cinese, ma sono introdotti nuovi concetti di origine occidentale, quali le dodici posizioni astrologiche. La parte principale del testo è quella menzionata nel punto g), ossia le tavole delle posizioni mensili dei cinque pianeti, nonché di Luohou e Jidu. È da notare che il mese usato come unità temporale non è il mese sinodico (l'intervallo di tempo perché la Luna torni nella medesima posizione relativa rispetto alla Terra e al Sole) bensì quello solare (il periodo di ritorno nella medesima posizione rispetto al Sole), come è caratteristico del calendario indiano, nel quale un anno solare è diviso in dodici 'mesi solari' (sauramāsa) in base all'ingresso del Sole in un nuovo segno zodiacale. Così, ogni effemeride ha dodici righe, ciascuna corrispondente a un mese solare. In ciascuna effemeride, l'inizio del primo mese dell'anno può essere equiparato al cinese yushui, uno dei 24 jieqi ('divisioni solari' o qi nodali), quando la longitudine solare è di 330°. L'epoca delle effemeridi dei cinque pianeti è il decimo anno del periodo Zhenyuan (794), mentre quella di Luohou e di Jidu corrisponde al primo anno del periodo Yuanhe (806).
Ciascuna effemeride consiste di un numero di colonne corrispondente al numero di anni (A) in cui il pianeta compie un numero intero di rotazioni siderali (R), e dunque effettua un numero intero (N) di congiunzioni con il Sole; questi numeri interi sono forniti nel preambolo delle tavole. È da notare che i periodi di 83, 79, 59 e 8 anni, riferiti rispettivamente a Giove, Marte, Saturno e Venere, indicati nella Formula per impedire i disastri causati dai sette astri, si trovano anche nei pronostici mesopotamici (Neugebauer 1975). è possibile così calcolare il periodo sinodico (P) dividendo A per N, e confrontare i risultati con il periodo moderno, come mostra la tab. 1. I periodi sinodici dei cinque pianeti sono prossimi a quelli attestati nel Calendario Wuji (Wuji li), ufficialmente usato in Cina dal 762 al 783.
Come il Sūtra delle case e degli astri, anche la Formula per impedire i disastri causati dai sette astri non suscitò molto interesse tra i lettori cinesi e andò quindi perduta in Cina, tuttavia, dopo essere stata portata in Giappone da un monaco buddhista, fu usata dagli astrologi buddhisti come strumento per ottenere le posizioni planetarie.
Un altro testo collegato alla Formula per impedire i disastri causati dai sette astri e accomunato da uno stesso destino fu il Calendario Futian (Futian li), di origine centroasiatica. Anche quest'opera andò perduta in Cina, ma si salvò perché fu portata in Giappone e usata dagli astrologi buddhisti per calcolare le posizioni planetarie necessarie ai loro oroscopi.
Bibliografia
Chao Huashan 1978: Chao Huashan, Discovery of a grave of the T'ang dynasty astronomer Jutan xuan, "Wen wu", 1978, pp. 49-53.
Hayashi 1997: Hayashi, Takao, Āryabhata's rule and table for sine-differences, "Historia mathematica", 24, 1997, pp. 396-406.
Nakayama 1964: Nakayama, Shigeru, The significance of the Fut'ien li, on the history of astronomy, "Kagakushikenkyu", 71, 1964, pp. 120-123.
Neugebauer 1975: Neugebauer, Otto, A history of ancient mathematical astronomy, Berlin, Springer, 1975, 3 v.
Yabuuti 1979: Yabuuti, Kiyoshi, Researches on the Chiu-chih li Indian astronomy under the T'ang dynasty, "Acta asiatica", 36, 1979, pp. 7-48.
Yano 1979: Yano, Michio, The Chiu chih-li and the Ardharatrika-paksa, "Journal of Indian and Buddhist studies", 27, 2, 1979, pp. 953-956.
‒ 1986: Yano, Michio, The Ch'iyao jang-tsai-chueh and its ephemerides, "Centaurus", 1986, pp. 28-35.
‒ 1987: Yano, Michio, The Hsiu-yao Ching and its Sanskrit sources, in: History of oriental astronomy, edited by G. Swarup, Cambridge, Cambridge University Press, 1987, pp. 125-134.
‒ 1990: Yano, Michio, Ptolemy in China, in: Documents et archives provenant de l'Asie centrale, Actes du colloque franco-japonais, Kyōto International Conference Hall à l'Université de Ryukoku, 4-8 octobre 1988, Kyōto, Association Franco-Japonaise des Études Orientales, 1990, pp. 217-220.
‒ 1995: Yano, Michio, A planetary ephemeris in Japanese Buddhist astrology. A case of transmission, in: East Asian science. Tradition and beyond, edited by Hashimoto Keizo, Catherine Jami and Lowell Skar, Osaka, Kansai University Press, 1995.
Zysk 1991: Zysk, Kenneth G., Asceticism and healing in ancient India. Medicine in the Buddhist monastery, New York, Oxford University Press, 1991.