La scienza in Cina: dai Qin-Han ai Tang. La matematica
La scienza in Cina: dai Qin-Han ai Tang. La matematica
La matematica
Le bacchette
di Alexei Volkov
Il sistema di numerazione cinese, sistema decimale e principio posizionale
Il sistema di numerazione cinese era essenzialmente decimale; vi erano anche due serie di segni per un ciclo sessagesimale usato nella compilazione del calendario, i quali tuttavia non furono mai utilizzati per rappresentare numeri, sebbene talvolta potessero servire per il conteggio di oggetti o di persone; questi segni furono adoperati più tardi, nei testi matematici influenzati dall'Occidente, per denotare elementi (in particolare punti) nelle figure geometriche.
Nei primi documenti della storia cinese ‒ cioè nelle iscrizioni su ossa animali o gusci di tartaruga dei secc. XIV-XI a.C. ‒ i numeri naturali da 1 a 9 erano già rappresentati ciascuno da un segno particolare (cifra); per numeri maggiori di 9 si ricorreva a combinazioni delle cifre con termini che indicavano le potenze di 10: shi, dieci; bai, cento; qian, mille; wan, diecimila. Per collegare questi termini occasionalmente si usava anche la parola ausiliaria you (che significa 'anche', 'e'); per esempio, il numero 56.789 si leggeva (traslitterato in dialetto mandarino moderno) wuwan [you] liuqian [you] qibai [you] bashi [you] jiu, cioè 'cinque-[volte-]diecimila [e] sei-[volte]mille [e] sette-[volte-]cento [e] otto-[volte-]dieci [e] nove'. I numeri del tipo sette-[volte-]cento e simili si rappresentavano graficamente con un singolo ideogramma che combinava la potenza di 10 che interessava (qui 100) con il moltiplicatore (qui 7); questa circostanza permette di considerare il modo di rappresentazione dei numeri che ne risulta come una forma embrionale di notazione posizionale (uno stesso simbolo ha valore diverso se scritto in una particolare posizione rispetto agli altri). I numeri 20, 30 e 40 erano indicati con 2, 3 e 4 tratti verticali, uniti insieme, ognuno dei quali rappresenta il numero 10.
La combinazione delle nove cifre con i quattro termini per le quattro prime potenze di 10 (da 10=101 a 10.000=104) permetteva di esprimere numeri naturali relativamente grandi; il numero più grande che è stato trovato nelle iscrizioni è 30.000. Per quanto riguarda i numeri ancora più grandi, già alla fine del I millennio a.C. si usavano termini per potenze di 10 maggiori della quarta. Nelle Memorie sui metodi di numerazione (Shushu jiyi) di Xu Yue (attivo attorno al 220 ca.), uno dei dieci canoni della matematica cinese, sono descritti un insieme di dieci termini per tali potenze (il primo di essi è yi, l'ultimo è zai) e tre diversi metodi per assegnare a essi valori numerici; si tratta quindi di tre differenti sistemi di notazione numerica. Per le frazioni decimali, ossia le frazioni che hanno per denominatore una potenza di 10 (1/10, 1/100 e così via) si usavano nomi di unità di misura decimali.
La notazione standard per i numeri della Cina antica risale alla fine del I millennio a.C. Gli elementi grafici per le cifre decimali erano scritti separatamente dai caratteri che indicavano le potenze di 10; a volte potevano essere usate forme arcaiche per i numeri 20 o 30. La presenza di termini particolari per le potenze di 10 indica che non si è ancora in presenza di una notazione posizionale vera e propria. Non esisteva nemmeno un segno per lo zero; tuttavia, a partire dall'VIII sec. d.C., se non prima, fu introdotta in Cina la notazione indiana la quale usava punti per le posizioni vuote nella moltiplicazione e nella divisione.
La rappresentazione dei numeri con le bacchette e, più tardi, con l'abaco ‒ i due più antichi strumenti di calcolo tradizionali cinesi ‒ incorporava invece il principio base del sistema di numerazione posizionale decimale, secondo il quale a ogni numero corrispondeva il disporre un certo numero di bacchette in certe posizioni su una superficie di calcolo (v. oltre), le quali indicavano l'ordine di grandezza del numero, ossia se relativo a unità, a decine, ecc. o a decimi, centesimi, e così via (v. oltre); qualcosa di simile, ma mediante palline che potevano scorrere lungo asticciole 'di posizione', avveniva nell'abaco. I disegni o le immagini a stampa dei numeri rappresentati con le bacchette sono spesso considerati i primi esempi di questo genere di notazione decimale in Cina, anche se, a rigore, non si tratta di una notazione numerica indipendente.
Lo zero era indicato da una 'posizione' vuota nel caso delle bacchette e da una disposizione particolare delle palline nel caso dell'abaco. Si pensa generalmente che il simbolo rotondo per lo zero sia apparso in Cina nel trattato Scritti sui numeri in nove capitoli (Shushu jiuzhang, 1247) di Qin Jiushao (1202-1261 ca.); in questo testo, però, esso indica soltanto alcune posizioni vuote corrispondenti ai termini nulli di un'equazione, termini cioè nei quali lo zero è necessario per evitare confusione. Meno noto è il fatto che, come ha messo in evidenza Yan Dunjie (1947), il simbolo rotondo per lo zero è presente in alcuni testi matematici in calendari risalenti al XII secolo. Osserviamo incidentalmente che, poiché nella notazione con le bacchette presente nei manoscritti ritrovati a Dunhuang precedenti il X sec. non si trova alcun particolare simbolo per lo zero, si può supporre che tale simbolo scritto sia apparso in Cina non molto prima del XII sec., anche se le basi concettuali erano state poste già da tempo.
I primi riferimenti alle bacchette
La descrizione più antica e dettagliata delle bacchette si trova nel capitolo intitolato Trattato sui tubi sonori e sul calendario (Lüli zhi) dell'opera Storia della dinastia Han [anteriore] (Hanshu), scritta da Ban Gu (32-92 d.C.), anche se la maggior parte del capitolo in questione va attribuita ‒ come suggeriscono anche le considerazioni introduttive dello stesso Ban Gu‒ a Liu Xin (m. 23 d.C.), autore del Calendario Santong (Santong li).
Nei testi più antichi si parla di strumenti chiamati ce, suan, chou, chousuan, chouce, e suanchou, che molti studiosi moderni considerano identici alle bacchette per il calcolo; queste sono dette comunemente suanzi a partire dalla dinastia Song (960-1279). Il termine suan ha senza dubbio il significato di bacchette sia nella Storia della dinastia Han [anteriore] e nei Nove capitoli, sia nel commentario di Liu Hui (III sec. d.C.) a quest'ultima opera. Nei Nove capitoli, nello Gnomone dei Zhou (Zhoubi) e nel trattato filosofico intitolato Libro del Maestro dello Huainan (Huainanzi, 139 a.C. ca.), si trova il termine zhi ('disporre [il numero mediante le bacchette]') invece di suan; tuttavia nell'ultimo dei trattati elencati le bacchette sono menzionate esplicitamente, mentre in altri testi di questo periodo compare il termine zhi ma non il termine suan. Il termine zhi è usato anche nel più antico trattato matematico a noi pervenuto, il Libro dei procedimenti matematici (Suanshu shu), nelle numerose descrizioni di algoritmi, pensati molto probabilmente per le bacchette, come d'altra parte suggerisce la presenza del termine suan nel titolo originale.
L'elenco fornito da Joseph Needham dei testi cinesi antichi che menzionano le bacchette contiene riferimenti riguardanti scopi diversi dai calcoli matematici ‒ per esempio, per pianificare campagne militari ‒ e il termine suan non si riferisce sempre alle bacchette per il calcolo, così come erano descritte nella Storia della dinastia Han [anteriore] e usate secondo i modi consueti (Needham 1959). Il capitolo Cerimonia [della gara] con l'arco nel distretto (Xiang she li) del Cerimoniale (Yili), un classico del confucianesimo che tradizionalmente si considera scritto prima della dinastia Qin (221-206 a.C.) ed edito tra il I sec. a.C. e il I sec. d.C., menziona l'uso di bastoncini (suan) senza precisarne meglio l'aspetto. Dal testo si deduce che questi bastoncini erano usati per tenere il conto dei colpi andati a segno nel corso di una gara di tiro con l'arco e mai per rappresentare numeri su una superficie di calcolo. L'appendice al capitolo intitolata Note (Ji), compilata dopo che era stato scritto il testo principale, non menziona i bastoncini chiamandoli suan, bensì li definisce 'bastoncini-freccia' (jianchou), e spiega che ve n'erano 80, che un jianchou era lungo 1 chi (23 cm ca.) e aveva una 'impugnatura' senza la corteccia oppure 'senza colore' (wuse); probabilmente quando furono scritte le Note, la parola suan indicava, ormai comunemente, le bacchette solitamente utilizzate per il calcolo descritte nella Storia della dinastia Han [anteriore], e questo spiegherebbe il cambiamento di nome.
Un possibile riferimento all'uso delle bacchette in un periodo precedente si trova in un passo del Commentario di Zuo alle 'Primavere e autunni' (Zuozhuan, o Zuoshizhuan), compilato nel V-IV sec. a.C. ed edito durante la dinastia Han (206 a.C.-220 d.C.), che fa riferimento all'anno 542 a.C.; si parla infatti dell'interpretazione di un certo carattere cinese come la combinazione del numerale 2 e di tre numerali 6, rappresentati in una forma del tipo di quelle in cui si adoperano le bacchette, anche se la forma arcaica del carattere in questione potrebbe essere considerata la combinazione di forme scritte dei numerali per 2 e per 6; inoltre, se i 6 fossero davvero scritti nella forma del calcolo con le bacchette, come suggeriscono gli autori, il principio fondamentale dell'alternanza dell'orientamento delle bacchette nelle posizioni decimali pari e dispari (v. oltre) sarebbe apertamente negato.
Il passo più frequentemente citato a proposito dell'antica origine del calcolo con le bacchette è una frase del Libro della Via e della Virtù (Daode jing; le versioni a noi pervenute risalgono a non prima del III sec. a.C.): "shan shu bu yong chou ce" (Daode jing, 27), tradizionalmente interpretata come "un buon matematico non usa bastoni né pezzi di bambù". Si è ritenuto che questa frase potesse riferirsi alle bacchette ('un buon matematico non usa le bacchette'), ma l'ipotesi che chou e ce si riferiscano alle bacchette in realtà si basa sul significato moderno del termine shu ('numero', 'il contare') e, cosa ancora più importante, sulla tesi, ancora tutta da dimostrare, che l'uso delle bacchette risalga a una remota Antichità. Questa tesi era già stata adottata da Liu Hui, che in uno dei commenti ai Nove capitoli cita, cinque secoli dopo, il Libro della Via e della Virtù in un contesto puramente matematico (cambiando ce in suan) e usa inoltre in un'occasione il termine ce con riferimento alle bacchette. La frase del Classico taoista sembra essere interpretata allo stesso modo nel commentario alle Memorie sui metodi di numerazione (Shushu jiyi) di Xu Yue scritto da Zhen Luan (VI sec.), il quale usa però i termini suanchou invece di chouce.
La parola shu nel contesto del trattato taoista poteva invece avere un significato più ampio, riferendosi sia all'atto del 'contare/calcolare' (in senso molto lato) sia alla 'divinazione'. La frase del trattato poteva quindi riferirsi non esclusivamente a calcoli matematici effettuati con le bacchette, come suppone la maggior parte degli autori moderni, ma anche a forme di conteggio semplici o a pratiche di 'calcolo [del destino]', cioè di divinazione, inclusi casi particolari, come il calcolo per prevedere l'esito di operazioni militari. D'altronde, la parola ce ha anche il significato di 'stratagemma', che ben si addice a indicare operazioni militari; fu proprio uno strumento per pianificare le campagne militari della fine del III sec. a.C. a essere designato con il termine chouce nelle Memorie di uno storico (Shiji) dei primi anni del I sec. a.C., menzionato da Needham. Il contesto generale del Classico taoista non permette di scegliere un'interpretazione piuttosto che un'altra.
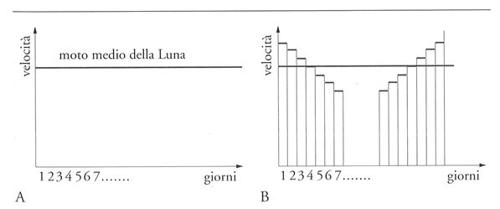
Infine, per quanto riguarda le testimonianze archeologiche a sostegno dell'antichità delle bacchette sono stati spesso citati i numeri ritrovati sulle iscrizioni delle ossa animali e dei gusci di tartaruga dei secc. XIV-XI a.C., o sulle monete dei secc. V-III a.C. Recentemente lo studioso Redouane Djamouri (1994) ha però sostenuto che le più antiche forme grafiche menzionate da Needham non si possono considerare semplicemente numeri, ma piuttosto parti di caratteri cinesi che rappresentano i mesi, e quindi includono necessariamente anche l'elemento che significa 'Luna' (il carattere cinese yue significa sia mese sia Luna).
Un altro studioso, Chen Liangzuo (1978), ha sottolineato che molti problemi riguardanti la scrittura dei numeri sulle monete pre-Qin restano aperti; egli fornisce una tavola con 52 numeri maggiori di 10 trovati sulle monete, 31 dei quali hanno almeno una cifra maggiore di 5, ma soltanto in uno di questi (657) le cifre sono rappresentate come con il sistema delle bacchette (per esempio, per la cifra 6 si ha una combinazione di un tratto orizzontale e uno verticale), mentre in 30 casi le cifre da 5 a 9 sono standard. Chen suggerisce inoltre che le combinazioni di 1+n tratti ortogonali (per n che va da 1 a 4), che solitamente sono state interpretate come le cifre da 6 a 9 nel sistema delle bacchette, potrebbero invece rappresentare i numeri da 11 a 24. La principale differenza tra la rappresentazione dei numeri con il sistema delle bacchette, descritta nei trattati matematici, e quella con le aste delle iscrizioni consiste nel fatto che in quest'ultima le unità sono orizzontali e le decine verticali, mentre nella prima si verifica il contrario.
È quindi assai difficile stabilire se i 'bastoncini' menzionati nei testi più antichi o trovati nel corso di scavi archeologici fossero usati per calcoli matematici, oppure per contare oggetti, per la divinazione o per pratiche magiche e rituali. Si può però affermare che i metodi di rappresentazione dei numeri con le bacchette e i procedimenti per eseguire operazioni aritmetiche siano apparsi, al più tardi, nel III sec. a.C. Inoltre, sempre sulla base dei dati esistenti, non risulta che alla metà del I millennio d.C. fossero già stati definiti, in modo stabile, né la forma, il materiale e le dimensioni dello strumento di calcolo, né i metodi di rappresentazione dei numeri positivi e negativi (colori, sezioni).
La tavola di calcolo: mito o realtà?
I calcoli con le bacchette erano effettuati su una superficie piana, per esempio su un tavolo o per terra; a volte un panno particolare ricopriva la superficie, e di questo panno si fa cenno nel commentario di Liu Hui al problema 18 del cap. 8 dei Nove capitoli. Non sappiamo se su questa superficie fossero effettivamente segnate celle quadrate o rettangolari per indicare le posizioni decimali, o se queste fossero rappresentate soltanto idealmente. Anche se in teoria una qualunque superficie piana poteva andare bene, alcuni storici, quali Li Yan, Needham e Libbrecht, hanno sostenuto che fosse in uso una tavola (di legno) sulla quale erano disegnate le celle. Libbrecht ha ricostruito una tavola affermando che aveva 'la forma di una scacchiera' ed era chiamata suanpan, il termine usato in Cina per l'abaco; tuttavia egli non ha fornito alcuna testimonianza basata su testi originali che dimostri che un tale strumento sia effettivamente esistito.
Oggi la teoria di una tavola di legno sulla quale erano effettuate operazioni aritmetiche è decisamente messa in discussione (Hua Yinchun 1987). A sostegno di questa posizione si è osservato che, poiché la lunghezza delle bacchette riportata dalle fonti storiche era di circa 10 cm, per rappresentare, per esempio, il numero 1.644.866.437.500, che si trova nel problema 24 del cap. 4 dei Nove capitoli, la tavola avrebbe dovuto essere lunga più di un metro; uno strumento così grande non poteva certo non essere ricordato nei lavori di storici e letterati che parlavano di matematica e di astronomia (così come erano menzionate spesso le bacchette), ovvero si dovrebbe trovare raffigurato in ritratti antichi e medievali di matematici, e in questo caso gli archeologi ne avrebbero certamente trovato dei frammenti. Tuttavia, non vi è traccia di un tale strumento nelle fonti cinesi antiche e medievali, né sono stati trovati resti di legno a esso attribuibili (Martzloff 1987), mentre in numerose opere letterarie si parla invece di bacchette disposte su un tavolo, su un letto o per terra. Tutti questi elementi suggeriscono che le 'tavole per calcolare' non siano mai esistite; in realtà, un panno o un foglio di carta (con le celle segnate) poteva risultare molto più comodo da usare, trasportare e riporre. Dal momento che in Giappone si usava un foglio di carta, è lecito supporre che lo stesso avvenisse anche in Cina.
A sostegno della tesi dell'esistenza di una vera e propria tavola di calcolo, Needham (1959) propone l'esempio di una 'tavola per calcolare' ripresa dall'edizione del 1593 delle Origini generali dei metodi matematici (Suanfa tongzong, 1592) di Cheng Dawei (1533-1606). L'illustrazione intitolata Maestro e allievi: domande difficili (Shisheng wennan) mostra un uomo anziano (apparentemente il maestro) e due giovani (gli allievi) intorno a un tavolo sul quale si trova un oggetto rettangolare.
L'incisione è piuttosto scadente, e l'oggetto in questione è una tavola, o un telaio, rettangolare di dimensioni presumibili di circa 50-70 cm, su cui a prima vista sembra essere rappresentata una griglia di 5×10 celle rettangolari; le celle sono però tutte vuote, e non si vedono bacchette, né sulla tavola, né nelle mani dei personaggi, anche se per l'incisore non sarebbe stato difficile riprodurle. Dato che la figura si trova nella prefazione di un trattato dedicato essenzialmente all'introduzione delle operazioni con l'abaco, nel quale non si parla mai in maniera esplicita di bacchette, e che all'epoca della pubblicazione le bacchette con tutta probabilità non erano più in uso, si può effettivamente individuare nell'oggetto riprodotto un abaco.
A confortare questa ipotesi, Li Yan (1945) ha presentato una riproduzione della figura in questione, tratta da una non precisata copia a stampa delle Origini generali dei metodi matematici di Cheng Dawei della dinastia Ming (1368-1644), conservata in Giappone. È molto diversa da quella di Needham, ma porta lo stesso titolo e riproduce anch'essa un maestro con due allievi, uno dei quali tiene in mano un abaco con 11 posizioni decimali (secondo un calcolo fatto da Li Yan). Infine, nel cap. 13 dell'edizione del 1716 del trattato di Cheng Dawei si trova un'altra versione della figura, graficamente vicina a quella della dinastia Ming trovata in Giappone, nella quale uno dei due allievi tiene in mano un abaco con nove posizioni decimali (Suanfa tongzong jiaoshi, p. 804). L'ipotesi più probabile è che la raffigurazione presentata da Needham sia una cattiva riproduzione a stampa del XIX sec. di un abaco.
Un disegno del 1795 mostra un uomo che esegue operazioni con bacchette disposte su una superficie piana (molto probabilmente un foglio di carta) poggiata per terra e sulla quale è una griglia 5×5; come ci si poteva aspettare, le dimensioni della superficie sono piuttosto grandi (60 cm×90 cm, secondo una stima approssimata).
Bacchette e cosmologia
Secondo Liu Xin, un insieme tipo di bacchette comprendeva 271 bacchette, un numero 'figurato' corrispondente a una disposizione delle bacchette nella sezione trasversale della quale si individuano nove strati esagonali più una bacchetta centrale; i numeri coinvolti in tale disposizione, 6 e 9, hanno un ruolo di primo piano nelle considerazioni numerologiche che sono presenti nel capitolo di Liu Xin.
Liu Xin afferma esplicitamente che le bacchette erano usate nei calcoli relativi al calendario. Un'analoga affermazione sull'uso delle bacchette in tale contesto matematico si trova anche nel lemma Bambù [e questioni connesse] (Zhu) del dizionario Spiegazione delle figure e interpretazione dei caratteri (Shuowen jiezi) (121 d.C. ca.): "Le bacchette [in questo testo si adopera un altro termine che indichiamo con suan] sono lunghe 6 cun [13,8 cm ca.] e si usano nei calcoli del calendario. [Suan] è composto dal carattere zhu ['bambù'] e nong ['operare con, manipolare']. Ciò significa: [se si] opera sempre [con questo strumento], allora non si fanno errori" (Shuowen jiezi, p. 198). Queste osservazioni sono importanti perché talvolta è difficile stabilire se le bacchette menzionate in fonti precedenti fossero usate per calcoli matematici, oppure semplicemente per contare, per la divinazione o per altri scopi.
Il più antico riferimento a numeri negativi rappresentati con le bacchette si trova nel commentario di Liu Hui ai Nove capitoli. In riferimento al metodo di risoluzione di sistemi di equazioni lineari che si ritrova in questo Canone della matematica Liu Hui parla di bacchette colorate rosse e nere per rappresentare i coefficienti delle equazioni (rispettivamente, usando sempre la terminologia moderna, coefficienti positivi e negativi). Alcune fonti parlano anche di bacchette nere e bianche usate con tutta probabilità allo stesso scopo (Needham 1959, p. 71), mentre altre affermano che il segno di un numero era rappresentato da bacchette a sezione triangolare (per i numeri positivi) e quadrata (per quelli negativi). L'idea di utilizzare bacchette con sezione diversa è molto antica (un accenno si trova già nel citato commentario di Liu Hui, v. oltre), ma la prima descrizione esplicita è contenuta nel capitolo Trattato sui tubi sonori e sul calendario (Lüli zhi) della Storia della dinastia Sui (Suishu):
I bastoncini [che indicano] '[cose] reali' (zhengce) [cioè le bacchette per i numeri positivi] hanno tre lati; sono in totale 216, [insieme] formano un esagono [se si osserva una sezione trasversale del fascio di bacchette]; sono i contrassegni di qian [cioè del simbolo preso dal Classico dei mutamenti (Yijing), che rappresenta il cielo e il principio cosmico yang]. I contrassegni '[per cose] dovute' (fuce) [le bacchette per numeri negativi] hanno quattro lati, e sono in totale 144 e formano un quadrato; sono i contrassegni di kun [il simbolo che rappresenta la Terra e il principio cosmico yin]. I diametri dell'esagono e del quadrato sono entrambi pari a 12 [unità, cioè bacchette]; è il grande numero del Cielo e della Terra [cioè 12=3×4, dove 3 è il 'numero del Cielo' e 4 il 'numero della Terra']. (Suishu, 2, p. 387, righe 5-6)
Il numero dei lati dei poligoni ottenuti come sezione delle bacchette è così inserito nel quadro della 'cosmologia numerologica': la forma triangolare è associata al 'principio positivo' yang, collegato al cielo, al cerchio e ai numeri dispari (in particolare 3, da cui il triangolo), mentre la forma quadrata è associata al 'principio negativo' yin, collegato alla Terra, al quadrato e ai numeri pari (in particolare 4). Le quantità 216 e 144 bastoncini che si ritrovano in questo passo erano menzionate già nel cosiddetto Grande commentario o Sentenze aggiunte (Dazhuan o Xici) del Classico dei mutamenti, risalente al periodo compreso fra la metà del III e gli inizi del II sec. a.C.
Alcuni autori ritengono inoltre che una bacchetta supplementare posta di traverso sull'ultima cifra del numero indicasse che questo era negativo, oppure che i numeri negativi fossero rappresentati da bacchette in posizione obliqua. Queste interpretazioni nascono probabilmente da un fraintendimento di quanto scrive Liu Hui nel suo commentario ai Nove capitoli: "Le bacchette 'reali' [quelle per i numeri positivi], sono rosse, quelle 'dovute' [per i numeri negativi] sono nere. Se non [si usano bacchette rosse e nere] la distinzione [tra quantità positive e negative] si fa tra bacchette oblique e dritte" (Suanjing shishu, I, p. 225, riga 3). La frase di Liu Hui si riferisce molto probabilmente alle bacchette a sezione triangolare ('obliqua') e quadrata ('dritta') menzionate successivamente, come si è visto, anche nella Storia della dinastia Sui. È vero che un tratto obliquo posto di traverso sull'ultima cifra di un numero indicava il segno negativo nei testi matematici della dinastia Song (960-1279) e in quelli dell'inizio della dinastia Yuan (1279-1368), ma in questo caso si è in presenza soltanto di un metodo di rappresentazione grafica dei numeri positivi e negativi e non si tratta dell'effettiva disposizione delle bacchette. Un altro modo per distinguere coefficienti positivi e negativi era l'uso d'inchiostro rosso e nero, oppure dei caratteri 'reale' (zheng) o 'dovuto' (fu) posti accanto ai numeri.
Il riferimento alla cosmologia numerologica si ritrova nel commentario alle già citate Memorie sui metodi di numerazione di Xu Yue scritto da Zhen Luan, un autore attivo attorno al 560 ca.; egli parla di bacchette di bambù lunghe 4 cun e a sezione quadrata di lato uguale a 3 fen. Il numero 3 era associato alle 'Tre potenze' (Cielo, Terra e Uomo), e il numero 4 alle 'Quattro stagioni' (sishi); analoghe corrispondenze simboliche compaiono nella descrizione di altri strumenti. È interessante notare che le bacchette descritte da Zhen Luan e quelle per i numeri negativi descritte più tardi nella Storia della dinastia Sui sono molto diverse da quelle menzionate nella Storia della dinastia Han [anteriore]; infatti, sono a sezione quadrata, più corte e molto più spesse, e perciò simili alle bacchette giapponesi (sangi), che faranno la loro comparsa molto più tardi. Si può supporre che le bacchette menzionate da Zhen Luan, avendo la stessa sezione (quadrata), dovevano essere di due diversi colori (come quelle giapponesi).
I materiali delle bacchette erano vari, come del resto varie erano forme e dimensioni. Le bacchette descritte da Liu Xin nella Storia della dinastia Han [anteriore] misuravano 6 cun di lunghezza, ossia 13,8 cm (1 cun all'epoca misurava 2,3 cm ca.), e 1 fen, ossia 0,23 cm ca., di diametro (essendo 1 fen pari a un decimo di cun); le bacchette descritte da Zhen Luan erano lunghe 9,24 cm ca. (non è nota tuttavia la data esatta in cui fu terminato il commentario di Zhen Luan: 1 cun misurava 2,4 cm ca. prima del 565 d.C. e 2,7 cm ca. negli anni 565-580), mentre il lato della sezione quadrata misurava 0,7 cm ca. Infine, la Storia della dinastia Sui (Suishu, VII sec. d.C.) menziona bacchette di bambù di 3 cun, ossia 9,0 cm ca. con le misure delle dinastie Sui e Tang; la 'larghezza' delle bacchette (probabilmente si trattava del lato del quadrato o del triangolo equilatero della sezione) era di 2 fen, cioè 0,6 cm ca.
Per quanto riguarda il materiale, oltre al bambù le fonti storiche nominano osso, avorio, ferro e giada. Recentemente sono stati trovati, in tombe dei secc. II-I a.C., alcuni oggetti considerati come i più antichi esemplari di bacchette per il calcolo, alcuni di bambù, altri di osso.
Rappresentazione dei numeri e operazioni
Come è stato accennato, le operazioni con le bacchette erano effettuate su una superficie piana suddivisa, mediante righe orizzontali e verticali (reali o ideali, v. oltre) in un certo numero di 'celle' o 'posizioni'. Le 'posizioni' su una riga orizzontale potevano corrispondere, per esempio, alle varie posizioni decimali di un numero, in relazione a potenze intere positive di 10, iniziando da quella nulla; a partire da una 'posizione' su una riga riservata alle unità (100=1), la posizione immediatamente a sinistra corrispondeva alle decine (101=10), quella ancora a sinistra alle centinaia (102=100) e così via; le 'posizioni' a destra a partire dalla cella delle unità servivano per le potenze negative di 10, ossia, nell'ordine, 10−1 (=decimi), 10−2 (= centesimi) e così via. Non sappiamo se prima di rappresentare i numeri fosse fissata, in base a considerazioni riguardanti i dati numerici e le operazioni da compiere, la posizione delle unità, assegnando in tal modo provvisoriamente una potenza di 10 a tutte le posizioni sulla riga nel modo dianzi indicato, o se invece le posizioni fossero già definite sulla superficie di calcolo. Questo secondo caso implica, tuttavia, una notevole limitazione delle possibilità dello strumento, dato che i numeri potevano variare di molto, e inoltre molti documenti suggeriscono di sistemare le bacchette su una qualunque superficie piana (su un tavolo, per terra, ecc.) e non su una tavola predisposta, confermando quindi che forse la prima ipotesi è più veritiera.
Il metodo di rappresentare le cifre decimali con le bacchette è descritto nel Canone matematico del Maestro Sun (Sunzi suanjing) e nel Canone matematico di Xiahou Yang (Xiahou Yang suanjing), e anche nel manoscritto di Dunhuang (Pelliot 3349) intitolato Canoni di matematica (Suanjing), un testo che, insieme ad altri due manoscritti di Dunhuang (Stein 19 e Stein 5779), costituisce un trattato precedente al X sec. d.C. il quale ha una prefazione molto simile a quella del citato Canone matematico del Maestro Sun. Secondo tutti questi trattati, le bacchette erano alternativamente poste verticalmente od orizzontalmente a seconda della potenza di 10 che era rappresentata in quella posizione; precisamente, le bacchette per le unità erano verticali, per le decine orizzontali, per le centinaia verticali e così via (quindi verticali per le potenze del tipo 102n, orizzontali per 102n+1, con n intero o nullo). Le cifre da 1 a 5 erano rappresentate da un numero corrispondente di bacchette verticali (od orizzontali, a seconda della parità o meno della posizione decimale), mentre quelle da 6 a 9 avevano le stesse bacchette delle cifre da 1 a 4 rispettivamente, sormontate però da una posta in posizione perpendicolare che rappresentava cinque unità. La posizione per lo zero era lasciata vuota.
La ragione principale per l'alternanza verticale-orizzontale sembra essere stata quella di evitare ogni possibile confusione tra le bacchette di due posizioni decimali contigue. Se tutte le cifre fossero state rappresentate verticalmente, sarebbe stato facile confondere, per esempio (indichiamo fra parentesi la rappresentazione del numero mediante bacchette), il numero 12 (| ||) con il numero 3 (|||), mentre alternando non vi era possibilità di confusione: 12 (-||) e 3 (|||). Tuttavia, questa alternanza forse sarebbe stata superflua se la superficie di calcolo avesse avuto già le celle; si può supporre quindi che questo sistema fosse collegato invece alle nozioni stesse di 'orizzontale' e 'verticale' della cosmologia simbolica, e fossero quindi poste in corrispondenza con Terra e Cielo, e in definitiva con yin-yang, le due forze primarie opposte e complementari. Una testimonianza di questo particolare significato dell'orientamento relativamente alle bacchette usate nella divinazione si trova in un testo del VI sec. d.C., il Compendio delle Cinque fasi (Wuxing dayi): le bacchette che rappresentano i Tronchi celesti (tiangan) sono poste verticalmente, mentre quelle che simboleggiano la categoria complementare, cioè quella dei Rami terrestri (dizhi), sono orizzontali. Anche se il Compendio fu compilato relativamente tardi, il principio della disposizione delle bacchette divinatorie risale certamente a un'epoca molto precedente; l'alternanza verticale-orizzontale avrebbe quindi seguito, in origine, lo schema simbolico generale e non sarebbe stata motivata da uno scopo puramente pratico.
Nonostante la semplicità del sistema, con le bacchette si potevano rappresentare numeri piuttosto grandi; un semplice calcolo mostra che con l'insieme tipo di 271 bacchette menzionato nella Storia della dinastia Han [anteriore] si poteva rappresentare un qualunque numero naturale da 1 a 25…5…54 (in questo ultimo numero la cifra 5 si ripete 53 volte). È vero che per rappresentare quest'ultimo numero con bacchette da 4 cun sarebbe stata necessaria una tavola lunga più di 5 metri, ma è storicamente accertato che i matematici cinesi operavano effettivamente con numeri molto grandi, come dimostra il calcolo delle possibili configurazioni del gioco del go (weiqi in cinese) effettuato da Shen Gua (1031-1095). Questi aveva calcolato 3361 configurazioni (affermando in modo errato che erano ca. 10208), un numero che non può essere rappresentato usando le 271 bacchette della dinastia Han; esso richiede infatti 486 bacchette per le 173 cifre nella notazione decimale.
I testi matematici degli inizi del I millennio d.C. che ci sono pervenuti contengono algoritmi per varie operazioni da eseguire con le bacchette. Nel Canone matematico del Maestro Sun e nel Canone matematico di Xiahou Yang sono descritti algoritmi per due delle quattro operazioni fondamentali, ossia la moltiplicazione e la divisione tra numeri interi (Tav. II).
Le restrizioni che il numero delle bacchette a disposizione e le dimensioni della tavola imponevano, come pure il gran numero di operazioni intermedie che intervengono anche in operazioni semplici come la moltiplicazione e la divisione, stimolarono la ricerca di algoritmi più semplici e rapidi. Nei trattati di matematica, fin dal Canone matematico di Xiahou Yang, si citano numerosi metodi di 'calcolo più rapido'. Poiché in alcuni di questi metodi i due numeri con i quali si operava potevano essere posti sulla stessa riga, con qualche leggera modifica essi furono adottati per i calcoli con l'abaco.
Nei Nove capitoli (v. par. 2) sono descritti algoritmi per le operazioni aritmetiche con frazioni, per le estrazioni di radici quadrate e cubiche e per la risoluzione di sistemi di equazioni lineari (un algoritmo valido in generale, con esempi sino a cinque incognite). Quest'opera mostra inoltre che un procedimento di risoluzione numerica delle equazioni di secondo grado del tipo x2+ax=b (con a,b>0), basato su una modificazione del procedimento di estrazione di radice, era stato elaborato fin dal I sec. d.C.
Dai calcoli aritmetici all'algebra simbolica
L'idea fondamentale del rapporto tra posizione e valore che si esprime nella notazione con le bacchette fu in seguito generalizzata e utilizzata nella rappresentazione di equazioni di grado superiore. Autori del XIII e XIV sec., quali Qin Jiushao (1202-1261 ca.), Li Zhi (noto anche come Li Ye, 1192-1279 ca.), Yang Hui (XIII sec.) e Zhu Shijie (XIII-XIV sec.) si servivano nei loro lavori di un algoritmo per la risoluzione numerica di equazioni di grado superiore che faceva uso delle bacchette. Alla sua formulazione potrebbero aver contribuito Jia Xian (attivo intorno al 1050 ca.) e altri autori del periodo compreso fra la fine del I e l'inizio del II millennio, le cui opere sono andate perdute. Da un punto di vista moderno esso è simile al cosiddetto metodo di Ruffini-Horner; i polinomi coinvolti nelle equazioni sono rappresentati dalle colonne dei loro coefficienti mediante le bacchette. L'algoritmo si avvicina concettualmente al procedimento di estrazione delle radici quadrate e cubiche trovato già all'epoca dei Nove capitoli, ma il metodo degli autori dei secc. XIII e XIV non fa uso dello sviluppo del binomio.
Il sistema di calcolo con le bacchette e la sua generalizzazione nella rappresentazione di equazioni di grado superiore diede origine a una sorta di algebra simbolica nella quale si operava con polinomi in più variabili, rappresentati disponendo i coefficienti in un quadro bidimensionale. Alla base dell'algebra cinese medievale vi era il principio classico dell'esistenza di una relazione (esponenziale) tra le posizioni ordinate linearmente sulla superficie di calcolo e le potenze successive di un dato numero. Il sistema posizionale delle bacchette (il numero in questo caso è la base 10), come pure la rappresentazione di equazioni di grado superiore (dove al posto del numero vi è un'incognita), si basano sullo stesso principio. La superficie di calcolo e le bacchette divennero così uno strumento utilissimo non soltanto per effettuare calcoli numerici, ma anche per un'algebra di tipo quasi simbolico.
Dalle bacchette all'abaco
Il calcolo con le bacchette, che nella sua forma classica risale al più tardi al III sec. a.C., fornì ai matematici cinesi un potente mezzo di espressione che permise loro di affrontare la serie (potenzialmente infinita) delle potenze positive e negative di 10, e più tardi potenze di variabili (nel caso di polinomi) o d'incognite (nel caso di equazioni). Tale metodo svolse quindi un ruolo cruciale nello sviluppo della matematica in Cina; in particolare, le bacchette, insieme alla loro raffigurazione, resero possibile la rappresentazione di oggetti matematici a struttura bidimensionale, quali le operazioni con le frazioni costituite da coppie di numeri naturali, la risoluzione di sistemi di equazioni con un numero qualunque d'incognite, l'estrazione di radici e la risoluzione di equazioni di grado elevato; l'insieme di questi due aspetti permise di sviluppare non più tardi del XIII sec. metodi per la risoluzione di sistemi di equazioni non lineari fino a quattro incognite.
La notazione algebrica che fa uso dell'immagine grafica delle bacchette era molto diffusa tra i matematici della dinastia Song meridionale (1127-1279). Nel XIV sec. An Zhizhai nelle Spiegazioni dettagliate dei metodi di matematica (Xiangming suanfa, 1373), Ding Ju nei Metodi matematici di Ding Ju (Ding Ju suanfa, 1355) e Jia Heng nella Raccolta delle massime potenzialità dei metodi di matematica (Suanfa quanneng ji) menzionano ancora il calcolo con le bacchette. Una testimonianza dell'uso delle bacchette nei secc. XIV-XV potrebbe provenire da una figura presente nell'opera Caratteri eterogenei delle 'Quattro parole a coppie' (Kuiben duixiang siyan zazi, 1371) e nella sua riedizione Nuova edizione delle 'Quattro parole a coppie' (Xinbian duixiang siyan, 1436), ma tale conclusione sarebbe affrettata; le bacchette (suanzi) raffigurate in questo manuale per bambini formano infatti una figura di carattere divinatorio, e non una configurazione su una tavola di calcolo. Lo Specchio prezioso della dottrina del calcolo (Suanxue baojian) di Wang Wensu (nato intorno al 1465) menziona ancora il calcolo con le bacchette, ma il libro di Mei Wending (1633-1721) Scritti completi sui calcoli per il calendario (Lisuan quanshu) afferma che alla fine del XVII sec. il calcolo con le bacchette non era più in uso. La scomparsa delle bacchette si può allora datare tra il periodo a cavallo fra il XV e il XVI sec. (seguendo la testimonianza fornita dal libro di Wang Wensu) e la fine del XVII sec. (secondo quanto si ricava da quello di Mei Wending).
La versione 'rapida' delle operazioni matematiche, pensata originariamente per il calcolo con le bacchette (presumibilmente), fu trasferita in seguito ai calcoli con l'abaco. La praticità e la velocità che l'abaco offriva sono spesso considerate la ragione principale per la diffusione di questo strumento tra le diverse categorie di cittadini (mercanti, artigiani, funzionari) e in seguito anche tra i matematici professionisti. Il fatto però che l'abaco abbia finito per sostituire le bacchette non può essere spiegato soltanto con la praticità di effettuare le operazioni aritmetiche più semplici; l'esistenza contemporanea delle bacchette e dell'abaco per molti secoli in Corea, e forse anche nel Vietnam, non ci permette infatti di concludere che la scomparsa del calcolo con le bacchette sia dovuta alla maggiore efficienza dell'abaco (che invece è alquanto limitata); essa va piuttosto attribuita ai profondi cambiamenti che subì la struttura sociale e cognitiva della matematica cinese tradizionale nei secc. XIV-XVI.
I 'Nove capitoli sui procedimenti matematici': la costituzione di un canone nella matematica
di Karine Chemla
Un libro con un destino singolare
L'opera i Nove capitoli sui procedimenti matematici (Jiuzhang suanshu, nel seguito abbreviato in Nove capitoli) è il più antico testo cinese di matematica tramandato dalla tradizione scritta; composto probabilmente tra il I sec. a.C. e il I sec. d.C., il titolo è attestato in un'iscrizione su un recipiente per misure di capacità vistato dal Ciambellano della Tesoreria dello Stato (Dasinong) nel 179 d.C.; si tratta di un'indicazione interessante sulla quale torneremo in seguito.
La ragione principale per la quale i Nove capitoli non sono andati perduti può ben essere il fatto che questo testo divenne un canone (jing) poco dopo essere stato ultimato: 'canone' è il termine usato da Liu Hui, l'autore del primo commento al testo che sia giunto fino a noi. L'opera è stata infatti oggetto di numerosi commenti; due di questi furono scelti dalla tradizione per essere tramandati assieme al testo, e precisamente il commento di Liu Hui, completato nel 263, e quello composto da un gruppo di studiosi, con la supervisione di Li Chunfeng, all'interno della raccolta di Canoni matematici della dinastia Tang (618-907), presentata all'imperatore nel 656. Tutte le edizioni a noi pervenute dei Nove capitoli contengono questi due commenti; analogamente a quanto accadde per la medicina, l'edizione Tang dei Classici di matematica offuscò le versioni precedenti. I commenti di Liu Hui e di Li Chunfeng menzionano le opere di altri studiosi ‒ Zhang Heng (78-142), Zu Chongzhi (429-500) e il figlio Zu Geng ‒, attestando una tradizione di ricerca sugli argomenti trattati nei Nove capitoli che è confermata da testimonianze storiche.
Con la dinastia Song si assiste a una ripresa d'interesse per i Nove capitoli. Il Dipartimento della Biblioteca imperiale (Mishu sheng) lo stampò nel 1084; la ristampa di questa edizione, curata da Bao Huanzhi, nel 1213, è la più antica edizione dell'opera in nostro possesso. Inoltre, furono composti due nuovi commenti: Procedimenti dettagliati del Canone dell'Imperatore Giallo dei Nove capitoli sulla matematica (Huangdi jiuzhang suanjing xicao) di Jia Xian, nella prima metà dell'XI sec., e Spiegazione dettagliata dei 'Nove capitoli sui metodi matematici' (Xiangjie jiuzhang suanfa) di Yang Hui, nel 1261. In questo periodo lo status dei Nove capitoli come canone fu sistematicamente e risolutamente messo in risalto, come si desume da una delle prefazioni di Yang Hui, nella quale egli afferma, citando la prefazione di Rong Qi al commento di Jia Xian stampato nel 1148: "Quando il governo istituì gli esami di matematica al fine di selezionare i funzionari i Nove capitoli furono scelti come il più importante classico matematico, perché in verità esso è come i Sei classici del confucianesimo, il Canone delle difficoltà (Nanjing) e la Grande semplicità (Taisu) delle Scuole di medicina e il Libro del Maestro Sun dell'arte militare". Il raffronto con i Classici del confucianesimo esprime certamente l'enorme valore che a esso era conferito, e rispecchia anche il fatto che si credeva fosse stato scritto da un mitico imperatore o da un saggio dell'Antichità. Comunque, per tutti i matematici del periodo Song e Yuan i Nove capitoli costituirono una fonte d'ispirazione e un testo di riferimento.
Dato il grande significato di quest'opera per le tradizioni matematiche dall'inizio dell'era volgare fino al periodo aureo Song e Yuan e oltre, essa merita un'analisi approfondita da due punti di vista. Innanzitutto esamineremo il suo contenuto matematico e gli aspetti principali della pratica matematica che rappresenta; entrambi questi elementi determineranno gli interessi e le pratiche della matematica nell'antica Cina. Considereremo poi il testo dal punto di vista dei commenti, allo scopo di capire che cosa significasse considerare il libro un canone ‒ ossia come questa circostanza ebbe un influsso sulle aspettative nel confronto del libro e sulla lettura di esso ‒ e scoprire quali attività di carattere matematico furono sviluppate per condurre l'esegesi dell'opera.
La struttura dei Nove capitoli
Cominciamo con una rapida rassegna in merito alla struttura del libro, il quale consta principalmente di problemi, delle loro soluzioni, nonché degli algoritmi di risoluzione.
Nella Cina antica le conoscenze matematiche erano esposte essenzialmente sotto forma di algoritmi; ciò riflette l'importanza che i matematici hanno sempre dato proprio agli algoritmi. Contrariamente ai commenti che furono stesi successivamente, nei Nove capitoli non vi è alcun riferimento ad ausili visivi, anche se la descrizione degli algoritmi fa spesso riferimento a una superficie ‒ come si è detto, in molti casi si trattava probabilmente di una qualunque superficie piana orizzontale ‒ per eseguire i calcoli descritti, sulla quale i numeri erano rappresentati da bacchette. Tuttavia, soltanto molto più tardi, nelle opere delle dinastie Song e Yuan, i vari stadi del procedimento di risoluzione e le disposizioni successive delle bacchette sulla superficie di calcolo cominciarono a essere rappresentati nei testi. Il modo in cui gli algoritmi erano eseguiti sulla superficie di calcolo, così come descritto nei Nove capitoli e nelle testimonianze di scrittori più tardi, determinerà in maniera decisiva l'approccio alla matematica e quindi agli algoritmi stessi nell'antica Cina.
Vediamo ora un po' più da vicino i vari elementi contenuti nel testo. Nei problemi presentati nei Nove capitoli si considerano sempre valori particolari relativi alle entità trattate. Per esempio, l'algoritmo per moltiplicare due frazioni fa seguito a un problema che recita: "Supponiamo che qualcuno possegga un campo largo 4/7 di bu e lungo 3/5 di bu (1 bu=6 chi=1,38 m ca.). Si chiede quanto è grande il campo". Così, nell'enunciato di un problema interviene di solito una situazione particolare. Il confronto tra il problema che segue, che richiede una somma di frazioni, e l'esempio precedente mostra che però non è sempre così: "Supponiamo che qualcuno abbia 1/3 e 2/5. Si chiede quanto ottiene unendo ciò che ha". In questo enunciato si fa riferimento a frazioni particolari, ma senza un contesto specifico concreto; infatti, in molti casi i termini di un problema si riferiscono a una situazione astratta, come la precedente. Malgrado ciò, l'aspetto generale dei Nove capitoli ha spinto gli storici a conclusioni spesso affrettate, a considerare cioè quest'opera come una specie di libro di testo per le scuole elementari, concepito per aiutare i lettori a risolvere problemi suggeriti da attività concrete. Occorre invece guardarsi dall'apparenza; infatti, un'analisi più accurata, che tenga conto di come i commentatori hanno utilizzato i problemi nella loro attività matematica, rende possibile capire come nella Cina antica i problemi costituissero un ente matematico sottoposto a una pratica particolare che possiamo e dobbiamo ricostruire.
Oltretutto, un algoritmo può a volte essere proposto indipendentemente da qualsiasi problema; è il caso, per esempio, della regola del tre, che costituisce l'argomento principale del cap. 2 ed è formulata in modo astratto. La descrizione fa intervenire il concetto di lü, che i commentatori riconosceranno più tardi come centrale per la comprensione della matematica. Il termine lü qualifica le due quantità che determinano come convertire, mediante la regola del tre, qualcosa di un certo tipo e della quale si sia in possesso in una di tipo cercato; la qualifica di lü per entrambe le quantità sottolinea il fatto che esse sono definite soltanto una relativamente all'altra, nel senso che esse possono essere moltiplicate o divise per uno stesso numero senza che il significato della coppia venga meno. La regola del tre poggia dunque sulla 'quantità di ciò che si ha' e sulla coppia costituita dal 'lü di ciò che si ha' e dal 'lü di ciò che si cerca' per dare luogo alla 'quantità di ciò che si cerca'. Di nuovo, qui i commenti metteranno in luce l'importanza della nozione e il carattere fondamentale di questo algoritmo astratto.
Ciò ci conduce all'altra componente principale dei Nove capitoli, ossia l'insieme dei procedimenti. L'apparenza della maggior parte dei problemi non deve trarre in inganno, in quanto gli algoritmi di risoluzione sono di carattere generale. Per esempio, per l'addizione di frazioni è descritto il seguente procedimento: "I denominatori moltiplicano i numeratori che non corrispondono a essi; sommare; prendere questo come dividendo (shi). I denominatori moltiplicati fra loro formano il divisore (fa). Dividere […]. Se i denominatori sono uguali si sommano [i numeratori] tra loro direttamente", e cioè (a/b)+(a′/b′)=(ab′+ba′)/bb′. Si osservi come sia chiaro il carattere generale dell'algoritmo; esso permette infatti di sommare quante si vogliano frazioni. I commentatori si aspettano anzi che un algoritmo sia il più generale possibile e che un problema rappresenti una classe di problemi tra loro simili.
Quando un algoritmo nei Nove capitoli non è abbastanza generale, ma utilizza, invece, le condizioni particolari di un problema, vediamo Liu Hui affrontare la questione e fornire un altro algoritmo, generale, che copre una più ampia gamma di problemi dello stesso tipo. Questo è uno tra i tanti esempi che mostra come, malgrado lo status di canone che ha il libro, Liu Hui mantenga un atteggiamento critico verso il contenuto. Non si tratta però solamente di questo, giacché siamo di fronte a una scelta che rappresenta una caratteristica molto più fondamentale della pratica della matematica nella Cina antica, ossia siamo di fronte al fatto che i matematici davano più importanza alla generalità che all'astrazione, e questo è un punto sul quale è opportuno riflettere.
Oltre alle conoscenze di aritmetica e di algebra, anche quelle di geometria prendono la forma di algoritmi. È quello che mostra il procedimento per calcolare l'area di un cerchio: "Moltiplicando metà della circonferenza e metà del diametro tra loro si ottiene il bu del prodotto (l'area)". Occorre notare che questo algoritmo è corretto, ed è con questo enunciato che Liu Hui ne stabilisce la correttezza. Dato che, come sottolinea il commentatore, l'algoritmo in quanto tale non dà luogo a calcoli, se ne conclude che un algoritmo era visto non soltanto come la prescrizione di un calcolo, ma anche come l'espressione di una relazione tra grandezze.
Queste sono le caratteristiche fondamentali dei problemi e degli algoritmi che compongono quest'opera e sono organizzati in nove 'capitoli' (juan). La questione è ora di cogliere la natura dell'attività matematica svolta con questi elementi nell'antica Cina. Poiché nei Nove capitoli non vi sono osservazioni 'di secondo ordine' riguardo ai procedimenti, dobbiamo basarci soltanto sulle descrizioni di questi se vogliamo cogliere alcuni aspetti della pratica particolare rappresentata dagli algoritmi e dalle superfici di calcolo. Soltanto l'esame dei commenti può gettare luce sul modo di trattare i problemi e sul significato dell'organizzazione delle conoscenze in nove parti.
Prima di esaminare la pratica della matematica che ci rivelano i Nove capitoli vogliamo spendere alcune parole sulla composizione del testo così come è storicamente avvenuta. In quanto canone, l'opera non è attribuita ad alcun autore. Nella sua prefazione, Liu Hui cita il contribuito all'edizione di due studiosi, Zhang Cang (250-152 a.C. ca.) e Geng Shouchang (attivo intorno al 50 a.C.), un'indicazione di come molto presto si sia pensato che il processo di costituzione dell'opera fosse durato secoli (e forse Liu Hui ne estendeva ulteriormente la durata). A questo proposito, è interessante ricordare i risultati della ricerca storica recente riguardo al processo di composizione di altri due classici del periodo Han (206 a.C.-220 d.C.). Basandosi sui manoscritti di carattere medico trovati nelle ultime decadi del XX sec. in tombe Han, è stata formulata riguardo alla composizione del Canone interno dell'Imperatore Giallo (Huangdi neijing) l'ipotesi che il testo sia una raccolta di trattati minori precedenti, alcuni dei quali vicini ai manoscritti portati alla luce; ciò ha aperto un campo di ricerca sulla formazione dei canoni, non soltanto nella medicina. Sulla stessa linea, un'analisi di tipo 'internista' ha portato Christopher Cullen (1996) a supporre che un processo analogo di accumulo di vari testi potesse essere responsabile della composizione di un classico Han dedicato alla matematica e all'astronomia, lo Gnomone dei Zhou (Zhoubi, cap. XV). Il ritrovamento, nel 1984, in una tomba anteriore alla fine del II sec. a.C., di un manoscritto matematico, il Libro dei procedimenti matematici (Suanshu shu) ‒ il più antico testo matematico cinese a noi pervenuto (e di cui non si trova traccia nella tradizione scritta) ‒ fece sperare che esso potesse gettare luce sul processo di compilazione dei Nove capitoli; tale speranza però svanì dopo la sua pubblicazione, poiché, anche se esso ha certamente molti aspetti in comune con i Nove capitoli, non può in alcun modo essere considerato né un prototipo di questo né una sua parte. Ancora non sappiamo, perciò, se l'opera i Nove capitoli sia stata composta secondo un procedimento analogo a quello degli altri testi citati. Comunque, il manoscritto del Libro dei procedimenti matematici fornisce interessanti indicazioni sui gruppi sociali che possono aver preso parte alla produzione delle conoscenze registrate nei Nove capitoli.
Se consideriamo tale questione dapprima da una prospettiva interna al testo, vediamo che le situazioni in gioco nei problemi raccolti nei Nove capitoli rinviano sistematicamente a problemi concreti che la burocrazia della dinastia Han doveva affrontare, e precisamente a problemi per i quali era responsabile il Ciambellano della Tesoreria dello Stato, come la paga dei 'dipendenti pubblici', la gestione dei granai e delle opere civili e della definizione degli standard di misura per il grano. Come abbiamo ricordato, il primo documento che riporta il titolo dell'opera è proprio un'iscrizione su un recipiente che costituiva una misura campione di capacità stabilita dall'amministrazione; i volumi di queste misure per il grano suscitarono l'interesse dei matematici per secoli (Volkov 1995). Il sesto dei Nove capitoli ha lo stesso nome di una regola per un'equa imposizione dei tributi sostenuta effettivamente da un Ciambellano della Tesoreria dello Stato, Sang Hongyang (152-80 a.C.); nel capitolo citato si fornivano le tecniche matematiche necessarie. Questi rimandi tra i compiti di particolari settori della burocrazia e alcuni problemi matematici sono in accordo con il fatto che molti studiosi noti nell'epoca Han per la loro abilità matematica sono anche ricordati per aver lavorato, in un periodo della loro vita, per l'amministrazione dello Stato; tra questi, Geng Shouchang citato da Liu Hui per il contributo ai Nove capitoli e Zhang Cang, il quale si occupò anch'egli di contabilità e finanza ad alti livelli dell'amministrazione. Il Libro dei procedimenti matematici ha permesso di chiarire ulteriormente la questione, poiché esso era certamente usato da questi funzionari.
Apparentemente, quindi, la matematica si è sviluppata in Cina nell'epoca Han in rapporto con l'amministrazione responsabile delle questioni economiche (Chemla 1997a). Bisogna tuttavia fare attenzione a non guardare alle questioni storiografiche senza considerare anche il contesto. Infatti, alcuni problemi dei Nove capitoli che oggi saremmo tentati di definire 'ricreativi' erano invece considerati da studiosi più tardi, quali il matematico Wang Xiaotong (VII sec.), come attinenti a questioni astronomiche; questi esperti coglievano quindi nel libro il riflesso di un'interazione tra astronomia e matematica, a lungo considerata cruciale per il modo in cui quest'ultima si era sviluppata in Cina. Le fonti ci dicono inoltre che sia Zhang Cang sia Geng Shouchang si occuparono di astronomia. Se ora si confronta il contenuto dei Nove capitoli con lo Gnomone dei Zhou e altri scritti di astronomia, si osserva che le parti dei Nove capitoli che non si trovano nel Libro dei procedimenti matematici hanno lo stesso punto di partenza dei procedimenti utilizzati in attività astronomiche, e cioè estrazioni di radici e questioni relative a proprietà del triangolo rettangolo. Tutto ciò potrebbe indicare che, essenzialmente, la matematica esposta nei Nove capitoli unificava in un unico corpus di conoscenze elementi che si erano sviluppati nei due principali campi di attività dell'amministrazione statale, ossia l'astronomia e la finanza.
Esaminiamo ora la pratica matematica degli algoritmi così come è possibile desumerla dai Nove capitoli. Vedremo che l'uso concreto della matematica non ne preclude sviluppi teorici sulla base dei procedimenti stessi.
La superficie di calcolo e la natura algoritmica della matematica in Cina
L'algoritmo sviluppato nel cap. 8 dei Nove capitoli (Misure in un quadrato) per un sistema di n equazioni lineari in n incognite poggia su un'organizzazione precisa dei coefficienti, all'interno di una tavola sulla superficie di calcolo, dove si eseguono le procedure (tale algoritmo corrisponde a quello che oggi va sotto il nome di 'metodo di eliminazione di Gauss').
Più in generale, la disposizione delle varie posizioni sulla superficie obbedisce a regole molto precise basate principalmente sull'uso di assi orizzontali e verticali per spiegare tutte le notazioni (Chemla 1996a), e ciò ha condizionato lo sviluppo di un particolare tipo di ricerca sugli algoritmi stessi che cercheremo di capire più avanti. La rappresentazione di un sistema di equazioni fa intervenire una notazione posizionale analoga a quella del sistema decimale di numerazione; le incognite sono infatti rappresentate da posizioni, e quindi un numero (rappresentato dalle bacchette) posto sulla superficie acquista il significato di coefficiente in base alla posizione che occupa. L'utilizzazione di notazioni posizionali per rappresentare vari tipi di oggetti matematici nel lungo arco di tempo che va dall'inizio dell'era volgare agli inizi del XIV sec. è una particolarità della tradizione matematica cinese che non si trova in altre antiche tradizioni. Osservando come erano gestite le posizioni sulla superficie di calcolo e come era svolta la ricerca sugli algoritmi, in altre parole, descrivendo le caratteristiche della pratica matematica nell'antica Cina, possiamo sperare di capire perché questa proprietà posizionale ricorre in molte notazioni.
Ciò che in termini moderni è descritto come un'eliminazione di equazioni diventa sulla superficie di calcolo un'eliminazione di colonne; ne segue che la corretta disposizione dei coefficienti sulla superficie è quindi un requisito chiave per un uso corretto del procedimento. L'algoritmo opera uniformemente, ripetendo la stessa operazione sulle varie posizioni di una colonna o su diverse colonne, una proprietà che ricorda gli algoritmi dell'aritmetica elementare che ripetono la stessa operazione su ogni cifra del numero su cui si applicano (per es., v. Tav. II). L'uniformità nel funzionamento di un algoritmo è una proprietà tenuta in gran conto dai matematici dell'antica Cina, e rappresenta per gli algoritmi ciò che per le notazioni è il modello posizionale. Inoltre l'algoritmo è generale, poiché può essere applicato ‒ e nel citato cap. 8 dei Nove capitoli lo è ‒ a un sistema a un numero qualunque di equazioni, e le dimensioni della superficie guidano l'applicazione a un qualunque numero di equazioni. La sua potenziale generalità è svelata passo dopo passo nel corso del capitolo.
L'eliminazione di colonne richiede che vi siano posizioni vuote ‒ coefficienti uguali a zero, se si vuole ‒ che entrano nel calcolo; richiede anche che siano introdotti numeri positivi e negativi, e che con essi si proceda nel calcolo. Nei Nove capitoli sono introdotti, per la prima volta nel corso dei calcoli, numeri negativi per effettuare l'eliminazione e completare l'algoritmo in alcuni casi particolari: ciò costituisce una prima estensione della sua applicabilità. Nei problemi immediatamente seguenti intervengono coefficienti positivi e negativi, estendendo così il numero dei sistemi che possono essere presi in considerazione e risolti dallo stesso algoritmo. Il procedimento, descritto una prima volta per equazioni aventi soltanto coefficienti positivi, è così esteso una seconda volta, accrescendone la generalità.
Questi numeri positivi e negativi vanno però distinti dai numeri come li intendiamo noi oggi. Indipendentemente dal fatto che essi siano introdotti nel corso di un calcolo per completare un algoritmo oppure per rappresentare sistemi più generali, si tratta sempre di contrassegni algoritmici e non di numeri effettivi. La differenza principale sta nel fatto che la soluzione per un sistema non può mai essere zero, né un numero negativo, ma nemmeno un numero positivo, in quanto si tratta soltanto di un numero senza segno; 'positivo' e 'negativo' sono invece contrassegni dati ai numeri sulla superficie per precisare come devono essere effettuate le operazioni fondamentali dell'algoritmo, e resteranno legati a questo contesto per molto tempo (Chemla 1994); se ne affrancheranno infatti solamente nel periodo Song e Yuan per permettere ‒ in modo analogo ‒ l'estensione dell'applicabilità di un algoritmo per la risoluzione di equazioni algebriche. Ciò sottolinea l'interesse, che perdura nei secoli, per l'estensione dell'applicabilità di un dato algoritmo e indica, da un'ulteriore nuova prospettiva, il ruolo centrale che ha l'algoritmo e il valore che è attribuito alla sua generalità. Vedremo più oltre altre manifestazioni di questo fatto.
L'algoritmo che stiamo esaminando mostra un altro aspetto interessante, e precisamente il fatto che, al contrario delle operazioni con carta e penna, i calcoli svolti sulla superficie non permettono di conservare traccia dei passaggi intermedi. Composta di bacchette, la colonna nella quale avviene l'eliminazione scompare ed è sostituita dalla colonna risultante, ed è quest'ultima che interviene nella nuova operazione al posto di quella che è stata sostituita finché non è anch'essa modificata. Ciò implica che l'algoritmo, descritto in termini di eliminazione successiva di colonne, non opera tanto su numeri, quanto su 'posizioni' sulla superficie, il contenuto delle quali cambia lungo tutto il calcolo. Questo significa che la descrizione dell'algoritmo, nella quale compaiono i nomi delle posizioni e mai il valore di ciò che in queste posizioni si trova, utilizza quello che oggi si chiama 'assegnazione di variabili'. Con le posizioni è quindi introdotto un oggetto matematico cruciale per la tradizione che si è sviluppata sulla base dei Nove capitoli.
L'algoritmo come elenco di operazioni: la natura algebrica della pratica algoritmica
I procedimenti che costituiscono il nucleo centrale del cap. 7 (Eccesso e difetto) mostrano proprietà che rivelano una pratica interessante nel trattamento degli algoritmi. Questo capitolo si apre enunciando l'algoritmo denominato 'procedimento per eccesso e per difetto', denominato in Occidente 'regola della doppia falsa posizione', per la risoluzione della maggior parte dei problemi nel capitolo medesimo; un esame di come questi problemi si risolvono mediante l'algoritmo dimostra che non tutti si trovano con questo nella stessa relazione.
Il procedimento consta di tre fasi, indicate come I, II e III, che peraltro non si applicano in tutti i casi; anzi, i problemi che abbiamo definito del 'primo tipo' sono risolti dalla successione di operazioni I+II, mentre per i problemi del 'secondo tipo' opera la successione I+III. In un calcolo concreto su una superficie di calcolo non è possibile infatti applicare la fase III dopo la II; la successione II+III rappresenta dunque un'alternativa: con le quantità calcolate con la fase I si può passare alla II o alla III, a seconda del problema.
Questo fatto si riflette nel modo in cui un problema si collega all'algoritmo. La 'regola della doppia falsa posizione' richiede quattro termini che chiameremo a, a′, b, b′; per i problemi del primo tipo, a e a′ sono ipotesi arbitrarie sulle incognite e b, b′ sono dedotti da queste ultime. Nel secondo tipo di problemi i quattro termini sono invece quantità che esprimono una relazione tra le incognite, costituendo i termini del problema; in tal modo, anche se rispetto ai due problemi i quattro termini hanno un significato completamente diverso, è fornito un unico algoritmo per le due situazioni. Vediamo come ciò sia possibile.
La struttura dell'algoritmo fornisce una parte della risposta. Anche se i problemi sono di natura diversa, le liste delle operazioni da fare per risolverli si possono compilare in modo che presentino tutte la stessa successione iniziale di calcoli da eseguire (fase I); poi, a seconda del problema da risolvere, si sceglie il primo o il secondo modo di concludere l'algoritmo. Il significato della fase I varia a seconda del problema; infatti, i calcoli possono essere interpretati (nel primo tipo) come la produzione di nuove ipotesi sulle incognite oppure (nel secondo tipo) come la produzione di nuove relazioni fra le incognite. Ne segue che, malgrado il significato dei calcoli iniziali cambi al variare del problema, la loro identità formale permette di unificarli in un unico algoritmo. Ciò mette in luce il carattere algebrico della pratica algoritmica nell'antica Cina. Inoltre, tale interesse dei matematici dell'antica Cina verso un unico algoritmo è tanto più interessante se si tiene conto del fatto che in questo caso i procedimenti non possono essere identificati, in quanto le sezioni finali nei due casi sono assolutamente diverse. Per la scrittura dell'algoritmo, i Nove capitoli si servono di un 'condizionale'. Per produrre un testo che unisse le procedure per i problemi dei due tipi, gli autori dovevano confrontare liste di operazioni come tali, senza tenere conto del loro effettivo significato nel particolare contesto in cui sono effettuate, e riscriverle per mettere in risalto la parte che hanno in comune, base per unificare le procedure in un unico algoritmo. Questa proprietà rivela l'aspetto teorico di questa pratica algoritmica e accresce una volta di più l'interesse nell'estensione del campo di applicazione di una data procedura sottolineando l'importanza attribuita alla generalità.
L'algoritmo come successione di cambiamenti sulle posizioni: la definizione di nuovi oggetti matematici
Consideriamo infine gli algoritmi per l'estrazione di radice, presentati nel cap. 4 (Piccola larghezza), che rappresentano una sintesi di tutti gli aspetti considerati finora e mettono in luce l'originalità propria di questa pratica matematica. Gli algoritmi fanno intervenire il sistema di numerazione posizionale decimale con il quale i numeri sono rappresentati sulla superficie di calcolo e determinano le cifre della radice una alla volta. Vediamo alcune caratteristiche dell'algoritmo per la radice quadrata (Tav. VI); la descrizione è completamente astratta e utilizza costantemente la terminologia della divisione (v. Tav. IIb), determinandosi in questo modo una relazione tra questa operazione e l'estrazione di radice quadrata. Infatti, la radice è designata come 'quoziente' e posta nella riga superiore della superficie, mentre il numero di cui si cerca la radice è detto 'dividendo'(shi) e quindi, analogamente a un dividendo, posto nella riga mediana; il termine 'divisore' (fa) designa una sequenza di numeri che si sostituiscono l'un l'altro nella riga sottostante (torneremo su questo punto più avanti).
Un rapido sguardo alla struttura dell'algoritmo rivela come la descrizione che ne è fatta usi tutte le risorse che abbiamo incontrato. Dopo una prima fase dedicata a determinare la prima cifra ‒ passi da (a) a (d) ‒ si è di fronte a un 'condizionale', ‒ ossia un'alternativa, passo (f) ‒: o si legge il quadro di numeri fin qui ottenuto come un risultato approssimato, o si va avanti e si calcola la cifra successiva. In quest'ultimo caso si seguono i calcoli prescritti fino al successivo 'se' ‒ passo (f′) ‒ dove si è davanti alla stessa alternativa ma con una cifra in più: se si sceglie di calcolare una nuova cifra si è rinviati al passo precedente (f) e si ripetono le operazioni. L'algoritmo è quindi una combinazione di un'iterazione e di due scelte o 'condizionali'. Un'analisi più precisa metterebbe in luce quanto sottile sia la posizione delle alternative nella successione delle operazioni (Chemla 1987, 1994).
Per quanto riguarda l'iterazione tra i passi (f) e (f′), è necessario che i termini usati nella descrizione non indichino numeri specifici, bensì 'posizioni' sulla superficie (quoziente, dividendo, divisore), cioè in altri termini il contenuto di una riga al momento in cui questa entra in gioco nel calcolo. L'uso di un'iterazione implica inoltre una certa omogeneità dell'algoritmo, di nuovo in analogia con l'omogeneità propria del sistema di numerazione posizionale. Anche l'iterazione è collegata alla ricerca della maggior generalità possibile; essa mostra, infatti, come le stesse operazioni si applichino a tutte le cifre successive alla prima. Tutte queste proprietà della descrizione dell'algoritmo richiedevano certamente un lavoro specifico che incideva sulla lista dei calcoli.
Torniamo ora ai termini tecnici della divisione e al loro uso nella descrizione dell'algoritmo per l'estrazione della radice quadrata. Nella riga superiore le cifre della radice sono segnate una dopo l'altra a mano a mano che sono ottenute, come lo sarebbero quelle di un 'quoziente'. Il numero posto nella linea mediana è diminuito ‒ proprio come un 'dividendo' ‒ sottraendo il prodotto tra le cifre della riga superiore e le quantità poste nella riga sottostante.
Per quanto riguarda la riga sotto al 'dividendo', un cosiddetto 'divisore' è aggiornato progressivamente, passi (c), (d), (i) e (j); l'estrazione di radice rientra così nel modello dinamico della divisione. Infatti, se si considerano i movimenti che subisce la posizione del divisore, essa viene dapprima spostata in avanti il più possibile all'inizio del calcolo, poi è progressivamente spostata all'indietro; entra nel calcolo moltiplicandola per la riga superiore, per sottrarre quindi il prodotto dalla riga di mezzo (a tale proposito, si osservi per esempio come il calcolo di A−a2102n sia presentato come un'eliminazione del 'divisore' a102n, corrispondente alla cifra a, dal 'dividendo' A). La posizione sotto il 'dividendo' riproduce in questo modo il comportamento di un divisore quando si effettua una divisione.
Di conseguenza, i termini usati si riferiscono a 'posizioni' sulla superficie di calcolo, che nel corso dell'algoritmo sono soggette a operazioni simili a quelle che durante una divisione interessano le posizioni che hanno lo stesso nome: avere lo stesso nome significa perciò avere lo stesso comportamento nel corso del calcolo. È così che la dinamica dell'estrazione di radice è costruita come una sorta di divisione. Si osservi come, esattamente nello stesso modo, la moltiplicazione sia impostata come un'operazione inversa della divisione (v. Tav. II). Per l'estrazione di radice, l'aggiornamento del valore del 'divisore' richiede calcoli ausiliari; in questo caso il comportamento della riga aggiunta di volta in volta a questo scopo sotto quella del 'divisore' non può essere collegato con alcuna delle righe dell'operazione di divisione, e di conseguenza a questa riga non è dato alcun nome. Ciò conferma quanto abbiamo osservato a proposito della relazione tra nomi e comportamenti. Si tratta di un fatto importante, in quanto alcune descrizioni più tarde lavoreranno proprio su questo punto, descrivendo in un modo nuovo l'evoluzione di tali righe inferiori durante l'algoritmo e, a causa di ciò, attribuendo a esse ‒ come si è visto sopra ‒ il nome di 'divisore' (fa). In tal modo, se non si fa attenzione a questa pratica singolare riguardante 'posizioni' e nomi, non si possono cogliere i cambiamenti avvenuti nel corso dei secoli. In conclusione, stabilire e rielaborare relazioni tra algoritmi a partire dal modo in cui erano eseguiti sulla superficie di calcolo sembra essere stata pratica comune dei matematici, che può essere ricostruita, come abbiamo fatto, a partire dai Nove capitoli e che proseguirà per alcuni secoli.
Tale pratica, che richiedeva di saper manipolare i cambiamenti di 'posizione' e di visualizzare l'algoritmo come una successione di trasformazioni sulla superficie di calcolo, può inoltre spiegare come si siano formati alcuni concetti matematici nell'antica Cina. Siamo di fronte a un chiaro esempio di come un ambiente di lavoro e una particolare pratica matematica possano dare un'impronta ai concetti matematici e ai risultati che si ottengono. La nozione di equazione di secondo grado, così come è introdotta nei Nove capitoli, ne è un esempio. Per capirla dobbiamo ritornare all'estrazione di radice eseguita sulla superficie di calcolo.
Se guardiamo il quadro di numeri dopo il passo (d) dell'algoritmo nella Tav. VI, lasciando da parte la prima parte della radice già calcolata, restano due posizioni: un dividendo (shi) G e una sorta di divisore (congfa, divisore aggiunto), g. L'applicazione a questi della parte rimanente dell'algoritmo dell'estrazione di radice equivale a risolvere un'equazione di secondo grado, x2+gx=G (con g, G>0), e questo è proprio il modo in cui le equazioni di secondo grado sono introdotte nei Nove capitoli. Questo tipo di operazione aritmetica fa intervenire due termini (un 'dividendo' e una sorta di 'divisore'), in altre parole due 'posizioni', e il relativo risultato si ottiene applicando l'algoritmo per l'estrazione della radice quadrata privato della prima parte. Si tratta di una concezione caratteristica della Cina, che definì il quadro entro il quale si sviluppò l'approccio alle equazioni fino al XIII secolo. Tale concezione differisce da quella odierna in quanto queste equazioni non sono enunciati di uguaglianze e quindi manipolarle non implicava la trasformazione degli enunciati. Tuttavia, malgrado fosse strettamente legata a un contesto molto particolare, questa nozione di equazione si diffuse lo stesso nel mondo matematico, attraverso il mondo arabo (Chemla 1992).
Si osservi che questo modo d'introdurre l'equazione di secondo grado come un quadro di numeri sul quale opera l'algoritmo dell'estrazione di radice riproduce il modo in cui fece la sua comparsa l'equazione lineare generale, ossia con coefficienti sia positivi sia negativi (v. sopra). Si parte in entrambi i casi dagli algoritmi che operano su configurazioni di 'posizioni' sulla superficie di calcolo, e alcuni degli stati in cui questi quadri di numeri si trovano provvisoriamente durante il calcolo, come pure la parte dell'algoritmo che li riguarda, ricevettero lo status di oggetti matematici autonomi. Entrambi i casi attestano uno stesso modo particolare di definire nuovi oggetti che dipende in modo essenziale dalla superficie di calcolo. Notiamo infine che l'algoritmo per l'estrazione di radice introduce nuovi oggetti anche in un altro modo. Esso prescrive infatti che nel caso in cui il numero N non è esaurito, una volta determinate le unità della radice, occorre dare il risultato come 'lato di N', cioè, in termini moderni, come N1/2. Ne segue che, nell'antica Cina gli irrazionali quadratici sono stati istituiti affinché l'estrazione di radice avesse sempre un risultato esatto; i commenti successivi presentano anche calcoli con queste quantità (Volkov 1985; Li Jimin 1990; Chemla 1995). Allo stesso modo, le frazioni sono state introdotte affinché le divisioni dessero sempre un risultato esatto (v. Tav. IIb). È notevole il fatto che tutti questi elementi dei Nove capitoli si trovino anche nei più antichi testi matematici indiani.
Ricapitolando, i Nove capitoli espongono la matematica sotto forma di algoritmi. La nostra analisi ha messo in luce come quest'opera attesti alcuni modi specifici di ricerca sugli algoritmi, come pure alcune tendenze teoriche di questa pratica matematica. Gli algoritmi appaiono sia come liste di operazioni sia come trasformazioni delle 'posizioni' sulle superfici di calcolo; in base a ciò, due obiettivi principali sembrano avere guidato la ricerca, e precisamente trovare relazioni tra algoritmi apparentemente diversi ed estendere il loro campo di applicazione per renderli il più possibile generali.
È possibile che quest'ultimo obiettivo sia collegato all'ideazione di algoritmi con proprietà algebriche e quindi a una particolare attenzione nei confronti degli aspetti formali nella matematica. Il primo obiettivo può invece essere messo in relazione con una pratica di concettualizzazione e di confronto di algoritmi attraverso le trasformazioni che essi operano sulle 'posizioni' nella superficie di calcolo; un'indicazione del ruolo chiave che le 'posizioni' e il loro comportamento sulle superfici per calcolare devono aver giocato nella matematica dell'antica Cina. A questi oggetti era dato un nome e abbiamo visto come questo uso dei nomi sia stato di aiuto nello stabilire relazioni tra procedure diverse. Le 'posizioni' offrirono anche una base per creare nuovi oggetti matematici, suggerendo quindi un modello per nuove ricerche su di esse; la descrizione fin qui presentata di questa antica pratica aiuterà nel seguito a capire in quale modo si sono sviluppate queste ricerche.
Esegesi e dimostrazione: i commentari ai 'Nove capitoli sui procedimenti matematici'
di Karine Chemla
Rivolgiamo ora l'attenzione ai due più antichi commentari ai Nove capitoli sui procedimenti matematici, che sono stati tramandati assieme a quest'opera: il commentario di Liu Hui, terminato nel 263, e i 'commentari di Li Chunfeng', scritti in realtà da un gruppo di studiosi con la supervisione di Li Chunfeng e terminati nel 656. Studiare quale genere di matematica era sviluppato in un commentario nell'antica Cina rappresenta un punto essenziale, in quanto in essi si trovano nuovi elementi, molto importanti per la storia della matematica. Per prima cosa, contrariamente ai Nove capitoli, che è un testo costituito essenzialmente di problemi e procedimenti di risoluzione, i commenti di Liu Hui e Li Chunfeng contengono ausili visivi: figure (tu) per la geometria piana e solidi (qi) per la geometria dello spazio. La più antica testimonianza dell'uso di ausili visivi nella matematica dell'antica Cina si trova nei commenti ai canoni; questo fatto è confermato da disegni presenti nel commento di Zhao Shuang (III sec.) allo Gnomone dei Zhou, quale quello nella fig. 7, tratto dall'edizione del 1213. Non ci sono pervenuti disegni di carattere matematico di epoca precedente; quelli ai quali fanno riferimento i commenti ai Nove capitoli sono andati perduti. I disegni presenti nel commento di Zhao Shuang hanno probabilmente subito un deterioramento nel passare ai posteri (l'edizione del 1213 contiene infatti figure errate); tuttavia, essi forniscono indicazioni preziose su come le figure potevano essere utilizzate nell'antica Cina. Le forme geometriche sono rappresentate su una griglia con quadrati unitari. Ciò può essere in relazione con l'usanza di far uso di dimensioni determinate quando si opera su una data situazione geometrica, e che rimanda al fatto che i problemi dei Nove capitoli sono sempre presentati con valori particolari. Inoltre, la sovrapposizione di due quadrati con griglie diversamente orientate può rappresentare un indizio che le figure erano ritagliate su carta quadrettata. Vi è una seconda differenza più importante, ed è che i commenti contengono anche le dimostrazioni della correttezza degli algoritmi che si trovano nei Nove capitoli. Le dimostrazioni hanno luogo in un contesto diverso da quello dei testi greci dell'Antichità, dove lo scopo è stabilire la verità degli enunciati matematici. La descrizione delle dimostrazioni di correttezza degli algoritmi, oltre a farci conoscere meglio la concezione che si aveva degli algoritmi nell'antica Cina, mette in evidenza un originale metodo di dimostrazione.
La situazione ora descritta fa nascere molte questioni interessanti. Le prime riguardano le dimostrazioni: per quale ragione il tipo particolare di esegesi di Liu Hui e Li Chunfeng, nell'ambito della matematica, assume la forma della scrittura di dimostrazioni? Viceversa: quale tipo di dimostrazioni era seguito a scopo di esegesi? E quale posizione assegnare a esse nella storia universale della dimostrazione? Un secondo gruppo di questioni riguarda il tipo di testo: quali indicazioni può dare la matematica su un testo particolare quale è un canone (jing) e sulla pratica del commento? Di quale atteggiamento verso i canoni, di quali modi di lettura, di quali operazioni sono testimonianza i commentatori? Infine, nel caso specifico della matematica, sfruttando il fatto che i commenti sono più espliciti dell'opera commentata, quale aiuto possiamo trarne per la lettura e la comprensione dei Nove capitoli, nonché per la ricostruzione della prassi matematica a cui l'opera si riferisce, così come la intendevano i più antichi lettori che conosciamo? Esaminiamo ora i commenti con in mente queste domande.
Le dimostrazioni di Liu Hui: schemi stabili di ragionamento
Si può verificare facilmente che i commentatori vedessero nei loro ragionamenti una spiegazione della correttezza degli algoritmi dei Nove capitoli; ogni ragionamento è infatti regolarmente concluso con espressioni del tipo 'da cui il risultato' (jide), che ricordano il classico latino 'q.e.d.' (quod erat demonstrandum). L'utilizzazione di schemi di ragionamento che ricorrono indica poi che le dimostrazioni non sono ad hoc, ma seguono determinate regole. Per esempio, ciò appare evidente nelle dimostrazioni, piuttosto elaborate, per mezzo delle quali Liu Hui stabilisce la correttezza degli algoritmi per l'area del cerchio e il volume della piramide, che sono due casi in cui nel trattare suddivisioni infinite i ragionamenti condividono la stessa struttura (Chemla 1992).
In primo luogo, si suddivide l'oggetto in questione; precisamente, nel cerchio sono inscritti poligoni, facendo riferimento a una figura (tu), e la piramide è suddivisa in solidi (qi); questi due ausili visivi sono quindi introdotti per condurre la prova. In un secondo passo, in base a queste divisioni si mettono in evidenza relazioni esatte che sussistono in una determinata parte dell'oggetto studiato e che alla fine convergono nell'algoritmo del quale si vuole dimostrare l'esattezza. Per il cerchio si tratta della relazione tra il semiperimetro di un poligono regolare inscritto, il raggio e l'area di un poligono con un numero di lati doppio del precedente; per la piramide la suddivisione permette di stabilire il risultato per un solido che è una parte di quello dato; per mostrare la relazione, i poligoni sono trasformati in rettangoli, mentre il solido entro il quale si considera la piramide (qiandu) è trasformato in un parallelepipedo. In terzo luogo, si può iterare la suddivisione dell'oggetto, che permette di mettere in evidenza quali sono queste relazioni; si crea così una successione di situazioni simili, per le quali sono valide le stesse relazioni, e dove è considerata una parte sempre maggiore dell'oggetto geometrico. Il quarto punto in comune è fondamentale e consiste nel fatto che prima di arrivare alla conclusione si calcola sempre di quanto diminuisce la parte dell'oggetto non ancora trattata nel corso dell'iterazione della procedura di suddivisione. L'algoritmo è dichiarato corretto soltanto quando si dimostra che nel procedimento seguito la grandezza di questa parte tende a zero.
Il ragionamento matematico che entra in gioco ricorda quello di testi greci come gli Elementi di Euclide o la Dimensio circuli di Archimede, nei quali il problema è affrontato con uno schema di ragionamento che nel XVII sec. verrà identificato e denominato 'metodo di esaustione'. È in modo del tutto simile che lo schema di ragionamento seguito da Liu Hui diviene per noi visibile. Questa analogia tra i testi greci e quelli cinesi relativamente ai fatti utilizzati nei ragionamenti non deve però nascondere le differenze strutturali presenti nel modo di ragionare. I testi matematici greci citati fanno uso costante della reductio ad absurdum e implicano un numero di passi potenzialmente infinito, mentre i commentari cinesi procedono attraverso un ragionamento diretto e fanno entrare in gioco ciò che sembra un'infinità attuale di operazioni. Un'altra differenza fondamentale è che gli algoritmi usati da Liu Hui riguardano non soltanto la geometria, ma anche l'aritmetica e l'algebra. Rivolgendoci ora a questa parte dei commenti vedremo più chiaramente certe caratteristiche del loro modo di condurre una dimostrazione.
Le dimostrazioni di Liu Hui: ricerca dei procedimenti fondamentali
Il commento di Liu Hui all'algoritmo per la somma di frazioni, descritto dopo il problema 9 del cap. 1, è un punto cruciale del testo. Prima di descriverlo, vediamo gli oggetti che sono coinvolti nel ragionamento. L'espressione per m/n usata nei Nove capitoli, ossia 'm di n parti' ('n' fen zhi 'm'), esprime il fatto che la frazione è considerata composta di 'parti', e mostra anche un numeratore e un denominatore. Da un lato, il problema che richiede di sommare frazioni mette insieme varie parti per formare una data quantità; quest'ultima deve essere quindi stimata. Dall'altro lato, l'algoritmo prescrive calcoli sui numeratori e sui denominatori per ottenere una frazione. Stabilire la correttezza dell'algoritmo significa quindi provare che la frazione ottenuta esprime effettivamente la quantità formata.
Anzitutto, nel considerare le frazioni così come sono manipolate dall'algoritmo, Liu Hui sottolinea che una frazione si può esprimere in molti modi, in quanto si possono moltiplicare e dividere numeratore e denominatore per uno stesso numero senza che cambi il suo valore. Si può quindi dividere per semplificare; l'operazione opposta, 'complicare', introdotta da Liu Hui serve soltanto nelle dimostrazioni. Considerando poi le frazioni come parti, egli fa corrispondere le frazioni semplificate alle parti più grezze e quelle complicate alle parti più fini, sottolineando che la quantità non varia anche se essa è formata in modi diversi. Per dimostrare che (a/b)+(a′/b′)=(ab′+a′b)/bb′ si mostra come, con la moltiplicazione, l'algoritmo si riduce ad adattare parti diverse affinché abbiano la stessa grandezza. Citando i Nove capitoli, Liu Hui spiega l'effettivo significato di ciascun passo in termini di parti e in termini di numeratori/denominatori. Quando "si moltiplicano i denominatori uno con l'altro", un'operazione che nel corso della dimostrazione egli chiama "rendere uguale", è calcolato il denominatore comune a tutte le frazioni e si definisce la misura che le diverse parti hanno in comune per poter essere quindi sommate; inoltre, quando "i denominatori moltiplicano i numeratori che non corrispondono a essi", per dare ab′ e ba′ i numeratori ‒ egli dice ‒ sono resi omogenei con i denominatori a cui corrispondono, e quindi le quantità originali non sono perdute. Anche qui egli dà, en passant, un nome a questo insieme di operazioni: 'rendere omogeneo'; 'rendendo uguali' i denominatori e 'rendendo omogenei' i numeratori l'algoritmo fornisce effettivamente una misura corretta della quantità ottenuta mettendo insieme varie frazioni. È interessante osservare come questa descrizione dell'algoritmo, introdotta a fini di dimostrazione, sarà poi effettivamente utilizzata da Liu Hui e da altri matematici di periodi successivi ‒ tra gli altri Zhu Shijie ‒ per sommare frazioni.
Noi lettori di oggi vediamo in questo testo una dimostrazione della correttezza dell'algoritmo. Cosa cercava però Liu Hui? Questo punto è chiarito nel seguito del commento. L'autore infatti non si ferma qui, ma prosegue con considerazioni molto astratte e anche di carattere filosofico, concludendo poi con un'affermazione fondamentale: "Moltiplicare per disaggregarli, semplificare per unirli, rendere omogenei e rendere uguali affinché possano comunicare: come potrebbero non essere questi i punti fondamentali della matematica?".
Anche se può sembrare poco chiara, questa affermazione è cruciale. Essa mostra infatti che la dimostrazione non riguarda soltanto la correttezza del procedimento, dal momento che entra in gioco molto di più. Essa mostra in azione nell'algoritmo le operazioni (moltiplicazione, divisione, rendere uguale o rendere omogeneo) che costituiranno l'argomento delle considerazioni successive; infatti, uno degli scopi della dimostrazione è proprio mettere in evidenza queste operazioni. Introdotte in relazione alle frazioni, il rendere uguale e il rendere omogeneo non sono semplicemente operazioni che si effettuano su numeratori e denominatori; in quanto la loro rilevanza va molto al di là se nelle osservazioni conclusive Liu Hui le considera punti chiave della matematica. Come interpretare tutto ciò?
In effetti, queste operazioni si presentano in numerose altre dimostrazioni del commentario di Liu Hui. Un esame attento di alcune di esse consente di trarre qualche conclusione su come la dimostrazione della correttezza di un algoritmo si colleghi all'esposizione delle operazioni fondamentali che entrano in gioco. Il commento di Liu Hui sull'algoritmo per risolvere sistemi di equazioni lineari presentato nei Nove capitoli sottolinea dapprima la proprietà che tutti i numeri presenti in un'equazione possono essere moltiplicati o divisi per una stessa quantità senza modificare il significato dell'equazione; le operazioni di moltiplicazione e divisione che Liu Hui aveva definito fondamentali si ritrovano anche qui. Per riferirsi alla proprietà detta, Liu Hui qualifica i coefficienti come lü, estendendo in tal modo il campo di applicazione di un concetto che il canone introduceva nel contesto della regola del tre. Nei Nove capitoli il concetto faceva riferimento a due numeri che esprimono l'equivalenza fra due cose che la regola del tre deve convertire l'una nell'altra e che individua la proprietà per cui quei numeri sono definiti soltanto attraverso il loro rapporto, cosicché moltiplicarli o dividerli entrambi per lo stesso numero non potrebbe danneggiare la loro capacità di esprimere la citata equivalenza. Nel ricorrere a questo concetto anche per individuare ciò che contraddistingue i coefficienti di un'equazione lineare, Liu Hui sottolinea la rilevanza generale un concetto introdotto dal Canone dei Nove capitoli in un contesto specifico.
Desiderando mostrare come l'eliminazione tra due equazioni permette di annullare il coefficiente posto più in alto (cioè il termine in x) in una di esse, il commentatore vede una nuova applicazione delle operazioni del 'rendere uguale' e del 'rendere omogeneo'. A questo scopo, mostra come l'algoritmo sia equivalente a un altro procedimento, ossia al moltiplicare le due colonne (cioè le due equazioni) ciascuna per il numero che si trova nella posizione più in alto (cioè il coefficiente della x) dell'altra. I numeri nelle posizioni più alte sono così resi uguali, e gli altri omogenei, ed è per questa ragione che l'eliminazione è possibile. La dimostrazione introduce perciò un nuovo algoritmo per risolvere il problema, e fa vedere che esso è equivalente a quello del quale si vuole dimostrare la correttezza. Il nuovo algoritmo sarà utilizzato dallo stesso Liu Hui e da altri per risolvere sistemi di equazioni. L'autore spiega poi quello che secondo lui è il motivo per cui quest'ultimo algoritmo non si trova nei Nove capitoli: esso porta a equazioni che sono più complicate del necessario perché hanno coefficienti con divisori comuni molto grandi. Il nuovo procedimento introdotto serve però a mettere in evidenza, mediante il confronto, il significato (yi) dell'algoritmo fornito nel cap. 8 e la sua strategia formale; esso equivale cioè a un procedimento che 'rende uguali' alcuni coefficienti e 'omogenei' gli altri.
Possiamo ora tornare all'affermazione di Liu Hui prima riportata per cercare di approfondirne il senso confrontando le dimostrazioni date per gli algoritmi per sommare frazioni e quelle per risolvere sistemi di equazioni lineari. Questo confronto rivela in primo luogo che le espressioni 'rendere uguali' e 'rendere omogenei' che compaiono nelle due dimostrazioni, oltre al significato relativo alle operazioni a cui si fa riferimento nel contesto in cui sono usate ('rendere uguali' significa rendere uguali i denominatori delle frazioni oppure i coefficienti delle equazioni), ne hanno anche uno formale che si riferisce al 'modo di funzionare' degli algoritmi; in entrambi i casi il procedimento consiste nel rendere uguali alcune quantità e omogenee altre. Il parallelismo stabilito tra le due dimostrazioni rende evidente che gli algoritmi seguono effettivamente la stessa strategia formale, e ciò si esprime nel fatto che uno stesso algoritmo fondamentale giustifica la loro correttezza. Una stessa strategia permette di risolvere i problemi dei due tipi, malgrado il significato concreto delle operazioni sia diverso a seconda del contesto. Ciò si collega al tipo di lavoro sugli algoritmi che portò forse a sviluppare le regole della 'doppia falsa posizione' presenti nei Nove capitoli (v. par. 2); sulla base delle ragioni effettive che giustificano la correttezza degli algoritmi è possibile rilevare un sotterraneo legame formale tra i procedimenti.
Il confronto rende chiaro che uno dei motivi per cui Liu Hui esegue le dimostrazioni è proprio il desiderio di portare alla luce queste strategie formali di carattere fondamentale comuni ai vari procedimenti dei Nove capitoli; esse permettono di ridurne la varietà rivelando che è sempre applicato un piccolo numero di strategie. Moltiplicare e dividere tutti i numeri di un dato insieme, rendere uguali od omogenee certe quantità sono operazioni alla base di molti degli algoritmi del Canone; è per questo che, quando esse compaiono per la prima volta, Liu Hui ne sottolinea subito l'importanza. In tal modo, nell'affermazione di cui abbiamo detto sopra egli riassume gli algoritmi più importanti che sono alla base dei procedimenti dei Nove capitoli e che le dimostrazioni del suo commento permettono di scoprire.
Concludiamo indicando come le due dimostrazioni di proprietà geometriche considerate prima si ricollegano a questa interpretazione del lavoro di Liu Hui. Le trasformazioni geometriche fondamentali che sono all'opera nei ragionamenti relativi al cerchio e alla piramide si presentano come manifestazioni della stessa operazione generale: "usare l'eccesso per riempire il vuoto" (yi ying bu xu). Liu Hui sottolinea ripetutamente il fatto che negli algoritmi in contesto geometrico questa trasformazione entra in gioco sistematicamente. Quindi, anche in questo ambito, per il tramite della dimostrazione si mette in evidenza la strategia formale comune a vari algoritmi (in questo caso, un tipo di trasformazione geometrica). Si può inoltre aggiungere, ritornando alla dichiarazione fondamentale di Liu Hui, che tale operazione, la cui efficienza va oltre i limiti della matematica, è una delle forme generali sotto le quali si può presentare una successione di moltiplicazioni e divisioni.
I problemi come condizione per evidenziare strategie formali
Vediamo ora quali condizioni sono necessarie per scoprire che un certo algoritmo si fonda sul 'rendere omogenee' e sul 'rendere uguali' certe quantità. Sarebbe certamente interessante esaminare come opera Liu Hui per ritrovare tale algoritmo nella risoluzione di sistemi di equazioni lineari o nella 'regola della doppia falsa posizione' (Chemla 1991); noi ci concentreremo però sulla moltiplicazione delle frazioni, che, come abbiamo visto in precedenza, i Nove capitoli introducono a proposito di un problema che richiede di calcolare l'area di un rettangolo.
Dopo una prima dimostrazione della correttezza, e con l'intenzione esplicita di "farlo capire in tutta la sua generalità", Liu Hui ne dà una seconda, che in formule possiamo esprimere così: (a/b)(c/d)=[(ac)/(bc)][(bc)/(bd)]=(ac)/(bd). Nelle parole di Liu Hui, ac e bd sono 'resi omogenei' rispetto a bc, il termine 'reso uguale'. È molto interessante il modo in cui egli mette in evidenza come entrano di nuovo in gioco le operazioni di 'rendere omogeneo' e 'rendere uguale': mette da parte il problema originale, nel quale a/b e c/d sono l'altezza e la base di un rettangolo, e, ai fini della dimostrazione, introduce un nuovo problema: "5 [ossia b] cavalli valgono 3 [ossia a] jin d'oro [un jin equivale a 220 o 250 g ca.]; se ne sono venduti 4 (c), e se 7 (d) persone si dividono [il ricavato], quanto riceve ogni persona?". Si tratta di un problema equivalente ‒ come osserva lo stesso Liu Hui ‒ al seguente: "Un cavallo vale 3/5 (a/b) di jin d'oro. Se una persona vende 4/7 (c/d) di cavallo quanto ricava?". Dal nostro punto di vista, il problema originale del Canone è identico a questo; il fatto che per Liu Hui siano problemi diversi mostra una pratica matematica originale, vale a dire il considerare i problemi in relazione alle dimostrazioni. Dov'è la differenza? I primi due passi della moltiplicazione di due frazioni, cioè il calcolo di ac e bd, risultano ora parte della trasformazione del primo problema nel seguente: "20 (bc) cavalli valgono 12 (ac) jin d'oro. Se uno vende i 20 (bc) cavalli e se 35 (bd) persone si dividono il ricavato, quanto ricava ogni persona?". La soluzione di quest'ultimo problema si ottiene con la divisione che costituisce l'ultimo passo della moltiplicazione di due frazioni. Il procedimento del Canone è così interpretato, passo dopo passo, secondo una successione di problemi, ed è inserito in un insieme più ampio di operazioni che consentono di determinare un certo numero di cavalli, sempre pari a bc. In questo contesto più ampio le prime due operazioni effettuate nel moltiplicare le frazioni si possono considerare operazioni che 'rendono omogenee' due quantità in relazione al 'rendere uguale' il numero dei cavalli. La differenza decisiva sta proprio qui, in quanto la nuova situazione permette a Liu Hui di far apparire il rendere uguale nel caso del numero dei cavalli, mentre il problema originale non poteva offrire un'interpretazione per questo calcolo.
Nell'antica Cina i problemi non sono soltanto enunciati che richiedono un procedimento di risoluzione, in quanto essi mostrano anche situazioni che permettono d'interpretare le operazioni effettuate. L'abbiamo visto in un caso nel quale le potenzialità offerte dal problema del Canone non erano abbastanza ricche. È anche un segno del modo in cui Liu Hui legge e utilizza in generale i problemi dei Nove capitoli; l'esame del lavoro dei commentatori ci permette così di evitare anacronismi nella lettura del Canone, in particolare dei problemi che lo compongono. Seguendo Liu Hui, dobbiamo considerare un problema sia come un rappresentante di una classe di problemi simili sia come un terreno per l'interpretazione. L'interpretazione delle operazioni costituisce un elemento essenziale per dimostrare che un procedimento è corretto. L'oro, le persone e i cavalli che Liu Hui introduce permettono di esporre l'intero schema del 'rendere uguale' e 'rendere omogeneo', e spiegare così il procedimento usato nei Nove capitoli. In tal modo si può capire come la moltiplicazione di frazioni si colleghi a questo e ad altri procedimenti.
Le possibilità d'interpretazione offerte da un problema sono una condizione fondamentale per mettere in evidenza il modo in cui questa strategia formale entra in gioco nel procedimento. In assenza di simbolismo, il calcolo formale era quindi effettuato interpretando opportunamente le operazioni. Il punto cruciale è che l'operazione di 'rendere uguale' non appartiene in senso stretto al procedimento, ed è per questo che il problema non era in grado di fornirne un significato; esso appartiene invece alla dimostrazione, come sottolinea lo stesso Liu Hui, e ciò chiarisce in quale modo gli algoritmi fondamentali, che permettono di stabilire collegamenti formali tra procedimenti diversi, vengano alla luce attraverso la dimostrazione, come dire che tali algoritmi non esprimono soltanto prescrizioni, ma possono anche esprimere una dimostrazione (Chemla 1997a).
L'affermazione fondamentale di Li Chunfeng
In un testo ufficiale scritto sotto la supervisione di Li Chunfeng, Trattato sui tubi sonori e sul calendario (Lüli zhi, che fa parte della Storia della dinastia Sui), si ritrova un'affermazione fondamentale che coincide in molti punti con quella di Liu Hui ma ne diverge in altri. Il commentatore del VII sec. scrive: "Per quanto riguarda ciò che si chiama lü vi sono nove [parti della matematica] che ne scaturiscono: la prima si chiama Campi rettangolari [qui Li Chunfeng elenca i titoli dei capitoli dei Nove capitoli e le precisazioni di Liu Hui sulle questioni che è possibile trattare in ciascuno dei capitoli], tutti moltiplicano per disaggregarli, dividono per unirli, 'rendono omogenei' e 'rendono uguali' affinché siano posti in comunicazione, applicano la regola del tre per collegarli, quindi i metodi dei procedimenti matematici si esauriscono qui" (Suishu, 24). Si conferma così l'importanza che queste affermazioni debbono aver avuto per i commentatori. Li Chunfeng deve avere svolto un'opera di carattere esegetico del genere di quella di Liu Hui per fare affermazioni analoghe, anche se non identiche. Le differenze fondamentali rispetto a quello che afferma Liu Hui sono tre: in primo luogo, un nuovo algoritmo, cioè la regole del tre, è aggiunto all'elenco delle operazioni fondamentali; in secondo luogo, il concetto di lü mediante il quale il Canone descriveva la regola è ora posto alla radice della struttura, come ciò da cui tutto deriva; infine, l'affermazione di Li Chunfeng riguarda chiaramente tutta la matematica.
Riguardo al primo punto, l'inclusione della regola del tre tra gli algoritmi fondamentali è in relazione con il fatto che quest'operazione, come quelle di 'rendere uguale' e di 'rendere omogeneo', è messa in evidenza in molti commenti che si occupano di stabilire la correttezza dei procedimenti. Attraverso la ricerca dei motivi per i quali un algoritmo risulta corretto si può scoprire che esso chiama in causa un procedimento fondamentale di tipo formale, ossia la regola del tre. Un'affermazione simile di Yang Hui, nella prefazione al suo commento Spiegazione dettagliata dei 'Nove capitoli sui metodi matematici' (Xiangjie jiuzhang suanfa, 1261), testimonia il perdurare di questa ricerca. Attraverso le dimostrazioni, i commenti mettono in luce come differenti procedimenti facciano uso di questi algoritmi in modo nascosto; si riduce in tal modo la varietà di questi ultimi e si stabiliscono legami tra di essi.
I vari commentatori sembrano aver sviluppato le dimostrazioni secondo una prassi simile e condividendo gli stessi obiettivi, come si desume dalle loro dichiarazioni; così, provare la correttezza di una procedura diventa un metodo per cercare un minimo numero di algoritmi fondamentali che soggiacciono alle varie procedure del Canone, e gli algoritmi fondamentali, sui quali vertono le affermazioni dei commentatori, variano da un commento all'altro. D'altra parte, Li Chunfeng non organizza la sua dichiarazione allo stesso modo di Liu Hui; dove quest'ultimo fa riferimento soltanto a operazioni, il primo identifica nel lü il concetto che sta alla base degli algoritmi fondamentali e della loro validità. In altre parole, oltre alle operazioni Li Chunfeng presenta una proprietà formale, comune a tutte le quantità alle quali sono applicate le operazioni fondamentali e che rende conto della loro efficienza.
Il modello della regola del tre mostrato in un esempio ci permetterà una migliore comprensione della pratica della dimostrazione dei nostri commentatori, in due diverse direzioni; considereremo infatti più in dettaglio il modo in cui una procedura si collega agli algoritmi fondamentali sui quali essa si basa. La dimostrazione della validità dell'algoritmo dei Nove capitoli per risolvere un certo problema può anche dare luogo a un procedimento alternativo che consta di una combinazione di algoritmi fondamentali, mentre nel contempo è anche resa esplicita l'argomentazione soggiacente a questo procedimento dimostrandone quindi la correttezza: è questo il caso del problema 10 del cap. 6.
Il commentatore mostra su questo esempio come la duplice applicazione della regola del tre porti al risultato. Ancora più interessante è il passo successivo; qui l'algoritmo del quale si vuole dimostrare la validità è messo in relazione con le operazioni fondamentali sulle quali esso si basa. A partire dal procedimento suggerito il commentatore applica opportune modifiche alla lista delle operazioni per trasformarla nell'algoritmo del quale si vuole dimostrare la correttezza.
Si tratta di un modo di procedere che ricorda le dimostrazioni di tipo algebrico, nelle quali per ottenere la formula cercata si applicano opportune trasformazioni a una formula che si sa essere giusta; le dimostrazioni di questo tipo, che entrano in gioco in entrambi i commenti che stiamo esaminando, si possono infatti considerare come "dimostrazioni algebriche in un contesto algoritmico" (Chemla 1997-98). La trasformazione di un algoritmo in un altro fa intervenire le operazioni fondamentali. Fino a quale punto queste dimostrazioni algebriche, o in generale le dimostrazioni della validità degli algoritmi, hanno contribuito alla nascita delle dimostrazioni matematiche di tipo algebrico? Il problema è ancora aperto; abbiamo comunque un'indicazione del modo in cui potranno essere inserite, in una futura storia universale della dimostrazione, le fonti cinesi.
Nel problema specifico, infine, vi è un altro aspetto interessante. I commenti sottolineano spesso che i procedimenti del cap. 6 del Canone si riducono a parecchie combinazioni della regola del tre; di conseguenza, nelle dimostrazioni della correttezza delle procedure raccolte in quel capitolo si rivela quale sia il vero argomento di questa parte del libro, che è espresso in termini di algoritmi fondamentali. In tal modo i commenti forniscono chiarimenti sull'organizzazione del testo in nove capitoli; ciò ci riporta alla dimensione esegetica dei commenti.
Atteggiamenti nei confronti del Canone: dimostrazione ed esegesi
Uno degli aspetti dell'affermazione di Li Chunfeng che abbiamo sottolineato è che l'analisi dei Nove capitoli lo porta a considerazioni che riguardano tutta la matematica. Ciò si collega, prescindendo da qualche sfumatura che qui non possiamo considerare, con l'atteggiamento che altri commentatori manifestano verso il Canone. Nella sua prefazione a questo testo, Liu Hui scrive: "[I Nove capitoli] sono per la maggior parte resi semplici e tuttavia sono in grado di raccogliere […]. Benché si parli delle 'nove parti della matematica', essi sono in grado di esaurire il sottile [xian], di penetrare nelle minute [wei] e di sondare ciò che non conosce limiti" (Jiuzhang suanshu, p. 91). Il fatto che il Canone possa raccogliere tutta la matematica è riaffermato con vigore nella prefazione di Yang Hui. Se ciò può risultare sorprendente per un lettore moderno ‒ ci si può chiedere come possa un solo libro comprendere tutta la matematica ‒, si tratta di un'affermazione la cui importanza è sottolineata dal fatto che si ripete nei secoli, e che va attentamente interpretata e non semplicemente respinta come priva di senso. Se infatti consideriamo queste affermazioni nel più ampio contesto dell'atteggiamento verso i canoni che si aveva nell'antica Cina, vediamo che i Classici del confucianesimo suscitavano regolarmente le medesime attese presso i commentatori; pertanto, una tale affermazione significa probabilmente soltanto che i Nove capitoli erano reputati un canone.
Cogliere il significato che questa affermazione potrebbe avere per la matematica, secondo i nostri commentatori, può farci capire più in generale un tale atteggiamento verso i canoni. L'affermazione di Li Chunfeng è cruciale, e ci mostra la strada da seguire; essa infatti chiarisce come la sua analisi dei nove capitoli del Canone lo porti a identificare gli algoritmi fondamentali che entrano in gioco in tutti i capitoli e che permettono di spiegarli tutti. Abbiamo visto come l'approccio a questi algoritmi avvenisse tramite la pratica della dimostrazione e il confronto. È chiaro che la loro caratterizzazione come 'fondamentali' è dovuta al fatto che tutte le dimostrazioni dei Nove capitoli convergono verso gli stessi algoritmi. Questo è quanto possiamo concludere sulla base dei commentatori. Dalla constatazione che le procedure dei Nove capitoli si riducono tutte a questi algoritmi, Li Chunfeng deduce che essi esauriscono i metodi dei procedimenti matematici. Il Canone indicherebbe allora gli schemi fondamentali delle operazioni con i quali realizzare ogni procedimento, presentando un numero finito di essi. In questo senso l'opera abbraccerebbe tutta la matematica; così, interpretare il Canone significa individuare gli algoritmi fondamentali che esso indica.
Si può inoltre sostenere che in questo modo i commenti rivelano la valenza universale del Classico, come essi lo vedono nell'ambito della cosmologia; essi mostrano come, in ultima analisi, tutti i procedimenti matematici discendano da un'interazione di un piccolo numero di trasformazioni fondamentali. Inoltre, se guardiamo più da vicino i loro risultati, è molto interessante osservare come venga costantemente sottolineato il ruolo svolto da due principî opposti ma complementari, che nella matematica prendono la forma della moltiplicazione e della divisione.
In conclusione, ciò che ci si aspetta dai Nove capitoli in quanto Canone, e cioè in quanto testo che comprende tutta la matematica, si accorda con una particolare pratica di dimostrazione che tende a mettere in luce gli algoritmi fondamentali ai quali il Canone fa riferimento in modo indiretto e che si applicano in ogni situazione matematica. L'esegesi e la dimostrazione diventano in questo modo le due facce di una stessa medaglia.
L'evoluzione della matematica dalla dinastia Han alla dinastia Tang
di Karine Chemla
I più antichi testi matematici cinesi conservati, composti tra l'inizio e il VII sec. dell'era volgare, hanno avuto un comune destino. O, più precisamente, fin dall'inizio sono stati pensati per condividere uno stesso destino: furono tutti scelti per far parte di una raccolta, Dieci canoni di matematica (Suanjing shishu, che include i Nove capitoli), all'interno della quale ci sono pervenuti. Subito dopo la presentazione della raccolta all'imperatore Gaozong (650-683) della dinastia Tang da parte di Li Chunfeng, nel 656, questi libri sarebbero serviti come manuali nella Scuola di matematica, che era controllata dalla Direzione dell'istruzione (Guozijian), e per la scelta degli argomenti agli esami di matematica che furono istituiti in quel periodo. I testi dell'amministrazione statale in nostro possesso dimostrano chiaramente che i curricula e gli esami erano basati su questi libri. Come accadde per la medicina, l'edizione Tang dei Classici utilizzati nell'istruzione statale sostituì definitivamente le versioni precedenti. Tutte le edizioni che la tradizione scritta ci ha consegnato comprendono i commenti composti per questa edizione sotto la supervisione di Li Chunfeng. Grazie all'importanza che avevano nell'istruzione pubblica, i Dieci canoni di matematica ebbero anche un ruolo assolutamente centrale nella diffusione della cultura sviluppatasi in Cina nell'Asia orientale; la raccolta passò in Giappone e in Corea, nel momento in cui, durante la dinastia Tang, i due paesi traevano ispirazione dalle istituzioni cinesi, per quanto riguardava il sistema degli esami.
L'interesse particolare che la dinastia Song (960-1279) ebbe per i canoni si manifesta anche riguardo alla matematica. Nel 1084 il Dipartimento della Biblioteca imperiale (Mishusheng) fece stampare la raccolta; si tratta della prima stampa in assoluto di un libro di matematica. Lo status di canone che era stato attribuito a questi scritti ebbe un ruolo chiave nel richiamare l'attenzione degli studiosi dell'epoca Song. La raccolta aveva però nel frattempo subito danni; già all'epoca un canone composto da Zu Chongzhi (429-500) era andato perduto, e non poté quindi essere incluso nella raccolta. Un altro testo mancante, il Canone matematico di Xiahou Yang (Xiahou Yang suanjing), era stato sostituito da un libro del periodo Tang, assicurando a questo, per il solo fatto di essere compreso tra questi scritti prestigiosi, la trasmissione ai posteri. Nessun altro libro della dinastia Tang ci è infatti pervenuto attraverso la tradizione scritta.
Nel 1213 Bao Huanzhi ristampò questa edizione, aggiungendovi le Memorie sui metodi di numerazione (Shushu jiyi) di Xu Yue, da lui stesso trovate in un monastero taoista e considerate uno dei canoni in uso nella Scuola di matematica sotto la dinastia Tang. Si tratta della prima edizione della raccolta che effettivamente possediamo, anche se soltanto in parte, e ciò grazie alle collezioni di libri a stampa raccolti dai bibliofili Ming (1368-1644) e Qing (1644-1911). Infatti, nella matematica come nella medicina, le stampe di epoca Song dei canoni sono le più antiche edizioni esistenti, e sono perciò quelle che hanno avuto un ruolo chiave nella trasmissione dei testi antichi; gli unici libri di matematica scritti prima della dinastia Tang a noi pervenuti sono quelli che gli studiosi Song pensavano facessero parte della raccolta. Cercheremo quindi di cogliere alcuni aspetti delle attività matematiche che si svolgevano in Cina fino all'epoca Tang basandoci su quanto messo in luce da questa raccolta.
Diversi tipi di libri
Il confronto tra i vari libri della raccolta Dieci canoni di matematica mostra una certa evoluzione nello scrivere di matematica dalla dinastia Han alla dinastia Tang. Alcuni di questi canoni, come il Canone matematico del Maestro Sun (Sunzi suanjing) o il Canone matematico di Zhang Qiujian (Zhang Qiujian suanjing) seguono in gran parte il modello del Canone Han i Nove capitoli, e mettono insieme problemi che richiedono procedimenti di risoluzione diversi. Dal III sec. cominciano però a comparire libri dedicati a particolari settori della matematica: le Memorie sui metodi di numerazione, attribuite a Xu Yue, che trattano della rappresentazione dei numeri; il Canone di matematica che continua gli antichi (Jigu suanjing), di Wang Xiaotong, dedicato alla risoluzione dei problemi mediante equazioni algebriche; il Canone di matematica dell'isola marina (Haidao suanjing) di Liu Hui, che si occupa di una categoria di problemi riguardanti il triangolo rettangolo.
In quest'ultimo caso, però, può trattarsi di un'evoluzione del testo in epoca Tang; pensato in origine da Liu Hui come un capitolo aggiuntivo ai Nove capitoli, venne trasformato successivamente in libro indipendente e attribuito allo stesso Liu Hui. Siamo così di fronte a un secondo cambiamento, consistente nel fatto che, a differenza dei canoni Han, si tende sempre più spesso ad attribuire ad autori precisi la paternità dei testi. La comparsa di libri specializzati e l'indicazione sempre più precisa dell'autore sono fenomeni presenti anche nel campo della medicina.
A differenza dei canoni del periodo Han, nei libri successivi vi sono numerosi dettagli su come operare sulla superficie di calcolo. Il Canone matematico del Maestro Sun spiega come rappresentare i numeri con le bacchette e descrive gli algoritmi per eseguire le operazioni di moltiplicazione e divisione, mentre i Nove capitoli sembrano dare per scontati i due argomenti. Inoltre, a parte alcuni modi elaborati di disporre i dati sulle superfici di calcolo, il Canone Han non spiega come disporre i numeri per eseguire gli algoritmi descritti, mentre il Canone matematico del Maestro Sun e il Canone matematico di Zhang Qiujian, assieme ad altri, su questo abbondano di particolari; si tratta di testimonianze preziose per ricostruire la pratica di computo sulla superficie di calcolo nell'antica Cina (Chemla 1996a). In nessuno di questi libri si trova però raffigurata la superficie con la disposizione dei dati, diversamente dai libri matematici di epoca Song-Yuan, che invece forniscono in vario modo queste illustrazioni.
Sviluppo di argomenti precedenti
Per alcuni argomenti trattati nei Nove capitoli si assiste a notevoli sviluppi nei secoli successivi. Per illustrare questo punto prenderemo in considerazione gli algoritmi per l'estrazione di radice e per la risoluzione di equazioni algebriche. Come abbiamo visto, gli algoritmi per l'estrazione di radici quadrate o cubiche dei Nove capitoli erano descritti in modo da mostrare che queste operazioni erano una specie di divisione. Infatti, entrambi gli algoritmi richiederanno un 'quoziente', un 'dividendo' e un 'divisore', e calcoli ausiliari per far rientrare le operazioni nello schema della divisione. Molti dei successivi Dieci canoni riprendono questo argomento ma, anche se a prima vista gli algoritmi esposti sembrano gli stessi del Canone Han, vi è in realtà una differenza essenziale: l'estrazione di radice quadrata è descritta come una divisione con due divisori, mentre per la radice cubica si parla di tre divisori; ciò implica che nei nuovi algoritmi entrano in gioco soltanto le posizioni nella superficie di calcolo, il cui comportamento si può far corrispondere a quello delle posizioni che intervengono nel caso della divisione.
Per cogliere quest'evoluzione occorre quindi prestare attenzione alla successione di eventi a cui sono soggette le righe della superficie nel corso del calcolo; in altre parole, occorre una lettura simile a quella che permette di cogliere la relazione tra estrazione di radice e divisione nei Nove capitoli, o la relazione tra moltiplicazione e divisione: ciò dimostra la continuità di una tradizione di lavoro mediante algoritmi. Ma in che cosa è significativa quest'evoluzione?
Intanto, essa è significativa riguardo ai valori che il Canone Han apprezza maggiormente. L'omogeneità nel corso di tutta l'operazione sembra essere una proprietà richiesta nei Nove capitoli, e da questo punto di vista i nuovi algoritmi per l'estrazione di radice contenuti nei canoni più recenti rappresentano un passo avanti; in questa direzione si proseguirà fino alla dinastia Song (Chemla 1994). Inoltre, questo cambiamento è anche significativo da un punto di vista moderno, in quanto sono ora messi in luce i coefficienti delle successive equazioni che sono alla base dell'estrazione di radice. Lungi dall'essere una semplice riscrittura, la nuova forma dell'algoritmo apre nuove prospettive e si accompagna a un'estensione dell'ambito di applicazione delle equazioni algebriche considerate.
I Nove capitoli introducevano l'equazione di secondo grado come dipendente dall'estrazione di radice quadrata e legata alla figura dello gnomone; anche il Canone matematico di Zhang Qiujian fa uso di equazioni quadratiche per risolvere problemi geometrici. Tuttavia, per quanto riguarda la radice cubica, l'algoritmo descritto nei Nove capitoli non poteva dar luogo a un'equazione cubica come sottoalgoritmo; nei nuovi algoritmi di estrazione della radice cubica, invece, nei quali si disponevano i diversi 'divisori' su righe distinte, le equazioni cubiche potevano essere introdotte come operazioni aritmetiche che interessavano tre posizioni e risolte mediante un sottoalgoritmo; ciò è quanto è possibile rilevare dal Canone di matematica che continua gli antichi di Wang Xiaotong, ed è forse questo l'argomento del canone di Zu Chongzhi che è andato perduto. Si tratta di un esempio del modo di creare un nuovo oggetto matematico a partire dalla pratica della superficie di calcolo, procedimento analogo a quello esaminato in riferimento ai Nove capitoli. Ciò permette di capire il significato della successiva riformulazione di un algoritmo che poteva invece sembrare lo stesso procedimento.
Analogamente a come è introdotta l'equazione di secondo grado nei Nove capitoli, cioè come un'operazione su due posizioni (nel nostro linguaggio, il coefficiente di x e il termine noto), l'equazione cubica è introdotta come un'operazione su tre posizioni (i coefficienti di x2 e di x e il termine noto). L'equazione completa con tutti i coefficienti e in notazione posizionale compare in Cina soltanto più tardi, durante le dinastie Song e Yuan, in relazione a un ulteriore modo di estrarre radici. Prende corpo una tradizione che concepisce le equazioni come operazioni numeriche dipendenti dall'estrazione di radice e che continuerà a svilupparsi fino alla dinastia Yuan. Tuttavia, con il progressivo declino della matematica al quale si assiste nel seguito, i testi del XVI sec. ritorneranno a un trattamento delle equazioni algebriche più vicino a quello del periodo Tang. Questa tradizione era quindi ancora viva quando, nel XVII sec., i primi missionari gesuiti arrivarono in Cina.
Decadenza di alcuni argomenti antichi
Se alcuni argomenti dei Nove capitoli, quale l'estrazione di radice, sono sviluppati in canoni seguenti, ve ne sono altri che decadono. Per esempio, la necessità, sostenuta nei Nove capitoli, di dare in alcuni casi il risultato dell'estrazione di radice quadrata come N1/2 scompare dai libri che seguono, poiché quando l'operazione non può essere completata è lasciata la forma approssimata del risultato. Inoltre, sia il Canone matematico del Maestro Sun sia il Canone matematico di Zhang Qiujian ritornano sulla risoluzione di sistemi di equazioni o sulla 'regola della doppia falsa posizione', ma in nessuno dei due testi gli algoritmi sono così eleganti e completi come nel Canone Han. Riguardo al primo argomento, tanto il modo di disporre i dati quanto gli algoritmi sono nei due Canoni essenzialmente gli stessi dei Nove capitoli, ma non è più menzionata la possibilità di far uso di contrassegni per numeri sia positivi sia negativi per estendere la portata dei sistemi che si possono risolvere con il procedimento esposto. Le regole della doppia falsa posizione sono menzionate, ma senza la generalità e la precisione che hanno nei Nove capitoli. A questo proposito, il Canone matematico del Maestro Sun comprende i due tipi di problemi risolti nei Nove capitoli mediante il procedimento per eccesso e quello per difetto, anche se il secondo compare soltanto in una forma semplificata; tuttavia, gli algoritmi per risolverli (nella notazione del par. 2, riferentesi a tre fasi: I, II e III) sono descritti come distinti, in quanto il procedimento I+II serve a risolvere problemi del primo tipo, mentre per i problemi del secondo tipo è dato un altro procedimento, che equivale a I+III. Il Canone matematico di Zhang Qiujian contiene soltanto problemi del primo tipo, per i quali è dato il procedimento I+II, quindi la possibilità di usare un simile procedimento per risolvere il secondo tipo di problemi non è contemplata in questo testo.
Nuovi argomenti
I canoni matematici pubblicati dopo la dinastia Han testimoniano anche un interesse per argomenti che non compaiono nei Nove capitoli. Uno di questi è l''analisi indeterminata' o 'teoria delle congruenze'. Un problema di congruenze analogo a quello che nel XIX sec. sarà chiamato 'teorema cinese dei resti' compare per la prima volta in un libro di matematica nel Canone matematico del Maestro Sun, ma si tratta solamente della punta di un iceberg; infatti, esso si rivela in tutta la sua estensione soltanto nel contesto della compilazione di calendari, al quale era collegato (v. par. 5). Il Canone matematico di Zhang Qiujian ci segnala anche un interesse per l'analisi indeterminata con il problema che è diventato famoso come 'problema dei cento polli'; esso richiede due equazioni lineari in tre incognite per le quali sono forniti una successione di soluzioni e un procedimento che spiega come trovarle tutte a partire da una di esse. I due problemi ebbero una diffusione molto ampia e si ritrovano in numerosi scritti arabi di epoca medievale. Ciò c'introduce al nostro ultimo punto.
La diffusione della matematica dell'antica Cina
La matematica dell'antica Cina così come appare nei Dieci canoni ha avuto sbocchi nella matematica moderna? E se sì, in quale modo? Abbiamo già detto che i Dieci canoni circolarono molto presto in Giappone e in Corea, e apparentemente anche in Vietnam. Su un altro fronte, i più antichi trattati indiani di matematica e i commenti relativi dal VI sec. in poi hanno in comune con le fonti cinesi molti concetti e algoritmi: il sistema posizionale decimale e gli algoritmi fondamentali dell'aritmetica; il concetto di frazione e l'aritmetica a esso relativa; gli irrazionali quadratici, la regola del tre e l'uso che se ne faceva per dimostrare gli algoritmi; la misurazione della distanza alla quale si trova un luogo non raggiungibile (Vogel 1986). Dato lo stato delle fonti disponibili non siamo in grado di stabilire priorità, ma i contatti tra Cina e India sono stati certamente piuttosto importanti dal momento che vi sono così tanti punti in comune.
Il tramite dell'India spiega alcuni aspetti comuni che si riscontrano tra fonti arabe e cinesi, ma molti fatti lasciano supporre uno scambio diretto tra queste due regioni del mondo. Tra l'altro, numerosi elementi comuni delle fonti arabe e cinesi non hanno finora trovato corrispondenti in quelle indiane. Nelle fonti arabe la regola della doppia falsa posizione appare dal IX sec. in poi (nell'Europa medievale più tardi); in tutte le fonti la regola è applicata soltanto ai problemi che abbiamo chiamato del primo tipo; ciò parla in favore di un processo di trasmissione, ma finora questa regola non si è trovata nelle fonti indiane. Inoltre, il modo particolare di affrontare le equazioni algebriche in Cina compare improvvisamente alla fine del XII sec. nel mondo arabo nel lavoro di Sharaf al-Dīn al-Ṭūsī (Chemla 1995), e nemmeno questo modo si è finora ritrovato nelle fonti indiane. Infine, in alcuni testi provenienti dall'Oriente islamico si trovano algoritmi per l'estrazione di radice che sono più vicini a quelli cinesi che non a quelli indiani; se ne conclude che le strade attraverso le quali l'aritmetica asiatica è entrata nel mondo arabo possono essere più d'una (Chemla 1994).
I fatti qui considerati, assieme ad altri, possono dimostrare uno scambio continuo e diretto delle conoscenze matematiche nell'Asia centrale, anche prima della fondazione dell'Impero mongolo. Quest'ipotesi è suffragata dai manoscritti matematici, di contenuto vicino in qualche caso ad alcuni dei Dieci canoni di matematica, trovati nel tempio a Dunhuang, sigillato intorno al 1000; i libri di matematica cinesi erano dunque presenti nelle regioni a est già prima del X sec., e in tal modo le conoscenze matematiche della Cina antica trovarono forse una loro via verso la matematica moderna. Per quanto riguarda, infine, la trasmissione delle conoscenze matematiche all'interno della Cina stessa, non ci sono pervenuti scritti posteriori al Canone matematico di Xiahou Yang e precendenti il periodo della ripresa dell'attività matematica agli inizi della dinasta Song. Un'analisi di quanto sia potuto accadere nel frattempo è quindi piuttosto difficile. È possibile che nessuno scritto sia stato diffuso, e in questo caso non sapremo mai che cosa si facesse in matematica, ma ciò può anche significare che la matematica fu parzialmente dimenticata per qualche tempo, in questo modo si spiegherebbe anche per quale motivo era così difficile nel periodo della dinastia Song trovare copie di canoni di epoca precedente. In ogni caso, malgrado vi fossero durante la dinastia Tang sia un insegnamento ufficiale sia esami di Stato di matematica, non è rimasto alcun segno di una particolare attività matematica di quel periodo.
Metodi matematici nella compilazione dei calendari
di Qu Anjing
La compilazione di calendari nella Cina antica e medievale si è valsa dei risultati ottenuti nel campo dell'astronomia matematica. Gli elementi più interessanti di un calendario cinese tradizionale, in particolare dal punto di vista matematico, sono le costanti astronomiche e gli algoritmi. Il testo calendaristico più antico in nostro possesso è il Calendario Taichu (Taichu li), assai simile al Calendario Santong (Santong li), anche se è probabile che molti altri lo abbiano preceduto. Si ha notizia di un centinaio di calendari compilati tra il I sec. a.C. e la metà del XVII sec. d.C., di cui solamente meno della metà è giunta sino a noi, conservata nelle venticinque storie dinastiche relative a quel periodo; di un'altra ventina ci restano solamente alcune costanti astronomiche, mentre degli altri conosciamo soltanto il nome.
Prima del III sec. d.C. la velocità del moto apparente dei corpi celesti era considerata costante e un algoritmo molto semplice permetteva di calcolarla; a partire da questa data si scoprì che il moto della Luna era irregolare, e così s'iniziò a usare metodi d'interpolazione lineare (fig. 8). La scoperta dell'irregolarità del moto del Sole e dei pianeti avvenne invece nel 560 d.C. a opera di Zhang Zixin (m. 577). Dopo di lui, Liu Xiaosun propose una correzione del moto del Sole nel Calendario Wuping (Wuping li, 576 d.C.), calendario che non fu mai usato e che è andato quasi interamente perduto, a cui seguirono altre proposte di metodi numerici per approssimare la posizione di numerosi corpi celesti.
Nei calendari cinesi tradizionali la lunghezza dell'eclittica in du ('gradi', pressoché coincidenti con quelli sessagesimali) era uguale alla lunghezza in giorni di un anno sidereo. Il moto medio del Sole era perciò di 1 du al giorno e l'eclittica era divisa in 365,25 du ca. invece dei 360 du usuali. Questo sistema rimase in uso per più di duemila anni, sino a quando nel XVII sec. si cominciò a sentire anche nell'Impero di Mezzo l'influenza della moderna astronomia matematica europea. Per il computo dei giorni e degli anni si disponeva di un sistema ciclico sessagesimale. Il sistema era costruito su un gruppo di dieci caratteri, detti 'Tronchi celesti' (tiangan), il quale era associato alternativamente a un altro gruppo di dodici caratteri, detti 'Rami terrestri' (dizhi), in modo da ottenere sessanta combinazioni; un numero del ciclo sessagesimale era dunque individuato da due caratteri, uno dei Tronchi celesti e l'altro dei Rami terrestri.
Il sistema delle costanti astronomiche e il metodo delle congruenze
Nella compilazione dei calendari cinesi antichi svolgeva un ruolo molto importante la determinazione della 'Suprema origine' (shangyuan), ossia l'inizio del ciclo cosmico; si trattava di un compito non semplice, perché questa data doveva soddisfare rigide condizioni. La Suprema origine doveva infatti cadere nel primo anno di un ciclo sessagesimale degli anni, alla mezzanotte del primo giorno di un ciclo sessagesimale dei giorni e durante la Luna nuova, al passaggio del Sole al solstizio d'inverno in una particolare casa lunare, con la Luna al perigeo e in nodo ascendente, e quando i cinque pianeti visibili passavano contemporaneamente per il solstizio d'inverno. Queste condizioni furono mantenute nella compilazione dei calendari dal I sec. a.C. al XIII d.C.; tuttavia, dal momento che non era possibile individuare una Suprema origine che verificasse tutte queste condizioni ideali, potevano essere trascurate una o due di esse, come, per esempio, il nome dell'anno. Il numero di anni trascorsi tra la Suprema origine e il momento in cui era compilato un determinato calendario doveva soddisfare un certo sistema di congruenze.
La Suprema origine era collegata a un unico sistema di costanti per ciascun calendario. Quasi tutte queste costanti erano frazioni; se maggiori di 1, erano espresse come un intero più una frazione propria. Dopo il Calendario Linde (Linde li, 664 d.C.), in tutti i calendari queste costanti avevano lo stesso denominatore (A); alcuni numeratori di costanti erano decimali a quattro o anche a sei cifre. Le costanti astronomiche indipendenti erano le seguenti dieci: il mese sinodico o lunare (B/A), l'anno tropico (T/A), l'anno siderale (S/A), il mese anomalistico (G/A), il mese nodale (J/A) e il periodo sinodico di Giove (M6/A), di Marte (M7/A), di Saturno (M8/A), di Venere (M9/A) e di Mercurio (M10/A). Nella compilazione dei calendari ogni costante era in una relazione particolare con la Suprema origine; essa poteva essere una costante fondamentale, utilizzata per determinare l'inizio del ciclo, oppure una costante derivata, che era corretta affinché corrispondesse a esso. Costanti fondamentali per la determinazione della Suprema origine erano considerati l'anno tropico e il mese sinodico, i cui numeratori erano di norma interi, ossia formavano una terna di dati tale che due di essi permettevano di determinare il terzo. Una volta determinata la Suprema origine, era possibile stabilire con alcuni semplici metodi un legame ideale tra questa e le costanti derivate; questo algoritmo, che non varia di molto al variare delle costanti dei diversi calendari, è stato d'importanza fondamentale per la compilazione dei calendari cinesi in epoca antica e medievale.
Nella compilazione di un calendario, la Suprema origine era tanto più utile quanto più era vicina nel tempo, cioè quanto più era minore il numero di anni trascorsi tra la Suprema origine e il momento in cui il calendario era compilato. Per ottenere un conveniente inizio del ciclo cosmico a partire da un sistema di congruenze, occorreva fare degli arrotondamenti ad alcuni resti, come quelli del solstizio d'inverno e del tempo che intercorre tra il solstizio d'inverno e la Luna nuova nel periodo del solstizio.
Si può pensare che la Suprema origine ideale dovesse soddisfare due condizioni: non doveva risalire a più di cento milioni di anni e l'errore sui resti non doveva superare ±0,01 giorni (Qu Anjing 1991). Si può dimostrare che, con queste due sole condizioni, quasi ogni inizio di ciclo cosmico fissato nei calendari cinesi tradizionali è l'unica soluzione di un sistema di tre congruenze, che corrispondono al ciclo sessagesimale dei giorni e degli anni e alle costanti dell'anno tropico e del mese sinodico. Tutte le altre costanti che non erano calcolate per la scelta della Suprema origine necessitavano di una correzione.
Già nel Canone matematico del Maestro Sun (400 d.C. ca.) si trovano un problema e un algoritmo relativi a congruenze lineari. Un alto livello di sviluppo di questi argomenti si evidenzia negli Scritti sui numeri in nove capitoli (Shushu jiuzhang, 1247 d.C.) di Qin Jiushao; l'autore discute due tipi di algoritmi per sistemi di congruenze lineari risolvendo il problema in modo quasi perfetto. Uno di questi algoritmi era chiamato yanji shu, dal termine yanji usato per indicare la Suprema origine a partire dal Calendario Dayan (Dayan li, 724 d.C.) di Yixing; Qin utilizza l'epoca del Calendario Kaixi (Kaixi li, 1207 d.C.) come esempio per dimostrare il procedimento dello yanji shu, scegliendo per prima cosa le costanti fondamentali: il mese sinodico e l'anno tropico. Il procedimento utilizzato per stabilire la data della Suprema origine fu abbandonato dopo il Calendario Shoushi (Shoushi li, 1280 d.C.), e il metodo non fu più applicato.
Compilare un calendario richiedeva grande precisione e perciò gli antichi compilatori cercavano, attraverso un accurato lavoro, di migliorare vecchi metodi di calcolo o di trovare nuovi algoritmi più adatti alla costruzione di nuovi e plausibili modelli celesti. L'interpolazione è il metodo numerico più importante nel tradizionale sistema cinese di compilazione dei calendari, in particolare l'interpolazione lineare. Intorno al 600 d.C. Liu Zhuo (544-608) ideò nel Calendario Huangji (Huangji li) quella che oggi si definisce un''interpolazione quadratica a tratti', da cui derivarono successivamente molti tipi d'interpolazione polinomiale.
Bibliografia
Aston 1972: Aston, William G., Nihongi. Chronicles of Japan from the earliest times to A.D. 697, translated from the original Chinese and Japanese by William G. Aston, with an introduction to the new edition by Terence Barrow, Rutland-Tōkyō, Charles E. Tuttle, 1972 (1. ed.: London, Allen and Unwin, 1956).
Bréard 1999: Bréard, Andrea, Re-Kreation eines mathematischen Konzeptes im chinesischen Diskurs. Reihen vom ersten bis zum 19. Jahrhundert, Stuttgart, Steiner, 1999.
Brenier 1994: Brenier, Joël, Notation et optimisation du calcul des grands nombres en Chine. Le cas de l'échiquier de Go dans le Mengqi bitan de Shen Gua (1086), in: Nombres, astres, plantes et viscères. Sept essais sur l'histoire des sciences et des techniques en Asie orientale, textes préparés pour la publ. par Isabelle Ang et Pierre-Étienne Will, Paris, Collège de France - Institut des Hautes Études Chinoises, 1994, pp. 89-111.
Chemla 1987: Chemla, Karine, L'aspect algorithmique récurrent dans les mathématiques chinoises. Paysages d'algorithmes, algorithmes de paysages, "Cahiers d'histoire et de philosophie des sciences", 20, 1987, pp. 86-104.
‒ 1991: Chemla, Karine, Theoretical aspects of the Chinese algorithmic tradition (first to third century), "Historia scientiarum", 42, 1991, pp. 75-98.
‒ 1992: Chemla, Karine, Résonances entre démonstration et procédure. Remarques sur le commentaire de Liu Hui (3e siècle) aux 'Neuf Chapitres sur les Procédures Mathématiques' (1er siècle), "Extrême-Orient, Extrême-Occident", 14, 1992, pp. 91-129.
‒ 1994: Chemla, Karine, Similarities between Chinese and Arabic mathematical documents (I). Root extraction, "Arabic sciences and philosophy", 2, 4, 1994, pp. 207-266.
‒ 1995: Chemla, Karine, Algebraic equations East and West until the Middle Ages, in: East Asian science. Tradition and beyond, edited by Hashimoto Keizo, Catherine Jami and Lowell Skar, Osaka, Kansai University Press, 1995, pp. 83-89.
‒ 1996a: Chemla, Karine, Positions et changements en mathématiques à partir de textes chinois des dynasties Han à Song-Yuan. Quelques remarques, "Extrême-Orient, Extrême-Occident", 18, 1996, pp. 115-147.
‒ 1996b: Chemla, Karine, Relations between procedure and demonstration. Measuring the circle in the 'Nine chapters on mathematical procedures' and their commentary by Liu Hui (3rd century), in: History of mathematics and education. Ideas and experiences, edited by Hans Niels Jahnke, Norbert Knoche and Michael Otte, Göttingen, Vandenhoeck und Ruprecht, 1996, pp. 69-112.
‒ 1997a: Chemla, Karine, Croisements entre réflexion sur le changement et pratique des mathématiques en Chine ancienne, in: En suivant la voie royale. Mélanges offerts à Léon Vandermeersch, réunis et présentés par Jacques Gernet et Marc Kalinowski, avec la collaboration de Jean-Pierre Diény, Paris, EFEO, 1997, pp. 191-205.
‒ 1997b: Chemla, Karine, Reflections on the world-wide history of the rule of false double position, or: how a loop was closed, "Centaurus. International magazine of the history of science and medicine", 39, 1997, pp. 97-120.
‒ 1997c: Chemla, Karine, Qu'est-ce qu'un problème dans la tradition mathématique de la Chine ancienne? Quelques indices glanés dans les commentaires rédigés entre le 3e et le 7e siècles au classique Han 'Les neuf chapitres sur les procédures mathématiques', "Extrême-Orient, Extrême-Occident", 19, 1997, pp. 91-126.
‒ 1997d: Chemla, Karine, What is at stake in mathematical proofs from third century China?, "Science in context", 10, 2, 1997, pp. 227-251.
‒ 1997-98: Chemla, Karine, Fractions and irrationals between algorithm and proof in ancient China, "Studies in history of medicine and science", n.s., 15, 1-2, 1997-1998, pp. 31-54.
Chen Liangzuo 1977: Chen Liangzuo (Chen Liang-ts'o), Woguo chousuan zhongde kongwei 'ling' ji qi xiangguande yixie wenti [Lo zero, la posizione vuota dell'abaco in Cina e alcuni problemi connessi], "Dalu zazhi", 54, 1977, pp. 238-250.
‒ 1978: Chen Liangzuo (Chen Liang-ts'o), Xian Qin shuxue de fazhan ji qi yingxiang [Influenze e sviluppo della matematica nel periodo precedente alla dinastia Qin], "Lishi yuyan yanjiusuo jikan", 49, 1978, pp. 263-320.
Chen Meidong 1995: Chen Meidong, Guli xintan [Nuove ricerche sull'antica scienza dei calendari], Shenyang, Liaoning jiaoyu chubanshe, 1995.
Cullen 1996: Cullen, Christopher, Astronomy and mathematics in ancient China. The Zhou bi suan jing, Cambridge, Cambridge University Press, 1996.
Djamouri 1994: Djamouri, Redouane, L'emploi des signes numériques dans les inscriptions Shang, in: Sous les nombres, le monde. Matériaux pour l'histoire culturelle du nombre en Chine ancienne, préparé par Alexei Volkov, Paris, Presses Universitaires de Vincennes, 1994.
Du Shiran 1966: Du Shiran, Shilun Song Yuan shiqi Zhongguo he Yisilan Guojia jian de shuxue jiaoliu [Discussione sugli scambi nell'ambito della matematica tra la Cina e i paesi islamici], in: Song Yuan shuxueshi lunwenji [Raccolta di saggi sulla storia della matematica durante le dinastie Song e Yuan], [a cura di] Qian Baocong, Beijing, Kexue chubanshe, 1966, pp. 241-265.
Fu Daiwie 1988: Fu Daiwie, Lun 'Zhoubi' yanjiu chuantong de lishi fazhan yu zhanzhe [Studio sullo sviluppo storico e la trasformazione della tradizione di ricerca del 'Zhoubi'], "Tsinghua journal of Chinese studies", 18, 1988, pp. 1-41.
Guo Shuchun 1992: Guo Shuchun, Gudai shijie shuxue taidou Liu Hui [Liu Hui, figura importante nell'antico mondo della matematica], Jinan, Shandong kexue jishu chubanshe, 1992.
Henderson 1991: Henderson, John B., Scripture, canon and commentary. A comparison of Confucian and Western exegesis, Princeton (N.J.), Princeton University Press, 1991.
Hua Yinchun 1987: Hua Yinchun, Zhongguo zhusuan shigao [Breve presentazione della storia del calcolo con l'abaco in Cina], Beijing, Zhongguo caizheng jingji chubanshe, 1987.
Jami 1994: Jami, Catherine, History of mathematics in Mei Wending's (1633-1721) work, "Historia scientiarum", 4, 2, 1994, pp. 159-174.
Kalinowski 1994: Kalinowski, Marc, La divination par les nombres dans les manuscrits de Dunhuang, in: Nombres, astres, plantes et viscères. Sept essais sur l'histoire des sciences et des techniques en Asie orientale, textes préparés pour la publ. par Isabelle Ang et Pierre-Étienne Will, Paris, Collège de France, Institut des Hautes Études Chinoises, 1994.
Kim Yong Un 1994: Kim Yong Un, Korean mathematics, in: Companion encyclopedia of the history and philosophy of the mathematical sciences, edited by Ivor Grattan-Guinness, London-New York, Routledge, 1994, 2 v.
Lam Lay Yong 1986: Lam Lay Yong, The conceptual origins of our numeral system and the symbolic form of algebra, "Archive for history of exact sciences", 36, 1986, pp. 183-195.
‒ 1992: Lam Lay Yong - Ang Tian Se, Fleeting footsteps. Tracing the conception of arithmetic and algebra in ancient China, Singapore-London-Hong Kong, World Scientific, 1992.
Libbrecht 1973: Libbrecht, Ulrich, Chinese mathematics in the thirteenth century. The Shu-shu chiu-chang of Ch'in Chiu-shao, Cambridge (Mass.), M.I.T. Press, 1973.
‒ 1982: Libbrecht, Ulrich, Mathematical manuscripts from the Dunhuang caves, in: Explorations in the history of science and technology in China, chief editors Li Guohao, Zhang Mengwen, Cao Tianqin, Shanghai, Chinese Classics Pub. House, 1982, pp. 203-229.
Li Jimin 1987: Li Jimin, Cong 'yanji zhifa' yu 'dayan zongshushu' kan Qin Jiushao zai suanfa shang de chengjiu [Il risultato di Qin Jiushao nel calcolo degli algoritmi secondo il metodo Yanij e Dayan], in: Wu Wenjun, Qin Jiushao yu 'Shushu jiuzhang' [Qin Jiushao e il 'Shushu Jiuzhang'], Beijing, Beijing Shifan daxue chubanshe, 1987, pp. 203-219.
‒ 1990: Li Jimin, Dongfang shuxue dianji 'Jiuzhang suanshu' ji qi Liu Hui zhu yanjiu [Studio su un classico orientale, il 'Jiuzhang suanshu' e i commentari di Liu Hui], Xi'an, Shaanxi renmin jiaoyu chubanshe, 1990.
Li Yan 1945: Li Yan, Chousuan zhidu kao [Indagini sul sistema del calcolo con l'abaco], in: Li Yan, Zhongsuan shi luncong [Saggi sulla storia della matematica cinese], Shanghai, Shangwu yinshuguan, 1931-1947, 4 v.; v. III, 1945, pp. 29-36.
‒ 1954: Li Yan, Zhongguo suanxueshi luncong [Raccolta di documenti sulla storia della matematica in Cina], Taipei, Zhengzhong shuju, 1954.
‒ 1987: Li Yan - Du Shiran, Chinese mathematics. A concise history, transl. by John N. Crossley and Anthony W.-C. Lun, Oxford, Clarendon Press; New York, Oxford University Press, 1987.
Martzloff 1987: Martzloff, Jean-Claude, Histoire des mathématiques chinoises, Paris, Masson Press, 1987.
Mikami 1913: Mikami, Yoshio, The development of mathematics in China and Japan, Leipzig, Teubner; New York, Stechert and Co., 1913.
Nakayama 1964: Nakayama, Shigeru, The significance of the Fut'ien li on the history of astronomy, "Journal of history of science", 71, 1964, pp. 120-123.
Needham 1959: Needham, Joseph, Mathematics and the sciences of the heavens and the earth, in: SCC, III, 1959, pp. 1-168.
Qian Baocong 1966: Song Yuan shuxueshi lunwenji [Raccolta di saggi sulla storia della matematica durante le dinastie Song e Yuan], [a cura di] Qian Baocong, Beijing, Kexue chubanshe, 1966.
Qu Anjing 1990: Qu Anjing, Zhongguo gudai lifa zhong de shangyuan jinian jisuan [Metodo di calcolo negli antichi calendari cinesi], in: Shuxueshi yanjiu wenji [Raccolta di saggi di storia della matematica], [a cura di] Li Di, Hothot, Neimeng daxue chubanshe, 1990.
‒ 1991: Qu Anjing, Tang Song lifa yanji shangyuan shili ji suanfa fenxi [Esempi di 'yanji shangyuan' e i loro algoritmi nei calendari Tang e Song], "Ziran kexueshi yanjiu", 10, 1991, pp. 315-316.
‒ 1994: Qu Anjing, Zhongguo gudai shuli tianwenxue tanxi [Studi sull'astronomia matematica nella Cina antica], Xi'an, Xibei daxue chubanshe, 1994.
‒ 1996: Qu Anjing, Bian Gang. A mathematician of the 9th century, "Historia scientiarum", 6, 1, 1996, pp. 17-30.
Smith 1914: Smith, David E. - Mikami, Yoshio, A history of Japanese mathematics, Chicago, The Open Court Publishing Company, 1914.
von Verschuer 1985: Verschuer, Charlotte von, Les relations officielles du Japon avec la Chine aux VIIIe et IXe siècles, Genève, Droz, 1985.
Vissière 1892: Vissière, Arnold, Recherches sur l'origine de l'abaque chinois et sur sa dérivation des anciennes fiches à calcul, "Bulletin de géographie", 28, 1892, pp. 54-80.
Vogel 1994: Vogel, Hans U., Aspects of metrosophy and metrology during the Han dynasty, in: Sous les nombres, le monde. Matériaux pour l'histoire culturelle du nombre en Chine ancienne, préparé par Alexei Volkov, Paris, Presses Universitaires de Vincennes, 1994.
Vogel 1986: Vogel, Kurt, Ein Vermessungsproblem reist von China nach Paris, "Historia mathematica", 10, 1986, pp. 360-367.
Volkov 1985: Volkov, Aleksej, Ob odnom drevnekitaiskom matematičeskom termine [Su un termine matematico dell'antica Cina], in: Tezisy konferentsii aspirantov i molodykh naučnykh sotrudnikov IV AN SSSR, Moskva, Nauka Press, 1985, v. I.1, pp. 18-22.
‒ 1994: Volkov, Alexei, Large numbers and counting rods, in: Sous les nombres, le monde. Matériaux pour l'histoire culturelle du nombre en Chine ancienne, préparé par Alexei Volkov, Paris, Presses Universitaires de Vincennes, 1994.
‒ 1995: Volkov, Alexei, Quantitative analysis of Liu Xin's standard measuring vessels, in: East Asian science. Tradition and beyond, edited by Hashimoto Keizo, Catherine Jami and Lowell Skar, Osaka, Kansai University Press, 1995, pp. 377-384.
Wagner 1979: Wagner, Donald B., An early Chinese derivation of the volume of a pyramid. Liu Hui, third century A.D., "Historia mathematica", 6, 1979, pp. 164-188.
Wu Chengluo 1957: Wu Chengluo, Zhongguo duliangheng shi [Storia dei pesi e delle misure in Cina], Shanghai, Shangwu yinshuguan, 1957 (1. ed.: 1937).
Wu Wenjun 1982: Wu Wenjun, Churu xiangbu yuanli [Il principio 'Ciò che viene e ciò che va si compensano l'un l'altro'], in: Jiuzhang suanshu yu Liu Hui [Il 'Jiuzhang suanshu' e Liu Hui], [a cura di] Wu Wenjun, Beijing, Beijing Shifan daxue chubanshe, 1982, pp. 58-75.
Yamazaki 1959: Yamazaki, Yoemon, The origin of the Chinese abacus, "Memoirs of the Research department of the Tokyo Bunko", 18, 1959, pp. 58-70.
‒ 1962: Yamazaki, Yoemon, History of instrumental multiplication and division in China from the reckoning blocks to the abacus, "Memoirs of the Research department of the Tokyo Bunko", 21, 1962, pp. 102-120.
Yan Dunjie 1947: Yan Dunjie, Song Yuan suanxue congkao [Ricerche sulla matematica in epoca Song e Yuan], "Kexue", 29, 4, 1947, pp. 109-114.