La scienza in Cina: i Ming. Matematica e astronomia
La scienza in Cina: i Ming. Matematica e astronomia
Matematica e astronomia
La perdita delle conoscenze matematiche e astronomiche
di Guo Shirong
Durante la dinastia Ming (1368-1644) le scienze matematiche e l'astronomia attraversarono un periodo di grave decadenza che causò la perdita di molte delle conoscenze acquisite nelle epoche precedenti. In questo periodo la comprensione delle teorie matematiche tradizionali subì una battuta d'arresto, le opere furono caratterizzate quasi esclusivamente da un intento divulgativo e pragmatico, e alcuni dei più importanti risultati conseguiti nella matematica durante le dinastie Song (960-1279) e Yuan (1279-1368) caddero nell'oblio. Anche nel campo dell'astronomia sia gli strumenti sia i calcoli calendaristici decaddero a un livello molto inferiore rispetto a quelli dell'epoca Yuan.
Il declino dell'attività matematica
Tra la metà del XIV e la fine del XVI sec. gli scritti matematici delle epoche precedenti divennero estremamente difficili da reperire; ciò costrinse gli studiosi desiderosi di leggerli a estenuanti ricerche. Il catalogo intitolato Catalogo della biblioteca Wenyuan ge (Wenyuan ge shumu), compilato da Yang Shiqi (1365-1444) tra il 1421 e il 1441 sulla base delle collezioni della Biblioteca imperiale, documenta che essa conservava 22 opere matematiche diverse; tra queste vi erano sette dei Dieci canoni di matematica (Suanjing shishu) (la raccolta compilata durante la dinastia Tang). Per quanto riguarda invece gli autori del XIII sec., la biblioteca custodiva le opere di Li Ye e di Qin Jiushao, tuttavia la raccolta delle opere di Yang Hui era incompleta e gli scritti matematici di Zhu Shijie non erano citati. Se confrontiamo il Catalogo della biblioteca Wenyuan ge con la precedente Grande enciclopedia dell'era Yongle (Yongle dadian, 1408), una raccolta di monografie su tutti gli argomenti, costituita da 22.877 capitoli e curata da Xie Jin (1369-1415) e Yao Guangxiao (1335-1418) in collaborazione con altre 2167 persone, scopriamo che i testi matematici antichi aggiunti alla collezione della Biblioteca imperiale tra il 1408 e il 1441 erano stati ben pochi. D'altra parte, la raccolta di testi antichi Tecniche segrete dei nostri tempi (Jindai mishu), composta da 141 scritti curati da Mao Jin (1599-1659), un noto collezionista di libri, comprendeva solamente due testi matematici. Nel complesso, quindi, il numero di opere circolanti su questo argomento era molto ridotto. La Biblioteca imperiale disponeva di alcuni importanti testi di matematica delle dinastie Song e Yuan, essi tuttavia erano inaccessibili alla maggior parte dei matematici e potevano essere consultati soltanto da alcuni bibliotecari, dagli alti funzionari della corte o da persone in possesso di un permesso speciale. Nel XV sec. l'unico matematico che, per quanto ne sappiamo, ebbe la possibilità di consultare i testi della Biblioteca imperiale fu Liu Shilong, uno degli studiosi incaricati di compilare la Grande enciclopedia dell'era Yongle.
L'esame delle collezioni appartenute ai matematici più importanti dell'epoca illustra chiaramente quale fosse la situazione. Wu Jing, uno studioso della metà del XV sec., esaurì tutte le sue energie nella ricerca del testo completo dei Nove capitoli sui procedimenti matematici (Jiuzhang suanshu, testo canonico della matematica cinese, scritto tra il I sec. a.C. e il I sec. d.C., e in seguito ricordato come Nove capitoli), nonostante vivesse a Qiantang (l'attuale Hangzhou) e si recasse di frequente nel Zhejiang e nel Jiangsu, regioni che ospitavano i maggiori centri culturali della Cina. Benché godessero di chiara fama fra i contemporanei e, come alti funzionari, avessero molte occasioni di viaggiare e collezionare libri, Gu Yingxiang (1487-1565) e Tang Shunzhi (1507-1560) disponevano di pochissimi testi matematici e non avevano il permesso di consultare la Biblioteca imperiale. Tang Shunzhi possedeva una trascrizione delle Misurazioni del cerchio sullo specchio del mare (Ceyuan haijing) di Li Ye, che Gu aveva preso in prestito e studiato, mentre lo stesso Gu affermava di aver letto uno dei Dieci canoni di matematica, lo Gnomone dei Zhou (Zhoubi), oltre allo Specchio di giada delle quattro incognite (Siyuan yujian) di Zhu Shijie. Anche Wang Wensu, un autore della prima metà del XVI sec., cita nel suo Prezioso specchio della matematica antica e moderna (Gujin suanxue baojian, prefazione del 1524) numerose opere che riteneva composte dopo la metà del XIV sec., tuttavia, per quanto riguarda i più importanti scritti matematici delle dinastie Song e Yuan, si limita a menzionare quelli di Yang Hui. Infine, una testimonianza importante è fornita da un catalogo di testi matematici compilato da Cheng Dawei (1533-1606) intitolato Fonti e sviluppo dei canoni di matematica (Suanjing yuanliu). Posto in appendice alle sua opera sulle Origini generali dei metodi matematici (Suanfa tongzong, 1592), il catalogo include tutti i libri di matematica antichi e contemporanei che Cheng conosceva o di cui aveva sentito parlare, per un totale di 51 opere (v. par. 2). Oltre ai Dieci canoni di matematica il catalogo comprende circa 22 titoli di opere matematiche composte prima del XIV sec.; fatta eccezione per gli scritti di Yang Hui, soltanto una di queste compare anche nel Catalogo della biblioteca Wenyuan ge. Tuttavia, tranne le opere di Yang Hui, due delle quali sono citate nel suddetto Catalogo, Cheng non possedeva né aveva mai letto personalmente quasi nessuno di quei libri. Nell'elenco non compaiono né le opere di Qin Jiushao, né quelle di Zhu Shijie e, nonostante vi fossero citate le Misurazioni del cerchio sullo specchio del mare di Li Ye, l'inesattezza dei commenti di Cheng Dawei dimostra che egli non aveva mai avuto occasione di consultarle direttamente.
Durante gli anni di regno della dinastia Ming circolava quindi un numero molto ridotto di opere di matematica, e sembra che gli studiosi del tempo ignorassero molte delle più importanti scoperte effettuate nelle epoche precedenti. La ricerca matematica, inoltre, mutò radicalmente i propri obiettivi e i cultori della materia cominciarono a interessarsi ad aspetti molto diversi da quelli tradizionali. Gli studi matematici si orientarono progressivamente verso le applicazioni pratiche e divennero comuni le trascrizioni in versi delle formule e dei problemi matematici; la maggior parte degli studiosi mostrava, infatti, un crescente interesse per la divulgazione delle conoscenze matematiche fra la popolazione e per la loro applicazione alle attività della vita quotidiana. Tali tendenze sono evidenti nelle opere matematiche composte fra il XIV e il XVII sec. che è possibile suddividere in quattro gruppi: (a) testi composti allo scopo di permettere a settori più vasti della popolazione di usare la matematica in diversi generi di attività; (b) opere basate sul sistema tradizionale dei Nove capitoli; (c) scritti sull'abaco; (d) opere su problemi matematici specifici. I testi appartenenti al primo gruppo si occupavano di argomenti come le unità di misura e di capacità, i pesi, il calcolo dell'area dei campi, i numeri grandi e quelli piccoli, le variazioni di peso; tuttavia, anche se ben accolti dal pubblico, essi non apportarono alcun contributo significativo al progresso della scienza matematica. Tra queste opere ricordiamo i seguenti scritti risalenti al XIV sec.: i Metodi matematici di Ding Ju (Ding Ju suanfa, 1355) di Ding Ju, la Raccolta delle massime potenzialità dei metodi di matematica (Suanfa quanneng ji) di Jia Heng, le Origini della matematica (Tongyuan suanfa, 1372) di Yan Gong, le Spiegazioni dettagliate dei metodi di matematica (Xiangming suanfa) di An Zhizhai e He Pingzhi e due opere anonime intitolate Metodi dettagliati [di matematica] svelata (Toulian xicao) e Borsa ricamata [istruzioni] delle origini illuminanti [della matematica] (Jinnang qiyuan). Al secondo gruppo appartengono i testi che riassumevano le conoscenze matematiche del tempo, presentandole secondo la suddivisione tradizionale in nove capitoli principali, integrati a volte da capitoli preliminari nei quali erano trattati alcuni algoritmi generali (l'addizione, la sottrazione, la moltiplicazione, la divisione, le frazioni, le proporzioni, l'uso dell'abaco), le rime per la formulazione degli algoritmi e i passi da percorrere nello studio della matematica. Sono inclusi in questo gruppo l'Esame dei 'Nove capitoli sui procedimenti matematici' con [problemi] analoghi (Jiuzhang suanfa bilei daquan, 1450) di Wu Jing e le opere citate precedentemente, Prezioso specchio della matematica antica e moderna di Wang Wensu e Origini generali dei metodi matematici di Cheng Dawei, oltre a uno scritto di Liu Shilong intitolato Nove capitoli sui metodi di matematica generali e comprensibili (Jiuzhang tongming suanfa, 1424), andato in seguito perduto. Gli scritti sull'abaco, che costituiscono il terzo gruppo, rappresentano invece una novità. L'abaco cinese, che fece probabilmente la sua comparsa come strumento di calcolo verso la fine della dinastia Yuan (la sua origine è tuttavia controversa), durante la dinastia Ming era così diffuso da sostituire completamente le tradizionali bacchette (v. oltre). Le prime opere affidabili su questo strumento furono composte solamente verso la fine del XVI sec.; fra queste ricordiamo i Metodi di calcolo per le perle in un piatto (Panzhu suanfa, 1573) di Xu Xinlu, le Regole generali della matematica (Shuxue tonggui, 1578) di Ke Shangqian, i Metodi matematici di Yi Hong (Yi Hong suanfa, 1584) di Yu Kai, la Raccolta [dei metodi fondamentali delle 'Origini generali'] dei metodi matematici (Suanfa zuanyao, 1598) di Cheng Dawei e la Bussola per i metodi matematici (Suanfa zhinan, 1604) di Huang Longyin. Infine, al gruppo di testi che affrontano problemi matematici specifici appartengono gli scritti di Gu Yingxiang intitolati Procedimenti per il calcolo di 'segmenti e archi' (Hushi suanshu, 1552) e Procedimenti matematici per il triangolo rettangolo (Gougu suanshu, 1533), e il Nuovo resoconto della scienza del calcolo (Suanxue xinshuo, terminato prima del 1581 e pubblicato nel 1603) di Zhu Zaiyu (1536-1610 ca.) in cui è trattato l'uso della matematica nella musica. La natura di questi testi rispecchia le caratteristiche della ricerca matematica nell'epoca Ming, incentrata sulle applicazioni pratiche. L'unico matematico del passato che continuò a esercitare una qualche influenza teorica in questo periodo fu Yang Hui, mentre la maggior parte delle teorie e dei metodi sviluppati durante le dinastie Song e Yuan andò perduta per cui spesso i matematici Ming non erano più in grado di comprendere molti procedimenti. È il caso del metodo seguito da Qin Jiushao per la risoluzione delle equazioni di grado superiore con coefficienti numerici, detto 'metodo per l'estrazione di radice mediante addizione e moltiplicazione' (zengcheng kaifang fa), risalente al 1247. Questo procedimento (che era efficiente quanto il cosiddetto metodo Ruffini-Horner, divulgato in Europa nel 1819) non compare in nessuna delle opere di matematica pubblicate fra la metà del XIV e la fine del XVI secolo. Per quanto riguarda invece il triangolo di Jia Xian (conosciuto in Europa con il nome di 'triangolo di Pascal'), risalente all'XI sec., esso è citato negli scritti di Wu Jing, Wang Wensu e Cheng Dawei, tuttavia soltanto Wang lo applica alla risoluzione di equazioni.
Un altro esempio del declino degli studi matematici in epoca Ming è l'interpretazione del metodo di Qin Jiushao per la risoluzione di sistemi di congruenze lineari. Un certo numero di problemi di questo tipo si trova nelle opere di Wu Jing, Xu Xinlu e Cheng Dawei, che tuttavia si limitano a fornire le soluzioni di sistemi specifici senza indicare un metodo generale di risoluzione. Nelle Origini della matematica di Yan Gong troviamo un numero maggiore di problemi, ma il metodo suggerito è valido soltanto per il particolare tipo di questioni affrontate nel suo libro e non può essere considerato un algoritmo generale. Wang Wensu presentò due procedimenti del tipo 'prova ed errore'; la sua spiegazione del metodo di Qin Jiushao dimostra però un'incomprensione dell'aspetto più importante di tale procedimento, ossia del fatto che poteva essere applicato alla risoluzione di sistemi di congruenze anche in presenza di moduli che non erano tutti primi tra loro. Inoltre, l'ultima applicazione durante la dinastia Yuan del metodo dell'incognita celeste si trova nel Trattato generale sulla gestione del fiume (Hefang tongyi, 1321) di Shakeshi (1278-1351); durante i tre secoli successivi nessun matematico riuscì a comprendere correttamente questo metodo che coinvolgeva lo studio dei polinomi in un'indeterminata, e tanto meno la sua generalizzazione al metodo delle quattro incognite. L'analogia sostanziale di tali metodi con l'algebra sviluppata in Occidente e introdotta in Cina dai missionari europei nel XVII sec. fu messa in luce per la prima volta da Mei Gucheng (1681-1763). Il termine 'incognita celeste' (tianyuan) compare negli scritti di Wu Jing e di Cheng Dawei, che tuttavia non ne comprendono appieno il significato e lo utilizzano in modo non appropriato. Wang Wensu lo usa in combinazione con quadrato, cubico e così via e parla, per esempio, di 'incognita celeste cubica' (lifang tianyuan), ma tale interpretazione del termine non corrisponde al suo significato originale. Infine, pur avendo avuto la possibilità di leggere e studiare la monografia di Li Ye sull'argomento, neanche Gu Yingxiang e Tang Shunzhi furono in grado di comprenderla. Gu scrisse due libri basandosi sullo studio delle Misurazioni del cerchio sullo specchio del mare di Li Ye, ma decise di omettere e ignorare i 'metodi dettagliati' (cao) contenenti l'esposizione del procedimento dell'incognita celeste; egli giustifica nel modo seguente la sua scelta: "benché i metodi dettagliati annessi a ciascun problema permettano di risolverlo facendo ricorso direttamente all'incognita celeste, [nell'opera di Li] non è fornito alcun metodo per utilizzarla, privando gli studiosi dei dati necessari a una sua piena comprensione. Ho dovuto quindi omettere i dettagli della risoluzione dei vari problemi e scegliere un'esposizione diversa" (Ceyuan haijing fenlei shishu, prefazione). E ancora: "I dettagli della risoluzione di ciascun problema possono essere compresi soltanto facendo ricorso all'incognita celeste e risultano pertanto di difficile comprensione" (Zhongguo kexue jishu dianji tonghui. Shuxue juan, p. 1109). Un ultimo caso esemplare è quello relativo ai metodi di somma delle serie (duoji, lett. 'problema di accumulazione') e di interpolazione (zhaocha). Del primo si erano occupati nel XIII sec. Zhu Shijie e, anche se in modo meno approfondito, Yang Hui, mentre l'interpolazione era stata applicata da Guo Shoujing, alla fine del XIII sec., al calcolo calendaristico. Anche questi metodi caddero in disuso durante la dinastia Ming; nelle opere matematiche del tempo sono trattati alcuni problemi di somma delle serie, facendo però riferimento soltanto ai risultati di Yang e ignorando quelli più perfezionati di Zhu Shijie.
Gli ostacoli agli Studi di astronomia
In epoca Ming l'astronomia attraversò un periodo di declino inarrestabile e molti risultati raggiunti in epoca Song e Yuan andarono perduti. Gli strumenti astronomici utilizzati erano ormai obsoleti e sia i calcoli calendaristici sia le previsioni delle eclissi e dei moti del Sole e della Luna risultavano spesso errati. Per tutta la durata della dinastia Ming restò in uso il Calendario Datong (Datong li) elaborato da Liu Ji (1311-1375); infatti, i tentativi di riformarlo furono osteggiati dalla corte, con il risultato di accumulare errori sempre più gravi nel corso degli anni. Per quanto riguarda gli strumenti di misurazione del tempo, non furono realizzati progressi significativi. Il miglioramento e lo sviluppo di nuovi tipi di clessidra furono impediti dall'emanazione, all'inizio della dinastia Ming, di un decreto imperiale che imponeva l'unificazione di tutti i tipi di clessidra in uso nel paese. Sia il sistema di misurazione del tempo sia le indicazioni sugli strumenti erano piuttosto imprecisi; per esempio, la bacchetta che fungeva da indicatore era suddivisa sommariamente in quarti. In seguito non fu effettuato alcun tentativo di miglioramento o di rinnovamento degli strumenti di misurazione del tempo e ad aggravare la situazione si aggiunse la distruzione di alcune clessidre del periodo Yuan. Nella Storia della dinastia Ming (Mingshi) si racconta che quando nel 1368 al primo imperatore Ming, Hongwu (Zhu Yuanzhang, 1368-1398), fu presentata una clessidra meccanica di epoca Yuan, dotata di un segnalatore automatico costituito da due statuine di legno che suonavano, a intervalli di un'ora, un tamburo e un zheng (uno strumento a percussione a forma di campana utilizzato anticamente dalle truppe in marcia), l'imperatore, considerandolo soltanto un complicato giocattolo che poteva distrarlo dai suoi doveri di sovrano, ordinò che fosse fatto a pezzi. Questo episodio emblematico può aiutare a comprendere come l'atteggiamento degli imperatori Ming influisse negativamente sullo sviluppo degli strumenti di misurazione del tempo.
Gli strumenti astronomici versavano in condizioni altrettanto disastrose; l'osservatorio della capitale, a Pechino, rimase privo di strumenti fino al 1438, anno in cui ne furono realizzati due, una 'sfera armillare' (hunyi) e una sua versione semplificata (jianyi), in base ai modelli di legno degli strumenti dell'osservatorio di Nanchino ideati da Guo Shoujing all'inizio della dinastia Yuan. La realizzazione di tali strumenti e il loro impiego a Pechino presentarono molti problemi che furono risolti soltanto più tardi. L'armilla semplificata non era stata graduata fino all'eclittica e ulteriori graduazioni furono aggiunte nel 1446. Inoltre, la differenza di latitudine fra Nanchino e Pechino da un lato causava imprecisioni che divennero note soltanto nel 1447, dall'altro lato rendeva gli strumenti realizzati per Nanchino inutilizzabili nella nuova capitale. Infine, non era stato preso in considerazione il fenomeno della precessione degli equinozi dovuto al movimento conico dell'asse di rotazione della Terra; nella sfera armillare gli equinozi erano semplicemente copiati dal modello più antico e solamente nel 1489 si acquistò consapevolezza di questo problema.
L'atteggiamento dei sovrani Ming provocò anche un declino negli studi teorici della disciplina; la corte vietò infatti alla gente comune di studiare astronomia e di collezionare libri sull'argomento, mentre stabilì che la carica di astronomo presso l'Ufficio astronomico imperiale divenisse in pratica ereditaria. Un documento del sesto anno della dinastia Ming (1373) riporta la seguente proibizione: "Agli astronomi dell'Ufficio astronomico imperiale non è permesso di cambiare professione. I loro discendenti hanno l'obbligo di studiare astronomia e matematica e non sarà loro permesso studiare altre discipline a scopo professionale. I discendenti degli astronomi ufficiali che non studino astronomia e matematica saranno deportati nei Mari del Sud e condannati ai lavori forzati" (Da Ming huidian, p. 2959). Sulla prima pagina del Calendario Datong era scritto: "Chiunque falsifichi il calendario sarà punito con la morte, secondo la legge, e chi denuncerà i contraffattori riceverà come ricompensa 50 liang [di argento]. Un calendario privo di questo timbro è da considerarsi contraffatto" (Jiang Xiaoyuan 1991, p. 120). Era persino vietato lo scambio di idee fra astronomi impiegati in dipartimenti diversi dell'Ufficio astronomico imperiale e vi furono casi di funzionari fustigati a morte per aver parlato di fenomeni celesti. Date le circostanze, le persone interessate a studiare astronomia divennero sempre più rare e, per proteggere sé stessi e le loro famiglie, gli astronomi evitavano di esprimere apertamente il proprio parere. Persino lo stesso autore del Calendario Datong, Liu Ji, che aveva sostenuto Hongwu nella fase della fondazione della dinastia Ming, non volle che i suoi discendenti studiassero astronomia. Nella Storia della dinastia Ming si legge che "quando, gravemente ammalato, tornò a casa, Liu Ji affidò il Libro di astronomia al figlio Lian, esortandolo a rimetterlo immediatamente alla Corte e a non permettere a nessuno dei suoi discendenti di studiarlo" (Mingshi, p. 3781). Altri documenti attestano che i funzionari di corte avevano timore a studiare astronomia: "Un giorno l'imperatore chiese a Yang Shiqi e ad altri funzionari della corte: "Avete osservato il cielo stellato la notte scorsa?" Rispose Yang: "Noi non conosciamo la scienza del cielo". Disse l'imperatore: "Chiunque sia chiamato ru ['seguace di Confucio', 'letterato'] deve conoscere il cielo, la Terra e l'uomo. Come mai non conoscete la scienza del cielo?" Gli fu risposto: "Non osiamo studiare astronomia, perché è vietato dalla legge"" (YWsq, 867, pp. 211-212).
L'Ufficio astronomico divenne così un organismo sempre più inadeguato, chiuso a ogni innovazione e inavvicinabile per gli studiosi di talento. Soltanto sporadicamente la corte tentò di prendere qualche provvedimento nel tentativo di riformare questa struttura. Durante il regno di Hongzhi (1488-1505) la proibizione di dedicarsi agli studi di astronomia fu in parte revocata e fu chiesto agli studiosi della materia di presentarsi a corte, ma nessuno si fece avanti. Nel corso del XVI sec. un numero crescente di persone si rese conto che il divieto andava revocato del tutto; molti funzionari cominciarono a parlare apertamente di astronomia e alcuni tentarono persino d'incoraggiare lo studio della materia al di fuori dell'Ufficio astronomico. Vi furono, infine, individui particolarmente audaci, come il principe Zhu Zaiyu (1536-1610 ca.) e Xing Yunlu, un funzionario dello Shaanxi, che osarono scrivere libri di astronomia o compilare nuovi calendari.
Nella tradizione cinese era estremamente importante possedere calendari in grado di prevedere correttamente le eclissi e i moti del Sole e della Luna; ciò nonostante, durante la dinastia Ming le previsioni delle eclissi risultavano spesso poco accurate a causa dell'uso di un calendario estremamente impreciso che era stato compilato poco prima della fondazione della dinastia da Liu Ji. Uomo di fiducia del nuovo imperatore, che però non possedeva le conoscenze astronomiche necessarie a un simile compito, Liu Ji si basò infatti completamente sul Calendario Shoushi (Shoushi li) elaborato da Guo Shoujing e risalente al 1281. Nel 1384 Yuan Tong, un astronomo dell'Ufficio astronomico imperiale, fece notare che in sostanza il Calendario Datong era soltanto una copia del calendario di Guo Shoujing e ne propose la revisione allo scopo di correggerne le imprecisioni che andavano aumentando col passare del tempo. La sua proposta fu accolta e Yuan Tong fu nominato direttore dell'Ufficio astronomico con l'incarico di riformare il calendario. In questa veste pubblicò la Norma generale del calendario Datong (Datong lifa tonggui), in cui spiegava in modo particolareggiato i metodi per prevedere le eclissi e i calcoli calendaristici da lui usati. La nuova edizione, tuttavia, si basava ancora sostanzialmente sul calendario di Liu Ji e conteneva soltanto alcune modifiche di importanza secondaria; l'epoca, ossia la data a partire dalla quale erano stati eseguiti i calcoli calendaristici, fu spostata dal 1280 al 1384, ma la precessione degli equinozi vi era del tutto ignorata e la durata del giorno era ancora indicata con l'ora di Nanchino in tutto l'Impero.
Il Calendario Shoushi di Guo Shoujing era stato estremamente preciso, tuttavia rimase in uso troppo a lungo senza che vi fossero apportate le necessarie correzioni e il margine di errore aumentò sempre più con il passare del tempo; nel 1450 la sua scarsa affidabilità era divenuta ormai evidente. Per esempio, gli Annali della dinastia Ming (Ming shilu), cronaca ufficiale delle attività quotidiane degli imperatori, riportano che il quindicesimo giorno del primo mese del primo anno del periodo di regno Jingtai (1450-1456), ossia il 28 gennaio 1450, "l'eclissi lunare si verificò al terzo quarto dopo mao zheng [ore 6.45], mentre le previsioni indicavano che sarebbe avvenuta al primo quarto dopo chen chu [ore 7.15]" (Ho Peng-Yoke 1986, p. 236); si trattava di un errore di ben due quarti d'ora. In seguito a ciò, un certo numero di astronomi e di funzionari dell'Ufficio astronomico fu punito in vario modo per aver sbagliato le previsioni. Molti testi dimostrano che non tutti ignoravano la scarsa precisione del calendario; nella Storia della dinastia Ming, ultimata nel 1739, si legge: "Sin dal periodo di regno di Chenghua, le previsioni delle eclissi non hanno mai corrisposto alla realtà" (Mingshi, p. 516). Nel 1611 in un memoriale all'imperatore, Fan Shouji scriveva: "Dal primo anno di regno di Wanli fino a oggi, le previsioni di una dozzina di eclissi sono state imprecise, con errori di uno, due o persino quattro quarti d'ora" (Ho Peng-Yoke 1986, p. 641). Queste notizie sono indicative dei problemi posti dal Calendario Datong, le cui previsioni finirono per essere considerate meno affidabili di quelle del Calendario islamico (Huihui li), molto più accurato. Per esempio, nel comunicato dell'Ufficio astronomico sull'eclissi solare del primo giorno dell'undicesimo mese del dodicesimo anno di regno di Wanli (1584), si legge che "secondo il Calendario Datong, l'eclissi sarebbe dovuta durare 92 secondi, mentre secondo il Calendario islamico non si sarebbe verificata. I fatti hanno dimostrato che erano giuste le previsioni del Calendario islamico" (ibidem, p. 600). Per evitare punizioni, l'Ufficio astronomico imperiale fornì all'imperatore le previsioni basandosi su entrambi i metodi. Li Dexiu, vicedirettore dell'Ufficio astronomico, avanzò nel 1393 alcune critiche sul Calendario Datong di Yuan Tong in seguito alle quali la corte respinse circa dieci proposte di revisione con motivazioni diverse. Nel 1483 l'Ufficio astronomico non accolse una proposta con la motivazione che "non si può modificare il vecchio calendario, in quanto è stato adottato al momento della fondazione della dinastia" (ibidem, p. 364); nel 1497 un'altra proposta fu rigettata perché "per oltre 100 anni non sono stati rilevati errori nel calendario" (ibidem, p. 424). In seguito per tre volte ancora, fra il 1519 e il 1523, tre astronomi chiesero senza successo che fossero apportate modifiche al calendario. Per molti funzionari, appartenenti non soltanto all'Ufficio astronomico ma anche ad altri settori della corte, la modifica del calendario doveva essere affrontata con la massima cautela, trattandosi di un importante documento imperiale. Inoltre, gli astronomi di corte erano giudicati incapaci di portare a termine il compito di revisione. Nel 1595 il nuovo calendario di Zhu Zaiyu fu accolto da aspre critiche; secondo i suoi avversari "il Calendario Datong, compilato durante il regno dell'imperatore Hongwu e utilizzato per oltre 200 anni, non potrà mai essere modificato. Un cambiamento […] sbalordirebbe tutti, non soltanto in patria, ma anche all'estero" (ibidem, p. 616).
Molti astronomi furono puniti o minacciati per aver proposto la revisione del calendario; per esempio, Yu Zhengji fu condannato per aver fatto commenti sconvenienti nella sua proposta di revisione del calendario del 1481. Un caso analogo fu quello di Zhu Sheng che nel 1497 propose di rettificare il calcolo della precessione e fu minacciato di punizione per aver studiato astronomia senza autorizzazione. Quando nel 1596 Xing Yunlu presentò all'imperatore un memoriale in cui proponeva la revisione del calendario, i funzionari dell'Ufficio astronomico si irritarono e Zhang Yinghou, Direttore dell'Ufficio, lo accusò di abuso di potere e di aver contravvenuto alle leggi che vietavano di studiare il calendario. Un caso molto interessante è la disputa del 1542; il giorno in cui fu pubblicato il calendario del nuovo anno, fra alcuni studenti dell'Ufficio astronomico nacque in proposito un acceso dibattito e poiché ognuno restava della propria opinione decisero di ricorrere al giudizio dell'imperatore. Essi non soltanto non riuscirono a farsi ricevere, ma furono anche puniti per aver contravvenuto alla legge; 13 studenti di entrambe le parti furono espulsi e nello scandalo furono implicati anche i loro insegnanti e alcuni funzionari, mentre le questioni sollevate rimasero senza risposta.
In conclusione, il principale ostacolo alla revisione del calendario fu la stessa corte imperiale; gli autori della Storia della dinastia Ming riportarono che "i funzionari dell'osservatorio restarono ostinatamente aggrappati al passato e la paura di ogni cambiamento immobilizzò tutte le persone interessate in una posizione di stallo, impedendo che si procedesse alla revisione del calendario" (Mingshi, p. 516). Nonostante il susseguirsi delle proposte, la questione della revisione del calendario non fu mai risolta.
Un'opera per la divulgazione della matematica: le 'Origini generali dei metodi matematici' di Cheng Dawei
di Li Zhaohua
Cheng Dawei (1533-1606) era originario della regione dell'Anhui, all'epoca molto vivace dal punto di vista economico e culturale. Fin da giovane dimostrò grande intelligenza e varietà d'interessi: matematica, paleografia, calligrafia e poesia. A vent'anni intraprese la carriera commerciale seguendo la tradizione familiare; nel corso dei suoi numerosi viaggi nella regione bagnata dal tratto medio e inferiore del Fiume Azzurro raccolse opere di matematica cinese di tutti i tempi, ed ebbe occasione di formarsi una notevole cultura matematica, anche grazie agli scambi avuti con studiosi della disciplina. Dopo il ritorno alla sua città natale, a 40 anni, egli si dedicò completamente ai suoi studi. Nel 1578 il Primo ministro Zhang Juzheng (1525-1582) diede ordine di eseguire, in tutte le province del paese, misurazioni sistematiche dei terreni, necessarie per applicare il nuovo sistema di tassazione detto 'l'unica sferza' (yitiaobian fa) ‒ che semplificava la riscossione delle imposte‒ stabilendo un limite di tre anni per il completamento dei lavori; Cheng vi prese parte, nel 1581, nella zona di Xiuning, sua città natale, probabilmente in ragione delle sue conoscenze matematiche. Intorno ai 60 anni, Cheng Dawei terminò la stesura del Nuovo trattato sistematico sulle origini unificate dell'aritmetica (Xinbian zhizhi suanfa tongzong, 1592, in 17 capitoli, più noto come Suanfa tongzong, cioè Origini generali dei metodi matematici), avvalendosi dei testi che aveva raccolto, degli studi fatti e della pratica acquisita; sei anni dopo ne pubblicò una versione abbreviata, la Raccolta [dei metodi fondamentali delle 'Origini generali'] dei metodi matematici (Suanfa zuanyao, 1598) in 4 capitoli.
L'opera Origini generali dei metodi matematici rappresenta lo stato delle conoscenze matematiche in Cina all'epoca dell'arrivo dei missionari europei; essa ebbe un grande influsso sia in Cina, sia in Corea. Cheng riprende lo stile e la struttura generale dei Nove capitoli; dopo una parte introduttiva, espone alcuni aspetti della matematica tradizionale e nozioni di uso quotidiano, per finire con problemi difficili e metodi risolutivi di varia natura. La prima sezione e il terzo capitolo del libro parlano dell'origine della matematica collegandola ad alcuni elementi di numerologia presenti nell'esposizione della teoria sul quadrato e il cerchio, e nella considerazione di configurazioni numeriche quali il Diagramma del Fiume [Giallo] (Hetu, per i numerali da 1 a 10) e il Documento del Fiume Luo (Luoshu, per quelli da 1 a 9). I primi due capitoli trattano di matematica elementare e presentano un'esposizione esaustiva dei metodi di calcolo con l'abaco. Nei dieci capitoli centrali sono presentati dieci tipi di algoritmi: fangtian ('misurazione dei campi'), subu ('miglio e tessuti'), cuifen ('distribuzione per proporzioni'), shaoguang ('ridurre l'ampiezza'), fentian jieji ('divisione dei campi e distribuzione dei prodotti'), shanggong ('discussioni su problemi edili'), junshu ('tassazioni eque'), yingnü ('eccesso e difetto'), fangcheng ('calcoli facendo uso di tabelle') e gougu ('triangolo rettangolo'). Negli ultimi cinque capitoli l'autore espone in versi numerosi problemi e vari metodi di risoluzione. Alla fine dell'ultimo capitolo si trova, per la prima volta in un'opera matematica cinese, una bibliografia che raccoglie 51 titoli di antichi testi scritti tra il 1084, in epoca Song, e il 1588, sedicesimo anno di regno di Wanli (1573-1619), in epoca Ming. Ciascuno dei dieci capitoli centrali dell'opera introduce qualche elemento originale. Nel cap. 3, per esempio, è citata la 'ruota per misurare' (zhangliang buche), uno strumento usato per misurate i terreni simile all'odierno metro a nastro e molto più avanzato dei compassi di legno tradizionalmente utilizzati, inventato dallo stesso Cheng. L'algoritmo chiamato jieliang chengjin (lett. 'tagliare un liang per ottenere un jin', che corrisponde a un'addizione a base 16), descritto nel cap. 4, espone un metodo di addizione con l'abaco molto semplice e pratico. Infine, nel cap. 6, l'estrazione della radice cubica sull'abaco è realizzata utilizzando la divisione con un divisore a due o più cifre; si tratta della più antica documentazione di metodi di questo tipo. Gli errori presenti nell'opera dimostrano, tuttavia, il declino della matematica cinese alla fine della dinastia Ming: nel cap. 3, quando si parla della riduzione di una frazione che appare come denominatore, è frainteso il significato di mingfen (lett. 'nominare una frazione', che corrisponde all'approssimazione di frazione nell'estrazione di radice in una equazione); nel cap. 6, nella sezione in versi sulla ricerca della soluzione di un'equazione di secondo grado, nella risoluzione del problema per determinare i tre lati di un triangolo rettangolo quando sono noti il prodotto tra i cateti e la differenza tra l'ipotenusa e il cateto maggiore (o minore), Cheng sbaglia nell'usare un'equazione di secondo grado; le formule per l'arco e il vettore di un segmento circolare usate nel cap. 7 non hanno un carattere generale; la formula in versi per determinare il volume di una diga, contenuta nel cap. 8, è errata; infine, nel cap. 12, dove si richiede di determinare un triangolo rettangolo essendo noti un cateto e la differenza dei due cateti, anziché calcolare la lunghezza dell'ipotenusa, si calcola quella del cateto maggiore, e nell'ultimo problema del capitolo la formula per misurare l'altezza e la distanza di un'isola è errata.
La cultura matematica di Cheng e il suo lavoro di raccolta di materiali e di compilazione si riflette nei contenuti delle Origini generali dei metodi matematici, molti dei quali sono ripresi dalle opere di Yang Hui (Metodi rapidi di moltiplicazione e divisione per le superfici dei campi e problemi analoghi, 1275, e Scelta di curiosità nel solco della tradizione, 1275) e di Gu Yingxiang (Procedimenti matematici per il triangolo rettangolo e Procedimenti per il calcolo di ' segmenti e archi', v. par. 1). Vi sono inoltre somiglianze con varie opere di epoca Ming, quali le già citate Spiegazioni dettagliate dei metodi di matematica di An Zhizhai (confrontando le Origini generali dei metodi matematici con l'edizione che ci è pervenuta, stampata con blocchi di rame in Corea, ricomposta secondo l'edizione a incisione del 1373) ed Esame dei 'Nove capitoli sui procedimenti matematici' con [problemi] analoghi di Wu Jing. Per esempio, la soluzione in forma grafica dell'estrazione di radice contenuta nel cap. 6 si trova nel libro di Yang Hui; la formula errata del cap. 8 alla quale abbiamo accennato sopra è la stessa che si trova nel libro di An Zhizhai; quella dell'arco-vettore del cap. 7 coincide con quella del libro di Wu Jing; l'esposizione e l'argomentazione sul quadrato e il cerchio del cap. 3 sono prese dal libro di Gu Yingxiang; e si potrebbe proseguire. Per quanto riguarda l'abaco invece, nessuno dei testi sul calcolo con questo strumento apparsi prima delle Origini generali dei metodi matematici e giunti fino a noi (fra cui le opere di Xu Xinlu, Ke Shangqian, Yu Kai e Zhu Zaiyu, v. par. 1) presenta un'esposizione sistematica sull'argomento comparabile a quella elaborata da Cheng.
L'opera di Cheng rappresenta bene la tendenza verso lo studio e l'uso dell'aritmetica per fini pratici tipici della matematica del periodo Ming. Essa fu ben accolta sia dalla gente comune, interessata alle applicazioni pratiche, sia dai matematici, che apprezzavano l'esposizione sistematica dei problemi, il ricco contenuto, lo stile e la presentazione simili a quelli dei Nove capitoli. L'opera Origini generali dei metodi matematici si prestava quindi a essere largamente diffusa e ha avuto molte edizioni di cui non è noto ancora il numero esatto. Ci sono pervenute cinque copie di un'edizione in 17 capitoli; 4 copie di un'altra, sempre in 17 capitoli; una in 12 capitoli e una in 13, oltre a varie edizioni rivedute. Di queste, la migliore è quella in 17 capitoli (quattro copie), un'incisione opera di Cheng Guangshen che risale al 1716, periodo di regno Kangxi della dinastia Qing. In Giappone si trova oggi un'edizione in 17 capitoli con una tavola di simboli giapponesi (cinque copie), incisa e pubblicata nel 1675.
L'abaco
di Alexei Volkov
Il termine cinese moderno per abaco è suanpan, letteralmente 'vassoio (o piatto) per calcolare (o per contare, o per le bacchette per contare)'. Le versioni moderne dello strumento, che sono sia cinesi sia coreane o giapponesi, sono formate da una struttura rettangolare, solitamente di legno, e da asticelle metalliche, poste tra i lati maggiori del telaio. I tipi più diffusi sono due: uno ha sette dischetti (o palline) mobili su ogni asticella, l'altro soltanto cinque. La struttura è divisa in due aree da un listello trasversale; la parte più grande, di solito quella inferiore, contiene quattro o cinque palline, e quella superiore le restanti (una o due, rispettivamente). Ogni asticella rappresenta una posizione decimale, cioè i valori 10k, 10k+1, 10k+2, ecc., a partire da destra, dove k (ossia, la prima posizione decimale adoperata) dipende dall'ordine di grandezza del numero da rappresentare. Le cifre da 0 a 4 si rappresentano spostando verso il listello trasversale un numero corrispondente di palline della parte inferiore, mentre quelle del settore superiore ne sono tenute distanti; le cifre da 5 a 9 si segnano invece con una pallina della parte superiore spostata verso il listello, e da 0 a 4 palline della parte inferiore spostate anch'esse verso il listello. La quantità di posizioni decimali del numero da rappresentare sull'abaco è dunque limitata dal numero delle asticelle. Nel Classico di Lu Ban (Lu Ban jing), un testo di falegnameria del XV sec. d.C. che contiene la più antica descrizione cinese dell'abaco pervenutaci, questo numero non è specificato, né si può ricavare dalle dimensioni dello strumento che sono fornite, in quanto la descrizione è probabilmente alterata; è stato però suggerito che potevano essere 12. L'abaco con sette palline, più diffuso oggi in Cina, ha 13 asticelle, mentre quello con cinque, noto come abaco giapponese, ne ha 21.
L'abaco era sicuramente più pratico da utilizzare rispetto al sistema con le bacchette, ma aveva l'inconveniente, dovuto alla sua struttura, di rendere molto difficile la rappresentazione di un numero che avesse molte posizioni decimali, e ciò a causa della mancanza di spazio, circostanza evidente quando si dovevano compiere operazioni aritmetiche, anche le più elementari, che richiedevano la rappresentazione simultanea di due numeri e dei risultati parziali. Questa difficoltà è riportata esplicitamente nei resoconti di chi si serviva di più abachi contemporaneamente. Il celebre matematico Zhu Zaiyu (v. par. 1) affermava, per esempio, che per l'estrazione di radice serviva un abaco con 81 posizioni decimali e 567 palline, oppure occorreva utilizzare contemporaneamente quattro o cinque abachi normali. Al riguardo è interessante ricordare che anche i più antichi esemplari dell'abaco russo chiamato sčëty, risalenti al XVI sec. d.C. ca., presentano due o quattro abachi uniti insieme, con nove o dieci palline su ciascuna asticella. La dimensione normale di un abaco era però sufficiente per effettuare operazioni con cifre che avessero un numero ragionevole di posizioni decimali; come nel caso del calcolo con le bacchette, le operazioni si effettuavano cifra per cifra e per utilizzare razionalmente lo spazio disponibile si sostituivano le cifre non più utilizzate con quelle dei risultati intermedi.
Nei trattati medievali di matematica cinese si trovano molti procedimenti per effettuare le varie operazioni aritmetiche; quello per la moltiplicazione chiamato liutou cheng, che si può tradurre approssimativamente con 'moltiplicazione che conserva la testa', dove 'testa' è un termine tecnico per indicare la prima posizione di uno dei due fattori (in questo caso il secondo), fu concepito originariamente per il metodo delle bacchette, come descritto nella Introduzione allo studio della matematica (Suanxue qimeng, 1299) di Zhu Shijie. Esso ricorre in molti trattati dedicati al calcolo con l'abaco ed è presentato come il più importante metodo di moltiplicazione nelle Origini generali dei metodi matematici di Cheng Dawei; una variante di questo procedimento sarà in uso in Giappone dal XVII secolo.
La comparsa dell'abaco
Quando esattamente l'abaco sia comparso in Cina è un problema aperto. Forse è troppo prudente affermare che questo strumento "divenne di uso comune in Cina a partire dalla seconda metà del XVI sec." (Martzloff 1997, p. 215); quasi sicuramente esso era già utilizzato al più tardi all'inizio del XV sec., e alcune testimonianze suggeriscono un uso abbastanza diffuso già alla fine del XIII secolo. Le affermazioni di alcuni studiosi secondo cui l'abaco esisteva già nel II o III sec. d.C. si basano tutte soltanto su un passo del trattato Memorie sui metodi di numerazione (Shushu jiyi) attribuito a Xu Yue (attivo nel 220 d.C.), e al commento a quel passo scritto da Zhen Luan (attivo intorno al 560 d.C.), dove si fa riferimento allo strumento per il 'calcolo con le perle' (zhu suan, v. oltre). Non abbiamo però alcuna prova che l'abaco fosse usato in Cina prima dell'anno 1000.
Una delle più antiche raffigurazioni dell'abaco esistenti si trova nel quadro di Wang Zhenpeng (1288-1350 ca.) Dipinto del Cielo e della Terra trasportati insieme (Qian Kun yi dan tu, datato al 1310), in cui è rappresentato un commesso viaggiatore che trasporta un enorme secchio contenente vari oggetti, tra i quali un abaco. Lo strumento è riprodotto con molta precisione: ha cinque palline nella parte inferiore, mentre il numero di quelle nella parte superiore, una o due, è impossibile da determinare; secondo alcuni, il dipinto dimostrerebbe che l'abaco era molto diffuso all'epoca della dinastia Song (Hua Yinchun 1987). Una raffigurazione di un abaco con 10 aste e 7 palline per asta si trova nel manuale per bambini Caratteri eterogenei delle 'Quattro parole a coppie' (Kuiben duixiang siyan zazi, 1371); in questo libro, stranamente, le bacchette (suanzi) sono rappresentate accanto all'abaco. Un'altra edizione a stampa del libro, intitolata Nuova edizione delle 'Quattro parole a coppie' (Xinbian duixiang siyan, 1436), contiene un disegno leggermente diverso. Infine, in un famoso quadro del XII sec. opera di Zhang Zeduan, Quadro del [risalire] il fiume [durante] la festività del Qingming (Qingming shanghe tu, forse risalente agli anni tra il 1100 e il 1126), si trova raffigurato un oggetto simile a un abaco; se questa identificazione è corretta il quadro sarebbe la più antica testimonianza dell'esistenza dello strumento nei primi anni del XII secolo.
L'abaco è menzionato in molte opere letterarie delle dinastie Song e Yuan e in quelle dell'inizio della dinastia Ming. Il trattato Nuovi scritti dal dipartimento meridionale (Nanbu xinshu) di Qian Yi (attivo negli anni 1008-1016) parla di un 'metodo [per calcolare?] le perle' (guzhu zhi fa) riferendosi molto probabilmente a uno strumento per calcolare con le 'perle' (zhu), ossia delle palline, simile a uno di quelli descritti nelle citate Memorie sui metodi di numerazione, mentre invece il titolo del poema di Liu Yin (1249-1293) Suanpan ('abaco' in cinese moderno) paradossalmente non sembra fare riferimento all'abaco (Hua Yinchun 1987). Per quanto riguarda i testi matematici sull'abaco, che come si è visto costituiscono una parte importante della produzione matematica di epoca Ming (v. par. 1), il primo a noi pervenuto nel quale è raffigurato l'abaco è il libro già citato di Xu Xinlu Metodi di calcolo per le perle in un piatto (1573). Lo strumento raffigurato ha nove aste, ciascuna con una pallina nella parte superiore e cinque in quella inferiore. I numeri da 1 a 5 si rappresentano spostando verso il listello divisorio da una a cinque palline della parte inferiore, e i numeri da 6 a 9 con una pallina della parte superiore spostata verso il basso e da una a quattro di quelle della parte inferiore spostate verso l'alto; quindi, contrariamente ad altri che lo seguiranno, questo abaco utilizza un sistema di rappresentazione dei numeri analogo a quello del calcolo con le bacchette. Si può citare tuttavia un altro testo che descrive lo stesso sistema a nove aste, la Bussola per i metodi matematici (Suanfa zhinan, 1604) di Huang Longyin. L'abaco rappresentato da Ke Shangqian nelle Regole generali della matematica (1578) ha invece 10 aste e 2+5 palline (cioè il sistema moderno); il numero 5 era rappresentato da una pallina nella parte superiore; uno strumento dello stesso tipo è presentato da Cheng Dawei nelle Origini generali dei metodi matematici, con la differenza che questo ha quindici aste (v. par. 2 e Mei Rongzhao 1983, dove sono elencati molti altri trattati del XVI sec. che spiegano come eseguire calcoli con l'abaco). Per quanto riguarda le menzioni di epoca precedente nei testi matematici, nell'Esame dei 'Nove capitoli sui procedimenti matematici' con [problemi] analoghi di Wu Jing (v. par. 1), l'abaco è citato due volte, in modo vago e generico; secondo alcuni autori, almeno due delle opere contenute nella sezione bibliografica delle Origini generali dei metodi matematici hanno titoli che possono riferirsi all'abaco, ma poiché entrambi i libri sono andati perduti è impossibile verificare se effettivamente si parlasse proprio di questo strumento. Infine, anche in un'opera del matematico Xie Chawei (attivo probabilmente nella prima metà dell'XI sec.) si trovano altre affermazioni che, secondo alcuni studiosi moderni, potrebbero riferirsi all'abaco. Un oggetto simile a una pallina dell'abaco moderno risalente al 1108 d.C. fu trovato nel 1921; l'esemplare più antico in nostro possesso è stato però trovato in una tomba degli ultimi anni del XVI o dei primi del XVII sec.; ha 15 aste con 1+5 palline, e si tratta perciò del tipo descritto nel già citato Metodi di calcolo per le perle in un piatto. Numerosi autori hanno osservato che l'abaco cinese e lo strumento per il 'calcolo con le perle' del commento di Zhen Luan alle Memorie sui metodi di numerazione assomigliano all'abaco romano, una piccola struttura metallica con numerose scanalature e dischetti scorrevoli. Alcuni autori suggeriscono che l'abaco romano fu portato in Cina dall'Europa, e dalla Cina in Giappone e in Russia; questa conclusione appare un po' affrettata e il problema delle origini dell'abaco (come quello del rapporto fra abaco cinese e sčëty russo) resta tuttora aperto.
La rappresentazione dei numeri e le corrispondenze cosmologiche: i precursori dell'abaco
Nelle Memorie sui metodi di numerazione attribuite a Xu Yue è contenuta la descrizione di uno strumento che apparentemente assomiglia e si basa su principî simili a quelli dell'abaco. Quest'opera si fa risalire tradizionalmente a un periodo compreso tra la fine del II e l'inizio del III sec., e il commento scritto da Zhen Luan, nel VI sec., è considerato da alcuni una prova dell'esistenza dell'abaco prima di questo secolo, al quale è spesso ritenuto appartenere (Needham 1959; Yamazaki 1959). Nelle Memorie sui metodi di numerazione sono elencati diversi metodi di rappresentazione dei numeri naturali per mezzo di strumenti; questi ultimi sono menzionati molto brevemente e la loro interpretazione moderna segue essenzialmente il commento di Zhen Luan. Il passo rilevante per quanto riguarda il metodo che potrebbe rappresentare l'origine dell'abaco recita: "Calcolo con le perle: controllare e guidare le Quattro Stagioni, [fornire] trama e ordito per le Tre potenze". Il commento di Zhen Luan spiega così questa frase:
Intagliare una tavola di legno e suddividerla in tre parti. Due ‒ le parti superiore e inferiore ‒ servono a tenere fisse le 'perle mobili'. La parte collocata tra le due è per stabilire le posizioni [decimali] per il calcolo. In ciascuna posizione vi sono cinque perle. I colori di una perla della [parte] superiore e delle quattro perle della [parte] inferiore sono [tutti?] diversi. Una perla nella sua [parte] superiore [= della tavola], e che ha un colore diverso, corrisponde alle quattro perle poste nella sua [parte inferiore]. Ogni perla [nella parte inferiore] è guidata [controllata] secondo l'arrivo della perla [della parte superiore] alle quattro perle nella [parte] inferiore; ciò spiega perché è detto 'controllare e guidare le Quattro Stagioni'. Le perle si muovono nelle tre posizioni; ecco perché si dice '[fornire] trama e ordito per le Tre potenze'. (Suanjing shishu, II, p. 546)
Anche se è piuttosto oscura, non vi è dubbio che questa descrizione si riferisce a una tavola di legno con tre scanalature (le tre 'parti'), nelle quali sono poste delle palline ('perle', zhu) di 'colori diversi'. Non si parla di aste alle quali le perle siano attaccate. Una cifra è rappresentata da una combinazione di perle prese dalle due parti superiore e inferiore dello strumento e poste nella parte mediana. Le tre parti, superiore, inferiore e mediana, rappresentano le Tre potenze della filosofia classica cinese, vale a dire Cielo, Terra e Uomo. Rimane abbastanza oscuro il criterio con cui i numeri erano rappresentati con questo strumento. Secondo un'ipotesi accettata dalla maggior parte degli studiosi moderni, esso era analogo a quello dell'abaco moderno. Le perle nei settori superiore e inferiore erano di due colori diversi; le cifre da 1 a 5 erano rappresentate dal corrispondente numero di perle di un colore del settore inferiore, mentre una cifra n da 5 a 9 era rappresentata da una perla di un altro colore (e avente valore 5) del settore superiore e n−5 perle del settore inferiore. Yoshio Mikami suggerì che la descrizione poteva riferirsi a un qualche tipo di abaco "benché l'abaco fosse allora di forma alquanto diversa da quella che avrà in seguito" (Mikami 1913, p. 111); successivamente, avendo verificato che tutte le edizioni pervenute del trattato contenevano la stessa oscura descrizione dello strumento, egli confermò la sua ipotesi osservando che se si aggiunge un carattere (e cioè il numerale 'cinque') e si cambia conseguentemente la punteggiatura, il testo si può interpretare come un chiaro riferimento a uno strumento simile all'abaco: "una perla nella sua [parte] superiore [della tavola], che ha un colore diverso, corrisponde a 5; [per quanto riguarda] le quattro perle poste nella [parte] inferiore, ogni perla corrisponde a 1" (Qian Baocong 1921, p. 3). Anche se il testo non è emendato in questo modo, la descrizione dello strumento si presta a essere interpretata effettivamente come una prima testimonianza del sistema di rappresentazione dei numeri dell'abaco, vi è tuttavia un'altra possibile interpretazione, che parte dall'esame degli altri strumenti per rappresentare numeri ed eseguire dei calcoli menzionati nel trattato.
La maggior parte dei 'metodi di calcolo' descritti brevemente nelle Memorie sui metodi di numerazione (i quali utilizzano tutti strumenti, eccetto uno, e sono spiegati in dettaglio da Zhen Luan) combina, per rappresentare i numeri naturali da 1 a 9, sia posizioni sia colori dei dischetti. Nel metodo detto del 'Grande Uno' (tai yi), la tavola di legno ha nove scanalature parallele e un'asta a esse perpendicolare serve a indicare le nove cifre: una 'perla' è libera di scorrere lungo l'asta, e la sua posizione sopra il punto d'intersezione dell'asta e dell'n-esima linea orizzontale (contando a partire da uno dei lati della tavola) rappresenta la cifra n tra 1 e 9. Per poter rappresentare un numero con m posizioni decimali sono necessarie m aste. L'aspetto importante di questo strumento è che, analogamente all'abaco, utilizza l'idea di perle che scorrono su un'asta. Nel metodo dei 'due schemi' (liang yi) la tavola di legno ha invece cinque scanalature parallele e, come nel metodo precedente, un'asta perpendicolare alle cinque linee serve a denotare le posizioni decimali. Ogni asta contiene una sola perla, di colore blu o giallo e i numeri 1, 2, 3 e 4 si rappresentano con una perla gialla posta all'intersezione dell'asta con la prima, la seconda, la terza e la quarta riga, rispettivamente, partendo dal basso; mentre un numero n da 5 a 9 si rappresenta con la perla blu all'intersezione dell'asta verticale con l'(n−4)-esima riga a partire dall'alto; le perle gialle rappresentano la Terra e quelle blu il Cielo. Infine, nel metodo detto 'calcolo dei Nove Palazzi' (jiugong suan), per rappresentare i numeri si usano perle e 'fili' (xian) colorati: i colori corrispondono ai punti cardinali, alle Cinque fasi e ai valori numerici da 1 a 5. Questo genere di corrispondenza ricorre più volte nel trattato ed è utilizzato anche a proposito di un altro metodo, il 'calcolo con i numeri del compimento' (chengshu suan).
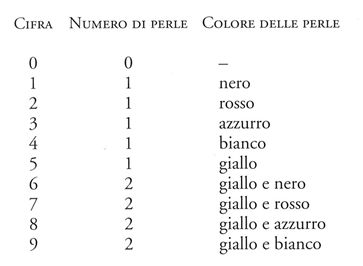
Questi esempi mostrano che il 'calcolo con le perle' è soltanto uno dei diversi metodi di rappresentazione dei numeri basati sul sistema di corrispondenze tra colori, posizioni nello spazio e numeri diffuso nella cosmologia tradizionale cinese simbolica e numerologica, che si affermò alla fine del I millennio a.C. Su questa base è possibile ipotizzare un'altra ricostruzione del metodo di 'calcolo con le perle', che scardinerebbe l'unico argomento a favore dell'ipotesi di un'origine antica del metodo di rappresentazione dei numeri dell'abaco (intorno al VI sec.) piuttosto che durante il periodo Song. Nel metodo di calcolo dei Nove Palazzi, così come in quello detto con i numeri del compimento, contrassegni di colore nero, azzurro, rosso, bianco o giallo denotavano rispettivamente i numeri naturali da 1 a 5, mentre quelli da 6 a 9 erano rappresentati da combinazioni di due contrassegni, uno giallo e uno di un colore nero, azzurro, rosso e bianco. Secondo questa ricostruzione alternativa del metodo di calcolo con le perle, la parte inferiore della tavola conteneva perle di quattro dei colori menzionati (nero, azzurro, rosso, bianco), mentre quelle della parte superiore erano gialle; le cifre da 1 a 9 erano rappresentate da una o due perle nella parte mediana, secondo la seguente
Questa ricostruzione è in accordo sia con il testo sia con il commento di Zhen Luan (emendato o no come suggeriscono Qian Baocong e Yoshio Mikami) ed è confermata dal riferimento esplicito alle Quattro Stagioni in relazione alle quattro perle poste nella parte inferiore; si stabiliva così una corrispondenza tra le perle e i colori tradizionalmente associati alle Quattro Stagioni.
Nell'abaco del periodo Song-Yuan si ritrova una corrispondenza tra le posizioni dei contrassegni e i numeri rappresentati; non sappiamo però se i metodi e gli strumenti descritti nelle Memorie sui metodi di numerazione (in particolare il 'calcolo con le perle') siano effettivamente esistiti, se siano mai stati usati dai matematici, e se uno tra questi sia poi diventato l'abaco Song e in quale epoca. Occorre anche ricordare che la versione in nostro possesso delle Memorie è stata trovata, in un monastero taoista, nei primi anni del XIII sec., e come dimostra un esame anche sommario, è possibile che sia diversa da quella risalente al periodo tra la fine del I millennio e l'inizio del II d.C. Se l'epoca della prima diffusione dell'abaco si può far risalire ai secc. XI e XII, l'origine dello strumento rimane quindi oscura. L'abaco fu concepito sulla base del sistema di corrispondenze simboliche che molto tempo prima aveva prodotto il più potente strumento di calcolo cinese: il calcolo con le bacchette. Quest'ultimo, comparso alla fine del I millennio a.C., stabiliva molteplici relazioni tra numeri, posizioni, forme e colori, e permetteva di rappresentare, o meglio di costruire, vari oggetti matematici, mentre gli strumenti di calcolo servivano a convalidare il modello astratto di questi oggetti concepito nel quadro del sistema simbolico.
Riguardo alla rappresentazione di alcuni oggetti matematici e al loro studio, l'abaco era uno strumento molto meno potente del calcolo con le bacchette. Un tipico esempio di oggetto difficile da rappresentare con l'abaco è una tabella bidimensionale del tipo di quelle che intervengono nello studio dei sistemi di equazioni lineari o di grado superiore. I matematici che cercavano di adattare all'abaco gli algoritmi pensati per il calcolo con le bacchette, devono aver incontrato notevoli difficoltà; lo strumento era in grado di eseguire abbastanza bene soltanto alcuni degli algoritmi che si trovano negli antichi testi cinesi. Pertanto, non è forse una semplice coincidenza che l'epoca in cui l'abaco sostituì il calcolo con le bacchette e divenne di uso comune sia generalmente considerata un periodo di declino nella storia della matematica tradizionale in Cina, un periodo nel quale i metodi sofisticati sviluppati in precedenza, erano stati dimenticati o fraintesi.
L'introduzione della matematica occidentale in Cina nel XVII secolo
di Peter Engelfriet
Nonostante in precedenza non fossero mancati contatti con culture sorte a occidente della Cina, fu soltanto a partire dai primi anni del XVII sec. che lo sviluppo della matematica iniziò a essere nettamente influenzato dall'esterno. La traduzione in cinese, eseguita dai gesuiti, di opere matematiche diffuse nell'Europa contemporanea fece parte di un confronto tra culture che mise in luce incompatibilità di principî e di pratiche in diversi campi, ma non in quello della matematica, dove invece le idee occidentali furono accolte e accettate senza difficoltà. Questo fatto fu espresso felicemente da Li Zhizao, il quale, nella prefazione al suo Trattato sui metodi di calcolo [occidentale e orientale] (Tongwen suanzhi, 1613), uno dei primi adattamenti cinesi di opere europee, spiega come mai la matematica occidentale e quella cinese fossero tanto simili: "non è forse perché le menti sono le stesse, i principî gli stessi, e i numeri naturali del cielo e della Terra sono gli stessi [ovunque]?" (Ming Qing jian Yesuhuishe yizhu tiyao, p. 257). Da questa esplicita fiducia nel significato universale della matematica sarebbe però sbagliato dedurre che da quel momento venisse meno ogni differenza tra la matematica cinese e quella 'occidentale'. Benché Joseph Needham abbia affermato che quasi subito dopo l'introduzione della matematica occidentale quest'ultima e quella cinese si sono 'fuse' in una 'matematica universale' (Needham 1970), studi successivi e più dettagliati hanno mostrato che questa tesi non è sostenibile. Il risultato principale dell'incontro fra due tradizioni matematiche fu un rinnovato interesse per la matematica in sé e la comparsa di una varietà di tentativi, da parte dei principali studiosi, volti a confrontare la matematica importata dall'Occidente con quella sviluppata in Cina e a sistemare, dove possibile, la nuova terminologia, i nuovi metodi e le nuove idee nel quadro offerto dai lavori matematici cinesi che erano ancora accessibili, cercando in tal modo di formulare una sintesi creativa d'insieme. Anche se alcuni importanti aspetti della matematica in Cina erano andati perduti, i lavori di epoca Ming conservavano una parte abbastanza consistente del patrimonio tradizionale perché si potesse valutare quest'ultimo, in generale, non inferiore, sotto ogni riguardo, al materiale europeo recentemente tradotto. Così, cercare di ritrovare i contenuti e lo spirito di quanto era stato fatto in campo matematico nelle epoche precedenti della storia cinese divenne un obiettivo tanto importante quanto quello di 'sviluppare una nuova matematica'.
Le circostanze particolari che caratterizzarono l'introduzione in Cina della matematica occidentale ‒ effettuata da un piccolo gruppo di missionari gesuiti guidati da un'intensa motivazione ideologica e guardati con sospetto sia in Cina sia in Europa ‒ resero tale trasferimento culturale assai differente da altri fenomeni storici di natura analoga, quali, per esempio, quelli avvenuti a Bagdad nei secc. VIII e IX, e in Andalusia nei secc. XI e XII. Lungi dall'essere uno 'scambio culturale aperto', si trattò di qualcosa di limitato sia nello scopo sia nella portata; l'importanza principale fu attribuita allo sviluppo delle applicazioni pratiche, al punto che si trascurò di trasmettere i più importanti risultati teorici della matematica europea del XVII secolo. Inoltre, va considerato che l'interesse dei missionari per la matematica cinese tradizionale, che peraltro in qualche caso avrebbe potuto arricchire la matematica occidentale, rimase sempre molto scarso.
Le prime traduzioni: l'incontro fra due tradizioni matematiche
Appena Matteo Ricci (1552-1610) giunse a Pechino, dove si stabilì nel 1601, incontrò Xu Guangqi (1562-1633) e Li Zhizao (1565-1630), entrambi alti funzionari governativi, i quali non soltanto si dedicarono ad appoggiare la causa dei gesuiti, ma s'impegnarono anche nelle prime traduzioni di testi matematici. Xu Guangqi tradusse, insieme a Ricci, i primi sei libri degli Elementi di Euclide, che uscirono in edizione cinese nel 1607 con il titolo Elementi di geometria (Jihe yuanben; i libri restanti dovranno attendere il 1857), e Li Zhizao si occupò di un'altra parte della classica divisione della matematica occidentale, l'aritmetica. Aritmetica e geometria avevano status molto diversi rispetto alla tradizione matematica cinese: la geometria deduttiva nello stile di Euclide era certamente un'idea completamente nuova, mentre l'aritmetica e l'algebra retorica 'presimbolica' erano già presenti nella tradizione cinese, e l'unica novità consisteva nell'introduzione del calcolo 'scritto', ossia effettuato in modo sistematico con carta e penna. Le conoscenze europee in questo campo che si diffusero in Cina fino alla fine del XVII sec. furono essenzialmente quelle provenienti dalla scuola di Cristoforo Clavio (1537-1612), professore nel Collegio romano, al quale si deve in gran parte la strutturazione del curriculum di studi matematici negli istituti retti dai gesuiti (Baldini 1992). Molti dei gesuiti attivi in Cina, compreso Ricci, si erano formati nella sua 'accademia matematica' e le sue opere costituirono la fonte principale per la maggior parte delle traduzioni in cinese. Fu così che la prima edizione della versione latina di Clavio degli Elementi di Euclide ‒ un'opera erudita pubblicata nel 1574 il cui scopo era anche quello di servire come manuale pratico ‒ formò la base della traduzione di Xu Guangqi e Ricci, intitolata, come già detto, Jihe yuanben (lett. 'elementi di quantità'), mentre l'Epitome arithmeticae practicae (1583) di Clavio fu il punto di partenza per il Trattato sui metodi di calcolo [occidentale e orientale] di Li Zhizao. Come molte traduzioni cinesi di opere occidentali, l''Euclide cinese' fu il risultato di un procedimento per il quale una prima traduzione orale dal latino al cinese era poi rielaborata in una lingua conforme agli standard del cinese classico da parte di studiosi cinesi. In questo modo Xu e Ricci elaborarono la loro mirabile traduzione, che avrebbe lasciato il segno nella terminologia della geometria cinese moderna. Invece di traslitterare semplicemente i termini ‒ ossia di rendere il suono delle parole usando caratteri cinesi privi del giusto significato ma la cui pronuncia approssimava il suono dei caratteri stranieri, secondo una tecnica che nel passato è stata largamente usata in Cina ‒ essi cercarono di trovare un termine cinese equivalente per rendere ogni determinato concetto. Benché questa scelta presentasse il vantaggio di dare luogo a un linguaggio elegante e di immediata comprensibilità, essa aveva però l'inconveniente di mettere in ombra, in vari casi, importanti differenze di sostanza. In effetti, analisi critiche di questo tipo di traduzione hanno rivelato alcuni punti che potevano causare confusione e ostacolare la comprensione (Martzloff 1980).
Una difficoltà di questo genere si presenta già nel titolo stesso dell'opera, Jihe yuanben. La questione non riguarda tanto la scelta del secondo termine, yuanben, che vuol dire 'fonte', 'origine', quanto piuttosto quella del primo termine, jihe, che fu adottato per rendere il concetto di 'quantità in generale' (lat. quantitas). In questo modo però si faceva riferimento a una nozione specifica della matematica greca che non aveva corrispondenza nella matematica cinese, e precisamente alla divisione della matematica, appunto sulla base del concetto di quantità, in due parti: la geometria, avente a che fare con quantità continue (grandezze: du), e l'aritmetica, concernente invece quantità discrete (numeri: shu). Nella matematica in Cina le grandezze geometriche erano sempre considerate come 'quantità misurate'; poiché jihe era un termine che ricorreva frequentemente nei testi matematici cinesi col significato di 'quanto grande' oppure 'quanto numeroso', la scelta di questa particolare espressione avrebbe portato facilmente al venir meno di quella distinzione. Il Jihe yuanben aiutò nell'identificare la geometria come una ben distinta parte della matematica e, abbastanza ironicamente, jihe diventò il termine cinese per 'geometria' in senso stretto (difatti, il titolo cinese della traduzione è stato reso nelle lingue occidentali con Elementi di geometria). Tuttavia, il discorso geometrico contenuto nell'opera di Euclide non fu pienamente apprezzato a quei tempi; a sua volta, questo mancato collegamento può aver costituito un ostacolo per la comprensione della struttura deduttiva degli Elementi, che non fu mai adottata rigidamente. La prefazione di Ricci all'opera ‒ un abile adattamento per il pubblico cinese dei famosi prolegomena di Clavio ‒ sottolinea ampiamente e con grande eloquenza l'utilità della matematica per la società; a essa segue un'appassionata prefazione di Xu Guangqi, nella quale lo studioso cinese introdusse alcuni dei temi che avrebbero profondamente segnato i modi della ricezione della matematica occidentale. Il messaggio fondamentale di Xu era che nella società ideale delle Tre Dinastie (all'incirca prima del 1700 a.C.), che costituiva un quadro di riferimento quasi sacro per i letterati cinesi, le scienze matematiche erano fiorenti e svolgevano una funzione importante nell'organizzazione della società; nelle epoche successive, per mancanza di ordine, questa tradizione era stata trascurata. La matematica occidentale poteva avere un ruolo essenziale nel ristabilire questo aspetto dell'arte di governo e della cultura; si sottolineava in tal modo la continuità con il passato, senza mai sostenere che la matematica occidentale avrebbe dovuto soppiantare quella cinese.
L'attività matematica dello stesso Xu Guangqi fu pienamente coerente con queste idee. In primo luogo, con l'intento d'introdurre materie utili alla società, egli pubblicò, insieme a Ricci, una breve opera sui metodi di misurazione del terreno, la Spiegazione dei metodi di misurazione (Celiang fayi, 1607), basata ancora su quanto Ricci aveva appreso a Roma. Questo problema era trattato nelle opere matematiche cinesi dell'epoca; ma dopo un attento studio dei testi allora in circolazione, egli arrivò alla conclusione che si trattava di fonti spesso carenti sotto molti aspetti e che tali manchevolezze erano dovute alla trasmissione incompleta delle nozioni. Nonostante ciò egli fu portato a concludere che la matematica cinese e quella europea usavano gli stessi metodi; tuttavia, mentre le fonti cinesi non dimostravano perché questi metodi (algoritmi) fossero corretti, né come si fosse giunti a essi, la matematica occidentale forniva invece spiegazioni complete. Lo stile del discorso matematico occidentale poteva quindi mostrarsi d'aiuto nel tentativo di capire la tradizione matematica cinese; Xu compose alcune brevi opere per spiegare in quale modo portare avanti questo lavoro. Così, nelle Differenze e somiglianze [tra oriente e occidente nei metodi] di misurazione (Celiang yitong, 1609) confrontò sei metodi di misurazione del terreno contenuti nella citata opera sull'argomento scritta insieme a Ricci, con i loro equivalenti cinesi; nelle Spiegazioni del triangolo rettangolo (Gougu yi, 1609) cercò di dimostrare geometricamente, secondo i criteri della matematica occidentale, 15 degli algoritmi cinesi tradizionali associati al triangolo rettangolo (gougu); infine, in un'opera rimasta probabilmente inedita, Metodi di estrazione [della radice] quadrata con divisore fisso (Dingfa pingfang suanshu), spiegò geometricamente gli algoritmi per l'estrazione di radice, compresa la forma generalizzata nella quale essi erano utilizzati tradizionalmente per trattare problemi che, nella matematica moderna, comportano equazioni di secondo e di terzo grado a una incognita.
Questo programma di ricerca di carattere comparativo intrapreso da Xu Guangqi fu condiviso da Li Zhizao, che da lungo tempo s'interessava alla geografia e fu spinto verso la cultura occidentale dalla versione cinese del Mappamondo di Ricci. Dopo aver svolto studi di astronomia occidentale sotto la guida di Ricci, Li scrisse, completandolo nel 1605, un trattato sulla costruzione e sull'uso dell'astrolabio, basato sull'Astrolabium (1593) di Clavio. In questo contesto tradusse anche un'opera di geometria intitolata Spiegazioni delle differenze [nell'area e nel volume] tra [figure] contenute in un cerchio e in una sfera (Yuanrongjiao yi, 1607), un breve trattato che Clavio aveva inserito nel suo commento al De sphaera mundi di Giovanni di Sacrobosco (attivo nel 1230), intitolato In Sphaeram Ioannis de Sacro Bosco Commentarius (1570), lavoro che era senza dubbio servito da 'sostegno matematico' al modello cosmologico introdotto dai gesuiti. Il Trattato sui metodi di calcolo [occidentale e orientale], la sua opera più importante, è formata da tre parti scritte in tempi diversi. La prima parte, elaborata insieme a Ricci (sulla base dell'opera di aritmetica pratica di Clavio prima citata) nel 1607, introduce gli algoritmi per effettuare le quattro operazioni aritmetiche fondamentali con carta e penna. La seconda parte, pubblicata nel 1613 insieme alla prima, illustra bene l'evoluzione delle ricerche di Li Zhizao, infatti, anche se è ancora basata sull'originale di Clavio, comprende molto materiale tratto da opere cinesi contemporanee, come le Origini generali dei metodi matematici di Cheng Dawei (v. par. 2), con i relativi commenti di tipo comparativo. L'ultima parte ci è pervenuta soltanto parzialmente, e tratta di trigonometria. L'integrazione nell'aritmetica pratica occidentale di importanti aspetti della matematica cinese consentì a Li Zhizao di estendere la sua trattazione ad argomenti della tradizione dei Nove capitoli sui procedimenti matematici, quali le frazioni, le somme di serie, le estrazioni di radici e la 'regola del tre'. Di particolare interesse è la sezione sul 'metodo della doppia falsa posizione', che egli riconosce analogo al tradizionale metodo ying bu zu (lett. 'troppo e non abbastanza'), corrispondente al cap. 7 dei Nove capitoli; in origine, tale metodo potrebbe essere pervenuto in Cina dall'Europa. Egli si occupa anche del modo cinese tradizionale di trattare i problemi in cui intervengono quelli che oggi chiamiamo 'sistemi di n equazioni lineari in n incognite', il quale poteva essere applicato quando quello della doppia falsa posizione diventava farraginoso, e osserva che il vecchio nome di questo metodo era fangcheng ('calcoli facendo uso di tabulazioni', così denominato in quanto in esso si risolvevano i problemi organizzandone i dati in una tabella), corrispondente al cap. 8 dei Nove capitoli. Più tardi, Mei Wending arriverà ad affermare esplicitamente che il metodo del fangcheng non esisteva nella tradizione matematica occidentale; Li Zhizao non si spinge così in là, ma egli indica comunque un aspetto a proposito del quale la matematica occidentale poteva trovare un arricchimento confrontandosi con la tradizione cinese, sviluppando in tal modo il programma di ricerca comparativo nato dall'incontro tra le due tradizioni (per una trattazione moderna di questi temi).
Le ricerche comparative e la ricostruzione della tradizione matematica cinese: sviluppi successivi
Sebbene le antiche traduzioni ricordate in precedenza fossero, sin dall'inizio, molto ammirate, la conoscenza e l'interesse attivo nei riguardi dei loro contenuti non andarono molto oltre l'ambito d'influenza dei gesuiti. D'importanza maggiore per la diffusione di metodi matematici importati dall'Occidente furono le traduzioni preparate nel contesto della riforma del calendario (v. par. 5); Xu Guangqi e Li Zhizao riuscirono a ottenere che alcuni gesuiti entrassero a far parte del comitato incaricato di migliorare l'accuratezza delle osservazioni e dei calcoli astronomici occorrenti allo scopo e la vasta raccolta di nuove traduzioni prodotte come risultato del lavoro di questo comitato, nota come Trattato sulla scienza calendaristica del periodo Chongzhen (Chongzhen lishu), fu presentata al sovrano tra il 1631 e il 1634. La raccolta includeva molti testi nuovi, riguardanti soprattutto i metodi matematici utili per le misurazioni astronomiche e i relativi calcoli. Erano presenti, infatti, vari trattati di trigonometria piana e sferica, fra cui due testi scritti da gesuiti, Grandi misurazioni (Dace) di Johann Schreck (1576-1630, noto anche come Terrentius) e Spiegazione completa della misurazione (Celiang quanyi) di Giacomo Rho (1593-1638); in quest'ultima opera erano considerati anche i solidi platonici e alcune proposizioni archimedee sulla sfera e sul cilindro, senza però le relative dimostrazioni. Anche l'introduzione di alcuni dispositivi per il calcolo, quale il compasso geometrico militare di Galileo, i cui vari usi sono illustrati nella Spiegazione del compasso per proporzioni (Biligui jie), sempre di Rho, destò molto interesse. Più tardi, fu aggiunto un altro trattato scritto dal gesuita Giulio Aleni (1582-1649), Procedimenti essenziali 'di geometria' (Jihe yaofa, 1631), dedicato a problemi di costruzione e geometria pratica. La pubblicazione di questi testi ispirò negli anni successivi numerosi intellettuali a condurre ricerche matematiche per proprio conto; nella seconda metà del XVII sec. il programma di ricerca intrapreso da Xu Guangqi e Li Zhizao portò a nuovi contributi creativi. Nel frattempo, l'ambiente culturale interessato alla matematica occidentale era cambiato; le ricerche matematiche erano ora condotte soprattutto dai letterati confuciani privati del potere politico, i quali consideravano gli studi matematici come parte di una più vasta impresa intellettuale fortemente accentrata sul passato.
I matematici della generazione fiorita durante e dopo la caduta della dinastia Ming elaborarono e svilupparono ulteriormente il 'progetto' di confrontare e comparare la matematica recentemente importata con l'eredità matematica cinese e d'integrare i nuovi concetti e metodi nella cornice della tradizione cinese che nel contempo si tentava di ricostruire. La suddivisione della matematica nelle varie branche rimase in gran parte quella tradizionale e la forma 'problema-algoritmo' continuò a dominare lo stile di presentazione delle nozioni e dei ragionamenti; tuttavia, l'idea di dimostrazione matematica, nel senso di una spiegazione euristica, guadagnò sempre più importanza. Un esempio tipico di 'letterato-matematico' di questo periodo è Fang Zhongtong (1634-1698) i cui studi matematici sono raccolti in una voluminosa opera intitolata Rivelazione di numeri e grandezze (Shudu yan), completata nel 1661 ma inedita sino al 1687. Il valore di questo testo non sta tanto nell'aver fornito materiale nuovo, poiché si trattava soprattutto di una compilazione di testi preesistenti, quanto piuttosto nel fatto che il lavoro offriva una visione della struttura e della natura della matematica che era collegata alla cosmologia neoconfuciana. Nel tentativo di organizzare tutta la matematica, sia occidentale sia cinese, il materiale era ripartito in nove branche corrispondenti alle divisioni dei Nove capitoli. In questo modo, l'autore cercò d'integrare tutta la matematica nella cornice cinese tradizionale accordando, tuttavia, una priorità alla geometria sui numeri (Fung Kam Wing 1995).
Du Zhigeng (attivo tra il 1681 e il 1700), nell'organizzazione dei materiali contenuti nella sua Chiave per la matematica (Shuxue yao, 1681), ha combinato la suddivisione della matematica tradizionale con la struttura dei sei libri degli Elementi di Euclide tradotti nei Jihe yuanben. Egli presenta un insieme sistematico di sei capitoli, ciascuno dei quali a sua volta diviso in sezioni corrispondenti alle nove divisioni dei Nove capitoli. Ogni capitolo è preceduto da un insieme di fanli, termine non matematico in origine, che si può tradurre come 'principî generali' e che egli usa per riferirsi sia a definizioni e postulati nello stile degli Elementi di Euclide, sia a definizioni di concetti della matematica cinese tradizionale. Il corpo del testo non consisteva però di proposizioni seguite da dimostrazioni come negli Elementi, bensì di problemi seguiti dagli algoritmi necessari per risolverli secondo la tradizione cinese. Tuttavia, gli algoritmi erano seguiti a loro volta da una spiegazione o da una dimostrazione; inoltre, i problemi erano disposti dal più semplice al più complesso; nel caso del più complesso si supponeva noto il caso più semplice e a questo si faceva riferimento, così come nei teoremi degli Elementi di geometria si richiamavano risultati già stabiliti. Oltre alla Chiave per la matematica, Du Zhigeng pubblicò una versione ridotta dei Jihe yuanben, intitolata Epitome degli 'Elementi [di geometria]' (Jihe lunyue, 1700), nella quale aggiunse 10 proposizioni da lui stesso trovate. Come precisa nella prefazione, l'adattamento della traduzione di Ricci e Xu si era reso necessario perché, a suo avviso, lo stile prolisso di questa traduzione respingeva i lettori. Un'osservazione simile era stata avanzata da Li Zijin (1622-1701), il quale aveva notato che in essa i risultati più profondi e quelli più ovvi erano dimostrati con la stessa profusione di dettagli; molti lettori si rivolgevano allora al lavoro di Aleni prima citato, Procedimenti essenziali 'di geometria', considerati un riassunto della traduzione di Xu e Ricci; con la sua Raccolta di testi semplificati sugli 'Elementi [di geometria]' (Jihe yijianfa, 1679), Li Zijin cercò di trovare un punto di equilibrio tra troppe e troppo poche spiegazioni.
Un lavoro di sintesi di questi diversi contributi nati dall'incontro con la matematica occidentale fu fatto da Mei Wending (1633-1721), senza dubbio il più prolifico e dotato scrittore di matematica del suo tempo. Lo stile di scrittura di Mei risente molto dell'influenza della geometria occidentale; egli fa quasi sempre uso di spiegazioni e giustificazioni, anche se lo scopo è quello di far capire, piuttosto che fornire dimostrazioni rigorose. Nelle sue ricerche sulla matematica cinese tradizionale, Mei Wending prosegue il lavoro di Li Zhizao e sviluppa sistematicamente lo studio del fangcheng, uno dei capitoli tradizionali, nell'opera Sulle misure di un quadrato (Fangcheng lun); inoltre classifica i problemi di questo capitolo in quattro tipi, mostra come risolverli (usando carta e penna) mediante eliminazioni successive e fornisce esempi nei quali compaiono sino a sei incognite; infine sottolinea la differenza essenziale tra il fangcheng e il 'metodo della doppia falsa posizione', che nell'opera di Li Zhizao è utilizzato anche nei casi in cui il fangcheng sarebbe stato invece molto più conveniente. Tuttavia, l'interesse principale di Mei era rivolto alla geometria e all'astronomia. Egli cercò di portare ordine in alcuni degli argomenti che riteneva fossero stati trattati in modo troppo affrettato nel Trattato sulla scienza calendaristica del periodo Chongzhen, esponendo in modo sistematico la trigonometria piana e sferica in due lavori, intitolati Aspetti essenziali di trigonometria piana (Ping sanjiao juyao) e Aspetti essenziali di trigonometria sferica (Hu sanjiao juyao). Egli andò anche oltre quello che era presente nelle traduzioni contenute nella raccolta; in particolare, sviluppò ulteriormente la stereometria, ossia la geometria delle figure solide, nel Supplemento agli 'Elementi [di geometria]' (Jihe bubian). Un forte stimolo a queste ricerche erano stati alcuni punti oscuri che aveva incontrato nei testi occidentali (Martzloff 1993a); Mei era stato colpito in particolare dal fatto che la divisione di un segmento in media ed estrema ragione era detta 'divina' o 'aurea', ma in nessun punto era spiegato perché (infatti, di Euclide erano stati tradotti soltanto i libri di geometria piana). Mei Wending scoprì presto che questo concetto era molto importante nella geometria solida; egli calcolò il volume e la lunghezza dei lati dei solidi platonici e di due dei solidi archimedei, non presenti nelle traduzioni in cinese, per i quali si servì di una sorta di approccio descrittivo di natura intuitiva, immaginando che i solidi fossero sezionati oppure inscritti l'uno nell'altro. Corresse in tal modo alcuni errori nei dati numerici riguardanti figure solide nella traduzione di Rho Spiegazione completa della misurazione.
Mei riconsiderò l'approccio di natura comparativa seguito dai suoi predecessori, infatti, invece di ricorrere alla geometria euclidea per spiegare gli algoritmi tradizionali, egli mostrò come molte proposizioni degli Elementi di Euclide, appartenenti a quella che è stata chiamata modernamente 'algebra geometrica', potessero essere riformulate usando la terminologia tradizionale relativa al 'triangolo rettangolo' (gougu) e come potessero essere dimostrate a partire dalle relazioni note della matematica tradizionale. Il successo della dimostrazione di questa equivalenza lo portò alla ben nota conclusione che nei Jihe yuanben non vi era più matematica di quella contenuta nella tradizione cinese e che l'essenza degli Elementi risiedeva nel teorema di Pitagora e nella misurazione di aree e di volumi. L'opera di Mei Wending, tenuta in alta considerazione dalle generazioni successive, costituì un fondamentale punto di riferimento per avvicinarsi alle conoscenze importate dall'Occidente.
Le prime reazioni all'astronomia occidentale
di Chu Pingyi
Nella Cina tradizionale l'astronomia era parte integrante del processo di legittimazione del potere politico; l'imperatore era considerato Figlio del Cielo e avvalorava il suo mandato presentando un calendario esatto che comprovava la sua relazione diretta con il Cielo. Nei Classici confuciani si fa cenno a tale relazione, ma durante la dinastia Han essa divenne una teoria sistematica di corrispondenze tra la condotta dell'imperatore e il volere del Cielo. All'inizio di ogni nuova dinastia la pubblicazione di un accurato calendario simboleggiava la benedizione del Cielo sull'imperatore e sulla sua dinastia. La rilevanza politica del calendario giustificava lo stretto controllo sugli studi astronomici da parte dello Stato, effettuato attraverso l'Ufficio astronomico; ma di fatto, se questi studi non sovvertivano l'ordine sociale, tale controllo era esercitato assai di rado in maniera rigorosa; nella maggior parte dei casi si trattava di un gesto simbolico inteso a proclamare il monopolio statale degli affari astronomici. Il mancato esercizio di un controllo rigoroso dello Stato favorì la fioritura degli studi astronomici non soltanto fra gli astronomi di corte ma anche tra indovini ed eruditi. Pure i Ming, una volta saliti al trono, fecero realizzare un nuovo calendario e lo pubblicarono, ma in realtà, si trattava dello stesso calendario di epoca Yuan con un nome diverso (v. par. 1). Il personale in servizio presso l'Ufficio astronomico Yuan rimase alle dipendenze dei nuovi governanti, i quali avevano delle ottime ragioni per adottare questo tipo di politica; grazie al complesso insieme di calcoli elaborati da Guo Shoujing, l'astronomia tradizionale cinese aveva infatti raggiunto il suo apice.
All'interno dell'Ufficio astronomico era presente un dipartimento dedicato a una tradizione astronomica diversa da quella cinese, l'astronomia islamica. In epoca Yuan l'astronomia islamica, usata nella determinazione delle festività religiose dei musulmani dell'Impero, aveva svolto anche un'eccellente funzione nella calibratura dell'astronomia cinese. Nei primi anni del suo regno, il fondatore della dinastia Ming, Hongwu, ordinò la traduzione di opere astronomiche islamiche, ed essa fu utilizzata per tutto il periodo Ming. Le previsioni delle anomalie celesti erano effettuate sulla duplice base del sistema cinese e di quello musulmano, e i risultati erano poi confrontati con le osservazioni astronomiche. Il calendario islamico era comunque molto diverso da quello cinese e fu forse proprio questo il motivo per cui non si tentò di assimilare questa tradizione alla calendaristica cinese, anche se il dipartimento di astronomia musulmana (chiamato Dipartimento del calendario musulmano) fu mantenuto.
Alla metà del XV sec. l'astronomia cinese versava in una situazione di profonda crisi; gli astronomi Ming erano infatti in grado di produrre calendari utilizzando le tavole astronomiche trasmesse loro dagli Yuan, ma non riuscivano a padroneggiare le complicate tecniche di calcolo e a regolare il calendario per correggere eventuali sfasature. Ciò era dovuto in parte agli errori accumulatisi nei duecento anni di utilizzazione del medesimo calendario, e in parte al mancato adeguamento dei parametri fondamentali legati alla latitudine resosi necessario in conseguenza del trasferimento della capitale da Nanchino a Pechino. Comunque sia, la responsabilità doveva attribuirsi in gran parte all'incompetenza degli astronomi di corte, che monopolizzavano gli studi calendaristici tramandandosi spesso la carica di padre in figlio e mantenendo segrete le proprie conoscenze. Questo retaggio intellettuale era sufficiente per realizzare un calendario, ma si rivelò del tutto inadeguato per il compito di correggere gli errori rilevati; come osservato dal letterato confuciano Xie Zhaozhe (attivo nella seconda metà del XVI sec.), i funzionari dell'Ufficio astronomico erano diventati lo zimbello della corte imperiale. I letterati-funzionari, che erano da molto tempo a conoscenza dei gravi problemi della calendaristica cinese, proposero numerose riforme, ma l'atteggiamento difensivo e geloso degli astronomi imperiali rese vano qualsiasi tentativo di correzione e le proposte di riforma, invece di contribuire a creare un clima di tolleranza intellettuale, alimentarono i dissapori tra i riformisti e gli astronomi di corte. Inoltre, ogni sforzo fu ostacolato dalla corruzione politica, che aveva iniziato a dilagare sin dalla metà della dinastia Ming. L'Imperatore Wanli (1573-1619), che non dava udienza ai suoi funzionari ormai da decenni, sordo a qualsiasi progetto di riforma, lasciò in uso il vecchio calendario pieno di errori.
L'arrivo dei gesuiti europei diede nuovo impulso all'annosa causa riformista; sebbene gli obiettivi dei gesuiti fossero essenzialmente di natura religiosa, essi sfruttarono la necessità di un calendario esatto per assicurarsi una posizione sicura a corte. Questa scelta strategica era tipica dei gesuiti che, nella loro opera di conversione, cercavano anzitutto l'avvicinamento delle massime autorità alla fede cristiana. La sede dell'Ufficio astronomico si trovava all'interno della città imperiale e i gesuiti ritenevano che la loro vicinanza avrebbe aumentato le probabilità di riuscire a convertire il sovrano al cristianesimo. Matteo Ricci era certo che questa strategia avrebbe dato i suoi frutti; la tattica principale adottata dai missionari fu quella di ricoprire la funzione di consigliere tecnico, avvalendosi degli adeguati supporti da Roma. Per avere accesso alla corte, i gesuiti dovevano innanzi tutto entrare in relazione con potenti protettori. Una volta compresa la natura della gerarchia sociale cinese, Ricci iniziò a presentare i missionari come letterati confuciani, non soltanto adottando la tunica con le maniche lunghe tipica dei letterati cinesi, ma anche citando puntualmente i Classici confuciani, nel tentativo di convincere i Cinesi che il cielo menzionato nei Classici era la stessa entità del Dio dei cristiani. Inoltre, per accattivarsi il favore dei funzionari inviava loro insoliti regali, piccoli prodigi della scienza che riempivano di stupore i letterati cinesi; in questo modo i gesuiti, dimostrando la loro superiorità scientifica, conferivano implicitamente maggior prestigio alla loro teologia. I destinatari di tali doni ricambiavano i missionari con lettere, poesie e soprattutto con la loro protezione, che si rivelò preziosa per il coinvolgimento dei gesuiti nella riforma del calendario. Come abbiamo visto, tra i sostenitori dei missionari due personalità di rilievo erano Xu Guangqi e Li Zhizao. Dopo che gli astronomi cinesi fallirono la previsione dell'eclissi solare del 1610, Zhou Ziyu, un astronomo ufficiale che era in buoni rapporti con Ricci, avanzò la proposta di tradurre le opere astronomiche occidentali, facendo leva sul fatto che già in precedenza, nel primo periodo della dinastia Ming, erano stati tradotti gli studi degli astronomi musulmani. Questo costituì un primo passo nel tentativo di conformare le conoscenze occidentali al sistema astronomico ufficiale; i gesuiti furono stimolati a studiare l'astronomia cinese, soprattutto grazie alle monografie sul calendario presenti all'interno delle storie dinastiche o alle recenti pubblicazioni sull'argomento, e a redigere proposte di riforma. Nel 1613 Li Zhizao suggerì che l'incarico di riformare il calendario fosse assegnato ai missionari stranieri, ma l'imperatore non accolse la richiesta e, pochi anni dopo, la persecuzione del 1616 rese ancor più difficile il tentativo di coinvolgere i gesuiti in questo progetto.
Nel 1629 gli astronomi di corte non seppero prevedere un'altra eclissi solare e questo fallimento fu considerato un indizio dell'indebolimento del mandato celeste del sovrano Ming. L'imperatore Chongzhen (1628-1644), che aveva assunto di recente il titolo imperiale, si era trovato a dover far fronte all'invasione dei Mancesi dall'esterno e a una violenta rivolta contadina all'interno del paese; tutte queste circostanze lo portarono alla decisione di avviare i lavori per la riforma del calendario. L'appoggio del sovrano offrì ai gesuiti una nuova opportunità: Xu Guangqi fu promosso Direttore dell'Ufficio dei riti e creò, dirigendolo personalmente, un dipartimento speciale dell'Ufficio astronomico che aveva il compito di tradurre i testi astronomici occidentali e di fabbricare strumenti sul modello occidentale. Da quel momento i suoi amici gesuiti entrarono ufficialmente a corte; essi si prodigarono in tutti i modi per acquisire le più recenti scoperte europee.
L'aggiornamento del calendario cinese presentava difficoltà enormi; poiché il calendario lunisolare cinese era strutturalmente diverso da quello solare gregoriano, era impossibile trasferire direttamente i frutti della recente riforma europea del calendario (1582) e, pur valendosi della tecnica occidentale, i gesuiti dovettero creare, pezzo per pezzo, un calendario che si adattasse al modello cinese. Il Vaticano era tempestato dalle richieste di informazioni astronomiche da parte dei missionari e furono organizzati molti viaggi in Europa per recuperare libri e reclutare gesuiti esperti di astronomia, tra i quali il già citato Giacomo Rho e più tardi Adam Schall von Bell (1592-1666), che svolsero un ruolo fondamentale nella riforma. Furono interpellati persino Galileo Galilei (1564-1642) e Johannes Kepler (1571-1630); il primo non offrì alcuna collaborazione, mentre Kepler inviò addirittura delle tavole astronomiche. In seguito all'impegno dei gesuiti, fu trasmesso in Cina un sistema semiticonico ‒ ispirato quindi al sistema solare ipotizzato da Tycho Brahe (1546-1601), in parte eliocentrico, in parte geocentrico ‒, grazie soprattutto all'opera di Christen Sørensen, detto Longomontanus (1562-1647), e furono importati telescopi, strumenti ticonici, formule di trigonometria e logaritmi, che divennero più tardi indispensabili per gli astronomi cinesi. Tuttavia, il calendario costruito a frammenti dai gesuiti creava altri problemi e rendeva l'impresa della riforma assai ardua; le unità di base per le misurazioni astronomiche, per esempio, erano diverse: i quadranti cinesi dividevano il giorno in 100 unità, mentre quelli europei lo dividevano in 96 quarti di un'ora; la circonferenza cinese era di 365,25° anziché di 360°. Queste divergenze rendevano le tavole astronomiche cinesi quasi del tutto inutili per i gesuiti, i quali persero molto tempo a cercare di convertirle, e ben presto divenne chiaro che era necessario importare in toto la tecnica calendaristica dall'Europa. Con l'introduzione di nuovi apparecchi e strumenti di calcolo, i gesuiti sottoponevano l'astronomia cinese a una gran forzatura, che riguardava persino i concetti basilari su cui poggiava il metodo di compilazione del calendario. Basando i loro calcoli astronomici sulla velocità reale del Sole invece che sulla sua velocità media, i metodi tradizionali di determinazione del mese intercalare, elemento fondamentale del calendario cinese, erano modificati radicalmente. Sin dai tempi degli Han l'astronomia cinese aveva seguito modelli algebrici; con l'arrivo dei gesuiti iniziò a basarsi prevalentemente sulla geometria, sebbene il formato del calendario fosse rimasto lo stesso, la tecnica per realizzarlo era stata trasformata profondamente.
Questi sforzi immani non sembravano però vani poiché, fino a che gli astronomi cinesi continuavano ad acquisire nuove conoscenze, i gesuiti potevano consolidare la loro posizione a corte attraverso il monopolio del sapere astronomico. Tuttavia, tali cambiamenti provocarono la reazione degli astronomi cinesi, che misero in luce come i principî dell'astronomia tradizionale fossero ormai divenuti inapplicabili. Nonostante tutto l'impegno, disfarsi dei metodi tradizionali non era così facile; sin dalla costituzione del Dipartimento dedicato all'astronomia occidentale nel 1629, Xu Guangqi e i gesuiti suoi collaboratori dovettero far fronte alla rivalità dei loro colleghi cinesi dell'Ufficio astronomico imperiale e degli studiosi che lavoravano all'esterno, come Wei Wenkui, che offrì in dono all'Ufficio dei riti un calendario da lui stesso creato. Xu era solito difendersi affermando la superiorità dei metodi occidentali e, quando si presentava l'occasione, coinvolgeva i suoi rivali in dibattiti; in una di queste occasioni Xu si scagliò contro i metodi di calcolo utilizzati da Wei perché, confrontati alla trigonometria occidentale, erano di gran lunga più imprecisi; Wei dovette ammettere la sua inferiorità e chiese una copia delle tavole trigonometriche, ma naturalmente Xu non svelò le sue armi segrete. Attraverso i nuovi strumenti, come il telescopio, Xu diede una forma tangibile e sorprendente alle conoscenze occidentali e provò che con essi egli era in grado di osservare e prevedere meglio i fenomeni celesti; dal 1629 sino alla sua morte, avvenuta nel 1633, presiedette a numerose dimostrazioni del primato dell'astronomia occidentale, per la maggior parte previsioni di eclissi lunari, che servivano a provare la superiorità dell'astronomia europea e a verificare la precisione delle tavole e degli strumenti astronomici.
Nonostante Xu e i suoi colleghi gesuiti avessero dato prova della loro abilità nel prevedere i fenomeni celesti, l'imperatore non si decideva a dare la sua approvazione; al contrario, nel 1634, subito dopo la morte di Xu, fu creato un nuovo dipartimento astronomico diretto da un astronomo privato. Il tentativo di Xu di annientare i suoi avversari antiriformisti era fallito; il suo successore Li Tianjing s'impegnò a fondo nella traduzione dei trattati occidentali, ma non era abbastanza potente da riuscire a proteggere i gesuiti, i quali, dal canto loro, lamentavano l'inettitudine e l'incapacità di Li a imporre la sua autorità. Questi elementi fecero sì che nell'ultimo decennio della dinastia Ming coesistessero a corte quattro diversi sistemi astronomici che producevano ognuno il proprio calendario, in costante conflitto tra loro. Nel 1634, come già detto, fu completata la traduzione dei testi astronomici occidentali conosciuta con il nome di Trattato sulla scienza calendaristica del periodo Chongzhen (Chongzhen lishu), ma l'imperatore continuò a servirsi di tutti i diversi sistemi per verificare l'esattezza delle osservazioni astronomiche e delle previsioni. I rapporti ufficiali dell'epoca riportano che i metodi occidentali avevano sempre la meglio in queste competizioni e Li Tianjing, nel frattempo, si affannava nel tentativo di convincere l'imperatore ad avallare il calendario realizzato con il metodo occidentale, ma il sovrano continuava a esitare. Qualsiasi cambiamento riguardante il calendario richiedeva infatti la massima prudenza da parte dell'imperatore. Se da un lato molte delle costanti astronomiche necessarie per realizzare un calendario dovevano essere calcolate con i metodi occidentali, dall'altro lato tra i sistemi adottati con successo a corte vi era anche quello dell'astronomia musulmana; quindi, l'astronomia europea non doveva pretendere di avere una superiorità sugli altri sistemi. L'imperatore Chongzhen considerava l'astronomia occidentale come uno dei tanti sistemi al servizio dei propri interessi e pensava che gli astronomi delle diverse tradizioni dovessero lavorare insieme per lui; più di una volta ordinò loro di collaborare per realizzare un calendario preciso e coerente. Li Tianjing era costretto ad ammettere che l'astronomia occidentale era più accurata, ma anche totalmente incompatibile con gli altri sistemi; pertanto, se il sovrano desiderava un calendario preciso non gli rimaneva che scegliere il metodo occidentale e scartare gli altri.
Oltre a fattori tecnici e istituzionali che impedivano all'imperatore di approvare senza indugio il calendario dei gesuiti, anche fattori di natura culturale giocavano un ruolo assai importante nella competizione per la scelta del calendario del tardo periodo Ming. L'adozione della tecnologia europea si era rivelata molto più semplice del cambiamento delle pratiche astronomiche cinesi. Per adeguare il sistema cinese a quello europeo, i gesuiti avevano dovuto inevitabilmente respingere tutti quei metodi che per millenni erano stati utilizzati dai Cinesi per realizzare il calendario e, data l'importanza politica e simbolica di questo, tali cambiamenti suscitavano sospetti. A rafforzare le obiezioni degli astronomi di corte, direttamente interessati alla questione, vi erano anche alcuni funzionari, i quali sostenevano che i gesuiti utilizzavano le loro conoscenze con l'unico scopo di far proseliti. Le accuse del letterato confuciano Lin Qilu esprimono bene questi punti di vista. Egli criticava aspramente il tentativo dei missionari di imporre ai Cinesi il calendario gregoriano e l'intera cosmologia europea, sostenendo che la teoria della rotondità della Terra era una pura assurdità e che impostare i mesi su un periodo di trentuno giorni, come facevano i gesuiti, anziché inserire il mese intercalare, era un raggiro. Inoltre, il loro calendario non contemplava alcuna cerimonia particolare per le eclissi solari; pertanto, l'impiego di tale calendario era non soltanto inutile ma anche dannoso, poiché senza il corretto svolgimento dei rituali di Stato l'ordine sociale sarebbe stato sconvolto. Secondo Lin Qilu, i gesuiti si servivano delle loro conoscenze in campo astronomico solamente per consolidare il loro ruolo a corte; come poteva il grandioso Impero Ming tollerare la vicinanza al Figlio del Cielo di questi barbari dagli occhi verdi e il naso lungo? Oltre a ciò, era ovvio che la loro presenza aveva come unico scopo la conversione dei Cinesi al cristianesimo; la diffusione della dottrina cristiana avrebbe certamente annientato il confucianesimo, quindi i gesuiti meritavano una severa punizione.
Queste argomentazioni non furono mai presentate direttamente al sovrano; tuttavia dimostrano come molti letterati confuciani avessero colto le motivazioni del lavoro dei gesuiti, che non erano comuni astronomi la cui attività di ricerca era circoscritta al calendario o alle osservazioni del cielo. L'astronomia occidentale non era un semplice sistema di conoscenza, ma era considerata una fonte di disordine sociale e, quindi, adottare un sistema astronomico anziché un altro non era un problema puramente tecnico, ma anche culturale. I gesuiti erano consapevoli di questi problemi; Adam Schall fece notare che gli oppositori dei missionari chiamavano l'astronomia europea 'metodi occidentali' anziché 'nuovi metodi', locuzione adoperata invece dai gesuiti e dai loro sostenitori cinesi. Questa battaglia combattuta sul fronte della terminologia chiarisce la natura culturale del conflitto; i gesuiti erano considerati stranieri alla stessa stregua dei Mancesi che, proprio mentre la riforma del calendario era in atto, iniziavano a rappresentare una crescente minaccia per l'Impero Ming. Nel 1643 l'imperatore riconobbe finalmente la superiorità dell'astronomia occidentale e adottò il nuovo calendario, a condizione che mantenesse invariato il vecchio nome. Probabilmente questo gesto simbolico mirava a salvaguardare la continuità della tradizione calendaristica cinese e il mandato celeste dell'imperatore Chongzhen. La dinastia non sarebbe comunque durata molto e l'anno successivo fu sopraffatta da una rivolta contadina; per ironia della sorte, i frutti della riforma del calendario caddero proprio nelle mani dei nemici dei Ming e servirono a legittimare l'investitura del nuovo sovrano mancese.
Bibliografia
Baldini 1992: Baldini, Ugo, Legem impone subactis. Studi su filosofia e scienza dei Gesuiti in Italia. 1540-1632, Roma, Bulzoni, 1992.
Chemla 1996: Chemla, Karine, Les mathématiques européennes vues de Chine, in: L'Europe mathématique. Mythes, histoires, identités. Mathematical Europe. Myth, history, identity, sous la dir. de Catherine Goldstein [et al.], Paris, Éd. de la Maison des Sciences de l'Homme, 1996, pp. 221-245.
D'Elia 1960: D'Elia, Pasquale M., Galileo in China. Relations through the Roman College between Galileo and the Jesuit scientist-missionaries, 1610-1640, Cambridge (Mass.), Harvard University Press, 1960.
Deane 1994: Deane, Thatcher E., Instruments and observation at the Imperial astronomical bureau during the Ming dynasty, "Osiris", 9, 1994, pp. 127-140.
Fung Kam Wing 1995: Fung Kam Wing, Fang Zhongtong ji qi Shudu yan [Fang Zhongtong e il suo 'Shudu yan'], "Lun heng", 2, 1995, pp. 128-209.
Guo Shirong 1996: Guo Shirong, 'Suanfa tongzong suanjing' yuanliu ji qi xueshu jiazhi [Origine e sviluppo del classico di matematica 'Suanfa tongzong' e il suo significato scientifico], "Zhongguo keji shiliao", 17, 1996, pp. 21-27.
Henderson 1986: Henderson, John B., Ch'ing scholars' views of western astronomy, "Harvard journal of Asian studies", 66, 1, 1986, pp. 121-148.
Ho Peng-Yoke 1986: Ho Peng-Yoke - Chiu Ling Yeong, Preface, in: Mingshilu zhong zhi tianwen ziliao [Documenti sull'astronomia nel Mingshilu], [a cura di] Ho Peng-Yoke, Chiu Ling Yeong, Hong Kong, Xianggang daxue Zhongwenxi, 1986, 2 v.
Huang Yi-Long 1991: Huang Yi-Long, Court divination and christianity in the K'ang-Hsi era, "Chinese science", 10, 1991, pp. 1-20.
‒ 1996: Huang Yi-Long, Tianzhujiao tu Sun Yuanhua yu Mingmo chuan Hua de Xiyang huopao [Il cristiano convertito Sun Yuanhua e l'importazione dei cannoni occidentali alla fine dei Ming], "Zhongyang yan jiuyuan lishi yuyan yanjiusuo jikan", 67, 1996, pp. 911-966.
Hua Tongxu 1991: Hua Tongxu, Zhongguo louke [La clessidra cinese], Hefei, Kexue chubanshe, 1991.
Hua Yinchun 1987: Hua Yinchun, Zhongguo zhusuan shigao [Breve presentazione della storia del calcolo con l'abaco in Cina], Beijing, Zhongguo caizheng jingji chubanshe, 1987.
‒ 1990: Hua Yinchun - Li Peiye, Zhonghua zhusuan dacidian [Grande dizionario del calcolo con l'abaco], Hefei, Anhui jiaoyu chubanshe, 1990.
Jami 1991: Jami, Catherine, Scholars and mathematical knowledge during the late Ming and early Qing, "Historia scientiarum", 42, 1991, pp. 99-109.
‒ 1993: Jami, Catherine, L'histoire des mathématiques vue par les lettrés chinoises (XVIIe et XVIIIe siècles). Tradition chinoise et contribution européenne, in: L'Europe en Chine. Interactions scientifiques, religieuses et culturelles aux XVIIe et XVIIIe siècles, édité par Catherine Jami et Hubert Delahaye, Paris, Collège de France, Institut des Hautes Études Chinoises, 1993, pp. 147-167.
‒ 1996: Jami, Catherine, From Clavius to Pardies. The evolution of the Jesuits teaching of geometry in China (1607-1723), in: Western humanistic culture presented to China by Jesuit missionaries (17th-18th centuries), edited by Federico Masini, Roma, Institutum Historicum S.I., 1996.
Jiang Xiaoyuan 1991: Jiang Xiaoyuan, Tianxue zhenyuan [Il vero significato della scienza del cielo], Shenyang, Liaoning jiaoyu chubanshe, 1991.
Liu Dun 1990: Liu Dun, Mei Wending zai jihexue lingyu zhong de ruogan gongxian [Contributo di Mei Wending nel campo della geometria], in: Ming Qing shuxue shi lunwen ji [Saggi sulla storia della matematica durante i Ming e i Qing], [a cura di] Mei Rongzhao, Nanjing, Jiangsu jiaoyu chubanshe, 1990, pp. 53-83.
‒ 1995: Liu Dun, Fang Tai suojian shuxue zhenji [Preziosi testi di matematica di Fang Tai], "Zhongguo keji shiliao", 16, 1995, pp. 8-21.
Martzloff 1980: Martzloff, Jean-Claude, La compréhension chinoise des méthodes démonstratives euclidiennes au cours du XVIIe siècle et au début du XVIIIe, in: Les rapports entre la Chine et l'Europe au temps des lumières. Actes du IIe Colloque international de sinologie, Centre de recherches interdisciplinaires de Chantilly, 16-18 septembre 1977, Paris, Les Belles Lettres, 1980.
‒ 1993a: Martzloff, Jean-Claude, Éléments de réflexion sur les réactions chinoises à la géométrie euclidienne à la fin du XVIIe siècle, "Historia mathematica", 20, 1993, pp. 160-179.
‒ 1993b: Martzloff, Jean-Claude, Espace et temps dans les textes chinois d'astronomie et de technique mathématique astronomique aux XVIIe et XVIIIe siècles, in: L'Europe en Chine. Interactions scientifiques, religieuses et culturelles aux XVIIe et XVIIIe siècles, édité par Catherine Jami et Hubert Delahaye, Paris, Collège de France, Institut des Hautes Études Chinoises, 1993.
‒ 1997: Martzloff, Jean-Claude, A history of Chinese mathematics, with forewords by Jacques Gernet and Jean Dhombres, Berlin-New York, Springer, 1997.
Mei Rongzhao 1983: Mei Rongzhao, The decimal place-value numeration and the rod and bead arithmetics, in: Ancient China's technology and science, compiled by the Institute of the History of Natural Sciences, Beijing, Foreign Languages Press, 1983.
‒ 1990: Ming Qing shuxue shi lunwen ji [Saggi sulla storia della matematica in epoca Ming e Qing], [a cura di] Mei Rongzhao, Nanjing, Jiangsu jiaoyu chubanshe, 1990.
Menninger 1969: Menninger, Karl, Number words and number symbols. A cultural history of numbers, Cambridge (Mass.), M.I.T. Press, 1969.
Metallo 1990: Metallo, Frances R., The abacus. Its history and applications, Arlington (Mass.), COMAP, 1990.
Miao Shufang 1995: Zhongguo zhusuan daquan [Grande compendio sull'abaco cinese], [a cura di] Miao Shufang, Lu Caiwu, Lu Chuanfeng, Beijing, Zhongguo Huaqiao chubanshe, 1995.
Mikami 1913: Mikami, Yoshio, The development of mathematics in China and Japan, New York, Chelsea Publishing Company, 1913.
Moon 1978: Moon, Parry H., The abacus. Its history, its design, its possibilities in the modern world, New York, Gordon and Breach Science Publishers, 1978 (1. ed.: 1971).
Needham 1958: Needham, Joseph, Chinese astronomy and the Jesuit mission. An encounter of cultures, London, China Soc., 1958.
‒ 1959: Needham, Joseph, Mathematics and the sciences of the heavens and the earth, in: SCC, III, 1959.
‒ 1970: Needham, Joseph, Clerks and craftsmen in China and the West. Lectures and addresses in the history of science and technology, Cambridge, Cambridge University Press, 1970.
Peterson 1986: Peterson, Willard J., Calendar reform prior to the arrival of missionaries at the Ming court, "Ming studies", 21, 1986, pp. 3-61.
Pullan 1970: Pullan, John M., The history of the abacus, London, Hutchinson, 1970 (1. ed.: 1968).
Qian Baocong 1921: Qian Baocong, Jishufa yuanlin kao [Origini e storia del sistema metrico decimale cinese], "Xueyi zazhi", 3, 1921, pp. 1-6.
‒ 1964: Qian Baocong, Zhongguo shuxue shi [Storia della matematica in Cina], Beijing, Xinhua shudian, 1964.
Ruitenbeek 1993: Ruitenbeek, Klaas, Carpentry and building in late imperial China. A study of the fifteenth-century carpenter's manual Lu Ban jing, Leiden-New York, E.J. Brill, 1993.
Sivin 1973: Sivin, Nathan, Copernicus in China, "Studia copernicana", 6, 1973, pp. 1-53.
Smith 1914: Smith, David E. - Mikami, Yoshio, A history of Japanese mathematics, Chicago, Open Court, 1914.
Terrien de Lacouperie 1883: Terrien de Lacouperie, Albert, The old numerals, the counting-rods and the swan-pan in China, London, [s.n.], 1883.
Volkov 1994: Volkov, Alexei, Large numbers and counting rods, in: Sous les nombres, le monde. Matériaux pour l'histoire culturelle du nombre en Chine ancienne, préparé par Alexei Volkov, Paris, Presses Universitaires de Vincennes, 1994.
Wang Ping 1980: Wang Ping, Xifang lisuanxue zhi shuru [Introduzione della matematica e dell'astronomia occidentali in Cina], Taipei, Zhongyang yanjiuyuan jindaishi yanjiusuo, 1980.
Yamazaki 1959: Yamazaki, Yoemon, The origin of the Chinese abacus, "Memoirs of the Research department of the Tokyo Bunko", 18, 1959, pp. 91-140.
‒ 1962: Yamazaki, Yoemon, History of instrumental multiplication and division in China from the reckoning blocks to the abacus, "Memoirs of the Research department of the Tokyo Bunko", 21, 1962, pp. 125-148.
Yan Dunjie 1987: Yan Dunjie, Ba chongxin faxian zhi Yongle dadian suanshu [Opere di matematica ritrovate nel Yongle dadian], "Ziran kexue shi yanjiu", 6, 1, 1987, pp. 1-19.