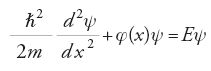La seconda rivoluzione scientifica: fisica e chimica. Completare un vecchio lavoro

La seconda rivoluzione scientifica: fisica e chimica. Completare un vecchio lavoro

Completare un vecchio lavoro

La teoria della relatività di Einstein e la teoria dei quanti di Planck, Sommerfeld e Bohr, che avrebbero determinato una nuova visione del mondo, alla fine della Prima guerra mondiale erano già parte integrante del patrimonio di conoscenze della fisica.

La teoria della relatività aveva assunto quasi la sua forma definitiva, mentre la teoria quantistica degli atomi e della radiazione era in una fase di transizione, precorritrice della meccanica quantistica che sarebbe apparsa soltanto verso la metà degli anni Venti del XX secolo.

Relatività generale e cosmologia

Alla fine del 1915 Albert Einstein (1879-1955) aveva ultimato la formulazione delle equazioni covarianti che descrivevano la gravitazione in forma generale: era nata la teoria della relatività generale, di gran lunga più ambiziosa e matematicamente più complessa di quella della relatività speciale. Dopo il 1918, quando divenne chiaro che la teoria di Einstein avrebbe completato quella di Isaac Newton, tutto l'interesse si concentrò sulla verifica sperimentale di tre effetti cruciali previsti dalla relatività generale. Uno di essi era già stato rilevato, in quanto riguardava un fenomeno noto da molto tempo; osservazioni accurate mostravano infatti un'anomalia nella precessione del perielio di Mercurio attorno al Sole di 43″ d'arco per secolo, un valore di cui la nuova teoria di Einstein poteva rendere ragione quasi perfettamente.

La teoria prevedeva inoltre che, per effetto della gravità, la luce dovesse essere deflessa in vicinanza di corpi di grande massa a causa della distorsione della geometria dello spazio determinata dal corpo stesso. Secondo la teoria relativistica della gravitazione, un raggio di luce che fosse passato molto vicino al Sole avrebbe dovuto subire una deflessione di un angolo pari a 1,7″, rilevabile misurando la posizione delle stelle durante un'eclisse solare. Arthur S. Eddington (1882-1944) ebbe un ruolo centrale nel pianificare e condurre una spedizione astronomica che avrebbe confermato la previsione; le analisi delle fotografie scattate nel 1919 durante l'eclisse totale di Sole mostrarono infatti una deflessione della luce stellare in accordo con quanto previsto. I risultati della spedizione inglese, ampiamente accettati, furono considerati una conferma della teoria di Einstein e, in assoluto, un esperimento di valore cruciale.

La terza prova era più problematica. Già nel 1907 Einstein era arrivato a concludere che la gravità rallenta il ritmo di un orologio, inteso come frequenza di un segnale elettromagnetico; la luce monocromatica emessa da un corpo di grande massa è infatti ricevuta con una lunghezza d'onda spostata verso il rosso (corrispondente a una frequenza minore) rispetto al valore specifico della stessa radiazione misurata in laboratorio. Lo spostamento verso il rosso della luce proveniente dal Sole, dovuto alla gravità, era un effetto molto difficile da misurare e, per un certo tempo, i ricercatori non furono in grado di rilevarlo. Soltanto all'inizio degli anni Venti del XX sec. furono disponibili misure in accordo con la teoria, in una situazione sperimentale tutt'altro che limpida, destinata a rimanere tale per quasi quattro decenni. Dal momento che la teoria era confermata dalle prime due prove, riguardo alla terza si poteva tutt'al più affermare che non implicava contraddizioni.

La relatività generale non risultò di grande aiuto per gli astronomi e tuttavia nel 1924 Eddington mostrò che poteva essere applicata per risolvere problemi di astrofisica. Egli era interessato alla stella doppia Sirio e, in particolare, alla piccola stella compagna Sirio B, della quale sospettava avesse una densità estremamente alta (che fosse quindi quella che oggi si chiama una nana bianca).

Se l'ipotesi era corretta, la luce proveniente da Sirio B doveva essere spostata verso il rosso per effetto gravitazionale, come confermarono le misurazioni effettuate al Mount Wilson Observatory in accordo con la relatività generale e con la congettura di Eddington relativa all'esistenza di stelle piccole e densissime. Un lavoro svolto successivamente nel settore delle stelle molto compatte condusse Lev Davidovič Landau (1908-1968) e Subrahmanyan Chandrasekhar (1910-1995) a concludere, all'inizio degli anni Trenta del XX sec., che tali stelle subissero un completo collasso gravitazionale (risultato ritenuto inaccettabile da Eddington).

Molti fisici ritenevano che la conferma sperimentale della relatività generale non fosse in realtà così rilevante, si aspettavano di più da una teoria di una simile portata concettuale e complessità matematica. La relatività speciale era divenuta uno strumento quotidiano dei fisici, mentre alla teoria generale mancava il nesso con la fisica di laboratorio e, pertanto, la maggior parte dei fisici continuava a ignorarla. Coloro che avevano sia l'interesse sia la preparazione per dominarla ne elogiavano la struttura matematica piuttosto che la capacità di risolvere problemi empirici. Hermann Weyl (1885-1955) scrisse a tal proposito nel suo Raum-Zeit-Materie (Spazio-tempo-materia): "Il supporto principale della teoria deve essere trovato non tanto nell'esperienza quanto piuttosto nella sua intima coerenza logica" (Weyl 1918, p. 198).

L'idea iniziale di Einstein diede luogo ad altre teorie della gravitazione da parte del matematico e filosofo Alfred North Whitehead (1861-1947) nel 1922 e del matematico George D. Birkhoff (1884-1944) nel 1927. Qualche fisico trovò interessanti queste e altre teorie, ma nessuna di esse si rivelò in grado di competere con la teoria generale della relatività. Alcuni fisici teorici, persuasi della sostanziale correttezza della relatività generale, l'ampliarono o la riformularono matematicamente. Attorno al 1920 Weyl, Einstein ed Eddington cercarono di estendere la teoria della gravitazione in modo da includere anche i fenomeni elettromagnetici, secondo una linea di ricerca accolta anche dal giovane Wolfgang Pauli (1900-1958). Ne seguirono sviluppi di grande interesse in matematica, ma non verificabili sperimentalmente in fisica.

Un differente approccio verso l'unificazione fu seguito dal matematico Theodor Kaluza (1885-1954), il quale ritenne utile aggiungere una quinta dimensione alle usuali quattro dello spazio-tempo. La sua teoria della relatività pentadimensionale, comprendente sia la teoria relativistica della gravitazione sia le equazioni dell'elettromagnetismo, suscitò una certa attenzione ma presto subì la stessa sorte di tante altre teorie unificate e, sebbene formalmente interessante, sembrava non avere alcuna connessione con la realtà fisica. Nonostante ciò, la teoria della relatività a cinque dimensioni continuò a essere coltivata da alcuni fisici, tra cui lo stesso Einstein. Nel 1926 il fisico svedese Oskar Klein (1894-1977) fece un importante passo avanti nel mettere in relazione la quinta dimensione con la meccanica quantistica. L'approccio di Kaluza e di Klein rappresentava un ambizioso tentativo di costruire una teoria veramente unificata ma, anche in questo caso, nessuno riuscì a ricavarne effetti rilevabili sperimentalmente.

La maggior parte degli astronomi poteva trovare più utile, rispetto ai fisici, la relatività generale; esisteva infatti un ambito disciplinare, la cosmologia relativistica, in cui la teoria non soltanto era utile ma aveva anche un effetto rivoluzionario. Tale disciplina, che rappresenta la struttura matematica della cosmologia moderna, risale all'articolo di Einstein del 1917 Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie (Osservazioni cosmologiche sulla teoria della relatività generale). Includendo nelle sue equazioni per il campo gravitazionale un termine cosmologico egli derivò come soluzione un modello di Universo statico e uniformemente riempito di materia poco densa. L'Universo di Einstein era chiuso e tuttavia illimitato, risultato reso possibile dalla curvatura positiva dello spazio. Egli fu sorpreso, nel 1917, nell'apprendere che l'olandese Willem de Sitter (1872-1934) aveva trovato per le stesse, identiche equazioni una soluzione corrispondente invece a un Universo molto diverso. L'Universo di de Sitter era vuoto, spazialmente chiuso e con la peculiare proprietà per cui gli orologi (intesi come atomi irradianti) avrebbero dato l'impressione di ticchettare più lentamente quanto più si fossero trovati lontani dall'osservatore. Come quello studiato da Einstein, esso era concepito come un Universo statico, nel senso che la curvatura dello spazio non variava nel tempo.

Durante gli anni Venti del Novecento la cosmologia matematica fu interessata in particolare all'analisi dei due modelli per stabilire quale descrivesse meglio l'Universo reale. Si trattava tuttavia di una prospettiva limitata, come mostrò chiaramente la scarsa attenzione prestata all'articolo dal titolo Über die Krümmung des Raumes (Sulla curvatura dello spazio), redatto nel 1922 dal fisico russo Aleksandr Aleksandrovič Friedmann (1888-1925) e pubblicato su "Zeitschrift für Physik". Friedmann dimostrava che esistevano soluzioni diverse alle equazioni di campo cosmologiche, includendo modelli sia ciclici sia in espansione uniforme a partire da una singolarità.

Soltanto nel 1930 i maggiori astronomi giunsero alla conclusione che dovessero essere considerate altre soluzioni oltre quelle proposte da Einstein e de Sitter. Con la scoperta osservativa di Edwin P. Hubble (1889-1953), l'anno precedente, di una relazione lineare tra lo spostamento verso il rosso delle galassie e le distanze, i tempi erano maturi per accettare un Universo in espansione. Pur senza conoscere il lavoro di Friedmann, nel 1927 l'abate belga Georges édouard Lemaître (1894-1966) aveva derivato le medesime soluzioni dinamiche e suggerito un modello di Universo dello stesso tipo. Le osservazioni di Hubble e la teoria di Lemaître furono argomentazioni molto potenti contro l'idea di un Universo statico. Sebbene Edward Arthur Milne (1896-1950) in breve tempo avesse elaborato una teoria di Universo in espansione su basi non einsteiniane, la maggior parte degli astronomi e dei fisici considerarono il nuovo paradigma cosmologico come un trionfo della teoria della gravitazione di Einstein.

L'accettazione di un Universo in espansione non implicava comunque anche l'immediato consenso verso l'idea di un Universo di età finita. L'audace ipotesi di un inizio, un big bang, fu proposta per primo da Lemaître nel 1931 ma, per più di un decennio, non fu presa seriamente in considerazione. Un modello di Universo proposto da Einstein e de Sitter nel 1932 era formalmente del tipo big bang, in quanto iniziava in una singolarità (R=0) e continuava a espandersi secondo la relazione R(t)≈t^2/3. All'Universo di Einstein-de Sitter poteva dunque essere attribuita un'età definita, vale a dire due terzi dell'inverso della costante di espansione trovata da Hubble; sfortunatamente quel valore, per le conoscenze dell'epoca, denotava un Universo più giovane di alcune sue parti costituenti, inclusa la Terra.

Nuclei e particelle

Fino al 1920 si era creduto che l'atomo consistesse di elettroni in rivoluzione attorno a un piccolissimo nucleo costituito da un sistema saldamente legato di protoni ed elettroni. In questa prospettiva, un atomo con numero atomico Z e numero di massa A includeva nel proprio nucleo A protoni e A-Z elettroni. Il modo in cui queste particelle potessero essere accoppiate nel nucleo suscitava molte speculazioni, da parte, tra l'altro, anche di Ernest Rutherford (1871-1937) che, per un certo periodo, difese un modello satellitare del nucleo in base al quale i protoni e gli elettroni circondavano un nocciolo centrale dotato di massa. La configurazione da lui proposta, dimenticata dopo il 1930, non era dissimile dal modello atomico di Bohr ma si presentava a una scala molto inferiore e con assai minori evidenze sperimentali.

Attorno al 1933 una nuova descrizione dell'atomo sostituì quella a due particelle. Nel 1920 Rutherford aveva proposto l'ipotesi che alcuni protoni nucleari potessero unirsi con elettroni per formare quelli che egli chiamò neutroni. Per più di un decennio queste entità rimasero tuttavia pure ipotesi e, quando furono identificate, risultarono essere ben diverse da quanto previsto da Rutherford. Qualunque fosse il credito dato al suo neutrone, era ancora unanimemente accettato che la materia fosse costituita da due soli mattoni fondamentali: l'elettrone e il protone.

Il paradigma a due particelle cominciò a dare qualche segno di cedimento alla fine del 1930, dopo la formulazione dell'ipotesi di Pauli, secondo la quale lo spettro continuo della radioattività beta suggeriva che l'elettrone fosse espulso dal nucleo insieme a una particella neutra e molto leggera. Molti fisici erano del parere che postulare una nuova particella elementare per spiegare un rebus sperimentale fosse un azzardo, ma l'alternativa sembrava essere una violazione del principio della conservazione dell'energia. Niels Bohr preferiva accettare il fatto che l'energia non fosse conservata nella radioattività beta, mentre Pauli confidava troppo rigorosamente nelle leggi di conservazione per considerare tale eventualità; inoltre, la sua ipotetica particella non era soltanto una soluzione ad hoc, in quanto poteva offrire anche una spiegazione per lo spin del nucleo dell'azoto 14. Basandosi sull'assunzione per cui esso era composto da quattordici protoni e sette elettroni, tutti dotati di spin semiintero, anche il suo spin totale sarebbe stato semiintero, contrariamente a quanto mostravano gli esperimenti. Pauli ipotizzò che la sua particella fosse un componente del nucleo e con spin 1/2, una specie di elettrone leggero e neutro. Un numero dispari di particelle di Pauli nel nucleo dell'azoto ne avrebbe reso intero lo spin.

Il neutrino di Pauli, come venne chiamata questa ipotetica particella, presentava numerosi lati oscuri ed era considerato con molto scetticismo. L'ipotesi non piaceva a Bohr e, ancora nel 1936, P.A.M. Dirac (1902-1984) considerava che la non conservazione dell'energia fosse un'alternativa preferibile. Soltanto con la teoria quantistica dei campi per il decadimento beta formulata da Enrico Fermi (1901-1954) il neutrino acquisì maggiore legittimazione e, verso il 1935, gran parte dei fisici accettò di considerarlo come una particella elementare reale, anche se non ancora osservata. Nella teoria di Fermi il neutrino non aveva massa e, contrariamente a quanto sostenuto da Pauli, non era un costituente del nucleo. Il neutrino si formava nel processo della radioattività beta, quando un neutrone decadeva in un protone e in un elettrone. Non fu il neutrino comunque a inaugurare una nuova era nella fisica nucleare, ma un'altra particella neutra.

In un celebre esperimento del 1932, James Chadwick (1891-1974) raggiunse la seguente conclusione: ciò che altri fisici avevano creduto essere un fotone gamma era in realtà una particella dotata di una massa approssimativamente uguale a quella del protone. Chadwick, in un primo momento, ritenne di aver trovato il neutrone composto a lungo cercato da Rutherford e trascorse più di un anno perché ci si rendesse conto che egli aveva scoperto un costituente nucleare fondamentale quanto il protone: in questa nuova prospettiva, nel nucleo atomico non c'era più spazio per gli elettroni. Il numero atomico di una data specie di atomi era ora identificato con il numero di protoni e il suo numero di massa con la somma del numero dei suoi protoni e dei suoi neutroni. Questo chiarì il problema dello spin del nucleo di azoto, che si era compreso avere un numero pari di particelle, ciascuna con spin semiintero. Il neutrone non ebbe soltanto rilevanza sostanziale nella comprensione della struttura dei nuclei ma era destinato a rivestire grande importanza anche nella produzione di alcune reazioni nucleari.

Sulla base della sua teoria relativistica per l'elettrone, Dirac ipotizzò nel 1929 che potessero esistere antielettroni carichi positivamente, che egli immaginò come 'buchi' nel continuum di elettroni con energia negativa. Ipotizzando inoltre che l'antielettrone coincidesse con il protone, egli credeva di aver ridotto tutta la materia a diverse manifestazioni di una stessa particella. La sua ambiziosa teoria unitaria entrò presto in conflitto sia con gli esperimenti sia con la teoria dei quanti. Tuttavia Dirac trasformò questo fallimento in uno sbalorditivo successo, affermando che l'antielettrone esisteva come ulteriore particella, seppure ancora ipotetica; anche il protone avrebbe dovuto avere la sua antiparticella ed esistevano probabilmente stelle costituite da antimateria in angoli remoti dell'Universo. Stelle non ne sono mai state rilevate ma gli antielettroni furono individuati fra gli anni 1932 e 1933, quando Carl D. Anderson (1905-1991) scoprì, mediante una camera a nebbia, tracce di raggi cosmici attribuibili agli elettroni positivi. La scoperta dei positroni, come furono chiamati, identificati con gli antielettroni ipotizzati da Dirac, fu confermata da altri scienziati, in particolare da Patrick M.S. Blackett (1897-1974).

Nel 1931 l'antielettrone non era l'unica particella congetturata da Dirac, in quanto egli aveva fornito argomentazioni nell'ambito della meccanica quantistica a sostegno anche dell'esistenza di monopoli magnetici, non prevista dalla teoria classica dell'elettromagnetismo. A tutt'oggi, nessun monopolo magnetico è stato tuttavia rilevato.

Negli anni Trenta l'oggetto di studio privilegiato per la ricerca di nuove particelle era la radiazione cosmica, che costituiva anche il banco di prova per le teorie riguardanti la fisica delle alte energie. Esperimenti condotti con palloni di alta quota rivelarono l'esistenza non soltanto dell'elettrone positivo ma anche di un tipo di elettrone pesante, con massa intermedia fra quella del protone e quella dell'elettrone. Questo è quanto Anderson e Seth Neddermeyer conclusero nel 1937; altri ricercatori presto confermarono la loro scoperta. A differenza del positrone, l'elettrone pesante o 'muone' non era presente in alcuna teoria quantistica dei raggi cosmici. In una teoria riguardante le forze nucleari il fisico giapponese Hideki Yukawa (1907-1981) aveva però ipotizzato due anni prima l'esistenza di una nuova particella, che avrebbe agito come quanto del campo nucleare. Yukawa aveva stimato che il suo 'mesone' avesse una massa pari a 200 volte ca. la massa dell'elettrone; quando tale ipotesi divenne nota in Occidente, i fisici identificarono tale particella con quella di Anderson-Neddermeyer, incorrendo in un errore che si sarebbe rivelato ancora più grave.

A distanza di due decenni dal 1920, quando le uniche particelle elementari dotate di massa note erano l'elettrone e il protone, erano state introdotte nel novero delle particelle fondamentali anche il neutrone, il mesone e il positrone; molti fisici accettavano inoltre il neutrino, mentre il fotone o quanto di luce era stato riconosciuto come 'particella elementare' sin dalla metà degli anni Venti. Il numero di particelle note stava aumentando, ma quello che ai fisici degli anni Trenta sembrò un incremento sorprendente fu soltanto il preludio di quanto sarebbe avvenuto nei decenni successivi alla Seconda guerra mondiale.

La teoria dei quanti e la fisica nucleare si dimostrarono di grande importanza per l'astrofisica, una scienza che si era trasformata profondamente durante il periodo tra le due guerre. In alcuni articoli del 1920 e 1921 il fisico indiano Meghnad Saha (1893-1956) introdusse la teoria quantistica nello studio delle atmosfere stellari, concentrando la propria attenzione sui processi di ionizzazione e sull'influenza della pressione. L'equazione fondamentale di Saha determina in che modo lo stato di ionizzazione dipenda dalla densità e dalla temperatura di un gas. La teoria di Saha incoraggiò il lavoro di Ralph H. Fowler, Henry N. Russell, Albrecht Unsöld, Milne e altri. Alla fine degli anni Venti lo studio di uno spettro stellare consentiva ai fisici di dedurre, con una certa affidabilità, non soltanto la pressione e la temperatura dell'atmosfera di una stella ma anche la sua composizione chimica.

Nella sua monografia del 1925, Stellar atmospheres, Cecilia H. Payne (1900-1979) concludeva da studi di spettroscopia che l'idrogeno e l'elio sono di gran lunga più abbondanti degli altri elementi, risultato che la maggior parte dei suoi colleghi trovava incredibile. La sua conclusione era tuttavia corretta e, una volta accettata, divenne centrale per le teorie sulla formazione degli elementi e sulla produzione di energia stellare. Uno dei risultati dell'astrofisica fu l'eliminazione dal novero degli elementi chimici del nebulio, suggerito alla fine del XIX sec. sulla base di alcune righe spettrali non identificate, dovute in realtà a ferro altamente ionizzato.

Nel suo classico lavoro The internal constitution of stars (1926) Eddington ipotizzò che la principale fonte dell'energia solare fosse un processo di fusione, nel quale quattro protoni si univano con due elettroni per formare un nucleo di elio (una particella alfa). Tre anni dopo, Friedrich Georg Houtermans (1903-1966) e Robert d'Escourt Atkinson (1898-1982) considerarono, evidenziandolo, l''effetto tunnel' della meccanica quantistica, che permette alle particelle nucleari di interagire anche a energie classicamente proibite. Come già Eddington, anche Houtermans e Atkinson considerarono la trasmutazione di quattro protoni in un nucleo di elio, ma per cattura successiva di protoni da parte di un nucleo leggero e per successiva espulsione di una particella alfa.

La teoria di Houtermans e Atkinson fu il primo passo nello sviluppo dell'astrofisica nucleare, che celebrò un grande successo negli anni 1938-1939 quando Hans Bethe formulò una teoria quantitativa per la produzione dell'energia solare. Secondo tale teoria due tipi di processi nucleari generavano l'energia nelle stelle di sequenza principale, come il Sole, e in entrambi i casi l'idrogeno si trasformava in elio, ma in modi distinti e con differenti vite medie. Il ciclo protone-protone (ciclo PP) coinvolgeva soltanto isotopi di elio e di litio, mentre il più complesso ciclo del carbonio (ciclo CNO) faceva riferimento a isotopi di carbonio, azoto e ossigeno come passaggi intermedi nella formazione dell'elio. Bethe mostrò che, nel primo caso, il tasso di produzione di energia sarebbe variato con la temperatura come T⁴, nel secondo invece la dipendenza sarebbe stata molto più marcata, come T¹⁷. Con questo lavoro l'astrofisica nucleare era divenuta una disciplina formalmente compiuta, basandosi in modo sostanziale sui dati di laboratorio della fisica nucleare. Bethe tuttavia non era molto interessato all'origine degli elementi utilizzati per produrre l'elio, un problema del quale si sarebbe occupato George Gamow (1904-1968) un decennio più tardi, facendone la pietra angolare della propria cosmologia.

La meccanica quantistica come soluzione ed enigma

Secondo la teoria quantistica degli atomi formulata da Bohr e successivamente sviluppata da Arnold Sommerfeld, gli elettroni si muovono attorno al nucleo su orbite caratterizzate da due o tre numeri quantici. Bohr giunse a basare la formulazione della teoria sul principio di corrispondenza, l'idea secondo cui, per grandi numeri quantici, la teoria atomica avrebbe fornito gli stessi risultati numerici di quelli predetti dalla fisica classica. Dal suo inizio nel 1913 fino al suo declino dodici anni dopo, la teoria quantistica degli atomi di Bohr e Sommerfeld ottenne successi empirici in ambito molto ristretto, in quanto poteva spiegare lo spettro dell'idrogeno (compresa la sua struttura fine), l'effetto Stark, la divisione Zeeman semplice ('normale') e la periodicità della tavola degli elementi, anche se falliva per tutto il resto. Per accennare solo a due delle anomalie più ampiamente discusse, il più complesso effetto Zeeman anomalo resisteva a tutti i tentativi dei fisici quantistici, i cui lunghi calcoli non riuscivano a riprodurre in modo soddisfacente lo spettro e l'energia di ionizzazione dell'elio, il più semplice, dopo l'idrogeno, tra tutti gli elementi chimici.

Nel 1924 i fisici più accreditati concordavano unanimemente sul fatto che la teoria di Bohr e Sommerfeld dovesse essere sostituita, perché non soltanto mostrava i propri limiti nel trattare molti problemi sperimentali ma sembrava discutibile anche nella sua struttura logica e concettuale. I fisici tesero a considerarla come uno strumento tecnico privo di quella semplicità, portata e bellezza che una teoria dei fondamenti avrebbe dovuto mostrare. Il successo, parziale ma significativo, della teoria di Bohr e Sommerfeld indicava però che essa non era del tutto sbagliata e che qualsiasi teoria futura avrebbe dovuto necessariamente confrontarsi con essa.

La strada per la meccanica quantistica s'indirizzò verso la teoria della radiazione, includendo la natura della radiazione ad alta frequenza come i raggi X. Arthur H. Compton (1892-1963) concluse nel 1923 che i risultati dei suoi esperimenti di diffusione di raggi X da parte degli atomi potevano essere ricondotti a collisioni tra i quanti di raggi X ed elettroni quasi liberi, nelle quali si conservassero l'energia e l'impulso. I quanti ‒ o fotoni, come sarebbero stati chiamati di lì a poco ‒ trasportavano impulsi ed energie (rispettivamente hν/c e hν) in accordo con la vecchia ipotesi dei quanti di luce di Einstein del 1905. La scoperta di Compton fu considerata di grande rilevanza ma, a Copenaghen, Bohr respingeva la sua interpretazione in termini di collisioni tra quanti ed elettroni. Come alternativa, egli e Hendrik A. Kramers (1894-1952) svilupparono un'idea di John C. Slater (1900-1976) in una teoria della radiazione che rigettava i quanti e utilizzava al loro posto ipotetici oscillatori virtuali associati agli atomi che emettevano luce. È da notare che la teoria di Bohr-Kramers-Slater soddisfaceva il principio di conservazione dell'energia soltanto statisticamente e non in senso assoluto e nei singoli eventi.

Nonostante gli esperimenti avessero obbligato Bohr e altri ad abbandonare la teoria, a partire dalla primavera del 1925 essa rivestì un ruolo importante come base e ispirazione per un nuovo approccio a quella della dispersione. Kramers propose tale teoria nel 1924, sviluppandola più a fondo l'anno successivo insieme a Werner Heisenberg (1901-1976). Le formule della dispersione trovate da Kramers e Heisenberg utilizzavano solamente le frequenze e l'intensità della luce emessa dagli atomi. I loro risultati furono di grande importanza per le prospettive che si sarebbero aperte all'inizio dell'estate del 1925, quando Heisenberg riuscì a dare una formulazione astratta della meccanica quantistica che prometteva di essere una teoria di carattere fondamentale, logicamente consistente e priva delle difficoltà che gravavano sulla teoria delle orbite di Bohr e Sommerfeld. Nello sviluppo della meccanica quantistica proposto da Heisenberg il principio di corrispondenza di Bohr ebbe un ruolo essenziale.

La meccanica quantistica, distinta dalla vecchia teoria dei quanti, apparve tra il 1925 e il 1926 in tre o quattro formulazioni differenti. Il pionieristico articolo di Heisenberg, Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen (Una reinterpretazione quantistica delle grandezze cinematiche e meccaniche) presentava una teoria nuova e molto astratta basata su proprietà osservabili associate a simboli disposti in righe e in colonne. Guidato dal criterio filosofico di 'osservabilità' e dal programma di 'traduzione' della teoria di Kramers-Heisenberg, Heisenberg abbandonò le orbite elettroniche e sostituì le quantità che le definivano (velocità angolari, momento elettrico e magnetico) con simboli connessi all'osservazione e alle transizioni quantistiche (frequenze spettrali e intensità). Max Born (1882-1970), professore di Heisenberg a Gottinga, comprese che i simboli della meccanica quantistica di Heisenberg erano matrici: ciò spiegava (anche se soltanto in senso matematico) il sorprendente risultato secondo il quale, in generale, due variabili non commutano. Con il cosiddetto Dreimännerarbeit (lavoro di tre uomini) del novembre del 1925, scritto da Heisenberg, Born e da un altro suo studente, Pascual Jordan (1902-1980), la nuova meccanica quantistica ottenne una formulazione più salda e generale. Quasi contemporaneamente, Dirac sviluppò la sua elegante versione algebrica della meccanica quantistica, nota per un certo tempo come l'algebra dei q-numeri. Da un punto di vista formale la meccanica quantistica, o meccanica delle matrici, sembrava essere una teoria soddisfacente ma molto incerta dal punto di vista empirico. Soltanto dopo mesi di duro lavoro Pauli e Dirac, utilizzando metodi differenti, furono in grado di derivare lo spettro corretto per l'idrogeno, anche se nell'approssimazione non relativistica.

Nello stesso periodo, verso la fine del 1925, Erwin Schrödinger (1887-1961) stava sviluppando una versione assai diversa della meccanica quantistica, basata sul dualismo onda-particella proposto da Louis de Broglie (1892-1987) nel 1924. Fondando le proprie argomentazioni sulla teoria della relatività, il fisico francese aveva suggerito una simmetria essenziale tra particelle e onde: così come Einstein ‒ e ora anche Compton ‒ attribuiva alla radiazione elettromagnetica un comportamento analogo a quello delle particelle, allo stesso modo egli sosteneva che a particelle dotate di massa come gli elettroni dovessero essere attribuite una frequenza e una fase d'onda, che le caratterizzavano. De Broglie propose audacemente che la lunghezza d'onda di un elettrone con impulso p fosse data da λ=h/p e, su questa base, interpretò la condizione di quantizzazione di Sommerfeld come un fenomeno di risonanza. Egli inoltre applicò la sua poco ortodossa teoria alla teoria statistica dei gas, un'area disciplinare nella quale era impegnato anche Einstein che, ritenendo promettenti le idee di de Broglie, si premurò di informare Schrödinger.

Questi sosteneva che, se gli elettroni atomici potevano essere descritti come onde, avrebbero dovuto essere governati da un'equazione d'onda. Si impegnò quindi per trovare l'equazione d'onda relativistica per un atomo di idrogeno, scoprendo infine che non forniva i valori di energia corretti. Deluso, egli concentrò la sua attenzione sull'approssimazione non relativistica e riuscì a sviluppare una teoria ondulatoria degli atomi, o meccanica ondulatoria, che pubblicò in una serie di articoli apparsi su "Annalen der Physik" tra la primavera e l'estate del 1926. Gli elementi cruciali nella versione di Schrödinger della meccanica quantistica erano due equazioni d'onda, una stazionaria e l'altra dipendente dal tempo.

Nel caso unidimensionale, indicate con ψ=ψ(x,t) la funzione d'onda e U(x) l'energia potenziale e posto ℏ=h/2π, l'equazione agli autovalori che determina i possibili valori E di energia si scrive

Per ottenere l'equazione del moto, l'energia deve essere sostituita dall'operatore E=iℏ∂/∂t che agisce sulla funzione d'onda ψ (dove i è l'unità immaginaria).

La teoria di Schrödinger forniva gli stessi risultati di quella di Heisenberg quando era applicata a semplici sistemi fisici. Le due versioni dovevano essere profondamente connesse ed entro l'estate del 1926 Pauli, Schrödinger e altri avevano trovato il modo per tradurre una teoria nell'altra.

Qual era il significato fisico della funzione ψ di Schrödinger? Questi ipotizzò che essa rappresentasse la densità di carica elettrica; per il caso dell'atomo di idrogeno ψψ*dV (dove ψ* è il complesso coniugato di ψ e dV un elemento di volume) sarebbe dovuta equivalere a una quantità elementare della distribuzione di carica elettronica. Born diede un'altra spiegazione, basata ampiamente su fenomeni aperiodici come sono i processi di collisione. Egli interpretò ψψ*dV come la probabilità per cui una particella in uno stato ψ sia localizzata all'interno dell'elemento dV. Con questa interpretazione, alla quale Schrödinger resisté fortemente quanto vanamente, Born introdusse una irriducibile componente probabilistica nella microfisica. Dopo ulteriori perfezionamenti matematici e concettuali, alla fine del 1926 si giunse a elaborare un formalismo generale e unificato per la meccanica quantistica, che non faceva distinzioni tra la meccanica delle matrici e quella ondulatoria.

Tuttavia alcuni problemi attendevano ancora una soluzione; tra questi lo spin dell'elettrone, concetto introdotto nell'autunno del 1925 da George E. Uhlenbeck (1900-1988) e Samuel Goudsmit (1902-1978) per spiegare l'effetto Zeeman anomalo e il momento magnetico non classico dell'elettrone. La loro proposta si adattava bene anche al principio di esclusione di Pauli, che attribuiva una non spiegata duplicità agli elettroni atomici per tener conto dei periodi e dei sottoperiodi della tavola degli elementi (il principio di esclusione, che anticipava il concetto di spin, proibiva che un atomo avesse due o più elettroni con gli stessi valori dei quattro numeri quantici con i quali Pauli definiva uno stato elettronico legato).

L'immagine semplificata di un elettrone in rotazione su sé stesso, come una trottola, mentre gira attorno al nucleo produceva serie difficoltà in relazione sia alla relatività (alcune regioni sulla superficie dell'elettrone si sarebbero mosse a una velocità superiore a quella della luce) sia alla teoria quantistica (lo spin non trovava immediata collocazione nell'equazione di Schrödinger); inoltre lo spin non forniva i corretti livelli energetici per la struttura fine dell'idrogeno. Questi problemi furono risolti con l'interpretazione dello spin come una quantità non meccanica, mediante l'attribuzione di due componenti alla funzione d'onda (una soluzione questa fornita da Heisenberg, Jordan e Pauli) e con la scoperta da parte di Llewellyn H. Thomas di un effetto relativistico fino ad allora trascurato (la precessione di Thomas).

Un altro problema riguardava la relazione tra relatività e meccanica quantistica. L'equazione di Schrödinger era non relativistica, e tuttavia una teoria fondamentale avrebbe dovuto soddisfare i principî della relatività, vale a dire trattare il tempo e lo spazio in una maniera Lorentz-invariante. Il problema si rivelò più difficile del previsto e la soluzione giunse da una direzione sorprendente. Più che fare uso della derivata temporale di ψ al secondo ordine, Dirac intuì che l'equazione d'onda dell'elettrone dovesse essere del primo ordine rispetto alle derivate sia spaziali sia temporali. Egli pubblicò la sua equazione Lorentz-invariante a quattro componenti all'inizio del 1928 e di lì a poco mostrò che essa spiegava con precisione la struttura fine dell'idrogeno. In più includeva lo spin dell'elettrone: il requisito di invarianza relativistica conduceva a trattare l'elettrone con il corretto momento magnetico. L'equazione di Dirac rappresentava un enorme passo avanti e le sue conseguenze si rivelarono gradualmente ai fisici; una di queste, e non la meno importante, risultò essere l'esistenza delle antiparticelle.

La nuova meccanica quantistica era più che una teoria della struttura atomica; essa era infatti anche una teoria del campo elettromagnetico e delle sue interazioni con particelle cariche. La teoria quantistica dei campi applicata alle interazioni elettromagnetiche, o anche elettrodinamica quantistica (QED, quantum electrodynamics), fu introdotta con l'articolo di Dirac The quantum theory of the emission and absorption of radiation (1927). Considerando l'interazione di un atomo con il campo elettromagnetico, egli fu portato a introdurre quantità che si possono interpretare come operatori di annichilazione e creazione di fotoni, in corrispondenza con i processi di assorbimento, emissione e diffusione. In questo e in altri articoli del 1927, Dirac applicò il suo formalismo per calcolare le probabilità di assorbimento, emissione e diffusione di fotoni e presentò inoltre una teoria completa per la dispersione, che comprendeva la formula di Heisenberg e Kramers che aveva ispirato la meccanica delle matrici.

Le pubblicazioni di Dirac sull'elettrodinamica quantistica, iniziate nel 1927, completavano lo schema della meccanica quantistica e, allo stesso tempo, introducevano un nuovo campo di ricerca che sarebbe presto stato all'avanguardia della fisica teorica. Come egli comprese, le teorie precedentemente elaborate erano incomplete, in quanto era ristretta ai bosoni (cioè ai fotoni) e non era relativisticamente invariante. La prima di queste limitazioni fu superata da Jordan ed Eugene Wigner, i quali nel 1928 utilizzarono gli stessi metodi della teoria della radiazione di Dirac per introdurre operatori di creazione e annichilazione modificati, applicabili ai fermioni (come gli elettroni).

La distinzione fra due classi di particelle, chiamate in seguito fermioni e bosoni, era stata introdotta da Dirac nel 1926: la funzione d'onda per due particelle dello stesso tipo negli stati m ed n poteva essere sia simmetrica sia antisimmetrica, ψ_mn(1,2)=ψ_mn(2,1) oppure ψ_mn(1,2)=−ψ_mn(2,1). Egli deduceva che il secondo caso si verifica per gli elettroni e altre particelle governate dal principio di esclusione di Pauli, mentre i fotoni sono descritti da funzioni d'onda simmetriche. Per entrambi i casi ricavò le corrispondenti proprietà statistiche, vale a dire la relazione tra il numero di particelle in un determinato stato, la temperatura e il numero degli stati con una certa energia. Sebbene Dirac non ne fosse al corrente, Fermi aveva ricavato la statistica quantistica dei fermioni alcuni mesi prima, pur non mettendola in relazione con la nuova meccanica quantistica. La statistica quantistica, per come fu introdotta principalmente da Dirac, Fermi e Heisenberg, divenne presto un argomento di punta della fisica teorica. I due tipi di particelle divennero note come particelle di Fermi-Dirac e di Bose-Einstein, nomi questi che Dirac nel 1945 propose fossero abbreviati rispettivamente in fermioni e bosoni.

La teoria della radiazione di Dirac fu il punto di partenza per l'ambizioso progetto di Heisenberg e Pauli di sviluppare una completa teoria quantistica dei campi in pieno accordo con il principio di relatività. Essi produssero due complessi articoli tra il 1929 e il 1930 che contenevano le equazioni canoniche per trattare i campi di materia e quelli di radiazione in interazione reciproca. Fu, tuttavia, l'ampio articolo di Fermi Quantum theory of radiation apparso sulle "Reviews of modern physics" nel 1932, piuttosto che gli articoli di Heisenberg e Pauli, a divenire il primo testo autorevole sull'elettrodinamica quantistica. La teoria di Heisenberg e Pauli non era soltanto matematicamente complessa, ma era anche minata da problemi di natura logica e concettuale. Il primo e più importante consisteva nel fatto che l'autoenergia dell'elettrone (assieme ad altre quantità) risultava essere infinita e quindi priva di significato fisico. J. Robert Oppenheimer (1904-1967) mostrò nel 1930 che le divergenze non potevano essere spiegate come artefatti matematici, giacché avrebbero avuto dirette implicazioni fisiche, come la produzione di uno spostamento infinito delle linee spettrali. Soltanto calcoli perturbativi all'ordine più basso fornivano risultati finiti, come la formula di Klein-Nishina per l'effetto Compton che Klein e Yoshio Nishina (1890-1951) avevano derivato nel 1929.

Il lavoro teorico e concettuale nell'elettrodinamica quantistica generò numerose idee nuove. Lo studio di processi ad alta energia nella radiazione cosmica si rivelò particolarmente fecondo, giovandosi anche dei gravi disaccordi iniziali tra aspetti teorici e sperimentali. Un'elaborata teoria relativa al moto di particelle veloci cariche attraverso la materia, sviluppata in particolare da Bethe e Walter Heitler (1904-1981), non permetteva di riprodurre dati sperimentali nella regione delle alte energie, tipicamente superiori a 137mc² (dove 137 sta per l'inverso della costante di struttura fine, la costante di accoppiamento per le interazioni elettromagnetiche). Tale limite energetico corrisponde a un elettrone con una lunghezza d'onda di de Broglie più piccola del raggio classico dell'elettrone e²/mc², una quantità questa che era spesso considerata alla stregua di una lunghezza fondamentale.

Una ragione dei dubbi sulla validità della QED ad alte energie era lo strano comportamento degli elettroni dei raggi cosmici che Anderson aveva studiato nelle sue fotografie ottenute con camera a nebbia. Bethe e Heitler proposero nel 1934 che le osservazioni indicassero un'incongruenza della meccanica quantistica e che la radiazione degli elettroni veloci potesse servire per sottoporre a una prova diretta la QED. Soltanto con l'ipotesi di Anderson e Neddermeyer secondo cui le particelle penetranti non erano elettroni ordinari, ma un nuovo tipo di elettroni pesanti (mesotroni), i fisici conclusero che una revisione della meccanica quantistica non era necessaria. Tuttavia rimanevano altre questioni aperte e la QED continuò a essere considerata problematica fino alla fine degli anni Quaranta, quando una nuova generazione di teorici sviluppò una teoria rinormalizzabile.

Interpretazione e filosofia

Mentre la teoria della relatività fu accolta con grande interesse tra i filosofi e gli uomini di cultura, durante il periodo tra le due guerre mondiali le implicazioni della meccanica quantistica furono discusse soprattutto dagli stessi fisici. Essi compresero che la nuova teoria differiva nei suoi fondamenti dalla fisica classica più radicalmente di quanto non avvenisse per la relatività e che le applicazioni tecniche della teoria non potevano essere separate facilmente dall'analisi concettuale di natura filosofica. In modo implicito, e in alcuni casi esplicitamente, essi si comportarono come filosofi. La meccanica quantistica, per come era stata concepita da Heisenberg, Born, Bohr e altri, era una teoria probabilistica nel senso che poteva soltanto predire la probabilità dei risultati di un esperimento. Si sarebbe potuto sperare che un futuro sviluppo della teoria potesse fornire lo stesso tipo di risposte non ambigue che offriva la meccanica classica?

Nel 1927 de Broglie rispose affermativamente al quesito pensando a una particella come a un pacchetto concentrato di energia guidato da un''onda pilota'. In questo modo egli poté dare una formulazione della meccanica quantistica come una teoria deterministica, senza abbandonare completamente la concezione di Born circa la natura probabilistica dei processi quantistici. La teoria di de Broglie, un parziale ritorno al determinismo classico, fu profondamente criticata da Pauli e non convinse anche altri importanti fisici quantistici. Conseguentemente, de Broglie abbandonò la 'teoria della doppia soluzione', che venne ripresa soltanto molti anni dopo, quando David Bohm (1917-1992) sviluppò una teoria analoga. L'insuccesso dell'approccio di de Broglie aprì la strada per l'ortodossia di Copenaghen.

In fisica classica due qualsiasi variabili commutano tra loro, ma in meccanica quantistica il prodotto di due operatori, xy, non è in generale uguale a yx. Il significato della non commutatività, come chiarito da Heisenberg nella primavera del 1927, prese la forma di un principio della filosofia naturale, il principio di indeterminazione. Heisenberg partì dal significato operazionale dei concetti fisici; secondo il suo pensiero di ispirazione positivistica, l'attribuzione di valori precisi e simultanei alla posizione e all'impulso di una particella era priva di significato se tali grandezze non potevano essere misurate esattamente. Egli provò che la meccanica quantistica proibisce per principio tali misurazioni, in quanto essa implica che le indeterminazioni Δq e Δp siano tra loro correlate e irriducibili, dal momento che il loro prodotto non può mai essere inferiore a h/4π. Heisenberg dimostrò una relazione simile tra tempo ed energia; per esempio, se la vita media di un atomo in uno stato eccitato è data da Δt, l'energia dello stato eccitato non può essere determinata con maggior precisione di ΔE=h/Δt, il che comporta una naturale e irriducibile larghezza delle linee spettrali. La mancanza di livelli di energia precisamente definiti era soltanto uno dei modi in cui la meccanica quantistica contraddiceva i postulati della vecchia teoria atomica di Bohr.

Giacché le relazioni di indeterminazione, valide per qualunque coppia di quantità fisiche coniugate, derivavano dalla meccanica quantistica, quasi tutti i fisici le accettarono. Ciò che era in discussione negli anni Trenta non erano tanto le relazioni in sé quanto le loro implicazioni filosofiche. Nel suo articolo del 1927, Heisenberg affermava che la causalità rigorosa era incompatibile con le relazioni di indeterminazione: lo stato iniziale di un sistema microfisico non può essere conosciuto con accuratezza illimitata e per questa ragione è impossibile conoscere con precisione qualunque stato successivo. In altre parole, la ragione alla base dell'indeterminazione non risiederebbe nell'equazione del moto di Schrödinger, ma nello stato iniziale di un sistema fisico.

Durante il Congresso voltiano tenutosi a Como nell'autunno del 1927, Bohr sostenne che l'osservazione di un sistema fisico non può essere effettuata senza che il sistema venga disturbato e che la misurazione e l'osservazione sono dunque connesse in modo essenziale. Questa è un'implicazione del suo principio di complementarità, che è talvolta visto come una generalizzazione del principio di indeterminazione. Tuttavia il principio di complementarità ha un differente senso epistemico in quanto non segue direttamente dalla meccanica quantistica e non conduce a predizioni. Bohr illustrò il suo principio facendo riferimento alle descrizioni, per esempio, di elettroni e onde luminose. Tali descrizioni sono complementari nel senso che richiedono concetti che sono mutuamente esclusivi anche se effettivamente non si contraddicono tra loro. A seconda della situazione sperimentale, un elettrone può comportarsi come una particella o come un'onda e per descriverlo in modo completo il fisico ha bisogno di darne una caratterizzazione con entrambi i linguaggi. Bohr sottolineò che i fenomeni quantistici e gli apparati sperimentali si presentano sempre in modo olistico. Ne segue che il fisico non può affatto sperare di penetrare oltre l'apparato sperimentale e ottenere la conoscenza di cosa sia in sé un oggetto quantistico.

D'altro canto, sebbene Bohr sottolineasse che la fisica quantistica attribuiva all'osservatore un ruolo nuovo e attivo nelle misurazioni, egli negava che questo conducesse ad ambiguità o a perdita di oggettività. Egli sosteneva che gli esperimenti potevano essere considerati senza ambiguità perché è propria del fisico la scelta di ciò che si debba misurare e in tal modo egli distrugge la possibilità che si possano realizzare aspetti in conflitto con essa. Il ruolo dell'osservatore nelle misurazioni, e quindi la distinzione fondamentale tra ciò che è oggettivo e soggettivo, divenne un problema negli anni Trenta e continuò a essere discusso vivacemente in seguito. Pochi fisici si unirono alla scuola di Bohr, e in particolare Jordan arrivò alla conclusione che le osservazioni non soltanto perturbano la quantità misurata ma letteralmente la producono.

Il principio di complementarità era una dottrina centrale in quella che divenne nota come l'interpretazione di Copenaghen della meccanica quantistica. Bohr e alcuni suoi sostenitori ritenevano che essa potesse essere applicata anche ad altri settori (filosofia, psicologia, religione, biologia e antropologia). A questo riguardo Bohr era un 'espansionista', secondo l'espressione dello storico della scienza Loren Graham; Einstein, d'altro canto, aveva sempre assunto un atteggiamento 'restrizionista'. Nella relatività o nella teoria quantistica egli si limitava a considerare l'ambito della fisica mentre si rifiutava di speculare sulla più ampia rilevanza di queste teorie oppure sulle loro possibili analogie in ambiti umanistici e sociali. Anche se il principio di complementarità non rivestiva quasi alcun ruolo nelle applicazioni dei fisici, esso era comunemente adottato come una valida meta-prospettiva e Pauli, Jordan, Heisenberg, John von Neumann (1903-1957) e Rudolf E. Peierls (1907-1995), fra gli altri, contribuirono a sostenerlo. Secondo l'autorevole e influente lavoro Mathematische Grundlagen der Quantenmechanik (Fondamento matematico dei quanti meccanici) di von Neumann, pubblicato nel 1932, la consapevolezza del ruolo dell'osservatore era essenziale nel processo delle misurazioni quantomeccaniche.

Einstein, a parte la segnalazione dell'ipotesi di de Broglie a Schrödinger, non diede alcun contributo alla nascita della meccanica quantistica. Dopo aver assimilato la nuova teoria, egli decise che essa non poteva essere corretta in alcun senso fondamentale. La sua diffidenza verso la meccanica quantistica, che durò tutta la vita, era epistemologicamente fondata. La fisica non si riduceva per lui a una formulazione statistica; come disse in una famosa lettera a Born, Dio non gioca a dadi con il mondo. L'insoddisfazione di Einstein verso la meccanica quantistica, o la sua interpretazione, divenne un tema importante alla Conferenza Solvay del 1927 e del 1930. Einstein inizialmente indirizzò i suoi argomenti contro le relazioni di indeterminazione nella speranza di dimostrare che i fenomeni atomici potessero essere descritti con maggior precisione di quanto permettesse l'equazione di Heisenberg. Durante il congresso del 1930 egli fece notare quella che lui riteneva essere una scappatoia per la discussione sulla relazione di indeterminazione tra energia e tempo, facendo riferimento a un esperimento mentale che considerava un orologio posto in una scatola contenente anche una qualche radiazione. Un dispositivo a otturatore consentiva la fuoriuscita di un singolo fotone e Einstein ipotizzò che pur considerando finita l'incertezza sul tempo di fuga del fotone (Δt), l'incertezza sulla sua massa o sull'energia (ΔE) poteva essere nulla; quindi ΔEΔt=0, in contraddizione con la relazione di indeterminazione. L'argomentazione di Einstein era ingegnosa, ma Bohr rispose con successo alla sfida invocando lo spostamento verso il rosso di origine gravitazionale predetto dalla relatività generale. Quando questo fattore fosse stato preso in considerazione, il fotone non avrebbe potuto più essere pesato con accuratezza e il valore minimo di ΔEΔt risultava essere la costante di Planck.

Irremovibile nelle sue convinzioni profonde rispetto alle argomentazioni di Bohr, Einstein modificò la propria strategia. Egli abbandonò il suo attacco alle relazioni di indeterminazione e provò invece a mostrare che si poteva avere del micromondo una conoscenza migliore di quanto poteva essere descritto dalla meccanica quantistica. Dopo essersi stabilito negli Stati Uniti, Einstein, collaborando con i suoi colleghi di Princeton Boris Podolsky (1896-1966) e Nathan Rosen (1909-1995), pubblicò sulla "Physical review" del 1935 un'obiezione breve ma famosa contro la completezza della meccanica quantistica, nota come 'paradosso EPR'. Secondo Einstein e i suoi coautori, una teoria poteva dirsi completa se conteneva una controparte per ogni oggetto o proprietà che esiste in una situazione fisica data e una quantità era reale se la teoria consentiva di predire i suoi valori senza disturbare il sistema. Nell'articolo relativo al paradosso EPR, intitolato Can quantum mechanical description of physical reality be considered complete?, essi sostenevano che la meccanica quantistica era incompleta in quanto entrava in contraddizione con qualunque ragionevole criterio di 'realtà'.

L'idea centrale dell'esperimento mentale EPR riguardava due particelle che interagiscono e successivamente si spostano lontano l'una dall'altra. Se gli impulsi iniziali sono noti e misuriamo quello di una particella dopo la collisione, è possibile calcolare l'impulso dell'altra. Potremmo anche decidere di misurare la posizione finale di una delle particelle e allo stesso modo conoscere la posizione dell'altra; la nostra decisione di compiere una particolare misurazione su una particella sembra allora influenzare istantaneamente lo stato dell'altra. Secondo Einstein, l'unico modo per sfuggire a un'azione istantanea 'spettrale' (proibita dalla teoria della relatività) sta nel concludere che le due particelle hanno sì impulsi e posizioni definiti, anche se non possiamo misurarli simultaneamente.

La replica di Bohr a questa conclusione paradossale non è meno famosa dell'argomento EPR. Egli respinse il ragionamento di Einstein in quanto esso presupponeva un criterio di realtà che riteneva non corretto. Einstein, Podolsky e Rosen avevano usato la frase 'senza turbare il sistema in alcun modo', e fu su questa frase che Bohr concentrò la sua critica. Secondo il punto di vista di Copenaghen, un oggetto atomico e l'apparato di misura non possono essere analizzati come parti separate. Misurare un sistema fisico, e quindi stabilirne la sua realtà, implicava necessariamente disturbarlo. Il dibattito tra Einstein e Bohr degli anni Trenta non diede luogo né a un accordo né a particolari chiarimenti, ma metteva in luce in maniera fruttuosa i disaccordi concettuali all'interno della comunità scientifica.

Chimica quantistica

L'applicazione alla chimica della teoria quantistica degli atomi fu immediata; nel 1911 Walther Hermann Nernst (1864-1941) fece notare che la teoria di Einstein per i calori specifici dei solidi si sarebbe dovuta estendere anche ai gas, un'idea, questa, approfondita dal chimico danese Niels Bjerrum (1879-1958). Applicando la teoria quantistica alla rotazione e alla vibrazione delle molecole di gas, Bjerrum ricavò risultati in buon accordo con gli spettri e con i calori specifici dei gas. Bohr contribuì molto all'applicazione della teoria quantistica alla chimica; la sua trilogia di lavori del 1913, intitolata significativamente On the constitution of atoms and molecules, trattava la struttura molecolare abbastanza dettagliatamente e abbozzava una spiegazione del sistema periodico degli elementi. Bohr descrisse il legame covalente come costituito da due elettroni in rotazione su un'orbita circolare comune a due atomi.

Su questa base egli calcolò il calore di formazione dell'idrogeno gassoso (H+H→H2) e ne ricavò un valore in buon accordo con il valore reale. Esperimenti e calcoli successivi provarono però che l'accordo era stato fortuito. Sebbene lo stesso Bohr e altri fisici avessero perfezionato il suo modello molecolare, il legame covalente rimaneva ancora un'anomalia fuori dell'ambito della teoria quantistica di Bohr e Sommerfeld. Più che adottare i modelli di dinamica molecolare proposti dai fisici quantistici, la maggior parte dei chimici preferì il modello statico che Gilbert N. Lewis (1875-1946) aveva introdotto nel 1916. Questo modello a coppie di elettroni era visualizzabile e utile dal punto di vista chimico, ma non consentiva il calcolo di quantità di interesse fisico più di quanto l'atomo dinamico di Bohr fosse utile per i chimici. Eppure, come Born scrisse ottimisticamente nel 1920, "abbiamo viaggiato abbastanza per vedere davanti a noi in lontananza i valichi che devono essere attraversati prima che la fisica possa imporre le sue leggi sulla sua scienza sorella" (Nye 1993, p. 229).

La prima applicazione della meccanica quantistica a un problema molecolare fu attuata da Øyvind Burrau, un fisico danese che nel 1927 risolse l'equazione di Schrödinger per la molecola più semplice possibile, lo ione carico positivamente della molecola di idrogeno. Di maggior rilievo fu, lo stesso anno, la prima soddisfacente trattazione quantomeccanica della molecola di idrogeno, fornita da Heitler e Fritz London (1900-1954) in un articolo che di fatto costituì il fondamento per una nuova disciplina scientifica, la chimica quantistica. La sostanza del loro metodo consisteva nel costruire in maniera simmetrica una funzione d'onda per la coppia di elettroni a partire dalle funzioni d'onda degli atomi separati. Nella teoria del legame di valenza di Heitler e London, l'energia di legame era di due tipi, un'energia coulombiana semiclassica e una molto più grande di scambio. Quest'ultima non ha una controparte nella teoria classica e in meccanica quantistica deriva dal fatto che due elettroni, che seguono la statistica di Fermi-Dirac, sono indistinguibili e possono essere interscambiati.

Un caso semplice di un sistema a due elettroni fu indagato inizialmente da Heisenberg, il quale nel 1926 aveva utilizzato la nuova statistica per introdurre il concetto di risonanza nell'ambito della meccanica quantistica. La sua teoria della risonanza costituiva un substrato per la teoria di Heitler e London sul legame dell'idrogeno molecolare. Infatti, la nuova nozione di energia di scambio si rivelò essere essenzialmente equivalente al fenomeno della risonanza discusso da Heisenberg. Fu ancora questi a dimostrare che le energie o le forze di scambio possono essere generalizzate ad ambiti diversi dal legame chimico. In relazione con il suo tentativo di comprendere le forze nucleari (o interazioni forti), egli introdusse, nel 1932, la forza di scambio tra protone e neutrone come l'equivalente della forza di scambio elettrone-elettrone.

La teoria di Heitler e London era un tentativo di spiegare il legame chimico facendo uso di proprietà degli atomi singoli. Essa funzionò bene per l'idrogeno ma la sua applicazione a molecole più complesse risultò difficoltosa, in quanto partiva dal presupposto per cui atomi singoli avrebbero mantenuto in linea di massima le proprie caratteristiche all'interno della molecola.

Con l'avvio della chimica quantistica nel 1927, i fisici e i chimici fisici iniziarono ad applicare la meccanica quantistica ad altre molecole e ad altri tipi di legami. Il più autorevole tra gli scienziati che per primi lavorarono in questa direzione fu l'americano Linus C. Pauling (1901-1994), il quale in una serie di lavori estese l'approccio di Heitler e London a molecole più complesse. In The nature of the chemical bond, il titolo generico di una serie di articoli pubblicati tra il 1931 e il 1933, egli introdusse dei metodi di approssimazione che gli permisero di trattare molecole troppo complesse per un approccio quantomeccanico rigoroso. Fra queste vi era il benzene (C6H6), il componente principale dell'importante classe dei composti aromatici, che egli poté spiegare sulla base del modello a risonanza tenendo conto delle funzioni d'onda delle singole strutture. Pauling esercitò una rilevante influenza grazie a contributi scientifici innovativi, lezioni e libri di testo. Nel 1935 egli pubblicò insieme con E. Bright Wilson il testo classico di meccanica quantistica Introduction to quantum mechanics, with applications to chemistry, un lavoro che svelò ai chimici l'utilità della meccanica quantistica. Quattro anni dopo, Pauling fornì un'ampia rassegna della teoria della valenza in un altro classico, The nature of the chemical bond and the structure of molecules and crystals.

La teoria del legame di valenza di Heitler, London e Pauling presupponeva che la molecola fosse formata mettendo insieme due o più atomi. Nella teoria alternativa degli orbitali molecolari le molecole erano considerate come i principali costituenti; i teorici iniziavano con i nuclei atomici e aggiungevano elettroni sugli orbitali molecolari a circondare due o più nuclei. Questa procedura fu proposta indipendentemente nel 1928 da Friedrich Hund (1896-1997) in Germania e da Robert S. Mulliken (1896-1986) negli Stati Uniti. Il lavoro di Hund, fondato sull'idea per cui una molecola è un'unità autosufficiente piuttosto che un aggregato di atomi, generalizzò il precedente trattamento di Burrau per la molecola dello ione idrogeno. Il metodo degli orbitali molecolari fu sviluppato ancora dal fisico tedesco Erich Hückel (1896-1980), il quale nel 1930 lo applicò alle molecole aromatiche e al legame doppio. Durante buona parte degli anni Trenta i principali sostenitori dei due metodi dibatterono animatamente sui rispettivi meriti, ma alla fine accettarono che entrambe le formulazioni non erano né equivalenti né incompatibili; si trattava di due approcci complementari al legame chimico. Il cosiddetto metodo dei determinanti sviluppato da John C. Slater (1900-1976) fu una sintesi e un compromesso fra i due modelli.

Sia i fisici sia i chimici fornirono importanti contributi alle prime fasi di sviluppo della chimica quantistica ma con approcci e strategie di ricerca differenti. Essi non sempre si compresero e, in particolar modo in Germania, furono spesso antagonisti. London non aveva simpatia per l'approccio più pragmatico dei chimici, che egli giudicava primitivo e semplicistico; secondo il suo punto di vista i chimici usavano il concetto di valenza per visualizzare le forze molecolari, un espediente per eseguire calcoli dettagliati di meccanica quantistica, una sorta di illusorio modo di pensare. Egli scrisse: "il chimico è fatto di legno duro e ha bisogno di avere regole anche se queste sono incomprensibili" (Gavroglu 1995, p. 95). In un articolo del 1929, Dirac affermò che la meccanica quantistica era in grado di spiegare tutta la chimica; Heitler e London condividevano quest'arrogante visione riduzionista di Dirac per cui la chimica non era altro che fisica applicata.

Ovviamente i chimici non erano d'accordo con questa prospettiva, sostenuti nella loro posizione da alcuni dei pionieri della chimica quantistica, come Pauling e Mulliken, che consideravano sterile per la chimica l'atteggiamento dei riduzionisti. Effettivamente la chimica apportò enormi contributi alla fisica durante gli anni Trenta, contributi che i fisici stessi non avevano previsto. Il progresso della scienza nucleare sperimentale dipendeva all'epoca da gruppi interdisciplinari che facevano uso di macchine e tecniche nuove per provocare reazioni nucleari e analizzarne i risultati. I fisici, compresi Fermi e Lise Meitner (1878-1968), ritenevano di aver identificato in nuclei con numero atomico maggiore di 92 alcuni radioelementi ottenuti dal bombardamento dell'uranio. Furono tuttavia i chimici Otto Hahn (1879-1968) e Fritz Strassmann (1902-1980) a riconoscere che alcuni di questi transuranici erano, chimicamente parlando, isotopi radioattivi di elementi già presenti nella tavola periodica.