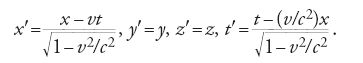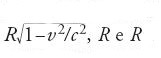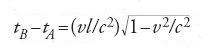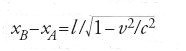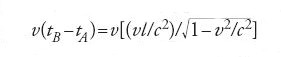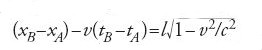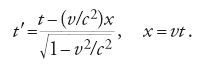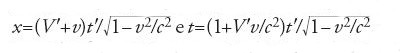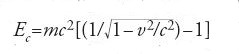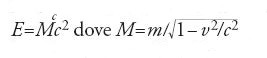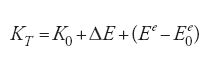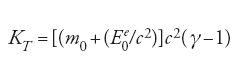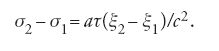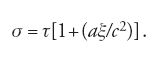La seconda rivoluzione scientifica: fisica e chimica. La relatività ristretta

La seconda rivoluzione scientifica: fisica e chimica. La relativita ristretta

La relatività ristretta

Può essere particolarmente utile studiare le origini della 'teoria della relatività ristretta, o relatività speciale', ponendo a confronto i metodi di ricerca di Albert Einstein (1879-1955) con quelli che il famoso matematico, filosofo e scienziato francese Jules-HenriPoincaré (1854-1912) utilizzò per affrontare gli stessi problemi teorici e lo stesso insieme di dati.Tale confronto consente di porre in rilievo quanto le concezioni einsteiniane sulla teoria fisica fossero, nel 1905, differenti da quelle di tutti gli altri fisici e, contemporaneamente, serve a spiegare il verificarsi di un evento unico nella storia della scienza: nel 1905, Einstein e Poincaré proposero approcci e soluzioni radicalmente diversi per lo stesso problema, pur avendo a disposizione i medesimi dati empirici. Le ragioni principali potrebbero essere le seguenti. (a) Einstein aveva una creatività basata sull'immaginazione visiva che gli consentiva d'integrare i dati disponibili a tutti i fisici con quelli che egli ricavava da un esperimento mentale (Gedankenexperiment). (b) La posizione di Poincaré nella ricerca scientifica si riduceva allo studio accurato dei dati empirici e alla formulazione di ipotesi sulla costituzione della materia; al contrario, Einstein sosteneva la necessità di accettare principî intesi come asser-indipendenti dalla costituzione della materia e da ogni verifica sperimentale (assiomi); in questo caso, fu il punto di vista di Einstein a prevalere. (c) Sia per Einstein, sia per Poincaré la posta in gioco era molto alta: per Poincaré, la teoria fisica doveva riuscire a rivelare la natura della realtà fisica, mentre Einstein, fin dal 1905, era giunto alla conclusione che la teoria fisica non era sufficientemente sviluppata per un obiettivo così ambizioso. Esisteva, quindi, una divergenza di opinioni su ciò che in fisica dobbiamo considerare un problema fondamentale e tale divergenza avrebbe influenzato la loro interpretazione del principio di relatività.

In un primo tempo, il contenuto del fondamentale articolo di Einstein del 1905, Zur Elektrodynamik bewegter Körper (Sull'elettrodinamica dei corpi in moto), in cui è esposta quella che oggi chiamiamo teoria della relatività ristretta o relatività speciale, fu apprezzato nella maggior parte dei casi per ragioni improprie. I fisici lo interpretarono come una generalizzazione della teoria degli elettroni (1904) del fisico olandese Hendrik Antoon Lorentz (1853-1928) e non come una sostanziale revisione delle nozioni ordinarie di spazio, tempo e sostanza. Due anni dopo, di fronte a questi errori di interpretazione e ai dati sperimentali che sembravano smentire una predizione chiave della teoria degli elettroni di Lorentz-Einstein, lo stesso Einstein si propose di estendere la sfera di applicabilità del suo lavoro del 1905 fino a comprendervi la gravitazione, cioè fino a enunciare una teoria generale della relatività (oggi detta relatività generale). Egli pubblicò questo nuovo risultato nell'articolo del 1907 Relativitätsprinzip und die aus demselben gezogenenFolgerungen (Il principio di relatività e le conseguenze che ne derivano).

Se riferito al contesto storico, lo sforzo compiuto da Einstein per estendere la teoria della relatività ristretta del 1905 alla gravitazione fu senza dubbio rilevante. D'altra parte, nel 1907, l'unica altra nuova teoria della gravità era quella che Poincaré aveva presentato nell'articolo del 1906 Sur la dynamique de l'électron.Sebbene in tale articolo Poincaré esponesse la novità della 'Lorentz-covarianza', la sua teoria era costruita su linee tradizionali, con un'equazione della forza analoga a quella di Lorentz per l'elettromagnetismo. Al contrario, l'obiettivo principale di Einstein era realizzare l'equivalenza tra fenomeni gravitazionali e accelerazione.Ancora una volta, com'era accaduto nella scoperta della relatività speciale, fu un esperimento mentale a suggerirgli la via da seguire.

Qui, in particolare, tenteremo di cogliere i nessi esistenti tra i concetti sui quali Einstein costruì la teoria della relatività del 1905 (per es., il carattere relativo dei campi elettrici e magnetici), il suo tentativo di generalizzare l'equivalenza tra la massa e l'energia e, infine, l'esperimento mentale del 1907 che gli permise di scoprire l'equivalenza tra gli effetti di un campo gravitazionale uniforme e un'accelerazione costante di retta in senso opposto.

Il problema fisico

di Arthur I. Miller

Prima del 1904, il principio di relatività della meccanica newtoniana era di solito indicato con il nome di principio del moto relativo. Nel 1900 Poincaré lo formulò nel seguente modo: "Il moto di un qualunque sistema deve obbedire alle stesse leggi, sia che venga riferito ad assi fissi, sia ad assi che si muovono di moto rettilineo". I particolari assi mobili di cui parla Poincaré sono sistemi di riferimento inerziali. Secondo il principio del moto relativo, le leggi della meccanica hanno la stessa forma in ogni sistema di riferimento inerziale; da qui segue che nessun espe rimento di meccanica è in grado di rilevare il moto di un sistema di riferimento inerziale.Nella meccanica newtoniana, il principio del moto relativo è un assioma, in quanto viene accettato senza alcuna verifica sperimentale. La situazione è molto diversa quando si passa all'elettromagnetismo.

Nell'Ottocento la teoria ondulatoria della luce era stata formulata sulla base del concetto di etere, in analogia con la propagazione del suono che ha bisogno di un mezzo (l'atmosfera) per trasmettersi. Tuttavia, nonostante i molti sforzi, i tentativi volti a rivelare sperimentalmente una qualche influenza dell'etere sui fenomeni ottici fallirono. Possiamo illustrare questi tentativi con il seguente esperimento mentale. Supponiamo che un'onda luminosa sia emessa da una sorgente in quiete; supponiamo poi di seguire un punto di quest'onda.Dopo l'emissione dell'onda, un osservatore, o piuttosto uno sperimentatore immaginario, che all'inizio si trovi in quiete in prossimità della sorgente, comincia a muoversi per raggiungere il punto segnato sull'onda luminosa. Consideriamo le due seguenti possibilità: (a) secondo la teoria della luce disponibile all'epoca, l'osservatore riuscirà a valutare gli effetti del suo moto relativo, per esempio, misurando la velocità dell'onda luminosa rispetto al suo laboratorio; (b) poiché le leggi dell'ottica sono indipendenti dallo stato di moto dell'osservatore, i fenomeni ottici misurati dall'osservatore in moto si manifestano come se egli stesso fosse in quiete rispetto all'onda luminosa: è quanto accade, assiomaticamente, per le leggi della meccanica nei sistemi di riferimento inerziale.

Le affermazioni (a) e (b) sono tra loro contraddittorie. Sia v la velocità dell'osservatore rispetto alla sorgente e c la velocità di un punto dell'onda rispetto alla sorgente; la velocità di un punto dell'onda rispetto all'osservatore sarà in questo caso, secondo (a):

[1] V′=c−v.

La [1] è la legge newtoniana di composizione delle velocità. Tuttavia secondo (b) si avrà sempre:

[2] V′=c.

Per la relazione [2], l'osservatore dovrebbe misurare i fenomeni ottici come se egli si trovasse in quiete rispetto all'onda luminosa.

Le equazioni fondamentali della teoria della luce erano, all'epoca, quelle introdotte da Lorentz nel 1892. Secondo quanto previsto dalle teorie fondate sul concetto di etere, queste equazioni dovevano essere formulate, inizialmente, in un sistema di riferimento in quiete rispetto all'etere. Si tratta di una classe speciale di sistemi di riferimento, poiché soltanto in essi la velocità della luce è esattamente c, indipendentemente dallo stato di moto relativo della sorgente luminosa; in questi sistemi di riferimento speciali vale quindi sempre la [2]. Il passaggio successivo consisteva nell'applicare le trasformazioni spaziotemporali della meccanica di Newton alle equazioni fondamentali dell'ottica espresse in un sistema di riferimento in quiete nell'etere. Queste trasformazioni (dette trasformazioni di Galilei) sono:

dove le quantità con l'indice r si riferiscono a un sistema inerziale, mentre quelle senza indice a un sistema di riferimento solidale con l'etere, e v è la velocità relativa tra il sistema di riferimento inerziale e l'etere. Con questa operazione si trasferisce il problema studiato in un altro sistema di riferimento in moto attraverso l'etere e si ottiene la [1] per il valore della velocità della luce nel sistema di riferimento in moto. Nel 1900, i fenomeni ottici nei sistemi di riferimento in moto erano quindi studiati con una combinazione di ottica ondulatoria e di meccanica.

Se esiste un etere, allora deve esserci un modo per rilevare sperimentalmente i suoi effetti, misurando di quanto la V′ nella [1] differisca da c. In base alla [1] e alla [2] possiamo stabilire quali siano gli esperimenti che ci consentono di rilevare l'etere. Supponiamo che la Terra, invece di muoversi attorno al Sole, sia in quiete e che l'etere scorra come l'acqua di un fiume. La velocità dei raggi di luce misurata sarà allora influenzata dalla velocità relativa v tra la Terra e l'etere, allo stesso modo in cui il moto di un nuotatore è influenzato dalla corrente di un fiume. Tuttavia, anche gli esperimenti più accurati risultavano coerenti con la [2].

Per rimuovere l'incoerenza tra la [1] e la [2], i fisici avanzarono alcune ipotesi; essi suggerirono, per esempio, che, a causa del moto della Terra attraverso l'etere, venissero modificate alcune caratteristiche dei corpi, così da essere cancellati gli effetti che dovremmo attenderci per la quantità v nella [1]: ossia, si riteneva che la quantità v fosse l'agente che produce effetti come la contrazione dei corpi in moto. Possiamo quindi affermare che i fisici formularono alcune ipotesi con l'obiettivo di costruire un principio del moto relativo per i fenomeni ottici in sistemi di riferimento in moto.

L'affermazione (b) (V′=c) relativa al nostro esperimento mentale non potrebbe essere soddisfatta semplicemente estendendo il principio del moto relativo alla teoria della luce? I fisici non sarebbero stati disposti a considerare questa una soluzione soddisfacente, perché essa avrebbe richiesto un radicale mutamento della visione del mondo, non molto diverso da quello che si ebbe con il passaggio da un Universo geocentrico a uno eliocentrico.Se essi avessero esteso il principio del moto relativo dalla meccanica di Newton alla teoria della luce avrebbero rifiutato la validità della [1] e, quindi, reso l'etere non necessario. Proprio in relazione a tale problema, nel Versuch einer Theorie der elektrischen und optischen Erscheinungen in bewegten Körpern (Trattato sui fenomeni elettrici e ottici nei corpi in moto) del 1895, Lorentz aveva proposto una nuova definizione di tempo per la teoria fisica.

In accordo con le nostre percezioni sensoriali, il tempo sembra essere una grandezza assoluta. Per questo, nella meccanica newtoniana si assume che in ogni sistema di riferimento inerziale il tempo sia lo stesso e tale ipotesi è usata nella derivazione della [1] (v. le altre due relazioni [3]). Nel 1895 Lorentz propose una versione migliorata della teoria della luce e dell'elettromagnetismo che aveva formulato nel 1892. Tale nuova versione conteneva uno strumento sistematico che permetteva di rimuovere le incoerenze esistenti tra la [1] e la [2] per una classe particolare di esperimenti che non erano riusciti a confermare l'esistenza dell'etere: si trattava di quegli esperimenti nei quali si può trascurare il quadrato del rapporto tra la velocità del sistema rispetto all'etere e la velocità della luce nell'etere privo di materia ponderabile, di solito indicato dai fisici come 'etere libero' o vacuum. Indicheremo questi esperimenti come approssimati al primo ordine del rapporto (v/c). Come ipotesi puramente matematica, Lorentz suppose che, in un sistema di riferimento in moto, il tempo dipenda dal moto relativo del sistema rispetto al laboratorio o all'etere, a seconda del tipo di esperimento considerato (per es., nell'esperimento di Armand-Hippolyte-Louis Fizeau del 1851, v è la velocità del flusso d'acqua rispetto al laboratorio). Lorentz parla di questo tempo matematico come di 'tempo locale', tl, ponendo, come scrisse nel citato Versuch,

Ovviamente il tempo fisico reale restava il tempo delle trasformazioni galileiane [3], t_r=t. L'ipotesi della coordinata tempo locale, insieme alle altre ipotesi su come l'etere influenzi la materia in moto, consentì a Lorentz di esprimere le equazioni della sua teoria come se il sistema inerziale in moto fosse in quiete nell'etere, purché si trascurassero i termini di ordine (v/c)2. Il principio del moto relativo di Lorentz era però approssimato, poiché poteva spiegare soltanto il fallimento di alcuni esperimenti sul trascinamento dell'etere. Benché utilizzasse un concetto assoluto di tempo, la meccanica di Newton conteneva un principio del moto relativo esatto e assiomatico, ma non era in grado di trattare né la luce, né i fenomeni riguardanti gli elettroni. A partire dal 1900 i tentativi sempre più complessi, volti a dedurre le leggi dell'elettromagnetismo da modelli meccanici dell'etere, cioè da un'immagine meccanica del mondo, persero molta della loro rilevanza di fronte sia ai successi ottenuti dalla teoria elettromagnetica di Lorentz nel trattare fenomeni riguardanti gli elettroni, sia al fallimento degli esperimenti sul trascinamento dell'etere, al primo ordine di (v/c). Lorentz assegnò un valore assiomatico alle equazioni dell'elet tromagnetismo e, nel 1900, formulò un programma di ricer ca secondo il quale tutte le leggi naturali avrebbero dovuto essere fondate su quelle della teoria elettromagnetica. I fisici si riferivano a questo programma di ricerca utilizzando la metafora dell''immagine elettromagnetica del mondo' (elektromagnetisches Welt-bild).

Quale applicazione importante dell'immagine elettromagnetica del mondo, la massa dell'elettrone avrebbe dovuto essere prodotta per autoinduzione dai suoi stessi campi elettrici e magnetici; la massa dell'elettrone dipenderebbe, quindi, dalla velocità dellstesso rispetto al laboratorio. Nel 1901 questa predizione fu verificata sperimentalmente dal fisico tedesco WalterKaufmann (1871-1947). Sebbene venisse ancora riconosciuta una certa importanza teorica all'esistenza dell'etere, la ricerca di una spiegazione completa di questi esperimenti divenne un problema secondario rispetto ai nuovi dati sulla massa degli elettroni veloci ottenuti da Kaufmann. Per discutere questi nuovi dati, i fisici svilupparono la teoria elettromagnetica di Lorentz; ma, pur ottenendo alcuni successi, la nuova versione della teoria impediva loro di spiegare il fallimento di tutti gli esperimenti compiuti per rivelare la presenza dell'etere. In Electromagnetische verschijnselen in een stelsel, dat zich met willekeurige snelheid kleiner den die van het licht, beweegt (Fenomeni elettromagnetici in un sistema in movimento con velocità più piccola di quella della luce, 1904) Lorentz formulò una teoria dell'elettrone in accordo con i dati di Kaufmann e, al contempo, spiegava il fallimento di tutti gli esperimenti volti a rivelare l'esistenza dell'etere.

L'approccio di Poincaré

di Arthur I. Miller

Come tutti i fisici all'inizio del secolo, Poincaré riteneva che il concetto di etere fosse necessario per la teoria elettromagnetica. La sua convinzione tuttavia era fondata piuttosto su ragioni filosofiche che scientifiche. Come egli scrisse in La science et l'hypothèse (1902), "la sola realtà obiettiva consiste di relazioni tra cose", o di sensazioni. Di conseguenza, visto che nella teoria elettromagnetica l'etere serve a connettere eventi o fatti, l'etere per Poincaré può essere considerato reale. L'origine della tesi di Poincaré, secondo la quale l'unica realtà obiettiva consiste di relazioni tra sensazioni, va ricercata nelle sue idee sulla genesi della geometria, la quale, a suo avviso, è alla base della nostra comprensione del mondo.

Noi formuliamo ipotesi a partire dai dati empirici. Poincaré chiamava 'leggi' le ipotesi di livello inferiore che sono più vicine ai dati empirici e 'convenzioni' le ipotesi di livello superiore. Le convenzioni sono dotate di un elevato potere di unificazione e "sono la generalizzazione naturale e diretta di principî sperimentali e particolari". In questo senso, il principio del moto relativo è una convenzione, non soltanto a causa del suo indiscutibile potere unificante ma anche perché, scrive Poincaré, "l'ipotesi contraria sarebbe particolarmente ripugnante per il pensiero". In altre parole, al di là delle sue basi empiriche (per es., la meccanica celeste), il principio del moto relativo è radicato nel pensiero prescientifico (infatti per noi ha senso parlare solamente di moto relativo degli oggetti). Più in generale, per Poincaré tutti i concetti scientifici hanno un'origine prescientifica. Rispondendo a BertrandRussell sul problema delle origini della scienza, egli affermava infatti: "Russell mi dirà che non è affatto un problema di psicologia, ma di logica ed epistomologia; io sarei portato a rispondere che non c'è né logica, né epistemologia senza psicologia". Proprio perché il relativismo è un aspetto essenziale del pensiero di Poincaré, di tutte le teorie dell'elettrone formulate tra il 1902 e il 1904 egli preferì quella di Lorentz; era infatti l'unica teoria che soddisfaceva i requisiti posti da Poincaré per l'etere e il relativismo. Nel settembre del 1904 Poincaré parlò di principio di relatività a proposito della spiegazione data da Lorentz del fallimento degli esperimenti sul trascinamento dell'etere; "secondo [tale principio] le leggi dei fenomeni fisici devono essere le stesse per un osservatore in quiete come per un osservatore trascinato in un moto di traslazione uniforme; così non abbiamo, né possiamo avere alcuno strumento per verificare se siamo o meno trascinati in questo moto". Il principio di relatività di Poincaré è quindi un'estensione del principio del moto relativo alla fisica dell'elettrone.

Poincaré sviluppò la sua discussione della teoria lorentziana dell'elettrone in due classici lavori aventi lo stesso titolo Sur la dynamique de l'électron; una versione abbreviata fu pubblicata sui "Comptes rendus" dell'Académie des Sciences di Parigi del 5 giugno 1905 e una, più estesa, nei "Rendiconti del Circolo matematico di Palermo" del marzo 1906. Poincaré dimostrò che, di tutte le possibili descrizioni elettromagnetiche dell'elettrone, soltanto la teoria di Lorentz era compatibile con il principio di relatività. Egli ottenne questo risultato aggiungendo alla lagrangiana dell'elettrone un termine che permetteva all'energia e alla quantità di moto delldi soddisfare correttamente la trasformazione di Lorentz; secondo la terminologia introdotta da Hermann Minkowski nel 1907, potremmo affermare che Poincaré elaborò un metodo che riusciva a trasformare queste quantità in un quadrivettore. Pur riconoscendo il disaccordo esistente tra la predizione lorentziana e i più recenti dati di Kaufmann per la massa dell'elettrone, Poincaré non giunse mai ad affermare che il principio di relatività diviene una convenzione quando lo si applichi alla dinamica degli elettroni. Anche dopo il 1908, quando furono trovati dati che confermavano la teoria degli elettroni di Lorentz (che allora molti fisici, a eccezione di Poincaré, chiamavano teoria di Lorentz-Einstein), le idee di Poincaré sulla struttura della teoria scientifica continuarono a impedirgli di elevare il principio di relatività al rango di convenzione; questo perché la sua teoria della gravitazione prediceva un valore dello spostamento del perielio di Mercurio che non si accordava con le misure in quel momento disponibili.

Nell'articolo Sur la dynamique de l'électron, Poincaré utilizzò la sua eccezionale abilità matematica per esprimere la teoria lorentziana degli elettroni in una forma che risultasse matematicamente equivalente alla teoria speciale della relatività di Einstein. Nello stesso mese in cui apparve sui "Comptes rendus" l'articolo di Poincaré, Einstein aveva infatti inviato agli "Annalen der Physik" il suo articolo Zur Elektrodyna mik bewegter Körper, che conteneva ciò che in seguito avrebbe chiamato la "ṣogenannt Relativitätstheorie" (cosiddetta 'teoria della relatività').

Nel 1905, i fisici ritenevano che la teoria elettromagnetica si stesse sviluppando nella giusta direzione e molti di essi consideravano la teoria degli elettroni di Lorentz la pietra angolare per una concezione di campo unificato della Natura. Quella di Lorentz era una teoria dinamica in grado di spiegare effetti come la presunta contrazione della lunghezza, la misura della variazione della massa dell'elettrone con la velocità, nonché la costanza della velocità della luce. Tutto era interpretato come conseguenza dell'interazione fra elettroni ed etere: erano state gettate le basi per una nuova grande era, scaturita da quello che tutti consideravano il problema fondamentale della teoria fisica.

La teoria della relatività ristretta

di Arthur I. Miller

Fin dall'inizio del 1905, l'approccio di Einstein differì radicalmente da quello di Poincaré, anche per i dati presi in esame. Dalla corrispondenza di Einstein e dall'analisi dei suoi lavori del periodo 1906-1907 sappiamo che fin dal 1905 egli aveva acquisito teoricamente che la luce può essere composta di particelle (quanti di luce, poi detti 'fotoni'), così come di onde. Poiché i quanti di luce non sono annoverati nella teoria di Lorentz, questa non può spiegare in che modo la massa dell'elettrone possa essere generata dai campi elettromagnetici che esso stesso produce; di conseguenza, la teoria di Lorentz non può essere a fondamento di ogni altra teoria fisica.

Einstein ricorda di aver disperato di scoprire le leggi 'vere' mediante "sforzi costruttivi" basati su fatti noti, ossia ricorrendo a teorie costruttive che rendessero ragione del verificarsi dei fenomeni con ipotesi sulla costituzione della materia. Per esempio, la teoria di Lorentz spiegava il fallimento degli esperimenti che cercavano di rivelare l'esistenza dell'etere con ipotesi sulle modalità con cui gli elettroni costituenti la materia interagirebbero con esso. Al contrario, le teorie di principio non spiegano i fenomeni e non fanno ipotesi sulla costituzione della materia; esse sono basate su principî generali che sono accettati come assiomi. Questi principî indicano la forma che le leggi fisiche devono assumere per impedire che certi fenomeni si verifichino: per esempio, nella termodinamica, il principio di conservazione dell'energia asserisce ab initio che tutte le teorie devono essere formulate in modo tale che l'energia si conservi. Un altro esempio è il principio newtoniano del moto relativo, il quale afferma, senza darne alcuna spiegazione, che le teorie della meccanica devono essere formulate in modo tale che le relative leggi restino le stesse in ogni sistema di riferimento inerziale.

Giunto al culmine della "disperazione", Einstein comprese che avrebbe dovuto affidarsi soltanto a una teoria di principio per andare oltre i "fatti noti". Gli indizi sul procedimento da seguire erano due.

a) Nel 1895 egli aveva concepito un esperimento mentale, simile a quello che è stato discusso in precedenza; ma, per Einstein, la [2] era richiesta da quella che egli chiamava l'"intuizione" dello sperimentatore ipotetico, secondo la quale, così come nessun esperimento meccanico può rivelare il moto di un sistema di riferimento inerziale, lo stesso deve aversi nel caso degli esperimenti con la luce. Nel 1905, Einstein avrebbe risolto l'incoerenza contenuta in questo esperimento; prima però egli avrebbe compreso un altro problema fondamentale, che costituisce il secondo indizio.

b) Mentre gli altri fisici lavoravano su quelli che essi consideravano i problemi principali, e cioè i dati di Kaufmann per gli elettroni veloci, Einstein rivolse la sua attenzione al fenomeno dell'induzione elettromagnetica, dove intervengono piccole velocità (molto minori di quella della luce). L'induzione elettromagnetica è il processo per cui in un circuito conduttore in moto rispetto a un magnete insorge una corrente elettrica; si tratta del processo che regola, per esempio, il funzionamento delle dinamo elettriche.Da letture personali e nei corsi seguiti dal 1896 al 1900 al Politecnico di Zurigo, Einstein era venuto a conoscenza dei problemi fondamentali che sono connessi con la progettazione delle dinamo elettriche. Il lavoro svolto, nel periodo 1902-1909, presso l'Ufficio brevetti di Berna, aveva ulteriormente attratto il suo interesse per l'induzione elettromagnetica nel caso del moto rotatorio relativo tra magnete e circuito; esso chiama in causa alcuni problemi concettuali circa la possibilità o meno che le linee di forza magnetiche ruotino insieme al magnete che le genera. Ancora più importante era il problema relativo alla possibilità che un campo magnetico esterno fosse prodotto da un magnete.Einstein comprese che era possibile indagare casi complessi di questo genere attraverso il caso, più semplice, dell'induzione elettromagnetica fra un magnete e un circuito conduttore in moto inerziale uno rispetto all'altro.

Secondo Einstein, la teoria elettromagnetica di Lorentz non riusciva a spiegare correttamente neppure un fenomeno semplice come l'induzione elettromagnetica. Le sue critiche principali non si basavano però su dati empirici, ma erano di natura per così dire 'estetica', vale a dire invocavano caratteristiche di simmetria che dovevano essere soddisfatte nella spiegazione di tale fenomeno. La teoria elettromagnetica dava ragione dell'induzione elettromagnetica in due modi diversi, a seconda che a muoversi fosse il circuito o il magnete.Nel primo caso, si genera una corrente che è prodotta da una forza agente sugli elettroni nel circuito; nel caso inverso, la nascita della corrente dipende da un campo elettrico prodotto dal magnete in movimento. Tuttavia, l'effetto misurabile ossia la corrente prodotta, dipende sempre dalla stessa causa, cioè la velocità relativa.

Secondo Einstein l'esistenza di due spiegazioni di un effetto dipendente unicamente dalla velocità relativa tra il magnete e il circuito rappresentava molto più che un difetto trascurabile nella teoria di Lorentz: si trattava di una ridondanza che egli interpretò come un'asimmetria "non inerente al fenomeno", come scrisse nell'articolo del 1905. Per eliminare l'asimmetria, egli impose la condizione che vi fosse equivalenza tra i punti di vista di due osservatori solidali con il conduttore e con il magnete. Colse così il significato dello stretto legame esistente fra meccanica ed elettromagnetismo per l'interpretazione dell'induzione elettromagnetica: si dovevano usare le leggi della meccanica per calcolare il moto relativo del filo e del magnete. Poiché il principio newtoniano del moto relativo è esatto e poiché sono necessari la meccanica e l'elettromagnetismo per spiegare l'induzione elettromagnetica, allora una versione del principio newtoniano del moto relativo deve essere applicata all'elettromagnetismo e all'ottica, come anche agli esperimenti sul trascinamento dell'etere. Con questo colpo magistrale, Einstein estese il principio newtoniano del moto relativo così da trattare sia la meccanica, sia l'elettromagnetismo, invece di tentare la riduzione di una disciplina all'altra. Di conseguenza, nell'elettromagnetismo non possono esserci sistemi di riferimento privilegiati e quindi, come egli scrisse nel 1905, l'etere diviene "superfluo". A questo punto Einstein si pose il problema di trovare una nuova possibilità di moto dei sistemi di riferimento che non portasse inevitabilmente alla legge newtoniana di composizione delle velocità.

Di tutti gli esperimenti con i quali si era tentato invano di rivelare l'etere, quelli che Einstein considerava più importanti erano gli esperimenti al primo ordine di (v/c), poiché potevano essere spiegati sistematicamente con il concetto lorentziano di coordinata tempo locale, definita nel Versuch di Lorentz; è da osservare che, nel giugno del 1905, Einstein non aveva ancora letto il lavoro di Lorentz dell'anno precedente sulla teoria degli elettroni, che conteneva la versione del tempo locale valida per tutti gli ordini di (v/c). Il tempo locale avrebbe quindi giocato un ruolo importante nel correlare i fenomeni rispetto a diversi sistemi di riferimento. Einstein passò poi a ricercare una nuova legge per la composizione delle velocità, che avrebbe dovuto sostituire la [1] e accordarsi con l'intuizione dello sperimentatore immaginario.Riuscì a realizzare ciò con una derivazione basata sulla coordinata tempo locale. Egli divise correttamente la prima delle [4] e l'ultima, ottenendo:

[5] V′=(V−v)/[1−(vV/c²)],

dove per Einstein i due insiemi di coordinate sono relativi a sistemi di riferimento inerziali, ossia V′ è la velocità di un punto nel sistema di riferimento S_r, V è la velocità di questo punto nel sistema di riferimento S e v è la velocità relativa tra S_r e S.Poiché per Einstein l'etere è "superfluo", allora i sistemi di riferimento S_r e S sono sistemi di riferimento inerziali nel significato che questo termine ha nella meccanica newtoniana, cioè sia S_r sia S possono muoversi. Questo non accade per i sistemi di riferimento che intervengono nella [4] e a maggior ragione nella [3], poiché la trasformazione galileiana [3] è matematicamente, ma non fisicamente, equivalente a quella della meccanica newtoniana; la ragione è che i sistemi di riferimento S sono fissi nell'etere. Quindi, la simmetria tra sistemi di riferimento che si ha nella trasformazione galileiana della meccanica newtoniana si perde nelle teorie elettromagnetiche fondate sul concetto di etere. Inoltre, le trasformazioni [3] e [4] contengono velocità della materia rispetto all'etere che sono incognite e vanno considerate, per ipotesi, responsabili del cambiamento delle caratteristiche fisiche dei corpi in moto. Perciò, sarebbe sbagliato sostenere che la versione della [5] presente nell'articolo di Poincaré Sur la dynamique de l'électron sia del tutto priva di ambiguità per il fatto che nelle teorie dell'etere si perde il concetto di quiete rispetto a un sistema di riferimento inerziale.

La legge einsteiniana di composizione delle velocità è coerente con l'intuizione dello sperimentatore immaginario quando il fenomeno studiato riguarda la luce, poiché nella [5] quando V=c, è anche V′=c. Questo risultato è decisamente bizzarro; senza che ne venga data alcuna spiegazione, la velocità relativa tra lo sperimentatore immaginario e il punto su un'onda luminosa risulta essere sempre la stessa, indipendentemente dal moto dello sperimentatore.

Nel 1898 Poincaré pubblicò un importante articolo dal titolo La mesure du temps, dedicato allo studio dei rapporti tra simultaneità, tempo e posizione degli orologi, con l'impiego di segnali luminosi. Egli aveva concluso che "non abbiamo né una intuizione diretta della simultaneità, né dell'uguaglianza di due durate". A prescindere da qualche sfumatura, lo scienziato francese avrebbe ripreso queste affermazioni nel suo libro del 1902 La science et l'hypothèse. Coerentemente con la sua concezione di una scienza fondata sui dati empirici e sulle percezioni sensoriali, e per la quale "l'esperimento è la sola fonte della verità", il problema relativo alla migliore definizione della simultaneità di due eventi distanti viene risolto da Poincaré con una definizione di tempo che "si basa sulla convenienza e la semplicità", il tempo assoluto delle trasformazioni galileiane. Anche quando discuteva su un qualche possibile significato fisico da assegnare al tempo locale, Poincaré concludeva che termini dipendenti dalla velocità relativa tra sistemi di riferimento vanno oltre le nostre percezioni sensoriali e quindi possono essere trascurati.

Einstein adottò un procedimento totalmente diverso non appena si rese conto, nel giugno 1905, che la formulazione coerente dell'elettrodinamica dei corpi in moto richiedeva che si esaminasse la cinematica da un punto di vista diverso da quello che chiama in causa le percezioni sensoriali: come scrisse nel 1946, riprendendo Poincaré, "non solo non abbiamo alcuna intuizione diretta dell'uguaglianza di due durate, ma non abbiamo neppure un'intuizione diretta della simultaneità di due eventi che si verificano in luoghi diversi". Il metodo einsteiniano del 1905 prevedeva un livello di astrazione superiore rispetto a quello della meccanica di Newton, con la sua legge di composizione delle velocità e i suoi concetti fondati troppo direttamente sulle nostre percezioni del mondo esterno.

Per comprendere e interpretare il concetto di tempo locale di Lorentz in modo radicalmente diverso da Poincaré, Einstein, per sua stessa ammissione, ricavò suggerimenti utili dalla lettura degli scritti filosofici di David Hume. L'analisi humiana delle percezioni sensoriali mostrava con grande chiarezza a Einstein che dai dati percettivi non possono essere tratte leggi naturali esatte. Einstein comprese così che l'alto valore numerico della velocità della luce non aveva permesso di comprendere quanto "il carattere assoluto del tempo, cioè della simultaneità, fosse rimasto ancorato nell'inconscio". Sebbene Einstein non concordasse pienamente con la replica di Immanuel Kant a Hume, egli si mosse in una direzione analoga a quella del filosofo tedesco, proponendo principî regolativi immodificabili di tipo kantiano: il principio di relatività (espresso in forma analoga a quello di Poincaré) e il principio secondo cui la velocità della luce è una costante definita, cioè indipendente dal moto relativo tra la sorgente e l'osservatore (principio che in seguito chiameremo assioma della luce). Come egli stesso scrisse nel 1907, il principio di relatività era la base di una teoria che indicava la forma che avrebbero dovuto assumere le leggi della fisica per essere ancora utilizzate nello studio della costituzione della materia.

Mentre i principî di relatività di Poincaré e di Einstein sono espressi in termini simili, il loro contenuto e le loro finalità differiscono radicalmente. Il principio di relatività di Einstein non spiegava per quale motivo la misura della velocità della luce sia sempre uguale a c. Il principio di relatività di Poincaré rappresentava invece il nucleo di una teoria costruttiva da porre a fondamento di una visione elettromagnetica del mondo. A differenza del principio di relatività di Einstein, quello di Poincaré non aveva un carattere assiomatico e dipendeva dai risultati negativi degli esperimenti sul trascinamento dell'etere. In breve, Einstein si muoveva coraggiosamente contro le principali correnti di fisica teorica del tempo per risolvere i problemi in modo radicale, cioè elaborando una concezione della fisica nella quale il verificarsi di alcuni problemi fosse escluso per principio e si dissolvesse il paradosso del 1895. Benché i dati sulle alte velocità avessero dominato la fisica teorica di base a partire dalla metà del 1905, per far entrare la fisica nel XX sec. Einstein aveva bisogno soltanto dei più familiari dati relativi alle basse velocità, come quelli provenienti dall'induzione elettromagnetica, oltre ai dati tratti da esperimenti mentali.

La contrazione delle lunghezze e la dilatazione del tempo

di Giulio Peruzzi

L'articolo di Einstein sulla relatività, del 1905, inizia con le seguenti parole:

È noto che l'elettrodinamica di Maxwell ‒ così come essa è oggi comunemente intesa ‒ conduce, nelle sue applicazioni ai corpi in movimento, ad asimmetrie che non sembrano conformi ai fenomeni. Si pensi per esempio alle interazioni elettrodinamiche tra un magnete e un conduttore. [...] Esempi come questo, come pure i tentativi falliti di individuare un qualche movimento della Terra relativamente al mezzo luminifero suggeriscono che i fenomeni elettrodinamici, al pari di quelli meccanici, non possiedono proprietà corrispondenti all'idea di quiete assoluta. Essi suggeriscono piuttosto che [...] per tutti i sistemi di coordinate per i quali valgono le equazioni della meccanica varranno anche le stesse leggi elettrodinamiche e ottiche. Eleveremo questa congettura (il contenuto della quale verrà detto in quanto segue principio di relatività) al rango di postulato; supporremo inoltre ‒ un postulato, questo, solo apparentemente incompatibile col precedente ‒ che la luce, nello spazio vuoto, si propaghi sempre con una velocità determinata c, che non dipende dallo stato di moto del corpo che la emette. (Einstein 1905b, pp. 891-892)

Questi due postulati sarebbero "apparentemente inconciliabili" in quanto, come già osservato in precedenza, due osservatori in moto relativo devono concludere che uno stesso fascio di luce ha per entrambi la stessa velocità c. Per comprendere come riconciliare i due postulati è necessario ripensare le nozioni di spazio e tempo, eliminando da queste alcuni caratteri mutuati dal senso comune e accogliendone di nuovi, come la relatività della simultaneità, la contrazione delle lunghezze e la dilatazione dei tempi. È questo il contenuto della prima parte dell'articolo di Einstein dove egli introduce una nuova cinematica, dimostrando quanto naturali, ancorché contrari al senso comune, siano questi nuovi caratteri dello spazio e del tempo. Questa parte è particolarmente significativa per comprendere sia la svolta radicale di Einstein rispetto agli approcci di Lorentz e Poincaré sia i contenuti della relatività ristretta. Inoltre la sua presentazione originale è di notevole efficacia: vale quindi la pena di riassumerne i tratti essenziali.

Nella prima sezione della cinematica, dal titolo Definition der Gleichzeitigkeit (Definizione di simultaneità), Einstein chiarisce che cosa si intende per 'tempo'. Ricordiamo innanzi tutto che un sistema di riferimento è un sistema di coordinate e un orologio e che un sistema di riferimeno è inerziale se in esso valgono le leggi della meccanica newtoniana (inoltre qualunque altro sistema di riferimento in moto rettilineo e uniforme relativamente a un sistema di riferimento inerziale è ancora un sistema di riferimento inerziale). Si consideri un punto materiale in quiete in un dato riferimento inerziale S; la sua posizione in S, come afferma Einstein, "può essere determinata con un campione di lunghezza rigido, utilizzando le regole della geometria euclidea, ed essere espressa in coordinate cartesiane" (x,y,z). Se ora vogliamo descrivere il moto di un punto materiale è necessario esprimere i valori delle coordinate in funzione del tempo. Questa descrizione matematica, osserva Einstein, "non ha significato fisico se prima non si chiarisce che cosa si intende per tempo". Per questo è importante notare che ogni nostro giudizio in cui interviene il tempo è un giudizio su eventi simultanei. Per esempio, quando affermiamo che un treno arriva alle ore 7 in pratica intendiamo dire che la posizione delle lancette dell'orologio sul 7 e l'arrivo del treno sono eventi simultanei. Per chiarire il significato fisico di tempo bisogna quindi partire da una definizione convincente di simultaneità.

fig. 4

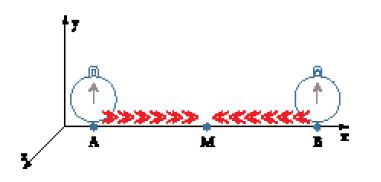
A questo fine consideriamo due osservatori A e B collocati in due punti dello spazio di un sistema inerziale che effettuano determinazioni di tempo per eventi che si verificano nelle loro immediate vicinanze. In tal modo abbiamo definito un tempo t_A per A e un tempo t_B per B. Per poter confrontare le letture dei tempi dei due osservatori è necessario 'sincronizzare' gli orologi. Questo viene fatto 'per definizione' nel modo seguente (usiamo qui una versione, equivalente ma semplificata rispetto a quella del 1905, esposta da Einstein successivamente). Supponiamo che da A al tempo t_A parta un raggio di luce verso B, e da B al tempo t_B parta un raggio di luce verso A. Diremo allora che i raggi sono stati inviati simultaneamente (cioè t_A=t_B) se la luce proveniente da A e quella proveniente da B vengono percepite da un osservatore M posto nel punto medio del segmento che congiunge la posizione di A con quella di B nello stesso istante t_M (fig. 4). Questa definizione di sincronizzazione è applicabile in modo coerente a un qualunque numero di orologi fermi in punti diversi del sistema inerziale. Da questa definizione, tratta da esperimenti fisici ideali, discende una definizione di 'simultaneità' e di 'tempo': "il 'tempo' di un evento è quello indicato, simultaneamente al prodursi dell'evento stesso, da un orologio stazionario situato nel luogo dell'evento e sincronizzato per ogni determinazione temporale con un dato orologio stazionario".

fig. 5

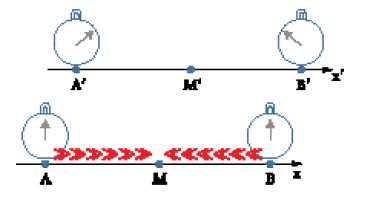
Cosa succede della simultaneità nel passaggio da un sistema inerziale a un altro? Per rispondere a questa domanda Einstein analizza nella seconda sezione dal titolo Über die Relativität von Längen und Zeiten (Relatività di lunghezze e tempi) un altro esperimento ideale. Prendiamo ancora due raggi di luce emessi simultaneamente da due sorgenti A e B, in quiete in un riferimento inerziale S e poste (per semplicità) in due punti dell'asse delle x di S. Sia S′ un altro riferimento inerziale. Per semplicità supponiamo che l'asse cartesiano delle X di S′ coincida con quello di S e gli assi Y e Z di S′ siano paralleli ai rispettivi assi di S. Sia inoltre S′ in moto uniforme rispetto a S con velocità v diretta lungo le x crescenti di S, e tale che all'istante t in cui per S si verificano i bagliori in A e B il punto medio M′ coincida con il punto medio M, A′ coincida con A e B′ con B (gli apici segnano i punti corrispondenti in S′). Se S′ fosse fermo, M′ verrebbe raggiunto simultaneamente dalla luce emessa da A e da B; siccome però M′ va incontro alla luce emessa da B e si allontana dalla luce emessa da A, allora esso sarà raggiunto prima dalla luce emessa da B e poi da quella emessa da A; i due eventi simultanei in S risulteranno non simultanei in S′ (fig. 5). Se ne conclude che la nozione di simultaneità non ha significato assoluto: il dissincronismo tra osservatori in moto implica che ci sono tanti tempi quanti sono i riferimenti inerziali. Questo risultato e la sua interpretazione segnano una svolta rispetto all'approccio di Lorentz e Poincaré: non esiste un tempo assoluto ma esistono solo tempi relativi ai diversi sistemi inerziali considerati.

A questo punto è essenziale per la descrizione fisica degli eventi specificare quali relazioni intercorrono tra le misure fatte da osservatori differenti in quiete rispetto a diversi riferimenti inerziali. E infatti nella terza sezione della cinematica Einstein espone la "teoria delle trasformazioni delle coordinate e del tempo" nel passaggio da un sistema inerziale all'altro. Per semplicità considera due riferimenti inerziali S e S′ con i rispettivi assi cartesiani X coincidenti e i rispettivi assi Y e Z paralleli; S′ si muove relativamente a S con velocità v diretta lungo l'asse delle x crescenti di S. Indichiamo con x,y,z,t le coordinate di un evento in S e con x′,y′,z′,t′ quelle dello stesso evento in S′. Insieme al postulato di relatività e a quello di costanza della velocità della luce, Einstein assume anche l'omogeneità e l'isotropia dello spazio e del tempo. Per l'omogeneità, le proprietà dei regoli e degli orologi non dipendono dalla posizione e dall'istante in cui si muovono, ma solo dal modo in cui si muovono; per l'isotropia, le proprietà dei regoli e degli orologi sono indipendenti dalla direzione in cui si muovono. Su questa base Einstein ricava le equazioni che esprimono le trasformazioni di coordinate cercate (le trasformazioni di Lorentz):

Al termine della sezione Einstein verifica la compatibilità dei due postulati. Supponiamo che all'istante t=t′=0, quando l'origine dei due sistemi S e S′ è comune, venga emessa da tale origine un'onda sferica che si propaga con velocità c nel sistema S. Si ha allora: x²+y²+z²=c²t². Utilizzando le trasformazioni di coordinate appena ottenute si ricava x′²+y′²+z′²=c²t′², cioè l'onda considerata anche nel sistema in moto continua a essere un'onda sferica che si propaga con velocità c. Sostituendo alle trasformazioni delle coordinate della meccanica di Newton le nuove trasformazioni delle coordinate si supera quindi l'apparente contraddizione tra i due principî. Questo implica però, come sarà chiaro in seguito (a partire in particolare dal contributo di Hermann Minkowski del 1908) una nuova struttura dello spaziotempo.

Vale la pena sottolineare che descrivere gli eventi attribuendo loro quattro coordinate invece di tre non ha nulla a che fare con la relatività di Einstein. Questo tipo di rappresentazione può essere usata anche nella meccanica newtoniana. La differenza sta nel modo in cui viene considerata la coordinata temporale. Per la fisica newtoniana il tempo è assoluto, uguale per tutti gli osservatori. Grazie a questo carattere assoluto del tempo il continuo quadridimensionale può essere scisso in un continuo tridimensionale e in uno unidimensionale: il passaggio dall'immagine statica (rappresentazione del moto in quattro dimensioni) all'immagine dinamica (rappresentazione del moto in tre dimensioni) possiede nella fisica classica un significato valido per tutti gli osservatori, cioè 'oggettivo'. Nella teoria della relatività invece la coordinata temporale è relativa al sistema di riferimento usato e muta nel passaggio da un sistema di riferimento all'altro. La scissione dello spazio quadridimensionale in uno a tre dimensioni e uno a una dimensione è un procedimento dipendente dall'osservatore, privo di significato oggettivo. L'immagine statica è quindi più conveniente e obiettiva di quella dinamica. Non è un caso che la geometria abbia acquisito un ruolo sempre più importante nella fisica dopo l'avvento della relatività di Einstein.

Nella quarta parte della sezione cinematica Einstein analizza il "significato fisico delle equazioni ottenute a proposito di corpi rigidi e orologi". La prima conseguenza è la contrazione delle lunghezze rispetto a diversi riferimenti inerziali. Consideriamo, scrive Einstein, una sfera rigida (cioè un corpo che esaminato in quiete abbia forma sferica) di raggio R in quiete in S′ e centrata nell'origine delle coordinate. L'equazione della sfera in S′ è x′²+y′²+z′²=R². Applicando le trasformazioni di Lorentz si ricava che in S l'equazione di questa superficie al tempo t=0 è

Quindi la sfera di S′ ha nel sistema S la forma di un ellissoide, i cui assi di rotazione sono

R e R: la dimensione lungo x (la direzione del moto) appare accorciata del fattore

una contrazione tanto maggiore quanto più il valore di v si avvicina a c (per v=c tutti i corpi del sistema in moto S′ appaiono in S come figure appiattite).

Questo risultato ci permette di chiarire anche l'esperimento ideale tramite il quale Einstein era giunto alla relatività della simultaneità. Consideriamo nel sistema S′ un'asta immobile con estremi A e B di coordinate x′_A (t′_A) e x′_B (t′_B). La lunghezza l dell'asta è data dalla differenza delle coordinate degli estremi presa allo stesso tempo t′=t′_A=t′_B:l=x′_B(t′)−x′_A(t′). Essendo l'asta immobile in S′ possiamo porre x′_A(t′)=0 e x′_B(t′)=l. Nel sistema S avremo dalle trasformazioni di Lorentz come coordinate per gli estremi dell'asta:

Per definire la lunghezza dell'asta in S dobbiamo misurare le posizioni dell'asta allo stesso istante t in S, ma abbiamo

per cui non possiamo più definire la lunghezza dell'asta come

ma dobbiamo sottrarre a questo valore lo spostamento dell'asta nel tempo t_B−t_A dato da

Il risultato finale è quindi

che è sempre minore di l. Si ritrova così la contrazione di Lorentz-Fitzgerald e si può constatare che la simultaneità in S′ (espressa da t′_A=t′_B) non corrisponde alla simultaneità in S (dove t_A è diverso da t_B). La seconda conseguenza delle trasformazioni di Lorentz riguarda il tempo segnato dagli orologi rispetto a diversi riferimenti inerziali. Immaginiamo, scrive Einstein, di collocare un orologio nell'origine del sistema di coordinate S′ (cioè con coordinate di posizione x′=y′=z′=0). Quale ritmo avrà questo orologio rispetto a S? Secondo le trasformazioni di Lorentz valgono evidentemente le relazioni:

Ne segue che

cioè t′ è minore di t: l'orologio in S scandisce il tempo più lentamente rispetto alla sua scansione in S′. I tempi si dilatano e al limite, se il valore di v è prossimo a c, l'orologio rallenta fino a fermarsi. A questo punto Einstein rileva "una conseguenza singolare" di questo risultato. Dati due orologi sincronizzati O₁ e O₂ inizialmente nella stessa posizione P, se uno di essi, per esempio O₂, si allontana percorrendo una curva chiusa, al ritorno in A sarà rimasto indietro rispetto a O₁. È la formulazione di quello che diverrà noto come 'paradosso dei gemelli'. Einstein nel 1916 chiarì che la relatività ristretta non è sufficiente a spiegare il fenomeno in quanto in esso entrano in gioco riferimenti non inerziali.

Dopo aver passato in rassegna le conseguenze fisiche delle trasformazioni di Lorentz, Einstein conclude la parte della cinematica ricavando dalle trasformazioni di Lorentz la legge di composizione delle velocità che sostituisce quella galileiana. La nuova relazione viene ottenuta con il seguente ragionamento. Sia x′=V′t′ la traiettoria di un corpo che si muove con velocità V′ nel sistema S′ lungo l'asse x′. Segue allora immediatamente dalle trasformazioni di Lorentz che

Allora la traiettoria in S del punto è data da x=Vt dove V è la velocità V=(V′+v)/(1+V′v/c²) (equivalente alla [5]).

Nella seconda parte dell'articolo dal titolo Elektrodynamischer Teil (Elettrodinamica), Einstein mostra che la nuova cinematica permette di rendere le equazioni di Maxwell compatibili con il principio di relatività semplicemente dimostrando che le equazioni di Maxwell sono invarianti per trasformazioni di Lorentz. Questo risultato permette a Einstein di trarre numerose e fondamentali conseguenze sulle quali non ci soffermiamo. Vale tuttavia la pena accennare al fatto che nelle pagine conclusive dove si tratta della dinamica dell'elettrone lentamente accelerato, Einstein ricava un'espressione dell'energia cinetica E_c (nella meccanica newtoniana E_c=mv²/2) che equivale alla nota formula E=Mc². Einstein scrive infatti che

Nulla però dice sul fatto che m sia la massa della particella nel sistema di riferimento in cui questa è in quiete (quella che in seguito sarà chiamata massa a riposo). Si limita a osservare che "m è la sua massa purché il suo moto sia lento": probabilmente vuole intendere 'lentamente accelerato' per poter sostenere l'approssimazione che la perdita di energia radiante sia trascurabile (e quindi che E_c è uguale all'energia sottratta al campo di forze che accelerano la particella), grazie alla quale ricava l'espressione di E_c. Nulla dice inoltre sul fatto che se si somma E_c con mc² si ottiene l'energia della particella e quindi che E=Mc² dove

La definitiva introduzione della più nota espressione legata al nome di Einstein richiederà anni di lavoro interpretativo.

Le derivazioni dell'equivalenza massa-energia

di Arthur I. Miller

Qualche tempo dopo aver sottoposto il suo articolo sulla relatività del 1905 agli "Annalen der Physik", Einstein si rese conto che l'equivalenza tra la massa e l'energia non era contenuta implicitamente nell'equazione dell'energia cinetica K₀ di un elettrone puntiforme che si trovi in un campo elettrostatico esterno agente nella direzione del moto dell'elettrone:

[10]  K₀=m₀ c² (γ-1),

dove γ=1/(1−v²/c²)^1/2, m₀ è la massa dell'elettrone nel suo sistema di quiete, v e c hanno il significato precedentemente indicato. Le derivazioni dell'equivalenza tra massa ed energia ottenute da Einstein nel 1905 e nel 1906 erano ancora insoddisfacenti per quanto concerne ciò che nel titolo dell'articolo del maggio 1907 avrebbe indicato come Über die vom Relativitätsprinzip geforderte Trägheit der Energie (Sulla inerzia dell'energia derivata dal principio di relatività). Si tratta di "un'assunzione di tale generalità", scrive Einstein a proposito dell'equivalenza massa-energia in quest'ultimo lavoro, da richiedere che la sua "necessità e correttezza [siano esaminate] nel modo più generale […]. Esistono casi che conducono a conseguenze incompatibili con questa ipotesi" (Einstein 1907b, p. 371). Un caso speciale che Einstein aveva in mente era la "dinamica della traslazione parallela" dei corpi rigidi, che egli trattava "dal punto di vista dell'attuale Relativitätselektrodynamik", cioè, senza alcuna ipotesi sulla costituzione della materia.

Egli considera un corpo rigido di forma qualunque che abbia una distribuzione di carica uniforme all'interno del suo volume e che si trovi in quiete nell'origine del sistema di riferimento inerziale k. Benché sia influenzato da una forza elettromagnetica esterna, il corpo resta in equilibrio nel suo sistema di quiete k. Rispetto al sistema del laboratorio K, la forza esterna fa aumentare l'energia del corpo di una quantità

[11]  ∆E=∫dt∫ϱv ∙ F dv,

dove F è il campo elettrico esterno, E è l'energia del corpo misurata in K, ϱ è la distribuzione di carica in K e dv è l'elemento di volume del corpo, misurato in K. Una trasformazione di Lorentz dà, nel sistema di quiete k del corpo,

[12]  ∆E=γv∫dτ(∑_ξK_ξ),

dove τ è la coordinata temporale in k e ∑_ξK_ξ è l'effetto totale sul corpo carico della componente ξ del campo elettrico lungo l'asse x di k. Sebbene la quantità ∑_ξK_ξ scompaia in k, dove il campo è in equilibrio, essa non deve annullarsi in K; infatti, a causa della relatività della simultaneità, i limiti di integrazione dipendono dalla coordinata ξ nel modo seguente:

[13]  τ₀=(t₀/γ)-(v_ξ/c²), τ₁=t₁-(v_ξ/c²).

Così, rispetto a K, l'energia del corpo è aumentata della quantità

[14]  ∆E=-(v/c)²γ(∑_ξK_ξ),

dove, per il calcolo dell'integrale in K, Einstein suppone che la forza sia o lentamente variabile oppure costante nell'intervallo di tempo considerato, e si annulli per t=t₀. La quantità ΔE è maggiore di 0, in quanto K_ξ e ξ sono dirette in senso opposto. La [14] è un "risultato singolare", scrive Einstein,

poiché se un corpo rigido, sul quale inizialmente non agisce alcuna forza, è sottoposto all'azione di forze che non producono alcuna accelerazione sul corpo stesso, queste forze, dal punto di vista del sistema di coordinate in moto rispetto al corpo, compiono sul corpo una quantità di lavoro ΔE dipedente dalla distribuzione della forza sul corpo e dalla velocità v. Secondo il principio di conservazione dell'energia, da ciò segue che l'energia cinetica di un corpo rigido sottoposto a una forza esterna è maggiore per una quantità ΔE rispetto all'energia cinetica del medesimo corpo, in moto con la stessa velocità, ma sul quale non agisce alcuna forza. (ibidem, p. 376)

Al fine di dimostrare un'altra proprietà inattesa della [14], Einstein si limita a considerare il caso in cui il corpo carico rimanga in moto inerziale solo per l'azione di forze elettromagnetiche proprie, cioè di forze prodotte dai suoi stessi campi elettrici magnetici. Ci si aspetterebbe che l'energia cinetica totale K_T del corpo sia

dove K₀ è dato dalla [10], E^e è l'energia del corpo dovuta ai suoi stessi campi elettrici e magnetici, ossia è l'energia elettromagnetica propria del corpo, ed E^e₀ è l'energia elettromagnetica propria del corpo quando è in quiete, cioè quando la sua massa è dovuta soltanto al suo stesso campo coulombiano. Nella [15], K_T dipende però dall'orientamento del corpo rigido e questo, sostiene Einstein, è impossibile. Tale 'contraddizione' può essere eliminata se si considera anche la quantità ΔE, poiché "l'energia cinetica del corpo in esame non può essere calcolata come se si trattasse di un corpo rigido sul quale non agisse alcuna forza" (ibidem, p. 378). Quindi, in luogo della [15], si deve scrivere:

da qui si ha:

La [17] è la versione della [10] per corpi carichi dotati di una certa estensione: "Un corpo carico elettrostaticamente possiede una massa inerziale che è superiore a quella del corpo non carico, di una quantità pari all'energia elettrostatica divisa per il quadrato della velocità della luce" (ibidem, p. 379). Einstein non si rendeva ancora conto del perché estendere questo risultato anche alla massa gravitazionale. Egli continuava a ricordare al lettore le molte ipotesi semplificatrici che gli avevano permesso di calcolare la [17] (ossia, la distribuzione di carica uniforme nel volume del corpo rigido).

Qual è però la natura della quantità ΔE, che dipende dalla relatività della simultaneità e, a un livello più profondo, dal principio di relatività? Su questo punto Einstein non poteva spingersi oltre poiché, egli scrive, siamo ancora ben lontani dal possedere una "dinamica della traslazione parallela dei corpi rigidi, [in assenza di] un'immagine del mondo [Weltbild] coerente con il principio di relatività", ossia di strumenti per analizzare gli effetti prodotti dalla costituzione della materia. Egli continuò a collegare la quantità ΔE a una "Qualität sconosciuta" (ibidem, p. 381) che si propaga con una "velocità finita" nei corpi osservati da un altro sistema di riferimento inerziale. Questa Qualität è necessaria perché, secondo il principio di relatività, se un corpo è in equilibrio in un sistema di riferimento inerziale, come nel caso precedente, allora esso deve trovarsi in equilibrio in ogni sistema inerziale: l'equilibrio non può essere modificato da una trasformazione di Lorentz.

L'articolo per lo "Jahrbuch" del 1907

di Arthur I. Miller

Nel settembre del 1907 Einstein ricevette l'invito del direttore dello "Jahrbuch der Radioaktivität und Elektronik", Johannes Stark, a scrivere un articolo di rassegna sulla sua teoria della relatività. L'articolo dal titolo Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen (Il principio della relatività e le conseguenze che ne derivano) fu inviato a Stark il 4 dicembre 1907.

A differenza delle precedenti formulazioni della teoria, in questo articolo Einstein sottolinea più volte che i sistemi di riferimento dove gli orologi sono sincronizzati e ha validità il principio di relatività sono i sistemi non accelerati. Forse Einstein intendeva preparare il lettore al paragrafo finale, dove invece avrebbe esteso il principio di relatività ai sistemi di riferimento accelerati. La rassegna einsteiniana della teoria della relatività si concludeva con un'analisi critica dei dati di Kaufmann del 1906, che erano in disaccordo con la teoria degli elettroni di Lorentz-Einstein. A questo punto, Einstein osservava acutamente che la deviazione sistematica tra le previsioni di Lorentz-Einstein e i dati di Kaufmann poteva essere imputata tanto a una fonte di errore non ancora riconosciuta come tale, quanto al fatto che i fondamenti della teoria della relatività non corrispondessero alla realtà. Einstein rinviava quindi a ulteriori esperimenti ogni decisione in merito a questo contrasto e liquidava i dati di Kaufmann, in quanto "secondo la sua opinione" essi confermavano teorie che "non comprendevano un insieme significativo di fenomeni" (Einstein 1907c, p. 439), vale a dire le teorie degli elettroni che non riuscivano a spiegare il fallimento degli esperimenti sul trascinamento dell'etere accurati al secondo ordine del rapporto v/c. Nel 1908 altri esperimenti sugli elettroni veloci avrebbero mostrato gli errori contenuti nei dati di Kaufmann e reso giustizia all'opinione di Einstein.

Nuovi risultati a favore della teoria della relatività sono contenuti nel paragrafo sulla dipendenza della massa dall'energia, dove Einstein migliora ulteriormente la precedente derivazione (1907) dell'equivalenza tra massa ed energia. Egli sostituisce l'artificio del corpo rigido elettricamente carico con un sistema di cariche circondato da un contenitore privo di massa e impenetrabile alla radiazione. Questo apparato gli consente di riprendere alcuni risultati ottenuti pochi anni prima da Max Planck (1858-1947) sulla pressione, temperatura ed entropia dei sistemi in moto. Planck aveva trovato che, anche in assenza di forze agenti su un sistema di corpi in quiete, un mutamento nello stato interno del corpo produce una forza misurabile in K; non esistono quindi corpi rigidi. I risultati di Planck potrebbero aver fornito a Einstein qualche suggerimento circa la natura della "Qualität sconosciuta", ma di ciò non vi è traccia nell'articolo, poiché nel frattempo egli aveva compreso come evitare l'ostacolo per andare direttamente al cuore dell'equivalenza massa-energia.

Per ragioni di generalità, Einstein assume che il corpo carico sia in moto rispetto al sistema di riferimento k. Egli evita il problema della "Qualität sconosciuta", assumendo che le forze esterne non agiscano al di fuori dell'intervallo di tempo definito in K e si annullino per i valori limite della variabile tempo t₀ e t₁; in tal modo, il contributo della forza ∑_ξK_ξ si annulla anche in K. Dalla [11] Einstein ricava:

[18]  dE=γdE',

la quale indica che l'energia di un sistema in moto uniforme può essere solo una funzione di due variabili, la velocità relativa v e il contenuto di energia E₀ rispetto al sistema di quiete k. Dalla [18] si ha poi:

[19]  E=[m₀+(E₀/c2)]γc²;

questa relazione ci dice che il sistema si comporta sotto tutti i punti di vista come se fosse un "punto materiale" avente una massa:

[20]  M=m₀+(E₀/c²).

"Questo risultato è di straordinaria importanza teorica ‒ commenta Einstein ‒ poiché una massa inerziale del sistema fisico e il contenuto di energia sembrano comportarsi come se fossero la stessa cosa", ossia la massa è energia confinata: era questo il significato generale dell'equivalenza massa-energia che egli aveva ricercato fin dal 1905.

Il significato principale della [20] riguardava il modo in cui viene misurata, anche in linea di principio, la variazione della massa; era proprio questo lo strumento che consentiva di generalizzare la [20] dalla "massa inerziale del sistema fisico" alla sua massa gravitazionale:

In precedenza abbiamo supposto implicitamente che una tale misura della variazione della massa possa essere eseguita con uno strumento di uso comune come la bilancia; quindi la relazione [20] vale non solo per la massa inerziale, ma anche per la massa gravitazionale o, in altre parole, inerzia e gravità [Schwere] sono sotto tutti gli aspetti esattamente proporzionali. […] La proporzionalità tra la massa inerziale e la massa gravitazionale è universalmente valida per tutti i corpi con tutta la precisione che attualmente è possibile raggiungere; così, a meno che non si dimostri il contrario, la dobbiamo accettare come se fosse universalmente valida. (ibidem)

In questo splendido passaggio, Einstein promuove l'equivalenza tra la massa inerziale e la massa gravitazionale da assunto valido "con la precisione che attualmente è possibile raggiungere" a principio "universalmente valido". Nell'articolo sulla relatività del 1905, egli aveva applicato un procedimento del genere a un altro concetto chiave; in quell'occasione, aveva elevato allo stato di principio, prescindendo da ogni verifica sperimentale, la "congettura" secondo la quale al primo ordine di (v/c) non c'è alcun moto assoluto né in meccanica, né in elettromagnetismo.

Come si è visto precedentemente, un aspetto essenziale che permise a Einstein di formulare la relatività nel 1905 era stato il carattere relativo dei campi elettrici e magnetici, per il quale aveva assunto un certo rilievo l'analisi del fenomeno dell'induzione elettromagnetica. In un manoscritto inedito del 1909 Einstein ricostruisce questo processo:

[La] differenza [tra gli osservatori solidali con il magnete e con il conduttore] non può essere una differenza reale ma piuttosto, a mio avviso, solo una differenza di scelta del punto di riferimento. […] L'esistenza di un campo elettrico deve quindi essere relativa e dipendere dallo stato di moto del sistema di coordinate usato. […] Quando nel 1907 mi trovai a scrivere un saggio di rassegna sulla teoria speciale della relatività per lo "Jahrbuch der Radioaktivität und Elektronik", cercai di modificare la teoria newtoniana della gravitazione in modo tale da ricomprenderla all'interno della teoria [della relatività]. I tentativi compiuti in questa direzione dimostrarono la possibilità di realizzare positivamente tale impresa ma non mi soddisfecero, poiché avevano bisogno di ipotesi prive di basi fisiche.

Mentre Einstein si trovava a riflettere sul fallimento di questa via apparentemente più orientata verso la teoria della gravitazione, nella sua mente si fusero la relatività dei campi elettrico e magnetico (1905) e l'evidenza che le energie di questi campi sono dotate di inerzia (1907):

A questo punto ebbi l'idea più felice della mia vita. Così come avviene per il campo elettrico prodotto dall'induzione elettromagnetica, analogamente anche il campo gravitazionale possiede un'esistenza relativa. Infatti, se consideriamo un osservatore in caduta libera, per esempio dal tetto di una casa, durante la caduta non esiste per lui alcun campo gravitazionale ‒ almeno non nelle sue immediate vicinanze. Quindi, se l'osservatore lascia andare alcuni corpi, questi restano rispetto a lui in uno stato di quiete o di moto uniforme, indipendentemente dalla loro particolare natura chimica o fisica (ovviamente, nell'esempio si trascura la resistenza dell'aria). L'osservatore ha quindi il diritto di considerarsi in uno stato di quiete. […] L'indipendenza della materia dall'accelerazione di caduta, che viene così provata sperimentalmente, costituisce un forte argomento a favore del fatto che il postulato della relatività deve essere esteso ai sistemi di coordinate che sono in moto non uniforme tra loro.

Al pari degli osservatori che nel 1905 cavalcavano il magnete e il conduttore, l'osservatore in caduta libera del 1907 "ha il diritto di considerarsi in uno stato di quiete".

Possiamo tentare di ricostruire quale fosse il procedimento da cui Einstein trasse il necessario supporto matematico per "l'idea più felice" della sua vita. Tuttavia non vi è dubbio che qualunque sia l'itinerario ipotizzato, colpisce, anche in questo contesto storico, quanto la fisica dell'esperimento mentale del 1907 sia incredibilmente semplice. Tutto dipende dall'ipotesi sostenuta dai fisici, e in particolare dagli astronomi, secondo la quale la massa inerziale e la massa gravitazionale sono esattamente uguali. Einstein riprende questa ipotesi e la estende fino a includervi l'accelerazione e la gravità.

Supponiamo che l'osservatore che cade liberamente dal tetto trasporti un sistema di riferimento K′, mentre un osservatore in quiete al suolo abbia un sistema di riferimento K. Gli assi y di K e K′ siano allineati; inoltre, le velocità che intervengono siano tutte sufficientemente piccole da consentire l'applicazione della meccanica di Newton. Allora, rispetto a K, l'equazione del moto per l'osservatore in caduta libera è:

[21] m_I(d²y/dt²)=-m_Gg+F,

dove m_I(m_G) è la massa inerziale (gravitazionale) del corpo in caduta, g è la sua accelerazione dovuta al campo gravitazionale esterno e F rappresenta le altre forze che agiscono sul corpo in caduta. Poniamo:

dove a è l'accelerazione costante del corpo rispetto a K e t′ è uguale a t. Allora si ha:

Qualunque fosse stata l'analisi matematica compiuta da Einstein nell'esperimento mentale, egli sarebbe arrivato a un'equazione analoga alla [23]. Assumiamo ora che sia m_I=m_G=m e facciamo un'ipotesi finale, per la quale è centrale l'immagine visiva dal forte contenuto teorico dell'osservatore in caduta libera. Poiché, come si è detto, nelle sue immediate vicinanze non c'è "campo gravitazionale, [egli] ha il diritto di considerarsi in uno stato di quiete" e quindi per lui deve essere a=−g. La [23] diviene allora:

[24] m(d²y'/dt'²)=F'.

L'osservatore in caduta libera che utilizza y′ e l'osservatore in quiete che utilizza y considereranno entrambi valide le leggi della meccanica newtoniana, anche se il primo non sperimenta alcun campo gravitazionale. Di conseguenza, così come il campo elettrico nell'induzione elettromagnetica ha un'esistenza relativa, anche il campo gravitazionale deve essere una quantità relativa.

Visto che all'epoca Einstein non conosceva gli esperimenti di Loránd Eötvös (1848-1919), è legittimo chiedersi quali indizi egli avesse per poter dichiarare in modo esplicito l'uguaglianza della massa inerziale e della massa gravitazionale. Un indizio era sicuramente contenuto in un libro che Einstein aveva letto prima del 1905, il già citato La science et l'hypothèse di Poincaré, in cui uno degli argomenti trattati riguardava la ricerca di ipotesi implicite nella scienza. Poincaré, per esempio, esamina con attenzione il modo in cui viene utilizzata la legge gravitazionale di Newton per misurare la massa di un pianeta che trasporti con sé un satellite: "Ciò che misuriamo con questo metodo non è la massa come rapporto tra la forza e l'accelerazione, ma la massa attraente; non l'inerzia di un corpo, ma il suo potere di attrazione". Secondo Poincaré, ciò che è implicito è il fatto che quando noi "pesiamo" questo pianeta cancelliamo la massa del satellite nei due membri dell'equazione F=m_Ia, dove la F è data dalla legge gravitazionale di Newton. L'assunzione tacita consiste nel considerare la massa inerziale e la massa gravitazionale del satellite esattamente uguali. Einstein aveva esteso questa tacita assunzione all'equivalenza tra un campo gravitazionale uniforme e un'accelerazione costante diretta in modo opportuno.

Proprio come nella relatività speciale, devono esistere trasformazioni delle coordinate e del tempo che ci consentano di passare da un sistema in moto (accelerato) a uno in quiete (quello con un campo gravitazionale uniforme diretto in senso opposto all'accelerazione dell'altro sistema). Un problema dinamico può essere così trasformato in uno statico, con un procedimento analogo a quello impiegato in elettrodinamica dopo il 1892. In particolare, sia nel 1905, sia nel 1907, Einstein riprendeva l'idea lorentziana dei tre sistemi di riferimento.

Nel paragrafo conclusivo dell'articolo pubblicato sullo "Jahrbuch" Einstein pone il seguente problema: "È concepibile che il principio di relatività sia valido anche per sistemi che sono accelerati rispetto a un altro sistema?". La risposta prende le mosse da una nuova versione dell'esperimento mentale. Un sistema di riferimento ∑₁ si muova nella direzione del suo asse x con un'accelerazione costante a rispetto a un sistema di riferimento ∑₂ in quiete; in ∑₂ agisca un campo gravitazionale costante, per cui tutti i corpi cadono con un'accelerazione −a.

Assumendo l'equivalenza tra la massa inerziale e la massa gravitazionale, le leggi newtoniane predicono gli stessi moti in ∑₁ e ∑₂; quindi, conclude Einstein, "in base alla nostra esperienza non riusciamo a individuare una qualche causa che ci consenta di distinguere tra ∑₁ e ∑₂; per questo, in ciò che segue ammetteremo la totale equivalenza fisica del campo gravitazionale e della corrispondente accelerazione del sistema di coordinate" (nel 1912, egli avrebbe chiamato questa asserzione 'principio di equivalenza'). L'accelerazione perde il suo carattere assoluto e diviene, insieme al campo gravitazionale, una quantità relativa, almeno nel caso in cui l'accelerazione sia costante. Einstein utilizza poi la teoria della relatività del 1905 come guida per ricercare una nuova definizione di simultaneità in un sistema di riferimento uniformemente accelerato ∑.

Nel periodo 1895-1904, Lorentz utilizzò alcune varianti dei tre sistemi di coordinate seguenti: (a) un sistema dell'etere S(x,y,z,t); (b) un sistema di riferimento S(x_r,y_r,z_r,t_L) dove x_r=x−vt, y_r=y, z_r=z, t_L=t−vx/c² è la coordinata matematica tempo locale e t_r=t; (c) infine, un sistema di riferimento matematico o fittizio S′(x′,y′,z′,t_r(=t)), nel quale, al primo ordine di (v/c), le equazioni dell'elettromagnetismo hanno la stessa forma che in S, dove x′=x_r, y′=y_r, z′=z_r. Nella teoria degli elettroni di Lorentz del 1904 la coordinata temporale diviene una versione della coordinata tempo locale, che risulta esatta per tutti gli ordini di (v/c); così, in S′ le equazioni dell'elettromagnetismo assumono la stessa forma che in S, per tutti gli ordini di (v/c).

Allo stesso modo, nell'articolo del 1905 Einstein utilizzò tre sistemi di coordinate per ricavare le equazioni di trasformazione relativistiche per le coordinate spaziali e temporali: K(x,y,z,t) e k(ξ,η,ζ,τ) sono sistemi di riferimento inerziali le cui coordinate spazio e tempo si accordano con il principio di relatività e con l'assioma della luce; a questi si deve aggiungere un sistema di coordinate intermedio S′, i cui assi sono allineati con quelli di k e le cui coordinate spaziali sono galileiane (x′=x, y′=y, z′=z), ma quella temporale è relativistica: t′=τ. Nel 1907 Einstein seguì un percorso analogo, con la sola differenza che S′ è un sistema di riferimento nel quale sono validi i principî della teoria speciale della relatività. Il sistema di riferimento k diventa il sistema ∑, uniformemente accelerato rispetto al sistema non accelerato S. Einstein cercò allora di dare una definizione di simultaneità nel sistema ∑. Supponiamo dunque che, al tempo t=τ=0, i due sistemi di riferimento ∑ e S siano in quiete relativa e i loro assi coincidano e che, subito dopo, ∑ inizi a muoversi di moto accelerato, con un'accelerazione costante a e di conseguenza con velocità v=at. A un dato istante di tempo il sistema inerziale S′ coinciderà con ∑.

Einstein suppone poi che l'accelerazione a sia così piccola che in ∑ non siano alterate la forma dei corpi e la rapidità degli orologi. All'istante t′, quando S′ e ∑ coincidono, gli orologi in ∑ possono allora essere sincronizzati al tempo t′. Einstein si chiede cosa sia possibile dire in merito alla rapidità degli orologi nel successivo elemento temporale τ. Poiché sono stati trascurati gli effetti dell'accelerazione, nel successivo istante di tempo t si applica l'assioma della luce, purché si considerino soltanto piccole traiettorie di luce. Chiamiamo 'tempo locale' σ il tempo degli orologi di ∑ che sono stati regolati a t=0, quando S e ∑ coincidevano ed erano in quiete relativa. Ma σ non è il 'tempo' di ∑, perché, sebbene gli orologi in ∑ restino sincroni con quelli in S, secondo la teoria speciale della relatività essi non sono sincroni con un qualunque altro orologio. Einstein definisce piuttosto il 'tempo' τ in ∑ come la lettura di un singolo orologio che si trovi nell'origine di ∑ e per il quale τ=t.

Per stabilire quale sia la relazione tra il 'tempo' σ e il 'tempo' τ di un evento, si deve utilizzare il sistema locale S′ di Lorentz. Due eventi sono simultanei in S′, e lo sono anche in ∑, quando è:

[25]  t₁-(vx₁/c²)=t₂-(vx₂/c²).

Se si considerano intervalli di tempo abbastanza piccoli in modo tale che

[26]  x₂-x₁=x'₂-x'₁=ξ₂-ξ₁,

dalla [25] si ottiene:

Ponendo σ₁=τ₁ e ξ₁=0, Einstein giunge alla relazione:

Per il principio di equivalenza la precedente equazione [29] diventa:

[30]  σ= τ[1+(Φ/c²)],

dove Φ è il potenziale gravitazionale tra l'origine e ξ. La [30] ci permette di prevedere un nuovo fenomeno, nel caso in cui come orologi si usino atomi eccitati, cioè 'generatori' di linee spettrali.

La luce proveniente dalla superficie del Sole "possiede una lunghezza d'onda che è maggiore della luce generata dallo stesso materiale che si trovi sulla superficie della Terra", ossia si deve avere quello che oggi si chiama red shift gravitazionale. In una nota al testo, Einstein si dice convinto che questo risultato debba valere anche per un campo gravitazionale non uniforme; la verifica definitiva del red shift gravitazionale sarebbe venuta soltanto con gli esperimenti effettuati da Robert V. Pound e Glen A. Rebka jr nel 1960.