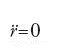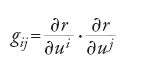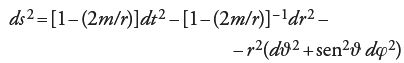La seconda rivoluzione scientifica: fisica e chimica. Relatività e gravitazione

La seconda rivoluzione scientifica: fisica e chimica. Relativita e gravitazione

Relatività e gravitazione

Problemi relativi alla gravitazione newtoniana

Il successo della teoria elettromagnetica di Maxwell, che utilizzava il concetto di etere (sebbene quasi del tutto implicitamente), suggerì l'idea che esistesse un etere specifico anche per la gravitazione newtoniana. Maxwell tentò questa strada nel 1865, proponendo un modello di campo gravitazionale mutuato dal campo elettrostatico; ma risultarono immediatamente evidenti difficoltà. Dato che cariche uguali si respingono, doveva esserci un cambiamento di segno quando si passava a esaminare la gravitazione. Ciò comportava un cambiamento di segno dell'energia e, poiché l'energia doveva essere positiva, Maxwell sostenne l'esistenza di una costante additiva molto grande che avrebbe dovuto corrispondere a una "energia intrinseca" dello spazio. Un altro tentativo lungo le stesse linee di ricerca fu effettuato nel 1911 da Max Abraham (1875-1922), ma andò incontro a difficoltà simili: se una particella oscillante avesse emesso onde gravitazionali trasversali queste avrebbero diminuito la densità di energia dello spazio quando avessero raggiunto zone distanti, e ciò avrebbe determinato di conseguenza un aumento di energia nella particella stessa, rendendola instabile.

Altri tentativi di giungere alla definizione di un etere gravitazionale, attraverso 'atomi vortice' o altri espedienti di questo tipo non ebbero miglior fortuna, sicché alla fine del secolo scorso il ripetuto insuccesso nel riformulare le idee newtoniane in termini di azione di contatto diede corpo all'idea che, intorno alla questione della gravitazione universale che agisce a distanza, esistesse un mistero ancora più grande di quello percepito nel XVIII secolo.

In questa fase, la ricerca fu resa marginale da due nuove difficoltà di tipo più pratico, la prima delle quali rappresentata dal problema della spiegazione delle irregolarità delle orbite dei pianeti del Sistema solare. Nel 1845, Urbain-Jean-Joseph Le Verrier (1811-1877) trovò che l'irregolarità di Mercurio era più grande, di 35″ d'arco a secolo, rispetto a quella prevista per gli altri pianeti. Sulla base di questa scoperta egli predisse l'esistenza di un altro pianeta, più vicino al Sole rispetto a Mercurio, cui diede il nome di Vulcano. Sfortunatamente la strategia che aveva funzionato così bene per i pianeti esterni non ebbe successo una seconda volta, e mezzo secolo di ricerche non fu sufficiente a dimostrare l'esistenza di Vulcano. Nel 1911, grazie a osservazioni e a calcoli più accurati, si era arrivati ad affermare che la discrepanza residua era di 43″ a secolo e Simon Newcomb arrivò alla conclusione che su Mercurio agisse qualche massa di materia sconosciuta, o che l'intensità della gravitazione non seguisse esattamente la legge di Newton. Tale modifica era stata proposta nel 1870 da Gustav Holzmüller per analogia con le modifiche dell'elettrostatica suggerite nel 1846 da Wilhelm Weber (1804-1891) e relative alle cariche in movimento. François Tisserand (1845-1896) applicò questa ipotesi alle orbite planetarie, ma arrivò a spiegare non più di un terzo dell'avanzamento osservato nel perielio di Mercurio (senza riscontrare modifiche significative per ciò che riguardava gli altri pianeti). Successivamente, furono proposte altre modificazioni ma esse si rivelarono tutte insoddisfacenti e la questione rimase completamente irrisolta fino al 1915.

La seconda difficoltà è più complessa e nasce nel contesto della teoria della relatività ristretta formulata da Einstein nel 1905. Come noto, secondo la nuova teoria la trasformazione tra due sistemi di riferimento possiede la forma [1], (si parla, ovviamente, di sistemi inerziali, per i quali valgono non soltanto la prima legge di Newton, o legge di inerzia, ma anche le equazioni di Maxwell, e ciò comporta, tra l'altro, che la luce si propaghi in linea retta):

[1]  x→x'=γ(x-vt),  t→t'=γ(t-vx/c²).

L'asse x è stato scelto nella direzione di spostamento di una delle due origini rispetto all'altra, mentre v è la velocità di separazione e γ=(1−v²/c²)^−1/2. Quando v è molto piccola rispetto a c, le [1] diventano, approssimativamente,

[2]  x→x'=(x-vt),  t→t'=t,

come nella meccanica newtoniana. Queste nuove trasformazioni sono definite 'trasformazioni di Lorentz' poiché furono ricavate nel 1904 da Hendrik Antoon Lorentz (1853-1928), sebbene in un contesto alquanto differente e con un significato diverso per la variabile temporale. Si dimostra facilmente che le trasformazioni di Lorentz lasciano invariante la forma differenziale

[3]  ds²=c²dt²-dx²-dy²-dz²,

che risulta invariante anche sotto l'azione del gruppo delle rotazioni. L'insieme di trasformazioni che lasciano invariante tale forma differenziale, noto come il 'gruppo di Lorentz', consiste di combinazioni di rotazioni e trasformazioni di Lorentz. Le equazioni di Maxwell sono invarianti rispetto al gruppo di Lorentz, mentre le leggi del moto newtoniane non lo sono: è necessaria una piccola ma significativa modifica (che implica l'aumento della massa con l'aumento della velocità, come è stato rilevato sperimentalmente da Walter Kaufmann nel 1901) per ripristinare l'invarianza. Nei termini di queste nuove trasformazioni, è ora possibile enunciare la seconda difficoltà pratica: la gravitazione universale di Newton non risulta invariante rispetto alle trasformazioni di Lorentz.

Queste due problematiche emersero in un clima in cui le discussioni astronomiche e cosmologiche avevano posto ulteriori questioni di tipo concettuale circa la legge di gravitazione newtoniana.

In particolare, come era stato osservato da Hugo Seeliger nel 1895, se l'Universo era infinito la formula newtoniana del potenziale gravitazionale avrebbe prodotto un risultato infinito, e lo stesso sarebbe accaduto per il valore della forza gravitazionale in ogni punto dello spazio. Carl Neumann aveva ipotizzato una correzione della formula del potenziale newtoniano (da 1/r a e^−αr/r), ma questa modifica avrebbe avuto l'effetto di introdurre una 'repulsione cosmologica' che bilanciava l'attrazione gravitazionale a grandi distanze.

Bisogna comunque osservare, dal punto di vista storico, che fu l'esigenza di rendere invariante rispetto alle trasformazioni di Lorentz la teoria newtoniana a fornire lo stimolo maggiore per lo sviluppo di una nuova teoria della gravitazione.

Il cammino verso la relatività generale

In realtà non esistevano grandi difficoltà nel formulare teorie della gravitazione invarianti rispetto alle trasformazioni di Lorentz. Una di queste fu fornita da Poincaré nel 1905 in quello stesso articolo in cui, contemporaneamente a Einstein, aveva formulato una variante della relatività speciale. Si trattava di una teoria dell'azione a distanza nella quale si sosteneva che l'effetto di una massa su un'altra non dipendeva dalla sua posizione istantanea (cosa che sarebbe impedita dall'invarianza di Lorentz, poiché una delle prescrizione della relatività speciale è che nessuna informazione può essere trasmessa più velocemente della luce) ma dalla posizione della prima massa in un dato istante precedente, cosicché l'effetto poteva essere trasmesso dall'una all'altra alla velocità della luce. Altre teorie degne di nota furono quelle di Gustav Nordström del 1912 e del 1913, nelle quali la forza era derivata da un potenziale scalare (proprio l'assenza di tale potenziale nella teoria di Poincaré avrebbe costituito, per Einstein, un'indicazione che essa era erronea). Queste teorie a una prima analisi sembravano abbastanza soddisfacenti, ma all'atto pratico si trovavano spesso in disaccordo con i risultati sperimentali e, inoltre, finivano con il sollevare altri problemi di natura teorica.

La soluzione finale al problema fu fornita da Einstein e richiese dieci anni di lavoro. Dapprima divenne chiaro che la questione era stata formulata male, perché nella meccanica newtoniana un campo gravitazionale uniforme può essere creato o rimosso, mediante una trasformazione di coordinate tra sistemi in moto accelerato l'uno rispetto all'altro. Per esempio, l'equazione del moto

diventa

in un sistema definito dalla trasformazione r→r′=r−(1/2)gt².

Nella meccanica newtoniana questo è un risultato familiare nell'analisi di sistemi di riferimento rotanti, dove le equazioni sono espresse in funzione delle forze di Coriolis e di quelle centrifughe. Di conseguenza, persino nella meccanica newtoniana, in un sistema accelerato la luce segue traiettorie curve, poiché se r=ct allora si ha:

[5]  r'=ct-gt²/2

che rappresenta una parabola. Se si assume che questo campo gravitazionale 'riducibile' possieda le stesse proprietà fisiche di quello 'irriducibile' intorno a un corpo pesante, ne segue che un raggio di luce che passa a una distanza R dal centro di una sfera gravitante di massa M subisce una deviazione di 2GM/(Rc²), un risultato già trovato da Johann Georg von Soldner nel 1801. Tale effetto poté essere individuato sperimentalmente esaminando la posizione apparente delle stelle la cui luce raggiungeva la Terra dopo aver sfiorato il disco solare. Questa osservazione è possibile soltanto durante un'eclissi totale di Sole. La ragione per cui il campo gravitazionale è l'unico cui si applicano tali considerazioni consiste semplicemente nel fatto che esso è un campo accelerato, ossia ‒ più esplicitamente ‒ che l'accelerazione su un corpo in un punto è indipendente dalla massa del corpo stesso. Questo elemento era già noto a Galilei e presente anche nei testi newtoniani, nei quali il capitolo sulle orbite planetarie non contiene, in sostanza, alcuna menzione delle masse inerziali. Tale proprietà fu verificata sperimentalmente con l'accuratezza di 1/1000 da Newton e con un'accuratezza di gran lunga maggiore da Loránd Eötvös nel 1889. Risultati più recenti l'hanno verificata in alcuni casi con un'accuratezza di una parte su 10¹¹ o 10¹². L'importanza di questo 'principio di equivalenza' cominciò a divenire chiara a Einstein nel 1907, quando in Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen (Il principio della relatività e le conseguenze che ne derivano), pubblicato in "Jahrbuch der Radioaktivität und Elektronik", dopo averla sollevata prese posizione sulla seguente questione: "è concepibile che il principio di relatività valga anche per sistemi che sono accelerati l'uno rispetto all'altro?". Egli considerò due sistemi, uno dei quali ha una accelerazione uniforme in una direzione fissa e l'altro si trova in uno stato di quiete in un campo gravitazionale uniforme diretto lungo la direzione opposta. Di qui arrivò alla conclusione che

per quanto ne sappiamo le leggi fisiche relative al primo sistema non differiscono da quelle relative al secondo; ciò è dovuto al fatto che in un campo gravitazionale tutti i corpi sono sottoposti alla stessa accelerazione. Quindi, allo stato attuale delle nostre esperienze, non abbiamo alcun motivo per ritenere che i due sistemi differiscano per qualche aspetto e assumiamo perciò la completa equivalenza fisica tra un campo gravitazionale e una corrispondente accelerazione del sistema di riferimento. Questa ipotesi estende il principio di relatività al caso di un sistema di riferimento in moto traslazionale uniformemente accelerato. (Einstein 1907c, p. 461)

In questo modo a Einstein era apparso chiaro che il problema della gravitazione era stato posto in maniera erronea. Non si trattava di un problema riconducibile all'invarianza di Lorentz, che riguardava soltanto trasformazioni tra sistemi in moto relativo uniforme; nondimeno, vi era qualcosa di corretto anche in questo modo di porre la questione, poiché il fatto che la gravitazione newtoniana non è invariante rispetto alle trasformazioni di Lorentz era il sintomo di un problema più profondo. L'effetto istantaneo che si sarebbe dovuto avere, secondo la legge del quadrato dell'inverso della distanza, entrava in conflitto con la caratteristica principale della luce, ossia con il fatto che nulla può viaggiare con una velocità superiore a essa.

Un altro esempio di sistema accelerato attirò l'attenzione di Einstein nel 1909, a partire da una discussione sui tentativi di Max Born (1882-1970) di formulare la nozione di un corpo rigido all'interno della teoria della relatività speciale. Così Einstein scriveva il 29 settembre 1909 ad Arnold Sommerfeld: "Mi sembra che la trattazione di un corpo rigido che ruota uniformemente sia di grande importanza, in quanto rappresenta un'estensione del principio di relatività a sistemi che ruotano uniformemente, che procede lungo linee di pensiero analoghe a quelle che tentai di sviluppare in merito alla traslazione uniformemente accelerata". Questo argomento rimase però sterile, mentre nel 1911 Einstein affrontò direttamente il problema dell'effetto della gravitazione sulla propagazione della luce. Egli ritornò, come punto di partenza, alle idee della meccanica newtoniana, facendo riferimento all'equivalenza tra l'accelerazione uniforme e il campo gravitazionale uniforme, e in Über den Einfluss der Schwerkraft auf die Ausbreitung des Lichtes (Sull'influsso della forza di gravità sulla propagazione della luce), pubblicato in "Annalen der Physik", asserì: "L'esperienza che tutti i corpi, in un campo gravitazionale omogeneo, subiscono la stessa accelerazione costante […] è una delle leggi più universali che l'osservazione della Natura abbia fornito; ma, nonostante ciò, tale legge non ha ancora trovato posto tra i fondamenti della rappresentazione fisica del mondo". Il punto più importante è quello che nella riflessione einsteniana appare un poco oltre: "Finché ci limitiamo a processi puramente meccanici in cui è valida la meccanica newtoniana, possiamo essere certi dell'equivalenza dei sistemi K (a riposo in un campo gravitazionale omogeneo) e K′ (uniformemente accelerato in uno spazio libero da campi gravitazionali). Questo punto di vista avrebbe un significato più profondo soltanto se i sistemi K e K′ fossero equivalenti rispetto a tutti i processi fisici, cioè, se le leggi della Natura relative a K fossero in completo accordo con quelle relative a K′. Assumendo che sia così, arriviamo a un principio che, se è effettivamente corretto, riveste un'enorme importanza euristica" (Einstein 1911, pp. 898-908).

Einstein utilizza questa equivalenza in un esperimento mentale sull'emissione di una certa quantità di energia radiante in un campo gravitazionale. Con una trasformazione nel sistema accelerato egli è in grado di dimostrare che l'energia della radiazione varia secondo la sua energia potenziale nel campo gravitazionale e che lo scorrere del tempo degli orologi, e quindi le frequenze della radiazione, sono influenzati allo stesso modo. Da quello che egli considerava come un suo precedente risultato, e cioè che la velocità della luce è la stessa in tutti i punti se misurata da un orologio non influenzato dal potenziale gravitazionale, conclude che in questo caso la velocità c è influenzata dal potenziale e quindi: "Il principio della costanza della velocità della luce è valido, nella presente teoria, in una formulazione diversa da quella normalmente posta a fondamento della ordinaria teoria della relatività". L'anno successivo egli spinse oltre questo punto di vista, prima di abbandonarlo completamente. Poiché la velocità della luce doveva cambiare con il potenziale gravitazionale, i due concetti non erano entrambi necessari per la teoria, e così nel 1912 egli utilizzò il valore della velocità della luce per definire il potenziale gravitazionale in un dato punto. In una nota aggiunta durante la correzione delle bozze egli sottolineò che, se l'hamiltoniana H è data da

[6]  H=-m(c²-v²)^1/2

e se c è ora una funzione della posizione, allora dalla condizione che ∫Hdt abbia un valore stazionario è possibile ricavare la corretta equazione del moto. Sebbene il campo gravitazionale riducibile potesse essere eliminato da una trasformazione accelerata, tuttavia non era necessario farlo, perché il principio hamiltoniano fornisce il cammino delle particelle direttamente nel sistema coordinato in cui il campo è presente. Nonostante ciò, Einstein era dell'opinione che nella sua analisi dei campi statici egli stesse trattando un caso speciale che corrispondeva all'elettrostatica nella teoria elettromagnetica e che il passo successivo era quello di considerare campi analoghi a quelli magnetostatici, prodotti per esempio da un anello che ruota. Così utilizzò il modello del disco rotante ed esso fu probabilmente il catalizzatore di un rilevante salto di qualità nelle sue idee.

Sebbene fosse impossibile descrivere compiutamente il disco rotante per mezzo della teoria della relatività speciale, è importante osservare come questa preveda che il risultato delle variazioni prodotte nel computo del tempo dalle trasformazioni di Lorentz sia un apparente accorciamento di un'asta nella sua direzione di movimento, rispetto alla lunghezza a riposo; 'apparente' perché prodotta semplicemente dalle diverse sincronizzazioni tra le misurazioni della posizione degli estremi nei due sistemi di riferimento, in uno dei quali l'asta è in quiete mentre nell'altro si muove. Anche senza un trattamento adeguato, si può inferire che aste rigide tangenti alla circonferenza del disco rotante mostrano un diverso accorciamento apparente rispetto ad aste simili disposte lungo il raggio, e che pertanto la relazione tra raggio e circonferenza è diversa da quella della geometria euclidea. La geometria apparente sulla superficie del disco deve dunque essere non euclidea; di conseguenza, il sistema di coordinate sulla superficie del disco non ha il suo usuale 'significato metrico immediato'. In seguito Einstein avrebbe ricordato l'ostacolo concettuale che lo aveva occupato per sette dei dieci anni di cui si è detto affermando che non era stato facile liberarsi dell'idea che le coordinate dovessero avere un significato fisico preciso. Nel 1912 Einstein aveva raggiunto la seguente conclusione: la teoria della relatività speciale aveva mostrato che il concetto newtoniano di tempo deve essere modificato e che, di conseguenza, la geometria del disco rotante non è euclidea. Questo sistema di riferimento è accelerato e un sistema linearmente accelerato è equivalente a un campo gravitazionale in cui le particelle si muovono soddisfacendo la condizione δ∫ds=0.

Einstein, dopo essere tornato a Zurigo nel 1912, cercò l'aiuto di un amico, il matematico Marcel Grossmann (1878-1936). Non esiste molta documentazione riguardo all'esatta natura dell'aiuto di Grossmann, tranne il fatto che da studenti avevano frequentato insieme a Zurigo il corso di Karl Friedrich Geiser (1843-1934) sulla teoria gaussiana delle superfici, di cui ci sono rimasti gli appunti di Grossmann utilizzati con tutta probabilità dal meno organizzato Einstein per superare gli esami finali. Sembra molto probabile però che sia stato proprio Grossmann ad aver spiegato a Einstein certi aspetti della teoria di Gauss che fecero vibrare una corda nella sua mente. Carl Friedrich Gauss (1777-1855), infatti, aveva espresso la sua teoria delle superfici in funzione di due parametri che definiscono una superficie come sistema di coordinate su di essa; cosicché le coordinate erano in effetti prive di significato metrico, che deve essere invece fornito dalla cosiddetta 'seconda forma quadratica': nella notazione moderna, se la superficie è definita come r=r(u¹,u²), allora

[7]  ds²=dr ∙ dr=g_ijduⁱdu^j,

dove

e si sottintende una somma su i,j=1,2 ogni qualvolta un suffisso letterale sia presente due volte in un termine. La forma metrica è una proprietà intrinseca della superficie, ossia indipendente dal modo in cui essa è immersa nello spazio esterno tridimensionale.

Altre espressioni determinano le proprietà locali della superficie in termini della sua curvatura e per la maggior parte non si tratta di proprietà intrinseche. Per esempio, un foglio di carta modellato in forma cilindrica conserva invariata la sua geometria intrinseca, e pertanto la misura della sua curvatura è una proprietà interamente estrinseca. Invece, la superficie di una sfera ha anche una sua curvatura intrinseca, rappresentata dal fatto che la somma degli angoli di un triangolo su di essa supera π di un ammontare proporzionale alla sua area. Gauss poté mostrare che la misura della curvatura della superficie può sempre essere scomposta in questo modo e che essa aveva una parte completamente intrinseca R, in cui entravano le derivate seconde delle g_ij come pure espressioni quadratiche nelle derivate prime.

Grossmann fu in grado di fornire questa più profonda comprensione dell'opera di Gauss e, inoltre, informazioni sul lavoro dei geometri differenziali italiani, i quali, in particolare Gregorio Ricci-Curbastro (1853-1925) e Tullio Levi-Civita (1873-1941), avevano generalizzato l'analisi di Gauss a un numero qualsiasi di dimensioni, dove la generalizzazione della R di Gauss era una matrice R_ijkl, il tensore di Riemann-Christoffel.

Era necessario studiare innanzi tutto il caso quadridimensionale e, naturalmente, sarebbero state disponibili soltanto le proprietà intrinseche del mondo a quattro dimensioni. Tutto ciò come poteva essere correlato con la gravitazione? Riflettendo sull'articolo del 1907, Einstein notò che la trasformazione accelerata cambia la forma metrica in qualcosa che non è più esprimibile in somme e differenze di quadrati, cosicché il campo gravitazionale apparente deve essere rappresentato in qualche modo dalle g_ij. L'ipotesi della variazione di c come un potenziale gravitazionale fu abbandonata: tale potenziale poteva essere descritto invece dai dieci parametri g_ij che definivano la forma metrica nello spazio quadridimensionale. Nell'articolo del 1913 apparso sul "Journal de physique" Einstein e Grossmann sostenevano che trasformazioni coordinate completamente generali, analoghe ai parametri arbitrari della teoria delle superfici di Gauss,

conducono alla seguente forma metrica ds²=g_ij dxⁱ dx^j, benché naturalmente con R_ijkl=0 (dato che la trasformazione da uno spazio all'altro in relatività speciale è un'operazione analoga a quella di piegare un foglio di carta in forma di cilindro); i cammini delle particelle sono dati da δ∫ds=0.

Tutto ciò aveva preparato il terreno per un grande balzo in avanti; tuttavia Einstein e Grossmann non erano ancora pronti per compierlo. Ciò di cui essi si resero conto era che l'eliminazione di un campo gravitazionale uniforme mediante una trasformazione accelerata può, almeno in parte, essere generalizzata: in questo modo qualsiasi campo gravitazionale può essere eliminato nell'intorno di un qualunque punto P, essenzialmente attraverso una trasformazione che avrebbe eliminato il campo uniforme che coincideva con il campo considerato nell'intorno di P.

La generalizzazione a un campo qualsiasi, anche nel caso di un campo irriducibile, ha però un prezzo per quanto riguarda il carattere locale della trasformazione e per il fatto che le trasformazioni corrispondenti in punti diversi non possono essere collegate fino a costituirne una sola, globale, che eliminerebbe l'intero campo. Bisogna fare dunque riferimento a una forma metrica generale ds²=g_ijdxⁱdx^j, senza le condizioni aggiuntive R_ijkl=0, e mantenere l'assunzione che i cammini delle particelle siano dati da δ∫ds=0. Il problema che Einstein e Grossmann, giunti a questo punto, non riuscivano a risolvere era rappresentato dal calcolo di g_ij.

In questo caso, sfortunatamente, l'analogia con la superficie di Gauss non risultava di alcun aiuto. I coefficienti metrici giocavano un doppio ruolo, descrivendo sia le relazioni temporali sia quelle spaziali in termini del sistema coordinato, e, inoltre, svolgendo il compito di potenziali gravitazionali. A giudicare da questo secondo aspetto, sembrava chiaro che vi era bisogno di un qualche analogo dell'equazione di Poisson per collegarli alla distribuzione e, possibilmente, al movimento della materia. Dal momento che esistono dieci g_ij indipendenti, occorre un insieme di dieci equazioni del campo e la densità ϱ che appariva nel membro di destra dell'equazione di Poisson poteva essere generalizzata abbastanza facilmente in un insieme di dieci quantità T_ij (che per polvere gravitante avrebbero assunto la forma T_ij=ϱg_ipg_jqv^pv^q, dove v è la quadrivelocità, v^p=dx^p/ds). Tuttavia, nella ricerca dell'analogo del membro di sinistra dell'equazione di Poisson, Einstein e Grossmann furono in grado di trovare soltanto una complicata matrice, che dava luogo a un insieme di dieci equazioni che non soltanto non erano invarianti rispetto a trasformazioni generali di coordinate, ma portavano addirittura a contraddizioni interne.

Il problema delle corrette equazioni di campo occupò Einstein per altri due anni. In una conferenza tenuta nel 1913 egli affermò che l'intero problema della gravitazione sarebbe stato risolto se si fosse potuto trovare un insieme di equazioni, covarianti rispetto a trasformazioni arbitrarie di coordinate, soddisfatte dalle quantità g_ij che determinano il campo gravitazionale. Questa posizione impostava correttamente la questione, ma per gran parte dei due anni successivi Einstein fu occupato dal tentativo di dimostrare che non era possibile trovare un simile insieme. Poi, quasi all'improvviso, verso la fine del 1915 egli scoprì come generalizzare correttamente l'equazione di Laplace e ciò fu sufficiente per usare la teoria a fini predittivi (attraverso un processo di introduzione di singolarità come nella gravitazione newtoniana).

Nell'articolo dell'anno seguente l'argomentazione è semplice: ci sono dieci g_ij da determinare; le dieci condizioni che le determinano devono essere in ogni caso soddisfatte se sono soddisfatte le venti condizioni R_ijkl=0; nella geometria differenziale esiste una procedura codificata per ricavare da R_ijkl un insieme di dieci quantità R_il=g^jkR_ijkl, detto tensore di Ricci; "Ciò ci induce a richiedere la condizione R_ij=0, per il campo gravitazionale privo di materia" (in questa argomentazione, le quantità g^pq sono ricavate come elementi della matrice inversa a quella i cui elementi sono g_ij). Dapprima Einstein scrisse l'equazione corrispondente a quella di Poisson, erroneamente, come R_ij=−T_ij; essa non è corretta perché T_ij, a differenza di R_ij, ha una divergenza che tende a zero. Comunque, il 25 novembre del 1915 Einstein riuscì a fornire le equazioni nella loro forma definitiva:

[10]  R_ij-g_ijR/2=-T_ij,

dove lo scalare di Ricci è definito da R=g^ijR_ij. La formulazione della teoria era finalmente completa.

I successi della relatività generale

La storia successiva della relatività generale attraversò differenti fasi, nella prima delle quali, tra il 1916 e la Seconda guerra mondiale, la teoria non era ben integrata con il resto della fisica. Inizialmente, l'interesse si concentrò sulle cosiddette 'tre verifiche cruciali' della teoria. Nella conclusione dell'articolo del 1916, Die Grundlage der allgemeinen Relativitätstheorie (Sul fondamento della teoria generale della relatività) pubblicato in "Annalen der Physik", Einstein aveva calcolato tre effetti, in prima approssimazione (non disponendo di una soluzione esatta delle equazioni di campo):

a) l'orbita di Mercurio, idealizzato come un pianeta singolo orbitante intorno a un Sole fisso, era solo approssimativamente ellittica e ruotava di 43″ a secolo;

b) la deviazione della luce, causata da un corpo dotato di massa, era esattamente il doppio del valore trovato da Soldner nel 1801;

c) le linee spettrali delle stelle, in un forte campo gravitazionale, dovevano risultare spostate verso il rosso.

Nel 1916 Karl Schwarzschild fornì la prima soluzione esatta delle equazioni del campo, corrispondente a una singolarità simmetrica sferica. Esprimendola in opportune coordinate essa aveva la seguente forma:

dove m è una costante di integrazione che più tardi fu identificata con la massa newtoniana (utilizzando opportune unità di misura in grado di rendere il valore numerico della costante gravitazionale pari a 1).

Nel 1919 si ebbe un'eclissi solare durante la quale fu possibile misurare il secondo dei tre effetti. Le spedizioni britanniche inviate a osservarlo ottennero risultati che furono salutati come una trionfale conferma della teoria. Tuttavia il loro livello di accuratezza era molto inferiore a quello corrente in astronomia. Arthur S. Eddington (1882-1944) ricavò i risultati in questione mediante un uso selettivo delle osservazioni, ignorando quelle del telescopio più grande sulla base della convinzione che il calore causasse una distorsione nello specchio. Risultati più accurati sono stati ottenuti nelle eclissi successive.

Per quanto riguarda il terzo effetto, esso fu verificato inizialmente con le linee spettrali del Sole; ma le misurazioni risultarono estremamente difficili a causa dello spostamento molto più grande delle linee causato da comuni fenomeni Doppler. L'effetto fu sottoposto a verifiche molto più accurate negli anni Cinquanta.

Il fatto che tra le due guerre la teoria della relatività sia stata ampiamente accettata è una conseguenza più della sua coerenza interna che delle conferme sperimentali. Nei primi stadi della sua elaborazione e della sua diffusione, il carattere non lineare e la complessità delle equazioni di campo fu un grande ostacolo per la scoperta di soluzioni esatte. Nel 1917, tuttavia, Hermann Weyl fu in grado di risolvere le equazioni dello spazio vuoto per il caso di simmetria assiale con una soluzione statica con due singolarità (due masse puntuali). Questa soluzione fu alquanto importante perché implica, oltre alle due masse puntuali, una singolarità non dotata di massa lungo la linea che le unisce e che, come una leggera asta rigida, le tiene separate. Ciò accade perché, contrariamente al caso newtoniano, il carattere non lineare della teoria rende impossibile, esattamente come ci si aspetta dal punto di vista fisico, una soluzione statica con due masse puntuali, che si attrarrebbero l'un l'altra e renderebbero la soluzione non statica. Questo solleva una questione ancora più ampia, e cioè se le equazioni del moto (che nell'articolo originario di Einstein assumevano la forma δ∫ds=0 ed erano quindi le geodetiche della metrica) siano in effetti completamente determinate dalle equazioni di campo. Che esse siano determinate in questo modo nel caso di una distribuzione continua di materia non coesa (la polvere) si ricava già dai risultati dell'originario articolo del 1913 scritto da Einstein in collaborazione con Grossmann.

La soluzione di Weyl mette però in risalto qualcosa di più notevole: il movimento delle singolarità delle equazioni di campo dello spazio vuoto è certamente vincolato, e potrebbe essere interamente determinato, dalle stesse equazioni. Weyl tentò di dimostrarlo nel 1923, ma la natura del problema divenne chiara soltanto nell'articolo di Einstein e Jakob Grommer che risale al 1927, e si dovette attendere fino al lavoro di Einstein, Leopold Infeld e Banesh Hoffmann del 1938 per avere qualcosa che assomigliasse a una soluzione soddisfacente del problema.

La chiave della difficoltà non risiedeva nella natura complicata delle equazioni, benché questa rendesse i calcoli lunghi e laboriosi, ma nel fatto che, per evitare qualsiasi ipotesi specifica sul tensore di energia, ciò che veniva studiato era precisamente il movimento delle singolarità. Tuttavia questa situazione era dovuta anche al fatto che, come per la polvere citata in precedenza, Einstein si opponeva a qualunque uso del tensore di energia, in quanto considerava che le equazioni di campo in cui esso compariva fossero relazioni tra una quantità geometrica nel membro di sinistra e una quantità fisica in quello destro, e per di più una quantità di cui normalmente non conosciamo nulla. Ciò sollevava enormi problemi concettuali legati alla natura della teoria. Così come, nella relatività speciale, la nozione di tempo era stata estesa oltre quella newtoniana e relativizzata rispetto a un particolare osservatore, allo stesso modo, nella teoria generale, doveva essere estesa e generalizzata la nozione newtoniana di spazio inteso come uno scenario fisso in cui hanno luogo gli eventi. La metrica spaziale è il campo gravitazionale in esame, e pertanto è determinata dalla distribuzione della materia; non vi è uno spazio di 'background' rispetto al quale la materia possa essere considerata come un oggetto. L'intera geometria differenziale riemaniana, in termini della quale veniva espressa la teoria della relatività generale, utilizza funzioni continue senza possibilità di avere singolarità; ciò vuol dire che le singolarità che si incontrano nell'analisi delle equazioni del moto devono essere considerate al di fuori della varietà spazio-tempo. La tecnica impiegata fu quella di circondare ogni punto nel quale ci si attendeva una singolarità con una piccola superficie e di cercare la soluzione delle equazioni del campo nella regione di spazio compresa tra le superfici, con condizioni al contorno espresse sotto forma di integrali di superficie. Sebbene i risultati ottenuti mostrassero che le particelle di massa piccola (tali cioè da non disturbare il campo gravitazionale) si muovevano lungo le geodetiche, e permettessero di calcolare le correzioni relativistiche al problema dei due corpi, ancora non si poteva affermare che si era giunti a una trattazione soddisfacente delle singolarità. Nel periodo tra le guerre si lavorò alla ricerca di soluzioni cosmologiche delle equazioni del campo.

Inizialmente Einstein fu spinto a cercare tali soluzioni a partire dall'idea che le sue equazioni del campo non potessero determinare univocamente i potenziali gravitazionali senza condizioni al contorno spaziali. Egli formalizzò un principio cosmologico ‒ secondo cui il campo doveva essere spazialmente isotropico in ogni punto ‒ con il requisito, a cui lo condusse la lettura di Ernst Mach, che "non vi può essere inerzia rispetto allo spazio, ma solo un'inerzia di masse l'una rispetto all'altra", come scrisse in Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie (Considerazioni cosmologiche sulla teoria generale della relatività) pubblicato nel 1917 in "Königlich Preussische Akademie der Wissenschaften Sitzungsberichte". La soluzione di Schwarzschild, in cui compare una sola massa, è un notevole esempio della insufficienza del principio di Mach nella relatività generale. Einstein sostenne, in parte per un'analogia newtoniana, la necessità di una modifica delle equazioni del campo nella forma

[12]  0=R_ij-g_ij(R-2λ)/2,

dove λ è una costante, di cui si sa che ha un valore piccolo. Le nuove equazioni di campo avevano una soluzione, nota ora come Universo di Einstein:

[13]  ds²=dt²-[1-(r²/R²)]^-1dr²-r²(dϑ²+sen²ϑdφ²),

dove λR²=1. Questa soluzione fa scomparire il problema delle condizioni al contorno perché tale Universo non aveva contorno, benché la sua estensione totale fosse finita. Einstein sicuramente riteneva che le nuove equazioni del campo non possedessero soluzioni per lo spazio vuoto, perché questo avrebbe riproposto il problema della relatività dell'inerzia, ma, sempre nel 1917, Willem de Sitter trovò la soluzione:

[14] ds²=[1-(r²/R²)]dt²-[1-(r²/R²)]^-1dr²-(dϑ²+sen²ϑdφ²),

dove ora λR²=3. Questa soluzione corrisponde a una pressione e a una densità pari a zero in tutti i punti. Einstein arrivò quindi alla conclusione che il termine aggiuntivo delle equazioni del campo non aveva ottenuto l'effetto che egli sperava e così, nel 1919, lo abbandonò ancora una volta. La soluzione di de Sitter è interessante anche per un altro aspetto. Le equazioni del moto mostrano che, se viene introdotta in un punto una particella di prova in stato di quiete (una particella, cioè, la cui massa non disturba la soluzione), essa comincia ad accelerare allontanandosi dall'origine, indipendentemente da dove venga collocata l'origine, perché la velocità, una volta che sia stata percorsa una distanza r, è proporzionale a r. In questo modo, la metrica di de Sitter suggeriva agli astronomi di cercare un allontanamento sistematico della materia distante. Era già noto, dalle osservazioni di Carl Wilhelm Wirtz del 1922 e di Edwin P. Hubble nel 1929, che le galassie a spirale, come era mostrato dai loro spostamenti verso il rosso, tendevano ad allontanarsi dalla Terra. In questo stesso periodo ulteriori ricerche di cosmologia diedero per scontati la recessione e gli spostamenti verso il rosso e cercarono un modello più realistico di Universo contenente materia in espansione.

Tra le due guerre si ebbe un progresso anche nello studio del collasso gravitazionale. L'idea risale inizialmente a Newton: poiché la legge di gravità produce forze di attrazione fra due masse qualsiasi (al contrario di quanto avviene, per es., in elettrostatica) una grande massa di materia sottoposta esclusivamente a forze gravitazionali collasserebbe verso il centro. Nella materia ordinaria sono sempre presenti altre forze, ma il principio di equivalenza sminuisce notevolmente l'effetto di resistenza al collasso che può derivarne: se la massa di un corpo viene aumentata attraverso l'aggiunta di materia addizionale, le forze gravitazionali continueranno ad aumentare; al contrario, le forze che mantengono la materia stabile, ossia le forze chimiche e quelle nucleari, raggiungeranno un punto di saturazione. Alla fine le forze gravitazionali saranno superiori alle altre; le forze chimiche vengono superate a una massa critica che è superiore solo del 20% rispetto alla massa del Sole e a quel punto la densità diventa molto alta. A tali alte densità, la massa critica è anche più piccola e così emerge un secondo punto di collasso che nella teoria newtoniana dà luogo alla situazione descritta in precedenza, e che, nell'ambito della relatività generale, fu studiata in profondità da J. Robert Oppenheimer e Hartland Snyder nel 1939. In questo nuovo contesto la situazione risulta più complicata e anche diversa per il seguente aspetto: il campo intorno a una sfera uniforme è dato dalla soluzione di Schwarzschild. È immediato rivelare per la [11] una singolarità in r=2m, oltre alla singolarità in r=0 derivante dall'utilizzazione di coordinate polari sferiche che sono singolari nell'origine. Le prime applicazioni di questa soluzione non trovarono alcuna difficoltà dovuta alla prima singolarità; nel caso del Sole, per esempio, si tratta solamente di 3 km. Così ogni effettiva soluzione del campo del Sole deve usare la forma di Schwarzschild soltanto fino al contorno del Sole, cioè per valori di r molto più grandi, e poi all'interno del Sole viene raccordata a essa una soluzione interna (che comporta alcune assunzioni fisiche in merito alla pressione e alla densità).

Questa procedura è del tutto simile a quella adottata nella gravitazione newtoniana. Al contrario, secondo Oppenheimer e Snyder, un corpo dotato di massa che collassa dovrà avere alla fine un raggio inferiore a 2m. Indagini successive hanno mostrato che tali singolarità, cui fu assegnato il nome di 'buchi neri', hanno proprietà insolite. I segnali luminosi possono essere seguiti dirigersi verso la sfera singolare a partire dall'esterno, ma non nel verso opposto, cosicché un tale corpo sarebbe invisibile al nostro occhio e potrebbe essere rivelato soltanto grazie alla forte intensità del suo campo gravitazionale.