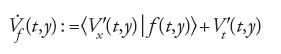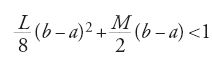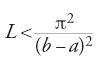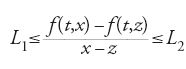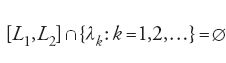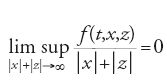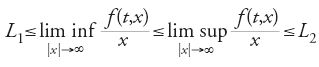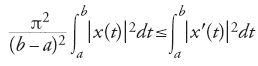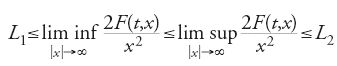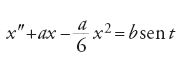La seconda rivoluzione scientifica: matematica e logica. Equazioni differenziali ordinarie

La seconda rivoluzione scientifica: matematica e logica. Equazioni differenziali ordinarie

Equazioni differenziali ordinarie

Accanto a sostanziali progressi nella teoria delle equazioni differenziali ordinarie lineari, sulle quali non ci dilunghiamo, nel periodo 1880-1950 si assiste alla nascita della teoria delle equazioni differenziali non lineari e alla scoperta delle principali tecniche che sono ancora oggi alla base dei suoi sviluppi. Nel presente capitolo vengono delineati gli aspetti principali di questa evoluzione.

Problema di Cauchy

Nel 1823 Augustin-Louis Cauchy (1789-1857) aveva dimostrato l'esistenza e unicità locale della soluzione y(t)= =(y₁(t),…,y_n(t)) del problema delle condizioni iniziali per un sistema di equazioni differenziali ordinarie:

[1] y'=f(t,y), y(t₀)=y₀,

associato al campo di vettori f=(f₁,…,f_n) utilizzando il metodo dei maggioranti nel caso delle f_j analitiche, e le approssimazioni poligonali di Euler quando la f e le ∂f/∂fy_k sono continue. Quest'ultimo caso fu poi generalizzato da Rudolf Otto Sigismund Lipschitz (1832-1903) nel 1868 al caso in cui il campo f è lipschitziano nella y. Motivato dall'approccio globale del comportamento delle soluzioni, che prenderemo in considerazione nel seguito, Jules-Henri Poincaré (1854-1912) studia nel 1890 la dipendenza della soluzione y(t;t₀,y₀) dai valori iniziali o dai parametri dai quali il campo dipende. Nello stesso anno, Charles-émile Picard (1856-1941) dimostra il teorema di Cauchy-Lipschitz con il metodo delle approssimazioni successive (o d'iterazione):

[2] y⁰=y₀,  y^k(t)=y₀+∫^t_t0f(s,y^k-1(s))ds, (k=1,2,...).

Il problema dell'esistenza di una soluzione quando f è continua, sollevato nel 1881 da Vito Volterra (1860-1940), fu risolto da Giuseppe Peano (1858-1932) nel 1886 nel caso di un'equazione scalare e, nel 1890, nel caso di un sistema. La convergenza delle approssimazioni poligonali è sostituita dall'applicazione del teorema di Ascoli-Arzelà. Constantin Carathéodory (1873-1950) generalizza nel 1918 i risultati di Cauchy-Lipschitz-Peano ai campi f misurabili in t, continui in y=(y₁,…,y_n), e dominati, quando le y sono limitate, da una funzione di t integrabile secondo Lebesgue. Erich Kamke (1890-1961) studia nel 1928 il prolungamento della soluzione della [1] su un intervallo aperto massimale I(t₀,y₀) e le proprietà delle soluzioni nelle vicinanze degli estremi dell'intervallo. Ispirato dai primi risultati di Oskar Perron (1880-1975) nel caso scalare, Mitio Nagumo introduce nel 1942 le prime condizioni tangenziali su ∂K assicurando l'esistenza di una soluzione della [1] quando f(t,y) è definita sul prodotto di un intervallo e di un insieme chiuso.

Teoria qualitativa

In una serie di quattro lunghe memorie pubblicate tra il 1881 e il 1886, Poincaré inaugura lo studio qualitativo delle equazioni differenziali non lineari: questo studio doveva precedere, secondo lo stesso Poincaré, quello quantitativo. Egli comincia con il considerare i sistemi autonomi piani:

[3]  u'=p(u,v), v'=q(u,v),

dove p e q sono polinomi, e si propone di studiare qualitativamente le orbite {(u(t), v(t)):t∈ℝ} delle traiettorie (u(t), v(t)) delle [3]. Le più semplici sono i punti singolari, orbite delle soluzioni costanti, soluzioni del sistema:

[4]  p(u,v)=0, q(u,v)=0.

Poincaré classifica questi punti secondo la natura degli autovalori della matrice jacobiana del campo di vettori (p,q) introducendo la terminologia oggi classica dei nodi (dove confluiscono un'infinità di orbite), fuochi (attorno ai quali le orbite si avvolgono a spirale), e punti di sella (dove si incontrano due orbite). Distingue anche i centri, circondati da una famiglia di orbite che sono dei cicli (curve di Jordan chiuse).

Poincaré associa alla [3] e a ogni ciclo Γ che non passa per alcun punto singolare della [3] un indice i[(p,q), Γ], che conta il numero algebrico dei giri del campo (p,q) intorno all'origine quando (u,v) descrive Γ nel senso positivo. Questa nozione è legata a quella di indice introdotta da Cauchy tra il 1831 e il 1837. Poincaré dimostra che un ciclo che non circonda punti singolari ha indice zero, e calcola gli indici dei vari punti singolari. Proiettando il suo sistema piano sulla sfera, Poincaré dimostra che il numero totale dei nodi e dei fuochi sulla sfera è uguale al numero totale delle selle più due: è la prima formulazione del famoso teorema di Poincaré-Hopf in topologia. La sfera non può dunque ammettere campi tangenti continui non nulli. Luitzen Egbertus Jan Brouwer (1881-1966) generalizzerà nel 1912 questo risultato a tutte le sfere di dimensione pari (teorema di Poincaré-Brouwer).

Nella seconda memoria, Poincaré introduce l'importante concetto di ciclo limite per la [3]: un'orbita chiusa sulla quale si avvolgono le orbite vicine. Utilizzando la nozione di arco senza contatti (non tangente al campo (p,q) in alcun punto) e quella di conseguente (intersezione successiva, con un arco senza contatto, di un traiettoria uscente da un punto di questo arco), Poincaré dà una prima versione di un risultato completato da Ivar Bendixson (1861-1935) nel 1901 (teorema di Poincaré-Bendixson), secondo il quale gli insiemi di punti di accumulazione per t→±∞ delle traiettorie della [3] possono essere soltanto punti singolari, cicli o unioni di archi che uniscono punti singolari (separatrici; gli archi essendo detti omoclini o eteroclini a seconda che finiscano in uno stesso punto singolare o in due punti diversi).

La terza memoria comincia con una discussione sulle condizioni di esistenza di un centro, esistenza che non può essere dimostrata a partire dal sistema differenziale linearizzato, ma richiede in generale la verifica di infinite condizioni. Poincaré riduce poi lo studio di equazioni differenziali (implicite) del tipo F(x,y,y′)=0 a quello di un'equazione differenziale su una superficie ∑, e dimostra che il numero totale dei nodi e dei fuochi su ∑ è uguale al numero totale dei punti di sella aumentato di 2(p−1), dove p è il genere di ∑. Si tratta del teorema di Poincaré-Hopf per una superficie di genere p (o caratteristica 2(p−1)). Il caso del toro viene studiato in dettaglio, e Poincaré pone il problema di sapere se in assenza di cicli ogni traiettoria sia ovunque densa. Nel 1932 Arnaud Denjoy (1884-1974) dimostra che la risposta è affermativa se il campo è di classe C², e negativa se è soltanto di classe C¹ (quest'ultimo risultato era stato ottenuto già nel 1916 da Piers Bohl).

La quarta memoria affronta lo studio qualitativo dei sistemi differenziali autonomi di dimensione qualunque:

[5] y'=p(y),

dove p=(p₁,p₂,…,p_n), e i p_j sono polinomi in y=(y₁,…,y_n). Poincaré utilizza abilmente una generalizzazione dell'indice data nel 1869 da Leopold Kronecker (1823-1891), che prefigura per campi di vettori di classe C¹ il grado topologico dei campi continui che sarà introdotto da Brouwer nel 1912. Gli archi senza contatto sono sostituiti da superfici senza contatto ∑={y:F(y)=0}, dove F è una funzione regolare reale. Tali superfici suggeriranno ad Aleksandr Michajlovič Ljapunov (1857-1918) il suo secondo metodo in teoria della stabilità. ∑ si dice senza contatto se il prodotto scalare ⟨F′(y)∣p(y)⟩ del gradiente di F per p non si annulla in alcun punto di ∑. L'indice del campo p su ∑ dipende allora soltanto dalle caratteristiche topologiche di ∑.

Poincaré utilizza l'indice di Kronecker per studiare la natura e il numero dei punti singolari della [5]. Per studiare i cicli egli introduce la nozione di superficie di sezione S (che taglia trasversalmente un'orbita in un punto) e quella di primo ritorno R. A ogni punto P di S, R associa il punto di intersezione ulteriore con S della traiettoria uscente da P. La dinamica della [5] è sostituita da quella delle iterate di R. I punti fissi di R forniscono le posizioni iniziali dei cicli. L'applicazione di questa idea ad alcuni problemi di meccanica celeste porta Poincaré a congetturare, nel 1912, l'esistenza di almeno due punti fissi per ogni applicazione continua di un anello del piano in sé che conservi le aree, lasci invariate le frontiere interna ed esterna, e muova i punti di queste in senso opposto. La dimostrazione sarà data l'anno dopo da George D. Birkhoff (1884-1944) (teorema di Poincaré-Birkhoff). Seguiranno numerose importanti generalizzazioni, varianti e applicazioni allo scopo di dimostrare l'esistenza di punti periodici o di curve invarianti, come in particolare i risultati del 1954 di Andrej Nikolaevič Kolmogorov (1903-1987), che introdurrà il metodo KAM (Kolmogorov-Arnold-Moser).

Il XVI problema proposto da David Hilbert (1862-1943) al Congresso internazionale dei matematici di Parigi nel 1900, richiedeva tra l'altro di determinare il numero massimo e la posizione dei cicli limite della [3] in funzione del grado di p e di q. Il problema resta aperto nonostante le numerose ricerche a esso dedicate, e la dimostrazione completa del 'teorema' di Henri Dulac (1870-1955) del 1923 sulla finitezza del numero di cicli limite dovrà attendere la fine del secolo scorso e l'uso di tecniche sofisticate.

Nel 1937 Aleksandr Aleksandrovič Andronov (1901-1952) e Lev Semenovič Pontrjagin (1908-1988) introducono i sistemi piani y′=f(y) strutturalmente stabili: la struttura topologica delle orbite di questi sistemi resta invariata per perturbazioni sufficientemente piccole del campo di vettori f. È il caso di un oscillatore lineare smorzato, e la nozione è importante per i sistemi differenziali che forniscono un modello per vari fenomeni naturali. Andronov e Pontrjagin enunciano condizioni di stabilità strutturale e risultati sulle possibili forme che può avere l'insieme delle orbite. L'insieme dei sistemi piani strutturalmente stabili è aperto e denso, ma ciò non è più vero in dimensione maggiore.

Metodi di perturbazione

Nel 1890 nella memoria Sur le problème des trois corps et les équations de la dynamique, per la quale riceverà il premio del concorso indetto dal re di Svezia e Norvegia Oscar II, Poincaré inaugura lo studio delle soluzioni T-periodiche di sistemi perturbati del tipo

[6]  y'=f(t,y,ε)

dove f è T-periodica in t, quando il sistema non perturbato y′=f(t,y,0) ammette una soluzione T-periodica y₀. Egli riduce lo studio delle soluzioni T-periodiche della [6] a quello dei punti fissi dell'operatore (detto di Poincaré o di traslazione) P definito dalla P(a)=y(t;a,ε), dove y(t;a,ε) è la soluzione del problema di Cauchy y′=f(t;y,ε), y(0)=a.

Quando l'equazione alle variazioni che è associata a y₀ z′=f_y′(t,y₀(t),0)z non ammette soluzioni T-periodiche non banali (caso della non risonanza), l'esistenza di una soluzione T-periodica della [6] vicina a y₀ è assicurata per ogni ε vicino allo zero. L'analisi è più delicata nel caso contrario (caso della risonanza), che ha sempre luogo quando si tratta di un sistema autonomo:

[7] y'=f(y,ε)

per il quale, inoltre, non è noto il periodo T(ε). Lo studio delle soluzioni periodiche di sistemi perturbati è opera di numerosi autori, che si basano sia sull'impostazione di Poincaré, sia su un metodo di studio delle equazioni integrali non lineari introdotto nel 1906 da Ljapunov e nel 1908 da Erhard Schmidt (1876-1959) (metodo di Ljapunov-Schmidt). In particolare, Eberhard Hopf (1902-1983) studia nel 1942 la comparsa di cicli limite a partire da un equilibrio instabile (biforcazione di Hopf) quando il parametro varia, problema già considerato nel 1938 da Andronov ed Evgenija Aleksandrova Leontovič-Andronova (1905-1996). Una situazione che si ritrova in numerose applicazioni, non soltanto fisiche o tecniche, ma anche in biologia e in dinamica delle popolazioni: lo studio matematico di quest'ultimo caso sarà sviluppato negli anni Venti del Novecento da Alfred J. Lotka (1880-1949) e da Volterra. Nel 1928 Andronov menziona i loro lavori quando stabilisce un legame tra i cicli limite di Poincaré e le oscillazioni autosostenute dell'equazione

[8]  x"+ε(x'³-x')+x=0

introdotta in meccanica da John W. Strutt (lord Rayleigh, 1842-1919) nel 1883, e dell'equazione:

[9]  x"+ε(x'²-1)x'+x=0

proposta nel 1920 da Balthasar van der Pol (1889-1959), come modello del comportamento di alcuni oscillatori elettronici a triodo. Andronov dimostra l'esistenza di cicli limite per ε piccolo utilizzando il metodo di perturbazione di Poincaré. Il problema dell'esistenza era già stato studiato nel 1925 da Élie Cartan e Henri Cartan e, nel 1928, da Alfred Liénard per classi più generali di equazioni del secondo ordine (equazioni di Liénard), utilizzando (senza dirlo esplicitamente) metodi qualitativi del tipo di Poincaré-Bendixson. Questi lavori ne ispireranno molti altri, dal momento che, come van der Pol aveva osservato, fin dal 1920, quando ε è molto grande le soluzioni periodiche corrispondono alle oscillazioni di rilassamento presenti in numerose applicazioni fisiche, tecniche e biologiche.

Un altro metodo perturbativo, che si riallaccia al metodo delle variazioni delle costanti della meccanica celeste e all'impostazione euristica di van der Pol per lo studio della [9], viene sviluppato a partire dal 1932 da Nikolaj Michajlovič Krylov (1875-1955) e da Nikolaj Nikolaevič Bogoljubov (1909-1992) (metodo del centraggio o della media). Tale metodo sostituisce un sistema della forma

[10]  y'=εg(t,y,ε),

con g T-periodica in t, con il sistema autonomo 'mediato':

Bogoljubov dimostra nel 1945 che per ε≠0 sufficientemente piccolo la differenza tra le soluzioni della [10] e della [11] con le stesse condizioni iniziali resta dell'ordine di ε su un intervallo di t dell'ordine di ε⁻¹. Il metodo si può applicare anche nel caso quasi-periodico (se si sostituisce il secondo membro della [11] con il limite a cui esso tende per T che tende all'infinito) e consentirà numerosi sviluppi e applicazioni, in particolare alla teoria delle varietà integrali, inaugurata nel 1950 da Norman Levinson (1912-1975).

Nella memoria del 1890, e nei tre volumi dei Méthodes nouvelles de la mécanique céleste (1892-1899) che ne costituiscono lo sviluppo, Poincaré studia anche le soluzioni asintotiche (per t→+∞ o t→−∞) e doppiamente asintotiche (per t→+∞ e t→−∞) verso un equilibrio o una soluzione periodica (soluzioni omocline o eterocline). Lo sviluppo di queste idee mediante la dinamica simbolica, introdotta da Jacques-Salomon Hadamard (1865-1963) e perfezionata da Marston Morse (1892-1977), come pure i lavori sull'equazione di Liénard forzata di cui parleremo nel seguito, conducono alla teoria del caos ampiamente studiata nell'ultimo quarto del XX secolo.

Stabilità

Il problema della stabilità delle soluzioni è posto in maniera precisa e studiato a fondo nel 1892 da Ljapunov nella sua tesi di dottorato. La stabilità di una data soluzione del sistema differenziale:

[12] y'=f(t,y)

si riduce per traslazione a quella della soluzione nulla, e quest'ultima è stabile se la sua dipendenza continua dalle condizioni iniziali è uniforme per i valori di t maggiori o uguali a t₀. Se inoltre y(t;t₀,y₀)→0 quando t→+∞, la stabilità si dice asintotica.

Scrivendo la [12] nella forma

[13]  y'=P(t)y+g(t,y),

dove g(t,y) raggruppa i termini di ordine superiore a 1 in y, il primo metodo di Ljapunov consiste nel cercare condizioni su P(t) sotto le quali la stabilità o l'instabilità della soluzione nulla del problema lineare

[14]  y'=P(t)y,

implichi quella della soluzione nulla della [13]. La forma delle soluzioni quando P è costante suggerisce a Ljapunov di definire (con il segno opposto e una diversa terminologia) l'esponente caratteristico di una soluzione y della [14] come:

Questa nozione, che ha un ruolo importante nelle moderne ricerche sulla teoria del caos, permette a Ljapunov di dimostrare, per la classe delle P(t) regolari, che contiene in particolare le P costanti o periodiche, la stabilità asintotica della soluzione nulla della [13] quando tutti gli esponenti caratteristici delle soluzioni della [14] sono strettamente negativi, e la sua instabilità quando uno di essi è strettamente positivo. In tali condizioni lo studio della stabilità o della instabilità per linearizzazione è matematicamente giustificato. Quando P è costante gli esponenti caratteristici sono le parti reali dei suoi autovalori, e quando P è periodica essi si esprimono in funzione dei fattori caratteristici introdotti da Gaston Floquet (1847-1920) nel 1883. Intorno al 1930 Perron apporta importanti complementi al metodo dandogli la sua forma attuale.

Ljapunov considera anche le situazioni nelle quali P costante ha un autovalore nullo, ovvero due autovalori immaginari coniugati ±iω, mentre gli altri hanno la parte reale strettamente negativa. È l'origine del metodo delle varietà centrali, che riduce lo studio del comportamento asintotico di un sistema differenziale a quello di un sistema di dimensione minore (uno o due in questo caso). In questa occasione Ljapunov ottiene il celebre teorema del centro per un sistema autonomo che ammette un integrale primo (per es., un sistema hamiltoniano):

[16]  y'=f(y).

Tale teorema dà condizioni di esistenza per una famiglia di soluzioni periodiche con ampiezza arbitrariamente piccola, il cui periodo tende a 2π/ω quando l'ampiezza diminuisce. Questo risultato avrà numerose generalizzazioni, sia locali sia globali.

Nello studio del caso P periodico, Ljapunov stabilisce le prime condizioni sufficienti sulla funzione T-periodica p per la stabilità delle soluzioni dell'equazione di Hill

[17]  x"+p(t)x=0.

Questo risultato ispirerà un'ampia letteratura a partire dal 1950, con i primi risultati conseguiti da Mark Grigorevič Krein (1907-1989).

La condizione di stabilità di Lagrange-Dirichlet per un sistema meccanico conservativo e la nozione di varietà priva di contatto di Poincaré suggeriscono a Ljapunov un secondo metodo per lo studio della stabilità e dell'instabilità della soluzione nulla della [12]. La stabilità è garantita se è possibile trovare una funzione reale definita positiva V(t,y) la cui derivata calcolata lungo le soluzioni della [13]

è negativa in un intorno dell'origine.

Nel 1934 Nikolaj Gurevič Četaev (1902-1959) migliora sostanzialmente i teoremi di instabilità di Ljapunov. Konstantin Petrovič Persidskij (1903-1970) nel 1933, e José L. Massera (1915-2002) nel 1949 dimostrano teoremi inversi di quelli di Ljapunov, facendo vedere che la stabilità e la stabilità asintotica dell'origine implicano l'esistenza di opportune funzioni di Ljapunov. Il secondo metodo di Ljapunov è uno strumento essenziale in teoria del controllo.

Problemi ai limiti

Motivato da risultati analoghi per le equazioni alle derivate parziali ellittiche, Picard studia, dal 1890, l'esistenza e l'unicità della soluzione di problemi ai limiti del tipo:

[19]  x"=f (t,x,x'),  x(a)=x(b)=0,

quando la funzione continua f è globalmente lipschitziana in (x,x′), con costanti rispettivamente L e M. Con il metodo delle approssimazioni successive Picard dimostra, nel 1896, l'esistenza e l'unicità della soluzione quando

Come si vede dal problema lineare, tale stima non è ottimale ma Picard ottiene nel caso particolare del problema:

[21]  x"=f (t,x),  x(a)=x(b)=0,

la condizione ottimale di unicità:

Per il problema del pendolo forzato:

[23]  x"+asenx=bsent,  x(0)=x(π)=0,

scritto sotto la forma equivalente di equazione integrale:

[24]  x(t)=∫^π₀G(t,s)[-asenx(s)+bsens]ds,

mediante la funzione di Green G(t,s) del problema lineare associato, Georg Hamel (1877-1974) dimostra nel 1922, sempre per iterazione, l'esistenza e l'unicità della soluzione quando ∣a∣⟨1 (caso ottimale). Il suo metodo applicato alla [21] avrebbe portato alla condizione [22]. Nello stesso anno Stefan Banach (1892-1945) estende il metodo delle approssimazioni successive alle equazioni astratte in uno spazio di Banach: y=F(y), dove F è lipschitziana di costante strettamente minore di 1 (contrazione). In questo linguaggio, l'impostazione di Hamel richiede soltanto che una certa iterata F^m di F sia una contrazione. Nel 1949 Charles L. Dolph (1919-1994) utilizza la tecnica di iterazione in L²(a,b) per dimostrare l'esistenza e l'unicità di una soluzione della [21] quando:

,

con

,

dove λ_k=k²π²/(b−a)² sono gli autovalori del problema:

[27]  x"+λx=0,  x(a)=x(b)=0.

La condizione λ≠λ_k(k=1,2,…) di esistenza e unicità del problema lineare forzato:

[28]  x"+λx=h(t),  x(a)=x(b)=0,

viene così estesa alla [21] per la classe di funzioni f che soddisfano una condizione del tipo [25].

Lo studio del problema [19] quando f è soltanto continua viene affrontato per la prima volta nel 1905 da Carlo Severini (1872-1951) con un approccio piuttosto indiretto. Se (p_k) è una successione di approssimazioni polinomiali di f su un dato compatto, e se x_k(t;c) denota la soluzione del problema di Cauchy:

[29]  x"=p_k(t,x,x'),  x(a)=0,  x'(a)=c,

la x_k(t;c) sarà soluzione del problema ai limiti:

[30]  x"=p_k(t,x,x'),  x(a)=x(b)=0,

se si può determinare c_k tale che x_k(b;c_k)=0 (metodo di tiro). Utilizzando il teorema di Bolzano, Severini dimostra che questa condizione è soddisfatta se la differenza b−a è sufficientemente piccola. Il teorema di Ascoli-Arzelà applicato alla successione degli x_k(t;c_k) permette a Severini di estrarre una soluzione della [19].

Nel 1922, Birkhoff e Oliver D. Kellogg (1878-1932) generalizzano il teorema del punto fisso di Brouwer allo spazio C¹([a,b]) delle funzioni con derivata prima continua. Essi dimostrano che ogni applicazione continua F di un insieme B convesso, limitato, chiuso ed equicontinuo di C¹([a,b]) in sé ha almeno un punto fisso. Il risultato di Severini è un caso particolare dell'applicazione che essi fanno di questo risultato a una classe di problemi ai limiti per un'equazione di ordine qualunque. Nel 1930 Juliusz Pawel Schauder (1899-1943) generalizza il teorema di Birkhoff-Kellogg alle applicazioni compatte di un convesso chiuso e limitato di uno spazio di Banach in sé e alle applicazioni continue di un compatto convesso di un tale spazio in sé. La sua sola applicazione alle equazioni differenziali ordinarie rappresenta una nuova dimostrazione del teorema di Peano per il problema di Cauchy [1].

Nello stesso anno Renato Caccioppoli (1904-1959) utilizza un approccio analogo per dimostrare l'esistenza di almeno una soluzione della [19] qualunque siano a⟨b quando f è limitata, condizione che indebolirà l'anno seguente nella:

Nel 1934, Jean Leray (1906-1998) e Schauder estendono il grado di Brouwer alle applicazioni compatte di uno spazio di Banach, e ne deducono una generalizzazione sostanziale del teorema del punto fisso di Schauder. Dolph utilizzerà questa generalizzazione nel 1949 per dimostrare l'esistenza di una soluzione della [21] quando

,

dove L₁ e L₂ soddisfano la [26], un risultato dimostrato nel 1933 nella tesi di Leray, sotto ipotesi di regolarità più restrittive, nel caso particolare L₁=L₂.

Un'interessante tecnica di studio della [19], basata sul principio di massimo, e che si trova in germe nei lavori di Picard, è il metodo delle sub e super soluzioni introdotto da Giuseppe Scorza Dragoni (1908-1996) nel 1931 e, nella forma attuale, da Nagumo nel 1937. Una sub (rispettivamente super) soluzione è una funzione α (rispettivamente β) tale che α(a)≤0, α(b)≤0 (rispettivamente β(a)≥0, β(b)≥0) e

[33]  α"(t)≥f(t,α(t),α'(t)),  β"(t)≤f(t,β(t),β'(t)).

Se la [19] ammette una sub e una super soluzione tali che α(t)≤β(t) e se per x compreso tra α(t) e β(t), f(t,x,z) soddisfa una condizione di crescita di tipo quadratico in z (condizione di Nagumo), l'esistenza di una soluzione x(t) della [19] compresa tra α e β è assicurata. Questo metodo si applica ad altre condizioni ai limiti e sotto ipotesi più deboli. Il problema [19] è l'equazione di Euler-Lagrange del calcolo delle variazioni per il funzionale φ definito dalla:

,

dove F(t,x):=∫^x₀f (t,s)ds. Nel 1915 Leon Lichtenstein (1878-1933) dimostra l'esistenza di una soluzione della [19] sotto l'ipotesi: F(t,x)≥−A, provando l'esistenza di un minimo per il funzionale minorato φ mediante una sottosuccessione convergente di una successione minimizzante (metodo diretto del calcolo delle variazioni). Nel 1930 Adolf Hammerstein (1888-1941) migliora questa condizione nella

,

con L che soddisfa la [22], generalizzando i risultati di Hamel e di Lichtenstein. Il suo metodo è piuttosto indiretto: riduzione a un'equazione integrale non lineare seguita da un approccio variazionale del tipo di Ritz applicato all'equazione integrale trasformata per darle una struttura variazionale. Una dimostrazione molto più diretta, nella linea di Lichtenstein, viene data nel 1938 da Silvio Cinquini (1906-1998) utilizzando la disuguaglianza di Poincaré

Il problema di sapere se, analogamente, è possibile sostituire la condizione [32] con la

,

è tuttora aperto. I metodi di tipo Leray-Schauder di super e sub soluzioni, e le tecniche variazionali, in particolare l'individuazione di punti critici mediante minimax, sono ancora i più usati nello studio dei problemi ai limiti non lineari.

Soluzioni periodiche

Lo studio delle soluzioni T-periodiche di un'equazione differenziale utilizza sia le tecniche qualitative sia quelle dei problemi ai limiti in quanto, se per fissare le idee consideriamo l'equazione del secondo ordine x″=f(t,x,x′), una soluzione è T-periodica se e soltanto se soddisfa le condizioni ai limiti x(0)=x(T), x′(0)=x′(T). Le motivazioni provengono dallo studio delle vibrazioni del pendolo forzato [23] trattato euristicamente da Georg Duffing (1861-1944) nel 1918 a partire dall'approssimazione

,

e dall'analisi dell'oscillatore di van der Pol eccitato periodicamente

[39]  x"+c(x²-1)x'+ax=h(t),

studiato formalmente a partire dal 1920 da van der Pol per c piccolo.

Il metodo diretto del calcolo delle variazioni viene utilizzato nel 1915 da Lichtenstein per dimostrare l'esistenza di una soluzione 2π-periodica di una classe di funzioni tra cui la [38], e nel 1922 da Hamel per il pendolo forzato: x″+asenx= =bsent. Nel 1943 Solomon Lefschetz (1884-1972) e Levinson dimostrano l'esistenza di una soluzione T-periodica di classi di equazioni di Liénard forzate utilizzando il teorema del punto fisso di Brouwer applicato all'operatore di Poincaré corrispondente. L'anno dopo Levinson definisce dissipativo o di classe D il sistema piano T-periodico in t

[40] y'=f(t,y)

se esiste R>0 tale che tutte le soluzioni della [40] soddisfano:

Egli dimostra che l'operatore di Poincaré P associato alla [40] ammette un punto fisso (che fornisce una soluzione T-periodica della [40]). Levinson, nel 1945, e Massera nel 1949, ottengono stime del numero di soluzioni periodiche di periodo minimale qT (q>1 intero) (soluzioni subarmoniche) dei sistemi dissipativi [40]. Levinson dimostra anche, nel 1944, l'esistenza di un dominio chiuso I invariante per P tale che, per ogni punto fuori di I, le iterate P^k(a) convergono a I. Utilizzando tecniche introdotte da Birkhoff nel 1922, Levinson dimostra che la struttura topologica di I può essere molto complicata (del tipo insieme di Cantor), traducendo una possibile irregolarità del comportamento delle soluzioni della [40]. Nel 1945 Mary Cartwright (1900-1998) e John E. Littlewood (1885-1977) annunciano che I può passare da un insieme costituito da un solo punto a uno topologicamente complicato quando si fanno variare i parametri dell'equazione [39] con h(t)=bλc cos(λt+α). Levinson conferma tale risultato nel 1949 dando un esempio semplice di equazione di Liénard forzata per la quale una 'curva' del piano (x,x′) ovunque discontinua invariante per P attira le iterate secondo P dei punti del piano salvo uno. Questi lavori costituiscono un'altra fonte importante per la futura teoria del caos.

Quando un sistema non è dissipativo occorre utilizzare altre tecniche per studiarne le soluzioni periodiche. Una di queste, introdotta da Tadeusz Wazewski (1896-1972) nel 1947, si basa sul teorema della non retrazione di una palla sulla propria frontiera, e si applica a equazioni come la [40] per le quali sulla frontiera di un certo insieme limitato B del piano il campo di vettori corrispondente entra ed esce alternativamente. Gli sviluppi di questa tecnica porteranno alla nozione di indice di Conley. Francesco Stoppelli sarà il primo, nel 1952, a usare il metodo di Leray-Schauder per dimostrare l'esistenza di una soluzione periodica di un'equazione non dissipativa. Un notevole sviluppo di tale metodo si avrà dalla fine degli anni Sessanta del Novecento.