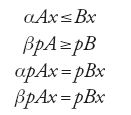La seconda rivoluzione scientifica: matematica e logica. L'economia matematica 1870-1950
La seconda rivoluzione scientifica: matematica e logica. L'economia matematica 1870-1950
L'economia matematica 1870-1950
Di matematica sociale comincia a parlare Condorcet nella Francia dei riformatori illuminati della seconda metà del XVIII secolo. Per Condorcet la matematica è lo strumento per la raccolta sistematica dei dati della realtà socioeconomica e l'introduzione di precisi criteri di razionalità nella gestione della cosa pubblica; essa rappresenta il modo in cui l'economia può raggiungere lo status di disciplina scientifica, seguendo il modello della fisica. La 'matematica sociale' viene coltivata anche in Italia negli ambienti illuministi che si muovono nella direzione di una laicizzazione della società e auspicano il passaggio dell'economia dalla sfera morale al campo scientifico.
Assai più significativo è il contributo di Augustin Cournot (1801-1877), il quale sostiene che l'obiettivo dell'introduzione della matematica nello studio dell'economia non è il calcolo numerico ma la determinazione delle relazioni tra le diverse variabili economiche. In Recherches sur les principes mathématiques de la théorie des richesses (1838) Cournot studia il comportamento del consumatore in relazione alla sua funzione di domanda e introduce la classificazione delle varie forme di mercato, dal monopolio al duopolio, all'oligopolio e al regime di concorrenza perfetta, ottenuta con un passaggio al limite quando il numero di agenti tende all'infinito.
Il marginalismo
Gli anni Settanta del XIX sec. sono quelli del marginalismo. Quasi contemporaneamente vengono pubblicati contributi come The theory of political economy (1871) di William S. Jevons, i Grundsätze der Volkwirtschaftslehre (Principî di economia, 1871) di Carl Menger e gli Eléments d'économie (1874-1877) di Léon Walras, dei quali ben presto si percepisce la coincidenza di temi, metodologia e approccio. Si sviluppano la teoria del comportamento dei vari agenti microeconomici e quella dell'equilibrio generale, che dominerà a lungo gli studi economici. Con il marginalismo, la matematica entra definitivamente a far parte dell'analisi economica e nasce l'economia matematica.
Rispetto agli economisti classici, i marginalisti assegnano al tema dello sviluppo un ruolo di secondo piano e concentrano tutta la loro attenzione sul problema dell'allocazione delle risorse; la ricerca delle condizioni che portano alla migliore ripartizione di risorse date diventa il problema centrale. Da qui la 'naturalezza' con cui la matematica diviene una normale presenza tra gli strumenti di ogni economista. Viene inaugurata la strada che porterà a considerare ogni problema economico come un problema di ottimo vincolato, con una funzione da massimizzare sotto vincoli. La centralità dell'allocazione ottimale indica l'adesione all'approccio utilitarista, alla tesi dell'astoricità delle leggi economiche e a una visione individuale: escono di scena le classi sociali, sostituite da aggregati minimi quali il consumatore e il produttore. Il valore diventa individuale e soggettivo: un oggetto ha valore nella misura in cui è desiderato da un soggetto.
La matematica diviene elemento dell'analisi economica attraverso le funzioni da massimizzare o minimizzare (la funzione di utilità, quella dei costi ecc.) ma, ancor prima, con la scelta di considerare argomenti centrali della ricerca lo studio di un sistema in equilibrio e l'individuazione dell'interdipendenza di tutte le variabili. In questo senso, Walras è il più lucido esponente della scuola marginalista; per Joseph A. Schumpeter (1883-1950) è addirittura il più grande economista di tutti i tempi.
Léon Walras (1834-1910) nasce in Normandia; anche suo padre Auguste era un economista, autore, tra l'altro, di una Théorie de la richesse sociale (1849). Léon si laurea in ingegneria a Parigi e, nel 1870, viene chiamato alla cattedra di economia politica della Facoltà di diritto dell'Università di Losanna, dove insegna fino all'inizio degli anni Novanta. La teoria di Walras va sotto il nome di 'equilibrio economico generale' perché si riferisce all'equilibrio dell'intero sistema economico, concepito come un sistema di quattro mercati interdipendenti: quello dei beni di consumo, con le equazioni dello scambio; quello dei servizi produttivi, con le equazioni della produzione; quello dei beni capitali, con le equazioni della capitalizzazione; infine, il mercato della moneta con le equazioni della circolazione. In questo, come nelle precedenti uguaglianze, i dati sono rappresentati dalle quantità iniziali delle risorse produttive, dalla tecnica produttiva e dai gusti dei consumatori (espressi con una funzione individuale di utilità). Le incognite sono i prezzi e le quantità dei beni prodotti e scambiati. Walras riesce a impostare un sistema di tante equazioni quante sono le incognite, deducendone l'esistenza e l'unicità dell'equilibrio. Si dimostra matematicamente che il sistema ammette una posizione d'equilibrio che assicura la massimizzazione delle singole utilità. In un'economia di puro scambio, la soluzione analitica del sistema è accompagnata poi dall'indicazione dei prezzi, raggiunti per approssimazioni successive, e coincide con questa soluzione, cui si perviene nel mercato con le fluttuazioni dei prezzi.
Quella di Walras è una costruzione grandiosa e di grande eleganza, in cui la matematica ha un ruolo strategico. Qualcuno pensa che sia "addirittura più dannoso che utile, presentare in forma matematica una dottrina che può sembrare per sé stessa abbastanza semplice e chiara", afferma Walras, aggiungendo: "In economia politica si danno e si ricevono tutti i giorni precise dimostrazioni che sono altro che affermazioni gratuite", ma "affermare una teoria è una cosa; dimostrarla è un'altra" (1974, p. 570). Da un punto di vista tecnico, la matematica usata si riduce all'algebra dei sistemi di equazioni lineari e ai primi elementi del calcolo differenziale. Molte ipotesi sono introdotte ad hoc: per il consumatore l'utilità è una realtà misurabile e, in particolare, una funzione additiva (l'utilità di un paniere di beni è uguale alla somma delle utilità procurate dai singoli beni del paniere); l'esistenza e l'unicità della soluzione sono garantite dal numero delle equazioni pari a quello delle incognite. Nonostante la necessità di opportuni raffinamenti, apportati nel corso del XIX sec., il successo arride al nuovo paradigma quasi immediatamente; tale successo tuttavia non coinvolge la prima generazione di marginalisti né tantomeno Walras, la cui teoria va incontro a serie difficoltà nell'ambiente francese. La rivoluzione marginalista ‒ se fu davvero una rivoluzione ‒ si afferma decisamente negli ultimi quindici anni del secolo.
In Inghilterra ne sono protagonisti Francis Y. Edgeworth (1845-1926) e Alfred Marshall (1842-1924). Il primo, convinto sostenitore dell'analogia con la meccanica e del parallelismo tra lo studio dei fenomeni fisici e di quelli socioeconomici, introduce un livello di argomentazioni analitiche più raffinate con l'abbandono, per esempio, della 'comoda' ipotesi di additività della funzione di utilità. Edgeworth può essere anche considerato un 'precursore' dell'econometria e della teoria dei giochi, con la teoria della contrattazione negoziale, il superamento di una necessaria unicità dell'equilibrio, la curva dei contratti, gli spunti per la teoria del core. Marshall, invece, fa un uso più moderato del formalismo matematico; infatti, il suo interlocutore privilegiato è quello che oggi si direbbe l'uomo d'azienda e la sua analisi è tesa a capire il funzionamento puntuale ed effettivo dei singoli ingranaggi del sistema. Da qui, la scelta di privilegiare la teoria degli equilibri parziali; manca perciò il grande affresco, ma l'indagine è penetrante e originale. I suoi Principles of economics (1920) godono di grande diffusione in Inghilterra e ancora oggi continuano a essere il testo di riferimento per l'insegnamento della microeconomia. Alle figure di Edgeworth e Marshall in Inghilterra si affianca negli Stati Uniti quella di Irving Fisher (1867-1947), autore di The rate of interest (1907), con la celebre teoria della determinazione dei tassi di interesse, e del successivo The purchasing power of money (1911), con l'altrettanto noto contributo alla teoria monetaria. Fisher è un grande divulgatore della teoria dell'equilibrio economico generale di Walras e Jevons e si distingue per il convinto sostegno alla tesi dell'analogia con la fisica e, in particolare, con la termodinamica, oltre che per l'estensione della stessa teoria al problema dell'allocazione intertemporale.
Il vero continuatore dell'opera di Walras è però Vilfredo Pareto (1848-1923), che nel 1892 diventa suo successore all'Università di Losanna. Ingegnere di formazione, acceso sostenitore delle tesi liberiste, Pareto comincia a occuparsi dei problemi dell'economia 'pura' alla fine degli anni Ottanta del XIX secolo. Le sue opere principali sono il Cours d'économie politique (1896), scritto con uno stile diretto e appassionato ‒ a volte quasi al limite della provocazione ‒, e il Manuale di economia politica (1906, tradotto in francese nel 1909), che si segnala per l'abbandono dell'ipotesi della misurabilità dell'utilità, in favore di una valutazione soltanto ordinale delle preferenze del consumatore. Dopo il Manuale, Pareto abbandona definitivamente gli studi economici per dedicarsi alla sociologia, prima di essere nominato senatore nel 1923 dal regime fascista.
Il confronto con Walras mette in evidenza una minore originalità dell'economista italiano. A Pareto, tuttavia, si deve una preziosa opera di approfondimento e di chiarificazione della teoria dell'equilibrio economico e di diffusione anche al di fuori del ristretto ambito degli studiosi di economia. Nel corso degli anni egli diventa un vero e proprio caposcuola, al quale fanno riferimento Pasquale Boninsegni, Umberto Ricci, Enrico Barone, Alfonso de Pietri-Tonelli e Luigi Amoroso, il quale si incaricherà di rappresentare 'ufficialmente', nei decenni successivi, la scuola paretiana. Questi economisti "tra il 1885 e il 1900, diedero sulle colonne del "Giornale degli Economisti" contributi così alti alla teoria pura economica da far rivaleggiare il tempo che fu detto della scuola di Losanna", scriveva Luigi Einaudi e, secondo Schumpeter, nel 1914 la scuola italiana non era seconda ad alcuno.
La matematica utilizzata da Pareto nei suoi studi economici è semplice: si tratta in sostanza dei primi elementi del calcolo differenziale, che sono spesso confinati in nota oppure nell'Appendice.
Nondimeno, l'uso della matematica è al centro di vivaci discussioni e di un'indubbia svolta metodologica, con dirette conseguenze anche sul piano sociopolitico. Pareto ne difende l'uso con grande vigore; di fronte alle critiche di matrice socialista, che avanzano seri dubbi sulla fondatezza dell'intero edificio dell'economia politica, sceglie di isolarne un nucleo teorico limitato ma inattaccabile nella sua 'naturalezza': l'homo oeconomicus e la massimizzazione dell'utilità quale unico criterio per spiegarne il comportamento. L'analogia è con la meccanica: come questa inizia il suo discorso con 'l'ente astratto che chiama punto materiale' così l'economia matematica prende le mosse dall'astrazione dell'homo oeconomicus. Il Cours inizia dichiarando che la scienza di cui intraprendiamo lo studio è una scienza naturale come la psicologia, la fisiologia, la chimica. L'economia si caratterizza dunque come una disciplina che studia un campo molto limitato e condivisibile (l'homo oeconomicus e la sua tendenza a massimizzare la propria utilità) e, come ogni scienza, ha uno status avalutativo. "Io studio la società dal di fuori, come un uomo può studiare l'automobilismo senza mai andare in automobile", scrive Pareto. Sono chiare le ragioni del successo del modello paretiano e dell'essenzialità della matematica nel renderne inattaccabili le conclusioni; chi non crede alle sue 'dimostrazioni' è Benedetto Croce, con il quale Pareto ha una pubblica discussione all'inizio del nuovo secolo. Un matematico come Émile Borel (1871-1956) avanza anch'egli alcune riserve sul compito affidato alla matematica di dissipare ogni dubbio nelle scienze sociali. A differenza di Walras, però, Pareto è in generale riconosciuto e apprezzato dalla comunità matematica, come mostra una recensione di Vito Volterra (1860-1940) del Manuale, che si sofferma sulla novità dell'approccio. Con l'opera di Pareto si conclude la prima stagione dell'economia matematica, che si colloca tutta all'interno della 'rivoluzione' marginalista e della teoria dell'equilibrio economico generale, costruita sul modello della fisica e della meccanica.
Gli anni del primo dopoguerra
Gli anni Venti e Trenta del XIX sec. presentano una situazione diversa. La fisica è cambiata dopo la teoria della relatività e la meccanica quantistica e anche la matematica si è trasformata. Gli 'oggetti' sui quali essa riflette non vengono più considerati in base alla loro natura e al loro 'contenuto' bensì in funzione delle relazioni che li collegano, ovvero delle strutture presenti nell''ambiente' che li ospita. Si elaborano schemi formali, tanto più apprezzati quanto più si prestano a essere impiegati in svariate situazioni. L'astrazione si afferma come il modo più 'economico' e unificante di cogliere la realtà.
Di conseguenza, cambiano radicalmente anche i rapporti tra contenuti interpretativi e sviluppi formali all'interno degli studi economico-matematici. Ben presto il termine modello matematico indicherà una situazione quasi rovesciata: non più il problema economico e poi la soluzione analitica (spesso in nota). Considerazioni economiche e sviluppo formale acquistano la stessa dignità e sempre più spesso i lavori di economia matematica sono articoli matematici nei quali al contenuto economico sono riservati introduzione e conclusioni.
A partire dagli anni Trenta si diffondono i modelli macroeconomici di derivazione keynesiana, che studiano questioni di equilibrio dinamico prendendo in considerazione grandezze macroeconomiche. Il modello di Roy F. Harrod ed Evsey D. Domar si sviluppa proprio negli anni della Seconda guerra mondiale. Compie i primi passi l'econometria: utilizzando anche gli strumenti del calcolo delle probabilità si tratta di risalire alle forme funzionali che esprimono la dipendenza di determinate grandezze economiche, a partire dai dati statistici disponibili, in modo da poter formulare previsioni con una certa approssimazione. La Società econometrica internazionale viene costituita all'inizio degli anni Trenta e, negli stessi anni, si sviluppa negli Stati Uniti l'analisi input output di Wassily Leontief (1906-1999; premio Nobel nel 1973) che intende rendere operativa la lezione walrasiana.
In Italia, negli anni del fascismo, per l'economia matematica ritornano le vecchie accuse di illecita intromissione della matematica nello studio dei fenomeni morali e della realtà economica. Il regime chiede che la disciplina si adegui ai nuovi dettami ideologici introducendo un homo corporativus del tutto distinto da quello oeconomicus. I contributi più originali vengono da Bruno de Finetti (1906-1985), un matematico noto soprattutto per le sue concezioni nel campo della probabilità. I suoi lavori esprimono una critica radicale al sistema liberista e al modello paretiano che ne è il fondamento teorico: non si tratta di attenuare l'astrattezza e la generalità degli studi economico-matematici ma, al contrario, di rafforzare l'impostazione matematica, con una separazione ancora più netta tra la teoria che ‒ sola ‒ può permettere il passaggio 'dal plurale al generale' e i fatti economici. L'originalità metodologica di de Finetti trova un riscontro anche sul terreno più 'tecnico'; le sue note di economia matematica contengono precise osservazioni sul concetto di ottimo paretiano e si inseriscono in quell'economia del benessere che richiama il nome di Arthur C. Pigou (1877-1959) e che approderà ai due teoremi fondamentali di Kenneth Arrow e Gérard Debreu del 1951. In particolare, nel caso vettoriale de Finetti anticipa per certi aspetti le condizioni oggi note come teorema di Kuhn-Tucker, che nel 1951 inaugura la programmazione non lineare.
Negli anni Trenta le sedi in cui la teoria dell'equilibrio economico generale viene approfondita e sviluppata sono soprattutto Londra e Vienna. Alla London School of Economics opera il gruppo di Lionel Robbins (1898-1984), rappresentato da personalità scientifiche come Friedrich August von Hayek (1899-1992) e John Hicks (1904-1989). Al centro della riflessione di Hayek c'è la volontà di conservare la centralità del concetto di equilibrio generale, aprendolo però all'analisi delle fluttuazioni cicliche. Gli eventi di quegli anni enfatizzano l'instabilità del sistema economico, sottolineando tra i vari fattori di instabilità il ruolo svolto dalla moneta. L'accenno alle fluttuazioni cicliche fa comprendere come la ricerca di Hayek sia orientata verso una generalizzazione dinamica del modello walrasiano-paretiano. In questo contesto appare fondamentale il ruolo delle aspettative; si può pensare a un sistema in equilibrio solamente quando gli agenti economici possono realizzare previsioni corrette sulla sua evoluzione. Hicks ‒ premio Nobel per l'economia (1972) come Hayek (1974) ‒ ha più volte ricordato i suoi debiti intellettuali nei confronti di Hayek e dei suoi seminari. Il suo Value and capital (1935) ha rappresentato uno dei veicoli più potenti della diffusione della teoria di Walras e Pareto nella comunità accademica degli economisti. Hicks studia l'equilibrio temporaneo raggiunto dal sistema economico in un determinato periodo, esaminando in particolare la sua stabilità e la tendenza a tornare alla configurazione di equilibrio quando ne sia stato allontanato per una ragione qualsiasi. Il movimento del sistema economico nel tempo è concepito come una successione di equilibri temporanei, diversi l'uno dall'altro e differenti anche dalle aspettative dei vari agenti economici.
Ancora più importante per l'evoluzione dei rapporti tra matematica e analisi economica è Vienna, all'epoca sede del celebre Circolo di Vienna, animato da personalità come Otto Neurath (autore del manifesto del neopositivismo logico), Moritz Schlick, Rudolf Carnap e Karl Menger (figlio di Carl appartenente alla prima generazione di marginalisti). Menger organizza il Mathematisches Colloquium dove si discute anche di economia matematica, al quale invita Karl Schlesinger, un banchiere con la passione degli studi e dell'economia 'pura', a tenere un seminario sull'equilibrio walrasiano. Schlesinger segnala ad Abraham Wald (1902-1950) il problema dell'esistenza di soluzioni non negative all'interno della teoria dell'equilibrio economico generale e lo aiuta ‒ anche economicamente ‒ nella fase iniziale delle sue ricerche, i i cui primi risultati furono pubblicati verso la metà degli anni Trenta. Al momento dell'Anschluss Menger è emigrato negli Stati Uniti da qualche mese; Schlesinger si uccide il giorno stesso dell'arrivo delle truppe naziste a Vienna; Wald, ebreo, riesce qualche mese dopo a raggiungere gli Stati Uniti; in tal modo, il Circolo di Vienna viene disperso e il Mathematisches Colloquium interrotto.
I contributi di Wald e von Neumann
Nei suoi scritti sull'equilibrio generale, Wald considera di fatto il modello propostogli da Schlesinger. Il vettore y=(y1,…,yn) indica il bene prodotto, mentre il vettore dato x=(x1,…,xn) indica le quantità disponibili dei servizi produttivi. Ogni bene finale è ottenuto con un unico processo produttivo, con rendimenti costanti di scala. Si ha allora, in particolare, la matrice input-output A di tipo (n,n) e la relazione:
[1] x=Ay+u
che lega le quantità disponibili dei servizi produttivi e quelle impiegate nella produzione (data la tecnologia a coefficienti costanti, individuata dalla matrice A). Il vettore u è a componenti non negative; in particolare è ui>0 per i beni liberi e ui=0 per quelli non liberi, completamente utilizzati nella produzione. In accordo con il principio della libera concorrenza, in condizioni di equilibrio prezzi e costi di produzione devono coincidere per tutti i prodotti:
[2] p=wA,
dove p e w sono i vettori dei prezzi, rispettivamente, dei prodotti finali e degli input. In particolare, è nullo il prezzo dei beni liberi:
[3] uiwi=0 i=(1,…,m).
Infine, il prezzo p di ogni bene è funzione della quantità domandata (ovvero prodotta, in condizioni di equilibrio) di quel bene:
[4] p=f(y),
dove f=(f1,…,fn) è quella che oggi si chiama funzione di domanda inversa. Le condizioni [1] … [4] rappresentano il modello studiato da Wald, il quale, in realtà, analizza due modelli leggermente diversi, con ipotesi differenti sulla funzione f. Nel primo introduce una condizione di convessità e di non saturazione, che in parte poi modifica richiedendo che, per un incremento Δy=(Δy1,…,Δyn) con almeno una componente negativa, la condizione pΔy≤0 implichi p′Δy⟨0, essendo p′=f(y+Δy), che oggi va sotto il nome di assioma delle preferenze rivelate.
Nei lavori di Wald compaiono per la prima volta nella teoria dell'equilibrio molti degli strumenti formali più usati dall'economia matematica del Novecento ossia, oltre all'assioma delle preferenze rivelate, le condizioni di complementarità e l'ipotesi di convessità. L'altra 'modernità' riguarda l'esigenza di discutere esplicitamente i problemi di esistenza e unicità, che Wald effettivamente risolve in entrambe le sue versioni del modello di equilibrio.
La stessa 'modernità' si trova nei lavori di John von Neumann (1903-1957), uno dei più grandi matematici del XX secolo. Nato a Budapest, nel 1926, dopo la laurea in ingegneria a Zurigo e un dottorato in matematica a Budapest, von Neumann si trasferisce a Berlino come Privatdozent. Grazie a una borsa di studio della Rockefeller Foundation studia con David Hilbert a Gottinga, prima di trasferirsi nel 1930 negli Stati Uniti, dove svolgerà tutta la sua carriera presso l'Institute for Advanced Study di Princeton.
Prima dei suoi contributi all'equilibrio generale, von Neumann pubblica nel 1928 l'articolo Zur Theorie der Gesellschaftsspiele (Per la teoria dei giochi di società), che può essere considerato uno dei passi fondamentali verso la costruzione della teoria dei giochi, dopo le anticipazioni di Cournot e di Edgeworth, un lavoro di Ernst Zermelo del 1913 sul gioco degli scacchi e un quasi contemporaneo intervento di Borel. L'applicazione della matematica all'economia, nata all'interno del marginalismo e a lungo identificatasi con la teoria dell'equilibrio e le sue generalizzazioni, comincia ad alimentare nuovi fronti, che acquistano via via una loro autonomia disciplinare. Nel modello walrasiano-paretiano ogni agente ottimizza i propri obiettivi incurante delle decisioni prese dagli altri agenti; il numero degli attori presenti sulla scena economica è talmente elevato che è ragionevole pensare che non si possano prendere in considerazione le scelte di tutti gli agenti, con le loro conseguenze. Von Neumann studia invece un piccolo sottoinsieme del sistema sociale, dove ciascuno è a conoscenza delle mosse degli altri e dove quindi ogni giocatore tenta di ottimizzare i propri obiettivi anche in funzione delle scelte degli altri giocatori.
Il lavoro del 1928 comincia con la definizione, rigorosa e assiomatica, di strategia e di forma normale di un gioco. Von Neumann studia il comportamento ottimale di due giocatori in un gioco a somma zero, dove ciò che guadagna un giocatore è quello che perde l'altro. Nella matrice A del gioco gli elementi della i-esima riga indicano i valori dei guadagni del primo giocatore, usando la i-esima strategia (in corrispondenza con ogni strategia dell'avversario); gli elementi della j-esima colonna rappresentano analogamente le perdite del secondo giocatore quando ricorre alla j-esima strategia. Nella peggiore delle situazioni, il primo giocatore calcola il minimo in ogni riga e fissa quindi la quantità maximinjaij; analogamente, il secondo giocatore fissa la sua attenzione sul valore minjmaxiaij. Il comportamento razionale dei giocatori porta a dire che la quantità v vinta dal primo giocatore ‒ quindi persa dal secondo ‒ soddisfa le disuguaglianze:
[5] maximinjaij≤v≤minjmaxiaij.
Nel caso in cui le disuguaglianze non diventino uguaglianze ‒ e quindi l'equilibrio non sia raggiunto ‒ von Newmann introduce il concetto di strategia mista, come distribuzione di probabilità nell'insieme delle strategie pure, e valuta il gioco attraverso un valore atteso. La sua soluzione è ricondotta alla ricerca di un punto di sella di una forma bilineare; qui dà, per la prima volta, la definizione di quasi-convessità ‒ solitamente attribuita a de Finetti e a Werner Fenchel ‒ e generalizza il teorema di punto fisso di Brouwer per le funzioni. Von Neumann riesce così a dimostrare il teorema di minimax, provando l'esistenza di soluzioni per ogni gioco finito (in cui i giocatori hanno un numero finito di opzioni possibili) fra due persone, a somma zero. È questa la base essenziale per le successive generalizzazioni (il caso di n giocatori) con il concetto di coalizione.
La data ufficiale della nascita della teoria dei giochi è comunque il 1944, quando viene pubblicato il volume Theory of games and economic behaviour di von Neumann e Oskar Morgenstern (1902-1977). Professore di economia all'Università di Vienna, Morgenstern aveva dovuto lasciare la capitale austriaca all'arrivo dei nazisti. Amico di Menger, era stato uno degli animatori del Mathematisches Colloquium, interessato in particolare alle ricerche di Wald. Morgenstern si proponeva di dare una veste assiomatica ai principî dell'economia, in polemica con l'impianto walrasiano che riteneva superato, sia per il livello di rigore sia per la modesta strumentazione analitica che vi veniva impiegata. Dall'incontro con von Neumann a Princeton nasce il progetto di una monografia, finalizzata alla descrizione dei fenomeni economici attraverso la teoria dei giochi. In tale monografia c'è in nuce tutto lo sviluppo che questa teoria ha conosciuto nella seconda metà del secolo: la presentazione dei nuovi strumenti matematici forniti dall'analisi convessa; una nuova dimostrazione del teorema di minimax, senza più fare riferimento ai teoremi di punto fisso; le basi per il passaggio ai giochi a somma diversa da zero e, infine, i motivi che ispireranno John F. Nash nel lavoro del 1950, in cui generalizza l'equilibrio di von Neumann e Morgenstern al caso di un gioco a n partecipanti, favorendo così un maggior impiego della teoria nello studio delle problematiche economiche.
Prima del volume scritto nel 1944 con Morgenstern, nel 1937 von Neumann pubblica l'articolo Über ein Ökonomisches Gleichungssystem und eine Verallgemeinerung des Brouwer'schen Fixpunktsatzes (Un sistema di equazioni e una generalizzazione del teorema del punto fisso brouweriano), in cui per la prima volta il problema dell'equilibrio viene affrontato con le tecniche di punto fisso. Se il termine di paragone più vicino nel tempo è costituito dai lavori di Wald, le differenze sono però molte, sia per gli strumenti usati sia per il punto di vista generale, che registra un deciso allontanamento dal quadro classico della teoria dell'equilibrio di Walras e Pareto, sostanzialmente conservato anche nelle successive generalizzazioni.
Il modello di crescita bilanciata analizzato da von Neumann differisce da quello walrasiano perché non considera il sistema economico in un determinato istante ma ne studia l'evoluzione lungo una successione di periodi. Viene poi a cadere la distinzione tra fattori produttivi e beni finali; il processo di produzione è circolare: i fattori produttivi impiegati in un periodo sono i beni prodotti in quello precedente. Il modello considera in particolare n beni e m processi produttivi (con rendimenti costanti di scala). L'economia è allora descritta da due matrici A e B di tipo (n,m), dove aij indica la quantità dell'i-esimo input necessario (unitariamente) per la j-esima tecnologia e, analogamente, bij indica l'output del bene i-esimo prodotto dalla j-esima tecnologia. Le condizioni di equilibrio derivano dall'osservazione che la quantità di un bene impiegata nella produzione in un periodo non può superare la quantità dello stesso bene resa disponibile nel periodo precedente, con la precisazione che, se è minore, il prezzo del bene è zero; analogamente, per ciascun processo produttivo, il ricavo non può superare il costo con le precisazioni che, se è minore, il processo produttivo è esercitato a livello nullo e che costi e ricavi ‒ riferendosi a periodi diversi ‒ vanno resi confrontabili, scontando i ricavi. Nell'ipotesi che il sistema economico si sviluppi a crescita bilanciata e che quindi i suoi vari livelli abbiano uno stesso saggio di espansione, von Neumann ottiene il sistema:
nelle incognite x (intensità dei processi produttivi), p (prezzo dei beni), α e β, rispettivamente saggio di crescita e saggio di profitto. L'esistenza del punto di equilibrio per il modello viene dimostrata riducendo la questione a un problema di minimax e questo, a sua volta, a un problema di punto fisso. Viene anche provato che, in equilibrio, saggio di crescita e saggio d'interesse coincidono.
Il modello di von Neumann ha esercitato una larga influenza sugli studi economico-matematici della seconda metà del secolo. Secondo E. Roy Weintraub è in assoluto il più importante lavoro mai apparso in questa disciplina, in quanto costituisce la genesi delle moderne dimostrazioni di esistenza nei modelli di equilibrio generale, della programmazione lineare, del teorema dell'autostrada e della teoria del punto fisso. Il modello di von Neumann ‒ come modello di produzione circolare ‒ si ritrova in Leontief, apre la via ai modelli multisettoriali e alle teorie normative della crescita degli anni Cinquanta-Sessanta e costituisce la premessa degli sviluppi dell'analisi delle attività e dei metodi della programmazione lineare.
Negli anni Trenta, dunque, cambiano molte prospettive negli studi economici e l'economia matematica non significa più soltanto equilibrio generale. Sono gli anni della grande teoria, in cui si impostano molti dei problemi al centro delle analisi dei decenni successivi.
La programmazione lineare
Il protagonista sovietico della programmazione lineare è Leonid Vital′evič Kantorovič (1912-1986), professore all'Università di Leningrado. Nella primavera del 1936 Kantorovič viene contattato per una consulenza da un'azienda che produceva legno compensato e voleva aumentare il livello di produzione di differenti tipi di compensato, realizzati in otto impianti dotati di diversa capacità produttiva. Kantorovič si rende conto che la questione ha una struttura matematica che la accomuna ad altre situazioni, apparentemente diverse all'interno del terzo piano quinquennale. Kantorovič dimostrerà l'esistenza delle variabili duali associate a ciascun vincolo ‒ chiamate moltiplicatori risolventi ‒ individuando un algoritmo risolutivo che verrà dimostrato equivalente a quello di George Bernard Dantzig.
La diffusione delle idee di Kantorovič è particolarmente lenta; come avvenuto con il fascismo, anche in Unione Sovietica in economia egli viene osteggiato. Stalin aveva classificato l'economia matematica come un semplice gioco con i numeri; la pianificazione e l'organizzazione ottimale delle forze produttive non erano considerate problemi di economia politica, bensì di politica economica. La situazione inizierà a modificarsi negli anni Cinquanta. Nel 1958 Kantorovič viene eletto membro dell'Accademia delle Scienze (che gli conferirà il premio Lenin nel 1965). A Mosca viene fondato il Laboratorio matematico-economico dell'Accademia delle Scienze e nel 1960 si terrà il primo convegno sull'impiego dei metodi matematici in economia e nella pianificazione.
Il 'padre' della programmazione lineare in Occidente è Dantzig che, durante la guerra, lavora al Pentagono come esperto di metodi di programmazione. Il suo metodo del simplesso risale all'estate 1947 e nell'autunno egli lo presenta a von Neumann, venendo così introdotto alla teoria della dualità e alla problematica dei rapporti con la teoria dei giochi. Il metodo è reso pubblico a Chicago nel 1949 nel corso di un convegno organizzato da Tjalling C. Koopmans (premio Nobel per l'economia nel 1975, insieme a Kantorovič). Nell'introduzione agli atti del convegno Koopmans ricorda le quattro distinte linee di ricerca che hanno portato alla nascita della programmazione lineare: le generalizzazioni intervenute in tema di equilibrio economico generale; la nuova economia del benessere; lo studio delle interdipendenze sollecitato dal modello di Leontief; lo specifico lavoro di Dantzig, motivato da questioni legate all'organizzazione della difesa e all'allocazione di risorse belliche.
Si torna dunque negli Stati Uniti, secondo un percorso legittimato dagli sviluppi dell'economia matematica statunitense della seconda metà del secolo scorso, fino alla loro supremazia, debitrice in misura determinante alla diaspora degli economisti europei negli anni Trenta. Lo stesso Koopmans era nato nei Paesi Bassi e aveva compiuto i suoi studi nelle Università di Utrecht e di Leida. Nel secondo dopoguerra si assiste negli Stati Uniti a una ripresa di interesse per l'approccio walrasiano e per la problematica dell'equilibrio generale. Nel 1947 vengono pubblicate le Foundations of economic analysis di Paul A. Samuelson, il quale nel 1938 aveva introdotto l'assioma debole delle preferenze rivelate e sosteneva che tutti i problemi dell'economia possono essere ricondotti a problemi di ottimizzazione vincolata. Gli sviluppi più importanti sulle questioni dell'esistenza, dell'unicità e della stabilità dell'equilibrio ebbero luogo, negli anni immediatamente successivi, ancora negli Stati Uniti.