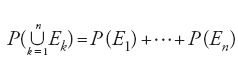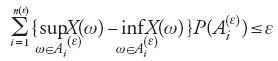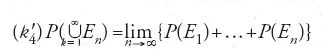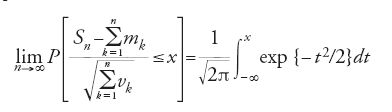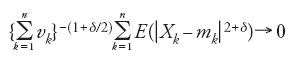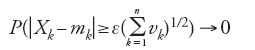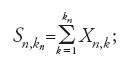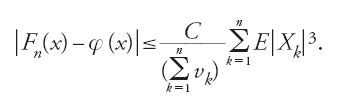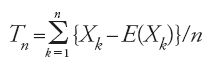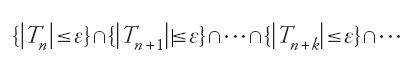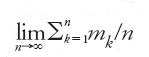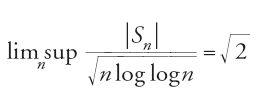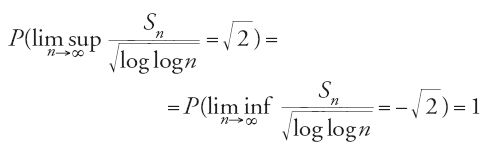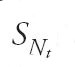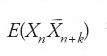La seconda rivoluzione scientifica: matematica e logica. La probabilità

La seconda rivoluzione scientifica: matematica e logica. La probabilita

La probabilità

Evoluzione della nozione di probabilità

La grande difficoltà in cui si dibattevano i cultori della probabilità dell'inizio secolo si può riassumere nel problema di formulare una definizione che, ispirandosi a una interpretazione ragionevole della probabilità, potesse altresì costituire il punto di partenza per la costruzione della corrispondente teoria matematica. Prima del 1930 la situazione non registra progressi significativi e Harald Cramér (1893-1985) ci ricorda che il perdurare di un sostanziale disordine in un'epoca in cui, invece, le branche classiche della matematica potevano ormai vantare fondamenti solidi, ingenerava sospetti e conseguente disinteresse della comunità scientifica verso gli studi probabilistici. Nell'intento di avviare a soluzione il problema di definire la probabilità, a partire dalla fine degli anni Venti alcuni studiosi proposero di affrontarlo in termini diversi da come era stato tramandato dalla tradizione plurisecolare. Più precisamente, ci si pose l'obiettivo della formulazione di un sistema di assiomi che, eventualmente prescindendo da qualunque significato sostanziale della probabilità, consentisse di accreditare il calcolo delle probabilità (CdP) come disciplina matematica a tutti gli effetti. Era indispensabile disporre di un quadro di riferimento sicuro, allo scopo di ordinare i risultati noti e di far fronte alle esigenze dello sviluppo, ormai in atto, della disciplina. L'atteggiamento assiomatico appariva come il più adatto per far raggiungere efficacemente gli obiettivi testé ricordati, anche se rischiava di lasciare completamente in ombra la questione fondamentale del valore della probabilità e dell'estensione del suo dominio di applicazione.

La concezione soggettiva di de Finetti

L'impostazione che Bruno de Finetti (1906-1985) ideò e perfezionò tra la fine degli anni Venti e l'inizio degli anni Trenta costituisce il primo tentativo riuscito di far discendere l'intera teoria matematica della probabilità da una interpretazione del suo significato concreto (de Finetti 1931a, 1931b). Tale impostazione è formulata assiomaticamente ma, a differenza di quella di Andrej Nikolaevič Kolmogorov (1903-1987), in cui i postulati riguardano direttamente la manipolazione aritmetica della probabilità, il sistema proposto da de Finetti si ricollega alla natura 'soggettiva' della stessa. Per un soggettivista, la probabilità di un evento esiste in relazione a un soggetto che la valuta; pertanto, essa è un indice numerico del grado di fiducia che quel soggetto ripone nel verificarsi dell'evento considerato. Il primo compito elementare della teoria delle probabilità è quello di fissare le condizioni minime a cui deve ubbidire una funzione a valori reali, definita su una data classe di eventi E, per poter essere considerata valutazione di probabilità su E. Quindi, per risolvere la questione, de Finetti fissò un unico postulato, noto come 'principio di coerenza', in base al quale tutte le funzioni P:E→ℝ, che non conducono a conseguenze negative secondo il giudizio di un individuo 'normale', possono riguardarsi come valutazioni di probabilità su E. Si tratta di precisare che cosa si debba intendere, nel contesto testé descritto, per conseguenze negative, secondo il giudizio di un individuo normale, di un'assegnazione di probabilità. Seguendo de Finetti, tratteremo subito del caso più generale della 'previsione' su una classe di numeri aleatori; successivamente, ritorneremo a quello della probabilità sulla base della corrispondenza tra eventi e loro indicatori.

Sia χ una classe di numeri aleatori limitati (si dice limitato un numero aleatorio per il quale si può determinare una coppia di numeri reali entro i quali variano tutte le sue realizzazioni possibili), tutti definiti sullo stesso spazio Ω di casi elementari. Valutare la previsione di un dato elemento di χ, da parte di un certo individuo, significa assegnare un numero che riassuma il grado di fiducia riposto da quell'individuo nel verificarsi dei diversi valori possibili del numero aleatorio preso in esame. Quando quest'ultimo è l'indicatore di un evento E (ossia il numero aleatorio che assume il valore uno in corrispondenza agli eventi elementari che implicano E e il valore zero in corrispondenza a tutti gli altri) allora la sua previsione è semplicemente la probabilità di E. Ancora una volta, compito della teoria delle probabilità è l'individuazione di tutte le funzioni ℙ:χ→ℝ che possono rappresentare una previsione su χ. Supponiamo che X₁,…,X_n siano elementi di χ e λ₁,…,λ_n elementi di ℝ, scelti in modo completamente arbitrario. Se risulta verificata la disuguaglianza:

[1]  λ₁X₁+...+λ_nX_n≥c

per ogni caso elementare in Ω e per un conveniente reale c, sembra ragionevole ritenere che la stessa disuguaglianza continui a essere soddisfatta dopo aver sostituito ciascun X_k con il valore della sua previsione:

[2] λ₁ℙ(X₁)+…+λ_nℙ(X_n)≥c.

Seguendo de Finetti, non sembra necessario imporre altre restrizioni a ℙ, oltre a quella menzionata che viene detta 'di coerenza'; quindi, ogni funzione ℙ:χ→ℝ tale che [1] implichi [2] è detta previsione su χ.

In un lavoro dedicato alla discussione delle principali impostazioni assiomatiche della probabilità, de Finetti dimostrò che, per ogni classe χ di numeri aleatori limitati, esiste almeno una previsione; ciò prova che la precedente definizione non perde mai di significato (de Finetti 1949).

Consideriamo ora una classe di eventi E (classe di sottoinsiemi di Ω) e l'insieme A(E) degli indicatori, A(E)={I_E:E∈E}, e denominiamo ogni previsione su A(E) 'probabilità' su E. Scriveremo P(E), in luogo di ℙ(I_E), per indicare la probabilità di E. Allora, si può facilmente verificare la validità delle seguenti proposizioni relativamente a ogni probabilità P:

(f₁) P(E)≥0 per ogni E in E;

(f₂) indicato con ∅ l'evento impossibile, se ∅ appartiene a ε si ha P(∅)=0; inoltre P(Ω)=1 se Ω è elemento di E;

(f₃) se E₁,…,E_n sono elementi di E a due a due incompatibili, e se la loro unione appartiene a E, allora

[3]  P(E₁ ⋃…⋃E_nP(E₁)+…+P(E_n).

Le condizioni (f₁)÷(f₃) sono dunque necessarie affinché P:E→ℝ possa considerarsi probabilità su E, coerente nel senso di de Finetti; esse sono anche sufficienti quando E è un''algebra', ovvero una classe di sottoinsiemi di Ω, chiusa rispetto alla negazione e all'unione di un numero finito qualunque di suoi elementi (un'algebra chiusa rispetto alle unioni numerabilmente infinite è detta 'σ-algebra'). Più precisamente: se E è un'algebra di sottoinsiemi di Ω, allora P:E→ℝ è una probabilità su E se e solo se:

(k₂) P(E)≥0 per ogni E in E;

(k₃) P(Ω)=1;

(k₄) per ogni E₁,…,E_n a due a due incompatibili in E, si ha

Nell'impostazione di cui stiamo trattando, i concetti di probabilità e di previsione sono introdotti in modo da ammettere una valutazione autonoma, purché compatibile con il principio di coerenza; difatti, tale principio è usualmente presentato mediante lo schema detto 'delle scommesse', che introduce un metodo di valutazione della probabilità e, più in generale, della previsione. Generalmente accade però che, assegnata una probabilità P su un'algebra E di sottoinsiemi di Ω, la valutazione della previsione di un generico numero aleatorio definito su Ω risulti più o meno strettamente condizionata dall'assegnazione di P; in taluni casi essa ne è univocamente determinata. Per esempio, se A₁,…,A_n è una partizione di Ω in E e X è il numero aleatorio (discreto con codominio finito) che assume il valore x_i su A_i (i=1,…,n), allora si dimostra che la previsione di X è univocamente determinata, risultando

[5] ℙ(X)=x₁P(A₁)+…+x_nP(A_n).

Più in generale, se X è un numero aleatorio limitato definito su Ω e tale che per ogni ε>0 esista una partizione finita di Ω in

,

per la quale

,

allora la previsione di X riesce univocamente determinata, risultando uguale all'integrale (del tipo di Riemann-Stieltjes) di X rispetto a P. In effetti, per il verificarsi di (i₁) basta conoscere la probabilità degli eventi A_x:={ω∈Ω:X(ω)≤x} ottenuti al variare di x in ℝ; la funzione F(x):=P(A_x), con x∈ℝ è nota come 'funzione di ripartizione' o di 'distribuzione' di X. Quindi, nota la funzione di ripartizione del numero aleatorio limitato X, la previsione di X è univocamente determinata, risultando

[7]  ℙ(X)=∫_ℝxdF(x).

In simili circostanze, conveniamo di denominare la previsione di X 'valore atteso' o 'speranza matematica' di X e di indicarla con il simbolo E(X).

Quelli che abbiamo brevemente ricordato possono riguardarsi come i passi elementari di base per la costruzione della teoria matematica della probabilità secondo de Finetti. I suoi tratti caratteristici possono essere sintetizzati nei punti seguenti: (a) la probabilità può essere definita su una classe qualunque di eventi, anche se non dotata di particolare struttura; (b) non si richiede alla probabilità di rispettare la condizione di additività per successioni infinite di eventi a due a due incompatibili ('additività completa'); (c) la nozione di previsione di un numero aleatorio prescinde da condizioni d'integrabilità del numero aleatorio stesso.

è doveroso riconoscere all'impostazione di de Finetti, chiarezza, semplicità e rigore concettuale, che la rendono particolarmente adatta per spiegare significativamente il ruolo degli assiomi generalmente accolti nelle trattazioni alterna tive e più diffuse del CdP.

L'impostazione assiomatica di Kolmogorov

Quando si parla d'impostazione assiomatica della probabilità, il pensiero dei più corre a quella di Kolmogorov (1933). Per la verità, un approccio del tutto simile era stato seguito in precedenza da Francesco Paolo Cantelli (1932), anche se con intendimenti diversi da quelli del matematico russo. Pur aderendo a concezioni frequentiste, i loro intenti furono dominati dall'esigenza di sviluppare il CdP come teoria puramente formale, a prescindere da ogni interpretazione concreta. Pertanto essi, e Kolmogorov in particolare, operarono in modo che il CdP apparisse come una derivazione naturale e legittima delle teorie della misura e dell'integrazione di Lebesgue, nell'indirizzo astratto di Fréchet. Kolmogorov apportò a tale indirizzo complementi tutt'altro che trascurabili, per consentirne l'aderenza più stretta alle esigenze di certi problemi probabilistici di primaria importanza; possiamo citare, a puro titolo semplificativo, il famoso teorema d'estensione. A partire dalle dichiarate pretese di chiarezza formale, Kolmogorov considera un insieme Ω di enti primitivi, deno minati 'casi elementari' e una classe E di sottoinsiemi di Ω, richiedendo che, oltre alle precedenti condizioni (k2)÷(k4):(k5)P(E_n) converga a zero al divergere di n, per ogni successione di eventi E_n appartenenti a E e decrescente verso l'evento impossibile.

La generica funzione P:E→ℝ, che soddisfi alle condizioni (k1)÷(k5), è detta 'misura di probabilità'. Quindi, sono probabilità secondo Kolmogorov soltanto quelle definite su algebre di eventi e che, oltre al requisito della coerenza definettiana, godono della proprietà di continuità (k5). Quest'ultima condizione, introdotta per ragioni di convenienza matematica, consente di legare la teoria delle probabilità alla più generale teoria della misura e dell'integrazione succitata. È noto che, valendo le (k1)÷(k3), le condizioni di additività finita e di continuità (k4) e (k5) equivalgono a quella di additività completa (detta anche di 'σ-additività'):

per ogni successione (E_n)_n≥1 di elementi di E, a due a due incompatibili e tali che

Supponiamo dunque che una certa misura di probabilità P sia assegnata su un'algebra E di sottoinsiemi di Ω. Un fondamentale teorema di Constantin Carathéodory (teorema d'estensione o di prolungamento) asserisce che esiste una e una sola misura di probabilità P* sulla σ-algebra più piccola fra tutte quelle che contengono E (la σ-algebra generata da E), tale che P*(E)=P(E) per ogni E appartenente a E. La già citata memoria del 1933 di Kolmogorov contiene interessanti applicazioni del precedente teorema; tra queste, la probabilizzazione della classe dei boreliani di ℝ (la σ-algebra generata dagli intervalli di ℝ) a partire da una data funzione di ripartizione. Al problema dell'estensione di una misura di probabilità, Kolmogorov ricondusse anche la questione della definizione della 'legge di probabilità' di un processo aleatorio: il celebre teorema di estensione che tanta parte avrebbe avuto nello sviluppo della teoria moderna dei processi aleatori.

Il teorema d'estensione di Carathéodory, relativo a una misura di probabilità definita su un'algebra di eventi, suggerisce l'introduzione della nozione di 'spazio di probabilità di Kolmogorov' (Ω‚ℋ,P), in cui Ω è lo spazio degli eventi elementari, ℋ una σ-algebra di sottoinsiemi di Ω (eventi) e P è una misura di probabilità su ℋ. Quindi, ogni elemento aleatorio viene definito come funzione 'misurabile' da Ω in un opportuno spazio garantendo, così, che la 'legge di probabilità' (altrimenti detta 'distribuzione di probabilità') di tale elemento risulti univocamente e completamente determinata dalla conoscenza di P su ℋ. La nozione di misurabilità richiede che sia definita una σ-algebra sullo spazio di arrivo dell'elemento aleatorio X preso in considerazione. Indicata tale σ-algebra con ℋ_X, allora X si dice misurabile se {ω:X(ω)∈B} appartiene a ℋ per ogni B scelto in ℋ_X. Pertanto, la distribuzione P_X dell'elemento X è determinata da

[8]  P_X(B)=P({ω : X(ω)∈B})  per ogni B∈ℋ.

Per quanto attiene alla nozione di previsione di un numero aleatorio, Kolmogorov non ne fornisce una definizione autonoma dalla distribuzione di probabilità del numero aleatorio in questione. Fermo restando il fatto che ogni numero aleatorio definito su (Ω‚ℋ,P) è da intendersi misurabile (con ℋ_X uguale alla σ-algebra dei boreliani di ℝ), si stabilisce facilmente che la previsione di ciascuno di tali numeri che sia anche limitato è univocamente determinata come integrale di X rispetto a P_X (o alla funzione di ripartizione di X). Perciò, nell'impostazione di Kolmogorov, i concetti di previsione e di speranza matematica vengono sostanzialmente a coin cidere. Così, nella memoria del 1933, Kolmogorov introduce direttamente il concetto di speranza matematica di un numero aleatorio (misurabile) X, defini to su (Ω‚ℋ,P), come integrale (secondo Lebesgue-Stieltjes, cosicché si possa trattare unitariamente anche il caso di numeri aleatori non limitati) di X rispetto a P_X. Quindi, mentre per de Finetti ogni numero aleatorio ammette una previsione (anche se qui abbiamo dovuto rinunciare, per ragioni di spazio, a esaminare il caso dei numeri aleatori non limitati) che può essere valutata in modi diversi purché compatibili col principio di coe renza, in un certo senso per Kolmogorov sono i numeri aleatori misurabili e integrabili i soli per i quali si possa parlare di previsione. Anche in questo passaggio possiamo scorgere la più stretta aderenza dell'impostazione di de Finetti alle ragioni intrinseche della probabilità e dei suoi impieghi, rispetto a quella di Kolmogorov più incline a ragioni di formalizzazione matematica secondo i canoni di ben collaudate teorie analitiche. Soltanto in tempi relativamente recenti si è assistito all'apparizione di studi probabilistici conformi al punto di vista di de Finetti (Dubins 1965).

La concezione asintotica di von Mises

L'idea di definire la probabilità come grandezza oggettiva, secondo un punto di vista antitetico a quello soggettivo, ha attratto l'attenzione di molti studiosi nel nostro secolo. I più hanno aderito a tale concezione pensando alla probabilità come al valore attorno al quale si stabilizza la frequenza di un evento in una successione di prove omogenee. Così, l'illustre geometra Guido Castelnuovo (1865-1952), al quale si deve un celebre trattato sul CdP apparso in prima edizione nel 1919, cercò di precisare i rapporti tra frequenza e probabilità mediante la cosiddetta 'legge empirica del caso': "In una serie di prove ripetute un gran numero di volte nelle stesse condizioni, ciascuno degli eventi possibili si manifesta con una frequenza (relativa) che è presso a poco uguale alla sua probabilità. L'approssimazione cresce ordinariamente col crescere del numero delle prove" (Castelnuovo 1945, p. 3).

Chiaramente, non è pensabile di poter fondare su tale constatazione empirica una qualsiasi teoria matematica delle probabilità, proprio a causa della vaghezza di certe espressioni contenute nella formulazione del 'postulato empirico'.

Altri studiosi si spinsero oltre, concependo la probabilità come frequenza limite. Il principale sostenitore dell'impostazione asintotica fu Richard von Mises (1883-1953).In lavori apparsi nel 1919 e nel 1931, egli cercò di conciliare le esigenze del punto di vista empirico con quelle del rigore matematico, fissando due assiomi in base ai quali oggetto del CdP sono le successioni di prove, dette Kollektiv, che soddisfano le seguenti proprietà: (m1) le frequenze con cui ciascuno dei risultati possibili si presenta nelle prime n prove, tendono a dei valori limite ‒ detti frequenze-limite o 'probabilità' ‒ quando n cresce indefinitamente; (m2) tali frequenze-limite rimangono inalterate se, invece di considerare tutte le prove della successione primitiva, se ne estrae una qualunque sottosuccessione fissando comunque il rango dei termini da conservare (in altri termini, nessun 'sistema di gioco'può alterare alla lunga i risultati; assioma di 'non-regolarità').

In un lavoro del 1937, de Finetti, oltre a una disamina sintetica dell'insufficienza formale dell'assioma (m₂) di non regolarità, discute di taluni aspetti concettuali della teoria, in relazione al significato della legge dei grandi numeri, alla definizione di Kollektiv e alla giustificazione del ragionamento induttivo. Gli spunti critici di de Finetti sono tali da minare le basi della teoria di von Mises più di quanto non riesca la formulazione ambigua e insufficiente dell'assioma di non regolarità. In effetti, i seguaci dell'impostazione si prefissero, principalmente, di riformulare gli assiomi originari di von Mises in modo da ottenere un assetto non contraddittorio della teoria, anche a costo di una drastica restrizione del campo di applicazione del CdP. Di alcuni di tali contributi, come quelli di Abraham Wald, William Feller e altri, e della di scussione che essi suscitarono, resta traccia in un resoconto critico, completo ed estremamente penetrante redatto da de Finetti (1938). Sembra che Maurice-René Fréchet, dopo la presentazione del contributo di Wald si chiedesse se questi, togliendo alla teoria di von Mises le contraddizioni che la infirmavano, non fosse riuscito "à l'écraser" anziché "à la justifier". La situazione cambiò, segnando un progresso, con l'apparizione dei concetti di 'algoritmo' e di 'funzione ricorsiva'. Infatti, nel 1940, Alonzo Church se ne avvalse per precisare regole appropriate di selezione in modo da garantire la validità di (m₂). Un progresso ulteriore fu realizzato da Kolmogorov nel 1963, grazie a un ampliamento della classe degli algoritmi che garantiscono l'invarianza del limite delle sottosuccessioni e, soprattutto, grazie a una riformulazione rigorosamente finitistica delloriginario di von Mises e Church. Significativa, inoltre, nella 'revisione' di Kolmogorov, è l'introduzione di una valutazione quantitativa della stabilità delle frequenze.

Eventi e numeri aleatori subordinati

Possiamo introdurre il problema con un esempio elementare. Un'urna contiene palline di due colori, bianco e nero, e la sua composizione è incognita; non è nota, in altri termini, la frazione di palline bianche sul totale. Si considerino cento estrazioni consecutive con reimmissione, dopo ogni osservazione, della pallina osservata. Gli eventi "si estrae pallina bianca nella centesima estrazione" e "si estrae pallina bianca nella centesima estrazione nell'ipotesi che nelle precedenti novantanove si siano osservate esattamente novanta palline bianche" sono evidentemente diversi. Il secondo è un 'evento su bordinato' o 'condizionato'. Generalmente, la previsione di fatti futuri coinvolge la valutazione di probabilità di eventi o, più in generale, la previsione di numeri aleatori, subordinati agli ipotetici risultati di precedenti esperienze.

Dati un numero aleatorio X definito su Ω e un sottoinsieme E (evento) di Ω, denotiamo con X∣E il 'numero aleatorio X subordinato a E', ossia il numero aleatorio che non è definito sul contrario di E e che, su E, coincide con X; formalmente, X∣E è la restrizione di X a E. Assumere la verità di E significa, in altri termini, supporre un aumento d'informazione che porta a eliminare dalle possibilità i casi elementari contenuti nel suo contrario. Se B è un altro evento (sottoinsieme di Ω), scriveremo B∣E per indicare l'evento che è vero se e solo se B ed E si verificano congiuntamente, falso se E si verifica e B non si verifica, privo di valore logico se E non si verifica: è un modo diverso per dire che I_B∣E è la restrizione di I_B a E. L'unica e ovvia restrizione nelle precedenti definizioni è che il condizionante E sia diverso dall'evento impossibile. Quando E=Ω, allora X∣E=X e B∣E=B.

Per quanto concerne la valutazione della previsione di X∣E e della probabilità di B∣E, ci sembra che le proposte più significative siano quelle legate alle impostazioni di de Finetti e di Kolmogorov. Nella prima, il punto di partenza è la solita condizione di coerenza che, per la natura del nuovo problema, si richiede debba valere subordinatamente a E.

L'atteggiamento di Kolmogorov rispetto alla definizione di speranza matematica e di probabilità condizionale è radicalmente diverso. Lungi dal tentare una definizione assiomatica di questi con cetti, Kolmogorov considera, nella più volte citata memoria del 1933, uno spazio di probabilità (Ω‚ ℋ,P), un elemento aleatorio Y definito su Ω e a valori in y e misurabile rispetto alla coppia ℋ-S (S è una σ-algebra di sottoinsiemi di y), e propone un procedimento per dedurre da P un nuovo ente che, per analogia col caso in cui Y assume un numero finito di valori, adotta come 'speranza matematica condizionale', o, a seconda dei casi, come 'probabi lità condizionale'. D'ora in poi useremo l'aggettivo condizionale per indicare le valutazioni ricavate in conformità all'approccio di Kolmogorov.

Connessioni tra frequenza e probabilità nelle concezioni non frequentiste

Si accennava in precedenza all'apparenza empirico-intuitiva del punto di vista di von Mises come causa del favore da esso riscosso. Per molti, infatti, è spontaneo collegare il concetto di probabilità a quello empirico di frequenza, salvo poi dover constatare difficoltà relative alla spiegazione e alla formalizzazione del rapporto tra i due concetti. Certi studiosi ritengono ingiustificato e arbitrario stabilire quel rapporto per via assiomatica. Per essi, l'analisi di tale rapporto deve poggiare su teoremi dedotti a partire da una definizione di probabilità libera da rimandi alla nozione di frequenza, in modo da evitare circoli viziosi nel ragionamento. Questa posizione è esplicitamente dichiarata dai soggettivisti ed è, ovviamente, implicita nelle considerazioni di chi aderisce all'impostazione assiomatica di Kolmogorov. De Finetti si occupò della questione con cura estrema, proponendone una soluzione originale e assai naturale, che chiarisce come il punto di vista soggettivo sia in grado di dare un'interpretazione soddisfacente del rapporto tra frequenza e probabilità. A questo fine, egli introduce la nozione di eventi scambiabili: E1,E2,…,E_n,… è una successione di 'eventi scambiabili' se, per ogni n≥1 e per ogni permutazione π(1),…,π(n) di 1,…,n, la distribuzione di probabilità del vettore di indicatori (I_E1,…,I_En) coincide con quella di (I_Eπ(1),…,I_Eπ(_n)).

Questa condizione probabilistica, già nota dal 1924 quando Jules Haag la fece oggetto di una comunicazione al Congresso dei matematici di Toronto, fu indipendentemente introdotta da de Finetti per tradurre in termini matematicamente precisi l'idea di prove analoghe dello stesso fenomeno, idea che è presente, in modo più o meno esplicito, in tutte le concezioni frequentiste della probabilità. Esprimere quest'idea in termini di scambiabilità equivale ad assumere che, in una successione di prove, l'informazione sostanzialmente rilevante sia rappresentata dal numero di successi e di insuccessi, senza riguardo all'individuazione delle prove che hanno prodotto successo e di quelle che hanno prodotto insuccesso. De Finetti espose le linee essenziali della teoria delle successioni di eventi scambiabili, compreso il celebre 'teorema di rappresentazione', in una comunicazione al Congresso dei matematici di Bologna, tenutosi nel 1928 (de Finetti 1937a). Chiarito il collegamento tra scambiabilità e le condizioni 'al contorno' abitualmente accolte dai frequen tisti, de Finetti studiò la questione delle connessioni tra frequenza e probabilità in relazione a una successione (E_n)_n≥1 di eventi scambiabili, riportandola allo studio della differenza tra la probabilità del verificarsi di E_n+1, subordinatamente al verificarsi di una prefissata (arbitraria) realizzazione dei primi n eventi, e della frequenza di successo relativa a quella realizzazione.

Nelle prossime sezioni, dedicate agli sviluppi tecnici del CdP, ci atterremo alla teoria kolmogoroviana, perché è nell'ambito di detta teoria che sono stati dedotti i principali risultati del CdP nei primi cinquant'anni del secolo.

Teoremi limite e leggi dei grandi numeri

La determinazione della legge limite di somme di numeri aleatori, al divergere del numero degli addendi, costituisce uno dei temi più studiati tra quelli classici del CdP. Esso è stato analizzato da due diversi punti di vista, in corrispondenza a due questioni di notevole interesse applicativo. La prima (che ha dato luogo agli studi sulle 'leggi dei grandi numeri') trae origine dall'osservazione del comportamento degli scostamenti di n numeri aleatori X1,…,X_n (corrispondenti a misure di una grandezza fisica, o, per es., a risarcimenti da parte di una compagnia di assicurazione ai propri assicurati, ecc.) da un valore di riferimento θ (rispettivamente, il vero valore della grandezza, o il premio di assicurazione, ecc.). La somma di tali scostamenti, valendo opportune condizioni, presenta un ordine di grandezza molto più piccolo del numero degli addendi. Perciò, sotto le medesime condizioni, si può asserire la convergenza di ∑ X_i/n verso θ (i=1, …,n). La seconda questione che ha determinato l'interesse per lo studio delle leggi limite di somme di numeri aleatori è legata a una diffusa evidenza empirica che pone in luce come certi caratteri collettivi, in una data popolazione, presentino una distribuzione di frequenze tendenzialmente 'gaussiana', purché il numero delle unità di tale popolazione sia sufficientemente grande. Classicamente, si è cercato di spiegare un simile comportamento interpretando i caratteri, per i quali si presenta, come conseguenza di un grande numero di piccole cause che si sommano. Queste ultime considerazioni sono alla base degli studi concernenti il 'problema centrale del limite'.

La formulazione sostanzialmente corretta dei descritti problemi e le prime proposte di risoluzione risalgono a epoche lontane dal periodo di cui dobbiamo qui occuparci. Bastino, dunque, le seguenti scarne citazioni: la pubblicazione postuma dell'Ars conjectandi (1713) di Jakob I Bernoulli (1654-1705), in cui viene dimostrata la legge debole dei grandi numeri per frequenze nello schema binominale; il teorema centrale del limite, entro i confini del medesimo schema, dimostrato da Abraham de Moivre (1667-1754) in un supplemento del 1733 alla Miscellanea analytica de seriebus et quadraturis, riprodotto anche nella terza edizione dell'opera The doctrine of chances; le varie edizioni (1812, 1814, 1820) della Théorie analytique des probabilités di Pierre-Simon de Laplace (1749-1827), in cui viene formulato il problema centrale del limite e presentata una dimostrazione del relativo teorema che, benché imprecisa e incompleta, lascia intravvedere l'esattezza del risultato; la generalizzazione, dovuta a Pafnutij L′vovič Čebyšev (1821-1894), della legge debole dei grandi numeri (1867) di Bernoulli, e una dimostrazione, basata sul metodo dei momenti, del teorema centrale del limite (1890-1891).

Il problema centrale del limite

Il contesto in cui, classicamente, si studiano le leggi limite di somme di numeri aleatori S_n=X1+…+X_n(n=1,2…) prevede che gli addendi siano stocasticamente indipendenti nel senso che, per ogni n=1,2,…, si abbia

[9] P({X₁≤x₁}⋂…⋂{X_n≤x_n}=P({X₁≤x₁})…P({X_n≤x_n})

in corrispondenza a ogni n-upla (x1,…,x_n) di numeri reali. Nella formulazione classica si assume, inoltre, che ogni X_n abbia speranza matematica m_n e varianza v_n=E((X_n−m_n)2) finite. Sotto queste condizioni, per 'teorema centrale del limite', secondo una terminologia, universalmente accolta, introdotta da George Pólya (1887-1985) nel 1920, s'intende qualunque teorema che asserisca la tesi

per ogni reale x. Il membro di destra della [10] è la funzione di ripartizione della legge 'gaussiana ridotta'.

In un articolo del 1901, Aleksandr Michajlovič Ljapunov (1857-1918), allievo di Čebyšev ed esponente della Scuola di San Pietroburgo, dimostrò che per la validità della [10] è sufficiente la condizione: esiste qualche δ>0 tale che

per n→∞.

Questa proposizione, che Ljapunov dimostrò utilizzando la trasformata di Fourier-Stieltjes delle funzioni di ripartizio ne coinvolte (fu Ljapunov il primo a denominare tale trasfor mata 'funzione caratteristica' del corrispondente numero aleatorio), viene usualmente ricordata per essere stata la prima versione rigorosa del teorema centrale del limite.

Un contributo decisivo al problema centrale del limite è quello del matematico finlandese Jarl Waldemar Lindeberg (1876-1932) che, nel 1922, formulò una condizione più debole di quella di Ljapunov, che si può anche dedurre da uno studio dello stesso anno di Sergej Natanovič Bernštejn (1880-1968), su possibili generalizzazioni del teorema di Ljapunov. Questo studio è molto meno noto di quello di Lindeberg, nonostante la sua fama di matematico superi di gran lunga quella di Lindeberg. A ogni modo, quel risultato segnò un significativo progresso per il problema centrale del limite, come emerge dai successivi sviluppi dovuti a Feller il quale, in un lavoro apparso nel 1935, dimostrò che la condizione di Lindeberg equivale al manifestarsi della [10] e della simultanea condizione di 'trascurabilità asintotica uniforme':

per n→∞, uniformemente in k.

Intuitivamente, quest'ultima condizione stabilisce che il contributo di ciascun numero aleatorio (X_k-m_k)/(∑ⁿ_k=₁v_k)^1/2 è piccolo rispetto alla somma (S_n-∑ⁿ_k=1m_k)/(∑ⁿ_k=₁v_k)^1/2. Così, il teorema di Lindeberg-Feller risolve il problema centrale del limite per numeri aleatori uniformemente asintoticamente trascurabili, sotto la condizione d'esistenza dei momenti del secondo ordine degli addendi. Negli stessi anni in cui il problema centrale del limite veniva risolto nella sua versione classica, Paul Lévy (1886-1971), uno dei più grandi probabilisti del secolo, enunciava una versione più generale dello stesso problema. Uno sguardo alla formulazione classica pone in evidenza che l'ufficio dei momenti di primo e secondo ordine è quello di trasformare le somme S_n in modo da evitare che probabilità positive 'scappino' verso valori indefinitamente grandi in valore assoluto. Non si può escludere, quindi, che conclu sioni dello stesso tipo possano valere con costanti diverse dai suddetti momenti, purché si ammetta, contestualmente, che le risultanti leggi limite riescano eventualmente diverse dalla gaussiana. Sulla base di queste considerazioni, nel 1925 Lévy poneva il problema: qual è la più ampia classe delle leggi limite, al divergere di n, di successioni del tipo (S_n/b_n−a_n)_n≥1 ottenute scegliendo opportunamente a_n e b_n, purché b_n sia divergente a +∞ per n tendente a +∞? Nonostante la generalità della nuova formulazione, si vengono ancora a escludere situazioni classiche come il teorema limite di Poisson che riguarda successioni con doppio indice (X_n,_k)1≤_k≤_kn con

Ciò suggerisce di riformulare così il problema: posto che X_n,1,…,X_n,_kn siano indipendenti per ogni n e uniformemente asintoticamente trascurabili (cioè che max P(∣X_n,k∣≥ε)→0 per n→∞ e per ogni ε>0), trovare la classe di tutte le leggi limite delle somme

e determinare, inoltre, le condizioni per la convergenza di tali somme a uno specifico elemento della classe succitata.

La risposta a quest'ultima questione, versione moderna del problema centrale del limite, si basa sulla nozione di 'legge infinitamente divisibile' introdotta da de Finetti (1929) per lo studio della legge di probabilità dei processi a incrementi indipendenti e stazionari. Ricordiamo qui che la di stribuzione di probabilità di un numero aleatorio X è infinitamente divisibile se, per ogni n naturale, esistono dei numeri aleatori X_n,1,…,X_n,_n, indipendenti e identicamente distribuiti, tali che la distribuzione di X coincida con quella di X_n,1+…+X_n,_n. In una fondamentale memoria del 1934, che generalizza precedenti risultati di de Finetti e Kolmogorov, Lévy fornì la caratterizzazione completa delle leggi infinitamente divisibili in termini di funzione caratteristica (Lévy 1934). La risposta al problema posto da Lévy si basa su un teorema del matematico russo Aleksandr Jakovlevič Chinčin (1894-1959) che, con Kolmogorov, è considerato caposcuola della nuova 'scuola russa'. Tale teorema (Chinčin 1937) afferma che la famiglia delle leggi limi te di somme S_n,kn di numeri aleatori come sopra descritti è esattamente quella delle leggi infinitamente divisibili.Due anni dopo, nel 1939, Boris Vladimirovič Gnedenko (1912-1995) e Wolfgang Doeblin (1915-1940) pubblicarono, indipendentemente, il criterio generale, ovvero condizioni necessarie e sufficienti, per la convergenza verso un membro assegnato della famiglia delle leggi infinitamente divisibili.

Contestualmente alla versione generale sopra descritta, Lévy poneva il problema del limite di somme (S_n/b_n−a_n)_n≥1 sotto l'ipotesi più restrittiva di addendi identicamente distribuiti, oltreché indipendenti. Egli stesso dimostrava che la famiglia delle leggi limite coincide, nel caso speciale preso in considerazione, con quella delle 'leggi stabili'. Una legge è detta stabile se, per ogni n, si possono determinare costanti α_n e β_n tali che la legge di (S_n/β_n−α_n)_n≥1 coincida con quella del singolo addendo. Successivamente, Lévy considerò il problema d'individuare l'insieme delle distribuzioni F di X1 per le quali, con opportuna scelta di a_n e b_n, (S_n/b_n−a_n)_n≥1 ammetta come legge limite un assegnato elemento G della famiglia delle leggi stabili. Si dice, allora, che F è nel 'dominio d'attrazione' di G. Il dominio d'attrazione della legge gaussiana venne determinato, indipendentemente, da Feller, Lévy e Chinčin nel 1935. Nel 1940, Doeblin e Gnedenko fornirono, indipendentemente, criteri generali per la determinazione degli altri domini d'attrazione.

Fin qui abbiamo accennato al teorema centrale del limite sotto l'ipotesi classica d'indipendenza stocastica degli addendi.Dopo i lavori di Andrej Andreevič Markov (1856-1922) relativi al teorema centrale per somme di numeri aleatori costituenti una catena markoviana omogenea e eventualmente non omogenea, ma a due soli stati, apparsi tra il 1907 e il 1910, Bernštejn (1926) studiò il problema dell'estensione dello stesso teorema a numeri aleatori 'debolmente indipendenti': gli eventi dipendenti (in senso ordinario) da X₁,…,X_k e quelli dipendenti da X_k+p,…,X_k+p+1… presentano una dipendenza stocastica che tende a svanire al divergere di p all'infinito. Inoltre, considerò somme di numeri aleatori dipendenti, dotati ‒ secondo la sua terminologia ‒ di mutua regressione quasi nulla. Egli anticipava, in questo modo, la nozione di martingala e, in definitiva, poneva le basi per lo studio del problema centrale del limite relativamente a martingale. Un contributo in questa direzione, di fondamentale importanza, dava anche Lévy nel 1935. Le idee di Bernštejn furono ripre se da Doeblin che, nel 1937, ottenne una legge del logaritmo iterato per catene markoviane, e da Michel Loève (1907-1979) che, in lavori del 1945 e del 1950, studiò estensioni della condizione di Lindeberg e della legge forte dei grandi numeri, nonché un'estensione del problema centrale del limite moderno.

Molti problemi concreti, come si ricordava all'inizio della sezione, portano a considerare somme di variabili aleatorie, e il teorema centrale precisa le condizioni sotto le quali la successione delle funzioni di ripartizione di tali somme ‒ F_n sia, per fissare le idee, la ripartizione della somma ridotta (S_n-∑ⁿ_k=1m_k)/∑ⁿ_k=1 v_k)^1/2 ‒ converge alla funzione di ripartizione φ della legge gaussiana ridotta (φ(x) = ∫^x_-∞ exp{-t²/2}dt(2π)^1/2,x∈ℝ). Il valore pratico del teorema, ai fini dell'approssimazione cosiddetta 'gaussiana' o 'normale', si accresce quando si conoscano stime dell'errore di approssimazione ∣F_n−φ∣. Ljapunov, nel lavoro già citato del 1901 e in uno precedente del 1900, stabilì un confine superiore per tale errore, che fu notevolmente migliorato da Andrew C. Berry (nel 1941) e, indipendentemente, da Carl-Gustav Esseen (nel 1945). Essi trovarono che, nel caso classico di somme di numeri aleatori indipendenti, di speranza matematica nulla e momento terzo finito, esiste una costante C tale che, per ogni x e n

Sotto condizioni più restrittive tra cui l'identità in distri buzione degli addendi, Harald Cramér fornì nel 1928 uno svilup po asintotico di F_x(x)−φ(x), nelle potenze di n^−1/2 e, in seguito, una generalizzazione al caso di addendi non identicamente distribuiti (Cramér 1937).

Una questione strettamente connessa alla valutazione dell'errore ∣F_x(x)−φ(x)∣ è quella delle 'grandi deviazioni' che si presenta quando x=x_n diverge a +∞ per n tendente a +∞. Poiché, in simili circostanze: 1−F_n(x_n)→0 e 1−φ(x_n)→0 (per n→+∞), è necessario ottenere confini sull'accuratezza 'relativa' dell'approssimazione, ossia confini per il rapporto { 1−F_n(x_n)}/{ 1−φ(x_n)} ; in particolare, è utile ottenere condizioni sotto le quali: { 1−F_n(x_n)}/{ 1−φ(x_n)}→1 per n→+∞. Nel 1938, Cramér affrontò il problema nel caso di addendi identicamente distribuiti, di speranza matematica nulla, e dotati di funzione generatrice dei momenti, sotto la condizione: x>1, x=o(√n) per n→+∞. Nonostante la situazione piuttosto particolare considerata da Cramér, i metodi da lui impiegati conservano una certa attualità.

Tra le ramificazioni del problema centrale del limite, merita di essere ricordato il cosiddetto 'principio d'invarianza' o, come qualcuno preferisce dire, la versione 'funzionale' del teorema centrale, studiata sistematicamente a partire dalla fine degli anni Quaranta.

Le leggi dei grandi numeri

La legge dei grandi numeri per antonomasia è quella che istituisce la convergenza alla probabilità della successione delle frequenze nello schema bernoulliano. Più in generale, il 'problema dei grandi numeri' può essere posto nei seguenti termini: data una successione di numeri aleatori X1,X2,…,X_n,…, dotati di speranza matematica finita, sotto quali condizioni ulteriori si può stabilire che

converge a zero, al divergere di n, in un senso da precisare?

Generalmente, la convergenza richiesta è 'in probabilità' e, allora, si ha una 'legge debole dei grandi numeri', oppure è 'quasi certa' e, allora, si ha una 'legge forte dei grandi numeri'. Ricordiamo il significato di questi due tipi di convergenza: asserire che T_n 'converge in probabilità' a zero significa che, per ogni ε>0, la probabilità dell'evento {∣T_n∣≤ε} converge a uno, al divergere di n; affermare che T_n 'converge quasi certamente' a zero equivale a stabilire (in uno spazio di probabilità di Kolmogorov) che, per ogni ε>0, la probabilità dell'evento

converge a uno, al divergere di n. La convergenza quasi certa implica quella in probabilità ma, in generale, non vale il viceversa. Si rileva facilmente che il fenomeno intuitivo dello stabilirsi della frequenza attorno al valore della probabilità, da un certo posto in poi, ha come corrispondente matematico lo schema della convergenza quasi certa e non quello più debole della convergenza in probabilità.

Dal punto di vista storico, la prima legge dei grandi numeri riguarda la convergenza in probabilità della frequenza di successo ‒ in una successione di prove indipendenti e identicamente distribuite ‒ verso la probabilità di successo in ciascuna prova; è il classico teorema di Bernoulli, già citato all'inizio. La prima estensione del teorema precedente a numeri aleatori con varianza uniformemente limitata risale a un lavoro di Čebyšev del 1867. La dimostrazione della conseguente legge debole si basa su una disuguaglianza, oggi detta di Bienaymé-Čebyšev (pare che Irénée-Jules Bienaymé l'abbia enunciata per primo, attorno al 1850). Nel 1899, Markov ottenne un lieve miglioramento della legge debole di Čebyšev. Si tratta, in ogni caso, di risultati che non risolvono il problema più pressante dello stabilirsi, definitivamente, della successione (T_n)_n≥1 attorno allo zero. Alcuni, soprattutto fra i pratici, ritenevano all'inizio del XX sec. che le precedenti leggi fossero sufficienti per convalidare quel fenomeno che, ai più, appariva tanto intuitivo. Che le cose non stessero esattamente in questi termi ni dovette accorgersi Émile Borel.Sia pure con ragionamenti non completamente corretti, egli stabilì, nel 1909, la prima legge forte dei grandi numeri in relazione alle frequenze di uno schema bernoulliano in cui la probabilità di successo è uguale a 1/2. Ancora qualche tempo doveva comunque passare prima che venisse fissata rigorosamente la distinzione tra convergenza in probabilità e convergenza in senso forte. Provvide a questa fondamentale separazione Francesco Paolo Cantelli, nel biennio 1916-1917, dopo un'analisi acuta e profonda del significato di legge dei grandi numeri; significativamente, egli introdusse il termine 'legge uniforme' e non 'legge forte', dovuto a Chinčin. A Cantelli si deve, anche, un'importante estensione del teorema di Borel, a numeri aleatori indipendenti (ma non necessariamente identicamente distribuiti) con successione limitata dei momenti quarti. Il procedimento dimostrativo si fonda, oltre che su certe disuguaglianze del tipo di quella di Čebyšev, sulla celebre proposizione, dimostrata in quell'occasione, nota oggi come 'lemma di Borel-Cantelli' (Cantelli 1917a).

Decisivi miglioramenti alla legge di Cantelli furono apportati da Kolmogorov. Questi, nel 1930, dimostrò che la convergenza della serie ∑^∞_n=1(v_n/n²) è condizione sufficiente per la validità della legge forte, in successioni di numeri aleatori indipendenti, anche se non identicamente distribuiti. Nel 1933, assumendo anche l'identità in distribuzione, Kolmogorov dimostrava che condizione necessaria e sufficiente per la validità della legge forte dei grandi numeri è che sia finita la speranza matematica del generico elemento della successione. La dimostrazione si avvale di una fondamentale disu guaglianza dovuta allo stesso Kolmogorov (1928) che migliora significativamente quella di Bienaymé-Čebyšev. L'analisi del problema dei grandi numeri condusse, in modo naturale, allo studio delle serie di numeri aleatori; anche in questo settore di ricerca, fondamentali furono i contributi di Chinčin e, soprattutto, di Kolmogorov, tra il 1925 e il 1930.

Fin qui abbiamo accennato alle ricerche sulle leggi dei grandi numeri relative a successioni di numeri aleatori indipendenti. L'ipotesi d'indipendenza è cruciale ma non mancano, per questo, risultati interessanti in presenza di particolari ipotesi di dipendenza. Storicamente, la prima legge (debole) dei grandi numeri per successioni dipendenti fu dimostrata da Markov nel 1907, nel caso di catene omogenee, con un numero finito di stati e con probabilità di transizione strettamente positive. Sotto queste ipotesi, in virtù del 'teorema ergodico di Markov', gli elementi della succesione riescono 'asintoticamente indipendenti'. Ed è proprio questa indipendenza asintotica che assicura la validità dello stesso risultato conseguito nell'ipotesi più restrittiva d'indipendenza. Queste considerazioni suggerirono a Bernštejn d'indagare se la stessa conclusione potesse essere raggiunta anche in condizioni più generali. Così, nel trattato del 1946 di Bernštejn si trova sostanzialmente affermato che la legge debole dei grandi numeri vale se: esiste

esiste K tale che v_n≤K per ogni n e il coefficiente di correlazione tra X_i e X_j, ϱ_ij, è tale che ∣ϱ_ij∣≤R(∣i−j∣), dove R(n) è funzione non negativa di n, per cui R(0)=1 e ∑ⁿ_k=1R(k)/n→0 per n→∞. L'ultima ipotesi sostituisce, in un certo senso, la condizione d'indipendenza asintotica delle catene markoviane con una forma più debole di 'ortogonalità asintotica'. In ogni caso, sembra essenziale per la validità della legge forte dei grandi numeri, nella sua formulazione classica, che la dipendenza tra due elementi della successione tenda a svanire all'allontanarsi progressivo dei posti degli elementi considerati.

Il concetto di stazionarietà ha origini fisiche: il teorema di Liouville che dà una misura invariante nel tempo per l'evoluzione dei sistemi dinamici conservativi nel loro spazio delle fasi. Chinčin, nel 1932, attuò una 'trasposizione' probabilistica del concetto fisico, in base alla quale si dice che una successione di numeri aleatori X₁,X₂,… è 'stazionaria' quando la legge di probabilità di n termini è invariante per traslazione rispetto agli indici, e ciò vale per ogni n=1,2,…. Nello scenario probabilistico, al teorema ergodico di Birkhoff corrisponde la legge dei grandi numeri seguente: se (X_n)_n≥1 è stazionaria e E∣X₁∣⟨∞, allora (∑ⁿ_i=1X_i/n_n)_n≥1 converge in senso forte verso un numero aleatorio che coincide con E(X₁∣ℱ), essendo ℱ la σ-algebra terminale relativa alla successione (X_n)_n≥1. Chiudiamo questa breve panoramica sulle leggi dei grandi numeri ricordando il teorema di convergenza delle martingale, di cui tratteremo più avanti.

La legge del logaritmo iterato

Indichiamo ancora con S_n la somma di n numeri aleatori indipendenti di valore atteso nullo. La legge forte dei grandi numeri asserisce, in questo caso, che l'ordine di grandezza delle oscillazioni di (∣S_n∣)_n≥1 è minore di n, risultando S_n/n→0, quasi certamente, per n→+∞. Un problema interessante è dunque quello di caratterizzare le fluttuazioni estreme delle medie S_n/n. Felix Hausdorff (1868-1942) dimostrò, nel 1913, che nel caso bernoulliano simmetrico (successioni di numeri aleatori indipendenti a valori −1 e 1, con probabilità uguali a 1/2) quasi tutte le realizzazioni della successione ∣S_n∣/nε+1/2 si mantengono limitate per ogni ε>0. L'anno successivo, Godfrey H. Hardy (1877-1947) e John E. Littlewood (1885-1977) migliorarono il precedente risultato sostituendo nε+1/2 con (nlogn)1/2; Chinčin ottenne un ulteriore miglioramento, nel 1923, potendo sostituire (nlogn)1/2 con (nloglogn)1/2. Infine, nel 1924, lo studioso russo dedusse la 'legge del logaritmo iterato' per il caso speciale in esame: se (X_n)_n≥1 sono numeri aleatori indipendenti, tali da assumere i valori ±1 con probabilità 1/2, allora

per quasi tutte le realizzazioni di (X_n)_n≥1 (Chinčin 1924).

L'interesse per le oscillazioni di (S_n)_n≥1 nel caso di successioni bernoulliane traeva origine dall'esigenza di caratterizzare meglio la distribuzione dei numeri normali, di cui si è detto precedentemente. Il metodo probabilistico adottato da Chinčin, per risolvere un problema di natura squisitamente analitica, indusse altri studiosi a indagare sulla possibilità di estendere la legge del logaritmo iterato a succesioni più generali di numeri aleatori. Kolmogorov riuscì nell'intento nel 1929.

In molte applicazioni gli elementi di (X_n)_n≥1 sono identicamente distribuiti, oltre che indipendenti, ma non soddisfano alle precedenti condizioni di limitatezza previste dal teorema di Kolmogorov. Viene pertanto naturale chiedersi se la legge del logaritmo iterato sussista anche nelle circostanze testé descritte. La risposta affermativa fu data, nel 1941, da Philip Hartman e Aurel Wintner. Questi studiosi, basandosi su un delicato procedimento di troncamento e sul metodo impiegato da Kolmogorov, stabilirono la seguente proposizione: se (X_n)_n≥1 è una successione di numeri aleatori indipendenti e identicamente distribuiti con valore atteso nullo e varianza unitaria, allora

Nel 1966, Volker Strassen dimostrerà che, nelle stesse condizioni d'indipendenza e di identità in distribuzione, l'esistenza della varianza è condizione necessaria per la validità della legge del logaritmo iterato.

Processi aleatori

L'analisi di fenomeni fisici e sociali complessi porta a dover considerare funzioni aleatorie più generali delle successioni considerate nella precedente sezione. Vi abbiamo già accennato, anche, per quanto riguarda le questioni attinenti alla definizione della corrispondente legge di probabilità. Queste sommarie considerazioni sono di per sé sufficienti a giustificare ricerche su ampie classi di processi aleatori. A esse si aggiungono, anche, naturali esigenze di indagine matematica sulle conseguenze della rinuncia all'ipotesi d'indipendenza stocastica che, sebbene fulcro del CdP classico, non può ritenersi adeguata per ogni circostanza concreta.

Gli inizi: i primi venti anni del secolo

Nei primi venti anni del secolo, le motivazioni per lo studio di schemi e modelli probabilistici complessi e, in ogni caso, diversi da quelli classici esaminati nel paragrafo precedente, furono di natura essenzialmente applicativa. In quel ventennio furono comunque gettati i semi della teoria generaleche si sarebbe sviluppata su basi matematiche più sicure dopo la pubblicazione della monografia di Kolmogorov del 1933. L'esame, sia pur necessariamente sommario, del lavoro compiuto nei primi venti anni del secolo è utile per comprendere alcune delle principali linee di ricerca della teoria dei processi aleatori, e quindi del CdP moderno.

Incominciamo dal 1900, quando Louis Bachelier (1870-1946) rese noto uno schema probabilistico, per lo studio delle oscillazioni dei prezzi del mercato azionario, basato su una formalizzazione del 'fenomeno browniano', il fenomeno, scoperto attorno al 1827 dal botanico inglese Robert Brown, del movimento irregolare di particelle organiche e inorganiche sospese inun liquido. Lo studio del Bachelier non ebbe molto seguito, nonostante l'originalità di impostazione; molti ritengono che furono le imprecisioni e la scarsa chiarezza del lavoro a provocarne la sostanziale caduta nell'oblio. Nel 1905, e in successivi lavori (1906, 1926), Albert Einstein (1879-1955) spiegò il fenomeno browniano nel contesto della teoria molecolare della materia. Pervenne a stabilire che la di stribuzione della posizione di una 'particella browniana' al tempo t, nell'ipotesi che la stessa si trovi in x al tempo t₀⟨t, è gaussiana con valore atteso x e varianza σ²(t₁−t₀), σ² essendo una costante positiva dipendente dal raggio della particella e dalla viscosità del liquido ma non dagli eventi precedenti t₀. Allora, se la posizione della particella, al tempo 0, è supposta uguale a zero, la legge di probabilità delle posizioni (aleatorie) X₁,…,X_n della particella, ai tempi 0⟨t₁⟨…⟨t_n, è gaussiana (n-dimensionale) con E(X_i)≡0, E(X_iX_j) (covarianza di (X_iX_j))=σ²min(t_i,t_j), Var(X_i)=σ²t_i. In questo modo, si origina un esempio notevolissimo di 'processo gaussia no', ossia di funzione aleatoria f(t), con t≥0, i cui valori, in corrispondenza a ogni n-upla t₁,…,t_n di valori del parametro temporale t, si distribuiscono secondo la legge gaussiana sopra descritta. Un altro processo gaussiano di notevole importanza, con parametro t∈(0,1), è il cosiddetto ponte browniano o, anche, 'processo di Wiener subordinato', caratterizzato dal fatto che la distribuzione di probabilità n-dimensionale corrispondente agli istanti 0⟨t₁⟨…⟨t_n⟨1 è gaussiana n-dimensionale con E(X_i)≡0, E(X_iX_j)=min(t_i,t_j)−t_it_j, Var(X_i)=t_i(1−t_i), essendo X_i il numero aleatorio corrispondente a t_i.

L'analisi fisica del fenomeno browniano fa ritenereche il moto della particella sia continuo. Per quanto osservato a proposito del teorema d'estensione di Kolmogorov, la probabilità della condizione di continuità delle traiettorie di un processo a parametro continuo (come quello in esame) non è univocamente determinata dalle di stri buzioni di dimensione finita. Verso la fine degli anni Trenta, venne formulata una teoria per trattare, in generale, questi problemi di 'non misurabilità'; qui basti ricordare che essa è dovuta principalmente a Doob. Nel 1923, molti anni prima dell'apparizione dei lavori di Doob, Norbert Wiener (1894-1964) pubblicò una fondamentale memoria in cui si dimostrava l'esistenza di una funzione aleatoria con le stesse distribuzioni di dimensione finita del moto browniano, sopra ricordate, e con le realizzazioni (o traiettorie) continue e ovunque non differenziabili. Il lavoro di Wiener fu così innovativo e importante che il processo gaussiano corrispondente al moto browniano viene oggi frequentemente chiamato 'processo di Wiener'.

Tra i lavori pionieristici nel campo dei processi aleatori va ricordata la tesi (sostenuta a Uppsala nel 1903) dallo svedese Filip Lundberg nella quale si definisce, per la prima volta, il 'processo di Poisson composto', per lo studio dell'andamento della funzione aleatoria che rappresenta l'ammontare dei rimborsi associati a una certa classe di sinistri assicurati da una compagnia. Si suppone che il numero di sinistri, N_t, nell'intervallo (0,t) costituisca un 'processo di Poisson', ovvero: quasi tutte le realizzazioni del totale dei sinistri sono funzioni non decrescenti su (0,∞), costanti a tratti e con salti di ampiezza unitaria; il numero di sinistri in (t,t+s) è indipendente dagli eventi che precedono t, per ogni t≥0 e s>0; la legge di probabilità di N_t+s−N_t non dipende da t. Inoltre, si assume che il rimborso dovuto per l'n-esimo sinistro sia un numero aleatorio X_n, indipendente dagli istanti in cui si verificano i sinistri e dai rimborsi relativi ad altri sinistri. Perciò, l'ammontare cumulativo dei rimborsi per i primi n sinistri è dato da S_n=X₁+…+X_n e, essendo N_t il numero (aleatorio) dei sinistri in (0,t),

rappresenta l'ammontare dei rimborsi nell'intervallo (0,t). Il processo

è detto 'processo di Poisson composto'. In un lavoro di Cramér (1976) si ricorda che Lundberg, sempre nella tesi di Uppsala, fece anche uso di un'equazione funzionale che è un caso particolare della famosa 'equazione in avanti' introdotta nel 1931 da Kolmogorov per lo studio dei processi markoviani a tempo continuo. L'origine di questi ultimi processi risale ai lavori di Markov, apparsi tra il 1907 e il 1910. Con essi il matematico russo iniziò lo studio delle catene che oggi portano il suo nome, per convalidare le classiche proprietà asintotiche delle somme di numeri aleatori in condizioni diverse da quella d'indipendenza stocastica.

Processi a incrementi indipendenti

Caratteristica comune dei processi {X_t:t≥0} testé descritti è l'indipendenza stocastica dei loro incrementi, X_st:=X_t−X_s, relativi a intervalli di tempo disgiunti; essi sono perciò detti 'processi a incrementi indipendenti'. Lo studio di questa classe di processi fu avviato da de Finetti in una serie di note lincee apparse tra il 1929 e il 1931, nell'intento di fornire una metodologia probabilistica atta a integrare o sostituire l'analisi classica all'atto in cui la scienza decidesse di rinunziare ai canoni del determinismo. In questo ordine di idee, de Finetti istituì una corrispondenza tra leggi di probabilità di funzioni a incremento aleatorio e leggi fisiche ordinarie, in accordo sostanziale con la classificazione di quest'ultime proposta da Volterra in Fonctions de lignes. De Finetti si limitò poi a considerare il caso degli incrementi indipendenti e 'stazionari' ('omogenei'): la legge di probabilità di X_t−X_s non dipende da s (proprio come nel caso del moto browniano e del processo di Poisson composto). Uno dei risultati più importanti ottenuti da de Finetti in questo contesto è l'asserzione che, nelle condizioni dichiarate, la legge di probabilità di X_t è necessariamente infinitamente divisibile.

Oltre ad acute considerazioni sulle traiettorie dei processi in questione, egli stabilì che la classe delle leggi infinitamente divisibili coincide con quella dei limiti (in distribuzione) di somme di numeri aleatoriindipendenti distribuiti secondo la legge di Poisson (de Finetti 1929). Il problema della caratterizzazione della classe delle leggi infinitamente divisibili occupò ‒ anche per le connessioni col teorema centrale del limite, messe in evidenza in precedenza ‒ i più illustri probabilisti dell'epoca.

Kolmogorov, nel 1932, fornì l'espressione della funzione caratteristica di una legge infinitamente divisibile, sotto l'ipotesi di esistenza della varianza; Lévy, nel 1934, e Chinčin, nel 1937, diedero la funzione caratteristica della più generale legge infinitamente divisibile, senza alcuna restrizione circa l'esistenza dei momenti.

Il succitato lavoro di Lévy ‒ che alcuni autorevoli studiosi hanno considerato tra le migliori memorie di CdP apparse nel XX sec. ‒ contiene il contributo più significativo per quanto riguarda la teoria generale dei processi aleatori a incrementi indipendenti.

A partire dalla fine degli anni Trenta, Lévy intraprese un'analisi molto profonda e matematicamente sofisticata delle traiettorie del processo di Wiener, pervenendo a risultati completi e definitivi, ancora oggi posti alla base delle trattazioni dell'argomento.

Processi markoviani

Si può dimostrare che ogni processo {X(t):t≥0} a incrementi indipendenti gode della seguente proprietà: se 0≤t1⟨t2⟨…⟨t_n, allora per ogni sottoinsieme boreliano B di ℝ, si ha

[19] P(X(t_n)∈B∣X(t₁),…,X(t_n-1))=P(X(t_n)∈B∣X(t_n-1)).

In altri termini, se è noto lo stato in cui si trova il proces so attualmente (tempo t_n−1), allora la previsione del futu ro (tempo t_n) è indipendente dal passato (tempi t1,…,t_n−2).

Questa proprietà di 'indipendenza condizionale' è con divisa da altri processi, non necessariamente a incrementi indi pendenti, con parametro variabile in ℱ⊂(0,∞). Essa è nota in letteratura come 'proprietà di Markov' o 'proprietà markoviana' e, di conseguenza, i processi che la posseggono sono detti 'processi markoviani'. In particolare, se ℱ=ℕ:={ 0,1,2,…} , allora il processo (successione) markoviano corrispondente è più comunemente denominato 'catena markoviana'. L'origine di queste denominazioni risale agli studi di Markov (già citati precedentemente) sulle somme di numeri aleatori X₁,X₂,… dipendenti. Il matematico russo aveva considerato il caso in cui X_n (n=1,2,…) assume valori in un insieme finito o numerabilmente infinito (per comodità si può, in questo caso, pensare a un sottoinsieme di ℕ) e, per l'appunto, la legge di probabilità 'lega' i termini X_n della successione in base alla regola (corrispondente alla condizione di Markov) P(X_n+1==j∣X₁=i₁,…, X_n=i_n)=P(X_n+1=j∣X_n=i_n) per ogni n, e i₁,…,i_n,j in ℕ. Tra le caratteristiche essenziali dei processi markoviani va menzionata la possibilità di descrivere le corrisponenti di stribuzioni di dimensione finita a partire da pochi dati elementari. Questa possibilità, evidenziata da Smoluchowski nel 1906 in relazione alla rappresentazione di Einstein del moto browniano, e prima ancora da Bachelier nel lavoro già citato, fu analizzata nelle sue conseguenze generali da Kolmogorov in un lavoro del 1931, a ragione ritenuto tra quelli che hanno gettato le basi della teoria generale dei processi aleatori (Kolmogorov 1931).

Ebbene, se {X(t):t∈ℱ) è un processo markoviano e se con p_s,t(B∣x) si indica la 'probabilità di transizione' P(X(t)∈B∣X(s)=x), per s e t in ℱ con s⟨t, allora resta provata la validità dell'equazione integrale (di Einstein-Smoluchowski, nel caso particolare del moto browniano)

[20] p_s,_t(B∣x)=∫_ℝp_s,t(dy∣x)p_t',_t(B∣y)

per ogni t′∈(s,t) che, nella letteratura dei processi aleatori, viene generalmente detta 'equazione di Chapman-Kolmogorov'.

Dal punto di vista della teoria generale, il problema della caratterizzazione della legge di un processo markoviano si riduce, per quanto detto sopra, a quello della ricerca, sotto opportune condizioni, di una classe di soluzioni dell'equazione [20] di Chapman-Kolmogorov. Per esempio, l'analisi delle proprietà fisiche del fenomeno browniano aveva permesso ad Einstein e Smoluchowski di ridurre la [20] a un'equazione differenziale lineare di tipo parabolico, oggi nota come 'equazione di Fokker-Plank', e quindi di ottenere la legge del processo gaussiano che ben conosciamo. Nel citato lavoro del 1931, Kolmogorov riuscì a individuare vaste classi di processi markoviani, con parametro continuo in (0,∞), le cui probabilità, o densità a seconda dei casi, di tran sizione sono caratterizzate dall'essere soluzione di certe equazioni differenziali denominate da Feller, rispettivamente, 'all'indietro' e 'in avanti'.

L'equazione di Fokker-Plank individuata nei lavori pionieristici sul processo del moto browniano è un caso particolare di equazione in avanti di Kolmogorov. In effetti il metodo di Kolmogorov, oltre che nel caso di processi markoviani con spazio degli stati finito o numerabilmente infinito, è valido per la classe dei'processi di diffusione' (di cui il processo del moto browniano è un importante rappresentante). Pertanto, le equazioni di Kolmogorov, oltre che in contesti strettamente probabilistici, intervengono anche nella formalizzazione di modelli reali di diffusione: la diffusione delle molecole di una sostanza attraverso materiali porosi; la propagazione di qualche proprietà tra le unità di una popolazione biologica, e così via.

Feller in una serie di importanti lavori, pubblicati a iniziare dal 1936 (Feller 1936), sviluppò l'indirizzo analitico di Kolmogorov: in un primo tempo studiando problemi di esistenza e unicità delle equazioni di Kolmogorov. Successivamente ‒ a causa del fatto che non sempre si verificano le 'caratteristiche locali' che portano alle equazioni di Kolmogorov e che, quando esistono, non sempre conducono a una determinazione univoca del processo ‒ Feller avanzò e sviluppò l'idea ‒ manifestatasi assai utile ‒ di impiegare la teoria dei 'semigruppi' dovuta a Hille e Yosida. In base a essa, l'equazione di Chapman-Kolmogorov equivale alla proprietà di semigruppo generalizzato; nel caso di processi omogenei, il semigruppo generalizzato si riduce a quello usuale. È interessante notare come, nell'approccio analitico di Kolmogorov e Feller, i valori attesi di certi funzionali di processi di diffusione corrispondano alle soluzioni di problemi al contorno per le equazioni di Kolmogorov.

Come è facile immaginare, questa connessione può essere foriera di interessanti e sensazionali scambi fra CdP e analisi matematica.

Accanto ai metodi analitici brevemente descritti, lo studio delle traiettorie dei processi markoviani richiede l'impiego di strumenti più propriamente probabilistici. Doeblin, in questa direzione, ottenne risultati di primaria importanza, in lavori pubblicati tra il 1937 e il 1940, concernenti processi markoviani omogenei. Doob contribuì significativamente allo studio delle traiettorie in condizioni più ampie di quelle considerate da Doeblin, scoprendo tipi di discontinuità ben più complicati di quelli posti in evidenza dal primo autore. Un approccio decisamente più probabilistico fu inaugurato da Itô nel 1944; esso consiste nella rappresentazione del processo di diffusione {X(t):t≥t₀} come soluzione della equazione differenziale stocastica (Itô 1944)

[21] dX(t)=a(t, X(t))dt +σ(t, X(t))dW(t)

dove W è un processo di Wiener con σ²=1.

In parole povere, X(t) è considerato legato a un moto browniano W(t) in modo che, se X(t)=x, allora l'incremento ΔX(t)=X(t+Δt)−X(t) sia press'a poco uguale a a(t,x)Δt++σ(t,x)ΔW(t).

Processi stazionari

Il concetto di successione stazionaria venne introdotto nel CdP da Chinčin (nel 1933) in relazione ad applicazioni nel campo della meccanica statistica. In un successivo lavoro del 1934, egli avviò ricerche su un'altra categoria di successioni aleatorie, quelle 'stazionarie in senso lato', che avrebbero poi trovato fecondi campi di applicazione, oltre che in meccanica statistica, anche in economia e meteorologia, per l'investigazione di fenomeni tendenzialmente periodici. I lavori di Chinčin ebbero un forte impatto anche sugli studi teorici, nelle direzioni che ora brevemente descriveremo (Chinčin 1934).

Ricordato che (X_n)_n≥0 si dice 'stazionaria' se le sue distribu zioni di dimensione finita sono invarianti rispetto a una trasla zione nel parametro, si ha che i termini di una successione stazionaria sono identicamente distribuiti; inoltre, se E∣X₁∣²⟨∞, allora risulta E(X_nX_n+k)=ϱ(k) per n,k≥0. Se E(X_n)≡0, ϱ è detta 'funzione di covarianza'. Ora, esistono successioni non stazionarie di numeri aleatori con momento secondo finito, con speranza matematica costante (possiamo supporla identicamente nulla, senza ledere la generalità del discorso) e tali che E(X_nX_n+k) sia funzione generalmente dipendente da k ma non da n; tali successioni si dicono 'stazionarie in senso salto'. Per ragioni di compattezza espositiva, conviene porsi in un contesto lievemente più gene rale, in cui i termini delle successioni considerate sono numeri aleatori a valori complessi; in tal caso la covarianza di (X_n,X_n+k) è definita da

dove con

si indica il coniugato di a. La definizione di stazionarietà, e i relativi fondamentali risultati dovuti a Chinčin, vennero adattati a processi con parametro continuo da Kolmogorov nel 1938. In successivi lavori del 1940 e 1941, lo stesso Kolmogorov inaugurò un nuovo approccio allo studio dei processi stazionari in senso lato, basato sulla constatazione che la classe dei numeri aleatori, con momento secondo finito e speranza matematica nulla, costituisce uno spazio di Hilbert quando il prodotto interno di due punti sia definito come covarianza dei corrispondenti numeri aleatori. Uno degli obiettivi principali di Kolmogorov era quello di risolvere il problema della previsione di un elemento della successione, non ancora osservato, sulla base dei precedenti elementi osservati (Kolmogorov 1941). Problemi di questo tipo, connessi fra l'altro con la difesa controaerea, furono attentamente considerati durante il secondo conflitto mondiale. Accade così che, contemporaneamente a Kolmogorov che lavorava in Unione Sovietica, negli Stati Uniti e in modo completamente indipendente, le stesse questioni venissero affrontate da Wiener e risolte nel 1942 anche se pubblicate qualche anno dopo (Wiener 1949).

Martingale

Consideriamo, ancora una volta, la successione di somme S_n di numeri aleatoriindipendenti, che assumono valori −1 e 1 con uguale probabilità; allora, posto S0≡0:

[22]  E(S_n+1∣Sn,…,S₁,S₀) = S_n per ogni n≥0.

Questo risultato conferma l'idea intuitiva che il valore atteso del capitale dopo (n+1) colpi a testa e croce (con una moneta equilibrata), nell'ipotesi che sia noto l'esito negli n colpi precedenti, coincida col capitale accumulato dopo n colpi (gioco equo!). Jean-André Ville, in una monografia sul concetto di Kollektiv usò il termine 'martingala' per designare una qualunque successione di numeri aleatori (X_n)_n≥0 tale che

[23] E(X_n+1∣X₀,…,X_n)=Xn per ogni n

(l'uguaglianza nell'espressione precedente è da intendersi 'quasi certamente').

Esempi di martingale ricorrono, come già ricordato, nei lavori di Bernštejn dedicati allo studio di somme di numeri aleatori non indipendenti e in lavori di Lévy a partire dal 1935; in questi ultimi lavori si trovano anche i germi della teoria generale. Fu comunque Doob, con un lavoro apparso nel 1940 e, successivamente, con il trattato più volte citato sui processi aleatori, a porre in evidenza le proprietà di successioni martingale e molte delle loro svariate applicazioni.

Fra i teoremi più importanti va menzionato il teorema di convergenza: se (X_n)_n≥1 è una martingala e

allora (X_n)_n≥1 converge quasi certamente a un numero aleatorio con speranza matematica finita.

Le 'scuole' dei probabilisti

Abbiamo scelto di descrivere lo sviluppo storico del CdP suddividendo i contributi originali per grandi temi di ricerca. Ciò non contribuisce a porre in luce il formarsi e l'avvicendarsi di 'Scuole' nelle varie aree geografiche interessate. A questa carenza cercheremo di rimediare, però, nella presente sezione conclusiva.

Le comunità scientifiche che all'inizio del secolo potevano vantare una tradizione di studi nel campo delle probabilità erano la russa e la francese.

Per quanto concerne la prima, abbiamo avuto modo di citare la cosiddetta Scuola di San Pietroburgo, creatasi intorno a Čebyšev e resasi illustre, anche, per l'opera di Ljapunov, Markov e Bernštejn. Caratteristiche riconosciute del gruppo costituitosi a San Pietroburgo furono il rigore nell'affrontare problemi classici, quali le leggi dei grandi numeri e il problema centrale del limite, la messa a punto di metodologie generali per l'analisi di ampie classi di questioni probabilistiche, e la proposta di nuovi schemi probabilistici, quali le catene di Markov. Il lavoro degli studiosi di San Pietroburgo non ebbe, purtroppo, tempestiva e adeguata diffusione nei paesi occidentali; unica eccezione l'Italia, dove divenne noto attraver so gli scritti di Cantelli e, soprattutto, grazie al trattato di Castelnuovo. Intorno al 1925, Mosca divenne il maggior centro degli studi probabilistici dell'Unione Sovietica. La cosiddetta 'Giovane Scuola di Mosca', nata sulla base degli indirizzi di Chinčin e Kolmogorov, sarebbe ben presto divenuta polo di riferimento mondiale, senza distinzioni settoriali perché, come abbiamo visto nei precedenti paragrafi, esercitò un influsso determinante su tutte le questioni più importanti poste all'attenzione dei probabilisti moderni. Nel 1956 vide la luce una rivista sovietica di probabilità "Teoriya Veroyatnostei i ee Primeneniya" che, tradotta in inglese dalla SIAM (Society of Industrial and Applied Mathematics) sotto il titolo "Theory of probability and its applications", ha occupato, e occupa, una posizione di grande prestigio nel panorama internazionale.

In Francia verso la fine del XIX sec. e gli inizi del XX, studiosi come Jules-Henri Poincaré (1854-1912) e Borel si dedicarono alla stesura di trattazioni ampie e sistematiche del CdP, senza però riuscire a ottenere risultati soddisfacenti, né dal punto di vista della buona organizzazione della materia né, tanto meno, sotto il profilo della critica dei fondamenti. Per esempio, i contributi degli studiosi russi di San Pietroburgo vi furono totalmente ignorati. Verso il 1920, fu attratto dal CdP un matematico già noto per i suoi studi di analisi funzionale nell'indirizzo di Volterra: Lévy. Il percorso degli studi di Lévy nel campo delle probabilità può essere suddiviso in tre tratti, non disgiunti: il primo dedicato alle leggi limite, il secondo ai processi a incrementi indipendenti e alle martingale, il terzo allo studio delle traiettorie del processo del moto browniano. Di alcuni dei contributi specifici del matematico francese in questi settori abbiamo già detto. Qui ricorderemo, invece, l'influenza del suo Calcul des probabilités (1925) sulla diffusione della disciplina nei paesi occidentali. Oltre a riscoprire e a sviluppare molti dei risultati dovuti a Čebyšev e discepoli (si veda l'analisi e l'uso della funzione caratteristica), Lévy procedette alla riformulazione generale di problemi classici, come quello centrale del limite, e a indicare i procedimenti appropriati per risolverli. Egli ebbe pochi allievi diretti (tra essi, Doeblin e Loève) perché, come annota Loève, non professòcorsi universitari veri e propri e, alla École des Mines o alla École Polytechnique dove insegnò, non fu titolare di un insegnamento di CdP. A dispetto di ciò, i suoi scritti influenzarono enormemente lo studio delle probabilità in Unione Sovietica e negli Stati Uniti e, naturalmente, anche l'attuale, molto attiva, scuola francese.

In altri paesi europei la storia del CdP si intreccia con quella degli studi attuariali: il CdP come strumento per le decisioni tecniche delle compagnie di assicurazione. Così fu in Svezia e in altri paesi scandinavi fino al 1930, e in Italia fino allo scoppio del secondo conflitto mondiale.

Caposcuola del gruppo di Stoccolma fu Cramér, i cui lavori abbiamo più volte ricordato nei precedenti paragrafi. Del gruppo di Stoccolma fece parte anche Feller, dal 1934 al 1939, anno del suo trasferimento definitivo negli Stati Uniti. Di lui abbiamo citato i lavori sul teorema centrale del limite e sui processi markoviani. Altri componenti del gruppo si occuparono, principalmente, di modelli stocastici connessi coi rami elementari delle assicurazioni, di teoria dei processi stazionari e delle loro applicazioni alldelle serie temporali, e di quel settore dell'inferenza statistica che, oggi, è comunemente designato come statistica dei processi aleatori. Per avere un'idea del buon livello raggiunto dal gruppo raccolto attorno a Cramér, basti ricordare i nomi di Hermann Wold, Ove Lundberg e Ulf Grenander che ne furono membri.

Per quanto concerne l'Italia, abbiamo già ricordato l'importanza che ebbe il trattato di Castelnuovo, pubblicato in prima edizione nel 1919, per la diffusione della probabilità classica in Italia. In effetti, gli studiosi di maggior prestigio internazionale furono Cantelli e de Finetti, che lavorarono in modo completamente indipendente e in direzioni di ricerca sostanzialmente diverse. Dei loro notevolissimi contributi abbiamo riferito nelle parti appropriate del presente scritto. Qui ricorderemo che Cantelli fondò nel 1930 il "Giornale dell'Istituto Italiano degli Attuari" (GIIA). Tale giornale, fino allo scoppio della Seconda guerra mondiale, ospitò i lavori dei più illustri probabilisti dell'epoca.

Verso la fine degli anni Trenta, lo studiodelle probabilità incominciò a essere considerato con crescente interesse anche negli Stati Uniti. Gli artefici di questa rinascita furono Feller e Doob. Del primo ricorderemo, ancora, la pubblicazione, nel 1950, del primo volume di un trattato (Feller 1950-71) che tanta parte avrebbe avuto nella formazione di base dei giovani probabilisti. Del secondo non si può non citare il trattato sui processi aleatori, a cui abbiamo fatto più volte riferimento, sia per l'originalità di molti dei risultati contenuti, sia per l'aver rappresentato, per molto tempo, la prima guida sistematica alla teoria generale dei processi aleatori. Oggi la qualità degli studi probabilistici negli Stati Uniti è di altissimo livello ed è testimoniata da una celebre rivista specializzata di CdP, "The annals of probability" che, con "The annals of statistics", sostituisce dal 1973 la vecchia rivista "The annals of mathematical statistics" nata nel 1930.

Dall'inizio degli anni Cinquanta, anche la presenza giapponese nella ricerca in campo probabilistico è tutt'altro che trascurabile. Basti qui richiamare i già citati contributi di Itô ai processi a incrementi indipendenti e all'elaborazione del calcolo stocastico.