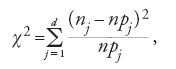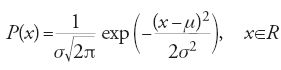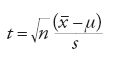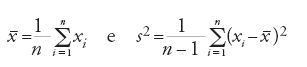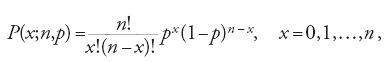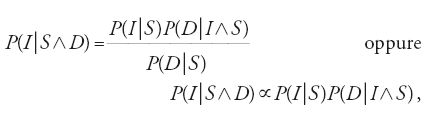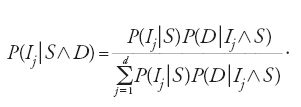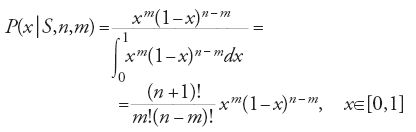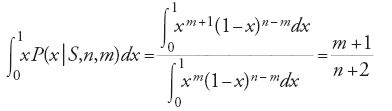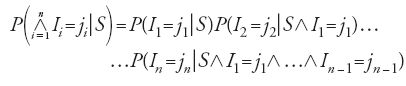La seconda rivoluzione scientifica: matematica e logica. La statistica metodologica

di Domenico Costantini - Storia della Scienza (2004)

Domenico Costantini

La statistica metodologica

La statistica metodologica è la disciplina che, sulla scorta della descrizione di certe caratteristiche di fenomeni riscontrate nel corso di osservazioni, sperimentali o meno, mira alla conoscenza delle medesime caratteristiche in fenomeni analoghi non ancora osservati. Nel seguito cercheremo di chiarire il significato di tale affermazione, per ora abbastanza oscura, che nondimeno pone in risalto come questa disciplina, detta anche statistica inferenziale, unitamente alle inferenze statistiche che la sostanziano, consista nell'affermare qualcosa circa avvenimenti non ancora accaduti o comunque sconosciuti per lo meno a chi compie l'inferenza. Degli altri due aggettivi con i quali a volte questa disciplina viene qualificata, ossia 'induttiva' e 'matematica', il primo ci appare corretto dal momento che fare asserzioni circa qualcosa che non si conosce è senza dubbio un modo di compiere un'induzione; il secondo, al contrario, è pleonastico poiché con esso si intende porre in risalto come nel compiere inferenze statistiche si faccia uso di strumenti matematici, e questo è ovvio dal momento che ogni moderna disciplina scientifica utilizza largamente gli strumenti concettuali elaborati della matematica.

Le questioni affrontate dalle inferenze statistiche sono essenzialmente di due tipi: da un lato, il controllo di ipotesi probabilistiche, dall'altro, la stima del valore sconosciuto di una grandezza. Le soluzioni proposte per le suddette questioni risultano diverse in accordo con le filosofie, a volte molto distanti, delle varie scuole di pensiero. Nelle pagine che seguono cercheremo di affrontare questa problematica da una prospettiva probabilisticamente corretta, situandola nel contesto storico in cui prese corpo e si sviluppò. Tuttavia, prima di prendere in esame le varie inferenze statistiche, intendiamo porre in evidenza un aspetto fondametale della statistica metodologica; ci riferiamo al fatto, inoppugnabile, che senza ipotesi non è possibile compiere alcuna inferenza statistica. A seconda del tipo di inferenza le ipotesi cambieranno: in alcuni casi saranno forti in altri meno; in ogni eventualità, senza avere ipotizzato alcunché, non è possibile andare al di là delle osservazioni.

I test di significatività

La struttura dei test di significatività è ipotetico-deduttiva in ragione del fatto che essi rappresentano l'adattamento del metodo galileano all'eventualità in cui le leggi, da sottoporre al vaglio dell'esperienza ed eventualmente confutare, siano probabilistiche. Sostanzialmente il metodo galileiano è un procedimento atto a controllare ipotesi avanzate nel corso della ricerca scientifica; consiste infatti nel sottoporre al vaglio dell'esperienza assunzioni ipotetiche per corroborarle o confutarle a seconda che le osservazioni siano in accordo o in disaccordo con le assunzioni avanzate. Tuttavia, non tutte le assunzioni che possono essere formulate sono di natura deterministica o, detto più chiaramente, sono affermazioni che non contemplano alcuna eccezione. Relativamente alle nascite umane, per esempio, l'assunzione da controllare potrebbe riguardare la percentuale delle nascite di sesso maschile ‒ e per differenza quelle di sesso femminile ‒ che, in prima istanza, potremmo porre pari al 50% dei nati. Proprio di questo tipo è un'ipotesi che troviamo avanzata nel primo test di significatività correttamente fomulato di cui si abbia notizia. Si tratta dell'analisi di John Arbuthnot Of the laws of change, or a method of calculation of the hazards of games (1692), volta a individuare la non accidentalità della prevalenza delle nascite maschili al fine di attribuirne la regolarità all'intervento della divina provvidenza. Nella seconda metà dell'Ottocento, principalmente ma non esclusivamente in ragione dell'affermarsi della teoria cinetica dei gas e di quella darwiniana dell'evoluzione, in ambito scientifico furono utilizzate maggiormente leggi statistiche con le quali non si afferma che tutti gli elementi (o unità statistiche) di un certo insieme (o popolazione) godano della stessa proprietà o attributo, ma piuttosto che solo porzioni di quegli elementi posseggano uno degli attributi, mutuamente esclusivi ed esaustivi, di una classe come, per esempio, quella delle possibili velocità di una molecola (Boltzmann 1909). Sorse allora impellente la necessità di controllare siffatte leggi che, non escludendo alcuna delle possibilità, non possono essere affrontate col metodo di Galilei. Tale metodo confuta una legge solo nel caso in cui le osservazioni rivelino la sua falsità, quando cioè si constata che un elemento si comporta diversamente da quanto la legge stabilisce essere valido per tutta la popolazione senza eccezione alcuna. Proprio a ragione della sua struttura, vale a dire dal contemplare possibili eccezioni, una legge statistica non potrà mai essere falsata, per lo meno in senso stretto, come può essere dimostrata falsa una legge quando l'osservazione sperimentale consenta di constatare l'esistenza di un'eventualità che quella aveva escluso.

La possibilità di confutazioni di questo genere era già stata esplorata fin dai primi studi sulla probabilità e la statistica, ma è solo nella seconda metà dell'Ottocento, segnatamente a opera di Wilhelm Lexis (1837-1914) e Karl Pearson (1857-1936), che i test di significatività furono chiaramente formulati. Il loro statuto epistemologico venne esplicitamente definito senza tuttavia essere approfondito nei dettagli; tale approfondimento peraltro non è ancora stato compiuto fino in fondo. Per le ragioni che abbiamo segnalato, lo scopo precipuo dei test di significatività consiste nel sottoporre a controllo, servendosi dei dati d'osservazione, asserzioni, di cui si è ipoteticamente assunta la validità, relative a distribuzioni di probabilità che potrebbero regolare la totalità delle osservazioni che possono essere compiute. È stato ideato un numero molto elevato di test di questo tipo ed è pertanto impossibile non solo passarli tutti in rassegna ma anche parlare di una consistente porzione di essi. Ci limiteremo a descriverne due dei più noti, che rappresentano i capostipiti di queste inferenze statistiche e che molto chiaramente ne evidenziano le caratteristiche salienti; dopo tale descrizione, cercheremo di mettere in risalto queste caratteristiche.

Nonostante il metodo proposto da Lexis possedesse già tutte le caratteristiche che individuano un test di significatività, fu solo con il test del chi-quadro, proposto all'inizio del Novecento da Pearson, che questi test entrarono a pieno titolo nel bagaglio della sperimentazione scientifica. Questo test è sostanzialmente un'inferenza statistica che intende stabilire se una distribuzione di probabilità si conforma a una distribuzione di frequenze relative ottenuta a seguito di n osservazioni eseguite per decidere di quali attributi, fra d possibili, godono n unità statistiche osservate. Avendo denotato con {n₁,…,n_j,…,n_d}, ∑^d_j₌₁n_j=n, i numeri, o frequenze, delle unità statistiche cui si addice il j-esimo (j=1,2,…,d) attributo, ci si chiede se le frequenze relative di tutte le possibili osservazioni, la cui cardinalità supponiamo numerabile, e di cui quelle compiute sono un sottoinsieme proprio, sono distribuite secondo la distribuzione di probabilità {p₁,…,p_j,…,p_d}, ∑^d_j₌₁p_j=1, detta distribuzione nulla (null), a volte indicata col simbolo H₀. La risposta a questo quesito, che per ragioni su cui torneremo può al più essere negativa, passa, dapprima, attraverso la determinazione del valore del chi-quadro

ossia di quel numero che Pearson aveva individuato per misurare la discrepanza fra le due distribuzioni coinvolte nel test di significatività: la distribuzione empirica, come si dice di solito, e la distribuzione teorica corrispondente alle frequenze che l'insieme delle unità statistiche osservate avrebbe dovuto presentare se queste fossero distribuite esattamente come si ipotizza sia distribuita la popolazione di riferimento. Questo valore, che è zero quando per ogni j, n_j=np_j, e aumenta con le differenze fra n_j e np_j, costituisce uno dei modi possibili di compendiare le discrepanze esistenti fra le frequenze di fatto osservate e le probabilità della distribuzione da controllare.

A questo punto è opportuno osservare che, di per sé, la [1] non consente di stabilire, se non in termini meramente numerici, se la discrepanza fra le distribuzioni empirica e teorica sia elevata o meno. Ciò significa che una volta determinato il valore della [1], rimane senza risposta il quesito se la discrepanza accertata indichi una significativa differenza fra la distribuzione empirica e quella teorica. L'idea che si fece largo nella seconda metà dell'Ottocento fu di misurare probabilisticamente il valore numerico della discrepanza, vale a dire di determinare la probabilità di verificarsi che avrebbe avuto il valore di fatto osservato se la distribuzione (di probabilità) teorica avesse regolato il fenomeno studiato. A questo riguardo è necessario notare che una simile idea era strettamente legata all'emergere di nozioni statistico-probabilistiche nelle scienze della Natura del periodo che stiamo esaminando, un periodo in cui si andava scoprendo che le caratteristiche macroscopiche di un gas sono riconducibili a caratteristiche microscopiche delle molecole che lo costituiscono: la temperatura alla velocità media delle molecole del gas, la pressione al numero medio delle loro collisioni con le pareti del contenitore.

Per rispondere al quesito che ha motivato il controllo è necessario illustrare con maggiori particolari la questione che si intende affrontare mediante un test del chi-quadro, vale a dire se le osservazioni compiute riassunte da {n₁,…,n_j,…,n_d} consentono di sostenere che la popolazione di riferimento è distribuita come {p₁,…,p_j,…,p_d}. Avendo chiaro questo punto fu abbastanza naturale, almeno nel clima culturale che abbiamo ricordato, fornire al quesito una risposta probabilistica, cioè giudicare la discrepanza [1] servendosi della distribuzione campionaria (sampling distribution), cioè delle probabilità di tutti i possibili gruppi di osservazioni, i campioni come si dice, che avrebbero potuto essere estratti dalla popolazione di riferimento. In linea teorica, a questa distribuzione si perviene supponendo che la popolazione di riferimento sia distribuita come {p₁,…,p_j,…,p_d} e calcolando poi la probabilità di tutti i possibili valori di χ². Questo calcolo, di per sé non semplice, è complicato ulteriormente dal fatto che non può essere eseguito una volta per tutte ma deve essere effettuato ogni volta in accordo con tutti i valori possibili di n. Per superare queste difficoltà, seguendo un'indicazione dello stesso Pearson, il calcolo della distribuzione campionaria viene compiuto supponendo n maggiore di qualunque valore fissato, cioè calcolando la probabilità nell'ipotesi che n tenda all'infinito. Si noti inoltre che questo calcolo viene solitamente eseguito assumendo che le varie osservazioni siano regolate dalla stessa probabilità e siano inoltre stocasticamente indipendenti; le osservazioni vengono quindi eseguite con modalità atte ad assicurare, almeno approssimativamente, la validità delle suddette supposizioni. Con queste assunzioni il calcolo della distribuzione campionaria diviene relativamente facile e consente di determinare la densità di probabilità con la quale un valore di χ² pari a quello trovato è contenuto in un dato intervallo e, quindi, anche la probabilità con la quale si sarebbe potuto osservare un campione che avesse presentato frequenze uguali a quelle del campione di fatto osservato, qualora la popolazione di riferimento sia distribuita come {p₁,…,p_j,…,p_d}. Se questa probabilità è inferiore a un valore dato ‒ per esempio 0,05, 0,01 oppure 0,005 ‒ si conclude che la popolazione da cui il campione esaminato è stato tratto non è distribuita come {p₁,…,p_j,…,p_d}.

La scelta di Pearson di ricorrere alla distribuzione limite fu criticata da Richard von Mises (1883-1953) che, proprio con riferimento ai contributi di Lexis, propose di misurare l'anzidetta discrepanza non già supponendo che la numerosità del campione cresca oltre ogni limite fissato, bensì determinando di volta in volta l'accettabilità o meno della discrepanza basandosi sulla constatazione che il campione osservato fosse interno, o meno, a un intervallo avente come punto centrale la media della distribuzione calcolata relativamente all'effettiva numerosità del campione. Questo suggerimento, che d'altro canto contiene in germe la possibilità di chiarire i fondamenti dei test di significatività, non fu purtroppo seguito anche, ma forse soprattutto, perché l'uso prevalente di tali test, almeno all'inizio del secolo scorso, fu operato nelle ricerche biologiche, in particolare in quelle connesse alla genetica di popolazione e alla sperimentazione agricola, compiute essenzialmente nei paesi di lingua anglosassone nei quali era preponderante l'influenza del pensiero di Pearson.

Il secondo test di significatività di cui ci occupiamo fu ideato da Student, lo pseudonimo con cui William S. Gossett (1876-1937) firmò l'articolo On the probable error of a mean (1908), in cui il test fu proposto: esso è universalmente noto con il nome di t di Student. Il quesito che in questo caso ci si pone è analogo a quello che si è appena visto ma la forma della domanda è diversa in ragione del fatto che ora si considera una popolazione, le cui unità statistiche sono caratterizzate da attributi misurabili, che si suppone abbia distribuzione di Gauss con valor medio μ noto e varianza, σ², sconosciuta, cioè una popolazione distribuita come

Di nuovo, avendo eseguito n osservazioni, che hanno condotto ai valori {x₁,…,x_i,…,x_n} supposti reali, ci si chiede se il valore medio della popolazione di riferimento sia conforme a quello del campione, vale a dire a quello che le osservazioni hanno permesso di riscontrare. Questa volta il valore di cui si calcola la distribuzione campionaria è il t di Student, ossia

in cui

sono la media e la varianza del campione. Anche in questo caso, servendosi della [2] si calcola la distribuzione campionaria della [3] e se il valore osservato di t giace in un intervallo la cui probabilità è inferiore a uno dei valori visti precedentemente, si conclude che il valore medio della popolazione non è conforme a quello del campione e pertanto che il campione esaminato non è stato tratto da una popolazione distribuita secondo la [2].

Anche la scelta della distribuzione gaussiana, e non di un'altra distribuzione di probabilità, è da ascrivere al contesto culturale tipico del periodo a cavallo tra XIX e XX secolo. La gaussiana, o distribuzione normale come la chiamano gli statistici anglosassoni, era stata individuata seguendo due diverse linee di pensiero: da Abraham de Moivre (1667-1754) e Pierre-Simon de Laplace (1749-1827), come il limite della distribuzione bernoulliana binomiale

quando n cresce oltre ogni limite fissato; da Carl Friedrich Gauss (1777-1855) come la distribuzione che regola il presentarsi degli errori nel corso della misurazione del valore sconosciuto di una grandezza. Questa distribuzione era quindi stata utilizzata, da un lato, nella determinazione dei valori della bernoulliana al fine di evitare il difficile calcolo dei fattoriali che vi compaiono, dall'altro nella teoria degli errori, segnatamente in astronomia, la disciplina relativamente alla quale Gauss aveva ideato la sua derivazione. Tuttavia verso la metà dell'Ottocento Lambert-Adolphe-Jacques Quételet (1796-1874) si era accorto che la gaussiana è in grado di rappresentare con sufficiente approssimazione il distribuirsi di caratteristiche antropometriche, come per esempio la circonferenza toracica dei coscritti scozzesi. Questa constatazione aveva diffuso la convinzione, confermata poi dalle osservazioni, che molte grandezze, non necessariamente legate allo studio di caratteristiche umane ma anche del regno animale o vegetale, avessero distribuzione normale. Gosset, non avendo alcuna indicazione circa la distribuzione della grandezza che intendeva studiare ‒ nel suo caso si trattava di ore di sonno acquisite a seguito dell'assunzione di bromuro di iosciamina ‒ aveva supposto che la grandezza oggetto della sua ricerca non fosse essenzialmente diversa dalle molte che si sapeva essere distribuite secondo la leggedi Gauss. Ecco la ragione della scelta, tutto sommato arbitraria, della distribuzione normale per la popolazione dalla quale il campione viene tratto.

Tornando ai test di significatività, la struttura di uno di essi è quindi la seguente: si suppone che una popolazione sia distribuita in accordo con una data legge di probabilità H0, l'ipotesi nulla; da questa popolazione si estrae un campione che, di volta in volta e in accordo con modalità diverse che ora non analizziamo, viene sintetizzato nel compendio C* (nei due test esaminati questi compendi erano [1] e [3]), si calcola poi, subordinatamente alla validità di H0, la densità di probabilità P(C∣H0), C∈A, dei valori di C appartenenti a un dato ambito A; infine, se il valore di P(C*∣I) è interno a un intervallo precedentemente fissato, si conclude che l'ipotesi relativa alla distribuzione della popolazione non è conforme alle osservazioni, cioè che H0 non è la di stribuzione della popolazione da cui è stato estratto il campione; al contrario, se ciò non avviene non si arriva ad alcuna conclusione.

Quello che abbiamo esposto relativamente ai test di significatività ne evidenzia le caratteristiche fondamentali. In primo luogo, l'intera argomentazione, una volta determinato P(C∣H0), si basa su P(C*∣H0), detta la verosimiglianza (likelihood) di H0. Questa è una probabilità ipotetica dal momento che è la probabilità di C*, il cui valore di verità, riferendosi a fattiaccaduti, è il vero, subordinatamente alla validità di assunzione, H0, il cui valore di verità è ignoto. Sul significato della verosimiglianza torneremo in seguito. In secondo luogo, un test di significatività consente solo di confutare un'ipotesi probabilistica, non di validarla: ciò deve essere tenuto ben presente; inoltre, la confutazione cui si perviene non è mai definitiva giacché ulteriori osservazioni, aggiunte ovviamente a quelle che hanno condotto a C*, potrebbero portare a un nuovo compendio C+≠C* esterno all'intervallo fissato.

I test di ipotesi

Molti autori, seguendo le indicazioni avanzate negli anni Trenta del Novecento da Jerzy Neyman (1894-1981) ed Egon Pearson (1895-1980), intendono i test di significatività come un caso particolare dei test di ipotesi, cioè di quelle inferenze statistiche che, oltre all'ipotesi nulla H0, prendono in considerazione anche un'ipotesi alternativa H1, sostanzialmente la negazione della prima. Dopo aver determinato le verosimiglmianze P(C*∣H0) e P(C*∣H1), servendosi di queste probabilità ipotetiche accettano, come dicono, H0 e conseguentemente rifiutano H1 oppure rifiutano H0 e conseguentemente accettano H1. Vengono pertanto introdotte le nozioni di errore di primo tipo, quello commesso quando l'ipotesi nulla è rifiutata mentre è corretta, e di errore di secondo tipo, quello che si commette quando l'ipotesi nulla è accettata mentre non è corretta. L'argomentazione consiste essenzialmente nel ragionare su due verosimiglianze incomparabili in ragione del fatto che si riferiscono a due ipotesi contradditorie. Per essere corrette dal punto di vista probabilistico, siffatte comparazioni, oltre alle probabilità ipotetiche, devono tener conto anche delle probabilità iniziali di cui parleremo fra breve.

I sostenitori dei test di ipotesi pretendono di essere in grado di trattare probabilisticamente due ipotesi evitando il ricorso alle probabilità iniziali e, a sostegno della loro pretesa, portano un modo ambiguo di intendere la probabilità. Infatti questo approccio all'inferenza statistica risente dei dubbi che a metà del Novecento erano sorti circa la validità dell'interpretazione frequentista della probabilità, per cui la probabilità di un evento è il limite cui nel lungo andare tende la frequenza relativa dell'evento in questione (Mises 1919), e della conseguente accettazione, almeno parziale, della definizione soggettivista della probabilità, per cui la probabilità è null'altro che la credenza che una ben individuata persona nutre nel verificarsi di un dato evento (de Finetti 1937b).

La stima

Contrariamente a ciò che avviene per i test di significatività, la natura delle stime statistiche è induttiva. Questo fondamentale aspetto della stima statistica fu messo chiaramente in luce già da Laplace in uno dei suoi primi lavori scientifici presentato nel 1774 nelle "Mémoire de l'Académie Royale des Sciences", dal titolo Mémoire sur la probabilité des causes par les événements. Il grande scienziato aveva affrontato il problema di pervenire, sulla scorta della conoscenza della frequenza con cui un certo evento era accaduto, alla probabilità con cui lo stesso evento si sarebbe verificato in una futura occasione. Questa probabilità era calcolata facendo riferimento alle probabilità delle cause che potrebbero aver determinato il verificarsi dell'evento.

Questo approccio induttivo alle inferenze statistiche fu prevalente dalla metà del Settecento fino alla fine dell'Ottocento, per la verità senza che ciò escludesse del tutto l'approccio ipotetico-deduttivo. Sono infatti della seconda metà del Settecento sia la memoria di Laplace che abbiamo testé ricordato sia quella di Thomas Bayes (1702-1761) in cui per la prima volta fu chiaramente esposto il principio delle probabilità composte, di cui parleremo fra breve. In un'altra formulazione questo principio è comunemente noto come teorema di Bayes che, per parte nostra, preferiamo chiamare regola di Bayes-Laplace dal momento che Laplace ne fece uso, verosimilmente senza conoscere il contributo di Bayes, con un rigore intellettuale e un'ampiezza di vedute del tutto assenti nel lavoro del pastore presbiteriano inglese.

Una stima statistica prende le mosse da una serie di osservazioni, sperimentali o meno, operate su un campione di unità statistiche tratte da una data popolazione con l'intento di indurre alcunché circa le osservazioni che successivamente potrebbero essere compiute sulle restanti unità della popolazione. Il principio probabilistico su cui si basano le stime è quello delle probabilità composte o regola del prodotto:

[6] P(I⋀I'∣S⋀D)=P(I∣S⋀D)P(I'∣S⋀D⋀I),

in cui I e I′ denotano le ipotesi, D i dati (evidence) cui si è pervenuti mediante le osservazioni sperimentali e S le conoscenze di sfondo, a volte dette di contorno, cioè quelle di sponibili prima di eseguire le osservazioni. Dalla [6] applicata prima a P(I∧D∣S) e poi a P(D∧I∣S), che sono ovviamente uguali, segue la regola di Bayes-Laplace:

in cui P(I∣S∧D) è la probabilità finale di I, P(I∣S) la probabilità iniziale sempre di I, P(D∣I∧S) la verosimiglianza di I e P(D∣S) è una costante di normalizzazione.

La [7] mostra la struttura logica di una stima statistica. Con ciò intendiamo affermare che operare una stima siffatta significa determinare la probabilità finale di un'ipotesi servendosi della sua probabilità iniziale e della sua verosimiglianza (Jeffreys 1961; Daboni 1982).

Ne consegue la grande importanza dei significati che possono essere attribuiti alle probabilità coinvolte nella regola di Bayes-Laplace. La probabilità finale è la probabilità di un'ipotesi determinata sulla base della conoscenza dei dati sperimentali e delle conoscenze di sfondo, vale a dire subordinatamente a tutto ciò che si conosce al momento di compiere la stima. La probabilità iniziale è invece la probabilità dell'ipotesi determinata sulla base delle sole conoscenze di sfondo, ossia subordinatamente a tutto ciò che si conosce prima di aver compiuto le osservazioni che hanno condotto ai dati. La verosimiglianza, infine, è la probabilità che i dati avrebbero avuto di essere accertati se il loro presentarsi fosse determinato, oltre che da tutto ciò che è specificato nelle conoscenze di sfondo, dalla validità dell'ipotesi di cui ci si sta interessando; quindi, la verosimiglianza è una probabilità ipotetica nel senso che, al fine di determinare questa probabilità, si assume la verità di un'ipotesi il cui valore di verità è ignoto.

Quando si prenda in considerazione una classe di ipotesi {I_j:j=1,2,…,d} mutuamente esclusive (due qualsivoglia di esse non possono essere contemporaneamente vere) ed esaustive (una di esse deve necessariamente essere vera), allora la [7] diviene

Si consideri una grandezza i cui valori possibili x siano tutti contenuti nell'intervallo [0,1]; per semplicità, supponiamo che si tratti della probabilità dei risultati del lancio di una moneta da un euro della quale non si sappia se è o meno truccata a favore di una delle sue facce: queste sono le informazioni di sfondo disponibili. Laplace aveva considerato un'urna che racchiude infiniti biglietti bianchi e neri in un rapporto ignoto e, dopo aver estratto dall'urna un dato numero di biglietti bianchi e neri, si era posto la domanda su quale fosse la probabilità che, estraendo un nuovo biglietto, esso fosse bianco. Nel nostro caso la probabilità alla quale siamo interessati è quella del verificarsi dell'evento 'testa'. Sulla scorta delle informazioni di sfondo non è consentito privilegiare alcuno dei possibili valori di x; queste conoscenze ci conducono alla densità di probabilità iniziale

[9] P(x∣S)=1, x∈[0,1].

Si supponga poi di aver lanciato n volte la moneta e di aver ottenuto m≤n volte 'testa' e, ovviamente, n−m volte 'croce'. Se la probabilità di 'testa' è x allora quella di 'croce' è 1−x e i principî della probabilità ci assicurano che la verosimiglianza di x è

[10] P(m,n∣x,S)=x^m(1-x)^n-m, x∈[0,1],

cioè la probabilità di ottenere m 'teste' nel corso di n lanci se la probabilità di 'testa' è pari a x. La [8] ci fornisce quindi una densità di probabilità finale pari a

formula che consente di risolvere il problema. Infatti, sex è la probabilità di ottenere 'testa' lanciando la moneta, allora

[12] xP(x∣S,n,m)

è la probabilità di ottenere 'testa' al prossimo lancio. Questa è la probabilità che stiamo cercando solo nell'eventualità in cui x sia la probabilità di ottenere 'testa' con la moneta in questione. Ma non sappiamo se questa probabilità è effettivamente pari a x e pertanto arriviamo alla probabilità cercata integrando la [12] su tutti i valori possibili di x, ossia

che è la celeberrima regola di successione di Laplace.

Nonostante la sua semplicità, la stima appena descritta consente alcune importanti considerazioni di natura generale. In primo luogo, come abbiamo già detto, stimare il valore sconosciuto di una grandezza significa trasformare una probabilità iniziale in una finale, nel caso appena visto la [9] nella [11], per il tramite della verosimiglianza, la [10]. Quindi un'inferenza statistica non individua alcun valore preciso e neppure esclude alcuno dei valori possibili, infatti tanto la [9] quanto la [11] sono definite sullo stesso intervallo [0,1] che contiene tutti i possibili valori della probabilità di 'testa'. Ciò che invece può cambiare, e il cambiamento può essere notevole in accordo con il valore di n, cioè delle osservazioni effettuate, sono le distribuzioni di probabilità sui valori possibili.Per esempio, nell'eventualità in cui si siano effettuati n=10 lanci dei quali m=2 sono risultati 'testa', la distribuzione finale differisce profondamente da quella iniziale; infatti, limitandosi a considerare i valori medi e le varianze abbiamo: 1/2=0,5 e 1/12≃0,08 per la distribuzione iniziale e 3/12=0,25 e 27/1872≃0,01 per la distribuzione finale; questi valori mostrano come il valore medio, abbandonando il punto centrale dell'intervallo, si sia notevolmente spostato verso il suo estremo inferiore mentre si è considerevolmente ridotta la varianza.

Una particolare considerazione deve essere dedicata alla probabilità iniziale. La scelta della [9], nota anche come la di stri buzione uniforme, non è ovviamente la sola possibile. Essa fu privilegiata dagli statistici del periodo classico, segnatamente da Laplace. Questo, se dapprima facilitò lo sviluppo della statistica metodologica, con il tempo influì negativamente sull'approccio probabilistico alla stima poiché, sulla scorta della grande autorità scientifica di Laplace, la di stribuzione uniforme fu usata anche in casi in cui non trovava alcuna giustificazione; in breve, divenne un dogma. Nel Novecento tuttavia furono individuate numerose altre di stribuzioni che, meglio dell'uniforme, possono rappresentare le conoscenze di sfondo disponibili.

Un'eventualità in cui la distribuzione iniziale uniforme è necessaria è quella che si presenta quando si compia un test di ipotesi. Infatti se la probabilità iniziale dell'ipotesi nulla, H0, e di quella alternativa, H1, sono uguali, vale a dire se P(H0∣S)=P(H1∣S), allora queste due probabilità scompaiono dalla regola di Bayes-Laplace; quindi, le probabilità finali P(H0∣S,D)=P(H1∣S,D) delle due ipotesi sono determinate dalle loro verosimiglianze P(D∣H0,S) e P(D∣H1,S) e, a meno di una costante di proporzionalità, tutto ciò che può essere detto per le une vale anche per le altre. Questa constatazione mostra come i test di ipotesi rappresentino in realtà un caso molto particolare di stima statistica.

La massima verosimiglianza

Il dogma della distribuzione uniforme di cui si è appena detto venne aspramente criticato all'inizio del Novecento, in particolare da Ronald A. Fisher (1890-1962), uno dei maggiori statistici di quel secolo. La sua critica non si incentrò solo sulla distribuzione uniforme ma anche sulla regola di Bayes-Laplace, che egli riteneva impossibile da applicare nella maggior parte delle eventualità che si presentano nel corso della ricerca scientifica. Conseguentemente Fisher propose di sostituire alla probabilità finale la verosimiglianza sostenendo, inoltre, che questa nozione è il solo strumento concettuale atto a compiere induzioni scientifiche. In tal modo egli si pose fuori dalla tradizione probabilistica proponendo di stimare il valore sconosciuto di una grandezza mediante il principio della massima verosimiglianza, vale a dire scegliendo come stima del valore sconosciuto il valore per il quale la verosimiglianza raggiunge il massimo. Nell'esempio precedentemente citato questo valore è 2/10=0,2 che, come si vede, non è molto diverso dal valore medio della distribuzione finale. Con il crescere di n, diminuisce la differenza fra il valore stimato mediante la massima verosimiglianza e il valore medio della distribuzione finale determinata a partire da una distribuzione iniziale uniforme, di modo che le due stime presentano notevoli analogie, anche in considerazione del fatto che, sempre con il crescere di n, la varianza della distribuzione finale diminuisce. Resta comunque immutata la profonda differenza concettuale esistente fra considerare come risultato di una stima un ben preciso valore, eventualmente corredato con un intervallo di incertezza, e intendere una stima come la determinazione delle probabilità di tutti i valori possibili della grandezza esaminata.

Stima per intervalli

La stima operata sulla base della massima verosimiglianza è un esempio di stima puntuale, cioè di una stima che si conclude individuando un valore ben definito. Altri tipi di stime, qualificate come stime a intervalli, non si limitano a indicare uno dei valori possibili della grandezza ma si concludono individuando intervalli, detti solitamente di fiducia (confidence), all'interno dei quali, con determinate probabilità, di solito prossime a uno, dovrebbe trovarsi lo sconosciuto valore della grandezza. Se la stima è compiuta in accordo con la regola di Bayes-Laplace la specificazione di questi intervalli è banale poiché, se si conosce la distribuzione sull'insieme di tutti i valori possibili, è immediata la determinazione della probabilità di un suo sottoinsieme. Alcuni autori, reputando insuperabili le difficoltà poste dalla determinazione della probabilità iniziale, hanno cercato di eliminare questa probabilità dalla stima. In alcuni casi ‒ a questo riguardo, particolarmente degno di nota è il lavoro compiuto da Neyman attorno alla metà del XIX sec. (Neyman 1952a) ‒ tale eliminazione è stata operata correttamente e il risultato ha portato all'individuazione di intervalli all'interno dei quali, qualunque sia la distribuzione iniziale, giace con una data (ed elevata) probabilità il valore sconosciuto. Tuttavia questa strada può essere percorsa solo quando si possa ragionevolmente confidare nel 'lungo andare' (long run) mentre non è percorribile qualora la stima non debba o non possa essere ripetuta un elevato numero di volte. Per la verità, sono state individuate altre presunte strade per arrivare agli intervalli senza essere vincolati alla probabilità iniziale: sono però affette da gravi errori logici e quindi non riteniamo necessario parlarne.

La predizione probabilistica

Un altro modo di effettuare la stima del valore sconosciuto di una grandezza si pone, sostanzialmente anche se a rigore non letteralmente, nel solco tracciato dalla regola di successione di Laplace tornando in certo senso agli albori della metodologia statistica. Ci riferiamo alle inferenze predittive su cui lavorarono dapprima Rudolf Carnap (1891-1970) in un contesto logico e successivamente Thomas S. Ferguson in un contesto più propriamente statistico. Un'inferenza consiste nell'applicare la regola del prodotto a una classe {I_i:n=1,2,…,n} contenente un numero finito di ipotesi, essendo I_i l'asserzione secondo cui all'i-esima osservazione si verificherà uno dei possibili eventi coinvolti nell'esperimento. Supponendo che le ipotesi riguardino i risultati dei successivi lanci di un dado, I_i potrebbe asserire che all'i-esimo lancio si verificherà l'evento '4', ossia una volta lanciato su un tavolo da gioco il dado mostrerà la faccia con impressa la cifra 4. Scritta relativamente alle ipotesi della classe, la [6] diviene

Concentrando l'attenzione sull'n-esimo termine di tale prodotto

[15] P(I_n=j_n∣S⋀I₁=j₁⋀…⋀I_n-1=j_n-1)

si nota che questa è la probabilità con cui all'n-esima osservazione si verificherà l'evento j_n, determinata subordinatamente alla conoscenza dei risultati delle n−1 osservazioni precedenti. Tale probabilità è solitamente qualificata come predittiva, intendendo affermare che si tratta della probabilità di una previsione, quella relativa al verificarsi di un evento. Al fine di determinare la [14] è necessario assumere la validità di certe ipotesi, di cui una delle più importanti asserisce essere la [14] scambiabile, cioè una probabilità invariante rispetto al variare dell'ordine dei risultati delle osservazionipassate o future.