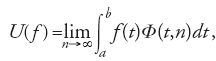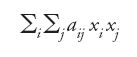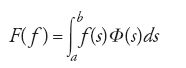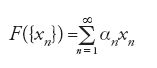La seconda rivoluzione scientifica: matematica e logica. Le origini dell'analisi funzionale
La seconda rivoluzione scientifica: matematica e logica. Le origini dell'analisi funzionale
Le origini dell'analisi funzionale
L'analisi funzionale acquista una precisa identità nel primo decennio del XX secolo. Le sue radici sono rintracciabili negli ultimi anni del XIX sec., in particolare nei lavori di Salvatore Pincherle (1853-1936) e Vito Volterra (1860-1940) in Italia. Essa differisce dall'analisi classica del XIX sec. in quanto tratta di funzioni nelle quali la variabile indipendente o la variabile dipendente, o entrambe, non sono numeri reali o complessi, ma elementi di una classe di funzioni 'ordinarie' o di un insieme astratto. In entrambi i casi, la classe di funzioni o l'insieme astratto sono dotati di una struttura topologica che permette l'uso dei concetti di limite e di continuità sulla base dell'estensione alla classe di funzioni o all'insieme astratto di importanti aspetti della teoria classica degli insiemi, per esempio quella di Georg Cantor (1845-1918).
Per esempio, se C[a,b] è l'insieme delle funzioni f (a valori reali) nella variabile reale s, definite e continue nell'intervallo chiuso [a, b], la 'distanza' tra due funzioni f e g può essere definita come il valore massimo assunto dalla differenza ∣f(s)−g(s)∣ al variare di s nell'intervallo [a, b], e denotata con ∥f−g∥. Ciò consente di trattare tali funzioni come vettori, con la lunghezza di f data da ∥f∥=∥f−0∥. Si può allora considerare C[a,b] uno spazio vettoriale di dimensione infinita. Il significato di convergenza di una successione {fn} a una funzione limite f, espressa dalla notazione ∥fn−f∥→0, è che fn(s) 'converge uniformemente' a f(s) su [a,b]. Ci sono molti altri esempi di spazi di funzioni.
In un certo senso, il ramo dell'analisi classica chiamato calcolo delle variazioni appartiene all'analisi funzionale, tuttavia la gamma completa delle idee dell'analisi funzionale non venne mai sviluppata nel XIX sec. nell'ambito della trattazione di tale teoria.
Spazi topologici e spazi metrici
L'introduzione della topologia insiemistica per classi di funzioni e per insiemi astratti si deve a Maurice-René Fréchet (1878-1973), che iniziò a lavorare su queste problematiche nel 1904, raggiungendo un livello di influenza decisiva nel 1906 con la pubblicazione della sua tesi. Fréchet partì dalla definizione assiomatica di 'L-classe', ossia un insieme di elementi astratti (chiamati punti), su cui è definita la 'convergenza' di una successione {xn} di punti a un punto x. In tale contesto definiva il concetto di punto limite di un insieme S di punti della L-classe: x è un punto limite di S se esiste una successione {xn} di punti di S, tutti distinti, convergente a x. Un punto limite di un insieme S può, ma non necessariamente deve, appartenere a S. Fréchet passava poi alla definizione di altri concetti, come quello di insieme derivato, insieme aperto, insieme chiuso, e così via, secondo il modello della teoria classica degli insiemi, creando una teoria topologica per una L-classe.
L'efficacia di questa costruzione per dimostrare teoremi utili era solo parziale. Una difficoltà derivava dal fatto che l'insieme di tutti i punti limite di un insieme S, detto l'insieme 'derivato' S′, non è necessariamente un insieme chiuso, come invece accade per la topologia classica dello spazio euclideo. Di conseguenza, Fréchet tentò un approccio differente, definendo la topologia degli insiemi di punti introducendo un nuovo sistema di assiomi. Partendo da un insieme astratto, a ogni coppia di punti x,y (distinti o coincidenti) egli faceva corrispondere un numero D(x,y), detto 'distanza tra x e y' (Fréchet inizialmente utilizzava il termine écart (scarto), ma poi lo sostituì con distanza). Gli assiomi per la distanza sono i seguenti: D(x,y)=0 se x=y, altrimenti D(x,y) è positiva; D(x,y) coincide con D(y,x); se x,y,z sono tre punti qualsiasi, D(x,z) è minore della somma di D(x,y) e D(y,z). Fréchet definiva poi il concetto di convergenza: una successione {xn} converge a un punto x se e solo se D(xn,x) converge a 0. In questo modo, l'insieme astratto diventa una L-classe, e Fréchet definì mediante la distanza una nuova topologia nella quale ogni insieme derivato era un insieme chiuso.
Il nome scelto per una classe dotata di una topologia basata su tali assiomi fu quello di 'spazio metrico'. Esso venne usato per la prima volta da Felix Hausdorff (1868-1942) nel libro Grundzüge der Mengenlehre (Lineamenti della teoria degli insiemi). L'invenzione degli spazi metrici fu uno dei risultati più importanti e utili del lavoro di Fréchet. Un altro notevole successo fu l'introduzione della nozione di compattezza. Egli chiamò 'compatto' un insieme S se ogni suo sottoinsieme infinito ammette almeno un punto limite (in una L-classe o in uno spazio metrico, a seconda di quale dei due casi è preso in considerazione), non necessariamente appartenente a S. Fréchet stabilì anche di considerare compatto ogni insieme finito. Aveva introdotto il concetto di compattezza in un lavoro ‒ pubblicato nel 1904 dall'Académie des Sciences di Parigi, prima del completamento della sua tesi ‒ sul seguente teorema, che considerava una generalizzazione di un teorema di Karl Theodor Wilhelm Weierstrass (1815-1897): se f è una funzione reale definita e continua su un insieme chiuso e compatto, allora essa è dotata di massimo assoluto nell'insieme stesso. L'enunciato del teorema di Weierstrass è del tutto analogo, con il termine limitato in luogo di compatto. Naturalmente Weierstrass lavorava con funzioni definite al variare di x sulla retta dei numeri reali o in uno spazio euclideo di dimensione maggiore o uguale a 2. Il concetto di limitatezza non ha significato in una L-classe nella quale non sia definita una distanza. La limitatezza ha significato in uno spazio metrico, ma è un concetto diverso dalla compattezza. In generale, gli insiemi limitati non sono necessariamente compatti.
Fréchet derivò probabilmente l'idea della compattezza dal teorema di Bolzano-Weierstrass, in cui si afferma (per gli insiemi di uno spazio euclideo) che un insieme infinito e limitato possiede almeno un punto limite (punto di accumulazione). Il teorema di Bolzano-Weierstrass è uno degli strumenti generalmente usati per dimostrare il teorema di Weierstrass generalizzato da Fréchet.
Due importanti concetti introdotti da Fréchet per gli spazi metrici astratti sono quelli di 'completezza' e di 'separabilità'.
Applicando il criterio di convergenza di Cauchy, il quale viene comunemente utilizzato nell'analisi moderna, Fréchet definisce uno spazio metrico 'completo' quando ogni successione {xn}, tale che la distanza D(xm,xn) tenda a 0 al crescere di m e n, converge a un limite x.
Lo spazio è separabile se è unione di un insieme numerabile S e del suo derivato S′. Uno dei risultati significativi della tesi di Fréchet è la scoperta di una stretta connessione tra il suo concetto di compattezza e un teorema riguardante i ricoprimenti aperti, un concetto che nella topologia degli spazi euclidei è utilizzato nel teorema di Heine-Borel (noto anche come teorema di Borel-Lebesgue). In un qualsiasi spazio topologico, per ricoprimento aperto di un insieme S si intende una famiglia F di insiemi aperti, tale che ogni punto di S sia contenuto in almeno uno di detti insiemi. La famiglia F può essere formata da un numero finito oppure infinito di insiemi.
Il teorema di Heine-Borel afferma che se F è un qualsiasi ricoprimento aperto di un insieme chiuso e limitato S in uno spazio euclideo, esiste una sottofamiglia finita di F che è un ricoprimento aperto di S. Vale inoltre il seguente teorema: in uno spazio metrico, un insieme S è chiuso e compatto se e solo se, dato un qualsiasi ricoprimento aperto F di S, esiste una sottofamiglia finita di F che è un ricoprimento aperto di S. Nella sua tesi Fréchet dimostrò una versione meno generale di questo stesso teorema.
Gli insiemi compatti di Fréchet non sono necessariamente insiemi chiusi. Alcuni decenni dopo, la definizione di insieme compatto venne riformulata in termini di ricoprimenti aperti. Il risultato, per gli spazi metrici, è che un insieme S in uno spazio metrico può essere chiamato compatto se e solo se, ogni sottoinsieme infinito di S ammette un punto limite in S (e non semplicemente nello spazio).
Parlare di uso del termine 'spazio' a proposito dei lavori di Fréchet è anacronistico. Il primo nome da lui usato per uno spazio metrico fu quello di 'una classe (E)' e, in seguito, di 'una classe (D)' (D sta per distanza). Tuttavia, la tendenza a pensare in termini di analogie con la geometria degli spazi euclidei caratterizzò il lavoro degli studiosi di analisi funzionale fin dalle prime fasi del suo sviluppo.
Spazi lineari di funzioni
Nei lavori del XIX sec. di algebra lineare e di geometria si preferiva un linguaggio geometrico, come per esempio i riferimenti alla nozione di dimensione, anche in un contesto essenzialmente algebrico. Antonie Frans Monna (1909-1995) nel libro Functional analysis in historical perspective (1973) traccia un quadro della storia della nozione di spazio lineare nel XIX secolo. La linearità di certe classi di funzioni è importante nel calcolo delle variazioni. Monna fa notare come, in un libro sul lavoro di Hermann Günter Grassmann (1809-1877) pubblicato nel 1888, Giuseppe Peano (1858-1932) avesse fornito una definizione assiomatica di spazio lineare astratto, che è sostanzialmente equivalente a quella moderna.
Nel primo decennio del XX sec. l'idea di linearità e la nozione di spazio metrico si combinarono nello studio di alcuni spazi lineari di funzioni. Le funzioni venivano pensate come vettori, con una nozione di lunghezza che permetteva di definire la distanza tra funzioni in quanto elementi di uno spazio metrico dotato di struttura lineare. Se ∥f∥ è la lunghezza, o norma, della funzione-vettore, la distanza tra f e g è ∥f−g∥. Le proprietà della norma sono: ∥f+g∥≤∥f∥+∥g∥,∥af∥=∣a∣∥f∥,∥f∥≥0 e ∥f∥=0 se e solo se f è la funzione identicamente nulla. Abbiamo già fatto l'esempio del caso dello spazio C[a,b] delle funzioni continue su un intervallo. Un altro spazio importante, studiato da David Hilbert (1862-1943) da un punto di vista geometrico, è lo spazio l2 delle successioni {xn} di numeri per i quali è convergente la serie infinita
[1] ∣x1∣2+∣x2∣2+∣x3∣2+….
Il tedesco Erhard Schmidt (1876-1959), che scrisse la sua tesi di dottorato a Gottinga e svolse un importante lavoro estendendo e migliorando i risultati di Hilbert, studiò l2 come spazio di funzioni, considerando {xn} come una funzione definita sugli interi positivi. Schmidt usò il simbolo ∥∥ per indicare la radice quadrata della somma che compare in [1] (Schmidt 1908). Altri esempi di spazi lineari di funzioni dotati di norma furono studiati prima che ‒ soprattutto con la pubblicazione della tesi di dottorato di Stefan Banach (1892-1945), presentata all'Università di Lwow nel 1920 e pubblicata due anni dopo nel terzo volume della rivista polacca "Fundamenta mathematicae" ‒ si diffondesse la definizione assiomatica di spazio lineare normato astratto. L'importanza e l'influenza della scuola polacca divennero enormi. Il lavoro sull'analisi funzionale fiorì in molti paesi; per un'intera generazione di matematici, una delle più importanti fonti di informazione e di ispirazione fu proprio la scuola polacca, e in particolare il libro di Banach, Théorie des opérations linéaires, pubblicato a Varsavia nel 1932.
Gli operatori lineari erano destinati a occupare il centro del palcoscenico dell'analisi funzionale per vari decenni, e furono studiati a fondo anche prima dell'epoca di Banach. Nel seguito faremo uso del linguaggio e di alcune notazioni impiegate per gli spazi lineari normati, anche se nel periodo iniziale che qui consideriamo erano adottati solo in parte.
Un operatore lineare definito su uno spazio lineare normato X, a valori in uno spazio lineare normato Y, è una funzione A di un punto variabile x, che assume valori A(x) in Y; la linearità di A è espressa dalle relazioni
[2] A(x1+x2)=A(x1)+A(x2), A(cx)=cA(x),
dove x1 e x2 sono punti qualsiasi in X e c è uno scalare (i punti x sono a volte chiamati vettori). Lo spazio lineare può essere reale o complesso, a seconda che gli scalari siano numeri reali o complessi. La continuità di A in un punto qualsiasi di X implica, quale conseguenza della linearità, la sua continuità in tutto X. Si può dimostrare che A è continuo se e solo se i valori ∥A(x)∥ sono limitati per tutti gli x tali che ∥x∥≤1. L'estremo superiore dei valori ∥A(x)∥, per ∥x∥≤1 viene denotato con ∥A∥ e chiamato norma di A. L'insieme di tutti gli operatori lineari A da X in Y forma effettivamente uno spazio lineare normato. Inizialmente l'importanza di questo risultato non venne compresa.
Piuttosto rilevante è il caso speciale in cui lo spazio Y dei valori A(x) è lo spazio lineare reale dei numeri reali, o lo spazio lineare complesso dei numeri complessi. In entrambi i casi la norma di un elemento è il suo valore assoluto. Gli operatori lineari continui a valori numerici si dimostrarono molto importanti nello sviluppo generale dell'analisi funzionale. Il primo matematico che provò a definire un metodo generale per rappresentare ogni elemento di una classe di operatori lineari continui a valori numerici fu Jacques-Salomon Hadamard (1865-1963), uno dei più celebri matematici francesi. Egli era stato l'insegnante di Fréchet in un liceo di Parigi e, in seguito, questi divenne il primo studente di dottorato di Hadamard.
Fu senza dubbio Hadamard, fautore dell'applicazione delle idee della topologia classica a classi di funzioni, che spinse Fréchet a intraprendere il progetto di trovare una generalizzazione del teorema di Weierstrass e, nel corso di tale progetto, a formulare il concetto di compattezza.
Hadamard cercava di definire un metodo per rappresentare analiticamente un qualsiasi operatore lineare continuo sullo spazio C[a,b]. Nel 1903 egli riuscì a dimostrare che un tale operatore U è esprimibile nella forma
dove f è un qualsiasi elemento di C[a,b] e Φ(t,n) è, per ogni intero positivo n, una funzione continua di t determinata in qualche modo da U. Il problema è che Φ non è univocamente determinata da U, come venne dimostrato quando, nel 1904, Fréchet ottenne un risultato del tutto simile, ma con una differente funzione Φ.
Hadamard coniò il termine francese fonctionnelle per un operatore funzionale a valori numerici. Nel 1922 uno dei suoi studenti di dottorato, Paul Lévy (1886-1971), pubblicò le sue Leçons d'analyse fonctionnelle e furono proprio le parole 'analyse fonctionnelle' a divenire il nome di questo ramo generale dell'analisi, sebbene Lévy lo usasse in un senso più limitato rispetto all'accezione più generale utilizzata in seguito.
Nel caso più semplice di un funzionale lineare continuo, con x e A(x) entrambi numeri reali, era noto da tempo che se A(x1+x2)=A(x1)+A(x2) per ogni coppia x1, x2 allora A(x) è un multiplo costante di x: A(x)=ax. In questo caso il fattore moltiplicativo a è determinato univocamente dal funzionale A. Per uno spazio lineare reale n-dimensionale di vettori x con componenti (x1,x2,…,xn), la forma di un generico funzionale lineare continuo A è A(x)=a1x1+a2x2+…+anxn. Una rappresentazione analoga per lo spazio C[a,b] non era ancora nota. Riuscì a scoprirla l'ungherese Frigyes Riesz (1880-1956) in un lavoro pubblicato per la prima volta nel 1909 nei "Comptes rendus" della Académie des Sciences di Parigi. Egli dimostrò che se A è un funzionale lineare continuo sullo spazio C[a,b], allora esiste una funzione reale a variazione limitata α(s), definita sull'intervallo [a,b], tale che la rappresentazione di A(f) per ogni f è
[4] A(f)=∫bαf(s)dα(s),
dove l'integrale è un integrale di Stieltjes. Nel 1909 Riesz non affrontò il problema della determinazione univoca della funzione α corrispondente al funzionale A, né studiò il rapporto tra α e la norma ∥A∥. Un metodo per determinare univocamente α esiste, anche se ciò può avvenire seguendo più di una regola. Una volta scelto il modo più appropriato, la norma ∥A∥ è pari alla somma di ∣α(a)∣ e della variazione totale della funzione α sull'intervallo [a,b].
Questo teorema di rappresentazione dovuto a Riesz occupa un posto di rilievo nella storia dell'analisi funzionale, in quanto ispirò molte importanti idee successive.
Spazi di Hilbert
Un evento di grande rilevanza, anche per le importanti conseguenze che ebbe sullo sviluppo dell'analisi funzionale negli anni immediatamente successivi, fu la pubblicazione nel 1900, da parte di Erik Ivar Fredholm (1866-1927), in Svezia, di un breve articolo e nel 1903 di un resoconto completo del suo studio sull'equazione integrale nell'incognita f
[5] f(s)+λ∫bαK(s,t)f(t)dt=g(t)
nella quale le funzioni f e g sono elementi di C[a,b], K(s,t) è una funzione continua di s e t, e λ è un parametro numerico. Si tratta, una volta assegnata la funzione 'nucleo' K, di stabilire quando la funzione incognita f possa essere determinata, dati λ e g.
Sulla base dei precedenti studi di Volterra, Fredholm dimostrò che l'equazione integrale [5] ammette una soluzione unica per f, qualunque sia il termine noto g, se λ non annulla una funzione D(λ) definita da una serie di potenze in λ, convergente per ogni valore di λ. Esiste al massimo un insieme numerabile di zeri di D(λ), tutti di ordine finito; sono punti isolati e quindi, se esiste una successione infinita di tali punti λn, la successione {∣λn∣} dei valori assoluti deve tendere a infinito. Se λ è uno zero di D(λ), l'equazione [5] con g=0 ammette un numero finito di soluzioni f linearmente indipendenti. Non c'è una soluzione unica per f se g≠0, ma può esservene una se si verificano determinate condizioni riguardanti il nucleo trasposto K(t,s) di un'equazione integrale. La situazione generale è in qualche modo analoga al problema algebrico della determinazione delle soluzioni dell'equazione vettoriale, x+λA(x)=y, con x e y vettori in uno spazio lineare n-dimensionale e l'operatore lineare A definito da una matrice quadrata di ordine n.
Il lavoro di Fredholm attirò l'attenzione di Hilbert a Gottinga; egli affrontò il problema di Fredholm da un punto di vista del tutto differente, che condusse al sorgere di una serie di problemi completamente nuovi, da lui trattati in vari lavori pubblicati negli anni 1904-1906, e 1910, raccolti in un libro del 1912 ristampato molti anni più tardi, nel 1953, negli Stati Uniti.
L'approccio scelto da Hilbert per sviluppare le idee suggeritegli dal lavoro di Fredholm sulle equazioni integrali lo spinse a usare quello che viene oggi chiamato un sistema ortonormale completo di elementi in C[a,b], per associare a una funzione f in C[a,b] una successione {xn} di numeri definiti come:
[6] xn=∫bαf(s)Φn(s)ds, n=1,2,…
essendo le funzioni Φn elementi del sistema ortonormale. Il sistema {Φn} è tale che l'integrale del prodotto Φn(s)Φm(s) è nullo per m diverso da n e vale 1 se m e n coincidono. Il sistema è completo in C[a,b] se la sola funzione continua f che rende nulli tutti gli xn è la funzione indenticamente nulla. Era noto che la serie ∣x1∣2+∣x2∣2+… è convergente, con somma minore o uguale all'integrale di ∣f(s)∣2 (la disuguaglianza è nota come disuguaglianza di Bessel). Per un sistema ortonormale completo di funzioni {Φn} continue, era noto che la disuguaglianza diventa un'uguaglianza, chiamata, per ragioni storiche, relazione di Parseval.
Hilbert affrontò problemi che Fredholm non aveva considerato. Cominciò con lo studiare le forme quadratiche e le forme bilineari, costruite con una doppia infinità di coefficienti aij, e i sistemi infiniti di variabili numeriche x1,x2,…,y1,y2,… tali che le serie infinite
[7] ∣x1∣2+∣x2∣2+…, ∣y1∣2+∣y2∣2+…
fossero convergenti. Hilbert dedicò grande attenzione al caso in cui tutti i numeri sono reali, ma si occupò anche del caso complesso. Probabilmente, il suo risultato più importante è legato al caso reale simmetrico, ossia quando aij=aji; prese comunque in considerazione anche il caso complesso in cui aji è il coniugato di aij (forma simmetrica hermitiana). Imponendo alla forma bilineare
una condizione di limitatezza, Hilbert riuscì a elaborare una 'teoria spettrale' delle forme quadratiche simmetriche limitate, un analogo infinito-dimensionale del metodo algebrico consistente nell'utilizzare una trasformazione ortogonale delle variabili x1,x2,…,xn nelle nuove variabili u1,u2,…,un per ridurre una matrice quadrata simmetrica a una matrice diagonale con tutti gli elementi non nulli appartenenti alla diagonale principale.
Il lavoro di Hilbert portò in primo piano lo spazio delle successioni infinite (reali o complesse), oggi noto come ℓ2. In effetti, egli non considerò tali successioni come elementi di uno spazio, ma utilizzò comunque la formula per la distanza tra due punti in ℓ2 per definire la continuità delle funzioni dell'insieme infinito di variabili x1,x2,…. Introdusse anche un tipo differente di continuità: la continuità completa.
La parte del lavoro di Hilbert che abbiamo presentato fu pubblicata per la prima volta nel 1906. In questa serie di articoli egli non fa mai riferimento alla allora completamente nuova teoria dell'integrazione proposta da Henri-Léon Lebesgue (1875-1941) nella sua tesi discussa a Parigi nel 1902.
L'integrale di Lebesgue, oggetto di grande attenzione, non era tuttavia accettato da tutti gli analisti. Nel 1906 Fréchet, Riesz e altri, tra i quali Ernst Sigismund Fischer (1875-1954) in Germania, conoscevano l'integrale di Lebesgue, e Riesz seguiva da vicino il lavoro di Hilbert. Nello stesso anno, inoltre, venne pubblicato un importante articolo: Séries trigonométriques et séries de Taylor del francese Pierre-Joseph-Louis Fatou (1878-1929).
Questi, studiando le funzioni a quadrato sommabile (in seguito dette 'funzioni di classe L2') definite nell'intervallo [0,2π], dimostrò che la relazione di Parseval vale per i sistemi ortonormali completi costituiti dalle ordinarie funzioni trigonometriche e per i coefficienti di Fourier delle funzioni di classe L2.
Nella primavera del 1907 l'articolo di Fatou e il lavoro di Hilbert ispirarono a Riesz il teorema noto come teorema di Riesz-Fischer. A quanto pare, qualcosa di simile accadde a Fischer. Per dare alla classe L2 (per l'intervallo [a,b]) la struttura di spazio metrico, con la distanza tra due suoi elementi f e g definita da
è necessario stabilire che due funzioni f1 e f2 definiscono lo stesso elemento di L2 se e solo se la loro differenza è 0 per tutti i valori di s in [a,b] tranne al più quelli contenuti in un insieme di misura nulla. In questo modo, L2 diventa uno spazio metrico completo (ciò è parte del teorema di Riesz-Fischer). Il teorema afferma anche che esiste un operatore lineare T che trasforma L2 suriettivamente in ℓ2 in modo tale che se T(f)={xn}, con {xn} elemento di ℓ2, allora ∥T(f)∥=∥f∥, dove ∥T(f)∥2 è la somma della serie infinita ∣x1∣2+∣x2∣2+… e ∥f∥2 è l'integrale di ∣f(s)∣2.
Per definire l'operatore lineare limitato T, basta scegliere una qualsiasi successione {Φn} di elementi di L2 che formi un sistema ortonormale completo, e definire xn come l'integrale di f(s)Φn(s).
Dopo qualche anno lo spazio ℓ2 fu chiamato 'spazio di Hilbert'. John von Neumann (1903-1957) formulò la definizione assiomatica di spazio di Hilbert astratto separabile, di cui L2 e ℓ2 sono esempi particolari, in un articolo pubblicato sulla rivista tedesca "Mathematische Annalen". Nel lavoro sui fondamenti della meccanica quantistica von Neumann usò certamente operatori non limitati nello spazio di Hilbert. Nato in Ungheria, residente in America dal 1930, egli fornì il più importante contributo alla teoria degli operatori su uno spazio di Hilbert e alle loro applicazioni alla fisica teorica dando inizio alla teoria delle algebre di operatori. Dopo il lavoro di Hilbert e prima di quello di von Neumann sugli spazi di Hilbert, Riesz presentò la sua versione della teoria spettrale degli operatori simmetrici limitati in l2, usando metodi del tutto differenti e molto originali. Ancora un altro lavoro di rilievo sugli spazi di Hilbert è il libro del 1932 scritto da Marshall H. Stone (1903-1989).
Spazi funzionali, topologia debole e operatori compatti
Il problema della rappresentazione analitica di un funzionale lineare continuo definito su L2 venne risolto da Fréchet e Riesz in due lavori pubblicati separatamente sullo stesso numero dei "Comptes rendus" dell'Académie des Sciences di Parigi il 24 giugno del 1907.
Se F è un tale funzionale, esiste un'unica funzione Φ di classe L2 tale che
per ogni f in L2. Tra gli spazi funzionali lineari normati di notevole interesse, troviamo gli spazi Lp, per p≥1, e gli spazi di successioni ℓp, sempre per p≥1. La natura di tali spazi per p>1 è di particolare interesse, in quanto per tali valori di p questi spazi sono 'riflessivi'.
In un importante articolo del volume 69 dei "Matematische Annalen", pubblicato a Lipsia nel 1910, Riesz presentò, insieme ad altri risultati, il teorema di rappresentazione per i funzionali lineari continui definiti su Lp, nel caso p>1. La definizione di Lp è analoga al caso p=2, con p al posto di 2 nella definizione della distanza D(f,g) e della norma ∥f∥. La trattazione comprende il caso p=2, tuttavia la dimostrazione di Riesz del teorema di rappresentazione non fa uso del teorema di Riesz-Fischer (che non ha analogo nel caso p≠2). Dato p, sia q=p/(p−1), e quindi 1/p+1/q=1. La relazione tra p e q è simmetrica, dunque p=q/(q−1). Riesz dimostrò che se F è un funzionale lineare continuo su Lp, allora per ogni f in Lp vale la [10] con Φ elemento di Lq univocamente determinato da F. Inoltre, la norma di F è uguale alla norma di Φ. Questo teorema, naturalmente, vale anche per funzionali lineari su Lq, scambiando il ruolo di p e q. Si osserva, allora, che la classe dei funzionali lineari continui su Lp può essere 'identificata con' Lq, nel senso che esiste un operatore lineare limitato T che stabilisce una corrispondenza biunivoca tra lo spazio lineare normato dei funzionali lineari continui su Lp e lo spazio Lq, con ∥T(F)∥=∥F∥. Lo spazio ℓp viene considerato più in dettaglio nel capitolo III del libro che Riesz pubblicò nel 1913. Brevemente, lo spazio in questione è formato da successioni {xn} tali che la serie ∣x1∣p+∣x2∣p+… è convergente con somma uguale alla potenza p-esima della norma dell'elemento {xn}. La rappresentazione generale di un funzionale lineare continuo su ℓp è data da
dove la successione {αn} è un elemento di ℓq univocamente determinato da F.
Ci sono molte altre cose importanti da dire a proposito dei funzionali lineari continui definiti sugli spazi lineari normati, perché il loro studio ha un ruolo significativo nella trattazione degli operatori lineari da uno spazio lineare normato in o su un altro. In proposito, faremo uso della notazione e della terminologia moderne. Lo spazio lineare normato di tutti i funzionali lineari continui definiti su X sarà denotato con X′; un suo elemento generalmente con x′. Lo spazio X′ è detto 'coniugato' di X o spazio duale di X. Il concetto di spazio duale venne introdotto esplicitamente per la prima volta per il caso astratto nel 1927 da Hans Hahn (1879-1934), professore a Vienna, che chiamò X′ lo 'spazio polare'. Se A è un operatore lineare limitato definito su X a valori in Y (un altro spazio lineare normato che può essere X stesso), si può definire un operatore lineare limitato A′, detto duale (o aggiunto) di A, definito su Y′ e a valori in X′. Si usa il termine trasformare per indicare la seguente relazione: A trasforma X in Y e A′ trasforma Y′ in X′.
Per spiegare la relazione tra A′ e A, si consideri l'espressione y′(Ax), che diventa y′(y) quando y=Ax. Tale espressione è un funzionale lineare continuo di x, e dunque uguale a x′(x) per qualche x′ in X′. Quindi x′ è determinato da y′ e da A, e dipende in modo lineare e continuo da y′. A′ è definito come l'operatore che trasforma y′ in x′:A′y′=x′. Si ha ∥A′∥=∥A∥.
Questo metodo per definire il duale di un operatore lineare limitato fu descritto da Riesz nell'articolo del 1910. Egli considerava un operatore lineare limitato T che trasforma Lp in sé stesso. Lo spazio Lq ha il ruolo di duale di Lp, e dunque l'operatore duale (che Riesz chiama il trasposto di T) trasforma Lq in sé stesso. Il lavoro di Riesz anticipava il metodo astratto più generale, sottolineando inoltre l'utilità dell'operatore duale. Egli dimostrò (nella sezione 13 dell'articolo citato) che se esiste una costante positiva M tale che per ogni f in Lp e per ogni Φ in Lq si abbia: ∥f∥≤M∥Tf∥, ∥Φ∥≤M∥T′Φ∥, allora l'operatore T trasforma Lp suriettivamente in Lp, con operatore inverso continuo T−1 (g=Tf,f=T−1g).
Nella teoria generale, un operatore lineare limitato A da X in Y per il quale punti distinti abbiano immagini distinte, stabilisce una corrispondenza biunovoca tra X e l'immagine di X in Y. In questo caso si dice che l'operatore A ammette un inverso A−1, non necessariamente definito su tutto Y e non necessariamente continuo. Vi sono molte relazioni tra le proprietà dell'applicazione definita da A e quelle dell'applicazione definita da A′. Per esempio, l'insieme dei valori A′y′, al variare di y′ in Y′, coincide con X′ se e solo se A ammette un inverso continuo. La dimostrazione standard di questa asserzione richiede l'uso di due importanti teoremi di analisi funzionale: uno è il teorema di Hahn-Banach; l'altro è un caso speciale del cosiddetto principio di uniforme limitatezza.
Il teorema di Hahn-Banach afferma che un funzionale lineare continuo, definito su uno spazio lineare normato contenuto in uno spazio lineare normato più grande, può essere esteso a un funzionale continuo sullo spazio più grande senza modificare la sua definizione nei punti dove è già definito e senza modificare il valore della sua norma. Un'idea che condusse al suddetto teorema è già contenuta nell'opera di Riesz, in particolare nell'articolo del 1910 sugli spazi Lp, e inoltre nel lavoro dell'austriaco Eduard Helly (1884-1943). Nel 1927 Hahn, e nel 1929 Banach, dimostrarono il teorema generale sulle estensioni dei funzionali lineari, che si rivelò indispensabile al fine di ottenere altri importanti risultati.
Prendiamo in esame ora una formulazione abbastanza generale del principio di uniforme limitatezza. Supponiamo che lo spazio X sia completo e sia S un sottospazio del duale coniugato X′. Se per ogni x in X esiste una costante C (dipendente da x) tale che ∣x′(x)∣≤C per ogni x′ in S, allora esiste una costante M tale che ∥x′∥≤M per ogni x′ in S. Un caso particolare di questo principio venne dimostrato da Helly nel suo articolo del 1912. Egli considerò il caso in cui X è lo spazio C[a,b] e S è formato da una successione {x′n} convergente per ogni x in X. Ci sono molte generalizzazioni che estendono il principio e le dimostrazioni moderne fanno in genere uso del teorema, dovuto a René-Louis Baire (1874-1932) che afferma che uno spazio metrico completo è di seconda categoria. Ricordiamo brevemente che uno spazio topologico si dice di 'prima categoria' se è unione di una famiglia numerabile di sottoinsiemi chiusi aventi parte interna vuota. Altrimenti si dice di 'seconda categoria'.
Nella teoria generale degli spazi lineari normati è definito il concetto di 'convergenza debole' di una successione di elementi dello spazio. Per definizione, {xn} converge debolmente a x se x′(xn) converge a x′(x) per ogni x′ dello spazio duale. Questo tipo di convergenza è stato studiato per la prima volta da Hilbert nel suo lavoro sullo spazio ℓ2, sebbene la sua definizione di convergenza non comprendesse il termine 'debole' e fosse formalmente diversa, anche se equivalente a quella data qui. L'uso dei termini debole (schwach) e forte (stark) in connessione con la convergenza in ℓ2 appare per la prima volta nel 1908 nella tesi di dottorato di Hermann Weyl (1885-1955). La 'convergenza forte' di {xn} in ℓ2 era usata per descrivere l'attuale 'convergenza secondo la metrica'. Riesz utilizzò i termini debole e forte nel suo importante articolo del 1910 sugli spazi Lp. Egli definiva la convergenza debole per mezzo dei funzionali lineari continui, come abbiamo descritto in queste pagine, e dimostrò un teorema da lui chiamato 'teorema principale sulla convergenza debole': in un insieme infinito e limitato di elementi di Lp esiste una successione di elementi distinti che converge debolmente a un elemento di Lp. Questo teorema viene oggi comunemente enunciato nella seguente forma: gli insiemi infiniti e limitati in Lp (per p>1) sono 'debolmente compatti' per successioni; formulazione, questa, che rimanda alla definizione originale di Fréchet della compattezza nelle L-classi.
Questo teorema di Riesz non vale in generale per spazi lineari normati; per esempio, non vale per Lp se p=1 o per lo spazio C[a,b]. Si ha comunque il seguente teorema generale: se lo spazio lineare normato X è riflessivo, allora da ogni successione limitata in X si può estrarre una sottosuccessione debolmente convergente. Lo spazio Lp è riflessivo per p>1. Il concetto di riflessività venne definito per la prima volta da Hahn, nel suo articolo del 1927, che usò l'aggettivo regolare in luogo di riflessivo. L'uso del termine riflessivo venne introdotto in un articolo del 1939 dall'americano Edgar R. Lorch (1907-1990). La definizione di riflessività è la seguente: lo spazio X è detto riflessivo se ogni funzionale lineare continuo sul duale X′ è rappresentabile nella forma x′(x) per qualche x in X. Uno spazio riflessivo è necessariamente completo.
Nel suo libro Théorie des opérations linéaires Banach dimostrò che se lo spazio lineare normato completo X è separabile e inoltre è tale che da ogni successione limitata sia possibile estrarre una sottosuccessione debolmente convergente a qualche elemento di X, allora X è riflessivo (Banach formulava diversamente il risultato). In effetti, il teorema vale anche senza la condizione di separabilità; questo è il risultato, in qualche modo sorprendente, che venne stabilito nel 1947 dall'americano W.F. Eberlein.
La nozione di convergenza debole di una successione in uno spazio lineare normato fu frequentemente usata prima che venisse rivolta l'attenzione alla definizione di topologia debole basata sulla nozione di intorno. In un lungo articolo pubblicato nei "Mathematische Annalen" del 1929, von Neumann diede sia la definizione di topologia forte sia quella di topologia debole in uno spazio di Hilbert astratto. Quest'ultima è basata su un sistema di intorni che definisce una topologia di tipo Hausdorff. Ogni intorno di un punto x0 è definito usando disuguaglianze con un numero finito di funzionali lineari continui per caratterizzare i punti x appartenenti all'intorno. Von Neumann sottolineò, e illustrò con un esempio, che nella topologia debole dello spazio di Hilbert un punto x può essere punto limite di un insieme S anche se non è limite di alcuna successione di punti di S.
Lo studio sistematico delle topologie deboli degli spazi lineari normati (applicando a questi spazi la definizione di intorno data da von Neumann) non progredì finché l'attenzione non venne rivolta, grazie alle pubblicazioni del russo Andrej Nikolaevič Kolmogorov (1903-1987) nel 1934 e di von Neumann nel 1935, al concetto di spazio lineare topologico. Nello studio di questi spazi fu decisivo il riconoscimento dell'importanza della convessità e del ruolo degli iperpiani (definiti da funzionali lineari continui) nello studio degli spazi lineari topologici. La fine degli anni Trenta e gli anni Quaranta furono periodi particolarmente fecondi per le origini di questo ramo dell'analisi funzionale.
L'ultimo argomento da trattare riguarda gli operatori lineari completamente continui, oggi chiamati generalmente operatori lineari compatti. L'importante articolo di Riesz su questo argomento venne pubblicato nel 1918, sulla rivista svedese "Acta mathematica". Egli studiò l'equazione g=f−λAf, dove f e g sono elementi di C[a,b], λ è un parametro complesso, e A è quello che Riesz denominò un operatore lineare vollstetig. Quest'ultimo aggettivo può essere tradotto in italiano come 'completamente continuo' e sta a indicare che A trasforma ogni successione limitata in una successione dalla quale si può estrarre una sottosuccessione convergente. Sebbene nell'articolo sia trattato il caso dello spazio C[a,b], questa definizione può essere estesa a un qualsiasi spazio lineare normato.
Il termine vollstetig è dovuto a Hilbert che lo usò nel suo studio sulle forme quadratiche limitate in ℓ2 per il caso speciale in cui la forma quadratica Q(x) è continua, secondo una definizione di continuità basata sull'uso di successioni debolmente convergenti in ℓ2. Nel lavoro di Hilbert si trova anche il teorema che afferma che in ℓ2 la 'sfera unitaria' formata dai punti x tali che ∥x∥≤1 è debolmente compatta per successioni (Hilbert non usò il termine 'debolmente compatto', ma conosceva il 'principio di selezione', al quale il teorema si ispira). Riesz modificò il significato di vollstetig in modo da poterlo applicare a un qualsiasi spazio lineare normato, nel quale la sfera unitaria non è necessariamente debolmente compatta per successioni. I risultati di Riesz sono molto vicini a quelli ottenuti da Fredholm nel suo celebre articolo del 1903. Riesz dimostrò che per tutti i valori di λ, tranne al più un insieme numerabile di valori isolati, l'applicazione che porta f−λAf in un punto g è un'applicazione iniettiva di C[a,b] su sé stesso, con inversa continua che definisce f come funzione di g. I valori isolati che fanno eccezione, λ1,λ2,…, se in numero infinito, sono tali che ∣λn∣ tende all'infinito. Per g=0 l'equazione 0=f−λnAf ha un numero finito di soluzioni f linearmente indipendenti non nulle. Riesz non considerò il coniugato dell'operatore A, caso studiato invece dall'ucraino Juliusz Pawel Schauder (1899-1943) nel 1930.
Come breve riepilogo conclusivo, si può affermare che gli oggetti che caratterizzavano l'analisi funzionale nel 1932, quando venne pubblicato il libro di Banach, erano gli spazi di funzioni e gli spazi astratti con una struttura algebrica di spazio vettoriale lineare, ma di dimensione infinita e dotati di una struttura topologica basata sul concetto di spazio metrico nel quale sia definita una norma. I principali oggetti di studio erano gli operatori lineari, generalmente quelli continui. Tali operatori erano di due tipi: quelli a valori numerici (i funzionali lineari) e quelli tra spazi di dimensione infinita. I funzionali lineari resero possibile una teoria della dualità, tra uno spazio e il suo coniugato e un operatore e il suo coniugato. Tale teoria favorì la ricerca di analogie con l'algebra delle trasformazioni lineari negli spazi lineari di dimensione finita, e l'abbandono, fecondo di risultati, del caso di dimensione finita. La prospettiva di possibili applicazioni a importanti problemi dell'analisi classica diede un impulso decisivo alla ricerca nell'ambito dell'analisi funzionale, ma il fascino e l'attrattiva della materia sono indipendenti dalle sue applicazioni. Dopo il 1932 sono sorti nuovi problemi e nuove tecniche di soluzione.
Tavola I - VITO VOLTERRA E LE ORIGINI DELL’ANALISI FUNZIONALE
È difficile individuare il nascere di una nuova branca della scienza: spesso accade che diversi concetti e risultati preesistano alla costituzione ufficiale di una teoria e solo a posteriori essi vengano riguardati come appartenenti alla teoria stessa. Ciò è particolarmente vero per l’analisi funzionale. Un aspetto importante di essa, il calcolo delle variazioni, già era comparso nella seconda metà del XVII sec. nell’opera di Isaac Newton (1642-1727) (problema del solido di rivoluzione di minima resistenza) e successivamente in quella di Jakob I (1654-1705) e di Johann I (1667-1748) Bernoulli (problemi della brachistocrona e isoperimetrici) per acquistare, poi, più ampio respiro con gli immortali contributi di Leonhard Euler (1707-1783), prima, e di Joseph-Louis Lagrange (1736-1813), dopo. Ma se si conviene di far coincidere il sorgere di una teoria con l’opera di chi ha manifestato di avere la piena coscienza che, con i suoi studi, stava aprendo un nuovo campo della scienza, non vi è dubbio che Vito Volterra (1860-1940) debba essere considerato come l’iniziatore dell’analisi funzionale. Egli, in una nota lincea del 1887, introduce le funzioni che dipendono da altre funzioni. Successivamente, considerando il grafico della funzione variabile indipendente piuttosto che la funzione stessa, adopera la locuzione ‘funzioni di linea’. In seguito egli adotta, definitivamente, il termine ‘funzionale’ proposto da Jacques-Salomon Hadamard (1865-1963).
Molti furono i problemi provenienti sia dalla matematica pura sia da quella applicata, i quali condussero Volterra a introdurre questo nuovo concetto nell’analisi. Fra essi, però, quelli che maggiormente giustificarono l’avvento di questa idea, più come ‘scoperta’ che come ‘invenzione’, furono i problemi dell’eredità elastica o elettromagnetica, come da lui poi esposti nella sua monografia del 1913, Leçons sur les fonctions de lignes, originata da un corso di lezioni tenuto alla Sorbona di Parigi nel 1912.
Volterra concepì i funzionali come funzioni dipendenti da un’infinità di variabili: tutti i valori della funzione u(t) variabile indipendente. Il metodo che egli adoperò per affrontare i problemi relativi ai funzionali o, più in generale, per gettare le fondamenta di un calcolo funzionale che estendesse ai funzionali i concetti e i risultati relativi alle comuni funzioni, oggetto del calcolo infinitesimale, fu quello da lui chiamato il passaggio dal finito all’infinito. Tale metodo può esser visto come una sorta di passaggio al limite da un insieme finito di variabili a un insieme infinito ma, nella sostanza, esso consiste non tanto in un processo di passaggio al limite, quanto in un principio di analogia, che, mediante opportune trasposizioni, trasferisce operazioni e simboli dello schema finito a quello infinito. Volterra non diede mai una definizione di cosa fosse il passaggio dal finito all’infinito,ma si servì di esso come di un procedimento euristico per trasportare concetti e risultati del calcolo infinitesimale a quello funzionale.
Il metodo di Volterra, per quanto suggestivo e ricco di notevoli risultati, ha però confini ben precisi, che ne limitano il raggio d’azione e gli impediscono di entrare nel vivo dei più importanti problemi dell’analisi funzionale. Infatti, ottenere i risultati dell’analisi funzionale da quelli dell’analisi infinitesimale classica con il passaggio dal finito all’infinito, tacitamente presuppone il sussistere del seguente principio: nulla può accadere negli spazi di dimensione infinita che già non accada in quelli di dimensione finita.
Tale affermazione è ben lontana dalla realtà. In effetti, i più significativi e profondi concetti e risultati, relativi agli spazi di dimensione infinita, quali, in genere, sono gli spazi funzionali, non hanno un significativo riscontro in quelli di dimensione finita. Gli uni e gli altri si appiattiscono infatti su concetti e risultati che, passando dalla dimensione finita a quella infinita, ammettono almeno due possibilità di generalizzazione; di esse il metodo di Volterra porta a considerare la più ovvia e, spesso, la meno importante. Si pensi ai concetti, fondamentali nell’analisi funzionale, di compattezza, di totale continuità e di convergenza debole, che nella dimensione finita coincidono con quelli di limitatezza e di chiusura, di continuità e di convergenza ordinari.
La grande, peraltro meritatissima, influenza che Volterra aveva sui matematici italiani fece sì che gli indirizzi coltivati all’estero da matematici come David Hilbert (1862-1943), Maurice-René Fréchet (1878-1973), Frigyes Riesz (1880-1956), Stefan Banach (1892-1945) e da altri, non fossero coltivati in Italia (tranne che per un’eccezione, di cui diremo fra breve), talché l’ingresso nella via maestra dell’analisi funzionale da parte degli analisti italiani fu ritardato di almeno vent’anni. Né giovò l’opera di Salvatore Pincherle (1853-1936), autore di un trattato sulle trasformazioni lineari che, scritto su un piano essenzialmente formale, incontrò la severa,ma purtroppo giusta, critica di eminenti analisti stranieri, primo fra tutti Edmund Landau (1877-1938).
Tuttavia a parte le limitazioni cui l’approccio di Volterra nell’analisi funzionale soggiace, la sua opera pionieristica rimane grande, specie per la filosofia cui essa era ispirata: affrontare con idee e metodi profondamente nuovi i grandi problemi delle applicazioni. Le sue indagini sui fenomeni ereditari e la sua teoria delle distorsioni elastiche, sviluppata fra il 1905 e il 1907, sono pietre miliari nella fisica matematica classica e anche nella matematica pura alcune sue pionieristiche idee si rivelarono in seguito feconde. L’intento di estendere ai funzionali, dipendenti da una linea o, più in generale, da una varietà, l’ordinario concetto di funzione armonica, portò Volterra a definire i funzionali armonici che, ripresi poi da William V.D. Hodge (1903-1975), dovevano condurre a quello che può considerarsi uno dei maggiori risultati matematici del Novecento: il teorema di esistenza di Hodge degli integrali armonici su una varietà di Riemann di dimensione n; teorema splendido in sé e gravido di importanti conseguenze per la geometria algebrica e la teoria dei gruppi continui. (G. Fichera)
Tavola II - CACCIOPPOLI E FANTAPPIÉ
Renato Caccioppoli (1904-1959), dopo Vito Volterra (1860-1940) e dopo le ricerche, rimaste purtroppo isolate, di Pia Nalli (1886-1964), fu il primo in Italia a studiare sistematicamente i grandi problemi dell’analisi funzionale, specie non lineare, cercandone l’applicazione ai problemi insoluti dell’analisi classica riguardanti le equazioni integrali e, specialmente, differenziali non lineari. Questi studi avevano ricevuto una formidabile spinta, in Polonia, con l’opera di Juliusz Pawel Schauder (1889-1943) e, in Francia, con quella di Jean Leray (1906-1998). I metodi che furono proposti da questi autori sono fondati sull’estensione agli spazi funzionali di procedimenti di natura geometrica, ben noti negli ordinari spazi di dimensione finita e frequentemente fondati su argomentazioni di carattere topologico. Caccioppoli contribuì in maniera notevole, e talvolta con autentica genialità, allo sviluppo di questi metodi e inoltre alla loro applicazione ai sopraddetti problemi di analisi classica.
Caccioppoli recò importanti contributi anche all’analisi funzionale lineare. Egli, nel 1934, si pose il problema, ripreso nel 1938, di dimostrare l’esistenza degli integrali abeliani di prima, seconda e terza specie su una superficie di Riemann compatta.
Gli interessi di Caccioppoli si estesero alla teoria della misura e dell’integrale, a quella delle funzioni pseudoanalitiche di una variabile complessa, alle funzioni analitiche di due variabili complesse, al calcolo delle variazioni per gli integrali multipli, al problema della quadratura delle superfici e, più in generale, della misura di varietà k-dimensionali in uno spazio a n dimensioni.
Anche se non sempre le sue trattazioni furono completamente esenti da imprecisioni, tanto da originare, talvolta, qualche critica troppo severa (Radó 1948), le idee in esse profuse ispirarono positivamente moltissimi matematici italiani. Il problema della quadratura delle superfici in forma parametrica (il caso, assai più semplice, di quelle in forma ordinaria era stato completamente trattato da Leonida Tonelli nel 1925), fu ripreso da Lamberto Cesari (1910-1990) e daTibor Radó (1895- 1965) che, indipendentemente l’uno dall’altro, giunsero, fra il 1942 e il 1946, a una sua soluzione esauriente.
Luigi Fantappié (1901-1956) fu un cultore di analisi funzionale con caratteristiche completamente differenti da quelle di Caccioppoli. A Fantappié si deve la creazione di un’originale teoria, quella dei funzionali analitici, alla quale, probabilmente ancora oggi, non è stato chiesto tutto quello che essa può dare.
Fantappié non si servì della geometria degli spazi di funzioni dove sono definiti i suoi funzionali, ma poté costruire la sua teoria per una via puramente algoritmica, sfruttando unicamente il fatto che ogni funzionale si considera come definito su classi di funzioni analitiche della variabile complessa z e che inoltre, se la funzione, variabile indipendente, dipende analiticamente, oltre che da z, da un parametro complesso α, allora il funzionale è per definizione funzione analitica di α. Solo in seguito fu notato che alle classi di funzioni dove sono definiti i funzionali di Fantappié può darsi una struttura di spazio topologico T0.
Particolarmente importante è la teoria nel caso dei funzionali lineari. Per questi Fantappié fornì un teorema di rappresentazione mediante il quale, poi, riuscì a edificare un rigoroso calcolo simbolico per una vasta classe di operatori lineari, rappresentando, sotto opportune ipotesi, l’operatore come un funzionale analitico della sua funzione caratteristica. Estese poi, seppure parzialmente, la teoria ai funzionali analitici dipendenti da funzioni analitiche di più variabili complesse per le quali riuscì a stabilire qualche risultato di per sé stesso interessante.
L’opera di Fantappié s’intreccia, spesso precedendola, con quella di numerosi autori che, fra le due guerre, studiarono la teoria delle funzioni analitiche di un operatore. (G. Fichera)