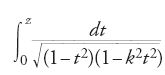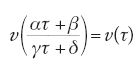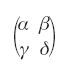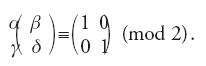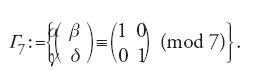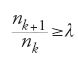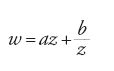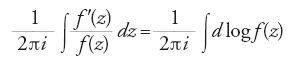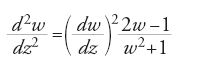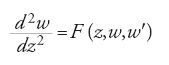La seconda rivoluzione scientifica: matematica e logica. Problemi di analisi complessa alla fine dell'Ottocento

La seconda rivoluzione scientifica: matematica e logica. Problemi di analisi complessa alla fine dell'Ottocento

Problemi di analisi complessa alla fine dell'Ottocento

La teoria generale delle funzioni complesse

Nel corso del XIX sec., a lungo si è scritto un integrale ellittico nella forma

dove il parametro k è detto modulo. I periodi della corrispondente funzione ellittica, e quindi del loro quoziente, sono naturalmente funzioni di questo parametro. Il quoziente si chiama funzione ellittica modulare, e nel 1878 era già chiaro da tempo che si trattava di un oggetto fondamentale per capire la teoria delle funzioni ellittiche. Solamente quell'anno Richard Dedekind (1831-1916) fu in grado di fornire una trattazione della funzione ellittica modulare che non si basasse sulla teoria vasta e difficile delle funzioni ellittiche.

La teoria creata da Dedekind era molto geometrica, e ruotava intorno a una funzione (successivamente chiamata da Felix Christian Klein funzione j) definita nel semipiano Im(z)>0, che verifica una semplice generalizzazione della condizione di periodicità:

dove

è una matrice a coefficienti interi e determinante 1. Associata a una tale funzione j esiste una regione, detta regione fondamentale, dove la funzione assume ogni suo possibile valore una e una sola volta la quale nel caso in esame è delimitata da un semicerchio e da due rette verticali. Utilizzando questa funzione Dedekind fu in grado di sviluppare una teoria quasi completa per rispondere a domande sui periodi e sui moduli, del tipo seguente: quali relazioni ci sono tra i moduli se il corrispondente rapporto dei periodi è moltiplicato per un numero primo? Si trattava di problemi classici, ma quello di Dedekind fu il primo approccio diretto, e rapidamente divenne il metodo standard.

L'anno successivo Klein diede un contributo significativo, ponendo in rilievo i legami con la teoria dei gruppi. Le matrici della forma [3] con coefficienti interi e determinante 1 formano un gruppo G contenente molti sottogruppi, tra i quali quello, già noto a Carl Friedrich Gauss (1777-1855), delle matrici per cui α e δ sono dispari e β e γ sono pari, che formano il sottogruppo delle matrici

Klein studiò come queste matrici agiscano geometricamente sul piano complesso spostando globalmente la regione fondamentale e con essa pavimentano il semipiano superiore. Le regioni fondamentali dei sottogruppi sono costituite da più copie della regione fondamentale della funzione j che formano un nuovo tassello mosso in blocco dal sottogruppo.

La scoperta più interessante di Klein riguarda il sottogruppo delle matrici

La sua regione fondamentale si compone di 168 copie della regione fondamentale della funzione j, formando un poligono a 14 lati mosso globalmente da Γ₇. I lati che si toccano nella pavimentazione definiscono coppie di lati nel tassello fondamentale che, quando sono incollati assieme, danno origine a una superficie di Riemann (in questo caso di genere 3). Il gruppo quoziente Γ/Γ₇ trasforma la superficie in sé. A partire da una descrizione così esplicita della superficie di Riemann, la prima di questo tipo, Klein fu in grado di determinare per essa un'equazione come curva nello spazio proiettivo.

Jules-Henri Poincaré (1854-1912) cominciò indipendentemente nel 1880 un programma di lavoro che generalizzava di gran lunga risultati conosciuti e creava una teoria geometrica delle funzioni complesse. Egli aveva scoperto un altro modo di costruire triangoli e poligoni analoghi a quelli di Klein, e aveva osservato che si spostavano sotto l'azione di gruppi opportuni in modo da ricoprire, di solito, un disco. Inoltre questo disco aveva una struttura geometrica non euclidea invariante per l'azione dei gruppi e quindi la corrispondente superficie di Riemann era localmente uguale a una porzione di spazio non euclideo bidimensionale. Molto rapidamente Poincaré (come Klein) giunse a congetturare che ogni superficie di Riemann corrispondesse a un gruppo di questo tipo e viceversa.

Ciò implicava che ogni superficie di Riemann si potesse ottenere da un poligono contenuto nella sfera di Riemann, o nel piano complesso o nel disco unitario. Fu solo nel 1907 che tale risultato, il cosiddetto teorema di uniformizzazione, fu dimostrato da Poincaré e Paul Koebe. Poincaré era stato guidato dal suo interesse per la teoria delle equazioni differenziali ordinarie lineari, a quel tempo oggetto di un premio bandito dalla Académie des Sciences. Nel 1884 annunciò di aver scoperto una classe di funzioni che generalizzavano le funzioni ellittiche e le funzioni theta, per mezzo delle quali si potevano esprimere le soluzioni di ogni equazione differenziale lineare ordinaria a coefficienti algebrici; un risultato sorprendente, anche se ardue difficoltà si ergevano di fronte ai tentativi di applicare questa scoperta, o anche solo di controllare i dettagli della dimostrazione.

Gli anni Ottanta del XIX sec. videro il rifiorire di interesse nei confronti della teoria delle funzioni complesse, in particolare in Francia, dove alla generazione di Poincaré e di Charles-émile Picard succedette, nell'arco di quindici anni, quella di émile Borel e di Jacques-Salomon Hadamard. Nel 1879 Picard aveva scoperto un miglioramento notevole del teorema di Casorati-Weierstrass: dimostrava che una funzione intera (definita su tutto il piano complesso, finita e priva di punti singolari) assume ogni valore finito, eccetto al più uno, e che in ogni intorno di un punto singolare essenziale una funzione assume ogni valore finito eccetto al più uno. Il suo metodo consisteva in un uso intelligente della funzione ellittica modulare, e quindi sollevò il problema di trovare una dimostrazione essenzialmente elementare, che non facesse uso di metodi apparentemente estranei ‒ i matematici cercano spesso questo tipo di dimostrazioni per essere sicuri di aver capito le ragioni per cui un teorema è vero.

Il lavoro di Picard doveva stimolare molte ricerche sulle funzioni intere. Il giovane Hadamard le mise in relazione con lo studio della funzione zeta di Riemann, mentre Borel fu il primo a dare una dimostrazione elementare dei teoremi di Picard. La caratteristica fondamentale di questo lavoro consiste nel problema di capire quali informazioni diano i coefficienti di una serie di Taylor sulla funzione che tale serie definisce e sulla natura dei punti singolari sul cerchio di convergenza o arbitrariamente vicini a esso. Jean-Gaston Darboux (1842-1917) diede inizio a queste ricerche con la pubblicazione di un articolo sull'approssimazione delle funzioni, che focalizzò l'attenzione sul modo in cui una serie di potenze diviene infinita sul suo cerchio di convergenza. Questo stimolò Hadamard a scegliere come argomento della sua tesi di dottorato le proprietà di una funzione definita da una serie di Taylor. Egli considerò una serie di potenze con raggio di convergenza unitario e studiò come la natura delle singolarità dipendesse dalla rapidità con cui crescono i coefficienti. Tra i risultati contenuti nella tesi c'erano condizioni necessarie e sufficienti sui coefficienti a_n affinché un dato punto sul cerchio di convergenza fosse una singolarità. Il principale tra questi è il teorema delle lacune di Hadamard, che afferma che se f(z)=∑a_nzⁿ, dove a_n=0 tranne che per una successione n_k per la quale esiste una costante λ>1 tale che per tutti i k

allora f(z) non può esere prolungata analiticamente fuori dal cerchio di convergenza della serie, la cui circonferenza costituisce quindi un bordo naturale per f.

Nel 1897 Hadamard pubblicò il famoso articolo, Sur certaines propriétés des trajectoires en dynamique, sulle funzioni intere, che gli valse il Grand Prix. Ciò che gli assicurò la gloria fu la dimostrazione rigorosa, contenuta in questo lavoro, di uno dei punti chiave che Riemann aveva utilizzato senza dimostrarlo nello studio della funzione ζ. Subito dopo Borel iniziò la pubblicazione di una serie di articoli sulla teoria delle funzioni intere, perfezionò e semplificò le definizioni relative alla descrizione della crescita di una funzione al crescere del modulo della variabile, e utilizzò i delicati risultati di Hadamard sul posizionamento degli zeri di una funzione intera e le proprietà del concetto di ordine per dare una dimostrazione del piccolo teorema di Picard.

La rilevanza della teoria delle funzioni complesse

Per ragioni legate all'ampiezza dello spettro delle sue applicazioni e al carattere matematico universale del concetto di funzione, l'analisi è stata, se non la principale, una delle aree importanti della matematica fin dall'invenzione del calcolo differenziale e integrale. Nel corso del XIX sec., essa assunse sempre di più il significato di analisi complessa; molte sottigliezze e applicazioni dell'analisi reale sono creazioni degli ultimi anni del XIX sec. o dei primi anni del XX.

Non c'era, naturalmente, convergenza di opinioni sul contenuto dei programmi per l'insegnamento della matematica nel XIX sec.; c'erano però due centri dominanti, le due Grandes Écoles di Parigi e l'Università di Berlino. Nella seconda metà del XIX sec. i leader riconosciuti dei matematici francesi scrissero i loro Traité, di solito in tre volumi, il cui contenuto sopravanzava di molto il programma svolto nei relativi corsi. La terza edizione del trattato di Camille Jordan (1838-1922) venne ristampata fino al 1959, ben dopo la sua morte. Il primo volume comincia con i fondamenti del calcolo differenziale, prosegue con le funzioni di una sola variabile complessa e si conclude con le applicazioni alla geometria (una combinazione molto francese, nel solco della tradizione della École Polytechnique). Il secondo, sul calcolo integrale, copre argomenti quali gli integrali di Euler, gli integrali di Fourier e il teorema di Green, tuttavia metà del volume riguarda ancora la teoria delle funzioni ellittiche. Il terzo volume infine è sulle equazioni differenziali, ordinarie e alle derivate parziali, reali e complesse. Il Traité di Picard è diverso ma ugualmente dedicato al campo complesso: è qui che la teoria delle superfici di Riemann fa il suo ingresso nei programmi francesi.

A Berlino Karl Theodor Wilhelm Weierstrass (1815-1897) teneva un corso di lezioni strutturato in quattro semestri che copriva l'analisi reale, fondamenti compresi, l'analisi complessa, le funzioni ellittiche e abeliane e alcune applicazioni (principalmente quelle di Adrien-Marie Legendre), e veniva rivisto ogni due anni. Tra le altre figure più in vista a Berlino, Leopold Kronecker ed Ernst Eduard Kummer erano considerati soprattutto cultori di analisi complessa. Fra i loro successori, Hermann Amandus Schwarz lavorava sia sul versante reale sia su quello complesso, mentre Lazarus Fuchs si occupava esclusivamente di analisi complessa. Naturalmente, questa enfasi si rifletteva anche altrove. Il ciclo di lezioni che Klein teneva a Gottinga (in concorrenza, a distanza, con Weierstrass) era prevalentemente dedicato agli aspetti complessi. È più facile nominare autori inglesi e americani di testi di analisi complessa piuttosto che di analisi reale, e lo stesso vale per l'Italia. è ragionevole pertanto domandarsi il perché. Una possibile risposta è che la geometria del tempo era naturalmente algebrica. Il teorema fondamentale dell'algebra ricompensa chiunque scelga i numeri complessi invece dei numeri reali e, di conseguenza, ogni teoria geometrica delle soluzioni delle equazioni polinomiali si colloca in modo naturale fra i numeri complessi. Si potrebbe pensare che questo sviluppo possa realizzarsi solo pagando un prezzo, quello di dover affrontare difficoltà maggiori nell'applicazione della teoria ai problemi del mondo reale. Tale supposizione assume innanzi tutto che il mondo reale accetti solo numeri reali come risposte, e poi che questo sia necessariamente un prezzo da pagare. Entrambe le supposizioni devono essere ridimensionate.

Cominciamo dalla seconda: in un momento di crescente autonomia della matematica pura, il fatto che una teoria ben sviluppata produca risposte nel campo complesso, forse inutili, non è necessariamente da condannare. Il punto di vista dell'epoca era duplice. Innanzi tutto una teoria complessa poteva offrire risposte che una teoria reale non poteva dare; è meglio, dopo tutto, avere risposte complesse a un problema, piuttosto che sapere solo che non esistono risposte reali. E poi non esisteva alcuna opposizione alla creazione di una teoria reale, ma la saggezza generata dall'esperienza suggeriva che le risposte, e perfino i problemi, potevano essere per loro stessa natura complessi. Questo ci riporta alla prima supposizione; che la matematica applicata richieda i numeri reali. Ciò è falso da tutti i punti di vista. Si pensi all'esempio, così comune e banale, del semplice trucco formale secondo cui una coppia di numeri reali x e y si possono fondere insieme in una singola quantità complessa x+iy. Un passo oltre questa ovvia osservazione è il teorema di de Moivre:

Durante il XIX sec. questa notazione è presente nelle applicazioni delle serie di Fourier. Basandosi sul precedente lavoro di Augustin-Jean Fresnel (1788-1827), Augustin-Louis Cauchy (1789-1857) introdusse la prima quantità fisica genuinamente complessa quando discusse la riflettività dei metalli. Un altro esempio, anche se dell'inizio del XX sec., può aiutare a chiarire questo punto: la teoria delle correnti alternate era molto più complicata della semplice algebra delle correnti continue e fu ampiamente formulata da Charles Proteus Steinmetz attraverso gli esponenziali complessi. Lo stesso trucco notazionale di scrivere z=x+iy e dz=dx+idy si dimostrò utile tanto nella teoria delle applicazioni conformi quanto nella cartografia teorica.

Divenne chiaro con la teoria delle funzioni ellittiche che tali funzioni, e gli integrali ellittici associati, erano necessariamente complesse. Questo non diminuì la loro utilità, e non ci fu mai nessuno che suggerisse la necessità di una teoria reale per giustificare il loro utilizzo nel mondo reale. Le prime esposizioni sistematiche delle funzioni di Bessel, quelle di Eugen Cornelius Joseph von Lommel e Carl Neumann, usarono in modo sistematico il teorema integrale di Cauchy e trattarono automaticamente le funzioni come funzioni di variabile complessa. Anche lo stretto legame tra funzioni complesse e armoniche contribuì a rendere naturale la teoria complessa. James C. Maxwell (1831-1879) l'aveva chiamata in causa nel suo Treatise on electricity and magnetism (1873). Klein scrisse e tenne lezioni sull'approccio di Riemann alla teoria delle funzioni complesse, partendo dall'elettrostatica. All'altro estremo dello spettro, negli anni Novanta del XIX sec., il pioniere russo dell'aeronautica, Nikolaj Egorovič Žukovskij (1847-1921), osservò che le funzioni della forma

potevano trasformare in modo conforme il cerchio unitario in una varietà di forme aventi approssimativamente l'aspetto di un profilo alare. Il flusso attorno a un cerchio si ottiene facilmente e da questo Žukovskij fu in grado di analizzare altri profili alari, stimandone la portanza generata. Egli si avvaleva anche dei primi esperimenti effetuati nella galleria del vento, che mostrarono una discrepanza (considerevole) tra la teoria e l'esperienza.

Non bisogna sovrastimare quanto la matematica si facesse, per così dire, complessa nel XIX sec. ma, ciononostante, è una tendenza da mettere in rilievo. Nei sessant'anni tra il 1859 e il 1919 furono scritti oltre sessanta libri sull'argomento, in almeno otto lingue. La Germania, naturalmente, era alla testa di questa tendenza, seguita dalla Francia. I testi inglesi e americani erano all'incirca tanti quanti quelli italiani. Esistevano poi testi russi, spagnoli, polacchi e danesi. I testi tedeschi da principio seguirono l'approccio di Riemann, quindi prevalsero i seguaci di Weierstrass, finché molti autori provarono a fondere le due impostazioni. I francesi dovettero attendere a lungo qualche autore che assimilasse quello che Riemann aveva cercato di dire.

Solo gli italiani, tra le altre nazioni, annoveravano ricercatori di punta nel campo della teoria delle funzioni complesse, e quindi i testi di Felice Casorati, Luigi Bianchi e Salvatore Pincherle rivestono un significato speciale, anche se gli ultimi due apparvero piuttosto tardi (rispettivamente, 1901 e 1899-1900). Gli autori inglesi e americani sembrano più che altro discepoli volenterosi. Andrew R. Forsyth provò a unificare le tre teorie principali, quelle di Cauchy, Riemann e Weierstrass, anche se William F. Osgood trovava che la sua trattazione lasciasse a desiderare. William Harkness e Frank Morley, d'altra parte, seguirono deliberatamente l'approccio di Weierstrass, sebbene si debba notare che una traduzione inglese del testo di Heinrich Durège era stata preparata per il mercato americano nel 1896.

Tutti gli autori francesi, o che scrivevano in francese, come Ernst Leonhard Lindelöf (1870-1946) e i tedeschi attratti dall'approccio di Riemann definivano una funzione complessa ponendo condizioni sulla derivata. Per ottenere i risultati necessari sulle serie di potenze, dimostravano il teorema integrale di Cauchy e la formula integrale di Cauchy. Ciò permetteva di dimostrare che gli zeri di una funzione complessa devono essere isolati, e quindi che una funzione complessa costante su un dominio D, piccolo a piacere, è costante su ogni dominio semplicemente connesso contenente D. Altri risultati fondamentali riguardano il teorema dell'indicatore logaritmico di Cauchy, del 1855, che afferma che il numero degli zeri meno il numero dei poli della funzione f(z) all'interno di una curva chiusa coincide con l'integrale

lungo la curva chiusa; e infine il principio del massimo: il massimo modulo di una funzione complessa definita su un dominio, se esiste, viene assunto sul bordo del dominio stesso. Applicazioni tipiche includevano il teorema fondamentale dell'algebra, il teorema di Liouville e la caratterizzazione delle funzioni razionali a partire dai loro zeri e poli.

Le differenze maggiori tra questi autori riguardavano le applicazioni. Per alcuni erano essenzialmente le funzioni ellittiche. Altri autori ritornarono alle motivazioni originali di Cauchy enfatizzando l'uso dei metodi complessi per valutare gli integrali reali. Durège si proponeva di esporre la teoria di Riemann dei moduli e riscriveva quella parte del suo libro a ogni nuova edizione. Autori successivi nel solco della tradizione riemanniana sono Axel Harnack (1851-1888) e Rudolf Otto Sigismund Lipschitz (1832-1903).

Gli autori della scuola di Weierstrass avevano a disposizione i vari cicli di lezioni del maestro come punto di partenza per le loro elaborazioni e visto che a queste lezioni partecipavano fino a 200 persone si può assumere che quasi tutti i matematici tedeschi e un buon numero di quelli stranieri fossero a conoscenza dei suoi principî. Tra gli effetti positivi del suo insegnamento c'era la distinzione tra poli finiti e singolarità essenziali, e di conseguenza il teorema di Casorati-Weierstrass, impostazione che implicava una significativa critica delle discussioni (piuttosto fuorvianti) fatte da autori precedenti sul fatto che funzioni come e^1/z sembrano assumere nell'origine ogni valore in dipendenza del modo in cui ci si avvicinava a zero. Tra gli effetti negativi c'era la rinuncia a utilizzare il teorema integrale di Cauchy e le conseguenti difficoltà per dimostrare il teorema di Laurent. Il primo libro nello stile di Weierstrass fu quello di Johannes Karl Thomae (1840-1921) del 1880. Egli ne fece seguire una seconda edizione (1898) nello stesso spirito, il che indusse Robert Fricke, uno stretto collaboratore di Klein, a osservare che agli studenti poteva risultare più semplice l'approccio basato sulle idee di Cauchy.

Il libro di Fricke del 1900, rivolto ai matematici applicati, era conforme a quella ipotesi, e approfondiva le applicazioni delle funzioni ellittiche. È interessante il fatto che Thomae scrisse nel 1890 un libro sulla teoria delle funzioni complesse completamente nello spirito di Riemann, suggerendo che gli studenti dovessero cominciare con il rigore di Weierstrass e quindi acquisire il gusto per l'ispirazione di Riemann. Il libro di Otto Biermann del 1887 era ancor più ligio all'ortodossia di Weierstrass, e sarebbe divenuto il miglior approccio iniziale alla teoria perché Weierstrass non scrisse mai un'esposizione del suo punto di vista. Si davano le dimostrazioni tipiche di Weierstrass del teorema di Liouville e del teorema fondamentale dell'algebra, che veniva dedotto dal teorema di Casorati-Weierstrass.

Tra gli autori italiani, Pincherle e Bianchi presentarono una miscela dell'approccio di Cauchy-Riemann e di quello di Weierstrass da cui partivano per trattare una varietà di argomenti più avanzati. Si lasciò a Giulio Vivanti il compito di scrivere un'esposizione ortodossa della teoria di Weierstrass, che August Gutzmer commentò così favorevolmente nel 1901 che accantonò l'idea di scrivere lui stesso un libro del genere e pubblicò invece nel 1906 una traduzione rivista e ampliata del libro di Vivanti. Un commentatore francese si lamentava riguardo al fatto che, a differenza dei geometri, i quali si muovevano ormai felicemente tra metodi analitici e metodi sintetici, gli analisti geometrici e algebrici sembravano sempre distanti tra loro. Il desiderio di unificazione in questa materia era ormai maturo per realizzarsi. Nel 1900 Weierstrass e gli altri fondatori della grande scuola matematica di Berlino erano ormai morti, e la loro tradizione si andava a poco a poco dissolvendo.

Il libro di Heinrich Burkhardt (1861-1914) del 1897, che fu ristampato in quattro edizioni, cominciava con il modo di Riemann di presentare le cose, e quindi passava a una presentazione più precisa, alla maniera di Weierstrass. Inoltre, Gottinga, dove lo spirito era dichiaratamente riemanniano, stava rapidamente diventando il centro universitario dominante in Germania. David Hilbert (1862-1943) tenne proprio a Gottinga nel 1896-1897 un corso di lezioni sulla teoria delle funzioni complesse; le annotazioni ai suoi appunti mostrano che egli raccomandava il libro di Durège per una prima introduzione, e con maggior calore l'Abriss di Thomae del 1890 per l'approccio di Cauchy-Riemann e il libro del 1888 di Thomae per l'approccio di Weierstrass. Venivano anche elogiati il Traité di Jordan e quello di Picard. Una tale panoramica sulla letteratura era tuttavia l'antitesi dell'approccio adottatto a Berlino, dove avevano preferito rielaborare il materiale e produrre la loro versione, senza riferimenti che suggerissero percorsi alternativi.

Il corso di Hilbert è uno dei primi a offrire qualcosa di simile all'attuale consenso in materia; tra i libri con tale impostazione ci sono quelli di Konrad Knopp del 1918 e di Ludwig Bieberbach del 1921 in Germania e l'esposizione francese, meno rigorosa, di Édouard Goursat del 1902. Una dimostrazione della maturità raggiunta dalla tradizione risulta evidente quando si rifletta che tutti i testi moderni compiono più o meno lo stesso percorso di quelli citati nell'approccio alla materia. Il testo di Lars Valerian Ahlfors (1907-1996) è tipico, e le note tra parentesi ne sottolineano gli aspetti più moderni. Sono definiti i numeri complessi e illustrate le loro operazioni algebriche fondamentali, quindi si definisce una funzione olomorfa come una funzione che ha una derivata (non necessariamente continua); essa soddisfa perciò le equazioni di Cauchy-Riemann.

Il primo risultato importante è il teorema integrale di Cauchy, dimostrato con il metodo di Goursat. Segue la formula integrale di Cauchy, servendosi della quale si dimostra che una funzione olomorfa è infinitamente differenziabile e ammette un'espansione in serie di Taylor; il principio del massimo modulo è utilizzato per garantire la convergenza. è sviluppata la teoria dei poli di ordine finito: il teorema dei residui di Cauchy, gli sviluppi in serie di Laurent e il calcolo del numero degli zeri e dei poli interni a una regione. Vengono quindi descritte le singolarità essenziali ed è dimostrato il teorema di Casorati-Weierstrass. Alcuni argomenti ulteriori sono a questo punto a portata di mano; tra essi, il teorema di Liouville, il teorema di Morera e il teorema della singolarità eliminabile di Riemann. Questo è un mero elenco degli argomenti che costituiscono il nucleo elementare della teoria delle funzioni complesse, secondo l'opinione generale. Esiste una certa flessibilità sui complementi; alcuni introducono un capitolo sulle funzioni armoniche, altri no. Il libro di Ahlfors segna il punto in cui il legame con le funzioni ellittiche venne rescisso; egli rinvia il lettore al libro di Edward T. Copson del 1935. Il cambiamento riflette il consenso che, a partire dal 1950, esiste sui programmi; c'è un nucleo fondamentale della materia e oltre a questo non una bensì molte aree di applicazione e di approfondimento della teoria. Tra gli argomenti di questo genere ci sono le funzioni ellittiche, il prolungamento analitico, la teoria delle funzioni intere e delle funzioni meromorfe e il teorema di rappresentazione di Riemann; le funzioni algebriche, le superfici di Riemann compatte e le famiglie normali; i teoremi di rappresentazione di Weierstrass e di Mittag-Leffler.

Il problema di Riemann-Hilbert

In alcune note pubblicate solo dopo la sua morte, Riemann aveva sviluppato un argomento secondo il quale esiste sempre un'equazione differenziale con n punti singolari e monodromia specificata in questi punti. In seguito, nel 1900, Hilbert presentò una variante di tale problema, il XXI dei suoi ventitre problemi, al Congresso internazionale dei matematici di Parigi. Egli chiese di mostrare che esiste sempre un'equazione differenziale ordinaria lineare fuchsiana con punti singolari e gruppo di monodromia dati. Tale problema non coincide con quello introdotto da Riemann, perché questi specificava la monodromia in ogni punto di ramificazione mentre Hilbert individuava solo il gruppo. Ancor più grave è il fatto che un semplice calcolo delle costanti dimostra che, in generale, ci saranno più coefficienti nelle matrici che in ogni equazione differenziale della classe fuchsiana con il dato numero di punti di ramificazione. Tuttavia si può o accrescere il numero di costanti nell'equazione differenziale introducendo singolarità apparenti o si può passare allo studio di un sistema di equazioni differenziali del primo ordine. Come Hilbert notò, questo percorso era già stato tracciato in una serie di casi speciali da L. Schlesinger usando la teoria di Poincaré delle funzioni zeta-fuchsiane: perciò Hilbert stesso invitò alla ricerca di un metodo che fosse perfettamente generale.

Un metodo fu trovato nel 1908 da Josip Plemelj (1873-1967) e indipendentemente nel 1913 da George D. Birkhoff (1884-1944), al quale fu fatto notare da Otto Toeplitz che aveva di fatto risolto il problema di Riemann-Hilbert. La soluzione rimase invariata fino al 1989 quando due matematici russi, Dmitrij Anosov e Andrej Bolibruch, annunciarono che in realtà questi risultati non erano corretti e che in effetti è possibile specificare punti singolari e dati di monodromia in modo che non esista nessuna equazione differenziale corrispondente nella classe fuchsiana. L'errore nei lavori classici proviene dalla confusione di due problemi. È facile mostrare che ogni equazione differenziale ordinaria lineare di ordine n può essere scritta come un sistema di n equazioni differenziali ordinarie del primo ordine; inoltre si può definire cosa sia un sistema di classe fuchsiana.

Non è vero tuttavia che ogni equazione differenziale fuchsiana produce un sistema fuchsiano: vero è invece che il problema di Riemann-Hilbert può essere risolto per ogni sistema che provenga da un'equazione differenziale di classe fuchsiana. Anosov e Bolibruch inoltre hanno caratterizzato i sistemi fuchsiani per i quali il problema di Riemann-Hilbert può essere risolto.

Equazioni differenziali non lineari

Lo studio delle equazioni differenziali non lineari è molto più difficile: durante il XVIII e il XIX sec. anche i migliori progressi furono frammentari. Per le equazioni del primo ordine erano state scoperte numerose tecniche; fra queste alcune erano antiche quasi quanto l'invenzione del calcolo stesso. Tali tecniche consistevano di vari cambiamenti di variabile, secondo regole che avevano lo stesso grado di difficoltà delle procedure per la valutazione degli integrali. Per esempio si poteva effettuare un cambiamento di variabile per ridurre una data equazione differenziale a un'altra le cui soluzioni potevano essere trovate per integrazione. Questo cambiamento implicava la moltiplicazione dell'equazione per una funzione detta 'fattore integrante'. Tali metodi furono sistematizzati da Sophus Lie (1842-1899), che spiegò fenomeni come quello dell'esistenza del fattore integrante tramite l'esistenza di un gruppo di simmetria dell'equazione. Lie affrontò anche i casi di ordine superiore ma questi si rivelarono estremamente più difficili.

Progressi ulteriori vennero con l'introduzione di idee provenienti dalla teoria delle funzioni complesse. L'equazione differenziale del primo ordine

[10] F(z,w,w′)=0

dove w′=dw/dz e F è un polinomio in w e w′, ha alcune soluzioni; la soluzione generale dipende da un parametro arbitrario. Nel caso lineare la posizione dei punti di ramificazione e dei punti singolari della soluzione è determinata dall'equazione differenziale e non dipende da parametri arbitrari; nel caso non lineare si può invece verificare questa eventualità. Era importante pertanto stabilire quando i punti di ramificazione fossero, in effetti, fissati; questo compito fu portato a termine da Fuchs nel 1884. Fu anche mostrato che tutti i punti singolari essenziali delle soluzioni sono fissati, cosa che però non si verifica per le equazioni differenziali non lineari del secondo ordine.

Un esempio elementare di quest'ultima eventualità è dato dall'equazione differenziale

la quale ha come soluzione generale

[12] w=tan(log(Az−B)),

dove A e B sono costanti arbitrarie. Il punto z=B/A è sia un punto di ramificazione sia un punto singolare essenziale; palesemente z dipende dalla scelta dei parametri arbitrari A e B.

Lo studio delle equazioni differenziali della forma

(dove F è razionale in w′, algebrica in w e analitica in z) si indirizzò per questo motivo al problema della caratterizzazione di quelle equazioni con punti di ramificazione e punti singolari essenziali fissi.

La classificazione conclusiva fu iniziata da Paul Painlevé (1863-1933) in una serie di articoli negli anni Novanta del XIX sec. e venne poi completata da Bertrand Gambier nel 1909. Il risultato comprendeva una lista di cinquanta tipi di equazioni delle quali sei potevano dirsi fondamentali. Queste sei nuove classi di equazioni definiscono corrispondenti funzioni complesse che sono dette oggi funzioni trascendenti di Painlevé.