La sfida della cupola

La sfida della cupola

Le cupole e la scienza

L’ideazione e la costruzione delle cupole, dal Quattrocento al Settecento, ha alimentato la sperimentazione e la formalizzazione della meccanica e della scienza delle costruzioni, così come ha contribuito all’idea del matematismo fisico. È nel cantiere della basilica di S. Maria del Fiore a Firenze che Filippo Brunelleschi (1377-1446) prova a passare dal mondo del pressappoco a quello della precisione, questione fondamentale per la formazione della scienza moderna. Analogamente, uscendo dal contesto italiano, è nel cantiere per la costruzione della cupola della chiesa di Sainte-Geneviève a Parigi, su progetto di Jacques-Germain Soufflot (1713-1780), che si metteranno a punto, grazie all’ingegnere Émiland-Marie Gauthey, alcune procedure per la valutazione della resistenza dei materiali.

Indubbiamente, la scienza delle costruzioni non può fare a meno dei processi astrattivi che conducono all’autonomia della teoresi. Nel contempo, questa scienza è intimamente legata alla sperimentazione e quindi a delle ragioni empiriche. Quello che la scienza moderna cerca di mettere in atto è l’unificazione di ciò che il mondo antico teneva diviso, cioè pensiero e percezione sensibile, argomentazione logica e verificabilità empirica, ragione ed esperienza. Lo fa proprio mettendo continuamente in relazione teoria e prassi, senza pretendere che l’una risolva l’altra. Con la scienza delle costruzioni la cupola diventa ‘calcolabile’ in quanto si ‘rappresenta’ come semisfera; e questa dapprima è un ente geometrico, per poi diventare, con René Descartes, un ente algebrico. Grazie alla geometria analitica, le figure geometriche sono formulabili attraverso funzioni algebriche che non hanno più bisogno di una rappresentazione grafica e i cui dati, inoltre, sono l’esito di una ‘quantificazione’ sempre più precisa degli enti sottoposti ad analisi o a manipolazione. Gli enti vengono tutti omologati come gravi, perdendo così il loro carattere, la loro specificità, la loro sostanza. Una mela non è una pera, ma ambedue hanno un peso. È su questa trasformazione degli enti in gravi che può essere formulata la legge della gravitazione universale di Isaac Newton. È anche per questo doppio registro, teorico e sperimentale, che si potrà dire non solo che un determinato materiale è più resistente di un’altro, ma anche, e con precisione, di quanto.

Si dirà che tale questione filosofica ed epistemologica ha poco a che vedere con l’ideazione e la costruzione di una cupola, ma noi crediamo che questi temi fossero sotto traccia nelle riflessioni comuni, per es., a Brunelleschi e a Paolo dal Pozzo Toscanelli (1397-1482). Quel Brunelleschi che, ‘inventando’ la prospettiva, sapeva benissimo che stava ‘geometrizzando’ il mondo, nel senso che lo stava ‘discretizzando’ per poterlo manipolare. Quel Toscanelli che, nella Firenze del primo Quattrocento, istruisce Brunelleschi sulla geometria di Euclide e disegna un planisfero in cui privilegia la rappresentazione del mondo rispetto alla sua simbolizzazione (il planisfero, oggi perduto, si dice sia stato usato da Cristoforo Colombo per il suo viaggio verso le ‘Indie’, che per molti segna il momento cruciale della stessa modernità); e che, inoltre, colloca sulla sommità della cupola di S. Maria del Fiore una piastra di ottone per convogliare la luce del Sole all’interno dell’edificio, trasformandolo così in una gigantesca meridiana, allo scopo di analizzare l’orbita terrestre intorno al Sole.

Al centro delle vicende che andiamo a raccontare vi sono, oltre a Brunelleschi e Toscanelli, Leon Battista Alberti (1404-1472) e Galileo Galilei (1564-1642). Quest’ultimo non è certo progettista o costruttore di cupole, ma senza di lui non sarebbe nata la meccanica moderna.

I progetti per la cupola di S. Maria del Fiore

Il caso iniziale di questo processo epistemico è la cupola di S. Maria del Fiore che, a differenza di quella del Pantheon, non viene metaforicamente legata alla terra, ma portata verso il cielo, per essere centro di ogni cosa. Il suo cantiere va considerato come una vera e propria impresa collettiva, nella quale si creano nuovi macchinari, nuovi sistemi organizzativi, nuove logiche costruttive. Insomma, un insieme organico di tradizione e innovazione.

Durante tutto il Trecento, Firenze conosce un fortissimo sviluppo economico e quindi una grande crescita edilizia. La nuova cattedrale doveva essere il simbolo di questo sviluppo. L’aveva progettata Arnolfo di Cambio che nel 1296 (quando si chiamava ancora S. Reparata) ne aveva posto la prima pietra, ma all’inizio del Quattrocento non era stata ancora completata. Uno dei motivi era che nessuno sapeva trovare una proposta convincente per la costruzione di quella che doveva essere la più grande cupola del mondo allora conosciuto. Nel 1366 l’Arte della Lana, la corporazione più potente e ricca della città, che sovrintendeva alla costruzione della chiesa, si rivolse al capomastro allora responsabile del cantiere, Giovanni di Lapo Ghini (m. 1373) e a un gruppo di artisti e ‘franchi muratori’ (organizzati in logge) guidati dal capomastro Neri di Fioravanti (m. 1374 ca.), chiedendo nuovi modelli per valutare quale soluzione scegliere. Ghini propose un modello gotico con murature non spesse, alte finestre e dei contrafforti a sorreggere la cupola. Neri propose una cupola «sorretta da una serie di catene di pietra o di legno incorporate nella struttura che girando intorno alla circonferenza, avrebbero sostenuto la cupola nei punti di possibile rottura, così come il cerchio di ferro tiene unite le assi di una botte» (King 2001, p. 19).

Fu scelto il modello di Neri. Questi aveva una significativa esperienza nella costruzione di coperture a volta. A lui si devono la progettazione e la costruzione di una volta a botte su luce di 18 m della grande sala del Bargello e degli archi ribassati del nuovo Ponte Vecchio, ricostruito dopo l’alluvione del 1333.

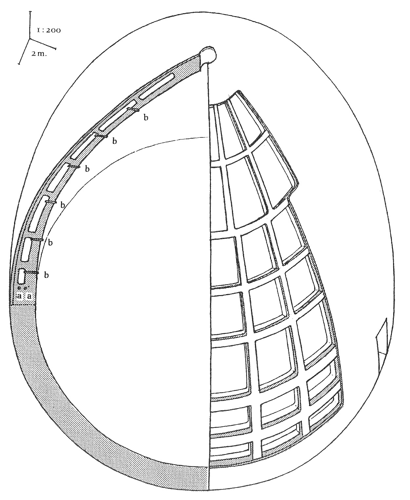
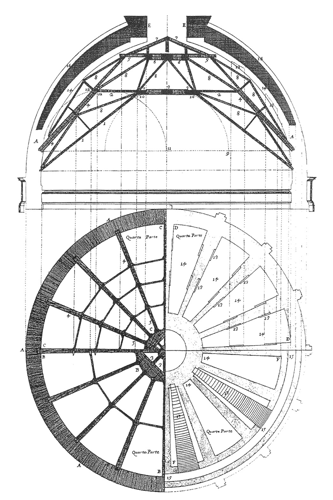
Una delle particolarità del modello di Neri era che prevedeva una struttura architettonica piuttosto rara: le cupole erano infatti due, una all’interno dell’altra. Possiamo trovare questa soluzione in edifici precedenti: nella basilica di S. Vitale a Ravenna (6° sec.) e, ancor più, nel battistero di S. Giovanni a Firenze (11°-12° sec.), che è una doppia cupola in quanto volta ottagonale sormontata da un tetto piramidale in legno. Curiosamente, però, l’esempio più simile si trova nella lontana Persia: è la tomba del sovrano mongolo Khudābanda Öljeytü a Sulṭāniyya, eretta tra il 1307 e il 1313. Si tratta di una struttura avente una luce paragonabile a quella fiorentina, caratterizzata da costolature (sia verticali sia orizzontali) di collegamento dei due paramenti, che hanno un parallelo evidente con gli ‘sproni’ e gli archi interni della cupola di Brunelleschi (fig. 1). Inoltre, la presenza di elementi in legno di pioppo – disposti radialmente con funzionamento a mensola e in seguito tagliati sul filo d’intradosso della calotta, con il chiaro scopo di sostenere locali impalcati provvisori – mostra con evidenza come la struttura sia stata realizzata senza l’uso di centine.

Il compito di Brunelleschi, vincendo il concorso del 1418, sarà quello di risolvere i complessi problemi tecnici posti dal progetto di Neri, che prevedeva una cupola a forma ogivale, con un diametro esterno di circa 54 m da elevare sino all’altezza di 105 m. Brunelleschi propose un modello ispezionabile, largo più di 2 m e alto 4. Per costruirlo vennero usati 49 carri pieni di calce e più di 5000 mattoni. Lo scopo fondamentale era quello di dimostrare che l’immane cupola poteva essere costruita senza centine.

Dal punto di vista concettuale, l’idea di base nella costruzione di una volta sferica, senza uso di centine, sta nel fatto di dotarsi, a ogni passo successivo del processo d’innalzamento, di un anello orizzontale chiuso e continuo in sommità. Questo anello funge da elemento di stabilizzazione del sistema, nel senso che su di esso trovano equilibrio, sotto forma di compressione, e secondo uno schema a simmetria assiale, le forze che tenderebbero a far ruotare verso il basso gli infiniti ‘archi incompleti’ che si ottengono sezionando la cupola, con piani verticali passanti per il suo asse centrale.

Ma quali sono i saperi e le tecniche che entrano in gioco in un’opera come questa? Brunelleschi abitava vicino al cantiere del duomo, e poteva osservare ogni giorno le macchine e l’organizzazione dei complessi processi costruttivi. Ne capiva le logiche e ne era inevitabilmente affascinato. Egli apparteneva alla corporazione degli orafi, considerati i ‘principi’ degli artigiani del Medioevo. Aveva costruito non solo gioielli, ma anche oggetti di vario tipo. Tra questi, degli orologi che agivano proprio grazie a meccanismi rigorosi, precisi ed efficaci, e soprattutto di piccole dimensioni. In tali esperienze, comprendendo e sperimentando la logica degli ingranaggi, delle leve, delle forze e delle molle, si era misurato con i concetti della meccanica.

L’impresa di Brunelleschi, proprio perché opera collettiva, è comprensibile solo se teniamo presenti le attività, non soltanto a Firenze, ma anche a Siena, delle botteghe rinascimentali, veri e propri laboratori dell’innovazione tecnico-artistica. In queste botteghe avviene la trasformazione del lavoro dei tecnici, da attività fondata sulla pratica e sull’esperienza, in disciplina basata su premesse teoriche assiomaticamente definite e messe in pratica attraverso metodi rigorosi di calcolo e di misurazione. È in queste botteghe che avviene la collaborazione tra umanisti e artisti-ingegneri e che vengono assimilati i testi dell’ottica classica e medievale come quelli della fisica e della geometria greca. È qui che si crea l’intreccio tra ‘ingegneria’, interpretazione della natura e filosofia.

Brunelleschi partecipa al concorso per le porte di bronzo del battistero scontrandosi con Lorenzo Ghiberti. Ne esce sconfitto e si reca, assieme a Donato Bardi, detto Donatello, a Roma; vi risiede per almeno due anni, guadagnandosi da vivere come orafo, ma sognando di poter risolvere il problema della costruzione della cupola. Per questo studia le fatiscenti rovine dell’antica città imperale. Si ritroverà ad analizzare il comportamento statico di alcuni monumenti antichi o tardoantichi della città, il Pantheon (27-25 a.C., ricostruito nel 115-127), le terme di Traiano (104-109) e il tempio di Minerva Medica (inizio del 4° sec.).

S. Maria del Fiore e il Pantheon

Il Pantheon è una cupola sferica del diametro di 43,3 m, che dispone sul perimetro di appoggio di una muratura verticale dall’enorme spessore di 6,5 m, alleggerita con nicchie radiali. Certo, nella Firenze di Brunelleschi non esiste né la possibilità di realizzare un volume sferico, né la disponibilità di una massa muraria così consistente all’appoggio. Vi è però nel Pantheon un’evidenza immediata: considerato che, anche in ragione del loro spessore, i muri perimetrali non presentano aperture, aria e luce penetrano attraverso un grande occhio zenitale, un foro circolare del diametro di 9 m, ricavato sulla sommità della cupola. Quest’occhio rappresenta una prova diretta del fatto che l’equilibrio necessario e sufficiente alla realizzazione senza centine poteva essere realizzato anche su una struttura di così enormi dimensioni.

Un altro suggerimento che si poteva trarre dall’osservazione del Pantheon deriva dalla presenza, all’intradosso della cupola, di una superficie a cassettoni. Certamente, la presenza dei cassettoni poneva il problema delle modalità costruttive di questa struttura. Assunto infatti che un’opera di quel tipo potesse essere realizzata senza utilizzare centine, i casseri avrebbero comunque richiesto un supporto locale. Tutto ciò poteva rappresentare uno spunto per immaginare una procedura di erezione che utilizzasse supporti locali, collegati in ogni fase di avanzamento alle strutture già realizzate.

Il tipo di spunti che Brunelleschi deve aver tratto dall’osservazione del Pantheon denota l’elaborazione di un sottile processo concettuale: nel considerare la superficie a cassettoni, egli deve aver compreso che su quella cupola era stata utilizzata almeno una centinatura parziale. Ma la presenza dell’occhio, la sua dimensione e la sua altezza, mostrano con evidenza come questa stessa centinatura, dal punto di vista prettamente statico, non fosse necessaria.

Ciò che appare straordinario in Brunelleschi è, dunque, come egli smonti idealmente la cupola del Pantheon, come si farebbe con le componenti di una macchina o con gli ingranaggi di un orologio. La smonta non per ricostruirla tale e quale a Firenze, ma per intuirne le logiche, i funzionamenti strutturali, i punti di forza e gli elementi di debolezza, e per dedurre, al termine di un procedimento del tutto concettuale, che a Firenze si sarebbe dovuto realizzare qualcosa di radicalmente diverso. Il risultato è che, nella cupola di S. Maria del Fiore, le scelte costruttive sono in realtà assolutamente autonome rispetto a quelle che avevano caratterizzato il Pantheon: diversi sono il materiale (la muratura in mattoni in luogo del calcestruzzo), la geometria (a padiglione anziché emisferica), la morfologia (a doppia anziché a singola calotta); diversa, infine, è l’architettura, che produce un oggetto a scala urbana, una cupola «magnifica e gonfiata» (F. Brunelleschi, Documento-programma per l’erezione della cupola, 1420, cit. in Di Pasquale 2002, p. 87), visibile dall’intera città, anziché un volume compresso e parzialmente nascosto. In altre parole, Brunelleschi non ha messo in atto un’analogia mimetica, ma una concettualizzazione dei processi; non ha riprodotto, ma ‘smontato’ l’oggetto per produrre qualcos’altro.

Le cupole e l’invenzione della prospettiva

È probabilmente il bisogno di rilevare queste architetture, per comprenderne la ‘figura’, ma anche il comportamento statico, che spinge Brunelleschi a ‘inventare’ la prospettiva. Da una parte viene ritrovato ciò che gli antichi già conoscevano e praticavano; dall’altra, con la formalizzazione del procedimento, prima geometrica e poi anche matematica, diviene possibile mettere in essere una ‘rappresentazione’ del mondo che, ‘discretizzandolo,’ permette un’analitica per parti, l’individuazione di leggi e la possibilità di rappresentare realisticamente l’irrappresentabile, l’immaginario, persino il fantastico. In sostanza, la prospettiva diviene il metodo per rappresentare oggetti tridimensionali su una superficie a due dimensioni, in modo da renderne calcolabili anche la posizione relativa, la dimensione o la distanza.

L’esperimento prospettico di Brunelleschi era un trucco ottico, quasi magico. Per alcuni aspetti anticipava i dispositivi ottici futuri come la camera oscura, i ‘panorami’, i diorami e l’arte catottrica.

Mettendosi all’interno di Santa Maria del Fiore, a poca distanza dal portale principale a circa 35 metri dal Battistero, dipinge su un piccolo pannello, in prospettiva perfetta, utilizzando un piano pittorico costruito geometricamente, tutto ciò che era visivamente contenuto entro la ‘cornice’ del portale della cattedrale: il Battistero e le vie adiacenti. […] Sostituì la raffigurazione del cielo con un pezzo di argento brunito, uno specchio che avrebbe riflesso in tempo reale le nuvole, gli uccelli e i cambiamenti intensi della luce. Infine, praticò un foro della dimensione di una lenticchia nel punto di fuga del dipinto, punto centrale all’orizzonte nel quale convergono tutte le rette di fuga. Il pannello fu quindi pronto per la dimostrazione. L’osservatore, posizionandosi a due metri all’interno del portale di Santa Maria del Fiore – in definitiva nel punto esatto dove Filippo aveva eseguito il dipinto – doveva girare il lato dipinto del pannello verso l’esterno e guardare attraverso il piccolo foro. Nell’altra mano aveva uno specchio, tenuto alla distanza della lunghezza del braccio, il cui riflesso (al contrario) mostrava l’immagine dipinta del Battistero e della piazza San Giovanni. L’effetto era così realistico che l’osservatore era incapace di dire se l’immagine attraverso il foro era quella attualmente in corso dietro il pannello oppure una perfetta illusione di quella realtà (King 2001, pp. 67-68).

Per misurare le distanze (tramite il metodo dei triangoli simili, ben noto all’epoca) bastava mettere davanti alla tavoletta uno specchio parallelo e della stessa forma, e calcolare poi quanta distanza serviva per inquadrare tutta l’immagine: più lo specchio era piccolo e più lontano doveva essere messo. Si poteva così stabilire un rapporto proporzionale costante tra immagine dipinta e immagine riflessa nello specchio (misurabile in tutte le dimensioni), e calcolare la distanza tra gli oggetti reali (il vero battistero) e il punto di osservazione, tramite un sistema di proporzioni. Quindi si poteva disegnare una sorta d’intelaiatura prospettica utile alla rappresentazione artistica, e inoltre era dimostrata l’esistenza del punto di fuga verso il quale gli oggetti rimpicciolivano.

La prospettiva non è solo una procedura controllabile di riproduzione e misurazione del mondo e, quindi, una parte dei processi di formazione del pensiero scientifico moderno. È anche un modo per ibridare la vita reale e quella immaginaria, per ingannare, stupire, mettere sotto scacco la realtà stessa. Non permette solo di riprodurre il reale, ma anche di produrlo. Nella prospettiva è in gioco sia ciò che chiamiamo scienza sia ciò che chiamiamo arte.

Il cantiere di S. Maria del Fiore

L’impresa pretende l’ingegno, e questo si mette in opera con l’astuzia, per far sì che la natura agisca a comando e diventi calcolabile. Il cantiere di S. Maria del Fiore era governato da Brunelleschi, si racconta, con assoluta determinazione e controllo. Vi lavoravano circa 300 operai, e il suo indotto esterno coinvolgeva tutti gli artigiani presenti nel comune di Firenze. Vi si potevano ammirare macchine aventi diverse funzioni, alcune ‘inventate’ dallo stesso Brunelleschi.

Uno dei problemi fondamentali era quello di trasportare il materiale da costruzione e metterlo in posizione con grande precisione. Per es., i blocchi di arenaria, pesanti circa 770 kg e presenti a centinaia, dovevano essere trasportati a oltre 50 m d’altezza. L’argano del cantiere sollevò in dodici anni marmo, mattoni, pietre e malte per un peso di 30 milioni di kg. Nel cantiere venne usata una delle funi più lunghe, resistenti e pesanti mai fabbricate: 182 m di lunghezza e 450 kg di peso.

Brunelleschi, tra l’altro, inventò una delle macchine più celebri del Rinascimento: un argano azionato non da uomini, ma da buoi. Una macchina mai vista prima. L’aspetto tecnologicamente significativo era che permetteva ai buoi di girare sempre dalla stessa parte, mentre l’andamento degli argani poteva essere reversibile. La variazione del senso di marcia era effettuata per mezzo di un dispositivo a vite senza fine, a filettatura elicoidale. A seconda del senso dell’avvitamento, sollevava o abbassava il rotore di molti centimetri, azionando l’una o l’altra delle ruote orizzontali con i pioli del subbio grosso, il più grande dei tre tamburi della fune. Così, un solo bue poteva sollevare un peso di 450 kg, a una altezza di 60 m, in 30 minuti.

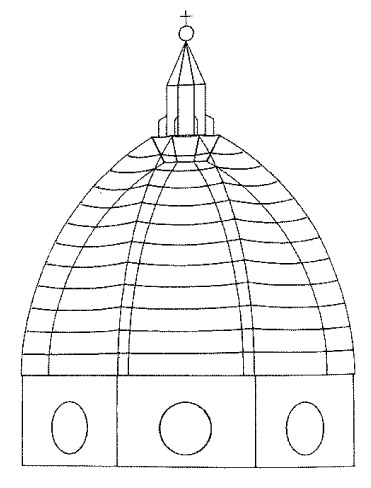
L’altra impresa e l’altra macchina (le due questioni stanno assieme) riguarda il sollevamento della lanterna alla fine della costruzione della cupola. La lanterna permette di chiudere la cupola, portando nel contempo la luce all’interno. Essa assume anche una connotazione retorica: chiude la costruzione verso il cielo; la rende in modo più evidente il centro di una spazialità urbana diffusa; permette di ribadire, grazie a colonne, capitelli e cornici delle finestrature, un determinato linguaggio architettonico, oggi si direbbe uno stile. La lanterna si era già vista, per es., nelle cupole della basilica di S. Marco a Venezia, nella cattedrale di Saint-Front a Périgueux e, pochi anni prima, nel 1420, nella Yeşil Cami (moschea verde) di Bursa in Turchia. Dopo la messa in opera della lanterna di Brunelleschi, peraltro prevista anche nel progetto di Neri, tutte le cupole che disegneranno i cieli delle città europee useranno questo stratagemma.

La struttura della cupola di S. Maria del Fiore

Proviamo ora a descrivere la cupola di S. Maria del Fiore. La larghezza della cupola interna doveva rastremare come quella del Pantheon, passando da 2 m alla base a 1,5 alla sommità; la calotta esterna doveva restringersi dallo spessore della base, leggermente superiore ai 60 cm, per arrivare a poco più di 30 cm all’altezza degli oculi. Allo stesso modo, gli otto costoloni verticali posti agli angoli dell’ottagono dovevano andare rastremando via via che si avvicinavano alla cima. Mentre il peso morto del Pantheon era alleggerito dall’uso di pomici e anfore vuote, in S. Maria del Fiore le calotte dovevano essere costruite in pietra per i primi 14 m, per continuare usando mattoni e tufo, una pietra leggera e porosa originata dalle ceneri vulcaniche.

All’altezza di «30 braccia» (F. Brunelleschi, Documento-programma…, cit. in Di Pasquale 2002, p. 88), i letti della muratura si sarebbero innalzati a formare un angolo di 30° in orizzontale al limite dell’angolo critico di slittamento. La sola forza d’attrito avrebbe tenuto insieme il laterizio a un angolo di 30°, anche con la malta ancora fresca; quindi non ci sarebbe stato bisogno di nessuna centinatura fino a quel punto. Al di sopra di quel livello, ogni corso di muratura avrebbe iniziato a inclinarsi in maniera decisa, raggiungendo un’angolazione massima in prossimità della cima.

La cupola esterna ha una duplice funzione: da un lato, serve a proteggere dagli agenti atmosferici la cupola interna, che costituisce il principale organismo strutturale; dall’altro, deve aumentare la magnificenza dell’oggetto architettonico. La cupola interna presenta su ogni spigolo un profilo a ‘quinto acuto’, ovvero ad arco di cerchio, centrato ai quattro quinti del diametro interno dell’ottagono di base, dalla parte opposta rispetto all’asse verticale di simmetria. Le due cupole sono collegate da 24 costoloni verticali, radialmente convergenti in pianta, dei quali 8 disposti in corrispondenza degli spigoli e 16 suddivisi nella larghezza delle 8 vele. Collegamenti su piani paralleli orizzontali, per mezzo di blocchi in pietra uniti con staffe metalliche, hanno luogo rispettivamente sul secondo e terzo camminamento interno. I costoloni di spigolo e quelli interni sono poi collegati per mezzo di ‘mattoni in atto d’arco’, ovvero archi in muratura, disposti su nove livelli paralleli, nel piano ortogonale alla superficie della cupola (Mainstone 1980, p. 2). Tra il primo e il secondo camminamento è visibile, nello spazio tra le due vele, una catena circonferenziale in legname, mentre risultano nascoste alla vista ulteriori catene in pietra e metallo. Il programma dei lavori si conclude con l’ordine di servizio: «murinsi la cupola nel modo di sopra, senz’alcuna armadura» (F. Brunelleschi, Documento-programma…, cit. in Di Pasquale 2002, p. 88).

Cupole e teoria archimedea

Se l’economia derivante dall’ipotesi di una costruzione senza uso di ‘armatura’ era apparsa immediatamente irrinunciabile, Brunelleschi convinse la commissione che doveva giudicare la bontà del suo progetto solo dopo aver visto un modello della cupola realizzato in scala significativa. Trascurando le componenti resistenti, che potevano riferirsi alle caratteristiche dei materiali e agli attriti sui letti di malta, un modello di questo tipo, in realtà, avrebbe potuto offrire indicazioni significative soltanto in termini di stabilità generale dell’equilibrio, mentre nessuna informazione poteva derivarne sulla resistenza della struttura, in particolare nel corso della sua realizzazione.

Del resto, fino all’epoca di Brunelleschi la conoscenza statica disponibile era in realtà unicamente legata al controllo degli equilibri: si trattava cioè di una statica (e di una relativa matematica di supporto) unicamente di tipo archimedeo. Nella proposizione VI del suo trattato Sull’equilibrio dei piani, Archimede traccia una primordiale dimostrazione della condizione matematica di proporzionalità inversa tra pesi e distanze che governa l’equilibrio della leva.

La teoria archimedea segna, in qualche modo, un’iniziale discontinuità rispetto alle posizioni della meccanica aristotelica, intesa come una teoria fisica generale, tendente ad abbracciare una visione globale del mondo. In quanto conoscenza universale, la fisica di Aristotele rifiuta infatti una descrizione del reale in termini matematici.

Galilei si colloca a metà tra la concezione neoaristotelica e quella neoplatonica. In lui, la scientia mathematicae non è più, come in Aristotele, strumento limitato e parziale di supporto alla conoscenza del mondo, né, come in Platone, struttura del mondo ideale, che si contrappone al regno dell’errore dei dati d’esperienza, ma diviene entità perfettamente sovrapponibile al mondo, e, in quanto tale, in grado di descrivere il reale nella sua effettiva verità. Nonostante questo, i residui di una logica aristotelica proiettano, in qualche modo, la propria ombra sull’elaborazione di una teoria meccanica che si fonda su questi presupposti. Galilei stesso incappa in un sorprendente errore di valutazione nell’analisi della resistenza di una barra. L’errore deriva da una concezione del mondo che eredita le logiche aristoteliche, collegate, per es., al concetto d’incompenetrabilità dei corpi.

Un parallelo diretto si ha nel campo della concezione strutturale delle cupole. Qui i ragionamenti sulle proprietà statiche di queste strutture, prima della modernità, individuavano, nella geometria emisferica, un’infinita successione di archi disposti in tutte le direzioni. Agli archi verticali, derivanti dal fatto di sezionare la struttura con piani passanti per il suo asse di simmetria, si contrappongono in questa immagine infiniti archi obliqui, e anche quei particolari archi che si ottengono sezionando la struttura orizzontalmente: archi che si trasformano in anelli e così facendo garantiscono l’equilibrio della cupola nelle fasi intermedie della sua realizzazione. Questa visione strutturale, concepita già chiaramente da parte di Alberti, esprime una primordiale lettura del comportamento spiccatamente iperstatico delle cupole e, in quanto tale, corrisponde a un’intuizione estremamente avanzata del loro funzionamento meccanico. Dice Alberti:

La volta sferica, una tra tutte, non richiede armatura: poiché essa non è fatta soltanto d’archi ma anche di anelli sovrapposti; e non è possibile immaginare fino a che punto gli uni e gli altri risultino reciprocamente collegati in innumerevoli intersezioni ed angoli uguali e diseguali, sicché in qualunque punto della volta si ponga una pietra, ci si accorgerà di aver posto con essa un concio appartenente ad innumerevoli archi ed anelli. […] E una volta che si siano costruiti gli anelli uno sull’altro, e allo stesso modo gli archi, anche facendo l’ipotesi che la costruzione voglia crollare, non si vede da che parte potrebbe cominciare (Di Pasquale 2002, p. 170).

Tuttavia, in queste analisi è del tutto assente qualunque esplicito riferimento al problema della resistenza del materiale alla compressione, o al ruolo della fessurazione per trazione, tipica del comportamento membranale, nel funzionamento di queste strutture. L’idea era dunque legata al fatto di ritenere che le parti della cupola non potessero crollare perché, toccandosi reciprocamente, avrebbero impedito gli spostamenti che sarebbero stati necessari al loro collasso. È come se, anche qui, le logiche derivanti dal concetto dell’incompenetrabilità dei solidi condizionassero le intuizioni statiche, riducendo il problema strutturale a un puro fatto di equilibrio dei corpi. Nel caso delle cupole che stiamo trattando, del resto, quest’approccio appare generalmente adeguato sul piano pratico, perché l’insegnamento di una secolare tradizione, in un legame con la conoscenza intuitiva simile a quello che si stabilisce tra l’ereditarietà e l’istinto, consentiva ai costruttori di definire sezioni resistenti sufficientemente spesse, tali da restare adeguatamente lontane da uno stato limite di rottura per compressione.

Le soluzioni di Filippo Brunelleschi

In un quadro dominato da fondamenti teorici del tutto primordiali, dunque, Brunelleschi deve mettere in atto una serie di espedienti costruttivi che tuttavia si basano su una profonda elaborazione concettuale e, come vedremo, sulla possibilità di dominare il processo costruttivo in termini di controlli.

Una volta resa manifesta la necessità di procedere alla costruzione senza uso di centine, egli tenta di ricostruire a Firenze le condizioni di stabilità, in fase costruttiva, che sono apparse un’evidenza ai suoi occhi nel caso del Pantheon.

In primo luogo, si tratta di ricreare le condizioni per il funzionamento di una cupola di rotazione, in una situazione in cui il preesistente tamburo ottagonale richiedeva invece la realizzazione di una cupola a padiglione. Brunelleschi disegna allora la cupola interna portante, di spessore tale da poter accogliere, al proprio interno, su ogni sezione orizzontale, un anello circolare. In questo modo ricostruisce virtualmente, all’interno della massa muraria, una cupola semisferica.

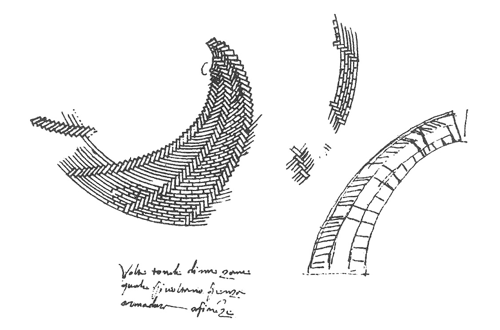
In secondo luogo, si tratta di far sì che quest’analogia risulti completa: ma per far questo è necessario evitare che la realizzazione della muratura per filari orizzontali comporti la formazione di spigoli lineari di raccordo in corrispondenza dei costoloni d’angolo. Questi spigoli avrebbero infatti rappresentato punti di discontinuità sul baricentro di ogni costolone. Sarebbe stato come realizzare una struttura a padiglione, a vele indipendenti, mentre una cupola sferica richiede continuità sull’intero anello orizzontale. Brunelleschi sceglie allora di murare la cupola, quando i filari abbiano raggiunto inclinazione significativa, per letti disposti su una superficie conica, con centro sull’asse di simmetria del sistema. Di qui la particolare forma a ‘corda molla’ assunta dai filari di mattoni tra le vele (fig. 2). In corrispondenza di ogni costolone di spigolo i letti di posa si trovano così su superfici ortogonali alla linea baricentrica del costolone stesso.

In terzo luogo, infine, si tratta di assicurare localmente la possibilità di murare la cupola nelle zone a forte inclinazione, senza il rischio che i mattoni, disposti sui letti di malta ancora freschi, scivolino verso il basso. Allora Brunelleschi, al livello del secondo camminamento interno, introduce un terzo espediente: la ‘spinapesce’ (fig. 3). Questa tessitura consente di connettere i mattoni dell’anello più avanzato a quelli dell’anello precedente, già realizzato, mentre il nuovo anello è ancora incompleto. L’interasse dei mattoni verticali, normalmente inferiore al metro, permette di limitare a un massimo di due o tre il numero di mattoni da posizionare tra elementi verticali adiacenti della spinapesce. Inoltre, la disposizione dei mattoni verticali secondo configurazioni concentriche riproduce, sul segmento della vela tra due costoloni, una suddivisione a conci del tipo delle strutture a piattabanda di tradizione romana, conferendo stabilità al corpo della vela.

L’importanza decisiva che questi dispositivi di natura costruttiva assumono per la cupola di S. Maria del Fiore determina una vera e propria rivoluzione nel modo di concepire il cantiere dell’opera rispetto alla tradizione. Infatti, la natura stessa di tali espedienti, il livello di precisione che la loro realizzazione richiede e il loro carattere di elemento essenziale, rispetto alla stessa conservazione in condizioni integre dell’organismo in costruzione, rendono fondamentale il ruolo dei processi di misurazione e controllo durante l’intera durata dei lavori.

Il risultato di questa formidabile serie d’innovazioni può essere apprezzato pienamente solo analizzando la cupola nei termini di una teoria contemporanea. Il funzionamento membranale delle cupole semisferiche prevede infatti che, durante l’applicazione del carico, tensioni di trazione circonferenziali abbiano luogo in corrispondenza degli anelli presso l’imposta. Quando queste tensioni superano la resistenza a trazione del materiale, si creano delle fessure che tendono a dividere la cupola in spicchi. Durante questi eventi fessurativi, che hanno luogo normalmente nel corso di molti anni, l’originario comportamento membranale della struttura viene perso. Ogni spicchio si comporta come la porzione di un arco verticale, in una configurazione che vede tutti questi archi connessi tra loro sulla calotta non fessurata presso la sommità della cupola. Nel caso di una cupola a padiglione vi è, nell’ambito del primo funzionamento membranale, una particolare tendenza alla concentrazione degli sforzi lungo gli spigoli. Qui infatti si compongono le sollecitazioni che derivano dalle vele in cui la volta è suddivisa. La forza lungo ogni diagonale, che cresce progressivamente verso le imposte, si fa carico di assorbire una parte via via maggiore dei carichi applicati alle vele adiacenti.

Contemporaneamente, i paralleli della cupola presso le imposte sono soggetti a trazioni orizzontali che equilibrano le compressioni delle diagonali. Rispetto a queste trazioni, i punti più deboli sono proprio gli spigoli, nei quali la presenza di forti compressioni indebolisce la muratura rispetto a una trazione orizzontale (come noto, la compressione è direttamente associata a una trazione su giacitura ortogonale). Quindi, la fessurazione si verifica inizialmente proprio sugli spigoli della cupola e porta, ancora una volta, alla perdita del suo comportamento membranale.

Nel caso della cupola di S. Maria del Fiore, gli espedienti di Brunelleschi hanno consentito di evitare questo comportamento. Le fessure principali procedono qui su linee meridiane presso la mezzeria delle vele soprastanti i pilastroni. Rappresenta un vantaggio, in questo senso, il fatto che le vele abbiano, in mezzeria, una sezione indebolita, corrispondente alla minima dimensione, in chiave, degli archi disposti sui paralleli.

A conferma dell’interpretazione di Salvatore Di Pasquale (2002) e di Rowland J. Mainstone (1980), il comportamento della cupola è quindi quello di una cupola di rotazione. È come se si fosse realizzata una struttura che originariamente, e in regime membranale, si comporta come il guscio di un uovo, mentre quando la cupola si fessura, secondo piani meridiani, presso il centro delle vele, si suddivide in spicchi. Ma questi spicchi, che presentano una piegatura caratteristica, nel punto in cui le due semivele si congiungono sul costolone, assumono una particolare resistenza, una rigidezza simile a quella che caratterizza una foglia, sulla piega del lembo, una proprietà che oggi definiremmo resistenza per forma.

Teorie strutturali e scientia geometriae: Leonardo da Vinci

Abbiamo già mostrato che nella costruzione delle cupole italiane, a partire dal Rinascimento, si assiste a una conferma di come i processi di definizione delle teorie strutturali vengano anticipati nella forma dell’intuizione statica.

L’idea che fosse possibile condurre un dimensionamento delle strutture secondo un approccio puramente geometrico persiste per molti secoli dopo il Medioevo. Questa concezione, che vede il prevalere della scientia geometriae nella definizione delle questioni costruttive, può essere interpretata come un’eredità della meccanica aristotelica, che concepisce le condizioni di equilibrio prevalentemente come configurazioni stabili per geometria. In una visione della fisica che ancora non incorpora il principio di azione e reazione, la stabilità viene interpretata come il raggiungimento di una simmetria, di un equilibrio geometrico, che consente di annullare la capacità delle forze di generare moto.

In questo senso, il contributo di Leonardo da Vinci (1452-1519) si presenta, nelle parole di Edoardo Benvenuto (1981, p. 324), come l’emergere, a livello intuitivo, dei «primi germi di idee che solo tre secoli dopo troveranno uno sviluppo» (il f. 82v del Codice Foster II di Leonardo studia la spinta orizzontale alle imposte degli archi).

Nell’ideazione di proposte strutturali per la ricostruzione del tiburio del duomo di Milano (tra il 1487 e il 1490), Leonardo appare cosciente del vantaggio offerto dalle soluzioni costruttive ad arco a sesto acuto in termini di efficienza nella trasmissione dei carichi verticali e di riduzione delle spinte orizzontali. Egli presenta se stesso alla fabbrica del duomo come un «medico architetto [che] ntenda bene che cosa è edifizio, e da che regole il retto edificare deriva» (lettera di Leonardo ai fabriceri del duomo di Milano, in Pedretti 1978, 1989, p. 35).

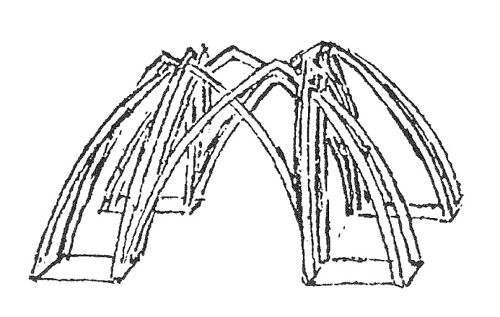
Leonardo si trova di fronte al problema di dare appoggio a un tiburio ottagonale su uno spazio libero a base quadrata, caratterizzato da quattro pilastri di spigolo, aventi anch’essi la sezione di un quadrato. Concepisce allora un sistema di sostegno costituito da quattro coppie di archi intrecciati (fig. 4), a sesto acuto (Codice Trivulziano, f. 27v, e figura assonometrica nel disegno del Manoscritto B, f. 27r, riguardante S. Lorenzo, quasi certamente relativa al duomo di Milano; si vedano anche gli studi di chiesa a pianta centrale nel Codice Windsor, f. 1913v). Si tratta di una soluzione ideale, troppo vincolante sul piano geometrico per poter essere adattata all’effettiva configurazione del duomo. Essa sembra però costituire la base concettuale per proposte maggiormente realistiche: l’arco a sesto acuto, che si forma sotto l’intersezione dei due archi complanari, viene riproposto nei più accurati disegni del Codice Atlantico (ff. 310r-b, 310v-b), che sezionano verticalmente la struttura.

Il 27 giugno 1490 l’incarico di riedificare il tiburio viene affidato a Francesco di Giorgio, Giovanni Antonio Amadeo e Gian Giacomo Dolcebuono: la proposta definitiva è quella di sovrapporre all’arco acuto un arco a tutto sesto, secondo un impianto strutturale più simile a quello originariamente previsto da Marco Solari. Ciò nonostante, è probabile che, come vedremo, la soluzione ad archi ‘intrecciati’ proposta da Leonardo abbia rappresentato nel Seicento un’importante fonte d’ispirazione per le successive innovazioni strutturali di una figura fondamentale nel progetto delle cupole in Italia, Guarino Guarini.

Secondo un approccio che segna il parallelo con la spiegazione, da parte di Alberti, del funzionamento statico delle cupole, Leonardo descrive l’arco come «una fortezza causata da due debolezze» (cit. in Benvenuto 1981, p. 324). Ma aggiunge che la struttura di un arco è formata da due quarti di cerchio, e mostra che ciascuno di essi, «debolissimo per sé desidera cadere e opponendosi alla ruina l’uno dell’altro le due debolezze si convertono in un’unica fortezza» (p. 324). Anche qui si anticipa, in qualche modo, quell’approccio cinematico che, come vedremo, segnerà il primo ingresso della scienza delle costruzioni nel mondo dell’architettura, nella settecentesca e avvincente vicenda che riguarda il consolidamento della cupola della basilica di S. Pietro a Roma.

Le opere di Brunelleschi posteriori alla costruzione della cupola di S. Maria del Fiore, le architetture di Alberti, sommamente autoriali, e il rilievo che assumono le opere di pittura di Leonardo rispetto alla sua debordante attività d’inventore e di analista, segnano il passaggio dal ‘facitore’ all’‘autore’, dall’artigiano all’artista, dal capomastro all’architetto. S’impone così l’attenzione alla questione della forma come valore a sé stante in quanto svincolata dalle modalità della sua realizzazione, autonoma nella sua stessa dimensione concettuale e valoriale, a partire dalle logiche stesse della sua ricezione. In altri termini, iniziano a emergere quelle caratteristiche che porteranno, nella seconda metà del Settecento, alla nascita dell’estetica e contemporaneamente della storia dell’arte.

La cupola di S. Pietro: progetti e costruzione

L’opera rinascimentale sulla quale si avrà il maggior investimento d’intelligenza artistica e tecnica, d’impegno economico e sociale e di valorizzazione simbolica e politica, sarà la basilica di S. Pietro a Roma. La cupola di questa chiesa fu progettata e realizzata in un periodo temporale che coinvolge quasi l’intero corso del 16° secolo. Attraverso la successione di alcuni papi, numerosi architetti furono coinvolti nell’impresa, che culminò nel 1588 con l’erezione della cupola vera e propria.

A oltre 150 anni dal completamento della cupola di S. Maria del Fiore, questa, di luce lievemente superiore a quella che si sarebbe dovuto costruire a Roma, imponeva la propria ingombrante presenza come prova diretta della realizzabilità dell’impresa. Nonostante ciò, nella cupola di S. Pietro i risultati costruttivi di Brunelleschi vennero in parte disattesi. L’evoluzione del progetto mostra infatti una sorprendente serie di incertezze in merito alle scelte strutturali.

La prima proposta per la cupola fu quella di Donato Bramante (elaborata tra il 1505 e il 1514), come rappresentata da Sebastiano Serlio in Il terzo libro dell’architettura (1540), che evidenzia il prevalere di un riferimento costruttivo allo schema del Pantheon, con la sola aggiunta della lanterna sopra l’oculus. La scelta strutturale appare però molto debole nel sottovalutare l’importanza che ha, per il Pantheon, la massiccia muratura perimetrale, direttamente gravante sulle fondazioni, che nel caso di S. Pietro viene sostituita da tre ordini di esili colonne da realizzare sopra le arcate della basilica.

Con il contributo di Antonio da Sangallo il Giovane (tra il 1521 e il 1546) si prende coscienza della necessità di rinforzare le sottostrutture, e in particolare gli archi di supporto, e dell’opportunità di adottare, per la cupola, un profilo maggiormente acuto, più simile a quello di S. Maria del Fiore. Permane tuttavia un’evidente debolezza nella scelta di alleggerire, ancora una volta, il tamburo con un colonnato perimetrale. Appare sovradimensionato lo spessore (e conseguentemente il peso) della cupola, che presenta inoltre un indebolimento alla base, ove s’introduce un ulteriore tamburo, costituito da un secondo ordine di colonne.

Dopo Bramante, è Michelangelo Buonarroti, tra il 1546 e il 1564, a dare il maggior contributo al progetto complessivo della basilica e alla concezione della cupola, in particolare sul piano dell’espressione plastica. Egli introduce lo schema fiorentino della struttura a doppia cupola, senza però che vi sia evidenza, nella sua proposta, della presenza di costoloni. Appare debole, dal punto di vista strutturale, l’adozione di un profilo a tutto sesto, che avrebbe comportato un allontanamento della curva delle pressioni dal profilo medio della cupola, con gravi conseguenze in termini di funzionamento statico. Questo schema avrebbe certamente generato importanti spinte, verso l’esterno, alla base della cupola, sulla sommità dell’attico.

L’effettiva costruzione della struttura inizia tuttavia nel 1588, su un progetto di variante elaborato da Giacomo Della Porta tra il 1588 e il 1591, a partire dal tamburo di Michelangelo. Con Della Porta s’introducono, sulla base del modello fiorentino a doppia cupola, 16 costoloni meridiani di collegamento delle due strutture, di larghezza decrescente dalla base al tamburo. Si migliora inoltre la stabilità della cupola, adottando un profilo intermedio tra quello proposto da Michelangelo e quello a sesto acuto della cupola fiorentina. Il raggio della superficie media, sezionata su un meridiano, corrisponde a circa 30,5 m, con un diametro interno del tamburo di 42,7 m.

Nel corso di questa lunga evoluzione progettuale, lo schema strutturale della cupola di S. Pietro si avvicina dunque parzialmente a quello di S. Maria del Fiore, rispetto al quale, tuttavia, permane una differenza cruciale proprio nel sistema costruttivo: l’esperienza romana abbandona definitivamente la soluzione realizzativa senza uso di centine.

È importante, a questo punto, ricordare come l’esecuzione di una cupola senza uso di centine richieda, in ogni fase del processo costruttivo, la disponibilità di un anello rigido sulla sommità dell’opera. Tuttavia, questa modalità costruttiva non è priva di conseguenze sulle dinamiche del cantiere: essa richiede al contrario un rilevante allungamento dei tempi di esecuzione. La cupola di Firenze ebbe infatti una durata di costruzione effettiva di sedici anni, e quella di S. Pietro solo di tre.

La costruzione della cupola di S. Pietro potrebbe essere avvenuta in questo modo: iniziale montaggio della centinatura; successiva realizzazione dei costoloni con la previsione di riseghe e selle di attesa, e forse di alcuni mattoni emergenti (per es., lateralmente); possibile avanzamento dei costoloni per spessori parziali, al fine di ridurre il carico gravante sulle centine, da completare, in seguito, parallelamente all’esecuzione delle vele; successiva realizzazione delle vele, in appoggio sulle selle e riseghe, predisposte sui costoloni già realizzati, sul sostegno di una centinatura leggera (o in assenza di essa).

Questa particolare ipotesi costruttiva sembra compatibile con le rappresentazioni di Domenico Fontana, che mostrano la presenza di riseghe laterali a una doppia quota, nell’elevazione di ogni costolone (fig. 5). Indipendentemente dal livello di conoscenza e intuizione di queste problematiche da parte degli esecutori coinvolti, va rilevato che nel caso di S. Maria del Fiore una modalità costruttiva come questa non sarebbe stata percorribile, perché avrebbe comportato, con ogni probabilità: a) la discontinuità strutturale tra costoloni e vele, sulle linee di collegamento tra questi elementi; b) la conseguente perdita dello schema statico a cupola di rotazione; c) il riconfigurarsi di un modello di funzionamento a padiglione, a ‘vele separate’, con fessurazione presso gli spigoli, e con le particolari criticità, sul piano strutturale, che tale modello comporta.

Le altre cupole italiane, dal Rinascimento al Barocco

Se la cupola di S. Maria del Fiore nasce da un impianto a croce latina in cui la struttura si posiziona nell’incrocio tra la navata principale e il transetto evocando centralità cosmogonica e razionalità, Leonardo cerca nei suoi disegni di architettura un’alternativa allo schema a croce latina: egli è alla ricerca di una continuità tra cielo e terra, tra ciò che viene sospeso e ciò che ‘porta’, tra logica geometrica e costruttiva. Vuole quindi che la cupola stessa sia l’elemento generatore dell’organismo architettonico. Disegna così una chiesa a pianta centrale, che verrà indubbiamente vista da Bramante, il quale proverà a utilizzarne la logica nel suo progetto per S. Pietro.

Questo schema sarà anche alla base del progetto della chiesa di S. Maria della Consolazione a Todi, costruita con il contributo prima di Cola da Caprarola, poi di Baldassarre Peruzzi e di Antonio da Sangallo il Giovane. Anche lo zio di quest’ultimo, Antonio da Sangallo il Vecchio, utilizzerà la pianta centrale per uno dei capolavori del Rinascimento, la chiesa di S. Biagio a Montepulciano.

Questo tema si radicalizzerà in una singolare architettura come il tempio di S. Stefano della Vittoria a Pozzo della Chiana presso Arezzo (1569), di Bartolomeo Ammannati (con un probabile contributo di Giorgio Vasari), nella chiesa votiva di S. Sebastiano a Milano (1578-86), di Pellegrino Tibaldi, e nella chiesa di Madonna di Campagna a Verona (1559-61), di Michele Sanmicheli.

Sarà inoltre utilizzato con grande capacità ‘retorica’ da Baldassarre Longhena nella basilica di S. Maria della Salute a Venezia (1631-87). Qui la chiesa è la cupola stessa; questa è costruita da una doppia calotta, quella in intradosso in mattoni e quella in estradosso in metallo, sopportata da una struttura lignea, secondo la tradizione costruttiva presente a Venezia sin dalla costruzione delle cupole di S. Marco. È l’unica architettura veneziana che utilizzi come fondazione una vera e propria platea, composta da ben 1.156.650 pali, i quali assorbono in modo uniforme i carichi che l’intero organismo architettonico scarica nel terreno. La chiesa, avendo una sorta di stilobate rappresentato dalla piattaforma, cresce dalla pavimentazione e sale verso la cupola.

Vi è un’ulteriore tipologia nell’ambito della progettazione delle cupole, soprattutto nel Manierismo e nel Barocco: la cupola ellittica o ovale. I modelli vengono dall’antica Roma e sono riproposti in alcuni disegni riportati da Serlio nei suoi Sette libri dell’architettura (1537-1575), in particolare con la pianta e la sezione longitudinale del ‘tempio ovale’ nel quinto libro (1547). Il tema troverà dapprima una soluzione architettonica nel tempietto di S. Andrea a Roma (1553 ca.), di Iacopo Barozzi, detto il Vignola. L’organismo architettonico cerca una propria unitarietà e un rigore formale; la cupola non viene caricata di significati, se non nel cambiamento tra le murature ortogonali del parallelepipedo che forma il blocco edile e che sostiene la piccola cupola, e le murature curve che circondano e sostengono l’andamento stesso della cupola. I materiali sono volutamente gli stessi. A dettare il codice linguistico e il riferimento all’antico è una facciata che viene concepita come pelle, mera scrittura, elemento grafico con nessuna ragione costruttiva.

Il ‘poliverso’ barocco che vuole perdersi nelle logiche ellittiche si affiderà spesso all’idea e al progetto della cupola ovale. Così, a Roma, Gian Lorenzo Bernini con la chiesa di S. Andrea al Quirinale (1658-78) e soprattutto Francesco Borromini con quelle di S. Carlo alle Quattro fontane (1634-44) e di S. Ivo alla Sapienza (1643-64).

Ma su Borromini, fondamentale per interpretare il Barocco, è doverosa una considerazione, che riprendiamo da un importante testo di Federico Bellini, Le cupole di Borromini: la ‘scientia’ costruttiva in età barocca (2004). Se è vero che il Barocco è l’età del grande sviluppo dell’algebra e del calcolo infinitesimale, e se «le curve dei grandi matematici del Seicento sono quasi sempre coniche: ellissi, parabole, iperboli; oppure curve più complesse: catenarie, cicloidi, spirali logaritmiche, conoidi; più raramente e più tardi funzioni trigonometriche», ebbene, queste sono «tutte curve che Borromini […] non usa mai: neppure una volta. Borromini usa un solo tipo di curva: la circonferenza» (p. 22). Egli disegna semplicemente delle curve policentriche:

Borromini è uno degli ultimi interpreti […] di una tradizione ben nota alla storia della geometria, che affonda le proprie origini in età romana, sopravvivendo per secoli all’intero medioevo e all’età rinascimentale: la cosiddetta ‘geometria operativa’ usata da agrimensori, navigatori, artisti e costruttori, fatta di metodi senza alcuna dimostrazione, talora di semplici ricette visive che fanno a meno del calcolo, e che quando ammettono il calcolo indulgono volentieri ad approssimazioni anche grossolane, indispensabili a fini pratici (p. 24).

Il risultato architettonico-artistico, comunque, pur essendo ancorato nei procedimenti a una tradizione millenaria, scardina non tanto l’assetto tecnico o tecnologico (costruttivo) quanto quello logico-formale:

Borromini si rivolge alla geometria con uno sguardo quasi infantile, ravvivato da un incontrollabile entusiasmo per le simmetrie che legano le maggiori figure del sistema euclideo, che lui intende quasi miracolisticamente, come una conferma della simmetria divina che dominerebbe la natura: più un candor pueri, dunque, che un furor matematicus. La sua attitudine a «cavar una cosa dentro l’altra» viene alimentato dal carattere logico-formale della geometria euclidea, che è un sistema chiuso e tautologico: iterando costruzioni regolari si ottengono composizioni geometriche sempre più complesse, ma del pari regolari: virtualmente all’infinito (p. 28).

Bellini segnala che, se Galilei afferma ne Il saggiatore (1623) che il libro della natura «è scritto in lingua matematica, e i caratteri son triangoli, cerchi e altre figure geometriche, senza i quali mezzi è impossibile intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro laberinto» (cit. in Bellini 2004, p. 28), Borromini costruisce per sé un labirinto geometrico. Come Galilei, anch’egli usa strumenti razionali, giacché nulla è più razionale di un labirinto. Ma se per Galilei la geometria serve a semplificare e chiarire, per Borromini, afferma Bellini, serve a «complicare e nascondere» (p. 28). Tuttavia, l’attività di chiarire e quella di complicare portano ambedue all’incontro con l’infinito, al paradosso della modernità, che riesce a rendere calcolabile ciò che per principio è incalcolabile, appunto l’infinito. Percorsi diversi, ma in un unico ‘sfondo’.

Tra le cupole ovali o ellittiche vanno ricordate le molte costruite a Roma nella seconda metà del Seicento da Carlo Rainaldi e, soprattutto, l’immensa cupola della chiesa del Pellegrinaggio di Vicoforte presso Mondovì, progettata nel 1596 da Ascanio Vittozzi.

Va ricordato anche il valore che la cupola assume nel magistero palladiano. Andrea Palladio aveva disegnato, nell’ultimo dei suoi Quattro libri dell’architettura (1570), la sezione del Pantheon e quella del tempio di Vesta a Tivoli (fine 2° sec.). Ridisegna anche il bramantesco tempietto di S. Pietro in Montorio a Roma (1481-1500), l’unica architettura del suo tempo che prende in considerazione. Quando progetta, negli anni Cinquanta e Sessanta del Cinquecento, la villa Trissino (a Meledo di Sarego, Vicenza) e la cosiddetta Rotonda (villa Almerico Capra a Riviera Berica, Vicenza), egli sa bene che, dotandole di una cupola, sta forzando una tradizione millenaria, la quale associava all’uso della cupola delle valenze simboliche di tipo religioso. Palladio sembra così attribuire all’abitazione nobiliare un valore espressivo, grazie proprio all’utilizzo della cupola, che trascende la dimensione religiosa dando nel contempo a quella laica una forza del tutto nuova. Egli libera la cupola dai vincoli di una simbolica teologico-cosmogonica senza che venga persa l’allusione alla centralità del potere, e segna così un momento significativo di quel processo di secolarizzazione che per molti caratterizza il passaggio dal mondo antico a quello moderno e a quello contemporaneo.

Non è un caso che ad accogliere e a promuovere questa ‘grammatica’ sarà, nel Settecento, la cultura architettonica anglosassone. Si vedano, per es., sia gli interventi di Colen Campbell sulla Burlington House a Londra dopo il 1717, cioè nel periodo in cui l’Inghilterra inizia a mettere in atto una strategia economico-politica di tipo imperiale, sia l’uso che Thomas Jefferson (futuro terzo presidente degli Stati Uniti) farà della cupola quando progetterà, nel 1768, la sua casa di Monticello (presso Charlottesville, in Virginia) come metafora di una nuova forma di universalità.

Ciò non significa affatto che la religione deve trovare altri linguaggi per esprimersi nell’architettura, ma che deve anch’essa sapersi misurare con una ‘ragione’ rappresentata dalla potenza del passato, e che tale potenza non è in sé solo religiosa. Questa sintesi avviene in due basiliche veneziane progettate da Palladio, S. Giorgio Maggiore (1565) e il Santissimo Redentore (1577). In particolare, in quest’ultima chiesa accade che la cupola con la sua imponenza ottenga sul piano della percezione ottica, anche per il fatto di dover essere osservata dalle Zattere (ovvero dal lato opposto del grande canale della Giudecca), la sintesi tra tipologia a croce latina e a croce greca, tra il linguaggio dell’antichità e quello della modernità.

Guarino Guarini

Guarino Guarini (1624-1683) inaugura una nuova stagione nell’arte di edificare cupole: le innovazioni che egli introduce non coinvolgono la sola sfera architettonica, ma anche aspetti di natura strutturale e costruttiva. L’idea nuova è quella di isolare, nella volta di rotazione, alcune componenti strutturali, aprendo il resto della superficie, in modo da farvi penetrare la luce del Sole. Come abbiamo visto, già Alberti aveva definito il concetto strutturale di cupola come insieme di molteplici archi, disposti in tutte le direzioni: egli aveva marcato le caratteristiche di un assetto che oggi definiremo iperstatico. A partire da questo assetto, l’apertura del sistema può allora avvenire individuando un particolare insieme di archi, tra gli infiniti possibili, a condizione di selezionare una configurazione stabile, e ricavando le aperture nell’ambito della geometria a essi complementare.

Un primo passo di questo processo, Guarini sembra realizzarlo nel progetto (1670) per la cupola della chiesa di S. Lorenzo a Torino, che corrisponde, sul piano costruttivo, a una volta nervata. Si tratta di una tipologia strutturale che ha importanti precedenti nella storia dell’architettura. Il miḥrāb (la nicchia da preghiera) della cosiddetta Grande moschea di Cordova in Spagna (8°-9° sec.) ha una geometria del tutto simile a quella della cupola torinese. Riferimenti ancora più diretti, rispetto alla vicenda biografica di Guarini, possono essere rintracciati nei disegni di Leonardo: molto evocativo è il foglio 24r del Manoscritto B, che traccia la planimetria di una chiesa a pianta centrale, ove l’orditura delle nervature riproduce fedelmente lo schema di S. Lorenzo. Più diffusi riferimenti al tema strutturale della volta nervata sono reperibili nell’ambito dell’architettura gotica, e potrebbero essere giunti a conoscenza di Guarini proprio per l’intermediazione di Leonardo: la volta della torre sud del duomo di S. Stefano (Stephansdom) a Vienna ripropone la geometria degli altri esempi citati. Rispetto a queste molteplici fonti, è tuttavia evidente la profonda innovazione introdotta nella cupola torinese, ove si assiste allo svuotamento delle porzioni della volta comprese tra gli archi strutturali, lasciando la luce penetrare all’interno dell’edificio.

Questo aspetto appare ancora più marcato nel progetto (1668) per la cappella della Sacra Sindone all’interno del duomo di Torino, in cui Guarini riprende il tema dell’arco, proponendone un nuovo ruolo strutturale e una nuova modalità di utilizzo nell’ambito della costruzione di una cupola. La struttura si costituisce qui come sovrapposizione di gruppi di sei archi, disposti in verticale, sui lati di un esagono regolare. La distanza tra due lati contrapposti dell’esagono interno è di poco inferiore a 14 m, mentre l’altezza interna della cupola corrisponde a circa 9,5 m. Ogni livello è ottenuto da quello inferiore, con una rotazione di 30°, in pianta, che porta la sezione d’imposta di ciascun arco a trovare appoggio sulla sezione in chiave dell’arco sottostante. A ogni livello le spinte alla base degli archi si equilibrano a vicenda, lasciando libera unicamente una componente radiale, che viene assorbita per mezzo delle catene orizzontali, presso la base di ogni arco. La struttura della cupola è completata da 12 costoloni meridiani, che intersecano gli archi ai vari livelli, presso l’imposta e sulla sezione in chiave, sotto la quale si inseriscono con un modiglione.

Lo schema strutturale qui descritto lascerebbe supporre che i rigidi costoloni verticali siano gli elementi destinati ad assorbire la gran parte dei carichi verticali agenti sulla cupola. In realtà, la muratura di questi elementi è disposta su letti orizzontali, anziché su superfici inclinate: il che porta a escludere che nel progetto originario questi elementi fossero concepiti come strutture portanti. Nei disegni originali di Guarini, del resto, si nota la presenza dei modiglioni, ma sono assenti costoloni meridiani: è come se l’architetto avesse all’inizio concepito la cupola priva di questi elementi, introducendoli solo in una fase successiva.

È possibile provare un’interpretazione di questo comportamento statico, nel quale le sollecitazioni sono portate non solo dai costoloni, ma anche, in modo significativo, dagli archi, a partire da un’ipotesi sul sistema costruttivo adottato nella costruzione della cupola. Il processo inizia con la realizzazione degli archi sul primo livello esagonale. In questa fase ogni arco presenta una centina in legno, sotto la quale è adagiata la catena metallica. La centina non lascia lo spazio per il modiglione, che dovrà quindi essere collocato in una fase successiva: questo spiega la dimensione dei modiglioni, più piccoli dello spazio disponibile per poter essere inseriti ad arco realizzato. La costruzione degli archi procede sui vari livelli sovrapposti. Una volta eliminate le centine di un livello, gli archi si caricano, assorbendo i pesi strutturali. Contemporaneamente le catene assorbono, in trazione, le spinte radiali non equilibrate dagli archi.

A questo punto entra però in gioco un’importante questione strutturale. Se si idealizzano come cerniere i punti di appoggio degli archi di un esagono su quelli dell’esagono sottostante, la cupola mostra in pianta una geometria poligonale (non triangolare): si tratta di un assetto strutturale caratterizzato da una intrinseca labilità. Questa labilità viene attivata in particolare per effetto di azioni radiali, di intensità non uniforme sui vertici del poligono. Ma azioni di questo tipo sono certamente connesse al processo costruttivo appena descritto, come effetto dell’ovvia impossibilità di disarmare gli archi tutti nello stesso istante. È possibile ipotizzare, dunque, che già in fase costruttiva, se non in un periodo immediatamente successivo, la labilità dello schema strutturale adottato si sia manifestata e abbia richiesto di adottare massicci costoloni meridiani, come elemento d’irrigidimento del sistema, originariamente non previsto.

Per garantire la stabilità, del resto, sarebbe stato sufficiente, in fase costruttiva, innalzare i costoloni sino al livello sottostante, rispetto all’ultimo raggiunto dagli archi, durante il processo di erezione della cupola. A supporto di questa interpretazione vi è la presenza di un tamponamento di chiusura, che riduce esternamente i vuoti della volta a fori di geometria rettangolare e dimensione ridotta: si tratta di un apparato murario che mostra, con evidenza, i tratti di un’aggiunta posteriore. Tutto ciò appare poi congruente con i livelli di compressione registrati sugli archi, come conseguenza del fatto che, una volta disarmato, ogni arco assorbe il proprio peso strutturale e lo trasmette agli archi del livello inferiore, a partire dal quale i costoloni iniziano a partecipare al naturale trasferimento delle forze verso la base della struttura.

Le fessure nella cupola di S. Pietro

Nella cupola di S. Pietro, dopo circa un secolo dalla costruzione comparvero fessurazioni sempre più preoccupanti. La sequenza costruttiva che abbiamo ipotizzato (con la realizzazione dei costoloni, su centine, in una prima fase e delle vele in una fase successiva) appare perfettamente in linea con il particolare quadro che, nel corso dei secoli, venne a determinarsi nella cupola, con la progressiva comparsa di fessure meridiane diffuse sulla superficie delle vele e con l’insorgenza di lesioni solo superficiali in corrispondenza dei costoloni.

La cupola romana si mostra del resto meno efficiente, dal punto di vista del comportamento statico, rispetto a quella di Brunelleschi. Questo appare evidente confrontando i valori probabili delle azioni strutturali sulla sommità del tamburo nei due casi. La cupola di S. Maria del Fiore, dal peso complessivo di 290 MN (meganewton), esercita alla base una spinta radiale di circa 210 kN/m, mentre quella di S. Pietro, pur gravando con un carico di 190 MN, determina una spinta di ben 290 kN/m. Questa differenza prestazionale spiega il progressivo aggravarsi delle lesioni sulla cupola romana: lesioni che, a partire dagli ultimi decenni del 17° sec., suscitarono una crescente preoccupazione e un intenso dibattito in merito alla ricerca dei possibili rimedi.

Tra il 1742 e il 1743, in seguito a una lunga attività di monitoraggio, Luigi Vanvitelli presentò un primo rapporto sullo stato della cupola e un rilievo dettagliato del suo quadro fessurativo. La sua analisi evidenziò numerose lesioni meridiane, che s’innalzavano dal tamburo sin quasi alla lanterna, sulla sommità della cupola. Nel mezzo secolo che precedette questi avvenimenti, si era registrato l’apparire dei primi studi scientifici sul comportamento strutturale degli archi e delle cupole, e sul comportamento a trazione delle barre metalliche.

Cosciente di questo clima culturale, nel 1742 papa Benedetto XIV chiese l’intervento di tre dei più importanti matematici dell’epoca, Thomas Le Seur, François Jacquier e Ruggero Giuseppe Boscovich, il cui Parere venne presentato l’8 gennaio 1743.

Si tratta di un documento di grande interesse scientifico, perché introduce, nell’ambito di un problema di sicurezza strutturale, procedimenti di calcolo fondati su un approccio di tipo matematico: il teorema dei lavori virtuali viene impiegato determinando una prima stima delle spinte radiali alla base della cupola, e si esegue un calcolo della forza agente su eventuali anelli cerchianti, da introdurre allo scopo di contenere questa stessa spinta. Nell’applicazione del teorema vengono descritti due cinematismi limite, che considerano la presenza di ‘cerniere’ alla base del tamburo, sulla sommità dell’attico e in corrispondenza della lanterna. Il primo cinematismo considera rigido il collegamento tra contrafforti e doppie colonne sul tamburo, assumendo che queste due componenti possano ruotare come un unico concio, mentre nel secondo, meno conservativo e più realistico del primo, si considera l’elevato livello di fessurazione presente in questa regione della cupola, assumendo che i due elementi debbano ruotare come conci separati. In seguito, anche Giovanni Poleni mostrerà il convincimento che la cupola, a partire dall’attico e dal tamburo, per effetto della fessurazione, fosse stata ripartita in spicchi, e che tali spicchi avessero subito un cinematismo, con attico e tamburo che ruotano verso l’esterno e cupola che ruota verso l’interno.

Il Parere non riporta nel dettaglio i calcoli svolti, né offre una descrizione esaustiva delle ipotesi formulate. È possibile però, alla luce della moderna teoria strutturale, cercare un’interpretazione dei risultati ottenuti. Questo tipo di valutazione può in qualche modo spiegare il forte allarme che traspare nel Parere: i suoi tre autori propongono di rinforzare la cupola con ulteriori cerchiature, ma anche con l’irrigidimento dei contrafforti e con incrementi di peso sul tamburo per contrastare le sollecitazioni. È la prima volta che la necessità di un rinforzo viene determinata con procedimenti scientifico-matematici.

Nonostante questo, le valutazioni espresse nel Parere vennero considerate eccessivamente prudenti, e furono generalmente ignorate da parte di coloro che, nelle settimane successive, lo analizzarono. Il papa reagì invece in modo tempestivo, e già il 12 gennaio coinvolse nell’analisi della cupola un altro eminente scienziato, il citato Poleni.

Questi affrontò la questione con un approccio di tipo spiccatamente scientifico-sperimentale. Infatti: a) esaminò l’applicazione del teorema dei lavori virtuali condotta dai tre matematici; b) ripercorse il problema del calcolo delle forze agenti sugli anelli cerchianti e ne fornì un’analisi di tipo sperimentale; c) applicò le emergenti teorie sulla meccanica degli archi (elaborate da Robert Hooke, Philippe de La Hire e James Stirling) e determinò, con una procedura sperimentale che superò le incertezze derivanti dall’applicazione di un calcolo esatto al caso concreto della cupola, la funicolare dei carichi sulla grande struttura, escludendone il tamburo; d) infine, eseguì dei veri e propri test di resistenza sul metallo da utilizzare per gli anelli cerchianti.

Come Le Seur, Jacquier e Boscovich, anche Poleni non rese esplicite, nei suoi scritti, alcune determinazioni di grande importanza, come la spina radiale alla base della cupola. È però interessante osservare come questo dato sia immediatamente disponibile nei risultati che descrive. La spinta è infatti semplicemente la componente orizzontale del vettore della forza, relativo alla funicolare dei carichi, presso la sezione d’imposta della cupola. Il valore che emerge da questa valutazione diretta, non esplicitata da Poleni, corrisponde a circa 300 kN/m. In realtà, nei termini di una teoria moderna si deve riconoscere come la spinta corretta corrisponda al valore minimo tra quelli associati a tutte le possibili configurazioni staticamente ammissibili. Poleni, invece, analizza un’unica funicolare, ma l’errore che commette è relativamente piccolo, oltre che a favore della sicurezza, perché deriva unicamente dall’arbitrarietà con cui egli ha fissato il passaggio della funicolare sul baricentro della cupola, all’imposta e in corrispondenza della lanterna. È possibile che la differenza tra questa determinazione e quella che deriverebbe dal portare sino in fondo il modello di calcolo dei tre matematici, di tipo cinematico, abbia sorpreso Poleni.

In ogni caso, anche se nei suoi scritti non compare esplicitamente un calcolo degli anelli di rinforzo, egli: a) scelse, con Vanvitelli, di adottare cerchiature per assorbire la spinta non equilibrata, argomentando correttamente che la cerchiatura può conferire resistenza aggiuntiva come la catena in un arco; b) portò così sul tamburo un carico prevalentemente verticale; c) eliminò di fatto la partecipazione del tamburo, difficile da analizzare per la sua articolata geometria, al problema della sicurezza strutturale, giustificando così la scelta di limitare lo studio della funicolare alla sola cupola.

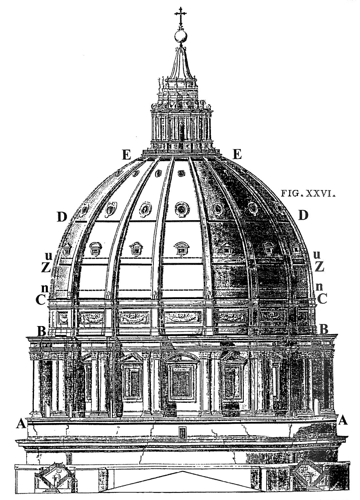
Una conferma dell’efficacia delle scelte strutturali adottate e della possibilità che il significato di queste scelte, nei termini di una determinazione scientifico-matematica, facesse già parte dei risultati che Poleni aveva raggiunto, deriva dal controllo della resistenza offerta dalle cerchiature introdotte, attraverso un calcolo del tutto immediato. Poleni, infatti, propose inizialmente l’introduzione di 5 anelli cerchianti (in posizioni da lui indicate con A, B, C, D, E: cfr. fig. 6), aventi sezione di 9,1×5,6 cm. Di questi anelli, due furono collocati nella regione della cupola che si trova immediatamente sopra il tamburo. Nella stessa regione vi sono 2 cerchiature esistenti (n e u, di sezione 6,0×4,0 cm).

Vi è quindi la possibilità che, pur non rendendo esplicito un calcolo matematico di resistenza del dispositivo di rinforzo adottato, Poleni avesse già, nei fatti, il risultato di questo calcolo, del resto molto immediato, date le evidenze del lavoro compiuto. Nella vicenda che lega il Parere all’attività di Poleni, saremmo allora di fronte a uno di quei passaggi in cui, nel mondo dell’architettura, un dispositivo tecnico, il rinforzo strutturale, viene selezionato in base a una valutazione di tipo scientifico supportata da un processo di controllo di tipo logico-matematico, e diviene quindi vero e proprio dispositivo tecnologico.

Nel cantiere di S. Pietro, riaperto per intervenire sulle fessurazioni, si scontrano più mondi, in particolare quello della nuova scienza e dei nuovi saperi e quello dell’esperienza e di una consolidata tradizione costruttiva. Mondi che in parte interagiscono e si rispettano, in parte confliggono. È il caso del rapporto tra Poleni e Vanvitelli. Quest’ultimo, nato come pittore, era anche esperto di idraulica, costruttore di ponti e porti, restauratore di monumenti, architetto. Nel rapporto tra i due personaggi si perpetua uno scontro tra le ragioni dell’empiria e quelle dell’astrazione, tra quelle della pratica e quelle della teoria, ma queste ultime iniziano progressivamente a prendere il sopravvento con il dominio congiunto di scienza e tecnica.

Considerazioni finali

Alcune considerazioni finali scaturiscono dalle risposte a qualche domanda.

In primo luogo, ci si chiede perché la trattatistica architettonica si interessi solo marginalmente degli aspetti costruttivi, e in particolare di quelli relativi alla complessa e pericolosa edificazione delle cupole, al punto che Bellini può scrivere quanto segue:

Sembrerà paradossale, ma la trattatistica tardorinascimentale, non si occupa né delle cupole né degli organismi di crociera, ossia dei tipi formali e costruttivi più rappresentativi della sua architettura (2004, pp. 42-43).

Il fatto è che per tutta la modernità si dà ancora il primato della prassi sulla teoria: la trattatistica architettonica, prima della nascita di un’editoria dedicata all’arte del costruire, svolge una valenza teoretica solo in quanto ragionamento attorno al linguaggio o ai linguaggi dell’architettura. Soltanto con molta fatica avviene quel processo di matematizzazione del reale che permette la formulazione di leggi universali e quindi un’assoluta autonomia della teoresi e lo sviluppo della scienza moderna. L’architettura viene considerata come ‘figura’ del cosmo, del potere, della natura, e quindi viene considerata linguaggio, e solo funzionalmente costruzione. La costruzione (come in generale la tecnica) sino alla fine del Settecento sarà considerata un semplice mezzo per un fine.

In secondo luogo, ci si chiede perché l’Italia sia (al di là del mondo islamico) il luogo in cui si è più diffusa la costruzione di cupole nell’architettura religiosa, e perché proprio in Italia nascano i primi ‘lemmi’ del linguaggio e delle logiche della scienza moderna, in particolare con Leonardo e Galilei. Si può rispondere ribadendo che in età rinascimentale dall’Italia emerge una forte volontà di matrice religiosa per un’universalizzazione astratta, e che, in sintonia con questo processo di universalizzazione, il rapporto con il passato che si ‘rinnova’, con l’Umanesimo, produce techno-loghíe.

Infine, ci si chiede come questo intreccio tra le figure (nel nostro caso quella della cupola) e la scienza (le scienze) si diffonda in Europa, e in che modo il ‘mondo’ delle cupole (con il suo immaginario, ma anche con i suoi cantieri) si offra alla teoresi scientifica. Il predominio nel resto dell’Europa dell’architettura gotica, e quindi di una logica costruttiva sommamente empirica, legata alla stereotomia e ai procedimenti della geometria operativa o della practica geometriae, si traduce nel tentativo di ‘incarnare’ una dimensione simbolica in chiave teologico-cosmogonica. L’Umanesimo, o ciò che chiamiamo modernità, interrompe questa unità, la dichiara presunta, e apre alla secolarizzazione, che verrà progressivamente accolta dalla cultura francese, da quella inglese e da quella tedesca. Ci si rivolge alle cupole per accettare questa rottura e per provare a liberarsi della ‘inclusività’ che l’arte gotica pretende, e persino per esprimere in modo diverso l’idea stessa di potere.

Tra le esperienze più significative che riprendono in vario modo il magistero italiano, si ricorda quella di Philibert Delorme che, dopo un periodo di studi e ricerche a Roma, introduce in Francia il tema della cupola con la cappella del castello di Anet (1544-52). All’esterno s’ispira al tempietto di S. Pietro in Montorio e all’interno si richiama alla suddivisone della volta del Pantheon, ma disegnando i lacunari secondo una trama orientata a 30° rispetto ai giunti orizzontali e abbandonando quindi la partizione orizzontale e verticale del Pantheon. Il risultato è una vertigine coinvolgente, che muove un comportamento a spirale non solo delle forme, ma anche delle ‘forze’.

Significativa è anche la chiesa di Saint-Louis des Invalides a Parigi (terminata nel 1691), di Jules Hardouin Mansard. Destinata a essere vista da lontano, è composta da una cupola tronca interrotta al livello delle finestre per lasciar penetrare la luce, da una calotta superiore che, così illuminata, metteva in scena l’affresco di Charles de La Fosse, e da una struttura composta da uno scheletro ligneo a modellare la copertura dorata.

Questa chiesa a pianta centrale è strettamente legata ai progetti del prozio dell’architetto, François Mansard, che per primo fissò l’importanza delle cupole come elemento fondamentale delle chiese di Parigi. Suo il progetto (1665-66) per la cappella funeraria dei Borboni nella cattedrale di Saint-Denis, con una cupola a doppio involucro che, pur non venendo mai costruita, influenzò Christopher Wren.

Questi, infatti, nella cattedrale di Saint Paul a Londra (iniziata nel 1675) riprende il progetto di Saint-Denis, pur confrontandosi con Saint-Louis des Invalides e con il tema delle ‘tre cupole’ di Hardouin Mansard. Al centro della navata concepisce una cupola formata da tre strutture: una semisfera interna in muratura, un cono intermedio, ancora in muratura, che sopporta il peso della lanterna, e una cupola esterna a centine in legno rivestita di lastre metalliche. La cupola interna risulta così soggetta al solo peso proprio, ed è strutturalmente autonoma dalle altre due; il cono sostiene la lanterna e la cupola lignea esterna, con il risultato di rievocare la maestosità delle cupole parigine e di S. Pietro. Wren non ricorre alla concezione di Michelangelo o di Brunelleschi di una cupola con struttura portante unitaria, poiché solo in quel modo avrebbe potuto ottenere il risultato voluto di una proporzionata cupola interna e una slanciata cupola esterna, ben più alta.

Risale al 1716 la chiesa di S. Carlo Borromeo (Karlskirche) a Vienna, di Johann Bernhard Fischer von Erlach. L’insolita imponenza della chiesa è dovuta alla triade formata da un portico simile a quello del Pantheon, inquadrato da due colonne giganti simili alla colonna Traiana di Roma; due corpi angolari simili a quelli del palazzo del Louvre di Parigi; e infine la cupola con tamburo finestrato. Il tutto a dimostrazione del potere che la fede cristiana ha di assorbire e trasfigurare gli splendori dell’antichità. Per Fischer von Erlach la cupola è posta al centro di ogni riflessione. L’ovale è il nucleo della composizione.

La costruzione della citata chiesa di Sainte-Geneviève a Parigi inizia nel 1757 a opera di Soufflot, che appronta una struttura per alcuni aspetti concettualmente analoga a quella della basilica di Santa Sofia di Costantinopoli (6° sec.), cioè una cupola sostenuta da arcate a loro volta sostenute da quattro grandi pilastrature controventate da pareti laterali di taglio. Con tale sistema, Soufflot voleva evitare una soluzione a tamburo massiccio come quella del Pantheon. Conscio della necessità di assorbire comunque diverse forme di azioni orizzontali tendenti a divaricare i sostegni, egli ritenne utile inserire una serie di rinforzi in metallo per compensare i possibili cedimenti, come fatto da Poleni per S. Pietro. Di fatto, si trattava di una forma di muratura armata, per alcuni versi analoga all’idea utilizzata in Inghilterra da John Smeaton nel faro di Eddystone (1755-59). La cultura ufficiale parigina dell’epoca s’indignò, ritenendo che la chiesa sarebbe presto crollata, perché la stabilità pareva affidata solo alla resistenza del metallo e le pilastrature sembravano troppo sottili per poter sopportare il peso della cupola. Soufflot, allora, si rivolse a Gauthey, che realizzò una macchina per sottoporre a prove di compressione la pietra utilizzata nei pilastri.

Sarà solo nel 18° sec., con la divulgazione dei trattati sull’arte del costruire che facevano riferimento alle nuove conoscenze scientifiche, che il bagaglio di nozioni del costruttore inizierà ad arricchirsi. Le riflessioni attorno alle tesi di Galilei relativamente alla frattura dei materiali porteranno progressivamente alla tabulazione dei risultati sperimentali utili al dimensionamento delle strutture e alle prime trattazioni sull’equilibrio delle stesse. È in questo periodo che si manifesta un crescente interesse, da parte dei matematici, per la ricerca di curve che possano risolvere per via geometrica problemi di natura costruttiva. I primi elementi per una vera e propria teoria statica degli archi e delle volte furono definiti da de La Hire e da Claude Antoine Couplet. Ai loro studi si collegano quelli di Bernard Forest de Bélidor, il cui sistema grafico-analitico sarà largamente impiegato fino alla fine del 18° sec., quando, grazie agli studi di Charles-Augustin Coulomb e di Lorenzo Mascheroni, sarà individuato il nuovo meccanismo flessionale.

Questa la trama generale, in cui troviamo personaggi, come Guarini e Wren, che giungono all’architettura attraverso un percorso di studio di tipo scientifico-matematico; come Bernardo Antonio Vittone e Giovanni Branca, che inseriscono nei loro trattati argomenti di algebra e geometria; come Bernini, che distingue le attività meccaniche da quelle artistiche, attribuendo alle prime un ruolo di servizio alle seconde; come Borromini, che concepisce la tettonica come parte del processo finale dell’ideazione.

Potremmo quindi concludere con una considerazione che è più di una suggestione: le ricerche attorno ai conglomerati cementizi, insieme all’industrializzazione della laminazione del vetro e della trafilatura dei metalli, insomma la progressiva e inarrestabile industrializzazione dei modi di produzione, non solo edilizi, con la ‘calcolabilità’ delle forme, tutto questo pone fine alla stagione delle cupole e ai suoi valori.

Il problema iniziale di come, nella costruzione della cupola di S. Maria del Fiore, poter fare a meno della centina, che costava troppo e della quale non si sapeva con certezza se avrebbe retto il carico di un’enorme costruzione, alla fine si traduce nella trasformazione della centina stessa in una struttura finita, portante, che si presenta essa stessa come opera. La centina ora non può e non deve più (ecco il funzionalismo) essere nascosta, ma rappresenta la verità stessa dell’opera. Se la centina nasce come una tecnica, cioè come un mezzo per un fine, ora è essa stessa un fine; se serviva a costruire l’opera, ora è essa stessa un’opera. Un cambiamento radicale. Si costruiranno ancora cupole, ma non avranno più lo stesso ‘valore’. Il dopo è reso con grande evidenza, per es., nella cupola in ghisa e vetro della Halle au blé a Parigi (1806-11, oggi Bourse de commerce), di Francois-Joseph Bélanger. Niente centine, solo travi metalliche autoportanti.

Si avrà, in conclusione, come processo inevitabile, il ‘canto del cigno’ di una stagione straordinaria, con l’apoteosi della cupola, nella basilica di Superga a Torino (1716-31), di Filippo Juvarra, o, di contro, con la sua ‘decostruzione’, messa in atto, per es., da Vittone, sempre nel Regno sabaudo, nelle sue fantastiche cupole a tre gusci o con lo svuotamento di pennacchi nel presbiterio della chiesa di S. Maria di Piazza a Torino (1747). Sempre, alla fine, tutto cerca di imporsi in modo definitivo o, al contrario, si decompone aprendosi ad altro.

Sullo sfondo, le immani cupole disegnate da Étienne-Louis Boulleé, l’architetto della Rivoluzione francese, le quali sembrano dichiarare che oramai tutto è possibile, che finalmente tutto è calcolabile e costruibile, e che dunque l’uomo può ‘accendere’ il giorno e la notte, come nel progetto per il ‘Cenotafio di Newton’ (1784), dove una cupola è diventata il mondo stesso.

Bibliografia

R.J. Mainstone, Development in structural form, Oxford 1975.

C. Pedretti, Leonardo architetto, Milano 1978, 1989.

R.J. Mainstone, Le origini della concezione strutturale della cupola di Santa Maria del Fiore, in Filippo Brunelleschi, la sua opera e il suo tempo, Atti del Convegno internazionale di studi, 1977, Firenze 1980.

E. Benvenuto, La scienza delle costruzioni e il suo sviluppo storico, Firenze 1981.

E. Benvenuto, An introduction to the history of structural mechanics, New York 1991.

Gli ingegneri del Rinascimento, da Brunelleschi a Leonardo, a cura di P. Galluzzi, catalogo della mostra, Firenze 1995.

Lo specchio del cielo. Forme significati tecniche e funzioni della cupola dal Pantheon al Novecento, a cura di C. Conforti, Milano 1997.

M. Mislin, Geschichte der Baukonstruktion und Bautechnik, Düsseldorf 1998.

R.J. Mainstone, Structure in architecture, Aldershot 1999.

U. Barbisan, R. Masiero, Il labirinto di Dedalo. Per una storia delle tecniche dell’architettura, Milano 2000.

R. King, La cupola di Brunelleschi. La nascita avventurosa di un prodigio dell'architettura e del genio che lo ideò, Milano 2001.

A. Becchi, F. Foce, Degli archi e delle volte. Arte del costruire tra meccanica e stereotomia, Venezia 2002.

S. Di Pasquale, Brunelleschi: la costruzione della cupola di Santa Maria del Fiore, Venezia 2002.

F. Bellini, Le cupole di Borromini. La ‘scientia’ costruttiva in età barocca, Milano 2004.

Guarino Guarini, a cura di G. Dardanello, S. Klaiber, H.A. Millon, Torino 2006.

M. Villani, L’architettura delle cupole a Roma: 1580-1670, Roma 2008.

P. Napoli, A structural description of the Chapel of the Holy shroud in Torino, «Nexus network journal», 2009, 11, pp. 351-68.

M. Como, Statica delle costruzioni storiche in muratura, Roma 2010.