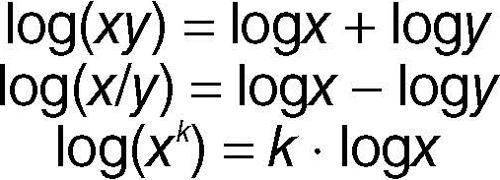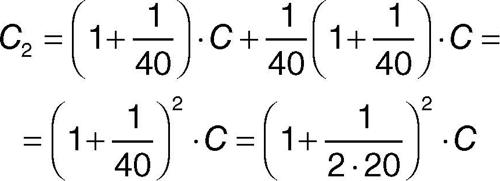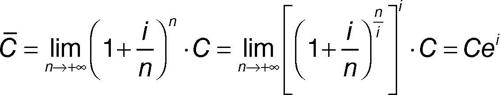La storia di un numero: e, il numero di Nepero

Enciclopedia della Matematica (2013)

Il numero denotato con il simbolo e è un elemento di RQ, cioè un numero reale non razionale. Le prime cifre della sua rappresentazione decimale sono 2,71828. Formalmente, il numero e può essere presentato come

dove la successione, il cui generico elemento è a_n = (1 + 1/n)ⁿ, ammette limite in quanto è monotòna (crescente). Esso può essere equivalentemente presentato come somma della serie degli inversi dei fattoriali dei numeri naturali:

Tramite quest’ultima definizione si prova l’irrazionalità di e. Si ragioni infatti per assurdo e si supponga che e sia razionale ovvero della forma p /q con p e q naturali e q almeno uguale a 2 (dato che e è compreso tra 2 e 3). Moltiplicando per q! = q · (q − 1) · (q − 2) · … · 3 · 2 · 1 entrambi i membri dell’uguaglianza

si ottiene al primo membro

che deve essere uguale a (secondo membro):

Questa uguaglianza è però assurda in quanto al primo membro figura il numero intero e · q!; al secondo membro compare invece un numero non intero in quanto è intero il numero in parentesi quadre mentre non lo è la somma di tutti gli altri che seguono.

La natura del numero e può essere ulteriormente precisata dicendo che si tratta di un numero (irrazionale) trascendente. Si dicono infatti algebrici i numeri che sono soluzione di un’equazione polinomiale a coefficienti razionali; i numeri che non sono algebrici vengono detti trascendenti in quanto – come affermò Eulero – trascendono la potenza dei metodi algebrici. La trascendenza di e fu dimostrata nel 1873 dal matematico francese Charles Hermite che non riuscì però a provare la trascendenza di π; quest’ultima dimostrazione fu ottenuta nel 1882 dal tedesco Ferdinand von Lindemann.

Nei corsi di calcolo, gli studenti incontrano e come base dei logaritmi naturali e come base di una particolare funzione esponenziale ƒ(x) = e^x. Il disagio di dover considerare come base di funzioni elementari, quali il logaritmo e l’esponenziale, un numero irrazionale quale è il numero e risulta compensato da una maggiore scorrevolezza nei calcoli. La derivata di ƒ(x) = e^x è infatti ancora e^x: quindi, ƒ(x) = ƒ′(x); in generale, invece, per ƒ(x) = a^x risulta ƒ′(x) = a^xlna. Analogamente, per ƒ(x) = Inx, si ha ƒ′(x) = 1/x mentre in generale da ƒ(x) = log_ax segue ƒ′(x) = Ina ⋅ 1/x. La retta tangente al grafico della funzione ƒ(x) = e^x in x = 0 è dunque parallela alla bisettrice del primo e terzo quadrante di equazione y = x (che forma un angolo di 45° con la direzione positiva dell’asse x) e lo stesso si può dire per la tangente al grafico di ƒ(x) = Inx in x = 1.

Le prime tracce della costante e nonché di un suo utilizzo numerico approssimato risalgono addirittura alle antiche civiltà egizie e greche, nella costruzione delle piramidi e del Partenone. In epoca e in termini moderni, la storia del numero e risulta legata a quella dei logaritmi e al nome di John Napier tanto che viene anche citato come «numero di Nepero» (nome italianizzato del matematico scozzese). In realtà, Napier non era un matematico nel senso moderno e professionale del termine; era piuttosto un gentiluomo di campagna che aveva studiato all’università di St. Andrews, la più antica della Scozia, ma che forse neppure aveva concluso i suoi studi (per via della morte della madre). Impegnato e brillante nella vita pubblica, a lungo coinvolto nelle diatribe teologiche e nelle meno nobili guerre di religione, Napier era un intellettuale a cui non mancavano senso di responsabilità civile e spirito pratico. Si interessò a quelli che sarebbero diventati i logaritmi nel tentativo di semplificare i calcoli di trigonometria sferica. Infatti, le proprietà fondamentali dei logaritmi:

permettono di trasformare moltiplicazioni e divisioni nelle più semplici operazioni di addizione e sottrazione e analogamente di trasformare i termini di una progressione geometrica negli elementi di una progressione aritmetica.

Napier scriveva in latino per assicurare una maggiore diffusione ai propri scritti: espose le sue idee nel Mirifici logarithmorum canonis descriptio e nel Mirifici logarithmorum canonis constructio che furono pubblicati postumi dal figlio Robert (il secondo con l’aiuto di Henry Briggs, matematico, amico e primo estimatore del nuovo calcolo, autore nel 1624 delle prime tavole di logaritmi). In Napier non c’è esplicitamente il numero e né il simbolo per indicarlo, appunto la lettera e; al matematico si deve invece la parola logaritmo che coniò unendo, per dare un’idea immediata delle proprietà fondamentali, le parole greche logos (rapporto) e arithmos (numero).

Si trova per la prima volta il numero 2,71828… (indicato però con la lettera b) in due lettere di Leibniz a Huygens del 1690 e del 1691. La lettera e fa finalmente la sua comparsa nel 1727 nel volume Mechanica del matematico svizzero Eulero: qui la lettera e sta forse per esponenziale oppure è semplicemente usata perché le precedenti lettere dell’alfabeto a, b, … erano state già impiegate. Sempre in Eulero si trova la descrizione di un semplice modello finanziario che assegna a un numero e un preciso significato economico. Se si indica con C il capitale iniziale dei 400.000 fiorini di cui parla Eulero e con i l’interesse annuo (nel suo esempio, i = 5% = 1/20), gli interessi maturati alla fine di un anno portano al capitale C₁ così calcolabile:

Se il calcolo degli interessi avvenisse semestralmente, alla fine del primo semestre, con un interesse del 2,5% (= 1/40), il capitale sarebbe uguale a (1 + 1/40)C per poi diventare alla fine dell’anno, indicando con C₂tale capitale:

Se gli interessi venissero computati n volte in un anno, ripetendo il ragionamento seguito per il calcolo semestrale degli interessi, alla fine il capitale sarebbe

cioè

Per n → ∞, cioè se il calcolo degli interessi fosse effettuato innumerevoli volte e al limite in modo continuo, la precedente espressione tenderebbe a diventare

Il numero e compare dunque in modo naturale, sia pure attraverso un passaggio al limite, considerando un capitale di 400.000 fiorini. In particolare, se nell’uguaglianza

si pone C = i = 1 si ottiene

il numero e fornisce pertanto il capitale maturato alla fine dell’anno con un investimento iniziale unitario (C = 1, cioè un’unità monetaria, euro o fiorino che fosse) e con una capitalizzazione continua che preveda un tasso di interesse annuo del 100% (i = 1).