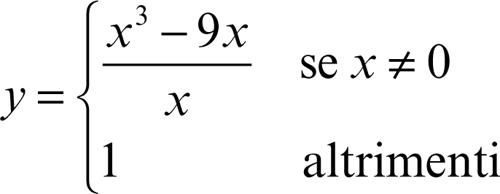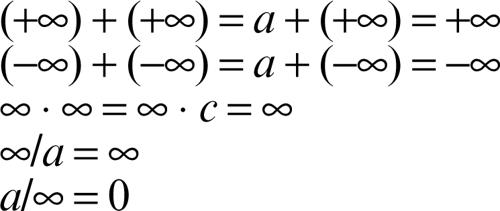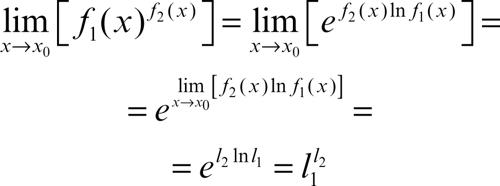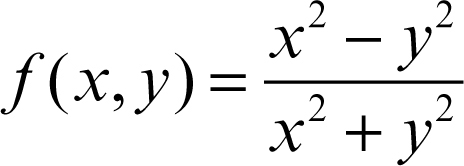limite

limite

limite nozione centrale nell’analisi matematica a cui vengono ricondotte le definizioni delle altre nozioni fondamentali (→ derivata, → integrale, → serie ecc.). Esprime in termini rigorosi l’esigenza di caratterizzare la tendenza di una quantità variabile (funzione, successione, serie) ad assumere valori arbitrariamente prossimi a un valore prefissato, rimanendo tuttavia in generale distinta da questo. Il suo significato, originariamente assunto come intuitivo ed espresso in modo non formale, senza una simbologia specifica, è stato chiarito nel xix secolo soprattutto attraverso l’opera di A.-L. Cauchy e di K. Weierstrass. Quest’ultimo ne diede la definizione riportata spesso come «ε − δ» e ormai classica. Il concetto è stato poi generalizzato nel xx secolo agli spazi astratti, dando luogo all’analisi funzionale moderna.

Limite di una funzione

Alla base della nozione di limite sta quella di intorno. Si considerino due spazi topologici X e Y: nel caso più semplice, si può prendere X = Y = R, ma la nozione si applica senza variazioni al caso euclideo multidimensionale X = Rⁿ, Y = R^m, a spazi metrici o normati e a qualsiasi spazio topologico. Sia poi y = ƒ(x) una funzione X → Y di dominio D(ƒ) ⊆ X e x₀ un punto di accumulazione di D(ƒ). Si dice allora che il limite di ƒ(x) per x tendente a x₀ è l, con l ∈ Y, e si scrive

se preso ad arbitrio un intorno V di l esiste in corrispondenza un intorno U di x₀ tale che, per ogni x ∈ U ∩ D(ƒ), x ≠ x₀, risulta ƒ(x) ∈ V. La condizione x ∈ D(ƒ) è indispensabile per calcolare ƒ(x), ma proprio per questo è ovvia e sovente viene tralasciata. Più delicata è la clausola x ≠ x₀, che significa che il valore di ƒ(x₀), anche se definito, è irrilevante. Questo permette, da un lato, di definire il limite anche per punti che non appartengono al dominio di ƒ, ma solo al suo derivato, dall’altro di assegnare un valore al limite anche quando il valore di ƒ(x₀) è definito in modo arbitrario. Nel caso in cui risulti l = ƒ(x₀), la funzione ƒ(x) si dice continua in x₀. Se

si dice anche, equivalentemente, che ƒ(x) tende (o converge) a l per x tendente a x₀, e si scrive ƒ(x) → l per x → x₀ (non si deve dire invece che il limite di ƒ(x) tende a l: le due parole «limite» e «tendere» hanno in sé un concetto dinamico che non deve essere ripetuto).

Nel caso particolare X = Y = R, si possono specificare gli intorni V di l e U di x₀ come gli intervalli V = (l − ε, l + ε) e U = (x₀ − δ, x₀ + δ), per cui la definizione si formula così: si ha che

se ∀ε > 0, e in particolare per ε arbitrariamente piccolo (si usa spesso dire «preso un ε positivo piccolo a piacere»), ∃δ > 0 tale che, ∀x ∈ D(ƒ), soddisfacente le limitazioni 0 < |x − x₀| < δ, risulta |ƒ(x) − l| < ε. La disuguaglianza 0 < |x − x₀| equivale infatti a x ≠ x₀. È essenziale notare l’ordine dei quantificatori: si sceglie ε (o, in genere, V) ad arbitrio, e in corrispondenza a esso si determina δ (o U). Tuttavia la dipendenza di δ da ε, indicata sovente con scritture come δ_ε o δ(ε), non è una dipendenza funzionale, perché i valori di δ corrispondenti a un determinato ε sono infiniti, e costituiscono un intervallo. Infatti, se l’implicazione |ƒ(x) − l| < ε è soddisfatta per tutti i valori di x che differiscono da x₀ meno di un certo δ, lo è a maggior ragione per tutti quelli che ne differiscono per meno di un valore δ′ più piccolo.

Quanto detto per la dipendenza δ = δ(ε) vale in genere per la dipendenza U = U(V). Vale per esempio, sempre nel caso di funzioni ƒ: R → R, quando uno o entrambi i valori x₀ o l siano ∞ (+∞ o −∞, se la retta viene estesa con due punti all’infinito). Basta infatti ricordare che un intorno di +∞ è una semiretta del tipo (a, +∞), un intorno di −∞ è una semiretta del tipo (−∞, a) e un intorno di ∞ è dato da {x: |x| > a}. Se il limite è ∞ (sia +∞, sia −∞), la funzione si dice divergente (positivamente, negativamente) per x tendente a x₀.

La definizione generale di limite si specificherà dunque in uno di questi casi sostituendo a uno e/o all’altro degli intorni V = (l − ε, l + ε) e/o U = (x₀ − δ, x₀ + δ) un intorno come sopra specificato. Per esempio, la scrittura

con l finito, significa: ∀ε > 0, ∃a tale che ∀x ∈ D(ƒ ), x > a si ha che |ƒ(x) − l| < ε. Analogamente,

significa che ∀b < 0, ∃δ > 0 tale che,

si ha che ƒ(x) < b.

La definizione generale consente poi di considerare (nel caso di funzioni ƒ: R → R) i limiti destro e sinistro, utilizzando gli intorni destro [x₀, x₀ + δ) o sinistro (x₀ − δ, x₀] di x₀, così come permette di indicare che il valore limite l è approssimato dall’alto o dal basso. Queste specificazioni vengono indicate da un suffisso + o −: per esempio,

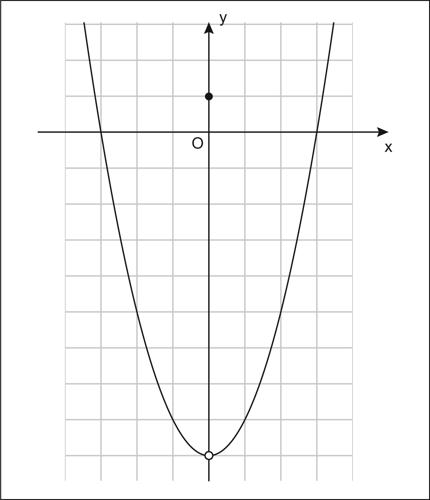
significa che ∀ε > 0, ∃δ > 0 tale che, ∀x ∈ D(ƒ), con x₀ < x < x₀ + δ risulta l − ε < ƒ(x) ≤ l. Se i limiti destro e sinistro coincidono, tale valore è il limite di ƒ(x). Per esempio, nella funzione ƒ(x) così definita

il cui grafico è una parabola, privata del suo vertice più il punto (0, 1), si ha che sia il limite destro sia il limite sinistro per x tendente a 0 è −9 ed è quindi:

Tale limite non coincide con il valore della funzione per x = 0 dove la funzione ha un punto di discontinuità.

I principali problemi connessi alla nozione di limite sono:

• sapere se un determinato limite esiste o non esiste;

• in caso affermativo, calcolare o approssimare il valore l di tale limite.

Teoremi sui limiti di funzioni

Per quanto riguarda il problema dell’esistenza, il criterio di convergenza di → Cauchy fornisce una condizione necessaria e sufficiente per l’esistenza del limite finito, mentre l’ipotesi di monotonia garantisce l’esistenza del limite, finito o infinito. Vale infatti il teorema del limite delle ƒunzioni monotone: se ƒ(x) è monotona in un insieme E ⊂ (a, b) avente b come punto di accumulazione da sinistra, esiste

È possibile che b e/o L siano +∞. Analogamente se a è punto di accumulazione da destra per E esiste

potendo essere sia a che l uguali a −∞.

Un altro teorema che garantisce l’esistenza del limite è il teorema del conƒronto: se ƒ₁(x) ≤ ƒ(x) ≤ ƒ₂(x) in un intorno di x₀, punto di accumulazione del loro dominio, e se esistono i due limiti

e questi assumono lo stesso valore l

allora anche ƒ(x) ammette limite per x → x₀ e risulta, quindi:

Per esempio, dalle disuguaglianze 1 < x/sinx < 1/cosx e dal fatto che cosx è continua per x = 0 si deduce il limite notevole

Le due funzioni ƒ₁(x) e ƒ₂(x), se esistono, costringono la funzione intermedia a seguire il loro stesso andamento: per questo il teorema è stato anche scherzosamente chiamato teorema dei carabinieri (che accompagnano l’arrestato, affiancandolo da entrambi i lati). Se la funzione però non ammette limite, come per esempio, la funzione sin(1/x) per x → 0, il teorema non aiuta: in tali casi si deve far ricorso alle nozioni di massimo limite e di minimo limite (→ massimo e minimo limite).

Il limite, se esiste, è comunque unico (teorema dell’unicità del limite, valido in spazi topologici purché soddisfacenti l’assioma di separazione, quindi in particolare in tutti gli spazi metrici).

La determinazione del valore del limite, se esso ha un’espressione analitica esplicita, è immediata se ƒ(x) è continua in x₀, altrimenti si utilizzano alcuni teoremi, che indicano le possibili operazioni con limiti, in cui si suppone che

esistano finiti. I teoremi sono i seguenti (in corsivo è indicata la proprietà dei limiti che essi rispettivamente esprimono):

da cui si ricava ovviamente la possibilità di sommare limiti;

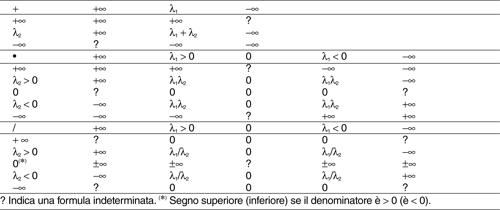
I risultati precedenti si estendono al caso di limiti infiniti con le seguenti regole:

dove a, c sono numeri reali non nulli e dove vale per prodotti e quozienti la regola dei segni: per esempio, (+∞) ⋅ (−3) = −∞.

Rimangono esclusi i casi (+∞) − (+∞), 0 ⋅ ∞, ∞/∞, 0/0 che costituiscono delle forme indeterminate, talvolta dette di indecisione in quanto bisogna stabilire quale sia l’infinito o infinitesimo predominante; per esse si ricorre di volta in volta a metodi particolari, quale per esempio quello legato al nome di → L’Hôpital, che consente, sotto opportune ipotesi, di riportare il problema al calcolo del limite del quoziente delle derivate ƒ′ (x)/g′ (x).

Essenziale poi è il teorema sul limite delle funzioni composte. Siano date le funzioni y = ƒ(x), z = g(y), e si consideri la funzione composta z = h(x) = g(ƒ(x)). Se

ci si attende che risulti

Ciò è vero se la funzione g è continua in y = l, altrimenti la tesi può non essere verificata. Per esempio, sia g(y) = 0 per y ≠ 0, g(0) = 1 (quindi, g(y) → 0 per y → 0, ma essa non è continua in y = 0). Allora se ƒ(x) = xsin(1/x), la funzione h(x) vale 1 per x = 1/(kπ), 0 altrove, e quindi non ammette limite per x → 0. Se invece ƒ(x) = g(x), risulta h(x) = 1 per x ≠ 0, h(x) = 0 per x = 0, e quindi h(x) → 1 ≠ 0.

Metodo utile nella rimozione delle indeterminazioni del tipo ∞^∞, 0⁰, 1^∞ risulta la seguente sostituzione

se entrambi i limiti sono finiti e non entrambi nulli (si deve avere ƒ₁(x) > 0, e quindi l₁ ≥ 0 per il teorema della → permanenza del segno). Si ha poi, simbolicamente, l₁^+∞ = +∞ se 1 < l₁ ≤ +∞, l₁^+∞ = 0⁺ se 0 ≤ l₁ < 1 e viceversa l₁^−∞ = 0⁺ se 1 < l₁ ≤ +∞, l₁^−∞ = +∞ se 0 ≤ l₁ < 1.

￭ Limite di una successione Nel caso di una successione {s_n}, la nozione di limite non muta, ma si deve notare che ha senso solo il

Si ha dunque

finito se, ∀ε > 0, ∃N = N(ε) tale che, ∀n > N, si ha |s_n − L| < ε. Continuano a valere i teoremi sui limiti di funzioni (le successioni sono una particolare classe di funzioni) come l’esistenza del limite per successioni monotone, il teorema del confronto e tutte le regole di calcolo sopra indicate.

Una successione convergente o divergente è detta regolare, altrimenti è detta irregolare. Ogni successione monotona è regolare. La successione {aⁿ} è convergente a 0 se |a| < 1, è convergente a 1 se a = 1, è divergente positivamente se a > 1, è indeterminata se a ≤ −1.

Limite di una successione di funzioni

Il concetto di limite si estende opportunamente a successioni di funzioni, cioè a successioni i cui termini ƒ_n siano funzioni. La definizione di funzione limite in questo contesto si avvale di alcuni concetti quali quello di convergenza puntuale e di convergenza uniforme per i quali si rinvia al lemma → successione di funzioni.

Limite di funzioni in n variabili

Nel caso di funzioni di più variabili, ƒ: Rⁿ → R^m, vale la definizione generale, nella quale intervengono gli intorni V di l e U di x₀; tutti i risultati precedenti continuano a valere, salvo quelli legati all’ordinamento di R (limite destro e sinistro). Ha invece significato considerare le restrizioni, in particolare quelle lungo parallele agli assi coordinati (cioè lungo le loro rispettive direzioni). Supponendo per esempio, per semplicità, che ƒ(x, y) sia definita in un intorno dell’origine, si possono considerare il limite

e i limiti

Se esiste l gli altri due limiti esistono e sono uguali a l. È però possibile che esistano l₁ e l₂ e siano differenti: per esempio, la funzione

ha l₁ = 1, l₂ = −1. In questo caso l non può esistere. Viceversa, da l₁ = l₂ non si può dedurre nulla sull’esistenza di l: per esempio, la funzione

ha l₁ = l₂ = 0, ma l non esiste, in quanto sulla retta y = x si ha ƒ(x, x) = 1 e 1 ≠ 0.