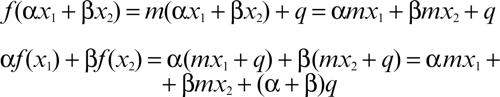lineare

lineare

lineare termine che, se riferito alla rappresentazione analitica di un fenomeno, indica la possibilità di formalizzarlo con una espressione di primo grado. Una → ƒunzione lineare è, quindi, una funzione polinomiale di primo grado; una equazione lineare (→ equazione algebrica) è un’equazione di primo grado e un → sistema lineare è costituito da tutte equazioni di primo grado; una crescita, o una decrescita, si dice lineare, se espressa da una funzione lineare. La formalizzazione matematica di un fenomeno ottenuta utilizzando soltanto espressioni di primo grado costituisce il modello lineare del fenomeno; nei metodi di risoluzione numerica si ricorre spesso a modelli di questo tipo per una prima valutazione dell’andamento di un processo.

L’aggettivo si riferisce in modo naturale a diversi oggetti matematici in cui sono coinvolte espressioni polinomiali di primo grado e per la cui definizione si rimanda ai singoli lemmi.

□ In algebra elementare si parla, oltre che di equazioni e sistemi lineari, di → combinazione lineare.

□ In analisi, oltre a considerare le funzioni elementari, si studiano le → equazioni differenziali lineari e, in generale, le proprietà di una → forma algebrica, lineare o multilineare, così come si analizza la linearità di un → operatore.

□ In statistica si ricerca l’andamento di un fenomeno attraverso l’→ interpolazione lineare di dati rilevati e nell’esame della dipendenza tra due fattori si introduce il concetto di → regressione lineare; mentre nelle applicazioni della matematica, i problemi di ottimizzazione più semplici sono studiati attraverso gli strumenti della → programmazione lineare.

□ In → algebra lineare sono importanti i concetti di → dipendenza lineare, di → applicazione lineare e di → trasformazione lineare. Il nome di tale settore disciplinare dipende appunto dal fatto che esso ha come oggetto di studio gli → spazi vettoriali (talvolta detti anche spazi lineari) e le loro trasformazioni.

□ In termini più generali, l’aggettivo lineare si attribuisce a una legge espressa da una funzione reale ƒ di variabile reale tale che per ogni x₁, x₂ del suo dominio e per ogni α, β ∈ R si ha ƒ(αx₁ + βx₂) = αƒ(x₁) + β ƒ(x₂) (proprietà di linearità). Per l’uso del termine in questo più ampio significato si vedano → applicazione; → funzionale; → operatore; → trasformazione lineare. La funzione quadratica ƒ espressa da y = x ² non gode della proprietà di linearità perché ƒ(x₁ + x₂) = (x₁ + x₂)² non è uguale a ƒ(x₁) + ƒ(x₂) = x₁² + x₂². Si osservi tuttavia che una funzione lineare ƒ(x), definita da y = mx + q, il cui grafico è una linea retta, gode della proprietà di linearità se e soltanto se il termine noto q è nullo e cioè esprime la relazione di diretta proporzionalità tra x e y. Infatti si ha:

□ In altri settori della matematica l’aggettivo lineare è poi utilizzato con ulteriori differenti significati dipendenti dal contesto. Si vedano perciò: → integrale di linea; → involucro convesso; → logica lineare; → ordinamento lineare; → serie lineare; → gruppi classici.