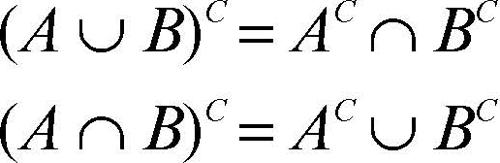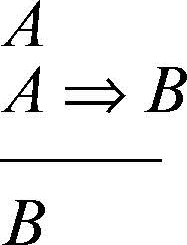enunciati, linguaggio degli

enunciati, linguaggio degli

enunciati, linguaggio degli linguaggio formale per esprimere affermazioni elementari a cui è attribuibile un valore di verità e per comporle tra loro, in modo tale che sia possibile determinare il valore di verità di una affermazione composta a partire dai valori di verità delle affermazioni elementari che la compongono. Le affermazioni dotate di valore di verità, che costituiscono gli elementi di tale linguaggio, sono dette enunciati o proposizioni (le due parole «enunciato» e «proposizione» sono utilizzate indifferentemente in letteratura, così come in questa enciclopedia, e sono considerate sinonimi). Nel linguaggio degli enunciati si distinguono gli enunciati elementari o atomici e gli enunciati composti, costruiti a partire da questi attraverso l’impiego dei → connettivi. Per esempio, la frase «il semaforo è rosso e la macchina è ferma» è un enunciato composto dai due enunciati elementari «il semaforo è rosso» e «la macchina è ferma», uniti tra loro dal connettivo della congiunzione ed è vera se e solo se sono veri i due enunciati che la compongono. Più formalmente, una proposizione o enunciato è una scrittura sintatticamente corretta (o, come si dice, ben formata) a cui può essere attribuito, in maniera univoca, un valore di verità: «vero» (V) oppure «falso» (F). Nei linguaggi naturali – quelli comunemente utilizzati per la comunicazione tra individui – ciò corrisponde a considerare come enunciato o proposizione una frase, affermativa o negativa, che esprima un giudizio di senso compiuto; non rientrano, quindi, tra essi le frasi che contengono forme interrogative o esclamative.

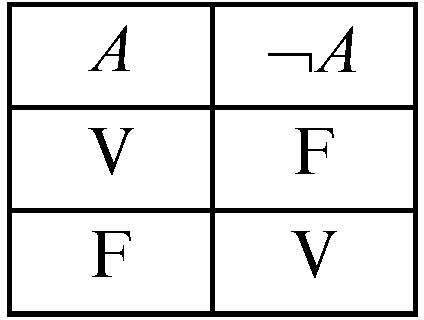
Gli enunciati elementari sono rappresentati nel linguaggio degli enunciati da lettere dell’alfabeto, dette lettere enunciative (o lettere proposizionali); esse costituiscono le minime scritture del linguaggio, sono cioè entità indivisibili in quanto la logica enunciativa non si interessa della loro struttura interna. Le lettere enunciative sono generalmente lettere minuscole, poiché si riservano le maiuscole per enunciati più complessi, non necessariamente elementari; nelle tavole di verità, tuttavia, gli enunciati sono indicati con lettere maiuscole poiché i valori di verità riportati su di esse valgono sempre, indipendentemente dal loro riferirsi a enunciati elementari o meno.

A partire dagli enunciati elementari si costruiscono quelli composti utilizzando i connettivi: la → negazione, la → congiunzione, la → disgiunzione, l’→ implicazione, la → doppia implicazione e gli altri che da essi si possono ricavare. I connettivi sono rappresentati da simboli, rispettivamente:

• la negazione di un enunciato a, che corrisponde nel linguaggio naturale all’espressione «non a», è rappresentata simbolicamente da ￢a;

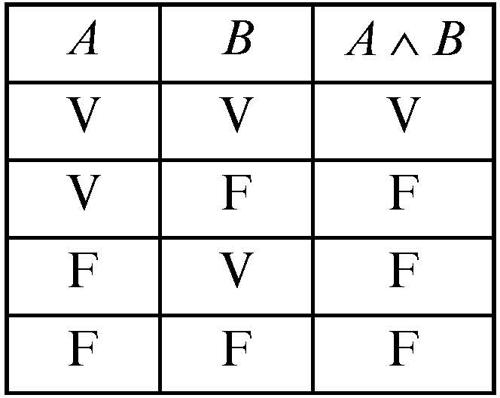
• la congiunzione di due enunciati, indicati con a e con b, che corrisponde nel linguaggio naturale all’espressione «a e b», è rappresentata simbolicamente da a ∧ b;

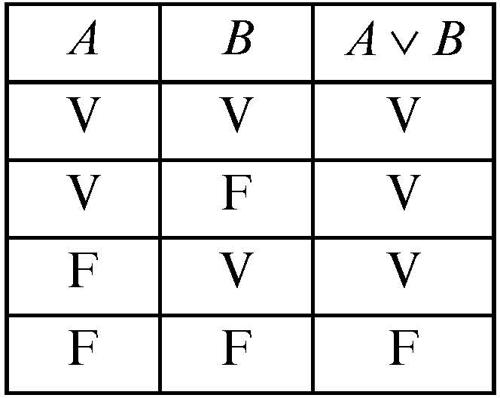
• la disgiunzione di due enunciati, indicati con a e con b, che corrisponde nel linguaggio naturale all’espressione «a o b», è rappresentata simbolicamente da a ∨ b. Questo connettivo rappresenta la disgiunzione inclusiva e non esclusiva; esso corrisponde al latino vel. La disgiunzione esclusiva, corrispondente al latino aut, può essere ricondotta alla disgiunzione inclusiva di due congiunzioni, così come avviene nel linguaggio naturale, giacché dire «o a o b» in senso esclusivo corrisponde a dire «a e non b oppure non a e b» dove «oppure» ha valore inclusivo;

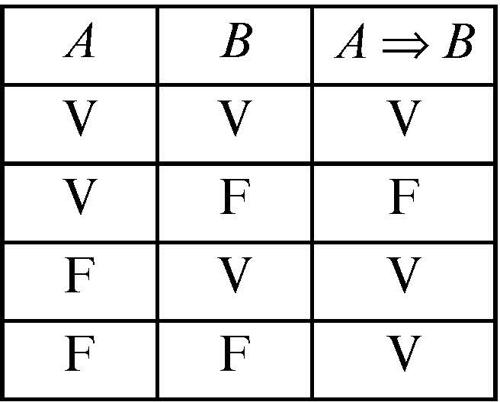
• l’implicazione fra due enunciati, indicati con a e con b, che corrisponde nel linguaggio naturale all’espressione «se a allora b», è rappresentata dal simbolo a ⇒ b. In questa scrittura, l’enunciato a è detto antecedente nell’implicazione, mentre l’enunciato b è detto conseguente. Se l’antecedente viene scambiato con il conseguente, si ottiene la cosiddetta implicazione inversa che ha la forma b ⇒ a (oppure a ⇐ b). L’implicazione a ⇒ b equivale alla frase «a è condizione sufficiente per b» oppure alla frase «b è condizione necessaria per a»;

• la doppia implicazione fra due enunciati, indicati con a e con b, che corrisponde nel linguaggio naturale all’espressione «a se e solo se b», è rappresentata dal simbolo a ⇔ b; questa scrittura simbolica può anche essere tradotta con la frase «a è condizione necessaria e sufficiente per b».

Per esemplificare la costruzione di proposizioni più complesse mediante l’uso dei connettivi, si consideri l’enunciato «se non piove allora gioco a pallone». Per tradurlo nel linguaggio degli enunciati si scelga una lettera enunciativa a che rappresenti l’enunciato elementare «piove» e una lettera b che rappresenti invece «gioco a pallone»; l’enunciato precedente può essere allora rappresentato dall’espressione ￢a ⇒ b. Talvolta inoltre, nel costruire le proposizioni, bisogna impiegare in maniera opportuna le parentesi. Per definire rigorosamente il linguaggio degli enunciati come linguaggio formale, occorre definire i suoi elementi: questi sono le → formule ben formate costruite a partire dal suo → alfabeto. L’alfabeto del linguaggio degli enunciati è formato da:

• un insieme infinito numerabile di lettere enunciative o proposizionali: a, b, c, ...;

• un insieme finito di connettivi rappresentati dai simboli: ￢, ∧, ∨, ⇒, ⇔;

• una coppia di parentesi: ( , ).

Utilizzando i simboli di questo alfabeto, si costruiscono le formule ben formate, mediante le seguenti regole:

• ogni lettera proposizionale a, b, c ... è una formula ben formata ed è detta formula atomica;

• se A e B sono formule ben formate allora anche ￢A, A ∧ B, A ∨ B, A ⇒ B, A ⇔ B, sono formule ben formate;

• le formule ben formate sono tutte e sole le espressione formali costruite secondo le due regole precedenti.

Le formule ben formate così costruite sono dette forme enunciative; dal punto di vista formale esse corrispondono agli enunciati e costituiscono, quindi, gli elementi del linguaggio degli enunciati. Una espressione quale ∧ B ￢⇒ non è una forma enunciativa perché non è ricavabile a partire dalle regole precedenti: è soltanto una giustapposizione di simboli del suo alfabeto.

A ogni lettera proposizionale è attribuito un valore di verità («vero» o «falso»). Il valore di verità di un qualsiasi enunciato A, formato da lettere proposizionali combinate fra loro per mezzo dei connettivi, può essere determinato in base al valore di verità delle singole lettere proposizionali che lo compongono e al modo di operare dei connettivi impiegati. A titolo di esempio sono qui riportate le tavole di verità di alcuni connettivi:

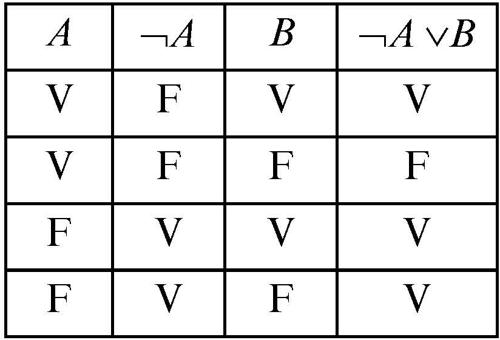
Utilizzando le tavole di verità è possibile determinare il valore di verità di una qualsiasi forma enunciativa. Nel caso dell’enunciato ￢A ∨ B la tavola di verità è la seguente:

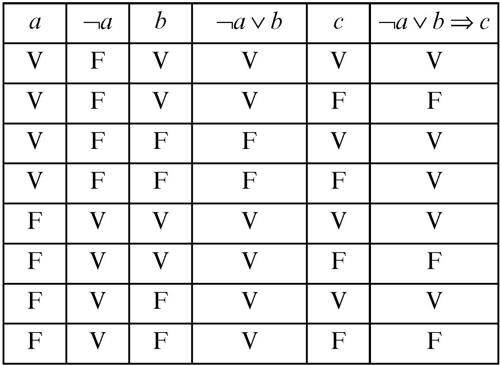
Per l’enunciato (￢a ∨ b) ⇒ c (che si legge «non a o b implica c») si costruisce una tabella le cui righe indicano tutti i possibili valori di verità che si possono associare alle tre lettere enunciative a, b e c (poiché ciascuna di essa può essere vera o falsa, cioè assumere due valori, le possibilità complessive sono 2³ = 8):

L’enunciato è falso quando è falso solo c, quando sono falsi c e a, quando sono falsi tutti e tre gli enunciati elementari.

In generale se una forma enunciativa F è formata da n lettere enunciative, variamente connesse fra loro, allora è possibile costruire una tavola di verità che calcoli il valore di verità di F in corrispondenza dei valori di verità delle lettere enunciative che la compongono. Questo corrisponde a ricavare la verità di un enunciato composto a partire dalla verità degli enunciati elementari che lo compongono. Dato che gli enunciati elementari sono n e ciascuno può assumere due valori (vero o falso) si avranno, come conseguenza, 2ⁿ possibilità diverse, perciò la tavola di verità di F avrà 2ⁿ righe.

La tavola di verità della forma ￢A ∨ B, precedentemente considerata, mostra che essa è sempre vera tranne nel caso in cui A sia vera e B sia falsa; il valore di verità di questa forma enunciativa (ultima colonna della tavola) è uguale al valore di verità di A ⇒ B, in corrispondenza di tutti i casi possibili. Si dice che le due forme enunciative (e, quindi i due enunciati) ￢A ∨ B e A ⇒ B sono logicamente equivalenti e possono essere sostituite l’una con l’altra all’interno di una forma enunciativa senza alterarne il valore di verità (→ equivalenza logica). L’equivalenza logica tra forme enunciative consente di ridurre il numero di connettivi necessari a costruire il linguaggio degli enunciati. Infatti, il connettivo ⇔ può essere sostituito dalla congiunzione di due implicazioni: A ⇔ B è logicamente equivalente a (A ⇒ B) ∧ (B ⇒ A). Inoltre, per l’equivalenza tra A ⇒ B e ￢A ∨ B entrambi i connettivi dell’implicazione e dell’implicazione doppia non sono essenziali per la costruzione del linguaggio. Infine, in base alle leggi di De Morgan è possibile convertire una disgiunzione in una congiunzione e viceversa (→ De Morgan, leggi di). Infatti: A ∧ B è logicamente equivalente a ￢(￢A ∨ ￢B) così come A ∨ B è logicamente equivalente a ￢(￢A ∧ ￢B).

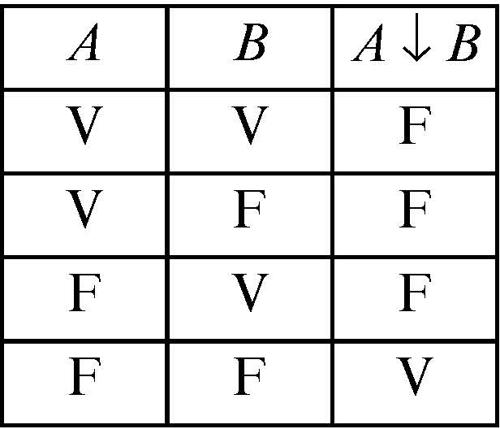
Ne consegue che con la negazione e la disgiunzione oppure con la negazione e la congiunzione è possibile costruire qualsiasi altro connettivo. Inoltre si può verificare, utilizzando le tavole di verità, l’equivalenza logica tra A v B e ￢A ⇒ B, così come tra A ∧ B e ￢(A ⇒ ￢B). Ne segue che il linguaggio degli enunciati può essere costruito inserendo nel suo alfabeto un sistema minimo di connettivi, detto anche base di connettivi, adeguato a esprimere la verità di qualsiasi forma composta; esso è costituito dalla negazione e da uno qualsiasi dei connettivi ∨, ∧, ⇒. È addirittura possibile un’ulteriore riduzione (→ Sheffer, funtori di), introducendo un solo connettivo: la negazione congiunta (spesso indicato con ↓) che ha la seguente tavola di verità:

A ↓ B è vera se e solo se né A né B sono vere. Ne risulta che ￢A è logicamente equivalente a A ↓ A; analogamente si trovano le equivalenze logiche che rendono tale connettivo in grado di esprimere i valori di verità di forme enunciative costruite con gli altri usuali connettivi.

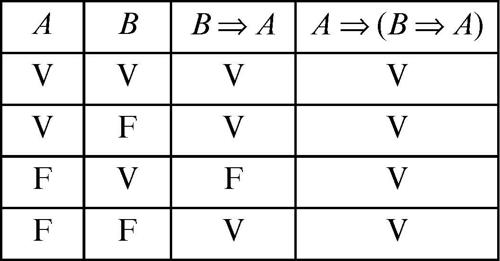
Dire che due forme enunciative F e G sono logicamente equivalenti vuol dire che la forma F ⇔ G è sempre vera, qualunque siano i valori di verità di F e G. Le forme (e i corrispondenti enunciati) che risultano sempre veri, per ogni valore di verità delle lettere che li compongono, si dicono tautologie; quelli che risultano sempre falsi sono invece detti contraddizioni. Per esempio, l’enunciato A ⇒ (B ⇒ A) è una tautologia come si evince dalla seguente tavola di verità

La tautologia A ⇒ (B ⇒ A) è anche nota sotto il nome di legge dell’a fortiori. Altri esempi di tautologie sono le seguenti forme:

• A ∨￢A

(principio del terzo escluso o «tertium non datur»)

• ￢(A ∧ ￢A)

(principio di non contraddizione)

• ￢￢A ⇔ A

(doppia negazione)

• A ⇔ A

(riflessività della doppia implicazione)

• (A ⇔ B ) ⇔ (B ⇔ A)

(simmetria della doppia implicazione)

• ((A ⇔ B) ∧ (B ⇔ C)) ⇔ (A ⇔ C)

(transitivà della doppia implicazione)

È possibile costruire un modello insiemistico per il linguaggio degli enunciati, creare cioè una corrispondenza fra enunciati e insiemi. Ogni proposizione acquista significato e ha un valore di verità se riferita a un insieme di elementi di riferimento, detto insieme universo e indicato con la lettera U; per esempio, proposizioni come «n è pari» o «m è multiplo di n» hanno senso se riferite all’insieme dei numeri naturali. In quest’ottica è possibile associare a ogni enunciato a un sottoinsieme di elementi per cui quell’enunciato risulta vero; per esempio all’enunciato a: «n è un numero naturale minore di 3» risulta associato l’insieme A = {0, 1, 2} che è un sottoinsieme dell’insieme dei numeri naturali. Questo modo di procedere può essere esteso a una qualunque forma enunciativa secondo la corrispondenza seguente:

• a ogni lettera enunciativa a si associa un insieme A, sottoinsieme dell’universo U;

• alla formula ￢a si associa l’insieme complementare di A nell’universo U, indicato con A^C (si legge «complementare di A»). Per esempio, se a è l’enunciato «n è pari» allora il sottoinsieme associato ad a è l’insieme dei numeri pari, mentre il sottoinsieme associato a ￢a è l’insieme dei numeri dispari;

• alla formula a ∨ b si associa l’unione del sottoinsieme A associato ad a e del sottoinsieme B associato all’enunciato b (in simboli A ∪ B);

• alla formula a ∧ b si associa l’intersezione del sottoinsieme associato ad a e del sottoinsieme associato a b (in simboli A ∩ B).

Grazie a questa corrispondenza, ogni proprietà enunciata per gli insiemi può essere estesa alle proposizioni e viceversa. In particolare le leggi di De Morgan espresse per i connettivi, hanno la loro forma equivalente per gli insiemi e possono quindi essere scritte per gli insiemi nel modo seguente:

In parole, il complementare dell’unione di due insiemi è l’intersezione dei loro rispettivi complementari, mentre il complementare della loro intersezione è l’unione dei loro rispettivi complementari. Allo stesso modo, alle leggi distributive fra unione e intersezione, espresse per gli insiemi come

corrispondono le due tautologie

Ciò significa che dalle equivalenze logiche fra enunciati possono essere ricavate proprietà nei vari modelli del linguaggio degli enunciati. Gli stessi connettivi possono essere visti come operazioni e le equivalenze logiche come loro proprietà: si delineano così, nell’insieme delle forme enunciative, una struttura algebrica e delle regole di semplificazione delle espressioni e quindi una possibilità di calcolo. L’idea della riduzione della logica enunciativa al calcolo algebrico è alla base dell’algebra di → Boole.

Il linguaggio degli enunciati fornisce gli elementi di base per un calcolo logico, detto calcolo degli enunciati o calcolo delle → proposizioni, in cui viene tradotto in termini formali il concetto di dimostrazione matematica. Per questo viene stabilita una teoria formale assiomatica che esprime il linguaggio degli enunciati a partire da:

• i simboli del’alfabeto: questi sono le lettere enunciative, le parentesi e due connettivi, di cui uno è la negazione, per esempio i connettivi ￢e ⇒;

• l’insieme di formule ben formate (fbf); sono le forme enunciative costruite a partire dall’alfabeto di simboli, secondo le seguenti regole: a) tutte le lettere enunciative sono fbf; b) se A e B sono fbf lo sono anche (￢A) e (A ⇒ B); c) le fbf sono tutte e sole le forme costruite seguendo queste due regole.

• gli assiomi sono le seguenti fbf, essendo A, B e C tre qualsiasi fbf:

a) A ⇒ (B ⇒ A)

b) (A ⇒ (B ⇒ C)) ⇒ ((A ⇒ B) ⇒ (A ⇒ C))

c) (￢ B ⇒ ￢A) ⇒ ((￢ B ⇒ A) ⇒ B)

Gli assiomi costituiscono tre tautologie (il primo assioma è la legge dell’«a fortiori»);

• come regola di inferenza (o di deduzione) si sceglie il → modus ponens, che consente di dedurre, dalle due fbf A e A ⇒ B, la fbf B. In simboli:

La linea orizzontale separa le premesse (A e A ⇒ B) dalla conclusione B.

In questa teoria formale si introducono gli altri usuali connettivi, scrivendo:

• A ∧ B in luogo di ￢ (A ⇒ ￢B)

• A ∨ B in luogo di ￢ A ⇒ B

• A ⇔ B in luogo di (A ⇒ B) ∧ (B ⇒ A)

Una fbf F deducibile dagli assiomi attraverso la regola di deduzione si dice dimostrabile all’interno della teoria formale introdotta: si scrive ⊢ F e la sua dimostrazione è la catena di deduzione che va dagli assiomi a F. Il teorema di deduzione stabilisce che se Γ è un insieme di fbf e A e B sono due fbf, allora se da Γ e A si deduce B, allora da Γ si deduce A ⇒ B. Quindi, se dagli assiomi e dalla fbf A si deduce B allora A ⇒ B è un teorema nel sistema formale del calcolo degli enunciati ed è dimostrabile in esso. Nel calcolo degli enunciati, così formalizzato, vale il teorema di completezza semantica (→ completezza logica) che stabilisce che le formule in esso dimostrabili, cioè i suoi teoremi, coincidono con le tautologie. In termini più specifici è possibile dimostrare che:

• se una formula F è dimostrabile nel calcolo degli enunciati allora F è una tautologia (teorema di correttezza);

• viceversa, ogni tautologia è dimostrabile formalmente nel calcolo degli enunciati (teorema di adeguatezza).

È importante notare che il calcolo degli enunciati, pur essendo semanticamente completo come stabilito dal teorema precedente, risulta tuttavia sintatticamente incompleto nel senso che, data comunque una fbf F, non è detto che esista una dimostrazione di F o di ￢F. Si consideri per esempio una lettera enunciativa a: né a né￢a sono tautologie e quindi nessuna delle due è dimostrabile nel calcolo degli enunciati.