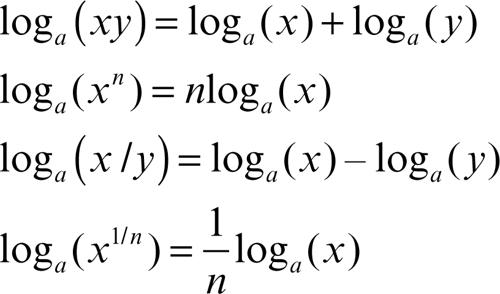logaritmo

logaritmo

logaritmo di un numero reale positivo x rispetto a una base a (dove a è un numero reale positivo diverso da 1) è l’esponente y che bisogna attribuire ad a per ottenere x. Si scrive allora y = log_a(x), x è detto argomento del logaritmo e y è detto logaritmo in base a di x. Per definizione quindi y = log_a(x) se e solo se a^y = x. Per esempio: log₂(8) = 3 perché 2³ = 8; log₁₀(1000) = 3 perché 10³ = 1000; log₁₀(0,1) = −1 perché 10⁻¹ = 1/10 = 0,1 e, qualunque sia la base, log_a(a^k) = k. Se non ci sono equivoci, l’argomento del logaritmo può anche essere scritto non racchiuso tra parentesi. Come base dei logaritmi può essere scelto qualunque numero reale positivo a diverso da 1, ma di fatto le basi prevalentemente usate sono:

• base e: si assume come base il numero di Nepero e = 2,718281... e il logaritmo è allora detto logaritmo naturale (o anche logaritmo neperiano). Per il logaritmo naturale si omette di scrivere la base e si utilizza la notazione ln (utilizzata anche nelle calcolatrici); il logaritmo naturale è anche detto logaritmo iperbolico perché, se 0 < a < b, l’espressione lnb − lna fornisce l’area sottesa all’iperbole di equazione y = 1/x nell’intervallo (a, b). Alcuni autori, se dal contesto è chiara la base e, indicano il logaritmo naturale anche semplicemente con log;

• base 10: il logaritmo è allora detto logaritmo decimale. Per i logaritmi decimali si omette di scrivere la base e si utilizzano le notazioni log, Log o lg. Va tuttavia osservato che vi è difformità nella letteratura internazionale: alcuni autori, se dal contesto è chiara la base decimale, utilizzano log per tale logaritmo e anche nelle calcolatrici il tasto log indica il logaritmo decimale. Nella tradizione italiana, per il logaritmo decimale è utilizzata talvolta anche la notazione Log (con la lettera L maiuscola). Tale logaritmo in base 10 è anche talvolta detto logaritmo volgare o logaritmo di Briggs, dal nome del matematico inglese H. Briggs che comprese l’importanza dell’operatore logaritmo inventato nel xvii secolo da Nepero per semplificare i calcoli e ne curò la conversione in termini decimali;

• base 2: è utilizzata in teoria dell’informazione e in tale caso il logaritmo è anche detto logaritmo binario e indicato con lb.

Qualunque sia la base scelta, il calcolo del logaritmo rappresenta una delle due operazioni inverse dell’→ elevazione a potenza (l’altra essendo l’estrazione di radice). Di conseguenza, le proprietà dei logaritmi riflettono quelle delle potenze e sono date dalle formule seguenti (dove a è un numero reale positivo diverso da 1, n un qualsiasi numero reale, che dove è necessario è diverso da 0, e x, y due numeri reali positivi):

Le precedenti proprietà mostrano come, passando ai logaritmi, si riduce la complessità di una operazione perché l’elevazione a potenza si riduce a una moltiplicazione, la moltiplicazione a un’addizione e la divisione a una sottrazione. In questo fatto risiede l’origine dei logaritmi, inventati proprio per semplificare i calcoli. Infatti, prima dell’invenzione degli odierni strumenti di calcolo automatici, dati due numeri da dividere si passava ai loro logaritmi, letti nelle apposite tavole, si sottraevano questi numeri e quindi, sempre consultando le tavole, si effettuava la conversione inversa, trovando il numero di cui quello ottenuto è il logaritmo (detto anche antilogaritmo).

Le origini dei logaritmi

I logaritmi furono introdotti all’inizio del xvii secolo quando lo scozzese Nepero pubblicò le prime Tavole dei logaritmi utilizzando come base un’approssimazione del numero e. Tali prime tavole, compilate da vere e proprie schiere di “schiavi calcolatori”, erano chiamate «Tavole delle progressioni aritmetiche e geometriche»; anche il termine, introdotto da Nepero stesso, proviene dalla fusione dei due termini greci lógos («ragione, rapporto») e arithmós (numero) e identifica il logaritmo come “il numero (cioè l’esponente) della ragione in una progressione geometrica”. In effetti, il logaritmo agisce come un “trasformatore” che fa sì che i logaritmi dei termini di una progressione geometrica formino i termini di una progressione aritmetica. La progressione geometrica si ottiene da 10 moltiplicando per 10: 10 → 10² → 10³ → 10⁴ → … Passando ai corrispondenti logaritmi decimali si ha la progressione aritmetica, che si ottiene da 1 addizionando 1: 1 → 2 → 3 → 4 → … Come arguì Eulero, cui si deve la diffusione della scelta del numero e (iniziale del suo nome) come loro base “naturale”, i logaritmi si rivelarono utili in diversi ambiti della matematica (si vedano, per tali diversi utilizzi: → disequazione logaritmica; → equazione logaritmica; → scala logaritmica; → serie logaritmica; → spirale logaritmica).

Cambiamento di base

Noto il logaritmo di un numero in una base a, è comunque possibile calcolare il logaritmo dello stesso numero in una qualsiasi altra base b tramite la formula del cambiamento di base

Caratteristica e mantissa di un logaritmo

Dato un logaritmo decimale, si dice caratteristica del logaritmo il massimo intero, eventualmente negativo, che non lo supera, mentre si dice mantissa la differenza tra il logaritmo e la sua caratteristica. La determinazione della caratteristica del logaritmo decimale di un numero reale positivo x è immediata. Se x > 1, allora la caratteristica di log(x) è data dal numero delle cifre intere di x che precedono la virgola meno uno; se invece x < 1, allora la caratteristica di log(x) è data dal numero degli zeri che precedono la prima cifra decimale non nulla (ivi incluso anche lo zero che precede la virgola) con segno negativo. Per esempio, la caratteristica di log(4763,19) è 3, mentre la caratteristica di log(0,00038) è −4. Molto meno banale è invece la determinazione della mantissa di un logaritmo decimale, per la quale esistono apposite → tavole logaritmiche. Poiché log(x ⋅ 10^k) = k + log(x), la mantissa del logaritmo decimale di un numero x gode della seguente proprietà invariantiva: essa rimane inalterata se si moltiplica o divide x per una potenza di 10, vale a dire se si sposta la virgola all’interno delle cifre che compongono la scrittura decimale di x o se si aggiungono o sopprimono degli zeri in testa o in coda a esse: i logaritmi di tali numeri differiranno tra essi solamente per la caratteristica.

La funzione logaritmica

Il logaritmo (in una qualsiasi base a > 0) definisce una funzione, detta funzione logaritmica continua, monotòna crescente e derivabile infinite volte log_a: R⁺ → R, dove R⁺ indica l’insieme dei numeri reali positivi. Per la derivata di un logaritmo vale la formula

Nel caso particolare del logaritmo naturale, si ottiene quindi

Logaritmo di un numero complesso

Logaritmo di un numero complesso z ≠ 0 è un qualsiasi numero complesso w tale che e^w = z. Poiché nel campo complesso si considera come base sempre il numero e, in questo caso la notazione log, senza indicazione della base, non è ambigua. Risulta

dove arg(z) è l’argomento di z; poiché arg(z) è una funzione polidroma, con infiniti valori che differiscono per 2π, anche il logaritmo di un numero complesso log(z) risulta essere una funzione polidroma. Se si indica con Arg(z) l’argomento principale di z, allora vale

Si chiama logaritmo principale di z, indicato con Log(z), quel logaritmo di z che ha per argomento l’argomento principale di z, vale a dire Log(z) = ln|z| + iArg(z). Va osservato che il logaritmo di un numero complesso è non definito soltanto per 0, mentre è definito per numeri reali negativi. Per esempio Log(−e) = ln|−e| + iπ = 1 + iπ. Il logaritmo principale, come funzione complessa, è una funzione discontinua; tuttavia se si restringe il dominio al piano C privato di una semiretta R con origine nel punto 0, allora essa diviene una funzione olomorfa.