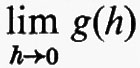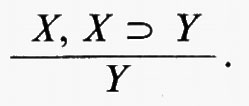Logica matematica

Logica matematica

*La voce enciclopedica Logica matematica è stata ripubblicata da Treccani Libri, arricchita e aggiornata da un’introduzione di Gabriele Lolli e un saggio di Beppo Levi.

sommario: 1. Introduzione. 2. L'evoluzione dei fondamenti della matematica. 3. Filosofia della matematica. 4. Fondamenti delle discipline matematiche. 5. Logica matematica. 6. Conclusione. □ Bibliografia.

1. Introduzione

La logica ha come oggetto le forme e le leggi del pensiero. La scoperta della grande efficacia del tipo di ragionamento matematico, unita alla considerazione che la matematica costituisce un campo naturale per l'applicazione e l'esemplificazione di argomenti logici astratti, ha fatto sì che nel sec. XX i legami tra logica e matematica si siano andati sempre rafforzando. È quindi abituale contraddistinguere la logica moderna per mezzo dell'aggettivo ‛matematica'. Cionondimeno questa disciplina è rimasta sostanzialmente quale era ai tempi di Aristotele. Non vi è motivo di tracciare una distinzione netta, come vorrebbero alcuni sostenitori della ‛logica matematica' o della ‛logica aristotelica', i primi per sottolineare la maggiore efficacia del loro indirizzo, i secondi per rivendicare la maggiore profondità del proprio.

Branca fondamentale della filosofia, la logica conserva la sua importanza ben oltre i campi della matematica e delle scienze esatte. Così il termine ‛logica filosofica', che è diventato di moda da qualche anno, si riferisce a taluni settori della logica, come la logica modale, che rivestono un particolare interesse per i filosofi. In questo articolo, comunque, fisseremo l'attenzione su quegli aspetti della logica e della matematica che mettono in evidenza l'interazione tra le due discipline.

Abbiamo diviso l'articolo in quattro parti. Dopo una breve rassegna sullo sviluppo storico della logica, nella prima parte, diamo nella seconda parte una descrizione piuttosto semplificata delle tendenze e delle correnti principali della filosofia della matematica. Sebbene i progressi contemporanei in questo campo siano stati in gran parte motivati o almeno influenzati dalla logica matematica, non si esige, a questo livello, una competenza tecnica in tale disciplina. Nella terza parte delineiamo i fondamenti dei principali settori disciplinari della matematica. Infine, nella quarta parte, descriviamo le caratteristiche più importanti dell'imponente edificio che costituisce oggigiorno la logica matematica. Tale esame risulterebbe incomprensibile se non includesse almeno qualche dettaglio di matematica formale.

2. L'evoluzione dei fondamenti della matematica

I primi passi dell'uomo nelle scienze matematiche furono motivati da problemi di carattere pratico o almeno da questioni poste dall'osservazione diretta dei fenomeni naturali. La matematica babilonese ed egiziana già comprendeva regole definite, acquisibili solo con l'aiuto del ragionamento deduttivo. Furono comunque i Greci a tentare per primi di fondare esplicitamente la matematica sul ragionamento puro. Nello sforzo di costruire su solide basi la matematica e la scienza in generale, i Pitagorici giunsero alla conclusione che tali fondamenti erano forniti dall'aritmetica, cioè dai numeri naturali. Il loro punto di vista divenne insostenibile di fronte alla scoperta delle grandezze incommensurabili, cioè, in termini moderni, dei numeri irrazionali. Per reazione a questa scoperta, i matematici greci edificarono la matematica su basi puramente geometriche. In tal modo, anche i risultati relativi alla teoria dei numeri sono presentati da Euclide in linguaggio geometrico, secondo una tradizione che sopravvive ancora oggi, quando, per esempio, parliamo del quadrato o del cubo di un numero.

Non affronteremo in questa sede il problema di determinare fino a che punto Euclide fosse influenzato da filosofi come Zenone, Aristotele o Platone, o quanto la sua teoria attingesse da Eudosso. In ogni modo, i tredici libri dei suoi Elementi mostrano che attorno al 300 a.C. i Greci avevano un'idea chiara dell'impiego del procedimento deduttivo in matematica. Il punto di partenza di Euclide era costituito da definizioni e da assiomi; questi ultimi erano suddivisi in due classi a seconda che l'autore li ritenesse di natura geometrica o puramente logica. Tali assiomi non erano considerati ipotesi arbitrarie, come gli attuali assiomi dell'algebra o della geometria, ma verità oggettive, e al tempo stesso si riteneva che le definizioni fornissero una chiara delimitazione degli oggetti da esse descritti. Ne segue che anche i teoremi erano considerati verità oggettive, ottenute dagli assiomi con un processo puramente deduttivo. Malgrado molte lacune, l'opera di Euclide e dei suoi immediati successori è espressione di un livello di chiarezza intellettuale che non venne superato per altri duemila anni, durante la maggior parte dei quali non fu neppure apprezzato. Sebbene in questo periodo la logica e la matematica non restassero ferme al punto di partenza, esse si svilupparono prevalentemente ciascuna per proprio conto. Nel sec. XVII si registra un rinnovato contatto tra la matematica e la logica o, più in generale, la filosofia. Così, per esempio, Cartesio considerava la sua opera geometrica un'applicazione dei principi generali dell'euristica che egli aveva sviluppato nella sua filosofia. E mezzo secolo più tardi Leibniz esponeva le sue idee pionieristiche nel campo della logica matematica al solo scopo, o quasi, di far progredire l'‛arte della scoperta'. Tuttavia, benché queste intuizioni - che erano già affiorate nel Medioevo - fossero importanti in linea di principio, non costituirono molto di più che una sorta di sprone psicologico per le grandi scoperte matematiche dei loro formulatori. Persino i contributi di Leibniz alla fondazione del nascente calcolo differenziale e integrale hanno soltanto una remota connessione con le sue idee sulla formalizzazione della matematica e sulla matematizzazione della logica.

Cionondimeno furono i problemi relativi al calcolo a imporre ai matematici e ai filosofi un rinnovato interesse verso i fondamenti della matematica. Per centocinquanta anni dopo Leibniz imperversò un accanito dibattito sulla corretta definizione delle nozioni fondamentali dell'analisi (o calcolo infinitesimale). A questo proposito, lo stesso Leibniz aveva suggerito l'introduzione di numeri infinitamente piccoli e infinitamente grandi, in aggiunta ai numeri reali la cui esistenza e il cui significato erano dati per scontati. Così, secondo Leibniz, la velocità di una particella avrebbe dovuto essere definita da una frazione il cui denominatore è la misura di un intervallo di tempo infinitamente piccolo e il cui numeratore è la distanza infinitamente piccola percorsa dalla particella in quell'intervallo di tempo. L'impostazione di Leibniz, malgrado l'intrinseca debolezza, nella misura in cui fu applicata tenendo conto delle sue contraddizioni interne, si dimostrò adeguata allo sviluppo dell'analisi e della geometria differenziale per oltre un secolo. Alla fine, comunque, tali contraddizioni, insieme al sorgere di problemi la cui soluzione richiedeva un apparato concettuale più sofisticato, portarono all'abbandono dell'impostazione leibniziana. Questa fu sostituita (dopo il 1850) dalla formulazione ‛ε, δ' di Weierstrass (prefigurata da Bolzano e, in qualche suo aspetto, da Cauchy), la cui caratteristica centrale è il concetto di limite, basato sul solo sistema dei numeri reali. A questo punto divenne necessario sottoporre anche questo sistema a un esame più approfondito. Si giunse così, da una parte, a un processo di riduzione in base al quale i numeri reali venivano ricondotti, in ultima istanza, ai soli numeri naturali e, dall'altra, all'indagine, effettuata da Cantor, su insiemi arbitrari di numeri reali, che costituì il punto di partenza per lo sviluppo di una teoria generale degli insiemi (infiniti). Vista superficialmente, questa ‛aritmetizzazione dell'analisi', come fu chiamata a quel tempo, sembrò segnare l'abbandono definitivo dell'impostazione geometrica di Euclide, in base alla quale ogni numero reale è rappresentato da un punto su una retta. A un livello diverso e più profondo, questo stesso sviluppo segnò comunque anche un ritorno allo standard di rigore proprio dei Greci e persino alle soluzioni da essi proposte per taluni problemi del calcolo.

Ad esempio, Euclide (o Eudosso, prima di lui) si era reso conto del fatto che il riferimento puro e semplice ai punti di una retta era inadeguato ai finì di una comprensione del sistema dei numeri reali. Conseguentemente egli basò la sua teoria delle proporzioni sul fatto che (in virtù dell'‛assioma di Archimede') i numeri irrazionali possono essere approssimati mediante numeri razionali con un grado di precisione arbitrario. La stessa concezione venne ripresa nel sec. XIX, questa volta al fine di definire i numeri reali in termini di numeri razionali.

Analogamente, sebbene i Greci non definissero le aree e i volumi per mezzo del concetto di limite, ma ne dessero semplicemente per scontata l'esistenza, Archimede impiegò un procedimento di approssimazioni successive (detto in seguito ‛metodo di esaustione') per calcolare aree e volumi in un modo non solo rigoroso, ma anche molto vicino alla formulazione ‛ε, δ' di Weierstrass.

All'inizio del sec. XIX si registrò un ulteriore sviluppo che, da una parte, polarizzò di nuovo l'attenzione sull'impostazione greca della matematica e, dall'altra, dimostrò la necessità di una sua revisione. Uno degli assiomi di Euclide è equivalente - presupponendo la validità degli altri assiomi - all'asserzione che, per una qualsiasi retta l in un dato piano p e per un qualsiasi punto Q di p che non appartenga a l, esiste una e solo una retta l′ nel piano p che passa per Q ed è parallela a l. A seguito dei molteplici tentativi che erano stati fatti per arrivare a dedurre questo assioma dai rimanenti, tre matematici (Gauss, Lobačevskij e Bolyai) svilupparono - indipendentemente l'uno dall'altro - una teoria in cui l'assioma delle parallele non è valido, mentre tutti gli altri assiomi (e postulati intuitivi) della geometria sono ancora soddisfatti. Essi pervennero alla conclusione che la nuova teoria non portava, apparentemente, ad alcuna contraddizione. Questa scoperta contribuì a creare un clima psicologico nel quale gli assiomi cessavano di essere considerati come verità assolute, sebbene indimostrabili, ma venivano piuttosto presi come proposizioni primitive di una teoria, quindi arbitrari, purché logicamente compatibili; l'arbitrarietà degli assiomi poteva essere eventualmente limitata dal contesto in cui si intendeva applicarli.

La rappresentazione di un punto mediante coordinate numeriche, che aveva per lungo tempo costituito un valido aiuto nella soluzione di problemi geometrici, veniva ora impiegata per ricondurre la coerenza della geometria alla (presunta) coerenza dell'aritmetica. Così, ad esempio, per stabilire la coerenza degli assiomi della geometria metrica tridimensionale sarebbe stato sufficiente dimostrare che essi possono essere interamente soddisfatti in una struttura i cui punti sono terne di numeri reali. Ma, mentre questa aritmetizzazione della geometria eliminava il problema della coerenza da tale disciplina, essa acuiva il bisogno di una approfondita indagine sui fondamenti dell'aritmetica e sugli strumenti logici usati nello sviluppo della matematica.

La modernizzazione della logica era stata avviata da Boole, attorno alla metà del sec. XIX, con un metodo algebrico che riecheggiava le idee già proposte da Leibniz un secolo e mezzo prima; fu proseguita durante la seconda metà del secolo da parecchi studiosi in Inghilterra, Germania, Italia e Stati Uniti. Forse chi più di ogni altro si adoperò per render saldi i fondamenti della nuova logica e, nello stesso tempo, fu in grado di applicarla al problema dei fondamenti della matematica fu G. Frege. Questa reciproca interazione - tra la matematizzazione della logica e la formalizzazione della ricerca sui fondamenti e sulla filosofia della matematica - è da allora un carattere determinante delle due discipline.

3. Filosofia della matematica

Daremo ora un quadro delle tendenze più importanti nella odierna filosofia della matematica. E interessante notare che, nonostante le origini remote e alcuni successivi sviluppi ed elaborazioni considerevoli, le varie impostazioni si manifestarono in tutta la loro compiutezza in un periodo relativamente breve, durante i primi venticinque anni del nostro secolo.

Per il ‛logicismo' la matematica è una branca della logica. Da questo punto di vista, la distinzione tra matematica e logica (data per scontata nel presente scritto) ha solo un significato pragmatico. Tutti i concetti matematici sono riducibili a relazioni o a insiemi e questi, a loro volta, sono solo astrazioni di concetti logici. La nozione di ‛insieme', per esempio, si ottiene per astrazione dalla nozione di ‛proprietà'. Una grave difficoltà per quest'impostazione fu scoperta da B. Russell, che peraltro deve essere ricordato come uno dei principali sostenitori del logicismo: si tratta del ‛paradosso (o antinomia) di Russell', che sorge qualora si ammetta il principio di astrazione (o comprensione) senza alcuna restrizione.

Consideriamo, per esempio, la totalità di tutti gli insiemi; sia a uno di essi. Si ha che a appartiene ad a, in simboli a∉a, oppure a non appartiene ad a, a ∉a. La prima alternativa può apparire al lettore come la più verosimile, ma, in ogni modo, egli concorderà sul fatto che deve valere una delle due possibilità. Ora, se A è l'insieme i cui elementi sono caratterizzati dalla proprietà di non appartenere a se stessi, sorge il problema di stabilire se A appartenga o no a se stesso.

Se A∈A, allora A non soddisfa la proprietà che definisce A, quindi A non può appartenere ad A, cioè A∈A. Ma se così è, A soddisfa la proprietà che definisce A e quindi A∈A. Entrambe le affermazioni conducono dunque a una contraddizione, in opposizione al ‛principio del terzo escluso', la cui validità viene di solito ammessa.

Il paradosso di Russell assestò un duro colpo alle convinzioni di Frege, che può essere considerato il fondatore del logicismo. Lo stesso Russell, comunque, giunse alla conclusione che la difficoltà non stava nelle caratteristiche di fondo dell'impostazione logicistica, bensì nell'ammissione senza restrizioni di qualsiasi formulazione che sembrasse non obiettabile dal punto di vista grammaticale. Conseguentemente, egli pose una limitazione alla definibilità di nuovi insiemi con la condizione che non si potesse definire un insieme a partire da elementi introdotti in termini dell'insieme da definire. Al fine di rispettare questa condizione (detta ‛principio del circolo vizioso'), Russell e Whitehead, nella grande opera comune Principia mathematica, introdussero un sistema matematico organizzato in successivi livelli stratificati o ‛tipi'. In effetti, in questo sistema, il paradosso di Russell non può presentarsi.

In ogni caso, la difficoltà sollevata da questa antinomia si presenta non solo nel logicismo, ma anche in qualsiasi sistema logico che non ammetta qualche restrizione del tipo indicato. Il paradosso di Russell è solo un membro di una numerosa famiglia, alcuni componenti della quale risalgono all'antichità. Queste antinomie possono essere classificate a seconda che la loro natura sia linguistica o matematica. Una copiosa letteratura è a esse dedicata. Esistono altre difficoltà che investono il logicismo in modo peculiare. La più importante fra di esse è forse quella relativa al problema dell'esistenza di insiemi infiniti. L'esistenza ditali insiemi è una caratteristica essenziale della matematica così come la conosciamo, eppure essa non può essere dedotta dai principi generali della logica. In ogni modo, Russell e Whitehead ammisero l'esistenza di insiemi infiniti postulandoli assiomaticamente. La matematica dei Principia mathematica è matematica ‛classica' e il lavoro di Russell e Whitehead tendeva semplicemente a poggiare tale disciplina su fondamenti stabili e sicuri senza alcuna intenzione di sottoporla a una revisione critica. Pertanto essi accettarono anche l'assioma della scelta, sebbene la sua necessità nella logica pura sia discutibile. Inoltre, per quanto il logicismo come filosofia sia apparentemente neutrale rispetto al problema del significato dell‛esistenza matematica', cioè della realtà degli oggetti matematici, gli scritti dei logicisti, compresi Russell e Whitehead, rivelano di solito una tendenza platonica o, in altre parole, la credenza nella realtà (in un certo senso) di quel mondo che il sistema logico-matematico intende descrivere.

Un punto di vista più rivoluzionario a proposito della matematica nel suo complesso fu adottato dalle varie scuole del costruttivismo, tra le quali quella di maggior rilievo è l'intuizionismo (detto anche neointuizionismo). È possibile trovare una motivazione psicologica per la comparsa del costruttivismo nel crescente grado di astrazione che aveva assunto la matematica nel corso del suo sviluppo nel sec. XIX e, in effetti, anche nel suo sviluppo successivo. Il grado d'astrazione che sembra accettabile a un matematico dipende dalle sue convinzioni soggettive e, tra l'altro, dalla sua prima educazione. Cionondimeno la nuova interpretazione dei metodo assiomatico, dianzi descritta, assieme alla comparsa della teoria degli insiemi di Cantor, produsse un forte spostamento dal concreto all'astratto. Una reazione contro questo tipo di sviluppo non tardò molto a manifestarsi e il primo a capeggiarla fu il grande algebrista L. Kronecker. A più riprese, Kronecker ribadì il punto di vista che per dimostrare l'esistenza di un oggetto matematico con una data proprietà non è sufficiente dimostrare l'asserzione: ‛esiste un oggetto A con la proprietà X', in modo puramente formale mediante l'impiego di principi logici generali. Secondo Kronecker, una dimostrazione effettiva di una simile asserzione deve anche fornire un metodo mediante il quale tale oggetto possa essere effettivamente costruito un passo dopo l'altro. Analogamente, ogni volta che venga introdotta una proprietà per caratterizzare alcuni oggetti in una collezione (per esempio, la proprietà di un polinomio di essere irriducibile), è necessario fornire anche un metodo concreto mediante il quale si possa decidere se un dato membro della collezione possieda o no la proprietà in questione. Il solo sistema infinito accettato da Kronecker come primitivo è il sistema dei numeri naturali (interi positivi).

Kronecker non si limitò a elaborare teorie; le mise anche in pratica. Così è a lui che dobbiamo parecchi metodi costruttivi di valore duraturo. Assai meno encomiabile fu la sua opposizione feroce all'opera di G. Cantor sulla teoria degli insiemi, che egli riteneva tanto astratta da essere priva di senso.

All'inizio del sec. XX, L. E. J. Brouwer divenne l'esponente guida di un'impostazione costruttivista della matematica. Brouwer si spinse molto più in là di Kronecker: egli sviluppò un sistema elaborato, partendo da una piattaforma filosofica generale e giungendo fino a una nuova teoria del continuo. Secondo Brouwer il punto di partenza della matematica è il carattere a priori (sintetico) del tempo.

Il ‟suddividersi degli eventi in parti qualitativamente distinte che possono riunirsi solo restando separate nel tempo" viene considerato da Brouwer come quel fenomeno fondamentale dell'intelletto umano che conduce al contare e quindi al sistema dei numeri naturali. Per questa sua filosofia, Brouwer adottò il nome di neointuizionismo, proprio perché essa si basava sull'intuizione del tempo, considerato sì come un concetto sintetico, ma a priori, in senso kantiano, mentre rifiutò esplicitamente una posizione analoga riguardo all'intuizione dello spazio. Per quanto riguarda la logica, egli la considerò un'astrazione del pensiero matematico, invertendo in tal modo l'ordine di priorità stabilito dai logicisti, e ridimensionò il valore della formalizzazione totale delle regole di deduzione matematica. Secondo l'intuizionismo, non vi è posto nel pensiero matematico per totalità infinite complete, che possono formarsi soltanto mediante una serie di passi successivi. Inoltre, la legge del terzo escluso (tertium non datur) cessa di avere una validità universale. Consideriamo infatti una affermazione matematica X, per esempio la seguente: ‛esiste un numero naturale che possiede la proprietà P'. Un matematico ‛classico' darebbe per scontato che o X o non-X deve essere un'affermazione vera dell'aritmetica. Pertanto egli si riterrebbe autorizzato a provare X mostrando che l'ipotesi non-X conduce a una contraddizione. Per un intuizionista questo è inammissibile, poiché dal suo punto di vista l'affermazione X significa che esiste un procedimento costruttivo per determinare un numero naturale con la proprietà P, e ciò non è affatto la stessa cosa che dimostrare l'assurdità di non-X.

Il contributo più rilevante di Brouwer ai fondamenti della matematica è la sua teoria delle funzioni di variabile reale, basata su una nuova teoria del continuo dei numeri reali. In accordo con la sua impostazione generale, questi numeri dovrebbero essere considerati non una totalità completa, ma una collezione (specie) di oggetti matematici che emerge gradualmente: tra questi vi sono, in primo luogo, numeri che possono essere calcolati mediante una regola esplicita, come ad esempio la radice quadrata di 2. Tuttavia Brouwer ammette, anche, la possibilità di prendere in considerazione quei numeri reali che siano ottenuti mediante una successione di scelte arbitrarie e, in tal modo, siano essi stessi emergenti gradualmente. Come conseguenza di questo graduale processo di creazione, Brouwer deve distinguere tra due tipi di disuguaglianza fra numeri reali: un tipo ‛forte' di disuguaglianza, per cui, assegnati due numeri, risulta possibile dimostrare (in base alle leggi di generazione dei numeri stessi) che la loro differenza è maggiore di un numero razionale positivo, e un tipo ‛debole' di disuguaglianza, che asserisce soltanto come la presupposta uguaglianza tra i numeri in questione conduca a una contraddizione. La teoria delle funzioni che così si ottiene non è semplicemente una versione più debole della teoria classica, come si potrebbe ritenere in base ai vincoli autoimposti dall'intuizionismo, ma contiene anche dei risultati, come l'asserzione che una funzione reale ovunque definita è necessariamente continua, che sono in contraddizione diretta con la matematica classica.

Malgrado l'avversione di Brouwer per la formalizzazione della matematica, esiste un'estesa letteratura, in continuo aumento, in cui le idee di Brouwer sono analizzate ed elaborate in un modo molto raffinato mediante gli strumenti della logica matematica. Sono state sviluppate anche impostazioni diverse da quella di Brouwer da parte di matematici che si sono andati convincendo della sostanziale correttezza del punto di vista costruttivista. Essi ritengono che solo una revisione radicale della matematica secondo le loro idee può salvaguardarla dal degenerare in una ricerca illusoria e velleitaria (v. intuizionismo).

Anche se non si condivide questa opinione, bisogna ammettere che parte del lavoro eseguito con queste motivazioni ha contribuito a convertire teorie matematiche astratte in metodi concreti di calcolo. Inoltre, la nozione stessa di calcolabilità ha dato luogo a un'intera branca della logica matematica moderna che, sebbene formulata all'interno dell'apparato concettuale della matematica classica, deve molto allo spirito del costruttivismo.

D'altra parte, anche se si condivide lo spirito dell'impostazione costruttivista e, in particolare, l'impressione che la matematica moderna sia eccessivamente spregiudicata nell'uso di principi logici e matematici astratti, risulta difficile decidere quali siano esattamente i principi che vanno mantenuti all'interno di un'impostazione correttamente costruttivista. Certamente l'intuizionismo di Brouwer e, in particolare, la sua teoria delle funzioni vanno ben oltre un punto di vista puramente finitista, in cui sono ritenute ammissibili solo proposizioni e argomentazioni relative a oggetti finiti (insiemi finiti, relazioni o funzioni su insiemi finiti, ecc.) o, al più, proposizioni e argomentazioni immediatamente riducibili alle precedenti.

All'altra estremità del campo del costruttivismo, su posizioni diverse da quelle degli intuizionisti, vi sono i predicativisti, i quali non si oppongono in linea di principio alle costruzioni infinitarie, e anche alle totalità infinite, purché esse siano concepite attraverso una serie di passi successivi. Un predicativista, per esempio, può sostenere che non esiste un sistema uniforme di numeri reali, ma una successione di lunghezze rappresentate da numeri razionali, limiti di successioni di numeri razionali e così via. Al centro dell'attenzione dei predicativisti è l'esigenza di evitare le definizioni circolari, non solo per non incorrere in antinomie, come nel caso di Russell, ma perché tali definizioni sono considerate inammissibili in un sistema concettuale dotato di senso. Un precursore del predicativismo fu il grande matematico H. Poincaré. Poincaré partecipò attivamente alle discussioni filosofiche sui fondamenti della matematica che ebbero luogo all'inizio del secolo e, come Kronecker, mostrò una profonda perplessità nei confronti del crescente grado di astrazione della matematica. I suoi contributi in questo campo furono molto discontinui dal punto di vista qualitativo, talvolta profondi e talvolta superficiali (benché brillanti), come del resto avvenne per le sue critiche alla logica matematica.

Un contributo di gran lunga più importante ai fondamenti filosofici della matematica fu dato da D. Hilbert, unico tra i contemporanei di Poincaré a essere un matematico di pari valore. Hilbert era ben consapevole del fatto che l'ammissione incontrollata di principi logici e assiomi matematici astratti avrebbe potuto condurre a disastrose contraddizioni. D'altra parte egli non era disposto a rinunciare a vaste aree della matematica, in particolare alla teoria astratta degli insiemi, al solo fine di evitare questo pericolo. Egli propose, quindi, di dividere tutto il pensiero logico-matematico in due stadi. Nel primo stadio incluse una trattazione del tutto concreta (intuitiva, anschaulich) degli elementi della logica e dell'aritmetica. La coerenza delle conclusioni ottenute in questo contesto doveva essere garantita dalla loro stessa concretezza. Il secondo stadio doveva contenere, su base assiomatica, le teorie matematiche comunemente accettate, quali l'aritmetica pura, la teoria degli insiemi astratti, la geometria. Secondo Hilbert il problema principale non consisteva nello stabilire se queste teorie fossero astratte o concrete o se avessero un qualsivoglia significato letterale - nello stesso senso in cui può avere un significato la descrizione, diciamo, del contenuto di una borsa -, ma il requisito fondamentale che una teoria doveva soddisfare era piuttosto quello di essere coerente (priva di contraddizioni).

Hilbert ritenne che la coerenza delle teorie matematiche accettate, e in primo luogo dell'aritmetica (cioè la teoria dei numeri naturali), avrebbe potuto e dovuto essere stabilita mantenendo la discussione nel sicuro contesto finitista del primo stadio. Egli sottolineò inoltre l'importanza di scegliere gli assiomi di una teoria matematica in modo che siano mutuamente indipendenti, vale a dire in modo che nessun assioma della teoria sia deducibile dagli altri. Infine Hilbert richiamò l'attenzione sull'esigenza di escogitare procedimenti, soprattutto per l'aritmetica, che forniscano un metodo sistematico per decidere se un'asserzione sia vera o falsa, oppure deducibile o no nell'ambito di una data teoria.

I tre punti elencati costituiscono il ‛programma di Hilbert'. Di essi solo il secondo, relativo all'indipendenza degli assiomi, è stato sistemato in modo soddisfacente. In effetti, ancor prima di volgere la sua attenzione ai fondamenti della matematica in generale, Hilbert aveva scritto un testo, ormai classico, sui fondamenti della geometria, in cui erano prese in considerazione e risolte varie questioni di questo genere. I corrispondenti problemi della teoria assiomatica degli insiemi si dimostrarono più difficili da trattare, ma oggi anch'essi sono stati risolti.

Per quanto riguarda la scoperta di procedimenti di decisione, dobbiamo distinguere, in generale, tra una situazione in cui siamo chiamati a decidere effettivamente (ad esempio mediante un programma di un calcolatore elettronico) se un dato teorema è deducibile da un insieme di assiomi specificato e il caso in cui ci si chieda di decidere se una asserzione è vera in una determinata struttura, per esempio in quella dei numeri naturali. Hilbert diede per scontato che fosse sempre possibile descrivere una data struttura mediante un sistema di assiomi, dal quale potessero essere derivate tutte le sue proprietà. In ogni caso, grazie all'opera rivoluzionaria di K. Gödel (1931), completata in alcuni aspetti importanti da A. Church e A. Tarski, oggi sappiamo che: 1) non esiste un procedimento effettivo per decidere se un'affermazione sia o no vera per il sistema dei numeri naturali; 2) non esiste un procedimento effettivo per decidere se un'asserzione relativa all'aritmetica sia o no deducibile dagli assiomi di Peano per l'aritmetica (si veda il prossimo capitolo); 3) non tutti i teoremi dell'aritmetica possono essere o dimostrati o confutati per mezzo degli assiomi di Peano; 4) non è possibile individuare un sistema di assiomi dal quale possano essere dedotte tutte le asserzioni vere dell'aritmetica.

Dovremmo dire a questo punto che, d'altro canto, esistono effettivamente procedimenti di decisione per teorie e strutture matematiche importanti, quali le teorie elementari dei numeri reali e dei gruppi commutativi. Tuttavia, considerando la posizione fondamentale occupata dall'aritmetica nello schema di Hilbert e, in generale, nella matematica, i risultati sopra menzionati assestarono un duro colpo al suo programma. Ancor più cruciale fu la scoperta, dovuta anch'essa a Gödel, del fatto che è dimostrabile l'impossibilità di stabilire la coerenza dell'aritmetica nell'ambito dell'universo finitista ammesso da Hilbert per questo scopo. Ciò dimostrava che anche il primo punto del programma di Hilbert non avrebbe potuto essere realizzato in modo soddisfacente.

Gran parte dell'opposizione al punto di vista di Hilbert non ha alcuna relazione con l'opera di Gödel e di fatto la precedette. Essa prese di mira piuttosto la tesi di Hilbert secondo la quale la matematica infinitista non ha a rigore alcun contenuto concreto, cioè non descrive alcuna realtà, fisica o platonica che sia. Pertanto Hilbert fu accusato di degradare la matematica riducendola a un gioco eseguito con serie di simboli prive di senso. Perfino al giorno d'oggi si trovano autori che tentano di combattere questo punto di vista più con sarcastico sdegno che con argomenti razionali. A questo proposito si dovrebbe ricordare che sia Hilbert sia coloro che condividono il suo punto di vista non cercano affatto di legiferare, ma semplicemente di descrivere la situazione come essi la vedono. Chiunque creda nella realtà obiettiva (benché platonica) delle meravigliose infinità evocate dalla matematica moderna dovrebbe ricordare le parole di un grande filosofo il quale osservò, riferendosi alle più famose questioni metafisiche, che l'idea di avere in tasca un tallero d'argento non significa avercelo realmente.

Nonostante il definitivo fallimento della parte tecnica del programma di Hilbert in alcuni dei suoi aspetti principali, la sua opera ebbe una grande influenza sullo sviluppo successivo della logica matematica. Il sistema deduttivo elaborato da lui e dai suoi seguaci è ancora largamente adoperato e gli strumenti teorici messi a punto, sia per raggiungere certi scopi, sia per mostrare che certi altri sono irraggiungibili, occupano una buona parte dell'arsenale del logico moderno.

Il problema dell'infinito è forse tuttora il problema centrale della filosofia della matematica, sebbene agli occhi di alcuni filosofi esso appaia ormai immerso in una problematica più generale. Per un nominalista, ad esempio, lo stesso concetto di insieme è privo di senso o, tutt'al più, è soltanto un'espressione linguistica, per cui un insieme finito non possiede un maggior grado di realtà di un insieme infinito. Per un positivista logico l'intera matematica è parte del linguaggio e il problema stesso dell'esistenza di entità infinite è privo di senso. In ogni caso questo è un problema che ha appassionato in egual misura filosofi e matematici fin dagli albori della scienza. La matematica moderna ha ricondotto la nozione geometrica di infinità alle infinità più astratte dell'aritmetica e della teoria degli insiemi. Potremmo, quindi, congetturare che le future generazioni di matematici trasformeranno ancora una volta i fondamenti della matematica e affronteranno il problema dell'infinito in una forma ancora sconosciuta.

4. Fondamenti delle discipline matematiche

La teoria degli insiemi considera le proprietà astratte di insiemi (aggregati, collezioni). Come già detto, questa disciplina fu fondata e sviluppata da O. Cantor (dopo il 1870). Da allora essa è divenuta uno dei campi fondamentali della matematica e tutta, o quasi tutta, la matematica può essere ricondotta a essa, almeno dal punto di vista tecnico. Cantor ritenne di poter sviluppare la teoria degli insiemi a partire da una base intuitiva, considerando come insieme una qualsiasi collezione di oggetti che potessero essere caratterizzati in un modo definito. E. Zermelo (1904), per dimostrare un'importante congettura di Cantor, si rese conto della necessità di introdurre un'ipotesi ad hoc che, sebbene apparentemente ragionevole, non poteva essere considerata vera per se stessa. L'ipotesi, nota come ‛assioma della scelta', stabilisce che, per ogni insieme S di insiemi non vuoti, esiste una funzione f(x) definita su tutti gli elementi di S e tale che, per ogni elemento a di S (in simboli: a∈S), f(a) appartiene ad a, f(a)∈a. Cioè, in breve, si suppone che f(x) assegni a ogni insieme in S un elemento di quell'insieme. Utilizzando questo assioma Zermelo fu in grado di dimostrare il ‛teorema del buon ordinamento', che stabilisce che ogni insieme A (per esempio l'insieme dei numeri reali) può essere totalmente ordinato in modo tale che ogni sottoinsieme non vuoto di A abbia un primo elemento rispetto alla relazione d'ordine. In quel periodo Zermelo si servì dell'assioma della scelta in concomitanza con altre ipotesi naturali sugli insiemi non esplicitate. Pochi anni più tardi egli formulò un sistema di assiomi più ampio che, in aggiunta all'assioma della scelta, conteneva altri assiomi, il cui scopo era quello di assicurare l'esistenza di insiemi infiniti e di insiemi costruiti in modo naturale a partire da insiemi dati, come ad esempio l'insieme dei sottoinsiemi di un insieme dato, oppure l'insieme di tutti gli elementi di un insieme dato che sono caratterizzati da una proprietà chiaramente formulata (‛definita').

Il sistema di Zermelo fu integrato in alcuni aspetti importanti da A. Fraenkel e il sistema che ne risultò è largamente usato ancora oggi. Sebbene, come abbiamo visto in precedenza, gli assiomi della geometria siano, fin dall'inizio del sec. XX, decaduti dal rango di verità assolute, molte discussioni riguardanti gli assiomi della teoria degli insiemi concernono ancor oggi il problema della loro verità (presumibilmente assoluta). Indipendentemente dall'atteggiamento personale verso tale questione, si vuol sapere a buon diritto se un dato assioma della teoria degli insiemi sia indipendente o no dai rimanenti in un dato sistema, ad esempio il sistema di Zermelo-Fraenkel. Fraenkel stesso dimostrò (1922) che, in tale sistema, l'assioma della scelta non può essere dedotto dagli altri assiomi, mentre Gödel provò alcuni anni più tardi (1938) che esso non può neppure essere rifiutato in base a questi assiomi, cioè che in ogni caso l'aggiunta dell'assioma della scelta non rende il sistema inconsistente (ammesso che esso sia inizialmente coerente).

Vi è un altro problema basilare della teoria degli insiemi che è indipendente sia dal sistema di Zermelo-Fraenkel, che include l'assioma della scelta, sia da ogni altro analogo sistema di assiomi. Questo problema riguarda la nozione di ‛cardinalità', che ci accingiamo a illustrare. Al fine di generalizzare la nozione di cardinalità da insiemi finiti a insiemi infiniti, Cantor attribuisce a due insiemi lo stesso numero cardinale se i loro elementi possono essere posti in corrispondenza biunivoca. In tali condizioni, due insiemi si dicono equivalenti (o equipotenti). È perfettamente possibile che un insieme infinito A sia equivalente a un insieme B e contemporaneamente anche a un sottoinsieme proprio di B (mentre ciò è impossibile nel caso di insiemi finiti). Tuttavia, se un insieme A è equivalente a un sottoinsieme proprio di B, ma non allo stesso B, si dice che il numero cardinale di A è minore del numero cardinale di B. Ne risulta un ordinamento dei numeri cardinali che estende il sistema dei numeri cardinali finiti, cioè dei numeri naturali. Il più piccolo numero cardinale infinito è proprio il numero cardinale dell'insieme dei numeri naturali. Esso è denotato dal simbolo ℵ₀, dove il segno ℵ - che si legge ‛alef' - è la prima lettera dell'alfabeto ebraico. ℵ₀ è anche il numero cardinale ℵ dell'insieme dei numeri razionali e anche dell'insieme di tutti i numeri algebrici, ma Cantor mostrò che ℵ₀è minore del numero cardinale א dell'insieme dei numeri reali. Ci si chiese a questo punto se esistesse un numero cardinale compreso fra ℵ₀ e ℵ. L'opinione di Cantor era che un tale numero cardinale non potesse esistere (‛ipotesi del continuo'). Nello stesso lavoro in cui trattò della coerenza dell'assioma della scelta, Gödel dimostrò anche che l'ipotesi del continuo è compatibile almeno con gli assiomi della teoria degli insiemi. In realtà egli adoperò un sistema di assiomi differente da quello di Zermelo-Fraenkel, ma le sue argomentazioni possono essere adattate anche a quest'ultimo. Infine, nel 1963, P. J. Cohen, usando i metodi di Gödel assieme ad alcune idee radicalmente nuove, dimostrò che è impossibile dedurre l'ipotesi del continuo dagli assiomi di Zermelo-Fraenkel. Ciò lasciò a chiunque creda nella realtà (platonica) del mondo degli insiemi il compito di trovare per la teoria degli insiemi un nuovo assioma che sia abbastanza evidente da essere accettato universalmente, o quasi, e tale che in questo sistema sia possibile decidere sulla legittimità o meno dell'inclusione dell'ipotesi del continuo. La ricerca di un tale assioma è tuttora in corso.

Vi è un altro gruppo di assiomi della teoria degli insiemi che può essere o no incluso in un sistema dato. Questi assiomi riguardano l'esistenza di insiemi il cui numero cardinale sia molto grande. Può essere dimostrato all'interno del sistema di Zermelo-Fraenkel (o di qualsiasi altro sistema assiomatico ‛ragionevole' per la teoria degli insiemi) che per ogni insieme S esiste un insieme S′ il cui numero cardinale è maggiore del numero cardinale di S. In particolare si può dimostrare che S′ è l'insieme dei sottoinsiemi di S. Tuttavia gli assiomi addizionali ai quali ci riferiamo postulano l'esistenza di insiemi la cui cardinalità è maggiore di qualsiasi cardinalità che sia possibile ottenere all'interno del sistema di Zermelo-Fraenkel. Sorprendentemente l'esistenza ditali insiemi condiziona anche le proprietà di insiemi infiniti relativamente ‛piccoli'.

Nel sistema in discussione la sola relazione fondamentale è la relazione di appartenenza, x∈y (si legga ‛x è un elemento di y'). A partire da questa si può dedurre la nozione di identità definendo x=y se, per ogni z, z∈x se, e solo se, z∈y, in altre parole se x e y hanno esattamente gli stessi elementi (carattere di ‛estensione' della nozione di insieme). Uno degli assiomi stabilisce poi che, se x=y, x e y appartengono esattamente agli stessi insiemi. Viceversa, possiamo assumere quest'ultima proprietà come definizione di identità (principio di Leibniz) e quindi sostituire la definizione precedente con un assioma corrispondente. L'insieme che contiene come unico elemento a è denotato con {a} ed è chiamato il singleton di a, l'insieme che contiene come elementi a e b è denotato con {a, b}. Un opportuno assioma ci assicura che questi insiemi esistono. Nella teoria degli insiemi si definisce ‛coppia ordinata' (a, b) l'insieme {{a}, {a, b}} e la definizione è analoga per le nozioni di terna ordinata, quaterna ordinata, ..., n-upla ordinata (a₁, a₂, ..., a_n). Una ‛relazione', infine, è definita come un insieme di n-uple e una ‛funzione' come una relazione R(x₁, ..., x_n, y) in cui, per ogni data n-upla x₁, ..., x_n, esiste al più un y che soddisfa la relazione. Un'‛operazione' in algebra o in aritmetica non è altro che una funzione. In questo modo, sulla base delle definizioni precedenti - che sono piuttosto tecniche e anche un po' artificiose -, ogni teoria matematica nota può essere espressa nell'ambito della teoria degli insiemi. Per questa ragione, e anche perché i problemi a essa relativi interessano direttamente molti altri rami della matematica, la teoria degli insiemi è giunta a essere considerata da molti come l'oggetto fondamentale della matematica pura, prendendo il posto che la geometria aveva occupato sotto l'egida di Euclide e persino il posto dell'aritmetica. Resta da vedere se questa situazione sia definitiva.

Come indica il suo nome, l'‛algebra' medievale era la scienza delle operazioni aritmetiche. In seguito si occupò principalmente della soluzione delle equazioni polinomiali. Da circa mezzo secolo tratta, più in generale, della struttura dei modelli (realizzazioni) di taluni insiemi di assiomi che si riferiscono (prevalentemente) a un certo numero di operazioni, quali l'‛addizione', la ‛moltiplicazione', l'‛intersezione', l'‛unione' e persino, per taluni suoi aspetti, la ‛differenziazione'. Sembra difficile determinare a priori quale tipo di sistema di assiomi debba essere considerato come algebrico e potremo solo elencare alcuni sistemi algebrici tra i più importanti.

1. Si chiama ‛gruppo' una struttura G che si basa su una singola operazione binaria, ab=c, detta moltiplicazione o, talvolta, addizione. L'operazione è associativa, cioè si ha (ab)c=a(bc) per tutti gli a, b, c in G. Esiste un elemento neutro o ‛identità', e, tale che ae=ea=a per tutti gli a in G. Inoltre, per ogni a in G, esiste un a′ in G tale che aa′=a′a=e. Il gruppo si chiama ‛commutativo' se ab=ba per tutti gli a e b in G. Esempi di gruppi commutativi sono forniti dagli interi, rispetto all'addizione, e dai numeri reali positivi, rispetto alla moltiplicazione. Un gruppo non commutativo è il gruppo delle rotazioni nello spazio, dove il ‛prodotto' di due rotazioni si ottiene eseguendole l'una dopo l'altra.

2. Si chiama ‛anello' R una struttura in cui sono definite due operazioni, addizione e moltiplicazione. R è un gruppo commutativo rispetto all'addizione, mentre la moltiplicazione è associativa e soddisfa le leggi distributive, a(b+c)=ab+ac e (b+c) a=ba+ca per tutti gli a, b e c in R. In un anello l'identità rispetto all'addizione è denotata con 0, come avviene per gli interi, che costituiscono un esempio di anello. Si dice che R possiede l'elemento unità 1, se a1=1a=a per tutti gli a in R. Non vi può essere più di un elemento di questo tipo.

3. Si chiama ‛corpo' F un anello con elemento unità 1, differente da 0, con moltiplicazione commutativa (ab=ba per tutti gli a e b in F) e tale che per ogni a≠0 vi è un a′ per cui aa′=1. In un corpo tutti gli elementi diversi da 0 costituiscono un gruppo rispetto alla moltiplicazione. I numeri razionali costituiscono l'esempio di un corpo.

4. Si chiama ‛corpo ordinato' un corpo in cui sia definito un ordinamento lineare (totale), a>b, tale che, per tutti gli a, b e c nel corpo, dalla condizione a>b segua che a+c>b+c e dalle due condizioni a>b e 0>c segua ac>bc. Un corpo ordinato è ‛archimedeo' se soddisfa il seguente ‛assioma di (Eudosso)-Archimede': sia 0>a>b; allora è sempre possibile ottenere un numero maggiore di b addizionando a a se stesso per un numero sufficiente di volte, cioè a+a+a+...+a⟨b.

I numeri reali costituiscono un corpo ordinato archimedeo, ma i numeri complessi, sebbene formino un corpo, non possono essere ordinati.

5. Si chiama ‛algebra booleana' una struttura B con due operazioni binarie, a⋃b e a⋂b, una operazione unaria, a′, detta complementazione, e due elementi distinti, 0 e 1, che soddisfano le seguenti condizioni: le operazioni ⋃ e ⋂ soddisfano la legge commutativa e la legge associativa. Esse sono collegate fra loro dalle leggi distributive a destra e a sinistra, e cioè per ogni a, b, e c in B risulta (a⋃b)⋂c = (a⋂c)⋃(b⋂c) e (a⋂b)⋃c = (a⋃c)⋂(b⋃c). Inoltre, per qualsiasi elemento a di B, risulta a⋃0=a, a⋂1=a, a⋃a′=1, a⋂a′=0.

Un esempio tipico di algebra booleana è l'insieme di tutti i sottoinsiemi di un dato insieme V, dove i simboli ⋃ e ⋂ denotano, rispettivamente, l'unione e l'intersezione di due insiemi. In questo sistema 1 e 0 indicano l'intero insieme V e l'insieme vuoto, rispettivamente. L'apice ′ denota la complementazione all'interno di V, cioè se a è un sottoinsieme di V, e quindi un elemento dell'algebra booleana, a′ è composto da tutti gli elementi di V che non appartengono ad a.

La ‛teoria dei numeri' o ‛aritmetica' si occupa delle proprietà del sistema dei numeri naturali, 0, 1, 2 .... Questo sistema può essere ricondotto direttamente alla teoria degli insiemi considerando i numeri naturali come numeri cardinali finiti, ove la nozione di finitezza è a sua volta definita puramente in termini di teoria degli insiemi. Tuttavia, anche se si accetta questa riduzione definitiva, l'aritmetica viene abitualmente fondata su di un sistema di assiomi dovuto a Peano, o su una sua variante. Il più interessante tra questi assiomi è ‛l'assioma di induzione (completa)', che afferma quanto segue: supponiamo che il numero 0 possieda una proprietà P e che ogni volta che P sia posseduta da un numero naturale n allora sia posseduta anche da n + 1. Allora tutti i numeri naturali possiedono la proprietà P.

Un'asserzione equivalente è che una proprietà Q non può essere posseduta da alcun numero naturale se, ogni volta che è posseduta da un numero naturale n, è posseduta anche da un numero naturale più piccolo di n. È questo il ‛principio della discesa infinita' che fu reso famoso da Fermat, ma che era già usato da Euclide. Euclide non lo formulò comunque in veste di assioma.

L'‛analisi' si basa su una gerarchia dei sistemi numerici, cioè i numeri naturali, sopra considerati, gli interi, i numeri razionali, i numeri reali e i numeri complessi. Mostreremo come, preso come dato di partenza il sistema dei numeri naturali, i sistemi rimanenti possono essere introdotti mediante definizioni.

Gli ‛interi' sono definiti come coppie ordinate di numeri naturali, α=(a, a′), β=(b, b′), ecc., dove α e β sono considerati eguali se a+b′=b+a′. La somma e il prodotto di interi sono definiti, in termini di addizione e moltiplicazione di numeri naturali, dalla α+β=(a+b, a′+b′), α•β=(ab+a′b′, a′b+ab′). Entro il sistema degli interi un numero naturale è identificato con (a, 0), mentre il numero che in notazione più familiare sarebbe stato scritto con −a è dato da (0, a). Scopo dell'introduzione degli interi negativi è di poter eseguire la sottrazione senza eccezioni.

Per essere in grado di dividere senza eccezioni, a parte la condizione che il divisore sia diverso da 0, si passa dagli interi ai ‛numeri razionali'. La rappresentazione di un numero razionale come coppia di interi α/β, dove β≠0, è ben nota e possiamo risparmiare al lettore i relativi dettagli.

Il passo successivo è costituito dal passaggio dai numeri razionali ai numeri reali; come già abbiamo accennato nella nostra breve rassegna storica, esso fu reso necessario dall'esistenza di lunghezze incommensurabili in geometria. Vi sono parecchi metodi (equivalenti) per introdurre i numeri reali, tutti concettualmente molto più profondi di quelli impiegati per introdurre gli interi e i razionali mediante coppie; ci contenteremo di una rapida descrizione di uno di essi. Esso fu proposto indipendentemente da G. Cantor e da C. Meray circa un secolo fa. Per capirlo meglio, consideriamo un numero reale come un punto di una retta sulla quale siano stati fissati i punti 0 e 1, secondo la nozione intuitiva comune in analisi fino a quell'epoca. Se {a_n} è una successione di numeri razionali, {a_n} può tendere a un limite razionale; per esempio la successione {0, 1/2, 2/3, 3/4, ..., (n−1)/n, ...} tende a 1. Oppure {a_n} può non tendere affatto a un limite, come ad esempio avviene se a_n=(−1)ⁿ, n=0, 1, 2, ... . Ma {a_n} può anche tendere a un limite che, tuttavia, è irrazionale, per esempio nel caso in cui a₀=1, a₁=1,4=14/10, a₂=1,41=141/100, a₃=1,414=1414/1000, ecc. Per di più, qualsiasi numero reale può essere ottenuto in questo modo come limite di una successione di numeri razionali. Cauchy, qualche tempo prima, aveva formulato la condizione necessaria e sufficiente perché una successione {a_n} tenda a un limite. Questa condizione è che la differenza a_n−a_m tenda a zero. Essa non implica la conoscenza del limite stesso. Conseguentemente Cantor e Meray decisero di definire un numero reale α come una successione di numeri razionali α={a₀, a₁, a₂, ...} che soddisfi la condizione di Cauchy. Si dice che α è uguale a un'altra successione di numeri razionali di questo tipo, β={b₀, b₁, b₂, ...}, se la differenza tra le due successioni, eseguita termine a termine, {a₀−b₀, a₁−b₁, a₂−b2, ...}, tende a 0. Inoltre, se α e β sono due numeri reali nel senso suddetto, anche la loro somma e il loro prodotto sono definiti termine a termine, α+β={a₀+b₀, a₁+b₁, a₂+b₂, ...} e a α•β={a₀b₀, a₁b₁, a₂b₂, ...}. Entro questo sistema di numeri reali un numero razionale a è identificato con la successione costante {a, a, a, ...}.

A tutti i sistemi numerici sinora considerati è associato un ordinamento naturale. Conseguentemente non esiste alcun numero reale il cui quadrato sia −1 o, in altre parole, un numero che soddisfi l'equazione x²+1=0. Il desiderio di avere sempre soluzioni, sia per questa particolare equazione, sia per tutte le altre equazioni algebriche xⁿ+c₁x^n-1+...+c_n-1x+c_n=0, n≥2, conduce all'ultima estensione del sistema dei numeri che interessa l'analisi classica: si definiscono, cioè, i ‛numeri complessi' come coppie ordinate di numeri reali, α=(a, a′), β=(b, b′), ecc., dove α è considerato uguale a β se e solo se a=a′ e b=b′. L'addizione è definita termine a termine, α+β=(a+b, a′+b′), mentre α•β=(aa′−bb′, ab′+ba′). Per poter considerare i numeri reali come un sottoinsieme dei numeri complessi si identifica un numero reale a con il numero complesso (a, 0). Ponendo i=(0, 1), risulta i² =ii=(−1, 0)=−1, cosicche i è la radice quadrata di −1 nel nuovo sistema. Un numero complesso α=(a, a′) può essere rappresentato da un punto di un piano, con coordinate x=a e y=a′. Questa visualizzazione, dovuta a Gauss, Argand e Wessel, favori l'assimilazione dei numeri complessi, a lungo ritardata malgrado la loro semplicità concettuale rispetto ai numeri reali. Invece di definire i vari sistemi numerici ‛geneticamente' attraverso gli altri sistemi, possiamo anche caratterizzarli direttamente mediante assiomi, come abbiamo fatto inizialmente per i numeri naturali. Ad esempio, i numeri razionali sono caratterizzati (‛a meno di isoformismi') dalla proprietà di costituire un corpo ordinato minimale, sono cioè tali da non avere alcun sottosistema proprio che sia un corpo. D'altra parte i numeri reali possono essere caratterizzati come corpo ordinato archimedeo massimale, tale cioè da non avere ampliamenti propri che siano ancora corpi ordinati archimedei. Sia in aritmetica che in analisi si ha a che fare in prima istanza con strutture matematiche specifiche, univocamente definite, mentre in algebra ci si occupa della totalità delle strutture che soddisfano un dato sistema assiomatico. Tuttavia un esame più accurato del punto di vista logico mostra che questa distinzione costituisce forse l'oggetto di una tendenza piuttosto che una realtà obiettiva. Ad esempio, sappiamo che oltre ai numeri naturali esistono, a seconda dell'interpretazione degli assiomi di Peano, molte altre strutture che soddisfano questi assiomi.

L'analisi, sia reale che complessa, può a questo punto essere sviluppata entro questo preciso contesto. La nozione centrale dell'analisi classica è il concetto di limite, che può essere illustrato dagli esempi seguenti. Sia g(h) una funzione a valori reali definita in un intorno di 0, per −a>h>a, ma non per h=0. Diciamo allora che g(h) tende al limite λ per h che tende a 0, in simboli:

dove λ è un numero reale, se per ogni ε⟨0, esiste un δ⟨0 tale che ∣λ−g(h)∣>ε, se 0>∣h∣>δ. Sia ora f(x) una qualsiasi funzione reale di una variabile reale e, per ogni x=ξ all'interno del suo intervallo di definizione, consideriamo il quoziente g(h)=(f(ξ+h)−f(ξ))/h. È questo il ‛rapporto incrementale' (la ‛pendenza') della funzione f(x) tra ξ e ξ+ h. Se il

esiste, λ è la ‛derivata' di f(x) per x=ξ. Questa è la nozione fondamentale del calcolo differenziale. È in apparenza un concetto puramente tecnico, ma prima che fosse formulato in questa forma precisa, la questione di trovare una definizione accettabile per la derivata di una funzione era considerata come il problema più importante per i fondamenti e addirittura per la filosofia (‛metafisica') della matematica.

I vari rami della geometria possono essere classificati, in prima approssimazione, in base alle nozioni che li caratterizzano. Così la geometria proiettiva tridimensionale si occupa di punti, rette e piani e delle loro proprietà di incidenza e d'intersezione. Nella geometria affine si introduce la relazione di parallelismo, che può essere soddisfatta da certi piani e da certe rette complanari che hanno una particolare posizione reciproca. La geometria affine può essere ottenuta dalla geometria proiettiva specificando un piano particolare come ‛piano all'infinito'. Introducendo, in più, il concetto di distanza, o di equidistanza, otteniamo i vari tipi di geometria metrica. Per tutte queste geometrie sono stati formulati in vari modi e studiati in grande dettaglio dei sistemi assiomatici. Di particolare interesse è la connessione tra le proprietà geometriche di un dato spazio e le proprietà algebriche del sistema numerico che può essere impiegato per introdurre in esso un sistema di coordinate.

Nel 1872 F. Klein, in una celebre conferenza, che divenne famosa come programma di Erlangen, mostrò come fosse possibile ottenere una più profonda comprensione dei rapporti reciproci tra le varie geometrie classificandole in base ai gruppi di trasformazioni che lasciano invariati i concetti e le proprietà di quelle geometrie. La geometria euclidea, per esempio, è la geometria del gruppo delle rotazioni e delle traslazioni dello spazio. Questa impostazione è applicabile con egual successo anche a geometrie n-dimensionali con n maggiore di 3. La convinzione che la geometria dovesse basarsi, in ultima analisi, sull'intuizione spaziale aveva creato delle difficoltà per la geometria pluridimensionale, difficoltà che svanirono allorché i punti dello spazio n-dimensionale furono identificati con n-uple di numeri reali, o anche complessi. Tuttavia esistono tipi di geometrie che non possono essere inclusi nel programma di Erlangen, in particolare la geometria riemanniana, che è data da una definizione analitica di distanza che può variare da punto a punto.

Più ampio è il gruppo di trasformazioni dello spazio che si prende in considerazione, più piccolo è il numero di concetti e proprietà che esso lascia invariati, e più generali sono questi concetti. La disciplina che si occupa dei concetti che rimangono invariati rispetto a tutte le tra- formazioni biunivoche e bicontinue (si tratta di un gruppo di trasformazioni molto ampio) si chiama ‛topologia'. Per esempio, il numero di buchi in un solido, o il problema relativo alla possibilità di connettere con una linea continua interna al solido stesso due suoi punti qualsiasi sono argomenti che fanno parte del campo d'applicazione della topologia. Anche in questo caso, invece di essere basata sulla geometria e in definitiva sui numeri reali, la nozione di spazio topologico può essere introdotta direttamente per mezzo di assiomi. Sia A un insieme di oggetti, chiamati ‛punti', e sia Ω un insieme di sottoinsiemi di A chiamati ‛insiemi aperti'. (Intuitivamente, un sottoinsieme U del dato insieme A è aperto se, per ogni punto p di U, ogni punto q di A sufficientemente vicino a p - in un senso non necessariamente metrico - appartiene anch'esso a U). Si dice, quindi, che la coppia (A, Ω) è uno spazio topologico se: a) A è aperto, cioè appartiene a Ω; b) l'insieme vuoto è aperto; c) l'intersezione di due insiemi aperti è un insieme aperto; d) l'unione di un qualsiasi numero di insiemi aperti è anch'esso un insieme aperto. Spesso uno spazio topologico soddisfa anche la condizione che, se p e q sono due punti distinti di A, esistono due insiemi aperti U e V privi di punti in comune, tali che p appartiene a U e q appartiene a V. Tale assioma si chiama ‛assioma di Hausdorff' sebbene Hausdorff abbia introdotto l'intero sistema di assiomi per una struttura topologica.

Malgrado la loro apparente semplicità, gli assiomi precedenti - insieme con ulteriori ipotesi, ove esse siano necessarie - sono estremamente efficaci. Nello stesso tempo, per la loro generalità, tali assiomi sono ampiamente applicabili e si dà il caso che essi siano soddisfatti e conducano a risultati interessanti anche in molte strutture che, dal punto di vista intuitivo, non hanno alcuna relazione con la geometria. D'altra parte, la teoria dei gruppi, concepita in origine in relazione a problemi algebrici, si è rivelata di grande importanza in topologia. Inoltre, alcune diramazioni della teoria dei gruppi sono state ulteriormente sviluppate in vista delle loro applicazioni topologiche, e queste, a loro volta, si sono dimostrate molto fruttuose anche in altri campi della matematica. Pertanto il metodo assiomatico, oltre al ruolo che svolge nel problema dei fondamenti della matematica, ha dimostrato la sua grande importanza anche per la scoperta di nuovi risultati.

5. Logica matematica

Si possono costruire dei linguaggi formali con diversi gradi di capacità espressiva. Tracceremo anzitutto le linee essenziali di un linguaggio base, il cui scopo è quello di illustrare il modo in cui le proposizioni possono essere modificate o associate tra di loro per dar luogo a nuove proposizioni. E questo il linguaggio del ‛calcolo proposizionale'. Per esempio, se p sta per ‛Giovanni ha otto anni' e q per ‛Giovanni è alto un metro e trenta', allora p⋀q vorrà dire ‛Giovanni ha otto anni ed è alto un metro e trenta'. La risposta alla domanda se p⋀q sia vera o falsa in una data situazione, cioè in riferimento a un particolare ragazzo chiamato Giovanni, in un dato momento, dipende allora solo dalla verità o dalla falsità di p e di q. Così p⋀q è vera se p e q sono entrambe vere, altrimenti è falsa. Analogamente, p⋀q, che vuol suggerire il significato espresso dalla congiunzione inclusiva ‛o', è falsa se p e q sono entrambe false, altrimenti è vera. I simboli ⋀ e ⋀ si chiamano ‛connettivi'. Un altro connettivo dal significato ovvio e intuitivo è ¬ (non). Così ¬p è falsa se p è vera ed è vera se p è falsa. Date p e q, vi sono esattamente 16 modi in cui possiamo assegnare i due ‛valori di verità' vero e falso (che indicheremo, rispettivamente, con le abbreviazioni V ed F) per le quattro possibili combinazioni dei valori di verità di p e q rispettivamente. Per alcuni di questi non esistono espressioni direttamente corrispondenti in italiano (o in altre lingue naturali). Per altri, invece, il linguaggio naturale non è sufficientemente preciso per una interpretazione non ambigua. Per esempio, sia p⊃q la proposizione definita stipulando che essa è falsa se p è vera e q è falsa e che essa è vera in tutti gli altri casi. La proposizione p⊃q si legge ‛se p allora q' oppure ‛p implica q', malgrado il disagio che sorge talvolta dal fatto che in questo modo ‛p implica q' può essere vera anche quando q è falsa, se p è anch'essa falsa.

Per n simboli o ‛variabili', p₁, ..., p_n, esistono 2²ⁿ possibilità di assegnare i valori. V e F per le 2ⁿ possibili combinazioni dei valori di verità di p₁, ..., p_n. Ogni assegnazione di questo tipo si chiama ‛funzione di verità'. Tutte le funzioni di verità possono essere ottenute, in vari modi, combinando un numero limitato di esse; per esempio ¬p e p⋀q sono sufficienti a questo scopo. In effetti p⋀q equivale, come funzione di verità, a ¬(¬p⋀¬q), p⊃q equivale a ¬p⋀q, e così via.

Finora non abbiamo fatto una netta distinzione tra i simboli e il loro significato. Per un'impostazione formalizzata procediamo come segue. Definiamo ‛linguaggio' un insieme di successioni di simboli ‛atomici' costruite secondo una serie di regole assegnate. Nel nostro caso i simboli atomici saranno: a) variabili, p, q, r, p₀, p₁, ...; b) connettivi, ¬, ⋀; 7; c) parentesi, (,). Le successioni, chiamate proposizioni o, con un termine più tecnico, formule ben formate, o sono variabili oppure sono ottenute da variabili per mezzo di un numero finito di applicazioni delle due regole seguenti: a) se X è una proposizione allora (¬X) è una proposizione; b) se X e Y sono proposizioni allora (X⋀Y) è una proposizione.

In questo linguaggio, se vogliamo ancora adoperare ⋀ e ⊃, le successioni risultanti possono essere considerate come abbreviazioni di proposizioni corrispondenti in termini di ¬ e ⋀, con (X ⋀ Y) al posto di (¬((¬X)⋀(¬Y)) e X⊃Y al posto di ((¬X)⋀Y). Si usa anche omettere le parentesi quando non possano sorgere equivoci, assumendo per convenzione che la negazione debba leggersi prima della disgiunzione, della congiunzione e dell'implicazione, cosa che faremo anche noi quando si presenterà l'occasione. Così ¬X⋀Y sta per ((¬X)⋀Y) e non per (¬(X⋀Y)).

Per ogni assegnazione di valori di verità alle variabili di una proposizione X otteniamo quindi un valore di verità per X secondo le regole stabilite in precedenza. Una proposizione X è una ‛tautologia' se assume il valore V (vero) per tutti i valori dati alle sue variabili. Per esempio ¬p⋀p, o più generalmente ¬X⋀X, dove X è una qualunque proposizione, sono tautologie.

Questa è la formulazione nel nostro sistema della legge del terzo escluso.

Una proposizione X si dice conseguenza (‛semantica') di un insieme di proposizioni S se X ha il valore V per tutte quelle assegnazioni per le quali tutti gli elementi di S assumono il valore V stesso. Ad esempio, quali che siano le proposizioni X e Y, Y è una conseguenza dell'insieme S formato da X e X⊃Y. Evidentemente possiamo decidere attraverso una valutazione diretta se una proposizione X è una tautologia e, almeno quando S è finito, se X è una conseguenza di S. Per ottenere lo stesso scopo esistono altre strade, che dipendono solo dalla forma della proposizione X assegnata (e degli elementi di S) oppure dalla forma delle proposizioni ottenute da X e dagli elementi di S per mezzo di certe trasformazioni standard.

Prendiamo ora in considerazione il compito di elencare tutte le tautologie di un linguaggio dato. È questo un compito differente da quello di decidere se una proposizione comunque data sia o no una tautologia. Si verifica facilmente che fornendo una risposta a quest'ultima domanda avremo anche risposto a quella iniziale. Per questo scopo, dobbiamo semplicemente disporre tutte le proposizioni del linguaggio in una successione X₀, X₁, X₂, ..., ed esaminare una proposizione dopo l'altra per vedere se essa sia o no una tautologia. Eliminando tutte le proposizioni che non lo sono, resta soltanto l'elenco richiesto di tutte le tautologie.

Per quanto il nostro problema sia così risolto, ne descriveremo ora un'impostazione completamente differente. Si tratta del ‛metodo assiomatico'. A prima vista esso appare del tutto equivalente ai procedimenti assiomatici discussi in precedenza per varie discipline matematiche, ma, come vedremo in seguito, esso può essere ampliato fino a includere tali procedimenti.

Il metodo che seguiremo consisterà nello scegliere alcune proposizioni del nostro linguaggio privilegiando una classe iniziale di proposizioni o ‛assiomi' e, successivamente, stabilendo una regola ben precisa (o, in altri casi, più regole) mediante la quale nuove proposizioni possano essere ‛dedotte', vale a dire possano essere aggiunte all'elenco di quelle già specificate, cioè agli assiomi. In generale, le proposizioni ottenute in questo modo si chiamano ‛teoremi' del sistema assiomatico (o deduttivo) in considerazione. Nel nostro caso ci proponiamo di costruire il sistema in modo tale che i suoi teoremi siano appunto le tautologie.

Gli assiomi del nostro sistema deduttivo saranno tutti costituiti da proposizioni di una delle quattro forme seguenti: 1. (X⋀X)⊃X; 2. X⊃(X⋀Y); 3. (X⋀Y)⊃(Y⋀X); 4. (X⊃Y)⊃((Z⋀X)⊃(Z⋀Y) - dove X, Y e Z sono proposizioni arbitrarie. Le proposizioni 1-4 si dicono ‛schemi d'assiomi', dal momento che ciascuna di esse non costituisce un singolo assioma, ma piuttosto uno schema che dà luogo a un'intera classe di assiomi.

La regola di deduzione del nostro sistema è la seguente: da due proposizioni qualsiasi, X, X⊃Y, si deduce Y. È questa la cosiddetta ‛regola del modus ponens', indicata schematicamente dalla

Intendiamo per ‛dimostrazione' una successione finita di proposizioni, Z₀, Z₁, ..., Z_n, n≥0, tale che ogni proposizione Z_j nella successione è un assioma, oppure esistono nella successione altre due proposizioni, Zk e Z_l (k>j, l>j), tali che la proposizione Z_l coincide con la proposizione Z_k⊃Z_j (cioè tali che Z_j può essere ottenuta da Zk e Z_l per mezzo del modus ponens).

Infine consideriamo come teorema ogni proposizione che compaia come proposizione finale in una dimostrazione. Cosi, in particolare, ogni assioma è un teorema, prendendo come dimostrazione la successione ridotta all'unico elemento costituito dall'assioma stesso.

Abbiamo, in tal modo, ottenuto la formalizzazione completa della nozione di deduzione nel nostro sistema. Sorge ora il problema di vedere se tale sistema sia adeguato, nel senso che i suoi teoremi siano proprio le tautologie: la risposta è affermativa.

Invece di elencare tutte le tautologie, che sono le proposizioni vere per tutti i valori delle variabili, potremmo voler elencare solo quelle proposizioni che sono vere per i valori delle variabili che rendono vere tutte le proposizioni appartenenti a un dato insieme S. Per questo scopo dobbiamo solo modificare il procedimento di cui sopra aggiungendo agli assiomi le proposizioni di S.

È evidente che il linguaggio formale finora considerato è troppo povero per fornire uno strumento adatto a formulare una teoria matematica anche relativamente semplice come l'algebra elementare. Considereremo, pertanto, un linguaggio destinato a descrivere qualsiasi struttura matematica assegnata mediante un insieme di singoli elementi e un certo numero di relazioni specifiche tra tali elementi. È questo il linguaggio del ‛calcolo predicativo del prim'ordine'. I simboli atomici del linguaggio comprendono: a) una scorta adeguata di costanti individuali per denotare oggetti, a, b, c, ...; b) ‛variabili', x, y, z, ..., usate come contrassegni privi di riferimento individuale; c) un insieme di ‛simboli di relazione' a uno, due, tre, ... posti, R( ), S(,), ecc., per denotare relazioni a un numero corrispondente di variabili (dove una relazione a una variabile è semplicemente un insieme); d) i ‛connettivi' ¬ e ⋀, che, come abbiamo visto, sono sufficienti; e) due ‛quantificatori': (∃), che vuol dire ‛esiste', e (∀), ‛per ogni'; f) parentesi, [e]. Partendo da questi simboli atomici, costruiamo ora, un passo dopo l'altro, in modo naturale, ‛formule ben formate' (in breve, formule). Iniziamo con ‛formule atomiche', che sono simboli di relazione i cui posti sono stati occupati da costanti individuali o da variabili. Impieghiamo i connettivi per ottenere nuove formule da formule date, come nel linguaggio proposizionale, in modo che, se X e Y sono formule, anche (¬X) e (X⋀Y) devono essere formule. Inoltre, se Q(x) è una formula, nella quale abbiamo messo in evidenza una variabile x in essa contenuta, anche [(∃x)Q(x)] e [(∀x)Q(x)] sono formule, purché (∃x) o (∀x) non siano già contenute in Q. Di nuovo permangono le convenzioni per omettere le parentesi e ⋀ e ⊃ sono ammessi come abbreviazioni.

Dobbiamo ora considerare la connessione tra le formule di un linguaggio e le effettive strutture matematiche del tipo cui si è accennato. Una tale struttura, M, doveva consistere di un insieme di individui, A, e di un insieme di relazioni ρ_j, j=0, 1, 2, ..., definite su A. Quindi, se ρ_j è una relazione a k posti, essa dev'essere identificata con l'insieme delle k-uple di elementi di A che soddisfano la relazione.

Cominciamo a scegliere nel nostro linguaggio dei ‛nomi' per le relazioni di M, cioè dei simboli di relazione R_n che denotano le relazioni ρ_n e tali che il numero di posti in R_n sia proprio il numero di posti nella relazione corrispondente. Analogamente, supponiamo che ciascun oggetto a in A abbia un nome a, che è una costante individuale nel linguaggio. Sia K l'insieme di tutte le formule i cui simboli di relazione e le cui costanti individuali denotino tutti entità di M, cioè siano nomi di entità di M. Daremo ora un certo numero di regole che determinano univocamente, per un qualsiasi elemento X di K, se X è soddisfatto da M o, il che è lo stesso, ‛è vero in M' o ‛vale in M'. Indicheremo questa relazione con M⊨X.

1. Supponiamo che X abbia la forma R(a₁, ..., a_n), dove R è un simbolo di relazione e le a₁, ..., a_n sono costanti individuali. Supponiamo che le a₁, ..., a_n denotino le α₁, ..., α_n in A, rispettivamente, ed R denoti la relazione ρ. Allora M⊨R(a₁, ..., a_n) se, e solo se, (α₁, ..., α_n) è nella relazione ρ (ricordando che ρ è un insieme di n-uple).

2. Supponiamo di aver già determinato per due elementi X e Y in K se essi sono o non sono soddisfatti da M. Allora ¬X è soddisfatto da M se, e solo se, X non è soddisfatto da M; X⋀Y è soddisfatto da M se, e solo se, almeno X o Y è soddisfatto da M.

3. Sia Q(x) una formula ben formata in cui compare una unica variabile x libera (non quantificata) che non compaia altrove nella formula sotto il segno di un quantificatore. Supponiamo di aver già determinato, per qualsiasi a che denoti un oggetto di M, se Q(a) è o non è soddisfatta da M. Allora M⊨(∃x)Q(x) se, e solo se, Q(a) vale in M per almeno una a siffatta e M⊨(∀x)Q(x) se, e solo se, Q(a) vale in M per ciascuna di queste a.

Le regole di cui sopra determinano univocamente se, per ogni formula ben formata X in K, M⊨K, purché X non comprenda alcuna variabile libera. Se X comprende le variabili libere x₁, ..., x_n, ed è quindi della forma Q(x₁, ..., x_n), si dice che Msoddisfa X se M⊨Q(a₁, ..., a_n) per tutte le a₁, ..., a_n che denotano elementi di M.

Se una formula X è valida in tutte le strutture M in cui essa è ‛definita', cioè tali che le costanti individuali e i simboli di relazione di X denotino entità di M, allora chiamiamo X una tautologia (sebbene alcuni riservino questo termine per il linguaggio proposizionale). Se S è un insieme di formule che sono definite e valide in una struttura M, scriviamo allora che M⊨S e diciamo che M è un ‛modello' di S. È sottinteso che, come si può prevedere, un simbolo che compare in più di una proposizione ha lo stesso significato (denotazione) in ciascuna di esse. Se X è un'espressione valida in tutti i modelli di un insieme di proposizioni S nel quale è definita, allora si dice che X è una conseguenza (semantica) di S.

Come abbiamo già fatto nel caso del linguaggio proposizionale, possiamo anche qui chiederci in che modo si possa decidere se una formula sia o no una tautologia, oppure in che modo si possano elencare tutte le tautologie, oppure in che modo sia possibile decidere, dato un insieme S di formule, se una data X sia o no una conseguenza di S, oppure, infine, come catalogare tutte le conseguenze di S. A prima vista si potrebbe pensare di poter rispondere alla prima di queste domande in modo simile a quello seguito nel caso proposizionale, e cioè calcolando semplicemente i valori di verità di una proposizione X per tutte le assegnazioni di valori di verità date alle sue variabili. Così potremmo risolvere qui lo stesso problema sfruttando la definizione iterativa della nozione di soddisfacibilità in una struttura. A questo punto, tuttavia, ci troviamo di fronte a una differenza fondamentale. Il numero di possibili assegnazioni di valori di verità alle variabili di una proposizione nel linguaggio proposizionale è finito, e per ciascuna di tali assegnazioni possiamo calcolare effettivamente il corrispondente valore di verità della proposizione. Invece il numero delle diverse strutture che dobbiamo prendere in considerazione è infinito, e persino nel caso di una sola particolare struttura M la decisione se (∀x)Q(x) o (∃x)Q(x) siano o non siano valide in M dipende dal numero (eventualmente) infinito di casi Q(a). Pertanto questa volta la nostra definizione non è effettiva. Naturalmente ciò non significa di per sé che non vi possa essere qualche altro metodo per decidere sistematicamente se, per qualsiasi Xdato, X sia o non sia una tautologia. Tuttavia, come ha mostrato A. Church con un risultato strettamente collegato all'indecidibilità dell'aritmetica, cui si è già accennato in precedenza, anche con un'interpretazione molto spregiudicata della nozione di ‛effettività' tale metodo non esiste. Ciò significa naturalmente che, in generale, anche la risposta alla terza delle domande di cui sopra è negativa, persino quando S è finito.

Diviene quindi ancora più importante trovare un procedimento che consenta almeno di elencare tutte le tautologie. E proprio questo lo scopo del ‛calcolo deduttivo', che ora diviene indispensabile, in una forma o nell'altra. In particolare, possiamo seguire lo schema stabilito per il linguaggio proposizionale. Adottiamo, dunque, gli schemi d'assiomi 1-4, descritti prima, ai quali aggiungiamo i seguenti: 5. Q(t)⊃[(∃x)Q(x)] e 6. [(≅x)Q(x)]⊃Q(t), dove t è o una costante o una variabile e x è una variabile qualsiasi, come in precedenza. Inoltre come regola di deduzione prendiamo, insieme alla regola del modus ponens, la seguente: se la formula Z non contiene la variabile libera (non quantificata) x, allora: a) da Q(x)⊃Z si deduce [(∃x)Q(x)]⊃Z e b) da Z⊃Q(x) si deduce Z⊃[(∀x)Q(x)]. Modificando la nozione di ‛dimostrazione' in modo da tener conto anche di queste due regole, definiamo di nuovo la nozione di ‛teorema'. Si può allora dimostrare che ‛una formula X è una tautologia se, e solo se, essa è un teorema'. Questo importante risultato è dovuto a K. Gödel (1930) e mostra che è possibile elencare tutte le tautologie mediante l'applicazione sistematica degli schemi d'assiomi e delle regole di deduzione. Lo stesso concetto si può esprimere dicendo, con una terminologia che a quel tempo ancora non esisteva, che è possibile ideare un programma in base al quale un calcolatore sarebbe in grado di stampare, una per una, l'elenco completo di tutte le tautologie. Analogamente, se S è un insieme finito di formule, possiamo predisporre un programma che fornisca tutte le conseguenze di S, e questo è ancora vero se S è infinito, purché definito in modo sufficientemente concreto (‛effettivo').

Sia ora S un insieme infinito di formule. Il principio seguente, noto come ‛principio di compattezza' del calcolo predicativo del prim'ordine, non solo si dimostrò di grande importanza per le sue applicazioni e i suoi ulteriori sviluppi, ma portò anche a un profondo chiarimento delle nozioni di ‛coerenza' e di ‛conseguenza' per questo linguaggio: ‛se ogni sottoinsieme finito di S possiede un modello, anche S possiede un modello; equivalentemente, se una formula X è una conseguenza di S, essa è già una conseguenza di un sottoinsieme finito di S'.

Non abbiamo finora assegnato un posto particolare al simbolo di uguaglianza =. Di fatto è possibile trattarlo alla stessa stregua di un qualsiasi altro simbolo di relazione a due posti che, in una data struttura, denoti una relazione riflessiva, simmetrica e transitiva e che permetta la sostituzione di ogni termine con un termine eguale. Ciò significa che a=a; se a=b, allora b=a; se a=b e b=c, allora a=c; infine, se (a₁, ..., a_n)∈R per una data relazione nella struttura e a₁=b₁, a₂=b₂, ..., a_n=b_n, allora (b₁, ..., b_n) e R. Con un'altra formulazione, possiamo interpretare a=b come asserzione del fatto che a e b denotano lo stesso oggetto. In tal modo il simbolo = denota l'identità, cioè una nozione che merita certamente di essere collocata in un sistema logico. Comunque, all'atto pratico, la differenza tra le due impostazioni non è poi così grande.

È anche possibile arricchire il linguaggio con l'introduzione di simboli di funzioni per denotare appunto funzioni. Come abbiamo illustrato in precedenza, ciò si può sempre evitare sostituendo una funzione di n variabili con una relazione tra n+1 variabili (per es. considerando la funzione di due variabili, x+y, come una relazione tra tre variabili x, y e z che soddisfino la x+y=z). L'introduzione di simboli funzionali è utile a molti fini e tutte le definizioni e i risultati esposti precedentemente possono essere opportunamente adattati per poter includere tali simboli nel linguaggio stesso.

Fino al 1930 la nozione di soddisfacibilità non veniva normalmente discussa, ma veniva piuttosto data intuitiva- mente per scontata. Non si trattava certo di una svista. Si riteneva che il vero oggetto della logica fosse la deduzione, la quale è meramente sintattica, nel senso che non va oltre le entità del linguaggio. La nozione di soddisfacibilità, invece, richiede non solo l'introduzione esplicita di strutture, cioè di entità estranee al linguaggio, ma, come abbiamo visto, essa introduce nella discussione anche un elemento infinitario. D'altra parte, finché non disponiamo della nozione di soddisfacibilità in una struttura, non possiamo formulare lo scopo di un calcolo deduttivo. E merito di A. Tarski l'aver chiarito questo fatto (1933).

L'analisi sistematica della relazione tra le formule (ben formate) o gli insiemi di formule, da una parte, e le strutture dalle quali queste formule sono soddisfatte, dall'altra, è nota come ‛teoria dei modelli'. In questi ultimi venticinque anni si è potuto constatare come questa analisi fornisca un riferimento naturale per alcune delle più importanti discipline matematiche e, in particolare, per l'algebra. Così, mentre in algebra si prendono spesso in considerazione tutti i modelli di un determinato insieme di assiomi (come nella teoria dei gruppi o nella teoria dei corpi), o anche le interconnessioni tra i modelli di determinati insiemi di assiomi, la teoria dei modelli stabilisce un quadro generale nell'ambito del quale si studiano esclusivamente le relazioni tra formule e strutture. Può sembrare stupefacente il fatto che questa impostazione molto generale sia in grado di produrre risultati non banali, ma è proprio quello che succede.

Illustriamo ora diverse nozioni basilari di questa teoria. Al posto del termine ‛formula' (‛ben formata') useremo d'ora in poi il termine più familiare ‛proposizione'. Un assioma è, di fatto, una proposizione. Tutte le proposizioni sono prese dal calcolo predicativo del prim'ordine. Una teoria T è un qualsiasi insieme ‛deduttivamente chiuso' di proposizioni in un dato vocabolario. Cioè, se X è una proposizione i cui simboli di relazione, le cui costanti individuali e i cui simboli funzionali compaiono in T e se X è una conseguenza di T, allora X appartiene di fatto a T. La teoria T è ‛completa' se, per qualsiasi X con simboli in T, come sopra, o X o ¬X è una conseguenza di T e, quindi, appartiene a T. Se, per qualche X, sia X che ¬X appartengono a T, allora T non può avere un modello.

Sia ora M una struttura qualsiasi e sia T l'insieme di tutte le proposizioni che valgono in M in un dato vocabolario. Allora T è una teoria. Sia M′ un'altra struttura con ‛le stesse' relazioni. Ciò significa, più precisamente, che i simboli di relazione di T sono interpretati anche in M′. Se le proposizioni di T valgono tutte anche in M′, diciamo che M′ è elementarmente equivalente a M (per il vocabolario dato). Se due strutture sono isomorfe, e cioè se è possibile porle in corrispondenza biunivoca in modo che le relazioni e le funzioni siano conservate, esse sono anche elementarmente equivalenti. Tuttavia l'inverso non è vero. E perfettamente possibile che due strutture siano elementarmente equivalenti senza essere isomorfe e perfino senza possedere la stessa cardinalità. Per fare un esempio, sia ℝ il corpo dei numeri reali e si consideri un vocabolario che comprenda uguaglianza, addizione, moltiplicazione, sottrazione, divisione e ordine. Possiamo formulare, con questi termini, molte proprietà importanti di ℝ per mezzo di proposizioni nell'ambito del calcolo predicativo del prim'ordine, e in particolare le due proprietà seguenti: a) ogni numero positivo ha una radice quadrata; b) ogni polinomio in una variabile e di grado n ha una radice (detta anche uno ‛zero' del polinomio), dove n è un intero dispari. Sia ora R′ un altro corpo ordinato che soddisfi a) e b) (per es. R′ può essere il sottocorpo di ℝ formato dai soli numeri reali algebrici). Un teorema di A. Tarski stabilisce che ℝ e R′ sono elementarmente equivalenti. In tal modo, un enunciato formulato nel nostro linguaggio, che sia stato dimostrato per il corpo dei numeri reali, è, in base a questa argomentazione, vero anche in molti altri corpi ordinati, e ciò anche quando non si possa più disporre del metodo di dimostrazione, che può implicare ad esempio considerazioni topologiche.

Un corpo ordinato che soddisfa a) e b) è detto reale chiuso. Il teorema di Tarski consiste nell'affermazione che la teoria dei corpi reali chiusi, cioè l'insieme delle proposizioni che valgono in tutti i corpi reali chiusi, è completa. In anni recenti è stata dimostrata la completezza di molte altre teorie. La tecnica di dimostrare un risultato per una struttura, e quindi trasferire tale risultato a un'altra struttura per mezzo di determinati principi della teoria generale dei modelli, viene applicata persino in alcuni casi in cui la seconda struttura non è elementarmente equivalente alla prima.

Si è accennato in precedenza che vi sono, oltre i numeri naturali, altri sistemi che soddisfano gli assiomi di Peano; si consideri pertanto un vocabolario che comprenda eguaglianza, ordine, addizione, moltiplicazione, i simboli numerici 0, 1, 2, 3,... e magari alcune altre funzioni e relazioni della teoria dei numeri. Sia T l'insieme di tutte le proposizioni formulate con questo vocabolario che sono soddisfatte dal sistema dei numeri naturali ℕ. In particolare appartiene a T la proposizione seguente, purché Q(x) sia formulata nel vocabolario dato:

[Q(0)⋀(∀x)[Q(x)⊃Q(x+1)]]⊃(∀y)Q(y).

Essa stabilisce che, se Q vale per 0 e se, dal fatto che vale per un qualsiasi n, segue che essa vale anche per n+1, allora Q è vera per tutti i numeri naturali.

La proposizione data è un esempio dell'assioma di induzione e, se Q è indeterminato, costituisce uno schema d'assioma che rappresenta il principio d'induzione nel calcolo predicativo del prim'ordine.

Qualsiasi struttura *N che soddisfi le espressioni di T possiede molte proprietà in comune con il sistema dei numeri naturali ℕ. Fu T. Skolem (1934) a notare per la prima volta che esistono delle strutture *N che sono estensioni proprie di ℕ, e cioè che contengono ‛numeri naturali infiniti' maggiori di ogni numero naturale ordinario. Tali sistemi si chiamano ‛modelli non-standard dell'aritmetica'. La loro esistenza è una conseguenza quasi immediata del principio di compattezza. Questo perché un modello non-tandard dell'aritmetica è, per definizione, un modello dell'insieme di proposizioni T che contiene un numero naturale infinito, denotato con a, che soddisfa, oltre T, le proposizioni 0>a, 1>a, 2>a, 3>a, ... .

Sia S l'insieme costituito dagli elementi di T con tutte queste disuguaglianze. Il principio di compattezza ci assicura che S ha un modello purché ogni sottoinsieme finito S′ di S abbia un modello. Tale sottoinsieme S′ può contenere solo un numero finito di proposizioni n>a, tutte contenute in una successione finita {0>a, 1>a, ..., k>a}. Ma tutte queste proposizioni, insieme a T, sono soddisfatte dallo stesso ℕ se interpretiamo a come il numero k+1. In tal modo lo stesso ℕ può essere considerato un modello di S′ se approfittiamo della libertà di scegliere il significato (la denotazione) di a a nostro piacere. Da ciò segue che tutto S possiede un modello *N. Ma in *N il numero a soddisfa le proposizioni n>a per ogni numero naturale n, cosicché a è infinito.

Skolem considerava l'esistenza di modelli non-standard dell'aritmetica come un'indicazione del potere limitato dei linguaggi formali. Ma alle stesse idee si può anche dare un indirizzo più positivo. Applicandole al corpo dei numeri reali, ℝ, possiamo ottenere una estensione propria di ℝ, *R, che contiene numeri infinitamente grandi e infinitamente piccoli e che condivide tutte le proprietà di ℝ nella misura in cui esse possono essere formulate nell'ambito del calcolo predicativo del prim'ordine, con un vocabolario ampliato a piacimento. Si verifica che questo è proprio il tipo di sistema richiesto per sviluppare l'analisi e in primo luogo il calcolo differenziale, secondo il metodo prospettato da Leibniz. Come abbiamo visto, questo metodo fu abbandonato nel sec. XIX perché ritenuto incerto nei suoi fondamenti e fu sostituito dal ‛metodo ε, δ' che abbiamo illustrato in precedenza. Tuttavia diviene ora possibile estendere qualsiasi funzione f(x) definita in un intervallo di ℝ a un intervallo di *R in modo tale che, se f(x) possiede una derivata λ per x=ξ, λ è data, a meno di un numero infinitamente piccolo, dal rapporto (f(ξ+h)−f(ξ))/h, dove l'incremento h è ‛infinitamente piccolo'. Idee del genere sono applicabili non solo al calcolo differenziale e integrale ma anche ad altri settori della matematica. È questo il metodo dell'analisi non-standard introdotto da A. Robinson nel 1960.

Il linguaggio del calcolo predicativo del prim'ordine, benché adatto a molti scopi, è ancora troppo povero per essere applicabile direttamente a tutti i rami della matematica o alla traduzione del discorso comune. La ragione di ciò sta nel fatto che in questo linguaggio la quantificazione (‛esiste' e ‛per ogni') è consentita solo in relazione a singoli oggetti, ad esempio numeri. In pratica, tuttavia, potremmo voler adoperare espressioni quali ‛per ogni insieme...', ‛esiste una funzione...', ‛per ogni gruppo di esseri umani...', vale a dire, potremmo voler quantificare anche relazioni e funzioni. Vi sono svariati modi per costruire le estensioni desiderate nel linguaggio formale, ma ciascuno comporta delle difficoltà. È naturale, quindi, supporre che a ciascuna proposizione Q(x), grammaticalmente corretta nel linguaggio formale, corrisponda l'insieme che la soddisfa; ma, come abbiamo già visto, l'applicazione senza restrizioni di questa concezione conduce all'antinomia di Russell. Un'altra possibilità è quella di introdurre un linguaggio ‛multigenere', in cui individui, relazioni e funzioni sono tutti considerati entità basilari sullo stesso piano, ma appartenenti a diversi ‛generi' o classi. L'interpretazione semantica delle formule di un linguaggio di questo tipo conduce tuttavia al problema di come assicurarsi che ogni relazione di un insieme dato sia ‛realmente' inclusa nella struttura che si suppone descritta dalle formule. Supponendo che a questa nozione si possa dare significato assoluto, si è allora portati di nuovo alla considerazione di modelli ‛non-intenzionali' o ‛non-standard' simili a quelli trattati in precedenza.

Le versioni più comuni della teoria assiomatica degli insiemi sono già state completamente trascritte nel linguaggio del calcolo predicativo del prim'ordine. Il sistema di Zermelo-Fraenkel, considerato in precedenza, consiste pertanto di assiomi che sono formulati nell'ambito del calcolo predicativo del prim'ordine mediante l'unica relazione ∈. In questo caso la formalizzazione è più importante di quanto essa non lo sia per una disciplina algebrica individuale, come ad esempio la teoria dei gruppi o la geometria euclidea. Uno degli assiomi di Zermelo, per esempio, afferma che per qualsiasi insieme x esiste un sottoinsieme y di x che consiste proprio di quegli elementi di x che possiedono una proprietà Q(z) definita, o, usando un termine intuitivo, ‛chiaramente definita'. Scrivendo x∈y per ‛x è un elemento di y', come è abituale nella teoria degli insiemi, invece di ∈(x, y), che sarebbe la forma stabilita dal nostro schema generale per il calcolo predicativo del prim'ordine, l'assioma in questione (l'assioma dei sottoinsiemi) diviene:

(∀x)(∃y)(∀z)[[z∈y⊃[z∈x⋀Q(z)]]⋀

⋀[[z∈x⋀Q(z)]⊃z∈y]].

Sorge ora tuttavia la questione relativa a che cosa si debba esattamente intendere per ‛proprietà definita' Q(z), e la risposta, ora comunemente accettata dopo alcuni anni di discussione, è che Q(z) sia semplicemente una qualsiasi formula ben formata che contenga soltanto il simbolo di relazione e e che non contenga x o y.

Dopo aver formulato gli assiomi della teoria degli insiemi nell'ambito del calcolo predicativo del prim'ordine, ci si imbatte nuovamente nell'esistenza di modelli non- standard per questi assiomi. Invero, come T. Skolem ha rilevato già nel 1920 sviluppando un'idea di L. Löwenheim, il sistema ha un modello ‛numerabile'. A prima vista ciò sembra strano dal momento che, come abbiamo già accennato, l'insieme di tutti i sottoinsiemi di un insieme numerabile - che si suppone contenuto nel modello - non può essere numerabile. Il paradosso è risolto dalla constatazione che anche in un modello numerabile della teoria degli insiemi un insieme può essere non numerabile ‛nell'ambito del modello'; vale a dire, tra le relazioni definite nell'ambito del modello, non ve n'è nessuna che fornisca una corrispondenza biunivoca tra l'insieme considerato e un insieme numerabile. Anche in questo caso il fenomeno dei modelli non-standard fu alla fine utilizzato con profitto. I contributi fondamentali di Gödel e di Cohen, a cui si è accennato in precedenza, si fondano quasi interamente sia su di esso sia su altre sofisticate argomentazioni della teoria dei modelli.

Un'ulteriore estensione naturale del calcolo predicativo del prim'ordine consiste nell'introduzione di formule infinitamente lunghe. Possiamo, in tal senso, ammettere congiunzioni infinite, disgiunzioni infinite e successioni infinite di quantificatori. Su queste ultime non si è ancora indagato sistematicamente, ma è noto che esse conducono a certe anomalie. D'altra parte, linguaggi comprendenti congiunzioni e disgiunzioni infinite non sono solo oggetti di studio interessanti in quanto tali, ma si presentano in modo naturale nella formalizzazione della matematica classica. L'assioma di Archimede, ad esempio, può essere espresso come una disgiunzione infinita; in parole: ‛se b è maggiore di a, e se a è maggiore di 0, a+a è maggiore di b oppure a+a+a è maggiore di b, oppure a+a+a+a è maggiore di b, oppure...'. In generale il principio di compattezza, di cui abbiamo già sottolineato l'importanza per il calcolo predicativo del prim'ordine, non si applica a linguaggi infinitari.

Occupiamoci ora di un altro ramo del pensiero matematico che richiede una dettagliata analisi logica. Si tratta dei concetti di ‛calcolabilità' e di ‛procedimento costruttivo' cui finora si è solo accennato. Dato che il contare rappresenta la vera essenza di un procedimento graduale, è naturale trattare in primo luogo la nozione di calcolabilità (o ‛computabilità') nel sistema dei numeri naturali, vale a dire cercare di stabilire in quali condizioni una funzione della teoria dei numeri - cioè una funzione con argomento e valori nei numeri naturali - possa considerarsi calcolabile. Il ramo della logica che si occupa di questo problema si chiama ‛teoria della ricorsività', per un motivo che verrà subito chiarito.

La procedura graduale del contare è espressa dalla funzione successore' s(x)=x′+1, per cui è naturale chiamare questa funzione computabile. Inoltre, se c è un qualunque numero naturale, una funzione costante f(x₁, .., x_n)=c può essere considerata computabile nei senso che, per qualsiasi valore assegnato all'argomento, possiamo immediatamente determinare il valore della funzione, cioè c. Un'altra classe di funzioni computabili in un senso banale si ottiene assegnando a ogni n-upla di numeri naturali (x₁, ..., x_n), n≥1, il valore del suo j-esimo elemento, 0≤j≤n. Si ottiene in tal modo la funzione g(x₁, ..., x_n)=x_j.

Le funzioni finora riconosciute come computabili si chiamano funzioni iniziali. Un metodo per ottenere da funzioni computabili altre funzioni, ovviamente computabili, è quello di sostituzione. In tal modo, se sappiamo come calcolare una funzione f(y₁, ..., y_m) e le funzioni g_k(x₁, ..., x_n), k=1, ..., m, possiamo calcolare anche la funzione F(x₁, ..., x_n)=f(g₁(x₁, ..., x_n), ..., g_m(x₁, ..., x_n).

Tuttavia il metodo di calcolo più caratteristico nell'ambito del sistema dei numeri naturali è la seguente regola di ‛ricorsività primitiva' (o di induzione): sia c un numero naturale qualsivoglia e sia g(x, y) un'assegnata funzione di due variabili. Si può definire allora, in modo unico, un'altra funzione f(x) mediante le condizioni:

f(0)=c f(x′)=g(x, f(x)).

Se, ad esempio, c=1 e g(x, y)=x′•y=(x+1)y, risulta f(0)=1, f(1)=1, f(2)=2•1, f(3)=3•f(2)=3•2•1 e in generale f(n)=n!. In tal modo vediamo che, se g(x, y) è computabile, possiamo calcolare a partire da essa la funzione f(x). Più in generale, f può dipendere anche da un certo numero di parametri x₁, ..., x_n. In tal caso anche g dev'essere specificata come una funzione di x, y e x₁, ..., x_n e la costante c è sostituita da un'altra funzione di x₁, ..., x_n che è stata già riconosciuta calcolabile.

Qualunque funzione ottenuta dalle funzioni iniziali mediante l'applicazione successiva delle regole di sostituzione e di ricorsività primitiva si dice ‛ricorsiva primitiva'. La definizione stessa mostra che tutte le funzioni ricorsive primitive sono computabili in senso intuitivo. Sebbene le regole introdotte in precedenza appaiano piuttosto rigide, la maggior parte delle funzioni che si possono trovare in un trattato di teoria dei numeri sono ricorsive primitive. Sorge ora il problema di accertare se questo sia vero per tutte quelle funzioni che dal punto di vista intuitivo sarebbero considerate senz'altro come computabili. Al fine di mostrare che ciò, di fatto, non si verifica, osserviamo che non è difficile ordinare effettivamente tutte le funzioni ricorsive primitive di una variabile secondo una successione infinita, con eventuali ripetizioni, specificando il modo in cui ciascuna funzione è ottenuta dalle funzioni iniziali mediante una successione finita di applicazioni delle due regole di derivazione. Sia f₀(x), f₁(x), f₂(x), ... la successione di funzioni ricorsive ottenute in tal modo. Si consideri la funzione F(x)=f_x(x)+1. Questa funzione è computabile in senso intuitivo, dal momento che, fissato un numero naturale n, possiamo ricondurci al ‛programma' stabilito per il calcolo di f_n(x), poi calcolare effettivamente f_n(n) e aggiungere 1. D'altra parte, F(x) non può coincidere con nessuna delle f_k(x). Supponiamo, infatti, che F(x)=f_k(X) per un particolare k. Allora F(k)=f_k(k). Ma, per costruzione, F(k)=f_k(k)+1. Il che porta alla f_k(k)=f_k(k)+1, cioè a una contraddizione che mostra che F(x), sebbene calcolabile, non è ricorsiva primitiva.

Come formulare una definizione che comprenda ogni procedimento effettivo per il calcolo di funzioni della teoria dei numeri? Non si tratta di un problema di matematica pura, dal momento che stiamo cercando di trovare la spiegazione logico-matematica corretta di un concetto che è in un certo senso empirico, per quanto sia ancora attinente al pensiero umano. La risposta a questo quesito, che è stato posto in parecchie formulazioni equivalenti, è nota come ‛tesi di Church'. Il fatto che differenti impostazioni abbiano di fatto portato allo stesso risultato rafforza la nostra fiducia nella sua correttezza. Descriveremo due di tali impostazioni.

Il punto di partenza per la prima di esse è costituito dagli schemi per costruire funzioni ricorsive primitive. Supponiamo di aver trascritto tutte le equazioni, comprese le funzioni iniziali, le sostituzioni e gli schemi di induzione che definiscono una particolare funzione ricorsiva primitiva. Ci rendiamo allora conto che il procedimento per calcolare effettivamente tale funzione è puramente formale. Esso consiste nel sostituire simboli numerici a variabili (dove identifichiamo n con 0′...‴ (n volte)) o nel valutare funzioni, cioè nel sostituire un simbolo numerico n a un'espressione g(k₁, ..., k_m), purché si sia già ottenuto g(k₁, ..., k_m)=n. Abbiamo visto che gli schemi che conducono alle funzioni ricorsive primitive sono troppo restrittivi per comprendere tutte le funzioni calcolabili. Ma il metodo impiegato per stabilire questo fatto sarebbe egualmente valido aggiungendo altri schemi, purché si decidesse a priori esattamente quali schemi ammettere. La ‛definizione di Gödel-Herbrand' di funzione ricorsiva (generale) sfugge a questa strettoia stabilendo che una funzione f(x₁, ..., x_n) è ricorsiva (cioè calcolabile) se può essere determinata in modo univoco applicando le sostituzioni e i calcoli sopra descritti a un certo sistema di equazioni E. In tal modo E è proprio un insieme finito di equazioni s=t, dove s e t sono espressioni formali ottenute mediante la concatenazione di simboli funzionali, i cui argomenti sono variabili, oppure 0; ad esempio s=f(g(x, y′), h(z′, 0, x)). Di questi simboli funzionali solo ′ ha un significato preassegnato, poiché denota la funzione successore', che a x fa corrispondere x′=x+1.

Un altro modo di introdurre le funzioni computabili si ottiene ricorrendo al concetto di ‛macchina di Turing'. Questa nozione è congeniale alla mentalità contemporanea, dal momento che rappresenta una versione idealizzata di un calcolatore elettronico. Sembra ormai provato che la stessa nozione astratta di macchina di Turing abbia notevolmente contribuito allo sviluppo concreto dell'invenzione del calcolatore. Una macchina di Turing - che prende il nome da A. M. Turing, che la ideò nel 1936 - è in grado di ‛leggere' lettere di un alfabeto finito, che sono stampate sui settori quadrati in cui è suddiviso un nastro infinito. A seconda della lettera presente nel quadrato esaminato e a seconda dello ‛stato interno' in cui si trova la macchina - fra un numero finito di stati possibili -, essa può cancellare la lettera esaminata e sostituirla con un'altra o esaminare lo spazio successivo sulla destra o sulla sinistra e, in tutti i casi, cambiare stato. Codificando in modo appropriato i simboli numerici mediante lettere dell'alfabeto, è possibile definire funzioni che possono essere calcolate da questa macchina. Si verifica che queste sono proprio le funzioni ricorsive definite precedentemente.

Connessa alla computabilità delle funzioni è la decidibilità dei problemi. Nel caso numerico, che qui stiamo trattando, sia A un insieme di numeri naturali assegnato in modo arbitrario ma definito. Il problema è quello di trovare un procedimento sistematico per decidere se un qualsiasi numero naturale n appartenga o no ad A. Tale problema può essere ricondotto a quello relativo al calcolo di funzioni, ponendo f_A(x)=0 per x appartenente ad A e f_A(x)=1 per x non appartenente ad A. Decidere se n appartenga o no ad A equivale allora a calcolare f_A(n). Così, se f_A(x) è ricorsiva, il nostro problema riceve una risposta affermativa e lo stesso A si dice ricorsivo. Può accadere che A sia non ricorsivo e che, tuttavia, rappresenti il codominio di una funzione ricorsiva, cioè sia costituito dall'insieme di numeri f(0), f(1), f(2), ... per una f(x) ricorsiva. Se l'insieme A e l'insieme B dei numeri naturali che non appartengono ad A sono entrambi numerabili ricorsivamente, e se A è il codominio di f(x) e B il codominio di g(x), allora A è ricorsivo. Infatti per decidere se un numero n appartiene ad A dobbiamo soltanto calcolare uno per uno f(0), g(0), f(1), g(), f(2), ..., per trovare prima o poi n come valore di f(x) o di g(x) per qualche x=k. Sebbene questa argomentazione non sia formale, essa può essere tradotta in un procedimento di decisione nel senso introdotto in precedenza. Osservazioni simili valgono per relazioni su numeri naturali, cioè su insiemi di n-uple di numeri naturali.

Nella celebre raccolta di problemi proposti da D. Hilbert nel 1900, il decimo richiede un procedimento effettivo per poter decidere se, per un dato pòlinomio a coefficienti interi, p(x₁, ..., x_n), esistano o no degli interi a₁, ..., a_n tali che p(a₁, ..., a_n)=0.

Sebbene il problema si riferisca ai numeri interi, non è difficile ricondurlo a uno relativo ai numeri naturali. Nel 1970, J. Matijasevič dimostrò non solo che non esiste un tale procedimento, ma anche che esistono polinomi p(x₁, ..., x_n, y₁, ..., y_m) per i quali manca un procedimento effettivo che consenta di decidere per quali valori di y₁, ..., y_m esistano valori di x₁, ..., x_n tali che si abbia p(x₁, ..., x_n, y₁, ..., y_m)=0.

Fino ad ora abbiamo considerato la nozione di computabilità per funzioni e insiemi numerici. Tuttavia questa nozione ha un significato intuitivo anche in altri casi. Al fine di trattare problemi analoghi anche in relazione a sistemi formali, K. Gödel introdusse l'‛aritmetizzazione' di tali sistemi. Supponiamo, quindi, che K sia l'insieme di tutte le proposizioni del calcolo predicativo del prim'ordine in termini di un certo numero finito di costanti, simboli di relazione e simboli funzionali. Assegniamo allora determinati numeri ai simboli atomici di K, ad esempio (nel caso aritmetico) assegniamo il numero 7 al simbolo ⋀, 9 a ¬, 11 a ∀, 13 a ∃, 15 a =, 17 a +, 23 al simbolo numerico 0, ecc. Assegniamo altri numeri alle successioni di simboli atomici e in particolare alle proposizioni di K e anche alle successioni di proposizioni di K, per esempio alle dimostrazioni, in un modo definito che ci consenta in tutti i casi di riottenere un simbolo o una proposizione o un insieme di proposizioni dal numero a essi assegnato (detto ‛numero di Gödel'). Vi sono molti modi per ottenere questo scopo, utilizzando la scomposizione in fattori primi dei numeri naturali. Si verifica allora che, conformemente alla tesi di Church, l'insieme di tutti i numeri che corrispondono alle proposizioni di K è ricorsivo. Questo è vero in particolare se K è l'insieme di tutte le proposizioni, vere o false, che hanno per oggetto i numeri naturali e che si esprimono in termini di addizione, moltiplicazione, uguaglianza e ordine e mediante i simboli numerici 0, 1, 2, 3 D'altra parte, l'insieme di tutti i numeri di Gödel delle proposizioni vere dell'aritmetica non è ricorsivo; cioè, identificando ancora la ricorsività con la computabilità, non esiste un procedimento effettivo per decidere se una proposizione dell'aritmetica sia vera o falsa.

Ora, sia P l'insieme degli assiomi di Peano per l'aritmetica cui si è accennato in precedenza. Questi assiomi possono essere effettivamente elencati. Corrispondentemente l'insieme dei numeri di Gödel delle proposizioni di P è numerabile ricorsivamente (e anche ricorsivo). Ne consegue che l'insieme T di tutte le proposizioni di K che possono essere ottenute da P, secondo le regole del calcolo deduttivo descritto in precedenza, può anch'esso essere effettivamente numerato. Quindi l'insieme S dei numeri di Gödel di T è numerabile ricorsivamente. Come abbiamo visto, T è anche l'insieme delle conseguenze (semantiche) di P. Ora, se T consistesse realmente di tutte le proposizioni che sono vere in aritmetica, il loro insieme sarebbe decidibile. Infatti, se X è una qualsiasi proposizione di K, potremmo determinare i numeri di Gödel di X e di ¬X, diciamo a e b, e soltanto uno di questi apparterrebbe a S. Elencando gli elementi di S dovremmo, prima o poi, imbatterci in a o in b. Nel primo caso X sarebbe vera in aritmetica, mentre nel secondo caso X sarebbe falsa. Ma ciò contraddice l'affermazione iniziale secondo cui non esiste un procedimento effettivo per decidere questo problema. Ne concludiamo che esistono proposizioni aritmetiche vere che non possono essere dedotte da P o, senza citare il concetto di verità, esistono proposizioni X nel vocabolario di P tali che né X né ¬X sono deducibili da P. È questo il ‛teorema di incompletezza di Gödel'.

Gödel pubblicò questo risultato nel 1931 nell'articolo più importante di tutta la storia della logica matematica. A quel tempo non erano state ancora formulate le questioni di indecidibilità connesse al teorema di Gödel; al contrario tali questioni e le relative scoperte furono senza dubbio ispirate, in ultima analisi, proprio dalle idee sviluppate in quell'articolo. Abbiamo qui enunciato il teorema per un sistema assiomatico formulato nel calcolo predicativo del prim'ordine, ma esso fu dato originariamente per un linguaggio più potente. La dimostrazione fa uso di un ‛procedimento diagonale' piuttosto simile a quello che si presenta nel paradosso di Russell, che a sua volta fu suggerito da un'argomentazione di Cantor. Non si basa sull'interpretazione nella teoria dei modelli degli assiomi di Peano P, ma sull'ipotesi esplicita che P sia esente da contraddizioni. Inoltre Gödel dimostrò nello stesso articolo che quest'ipotesi non può essere dimostrata nell'ambito dell'aritmetica; un risultato cui abbiamo già accennato a proposito del programma di Hilbert.

Attualmente l'analisi degli insiemi di numeri naturali e delle funzioni della teoria dei numeri, effettuata mediante la teoria della ricorsività e strumenti analoghi, ha dato luogo a un ampio campo di ricerche. Dopo l'opera pionieristica di Gödel gli sviluppi successivi sono dovuti soprattutto ai contributi di S. C. Kleene.

Fin qui abbiamo prestato solo scarsa attenzione ai dettagli della deduzione logica o matematica. È questo l'oggetto della ‛teoria della dimostrazione', che ebbe origine nel 1936 sempre in relazione al problema della coerenza dell'aritmetica. A quel tempo G. Gentzen mostrò che, nonostante i risultati di Gödel in questo campo, la coerenza dell'aritmetica può essere dimostrata nell'ambito di uno schema in qualche modo più ampio di quello considerato da Gödel. Tale schema non è strettamente finitistico nel senso originale di Hilbert, ma fornisce un'interessante dimostrazione della coerenza dell'aritmetica, purché si dia per scontata la coerenza di un frammento ‛moderatamente' infinitistico della teoria degli insiemi numerabili ben ordinati. A questo scopo Gentzen sviluppò un tipo speciale di sistema deduttivo, che egli chiamò ‛calcolo della deduzione naturale', che permette un'analisi dettagliata dei singoli passaggi di una dimostrazione e, se necessario, la loro modificazione. Da allora il calcolo di Gentzen è stato ampiamente applicato nella logica. Per quanto riguarda invece l'analisi sistematica e la correlazione delle dimostrazioni in matematica il lavoro è ancora quasi tutto da fare.

Per concludere questo esame panoramico della logica matematica, accenniamo brevemente a diversi altri argomenti. Contemporaneamente alla logica moderna si è sviluppato, a partire dai lavori di Boole e, prima ancora, di Leibniz, il desiderio di rappresentare tale disciplina in forma algebrica. Si considerino le proposizioni del calcolo predicativo del prim'ordine (per un vocabolario determinato) e si facciano appartenere alla stessa classe due proposizioni X e Y, se X⊃Y e Y⊃X sono tautologie. Se B è l'insieme di queste classi, B può essere convertito in un'algebra booleana definendo le operazioni algebriche come segue; siano a, b elementi di B, contenenti rispettivamente le proposizioni X e Y; allora a⋃b è la classe delle proposizioni X⋀Y, a⋃b è la classe delle X⋀Y e a′ è la classe delle ¬X. Queste definizioni sono indipendenti dalla particolare scelta di X e Y. Si verifica che l'elemento 1 di B è proprio la classe di tutte le tautologie, mentre 0 è la classe delle proposizioni contraddittorie, cioè delle proposizioni le cui negazioni sono tautologie. Segue dalle definizioni che le operazioni booleane riflettono l'azione dei connettivi nel calcolo predicativo. Diviene quindi naturale integrare l'algebra booleana introducendo operatori che riflettano la quantificazione. Questa idea è stata sviluppata in due versioni distinte (algebra cilindrica e algebra poliadica). Tali estensioni dell'algebra booleana hanno un considerevole interesse intrinseco, pur non avendo finora recato alcun contributo al nostro approfondimento della logica in quanto tale.

La matematica pura e la fisica classica sono formulate in modo naturale in termini di proposizioni dichiarative, sullo sfondo di un concetto di verità a due valori. Questa impostazione è troppo ristretta, sia per alcune discussioni filosofiche che per il linguaggio della vita di ogni giorno. Anche la fisica moderna ci presenta situazioni che non sono facilmente descrivibili nell'ambito dei linguaggi fin qui considerati. Pertanto ci si è dedicati con molta energia allo studio di ‛logiche non-standard', quali la ‛logica modale', - che incorpora nel suo linguaggio le ‛modalità' della possibilità e della necessità - e la ‛logica a più valori', in cui il semplice schema a due valori, vero e falso, è sostituito da un numero maggiore, o addirittura infinito, di valori di verità.

6. Conclusione

Non è facile prevedere quale sarà il giudizio delle generazioni future su un complesso di studi che si è svolto quasi tutto nell'arco di una vita. A noi sembra che gli ultimi cento anni abbiano visto una rivoluzione nella logica e nei fondamenti della matematica che è seconda solo a quella della matematica deduttiva nell'antica Grecia. In entrambi i casi, il mutamento rivoluzionario fu ottenuto rendendo espliciti modi di pensare che fino allora erano stati compresi solo intuitivamente e in maniera rudimentale. Credere che questo processo sia terminato sarebbe un errore. La nostra comprensione della componente euristica di una dimostrazione è ancora a uno stadio primitivo. Si ha l'impressione che molto rimanga ancora da dire su alcuni dei livelli più semplici dell'attività matematica, ad esempio sulle nozioni di sostituzione, di scambio delle variabili, di concatenazione di funzioni (logica combinatoria) e sull'uso e l'enunciazione dei simboli (semiotica). Un'altra caratteristica della logica contemporanea, che pone dei problemi ancora non risolti, è la regressione infinita che ci costringe a far uso di argomenti matematici a un livello più alto (metalivello) per far luce su argomenti simili a livello inferiore. Infine resta ancora aperto il problema dell'esistenza - o realtà o verità obiettiva - in matematica, specialmente se applicato ai concetti infinitari. Un'altra rivoluzione nella filosofia della matematica cambierà un giorno interamente la nostra impostazione del problema?

bibliografia

Casari, E., Questioni di filosofia della matematica, Milano 1964.

Cohen, P. J., Set theory and the continuum hypothesis, New York 1966 (tr. it.: La teoria degli insiemi e l'ipotesi del continuo, Milano 1973).

Fraenkel, A. A., Bar-Hillel, Y., Foundations of set theory, Amsterdam 1958.

Heijenoort, J. van (a cura di), From Frege to Gödel, Amsterdam 1967.

Heyting, A., Intuitionism. An introduction, Amsterdam 1956.

Robinson, A., Introduction to model theory and to the metamathematics of algebra, Amsterdam 1963 (tr. it.: Introduzione alla teoria dei modelli e alla metamatematica dell'algebra, Torino 1974).

Whitehead, A. N., Russell, B., Principia mathematica, vol. I-III, Cambridge 1925-1927.