Turing, macchina di

Turing, macchina di

Turing, macchina di automa universale, elaborato dal logico inglese A.M. Turing, che fornisce una traduzione formale del concetto intuitivo di → calcolabilità. Sebbene introdotta da Turing nella prima metà del secolo scorso (1937) come modello per analizzare i successivi passi secondo cui un essere umano esegue un calcolo, la macchina di Turing è tuttora utilizzata, nelle sue numerose varianti, come modello astratto del calcolo automatico sviluppato da un elaboratore. Utilizzando questo modello, per esempio, si studiano, in relazione alla complessità di calcolo delle funzioni, le proprietà di determinismo o non determinismo dei singoli passi, della sequenzialità o del parallelismo delle operazioni.

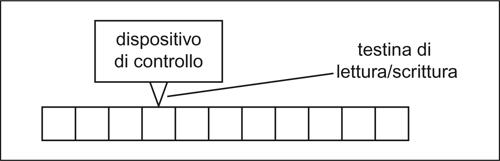
Una macchina di Turing può essere interpretata fisicamente come l’interazione tra due “oggetti”: un dispositivo di controllo, che può trovarsi in un numero finito di stati, e una memoria esterna sequenziale, costituita da un nastro potenzialmente infinito diviso in celle in ciascuna delle quali è possibile leggere o scrivere un carattere dell’alfabeto della macchina. L’interazione è data da una testina di lettura/scrittura. In ogni istante, in base allo stato del controllo e al carattere letto, la macchina può:

a) cambiare o meno lo stato;

b) cambiare o meno il carattere sul nastro;

c) spostarsi o meno di una cella a sinistra o a destra.

Il funzionamento della macchina può essere descritto da una funzione δ che a ogni coppia (stato, carattere letto) associa una terna (nuovo stato, nuovo carattere, mossa), dove il nuovo stato può anche essere lo stato stesso in cui la macchina si trova, così come il nuovo carattere può essere lo stesso carattere letto qualora questo non venga modificato; la mossa può essere uno spostamento a destra, uno spostamento a sinistra oppure nessuno spostamento. Indicati con Σ l’alfabeto dei caratteri con cui opera la macchina, con K l’insieme degli stati del suo dispositivo di controllo e con d, s, i le tre possibili mosse (traslazione di una cella a destra, di una cella a sinistra, traslazione identica cioè nessun movimento), la funzione δ che descrive il funzionamento della macchina di Turing è del tipo: K × Σ → K × Σ × {d, s, i }. L’alfabeto dei caratteri Σ = {σ₀, σ₁, …, σ_r} comprende un particolare carattere σ₀, indicato come «spazio» o «blank» (espresso in letteratura anche con il simbolo □); l’insieme degli stati K = (q₀, q₁, …, q_s} comprende due particolari stati, q₀ e q_ƒ che sono, rispettivamente, lo stato iniziale e lo stato finale. Una macchina di Turing è, quindi, costituita da una sestupla {Σ, σ₀, K, δ, q₀, q_ƒ }. Una sua configurazione è una stringa del tipo σ_i 1σ_i 2… σ_inq _j σ_in+1σ_in+2…σ_im, cioè un elemento dell’insieme Σ*KΣ⁺ dove Σ* indica l’insieme di tutte le stringhe costruite a partire dall’alfabeto Σ utilizzando i suoi caratteri, incluso il carattere vuoto, mentre Σ⁺ indica l’insieme di tutte le stringhe costruite con i caratteri di Σ escluso quello vuoto. Una configurazione è interpretabile come una triplice informazione:

• l’indicazione di una porzione finita di nastro σ_i 1σ_i 2…σ_inσ_in+1σ_in+2…σ_im contenente caratteri diversi dal blank, a differenza del resto del nastro che contiene solo il carattere blank;

• l’indicazione dello stato q_j in cui si trova la macchina;

• l’indicazione del carattere σ_in+1, su cui è posizionata la testina della macchina.

Una configurazione si dice iniziale se q_j = q₀ mentre si dice finale se q_j = q_ƒ.

Una transizione elementare di una macchina di Turing è una funzione C → C dove C è l’insieme delle sue possibili configurazioni e una transizione dalla configurazione c₁, alla configurazione c₂ è simbolicamente indicata con c₁ ⊦ c₂. Un calcolo di una macchina di Turing è una sequenza di configurazioni c₁, c₂, …, c_k, … tale che c₁ è una configurazione iniziale e per ogni i ≥ 1, c_i ⊦ c_i+1; se la sequenza c₁, c₂, …, c_k è finita, allora c_k deve essere una configurazione finale.

Una funzione aritmetica ƒ: Nⁿ → N, che a una n-pla di numeri naturali associa un numero naturale, è calcolabile secondo Turing (o Turing-calcolabile o T-calcolabile) se esiste una macchina di Turing M tale che da una configurazione iniziale contenente una qualsiasi n-pla x₁, …, x_n produce una configurazione finale contenente y, essendo y = ƒ(x₁, …, x_n). Trattandosi di una macchina logica astratta, la formalizzazione dei numeri naturali da rappresentare è semplificata al massimo: il numero 0 è rappresentato con un simbolo, per esempio una barretta |, mentre il numero n è rappresentato da n + 1 barrette; l’alfabeto Σ della macchina può essere così ridotto a due soli simboli: {|, □}. L’insieme delle funzioni Turing-calcolabili coincide con l’insieme delle funzioni rappresentabili con altri formalismi costruiti per dare una definizione rigorosa al concetto di calcolabilità (→ Post, sistema di; → lambda-calcolo); tutti questi formalismi descrivono tutte e sole le funzioni ricorsive. La tesi di → Church afferma appunto che l’insieme delle funzioni ricorsive coincide con quello delle funzioni calcolabili.

Il funzionamento di una macchina di Turing è descritto dall’insieme di istruzioni relative al modo di operare della funzione δ: K × Σ → K × Σ × {d, s, i }; tali istruzioni sono anch’esse memorizzate sul nastro e danno alla macchina la possibilità di scorrere tra la zona dove esse sono memorizzate e la parte del nastro stesso dove essa opera. L’importanza di tale modello logico sta, quindi, proprio nel fatto che l’automa è in grado di memorizzare sia dati che istruzioni sullo stesso supporto e con le stesse caratteristiche, sebbene in locazioni diverse. Estendendo tale processo, Turing descrisse macchine che compiono azioni elementari (quali copiare un dato, cancellare un carattere ecc…) e macchine più complesse ottenute come composizione di macchine elementari e giunse a descrivere il funzionamento di un automa universale, detto appunto macchina universale di Turing, in grado di simulare ogni altra macchina di Turing. Tale automa universale è alla base delle successive evoluzioni che hanno portato agli automi a programma e all’organizzazione logica dei moderni computer.

Pur nella sua grande potenza logica, la macchina di Turing ha tuttavia un limite intrinseco: data una configurazione iniziale di una macchina di Turing non è decidibile a priori la sua possibilità di giungere a un termine, cioè a una configurazione finale (indecidibilità della fermata di una macchina di Turing). Come ogni automa, la macchina di Turing può essere utilizzata come riconoscitore di un linguaggio, stabilendo che una stringa scritta sul nastro di una macchina di Turing M appartiene al linguaggio L costruito a partire dall’alfabeto Σ di M se la macchina è in una configurazione finale quando giunge al termine della stringa. Come riconoscitore di linguaggi, una macchina di Turing è un automa molto generale, che ha come casi particolari altri automi, quale per esempio l’automa a stati finiti. Corrispondentemente, un linguaggio riconosciuto da una macchina di Turing ha caratteristiche più generali di quelli riconosciuti da automi più specifici; così è, per esempio, un linguaggio regolare che è riconosciuto da un automa a stati finiti (→ automa). Si costruisce così una gerarchia di linguaggi che corrisponde alla gerarchia di automi, il cui livello più alto è appunto la macchina di Turing: la sua generalità va tuttavia a scapito della decidibilità perché quanto più è generale un automa e ampia la classe dei linguaggi che esso può riconoscere, tanto più numerosi sono i problemi non decidibili che riguardano tali linguaggi.