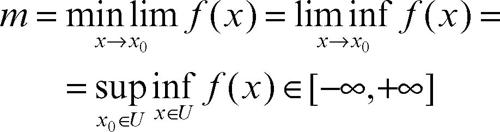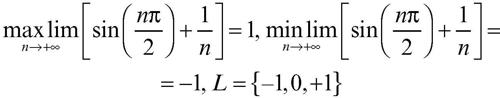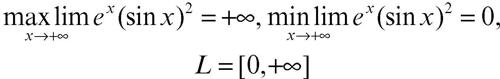massimo e minimo limite

massimo e minimo limite

massimo e minimo limite concetto che si utilizza nei casi in cui una funzione non ammetta limite ma, avendo per esempio un carattere oscillante, si approssimi tuttavia ad alcuni valori, diversi tra loro, senza mai “sceglierne” uno cui convergere.

Massimo limite

Formalmente, se ƒ(x): R → R è una funzione e x₀ un punto di accumulazione del suo dominio, si consideri un intorno U di x₀. L’estremo superiore

esiste (finito o +∞) e non cresce quando U diventa sempre più piccolo. Perciò esiste, senza alcuna eccezione, considerando la retta estesa con −∞ e +∞

Tale valore si designa con i simboli equivalenti

oppure

oppure ancora

ed è sempre possibile trovare una successione {x_n} ⊂ Dom(ƒ ), con x_n → x₀ tale che

Si possono distinguere per chiarezza i casi:

• per x₀ finito si ha

• per x₀ = +∞ si ha

(e analogamente per −∞).

Questa seconda scrittura è adatta in particolare al caso delle successioni:

Minimo limite

In modo analogo si introduce il minimo limite (o limite inferiore):

Questi due numeri esistono sempre e vale la disuguaglianza

Punto limite

Più in generale, ȳ si dice punto limite di ƒ(x) per x → x₀ se esiste una successione {x_n} ⊂ Dom(ƒ ), con x_n → x₀ e

L’insieme L di tutti i punti limite si chiama insieme limite; esso è sempre chiuso nella retta estesa [−∞, +∞] e i valori M e m ne sono rispettivamente il massimo e il minimo. Il limite l di ƒ(x) esiste (finito o infinito) se e solo se L si riduce al solo punto l o, equivalentemente, M = m = l.

Esempi:

lungo la successione {x_n} = {π/6 + 2n π} risulta per esempio