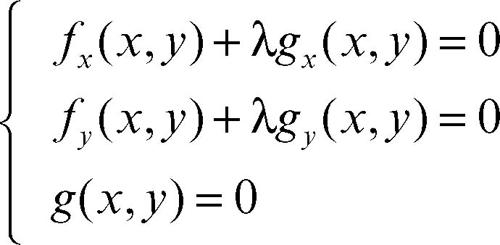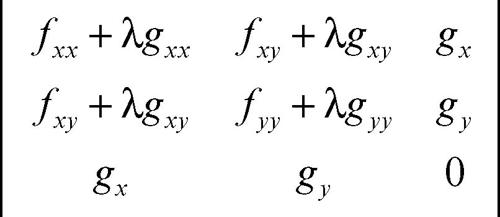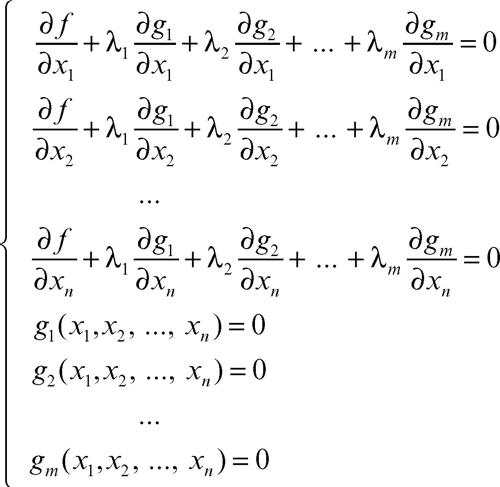massimo vincolato
massimo vincolato
massimo vincolato o massimo condizionato, valore massimo di una funzione in più variabili, quando queste siano legate da una relazione (vincolo) espressa come equazione nelle variabili stesse. Si distingue il caso di una funzione in due variabili e la sua estensione a una funzione di n variabili. Sia ƒ: R × R → R una funzione in due variabili definita in un dominio A del piano xy, e sia C una porzione di curva regolare in A, di equazione g(x, y) = 0 che rappresenta il vincolo. Un massimo vincolato di ƒ è un punto P appartenente alla curva che risulti di massimo per la funzione ƒ (le stesse considerazioni valgono per un minimo vincolato, con opportuna modifica dei termini). Nel considerare un punto P si escludono i punti nei quali le funzioni ƒ o g non sono derivabili o i punti che sono estremi della porzione di C in A. Se P è un punto di massimo (minimo) vincolato per la funzione ƒ, allora la curva C risulta tangente alla linea di livello della funzione F passante per P, da cui il sistema nelle tre incognite x, y, λ (→ Lagrange, moltiplicatori di)
che ha una soluzione data dalle coordinate del punto P e da un opportuno valore λ0 di λ Quindi, gli eventuali punti di massimo (minimo) vincolato vanno cercati tra le soluzioni del sistema precedentemente costruito. Se (x0, y0, λ0) è una soluzione di questo sistema, il punto P0(x0, y0) è poi di massimo vincolato se il determinante hessiano di L,
calcolato in (x0, y0, λ0), risulta maggiore di 0 (analogamente risulta di minimo vincolato se è minore di 0).
L’estensione a funzioni di più variabili si ha considerando una funzione ƒ(x1, x2, ..., xn) di n variabili, definita in un dominio n-dimensionale A, e m vincoli espressi dalle equazioni g1(x1, x2, ..., xn) = 0, g2(x1, x2, ..., xn) = 0, ..., gm(x1, x2, ..., xn) = 0 (con m < n); si ricercano i massimi e i minimi della varietà C definita dalle equazioni vincolari nel dominio A. Trascurando i punti nei quali si presentano fenomeni di singolarità, l’estensione del metodo di Lagrange fornisce un sistema di n + m equazioni nelle n + m incognite x1, x2, ..., xn, λ1, λ2, ..., λm:
