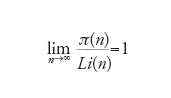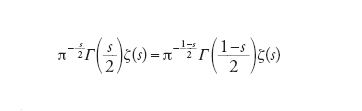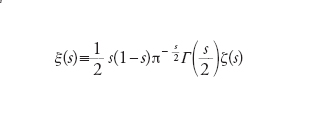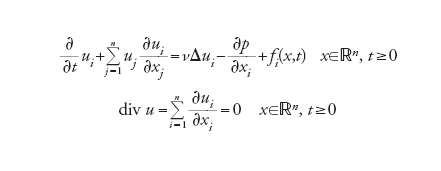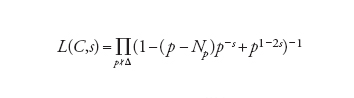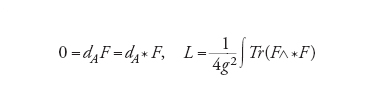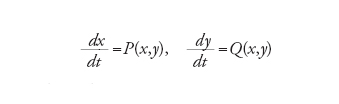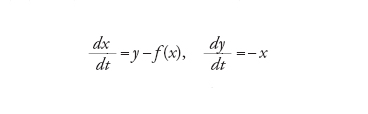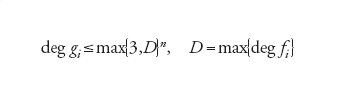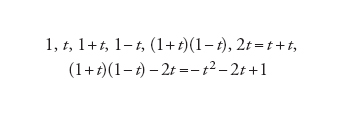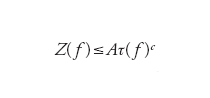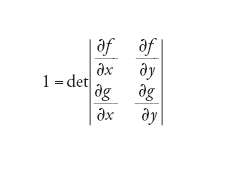Matematica: problemi aperti

Matematica: problemi aperti

Prima di parlare dei problemi aperti nella matematica è bene riflettere su quelli che ne hanno segnato la storia passata. Sono infatti proprio questi che a volte ci illuminano su quali possano essere gli sviluppi futuri di questa disciplina, nonostante proprio tale sguardo retrospettivo ci insegni che una delle loro principali caratteristiche è l'imprevedibilità della soluzione.

È facile formulare problemi semplici da spiegare ma la cui soluzione sfugge per secoli. Un tipico esempio sono i problemi sui numeri primi. La definizione di numero primo (un intero n divisibile solo per 1 e sé stesso) si apprende già nelle scuole elementari, ma è facile formulare domande difficilissime a partire da essa. Una, ben nota e classica, è la congettura di Goldbach, formulata in una lettera a Leonhard Euler nel 1742. Tale congettura afferma che ogni numero pari 2m si può scrivere almeno in un modo come somma di due numeri primi. Nonostante gli studi fatti sull'argomento, e l'inclinazione generale a credere che sia vera, non si ha idea di come provarla.

Ancora, il problema dei primi gemelli chiede se esistano infinite coppie di primi del tipo p, p+2. Un altro classico problema è se esistano infiniti numeri primi della forma n²+1, come per esempio 17=4²+1, 37=6²+1, 101=10²+1 (o più in generale espressi tramite un polinomio di grado maggiore di 1). Per il grado 1 vi è un famoso teorema di Peter Gustav Lejeune Dirichlet sull'esistenza di infiniti primi in una progressione aritmetica an+b, con a e b primi tra loro: la dimostrazione utilizza uno strumento analitico, le cosiddette serie L, che sono fra le più affascinanti e misteriose funzioni speciali. Su di esse esistono numerosi problemi aperti di difficilissima soluzione.

Un altro problema sui primi (che ha avuto recentemente nuova attenzione dopo il lavoro di Manindra Agrawal e altri sul test polinomiale di primalità e la discussione del problema P verso NP) è se esistano infiniti primi di Sophie Germain, ovvero della forma p=2q+1 in cui anche q è primo.

Abbiamo già detto che la matematica si sviluppa su tempi lunghi. Per i Greci era basata sulla geometria e anche i loro metodi di calcolo erano geometrici. Gli studiosi greci e poi alessandrini hanno lasciato aperti due grandi problemi risolti dopo quasi 2000 anni e le cui risposte sono rimaste capisaldi della matematica: (a) l'indipendenza dell'assioma delle parallele nella geometria euclidea, ovvero del quinto postulato di Euclide; (b) il problema della quadratura del cerchio.

A questo proposito, la risposta è che esistono geometrie non euclidee, cioè che non soddisfano il quinto postulato ma tutti gli altri. Per questo problema vanno citati i nomi di Friederich Gauss, János Bolyai, Nicolaj I. Lobačevskij.

L'analisi delle loro proprietà porta rapidamente allo studio delle geometrie secondo il loro gruppo di simmetrie (isometrie dello spazio) e questo conduce all'idea di spazio simmetrico, ovvero uno spazio con le usuali nozioni di retta e distanza che sia totalmente isotropo e inoltre simmetrico in ogni punto rispetto all'inversione di tutte le rette.

Un'altra importante direzione di ricerca è l'idea di geometria introdotta da Bernhard Riemann, che studia più in generale spazi non isotropi e quindi le variazioni della geometria locale. Qui la nozione moderna è quella di varietà differenziabile riemanniana. Si tratta di uno spazio che localmente ammette una descrizione in termini di coordinate come nella geometria cartesiana e in cui la distanza si calcola con i metodi del calcolo infinitesimale avendo a disposizione una descrizione euclidea in intorni sufficientemente piccoli di ogni punto.

La questione della quadratura del cerchio dipende invece dalla classificazione dei numeri in algebrici e trascendenti. Il problema parte dalla geometria dunque, ma si risolve tramite l'algebra e l'analisi matematica: la risposta che il cerchio non si può quadrare deriva dal fatto che π è trascendente, ovvero non è radice di un polinomio a coefficienti interi.

Passando all'era moderna, dopo che i matematici italiani del Cinquecento hanno trovato formule risolutive per le equazioni di terzo e quarto grado, la ricerca di analoghe formule per quelle di grado superiore diviene uno dei problemi più difficili dell'algebra. L'analisi dell'equazione di quinto grado porta molto lontano e si trasforma nella teoria dei numeri algebrici, delle forme modulari e così via.

Una delle idee fondamentali sia nella teoria delle equazioni sia nella geometria non euclidea è quella di simmetria, che si ripresenta in molti dei problemi aperti che discuteremo.

Problemi recentemente risolti

Periodicamente i matematici fanno il punto sullo stato dei problemi interni alla disciplina. Nel 1900 David Hilbert presentò una lista di 23 problemi per il XX sec. in occasione del Convegno internazionale di Parigi. Alcuni di essi sono stati risolti e su altri non si ha alcuna idea di quanto ancora resisteranno ai nostri sforzi.

A proposito dei quesiti da lui proposti, Hilbert afferma che un problema matematico deve essere difficile per stimolarci ma non del tutto inaccessibile, altrimenti rende frustrante ogni tentativo di risoluzione. Dovrebbe essere per noi una guida attraverso i sentieri intricati che portano alle verità nascoste, e finalmente un memento del piacere che otteniamo dal successo della sua soluzione.

I matematici essenzialmente cercano di provare nuovi teoremi e spesso per farlo devono eleborare nuove teorie. Il nome di molte di esse, formulate nel XX sec., non direbbe nulla a un matematico del Congresso del 1900: la topologia algebrica, l'algebra omologica, la teoria dei fasci, la teoria delle distribuzioni, i D-moduli. D'altra parte ci sono problemi, su cui i ricercatori di oggi lavorano o potrebbero farlo, che erano ben conosciuti ai matematici di cento anni fa o anche più antichi.

Tra questi ultimi, alcuni sono stati recentemente risolti, come per esempio la congettura formulata da Jules-Henri Poincaré nel 1904. Si tratta di un problema di natura geometrica e chiede se sia vero che una varietà tridimensionale compatta e semplicemente connessa sia omeomorfa a una sfera. Dopo che Steve Smale ne ha dimostrato la generalizzazione in dimensione maggiore o uguale a 5 e Michael Freedman in dimensione 4, la congettura originaria è stata finalmente dimostrata nel 2003 da Grigori Perelman.

Un altro di questi problemi è quello posto da Johannes Kepler, anche noto come problema dei pacchetti di sfere: quale è il modo più efficente di mettere insieme tante sfere? Formulato nel 1610, è stato risolto nel 1998 facendo uso del calcolatore da Thomas C. Hales e Samuel P. Ferguson con la dimostrazione che il modo migliore è quello che qualunque fruttivendolo conosce quando deve mettere in bella mostra mele o arance!

L'ultimo teorema di Fermat formulato nel 1637 e risolto nel 1995 da Andrew Wiles è forse l'esempio più famoso di equazione diofantea xⁿ+yⁿ=zⁿ; vedremo in seguito alcuni difficili problemi di tipo diofanteo.

Il problema dei 4 colori (bastano 4 colori per colorare una carta geografica?) formulato nel 1852 dal giovane matematico inglese Francis Guthrie è stato risolto nel 1976 da Heinrich Heesch, Kenneth Appel e Wolfgang Haken con l'aiuto di un IBM360. È uno degli input della moderna combinatoria e della teoria dei grafi e si lega a problematiche aperte della informatica teorica.

Per capire la continuità della matematica, possiamo subito enunciare un altro difficile problema aperto, che ha radici nella teoria delle equazioni algebriche. Circa trecento anni dopo la soluzione dell'equazione di terzo grado, il metodo di risoluzione viene finalmente portato al livello di una geniale teoria da Evariste Galois. Egli comprende in pieno il ruolo della simmetria, in questo caso delle simmetrie discrete delle radici a₁,a₂,…,a_n del polinomio f(x) di grado n che si sta studiando. Per simmetrie si intendono quegli scambi fra le radici, ovvero permutazioni, che trasformano in sé stesse le relazioni algebriche fra le radici espresse dall'annullarsi di polinomi g(a₁,…,a_n)=0, con g(x₁,…,x_n) polinomio a coefficienti nel campo di numeri su cui si considera il problema. Tali permutazioni formano un gruppo, il gruppo di Galois, e la risolubilità per radicali dipende dalla sua natura.

Segnaliamo inoltre un difficile problema aperto: dato un gruppo finito G esiste un polinomio a coefficienti razionali di cui G è gruppo di Galois? Per ora una risposta è nota solo per gruppi risolubili e per alcuni gruppi particolari.

I problemi del millennio

Ci sono probabilmente migliaia di problemi matematici aperti, ma solo pochi di questi sono considerati linee guida della ricerca futura.

Nel 2000, dichiarato anno della matematica, tramite Vladimir Igorevič Arnold la International Mathematical Union ha chiesto a vari matematici di presentare liste di problemi per il XXI sec., nello stesso stile di Hilbert. Fra questi, vale la pena di ricordare alcuni dei 18 presentati da Steven Smale e quelli da un milione di dollari della Clay Foundation.

Il primo da menzionare è l'ipotesi di Riemann, proposta dal grande matematico nel 1859. Essa si può formulare in vari modi ed è legata allo studio analitico della distribuzione dei numeri primi. È noto fin dai tempi di Euclide che questi ultimi sono infiniti, ciò nondimeno ci si può chiedere quanti fra i numeri sono primi.

Questa domanda si può formulare in modi differenti. Per esempio un classico (e semplice) teorema di Euler afferma che la somma ∑_p1/p, dove p varia sui numeri primi, diverge come la serie divergente ∑^∞_n=11/n, dove n varia su tutti i numeri naturali.

Un risultato più preciso è fornito dal cosiddetto teorema dei numeri primi, dimostrato alla fine del XIX sec. dal francese Jacques Hadamard e dal belga Charles de La Vallée Poussin seguendo una strategia sviluppata da Riemann. Indicando con π(n) il numero di primi minori o uguali a n, tale teorema può essere formulato nel modo seguente:

[1] formula

dove Li(n)≡∫ⁿ₂(logt)⁻¹dt

L'inizio dell'analisi consiste nel notare che la serie ζ(s)=∑^∞_n=11/n^s (con s variabile complessa) è convergente non appena la parte reale Re(s)>1. Riemann prova che la funzione ζ(s) ha una estensione meromorfa a tutto il piano con un polo semplice con residuo 1 per s=1 e soddisfa l'equazione funzionale

[2] formula

esprimente una simmetria rispetto all'asse Re(s)=1/2. Riemann introduce quindi la funzione

[3] formula.

Gli zeri interessanti della funzione ζ(s) si trovano sulla striscia critica 0≤Re(s)≤1 e coincidono con quelli della funzione ξ(s), olomorfa in tutto il piano. Inoltre, il numero di quelli compresi fra 0 e T è dell'ordine di (T/2π) log(T/2π)−T/2π. Fatto il cambiamento di variabili s=1/2+it e pensata la funzione come ξ(t), Riemann aggiunge l'ipotesi che nella coordinata t gli zeri siano solo reali: a oggi con il calcolatore si è dimostrato che i primi 1,5 miliardi di zeri soddisfano tale condizione! Egli prova poi che la distribuzione degli zeri della funzione ζ(s) è strettamente legata alla distribuzione dei numeri primi: l'ipotesi di Riemann è equivalente ad asserire che π(n)=Li(n)+O(n^1/2 logn). Si noti che per il teorema dei numeri primi basta provare molto meno, essenzialmente che non vi sono zeri sul bordo della striscia Re(s)=1.

L'ipotesi di Riemann ha avuto varie generalizzazioni, in quanto esistono vaste classi di natura aritmetica, come le serie L di Dirichelet, per cui analoghi di tale ipotesi si possono formulare. Le implicazioni in teoria dei numeri della validità di queste congetture sono molto estese.

Si deve notare che l'ipotesi di Riemann ha anche prodotto una vastissima serie di ricerche in geometria algebrica. In effetti già Julius Wilhelm Dedekind e Heinrich Martin Weber avevano notato una forte similitudine fra la teoria dei numeri algebrici e la teoria delle curve algebriche sui campi finiti. L'analogo dell'ipotesi di Riemann per le curve fu provato da Helmut Hasse e portò André Weil a un progetto, le congetture di Weil, che è stato alla base di una vera rivoluzione nella geometria e nell'algebra, avviata da Alexander Grothendieck e poi perfezionata da vari suoi allievi fra cui Pierre-René Deligne. Egli, completando il programma di Grothendieck, ha provato le congetture di Weil. L'idea di partenza è dimostrare che gli zeri (o numeri a essi associati) della funzione ζ si possono interpretare come autovalori di un qualche operatore. Dalle proprietà di quest'ultimo (per es., l'hermiticità) si dovrebbe derivare che gli zeri sono sulla retta reale. Nel caso degli analoghi della funzione ζ che vengono dalla teoria delle varietà algebriche sui campi finiti, la strategia di Weil è provare che si tratta dell'operatore di Frobenius indotto in spazi di un'opportuna coomologia costruita da Grothendieck (la coomologia étale).

Un'interpretazione analoga per la funzione di Riemann non è stata mai trovata ma queste idee si legano a tutti i programmi in cui appare la coomologia. Tra questi si annoverano vari problemi che qui discutiamo.

La congettura di Hodge

È forse il problema più difficile da spiegare, in quanto tratta di varietà kähleriane. Qui la topologia è solo un aspetto e la teoria è più vicina a quella delle funzioni algebriche. Senza dare una nozione generale, le varietà kälheriane compatte più comuni si trovano fra le varietà proiettive, ovvero le soluzioni (a meno di scala) di sistemi di equazioni polinomiali omogenee sui numeri complessi. Non sempre tali sistemi di equazioni possono risolversi localmente con parametri regolari a causa della presenza di singolarità (come nel vertice di un cono), ma quando questo avviene siamo in presenza di varietà di Riemann che alcune restrizioni notevoli dovute alla teoria algebrica rendono per definizione kälheriane.

è noto che esistono invarianti algebrici di una varietà X. In questo caso conviene considerare i gruppi di coomologia Hⁿ(X,ℤ). Il legame fra questi oggetti essenzialmente topologici e aspetti analitici delle varietà, stabilito nella prima metà del secolo scorso e oggi noto con il nome di calcolo differenziale intrinseco, è stata una delle grandi scoperte di Georges de Rham e William Hodge. Tale calcolo è basato sulle forme differenziali esterne del tipo ∑f_i1,…,ik(x₁,…,x_n)dx_i1 … dx_ik. In particolare de Rham mostra come i gruppi Hⁱ(X,ℝ) misurano l'ostruzione alla possibilità di integrare globalmente le forme differenziabili integrabili localmente. In termini più precisi, Hⁱ(X,ℝ) si identifica allo spazio delle i-forme differenziali ψ chiuse, ovvero con dψ=0, modulo quelle esatte e cioè della forma ψ=dϕ. Successivamente Hodge provò che in presenza di una metrica di Riemann si possono costruire un'operazione sulle forme differenziali, comunemente indicata con il simbolo *, un operatore δ≡*d* e un operatore di Laplace intrinseco Δ≡dδ+δ. Infine mostrò che le forme armoniche, ovvero quelle che soddisfano l'equazione di Laplace Δψ=0, si identificano con lo spazio di coomologia descritto da de Rham.

Nel caso in cui le varietà siano algebriche o più in generale abbiano coordinate complesse z_i, le forme si possono distinguere tramite le coordinate dz_i, dz-_i e si arriva alla nozione di p,q forme ∑f_i1,…,ik(z₁,…,z_n)dz_i1 … dz_ip dz-_j1 … dz-_jp e alla decomposizione di Hodge Hⁱ(X,ℂ)=⊕_p+q=iH^p,q. La congettura di Hodge riguarda la possibilità di costruire geometricamente le forme tramite sottovarietà, secondo una procedura classica; nel caso di varietà algebriche compatte non singolari, lega quindi la topologia e la struttura algebrica e chiede se le classi coomologiche razionali e di tipo p,p siano rappresentabili da cicli algebrici. Questa congettura si inserisce in un vasto programma di studio della geometria delle equazioni algebriche e della coomologia.

Il problema delle equazioni di Euler e di Navier-Stokes

È uno dei problemi più difficili dell'analisi e della fisica matematica e impone di studiare il comportamento delle soluzioni delle equazioni differenziali che sono alla base della dinamica dei fluidi incomprimibili. Le equazioni si possono formulare per un numero n qualunque di dimensioni spaziali.

Per n=2 la teoria è stata sviluppata da Olga A. Ladyzhenskaya ma questi risultati non si estendono al caso tridimensionale, più interessante per le applicazioni fisiche. Si tratta di equazioni differenziali non lineari nelle n+1 incognite u_i(x,t) (le componenti del vettore velocità) e p(x, t) (la pressione) che si scrivono nella forma

[4] formula

con la condizione iniziale

[5] u(x,0)=u⁰(x) x∈ℝⁿ.

I dati sono u⁰(x) e le componenti f_i(x,t) di un vettore che rappresenta una forza esterna (per es. la gravità), ν è una costante positiva che rappresenta la viscosità, Δ=∑ⁿ_i=1∂²/∂x_i² è il laplaciano.

Nonostante queste equazioni siano state studiate e molti risultati stabiliti, in particolare tramite lo studio delle cosidette soluzioni deboli, sembra che gli attuali metodi dell'analisi non siano sufficienti per farci comprendere se esistano soluzioni regolari (in presenza di dati regolari).

La congettura di Birch e Swinnerton-Dyer

È di nuovo una congettura di tipo analitico nel contesto della teoria dei numeri ma riguarda le soluzioni intere di speciali equazioni diofantee in due variabili, quelle del tipo y²=x³+ax+b con a,b interi. L'insieme C delle soluzioni complesse di una tale equazione è una curva ellittica (ovvero topologicamente analoga alla superficie di uno pneumatico) che ammette una struttura di gruppo abeliano. In particolare, i suoi punti interi (incluso l'infinito) formano un gruppo abeliano finitamente generato del tipo ℤ^r⊕F, con F gruppo finito, ma nonostante l'apparente semplicità del problema non sono noti metodi per calcolarlo (infatti si possono usare questi oggetti in crittografia). La congettura in oggetto asserisce che il numero r (il rango del gruppo) si interpreta tramite una funzione di variabile complessa, analoga alla ζ(s) di Riemann, detta serie L:

[6] formula

dove il simbolo p∤Δ indica il variare di p fra i numeri primi che non dividono il discriminante Δ, mentre N_p è il numero di soluzioni della stessa equazione cubica pensata come congruenza modulo p. L'ulteriore ipotesi è allora che L(C,s)=c(1−s)^r+termini di ordine superiore con c≠0 e in particolare L(C,1)=0 è equivalente all'esistenza di infinite soluzioni intere dell'equazione. Questa congettura ha vari raffinamenti e generalizzazioni ed è una parte essenziale del programma volta a comprendere le soluzioni intere delle equazioni algebriche a coefficienti interi (equazioni diofantee).

Esistenza di soluzioni quantistiche delle equazioni di Yang-Mills con lacuna per la massa

Il problema si inserisce nel più ampio contesto della ricerca di fondamenti rigorosi della teoria quantistica dei campi, in particolare della cromodinamica quantistica o di possibili teorie di gravità quantistica.

Per le equazioni di Maxwell il campo elettromagnetico è un tensore F=dA, con A (il potenziale) pensato come U(1)-connessione. Queste possono allora essere scritte come 0=dF=d*F, dove * è l'operatore di Hodge associato alla metrica dello spazio di Minkowski. Le equazioni classiche di Yang-Mills, di cui quelle di Maxwell sono un caso particolare, esprimono il tensore di curvatura F=dA+A A di una connessione A su un fibrato con gruppo strutturale G e hanno la forma (derivata dalla lagrangiana L)

[7] formula.

Esse sono una naturale continuazione del programma di Riemann sui fondamenti della geometria delle varietà, in quanto esprimono la variazione della curvatura di naturali campi su di esse.

La formulazione precisa del problema è allora la seguente: provare che, per ogni gruppo di Lie compatto G gruppo di gauge, esiste una teoria quantistica delle equazioni di Yang-Mills a 4 dimensioni per cui l'operatore H (hamiltoniana) ha uno spettro con una lacuna (0,Δ) con Δ>0. Le difficoltà matematiche hanno origine dal fatto che la quantizzazione non è un'operazione univocamente definita; esistono piuttosto vari metodi euristici per realizzarla, come i famosi integrali di Feynman, che al momento non hanno una formulazione rigorosa e quindi non possono essere applicati senza introdurre ogni volta opportune modifiche o nuove idee.

Il problema di P verso NP

Finora i problemi discussi hanno tutti solide origini nella matematica classica o nella fisica matematica, entrambe scienze con secoli di storia alle spalle. Il problema che discuteremo ora appartiene invece all'informatica, una scienza nata nel XX secolo. Gli aspetti teorici di questa disciplina sono essenzialmente matematici, anche se motivazioni e metodi spesso differiscono da quelli della matematica classica. Il tema generale è quello della complessità di un algoritmo, termine con cui si indica una serie di operazioni che possono essere eseguite da una macchina cui va sottoposto un determinato input per determinare l'output desiderato.

Un problema per cui si è sempre in cerca di un algoritmo ottimale è la fattorizzazione in fattori primi di un numero dato in input. Vari metodi di crittografia si basano sul fatto che non esistono (almeno al momento e forse mai) algoritmi rapidi per effettuarla e tra questi va ricordato il metodo RSA, utilizzato per compiere transazioni finanziarie su Internet che naturalmente si desidera siano sicure. Una loro drastica ottimizzazione permetterebbe di decrittare queste transazioni.

La rapidità di un algoritmo si misura in termini del suo tempo di esecuzione, ovvero del numero di passi elementari che la macchina deve fare per eseguirlo (resta, dal lato dell'hardware, il problema di far sì che i passi elementari siano i più veloci possibili). Naturalmente il tempo dipende dall'input, ma teoricamente si cerca di determinare a priori il massimo numero di passi necessari solo in termini della sua lunghezza in bit. La classe P è allora definita come la classe di problemi per cui esiste un algoritmo che produce la risposta in un numero di passi che è polinomiale nella lunghezza dell'input. Per esempio, recentemente è stato trovato un algoritmo deterministico che verifica in tempo polinomiale se un numero è primo ma al contrario si ritiene che il problema della fattorizzazione di un intero non sia in P.

Il fatto che sia possibile esprimere in termini matematici una domanda che riguarda il funzionamento dei computer dipende dai famosi risultati di Alan Turing (lo studioso inglese che decifrò il codice tedesco ENIGMA durante la Seconda guerra mondiale). Nel 1936, egli formulò una nozione teorica di calcolatore elettronico (il cui primo esemplare sarebbe stato costruito solo alcuni anni dopo) oggi indicata con il nome di macchina di Turing. Grazie a essa lo studio degli algoritmi può essere ricondotto alla teoria dei linguaggi.

Un linguaggio L, per definizione, è semplicemente un sottoinsieme dell'insieme costituito da tutte le parole ∑ in un alfabeto dato (che spesso per le macchine è quello binario). Sebbene la nozione intuitiva di linguaggio sia in questo modo certamente rispettata (almeno se fissiamo un dizionario), quelli che utilizziamo non hanno molto a che vedere con le lingue parlate e sono in genere insiemi infiniti di parole. L'idea di algoritmo viene così trasformata in quella di macchina di Turing che riconosce un dato linguaggio L, ovvero una macchina che accetta l'input, lo elabora con una serie di passi e si ferma accettandolo se è nel linguaggio dato oppure non si ferma o lo rigetta. Se per esempio consideriamo l'alfabeto formato dai soli simboli 0 e 1, allora una stringa si pensa come un numero scritto in forma binaria e il linguaggio PRIMO è formato da tutte le stringhe che rappresentano numeri primi. Una macchina di Turing riconosce PRIMO se, dando come input una stringa, si ferma e la accetta soltanto se rappresenta un primo.

Con queste convenzioni la classe P viene definita come la classe dei linguaggi per cui esiste una macchina di Turing che li accetta in tempo polinomiale. Per introdurre la classe NP (Nondeterministic polynomial time) è necessaria una premessa: oltre ai linguaggi, sottoinsiemi di ∑, possiamo pensare alle relazioni, che sono coppie di stringhe e cioè sottoinsiemi R⊂∑×∑′. Una relazione può essere essa stessa pensata come linguaggio; basta introdurre un nuovo simbolo, per esempio #, e codificare una coppia di parole (x,y) con l'unica stringa x#y. Con questa convenzione è chiaro cosa significhi affermare che la relazione R è in P.

NP viene allora definita come la classe di quei linguaggi L⊂∑ per cui esiste una relazione R⊂∑×∑′ che sia in P e per cui valga la proprietà seguente: una parola w è in L se e solo se esiste una y∈∑′ con (w,y)∈R tale che la lunghezza ∣y∣ di y sia limitata da ∣w∣^k per una costante fissata k. In altre parole l'algoritmo deve prima scegliere una parola ausiliaria ∣y∣ di lunghezza limitata da ∣w∣^k e poi procede in tempo polinomiale alla verifica. Il primo passo evidentemente non è polinomiale ed è per questo che, mentre è chiaro che P⊂NP, l'implicazione inversa può benissimo non essere vera.

Il problema è quindi determinare se P=NP e la sua importanza viene dalla scoperta che molti algoritmi apparentemente differenti sono in realtà sostanzialmente equivalenti.

Anche l'idea di confrontare due algoritmi ha un analogo in termini di linguaggi. Si introduce quindi un preordine in cui L≤_pL′, con L⊂∑ e L′⊂∑′, se esiste una funzione calcolabile in tempo polinomiale f:∑→∑′ con la proprietà

[8] w∈L f(w)∈L′.

Con questa definizione, un linguaggio L si dice NP-completo se L∈NP e per ogni linguaggio L′∈NP si ha L′≤_pL. Da essa si evince una sostanziale equivalenza fra i linguaggi NP-completi e dunque se fosse provato che uno qualunque di essi è in P si avrebbe P=NP.

Problemi di Smale e altri problemi

Vi sono molti altri problemi da un milione di dollari, alcuni dei quali non meno interessanti dei precedenti.

La congettura abc. Formulata da Joseph Oesterlé e David Masser nel 1985 dopo la soluzione del teorema di Fermat, è da molti considerata come la congettura più importante della teoria diofantea. Per enunciarla partiamo da un semplice concetto, quello di radicale rad(n) di un numero n: per definizione è il prodotto dei primi distinti che appaiono nella sua fattorizzazione e per esempio rad(100=5²×2²)=10=5×2, rad(50=5²×2)=10, rad(72=3²×2³)=6. La congettura asserisce che, posto c=a+b, per ogni ε>0 esiste una costante c_ε>0 per cui si ha

[9] max(a, b, c)〈c_ε(rad(abc))^1+ε.

per ogni coppia di numeri naturali a,b primi fra loro.

Consideriamo ora alcune questioni poste nella lista di Smale, iniziando con una variazione del sedicesimo problema di Hilbert.

Si consideri l'equazione differenziale in ℝ²

[10] formula

con P,Q due polinomi. Esiste una stima del numero K di cicli limite della forma K≤dq, dove d è il massimo dei gradi di P e di Q e q è una costante universale?

Per fare un esempio prendiamo l'equazione di Lienard

[11] formula

con f(x) polinomio con termine direttivo x^2k+1 e f(0)=0. Si prova che le traiettorie delle sue soluzioni girano intorno all'unico punto di equilibrio (0,0) e si può quindi definire una sezione di Poincaré T:ℝ⁺→ℝ⁺, dove ℝ⁺ è la parte positiva dell'asse y e T è il primo ritorno. I cicli limite sono esattamente i punti fissi di T. Per f(x)=x³−x abbiamo l'equazione di van der Pol con un unico ciclo limite.

Molti dei problemi di Smale sono legati alla complessità di calcolo.

Il primo è: dimostrare che non esiste un algoritmo polinomiale per decidere l'Hilbert Nullstellensatz. Per spiegare questa congettura ricordiamo prima di tutto che la Nullstellensatz (in forma equivalente) afferma che un sistema f₁(x₁,…,x_n)=0,…,f_k(x₁,…,x_n)=0 di equazioni polinomiali a coefficienti complessi non ha una soluzione f_i(ζ₁,…,ζ_n)=0 se e solo se esistono polinomi g_i con ∑^k_i=1g_if_i=1. Questo criterio è reso effettivo dal teorema di Brownawell, secondo il quale si possono scegliere i polinomi g_i di grado deg g_i limitato da

[12] formula.

Pertanto con l'usuale metodo di eliminazione di Gauss, o in alternativa utilizzando le basi di Gröbner, si può determinare se tali polinomi esistano.

Un altro curioso problema riguarda la complessità del calcolo del numero delle radici di un polinomio intero f(t) (in una variabile t). L'idea è di presentarlo come elemento finale di una sequenza di polinomi calcolati a partire da 1 e t applicando solo le operazioni +,−,×. Per esempio, nel caso f(t)=−t²−2t+1 una tale successione è data da

[13] formula.

Ovviamente infiniti programmi distinti possono dare lo stesso polinomio e per questa ragione si definisce l'invariante τ(f) come la minima lunghezza di un programma che calcola f. Detto Z(f) il numero di radici intere di f, la domanda è se questo sia polinomiale in τ(f) e cioè se esistano costanti A,c tali che per ogni polinomio intero f(t)∈ℤ[t] si abbia

[14] formula.

Il problema jacobiano

Si tratta di un famoso problema di algebra o geometria, formulato da Ott-Heinrich Keller nel 1939. Questa la sua forma più semplice: dati due polinomi f(x,y) e g(x,y) con determinante della matrice jacobiana uguale a 1 ovvero

[15] formula

è vero che x e y sono polinomi in f e g? La stessa domanda si può porre per n polinomi in n variabili.

Consideriamo ora la combinatoria, che anche a causa dell'uso intensivo dei computer è oggi al centro di varie investigazioni. Offriamo due problemi sull'argomento fra i numerosissimi noti.

Le matrici di Hadamard

Una matrice di Hadamard è una matrice H quadrata in cui ogni elemento è ±1 e due righe distinte sono ortogonali fra loro. In altre parole HH^t=n1_n, dove 1_n è la matrice identità e n è il numero di righe (o colonne) di H. È facile vedere che n deve essere un multiplo di 4 non appena n>2. Il problema è il seguente: esiste per ogni n siffatto una matrice di Hadamard di ordine n?

Vi sono alcune ovvie osservazioni, come il fatto che i numeri n per cui esiste una matrice di Hadamard sono chiusi per moltiplicazione. Il teorema più generale al momento è dovuto a Raymond Paley, secondo il quale esistono matrici di Hadamard per ogni numero del tipo 2^m(p^ℓ+1) con m>0 e p primo dispari.

Le matrici di Hadamard sono oggetti combinatori parte della cosidetta teoria dei disegni e analiticamente emergono come soluzioni del problema di Hadamard di determinare le matrici di determinante massimo fra quelle a coefficienti di modulo minore o uguale a 1. Esse possono essere utilizzate per costruire codici correttori di errori.

Un ulteriore problema combinatorio, apparentemente posto da Lothar Collatz nel 1937, è noto come problema di Ulam (ma anche come the mapping problem, Hasse's algorithm, Kakutani's problem, Syracuse algorithm, Syracuse problem, Thwaites conjecture). Preso un numero intero n, lo trasformiamo in T(n) con le seguenti regole: (a) se n=2m è pari si pone T(n)≡m, (b) altrimenti si pone T(n)≡3n+1. La domanda è la seguente: è vero che partendo da un qualsiasi numero e iterando l'operazione T prima o poi si arriva a 1? Per esempio, a partire da 1,2,3,4,5,6 abbiamo le sequenze:

[16] formula.

I numeri di passi necessari per raggiungere 1 sono 0, 1, 7, 2, 5, 8, 16, 3, 19, 6, 14, 9, 9, 17, 17, 4, 12, 20, 20, 7, …? Al momento nessuna correlazione tra la natura del numero di partenza e la corrispondente sequenza è stata realmente trovata.

Concludiamo con tre problemi di natura algebrica, di grande importanza anche se forse non altrettanto profondi dei precedenti.

Un problema di teoria degli invarianti

Gli algebristi del XIX sec. hanno dedicato molto tempo allo studiodegli invarianti delle forme binarie. Una forma binariaè semplicemente un polinomio omogeneo f(x,y)==∑ⁿ_i=0 a_ixⁿ⁻ⁱyⁱ. Effettuando un cambiamento lineare dideterminante 1 sulle variabili si ha una nuova forma e il problema classico è determinare le funzioni f(a₀,…,a_n) dei coefficienti che siano invarianti sotto queste trasformazioni. La teoria classica afferma che tali invarianti formano un'algebra finitamente generata la cui natura esplicita è però estremamente complicata, come mostrano le stime a priori sul numero dei generatori necessari per generarle o i calcoli delle serie i cui coefficienti sono le dimensioni in ogni grado degli spazi degli invarianti stessi. Un teorema di Melvin Hochster e Joel L. Roberts mostra che in ogni caso queste algebre hanno un'importante proprietà, detta di Cohen-Macaulay, che permette in linea teorica di spezzare in due passi il problema della determinazione degli invarianti, a partire dalla determinazione di un sistema di parametri. Calcoli algebrici mostrano che, per le forme binarie di grado n con n multiplo di 4, dovrebbe esistere un sistema di parametri formato da polinomi di grado 2,3,…,n−1. Infatti tali parameri dovrebbero essere i coefficienti del polinomio caratteristico di una trasvettante.

Il calcolo simbolico con le matrici. Poiché le matrici sono un'algebra non commutativa, per capire il loro calcolo simbolico è necessario utilizzare polinomi non commutativi. D'altro canto, se si fissa l'ordine delle matrici ci si convince rapidamente che esistono polinomi non commutativi formalmente non uguali a zero ma che si annullano identicamente quando calcolati sulle matrici: si tratta delle cosiddette identità polinomiali. Per esempio il polinomio

[17] (xy−yx)²z−z(xy−yx)²

è identicamente 0 se lo si calcola sulle matrici 2×2 ma non su quelle 3×3. Per le matrici n×n l'identità di grado minimo è quella di Amitsur-Levitzky:

[18] formula

dove σ varia fra le permutazioni di 2n numeri e sign(∙) è il segno. Si chiede di descrivere esplicitamente le identità polinomiali delle matrici n×n per ogni n. Questa domanda ha una risposta implicita, che però sembra difficile esplicitare. Se ci si limita alle espressioni multilineari di grado m, si può associare a un monomio una permutazione ciclica su m+1 elementi come per esempio

[19] x₁x₂→(1, 2, 3), x₂x₁→(2, 1, 3),

                                 x₁x₃x₂x₄→(1, 3, 2, 4, 5).

Le identità polinomiali corrispondono allora a quegli elementi dell'algebra del gruppo simmetrico S_m+1 che sono nell'ideale generato da un antisimmetrizzatore su n+1 elementi, uno spazio questo che si può descrivere esplicitamente.

Un problema collegato è quello di descrivere i polinomi centrali, ovvero che non sono identità ma il cui valore è sempre una matrice scalare. Esempi di tali polinomi sono noti per ogni n e vi è una caratterizzazione implicita nello stile della precedente, ma in generale non molto è noto su di essi. Il solo caso che si conosce in tutti i dettagli è quello con n=2 (a parte quello banale con n=1).

Un quesito ancora più difficile, legato allo studio dei corpi, chiede se dato un numero primo p esista un polinomio non commutativo f(x,y) che non sia centrale per le matrici p×p ma sia tale che f(x,y)^p sia centrale.

Questioni aperte

Abbiamo visto fino a ora problemi matematici formulati in modo preciso; tuttavia queste non sono le sole questioni aperte. Ci sono teoremi o teorie che non si sono sviluppate in passato per la complessità computazionale dei problemi affrontati e sfruttano i computer e la loro capacità di svolgere rapidamente calcoli impossibili da eseguire manualmente; si tratta di teorie spesso ai confini con la fisica o l'economia. Alcune di esse, specie quelle che vengono dalla modellizzazione dei sistemi complessi e in particolare della loro evoluzione dinamica, tendono ad avere anche degli aspetti sperimentali: non tutto è dimostrato rigorosamente e ci si accontenta dell'accordo tra simulazioni numeriche e fenomeni modellizzati. A partire da tali esperimenti si formulano quindi congetture matematiche.

Vi sono infine alcune controversie di tipo filosofico sul futuro della matematica. Ne metteremo in evidenza due.

È noto che nelle scienze esatte si è sempre parlato della matematica come del linguaggio in cui sono scritte le leggi della natura. Lo studio ormai assai avanzato della biologia e della complessità degli organismi viventi pone una forte sfida a tale assunto, sfida a cui si può rispondere in vari modi. È possibile che nel futuro svilupperemo una matematica del tutto nuova che ci permetta di descrivere la natura vivente, ma certo non possiamo escludere l'ipotesi che la sua complessità sia al di sopra delle nostre capacità di modellizzazione.

La seconda è parzialmente legata alla prima ed è relativa all'intelligenza artificiale. Possono pensare le macchine? Quali funzioni di ciò che chiamiamo intelligenza possono essere svolte da automi?

Abbiamo già visto che molto è stato fatto per dare un senso matematico alla nozione di macchina, algoritmo e così via, ma probabilmente solo la costruzione di automi sempre più versatili ci darà indicazioni più precise per rispondere a queste domande. Infine vi è un quesito che probabilmente non avrà mai risposta: la matematica che conosciamo è in qualche senso l'unica possibile? Sarebbe di grandissimo interesse poterla confrontare con quella di qualche altra specie intelligente, ma la possibilità che un tale incontro avvenga sembra decisamente remota.

Bibliografia

Agrawal 2004: Agrawal, Manindra - Kayal, Neeraj - Saxena, Nitin, PRIMES is in P, "Annals of mathematics", 160, 2004, pp. 781-793.

André 1996: André, Yves, Pour une théorie inconditionelle des motifs, Paris, Institut des Hautes Etudes Scientifiques, 1996.

Atiyah 1979: Atiyah, Michael F., Geometry of Yang-Mills fields, Pisa, Scuola Normale Superiore, 1979.

Bass 1982: Bass, Hyman - Connell, Edwin - Wright, David, The Jacobian conjecture: reduction.on degree and formal expansion of the inverse, "Bulletin of the American Mathematical Society", 7, 1982, pp. 287-330.

Birch, Swinnerton-Dyer 1965: Birch, Bryan - Swinnerton-Dyer, Peter, Notes on elliptic curves II, "Journal für die reine und angewandte Mathematik", 218, 1965, pp. 79-108.

Blum 1998: Blum, Lenore e altri, Complexity and real computation, New York, Springer, 1998.

Bombelli 1572: Bombelli, Rafael, L'algebra, Bologna, Stamperia di Giovanni Rossi, 1572.

Brenner, Cummings 1972: Brenner, Joel - Cummings, Larry, The Hadamard maximum determinant problem, "American mathematical monthly", 79, 1972, pp. 626-630.

Cardano 1545: Cardano, Girolamo, Ars magna, Norimbergae, per Ioh. Petreium, 1545.

Cipra 1998: Cipra, Barry, Packing challenge mastered at last, "Science", 281, 1998, p. 1267.

Deligne 1974: Deligne, Pierre, La conjecture de Weil I, "Publications mathématiques de l'IHES", 43, 1974, pp. 273-308.

Deligne 1980: Deligne, Pierre, La conjecture de Weil II, "Publications mathématiques de l'IHES", 52, 1980, pp. 137-252.

Faltings 1983: Faltings, Gerd, Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, ‟Inventiones mathematicae", 73, 1983, pp. 549-576.

Feynman, Hibbs 1965: Feynman, Richard - Hibbs, Albert R., Quantum mechanics and path integrals, New York, McGraw-Hill, 1965.

Feynman 1981: Feynman, Richard, The quantitative behavior of Yang-Mills theory in 2+1 dimensions, "Nuclear physics", B188, 1981, pp. 479-512.

Garey, Johnson 1979: Garey, Michael R. - Johnson, David S. Computers and intractability. A guide to the theory of NP-completeness, San Francisco, Freedman, 1979.

Grothendieck 1960-1970 : Grothendieck, Alexander, Eléments de géométrie algébrique, Paris, Institut des Hautes Etudes Scientifiques, 1960-1970.

Guy 1994: Guy, Richard K., Gaps between primes. Twin primes, in: Unsolved problems in number theory, 2. ed., New York, Springer, 1994, pp. 19-23.

Hales 1994: Hales, Thomas C., The status of the Kepler conjecture, "Mathematical intelligencer", 16, 1994, pp. 47-58.

Hirsch, Smale 1974: Hirsch, Morris - Smale, Stephane, Differential equations, dynamical systems, and linear algebra, New York, Academic Press, 1974.

Hochster, Roberts 1974: Hochster, Melvin - Roberts, Joel L., Rings of invariants of reductive groups acting on regular rings are Cohen-Macaulay, "Advances in mathematics", 13, 1974, pp. 115-175.

Hodge 1950: Hodge, William V.D., The topological invariants of algebraic varieties, in: Proceedings of the International congress of mathematicians, Cambridge, Mass., august 30-september 6, 1950, Providence (R.I.), American Mathematical Society, 1950, pp. 191-192.

Ilyashenko, Yakovenko 1995: Concerning the Hilbert 16th problem, edited by Yuri Ilyashenko, Sergej Yakovenko, Providence (R.I.), American Mathematical Society, 1995.

Keller 1939: Keller, Ott-Heinrich, Ganze Cremona-Transformationen, ‟Monatshefte für Mathematik", 47 1939, pp. 299-306.

Masser 1990: Masser, David W., Note on a conjecture of Szpiro. Les pinceaux des courbes elliptiques, ‟Astérisque", 183, 1990, pp. 19-23.

Mazur in preparazione: Mazur, Barry, Lectures on the ABC conjecture (in preparazione).

Mordell 1922-1923: Mordell, Louis J., On the rational solutions of the indeterminate equations of the third and fourth degrees, "Proceedings of the Cambridge Philosophical Society", 21, 1922-1923, pp. 179-192.

Osterwalder, Schrader 1973: Osterwalder, Konrad - Schrader, Robert, Axioms for Euclidean Green's functions, "Communications in mathematical physics", 31, 1973, pp. 83-112.

Osterwalder, Schrader 1975: Osterwalder, Konrad - Schrader, Robert, Axioms for Euclidean Green's functions, "Communications in mathematical physics", 42, 1975, pp. 281-305.

Riemann 1860: Riemann, Bernhard, Über die Anzhal der Primzahlen unter einer gegebenen Grösse, ‟Monatshefte der Königlichen Preussischen Akademie der Wissenschaften zu Berlin aus der Jahre 1859", 1860, pp. 671-680.

Riemann 1868: Riemann, Bernhard, Über die Hypothesen, welche der Geometrie zugrunde liegen (1854), ‟Abhandlungender Königlichen Gesellschaft der Wissenschaften zu Göttingen", 13, 1868.

Shanks 1993: Shanks, Daniel, Solved and unsolved problems in number theory, 4. ed., New York, Chelsea, 1993.

Smale 1998: Smale, Steve, Mathematical problems for the next century, "Mathematical intelligencer", 20, 1998, pp. 7-15.

Smale 2000: Smale, Steve, Mathematical problems for the next century, in: Mathematics: frontiers and perspectives, edited by Vladimir Arnold e altri, Providence (R.I.), American Mathematica Society, 2000.

Streater, Wightman 1964: Streater, Raymond F. - Wightman, Arthur S., PCT, spin and statistics, and all that, New York, Benjamin, 1964.

Sylvester 1868: Sylvester, James J., Problem 2511, ‟Mathematical questions and solutions", 10, 1868, p. 74.

Titchmarsh 1986: Titchmarsh, Edward C., The theory of the Riemann zeta-function, 2. ed., edited by R.D. Heath-Brown, Oxford, Clarendon, 1986.

Thwaites 1996: Thwaites, Bryan, Two conjectures, or how to win pound 1100, "Mathematical gazette", 80, 1996, pp.35-36.

Turing 1936-1937: Turing, Alan, On computable numbers, with an application to the Entscheidungsproblem, "Proceedings of the London Mathematical Society, Ser. 2", 42, 1936-1937, pp. 230-265.

Wiles 1995: Andrew, Wiles, Modular elliptic curves and Fermat's Last Theorem,. "Annals of Math". 141, 1995, pp.443-551.