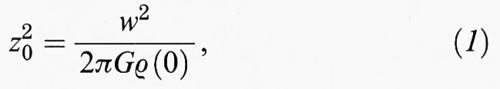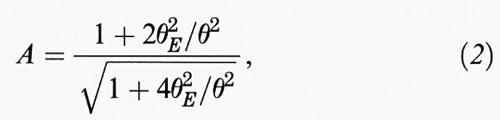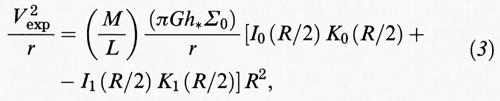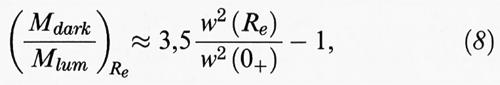Materia oscura

Materia oscura

SOMMARIO: 1. Introduzione.  2. Note storiche e metodologiche.  3. Le vicinanze del Sole.  4. Galassie a spirale.  5. Galassie ellittiche.  6. Gruppi e ammassi.  7. Teorie alternative della gravitazione.  8. Cosmologia. □ Bibliografia.

1. Introduzione

Attualmente, molti degli argomenti più scottanti e dei problemi irrisolti in astrofisica sono connessi con la materia oscura, cioè con la materia che non è osservabile attraverso la sua radiazione elettromagnetica. Telescopi e strumenti sofisticati, sulla Terra e nello spazio, permettono di esplorare l'universo da molte finestre aperte attraverso l'intero spettro delle onde elettromagnetiche - dalle onde radio ai raggi X; tuttavia, è ipotesi ormai generalmente accettata che in contesti differenti (nell'astronomia galattica ed extragalattica), debbano esistere quantità rilevanti di materia oscura, cioè non osservabile direttamente attraverso la sua radiazione elettromagnetica. È anzi possibile che il 90% dell'universo sia costituito da materiale finora non visto, della cui composizione a tutt'oggi non si ha ancora un'idea chiara e definitiva: non sappiamo, cioè, se sia costituito da corpi celesti a bassa luminosità come quelli conosciuti (pianeti o stelle nane; in questo caso essa viene spesso definita materia oscura ‛barionica'), o da buchi neri o, addirittura, da qualche particella elementare non ancora rilevata, possibile residuo del big bang iniziale (in quest'ultimo caso si parla di materia oscura ‛non barionica'). Diversi progetti sono in corso con l'obiettivo di identificare la natura di questa materia non vista.

È anche possibile che i costituenti principali della materia oscura siano differenti su scale diverse. D'altra parte, l'insoddisfazione derivante dall'incapacità di identificare da che cosa sia formata la materia oscura è così profonda, che è stato perfino suggerito che le leggi della fisica, così come sono state verificate su scala di laboratorio, non siano più valide, o almeno debbano essere riviste, quando si abbia a che fare con scale astronomiche (v. cap. 7). In questo caso la materia oscura sarebbe come l'‛etere cosmico', qualcosa che viene chiamato in causa per mascherare le nostre lacune nella conoscenza delle leggi della fisica. In effetti, basta guardare le immagini di un ammasso globulare o di una galassia per avere la prova diretta che la forza dominante è quella gravitazionale; tuttavia - come ha detto Feynman (v. Feynman e altri, 1963) - ‟non si può provare che la legge sia in questo caso esattamente quella dell'inverso del quadrato, ma solamente che, a queste enormi distanze, c'è ancora un'attrazione che tiene insieme il tutto". Infatti, le misure che attualmente pongono l'esigenza che esista del materiale inosservato sono il risultato proprio di quegli ‛esperimenti' che dovrebbero provare la validità delle leggi della fisica, e specialmente quella della legge di gravitazione, su grandi scale per distanze galattiche e intergalattiche.

D'altra parte occorre riconoscere che, secondo quanto appreso dagli esperimenti di laboratorio e da un piccolo numero di principî generali di simmetria e semplicità, le leggi della fisica hanno portato al quadro cosmologico del big bang che - nonostante varie questioni rimangano tuttora non risolte - ha ricevuto notevoli conferme osservative (come ad esempio la misura della radiazione di fondo cosmica). Forti di questo successo, in anni recenti i cosmologi hanno decisamente privilegiato uno scenario in cui Ω = ρ₀/ρ_crit = 1 (dove ρ₀ è la densità media attuale e ρ_crit la densità critica affinché l'universo sia chiuso; v. cap. 8), fornendo in tal modo un deciso contributo di entusiasmo e interesse a studiare il problema della materia oscura in astrofisica. La relazione principale tra la cosmologia e il problema della materia oscura, come vedremo, passa quindi attraverso il paragone tra la densità ρ_crit, interessante dal punto di vista cosmologico, e la densità reale ρ₀, quale risulta dalle osservazioni. È chiaro da molto tempo che la quantità di massa associata alla materia visibile porta a un valore piccolissimo di ρ₀; d'altra parte, il fatto che le osservazioni su scala galattica indicassero chiaramente come necessaria l'esistenza di materia oscura costituì presto una forte motivazione per accettare la possibilità che il valore di ρ₀ fosse in realtà molto più grande di quello osservato direttamente. Occorre notare però che la massa degli aloni oscuri intorno alle galassie è insufficiente a sostenere tale possibilità da un punto di vista cosmologico; in particolare, gli aloni potrebbero contribuire a portare la densità attuale fino al valore di ρ_crit solo se il loro raggio (dal centro della galassia) fosse dell'ordine di r_alone ≈ 2,5 h^-1 Mpc (

,

in cui H₀ è la costante di Hubble), mentre i dati suggeriscono dimensioni inferiori di un fattore 30 o più. In tal senso, mentre i risultati di molte ricerche negli anni settanta e ottanta hanno rafforzato la tesi dell'esistenza di materia oscura intorno alle galassie, il problema del divario tra la densità di massa dell'universo determinata dinamicamente e il valore di ρ_crit è divenuto sempre più acuto.

Nel seguito, concentreremo la nostra attenzione sulle principali misurazioni e sulle argomentazioni che hanno condotto alla conclusione che gli aloni oscuri esistono per quei sistemi per i quali si ritiene che le prove siano più solide e convincenti. In altri casi, si ha invece la sensazione che la prova si basi su fattori ‛estetici' piuttosto che su dati empirici diretti. L'astrofisica, del resto, è il teatro delle ipotesi più ardite e fantasiose, e talvolta l'esistenza degli oggetti astronomici più ‛esotici' (come le stelle di neutroni) è stata anticipata dall'immaginazione degli astrofisici teorici. È in questo spirito che devono essere interpretate le congetture e le argomentazioni indirette circa la presenza di materia oscura.

L'ampia letteratura su questi argomenti non ci permette di citare i singoli contributi, ma il lettore interessato potrà trovare la maggior parte dei dati relativi nelle opere riportate in bibliografia.

2. Note storiche e metodologiche

A partire dagli studi di J. C. Kapteyn (v., 1922) e di J. H. Oort, relativi ai moti stellari in vicinanza del Sole (v. cap. 3), e dagli studi di F. Zwicky dei moti galattici all'interno degli ammassi (v. cap. 6), si è congetturato che l'universo contenga molta più materia di quanta non appaia attraverso i telescopi a nostra disposizione. Sulla scala delle galassie e degli ammassi di galassie si è trovato che gli oggetti si muovevano più velocemente di quanto ci si potesse aspettare sulla base delle forze gravitazionali associate alla materia visibile. La spiegazione più naturale è quella di postulare la presenza di materia che, pur contribuendo al campo gravitazionale, semplicemente sfugge all'osservazione. Il problema relativo alla materia oscura è però divenuto di interesse primario tra gli astrofisici solo ai primi anni settanta, quando studi dettagliati dei moti dell'idrogeno atomico intorno alle galassie (v. cap. 4) condussero a ipotizzare che la presenza di aloni oscuri fosse un fatto generalizzato. Già negli anni sessanta si discuteva della possibile esistenza di aloni oscuri intorno alle galassie, ma solo nei tardi anni settanta e nei primi ottanta tale possibilità fu pienamente accettata dalla comunità scientifica. In molti casi la spinta a credere alla presenza di materia oscura è stata fornita dalle argomentazioni di natura cosmologica (v. cap. 8), anche se la quantità di materia oscura necessaria per spiegare la cinematica delle galassie, dove è più forte l'evidenza diretta della sua esistenza, è praticamente insignificante dal punto di vista cosmologico.

Da un punto di vista metodologico, è importante ricordare che le osservazioni astronomiche riguardano diverse finestre dello spettro elettromagnetico, ed è proprio da queste osservazioni che si ‛deduce' la massa degli oggetti astronomici. Molta della radiazione rivelabile otticamente proviene dalle stelle. Le teorie della struttura stellare permettono adesso di conoscere la massa di una stella, quando sia correttamente identificato il tipo cui essa appartiene. Tuttavia, se si considera la luce proveniente da una piccola regione di un disco galattico, essa risulta dall'emissione di molte stelle di tipi differenti, cioè da un'intera popolazione stellare, e occorre servirsi di un modello per effettuare una stima del cosiddetto rapporto massa-luminosità (M/L) che, a sua volta, è necessario per convertire i profili fotometrici osservati in profili di massa. Chiaramente, il modello dipende dal numero di stelle a bassa luminosità che si suppone siano presenti in una popolazione tipica, numero che è difficilmente determinabile sulla base dei dati osservativi. D'altra parte, le emissioni radio e di raggi X provengono, in prevalenza, rispettivamente dal gas freddo e caldo che si trova nelle galassie e nel mezzo intergalattico all'interno degli ammassi; la teoria dei processi di emissione normalmente fornisce un modo per stimare la quantità totale di gas responsabile dell'emissione. Tale quantità è però solo una frazione della massa totale del gas, perché potrebbero esservi grandi quantità di molecole che non contribuiscono direttamente all'emissione primaria. Per la maggior parte dei tipi di galassie, il gas costituisce solo una piccola frazione della massa totale. Inoltre, le nostre osservazioni sono complicate dalla presenza di polvere, che oscura parte della luce proveniente dalle stelle, anche se il suo contributo alla massa totale è assai modesto.

Tenendo conto di tutti questi problemi, la massa totale di un oggetto esteso come una galassia o un ammasso di galassie si misura meglio dinamicamente, procedendo come segue. In primo luogo, devono essere stabilite per ipotesi alcune proprietà geometriche del sistema considerato (spesso si assume una simmetria sferica o assiale, il che in casi specifici è in qualche modo giustificato dalle osservazioni); si adotta poi un modello che solitamente è caratterizzato da orbite semplici (come moti circolari in una galassia a disco) e da una condizione di sostanziale equilibrio (come l'equilibrio idrostatico per il gas caldo che emette raggi X o l'equilibrio del viriale per un gruppo di stelle o galassie). Infine, i dati cinematici disponibili sono interpretati e soggetti a un'operazione di fit, fornendo una misurazione dinamica della massa totale.

Quando la massa dinamica supera la massa stimata dei componenti visibili, si può essere indotti a ipotizzare la presenza di materiale inosservato. D'altra parte, la discrepanza potrebbe dipendere solo dall'eccessiva semplificazione del modello o dal fatto che alcuni dei suoi assunti non sono giustificati, e pertanto il problema della materia oscura in astrofisica non si riduce facilmente a semplici risposte affermative o negative. Qualche volta si è portati ad assumere un atteggiamento abbastanza ‛conservatore' e a concludere che la prova dell'esistenza di materia oscura ancora non esiste. Tuttavia, in astronomia questo tipo di argomentazione deduttiva, che in passato ha condotto a successi straordinari (si pensi per esempio alla scoperta di Nettuno nel 1846, basata sulle anomalie cinematiche di Urano), di recente ha indotto a credere alla scoperta di buchi neri (in particolare, un buco nero gigante nella galassia NGC 4258; v. Miyoshi e altri, 1995) o di pianeti intorno a una pulsar (v. Wolszczan e Frail, 1992).

Nell'ambito delle galassie, la necessità della presenza di materia oscura è di solito basata su due fattori che generalmente, almeno nei casi più convincenti, coesistono. Un fattore è costituito dal ‛valore' del rapporto massa-luminosità: popolazioni semplici di stelle, come quelle che si trovano nelle vicinanze del Sole, conducono a rapporti massa-luminosità (nella banda blu) di poche unità (in unità solari); se il valore dedotto risulta invece notevolmente superiore a 10, si è costretti ad ammettere la presenza di materia oscura. Il secondo fattore è l'‛incremento' del rapporto massa-luminosità con il raggio (il cosiddetto gradiente di M/L), che indica la possibile presenza di una quantità apprezzabile di materia oscura nelle parti esterne delle galassie.

Nel seguito mostreremo come un'applicazione di questi metodi ha convinto la comunità astronomica che la materia oscura in effetti esiste.

3. Le vicinanze del Sole

Il ragionamento che sta alla base del problema dell'esistenza di materia oscura nelle vicinanze del Sole, così come fu originariamente formulato da Kapteyn (v., 1922) e da Oort, può essere schematizzato nella maniera seguente: si consideri uno strato piatto di gas descritto da una densità ρ = ρ (z), dove z rappresenta la coordinata verticale. Se si suppone che il gas sia isotermo, cioè che la dispersione di velocità verticale delle particelle di gas, w, sia la stessa a differenti valori di z, le condizioni di equilibrio idrostatico definiscono una relazione fra il valore della densità sul piano equatoriale ρ (0), la scala di altezza z₀ della distribuzione di densità del gas, e la ‛temperatura' del gas w², tale che:

in cui G è la costante di gravitazione universale. Tale relazione quantifica semplicemente la previsione intuitiva che uno strato più caldo o più leggero sia più diffuso.

Usando le equazioni della dinamica stellare, il ragionamento precedente può essere riformulato per il ‛gas di stelle' nelle vicinanze del Sole; in tal modo lo strato di gas rappresenta il disco della nostra galassia. I dati disponibili sui moti delle stelle e la loro distribuzione in prossimità del Sole consentono di misurare w² e z₀: si ottiene così un valore dinamico di ρ (0) o, alternativamente, della densità (superficiale) proiettata σ = 2z₀ ρ (0). Inaspettatamente, la prima volta che fu fatta questa misurazione, si trovò una differenza tra il valore della densità di massa determinata dinamicamente e la quantità di massa, sotto forma di gas e stelle, risultante dalle osservazioni dirette. Si concluse così che circa la metà della massa che si trova nelle vicinanze del Sole doveva essere attribuita a materia inosservata.

Questo tipo di analisi si basa su numerose semplificazioni. Il modello considerato sopra, ad esempio, deve essere reso più aderente alla realtà per tener conto dell'esistenza di differenti popolazioni stellari, della disomogeneità radiale del disco e dell'esistenza di un campo gravitazionale di fondo generato da materiale non appartenente al disco, e va anche considerata la possibilità che i moti verticali non siano isotermi. Inoltre, per essere valido, il modello richiede che il campione di stelle sia rappresentativo. Infine, occorre valutare le barre di errore relative alle quantità misurate e le incertezze associate all'ammontare di massa determinato con mezzi di osservazione diretti (per esempio, la quantità di gas presente in forma molecolare).

Allo scopo di ottenere una misura sicura della possibile discrepanza tra l'ammontare del materiale osservato e la quantità di massa determinata dinamicamente, sono stati avviati due importanti programmi di lavoro. Il primo, a opera di J. N. Bahcall e dei suoi collaboratori, è arrivato alla conclusione che la discrepanza esiste, ed è grosso modo dell'ordine di quella originariamente riscontrata da Oort nei suoi studi pionieristici. I risultati del secondo e più recente programma, di K. Kuijken e G. Gilmore, sembrano in grado di conciliare la valutazione della massa dinamica con le stime dirette della massa nelle vicinanze del Sole, suggerendo così che la quantità di materia oscura in un disco ‛sottile' non sia significativa. La controversia è tuttora essenzialmente irrisolta, anche se prevale la tendenza verso una soluzione che sia una ‛via di mezzo' circa la quantità di materia nelle vicinanze del Sole. In ogni caso, sembra prevalere l'ipotesi che il disco possa essere più ‛leggero' di quello che risulta da vari modelli accreditati in passato per la distribuzione di massa nella nostra galassia.

Curiosamente, gli sviluppi recenti nella costruzione di modelli per la distribuzione di massa nelle vicinanze del Sole, da un lato mostrano che, contrariamente ai risultati ottenuti da Oort, potrebbe non essere necessaria la presenza di materia oscura nel disco, dall'altro ne riaffermano con forza la presenza dal momento che richiedono l'esistenza di un considerevole alone oscuro nella Galassia; infatti, se il disco è davvero così leggero da avere una densità locale di solo 40 ÷ 50 M_⊙/pc², il supporto alla ‛curva di rotazione' (localmente V_⊙ ≈ 220 km/s) ‛deve' derivare da un alone (oscuro) massiccio. A grandi linee, il 25% del supporto verrebbe dal disco, il 25% dal cosiddetto bulge o sferoide (cioè la componente luminosa sferoidale) e il 50% dall'alone oscuro (v. fig. 1; v. Merrifield, 1992). Il rapporto massa-luminosità (M/L) di un tale disco leggero sarebbe ben al di sotto di quanto ci si potrebbe attendere in base alla cosiddetta ‛decomposizione del disco massimo' (v. cap. 4).

Se si accetta la necessità dell'esistenza di un alone oscuro, occorre chiedersi quale sia la sua forma globale. La simmetria sferica o sferoidale è favorita per l'analogia con oggetti osservati, come gli ammassi globulari. Un ulteriore argomento a favore di questa ipotesi è rappresentato dal profilo di densità dell'alone oscuro che potrebbe somigliare a quello di una sfera isoterma (v. cap. 4). Naturalmente, un'analisi del tipo di quella adottata per la cinematica delle vicinanze del Sole non sarebbe in grado di distinguere tra un alone oscuro sferico e uno sferoide molto appiattito (o un disco piuttosto spesso). Un aspetto della forma che potrebbe essere controllato è la simmetria assiale globale del campo gravitazionale (e così dell'alone oscuro). Sono stati avanzati argomenti a sostegno di una apprezzabile triassialità (cioè deviazione dalla simmetria assiale), ma un esame locale delle costanti di Oort e della cinematica su larga scala delle stelle di carbonio suggerisce che il potenziale gravitazionale su grande scala sia dotato di simmetria assiale con un alto grado di approssimazione.

Negli ultimi anni, allo scopo di porre ulteriori vincoli alle proprietà dell'alone oscuro della nostra galassia, è stato iniziato un programma di osservazioni a lungo termine: un progetto è focalizzato sulle stelle in direzione del centro della nostra galassia, l'altro sulle stelle della Grande Nube di Magellano (una piccola galassia situata al margine dell'alone della Via Lattea): si spera che l'osservazione di milioni di stelle per un lungo periodo di tempo permetta di cogliere eventi di ‛effetto-lente' che potrebbero essere prodotti dagli oggetti oscuri dell'alone mentre passano lungo la linea ottica davanti alle stelle osservate. Utilizzando la relatività generale, è possibile calcolare le proprietà della ‛curva di luce' associata all'aumento temporaneo di brillanza della stella soggetta a effetto-lente, nell'ipotesi che gli oggetti che formano l'alone oscuro possiedano masse comprese entro un dato intervallo di valori. In particolare, il previsto fattore dell'amplificazione (per la densità di flusso da una data sorgente puntiforme) prodotta da un oggetto responsabile dell'effetto-lente posto lungo la linea di vista, è dato da:

dove θ misura la distanza angolare della sorgente dalla ‛lente' lungo il percorso incurvato del raggio di luce, e θ_E ∝ √m è la larghezza angolare del cosiddetto anello di Einstein per una ‛lente' in una data posizione geometrica e di massa m.

Alcuni eventi con le caratteristiche distintive dell'effetto-lente sono stati già identificati in direzione della Grande Nube di Magellano (v. fig. 2; v. Alcock e altri, 1993; v. Aubourg e altri, 1993). Questi eventi sono stati interpretati come dovuti alla presenza di oggetti ‛oscuri' di circa 0,1 M_⊙ di massa. L'esiguo numero di eventi osservati finora è in accordo con il numero atteso qualora l'alone oscuro della nostra galassia fosse dominato in parte significativa da oggetti di questo tipo. A loro volta le statistiche degli eventi di effetto-lente nella regione di cielo in direzione del centro della Galassia (v. Udalski e altri, 1993) sembrano indicare una quantità significativa di materia oscura nel ‛disco'. I progetti basati sull'effetto-lente, anche se interessanti e promettenti, sono caratterizzati da notevoli difficoltà dovute all'esiguità del numero di eventi attesi, all'analisi statistica impiegata nella selezione degli eventi positivi in presenza di altre cause di variabilità e all'interpretazione in termini di modelli dell'alone oscuro.

4. Galassie a spirale

In genere, il materiale nei dischi delle galassie a spirale ruota attorno al centro della galassia su orbite approssimativamente circolari (v. fig. 3). Il suo moto può essere misurato tramite studi spettroscopici, basati sull'effetto Doppler nelle righe di assorbimento o di emissione che forniscono le ‛curve di rotazione' V = V (r) - dove V è la velocità media associata alla rotazione - e quindi, indirettamente, una misura della forza gravitazionale che mantiene il materiale su quelle orbite. C'è ampia riprova, specialmente per le spirali senza una barra prominente, che il campo gravitazionale sottostante sia, con alto grado di approssimazione, a simmetria assiale. Questi studi spettroscopici possono essere eseguiti a lunghezze d'onda sia ottiche che radio. Nel caso del disco stellare bisognerebbe, in linea di principio, riferirsi alle righe di assorbimento delle atmosfere stellari, che però sono difficili da misurare. Quindi, la rotazione del disco ottico è di solito misurata sulla base delle righe di emissione dei gas caldi che circondano le regioni di formazione stellare recente. Di conseguenza, le curve di rotazione determinate otticamente riguardano, di solito, un campo di valori radiali relativamente piccolo. Non sorprende, quindi, che le osservazioni decisive per l'esistenza degli aloni oscuri provengano dagli studi radio dell'idrogeno atomico freddo (basati sulla riga di emissione di transizione iperfine a 21 cm), che - come si è spesso riscontrato - si estende a distanze talvolta due volte maggiori del raggio del disco facilmente visibile.

A grandi linee, il profilo di luminosità del disco delle galassie a spirale decresce esponenzialmente con il raggio, cioè come exp (- r/h_*), così che a 4 o 5h_* il disco ottico praticamente cessa (più del 90% della luce è contenuta all'interno di 4h_*). Se la luce stellare rappresentasse la distribuzione di massa si potrebbe calcolare facilmente, a parte un fattore di scala generale, l'attrazione gravitazionale

dovuta alla massa distribuita nel disco come funzione del raggio:

dove Σ₀ è la brillanza centrale del disco, R ≡ r/h_*, e le I e le K indicano le funzioni di Bessel; al di là del disco ottico, l'attrazione sarebbe presto ben approssimata dalla legge dell'inverso del quadrato. In altre parole, se il rapporto massa-luminosità M/L è costante con il raggio, si può mostrare che la curva di rotazione prevista, V (r), dovrebbe essere caratterizzata da una salita iniziale, fino a un raggio ≈ h_*, seguita da una rapida decrescita kepleriana V ~ r^-1/2. Se la distribuzione della luce non è esattamente esponenziale, o se l'assunto che il rapporto M/L sia costante è solo approssimativamente giustificato, si potrebbe in qualche modo ‛spiegare' la curva di rotazione osservata, ma esplorando il campo gravitazionale di una galassia a distanza sempre maggiore dal centro ci si aspetterebbe di trovare alla fine una decrescita kepleriana. A sua volta, la prova diretta dell'esistenza di aloni oscuri attorno alle galassie a spirale è offerta proprio dalla mancanza di tale decrescita nei profili delle curve di rotazione.

Tra le prime indicazioni dell'esistenza di curve di rotazione relativamente ‛piatte' nelle galassie esterne, dovrebbe essere menzionato lo studio di M31 (la galassia a spirale in Andromeda, che appartiene al nostro gruppo locale di galassie) a opera di van de Hulst, Raimond e van Woerden (v., 1957). Probabilmente, a quel tempo non si dava molto peso alla possibilità che la discrepanza incontrata tra la massa misurata dinamicamente e quella prevista divenisse un problema serio in astrofisica: così, per esempio, il modello di M. Schmidt della nostra galassia (1965) è caratterizzato da una rapida discesa kepleriana della curva di rotazione nella regione esterna al cerchio solare.

Se le curve di rotazione piatte osservate sono dovute a un alone oscuro essenzialmente sferico, così che a grandi distanze dal centro

in cui M (r) è la massa inclusa nella sfera di raggio r, il suo profilo di densità dovrebbe essere approssimativamente della forma ρ ~ r^-2. Questa è precisamente la forma attesa per una distribuzione isoterma di materia. Benché un alone oscuro non abbia motivo di essersi rilassato in una sfera isoterma, questo è un indizio evidente che la distribuzione di materia oscura richiesta in questo contesto non sarebbe ad hoc, ma anzi risulterebbe convincente dal punto di vista fisico. Si noti che la distribuzione di stelle in galassie ellittiche dentro la sfera che contiene metà della luminosità totale del sistema, nel caso in cui il rapporto M/L sia costante, è molto vicina a ρ_* ~ r^-2, in cui ρ_* indica la densità della materia luminosa.

Negli anni settanta la questione delle curve di rotazione piatte divenne ben presto l'oggetto di vari studi teorici e osservativi. Inizialmente, fu dato rilievo alla piattezza della curva di rotazione senza dar molto peso alla sua estensione radiale. In altre parole, l'esistenza di aloni oscuri fu spesso dedotta solo in base alle curve di rotazione derivate otticamente (specialmente nel lavoro di Rubin: v., 1987). Comunque, fu presto messo in luce che gli studi cinematici circoscritti al disco ottico non sarebbero stati in grado di fornire prove convincenti dell'esistenza di aloni oscuri; in realtà, includendo l'effetto del bulge, quando sia presente, si può mostrare che, in generale, il profilo fotometrico del disco può essere convertito, con un rapporto M/L costante, in una distribuzione di massa ragionevolmente in accordo con le curve di rotazione derivate otticamente. La prova decisiva per gli aloni oscuri discende dalle curve di rotazione radio ‛estese radialmente' (iniziando dal campione di galassie osservate da A. Bosma nel 1978), come provato dal caso chiaro e decisivo della galassia a spirale NGC 3198 (v. fig. 4; v. van Albada e altri, 1985). Lo studio di curve di rotazione radio di alta qualità mostra che la materia oscura è in effetti necessaria anche nei rari casi dove esse presentino un andamento decrescente nelle parti esterne. Si deve rilevare che, al fine di tradurre le misurazioni delle curve di rotazione in affermazioni significative a proposito del campo gravitazionale globale, il campo di velocità della galassia osservata dovrebbe essere altamente simmetrico, per non essere fuorviati da distorsioni che sono notoriamente indotte da barre o deformazioni del disco.

Se si assume l'atteggiamento prudente di chiamare in causa la minima quantità di materia oscura che i dati esigono, si è portati ad adottare una decomposizione (di una curva di rotazione osservata) in disco-bulge-alone che massimizza il contributo del materiale visibile. Questa è chiamata di solito la ‛soluzione del disco massimo', dal momento che sceglie, per il rapporto M/L del disco, il massimo valore compatibile con la curva di rotazione osservata; valori più bassi di tale rapporto sarebbero ugualmente accettabili, e corrisponderebbero a maggiori quantità di materia oscura. I modelli di disco massimo tendono a sottolineare il fatto che le curve di rotazione derivate otticamente non esigono necessariamente la presenza di materia oscura. Come ulteriore richiesta di natura fisica, in questi modelli le distribuzioni di densità di materia oscura vengono considerate come decrescenti uniformemente con il raggio. Il rapporto tra materia oscura e luminosa all'interno di una sfera che racchiude il disco ottico della galassia è dell'ordine dell'unità. Al di là del disco ottico, il contributo principale alla curva di rotazione deriva dall'alone invisibile.

Seguendo questo filo di ragionamento, negli anni ottanta è emerso ed è stato sottolineato un aspetto sconcertante, noto come ‛cospirazione', relativo alla piattezza delle curve di rotazione (v. van Albada e Sancisi, 1986): nello scenario sopra descritto la parte interna della curva di rotazione è sostenuta quasi esclusivamente dal disco, mentre la parte esterna è dominata dall'alone. Inoltre, su tutta l'estensione radiale, la curva di rotazione è spesso piatta e non presenta altre particolarità. Ci si domanda allora: come mai le proprietà dell'alone oscuro e del disco stellare sono così finemente accordate da produrre un andamento piatto e liscio della curva di rotazione, mentre ci si aspetta che il comportamento dinamico del disco e dell'alone siano, in linea di principio, disaccoppiati? Tale ‛cospirazione' rimane ancora un mistero. Un tipo simile di cospirazione è stato notato, pur se non in termini così chiari, anche nella discussione sulla distribuzione di massa delle galassie ellittiche (v. cap. 5).

Studi sulla dinamica verticale delle galassie spirale, un po' simili a quelli sulle vicinanze del Sole descritti brevemente nel cap. 3, possono gettare nuova luce sul problema della materia oscura. Per galassie convenientemente inclinate rispetto alla linea di vista, sono in corso tentativi volti a disaccoppiare la dinamica verticale da quella orizzontale che, in linea di principio, dovrebbero essere in grado di indicare se la soluzione del disco massimo è quella preferita in natura.

Negli anni settanta, l'importanza attribuita dagli studi teorici alla necessità di un alone oscuro derivava in gran parte da considerazioni di stabilità generale. Basandosi sullo studio delle proprietà degli ellissoidi classici, su alcune analisi modali lineari e su alcune simulazioni a N corpi di dischi galattici, J. P. Ostriker e P. J. E. Peebles avanzarono l'ipotesi secondo la quale i dischi autogravitanti con un eccesso di energia cinetica sotto forma di moti di rotazione sistematici (K_ordered) relativamente all'energia di legame gravitazionale (∣W∣)

dovrebbero presentare una spiccata ‛instabilità di barra'. Una maniera per stabilizzare il disco nei confronti di questi modi di barra può essere la presenza di un alone sufficientemente massiccio, che contribuirebbe ad aumentare il valore di ∣W∣ senza apprezzabile cambiamento di K_ordered. Curiosamente, la stima della massa oscura relativamente a quella luminosa all'interno del raggio ottico sulla base delle condizioni di stabilità è simile a quella ottenuta dallo studio delle curve di rotazione. In tal modo, la necessità empirica dell'esistenza di materia oscura risultava legata a una motivazione teorica più profonda e da ciò derivò una notevole spinta verso una generale accettazione dell'esistenza di aloni oscuri intorno alle galassie a spirale.

In tempi successivi, numerosi ‛controesempi' misero in dubbio la validità del criterio di stabilità generale usato per giustificare la presenza di aloni oscuri. Va tuttavia osservato che uno studio completo della stabilità dei dischi galattici, mirato a interpretare la struttura a spirale nelle galassie (v. Bertin e Lin, 1996), ha recentemente confermato il punto di vista secondo il quale una struttura non barrata su grande scala può essere sostenuta e giustificata, in generale, solo se il disco attivo è relativamente leggero, come accadrebbe se il disco fosse immerso in un alone massiccio. In altri termini, la conclusione di tali studi sulla morfologia dei modi a spirale su grande scala nelle galassie suggerisce che, se la soluzione del disco massimo fosse la regola (per esempio se fosse presente solo una quantità ‛minimale' di materia oscura), allora la maggior parte dei dischi galattici, se sufficientemente sottili, sarebbero instabili rispetto ai modi di barra.

La presenza di strutture barrate non ha niente di straordinario in sé. Il punto chiave risiede nel fatto che l'applicazione del criterio di Ostriker-Peebles presupponeva implicitamente il fatto che nelle galassie a spirale (a cominciare dalla nostra) molti dischi fossero non barrati, e ciò rendeva necessario ammettere la presenza di un alone oscuro considerevole. Adesso è noto che la presenza di una barra non è così rara. Recentemente, la possibilità di ottenere immagini nel vicino infrarosso (intorno a 2,2 µm) ha consentito di individuare più facilmente una barra nel disco sottostante composto da stelle evolute, e in realtà questa è presente in molti oggetti (come NGC 309 o NGC 1637) addirittura quando l'immagine ottica non la rivela. Altri oggetti (come NGC 4622), invece, non mostrano tracce di barre. Sarebbe auspicabile l'osservazione di un campione di galassie ampio e completo per verificare quanto frequentemente ricorre la morfologia barrata. Se la maggior parte delle galassie a spirale dovesse rivelare una barra nel disco stellare sottostante, allora la decomposizione del disco massimo sembrerebbe quella preferita in natura.

Le regioni esterne dei dischi galattici sono spesso soggette a ‛incurvamenti' che possono imporre alcuni vincoli dinamici sulle proprietà degli aloni oscuri su grande scala. È stato posto in evidenza che se si interpretano tali deformazioni come distorsioni stazionarie (‛stabili in maniera neutra'), che non propagano alcuna distorsione nel piano della galassia, allora si può concludere che l'alone è dominante, tale da rendere ‛sferico' il campo gravitazionale, o almeno, a seconda della forma della deformazione osservata, deve esserlo entro certi limiti (v. Sparke e Casertano, 1988). Si potrebbe obiettare che l'asserzione di persistenza, implicita in questi studi, non è giustificata dalla lunga scala temporale che caratterizza la periferia della galassia. Fortunatamente, se si considera il problema dal punto di vista dell'eccitazione e della propagazione ondulatoria, possono essere individuati altri vincoli dinamici interessanti. In particolare, il profilo di ampiezza della deformazione H (r), come risultato della conservazione dell'azione dell'onda, dovrebbe seguire la relazione H (r) ~ r^-1/2 σ^-1, dove σ è la densità superficiale; su questa base, il comportamento osservato suggerisce che debba essere presente un alone oscuro notevole (v. Bertin e Mark, 1980). D'altra parte, in assenza di alone oscuro, i modi di incurvamento sembrano mancare di un'adeguata sorgente di amplificazione, essenzialmente perché il termine di instabilità di Jeans, associato alle onde di densità, per le onde di incurvamento è sostituito da un termine che indica una forza di richiamo:

- 2πGσ ∣k∣ → + 2πGσ ∣k∣. (6)

Qui k è il numero d'onda radiale della perturbazione. Per contro, un alone oscuro sferoidale ruotante lentamente o non ruotante fornirebbe una sorgente naturale di eccitazione, attraverso una specie di instabilità a due correnti, secondo la quale il disco sventolerebbe come una bandiera (v. Bertin e Mark, 1980).

Se si ammette l'esistenza di aloni oscuri, si dovrebbero cercare dei vincoli sulle loro forme intrinseche. Innanzitutto, ci si dovrebbe chiedere se la loro simmetria sia conforme a quella del disco, cioè se essi possano essere considerati essenzialmente a simmetria assiale. Quindi ci si dovrebbe domandare se siano abbastanza rotondi oppure molto schiacciati. Il caso della nostra galassia (v. cap. 3) suggerirebbe una simmetria assiale e sarebbe in contrasto con una distribuzione della materia oscura in un disco sottile. Lo studio delle curve di rotazione estese radialmente nelle spirali mostra in effetti che in molti casi il potenziale gravitazionale sottostante deve essere essenzialmente a simmetria assiale. È stato anche suggerito che la piccola dispersione nella relazione di Tully-Fisher sarebbe incompatibile con aloni dominati da triassialità (v. Franx e de Zeeuw, 1992). Alcuni studi sulle galassie esterne basati sulle osservazioni di anelli polari attorno ai dischi galattici suggeriscono che gli aloni oscuri debbano essere sferoidali e abbastanza piatti (v. Sackett e altri, 1994).

5. Galassie ellittiche

Dalla discussione precedente, basata sull'uso delle leggi della fisica classica, dovrebbe essere chiaro che le galassie a spirale possiedono quantità significative di materia oscura nella forma di un alone diffuso. Se si segue questa linea di ragionamento, ci si attende che anche le galassie ellittiche possiedano aloni oscuri. Come può essere dimostrata la validità di questa previsione? Come può essere misurata la quantità e la distribuzione di materia oscura nelle galassie ellittiche? È da notare che in queste ultime, contrariamente al caso delle galassie a spirale, si può facilmente immaginare che l'alone abbia la stessa distribuzione spaziale della materia luminosa, dal momento che entrambi i componenti possono essere pensati come il prodotto di un collasso non dissipativo.

In generale, le galassie ellittiche mancano di un tracciante cinematico diretto, come l'emissione di idrogeno atomico che nelle galassie a spirale è usata per derivare le curve di rotazione. Per di più, mentre la determinazione della simmetria spaziale del potenziale gravitazionale sottostante nel caso delle spirali è stata sottoposta a verifiche convincenti, essa rappresenta il problema principale nel caso delle galassie ellittiche, non solo in generale, ma specialmente per oggetti singoli; in particolare, è difficile stabilire se il sistema in esame sia fondamentalmente a simmetria assiale o se invece esso sia triassiale. Tuttavia, le conseguenze che si possono trarre da modelli fisicamente accettabili consentono di affermare che ci sono, anche per le galassie ellittiche, molti oggetti per i quali si trovano aloni rilevanti. Invero, risulta che la distribuzione globale di materia per tali oggetti non si discosta molto dal comportamento rilevato nelle spirali (v. Bertin e Stiavelli, 1993). Nel seguito vengono riassunti alcuni dei problemi più interessanti relativi a questa classe di oggetti.

Molto raramente si trova dell'idrogeno atomico freddo attorno a galassie ellittiche; la sua distribuzione è generalmente irregolare, con alcune eccezioni, per esempio l'anello stretto e regolare intorno a IC 2006 (v. Franx e altri, 1994). La modellizzazione della cinematica del gas non è facile. In alcuni casi sembrano esistere prove della presenza di materia oscura. Per la galassia NGC 4278, sembra che il rapporto M/L debba aumentare di un fattore 2 dal centro a una distanza 6R_e (per una galassia ellittica, R_e è il raggio effettivo, definito come il raggio del cerchio che include metà della luminosità totale della galassia).

Spesso è presente del gas ionizzato caldo (osservato attraverso le linee di emissione ottiche), ma di solito esso ha solo una estensione radiale modesta; in questo caso è difficile, ancor più che per l'idrogeno atomico freddo, supporre che il gas abbia raggiunto uno stato di equilibrio non turbolento, come si richiede per poter utilizzare orbite chiuse come modello per il campo di velocità del gas. Uno studio dettagliato di NGC 5077, basato sulle orbite chiuse fredde per il gas in un potenziale triassiale, indica che la cinematica del gas osservata può essere riprodotta con un rapporto M/L costante fino a R_e; a tale scala, dunque, non si trova alcuna evidenza della presenza di materia oscura.

La scoperta che da molte galassie ellittiche vi è emissione di radiazione X estesa radialmente ha fatto subito pensare che questi dati potessero rappresentare una diagnostica indipendente della buca di potenziale di questi oggetti. Questa emissione di raggi X è dovuta alla presenza di un gas caldo diffuso, almeno negli oggetti più luminosi. Nel modello più semplice si suppone che questo gas caldo sia in equilibrio quasi-idrostatico, cioè in accordo con la seguente relazione:

in cui p è la pressione del gas. In tal modo, dalla densità osservata e dalla distribuzione di temperatura del gas si può dedurre la forza gravitazionale necessaria per legare la galassia. I primi lavori su questo argomento portarono a concludere che in realtà i raggi X forniscono una forte evidenza, forse l'unica attendibile, dell'esistenza di aloni oscuri attorno alle galassie ellittiche. Purtroppo, ricavare dei profili di temperatura attendibili per il gas caldo dalle informazioni spettroscopiche è un compito difficilissimo anche nei casi più favorevoli (v. Trinchieri e altri, 1994) e in ogni caso la fisica del raffreddamento dei gas caldi è molto complessa. Occorre dunque essere assai cauti (v. Fabbiano, 1989), specialmente perché le galassie brillanti che emettono raggi X sono state trovate solo in ammassi nei quali il confinamento del gas caldo non è dovuto unicamente al campo gravitazionale della singola galassia, ma anche alla pressione esterna esercitata dal mezzo intergalattico. Recentemente è stato dimostrato, per la galassia NGC 4472, che i dati relativi ai raggi X fino a 7R_e non permettono di stabilire se tra i modelli definiti dalle osservazioni della dinamica stellare siano da preferire quelli con o quelli senza materia oscura. Un fatto degno di interesse associato al gas caldo è che la forma dell'immagine ottica di una galassia ellittica (data dalla luce delle stelle) e la forma dell'immagine a raggi X (che si spera descriva la buca di potenziale gravitazionale) possono essere disaccoppiate. Tale disaccoppiamento, osservato in oggetti piuttosto piatti come NGC 720, suggerisce la presenza di un alone abbastanza rotondo, leggermente inclinato rispetto alla componente luminosa (v. Buote e Canizares, 1994).

Un'altra classe promettente di traccianti del campo gravitazionale nelle galassie ellittiche è quella degli oggetti singoli, in particolare ammassi globulari e nebulose planetarie, che si possono veder orbitare intorno alla galassia. Questo tipo di studi si trova attualmente in uno stadio avanzato per galassie relativamente vicine, come NGC 5128, M87 e NGC 4472; tuttavia, anche se le velocità radiali individuali possono essere misurate con buona precisione, l'uso di questi dati dipende dalla soluzione di complessi problemi di modellizzazione.

Studi spettroscopici della luce stellare (vale a dire informazioni cinematiche sulla distribuzione di stelle dedotte dalle righe spettrali di assorbimento della luce stellare) costituiscono la fonte più ovvia di dati relativi al campo gravitazionale nelle galassie ellittiche. Tuttavia, queste informazioni sono state a lungo considerate come lo strumento diagnostico meno utile, essenzialmente per due ragioni: da un lato, gli strumenti disponibili fino a tempi recenti non consentivano di ottenere profili cinematici a distanze sufficientemente grandi dal centro, e in realtà i profili, peraltro affetti da errori notevoli, si estendevano di solito solo fino a una frazione di R_e; dall'altro, si era piuttosto scettici sull'utilità di questi dati, poiché si sapeva che l'osservazione di un profilo di dispersione di velocità relativamente piatto poteva essere interpretato sia come dovuto a una variazione del rapporto M/L, cioè alla presenza di materia oscura, sia, alternativamente, come un'indicazione che il sistema era abbondantemente popolato da orbite tangenziali.

Adesso la situazione della diagnostica tramite la dinamica stellare è cambiata sostanzialmente. Anzitutto è possibile misurare con accuratezza profili cinematici ben oltre R_e. Inoltre, dal punto di vista della modellizzazione, è stato proposto un metodo valido per sistemi quasi sferici, basato sull'ipotesi che lo stato attuale delle galassie ellittiche sia quello risultante da un collasso non dissipativo; tale metodo consente di interpretare l'universalità dei profili di luminosità delle galassie ellittiche. Questa ipotesi suggerisce che il profilo della dispersione di velocità osservato possa cambiare notevolmente senza effetti significativi sulla distribuzione di densità della componente luminosa; in particolare, esso risulta più piatto in presenza di un alone oscuro. Usando questo modello dello stato dinamico delle galassie ellittiche, la quantità di materia oscura all'interno del raggio effettivo è data dalla semplice relazione:

dove w (R_e) è la dispersione di velocità osservata a R_e, e w (0₊) è la dispersione di velocità misurata al centro, escludendo eventuali peculiarità associate alla dinamica del nucleo. Alcune galassie, come NGC 3379, possono essere ben rappresentate da modelli senza alone oscuro, mentre altre, come NGC 4472, richiedono quantità significative di materia oscura. Sono state notate delle correlazioni in relazione alla dimensione della galassia, all'emissione di raggi X e alle proprietà radio degli oggetti che possiedono un alone oscuro (v. Bertin e altri, 1994). Al contrario, se i medesimi oggetti per i quali si è giunti alla conclusione che sia presente materia oscura, come NGC 4472 e NGC 7796, sono modellizzati con un rapporto M/L costante, allora la distribuzione delle orbite stellari dovrebbe essere per la maggior parte popolata da orbite tangenziali. È però assai arduo immaginare un processo di formazione che porti a moti in prevalenza quasi circolari senza dare origine a una rotazione globale. Per di più, quando la funzione di distribuzione si discosta significativamente da una gaussiana, sono prevedibili instabilità generali su scale di tempo veloci, così che i modelli in questione non sembrano fisicamente accettabili.

6. Gruppi e ammassi

Il Gruppo Locale è un insieme di circa 30 galassie che comprende la Via Lattea e alcuni oggetti ben conosciuti, come le Nubi di Magellano, Andromeda (M 31) e M 33. In un modello semplificato, potremmo supporre che la dinamica del gruppo sia dominata dalle due componenti più luminose, cioè la Via Lattea e M 31, e che la separazione attuale fra di esse, di circa 750 kpc, decresca a una velocità di circa 125 km/s. Dal momento che la scala di distanza ottenuta moltiplicando questa velocità per il tempo di Hubble è dell'ordine di 1 Mpc, sembra improbabile che si sia in presenza di un incontro casuale tra due galassie; è più plausibile, invece, considerare il sistema come legato gravitazionalmente e disaccoppiato dall'espansione di Hubble. In questo caso si ottiene un limite inferiore alla massa totale di M 31 e della Via Lattea supponendo che inizialmente le due galassie fossero vicine, che la loro separazione sia aumentata con l'espansione dell'universo e che ora esse stiano riavvicinandosi come conseguenza della mutua attrazione gravitazionale. Usando come età dell'universo 15 • 10⁹ anni, questo semplice modello porta a una massa totale di 4 • 10¹² M_⊙. Combinando questo valore con quelli noti delle luminosità totali delle due galassie, si ottiene un valore globale del rapporto massa-luminosità vicino a 100 M_⊙/L_⊙, il che implica che l'alone della nostra galassia (v. cap. 3) si estende verso l'esterno per almeno 100 kpc. Questo risultato è essenzialmente confermato dagli studi più recenti e dettagliati del Gruppo Locale, anch'essi basati sull'assunto che il sistema sia legato gravitazionalmente.

Il procedimento appena descritto può essere esteso considerando la dinamica delle coppie di galassie anche all'esterno del Gruppo Locale. Contrariamente al caso delle stelle binarie, per le quali le orbite possono essere misurate su intervalli di tempo significativi, qui si può solo misurare la separazione proiettata tra i due oggetti e le componenti radiali (lungo la linea di vista) della velocità orbitale a un certo istante. Un dato insieme di oggetti sarà in genere contaminato da coppie non fisiche; per di più, anche le coppie genuine possono risentire degli effetti di galassie vicine e di gruppi (come si verifica per M 31 e la Via Lattea). Inoltre, si devono avanzare delle ipotesi sul tipo di interazione gravitazionale che sussiste tra i due membri di una data coppia (specialmente se si rendono necessari aloni estesi, l'interazione non è quella semplice di due masse puntiformi) e sulla geometria delle orbite. Così non deve meravigliare che lo studio statistico delle galassie binarie non abbia portato per ora a conclusioni sicure sulla presenza di grandi quantità di materia oscura, benché lo studio delle coppie con dati cinematici di alta qualità (v. van Moorsel, 1987) suggerisca che gli aloni oscuri sono necessari per spiegare le osservazioni e ponga limiti significativi sulla loro estensione radiale. Ci si comincia a chiedere se gli aloni estesi che sono stati proposti possano entrare in contatto diretto, dando luogo a un decadimento dell'orbita, per attrito dinamico, a una velocità abbastanza elevata.

Tendenze e problemi analoghi, perfino più complessi, si incontrano nello studio dei cosiddetti ‛gruppi di galassie' (non esiste una definizione più precisa; il termine ammasso di galassie è solitamente riservato a sistemi più grandi, spesso costituiti da centinaia di galassie), con l'ulteriore complicazione che gli effetti cosmologici, dovuti all'espansione di Hubble e alla materia distribuita ‛fuori' dai gruppi, possono divenire un fattore rilevante. A dispetto di tutte le obiezioni che si possono sollevare, le masse dei gruppi vengono dedotte dal teorema del viriale,

2K + W = 0. (9)

o dai relativi ‛estimatori di massa'. I valori del rapporto massa-luminosità coprono intervalli piuttosto estesi, con valori tipici simili a quelli sopra riportati per il Gruppo Locale.

La scoperta da parte del satellite ROSAT (Roentgen Satellite) della presenza, in alcuni casi, di un'emissione diffusa di raggi X sulla scala di circa 200 kpc ha generato un nuovo interesse circa l'eventuale presenza e distribuzione di materia oscura nei gruppi di galassie. Risulta di particolare importanza il piccolo gruppo associato a NGC 2300, che apparentemente contiene solo tre galassie (v. Mulchaey e altri, 1993). Lo studio dei dati relativi ai raggi X per il gruppo a simmetria sferica di NGC 5044, costituito da una singola ellittica gigante circondata da un gran numero di nane, è basato su un modello dettagliato del flusso dovuto al raffreddamento del gas; esso fornisce un rapporto massa-luminosità di circa 130 M_⊙/L_⊙ (v. David e altri, 1994). Risultati analoghi sono stati ottenuti da Ponman e Bertram (v., 1993) nello studio del gruppo compatto di Hickson HCG 62. Se l'emissione di raggi X descrive la buca di potenziale sottostante, si deve concludere che la luce proveniente dalle galassie che appartengono al gruppo non descrive la distribuzione totale di massa. D'altra parte, se i gruppi sono pervasi da quantità considerevoli di materia oscura, l'attrito dinamico provocato da quest'ultima rende difficile prevedere per quanto tempo i componenti dell'ammasso possano sopravvivere alla fusione reciproca (o come siano stati in grado di farlo finora).

Come abbiamo detto nel cap. 2, sono stati gli studi sui moti di galassie in ammassi, a cominciare da quelli di F. Zwicky e S. Smith, a fornire la prima prova che nell'universo è presente una gran quantità di materia non luminosa. Studi più recenti hanno confermato le conclusioni generali dei primi lavori. I valori tipici dei rapporti massa-luminosità che sono dell'ordine di qualche centinaio sono in genere basati sull'assunto che materia oscura e galassie luminose abbiano la stessa distribuzione spaziale. Un caso ben studiato è quello dell'ammasso di Coma, formato da più di mille galassie luminose, principalmente ellittiche e lenticolari, posto a una distanza di circa 140 Mpc. I modelli che lasciano aperta la possibilità che la materia oscura non sia distribuita come quella luminosa permettono varie soluzioni, tutte ugualmente accettabili, con valori del rapporto massa-luminosità che arrivano fino a 500, i quali sarebbero senza dubbio interessanti da un punto di vista cosmologico (v. cap. 8). D'altra parte, uno studio dettagliato dei risultati ottici combinati con quelli ottenuti coi raggi X, come vedremo, per l'ammasso Coma riduce a 90 ÷ 250 M_⊙/L_⊙ l'intervallo consentito per il rapporto massa-luminosità; in realtà, il modello migliore sembra essere quello, caratterizzato da un intervallo 140 ÷ 190 M_⊙/L_⊙, nel quale la distribuzione di massa segue quella della luce.

Di solito, gli ammassi ricchi di galassie sono intense sorgenti di raggi X prodotti da un gas caldo all'interno dell'ammasso. Si è visto che è possibile rendere conto dei dati ottici e di quelli X trattando il gas come un plasma isotermo, coesistente con una distribuzione di galassie in moto in una buca di potenziale comune. Il modello prevede una relazione semplice ρ_gas ∝ ρ^β_galaxies tra i profili di distribuzione di densità delle galassie e quello del plasma caldo, dipendente da un parametro (β) che è il quadrato del rapporto tra la dispersione di velocità delle galassie e la velocità termica del gas. I valori tipici per le dispersioni di velocità radiali (lungo la linea di vista) delle galassie negli ammassi ricchi sono vicini a 900 km/s e le temperature caratteristiche del plasma sono intorno ai 7 keV. Il valore medio di β, ricavato dai calcoli relativi alle distribuzioni di densità, è 2/3, mentre quello ottenuto da misure dirette delle temperature del plasma e della dispersione di velocità delle galassie è 0,9, il che riduce la discrepanza notata in precedenza (v. Sarazin, 1988). Dal momento che l'emissione di raggi X sembra dovuta alla Bremsstrahlung termica, in linea di principio si può ricavare direttamente la massa del gas caldo all'interno dell'ammasso dai profili di brillanza superficiale dei raggi X osservati. In questo modo si ottiene un valore della massa del gas all'interno dell'ammasso simile o addirittura superiore alla massa totale associata alle singole galassie dell'ammasso; quest'ultima è dell'ordine del 10% della massa totale che risulterebbe dall'applicazione del teorema del viriale (9). Le incertezze sulla massa contenuta nelle regioni esterne sono compatibili con l'ipotesi che il 30 ÷ 60% della massa ricavata dal teorema del viriale sia dovuta al gas all'interno dell'ammasso (v. Sarazin, 1988). È possibile chiarire ulteriormente il problema relativo alla possibilità che le galassie luminose negli ammassi indichino la distribuzione di massa totale confrontando la forma delle isofote ottiche e di quelle a raggi X; uno studio di cinque ammassi Abell mostra isofote a raggi X sensibilmente più arrotondate rispetto alla distribuzione galattica sottostante.

Il principale problema irrisolto in relazione ai risultati discussi in questo capitolo concerne la possibilità di considerare un dato insieme di oggetti come un sistema autogravitante legato e isolato. Un diverso, e inatteso, modo di determinare la distribuzione di massa negli ammassi di galassie è fornito dagli archi luminosi giganti interpretati come dovuti all'effetto-lente gravitazionale, da parte dell'ammasso, di sorgenti molto distanti sullo sfondo (v. fig. 5). L'analisi spettrale conferma la validità di questa interpretazione. È interessante notare che i rapporti massa-luminosità derivati dai modelli di lente gravitazionale risultano ragionevolmente compatibili con quelli menzionati sopra. Nel futuro, questi studi sembrano destinati a porre vincoli significativi sulla distribuzione spaziale di materia oscura.

In conclusione, tutte le indicazioni derivate dalla dinamica interna degli ammassi ricchi, i quali occupano circa un decimillesimo dello spazio totale nell'universo, pongono un limite inferiore al loro contributo alla densità cosmologica. Questo contributo è almeno l'1% della densità critica (v. cap. 8; v. Peebles, 1993), e tale valore è indipendente da quello adottato per la costante di Hubble.

7. Teorie alternative della gravitazione

La discussione contenuta nei capitoli precedenti parte dal presupposto che le leggi della fisica, così come sono state derivate dagli esperimenti in laboratorio, siano applicabili alla scala delle galassie e oltre. I progressi nel campo dell'astrofisica forniscono continue conferme della sostanziale correttezza di questo assunto. Tuttavia, quando ci si trova di fronte a una seria discrepanza o a un problema irrisolto non è irragionevole chiedersi se ciò sia dovuto all'inapplicabilità delle leggi fisiche formulate sulla base di esperienze e osservazioni limitate alla scala planetaria. A tal proposito possono essere citati diversi esempi famosi, fra i quali alcune proposte eterodosse per spiegare la precessione anomala dell'orbita di Mercurio, prima che la relatività generale fornisse una spiegazione adeguata. Nel contesto della dinamica galattica, già nel 1923 J. H. Jeans avanzò la proposta che la legge della gravitazione potesse essere violata. Un primo suggerimento di soluzione del problema specifico della materia oscura in termini di modifica della legge di gravitazione fu fornito da A. Finzi.

In questo capitolo descriveremo brevemente le proposte avanzate per spiegare fenomeni come le curve di rotazione piatte prescindendo dalla presenza di materiale non osservato, a costo di modificare la dinamica newtoniana. Premettiamo questa discussione alla trattazione degli aspetti cosmologici del problema (v. cap. 8) perché vogliamo sottolineare come questa linea di pensiero non sia stata finora in grado di produrre una teoria generale della gravitazione sicura e convincente dal punto di vista teorico. Comunque, su una base semiempirica tale impostazione è stata in grado di interpretare con successo quasi tutte le osservazioni che vengono generalmente citate come prova della presenza di materia oscura (v. Sanders, 1990).

Una volta accettata l'idea di poter violare le leggi della dinamica newtoniana, si aprono diverse strade. Naturalmente, il principio guida consiste nel proporre modifiche che siano in grado innanzitutto di spiegare i problemi irrisolti. La via più naturale, e in effetti largamente seguita negli anni ottanta, è quella di immaginare che la violazione avvenga a una data ‛lunghezza di scala r₀', dell'ordine di pochi kpc, così che le curve di rotazione piatte che si osservano sarebbero una conseguenza della nuova dinamica (una proposta consisteva nel correggere l'usuale campo newtoniano con un potenziale alla Yukawa). Questi tentativi si rivelarono impraticabili per due ragioni principali. Innanzitutto, non si osserva alcuna correlazione tra il diametro galattico (al dato cinematico più esterno disponibile) e la discrepanza di massa attesa. In particolare, alcune galassie molto grandi, come UGC 2885, non richiedono materia oscura (nella trattazione dinamica newtoniana) sulla scala di 70 kpc, mentre altri oggetti molto piccoli, come UGC 2259, la richiedono al di sotto della scala dei 10 kpc. In secondo luogo, queste modifiche portano a una relazione tra velocità di rotazione asintotica e massa del tipo M ~ V²r₀, incompatibile con la relazione di Tully-Fisher, L ~ V⁴, tra luminosità e velocità.

L'approccio più promettente, che evita le due difficoltà appena menzionate, è quello in cui la violazione della dinamica newtoniana avviene al di sotto di un'accelerazione di soglia a₀ dell'ordine di 10^-8 cm/s², come suggerito da M. Milgrom. Si possono considerare due alternative. La prima prevede che la modifica riguardi la seconda legge della dinamica, cioè che la relazione tra forza e accelerazione cambi in regimi di piccole accelerazioni. Questo ha però conseguenze rilevanti e indesiderate sui principî fondamentali della meccanica classica. Il secondo approccio, preferibile, consiste nel modificare la forza di gravità, conservando la validità del secondo principio della dinamica. Un modo semplice di formulare questa proposta è quello di dire che il vero campo gravitazionale g è legato a quello newtoniano usuale g_n secondo la legge:

μ (g/a₀) g = g_n, (10)

dove μ (x) ~ 1 per x ≫ 1 (limite del campo newtoniano standard), e μ (x) ~ x per x ≪ 1 (campo di gravità modificata). Così la relazione per la velocità asintotica V⁴ ~ Ma₀ che segue dalla (10) è consistente con la relazione di Tully-Fisher. Utilizzando per la funzione di transizione μ l'espressione μ (x) = x (1 + x²)^-1/2, si è dedotto che i dati attuali sulle orbite planetarie nel sistema solare pongono un limite superiore all'accelerazione di soglia: a₀ ≤ 3,8 10^-7 cm/s² (v. Bracci e Fiorentini, 1989).

Questa modifica della gravità può essere formulata nel contesto di una teoria di campo, introducendo un'appropriata lagrangiana non relativistica. Va detto però che una teoria soddisfacente, generalmente covariante, non è ancora disponibile, per quanto è dato sapere. È stata notata una curiosa coincidenza numerica fra il valore di a₀, la costante di Hubble H₀ e la velocità della luce c, cioè a₀ ≈ H₀c.

Numerosi raffronti tra le previsioni derivanti da queste leggi di gravitazione modificate e diversi dati osservativi appaiono molto incoraggianti. In particolare, un singolo valore del parametro di accelerazione a₀ = 1,2 10^-8 cm/s² appare in grado di fornire un buon accordo per tutte le 11 galassie selezionate sulla base della qualità e della simmetria dei dati cinematici disponibili (v. Begeman e altri, 1991); la dimensione di questi oggetti varia tra 7 e 40 kpc (per i dati cinematici disponibili del punto più esterno). L'accordo diventa ottimo se la distanza della galassia è lasciata libera di variare leggermente rispetto al valore comunemente preso, cosa non irragionevole date le grandi incertezze sulla determinazione delle distanze. Per contro, per ottenere il medesimo accordo relativamente agli stessi oggetti utilizzando i modelli basati sulla dinamica classica newtoniana occorre ammettere una forte presenza di materia oscura, con profili di massa e di densità che possono essere giudicati ad hoc, dal momento che si tratta di materiale non visto. In conclusione, l'aspetto attraente della teoria modificata sta nella sua capacità di consentire previsioni confrontabili con osservazioni che, almeno fino a oggi, non hanno condotto a contraddizioni.

8. Cosmologia

All'interno dei modelli cosmologici classici e omogenei di Friedmann-Lemaître, una determinazione empirica del tipo di universo nel quale ci troviamo richiede la misura di tre parametri: la costante di Hubble H₀, il parametro di densità Ω, e la costante cosmologica Λ. I limiti astrofisici più interessanti sono quelli relativi alle prime due, mentre la costante cosmologica è spesso tacitamente trascurata. La costante di Hubble è spesso scritta nella forma H₀ = = 100 h km/(s Mpc), e un vasto corpus di risultati astronomici suggerisce che h sia compresa tra 0,5 e 0,9. La recente scoperta di Cefeidi nell'ammasso della Vergine porta alla determinazione della scala di distanza cosmologica, e conduce al valore h = 0,80 ± 0,17 (v. Freedman e altri, 1994). Un valore basso della costante di Hubble corrisponde a una scala di distanza grande e a una scala temporale lunga per l'età dell'universo. Il parametro di densità Ω = ρ₀/ρ_crit = = 8πGρ₀/(3H0²) è proporzionale alla densità media attuale dell'universo ρ₀. Il modello di Einstein-de Sitter considera Λ trascurabile e pone Ω = 1, con una relazione specifica tra tempo di Hubble (1/H₀ = 0,98 10¹⁰h^-1 anni) e l'età dell'universo t₀, data da H_0t0 = 2/3. Da notare che la densità critica associata alla soluzione di Einstein-de Sitter è ρ_crit = 1,88 10^-29h²g/cm³.

Le ragioni per cui i modelli cosmologici caratterizzati da Ω = 1 sembrano più interessanti dal punto di vista teorico spesso sono prese come dimostrazione che l'universo non può essere altrimenti (per una interessante descrizione dei molteplici e sottili aspetti coinvolti, v., per esempio, Peebles, 1993). L'argomento principale a sostegno di tale conclusione è intimamente connesso con la questione di come si dovrebbero fissare le condizioni iniziali per le equazioni che descrivono l'espansione dell'universo. In particolare, il nodo principale consiste nel riconoscere che i tre termini che compaiono nell'equazione di espansione, che per un universo dominato dalla materia si può scrivere come:

H² = H0² [Ω(1 + z)³ + Ω_R (1 + z)² + Ω_Λ]. (11)

con Ω + Ω_R + Ω_Λ = 1, e Ω_Λ ≡ Λ/3H0², scalano in maniera diversa con il tempo cosmico, così che il relativo ‛ordinamento' dei contributi della gravità, della curvatura e della costante cosmologica varia rapidamente avvicinandosi all'epoca iniziale (cioè per valori alti dello spostamento verso il rosso gravitazionale z), quando il termine gravitazionale è sicuramente prevalente. È giudicato ‛innaturale' postulare condizioni iniziali definite con tale precisione che lo stato attuale non sia completamente dominato dalla gravità (come sarebbe se si ponesse 0,1 ≤ Ω 〈 1) e tale da farci assistere, in tempi storici, alla transizione dal predominio della massa a quello della curvatura o della costante cosmologica. È ritenuto più ‛naturale' assumere Ω = 1 costante dall'inizio fino a oggi. L'analisi dettagliata del problema delle condizioni iniziali segue in realtà due principali linee di pensiero, una connessa con le proprietà del campo delle velocità medie imperturbato imposto da quelle condizioni iniziali, e l'altra relativa al problema di spiegare la crescita di strutture su vasta scala nella distribuzione di massa (come suggerito dall'esistenza di superammassi, ‛attrattori', ‛muri' e ‛vuoti'; v. figg. 6 e 7), in contrasto con l'isotropia che si osserva nella radiazione di fondo a microonde e a raggi X. Inoltre, il grado di omogeneità dell'universo osservato sembra essere difficile da conciliare, all'interno dei modelli cosmologici classici di Friedmann-Lemaître, con l'esistenza del ‛problema dell'orizzonte' (parti di universo che non sono in contatto causale sembrano aver raggiunto uno stesso stato di ‛rilassamento'). L'unico modello teorico plausibile proposto finora per risolvere tale difficoltà è quello dello ‛scenario inflazionistico', che sembra richiedere Ω = 1.

Sembra che tutte le prove accumulate con gli studi dinamici qui discusse portino a un valore di Ω ~ 0,1 entro un fattore 2 (v. Peebles, 1993; da notare che questo limite, data la determinazione empirica delle masse, è indipendente dal valore di h), che in realtà è compatibile con le conoscenze sulla nucleosintesi nei modelli del big bang. Le quantità relative di elementi leggeri misurati sono in accordo con quelle previste dai modelli di nucleosintesi (v. fig. 8) solo entro un piccolo intervallo della quantità Ω_Bh² (0,013 ± 0,005). Come indicato dal pedice B, il limite relativo a Ω si riferisce a materia barionica, e pertanto si può concludere che mentre la materia oscura prevista dinamicamente potrebbe essere tutta barionica e ancora compatibile con i modelli standard di nucleosintesi, la materia oscura cosmologica che è spesso richiesta per poter arrivare a Ω = 1 ‛deve' essere non barionica, altrimenti si avrebbero serie difficoltà nello spiegare le abbondanze nucleari osservate (specialmente quella del deuterio). All'inizio degli anni ottanta si sviluppò una tendenza generale ad accettare il valore Ω = 1 ammettendo che l'universo fosse dominato dalla materia oscura non barionica, anche se questo, a tutt'oggi, deve essere considerato un ‛passo coraggioso di natura teorica', data l'insufficienza di prove osservative. Dal punto di vista teorico, è necessario porre in rilievo che alcune delle proprietà interessanti dei modelli con Ω = 1 possono essere mantenute anche senza presumere l'esistenza di materia oscura non barionica, se si tiene conto di un contributo significativo della costante cosmologica Λ. Quest'ultima scelta - anche se meno attraente, dal momento che introduce un nuovo parametro nella teoria - ha il vantaggio potenziale di permettere nei modelli di espansione un tempo presente t₀ più lungo, il che potrebbe essere richiesto dalle età degli ammassi globulari più vecchi (da alcuni stimato in 16 ± 2 miliardi di anni).

Nei primi anni ottanta, alcuni esperimenti indicanti una massa del neutrino dell'ordine di grandezza desiderato determinarono la diffusa convinzione che la materia oscura potesse essere costituita da neutrini massivi. L'argomentazione che porta a determinare un tale valore della massa del neutrino si fonda sul fatto che la temperatura osservata della radiazione cosmica di fondo (T₀ = 2,73 K) limita l'attuale densità di neutrini per una loro famiglia a n_ν = 113 cm^-3, valore che produrrebbe la densità critica se la massa del neutrino fosse m_ν = 93 h² eV. Nuovi esperimenti hanno tuttavia invalidato i risultati precedenti, e il limite superiore attuale per la massa del neutrino (famiglia elettronica) è di 9 eV. Spesso ci si riferisce a neutrini massivi con l'espressione ‛materia oscura calda', poiché al tempo del disaccoppiamento, quando durante il raffreddamento dell'universo il plasma si trasformò in idrogeno atomico e la materia si disaccoppiò dalla radiazione, queste particelle avrebbero avuto velocità relativistiche. L'ipotesi della materia oscura calda è stata criticata anche perché richiede masse dei neutrini troppo grandi per spiegare la presenza degli aloni oscuri delle galassie nane sferoidali nelle vicinanze della Via Lattea e per la difficoltà di produrre sufficiente agglomerazione di materia in un tempo di Hubble partendo da condizioni iniziali lisce.

Verso la metà degli anni ottanta fu oggetto di attenti studi l'ipotesi dell'esistenza di ‛materia oscura fredda' (particelle più pesanti di 1 keV); essa presenta però il grande limite che le particelle di questo tipo devono essere di natura esotica e nessuna di esse è stata finora scoperta in laboratorio (come i fotini, spesso chiamati WIMPS, Weakly Interacting Massive Particles; v. Kolb e Turner, 1990). Naturalmente, il fatto che sia possibile scoprire tali particelle è largamente apprezzato dai fisici teorici che si occupano di sviluppare alcuni modelli di fisica delle particelle.

A conclusione di questa sommaria trattazione degli aspetti cosmologici relativi al problema della materia oscura, bisogna accennare ad alcune deduzioni dinamiche della densità media di massa ρ₀ che sono state suggerite da studi cosmologici; i valori dedotti cadono proprio nell'intervallo di valori indicato dagli studi sugli ammassi di galassie discussi nel cap. 6. Uno dei metodi generalizza le analisi statistiche della misurazione dinamica della densità di massa nelle vicinanze del Sole (v. cap. 3). Alla relazione statistica tra dispersione di velocità relativa a coppie di galassie in funzione della separazione proiettata e della densità media di massa è stato dato il nome appropriato di ‛teorema del viriale cosmico'. Vale la pena di notare che il metodo è concettualmente differente dallo studio delle galassie binarie di cui si è riferito nel cap. 6. È emerso che la dispersione di velocità cresce lentamente da 200 a 400 km/s circa nell'intervallo di separazione proiettato da 10 kpc a 5 Mpc, fornendo un Ω compreso tra 0,1 e 0,2, cioè un rapporto massa-luminosità M/L ≈ 300 hM_⊙/L_⊙ sulla scala di 1 Mpc. Stranamente, la dispersione di velocità è molto prossima alle velocità delle stelle misurate sulla scala di galassie singole.

A una scala maggiore si è trovata una relazione interessante tra i valori degli scostamenti su larga scala della velocità dal flusso imperturbato di Hubble, dovuti a perturbazioni di densità, e il valore osservato delle fluttuazioni di densità. In una teoria lineare delle perturbazioni, supponendo che le galassie luminose siano degli indicatori della densità di massa dell'universo, la perturbazione di velocità risulta proporzionale a Ω^0,6. Sulla scala della separazione tra il Gruppo Locale e l'ammasso della Vergine, cioè sulla scala di 20 Mpc, il contrasto di densità suggerito dai conteggi di galassie IRAS (Infrared Astronomical Satellite) è circa 1,4, e il corrispondente scostamento dal flusso imperturbato di Hubble (la velocità del Gruppo Locale misurata dal centro di Virgo) è circa di 170 km/s. Così, a meno di introdurre effetti significativi ‛di marea' indotti da concentrazioni di massa più distanti (come il cosiddetto ‛grande attrattore'), il valore che si deduce per Ω è di nuovo dell'ordine di 0,1-0,2.

Su una scala ancora maggiore, si possono applicare i concetti sopra esposti ai moti osservati su grande scala, dedotti dalla tecnica di ricostruzione del campo di velocità introdotta da E. Bertschinger e A. Dekel, e alla velocità di deriva rispetto alla radiazione cosmica di fondo del Gruppo Locale (circa 600 km/s). Da tutti questi metodi si ottengono risultati in ragionevole mutuo accordo, il che dimostra che essi sono strumenti di indagine interessanti, anche se si sono finora rivelati incapaci di definire il valore della densità media ρ₀ in maniera significativamente migliore degli strumenti descritti nel cap. 6.

Pur non addentrandoci nella discussione dell'interessante area di ricerca, in rapida evoluzione, che riguarda i modelli per la formazione di strutture nell'universo (cioè tutta la varietà degli scenari di formazione secondo l'ipotesi della ‛materia oscura calda' e della ‛materia oscura fredda', e la questione della ‛formazione preferenziale', il cosiddetto bias), vogliamo però richiamare l'attenzione sul vincolo che deriva dalla misurazione dell'anisotropia di quadrupolo della radiazione cosmica di fondo compiuta dal satellite COBE (Cosmic Background Explorer).

Vogliamo, infine, sottolineare che i tre principali interrogativi rimasti aperti sono quelli relativi a: 1) la costituzione della materia oscura; 2) il valore di Ω; 3) la forma degli aloni oscuri che circondano le galassie. Si tratta di questioni di grande importanza che ci auguriamo troveranno presto risposte concrete.

BIBLIOGRAFIA

Albada, T. S. van, Bahcall, J.N., Begeman, K., Sancisi, R., Distribution of dark matter in the spiral galaxy NGC 3198, in ‟Astrophysical journal", 1985, CCXCV, pp. 305-313.

Albada, T. S. van, Sancisi, R., Dark matter in spiral galaxies, in ‟Philosophical transactions of the Royal Society" (Series A), 1986, CCCXX, pp. 447-464.

Alcock, C., Akerlof, C. W., Allsman, R. A. e altri, Possible gravitational microlensing of a star in the Large Magellanic Cloud, in ‟Nature", 1993, CCCLXV, pp. 621-622.

Aubourg, E., Bareyre, P., Bréhin, S. e altri, Evidence for gravitational microlensing by dark objects in the Galactic halo, in ‟Nature", 1993, CCCLXV, pp. 623-625.

Begeman, K. G., Broeils, A. H., Sanders, R. H., Extended rotation curves of spiral galaxies. Dark haloes and modified dynamics, in ‟Monthly notices of the Royal Astronomical Society", 1991, CCXLIX, pp. 523-537.

Bertin, G., Bertola, F., Buson, L. M. e altri, A search for dark matter in elliptical galaxies: radially extended spectroscopic observations for six objects, in ‟Astronomy and astrophysics", 1994, CCXCII, pp. 381-391.

Bertin, G., Lin, C. C., Spiral structure in galaxies: a density wave theory, Cambridge 1996.

Bertin, G., Mark, J. W.-K., On the excitation of warps in galaxy disks, in ‟Astronomy and astrophysics", 1980, LXXXVIII, pp. 289-297.

Bertin, G., Stiavelli, M., Structure and dynamics of elliptical galaxies, in ‟Reports on progress in physics", 1993, LVI, pp. 493-556.

Bracci, L., Fiorentini, G., The missing-mass problem and the precession of perihelia, in ‟Il nuovo cimento della Società Italiana di Fisica. C", 1989, XII, pp. 121-127.

Buote, D. A., Canizares, C. R., Geometrical evidence for dark matter: X-ray constraints on the mass of the elliptical galaxy NGC 720, in ‟Astrophysical journal", 1994, CDXXVII, pp. 86-111.

David, L. P., Jones, C., Forman, W., Daines, S., Mapping the dark matter in the NGC 5044 group with ROSAT: evidence for a nearly homogeneous cooling flow with a cooling wake, in ‟Astrophysical journal", 1994, CDXXVIII, pp. 544-554.

Fabbiano, G., X rays from normal galaxies, in ‟Annual review of astronomy and astrophysics", 1989, XXVII, pp. 87-138.

Feynman, R. P., Leighton, R. B., Sands, M., The theory of gravitation, in The Feynman lectures on physics, vol. I, Reading, Mass., 1963, p. 7 (tr. it. in: La fisica di Feynman, 3 voll., Milano 1985).

Franx, M., Gorkom, J. H. van, Zeeuw, P. T. de, Evidence for axisymmetric halos: the case of IC 2006, in ‟Astrophysical journal", 1994, CDXXXVI, pp. 642-653.

Franx, M., Zeeuw, P. T. de, Elongated disks and the scatter in the Tully-Fisher relation, in ‟Astrophysical journal letters", 1992, CCCXCII, pp. L47-L50.

Freedman, W. L., Madore, B. F., Mould, J. R. e altri, Distance to the Virgo cluster galaxy M100 from Hubble space telescope observations of Cepheids, in ‟Nature", 1994, CCCLXXI, pp. 757-762.

Hulst, H. C. van de, Raimond, E., Woerden, H. van, Rotation and density distribution of the Andromeda nebula derived from observations of the 21-cm line, in ‟Bulletin of the Astronomical Institutes of the Netherlands", 1957, XIV, pp. 1-16.

Kapteyn, J. C., First attempt at a theory of the arrangement and motion of the sidereal system, in ‟Astrophysical journal", 1922, LV, pp. 302-328.

Kolb, E. W., Turner, M. S., The early universe, Redwood City, Cal., 1990.

Merrifield, M. R., The rotation curve of the Milky Way to 2.5 R₀ from the thickness of the H I layer, in ‟Astronomical journal", 1992, CIII, pp. 1552-1563.

Miyoshi, M., Moran, J., Herrnstein, J. e altri, Evidence for a black hole from high rotation velocities in a sub-parsec region of NGC 4258, in ‟Nature", 1995, CCCLXXIII, pp. 127-129.

Moorsel, G. A. van, Dark matter associated with binary galaxies, in ‟Astronomy and astrophysics", 1987, CLXXVI, pp. 13-24.

Mulchaey, J. S., Davis, D. S., Mushotzky, R. F., Burstein, D., Diffuse X-ray emission from the NGC 2300 group of galaxies. Implications for dark matter and galaxy evolution in small groups, in ‟Astrophysical journal letters", 1993, CDIV, pp. L9-L12.

Peebles, P. J. E., Principles of physical cosmology, Princeton, N. J., 1993.

Ponman, T. J., Bertram, D., Hot gas and dark matter in a compact galaxy group, in ‟Nature", 1993, CCCLXIII, pp. 51-54.

Rubin, V. C., Constraints on the dark matter from optical rotation curves, in Dark matter in the universe (a cura di J. Kormendy e G. R. Knapp), Dordrecht 1987, pp. 51-62.

Sackett, P. D., Rix, H.-W., Jarvis, B. J., Freeman, K. C., The flattened dark halo of polar ring galaxy NGC 4650A: a conspiracy of shapes?, in ‟Astrophysical journal", 1994, CDXXXVI, pp. 629-641.

Sanders, R. H., Mass discrepancies in galaxies: dark matter and alternatives, in ‟The astronomy and astrophysics review", 1990, II, pp. 1-28.

Sarazin, C. L., X-ray emission from clusters of galaxies, Cambridge 1988.

Sparke, L. S., Casertano, S., A model for persistent galactic warps, in ‟Monthly notices of the Royal Astronomical Society", 1988, CCXXXIV, pp. 873-898.

Trinchieri, G., Kim, D.-W., Fabbiano, G., Canizares, C. R., ROSAT PSPC observations of NGC 4636: interaction with Virgo gas?, in ‟Astrophysical journal", 1994, CDXXVIII, pp. 555-573.

Udalsky, A., Szymanski, M., KaLuzny, J. e altri, The optical gravitational lensing experiment. Discovery of the first candidate microlensing event in the direction of the Galactic bulge, in ‟Acta astronomica", 1993, XLIII, pp. 289-294.

Wolszczan, A., Frail, D. A., A planetary system around the millisecond pulsar PSR 1257 + 12, in ‟Nature", 1992, CCCLV, pp. 145-147.