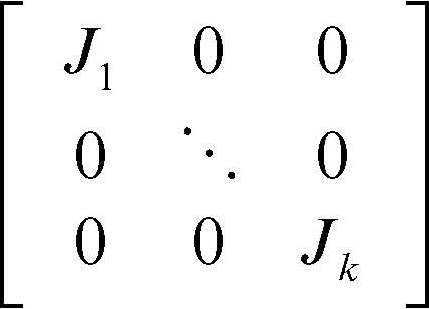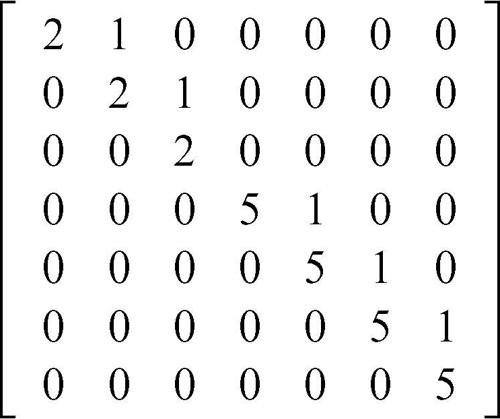Jordan, matrice di

Jordan, matrice di

Jordan, matrice di o matrice elementare di Jordan, matrice quadrata M che può essere così rappresentata

dove ogni J_i è un blocco di Jordan (→ Jordan, blocco di) e tutti gli altri elementi sono nulli. Per esempio, la matrice

è una matrice di Jordan i cui blocchi sono J_2,3 e J_5,4. Nella matrice M possono esserci più blocchi aventi lo stesso autovalore λ. La molteplicità algebrica di un autovalore di M coincide con la somma degli ordini dei blocchi di Jordan che possiedono tale autovalore; quella geometrica coincide con il numero di tali blocchi, in quanto a ogni blocco corrisponde un solo autovettore.

Se una matrice di Jordan è costituita da blocchi di rispettivi autovalori λ₁, λ₂, …, λ_k, il suo → polinomio minimo p(x), della forma

ha come esponente, per ogni autovalore, la dimensione del più grande blocco che gli corrisponde. I polinomi caratteristici dei singoli blocchi di Jordan si chiamano divisori elementari della matrice M. Ogni matrice è simile a una matrice di Jordan, definita a meno di una permutazione dei suoi blocchi; pertanto una matrice è diagonalizzabile se e solo se tutti i blocchi di Jordan hanno ordine 1.