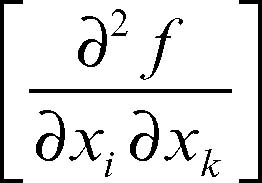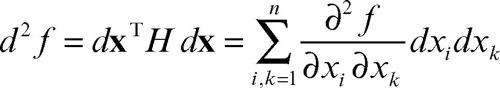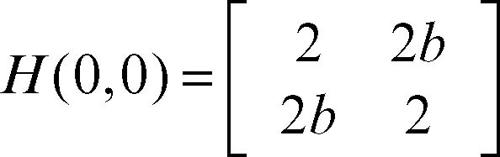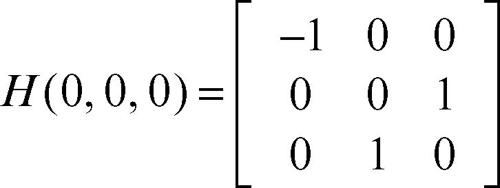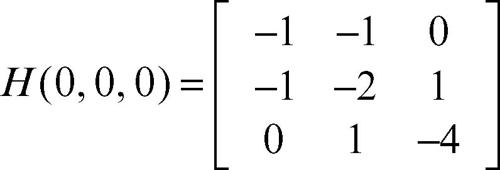matrice hessiana

matrice hessiana

matrice hessiana di una funzione ƒ: Rⁿ → R, due volte differenziabile, è la matrice H delle sue derivate seconde:

Il determinate della matrice hessiana è detto determinante hessiano (o semplicemente l’hessiano) di ƒ. La traccia della matrice H è il laplaciano di ƒ. Per il teorema di → Schwarz, se ƒ è di classe C ², allora H è una matrice simmetrica. Se dx ∈ Rⁿ indica il vettore incremento delle variabili indipendenti, il differenziale secondo di ƒ è dato da

per cui lo sviluppo di → Taylor di ƒ nell’intorno di un punto x è dato da

dove Dƒ(x) è la → matrice jacobiana di ƒ. Il segno della forma quadratica espressa dal differenziale secondo consente lo studio della concavità del grafico di ƒ nel punto x: precisamente se tale forma è definita positiva (negativa) il grafico giace, in un intorno di x, al di sopra (sotto) dell’iperpiano tangente, mentre se è indefinita il grafico attraversa tale iperpiano. In particolare, se il punto x è di stazionarietà (Dƒ(x) = 0), si avrà un minimo (massimo) relativo o un punto di sella. La verifica può essere fatta calcolando gli autovalori di H: se sono tutti concordi, la forma è definita; se vi è almeno un autovalore nullo e gli altri concordi, la forma è semidefinita; se ve ne sono di segni opposti, è indefinita.

Nel caso di hessiana semidefinita, è necessario un ulteriore studio per stabilire se il grafico attraversa o no l’iperpiano tangente.

Nei seguenti esempi l’origine è un punto di stazionarietà:

1) la funzione ƒ(x, y) = x ² + 2bxy + y ² ha come matrice hessiana nell’origine

Poiché l’hessiano è det(H) = 4 − 4b², se |b| < 1 la funzione ha un minimo nell’origine, se |b| > 1 ha una sella. Se b = 1, ƒ(x, y) = (x + y)² e la funzione ha minimi relativi sulla retta x + y = 0 nel piano z = 0; analogamente per b = −1 li ha sulla retta y = −x;

2) la funzione ƒ(x, y) = x ² + 2bxy + y ² − (x − by)⁴ si comporta nello stesso modo della precedente per |b| ≠ 1, ma per b = ±1 attraversa nell’origine il piano z = 0;

3) la funzione ƒ(x, y, z) = cosx + yz ha

i cui minori principali di guida valgono −1, 0, 1, per cui il grafico attraversa nell’origine l’iperpiano tangente;

4) la funzione ƒ(x, y, z) = cosx − xy − y ² + yz − 2z ² ha

i cui minori principali di guida valgono −1, 1, −3, per cui ƒ(x, y, z) ha un massimo nell’origine (→ matrice, minore di una).

Un’applicazione alle curve algebriche si ha considerando la cosiddetta curva hessiana (o semplicemente hessiana) di una curva Γ di equazione (in coordinate omogenee) ƒ(x₀, x₁, x₂) = 0. L’hessiana di Γ ha equazione det(H) = 0, e le sue intersezioni con Γ, se semplici, danno tutti e soli i punti di flesso di Γ.