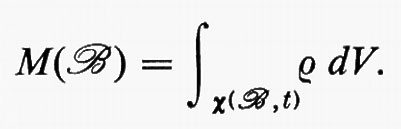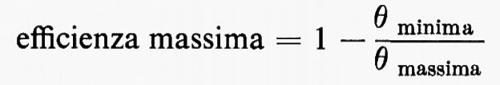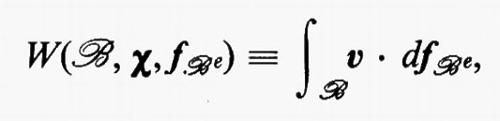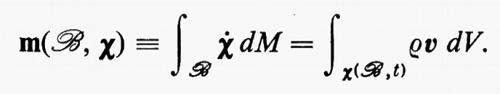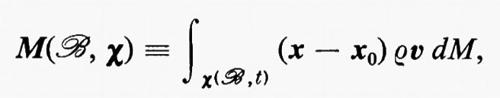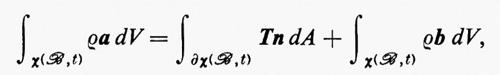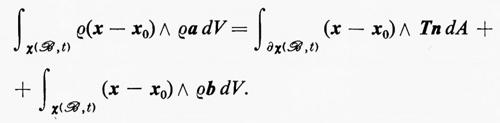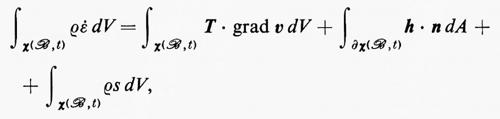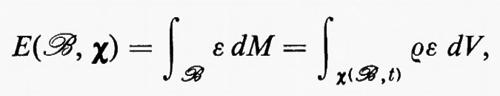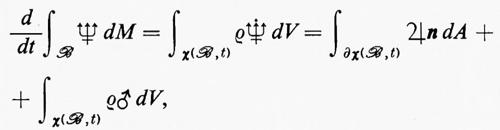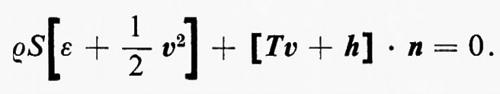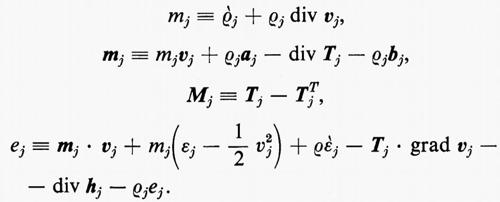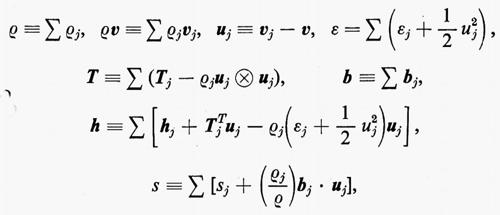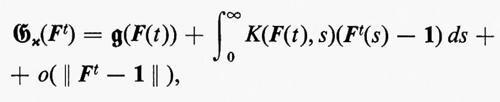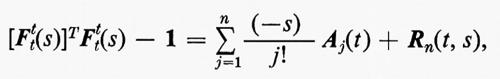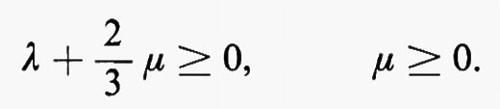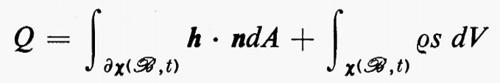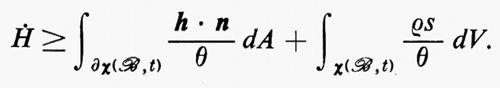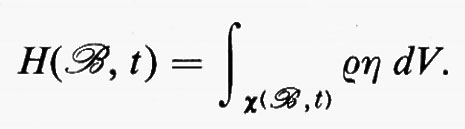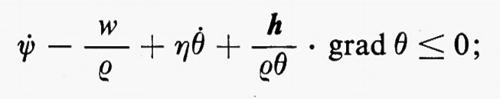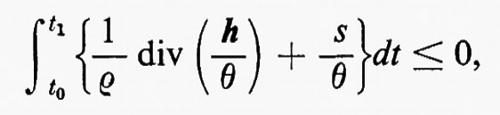Meccanica e termomeccanica razionali

Meccanica e termomeccanica razionali

di Clifford A. Truesdell

SOMMARIO: 1. Concetti e metodi: a) la natura delle scienze razionali; b) la nascita, l'apogeo e il lento declino della meccanica razionale; c) la natura e gli scopi della meccanica razionale a partire dal 1945; d) la termodinamica nel sec. XIX e la sua riduzione a termostatica; e) la natura e gli scopi della termomeccanica razionale creata negli anni sessanta. □ 2. Concetti fondamentali della meccanica razionale dei corpi deformabili: a) corpi; b) cinematica dei corpi continui; c) sistemi di masse, forze, coppie e riscaldamento; d) l'assioma di Noll sull'indipendenza della potenza dal riferimento. Le leggi del moto di Eulero; e) azioni di contatto e azioni a distanza. Esistenza dello sforzo e del flusso di calore; f) bilancio in generale. Equazioni generali di campo e condizioni di salto; g) relazioni costitutive. Assiomi di Noll; h) i materiali sempilci e i loro gruppi dei pari; i) miscele; j) mezzi polari e mezzi orientati; □ 3. Alcuni esempi importanti di meccanica razionale nel XX secolo: a) materiali elastici; b) fluidi semplici, flussi viscometrici; c) materiali con memoria evanescente; d) ipoelasticità. La zona elastica di un materiale semplice; e) sviluppi matematici delle teorie classiche. □ 4. Termomeccanica: a) esempi classici di materiali dissipativi: il fluido viscoso e il conduttore di calore rigido lineare; b) la disuguagllanza di Clausius-Duhem e le sue due applicazioni tradizionali; c) equazioni costitutive per materiali semplici. Equipresenza; d) l'interpretazione di Coleman e Noll della diseguaglianza di Clausius-Duhem; e) altre proposte per la seconda legge. Il principio di degradazione di Day; f) metodi inversi e seminversi. Serie di perturbazione; g) propagazione delle onde. □ 5. Alcuni esempi importanti di termomeccanica razionale: a) termodinamica dei processi omogenei; b) lo sviluppo della termoelasticità secondo Coleman e Noll; c) materiali con memoria. Teorema di Coleman; d) variabili interne di stato; e) miscele. Mezzi porosi. Reazioni chimiche. □ Bibliografia.

1. Concetti e metodi.

a) La natura delle scienze razionali.

Nella prefazione ai suoi Philosophiae naturalis principia mathematica (1687) Newton scriveva: ‟Poiché gli antichi (come ci dice Pappo) hanno ritenuto la meccanica della massima importanza nella ricerca sui fatti naturali, e i moderni, rigettando forme sostanziali e qualità occulte, si sono sforzati di assoggettare i fenomeni della natura alle leggi della matematica, ci è sembrato opportuno in questo trattato di coltivare la matematica per quanto essa si riferisce alla filosofia. Gli antichi infatti considerarono la meccanica in doppio modo: come razionale, che procede in modo accurato per dimostrazioni, e pratica. Alla meccanica pratica appartengono tutte le arti manuali, dalle quali la meccanica prese certamente il nome. Poiché però i maestri lavorano spesso con scarsa accuratezza, succede che la meccanica sia cosi distinta dalla geometria, sicché quanto è accurato è riferito alla geometria, quanto è meno accurato alla meccanica. Tuttavia gli errori non stanno nell'arte ma negli artefici. Chi lavora con minor accuratezza è un meccanico imperfetto, e se qualcuno può lavorare in modo accuratissimo, egli sarà il meccanico più perfetto di tutti [...]. Siccome noi non consideriamo le arti ma la filosofia, e scriviamo sulle potenze non manuali ma naturali, consideriamo specialmente quelle cose che si riferiscono alla gravità, leggerezza, forza elastica, resistenza dei fluidi e forze simili, vuoi attrattive vuoi impulsive: perciò proponiamo questo nostro lavoro come i principi matematici della filosofia. Infatti tutta la difficoltà della filosofia sembra consistere in questo, investigare le forze della natura dai fenomeni di moto e quindi dimostrare da queste forze altri fenomeni [...]"

Dunque Newton considerò la meccanica razionale come un'estensione della geometria, egualmente matematica sia nell'impostazione sia nel rigore logico. Egli ammise che il suo libro non raggiungeva lo scopo in tutti i suoi aspetti: ‟Avremmo desiderato derivare il resto dei fenomeni della natura attraverso lo stesso tipo di ragionamento da principi meccanici [...]".

Nell'interpretare queste affermazioni dobbiamo ricordare che nel sec. XVII la parola ‛meccanica' non aveva ancora acquistato il significato specialistico che ha oggi. Piuttosto nella ‛meccanica' Newton intendeva includere l'intero spettro di fenomeni che oggi sono considerati di pertinenza della ‛fisica' e forse anche gran parte di quelli appartenenti alla ‛chimica'.

Le scienze razionali sono quelle che seguono il programma di Newton. Certi fenomeni, scelti opportunamente, sono rappresentati da enti astratti corrispondenti a concetti matematici come quelli di insieme, scalare, vettore, tensore, posizione, tempo, corpo, massa, forza, coppia, energia, temperatura, calore, entropia. Questi enti sono introdotti a priori come primitivi. Si suppone che essi obbediscano a certi assiomi o postulati, i quali, posti in termini matematici, rappresentano gli aspetti più semplici per quanto non necessariamente i più immediatamente percepibili) dell'esperienza che si suppone essi modellino. Sulla base di questi assiomi, si dimostrano teoremi o proposizioni usando solo processi logici. La scelta dei teoremi da dimostrare, come la scelta degli assiomi posti inizialmente, è motivata dall'esperienza e dall'osservazione della natura. Infine, attraverso un'opportuna interpretazione, i teoremi sono messi in relazione con i risultati di esperimenti, sia che si tratti di esperimenti già effettuati, sia che si tratti di esperimenti nuovi suggeriti dalla teoria. Se le interpretazioni si adattano ai risultati empirici corrispondenti, si dice che la teoria spiega o predice quei risultati a seconda che essi siano stati ottenuti prima della formulazione della teoria o dopo di essa. I fisici hanno l'abitudine di dire che le loro teorie sono confermate dagli esperimenti, ma i filosofi naturali sono di solito più cauti nelle loro pretese.

Il compito di una teoria è tanto più difficile, quanto più ampio è l'arco dei fenomeni che si vogliono inquadrare in uno stesso modello. Così la meccanica razionale, cioè la parte della matematica che si occupa di corpi, forze, coppie e energie, oltre che di posizioni e tempi, è estremamente più complicata della geometria, che considera solo posizioni e tempi; tuttavia, a parte la geometria, la meccanica razionale è la più semplice di tutte le scienze razionali.

Se una teoria può essere costruita sulla base di un insieme di enti primitivi e di assiomi, può essere costruita anche sulla base di infinite altre scelte. Come in ogni altra parte della matematica, il gusto del teorico si riflette nella teoria che egli costruisce o nel modo in cui egli continua la ricerca nell'ambito di una teoria già esistente.

Il programma di Newton rimane ancora oggi il programma per una teoria razionale.

b) La nascita, l'apogeo e il lento declino della meccanica razionale.

Newton, dividendo con G. Bernoulli la gloria per aver sollevato la dinamica al rango di una scienza razionale, ha tracciato un sistema sufficiente a spiegare, attraverso le elaborazioni successive, la maggior parte dei fenomeni meccanici allora noti. La chiave del successo è stato il concetto di forza introdotto a priori; fu necessario un intero secolo dopo la morte di Newton per esplorare e sfruttare quel concetto. Ci furono formulazioni alternative e, addirittura, schemi rivali e la meccanica teorica che studiamo oggi li riflette assieme all'influenza di Newton.

I geometri del sec. XVIII, per quanto non escludessero la possibilità di modifiche allo schema newtoniano, ne erano tanto convinti da non risparmiare alcuno sforzo di calcolo pur di giustificarlo. L'esempio più lampante è fornito dal moto della Luna. Anche in quel caso nessuno di quei geometri pose in questione i principi di base newtoniani, ma per un certo tempo fu posta in dubbio l'equazione costitutiva del sistema solare, la cosiddetta ‛legge della gravitazione', a causa delle divergenze tra i dati astronomici e le predizioni della teoria.‛Infine, A.-C. Clairaut e Eulero scoprirono la ragione di quelle divergenze negli errori presenti nei loro calcoli approssimati e la teoria fu riabilitata. Fu una dimostrazione trionfale della potenza che ha la matematica nell'estrarre innumerevoli conseguenze complesse e pur precise da pochi assiomi apparentemente semplici.

Lo stesso punto di partenza condusse, nelle mani sommamente esperte di Eulero, a teorie definitive sui corpi rigidi, sui fluidi ideali sia comprimibili sia incomprimibili, sulle travi elastiche, sulle corde flessibili e sulle membrane, e su vari meccanismi. Qui, però, non si trattava affatto di eseguire dei calcoli; piuttosto Eulero e gli altri geometri del sec. XVIII dovevano innanzitutto precisare le idee di Newton, completarle aggiungendo nuovi concetti, quali quelli di campo vettoriale, di sforzo in una trave, di pressione interna, e, infine, creare nuovi strumenti matematici, quali il calcolo delle derivate parziali, la geometria differenziale e le equazioni alle derivate parziali.

Nel 1787 G. L. Lagrange pubblicò nel suo trattato Mécanique anailtique quella che egli dichiarò essere una sintesi generale della meccanica, che riduceva tutta la scienza a pura analisi. Quest'opera ha dato origine all'idea errata che la meccanica ‛classica' sia, in via di principio, un argomento ormai estinto. Se si limita l'attenzione ai corpi indeformabili, quest'impressione di chiusura e completezza è parzialmente giustificata. Tuttavia, per i solidi e i fluidi deformabili a tre dimensioni erano stati a malapena formulati fino al 1800 solo pochi modelli speciali, anche se notevoli, e i più importanti sviluppi della meccanica di tali corpi quando Lagrange scriveva erano ancora da venire.

Il programma di Eulero fu perseguito con un progresso senza interruzioni, nella prima metà del sec. XIX, da C.-L.M.-H. Navier, A.-L. Cauchy, S.-D. Poisson e G. G. Stokes, che crearono teorie per fluidi viscosi e per materiali elastici a tre dimensioni soggetti a piccole deformazioni. La sintesi maxwelliana della teoria elettromagnetica, che qui non consideriamo, potrebbe essere addotta come ulteriore esempio di ‛meccanica' in senso newtoniano.

Altri esempi possono essere trovati attraverso tutto il sec. XIX, ma nello stesso periodo si è sviluppata un'impostazione differente, l'impostazione della fisica teorica. In questa prospettiva la matematica è l'ancella del fisico, non la sua dea. Egli se ne serve a suo piacimento e la abbandona quando essa non riesce a soddisfare i suoi piaceri immediati. Le argomentazioni matematiche diventano strumenti di persuasione piuttosto che dimostrazioni. Come scrisse lord Rayleigh (The theory of sound, London 1894², vol. I, p. XXXV): ‟così, per quanto importante sia il mantenere una qualità costante di rigore nella matematica pura, il fisico farà bene ad accontentarsi di argomentazioni che siano sufficientemente soddisfacenti e conclusive dal suo punto di vista. Alla sua mente, esercitata a un ordine differente d'idee, le procedute più severe del matematico puro possono apparire non più convincenti ma meno".

La matematica si divise così dalla fisica e, quel che è peggio, sorsero le figure del ‛matematico puro' e del ‛fisico' che dimostrarono un crescente disprezzo reciproco. Anziché creare matematica nuova per risolvere problemi fisici, come avevano fatto C. Huygens e Newton, Bernoulli, Eulero e Cauchy, i fisici non si curarono più di seguire le scoperte matematiche e i matematici, a parte alcune notevoli eccezioni, come I.-H. Poincaré, D. Hilbert e J. Hadamard, si occuparono sempre più raramente di problemi legati alla fisica.

Nel sec. XX appare una nuova disciplina, detta ‛matematica applicata'. Per quanto si tratti di un termine mal definito, esso sembra dare importanza all'aggettivo ‛applicata' a spese del sostantivo ‛matematica', anche se spesso non è specificato l'oggetto cui dovrebbe riferirsi l'applicazione.

Entro il 1940 l'unità della scienza razionale proclamata da Newton e Eulero era scomparsa. Gli esperti della matematica del tempo partecipavano raramente alla formulazione di teorie sulla natura, mentre gli esperti in fisica mostravano scarso interesse per i criteri della matematica. La matematica applicata godeva a sua volta di scarsa considerazione da parte dei matematici e dei fisici, per quanto risultasse utile talvolta per la ricerca e lo sviluppo nel campo dell'ingegneria.

c) La natura e gli scopi della meccanica razionale a partire dal 1945.

Due campi della meccanica pura erano stati pressoché ignorati fino al 1945. Questi campi riguardavano materiali detti ‛fiuidi non newtoniani', quali vernici e soluzioni di gomma, e materiali capaci di deformazioni elastiche ampie, quali la gomma. Tali materiali apparivano sempre più frequentemente nell'uso comune e nei processi produttivi e pertanto numerosi teorici cominciarono a formulare teorie matematiche più o meno sufficienti a descriverli.

Divenne però ben presto chiaro che i concetti fisici e i metodi matematici già noti erano insufficienti allo scopo. Era quindi necessario creare tutta una serie di concetti nuovi con cui formulare una teoria atta a risolvere problemi specifici. Questo lavoro fu eseguito da diverse persone, provenienti dalla matematica, dalla fisica, dalla chimica, dall'ingegneria; esse lavorarono individualmente, non in gruppo, e ricevettero all'inizio scarsi riconoscimenti e poco aiuto. Alla fine, tuttavia, l'unificazione dei loro sforzi, in origine non coordinati, dette corpo a un'esauriente meccanica razionale dei mezzi continui, una nuova branca della matematica.

Questa scienza è ora approssimativamente nello stesso stato nel quale si trovava la dinamica dei sistemi di punti quando Lagrange compose la sua Mécanique analitique. È stata ottenuta una sintesi astratta e molti problemi chiave sono stati risolti, per quanto molti altri rimangano ancora aperti. Alcuni aspetti di questa sintesi e alcuni risultati specifici sono tratteggiati nel cap. 2.

La maggior parte del progresso recente nella meccanica razionale concerne i cosiddetti ‛corpi continui' o, brevemente, i ‛continui'. Naturalmente sono proprio questi i corpi di cui la geometria si è occupata principalmente fin dalle sue origini e la meccanica razionale dei continui è, in un certo senso, un'estensione diretta della geometria classica.

Anche la meccanica statistica, che rappresenta i corpi come insiemi molto numerosi di particelle soggette a certe ipotesi di probabilità, può essere trattata come una scienza razionale; in questo secolo sono stati fatti importanti progressi in questo campo, ma qui non ne parleremo dettagliatamente.

Siamo abituati oggi a concepire la meccanica classica come una scienza ‛applicata', destinata principalmente a risolvere i problemi dell'ingegneria. Essa non era stata presentata in tal modo da Lagrange. Il trattato di Lagrange è, secondo l'intenzione dell'autore, l'esposizione sistematica di una branca della matematica. Chi vuole applicare la meccanica analitica deve studiarla prima come una teoria generale. Lagrange stabilì i concetti, i principi e i teoremi principali, illustrandoli con alcuni esempi chiave, ma lasciò le applicazioni specifiche ad altri. La meccanica razionale dei ‛continui' del XX secolo segue l'esempio di Lagrange. Per quanto sia fortemente motivata dall'esperienza fisica, rimane pur tuttavia una branca della matematica.

La meccanica razionale dei continui si riallaccia alla tradizione del XVIII secolo anche per un altro verso. Piuttosto che ridurre il problema fisico alla dimensione delle tecniche matematiche che sono in grado di utilizzare, gli studiosi della meccanica razionale cercano di estendere il campo della matematica in modo da costruire il modello adatto per il fenomeno naturale in esame. Per quanto essi non siano prevalentemente impegnati nella creazione di matematica pura, non esitano a utilizzare i concetti e i metodi più nuovi della matematica pura, quando ciò sia necessario. Le ricerche recenti della meccanica razionale dei continui, essendo espresse in termini e in simboli spesso poco familiari a quanti abbiano studiato fisica, ingegneria, o matematica ‛applicata', sono esposte alle stesse critiche rivolte nel XVIII secolo a Eulero, a Lagrange e a coloro che svilupparono la meccanica razionale dei punti e dei corpi rigidi, disciplina, d'altra parte, oggi insegnata a tutti gli studenti di fisica e di ingegneria (v. Truesdell, 1966).

d) La termodinamica nel sec. XIX e la sua riduzione a termostatica.

La termodinamica classica sorse dai tentativi di spiegare il funzionamento della macchina a vapore e di calcolarne l'efficienza. Il corpo che esegue lavoro fu schematizzato come un corpo di gas la cui pressione soddisfa un'equazione termica di stato:

p = f(ρ, θ),

dove ρ è la densità di massa e θ è la temperatura. Si supponeva che il gas si contraesse e si espandesse in blocco, cosicché a p, a ρ e a θ si attribuiva ovunque lo stesso valore a un certo istante. L'efficienza della macchina è data dal rapporto tra calore assorbito e lavoro compiuto, quando entrambi siano misurati in unità meccaniche. I pionieri della termodinamica conclusero che l'efficienza massima di una macchina era determinata dalla temperatura massima e minima del corpo che esegue il lavoro:

Essi dimostrarono che tale efficienza era raggiunta in un qualunque ciclo di Carnot, cioè nel passaggio di ρ e θ da valori iniziali assegnati a quegli stessi valori attraverso un processo alternativamente ‛isotermico' e ‛adiabatico'.

Ritennero anche che nessun altro processo diverso da un ciclo di Carnot potesse raggiungere l'efficienza massima.

La potenza W delle forze agenti su un corpo gassoso di volume v fu senz'altro assunta come esprimibile nella forma seguente:

W= − pv• = pvρ•/ρ,

dove il punto indica una derivazione rispetto al tempo. Così, fin dall'inizio, si accettava una formulazione particolare e molto semplice della meccanica aggiungendo a essa concetti termici ed energetici.

Da queste premesse i pionieri della termodinamica derivarono una struttura teorica che può essere presentata come segue. Oltre alla temperatura θ(t), alla potenza sul corpo W(t) e al riscaldamento Q(t), vennero associate al corpo altre due grandezze: l'energia interna E(t) e l'entropia H(t). Queste grandezze soddisfano: 1) la prima legge della termodinamica (bilancio dell'energia): Á =W + Q; 2) la seconda legge della termodinamica (bilancio dell'entropia): θH• = Q.

La temperatura si suppone sempre positiva. Inoltre esiste un vettore k-dimensionale Y tale che

E = E(θ, Y), H = H(θ, Y).

Nel caso più semplice k = 1 e Y è proprio il volume del corpo. In un contesto diverso le k componenti di Y sono le masse di k dei k + 1 costituenti di una miscela. Infine la potenza W è una funzione lineare di Y•, cioè:

W = − p(θ, Y) • Y•,

dove p è la pressione termodinamica e p = p(θ, Y) è l'equazione termica di stato. Da queste ipotesi è facile derivare il teorema del potenziale termodinamico, una forma del quale è la seguente: l'energia libera Ψ ≡ E − θΗ è un potenziale per − p e − H:

− H = ∂_θΨ, −p = ∂_YΨ.

La relazione Ψ = Ψ(θ, Y) è un'equazione calorica di stato. Il teorema mostra che questa equazione determina non solo l'equazione termica di stato ma anche la funzione entropia.

Un processo è una coppia di funzioni θ(t), Y(t). Si dice che la teoria brevemente riassunta sopra tratta ‛processi reversibili' perché, se si descrive il processo all'indietro, si invertono i segni di W e Q e quindi anche di Á e H•.

La natura non offre generalmente una reversibilità di questo genere. Se si fa funzionare una macchina all'indietro non si riesce generalmente a recuperare tutto il calore necessario per farla funzionare in avanti. Calore e lavoro possono essere entrambi soltanto dissipati, mai creati. Questo fatto viene descritto col termine ‛irreversibilità'.

R. J. E. Clausius tentò di descrivere i processi irreversibili affermando che essi producono aumenti di entropia. Non è chiaro cosa egli intendesse per entropia in quei casi e ancor oggi alcuni ritengono che l'entropia ‛esista' solo per processi reversibili. M. Planck, d'altra parte, avanzò l'ipotesi che l'entropia potesse essere sempre introdotta, ma che non fosse in generale una funzione solo di O e Y. Egli riformulò la ‛seconda legge' di Clausius nella forma specifica:

θH• ≥ Q,

che si chiama anche disuguaglianza di Planck.

Nel XIX secolo, tuttavia, queste idee non furono mai sviluppate rigorosamente e i chimici considerarono generalmente inutile la teoria dei processi irreversibili allora disponibile. I fisici, anziché perfezionare e ampliare la termodinamica in modo adeguato a descrivere la deformazione, la conduzione del calore e la conseguente dissipazione di energia, calcarono sempre più l'accento sulle limitazioni della teoria già esistente. La circondarono di restrizioni, la più severa delle quali era che la teoria valesse solo per processi ‛infinitamente lenti' o ‛quasi statici', ‛vicini' all'equilibrio, ma non diedero mai alcun senso matematico a questi termini.

Infine J. W. Gibbs propose una trattazione radicalmente diversa dell'argomento. La variabile tempo non svolge alcun ruolo nella sua teoria, nella quale non vi sono processi. Si confrontano tra loro configurazioni di una certa classe e un principio variazionale determina quella che vale all'equilibrio. Le formule che si ottengono sono identiche a quelle corrispondenti della teoria dei processi reversibili, cosicché nelle applicazioni i risultati sono, in genere, esattamente gli stessi. Sfortunatamente Gibbs preferì chiamare la sua teoria ‛termodinamica', quale essa non è, invece di ‛termostatica', quale essa è. In effetti la teoria di Gibbs oltre a essere fondata su presupposti differenti, offre maggiori informazioni di quanto non faccia la termodinamica. Poiché l'equilibrio è definito attraverso l'esistenza di un minimo, ne seguono non solo il teorema del potenziale, ma anche alcune diseguaglianze che vincolano le derivate seconde di Ψ. La teoria di Gibbs, come altre teorie puramente statiche, comporta, implicitamente, un concetto di stabilità, mentre nella termodinamica, come in tutte le teorie che considerano le variazioni nel tempo, ogni criterio di stabilità ha un carattere accessorio.

Le idee di Gibbs si sono prestate facilmente all'assiomatizzazione e il lavoro più accurato in questo senso è stato svolto da C. Carathéodory, all'inizio del secolo. Nemmeno una perfetta termostatica, tuttavia, potrebbe servire gran che ad affrontare i problemi della termodinamica.

e) La natura e gli scopi della termomeccanica razionale creata negli anni sessanta.

La termodinamica classica non prende in considerazione la maggior parte degli aspetti della deformazione e tutto quanto attiene alla conduzione e alla radiazione di calore. La meccanica classica, a sua volta, esclude sia la temperatura che il calore. Nell'esperienza comune, invece, deformazione e riscaldamento sono intimamente connessi e di solito coesistono. Questo fatto evidente è diventato sempre più importante nell'ingegneria e, di conseguenza, gli ingegneri hanno trovato vari metodi speciali, alcuni a carattere teorico, per collegare i risultati piuttosto primitivi della termodinamica classica con le teorie di campo della meccanica classica dei continui, molto più sviluppate e astratte.

La termomeccanica razionale è una teoria compatta e unificata nella quale deformazione e calore sono introdotti entrambi fin dall'inizio. Quindi si tratta di una teoria generale di campo, che usa i concetti matematici e i metodi della meccanica razionale dei continui e allo stesso tempo incorpora ed estende largamente tutta la termodinamica classica, che vi appare come il caso speciale più semplice possibile.

Come il trattato di Lagrange forniva una struttura matematica entro la quale potevano essere formulati tutti i problemi concernenti insiemi di punti-massa e di corpi rigidi usando un unico metodo sistematico, la termodinamica razionale tende a offrire una struttura matematica che copra tutti i problemi concernenti corpi soggetti a deformazione e riscaldamento.

Fra gli studiosi che hanno dato i più importanti contributi alla termodinamica razionale ha particolare rilievo B. D. Coleman, che avremo spesso occasione di citare in questo articolo.

2. Concetti fondamentali della meccanica razionale dei corpi deformabili.

a) Corpi.

È tutt'altro che facile definire un ‛corpo', anche se questa nozione è così familiare nell'esperienza comune. Poiché la forma e la posizione di un corpo cambiano in generale nel tempo, non possiamo identificare i corpi con le porzioni di spazio che essi occupano. Ciononostante soltanto attraverso tali porzioni di spazio, che si possono chiamare ‛piazzamenti' dei corpi, possiamo distinguere e descrivere i corpi stessi.

Se si cercano le proprietà minime essenziali dell'insieme di tutti i corpi, troviamo facilmente che l'insieme costituisce un'algebra booleana. L'intersezione di due corpi è un corpo; tale è anche la loro unione. Ogni corpo ha un esterno, l'unione di due corpi è il corpo del quale ciascuno dei due fa parte, mentre l'intersezione dei due è il corpo che è una parte di entrambi.

Sfortunatamente non è stato ancora possibile costruire un sistema matematico in grado di descrivere la meccanica di corpi così complessi come quelli contemplati in generale dall'algebra booleana. In meccanica vari insiemi particolari di corpi, chiamati ‛universi materiali', sono studiati in dettaglio. Ne sono esempi sistemi di particelle, corpi rigidi, continui deformabili tridimensionali, aste, piastre, volte, miscele di corpi deformabili, mezzi porosi e compo- siti, corpi con struttura interna e così via.

In questo articolo concentreremo l'attenzione su continui deformabili ordinari tridimensionali. Tali corpi s'intende che costituiscano modelli matematici per la maggior parte dei corpi di materiali ordinari negli stati gassoso, liquido o solido.

S'incontrano i corpi solo in certi piazzamenti: essi occupano certi insiemi di posizioni x in uno spazio euclideo a tre dimensioni al tempo t. Una coppia ordinata (x, t) rappresenta un evento, ma un unico evento può essere rappresentato in infiniti modi differenti. Una qualunque di tali rappresentazioni, cioè un'applicazione di eventi su posizioni e tempi, è chiamata ‛sistema di riferimento'. Se lo stesso evento è rappresentato in due sistemi di riferimento diversi, le rappresentazioni (x, t) e (x*, t*) sono legate da un cambiamento di riferimento:

x* = c(t) + Q(t) + Q(x − x₀),

t* = t + a,

dove c è un'applicazione dell'asse dei tempi sulle posizioni, Q è un'applicazione sui tensori ortogonali, x₀ è una posizione particolare e a è un istante particolare. Queste trasformazioni rappresentano il concetto di cambiamento di osservatore. Lo stesso evento appare come (x*, t) a un osservatore, come (x*, t*) a un'altro. Poiché Q(t) è ortogonale, rappresenta una rotazione rigida, eventualmente preceduta o seguita da un inversione centrale. Possiamo immaginare un osservatore come un corpo rigido fornito di orologio. Due osservatori percepiscono esattamente gli stessi intervalli di tempo e le stesse distanze tra posizioni corrispondenti.

Un corpo tridimensionale ℬ è la chiusura di un insieme aperto su una varietà differenziabile, i punti X della quale sono chiamati punti materiali. A un certo istante, un corpo ℬ può essere applicato in modo bigettivo e bicontinuo, o persino con maggiore regolarità, sulla chiusura di un insieme aperto di posizioni x nello spazio euclideo a tre dimensioni. Una tale applicazione x:

x = x(X), X ∈ ℬ

è un piazzamento di ℬ e si dice che ℬ occupa la regione x(ℬ) nello spazio euclideo. Una serie di piazzamenti nel corso del tempo, cioè

x = x(X, t), X ∈ ℬ, t ∈ [t₁, t₂],

è un moto di ℬ rispetto al sistema di riferimento nel quale x è una posizione e t è il tempo. Il simbolo x(ℬ, t) indica il piazzamento di ℬ al tempo t e ∂x(ℬ, t) rappresenta la superficie limite di x(ℬ, t).

Rispetto al sistema di riferimento nel quale x* e t* sono rispettivamente posizioni e tempi, il moto è descritto dalle:

x* = x*(X, t*) = c(t) + Q(t)(x(X, t) − x₀),

t* = t + a.

La velocità v e l'accelerazione a di X nel moto x sono le derivate prima e seconda di x rispetto a t:

v ≡ x¨, a ≡ v• = x¨,

dove il punto soprascritto indica la derivata temporale di una funzione di X e di t. Con questa definizione x¨ e ẋ sono campi vettoriali su ℬ all'istante t. Poiché x è bigettivo, la velocità e l'accelerazione possono essere considerate anche come campi sul piazzamento di ℬ all'istante t. Useremo il punto anche per indicare la derivata materiale di tali campi su x(ℬ, t):

f• ≡ ∂_tf + (grad f)•v, w• ≡ ∂_tw + (grad w)v.

In particolare, a = v• = ∂_tv + (grad v)v (v. Noll, 1974; v. Truesdelì, 1977, cap. I).

b) Cinematica dei corpi continui.

La teoria del moto si chiama cinematica. Di solito questa teoria è costruita in termini di un piazzamento di riferimento, X = x(X), indipendente dal tempo. Allora il moto rispetto a un sistema di riferimento è equivalente alla trasformazione

x = x(x^-1)(x), t) ≡ x_x(X, t).

L'applicazione x_x è chiamata spostamento di ℬ, perché porta il piazzamento di riferimento di ℬ nel piazzamento di ℬ al tempo generico t.

Gli spostamenti possono essere analizzati con le tecniche usuali della geometria euclidea, dato che si tratta di applicazioni di regioni dello spazio euclideo su altre regioni di quello stesso spazio. Per esempio, possiamo definire il gradiente di spostamento F come la miglior approssimazione lineare di x_x alla posizione X nel piazzamento di riferimento x: F ≡ ∇x_x.

Tutti i cambiamenti di lunghezze e di angoli causati dallo spostamento possono essere espressi in termini di F. Un'ampia teoria matematica, chiamata ‛cinematica dei mezzi continui', mette in relazione varie grandezze definite in termini di F. Le più importanti ditali grandezze sono i tensori di deformazione C ≡ F^TF, B ≡ FF^T; il tensore di rotazione R, tale che F = R √-C = √-B-R; il gradiente di velocità G ≡ ∇v; il tensore velocità di deformazione D 1/2(G + G^T); il tensore di spin W ≡ 1/2(G − G^T) (v. Truesdelì e Noll, 1965, cap. CII).

c) Sistemi di masse, forze, coppie e riscaldamento.

La definizione di corpo data nel cap. 2, È a è limitata dall'ipotesi che il corpo sia un insieme misurabile. La massa M è una misura non negativa definita su corpi. La teoria della misura è stata ideata avendo in mente questa applicazione; essa fornisce esattamente la struttura matematica adatta a rappresentare il concetto fisico di ‛quantità di materia'.

Il concetto di forza è rappresentato da una funzione a valori vettoriali di coppie di corpi: f(ℬ, C) è la forza esercitata dal corpo C sul corpo ℬ. Se ℬ^e denota l'esterno di ℬ, allora f(., ℬ^e è una misura vettoriale definita sulle parti di ℬ.

La forza risultante su ℬ è f(ℬ, ℬ_e). Un sistema di forze è detto in equilibrio se la forza risultante su ogni corpo è nulla:

f(ℬ, ℬ^e) = 0 ∀ℬ.

Un teorema di Noll afferma che, se un sistema di forze è in equilibrio, allora, per corpi distinti ℬ e C,

f(ℬ, C) = − f(C,ℬ).

Questa relazione esprime il principio di azione e reazione: la forza esercitata da C su ℬ ha la stessa grandezza di quella esercitata da ℬ su C ma ha verso opposto.

Un sistema di ‛coppie' è una funzione F(ℬ, C) dello stesso tipo di f, ma i valori di questa funzione sono tensori antisimmetrici. L'esempio più importante di coppia è il momento di una forza rispetto a una posizione x₀, cioè (x − x₀) ⋀ f. Le proprietà matematiche di un sistema di coppie sono analoghe a quelle di un sistema di forze.

Il riscaldamento di un corpo ℬ da parte di un corpo distinto C è rappresentato da una funzione scalare Q(ℬ, C) che ha proprietà simili a quelle della funzione di forza f. In particolare Q(ℬ, ℬ^e) è il riscaldamento risultante di ℬ.

Forze, coppie e riscaldamenti sono indipendenti dal riferimento nel senso che:

f* = Qf, F* = QFQ^T, Q* = Q.

Cioè la forza, la coppia e il riscaldamento su un corpo sono gli stessi per tutti gli osservatori, tenuto conto della trasformazione ortogonale Q da un sistema all'altro: in questo senso si attribuisce ad essi un'effettiva realtà.

Si assume che la massa di un corpo abbia sempre lo stesso valore:

M(ℬ) = cost.

La massa è una funzione assolutamente continua del volume per ogni configurazione di ℬ:

La densità ρ è chiamata ‛densità di massa' di M in x(ℬ, t). Questo assioma è detto di ‛conservazione della massa' (v. Noll, 1974).

d) L'assioma di No/i sull'indipendenza della potenza dal rifrrimento. Le leggi del moto di Eulero.

La potenza W di un sistema di forze su ℬ^e in un certo riferimento è l'integrale della velocità rispetto alla forza:

dove f_ℬe è il sistema di forze esercitato da ℬ^e sulle parti di ℬ.

L'assioma di Noll afferma che la potenza è indipendente dal riferimento:

W* = W ;

da esso segue che il sistema di forze e di coppie è in equilibrio:

f(ℬ, ℬ^e) = 0, F(ℬ, ℬ^e) = 0 ∀ ℬ.

Questi enunciati costituiscono le ‛leggi della meccanica classica' in forma generale e per ogni sistema di riferimento.

La meccanica newtoniana presume l'esistenza di una classe speciale di riferimenti detti ‛inerziali', rispetto ai quali le forze e le coppie esercitate da tutti i corpi al di fuori del sistema Σ di corpi più ampio possibile hanno una forma particolarmente semplice. La forza d'inerzia su ℬ in un tale riferimento è

f(ℬ, Σ^e) = − m• (ℬ, x),

dove m è la quantità di moto di ℬ:

Chiamando f^a la risultante delle forze applicate:

f^a(ℬ) ≡ f(ℬ, ℬe_Σ),

ℬe_Σ e essendo l'esterno di ℬ in Σ, possiamo specializzare la legge generale f(ℬ, ℬ^e) = O per un riferimento inerziale:

f^a = m• (ℬ, x).

Similmente, chiamando M il momento della quantità di moto di ℬ:

si può provare che in un riferimento inerziale la coppia risultante applicata F^a soddisfa la relazione

F^a = M•(ℬ, x).

Le due relazioni f^a = m• e F^a = M•, dette leggi del moto di Eulero, esprimono il bilancio della quantità di moto e il bilancio del momento della quantità di moto in un sistema di riferimento inerziale. Si tratta di ampie generalizzazioni delle leggi di Newton, che esprimono i principi basilari della meccanica nella forma più largamente usata.

A esse va aggiunto il principio ugualmente importante del bilancio dell'energia, enunciato nel cap. 1 È d.

e) Azioni di contatto e azioni a distanza. Esistenza dello sforzo e delfiusso di calore.

Le forze sono di due tipi: quelle che i corpi esercitano l'uno sull'altro come conseguenza di un contatto e quelle che si esercitano sui corpi in virtù delle loro masse. Sono chiamate rispettivamente forze di contatto f_C e forze di massa f_B. Sistemi ditali forze sono definiti dalle condizioni seguenti:

∣f_B(A, C)∣≤ KM(A),

∣f_C(A, C)∣≤ KA(∂x(A, t) ⋂ ∂x(C, t)),

dove K è una costante, A denota area e ∂ indica frontiera. Cioè un corpo di massa piccola, qualunque sia il suo piazzamento, è soggetto a una forza di massa proporzionalmente piccola, mentre due corpi i cui piazzamenti abbiano un'area di contatto piccola sono soggetti a una forza di contatto proporzionalmente piccola, quali che siano le loro masse.

Secondo un teorema di W. Noll, questi due sistemi di forze soddisfano separatamente al principio di azione e reazione anche se nessuno dei due è in equilibrio. Un altro teorema di Noll afferma che le forze di contatto hanno una densità superficiale, chiamata vettore trazione t, e che questo campo vettoriale ha lo stesso valore in un certo punto su tutte le superfici che sono tra loro tangenti in quel punto. Un classico teorema di Cauchy assicura l'esistenza di un campo tensoriale degli sforzi T tale che

t = Tn,

dove n è la normale orientata alla superficie su cui agisce t. In conclusione, la prima legge del moto di Eulero prende la forma

ove b è la densità della forza di massa.

Similmente, la seconda legge di Eulero assume la forma

Ragionamenti analoghi possono essere applicati al riscaldamento Q e all'assioma del bilancio energetico. Il risultato è:

dove ε, la densità di energia interna rispetto alla massa, è chiamata l'‛energetico':

mentre h è detto ‛flusso di calore' e s ‛sorgente di calore'. Il vettore h rappresenta la conduzione di calore attraverso la frontiera ∂x(ℬ, t) del piazzamento di ℬ, mentre lo scalare s rappresenta il riscaldamento dovuto a radiazione (v. Truesdelì e Toupin, 1960).

f) Bilancio in generale. Equazioni genera/i di campo e condizioni di salto.

Le tre condizioni integrali ottenute nel paragrafo precedente sono della forma

dove ë, ♃ e ♂ sono certi campi scalari, vettoriali o tensoriali. Questa relazione, con campi non specificati, è una relazione generale di bilancio.

Se i campi ë, ♃ e ♂ sono sufficientemente regolari in una regione ℛ, si può prendere per x(ℬ, t) una sferetta, applicare il teorema della divergenza e far tendere il raggio della sfera a zero. Il risultato è l'equazione generale di campo:

ρ ë = div ♃ + ♂.

Questa equazione di campo deve valere in tutti i punti interni a ℛ; inversamente, se essa vale, l'equazione di bilancio è soddisfatta.

Per esempio, la condizione di bilancio della quantità di moto per mezzi continui assume la forma

ρα = div T + ρb,

con cui si esprime la prima legge del moto di Cauchy. Se questa equazione vale, si può dimostrare che la condizione di bilancio del momento della quantità di moto è equivalente alla condizione che il tensore di sforzo T sia simmetrico:

T = T^T.

Questa condizione è la seconda legge del moto di Cauchy. Similmente il principio del bilancio dell'energia può essere ridotto alla forma

ρε• = T • grad v + div h + ρs.

Queste sono le equazioni di campo della meccanica dei continui.

Le condizioni generali di bilancio non sono ristrette a campi regolari. Se ℛ contiene una superficie singolare sulla quale i vari campi che appaiono nelle equazioni di bilancio sono soggetti a salti, questi salti sono posti in relazione dalle condizioni generali di bilancio. La relazione fra le grandezze [ ] dei salti è espressa dal teorema di Kotchine:

[ρ ë S] − [♃]n = 0,

dove S è la velocità intrinseca di propagazione della superficie singolare ed n è il versore della normale. Applicando il teorema di Kotchine ai singoli casi appropriati, si ottengono le condizioni di conservazione della massa,

[ρS] = 0,

del bilancio della quantità di moto,

[T]n + S[ρv] = O,

e del bilancio dell'energia,

Queste condizioni si applicano in particolare alle onde d'urto.

g) Relazioni costitutive. Assiomi di Noll.

Le condizioni sviluppate finora sono leggi generali, nel senso che esprimono proprietà comuni a tutti i corpi presi in considerazione, cioè i continui tridimensionali. La varietà dei corpi dipende non solo dalle loro dimensioni e forme, ma anche dai materiali di cui sono fatti. Nella teoria sono introdotti materiali ideali, che fungono da modelli dei materiali che s'incontrano in natura. Questi materiali ideali sono definiti da relazioni costitutive, che legano i campi dinamici ed energetici, T e h, alle grandezze cinematiche come F oppure x_x stesso.

Gli assiomi per le equazioni costitutive di tipo puramente meccanico sono stati posti da Noll nel 1958 come segue.

1. Determinismo. Il tensore degli sforzi T in X ∈ ℬ e al tempo t è determinato dalla storia del moto di ℬ fino all'istante t. Cioè

T(X, t) = ???OUT-f???(x^tx^t(ℬ), X),

dove ???OUT-f??? è un'applicazione e x^t(ℬ) è la storia del moto di ℬ fino all'istante t.

Ciascuna applicazione particolare ???OUT-f??? definisce un materiale ideale; la relazione or ora stabilita è l'equazione costitutiva di quél materiale e l'applicazione ???OUT-f??? ne è la risposta. Poiché l'argomento x^t(ℬ) è la storia del moto di ℬ durante l'intero passato, la teoria comprende materiali con memoria. Tale memoria può essere, per quanto non lo sia necessariamente, infinitamente lunga.

2. Azione locale. Se in qualche intorno di X due moti hanno valore comune all'istante t e hanno avuto valore comune in tutti i tempi passati, gli sforzi T che essi determinano in X, t, in virtù dell'assioma 1, sono gli stessi.

3. Indifferenza del materiale al riferimento. La risposta di un materiale è indipendente dall'osservatore. Cioè, se ???OUT-f??? è l'applicazione la cui esistenza è affermata dall'assioma 1 e se x* è lo stesso moto x, ma riferito a un altro sistema definito dalla funzione Q (v. sopra, cap. 2, È a), allora, se poniamo

T*(X, t) = ???OUT-f???(x*^t(ℬ), X),

l'applicazione ???OUT-f??? dev'essere tale che

T* = QTQ^T.

Questi assiomi coprono quasi tutte le teorie speciali dei materiali studiate nel sec. XIX e molte di quelle introdotte recentemente, almeno per quanto riguarda la meccanica pura. Essi sono più generali di quanto non sia richiesto dalla maggior parte delle applicazioni.

h) I materiali semplici e i loro gruppi dei pari.

Un materiale è detto ‛semplice' se la risposta ???OUT-f??? dipende dal moto di ℬ solo attraverso il gradiente di spostamento F (v. sopra, cap. 2, È b). Cioè l'equazione costitutiva si riduce a

T(X, t) = G_x(F^t(X), x),

dove x denota il piazzamento di riferimento per lo spostamento a partire dal quale è definito F, cosicché X = x (X). I materiali semplici si prestano a sviluppi matematici molto ampi; sono stati a essi dedicati interi trattati e gran parte dell'attuale meccanica dei continui li concerne.

La risposta G _x, dipende dal piazzamento di riferimento x. È possibile, e in generale vero, che un punto materiale X in una posizione X′ di un piazzamento di riferimento differente x′ sia soggetto esattamente allo stesso sforzo, in ogni storia di piazzamenti riferita a x′ al quale sarebbe soggetto se la storia fosse riferita a x. In tal caso nessun esperimento descritto dalla teoria potrebbe far distinguere x da x′, cosicché x e x′ sono chiamati ‛pari'. I gradienti di spostamento che portano il piazzamento di riferimento x nei suoi pari formano un gruppo, chiamato il ‛gruppo dei pari', g_x(X), del materiale semplice rispetto a x in X. Questo gruppo rappresenta l'insieme di tutti gli esperimenti non distinguibili. Esso generalizza il concetto di ‛simmetn.a', familiare alla fisica fin dal XIX secolo, e gli dà un senso preciso.

Per facilitare l'interpretazione fisica si suppone che i vari piazzamenti di riferimento qui considerati abbiano la stessa densità di massa in X. Allora gli elementi di g_x sono necessariamente membri del gruppo unimodulare a. Un punto materiale X è chiamato ‛fluido' se per qualche x

g_x (X) = a.

È facile provare che allora g_x(X) = u per ogni x. Cioè un fluidò è un materiale per il quale nessun piazzamento di riferimento è distinguibile da un altro. X è isotropo se esiste un x, chiamato ‛piazzamento indistorto', tale che

g_x(X) ⊃ u,

dove o è il gruppo ortogonale. X è solido se esiste un x, detto ancora piazzamento indistorto, tale che

g_x(X) ⊂ o.

(Esprimendo a parole le due formule precedenti, si può dire che X è isotropo se può essere messo in un piazzamento tale che nessun esperimento successivo possa metterne in evidenza uno spostamento rigido; X è solido se può essere messo in un piazzamento tale che si può rivelare qualunque spostamento non rigido).

Se non vale nessuna delle tre possibilità di cui sopra, X è un cristallo fluido. Così i gruppi dei pari di X offrono la base per una classificazione esauriente dei materiali semplici.

L'applicazione di certi teoremi della teoria dei gruppi ci permette di affermare quanto segue: 1) tutti i fluidi sono isotropi e qualunque loro piazzamento è indistorto; 2) qualunque materiale isotropo è o fluido o solido; 3) per ogni piazzamento indistorto x di un solido isotropo è:

g_x = o.

L'ultima di queste affermazioni mostra che il concetto di isotropia nella teoria moderna è lo stesso di quello introdotto da Cauchy e usato tradizionalmente in fisica.

Le equazioni costitutive per i fluidi e per i solidi isotropi possono essere ridotte a forme particolarmente semplici e perciò molti degli sviluppi della teoria sono ristretti all'uno o all'altro di questi due tipi di materiali. Per esempio è possibile dimostrare che in un punto fluido che è stato sempre in quiete il tensore degli sforzi è della forma T = −p1, p essendo uno scalare. Quindi un fluido è un materiale che fluisce nel senso che non può rimanere in quiete se gli si applica uno sforzo di taglio. Per quanto il concetto di fluido sia molto generale, dato che permette anche una memoria infinitamente lunga, e benché il comportamento di un fluido che scorre possa essere molto più complesso di quanto non ammetta una qualunque delle teorie del sec. XIX, quando esso è in quiete obbedisce necessariamente alla teoria classica dell'idrostatica.

Se nessuno dei punti materiali di un corpo è distinguibile dagli altri attraverso la sua risposta locale, il corpo è uniforme. Se un qualche singolo piazzamento del corpo basta a mettere in evidenza questa uniformità, il corpo è omogeneo. Un corpo omogeneo è necessariamente uniforme e la maggioranza delle applicazioni della teoria riguardano corpi omogenei. Tuttavia è possibile che un corpo sia uniforme ma inomogeneo. Si consideri, per esempio, il seguente esperimento: si immagini di tagliare un pezzo di una striscia elastica infinita omogenea e senza sforzi, di piegarla di 180° a un estremo e di risaldare i due estremi fra loro. La striscia di Möbius così formata è ancora uniforme, ma in essa lo sforzo è diverso da zero e non c'è alcun piazzamento che porti tutte le sue parti in una condizione nella quale l'uniformità sia evidente. La striscia di Möbius di materiale elastico così ottenuta è un corpo elastico uniforme ma non omogeneo.

I corpi uniformi inomogenei posseggono alcuni degli attributi dei corpi che i fisici dello stato solido chiamano corpi con ‛dislocazioni'. Le equazioni di moto di un corpo uniforme non omogeneo sono state già stabilite e sono state ottenute e interpretate alcune loro soluzioni (v. Noll e altri, 1968; v. Wang e Truesdell, 1973, cap. V).

i) Miscele.

La teoria tracciata finora si riferisce a corpi composti, in ciascuna posizione e in ciascun istante, da un unico tipo di materiale. In chimica sostanze differenti si distinguono in base a proprietà chimiche differenti e possono combinarsi l'una con l'altra attraverso reazioni chimiche. Un effetto simile può presentarsi in situazioni puramente fisiche quando un atomo può essere eccitato a livelli diversi di energia in istanti differenti, o una molecola può spezzarsi in ioni. Per poter prendere in considerazione tali fenomeni su scala macroscopica, Truesdell ha proposto come modello una miscela di un numero finito di corpi costituenti sovrapposti, ℬ₁ i punti materiali dei quali possono essere indicati con X₁, X₂,..., X_k. In questa teoria una singola posizione x può essere occupata da un punto di ciascun corpo. Così invece di un moto unico si hanno k moti peculiari:

x = x_j(X_j, t), j = 1, 2..., k.

Ciascun costituente ha la sua velocità, accelerazione, tensore degli sforzi, vettore flusso di calore, ecc. peculiari. Per esempio, se si usa un accento grave sovrapposto per indicare la derivata temporale mentre X_j è tenuto costante, si può definire la velocità peculiare cosi:

v_i = x`_i.

Guidato dall'esempio del lavoro di J. Cl. Maxwell nel campo della teoria cinetica dei gas, Truesdelì ha proposto nel 1957 una struttura generale per teorie di questo tipo. I costituenti possono scambiare tra loro massa, quantità di moto ed energia, come conseguenza di reazioni chimiche e di mutamenti fisici. La sorgente di massa m_j, la sorgente di quantità di moto m_j, la sorgente di momento della quantità di moto M_j e la sorgente di energia e_j sono definite come segue:

Truesdell ha proposto assiomi di conservazione della massa, di bilancio della quantità di moto, di bilancio del momento della quantità di moto e di bilancio dell'energia nella seguente forma:

Σm_j = 0, Σm_j = 0, ΣM_j = 0, Σe_j = 0

dove tutte le somme vanno da 1 a k.

Avendo definito i campi appropriati per la miscela nel seguente modo:

Truesdell è riuscito a dimostrare che la miscela nel suo complesso obbedisce esattamente alle stesse equazioni di campo di un singolo continuo, quali sono presentate sopra nel cap. 2 È f. Il vettore u_j è chiamato velocità di diffusione del costituente j-esimo. Le definizioni di ε, T, h ed s mettono in evidenza gli effetti della diffusione sulle grandezze relative alla miscela. In base a queste definizioni, ciascuna affermazione riguardante la miscela diventa una conseguenza matematica di affermazioni riguardanti i costituenti e si è così costruito un metodo generale per derivare tali affermazioni.

Si può anche proporre una teoria generale delle equazioni costitutive per le miscele. Nel cap. 5, È e, citeremo alcuni risultati ottenibili in tal modo (v. Truesdell, 1969).

j) Mezzi polari e mezzi orientati.

Molti corpi che s'incontrano in natura non possono essere accuratamente descritti da varietà di punti. Una sbarra offre in proposito un esempio classico. Si può rappresentare una sbarra con una curva purché non si desideri tener conto di deformazioni più complicate di una flessione. Per rappresentare la torsione, si deve considerare la sbarra come una varietà formata non solo da una linea di punti, ma anche da vettori associati a ciascuno di quei punti, vettori che ruotano indipendentemente dalla deformazione della linea. La teoria classica delle sbarre elastiche usa due vettori su ciascun punto e ne considera importanti solo le direzioni, non le lunghezze; le direzioni si chiamano assi di torsione-flessione e il modo in cui le rotazioni di tali assi sono condizionate da forze e coppie applicate alla sbarra interviene nelle equazioni costitutive del materiale elastico. Una volta offre un altro esempio classico: tradizionalmente si può schematizzare una volta come una superficie a ciascun punto della quale è associato un vettore. La rotazione di questo vettore non è determinata dallo spostamento della superficie ma piuttosto da altre considerazioni. Si possono così rappresentare nella teoria sia le flessioni sia gli stiramenti nella volta.

Queste due teorie classiche sono approssimate sia in via di principio sia nel dettaglio. Una sbarra può essere rappresentata anche come un corpo speciale in una teoria tridimensionale, un corpo del quale due dimensioni sono molto più piccole della terza; un'analisi simile è possibile anche per una volta. I modelli monodimensionali delle sbarre e i modelli bidimensionali delle volte sono introdotti soltanto per ottenere una teoria matematica più semplice e più facilmente utilizzabile.

Vi sono altri corpi naturali per i quali la teoria tridimensionale sembra del tutto inadatta concettualmente. Un esempio è fornito da un materiale composto da molecole molto grandi e asimmetriche. Tale struttura molecolare è certamente riflessa nella risposta globale del materiale.

Alla fine del secolo scorso P.-M. Duhem suggerì che, per tener conto di tutte le possibilità, il moto di un corpo dovesse esser descritto da k + i applicazioni:

x = x(X, t), d_a = x_a(X, t), a = 1, 2, ..., k.

Il suo suggerimento fu seguito dai fratelli Cosserat, per quanto in un contesto piuttosto ristretto. Chiamando i vettori d_a ‛direttori' del corpo, J. L. Ericksen e Truesdell hanno costruito nel 1958 una cinematica e una dinamica generali su questa base. I direttori possono cambiare lunghezza oltre che direzione col passar del tempo. Materiali di questo tipo si dicono orientati. In generale vanno loro associate grandezze dinamiche ed energetiche addizionali. Il tensore degli sforzi per un tal corpo non è necessariamente simmetrico; in generale ci sono distribuzioni di momenti, che esercitano coppie in aggiunta ai momenti del campo del vettore trazione. I direttori possono aggiungere all'energia cinetica di traslazione ordinaria una energia di spin e analogamente ci può essere un momento di spin in aggiunta al momento ordinario della quantità di moto.

Il concetto di materiale orientato rende possibile disporre di modelli della risposta globale di materiali molto complicati. La generalità di tale concetto è così grande da renderlo inutile se non è opportunamente specificato in casi particolari. I casi principali studiati finora sono stati le aste elastiche, le volte elastiche, i materiali elastici con microstruttura e i fluidi anisotropi (v. Antman, 1972; v. Naghdi, 1972).

Teorie per fluidi anisotropi sono state sviluppate da Ericksen e collaboratori. A differenza delle teorie delle aste e delle volte, esse non sono estensioni della classe delle teorie descritte nelle sezioni precedenti di questo capitolo, ma si basano piuttosto sul concetto di materiali del tipo a scorrimento. Non si suppone che il tensore degli sforzi o le sue generalizzazioni siano determinati dalla storia dello spostamento; piuttosto si scrivono delle equazioni differenziali che legano queste grandezze e si cercano integrali ditali equazioni. Nei loro lavori, Ericksen e collaboratori tendono a circoscrivere la portata generale dell'impostazione proposta, mediante continui riferimenti diretti alle proprietà, rilevate sperimentalmente, di quei materiali naturali che vanno sotto il nome di e cristalli liquidi'; i ricercatori della scuola di Ericksen attribuiscono maggior valore a soluzioni ottenute in importanti casi particolari che ai teoremi generali (v. Ericksen, 1960, 1961, 1962 e 1976; v. Leslie, 1968).

3. Alcuni esempi importanti di meccanica razionale nel XX secolo.

a) Materiali elastici.

Un materiale elastico è definito dall'equazione costitutiva

T = g(F, X).

Lo sforzo è determinato dal gradiente di spostamento attuale F, indipendentemente dal tempo richiesto per effettuare lo spostamento e dai piazzamenti che il corpo ha occupato prima del piazzamento presente. Effetti di memoria sono del tutto assenti.

La teoria dell'elasticità è stata studiata ampiamente nel secolo scorso ed è oggi un ramo della scienza a sé stante. Quasi tutti i vecchi risultati si riferiscono alla teoria approssimata che si ottiene quando il piazzamento presente è quasi sovrapposto a quello nel quale T = O. Questa teoria può utilizzare il principio di sovrapposizione (v. Gurtin, The linear..., 1972).

Le equazioni generali della teoria non lineare senza restrizioni, chiamata talvolta ‛teoria finita', sono state ottenute oltre 150 anni fa, però, nonostante gli sforzi compiuti in questo secolo da A. Signorini e collaboratori, poco è stato ricavato da esse fin verso la fine degli anni quaranta, quando importanti soluzioni particolari, specialmente per i corpi isotropi incomprimibili, sono state trovate da R. S. Rivlin e da altri. L'attività in questo campo di ricerca è stata stimolata dal desiderio di predire correttamente il comportamento della gomma, materiale che sembra obbedire abbastanza fedelmente alle equazioni dell'elasticità finita sotto deformazioni che possono raggiungere il 200%.

Le soluzioni di Rivlin hanno fatto vedere che due fenomeni fin'allora considerati anomali erano di fatto conseguenze quasi inevitabili della teoria generale.

1. Effetto Kelvin. Per mantenere una deformazione di scorrimento semplice non è sufficiente applicare uno sforzo di taglio, ma è necessario aggiungere una pressione idrostatica proporzionale, al limite, al quadrato della dimensione della deformazione di scorrimento. Un corpo soggetto a uno sforzo di taglio puro cambia in generale il volume e il cambiamento è, al limite, proporzionale al quadrato della grandezza dello sforzo.

2. Effetto Poynting. Per realizzare una deformazione di scorrimento semplice, persino in un corpo incomprimibile, devono essere applicate al corpo trazioni normali diverse tra loro, le differenze essendo, al limite, proporzionali al quadrato della misura dello scorrimento. Sforzi di taglio puro causano in generale un allontanamento dei piani di scorrimento o un loro avvicinamento proporzionale, al limite, al quadrato della misura dello sforzo.

Questi fenomeni erano stati osservati sperimentalmente da W. Wertheim verso la metà del secolo scorso, ma non erano mai stati soddisfacentemente spiegati. Gli esperimenti di Wertheim riguardavano la torsione di un cilindro. Un fenomeno collegato a quello descritto era stato osservato verso la fine del XVIII secolo da Ch.-A. Coulomb: anche nei limiti entro i quali la coppia è proporzionale all'angolo di torsione, la rigidità torsionale dipende generalmente dalla tensione assiale. Anche questo fatto può essere spiegato dalla teoria generale, anzi la rigidità torsionale è stata calcolata esplicitamente da A. E. Green e R. T. Shield nel 1951.

Il successo ottenuto in tanti importanti casi particolari ha incoraggiato gli studiosi a sviluppare intensamente la teoria generale e sono stati così ottenuti teoremi di esistenza, unicità, andamento qualitativo, stabilità e instabilità, ecc. Sono stati pubblicati numerosi trattati e l'elasticità generale è oggi un campo attivo di ricerca specializzata (v. Knops e Wilkes, 1973).

b) Fluidi semplici, flussi viscometrici.

Nella meccanica classica dei fluidi il rapporto tra lo sforzo di taglio e lo scorrimento che esso produce è una costante chiamata viscosità. La viscosità dei fluidi si misura tradizionalmente coi viscosimetri; si tratta di strumenti basati su una configurazione nella quale il flusso del fluido e la coppia che esso esercita su una parte dell'apparecchio sono facilmente calcolati attraverso una teoria generale o particolare e facilmente misurati. Questi strumenti sono stati usati nella prima metà del secolo per la misura della ‛viscosità non lineare', un rapporto che dipende dallo scorrimento stesso ed è quindi incompatibile con la teoria classica. La viscosità non lineare è stata osservata principalmente nelle vernici e nei polimeri.

Un nuovo stimolo allo studio di tali materiali è derivato dallo sviluppo delle fibre artificiali. I loro processi di fabbricazione coinvolgono numerosi flussi che sono ovvia- mente incompatibili con la teoria classica dei fluidi viscosi. Per esempio, una colonna di un polimero allo stato fluido, estruso da una pressa, si rigonfia in generale fino a raggiungere un diametro molto maggiore di quello dell'ugello. Inoltre un'asta che ruoti in una tazza contenente tale fluido in generale attira su di sé il fluido stesso. Né l'uno né l'altro di questi fenomeni è previsto dalla teoria classica dei fluidi viscosi e la grandezza della viscosità del fluido non ha nulla a che fare con essi.

Negli anni quaranta e cinquanta numerosi studiosi hanno proposto equazioni costitutive particolari per i fluidi, in modo da spiegare questi fenomeni. La maggior parte di tali equazioni corrisponde a casi speciali del fluido semplice di Noll (v. sopra, cap. 2, È h). Il concetto cinematico di flusso viscometrico può a sua volta essere definito in modo preciso. Nel 1959 Coleman e Noll, generalizzando e semplificando precedenti importanti risultati di Rivlin, hanno fatto vedere che l'equazione costitutiva di un fluido semplice, quando è applicata a un flusso viscometrico, è equivalente a una formula semplice ed esplicita determinata da tre funzioni scalari dello scorrimento. Una di queste è la funzione di viscosità di taglio; le altre due sono le funzioni differenza dello sforzo normale. Come dicono i loro nomi, i valori di queste funzioni per un valore assegnato dello scorrimento sono lo sforzo di taglio e la differenza delle tensioni normali necessarie per rendere possibile il flusso. La teoria mette in relazione tutti i flussi viscometrici, mostrando che, in via di principio, i risultati di un programma sperimentale basato su un flusso viscometrico particolare sono sufficienti a determinare la natura di tutti i flussi viscometrici.

I fluidi semplici possono avere memoria complessa e di lunga durata. Però i flussi viscometrici sono tanto speciali da lasciare ben poco da ricordare alla memoria! Questa è la ragione per la quale tali flussi si prestano a una spiegazione esplicita e diretta per mezzo della teoria.

Un tipo di flusso viscometrico è il flusso in un tubo cilindrico a sezione circolare. È la teoria di questo flusso che fornisce la base per l'uso dell'ordinario viscosimetro a capillare. Se la sezione del tubo non è circolare, non è generalmente possibile un flusso rettilineo. Invece di procedere dritte lungo il tubo, le particelle del fluido sono soggette a un flusso secondario, che le spinge lungo traiettorie elicoidali. Per quanto questo flusso non sia viscometrico, le funzioni viscometriche del fluido sono sufficienti a descriverlo, almeno in via approssimata. Studi estesi di questi e di altri flussi secondari sono stati svolti da D. D. Joseph e da altri (v. Coleman e altri, 1966; v. Joseph e Fosdick, 1973; v. Joseph e altri, 1973; v. Truesdell, 1974; v. Joseph, 1974).

c) Materiali con memoria evanescente.

Negli esempi discussi nei due capitoli precedenti o il materiale era privo di memoria, oppure il moto era tale da non dar modo alla memoria di manifestarsi. Generalmente non si presenta nessuna di queste circostanze, ma l'esperienza comune indica che spesso la memoria dei materiali si attenua col tempo. Per esempio, una sbarra di metallo, se tenuta inflessa per un tempo abbastanza lungo, non ritorna al suo piazzamento originale, ma rimane completamente piegata o si adatta in una configurazione intermedia. In questi casi al momento della flessione iniziale lo sforzo può ben esser stato quello indicato dalla teoria dell'elasticità, ma decade poi nel tempo verso un valore più piccolo, che può persino ridursi a zero. Questo fenomeno si chiama ‛rilassamento dello sforzo'.

Per dare a quest'idea comune una forma precisa per i materiali semplici (v. sopra, cap. 2, È h) Coleman e Noll hanno supposto che il dominio del funzionale di risposta G_x sia un certo spazio di Banach delle storie F^t e hanno fatto l'ipotesi che l'applicazione G_x sia continua e differenziabile n volte nel senso di Fréchet sulle storie che corrispondono a uno stato di quiete. La topologia qui presupposta è quella determinata dalla norma ∥ ∥ nello spazio di Banach, che è una norma speciale, scelta in modo da dare maggior peso al presente e al passato recente che non al passato remoto. Il caso n = 0 è sufficiente a rappresentare il rilassamento dello sforzo. Se n 〈 0, G_x ha uno sviluppo di Taylor a n termini, valido per ∥ F^t − 1 → 0. Qui abbiamo scelto il piazzamento di riferimento in modo tale che F(t) = 1 per l'istante speciale t che stiamo considerando. Quando n = 1, G_x può essere ‛approssimato con un'applicazione lineare e ha quindi una rappresentazione in forma di integrale:

dove il nucleo K è un certo tensore del quarto ordine.

Per applicare questi risultati bisogna trovare situazioni nelle quali ∥ F^t - 1 ∥ è piccolo. Una di queste, ovviamente, è quella nella quale lo spostamento è sempre pressoché uguale all'identità, cioè esiste una quantità piccola ε tale che ∣ F^t(s) − 1 ∣ > ε per tutti gli s. Questo caso corrisponde a deformazioni infinitesime. Si può allora mostrare che l'espressione integrale scritta sopra si riduce a un'espressione proposta da L. Boltzmann un secolo fa. La teoria classica corrispondente si chiama ‛viscoelasticità accumulativa infinitesimale'. Il risultato appena ottenuto può essere espresso diversamente così: per una deformazione infinitesima l'equazione costitutiva di un qualunque materiale semplice con memoria evanescente è in prima approssimazione quella di un materiale elastico; la seconda approssimazione è offerta dalla teonà di Boltzmann.

Esiste poi un altro modo di rendere piccolo ∥ F^t − 1 ∥. Si considera un certo moto x(X, t) e s'introduce una famiglia corrispondente di moti ritardati:

x^r(X, t) ≡ x(X, rt),

in cui r è un numero positivo. Quanto più è piccolo r, tanto maggiore è il tempo necessario a X per compiere nel moto ritardato x^r una certa parte della traiettoria seguita nel moto originale x. Se r → 0, tutta la traiettoria di X, eccetto una porzione arbitrariamente piccola vicina a t = 0, è spinta arbitrariamente lontano nel passato o nel futuro. Così l'effetto del ritardo corrisponde esattamente all'idea di ‛moto lento'.

Per quanto riguarda questi moti,. Coleman e Noll hanno dimostrato un teorema di approssimazione. Per esprimere questo teorema, indichiamo con F_t il gradiente di sposta- mento quando il piazzamento presente è preso come riferimento e scriviamo:

dove ∣R(t, s) ∣ = o(sⁿ). Il tensore A_j così definito è detto j-esimo ‛tensore di Rivlin-Ericksen'. Dunque, ovviamente, il resto corrispondente Rr_n nel moto ritardato è tale che ∣ Rr_n(t, s) ∣ = o(rⁿsⁿ) quando rs → 0. Il teorema di Coleman e Noll afferma che ∥ Rr_n ∥ = o(rⁿ). In parole povere, per quel che concerne la memoria, la storia rappresentata nelle espressioni scritte sopra è determinata dalle sue prime n derivate a s = 0, con un errore che tende a zero più velocemente di rⁿ. Usando questo teorema Coleman e Noll hanno ottenuto per il funzionale di risposta G_x uno sviluppo in serie di polinomi nei tensori di Rivlin-Ericksen, A₁, A₂,..., A_n. Un materiale con un'equazione costitutiva di questo tipo è detto ‛matenale di tipo differenziale' di complessità n. Il teorema di Coleman e Noll afferma dunque che, in moti ritardati, la risposta di un materiale semplice con memoria evanescente coincide con quella di un opportuno materiale di tipo differenziale. Così gli effetti della memoria in un moto lento sono resi completamente espliciti.

Se lo si applica ai fluidi, il teorema di Coleman e Noll mostra che per un qualunque fluido semplice la teoria classica della viscosità è l'approssimazione di primo ordine in un moto lento. È facile calcolare approssimazioni di ordine superiore. La teoria che si ottiene per n = 2 è stata ampiamente studiata.

Ci sono anche altre definizioni matematiche di memoria evanescente, alcune più generali di quella di Coleman e Nolì e altre differenti. Applicazioni (‛funzionali') che descrivono effetti di memoria si presentano anche in biofisica. Lo studio dei funzionali di memoria è una branca dell'analisi matematica (v. Noll, 1974; v. Coleman e Noll, 1960; v. Coleman e Mizel, 1966).

d) Ipoelasticità. La zona elastica di un materiale semplice.

Gli aspetti generali dello snervamento e della deformazione plastica dei solidi sono noti da molto tempo. Teorie adatte a rappresentare questi fenomeni in un modo o nell'altro, di solito per deformazioni piccole, sono state proposte nel secolo scorso e intensamente sviluppate nella prima metà di questo secolo. Non occorre che se ne parli ulteriormente qui, perché questi studi riguardano principalmente applicazioni immediate a problemi speciali dell'ingegneria e non mirano a realizzare un'organizzazione dei principi generali (v. Geiringer, 1973).

Avanzando il suggerimento che una teoria corretta delle deformazioni plastiche ampie deve cominciare dai principi primi dell'elasticità e provare l'esistenza dello snervamento piuttosto che ipotizzarlo, Truesdell propose nel 1955, come studio-tentativo, una teoria di scorrimento detta ‛ipoelasticità'. Questa teoria è basata sulla seguente relazione differenziale per il campo del tensore degli sforzi T:

T• − WT + TW = f(T, D),

in cui D e W sono rispettivamente il tensore di deformazione e di rotazione e la funzione f è isotropa. La grandezza che compare a primo membro di questa relazione è il tasso di cambiamento dello sforzo, indipendente dal sistema di riferimento. L'equazione differenziale afferma che questo tasso di cambiamento è determinato dallo sforzo e dalla deformazione attuale.

Lo sforzo T può assumere un qualsiasi valore iniziale, in contrasto con quanto accade nella teoria dell'elasticità, in cui un unico valore di T è associato a ciascun piazza- mento del corpo. Ciononostante, vi sono delle forti analogie tra elasticità e ipoelasticità. Un integrale dell'equazione differenziale è presumibilm~nte determinato da un valore iniziale dello sforzo T₀ e ha la forma dell'equazione costitutiva di un materiale elastico, tranne per il fatto che esso dipende da T₀ come parametro. Ogni corpo elastico isotropo, per il quale la relazione sforzo-deformazione è invertibile, è ipoelastico. Tuttavia le due teorie sono differenti perché in generale materiali elastici anisotropi non sono ipoelastici e un materiale ipoelastico può essere elastico per certe condizioni iniziali di sforzo e non elastico per altre. Un materiale ipoelastico non è un materiale semplice e i teoremi generali che possono essere stabiliti per materiali semplici generalmente non gli si applicano. Per certi aspetti l'ipoelasticità è vicina alle teorie dei fluidi anisotropi di Ericksen (v. sopra, cap. 2).

Per un particolare caso di ipoelasticità, Truesdell ha fatto vedere che il comportamento in condizioni di taglio semplice è sostanzialmente indistinguibile dallo ‛snervamento' ipotizzato dalle vecchie teorie della plasticità. C'è una transizione continua da un comportamento puramente elastico a qualcosa che assomiglia molto a un cedimento improvviso.

La tendenza verso trattazioni matematiche sempre più generali ha fatto sì che l'ipoelasticità, una proposta dichiaratamente speciale, fosse messa da parte per un certo periodo. Più tardi si vide che essa si prestava alla soluzione numerica di problemi speciali su calcolatori e oggi è studiata specialmente da questo punto di vista.

L'idea che lo snervamento non debba essere semplicemente presupposto, ma che si debba piuttosto provarne l'eventuale comparsa in certe circostanze, come conseguenza di un'unica equazione costitutiva valida senza eccezione, si è mantenuta. Inoltre il fatto che l'ipoelasticità, come le vecchie teorie della plasticità, cada al di fuori della struttura teorica creata per i materiali semplici non ha scoraggiato gli studi tesi a dimostrare che anche i materiali semplici possono presentare fenomeni non distinguibili dallo scorrimento plastico e dallo snervamento.

Un notevole tentativo di questo genere è la teoria dei materiali con zona elastica proposta da D. R. Owen. Entro questa teoria Owen dimostra che la decomposizione del tensore delle deformazioni nelle componenti elastica e plastica, decomposizione assunta nelle precedenti teorie, è possibile per deformazioni elastiche piccole e solo per esse. Egli prova anche che le ipotesi chiamate ‛regole di scorrimento' nelle precedenti teorie valgono in condizioni molto generali come conseguenze dimostrate della teoria dei materiali semplici (v. sopra, cap. 2, È h; v. Owen, 1968 e 1970; v. Ting, 1973; v. Coleman e Owen, 1974).

e) Sviluppi matematici delle teorie classiche.

Nel sec. XIX certe teorie particolari dei mezzi continui, chiamate oggi ormai ‛classiche', furono seriamente considerate come branche della matematica. Per quanto nella prima metà del XX secolo siano state considerate principalmente le applicazioni, le approssimazioni e certe modificazioni suggerite dall'intuito, il rinato interesse per i fondamenti a partire dagli anni quaranta è stato accompagnato da uno studio matematico intenso e fruttuoso delle teorie classiche, considerate di nuovo come parti della matematica. Quest'attività è troppo tecnica perché possa essere riassunta qui, però è possibile almeno citare i campi di ricerca: onde d'urto nei gas (v. Courant e Friedrichs, 1948); frontiere libere in idrodinamica, argomento del lavoro di M. A. Lavrentev e J. B. Serrin (v. Gilbarg, 1960); aspetti analitici e qualitativi dell'elasticità lineare; stabilità idrodinamica, un campo inaugurato da Serrin (v. Joseph, 1976); teoria analitica e qualitativa della plasticità classica. C'è stata anche un'ampia e importante attività di ricerca su problemi concernenti l'esistenza e il comportamento qualitativo di soluzioni delle equazioni di Navier-Stokes per i fluidi viscosi e di altre equazioni differenziali non lineari alle derivate parziali.

4. Termomeccanica.

a) Esempi classici di materiali dissipativi: il fluido viscoso e il conduttore di calore rigido lineare.

Per due materiali dissipativi particolari erano state introdotte teorie locali esplicite ancor prima che fosse formulata la termodinamica. Innanzitutto c'era la teoria di Fourier-Duhamel del conduttore lineare rigido, definito dall'equazione costitutiva

h = − Kgrad θ,

dove il tensore K è la conduttività del materiale. Le equazioni differenziali della teoria erano state ottenute sostituendo questa espressione di h nell'equazione alla quale si riduce il principio del bilancio dell'energia (v. sopra, cap. 2, È f) per i moti rigidi e per una forma specifica di E. In questa teoria il fatto che il calore si diffonda spontaneamente dalle parti più calde verso quelle più fredde, e non il contrario, è espresso dalla condizione che il tensore K sia positivo. Questo fatto suggerisce la disuguaglianza di Fourier:

h • grad θ ≤ 0.

Il secondo esempio fu la teoria di Stokes-Duhem dei fluidi viscosi comprimibili. L'equazione costitutiva per lo sforzo è

T = − p1 + λ(tr D)1 + 2μD,

dove D è il tensore velocità di deformazione e dove p, λ e μ sono funzioni di ρ e θ. La funzione μ è la viscosità di taglio, mentre λ + 2/3 μ è la viscosità di volume. La funzione p è derivata da un'equazione calorica di stato tramite il teorema del potenziale termodinamico (v. sopra, cap. 1, È d). Il fatto che un corpo fluido che si deforma possa richiedere svolgimento di lavoro a causa dell'attrito, non essendo peraltro in grado di restituire spontaneamente quel lavoro, è espresso dalla condizione seguente:

(T + p1) • [λ(tr D)1 + 2μD] ≥ 0,

per tutti i valori possibili di D. La condizione è equivalente alle disuguaglianze di Stokes-Duhem:

Verso la fine del secolo scorso si finì per credere che queste due disuguaglianze riflettessero in qualche modo la seconda legge della termodinamica, ma siccome quella legge non era mai stata stabilita in una forma esplicita sufficientemente generale per poter essere applicata a questi due esempi di mutamenti irreversibili, tale analogia rimase nebulosa. Anche nella teoria dell'elasticità si ricorreva alla termodinamica per dedurre l'esistenza di una funzione potenziale, ma questo far riferimento alla termodinamica era altrettanto nebuloso. Per quanto la verità delle tre conclusioni fosse generalmente accettata, mancava loro un fondamento comune. Piuttosto che derivare da una qualche termodinamica generale dei processi irreversibili, esse indicavano la strada per arrivare a stabilire una tale teoria.

Per tutto il XIX secolo vi fu un solo esempio di una vera teoria termomeccanica di campo. Si trattava della base per il calcolo, dovuto a G. R. Kirchhoff, dell'assorbimento e della dispersione del suono in un fluido viscoso conduttore di calore. In questo esempio isolato le questioni concettuali sono nascoste. Si considerano solo gas ideali e le equazioni sono doppiamente approssimate: innanzitutto, si suppone piccola qualunque divergenza dall'equilibrio e poi si suppone piccola la frequenza dell'oscillatore eccitante. Per quanto la teoria di Kirchhoff sia un caso speciale approssimato assolutamente corretto della termomeccanica generale, quale la conosciamo oggi, e per quanto essa abbia fornito in verità un esempio importante di ciò che una teoria termomeccanica completa deve e può fare, le sue speciali caratteristiche resero difficile scoprirvi i principi di base.

b) La disuguaglianza di Clausius-Duhem e le sue due applicazioni tradizionali.

Se facciamo nuovamente riferimento alla forma generale del riscaldamento Q di un corpo continuo qual è presentata nel cap. 2, È e, cioè:

e la confrontiamo con le formulazioni di Clausius riguardanti processi irreversibili particolari, siamo portati a supporre che qualunque contributo q al riscaldamento dia anche un contributo pari almeno a q/θ all'aumento dell'entropia. In questo modo Truesdell e R. A. Toupin furono indotti a proporre nel 1960 la seguente forma della seconda legge, che essi chiamarono ‟disuguaglianza di Clausius-Duhem":

Già precedentemente, in questo secolo, P. M. Duhem e C. Eckart avevano introdotto l'integrale di superficie in certi casi speciali.

Una struttura assiomatica per i concetti di riscaldamento, entropià e temperatura può essere costruita lungo linee simili a quelle tracciate nel cap. 2, ÈÈ a ed e per la meccanica pura (v. Gurtin e Williams, 1967).

La disuguaglianza di Clausius-Duhem può essere interpretata in due modi: come una restrizione che riguarda i processi oppure come una restrizione che riguarda le relazioni costitutive.

La prima interpretazione è tradizionale nella dinamica dei gas. Le equazioni generali di quella teoria permettono onde d'urto di due tipi: quelle di condensazione e quelle di rarefazione. Le prime sono compatibili con la disuguaglianza di Clausius-Duhem, mentre le seconde non lo sono e, secondo la tradizione, sono escluse per questo motivo. La seconda interpretazione è già stata illustrata. Per concludere che K è non negativo nella teoria di Fourier-Duhamel dei conduttori di calore, abbiamo applicato la disuguaglianza di Fourier e abbiamo permesso a grad θ di assumere valori arbitrari. Per concludere che λ + 2/3 μ e μ sono non negativi nella teoria di Stokes-Duhem dei fluidi viscosi abbiamo applicato la disuguaglianza di Planck e abbiamo permesso a D di assumere valori arbitrari. Per queste due teorie speciali, la disuguaglianza di Clausius-Duhem si riduce rispettivamente alla disuguaglianza di Fourier e alla disuguaglianza di Planck, per quanto queste due teorie si escludano a vicenda.

In molti lavori recenti sulla termomeccanica dei continui la disuguaglianza di Clausius-Duhem è stata considerata come una formulazione approssimata della seconda legge della termodinamica e quindi è stata accettata come un assioma.

La forma locale della disuguaglianza di Clausius-Duhem è

ρη• ≥ div (h/θ) + ρs/θ,

dove η è l'entropia specifica, o ‛calorico', per la quale è:

La maggioranza degli sviluppi teorici si basa sull'uso delle formule che si ottengono eliminando ρs tra la disuguaglianza di Clausius-Duhem e il principio locale del bilancio dell'energia (v. sopra, cap. 2, È f). In termini dell'energetico libero ψ ≡ ε − ηθ, questa disuguaglianza di dissipazione ridotta diviene:

essa ha una struttura matematica semplice e può essere espressa in una forma astratta, e quindi ben più generale, introdotta da M. E. Gurtin.

Si supponga che π sia una funzione del tempo a valori scalari, che τ e λ siano funzioni del tempo i cui valori siano vettori k-dimensionali e σ e μ siano funzioni del tempo i cui valori siano vettori 1-dimensionali. Allora la disuguaglianza di dissipazione ridotta in forma astratta locale è

π• − τ • λ•+ σ • μ ≤ 0.

Nell'esempio che ha dato origine alla disuguaglianza di Clausius-Duhem k = 10 e l = 3, ma nelle teorie che tendono a rappresentare molti altri tipi di materiali una termodinamica può essere costruita lungo le stesse linee. Per esempio, per processi omogenei del tipo tradizionale l = 0 e k è arbitrario. Nelle teorie delle aste, delle volte e dei materiali con struttura interna (v. sopra, cap. 2, È j) k ha un valore particolare maggiore di 10. L'uso della disuguaglianza astratta di Clausius-Duhem rende possibile la trattazione degli aspetti termodinamici di tutte queste teorie differenti con un metodo unificato. I nomi dati a π, τ, σ sono rispettivamente accumulatore, tensione (termodinamica) e flusso di calore (generalizzato); λ ⊗ μ è chiamato il luogo.

La termomeccanica dei continui utilizza di solito la disuguaglianza di dissipazione astratta ridotta in una delle tre interpretazioni comuni. La prima è quella che abbiamo discusso sopra: π = ψ e λ = f ⊗ θ. Nella seconda p = ε e λ = F ⊗ η, mentre nella terza π = − η e λ = F ⊗ ε.

c) Equazioni costitutive per materiali semplici. Equipresenza.

La recente accelerazione del ritmo delle scoperte nella meccanica razionale dei continui è stata consentita da una distinzione chiara tra i principi generali, comuni a tutti i materiali di una classe ampia, e le relazioni costitutive, che modellano materiali particolari (v. sopra, cap. 2, È g). La termodinamica classica non aveva riconosciuto questa distinzione se non in contesti molto limitati. In verità la potenza W era stata presa da qualche precedente teoria della meccanica (v. sopra, cap. 1, È d) e così, in via di principio, si poteva adattare opportunamente qualunque relazione costitutiva puramente meccanica. Al contrario, la termodinamica stessa era stata sempre presentata in termini di equazioni di stato. Nel 1960 Truesdell e Toupin osservarono che, mentre la prima e la seconda legge sono certamente principi generali, alla pari con i principi del bilancio della quantità di moto e del momento della quantità di moto, le equazioni di stato sono relazioni costitutive, adatte solo per materiali molto speciali e che quindi non è corretto basare su di esse conclusioni generalizzate. L'osservazione era confermata dal fatto che l'uso della termodinamica in teorie di deformazione e dissipazione era rimasto limitato, fino allora, a quelle poche teorie meccaniche nelle quali le equazioni di stato termodinamiche tradizionali potevano essere incorporate quasi senza sforzo (v. sopra, cap. 4, È a).

La termodinamica razionale, per quanto abbia certamente antecedenti nelle ricerche del secolo scorso e in particolare negli studi di Duhem all'inizio di questo secolo, sembra cominciare da questa osservazione e dall'accettazione della disuguaglianza di Clausius-Duhem come una formulazione generale della seconda legge. Essa è la scienza delle equazioni costitutive della termomeccanica. Naturalmente la teoria puramente meccanica doveva esservi incorporata e principi quale quello di indifferenza del materiale dal riferimento (v. sopra, cap. 2, È g) dovevano essere estesi in modo da tener conto delle variabili termodinamiche. Tuttavia queste estensioni dirette non bastano. In questo articolo possiamo ignorare le estensioni più banali degli abbondanti risultati della meccanica e fissare l'attenzione sugli aspetti termodinamici più specifici della teoria combinata.

Si consideri, per esempio, un materiale elastico conduttore del calore. La sua risposta meccanica dipenderà certamente dalla temperatura:

T = g(F, θ).

Dall'esperienza risulta ugualmente ovvio che, se si vuole generalizzare la legge di Fourier della conduzione del calore, specialmente per materiali anisotropi, è necessario pensare il flusso di calore come dipendente sia dalla deformazione, sia anche, forse, dalla temperatura:

h = − K(F, θ) grad θ.

Per applicare le idee e i metodi della termodinamica, dobbiamo introdurre l'energetico ε e il calorico η e metterli in relazione con altre variabili. Le corrispondenti equazioni di stato sarebbero allora

ε = ε(F, θ), η = n(F, θ).

È certamente possibile procedere su questa base, ma una riflessione più attenta conduce subito a chiedersi perché, se h dipende da grad θ, si possa presumere che T, ε ed η non siano da esso influenzati e, se si permette ad h di essere il valore di una funzione generale di F e θ, perché mai si debba poi fare l'ipotesi che esso dipenda linearmente da grad θ.

Non vale affermare che devono essere gli esperimenti a dircelo, perché la termoelasticità delle grandi deformazioni è un campo nel quale gli esperimenti sono ancora rudimentali e danno risultati poco chiari. In questo campo, come in molti altri concernenti gli effetti di cambiamenti grandi e rapidi di forma e di temperatura, la pratica dell'ingegneria e le regole empiriche hanno proceduto bene al di là di quanto la fisica abbia suggerito e dev'essere una teoria razionale a indicare la strada per esperimenti critici. Senza un sostegno specifico nell'esperienza, il teorico non deve ipotizzare quello che può essere dimostrato e neanche ciò che può non essere vero. Dunque egli deve accettare la possibilità che T, h, ε ed η siano tutte funzioni di F, θ e grad θ.

Questo esempio illustra la regola di equipresenza proposta da Truesdell nel 1949. Secondo questa regola lo studioso che vuole formulare una teoria per una classe di fenomeni, dopo aver elencato le variabili indipendenti, o ^tcause', e anche le variabili dipendenti, o ‛effetti', deve ammettere a priori la possibilità che ciascuna causa contribuisca a ciascun effetto. Come è evidente da questa affermazione, la regola non è né una legge della fisica, né una profetica intuizione del risultato di qualche processo matematico. E una regola del senso comune da applicare nella formulazione delle teorie. Essa permette di scrivere ciascuna equazione costitutiva, indipendentemente dalla complessità dei fenomeni che è destinata a rappresentare, nella forma

e = f(c),

dove c ed e appartengono a spazi vettoriali opportuni. Lo spazio delle cause c è, in generale, di dimensione infinita, come, per esempio, lo spazio delle storie di funzioni i cui valori sono vettori di uno spazio di dimensione finita, mentre lo spazio degli effetti e è, in generale, di dimensione finita.

In termodinamica i materiali semplici, per esempio, vengono definiti prendendo c = λ^t ⊗ μ^t, dove λ e μ sono funzioni vettoriali che entrano nella disuguaglianza astratta di dissipazione ridotta (v. sopra, cap. 4, È b) ed e = π ⊗ τ ⊗ σ. Ciò significa che si presume che l'accumulatore, la tensione e il flusso di calore di un materiale semplice siano determinati dalla storia del luogo.

d) L'interpretazione di Coleman e Noll della disuguaglianza di Clausius-Duhem.

Avversando la regola di equipresenza, Coleman e Noll (v., 1963) in uno studio di grande originalità sono stati in grado di proporre un'interpretazione specifica della disuguaglianza di Clausius-Duhem: si tratta di una restrizione che riguarda le relazioni costitutive. L'applicazione costitutiva che definisce un materiale deve soddisfare la disuguaglianza di Clausius-Duhem identicamente, cioè per ogni argomento del dominio.

Naturalmente tutti i casi speciali classici della termodinamica (v. sopra, cap. 1, È d) e della termomeccanica (v. sopra, cap. 4, È a) sono compatibili con questa interpretazione (v. sopra, cap. 4, È b). Il grande merito di Coleman e Noll è quello di aver scelto, fra le diverse impostazioni della termomeccanica che conducevano a risultati equivalenti nelle teorie classiche, quella che si prestava meglio alla ricerca nel campo inesplorato delle grandi deformazioni accompagnate da grandi cambiamenti di temperatura nei materiali dissipativi.

Ne è seguita una nutrita serie di applicazioni, riuscite in quanto presentano rigorosamente risultati specifici dedotti da ipotesi esplicite, e il lavoro continua ancora. In questo articolo possiamo citare soltanto alcune delle applicazioni.

e) Altre proposte per la seconda legge. Il principio di degradazione di Day.

Contro la disuguaglianza di Clausius-Duhem sono state sollevate varie obiezioni. I sostenitori della termodinamica classica nella forma datale verso la fine del sec. XIX sono riluttanti ad accettare un concetto di entropia introdotto a priori. Essi ritengono che l'entropia abbia senso in condizioni di equilibrio o prossime all'equilibrio, e soltanto allora. Si rifiutano di utilizzare il concetto di entropia per cambiamenti ‛irreversibili' e preferiscono invece stabilire certe ipotesi sul risultato ditali processi se essi terminano in equilibrio. Ci sono anche termodinamici che preferiscono evitare l'uso della meccanica finché possibile. Essi lavorano direttamente con relazioni costitutive lineari cui impongono vari principi speciali: principi di dissipazione minima, regole di simmetria, ecc.

I. Müller ha proposto di sostituire il termine h • n/θ nella disuguaglianza di Clausius-Duhem con ϕ • n, dove ϕ è un flusso di entropia, da accettare alla pari di h come una variabile dipendente nelle relazioni costitutive. Egli ha anche proposto di sostituire 1/θ con una certa funzione ϑ(θ, θ•) chiamata ‛funzione di freddezza', funzione che si riduce, generalmente, a 1/θ solo all'equilibrio (v. Müller, 1973).

Se il caso che viene preso in considerazione è sufficientemente semplice, vuoi per il tipo di corpo, vuoi per le sue condizioni, tutte queste proposte conducono agli stessi risultati, ma ciò non si verifica in casi più complicati. Ed è proprio in questi casi più complicati che i risultati degli esperimenti non sono nè chiari nè sufficientemente ampi: è quindi per essi che la teoria deve servire come guida.

Quando le relazioni costitutive sono poste entro la struttura di Müller, si ottengono risultati un po' differenti da quelli classici. Per esempio, la teoria della conduzione del calore di Fourier e tutte le altre teorie basate sull'ipotesi fondamentale di Fourier prevedono che le perturbazioni della temperatura si muovano a velocità infinita. Ovviamente ciò non può esser vero in natura; per quanto la teoria di Fourier sia utile se applicata opportunamente, essa contiene qualche schematizzazione inadeguata e alcuni studiosi hanno tentato di trovare delle ragioni naturali e pressanti per introdurre un termine proporzionale a O sufficiente a condurre a una velocità specifica e finita. Una qualunque relazione costitutiva introdotta nella teoria generale della freddezza conduce a una tale velocità.

Un'altra idea frequentemente connessa con la termodinamica dei processi irreversibili è quella della reversibilità microscopica, ma non esiste ancora una sua trattazione completa basata sulla meccanica statistica. Tuttavia, W. A. Day ha fatto vedere che è possibile formulare un concetto d'inversione del tempo in certe teorie della meccanica dei continui. Materiali di questo tipo evidenziano certe simmetrie che hanno qualche relazione con quelle che i sostenitori della reversibilità microscopica dichiarano di saper derivare (v. Gurtin, Time-reversal..., 1972).

Ogni studioso di termodinamica sa che l'entropia è un concetto difficile per quanto di utilità centrale. Le presentazioni classiche dei processi reversibili superano la difficoltà dimostrando che, qualunque sia il suo significato, l'entropia esiste come conseguenza di certe ipotesi sul calore e sul lavoro. Entro le circostanze molto speciali prese in considerazione dalla termodinamica classica (v. sopra, cap. 1; È d), una tale dimostrazione può essere rigorosa e facile. Tuttavia nessun ragionamento semplice è stato esteso in modo da poterlo applicare alle teorie delle deformazioni grandi e rapide dei materiali dissipativi.

La principale speranza di successo sta nell'introduzione di un assioma termomeccanico che tenga conto esplicitamente della dissipazione. Un tale assioma fu proposto da lord Kelvin nel secolo scorso: ‟È impossibile ottenere, per mezzo di un dispositivo materiale inanimato, effetti meccanici da una qualunque porzione di materia raffreddandola al di sotto della temperatura degli oggetti più freddi che la circondano". Nonostante numerosi tentativi, finora questo assioma non è stato formulato in termini matematici.

Day ha cercato di ovviare alle obiezioni fatte all'introduzione di un concetto generale di entropia. Infatti, secondo Day, ‟il compito principale di una teoria della termodinamica dei materiali semplici con memoria [...] è quello di costruire l'entropia e di giustificare l'uso del nome entropia per il funzionale che si è costruito". Day stabilisce un assioma applicabile solo a processi ciclici che cominciano e finiscono in equilibrio:

t₀ e t₁ essendo gli istanti iniziale e finale. Per un'ampia classe di materiali questo assioma di degradazione è implicito nella disuguaglianza di Clausius-Duhem, ma non la implica. Comunque, Day mostra che, per i tipi più semplici di materiali, il suo assioma è sufficiente per ottenere gli stessi risultati che derivano, con minor difficoltà, dalle teorie che assumono l'entropia come un concetto primitivo, piuttosto che costruirla, come fa lui (v. Day, 1972).

Le idee di Day sono legate a un'altra linea di pensiero, dovuta, sembra, a Ericksen, secondo cui l'esistenza di una disuguaglianza per l'aumento dell'entropia, o qualcosa del genere, equivale a una specie di stabilità dell'equilibrio o a una conseguenza di tale stabilità. Ericksen stesso ha mostrato che se il moto di un materiale termoelastico è stabile in un senso dinamico, allora il piazzamento cui il materiale tende col tempo è necessariamente un piazzamento che soddisfa un criterio termostatico di stabilità. L'intero sistema di idee connesse con la stabilità, sia in meccanica pura sia in termomeccanica, è attualmente oggetto di intense ricerche.

Pur riconoscendo il carattere per ora discutibile della seconda legge della termodinamica per corpi formati da materiali complessi, soggetti a deformazioni grandi e rapide, in questo articolo citeremo soltanto i risultati che derivano dall'uso della disuguaglianza di Clausius-Duhem. Forse la ragione principale di questa scelta è che tale formulazione è l'unica che ha condotto, finora, a un vasto complesso di conclusioni specifiche.

f) Metodi inversi e seminversi. Serie di perturbazione.

Nelle teorie di campo formulate nel XIX secolo come sistemi di equazioni differenziali, varie condizioni iniziali e condizioni al contorno vanno imposte per determinare soluzioni particolari. Fisici e ingegneri hanno presentato delle soluzioni di quei problemi, generalmente in termini di serie infinite o di integrali coinvolgenti certe funzioni particolari, quali seni, coseni, esponenziali e funzioni di Bessel. Prendendo in considerazione, di solito, solo i casi nei quali le relative equazioni differenziali sono lineari, i matematici hanno dimostrato che tali soluzioni esistono e sono uniche e stabili, sotto condizioni molto deboli. L'uso di grandi calcolatori ha dato maggior forza a un programma di questo tipo. Così è nata l'idea che lo scopo del filosofo naturale sia quello di porre e risolvere ‛problemi al contorno' e talvolta quest'idea è usata come linea di demarcazione per distinguere il ‛fisico' o il ‛matematico applicato' dal matematico ‛puro'.

Ma solo relazioni costitutive molto semplici possono essere compatibili con una visione tanto arida della natura. L'obiettivo della scienza naturale, come ha sostenuto eloquentemente Newton, è di porre legami tra i fenomeni. Ciò non può essere ottenuto seguendo rigidamente quella linea di demarcazione, anche perché i problemi al contorno offrono una sola delle molte possibili strade per correlare i fenomeni

Nel XVIII secolo gli studiosi che per primi hanno derivato equazioni alle derivate parziali come condizioni per una teoria di campo hanno anche illustrato la validità delle loro idee indicando soluzioni speciali. Quando una parte di una soluzione particolare è postulata in partenza, mentre il resto è calcolato dalla teoria, il metodo si dice inverso. La teoria di Eulero sulla successione dei toni emessi da un corno è un esempio classico dell'uso dei metodi inversi. Tali metodi sono stati usati nella meccanica moderna razionale dei continui; le soluzioni di Rivlin per le deformazioni semplici di solidi elastici isotropi ne sono un valido esempio (v. sopra, cap. 3, È a).

Col metodo seminverso si assume a priori che una parte della soluzione dipenda da funzioni di certe variabili speciali; queste funzioni sono determinate poi in modo da essere compatibili con le equazioni generali. Un esempio classico del secolo passato è fornito dalle soluzioni date da A.-J.-Cl. de Saint Venant per la torsione e la flessione in elasticità lineare. Solo una parte delle condizioni al contorno appropriate sono soddisfatte, però le soluzioni particolari così trovate sono considerate come le più importanti fra tutte le soluzioni possibili. I metodi seminversi sono stati usati proficuamente nella meccanica razionale moderna dei continui, specialmente nella teoria dei flussi viscometrici (v. sopra, cap. 3, È b).

Nel metodo delle serie di perturbazione si parte da una soluzione semplice o persino banale e se ne cercano altre in qualche modo vicine a quella. Si tratta di solito di sviluppi in serie di potenze di qualche parametro che si riduce a zero per la soluzione nota. Il metodo può essere applicato alla relazione costitutiva stessa e il teorema relativo ai moti ritardati di Coleman e Noll ne è un esempio (v. sopra, cap. 3, È c). Più spesso esso è applicato simultaneamente alle equazioni differenziali e alla soluzione cercata. Esempi di questo tipo sono forniti dalla soluzione di Signorini del problema di trazione nell'elasticità finita e dalle soluzioni per i flussi secondari dei fluidi semplici (v. sopra, cap. 3, È d).

g) Propagazione delle onde.

Per quanto i metodi di perturbazione possano fornire un'ampia e interessante informazione, la loro applicazione è ristretta a casi non molto diversi da quelli per i quali una soluzione semplice è già stata ottenuta, di solito coll'uso del metodo inverso. Molti fenomeni di notevole importanza non sono trattabili coll'uso di tali metodi. Per esempio, se una palla di gomma è forata e rivoltata e quindi abbandonata a se stessa, assume una forma molto differente da quella originale; tale forma non può essere trovata per semplice perturbazione della forma di partenza, perché la serie di perturbazione si riduce sempre, per un qualunque corpo senza carichi sulla superficie, alla forma originale e a nessun'altra. I processi di perturbazione sono di solito associati a condizioni di unicità. In questo esempio, invece, il problema al contorno ha due soluzioni possibili (quella originale e quella eversa) piuttosto che una sola.

La distinzione è d'importanza decisiva per le teorie moderne, che tendono ad affrontare problemi di deformazioni grandi e con grandi differenze di temperatura. Le soluzioni ditali problemi di solito stanno al di là della zona delle piccole perturbazioni, per ragioni intrinseche. Un metodo diverso per ottenere risultati particolarmente semplici, ma importanti, è quello delle superfici singolari, introdotto da P. H. Hugoniot nel XIX secolo e applicato all'inizio del secolo presente, in modo del tutto generale, all'idrodinamica e all'elasticità finita, da Hadamard e Duhem. In questo metodo, la perturbazione può essere arbitrariamente grande, ma è idealizzata come una discontinuità ristretta su una superficie, anche se distribuita in modo liscio su di essa. Le discontinuità di questa specie hanno proprietà particolarmente semplici, che sono spesso facili da calcolare. In qualche caso la superficie singolare è costretta, per la natura stessa delle equazioni che descrivono il fenomeno, a propagarsi attraverso il corpo piuttosto che dividerlo permanentemente in due parti. In tal caso la superficie singolare si chiama onda.

Un'onda che trasporta una discontinuità normale di velocità è detta onda d'urto. Se la velocità è continua attraverso la superficie, ma l'accelerazione non lo è, l'onda è un'onda di accelerazione ed è interpretata talvolta come un'onda sonora.

La teoria locale delle onde ci permette d'immaginare chiaramente in che modo possono cambiare le condizioni di un corpo, per quanto non si sia in grado per ora di calcolare gli interi campi del moto e della temperatura. Un esempio classico è fornito dalla teoria delle onde d'urto e di accelerazione nei fluidi ideali. La teoria delle onde si è dimostrata un campo fertile per l'esplorazione delle proprietà costitutive di materiali di vario genere. Nella maggior parte dei casi, ma non in tutti, l'ampiezza a e la velocità intrinseca di propagazione S di un'onda di accelerazione soddisfano la condizione di propagazione:

(A − S²1)a = O,

dove il tensore acustico A è determinato dalla relazione costitutiva del materiale, dalle condizioni sul fronte d'onda stesso e dalla normale al fronte d'onda. Si può ottenere un'equazione differenziale per l'aumento o per il decadimento dell'ampiezza al procedere dell'onda. Per onde piane in molte differenti teorie si può provareche l'ampiezza obbedisce a un'equazione differenziale del tipo di Bernoulli:

dove μ dipende dalla classe dei materiali che si considera e dalle condizioni prevalenti nella parte del corpo a monte dell'onda, mentre β dipende solo dagli aspetti elastici della risposta del materiale. Quest'equazione, ottenuta nel 1965 da Coleman e Gurtin nel corso di ricerche su materiali con memoria evanescente (v. sopra, cap. 3, È c), è stata derivata e studiata successivamente da altri e specialmente da P. J. Chen, in altri contesti e con altre forme di μ e β.

Fino a poco tempo fa i due aspetti maggiori della propagazione delle onde erano stati studiati separatamente. Il primo aspetto era limitato alla dinamica dei gas e all'elasticità finita (v. sopra, cap. 3, È a). In queste teorie le discontinuità deboli di certi tipi d'onda diminuiscono in ampiezza durante la propagazione, mentre altre onde, in particolare quelle longitudinali di condensazione, si rinforzano durante la propagazione e le loro ampiezze, anche se piccole inizialmente, crescono oltre ogni limite in intervalli finiti di tempo. Questo fenomeno è di solito interpretato come la formazione di un'onda d'urto, per quanto non vi sia ancora alcuna dimostrazione matematica che gli urti siano realmente prodotti in questo modo.

Solo in una teoria non lineare l'ampiezza di un'onda può essere rinforzata mentre l'onda procede.

Le due teorie nelle quali è stata dimostrata la presenza di un tale rinforzo non tengono conto dell'attrito interno. Secondo le teorie classiche del suono che tengono conto di tale attrito, per esempio la teoria linearizzata di NavierStokes e la teoria di Boltzmann della viscoelasticità infinitesima, tutte le perturbazioni sono attenuate sistematicamente e non è possibile alcun rinforzo.

Nell'esperienza si incontrano entrambi i fenomeni. Suoni sufficientemente deboli svaniscono subito, ma gli strumenti musicali sono concepiti in maniera tale da concentrare l'energia e produrre, quasi immediatamente, un suono molto più forte di quello che li ha eccitati. Una stessa sostanza, l'aria, fornisce dunque l'esempio di entrambi i fenomeni. Corrispondentemente si dovrebbe poter disporre di una teoria unificata contenente entrambi i fenomeni come casi limite. In una teoria del genere dovrebbe esistere un'ampiezza critica, cioè un'ampiezza tale da separare le onde che si attenuano da quelle che si rinforzano.

È preciso merito di Coleman e Gurtin aver scoperto che la teoria dei materiali con memoria evanescente spiega effettivamente l'esperienza acustica comune. Essi hanno calcolato l'ampiezza critica per le onde piane, prestando particolare attenzione alle influenze termodinamiche su di essa. Successivamente sono state pubblicate molte ricerche sulla natura dell'ampiezza critica in altre teorie, o per altri tipi di onde (v. Coleman e altri, 1965; v. Chen, 1973).

Nel plexiglas le velocità di propagazione delle onde che approssimano superfici singolari sono abbastanza piccole per essere misurate e le osservazioni dei dettagli sono facilitate dalla trasparenza del materiale. Sono stati così condotti degli esperimenti sull'ampiezza critica e sui fenomeni ad essa collegati, sia in onde di accelerazione, sia in onde d'urto, ed è stato riferito che gli esperimenti collimano con la teoria di Coleman e Gurtin (v. Nunziato e altri, 1974).

5. Alcuni esempi importanti di termomeccanica razionale.

a) Termodinamica dei processi omogenei.

Se non si tiene assolutamente conto della deformazione e della conduzione del calore, tutte le grandezze della termomeccanica si riducono a funzioni del solo tempo. Per tali processi omogenei, la disuguaglianza di dissipazione ridotta (v. sopra, cap. 4, È b) diviene

π• − τ • λ• ≤ 0.

La generalizzazione ovvia del principio di determinismo (v. sopra, cap. 2, È g) è

π(t) = p(λ^t), τ(t) = t(λ^t),

dove p e t sono applicazioni che rendono soddisfatta la disuguaglianza di dissipazione ridotta per qualunque scelta di λ^t.

Se valgono equazioni di stato, p e t si riducono a funzioni della sola λ(t); allora la disuguaglianza di dissipazione ridotta richiede che sia:

t = ∂_λp

e il segno ≤ deve ridursi sempre a =. Di conseguenza, p è un potenziale per τ, ogni processo è ‛reversibile' e un processo è adiabatico se e solo se è isocalorico. Queste affermazioni astratte sono esattamente le conclusioni della termodinamica classica dei processi reversibili, basata su equazioni di stato (v. sopra, cap. 1, È d). Per esempio, se λ indica la coppia (θ, Y), se τ indica la coppia (−η, p) e se π sta per Ψ, allora il teorema or ora enunciato del potenziale si riduce a quello enunciato nel cap. 1, È d.

Una teoria di attrito lineare permette a τ di dipendere linearmente da λ•. Nell'interprètaziòne ricordata sopra,

W = − p₀(θ, Y) • Y• − Y• • π(θ, Y)Y•.

Allora la disuguaglianza di dissipazione ridotta è soddisfatta se e solo se

− H = ∂_θΨ, − p₀ = ∂_YΨ, X•p(θ, Y)X ≤ = ∀X.

Quindi Ψ non è più un potenziale termodinamico e un processo adiabatico non è più isentropico.

Truesdelì ha analizzato l'efficienza delle macchine termiche in questo contesto generale. Indicando con ΔΑ l'incremento di A nell'intervallo fra il tempo t₁ e il tempo t₂, egli ha mostrato che, se per un certo corpo è ‛DE − θ_minΔH ≤ 0, allora l'efficienza di quel corpo non può mai superare la stima classica 1 − θ_minima/θ_massima. Inversamente, se ΔE ≤ 0 e ΔH ≤ 0, l'efficienza 1 − θ_minima/θ_massima è raggiunta in un ciclo se e solo se tale ciclo è un ciclo di Carnot in un corpo tale che θH• = Q.

Se si applica questo teorema generale ai due esempi citati sopra si ottengono risultati differenti. Nel primo esempio è sempre θH• = Q e ogni ciclo di Carnot raggiunge l'efficienza massima classica. Nel secondo esempio, generalmente è θH• 〈 Q e nessun ciclo che non sia triviale raggiunge il massimo classico. Tuttavia, se si considera un processo ritardato (v. cap. 3, È c), allora per r → 0 l'efficienza dei cicli di Carnot tende verso il massimo classico. Così il concetto di processo lento può essere reso preciso.

b) Lo sviluppo della termoelasticita secondo Coleman e Noll.

Nei termini astratti usati nel paragrafo precedente e nel cap. 4, È b possiamo formulare putativamente le relazioni della termoelasticità nella forma seguente:

π = p(λ, μ), τ = t(λ, μ), σ = s(λ, μ).

È questa la teoria speciale, con interpretazioni specifiche per λ, μ, π, τ e σ, che Coleman e Noll hanno usato per dimostrare la validità della loro interpretazione della disuguaglianza di Clausius-Duhem e del principio di equipresenza. Affinché p, t e s soddisfino identicamente la disuguaglianza di dissipazione ridotta, è necessario e sufficiente che

π = p(λ), τ = _∂λp(λ), s(λ, μ) • μ ≤ 0.

Le prime due di queste relazioni esprimono il teorema del potenziale: il flusso di calore non influenza l'accumulatore e l'accùmulatore è un potenziale per la tensione. La terza relazione è la disuguaglianza di Fourier (v. sopra, cap. 4, È b). Se definiamo la dissipazione interna δ come segue:

δ ≡ π• − τ • λ•,

allora il teorema del potenziale implica che δ = O. Così in termoelasticità la disuguaglianza di Clausius-Duhem implica sia la disuguaglianza di Planck per la dissipazione, sia la disuguaglianza di Fourier per la conduzione del calore. In teorie più generali, come vedremo subito, non c'è una separazione tanto semplice degli effetti della deformazione e del flusso di calore.

c) Materiali con memoria. Teorema di Coleman.

In due importanti studi pubblicati nel 1964 Coleman è riuscito a costruire la prima termodinamica completa per materiali deformabili, dissipativi e con memoria a lungo raggio. La classe costitutiva da lui considerata è, in termini astratti, la seguente:

π(t) = B(λ^t, μ(t)), τ = I(λ^t, μ(t)), σ = G(λ^t, μ(t));

egli ha trattato esplicitamente le tre interpretazioni comuni delle variabili astratte (v. sopra, cap. 4, È b) e ha fatto l'ipotesi che le applicazioni B, I e G obbediscano al principio di memoria evanescente (v. sopra, cap. 3, È c). Il celebre teorema di Coleman può essere enunciato così: 1) assenza di interazione tra gradiente di temperatura e tensione. L'accumulatore è indipendente dal gradiente di temperatura: π(t) = B(λ^t); 2) potenziale termodinamico generalizzato. La risposta dell'accumulatore B determina la risposta della tensione I; dunque quest'ultima è indipendente dal gradiente di temperatura; 3) disuguaglianza di dissipazione. Vale là disuguaglianza di Planck: δ ≥ 0, e G(λ^t, μ(t))•μ(t) ≥ − δ; 4) compatibilità con la termostatica. Siano p e t le funzioni di α che sono i valori di B e I, rispettivamente, quando λ^t(s) = α, μ^t(s) = 0, 0 ≤ s 〈 ∞. Allora vale il teorema classico del potenziale termostatico: t = ∂_ap; 5) aspetto variazionale delle storie costanti di equilibrio. Nessuna storia che termini in un posto α ⊗ 0 può condurre a un valore dell'accumulatore più grande di quello che si ottiene dalla storia costante col valore α ⊗ 0. Cioè, se λ(t) = α, allora B(λ^t) ≥ p(α).

Questo importante teorema mostra che, per materiali con memoria evanescente, la termomeccanica razionale dei processi conduce a risultati assolutamente compatibili con la termostatica classica, li estende alla termodinamica e allo stesso tempo offre, in termini di processi, una controparte alle condizioni di stabilità implicate dalla termostatica di Gibbs. Quest'ultimo fatto è particolarmente importante e merita di essere enunciato nelle sue tre interpretazioni comuni per un materiale semplice: 1) tra tutti i processi che terminano nel luogo F ⊗ θ ⊗ 0, quello che ha sempre avuto il valore F ⊗ θ ⊗ 0 conduce al valore minimo dell'energetico libero ψ; 2) lo stesso enunciato 1), eccetto che il luogo è F ⊗ η ⊗ 0, l'energetico libero va sostituito coll'energetico ε; 3) lo stesso enunciato 1), eccetto che il luogo è F ⊗ ε ⊗ 0, l'energetico libero va sostituito con il calorico η e l'aggettivo minimo va sostituito con massimo.

Il lavoro di Coleman è basato sul concetto di memoria evanescente introdotto da Coleman e Noll (v. sopra, cap. 3, È c). Esso include la dimostrazione che un materiale di questo tipo si comporta come un materiale elastico (v. sopra, cap. 3, È a) in due casi limite: per deformazioni molto lente (moti ritardati) e per deformazioni molto veloci (onde deboli). Quale sia il materiale elastico particolare imitato dal materiale con memoria evanescente dipende dalle circostanze presenti e dalla storia di deformazione alla quale il materiale stesso è stato assoggettato.

Il lavoro di Coleman può essere, ed è stato infatti, generalizzato. Tuttavia, le proprietà ivi affermate non sono comuni a tutti i materiali concepibili. Materiali che non abbiano memoria evanescente o breve non presentano in generale la proprietà variazionale. Materiali con memoria a breve raggio non posseggono generalmente un potenziale termodinamico (v. Coleman e Mizel, 1964).

Il ruolo delle relazioni costitutive è essenziale in termomeccanica. Senza di esse non solo non si può dimostrare nulla di specifico, ma anzi è facile trovare controesempi per quasi tutte le affermazioni specifiche. Le differenze principali tra la termodinamica tradizionale e la termomeccanica razionale moderna sono due: le proprietà meccaniche dei materiali sono specificate espressamente ed esplicita mente e le relazioni costitutive termomeccaniche sono dichiarate e usate nelle dimostrazioni matematiche. C'è ancora un'altra differenza importante di base e cioè che la matematica è usata dall'inizio alla fine, esattamente come nel XVIII secolo, come il mezzo per estrarre innumerevoli conseguenze complesse eppur precise da pochi assiomi apparentemente semplici. Come il lettore avrà visto da sé, la termomeccanica razionale non pretende di proporre nuove leggi fisiche. Piuttosto tende a ottenere molte nuove conclusioni e previsioni da enunciati precisi delle leggi espresse in modo vago nel secolo passato, attraverso una specializzazione appropriata e procedimenti rigorosamente matematici.

d) Variabili interne di stato.

I tentativi di fisici e chimici di studiare i processi dissipativi si basano di solito sull'uso delle variabili interne di stato. Queste variabili possono essere considerate simili ai parametri Y₁, Y₂, ..., Y_k della teoria dei processi omogenei (v. sopra, cap. 5, È a), eccetto per il fatto che esse sono campi. Di solito sono scelte avendo in mente qualche proprietà fisica particolare: l'energia cinetica dello spin molecolare, la frazione di atomi eccitati a un certo livello di energia, il grado di avanzamento di una reazione chimica, ecc.

Per quanto riguarda la dinamica dei gas, la teoria delle variabili interne di stato è un caso speciale della teoria dei materiali con memoria. Dunque non sono necessari né una nuova analisi termodinamica, nè principi termodinamici addizionali (v. Coleman e Gurtin, 1967).

e) Miscele. Mezzi porosi. Reazioni chimiche.

Una struttura atta a specificare gli aspetti meccanici delle miscele è stata già descritta (v. sopra, cap. 2, È i). La teoria termomeccanica permette a ciascun costituente di avere la sua temperatura θ_j e il suo calorico η_j peculiari come anche la propria sorgente di calorico n_j, definita così:

ρn_j ≡ ρc_jη_j + ρ_jη`_j − div(h_j/θ_j) − ρ_js_j/θ_j.

L'assioma di dissipazione di Bowen e Truesdell afferma che

Σ n_j ≥ 0.

La disuguaglianza di dissipazione risultante per la miscela ha la forma proposta da Müller (v. sopra, cap. 4, È e), col flusso di entropia ϕ dato esplicitamente da:

ϕ = Σ (h_j/θ_j − ρ_jη_ju_j).

Secondo un principio generale di determinismo (v. sopra, cap. 2, È g), in base alla regola di equipresenza (v. sopra, cap. 4, È d), le relazioni costitutive devono specificare non solo T_j, h_j, ψ_j e η_j, ma anche le sorgenti m_j, m_j, e_j, come valori di applicazioni il cui dominio è lo spazio delle storie xt_l e θt_l su B_l, l = 1, 2, ..., k. Finora sono stati studiati solo materiali semplici, e tra questi solo quelli di una classe speciale.

Prima che fosse creata la termodinamica razionale, Truesdell aveva tentato di spiegare il fenomeno della diffusione con una teoria puramente meccanica di questo tipo. La teoria tradizionale di Fick trascura forze e inerzia e prevede che perturbazioni di densità si propaghino con velocità infinita. Entrambi questi difetti sono rimossi nella teoria di Truesdell, il quale ha anche mostrato che le relazioni di simmetria dedotte talvolta da un'assenta nuova legge della fisica corrispondono all'ipotesi che la miscela sia diluita in un senso ben specificato. Tuttavia la teoria di Truesdell, essendo meccanica, non offre un ponte verso la termochimica classica. Müller ha rimosso l'ostacolo presentando una teoria completamente termomeccanica che incorpora come approssimazioni o come casi limite tutti gli aspetti speciali noti, ma non ancora connessi, li mette in relazione gli uni con gli altri e offre i mezzi per calcolare approssimazioni migliori.

La termomeccanica permette anche di costruire una teoria razionale della filtrazione di fluidi attraverso mezzi porosi. Fino a poco tempo fa questo fenomeno era stato descritto attraverso un'approssimazione grossolana, la cosiddetta ‛legge di D'Arcy', senza relazione con altre parti della meccanica e priva di un qualunque aspetto termodinamico. Le idee che conducono alla legge di D'Arcy non offrono alcuna base per la costruzione di una descrizione più accurata. Müller ha formulato una tale descrizione entro la teoria generale delle miscele. Egli ha introdotto un campo di porosità come una variabile indipendente in aggiunta a quelle che descrivono i moti e le densità dei costituenti solidi e fluidi. La legge di D'Arcy appare allora come una prima approssimazione dell'equazione di bilancio della quantità di moto in questa teoria, così come, nella teoria delle miscele di fluidi in diffusione, la legge di Fick appare come la prima approssimazione della stessa equazione (v. Müller, 1971).

Una premessa necessaria per la costruzione di una teoria termomeccanica delle reazioni chimiche è la cinetica chimica. Nella sua interpretazione più stretta, tale teoria limita le possibilità generali di scambio di massa a combinazioni di atomi che formano varie molecole e alla dissoluzione e ricombinazione di quelle molecole per formare altre molecole. Anche se i costituenti di una miscela non sono pensati come composti di atomi nel senso chimico, essi possono seguire regole di combinazione e dissoluzione in rapporti fissi che vanno descritti da una cinetica. Ora, anche la cinetica chimica, un argomento ben studiato, è stata riformulata da R. A. Aris, R. M. Bowen e M. Feinberg in termini sufficientemente generali perché possa essere usata nella termomeccanica moderna (v. Feinberg, On chemical..., 1972).

Bowen, Müller e altri hanno costruito teorie termomeccaniche di miscele reagenti chimicamente. Per ottenere risultati sufficientemente definiti, in modo da consentire interpretazioni univoche, questi autori hanno considerato vari casi speciali entro quelli permessi dalla cinetica e dalla termomeccanica generale. Bowen si è interessato principalmente alla natura dell'equilibrio e ha proposto e analizzato un semplice criterio per distinguere l'equilibrio falso da quello forte. Nel primo si annulla l'ampiezza delle reazioni, mentre nel secondo si annullano anche le affinità chimiche. Le teorie tradizionali si basano su relazioni lineari tra affinità e ampiezze e quindi non sono in grado di distinguere un tipo di equilibrio dall'altro. Nella teoria di Bowen le tensioni in condizioni di equilibrio falso possono essere di un tipo più complicato di quello considerato nella termochimica classica, che è necessariamente quello valido in condizioni di equilibrio forte.

Le teorie di Müller sono fondate principalmente sulla struttura che risulta dall'uso della sua idea di freddezza (v. sopra, cap. 4, È f) e quindi determinano una velocità specifica, finita, di propagazione per perturbazioni della temperatura. Egli mette in particolare evidenza la verità o la falsità di certe relazioni di simmetria che giocano un ruolo importante nelle teorie non sistematiche proposte ad hoc, su basi intuitive e senza utilizzare le risorse della termomeccanica razionale. Müller ha considerato anche il caso che si verifica quando i costituenti di una miscela hanno temperature differenti nello stesso posto e ha discusso la possibilità che queste temperature tendano a un valore comune col procedere del moto.

Egli ha esteso l'impostazione della termomeccanica razionale in modo da applicarla a effetti elettromagnetici nell'ambito classico e relativistico (v. Müller, 1969; v. Alts e Müller, 1972). La grande complessità formale di queste teorie può essere dominata, fino a un certo punto, col ricorso alla tecnica dei moltiplicatori per eliminare i vincoli dalle disuguaglianze (v. Liu, 1972).

Bibliografia.

Alts, Th. S., Müller, I., Relativistic thermodynamics of simple heat conducting fluids, in ‟Archives for rational mechanics and analysis", 1972, XLVIII, pp. 245-273.

Antman, S., The theory of rods, in Encyclopedia of physics, vol. VI, a/2, Berlin-Heidelberg-New York 1972, pp. 641-703.

Chen, P. J., Growth and decay of waves in solids, in Encyclopedia of physics, vol. VI, a/3, Berlin-Heidelberg-New York 1973, pp. 303-402.

Coleman, B. D., Thermodynamics of material with memory, in ‟Archives for rational mechanics and analysis, 1964, XVII, pp. 1-46.

Coleman, B. D., On thermodynamics, strain impulses, and viscoelasticity, in ‟Archives for rational mechanics and analysis", 1964, XVII, pp. 230-254.

Coleman, B. D., Gurtin, M. E., Some properties of gases with vibrational relaxation when viewed as materials with memory, in ‟Meccanica", 1967, II, pp. 135-140.

Coleman, B. D., Gurtin, M. E., Herrera, R. I., Truesdell, Cl. A., Wave propagation in dissipative materials. A reprint of five memoirs, New York 1965.

Coleman, B. D., Markovitz, H., Noll, W., Viscometric flows of simple fluids, New York 1966.

Coleman, B. D., Mizel, V., Existence of caloric equations of state, in ‟Journal of chemical physics", 1964, XL, pp. 1116-1125.

Coleman, B. D., Mizel, V., Norms and semi-groups in the theory of fading memory, in ‟Archives for rational mechanics and analysis", 1966, XXIII, pp. 87-123.

Coleman, B. D., Noll, W., An approximation theorem for functionals, with applications in continuum mechanics, in ‟Archives for rational mechanics and analysis", 1960, VI, pp. 355-370.

Coleman, B. D., Noll, W., The thermodynamics of elastic materials with heat conduction and viscosity, in ‟Archives for rational mechanics and analysis", 1963, XIII, pp. 167-178.

Coleman, B. D., Owen, D.R., A mathematical foundation for thermodynamics, in ‟Archives for rational mechanics and analysis", 1974, LIV, pp. 1-104.

Courant, R., Friedrichs, K. O., Supersonic flow and shock waves, New York 1948.

Day, W. A., The thermodynamics of simple materials with fading memory, New York 1972.

Ericksen, J. L., Anisotropic fluids, in ‟Archives for rational mechanics and analysis", 1960, IV, pp. 231-237.

Ericksen, J. L., Conservation laws for liquid crystals, in ‟Transactions of the Society of Rheology", 1961, V, pp. 23-24.

Ericksen, J. L., Kinematics of macromolecules, in ‟Archives for rational mechanics and analysis", 1962, IX, pp. 1-8.

Ericksen, J. L., Equilibrium theory of liquid crystals, in ‟Advances in liquid crystals", 1976, II.

Feinberg, M., On chemical kinetics of a certain class, in ‟Archives for rational mechanics and analysis", 1972, XLVI, pp. 1-41.

Feinberg, M., Complex balancing in general kinetic systems, in ‟Archives for rational mechanics and analysis", 1972, XLIX, pp. 187-194.

Geiringer, H., Ideal plasticity, in Encyclopedia of physics, vol. VI, a/3, Berlin-Heidelberg-New York 1973, pp. 403-533.

Gilbarg, D., Jets and cavities, in Encyclopedia of physics, vol. IX, Berlin-Heidelberg-New York 1960, pp. 311-445.

Gurtin, M. E., The linear theory of elasticity, in Encyclopedia of physics, vol. VI, a/2, Berlin-Heidelberg-New York 1972, pp. 1-295.

Gurtin, M. E., Time-reversal and symmetry in the thermodynamics of materials with memory, in ‟Archives for rational mechanics and analysis", 1972, XLIV, pp. 387-399.

Gurtin, M. E., Thermodynamics and the energy criterion for stability, in ‟Archives for rational mechanics and analysis", 1973, LII, pp. 104-111.

Gurtin, M. E., Williams, W. O., An axiomatic foundation for continuum thermodynamics, in ‟Archives for rational mechanics and analysis", 1967, XXVI, pp. 83-117.

Joseph, D. D., Slow motion and viscometric motion; stability and bifurcation of the rest state of a simple fluid, in ‟Archives for rational mechanics and analysis", 1974, LVI, pp. 99-157.

Joseph, D. D., Stability of fluid motions, in Springer tracts in natural philosophy, voll. XXVII-XXVIII, Berlin-Heidelberg-New York 1976.

Joseph, D. D., Beavers, G. S., Fosdick, R. L., The free surface on a liquid between cylinders rotating at different speeds. II., in ‟Archives for rational mechanics and analysis", 1973, XLIX, pp. 381-401.

Joseph, D. D., Fosdick, R. L., The free surface on a liquid between cylinders rotating at different speeds. I., in ‟Archives for rational mechanics and analysis", 1973, XLIX, pp. 321-380.

Knops, R. J., Wilkes, E. W., Theory of elastic stability, in Encyclopedia of physics, vol. VI, a/3, Berlin-Heidelberg-New York 1973, pp. 125-302.

Leslie, Fr., M., Some constitutive equations for liquid crystals, in ‟Archives for rational mechanics and analysis", 1968, XXVIII, pp. 265-283.

Leslie, Fr., M., Theory of flow phenomena in liquid crystals, in ‟Advances in liquid crystals", in stampa.

Liu, I-Shih, Method of Lagrange multipliers for exploitation of the entropy principle, in ‟Archives for rational mechanics and analysis", 1972, XLVI, pp. 131-148.

Müller, I., Toward relativistic thermodynamics, in ‟Archives for rational mechanics and analysis", 1969, XXIV, pp. 259-282.

Müller, I., Entropy, absolute temperature and coldness in thermodynamics. Boundary conditions in porous materials, Wien 1971.

Müller, I., Thermodynamik, die Grundlagen der Materialtheorie, Düsseldorf 1973.

Naghdi, P. M., The theory of plates and shells, in Encyclopedia of physics, vol. VI, a/2, Berlin-Heidelberg-New York 1972, pp. 425-640.

Noll, W., The foundations of mechanics and thermodynamics. A reprint of selected papers, Berlin 1974.

Noll, W., Toupin, R. A., Wang, Ch.-Ch., Continuum theory of inhomogeneities in simple bodies. A reprint of six memoirs, New York 1968.

Nunziato, J., Schuler, K. W., Walsh, E. K., Barker, L. M., Wave propagation in non linear viscoelastic solids, in Encyclopedia of physics, vol. VI, a/4, Berlin-Heidelberg-New York 1974, pp. 1-108.

Owen, D. R., Thermodynamics of materials with elastic range, in ‟Archives for rational mechanics and analysis", 1968, XXXI, pp. 91-112.

Owen, D. R., A mechanical theory of materials with elastic range, in ‟Archives for rational mechanics and analysis", 1970, XXXVII, pp. 85-110.

Ting, Ts. W., Topics in the mathematical theory of plasticity, in Encyclopedia of physics, vol. VI, a/3, Berlin-Heidelberg-New York 1973, pp. 535-590.

Truesdell, Cl., A., Six lectures on modern natural philosophy, Berlin-Heidelberg-New York 1966.

Truesdell, Cl., A., Rational thermodynamics. A course of lectures of selected topics, New York 1969.

Truesdell, Cl., A., The meaning of viscometry in fluid dynamics, in ‟Annual review of fluid mechanics", 1974, VI, pp. 111-146.

Truesdell, Cl., A., Improved estimates of the efficiencies of irreversible heat engines, in ‟Annali di matematica pura ed applicata", 1976, CVIII, pp. 305-323.

Truesdell, Cl., A., A first course in rational continuum mechanics, vol. I, New York 1977.

Truesdell, Cl. A., Noll, W., The non-linear field theories of mechanics, in Encyclopedia of physics, vol. III/3, Berlin-Heidelberg-New York 1965, pp. 1-602.

Truesdell, Cl. A., Toupin, R. A., The classical field theories, in Encyclopedia of physics, vol. III/1, Berlin-Heidelberg-New York 1960, pp. 226-858.

Wang, Ch.-Ch., Truesdell, Cl. A., Introduction to rational elasticity, Leiden 1973.